Towards Millimeter-Level Accuracy in GNSS-Based Space Geodesy: A Review of Error Budget for GNSS Precise Point Positioning

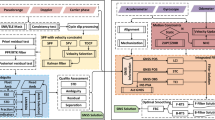
Abstract

The aim of the new generation of Global Geodetic Observing System is a millimeter-level accuracy in positioning, with a crucial role to be played by Global Navigation Satellites Systems (GNSS) in the Precise Point Positioning (PPP) mode. This is of course because GNSS constellations and receivers provide an efficient stand-alone technique with a homogeneous performance over large areas (positions, navigation and meteorology) when used in conjunction with the PPP mode, with also an ever-increasing data flow and different satellite line-of-sights. The requirement of accuracies reaching the millimeter or sub-millimeter implies a knowledge at this level of each line in the GNSS-PPP error budget, including, but not restricted to: clock biases, troposphere and ionosphere delays, multipath and ground deformations. In this review study, we consider this millimeter-/submillimeter level GNSS-PPP error budget, and possible mitigations and improvements in the frame of the existing global constellations: GPS, Galileo, GLONASS and BDS, in view of augmented constellations and/or Low Earth Orbit constellations, which will be available in the near future. We also pay a special attention to systematic biases that can/could exist between constellations.

Article Highlights

• The error budget of GNSS PPP is reviewed

• State-of-the-art improvements or mitigations for errors in GNSS PPP are discussed

• Systematic biases between four GNSS systems are analyzed in terms of each term in the list of error budget

1 Introduction

A prerequisite for improving our knowledge of the dynamic Earth and exploring a wide range of physical processes in the Earth system is establishing a comprehensive monitoring of the Earth system. The space geodetic techniques, e.g., GNSS, Very Long Baseline Interferometry (VLBI), Satellite Laser Ranging (SLR), Doppler Orbitography and Radio-positioning Integrated by Satellite (DORIS), were developed to provide both the reference frame for Earth system observations (the so-called International Terrestrial Reference Frame (ITRF), see Altamimi et al. 2016) and the continuous monitoring of crucial parameters related to changes in the Earth’s geometry, rotation and gravity field (Plag 2005). Each of these techniques contributes to different facets of this goal. In order to combine them together, the GGOS coordinating body has been established in 2003 by the International Association of Geodesy (IAG) (Rummel et al. 2005). As a GGOS technique, GNSS contributes to the determination of the polar motion rate and provides a global coverage for the establishment and maintenance of the ITRF (Boucher et al. 2015; Altamimi et al. 2016).

The concept of the Global Positioning System (GPS) emerged when it was realized in the early 1980s that the measurement of the phase of radio-waves with a decimeter wavelength could result, over a sufficient acquisition time, in a millimeter-level relative positional accuracy between ground-fixed GPS receivers located on the surface of the Earth. At this level of precision, the “static Earth” of the surveyors became the “dynamic Earth” of geophysicists, with also a flow of data for meteorology and ionosphere studies. Today, we have four operational global constellations of positioning satellites: GPS (USA), GLONASS (Russia), Galileo (Europe) and BDS (China), with the word GNSS attached to them, and also two regional augmented constellations: QZSS (Japan) and NavIC (India), generally referred as Regional Navigation Satellite System (RNSS). Accurate millimeter- to centimeter-level absolute positionings are now possible in real-time or near real-time for a single station, thanks to highly precise models of the GNSS satellite orbits, the drift of clocks, signal propagation delays, hardware biases and tidal effects. This is the so-called Precise Point Positioning mode, or PPP mode. The development, since 1994, of the International GNSS Service (IGS) infrastructure, with its online databases, is the backbone of these achievements (Teunissen and Montenbruck 2017). The concept of the single-receiver (stand-alone) PPP mode, based on the monitoring of large networks of static GNSS “reference” stations, was introduced (Héroux and Kouba 1995; Zumberge et al. 1997), as a way to alleviate differential positioning between two GNSS stations, only one of which is considered as a “reference”. This is still the operating mode for Real-Time Kinematic (RTK) and network RTK just because of the “real-time” requirement. The PPP mode is also a “cost-saving” mode, as by essence, one receiver is needed (Seepersad and Bisnath 2014). We also have to note that the PPP mode is also a strict requirement for GNSS meteorology, that is the modelling of the delays of radio-propagation caused by the neutral atmosphere. Differential GNSS gives only access to the differences between the states of the neutral atmosphere at the two receiver sites.

Because of its high-accuracy and consistent positioning with respect to a global terrestrial reference frame, the GNSS technique has made significant contributions to geophysics, e.g., (Genrich and Bock 1992; Bürgmann and Thatcher 2013; Zheng et al. 2017), seismology, e.g., (Nikolaidis et al. 2001; Larson 2009; Xu et al. 2013; Melgar et al. 2020), atmosphere sciences, e.g., (Shanmugam et al. 2012; Hammond et al. 2016; Larson et al. 2017; Jones et al. 2019), hydrology, e.g., (Hamilton and Whillans 2000; Tregoning et al. 2009; Argus et al. 2014), natural hazard science, e.g., (Gili et al. 2000; Sobolev et al. 2007; Grapenthin et al. 2014) and etc. (Bock and Diego Melgar 2016).

From their role as sources of unwanted noises, the neutral atmosphere (Bevis et al. 1992; Balidakis et al. 2018; Jones et al. 2019; Zus et al. 2019), the ionosphere (Pullen et al. 2009; Jakowski et al. 2012; Coster et al. 2017) and the multipath echoes (Martin-Neira 1993; Jacobson 2008; Larson et al. 2009; Rodriguez-Alvarez et al. 2009; Ferrazzoli et al. 2011; Löfgren et al. 2014) are now important applications by themselves, including but not restricted to terrestrial weather, space weather, soil moisture, snow depth and sea level monitoring.

This implies that what is informally referred to as the “GNSS error budget” is the topic of endless attention. It is not in fact a simple list of errors, but a full understanding of the different phenomena that are acting, in cascade or in parallel, on the propagation of the radio-wave from the electronics onboard the GNSS satellite to the electronics inside the ground/vehicle-based GNSS receiver (Herring 1999; Petrie et al. 2011). Actually, it is a “cascading” process, i.e., the reduction of the “error” associated with one item on the list implies a reduction of the “errors” of other items to the same, or even lower, levels. This is of course the main motivation of the IGS second and third data reprocessing campaigns (Griffiths 2019; Dach et al. 2021).

“Accuracy” is an application-dependent quantity. Geophysics and daily-life do not have the same level of requirements. Millimeter-level for the first, decimeter or above for the second. We will focus on this survey for the first type of applications. As the aim of the new generation of GGOS is millimeter-level accuracy (Plag 2005; Boucher et al. 2015) and the four fully operational GNSSs are providing global service nowadays, a review of error budget for GNSS PPP is thus very timely since it addresses the accuracy of current techniques and also indicates their limits. The up-to-date models or mitigations for errors excessing millimeter accuracy will be reviewed, with more emphasis on items where the four constellations are different or where confusions exist.

As far as we know, there are already several review articles and textbooks discussing the error budget for GPS, e.g., (Herring 1999; Hofmann-Wellenhof et al. 2001; Misra and Enge 2006; Xu 2007; Bock and Melgar 2016; Teunissen and Montenbruck 2017; Morton et al. 2020), but seldom for GNSS, e.g., (Teunissen and Montenbruck 2017). It is understandable because GPS has been developed for more than 40 years and other constellations may only have been fully operational for several years. Likewise, we will mainly focus on the error budget of GPS and extend to multi-constellations considering that they are not as well-documented as GPS.

To begin with, it is necessary to have an overview of the framework on which all the analysis is based. This is done in Sect. 2. An introduction of physical models and observation equations of the GNSS technique follows in Sect. 3, in order to give a thorough review of each error source in the observation equation. Various errors form the error budget of GNSS and are relevant for their origins. In Sect. 4, reviews of each error source are performed in separate subsections. Besides individual error sources, the impact of correlations between them and also the time correlations on PPP data processing are addressed in Sect. 5. Finally, a summary and an outlook are given in Sect. 6.

2 Analysis Framework

Before digging into the details of each GNSS technique, it is indispensable to give an overview of their common framework. At the core of this framework are a terrestrial (“linked” to the Earth’s surface) and a celestial (“linked” to the distant stars) reference frames, as well as a model of the proper time on the geoid, in a relativistic sense. The realization of these frameworks differs from constellation to constellation. A summary is given in Table 1. Even each of the four GNSS systems takes its own time system and coordinate system for broadcast satellite positions, as shown in Table 1 for an overview.

Table 1 An overview of global-based satellite systems (European GNSS Agency 2020; China Satellite Navigation Office 2021)

For simplicity and compatibility between multi-constellations, all receivers and satellite positions need to be defined in one common reference system, which is named “International Terrestrial Reference System” (ITRS) for the terrestrial reference frame and “Geocentric Celestial Reference System” (GCRS) for the inertial reference system. The corresponding realizations are the ITRF and the Geocentric Celestial Reference Frame (GCRF). Although all the coordinate systems adopted in WGS-84/PZ-90/GTFR/BDCS are Earth-Centered-Earth-Fixed (ECEF) coordinate systems, and are aligned to ITRF, the discrepancies between them can reach up decimeters (Demianov et al. 2000; Boucher and Altamimi 2001; Plag 2005; Cheng and Cheng 2017). In consequence, the so-called IGS terrestrial reference frame was realized by IGS based on the most recent ITRF. At present, the most commonly applied ITRF is the ITRF2014 and the corresponding realization, the IGb14 reference frame (see IGS Mail #7925 https://lists.igs.org/pipermail/igsmail/2020/007921.html). Nowadays, the high-precise products of IGS and its Multi-GNSS EXperiment (MGEX) products, such as satellite orbit and clock products, are generated in IGb14. The ITRF and GCRF are maintained and updated continuously by the International Earth Rotation and Reference Systems Service (IERS) over the past years, as well as the IGS reference frame by IGS. Recently, the newest realization of ITRS, i.e., ITRF2020, was released (https://itrf.ign.fr/en/solutions/ITRF2020), and the third reprocessing campaign of IGS also contributes to it. And the switch of the IGS products to the corresponding IGS reference frame IGS20 is now on its way (see IGS Mail #8282 https://lists.igs.org/pipermail/igsmail/2022/008278.html). Hence, it is recommended to check the consistency of the framework that IGS precise products are generated in when applying them for long-term analysis.

Transformations between ITRF and GCRF, as well to local coordinate systems are inevitable in space geodesy, with their own error budget, but this study is out of the scope of our review. Four rotation matrices are required for transforming a vector ${\varvec{r}}_{\text{ITRF}}^{\text{s}}$ given in the ITRF into the vector ${\varvec{r}}_{\text{GCRF}}^{\text{s}}$ given in the GCRF, as precession P, nutation N, rotation of the Earth S and the polar motion ${\varvec{P}}_{{\text{m}}}$ given in

$${\varvec{r}}_{{{\text{GCRF}}}}^{s} = \varvec{P}\left( t \right)\varvec{N}\left( t \right)\varvec{S}\left( t \right)\varvec{P}_{{\varvec{m}}} \left( t \right){\varvec{r}}_{{{\text{ITRF}}}}^{s}$$

(1)

These matrices require Earth rotation parameters to be built, like precession and nutation, polar motion, UT1 and Length Of Day (LOD). Details can be found in IERS 2010 memorandum (Petit and Luzum 2010).

The another two local coordinate systems that are usually taken into account in error models (Kouba 2015; Bock and Melgar 2016), i.e. the Satellite Body-Fixed coordinate Frame (SBFF) and the local horizontal coordinate frame East-North-Up (ENU), are outlined in Figs. 1 and 2. Similarly, through a rotation matrix ${\varvec{R}}_{{{\text{SBFF}}}}^{s}$, the vector $\Delta {\varvec{r}}_{{{\text{SBFF}}}}^{s}$ given in the SBFF, e.g., satellite antenna phase center offset, is transformed into the ITRF by

$$\Delta {\varvec{r}}_{{{\text{ITRF}}}}^{s} = {\varvec{R}}_{{{\text{SBFF}}}}^{s} \cdot \Delta {\varvec{r}}_{{{\text{SBFF}}}}^{s} ,$$

(2)

and with the rotation matrix ${\varvec{R}}_{{{\text{ENU}}, {\text{r}}}}$, a vector $\Delta {\varvec{r}}_{{{\text{ENU}}, {\text{r}}}}$ is converted from the ENU to the ITRF by

$$\Delta {\varvec{r}}_{{{\text{ITRF}}, {\text{r}}}} = {\varvec{R}}_{{{\text{ENU}}, {\text{r}}}} \cdot \Delta {\varvec{r}}_{{{\text{ENU}}, {\text{r}}}}$$

(3)

Fig. 1

Satellite body-fixed coordinate frame reproduced from Allahverdi-zadeh et al. (2016)

Fig. 2

The local horizontal coordinate frame ENU at receiver P

Likewise, for the reference time, a common reference time is needed. However, in fact, in order to synchronize and disseminate their internal time, the four GNSS constellations keep their “own” reference time system (see Table 1). With International Atomic Time (TAI) being the common substratum, these time systems are realized by different clock ensembles (Teunissen and Montenbruck 2017). As they are defined with respect to different origins, they have different offsets with respect to TAI. For GPS Time (GPST), the origin is at midnight on the night of 5th January 1980/morning of 6th January 1980 (Coordinated Universal Time (UTC) as maintained by the U.S. Naval Observatory (USNO)). Since then, GPST has differed from UTC because GPST is a continuous time scale, while UTC is corrected periodically with an integer number of leap seconds (Anthony F. 2021). A constant offset (19 s) between GPST and TAI exists from then on. But this practice of adding leap seconds will be put on hold from 2035 (Gibney 2022). Similarly, BeiDou Time (BDT) chose 1st January 2006 UTC as the origin of its time system (China Satellite Navigation Office 2021; Han et al. 2021), and thus constant offset between BDT and TAI is 33 s. While for Galileo System Time (GST), the origin is defined as 13 s before midnight between 21st August and 22nd August 1999 (Galileo ICD 2021). In this way, the GST is aligned to the GPST. The GLONASS Time (GLONASST), instead of depending on TAI like the other ones, aligns to the time scale of UTC, or more specifically to the Coordinated Universal Time of Russia (UTC(SU)) in Moscow (Russian Space Systems 2016). Unlike GPST, GLONASST has no integer offset from UTC and so leap seconds are added to GLONASST simultaneously to those added to UTC. However, due to the time zone difference between Greenwich and Moscow, the GLONASST offset differs by a constant three hours, to match Moscow standard time (Langley 2017). The relationships between the four GNSS time systems and TAI, as well as UTC, are summarized in Fig. 3. Since they can be converted from each other, a common practice for unifying multi-GNSS time systems is to refer to GPST for other GNSS constellations.

Fig. 3

Relationships between four GNSS reference time systems and TAI, as well as UTC. For the acronyms, see the text

It is also necessary to have a glance at the structure of GNSS signals, since these signals contain ranging codes and navigation messages that allow us to obtain the basic information that we are looking at (e.g., the signal travel time). All these GNSS systems continuously transmit or plan to transmit navigation signals in two common frequency ranges, i.e., the lower L-band (1164–1215 MHz) and the upper L-band (1559–1610 MHz) (European GNSS Agency 2020). A summary of signal characteristics of GNSS in open service is listed in Table 2.

Table 2 Signal characteristics of GNSS open service (Subirana et al. 2013; China Satellite Navigation Office 2021; Galileo ICD 2021; https://gssc.esa.int/navipedia/index.php/GLONASS_Signal_Plan; https://www.glonass-iac.ru/en/about_glonass/)

In the beginning, GPS chose signals in L-band because they are not influenced by operating weather phenomena (e.g., rain, snow or clouds) with frequencies in this range. Other requirements, like the corresponding antenna design, ionosphere delay and high bandwidth for code modulation, were also considered (Ogaja 2011). Therefore, two legacy frequencies L1/L2 were transmitted by GPS using the Code Division Multiple Access (CDMA) technique and the modulation method used was Binary Phase Shift Keying (BPSK). Since the choice of L-band frequencies had been proven to be advantageous, following the GPS pathway, other GNSS systems adopted compatible frequencies, common multiple access schemes and modulation schemes. Even GLONASS plans to transmit additional CDMA signals in G1/G2/G3 band during the GLONASS modernization, although traditionally, it uses a Frequency Division Multiple Access (FDMA) signal structure to distinguish the signals coming from different satellites. As far as we know, there are six GLONASS-M+ and -K1 satellites transmitting CDMA signal on the G3 frequency (Zaminpardaz et al. 2021). The first assessment of GLONASS CDMA G3 signal shows that its carrier-to-noise density has a lower noise level than GPS L1 (C/A), but has a similar signature to GPS L5 (Zaminpardaz et al. 2017). Indeed, the advent of GLONASS CDMA signal shows new possibilities in straightforward ambiguity resolution for PPP (Teunissen 2019; Zhang et al. 2023), which used to be impeded by the FDMA technique (see Sect. 4.10).

Improvements in other new GNSS signals mainly focus on two aspects: signal structure design and new advanced modulations. A pilot signal and a data signal are common designs in new signal structures, like L1C, GLONASS CDMA signals (G1a/G2a/G3) and almost all the signals in Galileo and BDS-3, which is expected to boost signal acquisition and reliability (Martínez Morán 2020). Instead of using traditional BPSK modulation, the new Binary Offset Carrier (BOC) modulation and its various implementations are adopted in order to obtain better multipath performance and easier signal tracking by using less bandwidth (Grewal et al. 2020; Morton et al. 2020). Specifically, we have a Time-Multiplexed BOC (TMBOC) modulation in GPS L1C, a BOC modulation in G1a/G2a, a Composite BOC (CBOC) modulation in E1, an Alternate BOC (AltBOC) in E5a + E5b, a Quadrature Multiplexed BOC (QMBOC) modulation in B1C and an Asymmetric Constant Envelope BOC (ACE–BOC) in B2. Reduced ranging noise and improved multipath resistance in these new signals have been reported by many studies (Circiu et al. 2017; Lu et al. 2019; Thoelert et al. 2019; Zhang et al. 2019b, 2021d; Andrei et al. 2020; Montenbruck et al. 2020). For more details about CDMA/FDMA, BPSK and variable BOC, we refer to Teunissen and Montenbruck (2017) and Xie et al. (2021). It is worth noticing that there are several signal structures sharing the same band (i.e., B1I/L1/E1, B2a/E5a/L5 and B2b/G3/E5b), which are designed for compatibility and interoperability between GNSS systems. As will be introduced in the following sections, multi-frequency is something of a double-edged sword. Sometimes, it can be challenging.

3 Physical Models and Observation Equations

The basic measurement made by GNSS is the propagation time (light-time) of the signal propagating from a satellite to a receiver through the vacuum, then the ionosphere and the Earth’s neutral atmosphere. Overall, there are three observables built around light-time: Pseudo-range, Carrier phase and Doppler. All three are generated by different acquisition procedures in the receiver (Misra and Enge 2006). The exact details of these procedures are highly technical and are outside the scope of this study. We refer the reader interested in these technicalities to, e.g., (Langley 1996; Tsui 2005; Doberstein 2012; Kaplan and Hegarty 2017).

Among all these three types of observables, carrier phase and pseudo-range observations are the most commonly used for geodetic applications. Generally speaking, the precision of pseudo-range measurements at the receiver level is considered as 1/100 of the chip (the fundamental unit of transmission of GNSS signals) length, while better than 1/100 of the wavelength of GNSS signals for carrier phase measurements (Xu 2007). For instance in the GPS L1 band at 1575.42 MHz, the precision of phase measurements is 2–3 mm compared to 0.3 m for pseudo-range P-code with a chip length of about 30 m (Bock and Melgar 2016). This can be improved by using a high-performance receiver: the noise of carrier phase measurements would be reduced to 0.2–0.3 mm, and the measured pseudo-range based on the C/A code would reach up to decimeter-level with a narrow correlator with 0.1 chip length (Grejner-Brzezinska 2008). Phase data, that is by definition the argument of the radio signal considered as a trigonometric sine function, contains the argument of the sine and an unknown integer-cycle bias called ambiguity. This ambiguity is not present for pseudo-range measurements. Unlike carrier phase and pseudo-range observations, the Doppler observations are more often used in the velocity estimation of a moving GNSS receiver, rather than high-precision positioning in a navigation system. This is because the accuracy of GNSS Doppler observations is at the centimeter-level (Gaglione 2015), e.g., 10 mm/sec, and their weak observation geometry (i.e., cones) would result in positioning accuracy orders of magnitude worse than pseudo-range-based one (Psiaki 2021). As all the current GNSS systems operate on frequencies that are very close, they offer comparable performances.

The basic principle of GNSS PPP can be simply interpreted as solving a set of observation equations for carrier-phase and pseudo-range observables at multiple frequencies to obtain the position vector of the receiver or any other relevant GNSS parameters, with the position of the emitter being “known”. The observation equations for carrier-phase and pseudo-range observables take the following form (Håkansson et al. 2017)

$$\Phi_{{f, {\text{r}}}}^{{{\text{sys}},{\text{s}}}} = \rho_{{\text{r}}}^{{\text{s}}} + c\left[ {{\text{d}}t_{{\text{r}}} - {\text{d}}t^{{\text{s}}} + b_{{f, {\text{r}}}}^{{{\text{sys}}}} - b_{f}^{{\text{s}}} + \tau^{{{\text{sys}}}} } \right] + c{\text{d}}t_{{{\text{rel}}}}^{{ {\text{s}}}} + d_{{{\text{trop}}, {\text{r}}}}^{{ {\text{s}}}} - d_{{{\text{ion}}, f, {\text{r}}}}^{{ {\text{s}}}} + \lambda_{f} N_{{f, {\text{r}}}}^{{ {\text{s}}}} + \lambda_{f} \varphi_{{pw, {\text{r}}}}^{{\text{s}}} + {\text{MP}}_{{f, {\text{r}}}}^{{{\text{sys}}}} + \varepsilon_{{f, {\text{r}}}}^{{{\text{sys}}}} ,$$

(4)

$$P_{{sig, {\text{r}}}}^{{{\text{sys}},{\text{s}}}} = \rho_{{\text{r}}}^{{\text{s}}} + c\left[ {{\text{d}}t_{{\text{r}}} - {\text{d}}t^{{\text{s}}} + B_{{{\text{sig}}, {\text{r}}}}^{{{\text{sys}}}} - B_{{{\text{sig}}}}^{{\text{s}}} + \tau^{{{\text{sys}}}} } \right] + c{\text{d}}t_{{{\text{rel}} }}^{{\text{s}}} + d_{{{\text{trop}}, {\text{r}}}}^{{ {\text{s}}}} + d_{{{\text{ion}}, f_{{{\text{sig}}}} ,{\text{r}}}}^{{ {\text{s}}}} + {\text{MP}}_{{{\text{sig}}, {\text{r}}}}^{{{\text{sys}}}} + \varepsilon_{{{\text{sig}}, {\text{r}}}}^{{{\text{sys}}}} ,$$

(5)

where the geometric (no light-time propagation) range between satellite and receiver antennas $\rho_{{\text{r}}}^{{\text{s}}}$ is given by

$$\rho_{{\text{r}}}^{{\text{s}}} = \|{\varvec{r}}_{{\text{r}}} - {\varvec{r}}^{{\text{s}}} + {\varvec{d}}_{{{\text{orb}}}}^{{ {\text{s}}}} + {\varvec{d}}_{{{\text{pco}}, f, {\text{r}}}}^{{ {\text{s}}}} + {\varvec{d}}_{{{\text{pcv}}, f, {\text{r}}}}^{{ {\text{s}}}} + {\varvec{d}}_{{{\text{tide}}, {\text{r}} }}\| .$$

(6)

Here, we use $\left( \cdot \right)_{{{\text{sig}}/f,{\text{ r}}}}^{{{\text{sys}},{\text{s}}}}$ henceforth representing for a term associated with a ranging code sig or carrier-phase frequency f (Hz), transmitted by satellite s and received by receiver r in a single GNSS sys. If one of them does not appear in a given term, it means that the term is independent of these quantities. And $\Vert \cdot \Vert$ denotes the norm of a vector. Other notations in (4–6) are defined as follows: $\Phi _{{f,{\text{r}}}}^{{{\text{sys}},{\text{s}}}}$—carrier-phase measurements (m), c—speed of light in vacuum (m/s), ${\text{d}}t_{{\text{r}}}$—receiver clock offset (s), ${\text{d}}t^{{\text{s}}}$—satellite clock offset (s), $b_{{f, {\text{r}}}}^{{{\text{sys}}}}$—receivers hardware bias for carrier phase (s), $b_{{f}}^{{\text{s}}}$—satellite hardware bias for carrier phase (s),—$\tau^{{{\text{sys}}}}$time offset between system time of different GNSS sys (s),${\text{d}}t_{{{\text{rel}}}}^{{\text{s}}}$—relativistic effect (s), $d_{{{\text{trop}}, {\text{r}}}}^{{ {\text{s}}}}$—tropospheric delay (m), $d_{{{\text{ion}}, f, {\text{r}}}}^{{ {\text{s}}}}$—ionosphere delay for carrier phase (m), $\lambda_{f}$—carrier wave length (m), $N_{{f, {\text{r}}}}^{{\text{s}}}$—carrier phase range integer ambiguity (cycle), $\varphi_{{{\text{pw}}, {\text{r}}}}^{{\text{s}}}$—phase windup effect of antennas (cycle), ${\text{MP}}_{{f, {\text{r}}}}^{{{\text{sys}}}}$—multipath effect of carrier phase (m), $\varepsilon_{{f{\text{, r}}}}^{{{\text{sys}}}}$—carrier-phase noise (m), $B_{{{\text{sig}}, {\text{r}}}}^{{{\text{sys}}}}$—receivers hardware bias for pseudo-range (s), $B_{{{\text{sig}}}}^{{\text{s}}}$—satellite hardware bias for pseudo-range (s), ${\text{d}}_{\text{ion,} \, \text{sig,} \, {\text{r}}}^{ \, {\text{s}}}$—ionosphere delay for pseudo-range (m), ${\text{MP}}_{{{\text{sig}}, {\text{r}}}}^{{{\text{sys}}}}$—multipath effect of pseudo-range (m), $\varepsilon_{{{\text{sig}}, {\text{r}}}}^{{{\text{sys}}}}$—pseudo-range noise (m), ${\varvec{r}}^{{\text{s}}}$—satellite position vector in GCRF (m), ${\varvec{r}}^{\text{s}}\text{=}{\left({\text{x}}^{\text{s}}\text{,} \, {\text{y}}^{\text{s}}\text{,}{ \, {\text{z}}}^{\text{s}}\right)}^{\text{T}}$, ${\varvec{r}}_{\text{r}}$—receiver antenna position in GCRF (m), ${\varvec{r}}_{\text{r}}\text{=}{\text{(}{\text{x}}_{\text{r}}\text{, }{\text{y}}_{\text{r}}\text{, }{\text{z}}_{\text{r}}\text{)}}^{\text{T}}$, ${\varvec{d}}_{\text{orb}}^{ \, {\text{s}}}$—satellite orbit errors (m), ${\varvec{d}}_{\text{pco,} \, {\text{f}}, \, {\text{r}}}^{ \, {\text{s}}}$—receiver and satellite antenna Phase Center Offset (PCO) (m), ${\varvec{d}}_{\text{pcv,} \, {\text{f}}, \, {\text{r}}}^{ \, {\text{s}}}$—receiver and satellite antenna Phase Center Variation (PCV) (m), ${\varvec{d}}_{\text{tide,} \, {\text{r}}}$—displacements induced by tidal forces exerting at receiver position (m). For brevity, some error sources are categorized as a stand-alone term in the observation, such as the ${\varvec{d}}_{\text{tide,} \, {\text{r}}}$ consists of many sub-components: solid Earth tides, ocean tides, atmospheric loading and pole tides, while the antenna phase correction is the sum of offsets caused by both satellite and receiver. Each of these terms will be reviewed separately in the following sections.

These error sources can be divided into two categories, scalar errors and vector errors (Seepersad and Bisnath 2014). The former one projects onto the range measurement (Eqs. 4, 5) while the latter one acts as displacements in a local coordinate system (see Figs. 1, 2) as shown in Eq. (6). Despite that it is more challenging to define the error budget of vector errors for GNSS PPP, a review is necessary to have a knowledge of the most recent advancements in mitigating these errors so as to indicate the current limitations and prospective future work.

4 Error Budget and Management

As previously mentioned, a number of error sources exist in the observation equations, which prevent us from obtaining the true “geometrical” distance between the satellite and the receiver. Each of them is overviewed in the following subsections, and a table gives an overall error budget as well as the corresponding mitigation strategies in each section. Please note that only errors that exceed the millimeter level in carrier phase observables are reviewed here.

4.1 Satellite Orbits

In order to obtain the geometric range between a satellite and a receiver, the position of the satellite (${\text{r}}^{\text{s}}$ in Eq. 6) is essential. Basically, a broadcast ephemeris that is designed for calculating the position of the satellite is modulated on the GNSS signal and transmitted to users. For GPS, a perturbed Keplerian orbit representation is used as the model of broadcast ephemeris, and the same is being done for BDS and Galileo, while the GLONASS constellation builds up on a numerical orbit propagation. The quality of the broadcast orbits and clocks has been improved over the years as shown in Fig. 4 (Warren and Raquet 2003; Steigenberger and Montenbruck 2017). The instantaneous accuracy of broadcast ephemeris for GPS nowadays is estimated to be around ± 1 m and accuracies are better for other new generation of GNSS constellations (Montenbruck et al. 2015a; Shi et al. 2020).

Fig. 4

Weighted RMS of broadcast orbit w.r.t. the IGS rapid products (left) (https://igs.org/acc/gps-only/#broadcast) and weighted RMS of individual Analysis Center (AC) orbit solutions w.r.t. the IGS final products (right) (https://igs.org/acc/gps-only/#final). Note that only GPS is included

A one-meter instantaneous accuracy is not compatible with millimeter-level applications. High-precision satellite orbit and clock products are required to conduct PPP, where we recall that the first P means “Precise”. The most important source of these products is IGS. In 1992, after the IGS was firstly set up by a proposal of the IAG, the first orbit solution was generated within a few weeks, with an instantaneous accuracy claimed to be at around 50 cm (Dow et al. 2005). It was not until 1994 that IGS became an official service. To meet the increasing demands for shorter latency from some communities like meteorology, “rapid” products are provided since 1996 and now various orbit products including final (latency 12–18 days), rapid (latency 17–41 h), ultra-rapid (latency 3–9 h) and real-time are all available. Considering that the accuracy degrades as latency shortens, we mainly focus on the final products with the highest precision in this review, that is, better than an instantaneous 2.5 cm accuracy for GPS and 3 cm for GLONASS (1D mean Root Mean Square (RMS)) according to the IGS (https://igs.org/products/#about).

Over the years, IGS has been providing free GPS orbit products to the scientific community with increased precision and timeliness through the internet (Fig. 4) (Kouba and Heroux 2001). In view of the ongoing modernization and the build-up of new constellations, the IGS established the MGEX project in 2012, which is now continued as an IGS pilot project to extend the service portfolio to these new constellations and to achieve a consistent data and product quality for all constellations, starting from 2016 (Montenbruck et al. 2017). Unlike broadcast ephemeris, precise satellite orbits and clocks products for all GNSS constellations are generated by using a network Least-Squares (LS) adjustment and making use of observation data from the IGS network (Tegedor et al. 2014). Until now (February, 2023), there are 513 well-distributed stations worldwide in the IGS network, among which 369 stations have the capacity to track multi-GNSS signals (https://igs.org/network/#station-map-list).

Before being fully operational, the potencies of these new GNSS constellations have been investigated by many studies. The multi-GNSS precise orbit products are generated by several IGS Analysis Centers (ACs) that contribute to the MGEX project, but the precise orbit determination strategy at each AC differs from each other. Despite that, methods for combining the MGEX products have been discussed in some papers, e.g., (Fritsche 2016; Sakic et al. 2018; Mansur et al. 2020), but there is still no official MGEX combination strategy today. Comparison between two orbit products from different ACs is one of the indicators for the underlying absolute accuracy. A general consistency of the Galileo orbits of the four ACs at the 5–30 cm level was reported by Steigenberger et al. (2014) for a period of twenty weeks in 2013. Except for Galileo, Guo et al. (2017) also compared the MGEX products of all ACs for BDS-2, and a consistency of 10–20 cm, 20–30 cm, and 3–4 m for BDS-2 MEO, IGSO, and GEO, respectively, was found. Likewise, a recent study shows that the current orbit consistency between ACs is at the level of a few centimeters for GPS, around one decimeter for GLONASS and Galileo, and a few decimeters for BDS-2 for the time period from 2015 to the middle of 2018 (Steigenberger and Montenbruck 2020). As for BDS-3, the orbit comparisons present consistencies of 9–22 cm for the C19–C37 satellites and of 50–120 cm for the C38–C46 (Shen et al. 2021).

All active BDS, Galileo and GLONASS satellites are equipped with Laser Retroreflector Arrays (LRAs) (Dell’Agnello et al. 2011; Zajdel et al. 2017) and the SLR observations can be used as an independent validation tool for the radial accuracy of orbits. However, for GPS, there were only two satellites SVN35 and SVN36 equipped with LRAs. Unfortunately, they were decommissioned in 2013 and 2014. Though being reactivated in 2015, SVN36 was only available until that year (Hugentobler 2016). According to the GPS modernization scheme, the new generation of GPS IIIF satellites will be all equipped with LRAs, but it is still on schedule (https://www.gps.gov/systems/gps/modernization/). Nevertheless, many results have already been published, e.g., range residuals with a Standard Deviation (STD) of about 2.7 cm for GPS SVN35/36 and of about 4.9 cm for GLONASS during 2001-early 2004 (Urschl et al. 2005). After analyzing 20 years of SLR observation from 1994 to 2014 for GPS and 12 years for GLONASS (2002–2013), a similar conclusion is drawn by Sośnica et al. (2015), that is, the RMSs of SLR residuals to GPS satellites are 2.28 cm and 2.36 cm for SVN35/36, respectively, and range from 3.7 to 4.6 cm for GLONASS satellites. Nowadays, with both multi-GNSS precise orbits and SLR observations from International Laser Ranging Service (ILRS), an accuracy of about 0.1–0.3 m for the Galileo, BDS-2 IGSO/MEO orbits is validated based on products of half a year from September, 2014 to April, 2015 (Guo et al. 2017). The accuracy of BDS-2 IGSO/MEO orbits has been improved when compared with the preliminary results presented by Shi et al. (2012) and Zhao et al. (2013). SLR residuals with a STD of about 5 cm for GLONASS, 4–9 cm for Galileo and of about 4–7 cm for BDS-2 MEO, 7–15 cm for BDS-2 IGSO for the time period 1 January–30 June 2016 are analyzed in Montenbruck et al. (2017), the error magnitude was updated by Steigenberger and Montenbruck (2020) to 4 cm for GLONASS, 5 cm for Galileo and 7 cm for BDS-2 IGSO/MEO based on orbit products for the first half of 2018. Weekly analysis of MGEX orbit products including SLR residual analysis and orbit comparisons is posted at the MGEX product analysis website (https://igs.org/mgex/analysis/). At the time of this writing (February 2023), SLR residuals with a STD of about 3–8 cm for GLONASS, 2–5 cm for Galileo, 3–5 cm for BDS-3 MEO, and of about 4–7 cm for BDS-2 MEO, 6–10 cm for BDS-2 IGSO were observed from January 2019 up to now.

Moreover, it is worth noting that discrepancies in the orbit model exist between different ACs and the corresponding SLR residuals, especially for Galileo (Montenbruck et al. 2017). By applying a more complex Solar Radiation Pressure (SRP) model like ECOM-2, the STD of SLR residuals reduces from 8 to only 4–5 cm compared to STD using legacy ECOM-1 SRP model. The SRP force is known as the largest error source in orbit modelling due to the lack of information on the optical properties (specular or diffuse reflection) and precise orientation of the satellite surfaces (plate model). Empirical SRP models were developed to improve orbit quality. The ECOM-1, firstly proposed by the Center for Orbit Determination in Europe (CODE) in the 1990s (Beutler et al. 1994), was widely used by many ACs, however, when applying it for GLONASS, shortcomings emerged, which are supposed to be addressed by the ECOM-2 model (quality of orbits and earth rotation parameters (ERPs)) (Arnold et al. 2015). For Galileo, in order to reduce the systematics in the SLR residuals, Steigenberger et al. (2014) proposed a model based on the combination of ECOM-2 and a priori box-wing model for satellites with stretched body shape (Steigenberger and Montenbruck 2017). Besides, hundreds of researchers, see for example (Vigue et al. 1994; Ziebart and Dare 2001; Priestley et al. 2011; Rodriguez-Solano et al. 2012; Montenbruck et al. 2015b; Steigenberger et al. 2018), are continuously working on modelling, with always upgraded precision, non-gravitational forces, e.g., SRP, antenna recoil from Earth thermal radiation (day and night sides), as well as satellite residual thrust from attitude corrections (non-yaw-steering events, see Montenbruck et al. 2017; Zajdel et al. 2017). Furthermore, the inclusion of additional observations like SLR, inter-satellite link, etc., do help to GNSS orbit determination as well (Hackel et al. 2015; Guo et al. 2016; Yang et al. 2020c), although they are still not yet employed operationally in the routine generations of products.

An overview of the error budget for satellite orbit can be found in Table 3. Even if the achievements are already significant, improvements are still needed. Nowadays, some error models in orbit determination are based on an empirical assumption (e.g., neglecting center-of-mass variation of satellite), typical shape model of the satellite (e.g., panel model in SRP modelling), or reconstructed from observations with a ground network (e.g., satellite antenna phase center). A better way to do so is by using exact satellite metadata provided by satellite manufacturers, which is preferred by the science community (Montenbruck and Steigenberger 2017). They will greatly improve the employed models and finally result in products with higher precision and more robustness. But unfortunately, satellite metadata is not widely available, even in limited sets. Likewise, operational information related to irregular movements for satellites, also known as manoeuvres, is not available from the GNSS service provider at present. Acting like discontinuities, they interrupt the normal processing, or the “smooth” satellite orbit and will impair the orbit modelling. So far, they can only be guessed or approximately reconstructed by analyzing phase residuals from ground stations (Montenbruck and Steigenberger 2017; Dai et al. 2019). Even though the amount of manoeuvres is moderate for the MEO constellation, it happens more frequently for QZSS or BDS GEO/IGSO constellations, especially for BDS GEOs (each month) (Tu et al. 2021). Further investigations are required since the satellite position can vary by tens of kilometers from the normal orbit during orbit manoeuvre.

Table 3 Error budget of satellite orbit, satellite clock and relativistic effect

4.2 Satellite Clocks

The onboard satellite clocks are a key components in the GNSS space segment for providing time and range information, as well as controlling all onboard timing operations including broadcast signal generation (Ferguson 2000). General relativity predicts that these clocks tick faster than ground clocks. This is discussed in Sect. 4.3. Besides, stringent technical and stability requirements need to be satisfied for these onboard clocks to build the essential backbone of a navigation system (Batori et al. 2020). Atomic clocks are of course chosen due to their excellent performance over quartz stabilized clocks (Ely et al. 2012), which are still in use for deep space applications because they can be extremely miniaturized at the opposite of current atomic clocks (Ely et al. 2018). Since the early days of GPS, the performance of the onboard clock has been always improving (Hauschild et al. 2013). At present, there are three types of atomic clocks onboard GNSS satellites: Rubidium (Rb), Cesium (Cs) and Hydrogen maser (H-maser) clock. Specifically, GPS and GLONASS satellites mount Cs and Rb atomic clocks, while Galileo and BDS-3 satellites mount Rb atomic clocks and passive H-maser clocks (Montenbruck et al. 2020; Jaduszliwer and Camparo 2021). The relative stabilities of these atomic clocks in terms of Allan deviation range from 10^–9 to 10^–13 s/s over a 1 s time window, and from 10^–14 to 10^–15 s/s for a 10⁵ s time window (Giorgi et al. 2019). In this section, we will focus on the stability and accuracy of these onboard atomic clocks, under rules called Atomic Frequency Standards (AFSs), to give a review of their overall performance.

To enable the virtual synchronization of the whole constellation of onboard clocks, the time offsets of each individual satellite clocks from the ground system time, as well as their linear frequency drift rates are provided as ancillary data in broadcast ephemeris (Jaduszliwer and Camparo 2021). In the absence of true values, precise clock products generated by IGS/MGEX are usually adopted as references. The expected accuracy of the precise products is generally considered to be at least one order of magnitude better than that of the broadcast ephemeris. The statistics of average broadcast-minus-precise clock correction values were computed based on a dataset in 2013/2014 by Montenbruck et al. (2015a). RMSs of clock differences ranged from 0.3 to 1.1 m in equivalent light-distances for GPS, 1.9 m for GLONASS, 1.6 m for Galileo and 0.8 m for BDS-2 MEO/IGSO. With respect to precise clock products generated by Deutsches Zentrum für Luft- und Raumfahrt (indicated by DLR), the RMS was improved from 1.11 to 0.30 m for Galileo during the period of 2014–2016 (Steigenberger and Montenbruck 2017), which is mainly due to the introduction of H-maser clocks and more frequent ephemeris uploads. For BDS-3, an overall satellite clock precision with STD of 0.54 m based on a dataset collected in the first half of 2019 was reported by Shi et al. (2020) w.r.t. precise clock products of Wuhan University (indicated by WUM).

Clock corrections in broadcast ephemeris are predicted based on observations from a set of monitoring stations, together with respect to modelling satellite orbits. These clock corrections are strongly correlated, especially in terms of the radial orbit component (Kouba and Springer 2001). The Signal In Space Range Error (SISRE) is widely used to indicate the contribution of orbit and clock errors to the modelled range measurements, as

$${\text{SISRE}} = \sqrt {\left( {w_{1}^{2} R^{2} - 2w_{1} RT + T^{2} } \right) + w_{2}^{2} \left( {A^{2} + C^{2} } \right)} ,$$

(7)

where R, A and C represent the orbit differences in radial, along and cross directions, respectively, and T denote the clock differences which are usually corrected by piece-wise systematic offsets. w₁ and w₂ are constellation-specific weighting factors which are provided by Montenbruck et al. (2018).

The SISRE improvements in GPS have been well-documented for more than two decades, from 4.5 m (RMS) to about 2 m (RMS) between 1990 and 1997, then achieved an accuracy of about 1 m for Block IIA satellites and 0.5 m for Block IIR and IIRM satellites during 2008–2010, then about 0.7 m between 2012 and 2013 with continuously improved broadcast ephemeris. SISRE of 0.35 m was reported for the new generation of Block IIF satellites equipped with Rb AFSs (Malys et al. 1997; Cohenour and Graas 2011; Liang et al. 2012). A comprehensive analysis of SISRE for multi-constellations was firstly given by Montenbruck et al. (2015a). Results show that SISREs are roughly 0.7 m, 1.9 m, 1.6 m and 1.5 m for GPS, GLONASS, Galileo and BDS-2 MEO/IGSO, respectively, over a 12-months period in 2013/2014. Most recently, remarkable SISREs values for Galileo and BDS-3 satellites, with onboard highly stable clocks, were found for a time period of 3 months in 2019: about 0.15 m for Galileo and 0.35 m for BDS-3 (Montenbruck et al. 2020). Likewise, An average SISRE of about 0.47 m for BDS-3 was reported over the whole month of July, 2019 (Yang et al. 2020b). These superior performances are also attributed to short upload intervals for the corrections. Overall, it should be noted that the clock performance dominates the performance of SISREs in all the above results.

The quality of multi-GNSS broadcast clock corrections has been considerably improved nowadays; nevertheless, they are still significantly less accurate than IGS/MGEX precise products and not sufficient for centimeter or millimeter-level applications. The main reason was identified by Teunissen and Montenbruck (2017): the broadcast navigation message is predicted according to the epoch of a data solution (orbits + clocks) derived from a small tracking network and uploaded regularly, which means that the accuracy will degrade within the time-span validity of the prediction. But even for Galileo with a 10–100 min update interval, the improved broadcast ephemeris is not as accurate as the IGS precise products. The nominal accuracy of GPS precise clock products that are provided by IGS is 75 picoseconds (RMS) (https://igs.org/products/#about), while for other satellite systems, MGEX products generated by several ACs are available, but there are still no official multi-GNSS precise clock products. Since the number of new GNSS satellites is always increasing, the IGS product portfolio will continuously be extended to cover precise ephemeris and clock products for all constellations (https://igs.org/mgex/). As a consequence, few publications have given thorough introductions of the accuracy of these MGEX products, and here only the consistency of products between different ACs is studied. Likewise, the SISRE strategy could also be applied as an indicator of accuracy, as well as the comparison between every two ACs. According to the clock products of five ACs during the first half of 2016, SISRE values of 1–3 cm for GPS, of about 5 cm for GLONASS, 3–7 cm for Galileo and 4–7 cm for BDS-2 IGSO/MEO, and about 0.3 m for BDS-2 GEO were found (Montenbruck et al. 2017). Similar results were shown by Steigenberger and Montenbruck (2020). By using precise clock products generated by six ACs of the first half-year of 2018, comparisons of precise clock products between every two ACs were presented: GPS has the smallest RMS at about 2 cm, while RMS ranged from 3 to 7 cm for GLONASS and 2 to 7 cm for Galileo. For BDS-3, Shen et al. (2021) presented the STDs of BDS-3 satellite clock products differences between five ACs during DOY 280 to DOY 317 in 2020, ranging from 4.5 to 8.9 cm for BDS-3 MEO. A summary of the error budget for the satellite clock before mentioned, as well as the SISRE values can be found in Table 3. To date, the most commonly used precise satellite orbit and clock products in GNSS PPP are from IGS/MGEX.

Since clock estimations refer to accurate models for delays of phase and pseudo-range measurements, like antenna phase centers, etc., improvements on accuracy are not only limited by the clock electronics but also limited by these external constraints. Nevertheless, strategies that can both enhance the efficiency and accuracy of clock timings were proposed over the years. There are mainly three types of approaches: undifferenced strategy (Hauschild and Montenbruck 2009; Laurichesse et al. 2013), differenced strategy (Mervart et al. 2008; Bock et al. 2009) and mixed-differenced strategy (Ge et al. 2012). The undifferenced strategy is commonly adopted in both post-processing and real-time products (Zhao et al. 2020). It is the most rigorous, but the less efficient method in terms of computer power because a huge number of ambiguity parameters need to be estimated when using Ionosphere-Free (IF) phase and code observations. The differenced strategy makes use of epoch- or satellite-differenced observations to eliminate ambiguity parameters. It is less computer-intensive, but at the cost of lower accuracy. By combining these two approaches, the mixed-differenced strategy exploits epoch-differenced phase observations and undifferenced code observations to achieve the same level accuracy of undifferenced strategy without degrading too much computer cost. By introducing at the receiver level external highly stable atomic clocks like the H-maser clock (Yao et al. 2021), the computation burden can be reduced significantly.

To characterize the stability of clocks, the Allan Deviation (ADEV) is the tool of choice (Allan and Barnes 1981). Typical Allan deviations for current GNSS satellite clocks are shown in Fig. 5(a). This figure shows ADEV clock in the 10^–14 to 10^–13 range at timescales of about 5 min to one day for H-maser clocks such as the ones onboard Galileo, or BDS-3 (produced by Shanghai Engineering Center for Microsatellites (SECM) and partially by China Aerospace Science and Technology Corporation (CASC)) (http://www.csno-tarc.cn/en/system/constellation). For the Cs clocks of GPS and GLONASS, the ADEVs fall by one order of magnitude to 10^–13 to 10^–12 per day (Batori et al. 2020; Jaduszliwer and Camparo 2021). More specifically, clock prediction uncertainties $c \cdot {\text{ADEV}}\left( \tau \right) \cdot \tau$ are illustrated in Fig. 5(b). While long-term stability is a key parameter for a navigation system, short-term stability is also vital for high-rate measurements and applications. However, it was not practical to evaluate short-term stability until the One-Way Carrier-Phase technique (OWCP) was proposed by Gonzalez and Waller (2007). A modified Allan deviation with limited short time scales was proposed by Griggs et al. (2015) based on data over half a year in 2014. For GPS satellites, deviations ranging from 10^–12 to 10^–13 over 1–200 s averaging intervals are reported (Fig. 5a), and for GLONASS satellites, the Cs clocks have comparable magnitudes but are not as good as the ones onboard GPS satellites. Rb clocks such as the ones onboard BDS-2 MEO and some Galileo satellites, demonstrate comparable or even better quality than GPS satellite clocks. Furthermore, Galileo H-maser clocks outperform most GLONASS and GPS clocks by almost one order of magnitude in many cases (Montenbruck et al. 2012; Hauschild et al. 2013).

Fig. 5

a Representative Allan deviations w.r.t. averaging time for typical GNSS clocks derived from the GFZ orbit and clock product for GPS week 1877 (December 27th, 2015–January 2nd, 2016), from Montenbruck et al. (2017), where short-term (1–100 s) values are from Griggs et al. (2015); b Standard deviations of GNSS clock predictions over different time scales, from Montenbruck et al. (2020). Triangles mark the typical upload intervals of broadcast ephemerides for the individual constellations

In retrospect, the improved performance of satellite clock is mainly due to the achievements in clock technology from Cs to Rb, then to the present H-maser, with improvements on a day-to-day basis (Morton et al. 2020) toward a common clock datum for all constellations, since each satellite navigation system maintains its own time system as we mentioned in Sect. 2 (see Fig. 3).

4.3 Relativistic Effect on Clocks

Time and reference frames are two backbones of GNSS (Weiss and Ashby 1997; Hofmann-Wellenhof et al. 2001). In a typical satellite navigation system, a global “time” is defined as the common time (TAI time for a practical point of view) of clocks resting on a particular equipotential surface of Earth, called the geoid, supplemented for orientation by what is called an Earth-centered “inertial” frame coordinate system. Earth-Centered Inertial (ECI) coordinate frames have their origins at the center of mass of Earth with the directions of axes defined with respect to distant stars. “Inertial” is in the sense of general relativity and means “only subject to gravitational forces, here mainly the Earth and the Sun”, in contrast to the ECEF frames, which remain “fixed” or “slowly varying” with respect to Earth’s surface (like the ITRF frame), and therefore rotates with respect to the distant stars. Relativistic effects in GNSSs applications, notated as ${\text{d}}_{\text{rel}}^{ \, {\text{s}}}$ in observation equations, are very significant (up to several meters in positioning accuracy) and rather complex to model precisely. Fortunately, they can be accurately computed and removed. A thorough review for the GPS constellation was given by Ashby (2003), therefore we will no repeat these calculations, but we will focus on the discrepancies of these effects between the four GNSSs constellations of today.

According to the theory of relativity, the beats of clocks depend upon their four-velocity along their world-lines. This effect can be split into two parts:

- A kinematic (symmetrical) part (Hofmann-Wellenhof et al. 2001):

$$\left( {\frac{{\Delta t^{\prime } - \Delta t}}{\Delta t}} \right)_{{{\text{sp}}}} = \left( {\frac{{f^{\prime } - f}}{f}} \right)_{{{\text{sp}}}} = - \frac{1}{2}\left( {\frac{{v^{{\text{s}}} }}{c}} \right)^{2} ,$$

(8)

where ∆t and ∆t^′ are time intervals on the ground and onboard satellite, respectively, and f, f^′ denote the corresponding frequencies while v^s is the velocity of the satellite with respect to the ground. For GPS, an onboard satellite clock with a velocity of 3.874 km/s runs slow by about 7 μs per day, and the typical magnitudes of other constellations are listed in Table 4.

Table 4 Representative GNSS satellite orbit parameters and corresponding relativistic effects (kinematic part and gravitational well part), which are modified based on Kulbiej (2016)

- A gravitational well part, or Schwarzschild reddening: This effect is non-symmetrical, and is due to the bending of space–time caused by the mass of Earth (Morton et al. 2020). As onboard satellite clocks are farther away from Earth masses than clocks located on the surface, they beat faster with a shift given by

$$\left( {\frac{{\Delta t^{\prime } - \Delta t}}{\Delta t}} \right)_{{{\text{ge}}}} = \left( { \frac{{f^{\prime } - f}}{f} } \right)_{{{\text{ge}}}} = - \frac{\Delta U}{{c^{2} }},$$

(9)

where ∆U is the difference of the Earth’s gravitational potential between the positions of the satellites and the receivers. By assuming a circular orbit and a point-like Earth, the onboard satellite clock runs faster by approximate 45 μs per day at an altitude of 20,184 km for a GPS satellite. The net effect on the satellite clock caused by the relative velocity and difference of gravitational potential between the satellite and the receiver may be linearly added (weak field approximation), i.e. Equation (8) + Eq. (9), and thus the satellite clock runs faster by about 38 μs per day than a clock on the ground, corresponding to about $- 4.4647 \cdot 10^{ - 10} {\text{s}}/{\text{s}}$ for frequency shift. Results for other constellations are listed in Table 4, see (Ashby 2003). This large secular effect is commonly compensated by giving before launch a small intentional offset of the frequency standard of the satellite clocks, which is known as a factory offset (Müller et al. 2008). For GPS, the nominal frequency of exactly (at the geoid level) f₀ = 10.23 MHz is offset by a $\Delta {\text{f = - 4}}{.4647} \cdot {10}^{{ - 10}} \cdot {\text{f}}_{{0}}$. The actual frequency of the satellite clock prior to launch is thus 10.22999999543 MHz as indicated in GPS-ICD-200 M (Anthony 2021). For GLONASS, the nominal frequency of f₀ = 5.0 MHz is offset by a $\Delta f = - 4.36 \times 10^{ - 10} \times f_{0}$, that is, 4.99999999782 MHz as indicated in GLONASS-ICD-2.0 (Russian Space Systems 2016). But this is not the remedy chosen for Galileo or BDS constellations. Instead of applying a factory offset, the correction is performed at the user receiver level. This relativistic effect on the Galileo satellite clock is absorbed into the satellite clock models broadcasted to users, which are estimated by the Orbitography and Synchronization Processing Facility (OSPF) and modelled with a second-order polynomial (Mudrak et al. 2015). The total satellite clock offset w.r.t. the UTC includes not only the relativistic effect but also the deviations due to its own frequency initialization uncertainty and instability. The same approach is applied to the BDS constellation (Han and Cai 2019).

However, all the relativistic effects discussed above are based on the assumption of a circular satellite orbit and a point-like gravitational field of the Earth. But there is always some orbital residual eccentricity even if satellite orbits are nominally circular for all constellations (Teunissen and Montenbruck 2017). The eccentricity e leads to a slightly elliptical orbit, and consequently, a periodical effect arises on the satellite clock, as

$${\text{d}}t_{{{\text{rel}}, {\text{per}}}}^{{\text{s}}} = - \frac{2}{{c^{2} }}\sqrt {a\mu } \cdot e \cdot \sin (E),$$

(10)

where μ is the gravitational constant of the Earth, a is the semi-major axis and E is the orbit eccentric anomaly angle. An alternative approach of the correction

$${\text{d}}t_{{{\text{rel}}, {\text{per}}}}^{{\text{s}}} = - 2\frac{{r^{{\text{s}}} \cdot v^{{\text{s}}} }}{{c^{2} }}$$

(11)

with position vector r^s and velocity vector v^s of the satellite that is more convenient and widely used, which is equivalent to Eq. (10) (over an osculating orbit,¹$\sqrt {a\mu } \cdot e \cdot \sin (E) = r^{{\text{s}}} \cdot v^{{\text{s}}}$) (Kouba 2002; Subirana et al. 2013). A maximum eccentricity of 0.02 for the GPS constellation corresponds to an added relativistic effect of about 45 ns, while for GLONASS and Galileo, the nearly circular orbits have smaller typical eccentricities of 0.003 and 0.0005, respectively (Kouba 2019; https://www.glonass-iac.ru/en/ephemeris/), which cause an additional effect of fewer than 7 ns and 1.2 ns, respectively. For the BDS, this additional effect can reach up to 26 ns for IGSO satellites and 20 ns for MEO satellites with a maximum eccentricity of 0.01 (http://www.csno-tarc.cn/system/constellation). In order to cope with this eccentricity-dependent effect, it is conventional to remove the effect by Eq. (11) in multi-GNSS precise clock products provided by IGS (Kouba 2015), but this removal should be avoided by users who want a precise understanding of the clock behavior. Although the GLONASS-ICD reports and several other technical reports have pointed out that this orbital eccentricity effect for GLONASS has already been transmitted with the navigation messages, and need not be accounted for by users (Russian Space Systems 2016), a conventional correction is still implemented by IGS ACs when generating the GLONASS precise products. Actually, this does not matter if the user adopted the same corrections.

Earth’s oblateness should also be taken into account. Even in a circular orbit, the satellite travels through a varying gravitational potential, which certainly causes a periodical effect on onboard clocks, but was considered to be masked by the clock noise or drifts (Formichella 2018). As the satellite clock precision/stability is always increasing (see Sect. 4.2), the J₂ oblateness term cannot be neglected any more at the sub-nanosecond level. Often referred to as J₂-correction, a simple analytical approximation of this effect has been developed by Ashby (2003) and Kouba (2004) as

$${\text{d}}t_{{{\text{rel}},\;J2}}^{{\text{s}}} = - J_{2} \frac{3}{2}\frac{{r_{{{\text{earth}}}}^{2} }}{{c^{2} }}\sqrt {\frac{\mu }{{a^{3} }}} \sin^{2} i \cdot \sin 2u,$$

(12)

where r_earth is the equatorial radius of the Earth, J₂ = 1.083·10^–3, i is the orbit inclination and u is the sum of orbit perigee angle and true anomaly. Typically, a periodic modulation at half the orbit period with an amplitude of about 0.04 ns and a rate of about 0.5 ns per day is caused by the J₂-correction. The magnitude reaches 0.06 ns for a Galileo MEO satellite while it is 0.1 ns for a GLONASS satellite. For satellites with high altitude and lowest inclination, like a BDS IGSO satellite, the value reduces down to about 0.036 ns (Müller et al. 2008; Teunissen and Montenbruck 2017). In short, the J₂-correction varies between approximately 1–3 cm of positioning accuracy, depending on the satellite constellation.

Furthermore, the Schwarzschild space–time bending adds a time delay on the propagation of electromagnetic waves, known as the Shapiro delay. It is classically given by Teunissen and Montenbruck (2017)

$$d_{{{\text{rel,stc}}}}^{{\text{s}}} = \frac{{2\mu }}{{c^{3} }}\ln \left( {\frac{{\left\| {{\varvec{r}}^{{\text{s}}} } \right\| + \left\| {{\varvec{r}}_{{\text{r}}} } \right\| + \rho _{{\text{r}}}^{{\text{s}}} }}{{\left\| {{\varvec{r}}^{{\text{s}}} } \right\| + \left\| {{\varvec{r}}_{{\text{r}}} } \right\| - \rho _{{\text{r}}}^{{\text{s}}} }}} \right),$$

(13)

where r^s is the position of the satellite and r_r is the position of the receiver, $\rho_{{\text{r}}}^{{\text{s}}}$ being the geometrical distance between the satellite and the receiver. This ranging delay reaches about 60 picoseconds for a MEO satellite and is a little larger for IGSO satellites (~ 70 picoseconds), therefore it is not neglectable in order to achieve millimeter level accuracy. Together with all the above terms, we finally come to the total relativistic effects.

One may notice that until now we only introduced the kinematic relativistic effect on the satellite clocks, actually, it also applies to the receiver clock, which is moving with respect to “inertial” space. During the time interval between the signal emission and signal reception, the receiver is moving with respect to inertial space because of the rotation of the Earth (approximately 0.5 km/s at the equator). It is called the Sagnac effect. The correction formula is given by Ashby (2003) as

$${\text{d}}t_{{{\text{rel}}, {\text{sag}}}}^{{\text{s}}} = \frac{{v_{{\text{r}}} \cdot \left( {r_{{\text{r}}} - r_{{\text{s}}} } \right)}}{{c^{2} }},$$

(14)

where v_r is the velocity vector of the receiver. The maximum effect is about 153 ns and 133 ns for Galileo satellites and GPS satellites, respectively, for a stationary receiver on the geoid. In general, these corrections are performed at the receiver software level (Mudrak et al. 2015; Sickle 2015). A similar eccentricity-dependent effect arises for a receiver, as discussed above, but it can be neglected in many cases. Since it affects all the observations from the same receiver in the same way and thus is able to be entirely compensated in the receiver clock offset estimation (Teunissen and Montenbruck 2017).

Table 3 gives an overview of the error budget of the relativistic effect in the GNSS PPP implementation. With the improvements in the accuracy of both satellite clocks and receiver clocks, a more accurate model of relativistic effect for time and frequency transfer at the picosecond level (10⁻¹⁶ s/s) is the next target. This entails the modelling of the relativistic effect to the order of c⁻³ (Giorgi et al. 2019). Small effects that were neglected in the past may need to be considered now. To take into account higher-order terms of the gravity field harmonic expansion is indispensable for reaching a sub-nanosecond level accuracy, in addition to the tidal potentials of the Sun, moon and other planets (Han and Cai 2019).

4.4 Ionosphere

The GNSS signals transit the atmosphere from satellites at an altitude of around 20,000 km to the receiver on or near the surface of the Earth. In the upper atmosphere, the ionosphere, which extends from about 50 to 1000 km above sea level, consists of ionised atoms and molecules and free electrons that significantly affect the radio wave propagation in a dispersive (i.e. frequency-dependent) way, including of course GNSS signals (Hernández-Pajares et al. 2011), both in code (group delay) and carrier (phase delay) observables (Jensen and Mitchell 2011), i.e. ${\text{d}}_{\text{ion,} \, {\text{f}}, \, {\text{r}}}^{ \, {\text{s}}}$ in Eq. (4) and ${\text{d}}_{\text{ion,} \, \text{sig,} \, {\text{r}}}^{ \, {\text{s}}}$ in Eq. (5). This propagation delay can vary from a few meters to tens of meters along the zenith direction (Klobuchar 1996). The amount of ionization/recombination varies greatly with the amount of radiation (mainly ultraviolet) received from the Sun, with not only diurnal and seasonal modulations, but also with a long-term modulation dictated by the solar cycle (around 11 years) and unpredictable solar flares. Ionization also varies with geographical location (polar, auroral zones, mid-latitudes, and equatorial regions). Propagation delays in the ionosphere are proportional to the integrated electron density N_e along the ray path, i.e., the number of free electrons per volume unit that is commonly used to characterize the state of the ionosphere. The total ionosphere delays, up to the third order (f⁻⁴, as the first order corresponds to f⁻²) for code and carrier-phase measurements, can be calculated analytically provided that the Earth’s magnetic field vector B₀ and the characteristics of the ionosphere (e.g., the Total Electron Content (TEC) along the signal propagation path) are known. For brevity, we only give the formula for carrier phase measurements in a simplified form

$$d_{{{\text{ion}},f,r}}^{{\text{s}}} = S_{1} + S_{2} + S_{3} - S_{{{\text{bend}}}} ,$$

(15)

where the S₁, S₂ and S₃ denote the first-, second- and third-order of the ionosphere delay, respectively, and S_bend represents the geometric bending caused by the ionosphere. The exact formula for each component can be found in the literature, e.g., (Brunner and Gu 1991; Bassiri and Hajj 1993; Fritsche et al. 2005; Petit and Luzum 2010). Although the code and the carrier phase measurements take a similar formulation, one should keep in mind that the ionosphere delay has an opposite effect on them due to by definition the group and phase velocity, as shown in observation equations Eqs. (4) and (5).

For a given signal frequency, the first order of the ionosphere delay, i.e. S₁, is proportional to the TEC along the ray path, in general, the delay in zenith being as small as 1 m during the night while being larger than 50 m at low elevation angle at daytime for both code and phase observables (Yunck 1993). During periods of high values of the TEC, the first-order ionosphere delay can reach up to a few hundred meters. Although it has been shown that the first-order ionosphere term explains up to 99.9% of the total ionosphere delay, the higher-order ionosphere terms can be greater than 1 cm, especially for high TEC cases. The second‐order term S₂, which is affected by both ionosphere electron content and the geomagnetic field is typically only 0.1% of the first order value in magnitude. The third‐order term S₃, which is not affected by the geomagnetic field, has a much smaller effect (less than 10% of the second-order value for GPS L1). Higher order terms are negligible at GNSS radio frequencies, e.g., for GPS L1 the fourth order is less than 0.1% of the third-order (Petit and Luzum 2010; Petrie et al. 2010). Another refraction error, i.e. the geometric bending term S_bend corresponds to the excess path length caused by the ionosphere refractivity is on the order of f⁻⁴, but could reach centimeters at low elevation angles (Hoque and Jakowski 2008). Therefore, we only limit our interest to ionosphere delays of no more than the third order in this review. Based on Xi and Wang (2021), we extended a typical result of ionosphere delay on carrier phase for the current multi-GNSS signals under a specific condition (i.e. a magnetic field with the magnitude of $B_{0} \cos \theta = 10^{ - 5} {\text{nT}}$ and the ionosphere has a Vertical Total Electron Content (VTEC) value of 143 TEC Units (TECU) $\left( {1 {\text{TECU}} = 10^{16} {\text{electrons}}/{\text{m}}^{2} } \right)$, as shown in Fig. 6. This result clearly indicates that the higher-order ionosphere terms, especially the second-order term, should be considered for millimeter-level applications.

Fig. 6

Typical ionosphere delays on carrier phase for the current multi-GNSS signals under a specific condition (see context, $B_{0} \cos \theta = 10^{ - 5} \;{\text{nT}},\;{\text{ VTEC}} = 143\;{\text{ TECU}}$), including first order (a), second order (b), third order (c) and ray bending (d). Variations w.r.t. elevation angle, and essentially Slant TEC (STEC) (black solid line in a), are calculated by applying a modified single layer mapping function on the given VTEC

Calibrations are required in order to eliminate or reduce these ionosphere delays for high-accuracy applications. Excellent reviews are (Yunck 1993; Klobuchar and Kunches 2000; Petrie et al. 2011). For GNSS PPP, there are mainly two ways for calibration, the first one depends on the ionosphere model and the second one is obtained by forming a linear combination of two or more observables with respect to different frequencies.

It is not easy to model the ionosphere to obtain highly variable TEC values for given positions and times due to its spatial and temporal variations. The ionosphere is largely impacted by solar and magnetic activities, as well as by the neutral atmosphere (Astafyeva 2019). Studies of the diurnal, seasonal and solar cycle behavior of TEC have been done by numerous researchers, e.g., (Klobuchar 1996; Mannucci et al. 1998; Zolesi and Cander 2014; Guo et al. 2015). In addition to periodic modulations, perturbations caused by solar flares, solar wind, aurora activity, and anthropogenic activities are present, such as travelling ionosphere disturbances, equatorial plasma bubbles, and scintillations (Hocke and Schlegel 1996; Béniguel and Hamel 2011; Béniguel et al. 2011; Taufiqurrahman et al. 2018; Belashov et al. 2021; Wan et al. 2021). Their impact can be huge, with sharp variations of the TEC causing losses of commercial communication channels. Moreover, 20% of daytime ionosphere variations are related to processes occurring in the lower atmosphere (Goncharenko et al. 2010).

Nevertheless, a global/regional ionosphere model is able to represent most of the spatial and temporal variations of the ionosphere. Two kinds of models are commonly used, including theoretical models, e.g., Parameterized Ionosphere Model (PIM) (Daniell et al. 1995), and empirical models, e.g., International Reference Ionosphere (IRI) model, broadcast model and Global Ionosphere Map (GIM) (Klobuchar 1987; Schaer 1999; Bilitza 2018). The theoretical model PIM is a global model of theoretical ionosphere climatology, which consists of diurnally reproducible runs of several physical ionosphere models, like the time-dependent ionosphere model of Utah State University (Schunk 1988), low latitude F region model developed by Anderson (1973). It produces profiles of electron content, electron density, ion composition (${\text{O}}^{+}$, $\, {{\text{N}}{\text{O}}}^{+}$, and ${\text{O}}_{2}^{+}$), etc. A similar product can also be provided by IRI. But the IRI is generated based on several terrestrial and spatial data sources (e.g., ionosonde and incoherent scatter radars) and the electron density is represented by analytic functions (Bilitza et al. 2011). Since both PIM and IRI only represent ionosphere climate, e.g., IRI describes monthly averages of ionosphere densities and temperatures, daily and sub-daily variations in the ionosphere are not well-modelled (Petrie et al. 2011; Prol and Camargo 2015). As a bonus, the GNSS product services made it possible to model TEC with dual-frequency receiver data at a global scale, like GIM (Schaer 1999; Nava et al. 2008; Oladipo and Schüler 2012). Different from IRI, the GIM has a higher time resolution (depending on the sample interval of GNSS observables) but only produces global VTEC values over a thin layer representing the ionosphere (generally located between 300 and 450 km above the Earth’s surface). Since 1998, the IGS has started to provide daily GIM products, and there are seven Ionosphere Associate Analysis Centers (IAACs) computing independently with different approaches and datasets (Hernández-Pajares et al. 2009). Results between these centers showed good consistency during one solar cycle (Roma-dollase et al. 2018). As the most commonly used ionosphere correction products, the IGS GIMs have typically errors of 10–20% of the RMS with respect to TEC derived from The satellite altimeter mission named after the ocean TOPography EXperiment (TOPEX) (Orús et al. 2002). Specifically, they are claimed to be as accurate as 2–8 TECU (Wielgosz et al. 2021; https://igs.org/products/#about). Another widely used empirical ionosphere model is the broadcast model, which is firstly proposed by Klobuchar (1987) for single-frequency GPS users, known as the Klobuchar model. It is a crude delay model of eight parameters and is usually broadcasted to input the so-called Ionosphere Correction Algorithm (ICA) with a 50% error average when compared to IF solution utilizing dual frequency observations (Klobuchar and Kunches 2000; Nahavandchi and Soltanpour 2008). Likewise, BDS-3 uses a new global ionosphere broadcast model, known as the BeiDou Global broadcast Ionosphere delay correction Model (BDGIM), but with a reduced about 20% average error with respect to daily site-specific GPS-derived TEC and GIM generated by the IGS (Yuan et al. 2019). While for Galileo, Ne-Quick model with 3 coefficients driven is applied and results show it outperforms Klobuchar model by 16% with respect to daily GIMs from the IGS and VTEC provided by JASON-1&2 satellite altimeters (Wang et al. 2017; Setti Júnior et al. 2019). However, there is still no individual broadcast ionosphere model for GLONASS (Hoque et al. 2015).

Recall that the geomagnetic field B₀, is also necessary for calculating higher-order ionosphere delays. In that case, the introduction of a more sophisticated model/measurement is recommended, such as the International Geomagnetic Reference Field (IGRF) (Wardinski et al. 2020). The relative differences between the IGRF and the traditional dipolar model can reach up to more than 60% w.r.t. the IGRF, and these differences are directly translated into the geodetic estimations (Hernández-Pajares et al. 2007).

As the combination of two frequencies corrects the first-order term of the ionosphere delay (e.g., the IF combination in GNSS PPP), a triple frequency combination is able to determine both the first- and second-order effects, and so forth (Kim and Tinin 2011). First-order correction is limited to 1–2 cm accuracy (Banville et al. 2017). Triple frequency implementations come at the cost of noise amplifications in the combined observables, balancing, or even ruining the gain in accuracy. In practice, the second- and third-order delays are often corrected in PPP mode by applying the GIMs and IGRF through analytical formulas. Based on simulations that are used to approximate the actual ionosphere, the residuals of these higher-order ionosphere models with respect to their simulations depend on the azimuth angle and the elevation angle of the signal path. An accuracy of roughly 1–2 mm at a VTEC level of 100 TECU was reported in Hoque and Jakowski (2007). Higher-order ionosphere delay models have not been yet routinely adopted by all IGS ACs. It is therefore recommended to check the consistency between different implementations of ionosphere corrections for practical applications (Hernández-Pajares et al. 2011), under penalties in accuracy (Zus et al. 2017).

The error budget of ionosphere delays for GNSS PPP is summarized in Table 5. Please note that short-term perturbations are not considered in this error budget. Current ionosphere models cannot predict short-scale variations in time and space (e.g., scintillations, Travelling Ionosphere Disturbances (TID), Equatorial Plasma Bubbles (EPBs) and atmosphere gravity waves induced by earthquakes) (Bahari et al. 2015). Models taking into account third- and higher-order terms are under assessment, especially for the ray bending terms, which have not been accepted as a routine correction by IGS ACs because there is still yet no consensus on it (Petrie et al. 2011).

Table 5 Error budget of ionosphere delays

4.5 Troposphere

As mentioned previously, when GNSS signals are travelling through the atmosphere, both refraction, diffraction and bending (to a lesser extent) occur. In the upper regions of the atmosphere, these effects are frequency-dependent (the ionosphere, see previous section). In the lower section of the atmosphere, they are frequency-independent, and this is why the literature speaks about the “neutral” atmosphere. Even closer to the surface, water vapor plays an important role. This “water–vapor layer” (around ten kilometers in depth) is called the troposphere, with corresponding tropospheric delay (${\text{d}}_{\text{trop,} \, {\text{r}}}^{ \, {\text{s}}}$ in Eqs. (4) and (5)) (Jensen and Mitchell 2011). Overall, this excess troposphere delay is typically about 2–3 m in the zenith direction, and can reach up to tens of meters at low elevation angles (Klobuchar 1996; Hakman et al. 2015).

The troposphere contains nitrogen, oxygen, trace gases, and by definition water vapor. Their effects on the propagation of GNSS signal are separated, for the commodity (Davis et al. 1985), in two parts: a hydrostatic (very often called improperly “dry”) and non-hydrostatic (very often called improperly “wet”) component (Barriot and Feng 2021). By commodity, we mean that the “dry” component only varies little over temporal and spatial scales of hours and kilometers, respectively, so it can be well-modelled and compensated with empirical models; at the opposite, the “wet” component is highly variable both in time and space and difficult to determine.

The hydrostatic component, which depends primarily on the total air pressure (including water vapor partial pressure), amounts to about 90% of the total tropospheric delay. It can be derived, quite precisely, from the empirical meteorology models or numerical weather prediction models, such as the Hopfield model (Hopfield 1971), the Saastamoinen model (Saastamoinen 1973), the Black model (Black 1978), and the European Centre for Medium-range Weather Forecasts (ECMWF) model (Chen and Liu 2016). A typical accuracy at 2–6 mm level in the zenith direction has been demonstrated, e.g., (Bock and Doerflinger 2001; Steigenberger 2014; Chen and Liu 2016), which is usually considered accurate enough for most geodetic applications. Nevertheless, this error can degrade down to 20 mm under severe weather conditions when the vertical wind acceleration reaches almost 1% of the gravity acceleration (Davis et al. 1985; Nilsson et al. 2013). The remaining 10% of the total tropospheric delays, i.e. the small “wet” part, highly variable in time and space, generally varies between 0 and 40 cm in the zenith direction (Petit and Luzum 2010; Nilsson et al. 2013). This wet part needs to be estimated from measurements, as the a priori model does not work very well. Even so, the residuals can reach up to several millimeters (~ 2–7 mm) (Teke et al. 2011; Ning et al. 2012; Steigenberger 2014; Kacmarik et al. 2017). A typical error budget of tropospheric delay is given in Table 6.

Table 6 Error budget of tropospheric delay (typical values)

A direct estimation of the tropospheric delays is difficult to implement (Hakman et al. 2015), as they are additive quantities in Eqs. (4) and (5), and therefore almost impossible to separate from the other additive quantities. A better parameterization of these delays is obtained by combining the so-called Zenith total Troposphere Delays (ZTD) and mapping functions (Marini 1972; Davis et al. 1985). The zenith total delay is itself subdivided into a Zenith Hydrostatic Delay (ZHD) and a Zenith Wet Delay (ZWD), with a corresponding hydrostatic mapping function ${\text{m}}{\text{f}}_{\text{non-hydro}}$ and a corresponding non-hydrostatic mapping function ${\text{m}}{\text{f}}_{\text{non-hydro}}$. The main weakness of this parameterization is that it is based on the assumption of a horizontal isotropy of the troposphere around the station. To overcome this weakness, horizontal gradients, taking into account the azimuthal variation of the refractivity, were introduced by Davis et al. (1993). In fine, the parameterization of the neutral delay takes the form (Bar-Sever et al. 1998):

$$\begin{aligned} d_{{{\text{trop}},{\text{ r}}}}^{{ {\text{s}}}} = & {\text{mf}}_{{{\text{hydro}}}} \left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right)\left[ {{\text{ZHD}} + \cot \left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right)\left( {G_{{{\text{N}}, {\text{r}}}}^{{{\text{hydro}}}} \cos \left( {{\text{Az}}_{{\text{r}}}^{{\text{s}}} } \right) + G_{{{\text{E}}, {\text{r}}}}^{{{\text{hydro}}}} \sin \left( {{\text{Az}}_{{\text{r}}}^{{\text{s}}} } \right)} \right)} \right] \\ & + {\text{mf}}_{{\text{non - hydro}}} \left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right)\left[ {{\text{ZWD}} + \cot \left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right)\left( {G_{{{\text{N}}, {\text{r}}}}^{{\text{non - hydro}}} \cos ({\text{Az}}_{{\text{r}}}^{{\text{s}}} ) + G_{{{\text{E}}, {\text{r}}}}^{{\text{non - hydro}}} \sin \left( {{\text{Az}}_{{\text{r}}}^{{\text{s}}} } \right)} \right)} \right], \\ \end{aligned}$$

(16)

where ${\text{G}}_{\text{N,} \, {\text{r}}}^{\text{hydro}},{ \, {\text{G}}}_{\text{E,} \, {\text{r}}}^{\text{hydro}},{ \, {\text{G}}}_{\text{N,} \, {\text{r}}}^{\text{non-hydro}},{ \, {\text{G}}}_{\text{E,} \, {\text{r}}}^{\text{non-hydro}}$ represent the north and west components of hydrostatic and non-hydrostatic horizontal gradients and ${\text{el}}_{{\text{r}}}^{{\text{s}}} , {\text{Az}}_{{\text{r}}}^{{\text{s}}}$ denotes the elevation angle and the azimuth angle of the signal path in the local ENU frame. A schematic representation of tropospheric delays as well as their mapping as ZTDs is shown in Fig. 7.

Fig. 7

Schematic representation of individual Slant Path Delays (SPDs), i.e. tropospheric delays from three GNSS satellites and their mapping to ZTDs, adapted from (Guerova et al. 2016)

Over the years, processing strategies and mitigation algorithms have evolved for tropospheric delays in GNSS PPP. With the emergence of multi-constellations, the Line-Of-Sights (LOS) receiver-satellites are more numerous, enhancing the precision of estimates of the tropospheric delays (Lu et al. 2015; Lu 2016; Zhao et al. 2019). Abdelazeem and El-Rabbany (2020) found 4.5% and 14% of improvements in GPS/Galileo and GPS/Galileo/BDS PPP solutions, respectively, when compared to GPS-only solutions and roughly a 10% of improvement on RMS of shipborne GNSS ZTD was investigated in Wang et al. (2019a) with respect to ZTD derived from GPS-only. A small decrease (2%) in STD of differences between the estimated gradients and Numerical Weather Model (NWM) gradients was reported when using GPS + GLONASS instead of GPS-only (Kačmařík et al. 2019). The choice of elevation cutoff in ZTD estimation is also an important parameter, as well as the elevation-dependent weighting function applied in GNSS data processing. Based on a dataset spanning over 14 years, Ning and Elgered (2012) analyzed Integral Water Vapor (IWV) estimates derived from ZWD w.r.t. 8 different elevation cutoffs. Their results show that the RMS at cutoff angles of 10° and 15° are smaller while the best correlation with radiosonde is obtained for a 15° cutoff. Four kinds of elevation-dependent weighting functions used for GNSS LS processing were investigated by Hadas et al. (2020). They found that the differences in estimated ZTD between these weighting functions are usually below the 5 mm level but can exceed 10 mm during the initialization period when the PPP solution is converging.

The mapping function is usually written in the form of a continuous fraction

$${\text{mf}}\left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right){ = }\frac{{{1 + }\frac{{\text{a}}}{{{1 + }\frac{{\text{b}}}{{\text{1 + c}}}}}}}{{{\text{sin}}\left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right){ + }\frac{{\text{a}}}{{{\text{sin}}\left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right){ + }\frac{{\text{b}}}{{{\text{sin}}\left( {{\text{el}}_{{\text{r}}}^{{\text{s}}} } \right){\text{ + c}}}}}}}} ,$$

(17)

in such a way it has a value of 1 when the elevation angle is zenithal. a, b and c are coefficients currently estimated either from climatological data. e.g., the Isobaric Mapping Function (IMF) and the Global Mapping Function (GMF) (Niell 2000; Boehm et al. 2006a), or NWM data, e.g., the Vienna Mapping Function (VMF), VMF1/VMF3 and Global Pressure and Temperature (GPT), GPT2w/GPT3 (Boehm et al. 2006b; Böhm et al. 2015; Landskron and Böhm 2018). In the past, mapping functions simply based on elevation angle, standard atmosphere parameters or meteorological data, such as Hopfield, Chao, Marini, Herring, Niell Mapping Function (NMF), Moffett, UNBabc and so on (Hopfield 1971; CC 1972; Marini and Murray 1973; Moffett 1973; Niell 1996; Guo and Langley 2003) were used. An overview of possible mapping functions can be found in Nilsson et al. (2013). Although these mapping functions have the advantage that they are independent of any external data, the mapping functions based on meteorological data, e.g., GMF/VMF1, have been shown to perform better. Comparisons with mapping functions used in GNSS have been done in many studies, e.g., (Boehm et al. 2007; Steigenberger et al. 2009). The unambiguous conclusion is that the VMF1 and VMF3 families are acknowledged to be the best nowadays overall (Barriot and Feng 2021). Durmus and Erdogan (2021) found a smaller RMS for PPP solutions in the vertical direction when using VMF1 (~ 6.75 mm) w.r.t. GMF/NMF/GPT2 (~ 7.0–7.5 mm), based on the processing of data from 190 IGS stations in 2018. Similar conclusions were also drawn from comparisons with respect to ray-tracing or radiosonde data, e.g., (Urquhart et al. 2014; Abdel-Monam Younes 2017). Besides the choices of meteorological inputs, another essential difference between different mapping functions in the form of continuous fractions is the method of solving for three coefficients in Eq. (16). These coefficients are typically estimated in a LS adjustment, in order to best fit the ratios of the delays at several selected elevations to the delays in the zenith direction (Niell 2000), which are both generated by ray-tracing the profiles provided in the meteorological input. More specifically, they can be determined altogether rigorously by iterative LS adjustment but with the risk of numerical instabilities, which is common for the non-hydrostatic coefficients due to the great departures from the spherically symmetric or exponential decay assumption with altitude in some cases (Landskron and Böhm 2018). To avoid these numerical instabilities, simplified methods, but without firm theoretical grounds, were proposed, e.g., only one coefficient a is estimated or calculated with fixed empirical b and c from ray-traced mapping factors at several specific outgoing elevation angles based on meteorological datasets like radiosonde. These methods are more simple and more efficient and have been applied in the most commonly used mapping function today, such as VMF1/VMF3 (Boehm and Schuh 2004; Landskron and Böhm 2018), but with mixed results. By combining the rigorous method (estimate a, b and c altogether) with the simplified methods (e.g., estimate a or a/b with the rest fixed), an improved mapping function modelling method was also introduced by Zhou et al. (2021).

The gradient parameters were introduced by Davis et al. (1993) based on an azimuthal Taylor series expansion of the vertical refractivity at a station up to degree one. They were interpreted as a titling of the mapping functions by Rothacher et al. (1998). A simple gradient model with a cotangent factor w.r.t. elevation angle was firstly proposed by MacMillan (1995). By applying the horizontal gradients definition (MacMillan 1995), Bar-Sever et al. (1998) found a 15% improvement in horizontal repeatability and a 25% improvement in the consistency of non-hydrostatic delays between GNSS PPP and Water Vapor Radiometer (WVR). Improvements in the accuracy of station coordinate and ZTD estimation have been investigated, e.g., (Iwabuchi et al. 2003; Li et al. 2015; Lu et al. 2016). New algorithms that claim to better represent the azimuthal anisotropy were studied over the years, such as the titling mapping function (Meindl et al. 2004), the adaptive mapping function (Gegout et al. 2011), high-order expansion of gradients model (Landskron et al. 2017), directional model of gradients (Masoumi et al. 2017) and so on. These algorithms have their merits, like a better capture of the azimuthal variability, leading to higher accuracy positioning and better baseline repeatability, but they also suffer, besides a lack of theoretical basis, from some practical ailments, such as the required use of pre-established models obtained by ray-tracing from NWM grids or over-parameterization (high correlation between solve-for parameters). Until now, the gradient model of MacMillan (1995) is still the most widely used in GNSS data analysis due to its simplicity and effectiveness.

Since the tropospheric delay is difficult to separate from other error terms, as shown in Eqs. (4) and (5), refinements in these error models contribute to improving its accuracy. The uncorrected higher-order ionosphere delays affect the estimation of tropospheric delay. Differences at a level of ~ 2 mm for ZTD parameters were reported by Fritsche et al. (2005) after correcting the second and third-order corrections of the ionosphere delays. The effect on estimated ZWD was at the same level, even after applying the most recent correction models of high-order corrections of the ionosphere delays (Zhang et al. 2020d). By using simulations generated from several models over the March in 2012, including IRI, IGRF12, and ERA-Interim reanalysis, a study performed by Zus et al. (2017) showed that high-order ionosphere delays have a significant impact on estimating tropospheric parameters in PPP mode around noon (epoch 15 UTC): a monthly average of up to − 1.5 mm for zenith delay, ± 0.05 mm for east gradient and 0.2 mm for the north gradient, w.r.t. estimates without correcting high-order ionosphere delays. During periods of solar storms and geomagnetic storms, the maximum differences between ZWDs estimated by PPP mode, with and without ionosphere high-order delay correction, can reach over 20 mm and the north gradients were found more likely to be affected when compared with east gradients (Zhang et al. 2018). Besides, the negative impact of the use of the a priori ZHD for the ZTD estimation was reported by Zhang et al. (2021b): an error of 10 mm in the a priori ZHD can lead to errors of approximately 0.4 mm in the PPP–ZTD and 1.0 mm in PPP-height solutions with a satellite elevation cut-off angle of 5°. Furthermore, antenna phase center correction also affects the estimation of ZWD, e.g., (Ortiz de Galisteo et al. 2010; Jarlemark et al. 2010; Ejigu et al. 2019).

Since 2006, the daily IGS Final Troposphere Estimates (FTEs) have been released with five-minute estimates of the zenith path delays and gradients w.r.t. a MacMillan model (MacMillan 1995; Bar-Sever et al. 1998; https://igs.org/products/#tropospheric_products). The accuracy is claimed to be better than 4 mm for zenith path delay (Byun and Bar-Sever 2009; Kouba 2015; Zhang et al. 2017), and the FTEs are thus used as the current routine benchmark for researchers testing their own solutions (Hakman et al. 2015). Though a millimeter-level accuracy of the modelling of tropospheric delay has been achieved, the classical assumption that errors of the a priori zenith hydrostatic delays can be compensated by the estimation of the remaining non-hydrostatic part is not rigorous, especially at low elevation angles (Nilsson et al. 2013). Except that, for short observing sessions with the specific weather condition, e.g., the passage of cold/warm atmospheric fronts with strong discontinuities, the atmospheric dynamics implies a large spatiotemporal correlation of the water vapor fields, that are therefore difficult to model (Bock and Doerflinger 2001). Therefore, refinements of mapping functions and gradients are still expected (Zhang et al. 2020b), with a full consideration of climate and terrain conditions.

Research into how to take full advantage of GNSS observables at low elevation angles is also ongoing, as such near-horizon data can be useful in separating propagation delays, e.g., the effects of the neutral atmosphere and the position of the receiver (Yunck 1993), with applications in meteorology because these rays probe the boundary layer close to the ground.

4.6 Antenna Phase Center

Antennas are one of the essential components of accurate GNSS applications. Antenna transmit/receive radiation patterns can be very complex, with main and side lobes (Balanis 2005). For computations, a so-called Mean Phase Center (MPC) is defined as the point-like center of an outgoing electromagnetic pulse radiated from the antenna, the phase front of which can be assimilated to a sphere or part of a sphere far from the device. In practice, the radiation pattern of an antenna, including its interaction with the surrounding structures/mountings, must be taken into account (Teunissen and Montenbruck 2017). This correction (called Phase Center Correction (PCC), see Fig. 8) for a fixed antenna, which can be seen as a propagation delay, depends on the orientation (called Phase Center Variation (PCV)) of the LOS of the considered satellite/receiver and a translation (called PCO for Phase Center Offset) between a reference (i.e. measurable) point of the antenna/support structure and the MPC (Dilssner et al. 2014). The reference point is the so-called Center-Of-Mass (COM) on the satellite side, because its attitude and motion are defined with respect to such a COM by Newtonian mechanics, and Antenna Reference Point (ARP) on the receiver side, with the implicit assumption that it is “fixed” (otherwise, there will be another COM).

Fig. 8

Geometrical diagram of the receiver PCC, similar for the transmitter. Modified based on (Teunissen and Montenbruck 2017)

Kröger et al. (2021b) write the PCC (satellite/receiver antenna) as

$$d_{{{\text{PCC}}, {\text{f}}}} = - {\varvec{k}} \cdot {\varvec{d}}_{{{\text{PCO}}, {\text{f}}}} + d_{{{\text{PCV}}, {\text{f}}}} \left( {{\text{el}}, \;{\text{az}}} \right) + r,$$

(18)

where k denotes the unit vector of LOS, f is the signal frequency and el, az are the elevation angle and the azimuth angle of the target (GNSS satellite/receiver antenna). A constant part r may exist but it is usually absorbed into the receiver clock error. Albeit the phenomenon is the same on both emitters and receivers, they are treated separately as they are expressed in different coordinate frames, e.g., SBFF on the satellite side and ENU on the receiver side.

The receiver antenna PCCs have been investigated since the very beginning of GPS (Willi et al. 2020) due to the fact that they are highly correlated to delays induced by other error sources, like atmospheric delays, receiver clocks bias, etc. Neglecting these millimeter- or even decimeter-level biases could lead to significant errors in other relevant parameters, especially in the station height (up to decimeter-level) (Markus et al. 1995; Dawidowicz 2018). For satellite antenna PCCs, let us first say that GNSS satellite antenna are fixed with respect to the satellite bus (i.e., no steer). Recalling that the precise satellite orbit and clock products provided by IGS refer to the COM of the satellites, while the observables refer to antenna phase center, the offset between two centers, i.e. satellite PCO and the potential LOS-dependent PCV, need to be corrected when applying these IGS precise products (Jarlemark et al. 2010; Montenbruck et al. 2018). In analogy to receiver antenna PCCs, the antenna PCOs of individual satellites can have perceptible effects on the clock, zenith path delay and station position, mostly in the station height (Zhu et al. 2003). Recalling that GNSS-derived station coordinates contribute to the realization of ITRS, that is, ITRF, these PCO-induced average effects in the station height, which implies a redefinition of the unit of length in TRF (i.e., the scale in TRF), will lead to bias in scale and thereby introduce bias in ITRF. For instance, a scale bias of 0.78∙∆z parts-per-billion (ppb) is induced by an error ∆z in the z-direction of PCO (Rothacher 1994; Brockmann 1997; Zhu et al. 2003) (hereafter, the z-direction refers to the direction along the z-axis in the SBFF, pointing towards the geocenter, or called nadir).

Therefore, calibrations of antenna phase centers on both the satellite and receiver sides are necessary for accurate GNSS applications. As far as we know, there are mainly three kinds of techniques for calibrating and modelling the receiver antenna PCCs on the receiver side, i.e., relative field calibration, anechoic chamber calibration, and absolute field calibration. Details will be discussed later in this section. Likewise, the antenna phase center on the satellite side can also be calibrated in an anechoic chamber, however, it could only be implemented before the satellite is launched. Unfortunately, for military reasons, details of some GNSS satellite antenna PCCs are not publicly available for scientific communities. An alternative way was developed to obtain them, i.e., estimate satellite PCCs based on GNSS observations from a global tracking network together with other parameters (Schmid et al. 2005a; Steigenberger et al. 2016), provided the absolute receiver antenna phase patterns were available. This prerequisite of absolute receiver antenna PCCs is needed because the nadir angle of LOS at the satellite side is a function of the zenith angle of LOS at the receiver side (see Schmid and Rothacher (2003)). In this case, an elevation-dependent phase center delay of the receiver antenna may be interpreted as a phase center delay of the satellite antenna w.r.t. the nadir angle, and vice versa (Rothacher 2001). Hence, either receiver antenna PCCs or satellite antenna PCCs can only be estimated once if the other one was known or fixed.

Let us first start with the receiver antenna PCCs. The relative field calibration system was developed by Rothacher et al. (1996) and Mader (1999), where several groups of receiver antennas PCCs were calibrated on a short well-known baseline w.r.t. a reference antenna. By combining several groups of receiver antenna PCC models derived from the relative field calibration and selecting the antenna Allen Osborne Associates Dorne Margolin T (AOAD/M_T) as the reference antenna, a set of standard antenna calibration values, named by igs_01.pcv, were regenerated by IGS in 1996 (Rothacher and Mader 1996). However, systematic errors in long-distance baseline, site-dependent multipath effect and other drawbacks were demonstrated (Rothacher 2001; Schmid et al. 2005a) when applying these relative PCC models. It is mainly due to the arbitrary assumption in the relative field calibration that the PCVs of the reference antenna are zero.

Alternatively, absolute calibration techniques including anechoic chamber and robot-based field calibration were developed at the same time. For anechoic chamber measurements, an antenna is set up in a room designed to reduce reflections and the absolute PCC may be obtained by measuring the phase delay of an artificial GNSS signal over the whole antenna hemisphere as the emitter is moved or the antenna is rotated (Sims 1985; Willi et al. 2018), then an expansion in spherical harmonic functions is commonly applied to model and express the radiation patterns of the antenna (Rahola et al. 2009; Schmitz et al. 2012). More details about anechoic chamber calibration can be found in Görres et al. (2006). Though several results have been derived by many studies (Schupler et al. 1996; Görres et al. 2006; Zeimetz and Kuhlmann 2008; Becker et al. 2010), calibration in an anechoic chamber is rather demanding in infrastructure and hard to carry out. Inspired by combining the advantages of the two methods above, robot-based absolute field calibration was proposed, that is, a high-precision robot rotates and tilts the antenna to be calibrated while the reference antenna is kept fixed (Wübbena et al. 1997), and then follows the same modelling method as applied in the anechoic chamber but with the real GNSS signal in the field. This technique was jointly developed by Geo++ GmbH company (Geo++) and Institut fur Erdmessung (IfE), Leibniz University Hannover and has been performed routinely over the years (Menge et al. 1998; Bilich et al. 2012). This absolute robot-based field calibration had been steadily refined by Geo++ since 2000, which provides absolute type-specific antenna PCC models for IGS. In November 2006, IGS decided to switch to absolute PCC models based on absolute calibration performed by Geo++ , which are published in ANTenna EXchange (ANTEX) format, i.e., igs05.atx. (Rothacher and Schmid 2010).

There is no essential difference for modelling receiver antenna PCCs w.r.t. different GNSS constellations and different frequencies. But GLONASS is somewhat special among them. Absolute field calibrations of receiver antenna PCCs for the GLONASS constellation were not sufficient before 2010 for the lack of enough operational satellites in the constellation at that time. Moreover, GLONASS FDMA is a troublesome issue to deal with, since frequency-dependent PCCs are mixed in observations from different carrier frequencies transmitted by the same satellite (Schmid et al. 2016). By estimating the changes of PCVs w.r.t. GPS of frequencies per 25 MHz, the PCVs for GLONASS frequency of each sub-channel were derived by Geo++ using robot-based field calibration (Wübbena et al. 2006). Together with updated robot calibrations of receiver antennas, the new antenna PCC models, named by igs08.atx, were adopted by IGS in 2011 and then further developments contributed to the switch to igs14.atx in 2017. From then on, the absolute calibrations have been routinely performed and added to the IGS ANTEX (e.g., igs14.atx). With the addition of new constellations, as well as new signals, receiver antenna calibrations for Galileo and BDS constellations were also performed. Since 2019, the Geo++ has been working on multi-frequency calibrations for all four GNSS constellations, and the preliminary results were presented to have a good repeatability of 0.2–0.4 mm (STD) (Wübbena et al. 2019). It also facilitated the birth of the antenna PCC models for the IGS repro-3 campaign, named by igsR3.atx, which was used for the ITRF2020 reprocessing effort of the IGS. Following this work, several antennas were also calibrated by other institutes, such as Eidgenössische Technische Hochschule (ETH) Zürich (Willi et al. 2020). All of them have contributed to the switch from igs14.atx to the newly released igs20.atx in IGS, where more patterns of multi-constellations and multi-frequency for receiver antenna PCCs are provided (see IGS Mail #8238 https://lists.igs.org/pipermail/igsmail/2022/008234.html).

In fact, the aforementioned three calibration methods have shown overall good agreements (1 ~ 2 mm) on modelling PCC of several different receiver antenna types (Rothacher 2001; Becker et al. 2010), although exceptions were also found in some certain antenna types (Aerts and Moore 2013; Krzan et al. 2020). But even by applying the same calibration method, the receiver antenna PCC models for individual antennas of the same type differ from each other (Schmid et al. 2005a; Wübbena et al. 2006). Their significant impacts on positioning results have been demonstrated, e.g., (Sidorov and Teferle 2012; Baire et al. 2014; Araszkiewicz and Völksen 2017). Although these positioning offsets usually do not exceed 2 mm in the horizontal direction (elevation angle el = 0°) and 4 mm in the vertical direction (elevation angle el = 90°) for most of the antennas (Kersten and Schön 2018; Krzan et al. 2020), the extreme ones still need to be considered. Moreover, discrepancies of up to 2–4 mm between the receiver antenna PCC models for identical frequencies from different constellations were found in some antenna-receiver combinations (Kröger et al. 2020, 2021a, b). All these discrepancies indicate that it is necessary to calibrate PCC models individually w.r.t. frequency/elevation/azimuth/radome, since each antenna has its own features. However, it is a heavy workload as the IGS global network consists of hundreds of individual antennas. So far, only the mean values from the same antenna type are adopted by the IGS and all of them are based on absolute robot-based calibrations. Until January, 2022, about 93.5% of the antenna/radome combinations operated (102 in total) within IGS global network now had been absolutely calibrated with azimuthal corrections according to Villiger and Dach (2022). Due to the large number of antenna types, we would just give statistics of these PCC models for multi-GNSS with multi-frequency to indicate their effects on GNSS PPP (see Table 7), please note that only robot-based calibrations are included in the statistics. One may refer to igs20.atx (https://files.igs.org/pub/station/general/igs20.atx) for more details.

Table 7 Error budget of receiver antenna phase center biases

The development of absolute receiver antenna PCCs makes it possible to estimate satellite antenna PCCs based on GNSS observations from a global tracking network. At the early stage of IGS (before the year 2006), the satellite antenna PCCs were ignored except for block-specific PCOs (Schmid et al. 2016), which had been shown to be inaccurate as the differences between individual satellites were significant, especially in the z-direction (Ge et al. 2005; Schmid et al. 2007). As a result, satellite-specific antenna PCCs are required. Schmid and Rothacher (2003) and Schmid et al. (2005b) firstly demonstrated the possibility of estimating nadir-/elevation-dependent satellite PCVs, as well as the azimuth-dependent PCVs with absolute robot calibrations for the receiver antenna. Later, in November 2006, the absolute satellite antenna PCC models were complemented by reprocessing multi-years solutions of global GNSS networks in several IGS ACs. The results were adopted by IGS, named by igs05.atx, within the frame of IGS05 (i.e., the IGS realization of ITRF2005).

Following the development of multi-GNSS constellations, the igs05.atx was then replaced by the igs08.atx with newly launched satellites before the year 2011, especially for GLONASS satellites (Dilssner et al. 2010; Dach et al. 2011b). Because of the fact that satellite antenna PCOs are not available and are correlated with the scale of ITRF, the satellite antenna PCOs are usually adjusted to the ITRF scales based on VLBI and SLR during the reprocessing (Villiger et al. 2020). Therefore, the satellite antenna PCOs of igs05.atx and igs08.atx cannot be compared directly since there is a significant scale difference (about − 1 ppb) between ITRF2005/IGS05 and ITRF2008/IGS08 (Rebischung et al. 2012). However, by ignoring scale-related biases, the accuracy of the satellite antenna PCOs is at centimeter-level (Schmid et al. 2016). The antenna PCCs of Galileo satellites were firstly included in igs08.atx in 2015 by adopting the models from Montenbruck et al. (2014) and Steigenberger et al. (2015). Subsequently, more accurate PCOs of Galileo satellites were estimated (Steigenberger et al. 2016), as well as the PCCs of BDS-2 IGSO/MEO within ITRF2008 (Dilssner et al. 2014; Guo et al. 2016; Huang et al. 2018). However, the differences among these estimated PCOs can reach up to decimeters according to the selected datasets, independent software and different applied models.

Although for satellite antenna PCCs, pre-launch calibrations (at 1 cm accuracy) performed by the satellite manufacturers are preferred by scientific communities (Montenbruck and Steigenberger 2017), some of them were not available at first. For antennas onboard GPS and GLONASS satellites, only the block-specific PCOs (i.e., one offset value per block, e.g., Block I and Block II for GPS) in the horizontal, also called the x-offsets and the y-offsets in SBFF, are available based on the manufacture information. Nowadays, PCCs of GPS Block IIR satellites and Galileo satellites, as well as PCOs of BDS-2/3 IGSO/MEO satellites, were disclosed by the Lockheed Martin Corporation (LMCO) (Dilssner et al. 2016), the European Global Navigation Satellite Systems Agency (GSA) (European GNSS Agency 2020), and the China Satellite Navigation Office (CSNO) (China Satellite Navigation office 2019), respectively.

But several studies have found that the manufacturer values could be untrustworthy and insufficient in high-precision positioning (Villiger et al. 2020; Geng et al. 2021). The comparison of PCCs between the ones estimated by space-based GPS observables and the pre-launch calibrations for GPS block IIR/IIR-M validates the accuracy and reliability of the estimations, as well as the calibration method itself (Dilssner et al. 2016). But when implementing the same method based on ground-based observations, disagreements between the estimated satellite PCOs and manufacture values have been demonstrated in many studies, including for GLONASS (Dach et al. 2019a), for Galileo (Steigenberger et al. 2016; Villiger et al. 2020; Geng et al. 2021) and for BDS-2/3 IGSO/MEO (Yan et al. 2019; Xia et al. 2020; Geng et al. 2021; Qu et al. 2021). These authors reported that these disagreements are at the centimeter-level in the horizontal and decimeter-level in the z-direction, respectively, and the re-estimated PCOs outperform the manufacturer values in terms of the performance of orbit determination and positioning. Two possible explanations for those discrepancies between estimate values and manufacturer values can refer to the context of Villiger et al. (2020): one is missing receiver antenna PCCs for Galileo/BDS when estimating PCOs based on ground-based GNSS observations, and the other reason is that the disclosed manufacturer values imply a certain scale as they will re-define the unit of the length in the TRF, which might be different from the scale of ITRF2014. Due to the correlation between satellite antenna PCOs and the scale of the TRF, the scale differences could be partially absorbed into the estimated PCOs when utilizing precise products or models aligned to ITRF2014.

Nevertheless, this commonly applied calibration method for estimating satellite antenna PCCs has difficulty in determining the horizontal PCOs, as in SBFF, the y-axis is aligned with the along-track direction and the x-axis points towards the sun, which means they are highly correlated with other orbit elements and clock parameters if all of them are estimated together. Thus, the horizontal PCOs were usually inherited from the manufacturer values, while only the offsets in the z-direction, the so-called z-offsets, are left to be estimated (Steigenberger et al. 2016). And it should be noted that a remaining problem accompanied by introducing the absolute antenna PCCs is that the scale of the corresponding ITRF has to be fixed for the estimation (Schmid et al. 2005a) because of the correlation between them. As a result, these satellite antenna PCC models need to be updated once a new ITRF is released. We have seen switches from igs05.atx to igs08.atx (ITRF2008), then to igs14.atx (ITRF2014) and it will be updated continuously (Rebischung and Schmid 2016; Schmid et al. 2016; Dawidowicz 2018; Dach et al. 2019b), e.g., recently igs20.atx (ITRF2020) (https://igs.org/news/igs20/). To date, the latest disclosed manufacturer values of Galileo satellite antenna PCCs from the GSA and the ones of BDS from the CSNO have been added into igs20.atx. Typical values of satellite antenna PCC models in igs20.atx are given in Table 8, and only statistics of individual satellite antenna PCC w.r.t. block type are shown for brevity.

Table 8 Error budget of satellite antenna phase center biases

In short, the modernization of GNSS brings up some unexpected problems in modelling antenna PCCs both for satellite and receiver. This frequency/elevation/azimuth/radome/constellation-dependent bias multiplies the requirements for calibration. To date, the antenna PCC models are not available for all the frequencies of multi-GNSS, which limits the high-accuracy multi-frequency multi-GNSS application (Geng et al. 2021). Routine calibrations and antenna models are essential for benefiting from millimeter-level GNSS observables in PPP mode. Though most of the calibrations are based on relative positioning or network adjustment, they are applicable in GNSS PPP. At present, the PCC models in GNSS PPP mainly depend on the ones used in precise products, for example, the IGS ANTEX products (e.g., igs14.atx), hence, the PPP users need to again make sure the consistency of antenna PCC models with precise products.

In the meantime, it is worth noting that the use of the disclosed pre-launch Galileo satellite antenna calibrations makes it possible for GNSS to contribute to the scale determination of a reference frame in GGOS (Villiger et al. 2020). Besides, new observation techniques have shown possibilities for modelling PCCs, such as introducing LEO observations for modelling satellite antenna PCCs without fixing the scale of the corresponding TRF (Haines et al. 2015; Schmid et al. 2016). Together with more precise PCC models, the correlation between PCC, tropospheric delay, receiver clock, station height and other geodetic parameters can be reduced, and hence after the combination of GNSS with other space-geodetic techniques is much easier.

4.7 Phase Wind-Up

Navigation satellites typically transmit Right-Hand Circularly Polarized (RHCP) carrier waves to allow optimum reception as well as receiver antennas. Rotating either the transmitter or the receiver antenna around its boresight direction changes the relative orientation to the electrical field, and so does the measured phase angle (Teunissen and Montenbruck 2017). As a result, the variations in relative orientations between the transmitter and receiver antennas will introduce additional carrier phase errors by a GNSS receiver (Petovello et al. 2007), introducing “ranging” errors even though the true relative range distance between antennas has not changed. This effect is known as Phase Wind-Up (PWU) or phase wrap-up, notated as $\varphi_{{{\text{pw}}, {\text{r}}}}^{{\text{s}}}$ in carrier-phase observation equations while it does not exist in pseudo-range observables.

The concept of PWU in a transmit-receiver system was firstly introduced in 1970s (Marini 1971). After the emergence of GPS, attentions have been paid on the PWU effect in the navigation system. Especially for PPP, the effect of PWU is more significant when fixing IGS precise orbit and clock, which can reach up to one half of the wavelength (Kouba 2015), or more specifically, about 9–10 cm for L1/G1a/E1/B1, 12–13 cm for L2/G2a/E5a/B2 and 11–13 cm for L5/G3/E5b/B3, respectively.

For correcting the effect of PWU, a representative theoretical framework can be found in Wu et al. (1992) and Tetewsky and Mullen (1996). A general analytical expression for the PWU correction model was derived by Wu et al. (1992) and Rao et al. (2013)

$$\varphi_{{{\text{pw}}, {\text{r}}}}^{{\text{s}}} = 2n\pi + \delta \varphi ,$$

(19)

$$\delta \varphi = {\text{sign}}\left( \zeta \right) \cdot \arccos \left( {\frac{{{\varvec{D}}^{\prime } \cdot {\varvec{D}}}}{{\left\| {{\varvec{D}}^{\prime } } \right\| \cdot \left\| {\varvec{D}} \right\|}}} \right), {\text{with}} \zeta = \hat{{\varvec{k}}} \cdot \left( {{\varvec{D}}^{\prime } \times {\varvec{D}}} \right) ,$$

(20)

where δφ is the fractional part of PWU and n is an accumulator that ensures the continuity between consecutive observations. The two effective dipoles for receiver D and transmitter D^′ are computed with the unit vectors in SBFF $\left( {\hat{{\varvec{x}}}^{\prime } , \hat{{\varvec{y}}}^{\prime } , \hat{{\varvec{z}}}^{\prime } } \right)$ and ENU $\left( {\hat{x}, \hat{y}, \hat{z}} \right)$, as well as the unit vector of LOS k

$${\varvec{D}} = \hat{{\varvec{x}}} - \hat{\varvec{k}} \left( { \hat{\varvec{k}} \cdot \hat{\varvec{x}} } \right) + \hat{\varvec{k}} \times \hat{\varvec{y}},$$

(21)

$${\varvec{D}}^{\prime } = \hat{\varvec{x}}^{\prime } - \hat{\varvec{k}} \left( { \hat{\varvec{k}} \cdot \hat{\varvec{x}} } \right) - \hat{\varvec{k}} \times \hat{\varvec{y}}^{\prime } .$$

(22)

The geometric relationships are illustrated in Fig. 9, and the framework can be referred to Sect. 2. Though this PWU model has been widely accepted and applied in GNSS PPP, and the residual of the model was claimed to be roughly at millimeter-level in some previous studies (Seepersad and Bisnath 2014), details need to be further discussed here to see if there is any difference between multi-constellations.

Fig. 9

Phase wind-up transmitter/receiver geometry

One may notice that the PWU correction is directly affected by the attitude of both the satellite and the receiver according to the equations above. For GNSS satellite, attitude control is required to make sure that its transmitting antenna always points toward the Earth and that the solar panel axis is perpendicular to the direction of the Sun, hence, it constantly rotates along the antenna axis as it orbits the Earth. This typically slow rotation corresponds to the attitude behavior of the satellite, characterized as the nominal attitude, which can be precisely modelled by the yaw angle, but it can become a faster and more unpredictable rotation during shadow crossings (Petovello et al. 2007). In shadow crossings, the satellite moves into the Earth’s shadow, where the Sun is invisible and hence the solar sensor onboard is no longer able to control the yaw attitude (Bar-Sever 1996). In this case, the satellite starts yawing with maximum hardware yaw rates (e.g., 0.1–0.2°/s for GPS satellites) (Kouba 2009). The attitude behavior corresponding to the rotation during shadow crossing is no longer the same as the nominal one so that mismodelling effects may arise (Bar-Sever 1996; Dilssner et al. 2011; Dai et al. 2015; Strasser et al. 2021). Influences of yaw-attitude mismodelling during shadow crossing have been quantified by Papanikolaou and Melachroinos (2016) based on GNSS data over two draconic years, i.e. 2015 and 2016. Results show that an attitude error of 180°, which corresponds to a carrier-phase error of half a cycle, may be induced for GLONASS-M and GPS II-A satellites, while for GPS IIR and IIF, a carrier-phase error of 0.25 cycles dominates the distribution of differences. For Galileo and BDS, a similar conclusion with errors up to 0.5 cycles can be found, e.g., (Fan et al. 2016; Cao et al. 2018; Liu et al. 2022). Investigations on predicting yaw attitude do help to correct PWU effects during shadow crossings (Xia et al. 2019). As for rotations of the antenna located on the receiver side, the effects are different for various receiver platforms. For instance, the effect of PWU due to the rotation of receiving antenna on static or slowly rotating platforms, such as cars, trains, and ships, is limited as the PWU is identical for all the signals in this case (Cai et al. 2016b), therefore, this common error will be absorbed by an epoch-wise parameter estimated in GNSS PPP, e.g., receiver clock. However, it is not applicable for fast rotating platforms like a sounding rocket and a guided missile (García-Fernández et al. 2008), and may degrade the performance in kinematic PPP mode (Le and Tiberius 2006).

Another thing that needs to be kept in mind is that Left-Hand Circularly Polarized (LHCP) component, caused by the Non-Line-Of-Sight (NLOS) signal reflected from surfaces at normal incidence, typically surrounding the antenna (Jiang and Groves 2014; Morton et al. 2020), also exists in the GNSS signals in reality. However, they are quite small when compared to the RHCP component of GNSS signal and are neglected in most applications (Beyerle 2009). Concerning that a pure RHCP transmitter signal is assumed by Wu et al. (1992) to give an approximation of PWU (hereinafter called PWU-RH for brevity), Beyerle (2009) justified it well with a more general expression (hereinafter called PWU-RHLH for brevity), including both RHCP and LHCP. It is important to note that for arbitrary orientations the expected deviations between PWU-RH and PWU-RHLH are in the sub-millimeter range, but in most ground-based applications, these two models (PWU-RH and PWU-RHLH) are equivalent considering that antenna bore-sight directions pointing towards the zenith at a static receiver. Taking both RHCP and LHCP into consideration, Rife et al. (2021) introduced equations to account for both geometric rotation and antenna phase pattern calibration (also known as antenna PCC in GNSS) based on Beyerle (2009), and they also pointed out that correctly computing phase wind-up requires to consider geometric rotation and antenna phase pattern together since they are not all equivalent w.r.t. the generation of PWU.

In summary, the well-known PWU correction model proposed by Wu et al. (1992) is sufficient for millimeter-level applications on a static or low-rotating platform, and it is commonly used in GNSS PPP nowadays. Nevertheless, the yaw attitude in eclipse season is still troublesome and needs to be investigated further for each constellation, which is the same as that described in Sect. 4.1 for satellite orbit determination. A PWU model that takes both geometric rotation and antenna phase pattern into account should be applied carefully to achieve better performance for a fast-rotating platform.

4.8 Multipath Effect

The GNSS signals may be affected by the local environment in various ways, like fading due to shadowing along the signal path, multipath, ambient noise, and interference, among which multipath has the most complicated and significant impact (Fig. 10). The multipath effect (notated as ${\text{MP}}_{{{\text{f}},{\text{r}}}}^{{{\text{sys}}}}$ and ${\text{MP}}_{{{\text{sig}},{\text{r}}}}^{{{\text{sys}}}}$ in Eqs. (4) and (5)) can reach up to 1/4 of wavelength for the carrier phase and 1/2 of the ranging code chip for the pseudo-range in the most severe conditions, that is, 4.76 cm for the GPS L1 carrier phase and 150 m for the GPS C/A code, respectively (Groves and Jiang 2013; Lu et al. 2021). In general, the phase observable suffers relatively small effects ranging from millimeters to centimeters as it depends on the environment surrounding the antenna. This site-dependent effect is difficult to reduce and remains to be one of the major limitations in positioning accuracy for GNSS PPP. Besides, resolution degradation and tracking errors, even a loss in signal could also be caused by the multipath (Genrich and Bock 1992). Therefore, one needs to be careful to deal with the multipath effect in the context of a given environment and application, especially in high-accuracy applications.

Fig. 10

The diagram of multipath at a GNSS receiver

The multipath effect actually refers to the total interference impacts caused by NLOS signals from the surrounding reflectors of a receiver antenna. As the reflected NLOS signals propagate longer geometry distances and are either weaken or distorted by the reflector (Lau and Cross 2007), they will be misaligned with the direct signals at the moment of reception. The misalignment induces a “ranging” error both on the code and the phase observations together with an attenuation of the received signals (Hofmann-Wellenhof et al. 2008). Meanwhile, most NLOS signals either have a LHCP or a mixed polarization (Zidan et al. 2020) due to the reflection, which can also induce phase wind-up error as we introduced in the last section. According to Schmid et al. (2005a), the multipath can be simply divided into two parts, one is the multipath caused by the near field of the antenna, such as marker, ground plane, and radome, while the other one is the multipath caused by the far-field environment. However, it should be kept in mind that this categorization is utilized only for illustration, since in fact they mingle with each other and cannot be well separated.

As far as we know, there is still no effective solution for eliminating the entire multipath effect in PPP mode; however, several schemes for mitigating or reducing its effect can be adopted in general. Concerning the GNSS antenna itself, either an advanced antenna design or suppressing reflections at the near field intentionally, can help reduce the multipath effect, such as a high-gain, directional antenna with smaller multipath effects, a choke ring antenna design, a pinwheel antenna design and an antenna with a large ground plane (Klobuchar 1996; Tranquilla et al. 1994; Kunysz 2000). Besides, considering the polarization diversity of signals received at the GNSS antenna (i.e., LHCP NLOS signals and RHCP LOS signals), especially at low incidence angles, an improvement can be achieved by employing an LHCP antenna to receive reflected signals and incorporating with the RHCP antenna as additional information for multipath mitigation (Dovis et al. 2004; Yang and Porter 2005). Despite that this method has been validated by several simulations, the complicated mixture of polarization of the reflected signals and the effects of antenna separation imply that it is not accurate enough and can only approximate the multipath effect (McGraw et al. 2020). To avoid the drawback of separated antennas, a single dual-polarized LHCP/RHCP antenna was used (Manandhar et al. 2004). Good performances on mitigating multipath effect by distinguishing NLOS signals from direct signals were shown both in simulation and in real GNSS datasets, e.g., (Brenneman et al. 2007; Izadpanah et al. 2008; Groves et al. 2010; Jiang and Groves 2014). But the requirement for calibration of such a dual-polarization antenna and knowledge of antenna orientation restrict its applications (Jiang and Groves 2014).

Advanced signal processing techniques in GNSS receivers were also investigated to resist multipath. Before going into details of these advancements, to have a better understanding of how multipath affects the received signal, let us give an overview of the signal tracking in a GNSS receiver first. The GNSS signal is periodic and can be replicated by the GNSS receiver. After the signal conditioning and acquisition are implemented to the GNSS signal received at the antenna, signal tracking follows in the receiver to make an accurate and continuous estimate of code delay and carrier phase. Typically, correlation-based code and carrier tracking structures are applied by aligning a locally generated replica of the signal with the received signal, in essence, to find the maximum correlation between them. This alignment is implemented by a feedback loop based on a feedback estimator. The most commonly adopted feedback delay estimator is called the Early-Minus-Late (EML) Delay Lock Loop (DLL) technique for code and EML Phase Lock Loop (PLL) technique for the carrier, respectively. For example, in a classical EML DLL procedure, the correlation between the local replica signal and the received signal is performed by an element called a correlator. Usually, two correlators (early correlator and late correlator) spaced at one chip from each other are used to form a discriminator function. Taking the output of the correlators as input, the DLL drives the output of the discriminator, i.e., the error of code delay, to zero in order to accurately track the signal. Until then, zero crossing of the discriminator determines the code delay of the received signal. The PLL procedure for estimating the carrier phase is similar to the DLL introduced above, therefore, we will not repeat it here. For more interest, we refer to Misra and Enge (2006) for details of the signal processing in a GNSS receiver. Now, let us consider a simplified case where the signal is BPSK modulated with infinite bandwidth. In this case, without multipath, the correlation function has a main correlation peak that is symmetrical about a lag of zero (see Fig. 11a). Recalling that the reflected NLOS signal has an additional propagation time delay and attenuated amplitude when compared to the direct signal, these multipath interferences composite and distort the shape of the correlation function as shown in Fig. 11b, c, and lead to tracking error (actually a shift in the crossing point of the discriminator) that consequently yields the pseudo-range measurements error, as well as the carrier phase measurement error (Teunissen and Montenbruck 2017).

Fig. 11

Diagram of the correlation function for a nominal signal (i.e., a direct signal without multipath), b a single in-phase (0° phase difference w.r.t. direct signal), delayed and attenuated multipath signal and c a combination of direct and the multipath signal (nominal signal plus multipath). Note that the separation of direct and multipath signals in (b) is not available in reality, which is used here only for illustration

As the classical EML fails to cope with the multipath effect, the narrow correlator EML technique, or in short called nEML, was developed by narrowing the spacing between the early and late correlator (Van Dierendonck et al. 1992; Mcgraw and Brassch 1999). This nEML technique was inspired by the fact that reducing the correlator spacing to a small fraction of one chip results in a reduction of tracking errors for a sufficient signal bandwidth (Van Dierendonck et al. 1992; Braasch 1997; Ray et al. 2001). However, the choice of correlator spacing depends on the receiver architecture, that is, the front-end bandwidth and the associated sampling frequency (Betz and Kolodziejski 2000). Alternatively, one can make use of the blanks between every two adjacent code chip transitions of the received signal to achieve a narrower correlator spacing (Mcgraw and Brassch 1999).

In order to further mitigate the impact of multipath, a narrow discriminator function is introduced, widely known as Double Delta Correlator (DDC) (Garin et al. 1996; Rouabah et al. 2011), and variants like Pulse Aperture Correlator (PAC) (Townsend and Fenton 1994), Strobe Correlator (SC) (Veitsel et al. 1998) and High Resolution Correlator (HRC) (Mcgraw and Brassch 1999), etc. Based on the classical EML technique, the DDC technique combines two early and two late correlators to construct a discriminator function as differencing of two EML-like discriminators spaced at different chip length. In this way, it offers better multipath rejection in medium-to-long delay (typically, more than 0.1 chip) multipath under a good Carrier-to-Noise density ratio (Bhuiyan and Lohan 2012), while it comes at the cost of slightly increased noise when compared to the classic EML technique (McGraw et al. 2020). Since all the techniques mentioned above do not claim any optimization, to obtain optimal multipath mitigations, several parameter-based techniques were proposed, e.g., the Multipath Estimating Delay-Locked Loop (MEDLL) (Van Nee 1992), the Modified Rake DLL (MRDLL) (Sun et al. 2012) technique, and the Multiple Gate Delay (MGD) correlator (Bello and Fante 2005). The main idea behind them is to model the signal or to estimate key parameters in forming a discriminator (e.g., the number of correlators), by using the maximum likelihood estimation method. Albeit these parameter-based techniques outperform nEML, common problems exist, such as significant hardware cost and model fidelity (i.e., the performance can be poor when the signal is under-/over-estimated). Some of them are even sensitive to the selected parameters (Hurskainen et al. 2008).

It should be noted that all these above-mentioned signal processing techniques are effective against medium-to-long delay multipath but are ineffective against the multipath signals arriving with a short delay (i.e., less than 0.1 chip). In fact, short- and medium-delay multipath are predominant in many environments (Teunissen and Montenbruck 2017). The A-Posteriori Multipath Estimation (APME) is therefore proposed to cope with the short-delay multipath (Sleewaegen and Boon 2001), based on the property of the signal amplitude measurements that they are highly correlated with the multipath error in code phase measurement, especially for short-delay multipath (Sleewaegen 1997). Improvement of short-delay multipath rejection up to 50% w.r.t. the nEML and the SC in high signal-to-multipath power ratio case was reported, see (Sleewaegen and Boon 2001), but deteriorations were introduced for medium-to-long delay multipath. Similarly, a slope-based multipath estimation technique was also developed to mitigate the short-delay, and the simulation result shows that it has the best overall performance when compared to the nEML and HRC in short-delay multipath cases (Bhuiyan et al. 2010). Until now, one may notice that the above techniques implemented in the receiver all focus on the code multipath mitigation, but actually, the carrier phase multipath mitigation has been studied with the same methods as well.

Another commonly adopted method for mitigating multipath is analyzing the time evolution of GNSS measurements. In the post-processing mode, one can mitigate the multipath effect by taking advantage of the fact that the periodic repeatability of each GNSS satellite induces a periodic variation in the multipath over a sidereal period at a stationary station. This sidereal period varies by constellations, e.g., every sidereal day for GPS, every eight days for GLONASS, every ten days for Galileo and every seven days for BDS MEO (Ye et al. 2015; Dong et al. 2016). As the multipath effect depends on both the characteristics of the surrounding environment and on the momentary geometry of the GNSS satellites, the multipath conditions are the same and its behaviors will repeat themselves over this period, provided the surrounding remains unchanged (Georgiadou and Kleusberg 1988; Håkansson 2020). Thanks to this characteristic of multipath, the Sidereal Filtering (SF) method was introduced to mitigate the multipath effect in GNSS PPP (Genrich and Bock 1992), which may be applied both in position domain (Takasu 2006; Hung and Rau 2013) and observation domain (Atkins and Ziebart 2016, 2017; Zheng et al. 2019b; Yang et al. 2020a). Instead of requiring an exact orbit repeat period for filtering (Cai et al. 2016a; Dong et al. 2016), the Multipath Hemispherical Map (MHM) model was introduced to project the multipath onto a hemisphere grid w.r.t. the elevation angle and azimuth angle of the incoming signal (Cohen and Parkinson 1991; Fuhrmann et al. 2015). Thereafter, the Modified MHM (M-MHM) model (Zheng et al. 2019a) and the Trend-surface MHM (T-MHM) model (Wang et al. 2019c) were proposed in order to improve the resolution of the grid and to better fit the spatial variation inside the grid. In most cases, a complete MHM model takes months or years of observations to obtain a good coverage of the hemisphere and to involve the characteristics of the multipath effect over both long- and short-term. Nevertheless, this technique is preferred in space-craft applications since the environment surrounding the antenna may be indefinitely static (i.e., almost always the same, without change) (McGraw et al. 2020). It should be noted that although these methods were firstly proposed based on the baseline measurements that usually appear in relative positioning, they have been now extended to GNSS PPP. Seepersad and Bisnath (2015) and Guo et al. (2021a) have shown the potency of an accurate multipath model on improving the accuracy and reducing the convergence time (i.e., time for positioning error being less than a pre-defined value) in GNSS PPP. This has been demonstrated in GPS PPP with MHM (Zheng et al. 2023), BDS-3 PPP with T-MHM model (Lu et al. 2022) and multi-GNSS PPP with SF/M-MHM models (Zheng et al. 2019a, b).

In fact, there is no essential difference in multipath effect between the four GNSS constellations except for discrepancies related to signal frequency and structure. Even with the two abovementioned post-processing methods for multipath mitigation, i.e., filtering and modelling, improvements of only about 40% can be found in multipath effect mitigation, and of course, the corresponding positioning accuracy is likewise improved. A brief summary of the error budget for the multipath errors can be found in Table 9 But there is still no consensus on mitigating multipath effects in GNSS PPP, and usually, they are neglected in the data processing. Therefore, it remains a nuisance in high-accuracy applications. More efforts are still needed to eliminate or reduce the predominant station-dependent multipath errors. As computational capabilities that are available to GNSS receivers continue to improve, more possibilities can be found with signal processing in the receiver. New techniques like Three-Dimensional (3D) mapping and neural networks (Suzuki and Kubo 2013; Adjrad and Groves 2018), or additional information from other datasets, e.g., aiding sensors, are also expected to help mitigate the multipath effects (McGraw et al. 2020).

Table 9 Error budget of phase wind-up and multipath effect

4.9 Inter-System and Inter-frequency Biases

When integrating observables from multi-GNSS into a positioning solution, the well-known Inter-System Biases (ISBs) need to be introduced for interoperability due to the different timescales, reference frames and signal structures employed by each individual GNSS system (Zhang et al. 2021c) (See Table 1). The ISBs have been demonstrated to be relevant to satellites, receiver types, frequency and structure of signals, which exist in both code and phase observables. If these biases are not calibrated properly when making use of observations from all systems, a poor result for PPP, maybe even worse than that of a single GNSS system in some cases, will be obtained (Jiang et al. 2017a). Since we aim at millimeter-level applications, the ISBs in carrier-phase observations are the primary topic in this section. Although the ISBs in code observations are also significant, an excellent review of both can be found in Håkansson et al. (2017) and we will not go into details here. Similarly, we will only focus on the carrier-phase observations for reviewing Inter-Frequency Bias (IFB) later, which is a particularity of GLONASS.

There are actually three components in the so-called ISBs, differences in geodetic references and timing systems, and biases induced by hardware in both satellites and receivers (Tian 2016). As we will discuss in the following that all three terms are commonly lumped together in the observation equation, here we just use the sum of them, i.e., the ISB, for the sake of brevity. The first two terms in ISB are the time and reference frame differences between systems. As we know, measurements from each GNSS constellation refer to satellite clock offsets with respect to their own time scale, and system time differences between them may vary from fractional seconds to several integral seconds (Dong et al. 2018). Systematic and system-specific errors will also be introduced if offsets between geodetic reference frames are not calibrated. Therefore, calibration of time scales and transformation between geodetic references need to be applied by multi-system users (Torre and Caporali 2015). Fortunately, one need not consider these two components any longer when using the precise clock products provided by MGEX because they already have been referenced to the GPS time scale conventionally, as well to a unify reference frame (e.g., the IGS realization of ITRS2014, IGb14 nowadays) (El-Mowafy et al. 2016; Steigenberger and Montenbruck 2020). All the adjustments are implemented in the integrated satellite orbit and clock determination.

The third term in ISB is the set of biases introduced by differences in the hardware of equipment. Due to the imperfection and physical limitations in hardware manufacturing, the GNSS signals suffer from digital delays in a sequence of signal tracking in the receiver, such as delays in the signal generator, signal distortion and correlator (Hegarty et al. 2005), as well as the effect of antenna, amplifier and so on (Phelts 2007). A similar delay at different frequencies can also be found at the satellite end of each system. These additional delays are called hardware biases, which have been shown by many studies (Odijk and Teunissen 2013; Aggrey and Bisnath 2014; Torre and Caporali 2015; Håkansson 2017, 2020; Zhang et al. 2021c) that they depend not only on satellite/receiver type, but also on the satellite-receiver combination. Their effects vary with carrier frequencies and signal structures, and even firmware can also make a difference. Although many manufacturers have been providing multi-GNSS receivers for many years, hardware biases between constellations are not calibrated in most geodetic receivers and antennas (Chen et al. 2015).

Nevertheless, the assumption that receiver hardware biases are identical for a certain frequency transmitted by satellites from the same constellation is generally adopted in PPP, which has been confirmed by the fact that in relative positioning the phase ambiguity can be fixed as integers after being double-differentiated (Håkansson et al. 2017). As can be seen from the observation equations, these two hardware biases ${\text{b}}_{\text{f,} \, {\text{r}}}^{\text{sys}}$ and ${\text{b}}_{\text{f}}^{\text{s}}$ are highly correlated with other parameters, e.g., phase ambiguity and receiver clock. They are inseparable and therefore it is impossible to estimate all the parameters unambiguously and simultaneously, otherwise, it would lead to an under-determined problem and rank deficiencies are inevitable. In practice, either lumping these parameters together or applying assumptions, like the a priori or some constraining information, is adopted in multi-GNSS PPP (Sirola et al. 2020). For example, the two hardware biases ${\text{b}}_{\text{f,} \, {\text{r}}}^{\text{sys}}$ and ${\text{b}}_{\text{f}}^{\text{s}}$ are usually combined together as one ISB term in the observation equation. Here, we give ${\text{b}}_{\text{f,} \, {\text{r}}}^{\text{sys}}$ and ${\text{b}}_{\text{f}}^{\text{s}}$ explicitly to distinguish their origins.

The phase ISBs have been shown to be stable over a short time period (typically, shorter than one day) (Odijk and Teunissen 2013; Paziewski and Wielgosz 2015; Zhang et al. 2020c), but it does not mean that they are constants. In fact, a slight intra-day variation of ISBs related to the receiver type has been illustrated by many studies (Gioia et al. 2015; Zhang et al. 2021c), while the daily and weekly repeatability is relatively stable. STDs of less than 0.6 ns were reported by Zhang et al. (2020c) for inter-day ISBs of four GNSSs based on almost one month of data from several MGEX stations, among which the ISB between Galileo and GPS was shown to be the most stable one with a STD of about 0.37 ns. A more thorough analysis given by Hong et al. (2019) indicates good consistency between the weekly stability and daily stability of ISBs. A discontinuity between adjacent days was also found in the ISBs time series (Dach et al. 2010; Hong et al. 2019; Zhang et al. 2021c), which can reach up to tens of nanoseconds. Since these discontinuities were proved to be irrelevant with receiver type and occur at the same time but with different magnitudes when applying multi-system precise products, they are ascribed to the different satellite clock datums of products from several MGEX ACs in different days (Liu et al. 2017a; Wang et al. 2019b).

According to the characteristics of ISBs, two methods are commonly applied to model their effects. One is introducing independent receiver clocks for each GNSS constellation, that is, observations from each GNSS constellation are processed separately as an individual system. The other one is to combine all the GNSS observations by estimating only one receiver clock and adding extra parameters to involve the ISBs for each GNSS constellation. The last, but not often used method, is to ignore ISBs as they can be absorbed in the clock bias and ambiguity parameters, which is applicable in the case where only a float ambiguity is required. It has been demonstrated that the former two methods are equivalent both in theory and numerical verification (Jiang 2019). In order to reduce the number of parameters and make full use of multi-GNSS constellations redundancy, the method with one receiver clock and ISB parameters are widely adopted (Angrisano et al. 2013; Cai et al. 2015; Zhang et al. 2016b; Pan et al. 2017a).

Based on the stability of short-term ISB, statistical modelling of ISB was also investigated. A Kalman filter method was proposed by Zhang et al. (2016a) to model and predict ISB in PPP mode by using IF combination, while a short-term station-dependent GPS/BDS ISB model combining a quadratic function and a periodic function was given by Jiang et al. (2017a) using undifferenced observations. Both results, based on a time period of one week, show that the positioning accuracy was improved by more than 10% in the east direction and the convergence time (with a threshold of 10 cm) was shortened by about 19.6% and 16.1% in the north direction and in the east direction, respectively. However, the statistical modelling of ISBs is considered to be more complicated than estimating ISB parameters directly as they are receiver-type dependent.

Recalling the daily variation of ISB, a parameterized estimation strategy of ISB was also investigated to better describe it. Initially, one constant ISB value over the interval of processing, e.g., one day, was applied in most IGS ACs, but soon several studies indicated that only one constant ISB per day was not sufficient because the results derived by introducing independent receiver clocks for each constellation outperform this “too basic” approach (Dach et al. 2010). This is easy to understand since a single constant is too rough for representing the daily ISB, especially for some types of receivers, which have a rather larger daily variation. Consequently, better modellings were proposed and investigated, mainly referring to the stochastic model of ISB parameters, including piece-wise constant, piece-linear, random walk, and white noise. Although ISB is estimated as a time constant or piecewise constant for every 30 min in most GNSS PPP currently, Zhang et al. (2021c) showed the effects of applying different stochastic models for ISB estimation on time and frequency transfer by multi-GNSS: random constant process and random walk process performs better than white noise process in terms of frequency stability at different time intervals. Influences on GNSS PPP were also analyzed with multi-GNSS precise products from several MGEX ACs, e.g., (Hong et al. 2019; Zhou et al. 2019). It is suggested to keep consistency with the strategies used by the providers of precise products (e.g., precise orbit, clock bias), where the ISBs are preferred to be estimated as constant over different intervals of processing, but in the case of the strategy choice at the provider is not known, random walk or white noise process is recommended to achieve more reliable positioning results. In addition, several studies verified that the previous estimation of ISBs can be added as pseudo-measurements to provide an a priori, or more precisely, an additional constraint condition (Cai and Gao 2009; Gioia et al. 2015; Dong et al. 2018). The a priori values obtained either from a model or pseudo-measurement do help to improve the accuracy and availability of positioning solutions, as well as to shorten the convergence time. For example, by using the a priori ISBs, one can fully exploit the multi-GNSS opportunity as only four mixed visible satellites are required to obtain a solution in this case, on the other hand, an improvement of up to 63% and 21% for 3D position accuracy and availability, respectively, can be achieved under the extreme condition where GNSS signals are blocked and strongly degraded without impairing performance in the normal conditions of operation (Dong et al. 2018).

Except for all the ISBs we discussed above, there is another special bias particular to GLONASS, which is known as IFB. As we mentioned in Sect. 4.6, unlike other GNSS, GLONASS employs FDMA rather than CDMA to distinguish the signals coming from individual satellites, for instance, the GLONASS G1 and G2 bands are divided into 14 sub-bands (the frequency numbers correspond from -7 to 6) and each satellite transmits in only one of them (Sleewaegen et al. 2012b). Signals of different frequencies suffer from different delays in the receiver hardware as they are tracked and processed by individual channels. As a result, IFBs are induced in both code and phase observations of GLONASS. Considering that code IFBs have different characteristics and that their accuracy is relatively lower, we here mainly focus on the phase IFBs for high-accuracy applications.

Although CDMA signals have been used in recently launched GLONASS satellites, the FDMA signals will continue to provide services for a long time to come (Tian 2020). As the magnitude of IFBs generally differs by millimeters among the same types of receivers or between G1 and G2, and by centimeters between different types of receivers, it has significant impacts on the PPP convergence period, integer ambiguity fixing and overall positioning accuracy with GLONASS observables (Aggrey and Bisnath 2014). In order to calibrate or eliminate IFBs, the characteristics of IFBs were analyzed first. A linear correlation between IFBs and the frequency numbers (corresponding from − 7 to 6) has been found and confirmed, e.g., (Pratt et al. 1997; Wanninger and Wallstab-Freitag 2007; Wanninger 2012). But it was not until 2012 that Sleewaegen et al. (2012a) revealed the origin of the IFBs, which is essentially the misalignment between phase and code observations, or called Differential Code-Phase Biases (DCPBs). This research also pointed out linear IFBs that arise in the analog radio-frequency hardware and the Digital Signal Processing (DSP) of the receiver, among which the DSP-induced biases are the major contributor while the RF-induced ones within sub-millimeters can be neglected. It indicates that IFBs vary with receiver types but they are stable enough to be directly derived from the receiver manufacturer and then be calibrated in advance. However, as elucidated by Wanninger (2012), calibrations were taken care by the manufacturers when there were few types of geodetic GPS/GLONASS receivers, and subsequently less attention was paid when more and more receiver types from different manufacturers were involved since 2006. These uncalibrated IFBs for different receiver types remain a challenge. Wanninger (2012) reported that the differences among 9 manufacturers can reach up to 5 cm or more for adjacent frequencies, that is, up to 73 cm for the entire G1 or G2 frequency bands. A similar result for 38 receiver types was obtained by Jiang et al. (2017b) based on long baseline studies. Besides, strong correlations between IFBs, firmware versions, and antenna types with the same receiver type were also illustrated in Aggrey and Bisnath (2014). Therefore, a station-specific correction model is preferred, which means a huge and continuous work burden. Although the IFBs have been recognized over the past years, Geng et al. (2017) argued that a rigorous DCPB model should be implemented rather than the IFB model, as the IFB is only an approximate deviation from DCPB which would lead to errors up to several millimeters across frequency channels. In analogy to ISBs, the IFBs induce no effects on PPP solutions with float ambiguity since they could be mixed into the undifferenced ambiguity, but lead to complications for PPP solutions requiring integer ambiguity resolution. Two methods are widely adopted to cope with the IFBs. One is calibrating with a linear model of frequency that is generated in advance, either based on zero or short baseline (Liu et al. 2017d). The other one and certainly a better one is correction by using third-party calibration, which is provided by several services like IGS (Schaer 2016; Sirola et al. 2020).

In a word, the ISBs and IFBs are of great importance when combing multi-GNSS observations into a PPP solution that requires integer ambiguity resolution. But for PPP solutions with float ambiguity, they have no explicit impact. Nevertheless, they are still worthy to be considered in the integer ambiguity resolution of PPP (see the next section). The error budget of the ISBs and IFBs is listed in Table 10. Since these biases can be easily absorbed into other parameters and the absolute values are impossible to obtain in many cases, here we just give their magnitudes as an indicator. In GNSS PPP, the phase ISBs can be estimated as additional parameters in the multi-GNSS data processing, and phase IFBs can be calibrated by pre-calibrated linear models. Corrections from a third party, such as Bias-Solution INdependent EXchange (Bias-SINEX) released by the IGS Bias working group and the Centre National d'Etudes Spatiales (CNES) (Schaer 2016; Liu et al. 2021), are also available for correcting IFBs and ISBs, but it should be noted that users need to follow the same parameterization and assumptions on biases as employed by the provider (Håkansson et al. 2017). With an increasing number of receivers and antenna hardware types, the error modelling for the code and carrier-phase biases is becoming more complex. It is strongly recommended that receiver manufacturers at least calibrate the GLONASS code and carrier phase IFBs to be identical for receivers of the same type (Liu et al. 2017c), and continuous efforts are also needed to put forward through service providers like station-specific calibrations (Geng et al. 2017; Villiger and Dach 2021).

Table 10 Error budget of inter-system bias and inter-frequency bias for phase observables

4.10 Integer Ambiguity Resolution

The high-precision carrier phase measurement comes at the cost of unknown integer ambiguity in itself and resolution of the integer ambiguity is a key to fast and high-precision applications for GNSS PPP (Collins et al. 2008; Ge et al. 2008). Since a receiver can only tell the fractional part of the carrier phase once the signal is locked, it cannot make out how many cycles are there between the receiver and the satellite, that is, the carrier phase ambiguity. Therefore, the precise carrier phase observables cannot be used directly as the pseudo-range ones unless the Integer Ambiguity Resolution (IAR) is done successfully. To a large extent, that is also why PPP usually takes a relatively long observation time span (tens of minutes) to achieve high precision (Morton et al. 2020). This long convergence time inhibits high-precision applications with a single station in PPP mode (Li et al. 2022b). A shorter convergence time and higher positioning accuracy (especially in the East component) can be expected if the IAR is achieved in a short amount of time (Geng et al. 2010). Considerable efforts have been put into this topic, good overviews can be found in many literature and textbooks (Hofmann-Wellenhof 2001; Teunissen and Verhagen 2009; Parkinson and Jr 2013; Leick et al. 2015; Teunissen and Montenbruck 2017).

Recalling the definition of the integer ambiguity parameter ${\text{N}}_{{{\text{f}},{\text{r}}}}^{{\text{s}}}$ we give in the basic observation equation Eq. (4), this ambiguity cannot be resolved to an integer value in a conventional PPP model as well (Shi and Gao 2014). This is because the estimated undifferenced ambiguities are biased by atmosphere delays and hardware biases in both receiver and satellite, e.g., ${\text{b}}_{{{\text{f}},{\text{r}}}}^{{{\text{sys}}}}$ and ${\text{b}}_{\text{f}}^{\text{s}}$, and hence their integer properties are lost (Geng et al. 2010). Strictly speaking, undifferenced IAR using the conventional PPP model is not feasible unless the atmospheric delays and all the hardware biases are corrected or calibrated properly.

To solve this issue, a new technique, known as PPP–RTK, has been proposed aiming at fast IAR in PPP mode (Wübbena et al. 2005). As a synthesis of the positive characteristics of both PPP and RTK concepts, the PPP–RTK technique has been developed over the past two decades (Wübbena et al. 2005; Collins et al. 2008; Ge et al. 2008; Laurichesse et al. 2009; Teunissen et al. 2010; Geng et al. 2011, 2012; Khodabandeh and Teunissen 2016; Odijk et al. 2016; Zhang et al. 2019a; Ma et al. 2020; Li et al. 2022d). In general, there are two major components in PPP–RTK, i.e., the server end and the user end. Based on observations of a GNSS network, precise satellite orbit/clock, information of hardware biases and atmospheric delays are derived at the server end, and then issued to the user end (Li et al. 2022b). From the point view of PPP, the goal of PPP–RTK is to augment PPP estimations at the user end with corrections/products from the server end, in such a way that the integer properties of ambiguities can be recovered to obtain a fast IAR (Teunissen and Khodabandeh 2015; European GNSS Agency 2019; Li et al. 2022b). More details about PPP–RTK can be found in literature like (Teunissen and Khodabandeh 2015; Li et al. 2022b), here we are mainly interested in the methods of ambiguity-resolved PPP in PPP–RTK, namely PPP–AR for brevity.

As we mentioned in the last section, rank deficiencies in the PPP model exist between the satellite/receiver clock, satellite/receiver hardware bias, ionospheric delays and ambiguities, which implies that one cannot estimate all the parameters unambiguously and simultaneously. That’s the same problem underlying the construction of PPP–RTK models (Odijk et al. 2016; Zhang et al. 2019a). A common practical method to solve the rank-deficient system is to apply the S-system theory (Baarda 1981; Teunissen 1985; Xu 1997): a minimum set of parameters to be estimated are chosen as a datum, also known as the S-basis, and then a full-rank of observation equations are formulated with estimable parameters formed by the so-called S-transformation (i.e., linear combinations of the S-basis). Since the choice of S-basis is not unique, several PPP–RTK models have been proposed and formulated over the years (Odijk 2002; Collins et al. 2008; Ge et al. 2008; Geng et al. 2009; Laurichesse et al. 2009; Teunissen et al. 2010; Zhang et al. 2011; Odijk et al. 2016). A comprehensive review of PPP–RTK models within the framework of the S-basis was given by Teunissen and Khodabandeh (2015), we here give a brief overview.

According to the methods of handling ionospheric delays, PPP–RTK models can be generally divided into three categories: ionosphere-float, ionosphere-free, and ionosphere-corrected models. In ionosphere-float models, the ionospheric delays are estimated as parameters, which can be applied to both between-satellite Single-Differenced (SD) observations and undifferenced observations. In the former case, the receiver-related code/phase biases are cancelled by differencing. Assuming m satellites are observed by n receivers in the network, this PPP–RTK model at the server end generally takes the form as (Teunissen and Khodabandeh 2015)

$$\begin{gathered} \Phi_{{f,{\text{u}}}}^{{{\text{sp}}}} = \rho_{{\text{u}}}^{sp} + d_{{{\text{trop}},{\text{u}}}}^{ sp} {-} c{\text{d}}t^{sp} {-} \mu_{f} l_{{\text{u}}}^{ sp} + \lambda_{f} N_{{f,{\text{u}}}}^{ sp} {-} \delta_{f}^{sp} \hfill \\ P_{{{\text{sig}},{\text{u}}}}^{sp} = \rho_{{\text{u}}}^{sp} + d_{{{\text{trop}},{\text{u}}}}^{ sp} {-} c{\text{d}}t^{sp} + \mu_{{{\text{sig}}}} l_{{\text{u}}}^{ sp} {-} \gamma_{{{\text{sig}}}}^{sp} , \hfill \\ \end{gathered}$$

(23)

where the between-satellite SD combinations are symbolized through (.)^sp = (.)^p − (.)^s with satellite s and satellite p (s, p = 1…m; s ≠ p), and a similar notation will be used for between-receiver differences, i.e., (.)_ru = (.)_u − (.)_r with user receiver u and reference receiver r hence after. Other symbol notations can be found as the same in Eqs. (4) and (5). Note that, for illustration, we use the satellite code/phase bias in meter (i.e., $\delta_{f}^{{\text{s}}} = {\text{cb}}_{f}^{{\text{s}}}$ and $\gamma_{f}^{{\text{s}}} = {\text{cB}}_{{{\text{sig}}}}^{{\text{s}}}$) and the ionospheric delay is given by the multiplication of the ionospheric delay $l_{{\text{u}}}^{{\text{ s}}}$ experienced on the first frequency f₁ and the frequency-dependent coefficients defined as the ratio μ_f = (f/ f₁)². For simplicity, we only consider a single GNSS system with dual-frequency here. Then, the SD satellite code bias $\gamma_{{{\text{sig}}}}^{sp}$ is usually selected as one of the S-basis, since it can be decomposed into the combination of the geometry-free $\gamma_{{{\text{IF}}}}^{sp}$ and ionosphere-free $\gamma_{{{\text{GF}}}}^{sp}$ components as

$$\gamma_{{{\text{sig}}}}^{sp} = \left( {\frac{{\mu_{2} }}{{\mu_{2} - \mu_{1} }}\gamma_{1}^{sp} - \frac{{\mu_{1} }}{{\mu_{2} - \mu_{1} }}\gamma_{2}^{sp} } \right) + \mu_{{{\text{sig}}}} \cdot \frac{1 }{{\mu_{2} - \mu_{1} }}\left( {\gamma_{2}^{sp} - \gamma_{1}^{sp} } \right) = \gamma_{{{\text{IF}}}}^{sp} + \mu_{sig} \gamma_{{{\text{GF}}}}^{sp} ,\;\;\;{\text{for}}\;\;{\text{sig }} = \, 1, \, 2.$$

(24)

In this way, it “disappears” in Eq. (23) after being “lumped” into clock parameter and ionospheric delay due to the same underlying coefficient 1 and ${\upmu }_{{{\text{sig}}}}$, respectively (see following Eqs. 25–26) (Zhang et al. 2019a). And with additional two S-basis vectors, i.e., the fixed SD vector of parameters [$\rho_{{\text{r}}}^{sp}$, $d_{{{\text{trop}}, {\text{r}}}}^{ sp}$] and SD ambiguities $N_{{f, {\text{r}}}}^{ sp}$ at a selected reference station r, a full-rank model can be formed by means of S-transformation as

$$\begin{gathered} \Phi_{{f,{\text{u}}}}^{sp} = \tilde{\rho }_{{{\text{ru}}}}^{sp} + \tilde{d}_{{{\text{trop}},{\text{ru}}}}^{ sp} {-} c\widetilde{{{\text{d}}t}}^{sp} {-} \mu_{f} \tilde{l}_{{\text{u}}}^{ sp} + \lambda_{f} \tilde{N}_{{f,{\text{ru}}}}^{ sp} {-} \tilde{\delta }_{f}^{sp} \hfill \\ P_{{\text{sig,u}}}^{sp} = \tilde{\rho }_{{{\text{ru}}}}^{{{\text{sp}}}} + \tilde{d}_{{{\text{trop}},{\text{ru}}}}^{ sp} {-} c\widetilde{{{\text{d}}t}}^{sp} + \mu_{{{\text{sig}}}} \tilde{l}_{{\text{u}}}^{ sp} , \hfill \\ \end{gathered}$$

(25)

where the estimable parameters at the server end become the Double-Differenced (DD) vector of parameters [$\tilde{\rho }_{{{\text{ru}}}}^{sp}$, $\tilde{d}_{{{\text{trop}},{\text{ru}}}}^{ sp}$], a biased version of “true” SD ionospheric delays $\tilde{l}_{{\text{u}}}^{sp}$, SD satellite clocks $\widetilde{{{\text{d}}t}}^{sp}$ and SD satellite phase biases $\tilde{\delta }_{f}^{sp}$, as well as DD ambiguities $\tilde{N}_{{f,{\text{ru}}}}^{ sp}$. Explanations for these parameters are as follows

$$\begin{gathered} \tilde{\rho }_{{{\text{ru}}}}^{sp} = \rho_{{\text{u}}}^{sp} {-} \rho_{{\text{r}}}^{sp} , r \ne u \hfill \\ \tilde{d}_{{{\text{trop}},{\text{ru}}}}^{ sp} = d_{{{\text{trop}},{\text{u}}}}^{ sp} {-} d_{{{\text{trop}},{\text{r}}}}^{ sp} , r \ne u \hfill \\ \tilde{l}_{{\text{u}}}^{ sp} = l_{{\text{u}}}^{ sp} {-} \gamma_{{{\text{GF}}}}^{sp} \hfill \\ \widetilde{{{\text{d}}t}}^{sp} = {\text{d}}t^{sp} + \frac{{\gamma_{{{\text{IF}}}}^{sp} }}{c} {-} \frac{{\rho_{{\text{r}}}^{sp} }}{c} \hfill \\ \tilde{\delta }_{f}^{sp} = \delta_{f}^{sp} {-} \gamma_{IF}^{sp} + \mu_{f} \gamma_{GF}^{sp} {-} \lambda_{f} N_{f,r}^{ sp} \hfill \\ \tilde{N}_{f,ru}^{ sp} = N_{f,u}^{ sp} {-} N_{f,r}^{ sp} , r \ne u \hfill \\ \end{gathered}$$

(26)

Although these parameters do not take the original forms anymore, they still work with the provided $\widetilde{{{\text{d}}t}}^{sp}$ and $\tilde{\delta }_{f}^{sp}$ (i.e., the PPP–AR at the user end can be achieved using SD observables). Since only one set of satellite clocks is estimated, this model is referred as the Common Clock (CC) model (Teunissen and Khodabandeh 2015). Based on the same choice of S-basis, a variant of the CC model, named the Distinct Clocks (DC) model (Odijk 2002; Teunissen et al. 2010), was adopted by simply lumping the common clock $\widetilde{{{\text{d}}t}}^{sp}$ and the satellite phase bias $\tilde{\delta }_{f}^{sp}$ into the so-called integer recovery phase clock (Laurichesse et al. 2009). Another choice of S-basis is to use directly the SD satellite phase biases $\delta_{f}^{sp}$, rather than the SD ambiguity ${\text{N}}_{{\text{f}},\text{ r}}^{ \, {\text{s}}{\text{p}}}$ in the CC model, called the CC-2 model. More details can be found in Teunissen and Khodabandeh (2015).

Nowadays, undifferenced and uncombined PPP–RTK models are of more use (Li et al. 2011; Zhang et al. 2011, 2022a; Odijk et al. 2016). They are very flexible in integrating observations from multi-GNSS (Schönemann et al. 2011), and introducing external information (e.g., the atmospheric delays) or dynamic constraints on all parameters directly to further strengthen the model itself (Zhang et al. 2019a). As indicated in Teunissen and Khodabandeh (2015) and Zhang et al. (2019a), all the aforementioned ionosphere-float models are also applicable in the undifferenced and uncombined cases. This is because during the reparameterizations of undifferenced and uncombined PPP–RTK models, several values are implicitly chosen as datums to solve the rank deficiencies (e.g., the receiver code/phase bias at a reference station) (Zhang et al. 2011, 2019a), and therefore the estimable parameters finally take the similar differenced forms (i.e., SD/DD). We will not repeat them but refer to Zhang et al. (2019a) and Zhang et al. (2022b) for details, since essentially, they only differ in the choice of S-basis vectors and parameterizations.

To eliminate the effect of the ionosphere and further reduce the number of parameters to be estimated, ionosphere-free models were also proposed based on IF combinations, e.g., Integer Recovery Clock (IRC) model (Laurichesse et al. 2009), Decoupled Satellite Clock (DSC) model (Collins et al. 2010), and Uncalibrated Phase Delay (UPD)/Fractional Cycle Bias (FCB) model (Ge et al. 2008; Geng et al. 2009, 2012). A combination of them is also possible, e.g., combining IRC and UPD in the modified UPD model (Geng et al. 2019a). Despite that these ionosphere-free models differ in employed procedure and estimation method, comparison between them have shown that they are equivalent in theory (Geng et al. 2010; Shi and Gao 2014), and therefore should have equivalent PPP–AR performances in practice, e.g., a daily (hourly) horizontal accuracy of better than 2 cm with IRC (DSC) model (Laurichesse et al. 2009; Collins et al. 2010) and an hourly accuracy with 0.5 cm in the horizontal and 1.4 cm in the vertical directions with UPD model (Geng et al. 2009). A more thorough comparative analysis can be found in Teunissen and Khodabandeh (2015), where the authors clarified that all the ionosphere-float and ionosphere-free models are intrinsically the same, but differs in the choice of S-basis vectors, parameterization and whether to eliminate the ionospheric delays. For instance, the S-basis in IRD/DSC models is identical to that of CC/DC models and the UPD/FCB is a reparameterization of the CC-B model. Hence, we will not repeat the details of these ionosphere-free models. The one-to-one transformations of user corrections between different PPP–RTK models were given by Teunissen and Khodabandeh (2015). The authors also pointed out that one needs to be careful when applying a fractional operator in UPD/FCB model to get the fractional part of a float ambiguity. Although the fractional operator has no effect on the integer properties of ambiguities at the user end, this operator would change the statistics of corrected observables and even destroy the integer properties of the ambiguities when improperly applied, e.g., (Geng and Bock 2013).

Since atmospheric delays also impair the integer properties of ambiguities at the user end, the inclusion of the atmospheric delays in PPP–RTK in the ionosphere-corrected model will benefit the model strength, reduce the ambiguity search space, leading to a faster PPP–AR (Banville et al. 2014). In that case, we have the so-called ionosphere-corrected model, which is straightforward based on the ionosphere-float model but can be cumbersome when using the ionosphere-free model (Morton et al. 2020). There are mainly two methods for implementing an ionosphere-corrected model. One is using the ionosphere model from external sources as constraints in the ionosphere-float model, e.g., the GIM (Banville et al. 2014; Zhang et al. 2022c). The other method is to derive the ionospheric delays together with other parameters in PPP–RTK networks at the server end and use them as fixed corrections or constraints at the user end (Li et al. 2022a). But the estimated ionospheric delays at the server end are not directly used, instead, they are modelled/predicted and then interpolated at the user end. There are several methods to do so, like VTEC modelling (Psychas et al. 2019), ionospheric tomography (Olivares-Pulido et al. 2019), best linear unbiased predictor (e.g., Kriging) (Teunissen et al. 2010; Zhang et al. 2011), distance-based interpolation (Nadarajah et al. 2018; Zha et al. 2021), etc. Some of them have achieved a millimeter-level positioning accuracy in the horizontal and single-epoch instantaneous PPP–AR, but they were restricted in a small local/regional network (dozens of kilometers) by the precision of the derived ionosphere information. Similarly, the tropospheric delays can be introduced in the same way as implemented in the ionosphere-corrected model. The troposphere model derived from meteorological datasets (Hadas et al. 2013) or estimated based on a GNSS network over a small/large region (Li et al. 2011; Shi et al. 2014; de Oliveira et al. 2017; Lou et al. 2018; Zheng et al. 2018) is usually applied. However, their contributions to PPP–RTK performance have been validated mostly with float ambiguities. For PPP–AR, recently, Song et al. (2022) reported the convergence times (with a threshold of 10 cm) of a static user were shortened by 2 min and 3.5 min in the horizontal and vertical directions, respectively, after introducing the tropospheric delays estimated based on a GPS network of 100 km spacing average at the server end.

In summary, no matter what form the PPP–RTK model takes, parameters of interest at a reference station/satellite are always required, serving as a datum to compensate for the rank deficiencies in the model. As shown in Teunissen and Khodabandeh (2015), this implies that the positioning at the user end with PPP–RTK corrections is in fact the relative positioning between the user station and the reference station, and the recovered integer ambiguities at the user end are essentially the DD ambiguities. Both are linked by introducing the PPP–RTK corrections at the user end.

However, it is not the case for GLONASS FDMA. As mentioned in the last section, GLONASS uses a troublesome FDMA mode with IFBs, one cannot form a single DD ambiguity with a pair of receivers and a pair of satellites. This prevents a typical straightforward PPP–AR of DD ambiguities as implemented in other CDMA signals (Leick et al. 2015; Zaminpardaz et al. 2021). Since both the code and phase IFBs have been shown to be hardware-related (e.g., receiver type/antenna type/firmware), one way to realize GLONASS FDMA IAR is to calibrate IFBs, that is, maintaining a large look-up table for IFB calibrations with all possible combinations of receivers, antennas, and firmware, e.g. (Reussner and Wanninger 2011; Sleewaegen et al. 2012b). But the work burden of such IFB calibrations can be huge and the table needs to be frequently updated. Alternatively, methods without IFB calibrations were investigated, such as choosing a PPP–RTK network consisting of homogeneous receivers (Liu et al. 2017c), estimating linear IFBs on the fly by simultaneously tracking two satellites with adjacent frequency channel numbers (Banville et al. 2013) and imposing external ionospheric constraints to prevent the IFB contaminating ambiguities (Geng and Bock 2016). Besides, a new formulation of the DD GLONASS FDMA model was introduced by Teunissen (2019), which takes a look-alike form to that of CDMA-based systems. In order to assess the applicability and performance of this new GLONASS FDMA model, Zhang et al. (2021a) applied it to GPS/GLONASS PPP–RTK. Results show that the convergence time (with a threshold of 10 cm) was shortened from 11(18) to 5(12) min in a homogeneous (heterogeneous) network (i.e., one with homogeneous receivers and the other with heterogeneous receivers) after both the GPS and GLONASS ambiguities were fixed. The possibility of GLONASS-only FDMA + CDMA IAR was also considered with the new GLONASS FDMA model (Zaminpardaz et al. 2021).

After applying the aforementioned PPP–RTK models, the integer properties of ambiguities at the user end are recovered. Following that, a typical procedure in PPP–AR is necessary to resolve the “recovered” integer ambiguities. Usually, it starts with a solution for all the parameters in observation equations by performing a LS adjustment, including the so-called float ambiguities (Deng et al. 2014). Secondly, these float ambiguities are adjusted to integers according to their integer constraints. In practice, there are different integer estimation principles available, such as the Integer Round (IR), Integer Bootstrapping (IB) (Teunissen 1998), and the Integer Least-Square (ILS). The IR estimator is the simplest as it only takes the nearest integers of float ambiguities, and therefore has the poorest success rate (i.e., the probability of correct integer estimation). The IB estimator combines the IR estimator with sequential LS estimation by utilizing some of the correlation between the float ambiguities, leading to a larger success rate (Teunissen and Montenbruck 2017). While the ILS estimator is the most complex, but optimal and proved to have the largest possible success rate, since it takes into account the correlations between the float ambiguities and follows the LS principle of the observation equation. However, an integer ambiguity search is required in the ILS estimator due to the integer constraints of ambiguities. This will lead to low efficiency for ILS estimator searching in a large space when high correlations between ambiguities exist (Zhang et al. 2015), especially for GNSS. To reduce the searching space of ambiguity and improve efficiency, the well-known Least Squares Ambiguity Decorrelation Adjustment (LAMBDA) was proposed based on the ILS approach by the means of decorrelation (Teunissen 1995). Nowadays, it has been widely adopted in GNSS data processing, while other estimators or a mixed form of them is also applicable, e.g., (Geng and Bock 2013).

Once the integer ambiguities are computed, acceptance tests are then needed to decide whether they should be accepted, since we do not know by definition the true integer ambiguities. There are basically two kinds of acceptance tests: the model-driven tests, e.g., ambiguity success rate test (Teunissen 1999) and the data-driven tests, including ratio test, difference test, projector test, etc. (Frei and Beutler 1990; Tiberius and de Jonge 1995; Han 1997). Unlike model-driven tests depending on the strength of the underlying GNSS model, data-driven tests are commonly adopted as they use real float solutions. But a critical pre-defined criterion (i.e., user-defined threshold) is required in data-driven tests, which is usually empirical and can vary with applications (Teunissen and Montenbruck 2017). To make the pre-defined threshold more adaptive and flexible, the so-called fixed failure-rate approach was proposed (Teunissen 2004; Verhagen and Teunissen 2006, 2013), where the threshold is computed with a given failure rate by taking the application model into account. And one can also implement the acceptance test without any a priori given testing function by using the optimal ambiguity tests, such as the constrained maximum success rate test and minimum mean penalty test (Teunissen 2004, 2005). We refer to literature, e.g., (Verhagen 2004, 2005; Verhagen and Teunissen 2006), for more details about these tests. Finally, with constraints of the accepted integer ambiguities, the float solution is re-adjusted into a fixed solution by virtue of their correlation with the ambiguities (Teunissen and Verhagen 2009). In practice, the Partial Ambiguity Resolution (PAR) proposed by Teunissen et al. (1999) is usually adopted since a full IAR is not always available or necessary, e.g., the success rate of the resolution of all ambiguities is too low (Teunissen and Verhagen 2009; Li and Zhang 2015). By choosing a sufficiently large subset of the ambiguities, the resolutions of which have success rates that are high enough to achieve IAR, the PAR significantly speeds up the PPP–AR convergence, especially at the initial stage, and thereby improves the overall positioning accuracy (Li and Zhang 2015; Psychas et al. 2020; Yan and Zhang 2022a).

Until now, we did not specify any specific GNSS system for implementing PPP–AR, which means it can be easily applied to any GNSS system and also their combinations in the same way. Indeed, the advancements of multi-constellations with multi-frequency enable better observation geometry and more redundancy in PPP–AR, thereby enhancing its robustness with a shorter convergence time (Morton et al. 2020). These have been shown in many PPP–AR studies integrating multi-GNSS with multi-frequency, see e.g., (Aggrey and Bisnath 2019; Xiao et al. 2019; Yao et al. 2019; Li et al. 2019b, 2020, 2022d, 2022c; Duong et al. 2020; Geng et al. 2020; Guo et al. 2021b; Cao et al. 2022; Yin et al. 2022; Ogutcu et al. 2022). Overall, in multi-GNSS multi-frequency cases, the convergence time (with a threshold of 5 cm in the horizontal direction) can be shortened to a few minutes at a global scale (e.g., 4.4 min (Li et al. 2022c)), and instantaneous PPP–AR is achievable in local/regional areas with or even without precise atmospheric delays (Tao et al. 2022). Meanwhile, positioning accuracy at millimeter-level in the horizontal and of about 1 ~ 2 cm in the vertical can be obtained.

But, on the other hand, such integrations between multi-GNSS with multi-frequency introduce a lot of biases as well, implying that all the above benefits are only available if and only if these biases are handled properly. To have a first look, let us start with the biases between frequencies in a single GNSS system. Traditionally, in dual-frequency PPP–RTK models, the satellite code biases of the two frequencies are decomposed and lumped into other parameters (see Eqs. 23–25). But when a third frequency or more frequencies are involved, additional satellite code biases of these frequencies need to be introduced in the model, named Differential Code Bias (DCB) in some literature (Zhang et al. 2011; Odijk et al. 2016). Fortunately, they are estimable and relatively time-stable, which means they can be estimated as additional parameters in the PPP–RTK model or calibrated with corrections from external providers (Wang et al. 2016; Villiger et al. 2019). Additional satellite phase biases are also required if observations used for satellite clock estimation and positioning are inconsistent (e.g., GPS L5 positioning with IF clock based on GPS L1/L2). As the time-varying phase biases can be absorbed into satellite clock offset during the satellite clock estimation (Pan et al. 2019; Li et al. 2020), this will lead to disagreements between satellite clocks, which is also known as the Inter-Frequency Clock-Bias (IFCB). It has been found that the IFCBs have equivalent daily variations of 10–20 cm in GPS Block-IIF satellites and of 6–26 cm in GLONASS-M+ satellites, respectively, while the marginal IFCBs in BDS-3 (1–3 cm) and in Galileo (less than 1–2 cm) can be neglected (Li et al. 2020; Chen et al. 2022; Zhang et al. 2023). A direct way to solve this is to provide distinct satellite clocks for the additional frequencies (Guo and Geng 2018), where IFCB no longer exists. But one needs to maintain distinct satellite clocks of all additional frequencies at the same time. Since the daily variations of IFCBs are stable with periodic properties, a more general solution is to model/estimate beforehand (Pan et al. 2019; Li et al. 2020; Zhang et al. 2023) or involve them in PPP–RTK model as additional parameters (Geng et al. 2019b). For instance, by correcting the pre-estimated IFCB, a triple-frequency UPD estimation was realized by Li et al. (2020), but limited by the number of GPS satellites transmitting L5 signal, only a 7.5% reduction in convergence time was reported when compared to dual-frequency GPS PPP–AR.

For the biases between multi-GNSS, both the code and phase ISBs are not negligible. As we mentioned in the last section that ISBs are system-specific and receiver-related, they cannot be cancelled out by double-differencing between diverse receiver types. Therefore, the inter-system DD ambiguities in the PPP–RTK model are no longer integers (Odijk and Teunissen 2013). Unless the ISB values are known, only intra-system PPP–AR (i.e., each GNSS system has its own reference satellite) is achievable with multi-GNSS. Although advancements of intra-system PPP–AR on shorter convergence time have already been reported in many studies (Geng and Shi 2017; Liu et al. 2017b; Pan et al. 2017b; Geng et al. 2020), a faster PPP–AR can be expected once the ISBs are known. In that case, the inter-system ambiguities are resolvable and thereby the availability of IAR solutions is improved (Odijk et al. 2017; Geng et al. 2019b). Similar to the methods applied for ISB in the conventional PPP model, ISBs can be calibrated or estimated as unknowns in PPP–RTK. Two general ways of introducing ISB parameters in the PPP–RTK model were given in Khodabandeh and Teunissen (2016): one is to generate corrections (i.e., satellite clocks/biases) for each individual GNSS system, which is essentially the intra-system PPP–AR, while the other one is to generate ISB-parameterized corrections by choosing one system as reference. The latter makes it possible to achieve inter-system PPP–AR. In practice, the server end can issue an ISB look-up table including all the receivers in the network, allowing the user end to realize their own ISB-corrected model. An alternative ISB estimation method based on the FCB model was proposed by Geng et al. (2019c), where the FCBs were estimated after correcting the Differenced ISBs (DISBs) derived from DD observables, and together with DISBs products, an inter-system PPP–AR was realized at the user end. By applying this method, a mean convergence time (with a threshold of 4 cm in the horizontal direction) of 10.8 min and 9.7 min was found in intra- and inter-GPS/BDS PPP–AR, respectively (Geng et al. 2019c).

Nowadays, the integration of multi-GNSS with multi-frequency makes the handling of biases in PPP–AR a bit more complicated. Besides all the aforementioned biases, they can be found in a large number of combination forms as well, depending on the choice of PPP–RTK models. Until now, each IAR-enabling clock/bias representation method had its own way to provide the necessary bias information (Schaer et al. 2021). But without standardization, these variants will eventually lead to confusion in positioning applications and impede any further development of PPP–AR. Therefore, a generally applicable bias parameterization for PPP–AR, named by the Observable-specific Signal Bias (OSB) representation was proposed (Villiger et al. 2019). The main idea of OSB is to specify the bias for the observables of each frequency in each GNSS system, and thereby any combined/differenced bias correction can be formed directly. Though originally introduced for the pseudo-range measurements, this OSB representation has been extended to carrier-phase observations in many studies (Schaer 2016; Liu et al. 2020; Schaer et al. 2021; Geng et al. 2022). A unified model of multi-GNSS multi-frequency biases based on OSB can be found in Li et al. (2022c). And the OSB representation has already been supported by the standard bias data interface, i.e., the Bias-SINEX (Schaer et al. 2021).

Overall, to achieve a fast and successful IAR in PPP mode, PPP–RTK is a promising way, showing its capability to obtain “instantaneously” millimeter-level positioning accuracy. But currently, it suffers from some restrictions. Relying on a regional network augmentation, the performance of PPP–RTK depends on the distribution and the inter-station distance in a regional network (Li et al. 2022b), implying a relatively high cost and computational burden (Khodabandeh 2021). Albeit a low-cost single-station PPP–RTK has been developed (Khodabandeh and Teunissen 2015, 2019; Khodabandeh 2021), instantaneous PPP–AR at large/worldwide scales is still limited by the precision of atmosphere information (Teunissen and Khodabandeh 2015; Choy et al. 2017; Li et al. 2022b; Yan and Zhang 2022b; Zhang et al. 2022c). While for the PPP IAR procedure, an underlying assumption is that the applied GNSS model is correct (i.e., no unmodelled and undetected biases present) (Verhagen et al. 2012). This is not always true in reality and a wrong integer estimation is still possible. Since a wrong/unsuccessful IAR can cause unacceptable errors in the position solution, which may even exceed the error of the ambiguity-float solution (Psychas et al. 2020), it is difficult to give the error budget of the IAR here as we did in previous sections. Thus, the method of validating the GNSS model is still missing, which essentially describes the sensitivity of IAR to unmodelled and undetected biased (Teunissen and Verhagen 2009; Verhagen et al. 2012).

Nevertheless, additional observations have shown their potential to relieve these limitations: Without a regional network, a much faster PPP–AR within a few seconds will be obtained with the augmentation of LEO constellations (Li et al. 2022b; Ma et al. 2022); With the integration of inertial navigation system, PPP–AR in the urban environment is significantly improved (Liu et al. 2016; Du et al. 2021). However, more investigations with real data are needed. Besides, the improvements in other error source modelling, such as the PCC model (Xin et al. 2020; Geng et al. 2021), have been found to help speed up the PPP–AR. Needless to say, a more reliable and faster PPP–AR can be expected with continuous efforts put in place.

4.11 Other Sources of Error

Except for all the error sources mentioned above, some additional error sources need to be considered in GNSS PPP. Most of them are site displacements, which are caused by various forces acting on the Earth’s crust, including the solid Earth tide, ocean loading (tidal), atmospheric loading (tidal), solid Earth, and ocean pole tide. They sum up to the d_{tide, r} term in Eqs. (4) and (5). In practice, they are served as offset vectors that imposed on the coordinates of the receiver, usually in the local coordinate frame. As these site-dependent displacements can reach up to several decimeters in some cases, such corrections are necessary for obtaining positioning results that are consistent with the ITRF in high-accuracy applications (< 10 cm). Considering that these site displacements have been reviewed by a lot of literature (Petit and Luzum 2010; Teunissen and Montenbruck 2017; Morton et al. 2020) and they are not relevant to constellations, we will just give a brief summary of these in this section. The error budget can be found in Table 11.

Table 11 Error budget of site displacements

The solid Earth tide refers to a subtle deformation of the Earth and its crust induced by the gravitational attraction of the Sun and Moon. A permanent displacement (up to 12 cm in mid-latitudes) and a periodical displacement (up to about 30 cm in the vertical and 5 cm in the horizontal, respectively) with a predominantly semi-diurnal and diurnal periods (Jentzsch and Jena 1997; Petit and Luzum 2010; Kouba 2015) have been found, and together sum up to about 0.4 m. However, they can be modelled with spherical harmonics, and for 5 mm accuracy, the second-degree tides and a height correction term are sufficient while more terms should be considered if higher accuracy is expected (Petit and Luzum 2010; Kouba 2015). This deformation arises not only for the solid Earth but also for the oceans, and thus results in site displacements with diurnal and semi-diurnal periods (Morton et al. 2020). The effect of ocean tide depends on the local geography of the ocean and land masses. Though it is most pronounced in the vertical direction and typically at the centimeter level, the displacement can reach up to 10 cm in coastal regions. In order to correct these displacements in GNSS PPP, sophisticated ocean tide models are applied based on hydrodynamic finite element models, (e.g., FES2014b) or altimetry observations (e.g., EOT20) (Carrère et al. 2016; Hart-Davis et al. 2021).

The atmosphere also exerts a load on the solid Earth. The changes in its temperature-driven pressure distribution result in deformations of the Earth’s crust. There are two components that consist of the atmospheric loading. One is the atmospheric pressure loading induced by atmospheric masses, that is, up to 2 cm, while the other one is the atmospheric tidal loading caused by variations of pressure at primarily diurnal and semi-diurnal time scales, essentially the variations of temperature in the atmosphere, which leads to a maximum effect of about 1.5 mm (Dach et al. 2011a). A correction model for atmosphere pressure loading is recommended by IERS Conventions (2010) (Ray and Ponte 2003), but still, no model is well recognized since there are several models developed for space-geodetic data (Petrov 2004; Tregoning and van Dam 2005; Boehm et al. 2009) and it is hard to tell which one is the best one.

Furthermore, polar motion of the Earth will lead to small periodic displacements of its crust, known as the solid earth pole tide. The resulting site displacements are predominantly seasonal or have Chandler (~ 430 days) periods and as such do not show up over a 24-h period (Morton et al. 2020). They can be determined by the pole coordinate variations from the mean poles and the maximum displacement may reach up to about 5 mm horizontally and 25 mm vertically, likewise, a model can be applied to correct this displacement (Petit and Luzum 2010). Not only the solid earth pole tide, the ocean pole tide is also caused by the centrifugal force due to the polar motion. Thereby, the same Chandler period and annual variations are found predominantly. Provided that the amplitude of the typical Chandler wobble parameters is of the order 0.3 arcsec, the load-deformation is no larger than about (1.8, 0.5, 0.5) mm in the (radial, north, east) components, respectively (Teunissen and Montenbruck 2017). Fortunately, a self-consistent equilibrium model of the ocean pole tide has been presented in Desai (2002), so that it can also be modelled accurately.

5 Remarks on Correlations

Until now, we have introduced error sources in PPP mode and their typical error budgets were given when applicable. But for evaluating the error budget for GNSS PPP, one needs to keep in mind that it is not a simple summation of them. One may notice that we have addressed several times that these error corrections are highly correlated, since most of them are often inseparable and generated by using a network adjustment with observations from the same global/regional network. Although it is necessary and useful to analyze the individual error budgets as they indeed show the characteristics and impacts on PPP solutions themselves, such an analysis is not sufficient for evaluating the overall performance of PPP solutions due to high correlations existing between individual error corrections (Khodabandeh and Teunissen 2015).

Potential pitfalls of ignoring correlations between error corrections in single station PPP–RTK have been demonstrated in Khodabandeh and Teunissen (2015): Based on the propagation of error, one would find the precision of the individual corrections is governed by the poor precision of pseudo-range observations, rather than the high precision of carrier-phase observations (see Psychas et al. 2022 for numerical examples); and after introducing a more precise correction (e.g., satellite phase bias) from another provider, the precision of the mixed corrections (e.g., satellite clock/biases) becomes worse when combining them together. To better understand the correlations, one can follow Khodabandeh and Teunissen (2018) using a canonical decomposition, where the undifferenced PPP–RTK model is decomposed into four blocks of decoupled and uncorrelated components, including the satellite-/receiver-averaged component, satellite-averaged SD component, receiver-averaged SD component and DD component. Since each component contributes to different estimable parameters in PPP–RTK, these parameters are implicitly correlated with each other by their constituents from the same component. Note that only ambiguities in the DD component are integer and resolvable, which means only the DD component takes the advantage of high-precision carrier phase observations, while the other three components are driven by pseudo-range unless the corresponding ambiguities are known. Therefore, even with IAR, the precision of the individual parameter/correction is pseudo-range dominated as the improvement from the relatively high-precision DD component is disguised by the other three components. As shown in Khodabandeh and Teunissen (2018), the high-precision DD component contributes to forming several parameters/corrections in PPP–RTK, e.g., the satellite phase bias/clock and ionospheric delays. In this case, improvements from the high-precision DD component can only be fully exploited once all the corrections are combined together. And it is clear now for the second pitfall, a more precise satellite phase bias from another provider, which is different from the original one, destroys the consistency between the four components. Although the precise satellite phase bias works, e.g., leading to a precise ambiguity estimation, it essentially introduces additional errors when combining all the corrections.

To further evaluate the performance of PPP–RTK with corrections in combined form, an analytical method was given by Khodabandeh and Teunissen (2015). Firstly, the Best Linear Unbiased Estimators (BLUE) of the PPP–RTK network combined corrections in an analytical form were derived using the conditional LS approach. It is formulated based on single-station corrections and adjusted by improvement from network information, in terms of time-/station-averaged network observations and time-/station-differenced network observations. Thereafter, the precision of the combined corrections is obtained by applying the variance propagation law, which will finally give an overall performance of the PPP–RTK corrections with a given precision of observations, number of epochs, number of network stations and the frequencies. We refer to Khodabandeh and Teunissen (2015) for details. Although this is exclusively for PPP–RTK, one can follow a similar way in general PPP, since they are essentially equivalent if the PPP–RTK is extended to a global scale (Choy et al. 2017).

When it comes to correlation, it is also worthwhile to pay attention to the correlations in GNSS PPP data processing, such as the time correlations existing in observations and the parameters to be estimated. The common data processing method for GNSS PPP is applying the so-called BLUE, e.g., the LS estimator and Kalman filter (Teunissen and Montenbruck 2017). To do so, in general, a function model and a stochastic model are indispensable. The function model of PPP mode, as shown in Eqs. (4) and (5), describes the mathematical relationships between observations and parameters to be estimated, while the stochastic model, often described by the a priori (co)variance matrix, reflects the precision of and correlation between observations (Bona 2000; Li 2016; Yue et al. 2022). Additional dynamic model also incorporates in the estimation as it specifies the time evolution of dynamic parameters (e.g., clock biases/tropospheric delays) in multi-epoch case (Goode et al. 2013; Teunissen et al. 2021; Hou et al. 2022). Likewise, to describe the uncertainty of the dynamic model, another stochastic model is required as well.

Since the basic assumption of being optimal for BLUE is that the observations are uncorrelated in time (Bona 2000; Goode et al. 2013; Teunissen et al. 2021), the stochastic models are of great importance because such assumption is embedded within them. A mis-specified/unrealistic stochastic model can destroy the minimum-variance property of BLUE, degrade the precision of estimated parameters, and more importantly, lead to an unreliable quality description as the incorrect stochastic model will propagate into error-variance matrices of all relevant parameters in the estimator (Parvazi et al. 2020; Khodabandeh 2021; Teunissen et al. 2021; Hou et al. 2022; Psychas et al. 2022). But unfortunately, unlike the well-documented function model of GNSS PPP, stochastic models that do reflect reality are usually unknown or partly unknown in PPP mode due to the lack of knowledge about them (Zhang et al. 2020a; Teunissen et al. 2021).

In practice, one may approximate the realistic stochastic model of observations with an a priori simple empirical stochastic model in GNSS PPP data processing, e.g., observation type based, satellite elevation angle based, carrier-to-noise-power density ratio based, and signal-to-noise ratio based stochastic models (Jin and De Jong 1996; Brunner et al. 1999; Satirapod and Wang 2000; Satirapod and Luansang 2008; Gao et al. 2011). These empirical models are reasonable because it partially reflects the quality of the real observations, i.e., the precision of pseudo-range is low and a low elevation angle, carrier-to-noise-power density ratio or signal-to-noise ratio means relatively noisier observations. Due to their simplicity and small computational burden, a stochastic model considering observation type and satellite elevation angle is nowadays adopted in most GNSS PPP data processing (Li 2016; Yue et al. 2022). However, it is far from reflecting reality since studies have shown that GNSS observations are not only correlated with the observation from different frequencies, but cross-correlated with those of different observation types, and even correlated in time with hardware-specific characteristics (Bona 2000; Parvazi et al. 2020). The possible cause for the time correlations includes multipath, antenna effects, tracking loop errors, lateral atmospheric variability and slowly changing satellite observation geometry (Olynik et al. 2002; Schön and Brunner 2008; Goode et al. 2013; Jansson and Persson 2013). Although attempts were made to capture time correlations with up-to-date time series analysis, like first-order auto-regressive noise process and harmonic functions (Borre and Tiberius 2000; Amiri-Simkooei and Tiberius 2007; Goode et al. 2013), their contribution to PPP solutions was not specified.

To obtain a more realistic stochastic model for GNSS observations, the (co)Variance Component Estimation (VCE) was firstly applied with zero/short baseline (Bona 2000; Tiberius and Kenselaar 2000, 2003; Amiri-Simkooei et al. 2013; Li 2016; Hou et al. 2022), but has been extended to GNSS PPP data processing nowadays (Cai and Gao 2013; Parvazi et al. 2020; Zhang et al. 2020a; Yue et al. 2022). Based on different estimation principles and assumptions of error distributions, it takes various forms in modern geodetic applications, such as the Minimum Norm Quadratic Unbiased Estimator (MINQUE) (Rao 1971), the Best Invariant Quadratic Unbiased Estimator (BIQUE) (Koch 1978; Crocetto et al. 2000), the Restricted Maximum Likelihood Estimator (RMLE) (Kubik 1970) and the Least-Squares Variance Component Estimator (LS-VCE) (Teunissen 1988; Teunissen and Amiri-Simkooei 2008). Nevertheless, the basic idea behind them is the same, i.e., the covariance matrix of observations can be considered as a linear combination of cofactor matrices, the coefficients of which are unknown parameters that must be estimated under a given estimation principle. Among these VCE variants, the LS-VCE was adopted more often in PPP mode due to its simplicity and flexibility. For example, by taking the correlations, cross-correlations and time correlations into account, the stochastic models of multi-frequency BDS and Galileo observations for receivers of different types were established by applying LS-VCE to the undifferenced geometry-free function model of PPP (Zhang et al. 2020a), showing comparable result with those using zero baselines; Ignoring the time correlation in observations, Parvazi et al. (2020) estimated stochastic model of four constellations observations with recursive LS-VCE. Compared to the commonly applied empirical stochastic model in GNSS PPP, 3D positioning accuracy was improved from 5.6 to 1.8 cm while the convergence time (with a threshold of 15 cm) was shortened from 5.3 to 3 min after applying the new stochastic model. Similar improvement in positioning accuracy, i.e., 18.4%, 10.7% and 8.6% in the ENU-directions, respectively, can be found in Yue et al. (2022) when applying the estimated variance-related information, however, further improvement is not significant after the covariance-related information was incorporated.

For the stochastic model of dynamic parameters, knowledge about them is still at a rather rudimentary level. The general solution is to assume that the time evolution of the parameter follows a typical stochastic process, e.g., random walk and Markov processes. And the system/process noise is usually given empirically based on the statistics of its temporal behavior. This assumption can be unrealistic/mis-specified, since we do not know the exact stochastic model. Again, the LS-VCE seems to be one possible solution as implemented by Hou et al. (2022). The stochastic model of the receiver code bias was jointly estimated with that of observations by using LS-VCE, and the consistency between the statistic property of residuals and the estimated stochastic model for receiver code bias validate its reliability. Indeed, the formal precision of related parameters (e.g., receiver clocks and ionospheric delays) were shown to be affected. Though it was based on zero/ultra-short baseline GNSS observations, it may also be applicable to PPP mode once most of the systematic errors in observations can be well-modelled and eliminated with the function model.

A more general way to cope with both the mis-specified stochastic models of observations and dynamic parameters was proposed by Teunissen et al. (2021). Regardless of the mis-specified stochastic model, the error matrices of a Kalman filter are calculated in a recursive way, thereby making use of the information provided by the filter itself. It has been shown that in this way, one can derive a better estimate of error-variance matrices, which ensures a proper quality description of the filter and also the detectability of mismodelled corrections, even with a mis-specified stochastic model. Therefore, this method is applicable and efficient particularly when time-varying parameters need to be recursively generated over time, like in PPP–RTK. In that case, the error-variance matrices can be computed in parallel to a recursive filter.

Last but not least, the uncertainty of corrections (e.g., orbits, clocks and ionospheric delays) is not neglectable when applying those corrections to GNSS PPP. As we know, in general, the corrections estimated by the server end are assumed to be precise enough with zero error variance so that they are commonly treated as deterministic/non-random corrections by PPP users (Psychas et al. 2022). Therefore, no information about the uncertainty of correction is provided for simplicity or due to the vast amount of information to be transmitted (Odijk et al. 2014). However, because of the intrinsic randomness of observations at the server end, the generated corrections are still random values accompanied by error-variance matrices, characterizing their uncertainties (Khodabandeh et al. 2023). In this case, if the uncertainty of corrections is neglected by the PPP user, unspecified stochastic processes from the corrections will be introduced in GNSS PPP, again leading to time-correlated observations at the user end. Likewise, the same problems that we mentioned above will show up.

This situation is even worse in real-time PPP–RTK, where the corrections are often provided with a time latency and the user needs to predict without the correct uncertainty information of the corrections. The negative impacts of time latency on IAR and positioning performance of PPP–RTK have been addressed in some studies, e.g., (Khodabandeh 2021; Psychas et al. 2022; Khodabandeh et al. 2023). A direct solution is to provide the uncertainties of core corrections to the user end, but it is not applicable as the amount of uncertainty information is huge, and it defies the purpose of PPP–RTK for minimizing the amount of necessary information. Instead of issuing the uncertainties, i.e., the full (co)variance matrices, one can make the dynamic model setting of the server end available to the user end, thereafter, a close-to-optimal result can be achieved by approximating the uncertainty of correction based only on its system/process noise variance part. Although with a close-to-optimal IAR performance, this close-to-optimal method is not able to describe the positioning performance properly. But once the server end shares more information with the user end (e.g., the measurement precision and filtering start time), the user is able to recursively estimate the (co)variance matrices based on a model-driven recursive engine as if the user would be provided with the uncertainties of corrections from the server end, showing optimal performance even with high latencies. For more details about these two methods, we refer to Psychas et al. (2022) and Khodabandeh et al. (2023).

6 Summary and Outlook

In this study, we reviewed the error budget of GNSS PPP. For the effects of these errors, their discrepancies between the four GNSS systems were addressed, as well as the mitigation methods. Since our analysis mainly focuses on errors excess millimeter-level in the measurements domain, several error sources such as receiver clock, receiver noise, and the earth rotation parameters are not discussed. Although the mapping from raw measurement error to final position error is complex, which depends on the tracking geometry and solution strategy employed, to first order the resulting error in position will be comparable to the measurement error (Yunck 1993).

It can be seen that GPS played a role as an exemplar in the historical evolution of GNSS PPP, which refers to that there are no significant differences in other systems when compared to GPS, except for GLONASS taking the FDMA mode. However, multi-GNSS does not mean multiple duplications of individual systems simply. The continuity and availability of observations, as well as the accuracy and reliability of corresponding solutions, were shown to be improved by integrating multi-GNSS. This fusion also brings out new opportunities. For instance, superior performances on both signal and satellite clock can be found in newly developed systems like Galileo and BDS-3, which provide reliable validations for modelling of related error sources, e.g., the relativistic effects, or in other words, better error models are required by the new generation of satellite clocks at the picosecond level. Another impressive progress is the official release of the manufacturer’s antenna PCC model for Galileo, which makes it possible for GNSS to contribute to the determination of the scale factor of the terrestrial reference frame independently. Therefore, satellite metadata is always preferred. On the one hand, the orbit model and the satellite antenna model can be refined, while on the other hand, hidden potencies of GNSS PPP are expected to be unveiled. Moreover, the multi-GNSS with multi-frequency have been demonstrated to be able to shorten the convergence time and speed up the PPP–AR with PPP–RTK.

It is also worth noting that possibilities have been revealed by combining GNSS PPP with other techniques, e.g., SLR, VLBI and Interferometric Synthetic Aperture Radar (InSAR). No observation system stands alone, even for GNSS, which indicates they may suffer from common error sources to different extents, especially for those ground-based measurements. In this case, an accurate error model can be established and shared with other techniques. Examples are found in SLR and LEO, which can help improve the GNSS orbit determination and calibrate the absolute satellite antenna PCC model of GNSS, respectively. Consequently, more accurate measurements will be obtained so that the error model can be further improved and vice versa. Though acting as a positive feedback system, better cooperation between systems is required. Unfortunately, there are often systematic technique-specific errors in most cases, preventing from doing so. It is thereby still challenging to find a way with optimal and holistic use of these techniques. In the long run, considering the enhancement of error models, data or information that was buried in the noise of these error models will show up. With most unmodelled systematic technique-specific errors being corrected, observations at low elevations may be fully exploited to probe the atmosphere, and combinations of GNSS with other space geodetic techniques will become easier.

In spite of all the benefits, the advent of multi-GNSS with multi-frequency introduces nuisances at the same time. Compatibility and interoperability need to be considered when combining the multi-GNSS observations. Due to the limitation of frequency resources and the growing number of GNSS signals, some frequency bands shared by several GNSSs (Dawoud 2012; European GNSS Agency 2020; Morton et al. 2020), e.g., B1I/L1/E1, B2a/E5a/L5, B2b/G3/E5b, are becoming crowded. Moreover, it has been reported that interferences appear and lead to performance degradation. While for interoperability, this not only refers to ISBs and IFBs, but to introduce all the error sources that are system-dependent or satellite-dependent, e.g., satellite clock and antenna PCC. Even a new type of GNSS hardware could lead to a new set of all the related error models for the new biases. As the number of biases increases, achieving PPP–AR will be more challenging. Together with the continuing modernization and extension of the GNSS constellations, these cases will become more complicated. As different MGEX ACs may adopt different error models for each system with different sets of global GNSS networks, the precise products generated by all the ACs may become inconsistent with each other, e.g., the clock datum. It is often recommended to apply the same models and processing strategies as used by the provider. However, they are not available with full details in many cases, especially over a long period of time. Until now, there are still no official precise products of multi-GNSS available from either IGS or MGEX. According to a workshop held online, that is, the third stop of the Tour de I’IGS, the orbit and clock combination for multi-GNSS may be released at around mid-2022 (https://igs.org/tour-de-ligs-presentations/), but there are still no official announcements of the combination products at the time of this writing (February 2023). More consistent and convenient IGS/MGEX precise products can be expected.

Still, due to correlations between error sources and lack of “true values” for comparison, it is hard to give the exact accuracy of ranging measurements after errors in GNSS observables are eliminated or corrected by models. Although we mainly focused on error models in static PPP modes with an ideal environment surrounding a stand-alone receiver, one needs to keep in mind that the requirements for error models (e.g., accuracy or model itself) could vary with PPP modes (i.e., static and kinematic), and high-precision observations are challenging to ensure as they also depend on the surrounding environment (e.g., signal blockage and multipath). Nonetheless, one can expect to fully exploit the observational potential of the carrier phase at the millimeter or even sub-millimeter level since the error mitigations are refined continuously in GNSS PPP with multi-GNSS as discussed above. To achieve this goal, more accurate error models are required to be further investigated, and delicate errors that used to be neglected also need to be considered at this stage. Thereafter, millimeter-level accuracy with the GNSS PPP–RTK technique is promising. The new potency of integrating different geodetic techniques is preferred to remedy original deficiencies of GNSS, which is not only good for GNSS itself but also facilitates the integration of all the geodetic techniques as a whole in GGOS.

Finally, if we look into the future, with the advent of augmented constellations, such as LEO constellations, new opportunities have been revealed by many studies (Hein 2020). Over the past two decades, LEO satellites piggybacked with payloads for scientific missions have been validated to have good performances, e.g., Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC) for GNSS radio occultation (Rocken et al. 2000), Gravity Recovery and Climate Experiment (GRACE) for gravity field retrieval (Tapley et al. 2004), etc. (Li et al. 2022e). Thanks to continuous improvements on the manufacturing and launching of the satellite, the cost of LEO satellite has been reduced gradually (Ge et al. 2022), which makes it possible to build and maintain large LEO constellations with hundreds of satellites to have a good coverage of the Earth’s surface. In fact, since 2015, more and more commercial enterprises have decided to deploy their own LEO constellations, e.g., Boeing (Selding 2016), Oneweb (Henri 2020), Starlink (McDowell 2020), and so on (Lawrence et al. 2017; Ge et al. 2022). Although most of them are mainly built for commercial purposes, i.e. providing all-weather and low-latency Internet service around the world (Zhang and Ma 2019), they can contribute to scientific studies by piggybacking some payloads as before mentioned. Besides, the possibility of providing Positioning, Navigation and Timing (PNT) services for LEO-augmented GNSS was also demonstrated systematically by Reid et al. (2016) and verified in the Luojia-1A satellite (Wang et al. 2018). As LEO satellites generally fly at an altitude of about 300–2000 km, one can not only receive the navigation-augmented signal from the LEO satellites through the ground-based stations, but also obtain observations from GNSS satellites by the LEO-based GNSS receiver. In this case, the LEO augmented constellation is able to fill observation gaps existing in today’s GNSS, especially in the area without ground stations, such as the ocean and polar regions (Ren et al. 2020). And therefore, with a better coverage of observations and better satellite geometry, the accuracy of precise products including orbit, clock, and ERP, as well as the ionosphere modelling, can be improved significantly, see e.g., (Männel and Rothacher 2017; Li et al. 2019a, 2021; Strugarek et al. 2019; Ren et al. 2020). Likewise, due to the lower altitudes, LEO satellites move faster, which gives the geometric diversity needed by PPP–AR and leads to PPP with a shorter convergence time (perhaps within 1 min in the future) (Li et al. 2019c; Ge et al. 2022). While for atmosphere monitoring, it will benefit from observations of higher spatial and temporal resolution from LEO satellites (Xiong et al. 2021) since they take longer trajectories than those of GNSS when passing through ground stations. However, all these opportunities are accompanied, at the same time, by challenges, including the design and maintenance of constellation, computational burden, etc. (Zhang and Ma 2019; Ge et al. 2022), and most of the above results are based on simulations or real datasets from a few LEO satellites today. Nevertheless, they have revealed the potencies of LEO-augmented GNSS, in terms of almost all error sources in GNSS PPP. To date, over 20 LEO satellite launch plans have been announced by famous companies or institutes (Ren et al. 2020). Thousands of LEO satellites will be fully operational once all the plans are finished. Until then, a new era would be expected to open not only for GNSS-based space geodesy but also for the GGOS.