Introduction

Precise point positioning (PPP), as a positioning technique, can obtain centimeter positioning accuracy using a single station without direct or explicit reference stations. The technique has made a lot of progress in the aspect of observation model, error modeling and data quality control since it was proposed (Malys and Jensen 1990; Zumberge et al. 1997; Kouba and Héroux 2001; Teunissen 2018). Usually, PPP needs about 30 min to converge to the centimeter level, which largely limits the application of PPP in real-time. One way to shorten the convergence time is to provide precise atmospheric corrections and constrain the corresponding parameters. However, this requires more expensive infrastructure to generate and broadcast the local ionospheric and tropospheric corrections. The integer ambiguity resolution, which converts the ambiguous carrier measurements into high-precision range observations, has been considered another important means of shortening the convergence time (Blewitt 1989; Ge et al. 2008). It has been the research hotspot among the GNSS community for the last 5 years (Laurichesse et al. 2010; Li and Zhang 2014; Geng et al. 2019).

Since the ambiguity parameters absorb the hardware delay and initial phase bias during the PPP filtering process in a single receiver mode, the additional corrections, uncalibrated satellite phase delay (UPD), are needed to restore the integer nature of ambiguities (Ge et al. 2008). Investigations on multi-constellation PPP-IAR are particularly conducted. Over 50% of real-time PPP-IAR solutions can be initialized in 5 min when involving GPS + GLONASS data while that of GPS is only 4% as reported in Geng and Shi (2017). The GPS + BDS-2 PPP-IAR solutions also outperform that of single-system PPP-IAR, the average time to first fix (TTFF) is shortened from 33.6 min to 24.6 min as reported in Pan et al. (2017). With GPS + BDS-2 + GLONASS combined, about 90.0% of PPP-IAR cases can be fixed within 10 min (Liu et al. 2017), which further demonstrated that multi-constellation plays an important role in the rapid convergence of PPP-IAR, with more satellites contributing to the PPP filtering process.

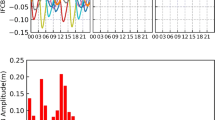
Most of the above studies are based on GNSS dual-frequency measurements. In particular, our earlier study reported that the positioning accuracy achieved with BDS/GPS/Galileo is better than 6 mm in horizontal components and 20 mm in vertical component with about 1.37 min convergence time (Zhao et al. 2021). However, it still does not reach the level of instantaneous IAR. This could be further improved by using additional third frequency signals, thanks to that the emerging navigation systems are designed for supporting more than two frequency signals. Since the satellite clock products are normally produced with L1/L2 ionosphere-free (IF) combinations, additional attention should be paid to the inter-frequency clock bias (IFCB) when involving more than two frequencies (Montenbruck et al. 2012). The research shows that IFCB has time-varying characteristics, in which the amplitude of GPS BLOCK IIF is the largest, about 10–25 cm, and other systems are relatively smaller and stable (Zhang et al. 2017; Gong et al. 2020). The time-varying signal is considered to be caused by the thermal change of the aircraft (Montenbruck et al. 2012).

The involvement of the third frequency promotes the integer ambiguity resolution. The TCAR (Three-Carrier Ambiguity Resolution) method and the CIR (Cascading Integer Resolution) method are proposed by forming combined observations with a longer wavelength and less noise (Vollath et al. 1999; Hatch et al. 2000). A typical TCAR method of selecting two ionosphere-reduced extra wide-lane (EWL) to instantaneously resolve wide-lane (WL) ambiguity is analyzed in Feng (2008). The results show that the TCAR procedure greatly shortens the TTFF from tens of minutes to a few minutes in long-distance RTK (Feng and Li 2010). PPP triple-frequency ambiguity resolution has also drawn a lot of attention in recent years. Geng and Bock (2013) first used the virtual GPS triple-frequency observation and adopted an ambiguity-fixed ionosphere-free (AFIF) method to quickly fix the wide-lane ambiguity. Results show that 99% of the ambiguities can be fixed within 65 s utilizing simulated triple-frequency GPS observations. Triple-frequency PPP can also be implemented using two ionosphere-free combinations, and TTFF is shortened with the addition of the third frequency as reported (Li et al. 2019). However, different selections of multiple ionosphere-free (IF) combinations undoubtedly aggravate the complexity of the function model. The uncombined model can directly process the individual frequency, thus making it more suitable for multi-frequency data processing. The uncombined model is adopted to successfully extract the EWL and WL phase bias utilizing a BDS-2 reference network (Gu et al. 2015). More research is conducted, and more evidence is reported that the third frequency has played an important role in PPP convergence. For example, the triple-frequency GPS/Galileo/BDS-2 combined solutions are evaluated in terms of positioning accuracy and convergence time in Li et al. (2020). Results show that the convergence time of triple-frequency PPP-IAR can be reduced by 15.6% compared with dual-frequency. It is also noticed that the contribution of the third frequency to the position accuracy is marginal after convergence. PPP-IAR tests with GPS/BDS-2/Galileo/QZSS combined are also conducted in Geng et al. (2020). Results show that the mean initialization time reduces from 9.2 min for dual-frequency PPP-IAR to 6.1 min for triple-frequency PPP-IAR. However, the instantaneous IAR is still not achieved yet from these earlier studies.

With the successful operation of the BDS-3 constellation, there are nearly 90 satellites that can broadcast multi-frequency signals at present. However, there are few reports on BDS-3-based triple-frequency PPP-IAR. This contribution focuses on the instantaneous convergence for PPP using triple-frequency raw observations from BDS-2/3, Galileo, GPS, and QZSS. Multi-GNSS observations for a selected day in 2021 from a regional network located in China are collected to determine satellite hardware delays, and another 20 stations are employed to validate the PPP-IAR performance.

First, the PPP model for triple-frequency raw observations is introduced, along with the satellite UPD extraction method and the ambiguity resolution strategy. Then, the dataset and processing strategy are described. Afterward, the results of UPD products and the positioning performance are analyzed, emphasizing the impact of multi-frequency and multi-constellation on the PPP convergence. Finally, our conclusions and findings are summarized.

Methodology

This section first describes the methodology of the proposed multiple-frequency PPP algorithms. Then, a cascading UPD derivation for EWL, WL and N1 ambiguity is given, followed by a simple description for triple-frequency PPP-IAR.

PPP model for triple-frequency raw observation

The uncombined geometry-based (GB) model can be expressed as follows:

$$E\left\{ {\delta p_{i,r}^{s,g} } \right\} = \mu_{r}^{s,g} \Delta x_{r} + \widetilde{\delta t}_{r}^{,g} + \gamma_{i}^{,g} \tilde{I}_{r}^{s,g} + m_{r}^{s,g} T_{r} + M_{i,r}^{s,g}$$
(1)
$$E\left\{ {\delta \emptyset_{i,r}^{s,g} } \right\} = \mu_{r}^{s,g} \Delta x_{r} + \widetilde{\delta t}_{r}^{,g} - \gamma_{i}^{,g} \tilde{I}_{r}^{s,g} + m_{r}^{s,g} T_{r} + \Psi_{i,r}^{s,g} + \lambda_{i}^{,g} \tilde{N}_{i,r}^{s,g}$$
(2)

where \(E\left\{ \cdot \right\}\) is the expection operator, and \(\delta p_{i,r}^{s,g}\) and \(\delta \emptyset_{i,r}^{s,g}\) are the observed minus computed (OMC) values. The observed values are code and phase measurements between satellite \(s\) of a constellation identifier \(g\), and stations \(r\) at frequency \(i \left( {i = 1,2,3} \right)\). The computed values are calculated from the precise orbit and clock and a prior coordinates of the station. \(\mu_{r}^{s,g}\) denotes the line-of sight (LOS) vector of unit length, and \(\Delta x_{r}\) is the incremental values with respect to the priori position. \(\widetilde{\delta t}^{s,g}\) is the reparametrized receiver clock term, which contains the actual receiver error and a combination of receiver code and phase hardware delays at frequencies 1 and 2; see Zhao et al. (2021). \({T}_{r}\) denotes the zenith tropospheric delay with its mapping function \({m}_{r}^{s,g}.\) \({\widetilde{I}}_{r}^{s,g}\) is the reparametrized ionosphere term that lumped the actual ionosphere delay and a combination of receiver and satellite code and phase hardware delays at frequency 1 and 2, see Zhao et al. (2021). Above-mentioned parameters are the same for both dual and three-frequency cases. \(\gamma_{i} = \left( {\lambda_{i}^{,g} /\lambda_{1}^{,g} } \right)^{2}\) and the corresponding wavelength \({ }\lambda_{i}^{,g}\). The ambiguity terms are parametrized as:

$$\begin{aligned} \tilde{N}_{{i,r}}^{{s,g}} = & N_{{i,r}}^{{s,g}} \\ & + \frac{1}{{\lambda _{i}^{{,g}} }}\left\{ {d_{{\emptyset _{{i,r}}^{{,g}} }} - d_{{\emptyset _{i} }}^{{s,g}} + \frac{{\gamma _{i}^{{,g}} + \gamma _{1}^{{,g}} }}{{\gamma _{2}^{{,g}} - \gamma _{1}^{{,g}} }}\left( {d_{{p_{{2,r}}^{{,g}} }} - d_{{p_{2} }}^{{s,g}} } \right) - \frac{{\gamma _{i}^{{,g}} + \gamma _{2}^{{,g}} }}{{\gamma _{2}^{{,g}} - \gamma _{1}^{{,g}} }}\left( {d_{{p_{{1,r}}^{{,g}} }} - d_{{p_{1} }}^{{s,g}} } \right)} \right\} \\ \end{aligned}$$
(3)

The code-specific hardware bias \(M_{i}^{s,g}\) and phase-specific hardware bias \({\Psi }_{i}^{s,g}\) are therefore derived as:

$$M_{{i,r}}^{{s,g}} = \left\{ {\begin{array}{*{20}c} {0,\;i = 1,2\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,} \\ {\frac{{\gamma _{i}^{{,g}} - \gamma _{1}^{{,g}} }}{{\gamma _{2}^{{,g}} - \gamma _{1}^{{,g}} }}\left( {d_{{p_{{1,r}}^{{,g}} }} - d_{{p_{{2,r}}^{{,g}} }} - d_{{p_{1} }}^{{s,g}} + d_{{p_{2} }}^{{s,g}} } \right) + \left( {d_{{p_{{1,r}}^{{,g}} }} - d_{{p_{{3,r}}^{{,g}} }} - d_{{p_{1} }}^{{s,g}} + d_{{p_{3} }}^{{s,g}} } \right),\;i > 2} \\ \end{array} } \right.$$
(4)
$$\Psi _{{i,r}}^{{s,g}} = \left\{ {\begin{array}{*{20}c} {0,\;i = 1,2\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;{\mkern 1mu} \;} \\ {\frac{{\gamma _{i}^{{,g}} - \gamma _{1}^{{,g}} }}{{\gamma _{2}^{{,g}} - \gamma _{1}^{{,g}} }}\left( {\delta d_{{\emptyset _{{1,r}}^{{,g}} }} - \delta d_{{\emptyset _{{2,r}}^{{,g}} }} - \delta d_{{\emptyset _{1} }}^{{s,g}} + \delta d_{{\emptyset _{2} }}^{{s,g}} } \right)} \\ { - {\text{ }}\left( {\delta d_{{\emptyset _{{1,r}}^{{,g}} }} - \delta d_{{\emptyset _{{3,r}}^{{,g}} }} - \delta d_{{\emptyset _{1} }}^{{s,g}} + \delta d_{{\emptyset _{3} }}^{{s,g}} } \right),\;i > 2} \\ \end{array} } \right.$$
(5)

where \(d_{{p_{i,r}^{,g} }}\) and \(d_{{p_{i} }}^{s,g}\) represent the constant part of code-specific hardware delays at receiver and satellite end, respectively, while \(d_{{\emptyset_{i,r}^{,g} }}\) and \(d_{{\emptyset_{i} }}^{s,g}\) represent the constant part of phase-specific hardware delays. The variation part of phase-specific hardware delays is further considered, with \(\delta d_{{\emptyset_{i,r}^{,g} }}\) and \(\delta d_{{\emptyset_{i} }}^{s,g}\) represent the variations at receiver and satellite end (Montenbruck et al. 2012).

It is noticed that \(M_{i,r}^{s,g}\) with \(i > 2\) not only includes the hardware delays of the third frequency, but also affected by that of the first and second frequency introduced by the clock parameters. The satellite part of \(M_{i,r}^{s,g}\) can be calibrated utilizing MGEX P1–P2/P1–P3 final differential code bias (DCB) products or observable-specific signal bias (OSB), while the receiver part of each constellation is regarded as common among satellites. Additional parameters for each constellation to absorb the receiver part of \(M_{3,r}^{s,g}\) should be set along with others during the filtering; otherwise, the code observations at the third frequency will be biased in this model. The constant part of phase-specific hardware delays can be absorbed into ambiguities, while the variations are lumped into \({\Psi }_{i,r}^{s,g}\). \({\Psi }_{i,r}^{s,g} = 0\) with \(i \le 2\) indicates that the variation part of phase-specific hardware delays for the first two frequency vanishes in the list of parameters. But this is not for\(i>2\), in particular, the case of GPS L5 measurements. The variation impact is corrected using the same strategy as proposed in Li et al. (2013), which will not be presented in detail in this contribution.

Satellite phase bias and ambiguity resolution.

Considering the hardware delays are also included in the estimates of phase ambiguity, the integer nature of ambiguity is contaminated and only float-PPP solution can be obtained if without correction of phase bias products. It is noticed from (3) that the float ambiguity consists of both code and phase measurements related to hardware delays; let us simplify the term as \(\tilde{N}_{i,r}^{s,g} = N_{i,r}^{s,g} + b_{i,r} - b_{i}^{s,g}\), where \(N_{i,r}^{s,g}\) is the integer ambiguity between station r and satellite s on frequency i; \(b_{i,r}\) and \(b_{i}^{s,g}\) are the corresponding fractional part originated from the stations and satellites, respectively. The integer part of hardware delays could also be absorbed into phase ambiguities.

Since ambiguities and ionosphere parameters are highly correlated, only taking raw ambiguities as input to extract UPDs results in low accuracy (Li et al. 2018; Zhao et al. 2021). A cascading strategy that forms the linear combinations first to mitigate geometric and ionospheric effects is more favored. Analogous to Gu et al. (2015), the fractional EWL, WL, and N1 biases are determined sequentially in this study. The corresponding ambiguity (i.e.,\(\tilde{N}_{ewl,r}^{s,g}\), \(\tilde{N}_{wl,r}^{s,g}\) and \(\tilde{N}_{1,r}^{s,g}\)) could be formed with the individual ambiguities at three frequencies and expressed as follows:

$$\left[ {\begin{array}{*{20}c} {\tilde{N}_{ewl,r}^{s,g} } \\ {\tilde{N}_{wl,r}^{s,g} } \\ {\tilde{N}_{1,r}^{s,g} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 & { - 1} \\ 1 & { - 1} & 0 \\ 1 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{N}_{1,r}^{s,g} } \\ {\tilde{N}_{2,r}^{s,g} } \\ {\tilde{N}_{3,r}^{s,g} } \\ \end{array} } \right]$$
(6)

For simplicity, we just take the extra wide-lane as an instance to demonstrate the processing strategy for the determination of UPD. Assume there are r stations and s satellites in the network, the observations matrix can be formed as:

$$\left[ {\begin{array}{*{20}c} {a_{ewl,1}^{1,g} } \\ {a_{ewl,2}^{1,g} } \\ \vdots \\ {a_{ewl,r}^{s,g} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {I_{r} \otimes e_{s} } & { - e_{r} \otimes I_{s} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {b_{ewl,1} } \\ {b_{ewl,2} } \\ \vdots \\ {b_{ewl}^{s,g} } \\ \end{array} } \right]$$
(7)

where \(\otimes\) is the Kronecker product; \(I_{r}\) and \(I_{s}\) are the unit matrix with r and s dimensions; \(e_{s}\) and \(e_{r}\) are a vector with one entries with dimension of \(s \times 1\) and \(r \times 1\). The fractional part \(a_{ewl,r}^{s,g}\) consisted of both satellite-related and receiver-related bias can be obtained by:

$$a_{ewl,r}^{s,g} = \tilde{N}_{ewl,r}^{s,g} - \tilde{N}_{ewl,r}^{s,g}$$
(8)

where \(\left\langle \cdot \right\rangle\) is the round operator. \(b_{ewl}^{s,g}\) of an arbitrary satellite is selected as zero to solve rank deficiency. Attention should be paid that \(a_{ewl,r}^{s,g}\) may be − 1 or 1 cycle biased with the actual value. The proper initialization of \(b_{ewl,r}\) and \(b_{ewl}^{s,g}\) values is therefore extremely important.

For the user side, the method of LAMBDA with partial ambiguity resolution is adopted to obtain the optimal integer solutions (Teunissen 1995). Instead of feeding the full ambiguities of three frequencies into the integer estimator in one step, the EWL/WL/N1 ambiguities, an explicit decorrelation from the raw ones, are resolved stepwise for the rovers. In each step, the LAMBDA method is applied. In this way, the ambiguity dimension and the search space are significantly reduced. The computational burden is therefore reduced. It is easier to pass the ratio test with the subset ambiguities. Keep in mind that the final ambiguity-fixed solutions only refer to the solutions with all EWL/WL/N1 ambiguities resolved in this contribution.

Data collection and processing strategy

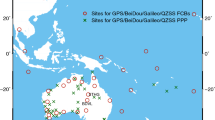
To verify the contribution of three frequency observations to PPP, the GNSS data of a regional network located in China on DOY 308 in 2021 are selected. The distribution of these stations is shown in Fig. 1, of which 36 stations are selected as a reference for estimating UPD products, and another 20 stations are used as rovers for PPP verification. These stations are equipped with UB4B0 receivers and Dywell antenna, which can fully support GPS L1/L2/L5, Galileo E1/E5a/E5b, BDS-2 B1/B3/B2b, BDS-3 B1/B3/B2a, and QZSS L1/L2/L5 observations. Due to the inclusion of the third frequency, the daily or monthly satellite DCB should be pre-corrected as illustrated in (4). MGEX products generated by Wuhan University (Zhang and Zhao 2018) are used for this purpose. The multi-GNSS products of WHU (WUM) are selected for BDS/Galileo/GPS/QZSS orbit and clock corrections (Guo et al. 2016).

Fig. 1
figure 1

Distribution of 36 reference stations (blue circle) and 20 rover stations (red star)

Full size image

The raw ambiguities of each frequency are estimated in an uncombined and undifferenced manner at the server. Earlier studies report that there is a non-negligible bias between BDS-2 and BDS-3 ISB parameters (Zhao et al. 2020). Therefore, we treat BDS-2 and BDS-3 as individual GNSS systems for data processing in this study. This is also convenient to select separate reference satellites for BDS-2 and BDS-3 satellites as they have different third frequencies. The prior noise of code and phase observations is set as 0.3 m and 0.003 m, respectively, for each frequency in all constellations, except for BDS-2 IGSO satellites. Due to the less precise orbit of BDS-2 IGSO, we down-weight the corresponding observation to 0.6 m and 0.006 m for pseudorange and phase observations, respectively. An elevation-dependent function, i.e., \(\left( {2 \cdot \sin \left( {{\text{ele}}} \right)} \right)^{2}\) for satellites with elevation lower than 30° and 1.0 for those above 30 degrees, for weighting observations is adopted to mitigate the multipath effects of low-elevation satellites. Considering the poor orbital accuracy of GEO satellites, C01–C05 satellites are excluded from data processing. The satellite-induced code biases of other BDS-2 satellites are corrected using an empirical model (Wanninger and Beer 2015). Other processing details are given in Table 1.

Table 1 Multi-GNSS processing strategy for UPD/PPP
Full size table

Results

In this section, the analysis of UPD products is first presented. Then, the positioning tests are carried out to verify the multi-frequency and multi-constellation PPP-IAR performance, emphasizing convergence time.

UPD

Figure 2 plots the EWL UPD series for GPS + QZSS/BDS-2/BDS-3/GAL. GPS has the largest STDs, while EWL UPDs of GAL and QZSS are the most stable. The average STD values of GPS/QZSS/BDS-2/BDS-3/Galileo are 0.017/0.003/0.010/0.014/0.003 cycle, respectively. Nevertheless, the EWL UPDs for all constellations seem to be a constant within a day, which is also observed in Geng and Guo (2020). Figure 3 plots the WL UPD for the same systems. The series exhibits slightly larger fluctuation compared with EWL, and the average STD values of the corresponding systems are 0.024/0.015/0.046/0.007/0.042 cycles. There seems to be discontinuous for all satellites in the BDS-2 constellation around 9 AM, which may be related to a change of reference satellites. It is noticed that BDS-3 exhibits a more stable WL series with an STD of 0.007 cycles than that of EWL, which may be due to some datum changes in the EWL series as observed in Fig. 2. For N1 UPDs, the wavelength of the raw ambiguity is around 20 cm, much smaller than EWL and WL ones, making it more susceptible to residual errors. As can be seen from Fig. 4, the series is much noisier than WL UPD, STDs for the corresponding systems are 0.060/0.030/0.059/0.048/0.042/cycle.

Fig. 2
figure 2

EWL UPD time series for GPS + QZSS/BDS-2/BDS-3/GAL on DOY 308, 2021

Full size image
Fig. 3
figure 3

WL UPD time series for GPS + QZSS/BDS-2/BDS-3/GAL on DOY 308, 2021

Full size image
Fig. 4
figure 4

N1 UPD time series for GPS + QZSS/BDS-2/BDS-3/GAL on DOY 308, 2021

Full size image

Convergence analysis

In this section, 20 stations evenly distributed in China, as depicted in Fig. 1, are selected for positioning analysis. In order to analyze the contribution of the multi-frequency and multi-constellation to PPP-IAR convergence, several positioning experiments are conducted. Considering that there are only four satellites in QZSS constellation, and QZSS and GPS are always analyzed together (still regarded as an individual constellation) in this study. Analysis of the impact of the third frequency and convergence verification is discussed in the following sections.

Contribution of the third frequency on the convergence

First, we focus on evaluating the impact on PPP convergence under the premise of introducing only one ambiguity resolution constraint of the EWL. The predefined cascading ambiguity essentially applies a preset Z-transformation based on (6) to the original ambiguities set (Teunissen et al. 2002). With the bootstrapping process, the search space of other ambiguity parameters can be reduced under the constraint of fixed EWL ambiguities in previous step. In order to make some quantitative analysis of the constraint effect, RO13 station is taken as an example to solve the triple-frequency PPP-IAR of single BDS constellation. The accuracy of the UPD-corrected EWL, WL and N1 ambiguities during the process is evaluated using the following expression for comparison:

$$\Delta b_{t,r}^{s,g} = \tilde{N}_{t,r}^{s,g} - \left( {\hat{N}_{t,r}^{s,g} + b_{t,r} - b_{t}^{s,g} } \right)$$
(9)

where \(\tilde{N}_{t,r}^{s,g}\) and \(\hat{N}_{t,r}^{s,g}\) are the float value of ambiguity and the final fixed integer ambiguity for type \(t\), respectively, and \(\Delta b_{t,r}^{s,g}\) is the difference. Let us call it residual, between the float values and the “ground truth values,” i.e., the correct fixed integers. We restart the PPP filter every 10 min to ensure that most of float ambiguities are in the beginning of convergence period. The ambiguities are then collected, and their residuals with respect to the “ground truth values” are depicted in Figs. 5 and 6.

Fig. 5
figure 5

Concentricity of float EWL ambiguity residuals (a), WL float ambiguity residuals (b) and WL float ambiguity residuals with EWL-fixed constraint (c)

Full size image
Fig. 6
figure 6

Concentricity of float N1 ambiguity residuals (a), N1 float ambiguity residuals with EWL-fixed constraint (b), N1 float ambiguity residuals with WL-fixed constraint (c) and N1 float ambiguity residuals with both EWL and WL fixed constraints (d)

Full size image

As Fig. 5a shows, the residual part of the float EWL ambiguity is rather close to zero after UPD corrections, with a percentage of 96.1% within ± 0.1 cycles and 99.6% within ± 0.2 cycle. The LAMBDA method or even rounding procedure can easily help us get correct integer EWL ambiguity solutions. The concentricity of float WL ambiguities with respect to the corresponding integers, illustrated in Fig. 5b, is much less than the case of EWL with 61.3% within ± 0.1 cycles and 79.1% within ± 0.2 cycles. Generally, the precision of code observation dominates the accuracy of ambiguities at the beginning of convergence. However, with the inclusion of the resolved EWL constraint, the concentricity of WL ambiguities is significantly improved. The percentage of the fractional part within ± 0.1 cycle and ± 0.2 cycle improves to 83.4% and 91.3%, respectively. The improvement of WL ambiguity concentricity can certainly improve the fixing rate of WL ambiguities, subsequently, shortening the convergence.

However, only fixing WL ambiguities is not the final goal; fixing N1 ambiguities is the key to achieving high accuracy and subsequent real convergence. Figure 6 shows the concentricity statistics of N1 ambiguity residuals under different ambiguity fixed constraints. The accuracy of N1 float ambiguity residuals is dominated by the precision of pseudorange observations during the convergence, which ranges from ± 2.0 to ± 3.0 cycles to the true values, as shown in Fig. 6. The percentage of ambiguity residuals within ± 1.0 cycle is 51.9%, which is improved by only 3.6% after EWL constraint. The effect on the WL ambiguity resolution is depicted in Fig. 6c for comparison. Improvement of only 9.2% is achieved compared without constraint, slightly better than that of EWL integer constraint. However, the EWL and WL constraints are jointly applied, and the percentages of residuals within 0.5 cycles and 1.0 cycles improve to 70.6% and 90.2%, respectively. This is more favorable for the final N1 ambiguity resolution than using only WL fixed constraint. Through our analysis, a preliminary conclusion can be made is that the introduction of the third frequency enables us to form and fix the EWL ambiguity so as to accelerate the success rate of fixing the WL ambiguity, consequently speeding up the fixing rate of N1 ambiguities, and eventually shorten the convergence of PPP positioning.

It is possible to investigate the positioning convergence with different ambiguity fixed modes: (1) all ambiguities are float, (2) EWL fixed and WL, N1 float, abbreviated as EWL-fixed, (3) WL fixed and EWL, N1 float, abbreviated as WL-fixed (4) EWL, WL fixed and N1 float, abbreviated as EWL + WL-fixed (5) all types of ambiguities fixed, abbreviated as N1-fixed. Figure 7 shows the BDS-only triple-frequency positioning series of RO13 under each ambiguity fixing mode. A typical convergence arc during the 6:00–8:00 is displayed for clear detail, and the accuracy of E/N/U components in the first 10 min is summarized in Table. 2. The accuracy improves in EWL-fixed and WL-fixed solutions with 13% and 35% on average, respectively. With both EWL and WL being constrained, the accuracy improvements of 86%, 86% and 85% are achieved for E/N/U directions compared with float solutions, respectively. The convergence of PPP can be greatly improved, which also confirms the preliminary conclusion as we made earlier. The final N1 integer ambiguities can be easily identified after EWL and WL combined constraint. The N1-fixed solutions can converge within one epoch, as depicted in Fig. 7, which reveals that after the inclusion of the third frequency, PPP has the potential to achieve instantaneous integer ambiguity resolution.

Fig. 7
figure 7

BDS-only PPP convergence series of RO13 in float, EWL-fixed, WL-fixed, EWL + WL-fixed and N1-fixed mode

Full size image
Table 2 BDS-only PPP accuracy of RO13 for the first 10 min under different positioning modes
Full size table

Contribution of the multi-constellation on the convergence

In order to analyze the impact of multi-constellation on convergence performance of triple-frequency PPP-IAR, we still take RO13 as an example and reset the filtering every 2 h to analyze convergence time. In each restart, all parameters are reinitialized so as to simulate the warm start of a GNSS receiver. The convergence criteria for horizontal and vertical positioning accuracy are set to be better than, respectively, 5 and 10 cm. As the BDS constellation has the largest number of satellites supporting multi-frequency signals, we take it as the primary constellation for all four strategies to evaluate the contribution of other constellations on convergence. The strategies are as follows: (1) BDS-only; (2) BDS + Galileo; (3) BDS + GPS + QZSS; (4) BDS + Galileo + GPS + QZSS.

Figures 8, 9, 10, 11 plot the PPP E/N/U time series of ambiguity-float and ambiguity-fixed solutions produced with the four strategies. As can be seen from Fig. 8, most of the restarts can converge below 10 cm after 20 min for BDS float solutions, but there are also some worse periods, such as 6:00–8:00 and 14:00–16:00, during which the series is rather unstable. It generally takes even more time to converge for the East component for all restarts. However, with the assistance of UPD corrections and the third frequency observations as discussed above, the integers of those ambiguities can be identified and fixed within 1–2 min. The positions are stably maintained at the centimeter level after ambiguity resolution, as depicted in Fig. 8. The average convergence time for E/N/U directions is 101/108/115 s. Some good restarts fulfill our convergence requirements within one epoch like 2:00–4:00, indicating instantaneous ambiguity-fixed could at least occasionally be achievable for BDS-only solutions. This piece of result has not been seen in previous studies. With the joint of Galileo, as plotted in Fig. 9, the convergence time is shortened for both float and fixed solutions, especially during the period of 6:00–8:00. For ambiguity-float solutions, the average convergence time is 807/410/753 s for E/N/U directions, with an improvement of 32%/56%/40% compared to BDS-only, respectively. For ambiguity-fixed solutions, most of the restarts can converge within one epoch under our convergence requirements for horizontal directions, which is rather promising. However, some worse restarts are as 16:00/20:00/22:00. The average convergence time is 32/52/67 s for E/N/U with an improvement of 68%/52%/42% compared to BDS-only, respectively. The results of BDS/GPS/QZSS are further plotted in Fig. 10, with similar performance compared with BDS/GAL strategy. Improvements of ambiguity-float solutions are 11%/43%/42% for E/N/U directions compared with BDS-only, slightly worse than that of BDS/GAL, especially in east directions, which may benefit from better satellite clocks of Galileo for BDS/GAL mode. Nevertheless, the average convergence time is 31/31/73 s for E/N/U directions, slightly better than that of BDS/GAL. The result of the last strategy is plotted in Fig. 11 with all constellations combined. In terms of ambiguity-float solutions, the best performance is observed in N/U directions among the four strategies, with improvements of 65%/56% compared to BDS-only solutions, respectively. The convergence time for ambiguity-fixed solutions is further shortened to 1 s for both horizontal and vertical directions, with only one exception at 20:00.

Fig. 8
figure 8

PPP (red) and PPP-IAR (blue) solutions of BDS for east (top), north (middle) and up (bottom) components

Full size image
Fig. 9
figure 9

PPP (red) and PPP-IAR (blue) solutions of BDS/Galileo for east (top), north (middle) and up (bottom) components

Full size image
Fig. 10
figure 10

PPP (red) and PPP-IAR (blue) solutions of BDS/GPS/QZSS for east (top), north (middle) and up (bottom) components

Full size image
Fig. 11
figure 11

PPP (red) and PPP-IAR (blue) solutions of BDS/Galileo/GPS/QZSS for east (top), north (middle) and up (bottom) components

Full size image

To find more evidence of fast convergence of triple-frequency PPP-IAR, a 10-min restart test utilizing the same products is conducted. The test lasted for 21 h and was repeated totally about 2520 times for all 20 user stations. The same criteria to determine the convergence are used as for the 2-h restart case.

Figures 12, 13, 14, 15 plot the positioning error in E/N/U directions for the over 2500 times resets for four strategies. The convergence criteria are plotted in dashed black lines for the corresponding directions. The cross points of the dashed line with red curve and the green curve indicate the convergence time used at 95% and 68% confidence level, respectively. If the dashed line is above the red or green curve, it means the instantaneous ambiguity-fixed is achieved at 95% or 68% confidence level. The last panel plots the average number of fixed satellites at each epoch as well as the ambiguity-fixed rate \({R}_{fixed}\) series, which is defined as the ratio of the number of cases with ambiguity-fixed solutions to the total number of resets. We further summarized the convergence time with the confidence level of 68% and 95% along with the average number of used satellites for each strategy in Table 3. Starting with the BDS-only solutions as depicted in Fig. 12, the average number of available satellites is 16.2, including 6.5 BDS-2 satellites and 9.7 BDS-3 satellites, and the average number of fixed satellites reaches 13.2. Those series in E/N/U directions are quite discrete as can be seen from the top 3 panels. Some very poor cases do not converge at the end of 10 min. Nevertheless, some good cases reach our convergence criteria in seconds, i.e., a few epochs. With the confidence level of 68%, 1 s and 127 s are needed for convergence in the horizontal and vertical direction, respectively, showing that BDS triple-frequency PPP-IAR has the potential to achieve rapid convergence as concluded above. However, with the confidence level of 95%, more than 600 s is needed, indicating that there is a large discrepancy in BDS-only PPP-IAR performance for different restarts.

Fig. 12
figure 12

Positioning errors for every 10-min restart (over 2520 times for 20 stations) with numbers of ambiguity-fixed satellites and the fix percentages for BDS-only mode, the dashed black line indicates the convergence criteria for the corresponding components

Full size image
Fig. 13
figure 13

Positioning errors for every 10-min restart (over 2520 times for 20 stations) with numbers of ambiguity-fixed satellites and the fix percentages for BDS + Galileo mode, the dashed black line indicates the convergence criteria for the corresponding components

Full size image
Fig. 14
figure 14

Positioning errors for every 10-min restart (over 2520 times for 20 stations) with numbers of ambiguity-fixed satellites and the fix percentages for BDS + GPS + QZSS mode, the dashed black line indicates the convergence criteria for the corresponding directions

Full size image
Fig. 15
figure 15

Positioning errors for every 10-min restart (over 2520 times for 20 stations) with numbers of ambiguity-fixed satellites and the fix percentages for BDS + Galileo + GPS + QZSS mode, the dashed black line indicates the convergence criteria for the corresponding components

Full size image
Table 3 Convergence time in horizontal and vertical direction with the confidence of 68%/95% for the four strategies along with the average number of used satellites
Full size table

Figure 13 shows the results of BDS and Galileo combined solutions; the average number of available satellites and fixed satellites reaches 23.2 and 19.2, which improves around 43% and 45% with respect to BDS-only. The positioning accuracy, as well as the \({R}_{fixed}\), is also significantly improved. With the confidence level of 68%, the convergence criteria are fulfilled within 1 s for both horizontal and vertical directions, which improves around 99% for the vertical component compared with that of the BDS-only solution. With the confidence level of 95%, the convergence criteria are fulfilled after 62 and 210 s for the horizontal and vertical direction, respectively, suggesting that there are still some extremely poor convergence cases even after combining BDS and Galileo.

Figure 14 plots the BDS and GPS/QZSS combined solutions. The average number of available and fixed satellites reaches 27.7 and 19.4. For those GPS satellites having only dual-frequency measurements, the period of 450 s continuous tracking is required to participate in ambiguity-resolution; the increments of the fixed satellites compared BDS-only therefore mainly consist of GPS BLOCK IIF/BLOCK IIIA and QZSS at the beginning, after that, the average number of fixed satellites increased slightly to 22.8. In terms of convergence time, similar performance with BDS/GAL can be obtained. With a confidence level of 68%, the horizontal and vertical criteria are fulfilled within 1 s, while the convergence criteria are fulfilled after 45 and 187 s, respectively, with a confidence level of 95%.

The results of the last strategy, which utilize all multi-frequency constellations, are plotted in Fig. 15. The average number of available and fixed satellites reaches 34.7 and 25.2. With GPS dual-frequency participating in ambiguity-resolution, the fixed number of satellites increases to 28.5. With the confidence level of 95%, the horizontal and vertical convergence criteria can be fulfilled within 1 and 2 s, respectively, suggesting instantaneous ambiguity resolution can be achieved in almost all cases after all multi-frequency constellations combined.

Summary and outlook

The PPP long convergence has been a major disadvantage for wider applications. The ambiguity resolution has been proven to be a powerful technique for solving it. This study presents a unified PPP-IAR model in an uncombined and undifferenced manner for dual- and triple-frequency observations. With the inclusion of the third frequency, the benefit of EWL integer constraint is investigated. Further, with multi-constellation available, especially after the successful operation of BDS-3, the contributions of different constellations on PPP convergence are analyzed. Finally, intensive restart tests on a large scale are conducted to verify our findings.

Firstly, we focus on the contribution of the third frequency to the PPP convergence. The introduction of the third frequency makes it possible to form EWL ambiguities. Analysis shows that the EWL float ambiguities are rather close to corresponding integers after UPD corrections with a percentage of 99.6% within ± 0.2 cycles, resulting in extremely fast ambiguity resolution. The concentricity of WL ambiguities can be significantly improved after the EWL constraint, consequently, speeding up the fixing rate of WL ambiguities at a very early stage of initialization. With both EWL and WL being constrained, the concentricity of N1 residual within 1 cycle improves from 51.5% of the original float solutions to 90.2%, making it more favorable for the final N1 ambiguity identification. The positioning verification on a selected rover station is performed. The accuracy improvement of 85% is observed in EWL and WL constraint solutions compared with float ones for the first 10 min of the initialization. This is further confirmed by the fast fixing of N1 integer ambiguities and instantaneous convergence in the position domain.

Secondly, four strategies with the primary constellation of BDS are designed for multi-constellation convergence verification: (1) BDS-only, (2) BDS + Galileo, (3) BDS + GPS + QZSS, (4) BDS + Galileo + GPS + QZSS. A 2-h restart is firstly conducted via taking RO13 as an example. Instantaneous PPP convergence is observed in BDS + Galileo + GPS + QZSS solutions except one exception at 20:00, while the average convergence time for BDS-only solutions is 101/108/115 s for E/N/U components, respectively. More evidence is found by performing over 2520 times repeats of 10-min triple-frequency PPP-IAR restart for 20 stations with the designed strategies. Within 68% confidence level, the convergence time of BDS-only in horizontal and vertical components is 1 s and 127 s, while that of BDS + Galileo and BDS + GPS + QZSS are both 1 s and 1 s for the same components. Those improvements can be attributed to the increasing number of multi-frequency satellites, which improves around 45–55% compared with BDS-only. With all BDS + Galileo + GPS + QZSS integrated, the used number of satellites increases to 34.7. Instantaneous convergence is observed with a confidence level of 95%, and the horizontal and vertical components fall into the convergence criteria within 1 s and 2 s. It is then concluded that instantaneous ambiguity resolution can be achieved in most cases after all multi-frequency constellations are combined. It should be mentioned that the results are obtained without atmosphere corrections.

PPP instantaneous ambiguity resolution allows us to expand the applications of real-time satellite-based augmentation. However, it should be mentioned that the kinematic PPP solutions are obtained using static stations with an open sky environment in this contribution. Dynamic tests will be further conducted to test the triple-frequency PPP-IAR performance in some more complex situations with real-time orbit and clock products. It is expected that with further completeness of GPS modernization and Galileo finalization, a more stable and fast convergence of positioning can be achieved in the near future.