Introduction

A first assessment of GLONASS CDMA L3 ambiguity resolution and positioning performance is provided. The navigation signals of the GLONASS system are traditionally transmitted on the basis of the frequency division multiple access (FDMA) technique (ICD-GLONASS 2008). As a consequence of the FDMA technique, inter-frequency biases are present that impede a straightforward integer resolution of the double-differenced (DD) ambiguities (Leick et al. 2015; Hofmann-Wellenhof et al. 2013). To resolve this issue, special calibration procedures have been proposed aimed at realizing GLONASS FDMA integer ambiguity resolution (Takac 2009; Yamada et al. 2010; Reussner and Wanninger 2011; Wanninger 2009). With the advent, however, of the GLONASS code division multiple access (CDMA) signals, double differences of the carrier-phase ambiguities become integer themselves and standard methods of integer ambiguity resolution can directly be applied to realize ambiguity-resolved precise positioning.

In February 2011, following the launch of the first GLONASS-K1 satellite, SVN 801 (R26) (IAC 2016), the Russian satellite system commenced transmitting CDMA signals on L3 (1202.025 MHz) (Urlichich et al. 2010; Thoelert et al. 2011; Oleynik 2012). The current constellation (March 2016) consists of 28 satellites of which 26 are of GLONASS-M series, and two are of GLONASS-K series, subseries GLONASS-K1 (IAC 2016). This constellation has four CDMA-transmitting satellites, i.e., SVNs 801 (R26) and 802 (R17) of series K, 755 (R21) and the newly launched 751 of series M, among which SVN 801 is undergoing a flight test (IAC 2016). All the satellites of the GLONASS-K series as well as the last seven satellites of the GLONASS-M series will be capable of transmitting CDMA signals on the L3 frequency (Oleynik 2012; Montenbruck et al. 2015).

It is expected that the last satellites of the GLONASS-M series will be launched by 2017 and that of the GLONASS-K1 series, 11 satellites will be launched through 2020. The GLONASS-K2 satellites will be launched in early 2017 (GPS World 2015). All these satellites will be able to transmit CDMA signals. Providing signals on the frequencies used by the other GNSSs (GPS L5 and L1) is also part of the future plan (Karutin 2012). An overview of these signals was presented in Urlichich et al. (2010, 2011) and Karutin (2012), and Thoelert et al. (2011) assessed the signal quality and the modulation quality of the L3 CDMA civil signal of SVN 801 received by a high-gain antenna.

We provide for the first time an analysis of the GLONASS L3 ambiguity resolution and corresponding positioning performance. Our analyses are based on L3 data of the GLONASS satellite pair R21–R26, received by two JAVAD receivers at Curtin University, Perth, Australia. We also compare our results with corresponding results obtained for the GPS L1 observables from the satellite pair G21–G29, having almost the same trajectories as those of R21–R26 for the periods considered in this contribution. We start first with the formulation of the four versions of the two-satellite models used in our analyses. These four versions are the geometry-free model, the geometry-based model, the height-constrained geometry-based model and the geometry-fixed model. We then study the noise characteristics of the GLONASS CDMA data and compare it to their GPS L1 counterparts. We present results on the carrier-to-noise density and on the estimated zenith-referenced measurement precision. Next, double-differenced (DD) ambiguity resolution is taken up. This is done for all four models, both for GLONASS and GPS. In this analysis, we present the empirical results and compare them for consistency with their formal counterparts. Following the ambiguity resolution analyses, the positioning performance is discussed. This is done both for the ambiguity float case as well as for the ambiguity fixed case. Besides, we illustrate a case of a near rank-deficiency and demonstrate that the PDOP and ADOP characteristics can be quite distinct and that one therefore should not confuse a poor PDOP with poor ambiguity resolution capabilities. Finally, a summary and conclusions are provided.

Two-satellite observational model

As our analyses are based on data from the GLONASS satellites R21 and R26, we first formulate the underlying two-satellite model. In the following, this formulation will be presented for four different models of different strengths, i.e., geometry-free, geometry-based, height-constrained geometry-based, and geometry-fixed model.

From geometry-free to geometry-fixed

With the expectation E{.} and dispersion D{.}, the corresponding two-satellite double-differenced (DD) system of observation equations reads

$$\begin{aligned} E\{ {\left[ \begin{aligned} p\\ \varphi\\ \end{aligned} \right]}\} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 1 & \lambda \\ \end{array} } \right]\left[ \begin{aligned} \rho \\ a\\ \end{aligned} \right] \hfill \\ D\{ {\left[ \begin{aligned} p\\ \varphi\\ \end{aligned} \right]}\} = \frac{1}{w}\left[ {\begin{array}{*{20}c} {\sigma_{p}^{2} } & 0 \\ 0 & {\sigma_{\varphi }^{2} } \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(1)

with p and φ being the DD code and phase observable, respectively, ρ the DD receiver-satellite range and a the DD integer ambiguity in cycles. The ambiguity a is linked to the DD phase observable through the signal wavelength λ. With the elevation-dependent weighting functions, w θ1 and w θ2 (see 4), for the first and the second satellite with elevation angles θ 1 and θ 2, respectively, the final weight becomes \(w = \tfrac{1}{2}[w_{\theta 1}^{ - 1} + w_{\theta 2}^{ - 1} ]^{ - 1}\). The zenith-referenced standard deviations of the undifferenced code and phase observables are denoted as σ p and σ φ , respectively.

We will be working with four different models (Teunissen 1997). They are arranged in ascending order of strength:

  1. 1.

    Geometry-free model (GFr): This is the model as formulated in (1). As it is parametrized in ρ, it is free from the receiver-satellite geometry;

  2. 2.

    Geometry-based model (GB): This model follows from linearizing (1) with respect to the unknown receiver coordinates. The receiver-satellite geometry is then taken into account through the parametrization

    $$\delta \rho \,\, = \,\, - c^{T} \,\delta b$$
    (2)

    with δρ being the receiver-satellite range increment, c the 3-vector containing the between-satellite single-differenced (SD) receiver-satellite unit direction vectors, and δb = [δN, δE, δH]T the unknown between-receiver baseline increment vector;

  3. 3.

    Height-constrained geometry-based model (H-GB): This model follows if one adds the (weighted) height constraint to the geometry-based model,

    $$E\{ \delta h\} = [0,0,1]\delta b;\quad D\{ \delta h\} = \sigma_{h}^{2}$$
    (3)
    1. 4.

      Geometry-fixed model (GFi): In this model the positions of the receiver and the satellite, and thus receiver-satellite range ρ, are assumed known.

Note that both the geometry-free and geometry-fixed model are solvable on an epoch-by-epoch basis, i.e., instantaneously. This is, however, not the case for the unconstrained and height-constrained geometry-based models. Two or more epochs are then needed for these models to be solvable.

Two-satellite positioning

Our solutions of the unconstrained and height-constrained geometry-based models are based on data from three epochs each. To realize a sufficient change of receiver-satellite geometry, the three epochs are every time chosen from three distinct segments of the satellite trajectories. In the skyplot of Fig. 1, this process is schematically shown for the satellites R21–R26. In this figure, the location of the satellites over the stated sub-periods is distinguished using different colors. Each position solution makes use of one pair of the DD observable (phase and code) over the red period, one pair over the blue period and one pair over the green period. For example, the satellites location indicated with the same markers in Fig. 1 are associated with those instants of which the observables are used in one position solution. Thus, each solution computed is in fact a triple-epoch solution, for which the ambiguities as well as baseline coordinates are assumed constant. As the sampling rate of the epoch-triples is 1 s, the so obtained ambiguity and position time series also has a 1 Hz rate.

Fig. 1
figure 1

Skyplot of the GLONASS CDMA-transmitting satellites at Perth, Australia, during UTC [04:47:00–06:55:00] on DOY 21 of 2016, with the cutoff elevation angle of 10°. The whole period is divided into three sub-periods distinguished using different colors. The black circles indicate the satellite positions at the first epoch of each sub-period, whereas the black pentagrams indicate them at 1000th epoch of each sub-period

Full size image

Noise characteristics

In this section, we study the noise characteristics of the GLONASS CDMA data and compare it to their GPS L1 counterparts. We present results on the carrier-to-noise density, the estimated zenith-referenced measurement precision and on the influence of multipath.

Measurement experiment

The data used in our analyses were collected by the two stations CUT3 and CUCC of an eight-meter baseline at Curtin University. Each station is equipped with a JAVAD receiver, capable of tracking GLONASS L3 CDMA signals as well as GPS L1 signals. The signals of the GLONASS satellite pair R21–R26 and of the GPS satellite pair G21–G29 were tracked. Their receiver-satellite geometry over the observation time span is shown in the skyplot of Fig. 2. For both the GLONASS and the GPS satellites, the broadcast ephemeris data are used. Further information is provided in Table 1. Note that the observation time spans are listed in three different days (DOYs 13, 21, 37). They were chosen such that the receiver-satellite geometries of GPS and of GLONASS repeat.

Fig. 2
figure 2

Skyplot of the GLONASS CDMA-transmitting satellites (purple) and GPS satellites (blue) at Perth, Australia, during UTC [04:47:00–09:31:00] on DOY 21 of 2016, with the cutoff elevation angle of 10°

Full size image
Table 1 Characteristics of the experiment conducted for this study
Full size table

Carrier-to-noise density

To get insight into the noise characteristics of the GLONASS CDMA L3 signal, we first consider its carrier-to-noise density (C/N0). Figure 3 shows the observed C/N0 of the GLONASS L3 and GPS L1 (all the visible satellites) signals. While the GLONASS L3 signal has a BPSK(10) modulation (Urlichich et al. 2011), the GPS L1 (C/A) signal has a BPSK(1) modulation (GPSD 2013). The C/N0 graph of the GLONASS L3 signal has a similar signature to that of GPS L5-signal (see Nadarajah et al. (2015)), which also has a BPSK(10) modulation.

Fig. 3
figure 3

Carrier-to-noise density (C/N0) for GPS L1 and GLONASS L3 signals tracked by JAVAD TRE_G3TH_8 receiver, connected to TRM59800.00 SCIS antenna at Perth, Australia, on DOY 21 of 2016 during UTC [04:47:00–09:31:00]

Full size image

Estimated precision (time correlation)

As another step to characterize the noise of the GLONASS L3 and the GPS L1 observables, we apply the least-squares variance component estimation (LS-VCE) method (Teunissen and Amiri-Simkooei 2008). The LS-VCE is applied to the short-baseline phase and code observables of the CUT3-CUCC receiver pair. Use was made of the exponential weighting function

$$w_{\theta } = \left[ {1 + 10\exp \left( { - \frac{\theta }{10}} \right)} \right]^{ - 2}$$
(4)

so as to capture the elevation dependency, where θ is the elevation of the satellite in degrees (Euler and Goad 1991). Incorporation of this elevation dependency in the LS-VCE allows one to estimate the zenith-referenced standard deviations of the undifferenced code and phase observables, σ p and σ φ . The corresponding VCE results are shown in Table 2. Note that the precision of the GLONASS L3 signal is significantly better than its GPS L1 counterpart. This is consistent with what was concluded from the C/N0 graph of Fig. 3. Also note that the table shows results for multipath-corrected standard deviations. The more detailed information on multipath correction is given in the next section. The so-obtained improvement is significant for both the GLONASS and GPS code observables, but most pronounced for GLONASS.

Table 2 Estimated zenith-referenced standard deviations of the undifferenced original (multipath-corrected) code σ p and phase σ φ observables
Full size table

Multipath

We now describe how the above-mentioned multipath was determined and how it was used as a means to correct the data. Consider the code-phase vector

$$\left[ \begin{aligned} m_{p} \\ m_{\varphi } \\ \end{aligned} \right]\,\, = \,\,\left[ \begin{aligned} p \\ \varphi \\ \end{aligned} \right]\,\, - \,\,\left[ \begin{aligned} 1\,\,\,\,\,\,\,\,\,0 \\ 1\,\,\,\,\,\,\,\,\lambda \\ \end{aligned} \right]\left[ \begin{aligned} \rho \\ a \\ \end{aligned} \right]$$
(5)

This vector is a zero-mean noise vector in case model (1) is correct, e.g., in case multipath is absent. In the presence of multipath, however, it captures the multipath on code, m p , as well as the multipath on phase m φ .

In our case, the epoch-by-epoch time series of the DD multipath vector [m p , m φ ]T was determined by computing ρ from the known receiver and satellite positions, while the reference integer a was computed using the very strong multi-epoch geometry-fixed model. Figure 4 displays the so-obtained DD code and phase multipath time series for the GLONASS L3 (R21–R26) and the GPS L1 (G21–G29) signals over the three time periods given in Table 1. Note that in all cases the time series of the three periods on DOYs 13, 21 and 37 indeed completely overlap each other.

Fig. 4
figure 4

DD code multipath (top) and DD phase multipath (bottom) for receiver pair CUT3-CUCC on DOY 13 during UTC [05:20:00–10:03:00] (blue), DOY 21 during UTC [04:47:00-09:31:00] (red) and DOY 37 during UTC [03:42:00–08:26:00] (green). Also, L3-signal of R21–R26 (left) and L1-signal of G21–G29 (right)

Full size image

As a further confirmation that the time series of the three DOYs 13, 21 and 37 capture the same phenomena, we now consider their day differences. These should then be showing zero-mean noise behavior with a variability that reflects the measurement precision. To do so, we first form the day-differenced DD code and phase multipaths, dm p and dm φ , by subtracting the DD multipath of DOY 37 from those of DOYs 13 and 21. Since the observables are highly dependent on the elevation of the satellites, the day-differenced DD multipaths are then normalized using the weight \(dw = \tfrac{w}{2}\). While w captures the DD observable weight of (1), the factor 2 in the denominator takes care of the differencing between the 2 days.

Figure 5 shows, for the 2 day pairs DOY 37-DOY 13 and DOY 37-DOY 21, the histograms obtained from the epoch-by-epoch time series of \(\sqrt {dw\,} dm_{p}\) and \(\sqrt {dw\,} dm_{\varphi }\) for both GLONASS and GPS. The red curve in each panel shows the normal probability density function (PDF) with its standard deviation given by the values of Table 2 and with its mean equal to the mean of the histogram. For both GLONASS and GPS, the 2 day pairs show a good consistency between the histograms and the formal PDFs. This consistency supports the conclusion that the time series of (5) indeed captures the mentioned multipath. Also note that Fig. 5 illustrates again the difference in measurement precision between the GLONASS and GPS signals.

Fig. 5
figure 5

Histograms (blue) and formal PDF (red) of the weighted day-differenced DD code and phase multipath for GLONASS (left) and GPS (right)

Full size image

For the results of Table 2, as well as for the results in the sections following, the data of DOYs 13 and 21 have been multipath-corrected on an epoch-by-epoch basis using the multipath time series of DOY 37. This epoch-by-epoch correction ensures that no time correlation enters. The doubling in noise that enters through the correction is accounted for in the analyses that follow.

Ambiguity resolution

In this section, the ambiguity resolution performance of the GLONASS L3 observables will be assessed and compared with that of the GPS L1 observables. Our assessment will be carried out using four different models: the geometry-free model, the unconstrained and height-constrained geometry-based model, and the geometry-fixed model.

From geometry-free to geometry-fixed

The data used for our analysis is that of DOY 21 of 2016 over the time period UTC [04:47:00-06:55:00]. The solutions computed are triple-epoch solutions as explained earlier (see Fig. 1). Each of these solutions are obtained with a 1 Hz sampling rate, thus producing a time series of 3500 solutions. As there is only one unknown DD ambiguity in each case, the ambiguity resolution can be done through simple integer rounding. We denote the float ambiguity as \(\hat{a}\), the fixed (integer rounded) ambiguity as aˇ, and the reference ambiguity as a. The reference DD ambiguity a has been obtained, as mentioned earlier, through the multi-epoch solution of the geometry-fixed model.

Figure 6 shows, for the receiver pair CUT3-CUCC, the time series of aˆ − a and aˇ − a for both the GLONASS satellite pair R21–R26 (left column) and the GPS satellite pair G21-G29 (right column). Float solutions are shown in gray, correctly fixed solutions in green, and incorrectly fixed solutions in red. These time series are given, from top to bottom, for the geometry-free model, the geometry-based model, the height-constrained geometry-based models using σ h  = 0.2 m and σ h  = 0.15 m, respectively, and the geometry-fixed model.

The results clearly show a much better ambiguity resolution performance for the GLONASS data than for the GPS data. This is due to the lower noise level of the GLONASS code data and the longer wavelength of L3. If we start with the geometry-free model (top in Fig. 6), we observe many incorrectly fixed solutions, both for GLONASS and GPS. The geometry-free model is simply too weak for successful ambiguity resolution. The variation in incorrectly fixed solutions is, however, much smaller for GLONASS than it is for GPS. In case of GLONASS, the range is only aˇ − a ∈ {−2, −1, 1, 2}.

Fig. 6
figure 6

DD ambiguity time series of aˆ − a and aˇ − a for both the GLONASS satellite pair R21–R26 (left) and the GPS satellite pair G21-G29 (right) using data from the receiver pair CUT3-CUCC on DOY 21 during UTC [04:47:00-06:55:00]. Float solutions aˆ − a are shown in gray, correctly fixed solutions in green, and incorrectly fixed solutions in red. The time series are given, from top to bottom, for the geometry-free (GFr) model, the geometry-based (GB) model, the height-constrained geometry-based (H-GB) models using σ h  = 0.2 m and σ h  = 0.15 m, respectively, and the geometry-fixed (GFi) model

Full size image

The ambiguity resolution performance improves if we switch to the stronger (unconstrained) geometry-based model (second row in Fig. 6). The incorrectly fixed GPS ambiguities do, however, still vary over a much larger range than their GLONASS counterparts. The performance improves further if we include a weighted height constraint (3rd and 4th row in Fig. 6). Now GLONASS and GPS have the same range of incorrectly fixed ambiguities, although the number of incorrectly fixed GLONASS solutions is of course still smaller than that of GPS. Finally, with the strongest model of all, being the geometry-fixed model (bottom row in Fig. 6), both GLONASS and GPS have all ambiguities correctly fixed. Thus, despite the larger noise level of the GPS ambiguities (compare the variability in the GLONASS and GPS float time series), all fixed ambiguities are now correct.

Distribution of the ambiguity residuals

So far we considered the float and fixed time series aˆ − a and aˇ − a, respectively (Fig. 6). We now consider the ambiguity residual, i.e., the difference between the float and corresponding fixed solution, \(\check{\varepsilon}=\,\) aˆ − aˇ. The ambiguity residuals form the basis for ambiguity validation (Verhagen and Teunissen 2013). Figure 7 displays the histograms of the DD ambiguity residuals for the five different models considered. The domain of the histograms is [−0.5, +0.5]. Note that the shape of the histograms changes when one goes from the weaker model (geometry-free) to the stronger model (geometry-fixed). Hence, the ambiguity residuals are not normally distributed, i.e., they are not normally distributed even if the data are.

Fig. 7
figure 7

Histograms (blue) and formal PDFs (red) of the DD ambiguity residuals \(\check{\varepsilon}=\,\) aˆ − aˇ that correspond with the time series of Fig. 6, for GLONASS (left) and GPS (right). The formal PDF of the ambiguity residual is given by (6)

Full size image

Assuming the data to be normally distributed, the ambiguity residuals have the distribution given by Teunissen (2002) as

$$f_{{\mathop \varepsilon \limits^{ \vee } }} (x)\, = \,\sum\limits_{{z \in {\mathbb{Z}}}} {\frac{1}{{\sqrt {2\pi } \sigma_{{\hat{a}}} }}} \,\exp \{- \frac{1}{2}\left(\frac{x - z}{{\sigma_{{\hat{a}}} }}\right)^{2}\}$$
(6)

with x ∈ [−0.5, 0.5]. This distribution has also been shown (red curve) for the five cases in Fig. 7. It demonstrates the consistency between the empirical and formal distributions. The distribution (6) has two limiting cases. The distribution tends to the uniform distribution when \(\sigma_{{\hat{a}}}\) gets larger and it tends to the impulse function when \(\sigma_{{\hat{a}}}\) gets smaller. This behavior is indeed clearly present in Fig. 7 when one goes from the rather weak geometry-free model toward the much stronger geometry-fixed model.

The ambiguity success rates

We computed the ambiguity success rates for the above five cases for GLONASS L3, GPS L1 and GPS L2, both formally as well as empirically. Being the probability of correct integer estimation, the formal ambiguity success rate is computed as (Teunissen 1998),

$${\text{Formal}}\,Ps\,\, = \,\,2\varPhi \left( {\frac{1}{{2\sigma_{{\hat{a}}} }}} \right)\, - \,\,1$$
(7)

with \(\sigma_{{\hat{a}}}\) being the ambiguity standard deviation and \(\varPhi (x) = \int_{ - \infty }^{x} {\tfrac{1}{{\sqrt {2\pi } }}} \exp \{ - \tfrac{1}{2}\nu^{2} \} d\nu\). The empirical success rate is computed as

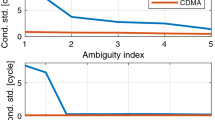
$${\text{Empirical}} \, Ps \, = \,\frac{{{{\# }}\,{\text{correct}}\,{\text{fixed}}\,{\text{DD}}\,{\text{ambiguities}}}}{{{{\# }}\,{\text{float}}\,{\text{DD}}\,{\text{ambiguities}}}}$$
(8)

The results of the empirical and formal success rates for the above five cases are given in Table 3. For the computation of the formal success rate, the ambiguity standard deviation was taken as an average of the formal standard deviations, thus \(\sigma_{{\hat{a}}} = \sqrt {\tfrac{1}{s}\sum\nolimits_{j = 1}^{s} {\sigma_{{\hat{a}}}^{2} (j)} }\), with \(\sigma_{{\hat{a}}}^{2} (j)\) being the variance of the float DD ambiguity of the jth solution. As the results of Table 3 show, the empirical values are in good agreement with the formal ones. Also, the stronger the model is (from top to bottom), the larger the success rates become. Similarly, we see an increase in success rate with wavelength.

Table 3 GLONASS L3, GPS L1, and GPS L2 ambiguity success rates, empirical and (formal), for the geometry-free (GFr) model, the geometry-based (GB) model, the height-constrained geometry-based (H-GB) model, and the geometry-fixed (GFi) model
Full size table

Positioning performance

In this section, we assess the GLONASS L3 observables performance in positioning. All results belong to the triple-epoch geometry-based model without any height constraint.

Two-satellite positioning: float solution

As discussed above, we make use of the 3500 triple-epoch solutions over the time period UTC [04:47:00-06:55:00] on DOY 21. Shown in Fig. 8 is the horizontal scatter plot for both the unconstrained float (gray) and correctly fixed (green) position solutions. Note that although the scatter plot of the fixed solutions has an ellipsoidal shape, the float scatter plot does not. The explanation lies in the significant change that the receiver-satellite geometry undergoes in the observational time span. This becomes clearer if we partition the time span in smaller time intervals and then assign different colors to these different time intervals, see Fig. 9. Now, we do recognize the ellipsoidal shapes in the scatter plot.

Fig. 8
figure 8

GLONASS R21–R26 horizontal position scatter plot (triple-epoch based) collected by the receiver pair CUT3-CUCC on DOY 21 during UTC [04:47:00–06:55:00]. Float solutions are shown in gray and correctly fixed solutions are shown in green

Full size image
Fig. 9
figure 9

GLONASS R21–R26 horizontal position scatter plot (triple-epoch based) collected by the receiver pair CUT3-CUCC on DOY 21 during UTC [04:47:00–06:55:00]. Float solutions are shown in blue, dark green, red, cyan, purple, beige, dark gray, each of which has a specific orientation. Correctly fixed solutions are shown in green

Full size image

As the confidence ellipses are the formal representatives of the scatter plots, the change in orientation that the float scatter plot undergoes from time interval to time interval can be explained by means of the properties of the confidence ellipses. The confidence ellipsoid of bˆ, having mean E(bˆ) = b, is given as

$$(\hat{b} - b)^{T} Q_{\hat{b}\hat{b}}^{ - 1} (\hat{b} - b) = r^{2}$$
(9)

With \(Q_{{\hat{b}\hat{b}}}\) the variance matrix of bˆ and constant r 2 chosen such that a certain confidence level is reached (e.g., 95 %). The confidence ellipsoid of the fixed solution is obtained by replacing bˆ and \(Q_{{\hat{b}\hat{b}}}\) by bˇ and \(Q_{{\mathop b\limits^{ \vee } \mathop b\limits^{ \vee } }}\), respectively.

The difference in shape between the float and fixed confidence ellipsoids is determined by the difference in the corresponding variance matrices. When solving the triple-epoch geometry-based model, the inverse variance matrices of the float and fixed solution can be shown to be related as

$$Q_{{\hat{b}\hat{b}}}^{ - 1} = Q_{{\mathop b\limits^{ \vee } \mathop b\limits^{ \vee } }}^{ - 1} - \frac{{k\bar{w}}}{{\sigma_{\varphi }^{2} }}\bar{c}\bar{c}^{T} \hfill \hfill (k=3)$$
(10)

in which \(\bar{w} = \tfrac{1}{3}\sum\nolimits_{i = 1}^{3} {\tfrac{w(i)}{2}}\) and \(\bar{c} = \tfrac{1}{{3\bar{w}}}\sum\nolimits_{i = 1}^{3} {\tfrac{w(i)}{2}} c(i)\). It is the second term on the right-hand side of (10) that determines the difference in orientation between the float and fixed scatter plots. Because of the very small value of the phase variance in the denominator of this second term, any change over time in the rank-1 matrix \(\bar{c}\bar{c}^{T}\) will be amplified and thus play an important role in the determination of the orientation of the float confidence ellipsoid.

From (9) and (10), it follows that the maximum and minimum differences between the float and fixed ellipsoids are realized in a direction parallel and orthogonal to the vector \(\bar{c}\), respectively. This is demonstrated in Fig. 10 by the horizontal scatter plots and corresponding ellipses. Figure 10 (top) shows the two float scatter plots (blue and gray) for two different orientations along with their correctly fixed counterparts, and Fig. 10 (bottom) shows their corresponding confidence ellipses. These ellipses are computed using the average float and fixed variance matrices over the period associated with the shown scatter plots. The brown colored vectors indicate the corresponding direction of the vector \(\bar{c}\), thus indeed pointing in the direction of maximum difference between the fixed and float ellipses. It is the change over time of this direction that makes the float scatter plot take the shape shown in Fig. 8.

Fig. 10
figure 10

[Top] GLONASS R21–R26 horizontal position scatter plots (triple-epoch based) collected by the receiver pair CUT3-CUCC on DOY 21 during UTC [04:47:00–06:55:00], left first 500 solutions; right last 500 solutions. Float solutions are illustrated in blue and dark gray, each having a specific orientation. Correctly fixed solutions are shown in green. [Bottom] The corresponding float and fixed confidence ellipses with the same color as their scatter plots. The brown vector indicates the direction of \(\bar{c}\) in (10)

Full size image

Two-satellite positioning: fixed solution

Now, we consider the scatter plot of the fixed solutions. In Fig. 11 (top), the unconstrained correctly fixed horizontal scatter plot along with the formal and empirical confidence ellipses (in red and blue) are shown, while Fig. 11 (bottom) displays the time series of the corresponding fixed height solutions. Both graphs show a good agreement between formal and empirical values. According to these values, the North and Height components are estimable with a standard deviation of about 25 mm, while the standard deviation of the East component is much smaller and around 5 mm.

Fig. 11
figure 11

(Top) GLONASS R21–R26 horizontal position scatter plot (triple-epoch based) of the correctly fixed solutions collected by the receiver pair CUT3-CUCC on DOY 21 during UTC [04:47:00–06:55:00]. The 95 % formal and empirical confidence ellipses are shown in blue and red, respectively. (Bottom) Time series of the correctly fixed height solutions. The blue dashed curves indicate the 95 % confidence interval

Full size image

That the East component can be determined so much better than the other two components can be explained by the behavior of the difference of the line-of-sight vectors to the two satellites R21 and R29. Figure 12 shows the absolute values of the weighted SD lines-of-sight \(\sqrt {\tfrac{w}{2}} \, \times \,c\) North, East, Height components for the satellites R21 and R29 over the observational period. The larger such component is, the better this component can be estimated. It therefore follows from Fig. 12 that one can indeed expect the North and Height components to be estimable with almost equal precision (see blue and red curves), while the East component would be much more precisely estimable (see green curve).

Fig. 12
figure 12

Time series of the weighted SD lines-of-sight components corresponding with the satellites R21 and R29 over UTC [04:47:00–06:55:00] on DOY 21 of 2016

Full size image

Interaction of positioning and ambiguity resolution

So far, the geometries of the triple-epoch geometry-based models have been such that the corresponding PDOP (Position Dilution of Precision) time series showed rather stable values over the chosen observational time periods. When we extend this time window, however, we note a period in which the PDOPs dramatically increase in value, see Fig. 13 (blue curve). This dramatic increase in PDOP must be due to a very poor relative receiver-satellite geometry. To explain the situation, we first show under which condition the multi-epoch geometry-based model becomes rank defect.

Fig. 13
figure 13

Triple-epoch time series of the unconstrained PDOP (blue) and ADOP (red), corresponding with the receiver pair CUT3-CUCC and GLONASS satellite pair R21–R26 on DOY 21 during UTC [04:47:00–08:10:00]

Full size image

Almost rank defect positioning geometry

When solving the multi-epoch geometry-based model, its k-epoch design matrix is formed by stacking the SD receiver-satellite unit vectors \(- c^{T} (i)\,{\text{for}}\quad i = 1,{ \ldots },k\) (see 2). Such a design matrix is rank defect if a vector \(d \in {\mathbb{R}}^{3}\) can be found such that

$$c^{T} (i)d = 0,\quad i = 1,{ \ldots },k$$
(11)

According to the definition of the vector c(i), the condition (11) means that at each epoch the two line-of-sight vectors make the same angle with the direction vector d. Geometrically this means that the rank deficiency occurs when the receiver-satellite unit line-of-sight vectors lie, at each epoch, on a cone having d as its symmetry axis (Fig. 14). The symmetry axis of the cone, i.e., the vector d, is then the direction in which the baseline solution becomes indeterminate. It is precisely this situation that explains the dramatic increase in PDOP values of Fig. 13.

Fig. 14
figure 14

Multi-epoch two-satellite positioning is indeterminate in direction d if the receiver-satellite unit directions u 1 r (i) and u 2 r (i) at each epoch lie on a cone having d as its symmetry axis (Teunissen 1990). The red and blue cones around d are formed by the receiver-satellite unit vectors at epoch 1 and epoch 2, respectively

Full size image

Figure 15 (top) shows the skyplot positions of the two GLONASS satellites R21 and R26 at the three epochs associated with the peak in the PDOP time series of Fig. 13 which is clearly depicted in Fig. 15 (bottom). The location of the satellites at the same epoch is shown with the same color. As the figure shows, the red and green satellite locations of R21 and R26 all lie on the same (red and green) cone having direction d (see 11), indicated as a purple circle, as its symmetry axis. Although the blue satellite locations of R21 and R26 lie on a different cone, this (blue) cone has again the same symmetry axis d. Hence, the geometry as shown in Fig. 15 is one in which the design matrix of the geometry-based model becomes (near) rank defect such that the baseline component in the direction of vector d becomes very poorly estimable. It is the very poor precision of this component that drives the PDOP to such large values.

Fig. 15
figure 15

(Top) GLONASS CDMA-transmitting skyplot for Perth, on DOY 21 of 2016 at three epochs, namely 05:59:25 (red), 06:22:45 (blue) and 07:46:05 (green) UTC. The purple circle illustrates the direction d along which the receiver position is poorest estimable. The two colored contour lines show the loci of the unit vectors that make the same 72 respective 81 degree angle with d. (Bottom) Triple-epoch time series of the unconstrained PDOP corresponding with the receiver pair CUT3-CUCC and GLONASS satellite pair R21–R26 on DOY 21 during UTC [04:47:00–08:10:00]

Full size image

Poor PDOP, good ADOP

Although the PDOP is often used as a quick diagnostic to infer whether the receiver-satellite geometry is favorable for positioning, one should be aware of the fact that the PDOP does not reveal whether or not one can expect ambiguity resolution to be successful (Teunissen et al. 2014). For that one needs the ADOP (Ambiguity Dilution of Precision). The ADOP is an easy-to-compute scalar diagnostic that measures the intrinsic model strength for successful ambiguity resolution. It is defined as the square-root of the determinant of the ambiguity variance matrix raised to the power of one over the ambiguity dimension (Teunissen 1997). The ADOP has several important properties. First, it is invariant against the choice of ambiguity parametrization. Second, it is a measure of the volume of the ambiguity confidence ellipsoid. And third, the ADOP equals the geometric mean of the standard deviations of the ambiguities, in case the ambiguities are completely decorrelated. Hence, in the one-dimensional case it simply reduces to the ambiguity standard deviation itself.

That the PDOP and ADOP can have a very different behavior over time is shown in Fig. 13. There where the PDOP increases dramatically in value, due to the near rank defect in the geometry-based design matrix, the time series of the ADOP still shows rather stable behavior over time. This difference between PDOP and ADOP has an interesting consequence for ambiguity resolution when weighted height-constraining is enforced. When a weighted height constraint is imposed on the geometry-based model, the variance of the float DD ambiguity can be shown to improve from its unconstrained value \(\sigma_{\hat{a}}^{2}\)to its weighted height-constrained value

$$\sigma_{{\hat{a}\,|h}}^{2} = \sigma_{{\hat{a}}}^{2} - [1 + \sigma_{h}^{2} /\sigma_{{\hat{h}}}^{2} ]^{ - 1} \sigma_{{\hat{a}\hat{h}}}^{2} \sigma_{{\hat{h}}}^{ - 2}$$
(12)

with \(\sigma_{{\hat{a}\hat{h}}}\) being the ambiguity-height covariance, σ h the a priori standard deviation of the height constraint, and \(\sigma_{{\hat{h}}}^{2}\) the variance of the unconstrained estimator of the height component. It can be seen that the ratio \(\sigma_{h}^{2} /\sigma_{{\hat{h}}}^{2}\) governs the benefit brought by the height constraint. One has the most benefit when σ 2 h  = 0 and the least benefit when σ 2 h  = ∞.

If σ 2 h is chosen much larger than \(\sigma_{{\hat{h}}}^{2}\), then the bracketed term of (12) becomes small. This means that if the receiver-satellite geometry is so strong that \(\sigma_{{\hat{h}}}^{2}\) is small, constraining the height with a variance σ 2 h much larger than \(\sigma_{{\hat{h}}}^{2}\) would have a negligible impact on ambiguity resolution. On the other hand, however, ambiguity resolution can benefit considerably from a weighted height constraint if \(\sigma_{{\hat{h}}}^{2}\) is large. The larger \(\sigma_{{\hat{h}}}^{2}\) is, the softer the weighted height constraint can be to still have an impact on ambiguity resolution. Thus, in case of a large PDOP, soft constraining of the height can still result in a very significant improvement of ambiguity resolution. The following examples shown in Fig. 16 make this clear.

Fig. 16
figure 16

[Top row] Triple-epoch time series of the unconstrained PDOP (left) and a zoom-in of it (right), corresponding with the receiver pair CUT3-CUCC and GLONASS satellites R21–R26 on DOY 21 during UTC [04:47:00–08:10:00]. [From second to the bottom row] The corresponding time series of the DD ambiguity estimations using the multipath-corrected observations (left) and DD ambiguity standard deviations (right), based on the unconstrained and height-constrained geometry-based model with the standard deviations of 2, 0.5, 0.2 and 0.1 m. Further, float solution (gray), correctly fixed solution (green), and incorrectly fixed solution (red)

Full size image

The first row of Fig. 16 shows the PDOP time series (and a zoom-in) of the triple-epoch, two-satellite geometry-based model of the GLONASS satellites R21–R26 for the period UTC [04:47:00-08:10:00] of DOY 21 in 2016. The second row of Fig. 16 shows in the left column the unconstrained DD ambiguity float and fixed time series, aˆ − a (in gray) and aˇ − a (in green and red), and in the right column the corresponding time series of the unconstrained ambiguity standard deviation. Similar time series are also shown in the third to bottom row of Fig. 16, but now as a result of imposing a weighted height constraint with increasing weight.

The results in the third row show that a soft height constraint of only σ h  = 2 m already has a significant impact on ambiguity resolution at the time instances for which the PDOPs are large. At these instances, the formal float ambiguity standard deviation has become much smaller, the variability in the float time series has reduced dramatically, and the ambiguity fixed solutions are now all correct. When we further increase the weight of the height-constraint, the results of the fourth to sixth row of Fig. 16 show that the ambiguity resolution improvements flow over to neighboring time instances such that finally in case of the bottom row now almost all of the 5000 ambiguity fixed solutions are correct.

Summary and conclusions

We provided an initial assessment of GLONASS CDMA L3 double-differenced integer ambiguity resolution and corresponding positioning performance. Our analyses are based on GLONASS L3 data from the satellite pair R21–R26 and on GPS L1 data from the satellite pair G21–G29. We studied the noise characteristics (carrier-to-noise density, measurement precision), the integer ambiguity resolution performance (success rates and distribution of the ambiguity residuals) and the corresponding ambiguity float and ambiguity fixed positioning performance. The results show that the GLONASS data have a significantly lower noise level than that of GPS, particularly in case of the code data. This difference is not only seen in the noise levels but also in their onward propagation to ambiguity time series and ambiguity residuals distribution. We also compared all our empirical results with their formal counterparts, thereby showing the consistency between data and models. The four different versions of the two-satellite model that were applied are as following: the geometry-free model, the geometry-based model, the height-constrained geometry-based model, and the geometry-fixed model. Finally, we demonstrated that PDOP and ADOP characteristics can be quite distinct and that one therefore should not confuse a poor PDOP with poor ambiguity resolution capabilities.