Machine Learning in Biomaterials, Biomechanics/Mechanobiology, and Biofabrication: State of the Art and Perspective

Abstract

In the past three decades, biomedical engineering has emerged as a significant and rapidly growing field across various disciplines. From an engineering perspective, biomaterials, biomechanics, and biofabrication play pivotal roles in interacting with targeted living biological systems for diverse therapeutic purposes. In this context, in silico modelling stands out as an effective and efficient alternative for investigating complex interactive responses in vivo. This paper offers a comprehensive review of the swiftly expanding field of machine learning (ML) techniques, empowering biomedical engineering to develop cutting-edge treatments for addressing healthcare challenges. The review categorically outlines different types of ML algorithms. It proceeds by first assessing their applications in biomaterials, covering such aspects as data mining/processing, digital twins, and data-driven design. Subsequently, ML approaches are scrutinised for the studies on mono-/multi-scale biomechanics and mechanobiology. Finally, the review extends to ML techniques in bioprinting and biomanufacturing, encompassing design optimisation and in situ monitoring. Furthermore, the paper presents typical ML-based applications in implantable devices, including tissue scaffolds, orthopaedic implants, and arterial stents. Finally, the challenges and perspectives are illuminated, providing insights for academia, industry, and biomedical professionals to further develop and apply ML strategies in future studies.

1 Introduction

In recent decades, cutting-edge engineering disciplines have increasingly converged with biological systems, significantly impacting the healthcare industry. Biomedical engineering, in particular, has rapidly emerged as an innovative and multidisciplinary field that has drawn extensive interest from research communities. Figure 1a illustrates some fast-growing disciplines within biomedical engineering, including biomaterials [1,2,3], biomechanics/mechanobiology [4,5,6,7], and biofabrication [8, 9]. These fields seamlessly integrate material sciences, mechanics, mathematics, physics, chemistry, computer science, and advanced manufacturing with biological sciences and clinical medicine, resulting in substantial benefits to human healthcare and socio-economic systems.

Fig. 1

Outline of review contents. a Machine learning (ML) in biomaterials, biomechanics/mechanobiology, and biofabrication. Created with BioRender.com. b The number of publications related to ML or data-driven approaches in conventional engineering since 2010. c The number of publications related to ML or data-driven approaches in biomedical engineering fields since 2010

Biomaterials present a broad class of natural and synthetic materials that are able to intimately interact with living biological systems. They exhibit multifunctionalities crucial for immune system support, cell interactions, and response to chemical, physical, and mechanical conditions within a local biological environment [10, 11]. So far, polymers, metals, ceramics, and composites are amongst the most typical biomaterials extensively utilised in various biomedical applications, including implantable and wearable devices [12, 13], regenerative medicine [14] and drug delivery [15]. Figure 2a depicts biomaterials employed in regenerative medicine for cardiac, bone, and skin tissue engineering, as well as drug delivery systems. These materials encompass a variety, incorporating polymeric, inorganic, and lipid-based nanoparticles. For decades, substantial efforts have been dedicated to exploration of novel biomaterials with desired chemical, physical, mechanical, and biological properties [1, 2]. Conventional routes for discovering and developing new biomaterials often relied heavily on trial-and-error experimental tests, proving workable but costly and time-consuming. In order to expedite the experimental processes and enhance success rates, advanced computational techniques have been widely employed as complementary approaches in modern biomaterial design [16, 17], which have proven effective in disclosing how material constituents and structures influence multifunctional properties from macroscale to nanoscale, thus offering compelling opportunities to achieve desired material performances as well as customised functionalities for patient-specific applications.

Biomechanics and mechanobiology often play critical roles in comprehending the responses and adaptation of living tissues to local environmental changes induced by prosthetic and therapeutic treatments. These disciplines closely engage with forces, deformation, stiffness, permeability, and other physical fields such as temperature and electromagnetic signals, exerting significant control over load-bearing characteristics and biotransportation across molecular, cellular, tissue, and organ levels [18,19,20,21,22,23,24], as depicted in Fig. 2b. While mechanobiology is closely correlated with biomechanics, it places a greater emphasis on actively regulating in vivo tissues or cellular behaviours such as tissue growth/remodelling and cell differentiation/proliferation [25,26,27,28,29]. As shown in Fig. 2b, mechanobiology regulates cellular behaviours with mechanical stimuli, thereby affecting osteoclasts, monocytes, pre-osteoblasts, osteoblasts, and osteocytes processes for bone adaptation and remodelling. The development of biomechanical and mechanobiological modelling techniques has been rapid, facilitated by advances in computational and data sciences integrated with innovative non-invasive imaging technologies [18, 30,31,32]. In both preclinical research and clinical trials, biomechanical and mechanobiological modelling have made significant contributions and theoretical breakthroughs in unveiling the complex relationships among a range of factors in engineering, biomaterials, and biomedicine. For example, disciplines like tissue engineering [33, 34], orthopaedics [35, 36], oromaxillofacial reconstruction [37,38,39], cardiovascular and pulmonary systems [40, 41] have widely embraced biomechanical and mechanobiological modelling techniques, thereby advancing multidisciplinary knowledge in this rapidly emerging field.

Fig. 2

Applications of biomaterials, biomechanics/mechanobiology, and biofabrication. a Biomaterials for implantable and wearable devices, including prosthetics, dental implants, scaffolds, and stents. Created with BioRender.com. b Illustration of biomechanics/mechanobiology for bone tissue engineering. Created with Biorender.com. c Biofabrication using bioink. Reproduced with permission. Copyright 2016, Elsevier [42]

Biofabrication encompasses a versatile set of advanced manufacturing techniques for creating non-living biomaterials, living constructs (cells or tissues), and hybrid components [43]. Recently, additive manufacturing (AM) has been rapidly developed to craft novel and sophisticated implantable or wearable devices, including bone scaffolds [44], fixation plates [45], dental implants [46], and smart surfaces [47]. For non-living materials, biomanufacturing can be mainly classified by different construction processes, such as fused deposition modelling (FDM), stereolithography (SLA) for polymers [48], selective laser sintering (SLS), and electron beam melting (EBM) for metals and alloys [49], as well as vat photopolymerisation and binder jetting (BJ) for bioceramics [50]. A more recent and notable development in this field is bioprinting, accomplished through ink-jet and valve-jet printing techniques that utilise customised bioink, combining living cells/tissues with supporting base materials to directly mimic structures of native organs/tissues [43]. Figure 2c illustrates bioprinting, depicting the creation of a microfibrous scaffold using a composite bioink encapsulating endothelial cells.

Lured by remarkable advances in computational sciences and computer technologies over the past decades, there has been a remarkable increase in data generation. For this reason, how to manage and make use of the unprecedented amount of data has inspired researchers to develop a range of data-driven approaches. Machine learning (ML), as a prominent class of data-driven approaches, employs computational algorithms learned from data, as opposed to experience or theory, to enhance performance in solving specific tasks. It stands as one of the most prevalent computational strategies utilised in a broad range of fields, including image and voice recognition, autonomous driving, online fraud detection, automatic language translation and medical diagnosis [51].

Engineering has undeniably witnessed profound impacts from various ML approaches, with significant efforts dedicated to material sciences [52], computational modelling techniques [33], and AM [53]. Figure 1b depicts the publication trend in these fields from the Web of Science Core Collection since 2010. Each subcategory, namely “machine learning” or “data-driven” combined with “materials”, “mechanics”, and “additive manufacturing/3D printing”, was counted. The publications in these fields have experienced remarkable growth since 2016. Material sciences, in particular, have emerged as the most dynamic discipline, with over 6,500 publications in 2023 alone, and the upward trend is expected to continue in the following years. While the percentages of publications in AM and mechanics are slightly lower than that of materials sciences, they are notably increasing, demonstrating potent applications across diverse disciplines within broad engineering fields.

Nevertheless, despite the unprecedented success of ML in other traditional engineering disciplines, biomedical engineering remains relatively underexplored. Figure 1c analyses the number of publications applying ML in biomaterials, biomechanics/mechanobiology, and biofabrication since 2010. The publications with topics containing keywords such as machine learning/data-driven plus biomaterial, biomechanics, mechanobiology, bioprinting, and biofabrication were counted from the Web of Science Core Collection. A rapid increase in publications has been more evident since 2017, with over 200 articles in 2023 alone. Biomechanics and mechanobiology constitute the largest portion of these publications (60.89%). While the total number of publications in these areas lags behind those shown in Fig. 1b, it reveals significant potential and tremendous opportunities for biomedical engineering to establish a new paradigm.

Therefore, the purpose of this review is to conduct a state-of-the-art evaluation of the development of ML in biomedical engineering and provide insights into its potential applications in relevant areas. We focus on various ML techniques applied in biomaterials, biomechanics/mechanobiology, and biofabrication from an engineering perspective, as outlined in Fig. 1a. It is important to note that these areas are highly interdisciplinary in nature; and other important disciplines, such as biophysics, biochemistry, and biology, may not have been reviewed comprehensively here.

The remaining sections are organised as follows. Section 2 briefs the ML approaches commonly used in the reviewed studies. Sections 3–5 review ML in disciplines of biomaterials, biomechanics/mechanobiology, and biofabrication, respectively. Section 6 focuses on typical applications in bone scaffolds, orthopaedic/dental implants, and arterial stents. Section 7 discusses the challenges and perspectives, followed by a conclusion in Sect. 8.

2 Machine Learning Approaches

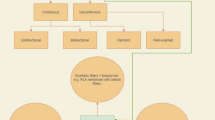
Machine learning integrates principles from statistics, neural networks, optimisation theory, computer science, system identification, and various other fields. Its overarching goal is to simulate or implement human learning behaviours, enabling the continuous improvement and reorganisation of known skills [54]. According to the differences in learning manners, ML can be categorised into supervised learning [55], unsupervised learning [56], semi-supervised learning [57], and reinforcement learning [58], as depicted in Fig. 3. Given the dynamic nature of ML techniques, the algorithms mentioned here may not represent an exhaustive enumeration of ML methods. Nevertheless, this section briefly reviews some typical ML models extensively utilised in biomedical engineering in open literature.

Fig. 3

The framework of machine learning models

2.1 Supervised Learning

Supervised learning utilises labelled training data to establish a mapping with new instances. Labels for training samples must be provided, and higher labelling accuracy generally leads to more effective learning outcomes. Supervised learning models aim to find an implicit functional relationship between input and output data based on given knowledge, making it suitable for classification and regression problems. Commonly used supervised learning models are summarised below.

2.1.1 K-Nearest Neighbour (KNN)

KNN, proposed by Fix et al. [59] and enhanced by Cover and Hart [60], stands as a prominent algorithm for classification and pattern regression [61]. It operates on the premise that similar instances are proximate, allowing the identification of new input features by calculating distances to existing sample data. Subsequently, inputs are classified into the nearest category. The essence of KNN lies in measuring distances between tested and training samples. In this context, Surya et al. [62] conducted a comprehensive review of KNN performance using various distance measures. The advantages of KNN stem from its simplicity in developing a training model [63]. Furthermore, the need for parametric regulation of complex models is eliminated [64]. However, it is worth noting that KNN may exhibit reduced efficiency with a substantial volume of sampling data. Nevertheless, KNN has found widespread applications in recommendation systems, text mining, finance, agriculture [65], and medical-related prediction [66,67,68], among other domains.

2.1.2 Decision Tree (DT)

DT is a fundamental method for classification and regression, encompassing both a classification tree and a regression tree. Among the most classical algorithms are ID3, C4.5, and C5.0 [69,70,71]. DT manifests a tree structure where internal nodes represent attribute tests, branches depict the outputs of these tests, and leaf nodes house the classification labels. It can be perceived as a compilation of if–then rules or as a conditional probability distribution defined in feature and classification spaces. Learning steps for DT typically involve feature selection, generation of DT structures, and model trimming. Due to its visual structure, DT is easily comprehensible and widely applicable across various domains, including data analysis in biomedical fields [72,73,74,75,76,77,78].

2.1.3 Random Forest (RF)

RF, proposed by Breiman [79], is composed of multiple DTs constructed with random feature subsets. Therefore, RF is recognised as an ensemble algorithm. Each DT functions as a classifier, and RF integrates the classification results from all DTs. The classification with the highest proportion is determined as the final output result. Due to the randomness inherent in DT construction, the common issue of overfitting can be alleviated to a considerable extent [80]. The RF algorithm has found certain applications in various biomedical fields to date [81,82,83,84].

2.1.4 Naïve Bayesian (NB)

Based upon the Bayes theorem, the NB algorithm classifies data samples using knowledge of probability statistics [85]. Unlike Decision Trees (DT), NB is firmly rooted in a more robust mathematical foundation. It assumes that all attributes are independent, allowing the NB algorithm to learn the joint probability distribution from input samples to output data. After training the NB model, it can generate output results with the greatest posterior probability when given input values. However, meeting the requirement of independence for dataset attributes can be challenging in many cases. Consequently, numerous studies have been conducted to address this assumption by considering attribute weighting, attribute selection, and structure extension [86]. The NB algorithm has extensive applications in various biomedical areas [87, 88].

2.1.5 Support Vector Machine (SVM)

SVM [89] has found extensive applications in statistical classification and regression analysis. In general, it belongs to a linearised classifier aiming to maximise the interval in feature spaces by solving convex quadratic programming problems. SVM maps the vectors of samples to a higher-dimensional space, where a hyperplane best separates two groups of mapped vectors. The advantages of SVM lie in its ability to learn data samples with good reproducibility and accuracy, ensuring that the model is generic and capable to new data, thereby maximising the proportion of correct labels [90]. SVM has been applied across various fields, such as text classification [91], image classification [92], biological sequence analysis, biological data mining [93], biomechanics [94,95,96,97,98], regenerative medicine [99, 100], and more.

2.1.6 Logistic Regression and Linear Regression

Logistic regression and linear regression [101, 102] are similar in many aspects, both falling under the umbrella of generalised linear models. The primary distinction lies in the types of their outputs. If the output is continuous, it is referred to as multiple linear regression and is employed to address regression problems. On the other hand, if the output follows a binomial distribution, it is recognised as logistic regression and is frequently used for classification issues. The process for both algorithms involves selecting data sets and output variables of interest, specifying a ML model, training the model parameters, and conducting model evaluation and validation [103]. These methods are fairly popular and widely utilised in various fields, such as biometrics [104], finance prediction [105], disease diagnosis [106], etc.

2.1.7 Backpropagation Neural Network (BPNN)

An artificial neural network (ANN) [107] is a complex system comprising numerous nodes (neurons) interconnected by pathways designed to emulate human brain functions. The outputs of an ANN are determined by various factors, including network structure, connection methods, weights, and activation functions. The weights in an ANN require training based on a sufficient dataset. Typically, an ANN consists of one input layer, one or more hidden layers, and one output layer. Among the learning frameworks for ANNs, it appears that the backpropagation neural network (BPNN) stands out. In a BPNN, initial weights are assigned randomly, and output data are generated as input data traverse the entire ANN model. These output data are then compared with known correct results, and any discrepancies are fed back from the output layer to the input layer to iteratively update the neural weights of the ANN model. Numerous techniques have been developed to optimise these weights, including the Levenberg–Marquardt (LM) method [108], scaled conjugate gradient (SCG) [109], one-step secant (OSS) [110], and others. This iterative process continues until the output errors fall within an acceptable tolerance.

2.1.8 Convolutional Neural Networks (CNN)

Convolutional neural network (CNN) [111] is one of the representative algorithms for deep learning, crafted to mimic the visual perception processes observed in animals. It is adaptable to both supervised and unsupervised learning paradigms. In this architecture, key components include input and hidden layers, with the hidden layers typically comprising convolutional layers, pooling layers, and fully connected layers. Convolutional layers play a pivotal role in extracting features from input data samples, while pooling layers serve to filter these features and convey new information to the fully connected layer. Regardless of implementing the supervised or unsupervised learning frameworks, CNNs leverage the concept of transferring error information backwards, akin to BPNN, facilitating the iterative adjustment of model parameters to enhance learning.

2.2 Unsupervised Learning

In contrast to supervised learning, unsupervised learning models are designed to unveil inherent structures or patterns within unlabelled data samples [112]. Despite this capability, the absence of corrective mechanisms inherent in supervised approaches makes it challenging to ensure the reasonability of learning models during the learning process. Unsupervised learning excels in discerning underlying laws among input data samples. Once trained and verified, these models find proper application in novel scenarios. Two prevalent techniques employed in unsupervised learning are clustering and dimension reduction [113]. Notable algorithms within this domain include K-means [114], Self-Organising Map (SOM) [115], Principal Component Analysis (PCA) [116], and CNN [117] as follows.

2.2.1 K-means

The K-means algorithm [118] is one of the most popular unsupervised ML models for its simplicity. The fundamental concept behind K-means is to categorise samples into the most similar groups based on the distances between each sample and category centre. Upon introduction of new samples into each cluster, the category centres undergo updates. The final classification of each sample is determined through iterative processes, ceasing when no further changes in category centres occur. However, due to the necessity of calculating distances between samples and all category centres, the K-means algorithm may exhibit sluggish performance when applied to large-scale datasets. Additionally, its sensitivity to noise may cause category centres to deviate to some extent from the correct ones in certain cases [114].

2.2.2 Self-Organising Map (SOM)

SOM [119] can be conceptualised as a straightforward neural network consisting only of an input layer and an output layer without hidden layers. SOM endeavours to map a dataset from any dimension into a one-dimensional or two-dimensional space by adaptively performing a transformation in an organised manner. Employing competitive learning, the winning neuron which is most closely aligned with the input data, is activated, prompting updates to the parameters of nodes neighbouring the activated neuron in terms of their distances from the winner. SOM facilitates the visualisation of database structures in a single image and has found extensive applications in clustering and data mining across various domains, including finance, industry, biomedical science, and more [120,121,122,123,124].

2.2.3 Principal Component Analysis (PCA)

PCA [125] is one of the most frequently utilised linear dimension reduction algorithms. It achieves the transformation of high-dimensional datasets into a lower-dimensional space through various forms of linear projection. PCA aims to maximise the variance of datasets in the projected dimensional space, enabling the utilisation of fewer dimensions while preserving the essential characteristics of the original datasets [126]. As a linear dimensional reduction method, PCA minimises the loss of features from the original dataset. Essentially, PCA seeks to distil key information from data samples, facilitating a simplified characterisation of the datasets [127]. Furthermore, PCA is adept at noise reduction within datasets and contributes on computational efficiency. This method finds applications in various biomedical areas [95, 128, 129].

2.2.4 Convolutional Neural Network (CNN) for Unsupervised Learning

In scenarios with limited labelled samples, CNN can be extended to the realm of unsupervised learning. Several models have been proposed in this context, including Variational Autoencoders (VAE) [130], Convolutional Restricted Boltzmann Machines [131], Deep Convolutional Generative Adversarial Networks [132], and so on.

2.3 Semi-supervised Learning

Semi-supervised learning [133] emerges as a valuable approach in scenarios featuring both labelled and unlabelled data samples, amalgamating principles from supervised and unsupervised learning. Often, full supervision proves unnecessary, and semi-supervised learning offers a less time-consuming and labour-intensive alternative for manually labelling training samples [134, 135]. Generally speaking, this methodology leverages a smaller set of labelled samples alongside a larger pool of unlabelled ones. The inclusion of unlabelled samples mitigates the challenges associated with performance degradation in conventional supervised learning when training samples are insufficient. Prominent algorithms in semi-supervised learning include self-training, semi-supervised support vector machine (S3VM), and graph-based methods.

2.3.1 Self-Training

Self-training represents the simplest method in semi-supervised learning, seeking to augment labelled datasets using unlabelled data samples [136, 137]. The process involves training with a limited number of labelled samples and subsequently labelling unlabelled samples with a well-trained ML model [138]. Given the potential inaccuracy of predictions from a model trained on an insufficient dataset, filtering techniques may be necessary in this context. A key drawback of self-training is the potential introduction of noisy labels by a well-trained ML model, prompting further studies to address this issue [139, 140].

2.3.2 Semi-supervised Support Vector Machine (S3VM)

As proposed by Bennett [57], Semi-Supervised Support Vector Machine (S3VM) extends the conventional SVM method in the realm of semi-supervised learning. In scenarios without unlabelled samples [141], it resembles SVM, aiming to identify a hyperplane with the maximum interval distance between support vectors. When considering unlabelled samples, S3VM attempts to establish a hyperplane that not only separates different types of labelled samples but also navigates through low-density areas in the dataset [142]. In this regard, Ding et al. [143] provide a comprehensive review of mainstream models in semi-supervised support vector machines, including Transductive SVM (TSVM), Laplacian SVM (LapSVM), MeanS3VM, and S3VM based upon cluster kernels.

2.3.3 Graph-Based Methods

Graph-based methods include minute [144], spectral graph transducer [145], Gaussian fields, harmonic function [146], etc. These methods share some similarities with the nearest-neighbour learning algorithms in supervised frameworks, differing in their incorporation of unlabelled samples to enhance ML model performance. Labelled and unlabelled data samples are treated as vertices connected by edge weights. The generation of graph edges, computation of edge weights, and execution of graph-based algorithms constitute crucial steps, with the effectiveness of this semi-supervised ML algorithm reliant on well-defined graph edges and edge weights [147].

2.4 Reinforcement Learning

Reinforcement learning [148] stands as the fourth fundamental category of ML methods, alongside supervised learning, unsupervised learning, and semi-supervised learning. In contrast to supervised learning, which aims to train ML models for producing correct outcomes, reinforcement learning places a strong emphasis on evaluating outcomes through reinforcing signals. Reinforcement learning models evolve through existing experiences and learning from mistakes to achieve improved results. Common reinforcement learning algorithms include Monte Carlo learning and Q-learning.

2.4.1 Monte-Carlo Learning

Monte Carlo learning involves the use of a substantial number of random samples to explore the entire knowledge space by directly learning from the environment [149]. This approach allows the construction of a relatively abstract model using known data samples, with the model parameters determined through the Monte Carlo technique to minimise residuals from original data. The Monte-Carlo algorithm learns from experiences, encompassing the state of samples, actions, and rewards. Upon extracting experiences from samples, reinforcement learning tasks can be addressed based on average sample returns [150, 151]. This type of reinforcement learning algorithm is less sensitive to initial values. However, the convergence of Monte-Carlo learning can be a key issue, and many studies have been carried out to deal with it [152, 153]. This reinforcement learning algorithm exhibits lower sensitivity to initial values. However, achieving convergence in Monte-Carlo learning can be a pivotal challenge, prompting numerous studies in the literature over time [154].

2.4.2 Q-learning

Q-learning, introduced by Watkins and Dayan [155], employs a Q-table as a reference to explore external states and receive rewards until a target state is attained. The training process of Q-learning primarily involves strengthening the ‘brain’ conventionally represented as the ‘Q’ table. It excels in identifying the most efficient path to reach the desired state effortlessly [156]. In comparison to the Monte Carlo reinforcement learning algorithm, Q-learning is more efficient but exhibits higher sensitivity to initial values [157, 158].

3 Machine Learning in Biomaterials

3.1 Overview

Biomaterials encompass versatile subclasses of organic/inorganic biocompatible materials that can intimately interact with living tissues. Apart from their mechanical and physical properties, tissue/cellular interactions with biomaterials have proven critically important [159, 160]. Table 1 summarises some typical biomaterials to illustrate the application spectrum. For example, polymers signify one of the major subclasses, varying from natural biopolymers such as proteins and polynucleotides [161] to synthetic degradable and non-degradable ones [162]. Their applications embrace a fairly broad range, such as connective hard and soft tissues [163], bioinks [43], drug delivery media, and tissue scaffolds [164]. Metals and their alloys are other important subclasses of biomaterials owing to their excellent mechanical properties and inertness [165], which have been well developed as a good alternative for either temporary or permanent replacement of failure tissues. Typical metallic biomaterials include stainless steel, titanium alloys, magnesium alloys, and shape memory alloys, which are widely used in orthopaedic devices [38, 39], dental devices [166,167,168,169,170,171,172,173], wearable devices [13] and arterial stents [41]. Similar to metallic biomaterials, ceramics have been used to replace or restore some diseased hard tissues (e.g., bone and teeth) owing to their excellent mechanical properties, chemical resistance, and transparency [33, 34, 174]. Composite biomaterials, generally composed of two or more materials with different compositions and microstructures, have also been studied and tested in medical applications such as orthopaedic implants and tissue scaffolds [175, 176], which could offer more freedom for engineers to customise various functionalities with ease.

Table 1 Typical biomaterials and their applications

Conventional routes for unravelling novel biomaterials rely on a large number of trial-and-error experiments in vitro and/or in vivo, which are generally time-consuming and uneconomic. Therefore, a so-called “rational design” using computational techniques has been more and more favoured for exploring novel biomaterials recently [212]. Latest advances in ML approaches have inspired biomaterials engineers and developers in rational design for their superior ability to handle a large volume of data over human experience, which has extensively influenced the design philosophy and development of new biomaterials as well as their clinical applications [213,214,215].

The ML applications in biomaterials can be categorised into three typical areas, namely data mining/processing, digital twins, and data-driven design. Data mining/processing allow identifying decisive factors affecting the target biomaterial properties, thus offering an intuitive way for characterising and understanding biomaterials. Digital twins establish quantitative relationships between those determinative factors and desired biomaterial properties, which can play a critical role in obtaining real-time responses of desired performances. Benefiting from the data mining/processing and digital twins, biomaterial design allows better customising those determinative factors for achieving desired and/or optimal functionalities [216, 217]. These three categories play important roles in exploring novel biomaterials, which are analysed in the following subsections. In this section, the analysis was conducted under the thematic umbrellas of biomaterials with data mining/data processing, digital twins, as well as data-driven design as follows.

3.2 Data Mining/Processing for Biomaterials

Biomaterials are generally associated with substantial data acquired from either experimental (in vitro and/or in vivo) tests or in silico modelling. ML techniques such as clustering, classification, and dimensionality reduction can be used to excavate such big data to determine the most relevant and dominant factors for the targeted biomaterial properties. In this aspect, Madiona et al. [177] employed the self-organising map (SOM) method to reduce the dimensionality of data describing surface interactions between polymers and living tissues (Fig. 4a), which provides an effective way to understand the molecular properties of polymer surfaces. In their study, the SOM was constructed with a network size of 8 × 8 and trained through a specified number of iterations, totalling 10,000 epochs. Figure 4a visually represents the data labels with distinct colours: polyethene terephthalate-red, poly(methyl methacrylate)-green, low-density polyethene-blue, poly(caprolactam)-sky blue, poly(undecanoamide)-lavender, poly(lauryllactam)-light yellow, poly(trimethyl-hexamethylene terephthalamide)-dark green, poly(hexamethylene adipamide)-indigo, Poly(hexamethylene azelamide)-dark red, and Poly(hexamethylene dodecanediamide)-light blue. Baier et al. [199] used the K-means clustering method to analyse micropores that could distinctively influence cellular physiology and new bone ingrowth in CaP bioceramics, in which five geometrical parameters (Fig. 4b) in each clustering group were investigated. In Fig. 4b, the three micropore clusters are based on Feret’s diameter and circularity as highlighted in black (1), red (2), and green (3). Shen et al. [189] studied the cell proliferation with titanium dioxide nanotube (TNT) using a DT model, where it was found that cell density and sterilisation could simultaneously impact the cell proliferation on various TNTs (Fig. 4c). The study involved a comparison between predicted and measured cell proliferation values using Decision Trees (DT). The DT employed an 80%/20% split for training and testing data. Additionally, a radar plot was generated to analyse the importance of each experimental feature. This encompassed factors such as the average diameter of TNTs, cell seeding density on the samples, samples annealed at high temperatures, cell incubation time, and sample sterilisation methods. Li et al. [188] used the SVM algorithm to identify the effects of various parameters on the mechanical behaviours of biodegradable magnesium (Mg) implants, which include metal forming processes and procedural temperature (Fig. 4d).

Fig. 4

Applications of data mining/processing in biomaterials. a Unsupervised self-organising map (SOM). Reproduced with permission. Copyright 2019, Elsevier [177]. b K-means clustering method to analyse bioceramic micropores. The yellow dots indicate the centres of each cluster. Reproduced with permission. Copyright 2019, Authors [199]. c The decision tree (DT) model for investigating cell proliferation on titanium dioxide nanotubes. Reproduced with permission. Copyright 2021, Authors [189]. d The flowchart uses the support vector machine (SVM) to estimate the mechanical properties. Reproduced with permission. Copyright 2021, Elsevier [188]. e A fully connected neural network to identify polymer configurations (globule, anti-Mackay, Mackay), including input layer, hidden layer, and output layer composed of neurons (circles). Reproduced with permission. Copyright 2017, American Physical Society [178]

It is worth noting that some ML-based studies on material sciences for engineering applications could also be rather useful [218,219,220,221,222,223,224]. For example, Wei et al. [178] employed an ANN model to classify different states of polymeric configurations, in which the classification can offer a novel and intuitive way to unravel the phase transitions between different polymers. Tripathi et al. [198] used the PCA method to filter noise data for identifying micro-damage in piezoelectric ceramics. Chittam et al. [187] investigated the performances of the logistic regression, SVM, and RF algorithms for data mining/processing in Mg-alloy, which presented a detailed framework on how to use these powerful data science tools in development of biomaterials.

3.3 Digital Twins for Biomaterials

Once pattern/feature recognitions on biomaterial datasets are achieved through some ML procedures, how to relate the identified parameters with material properties becomes a critical issue. In this regard, various ML approaches can be used to establish the relationships between identified parameters and desired biomaterial properties, which typically serve as digital twins [225,226,227,228] of their in vivo and/or in vitro experimental counterparts to predict real-time responses with sufficient accuracy when varying different parameters or patterns. The digital twin constructs a solid bridge between a physical biomaterial and its virtual counterpart, enabling to apply computational modelling techniques to accelerate the design process of new biomaterials [229, 230].

A number of studies have attempted to apply ML-based approaches for establishing digital twins for biomaterials in literature [231,232,233,234]. For example, Epa et al. [180] employed a three-layer NN to model the adhesion of human embryonic stem cell embryoid bodies (hEB) on the various polymeric surfaces. Rostam et al. [182] modelled the immune response of cells to polymer surfaces by using the RF, SVM, and NN models, offering a potential tool for the “immune-instructive” rational design of polymers. Vassey et al. [184] employed the gradient boosting regression method [235] to correlate structure-surface with cell-response, paving a futuristic way to modulate inflammatory responses by rational design of biomaterials as shown in Fig. 5a. The gradient-boosting regression model, trained on a dataset, predicted cell attachment and phenotype based on various surface features. The attachment of macrophages, categorised as high (blue), medium (green), or low (orange), was correlated with the sizes of topographical features in terms of total pattern area (μm²). Robles-Bykbaev et al. [181] investigated the osteocyte growth in scaffolds composed of type I collagen, in which the linear and nonlinear logistic regression models were used to simulate the degradation of collagen together with osteocyte growth and stem cell growth (Fig. 5b). The supervised RF algorithm classified the training samples into four distinct maps. The statistical learning model encompassed both linear/nonlinear regression and Long Short-Term Memory (LSTM) neural networks to predict biological activities. The proposed digital twins exhibited fairly promising results for estimating the biodegradation of collagen scaffolds through image data, which could serve as a potential tool for scaffold design. Burroughs et al. [179] used the RF to model cellular responses to topographically-patterned microscopic polymers, which provides an alternative numerical strategy in design of biomaterials for regenerative medicine (Fig. 5c). In Fig. 5c, the ChemoTopoChip layout features the colours representing various chemistries. The scatter plots illustrate (i) human immortalised mesenchymal stem cell (hiMSC) alkaline phosphatase intensity using a RF model with indicator variables for chemistries and topographical descriptors, and (ii) human macrophage polarisation using a RF model with indicator variables for chemistries and topographical descriptors. The line $y=x$ represents an ideal fit, and $R2$ corresponds to the goodness of fit.

Fig. 5

Applications of digital twins for biomaterials. a Machine learning predicting structure-surface with cell-response. Reproduced with permission. Copyright 2020, Authors [184]. b ML modelling of cellular growth and degradation of collagen. Reproduced with permission. Copyright 2019, Authors [181]. c Chemical and topographical features enhancing the responses of both cell types using ML. Reproduced with permission. Copyright 2021, Authors [179]. d ML prediction of drug release. Reproduced with permission. Copyright 2022, Royal Society of Chemistry [183]

Concerning biomaterials for drug delivery applications, Santana et al. [183] integrated a perturbation theory with ML approaches for predicting biological responses (e.g., probability of drug deviation from an anticipated dose) to nanoparticles that were designed for drug release. The study compared a number of regression models, including logistic regression, DT, NB, RF, and ANN models. The results, as depicted in Fig. 5d, revealed that the RF and NN models outperformed the others in terms of predictive accuracy. The investigation considered different drug release systems: No. 1, pristine nanoparticles with linked drugs; No. 2, coated nanoparticles with drugs linked to the nanoparticles; and No. 3, coated nanoparticles with drugs linked to coating agents. A combination of the trained perturbation theory and ML models was employed to predict the success of drug release systems using various molecular and coating descriptors.

In the material engineering field, substantial efforts have been made to apply various ML techniques for predicting or modelling mechanical and/or physical properties of materials, which can also be applied to design of biomaterials [236,237,238]. Typically, ML approaches can be used to predict polymeric material properties such as dielectric constant, glass transition temperatures, and bandgap, which are some important clues for biological responses [185]. Several studies have been reported to characterise mechanical and physical properties by ML techniques [190, 191, 193, 194], demonstrating great potential for biomedical applications. For example, Moghadam et al. [192] employed an ANN model to predict the bulk modulus of metal-organic materials, which enabled to establish structural-mechanical stability for 3358 base-materials with starkly different morphologies. Yang et al. [207] used a deep-learning CNN model to construct a digital twin for evaluating the stiffness of composite with different base materials. Various digital twins for ceramics were also widely reported [200,201,202,203], which are expected to be applied for future studies in biomedical engineering. Table 2 summarises more studies applying ML approaches in modelling material properties for the reference of biomaterial applications.

Table 2 A summary of machine learning (ML) applications in modelling/predicting various properties of biomaterials

3.4 Data-Driven and Machine Learning-Based Design for Biomaterials

ML approaches in data mining/processing enable to identify key patterns and/or parameters for constructing proper digital twins, which can be used for attaining desired material properties effectively. In literature, numerous studies have adopted different ML techniques for devising novel biomaterials. For example, Damiati et al. [186] explored the optimal design of a biodegradable polymer for drug delivery application. In their study, the drug delivery vehicles were based upon Poly (D, L-lactide-co-glycolide) (PLGA), where a non-steroidal anti-inflammatory drug (NSAID) Indomethacin (IND) was loaded. A multi-layer ANN model was employed to predict PLGA droplet sizes with respect to the input of PLGA concentration (Fig. 6a) and flow rates of both PLGA and aqueous phases, and thus the desired polymer particles can be tuned using the ANN model. Wu et al. [197] investigated the design of a titanium alloy with the desired Young’s modulus close to that of human bone. The study involved several key steps, including property prediction using two ANNs, mass spectrometry (MS) temperature filtering, and plotting combined maps, etc. These two ANN models were established to predict the martensitic transformation temperature (i.e., MS temperature) and the resulting Young’s modulus of the Ti-alloy, as illustrated in Fig. 6b. The constituents of the Ti-alloys, namely Ti, Nb, Zr, Sn, Mo, and Ta, were considered as the inputs. Using the ANN models, six groups of Ti-alloys were obtained, with Young’s modulus ranging from 40 to 65 GPa, validated through the dedicated experimental testing.

Fig. 6

Applications of machine learning (ML) in design for biomaterials. a Correlation between the observed and predicted PLGA droplet diameter. Reproduced with permission. Copyright 2021, Authors [186]. b Illustration of the operational process of βLow-assisted alloy design. Reproduced with permission. Copyright 2020, Elsevier [197]. c ML design of high-entropy alloys. Reproduced with permission. Copyright 2019, Elsevier [196]. d Microstructures of synthesised materials designed by ML. Reproduced with permission. Copyright 2020, Authors [204]. e ML design of hydroxyapatite nanopowders as bone fillers. Reproduced with permission. Copyright 2021, Elsevier [262]. f Hierarchical design construction and ML applicability for stronger and tougher microstructural materials. Reproduced with permission. Copyright 2018, Authors [209]

Wen et al. [196] conducted an ML-based design of high entropy alloys with a great hardness, as illustrated in Fig. 6c. The alloys were derived from the Al-Co-Cr-Cu-Fe–Ni HEA system. An experimental dataset containing material compositions and physical properties was utilised to train a SVM model for predicting the hardness. Iteration loop I involved constructing a ML-based surrogate model (${y}_{i}=f({c}_{i})$) with a training dataset, which was then applied to a search space to predict the properties and associated uncertainties. A utility function for Design of Experiment (DOE) was employed to select a candidate by balancing the exploitation and exploration. After synthesising and measuring the recommended candidates, the new data were incorporated into the training dataset, facilitating iterative improvement of the surrogate model. Iteration loop II was basically similar to Iteration loop I, with the introduction of a feature pool. In this loop, a ML-based surrogate model was trained from compositions (${c}_{i}$) and preselected physical features (${p}_{i})$, denoted as ${y}_{i}=f({c}_{i},{p}_{i})$. In their study, seventeen new alloys were optimised with higher hardness than the training dataset, showcasing a potential framework for tailoring the mechanical properties of other metallic alloys.

In design of bioceramics, similar strategies have also been taken to explore high-entropy ceramics [261]. For example, Kaufmann et al. [204] employed the RF method to explore the entropy-forming ability of disordered metal carbides. A set of material features reflecting essential chemistry, physics, and thermodynamics of each constituent was taken as inputs (Fig. 6d). In Fig. 6d, the first column presents an electron micrograph for each of the synthesised compositions. Columns 2–6 display the selected Energy Dispersive X-ray Spectroscopy (EDS) chemistry maps for each of the five metal cations present in every system. Column 7 is an electron backscatter diffraction (EBSD) map of the grain structure, revealing the effect on grain size in multi-phase compared to single-phase compositions. Compositions are listed from the largest to the smallest ML predicted entropy-forming ability (scale bar 100 µm). Yu et al. [262] investigated the structural behaviour of nanosized substituted hydroxyapatite (HA) powders using different ML techniques, in which a multi-layer perceptron (MLP) was adopted to model structural characteristics, and a genetic programming (GP) technique was employed to appraise the strength of the predictive model (Fig. 6e). Note that the ANN inputs the chemical compositions and outputs crystallite size (D), micro strain (η), and grain boundary volume fraction (f) of the various substituted HA nanopowders for design.

Design of biocomposites is commonly associated with a large design space, thus becoming a fairly demanding yet an active research field favouring some ML techniques [208, 211, 263]. For example, Gu et al. [209] systematically studied the design of bioinspired hierarchical composites using the ML techniques, as shown in Fig. 6f. The microstructure comprises a detailed assemblage of unit cells, which are then converted into a data matrix of building blocks encoding the individual unit cells. Strength and toughness ratios of designs were computed from the training data and ML output designs. Strain field plots were obtained from digital image correlation (DIC) measurement for ML optimisation. An ANN model was employed to predict the toughness and strength by taking material components in different locations of a unit cell as inputs. The new microstructural patterns obtained from the ANN model have exhibited a higher toughness and higher strength, the design of which was further prototyped by using AM techniques and validated by the experimental tests. Han et al. [210] proposed a ML framework for the design of bioactive glass used for biomedical applications. To precisely predict the dissolution behaviour of the bioglass composites, they compared the performances of several typical ML-based regression models, such as hybridising the RF model with the additive regression (AR-RF), SVM, ANN, linear regression, and Gaussian process regression models, where the AR-RF had proven to be of better performance over the other models. The proposed ML model could be used to design new bioglass composites with a controlled release and is expected to form a useful tool for considering other physical, chemical, biological, and mechanical properties. Table 3 summarises some more recent studies for the data-driven and ML-based designs of materials/biomaterials.

Table 3 A summary of machine learning (ML) in design for materials

4 Machine Learning in Biomechanics and Mechanobiology

Biomechanics plays a significant role in biomedical engineering, addressing a diverse array of healthcare objectives spanning from the body level to tissue and cellular levels [284, 285]. Mechanobiology signifies an emerging field that also investigates physical forces and mechanical properties of biological systems but focuses more on their spatial-temporal effects on regulating cellular/tissue activities. Recently, ML approaches have demonstrated their efficacy in the realms of biomechanics and mechanobiology, tackling the intricate knowledge required for these interdisciplinary features [36, 95, 286,287,288,289,290]. The following subsections detail the state-of-the-art developments in these fields and explore the computational strategies employed in multiscale modelling. It should be noted that in this review, the relevant studies were identified using such keywords as “machine learning” or “data-driven,” and combined with biomechanics, mechanobiology, and multiscale modelling in Web of Science Core Collection.

4.1 Biomechanics

4.1.1 Body Movements

ML techniques have been increasingly used to study biomechanics in the aspect of body movements, especially combining with signals acquired from various wearable and other devices. For example, several studies have showcased the applications of ML algorithms in analysing knee-specific biomechanics in conjunction with inertia sensors [83, 95, 291,292,293,294,295,296]. These studies focused on recording peak tibial acceleration, which exhibited a certain correlation with vertical ground reaction force (vGRF), knee flexion angle (KFA), knee extension moment (KEM), and sagittal plane knee power absorption (KPA) (Fig. 7a–c). For instance, Fig. 7c illustrates the model consisting of seven rigid segments and 16 Hill-type muscles (blue) with seven virtual inertial sensors (red): namely 1-iliopsoas, 2-glutei, 3-hamstrings, 4-rectus femoris, 5-vasti, 6-gastrocnemius, 7-soleus, and 8-tibialis anterior. In these biomechanical studies, the ML regression models (e.g., ANN, linear and nonlinear regression) could predict either global vGRF or knee-specific measures (e.g., KFA, KEM, KPA) by extracting various features such as shank and foot angle, running speed, ground slope (Fig. 7d). In general, the acceleration signals of a step are transformed into a feature vector representation, and a structured prediction algorithm enables to map the sequence of input vectors to the most likely gait segmentation sequence.

Fig. 7

Applications of machine learning (ML) in the measurement of body movements. a Sensors positioned on the lateral aspect of the torso, upper arm, forearm, and hand. Reproduced with permission. Copyright 2020, Authors [83]. b Marker placement for standard biomechanical gait analysis. Reproduced with permission. Copyright 2018, Authors [95]. c Conceptual drawing of a musculoskeletal model. Reproduced with permission. Copyright 2020, Authors [294]. d ML applied to the signals. Reproduced with permission. Copyright 2021, Elsevier [293]. e Alignment of the 3D triad to the images for trunk orientation and matching of the 3D scapula model to the images for scapula orientation. Reproduced with permission. Copyright 2019, Elsevier [297]

A similar strategy has also been reported for scapular kinematics [297], where humeral orientations and acromion process positions obtained from the motion capture data were used to train a multi-layer ANN model for the estimation of scapula orientation (Fig. 7e). Table 4 provides a summary of the studies using ML in biomechanics for body movements.

Table 4 A summary of machine learning approaches in biomechanics for body movements

4.1.2 Hard Tissue

Biomechanics of hard tissues is critically important for unravelling injuries, diseases, trauma, and design for implantable devices [312, 313]. Hard tissues, typically bones, are less prone to damage but often result in serious consequences when injuries occur [314]. While non-invasive imaging technologies such as X-ray and computed tomography (CT) have been widely used for detecting bone fractures, diagnoses relying on the human experience are often labour-intensive [315]. Moreover, micro-fractures are often challenging to be detected properly due to image ambiguity, noise, and other knowledge-dependent limitations [316]. To overcome this issue, ML approaches have been employed to classify bone fractures using image data [317,318,319,320,321,322,323,324,325]. Deep learning-based CNN and ANN models have proven effective in understanding bone microstructures and their fracture mechanics, as illustrated in Fig. 8a–d. For example, Fig. 8a illustrates a flowchart for three classification cases. Following a semi-automated cropping phase, a classic CNN was used as a baseline for classification, characterised by subsequent binary networks. The class activation map was then employed to visualise where the network was focusing. Instead of directly using images, Villamor et al. [326] established patient-specific FE models based on Dual-Energy X-ray absorptiometry; subsequently, the data extracted from finite element (FE) analyses, together with clinical information, were used to train the SVM capable of classifying potential hip fractures (Fig. 8e).

Fig. 8

Machine learning (ML) methods for detecting bone fractures. a Flowchart illustrating the three classification cases. Reproduced with permission. Copyright 2020, Elsevier [319]. b Optimised convolutional neural network (CNN) structures for the classification of cortical bone images and trabecular (cancellous) bone images. Reproduced with permission. Copyright 2021, Elsevier [317]. c Gradient-weighted Class Activation Mapping (Grad-CAM) activation heatmaps for the optimised CNN on pristine and failed cortical bone images, with the heatmaps overlaid on the original images. Reproduced with permission. Copyright 2021, Elsevier [317]. d Grad-CAM activation heatmaps for the optimised trabecular bone CNN on pristine and failed trabecular bone images, with the heatmaps overlaid on the original images. Reproduced with permission. Copyright 2021, Elsevier [317]. e Input parameters for predicting fracture risk, including geometry, bone density, boundary conditions, and material properties. Reproduced with permission. Copyright 2020, Elsevier [326]

Apart from bone fracture identification, ML approaches have also been widely employed for bone mechanics studies. Some early works can be traced back to 2004 when Lucchinetti et al. [327] employed an ANN model to inversely identify Young’s modulus and Poisson’s ratio of a small trabecular bone from experimental tests. Recently, Nazemi et al. [328] employed an ANN model to characterise the bone density-modulus relationships by correlating the stiffness of cortical and trabecular bone between the FE-based results and experimental tests. The comparisons of density-modulus relationships between the ANN-derived and literature are illustrated in Fig. 9a. Vukicevic et al. [329] used an evolutionarily assembled ANN model to predict bone fracture resistance curves under different age groups. As illustrated in Fig. 9b, the specimens from cortical bone underwent compact tension tests to prepare the R-curves with specific values of crack size and stresses. Then, evolutionary assembling of ANN was performed to obtain the age-specific R-curves. Rahmanpanah et al. [330] employed two ANN models to predict the load–displacement curves of a long bone, in which the trained ANN models can successfully predict responses of specific bone samples that were not used in the training process (Fig. 9c). In their study, the experimental tests were first conducted to obtain bone length ($l$), load exposure ($t$), limb side ($s$), horse age ($l$), and strain components (${\varepsilon }_{1},{\varepsilon }_{2}, {\varepsilon }_{3}, {\varepsilon }_{4}, {\varepsilon }_{5}, {\varepsilon }_{6}$). Then, these variables, along with the applied load that was predicted by the first ANN, comprised the input variables of the second ANN. Mouloodi et al. [331] employed the ANN as a regression model to predict bone stiffness under compressive cyclic loading, in which the applied force, exposure time, bone anatomy, and age were used as input variables and exhibited a fairly accurate prediction compared with the experimental results (Fig. 9d). More studies using ML approaches in bone mechanics are outlined in Table 5 for a reference.

Fig. 9

Machine learning (ML) in bone mechanics. a Artificial neural network (ANN)-derived density-modulus relationship for proximal tibial subchondral trabecular and cortical bone along with existing density-modulus relationships in the literature. Reproduced with permission. Copyright 2017, Elsevier [328]. b Prediction of bone fracture resistance curves using ML. Reproduced with permission. Copyright 2018, Taylor & Francis [329]. c ML model for predicting long bone load–displacement curves. Reproduced with permission. Copyright 2020, Elsevier [330]. d ML predicting bone stiffness. Reproduced with permission. Copyright 2021, Taylor & Francis [331]

Table 5 A summary of machine learning (ML) in bone mechanics

4.1.3 Soft Tissue

Soft tissues play a major role in connecting, supporting, and stabilising hard tissues and organs. Investigating soft tissues poses challenges due to their intricate nonlinear properties arising from heterogeneous and multiphasic microstructures, for which conventional methods may become inefficient and less effective [23, 287, 350, 351]. To tackle these challenges, promising solutions using ML techniques have gained particular interest from research communities recently.

For example, ML approaches have been utilised as surrogate models to predict stress distributions in arterial walls, which is crucial for estimating the rupture risks of atherosclerotic plaques [352, 353]. Specifically, the FE analyses were conducted to derive stress distributions in arterial walls. The resulting FE data served as labelled ground truth data to train the ML models, such as SVM [352] (Fig. 10a) or CNN [353], with the inputs encompassing geometric parameters and arterial pressure. In Fig. 10a, the colour-coded surfaces correspond to the predicted pressure risk ratios. The results underscore the potential of ML methods for real-time diagnosis directly utilising clinical data, thereby reducing or eliminating the need for extensive FE analyses.

Fig. 10

Machine learning (ML) in soft tissue mechanics. a Support vector regression using shape feature parameters. Reproduced with permission. Copyright 2017, Springer Nature [352]. b The ML model predicts the zero-pressure shape of the aorta. Reproduced with permission. Copyright 2018, John Wiley and Sons [354]. c The comparison between the SVM model and the ANN model to predict tissue deformation (magnitude errors). Reproduced with permission. Copyright 2017, Elsevier [355]. d The schematic of the ML approach to predicting elastic properties of collagenous tissue through images. Reproduced with permission. Copyright 2017, Elsevier [356]

Liang et al. [354] presented an inverse problem to predict the geometry of a zero-pressure aorta using a multi-layer ANN model (Fig. 10b). The approach parameterised the input shapes as sets of scalar values, named as shape codes. These shape codes were then transformed from input to output shapes through a nonlinear mapping, ultimately decoding into the zero-pressure shape. Similar methodologies have been applied to predict real-time tissue deformation by using the trained ML models such as ANN and SVM [355]. Ground truth data were obtained using the patient-specific FE models subjected to various boundary conditions, altering the magnitude or position of applied external forces (Fig. 10c).

In the realm of soft tissue modelling, ML-based approaches have been instrumental in developing frameworks to predict the elastic properties and nonlinear anisotropic strain–stress curves of collagen tissues [356]. As shown in Fig. 10d, a PCA model was used to parameterise the equal-biaxial stress–strain curves and quantify the overall stiffness. Subsequently, a customised CNN model extracted the structural patterns of collagen tissues and identified overall stiffness for classification purposes. Concurrently, the CNN model was used to perform the regression to predict the PCA parameters. Given the limited experimental data available for soft tissues, an unsupervised ML method combined with supervised learning and data augmentation was proposed to overcome this challenge effectively. Furthermore, Nguyen-Le et al. [357] introduced a novel deep learning framework to predict Pelvis soft tissue deformation. The FE analyses generated a simulation-based database for training and testing. LSTM neural network and deep neural network effectively handled high-frequency oscillation signals, demonstrating better accuracy in predicting soft tissue deformation in real time. Dalton et al. [358] proposed a ML-based framework for modelling soft tissue mechanics, leveraging a Graph Neural Network (GNN) trained in a physics-informed manner to minimise a potential energy function. This framework accommodates unique soft-tissue geometries of individual patients, thus enhancing computational efficiency and accuracy by avoiding low-order approximations.

ML approaches have also been instrumental in estimating constitutive parameters of cardiovascular tissues. For example, Cilla et al. [359] demonstrated the possibility of using ML techniques to fit the constitutive models based on a strain energy function, in which the nonlinear strain–stress curves obtained from the uniaxial experimental tests were used to train an ANN model which could substantially reduce computational costs. Liu et al. [360] successfully used a multi-layer ANN model to estimate constitutive parameters in a strain-invariant-based fibre-reinforced hyperelastic model [361], which was customised for aortic walls. In their study, the training data were generated by the FE simulations with pre-defined nonlinear and anisotropic elastic properties [362, 363]. Then, the systolic and diastolic deformations subject to two starkly different blood pressures were input to the ANN model, which comprised of an unsupervised shape encoding module and a supervised nonlinear mapping module to overcome the issue of data inefficiency, thereby enabling to identify in vivo material parameters in a time-efficient fashion. Gonzales-Saiz et al. [364] developed an ML-based framework to model complex and nonlinear material behaviours of soft tissue. They presented a multiphysics model-driven framework to optimally select the suitable model kinematics, rheological components, and their combination for a given set of experimental curves.

4.2 Mechanobiology

Mechanobiology aims to investigate mechanical effects on tissue or cellular behaviours, which can be traced back to the Wolff’s law for bone remodelling in response to mechanical forces in the 19th Century [365]. Due to recent advances in experimental tools and novel methods, in vivo mechanical forces can be accurately measured [366], providing meaningful ways to gain deep insights into how tissues and cells interact with their physical surroundings, thereby facilitating the development of future treatments from a mechanobiological perspective.

Notably, bony tissue plays a crucial role in safeguarding vital organs such as the brain, heart, and lungs, as well as contributing to load transfer and facilitating proper body movement [367]. The adaptive remodelling and regeneration of bony tissues are paramount for understanding such critical processes as bone healing, distraction [368], and its interaction with prosthetic devices [369]. Consequently, numerous studies have delved into mechanobiological modelling at various levels—organs, tissues, and cells [25, 37, 370]. In tissue scaffold engineering, for instance, dynamic bone growth outcomes have been demonstrated to be significantly important for bone scaffold design [34, 38, 371,372,373,374,375]. Lured by this promise, a number of significant studies have investigated tissue ingrowth in scaffolds based on different mechanobiological models [33, 34, 233, 371, 376,377,378,379,380,381,382,383,384,385,386,387,388], as summarised in Table 6.

Table 6 A summary of bone growth modelling in tissue scaffolds

The critical importance of bone osseointegration and remodelling around implants lies in their potential performance for either successful implantation or failure/loosening of positioned devices. In this regard, Ghosh et al. [389] carried out a design optimisation of implant surfaces to enhance osseointegration and bone growth, in which three different parameterised surface models were employed as design candidates. To reduce computational cost for evaluating bone growth during the optimisation process, a NN model was employed as a surrogate. As bone growth results could be evaluated in a real-time fashion, design optimisation can be performed using GA and the NN model without the need for time-consuming time-dependent FE analyses.

In effect, mechanobiology also plays a key role in depicting the behaviour of soft tissues and their associated diseases. Numerous studies are currently underway to explore biomechanical forces on vessels in vivo or in silico [390,391,392]. At a cellular level, mechanosensation and mechanotransduction can help understand cell proliferation and differentiation in response to mechanics [393,394,395,396,397,398,399].

Despite the crucial roles of mechanobiology in cells and tissues, there have been relatively fewer studies utilising ML techniques in this area compared to generic biomechanics. In this regard, Dattatrey et al. [400] employed an ANN model to predict bone remodelling parameters in response to patient-specific loads, offering a potential for regulating the neobone responses. Tiwari et al. [401] employed an ANN model to establish the relationship between the loading parameters (strain magnitude, frequency, and cycle) and bone remodelling parameters, intending to create a comprehensive in silico model for predicting bone remodelling under varying load conditions.

For regulating cellular behaviour, Bonnevie et al. [402] applied the ML approaches to investigate the mechanosensation of cells in heterogeneous microenvironments. In their study, a SOM model was employed to reduce dimensionality of cellular shapes, and a multi-layer ANN model to predict the mechanobiological state of Yes-associated protein and transcriptional coactivator with PDZ-binding motif with different cell morphology, which was further used to identify contractile cell populations distinctly.

4.3 Multiscale Modelling

Biological tissues exhibit intricate and often highly nonlinear and anisotropic material behaviours. To develop high-fidelity computational approaches, various typical constitutive models for tissue mechanics, such as hyperelastic [403], viscoelastic [404], and poroelastic [405] models, have been explored. The accuracy of these different constitutive models normally relies on correlating their model parameters with experimental data. Over the past decades, both hard and soft tissues have been identified to possess significant heterogeneity at the microscopic level [406, 407]. This recognition addresses the challenge of why a single constitutive model often falls short in adequately matching experimental results without sacrificing generality.

To overcome this difficulty, various multiscale finite element (FE²) techniques have been developed for modelling heterogeneous tissues, which are summarised in Table 7. Conventional multiscale finite element (FE²) methods commonly employ a homogenisation approach [408] to generate effective constitutive models for macro-FE analyses. However, the complex microstructures of biological tissues are randomly distributed, making the homogenisation process computationally expensive [348]. Extracting a single representative volume element (RVE) that characterises all heterogeneous microstructures and material behaviours can be demanding, if not impossible, necessitating further studies [409].

Table 7 A summary of conventional multiscale finite element-based (FE²) modelling in tissue/organs

For example, structures of tissue scaffolds play a crucial role in new bone regeneration, influencing the mechanical stimulation that regulates cell proliferation and differentiation [410]. Therefore, computational methods (in silico) have been introduced as an effective alternative to time-consuming and expensive in vitro and in vivo experiments [411,412,413,414,415]. Nevertheless, these scenarios necessitate multi-FE analyses at microscale. Particularly for design optimisation and inverse determination of scaffolding parameters, the computational costs of conventional FE² methods can become prohibitive, severely limiting their practical applications [409].

To overcome such computational hurdle, several promising ML studies have taken a significant step toward addressing the challenges imposed by conventional FE² methods. In bone remodelling studies, an ANN model was applied at the microscale level. Here, the nominal stress derived from macro-FE analyses and cyclic loading frequency served as inputs to predict the average bone density, effective damage, and bulk Young’s modulus of each representative volume element for macro-FE bone remodelling analyses (Fig. 11a) [441, 442]. In more detail, a whole bone was analysed using a macro-FE model. At the microscopic level, a micro-FE model was developed using a trained NN incorporated into the FE code Abaqus via a user subroutine UMAT. During the FE calculation at the macro level, the NN was invoked at every integration point to compute the averaged outputs representing the RVE behaviour at the mesoscale.

Fig. 11

Machine learning (ML) in multiscale mechanobiological modelling. a Multiscale approach for bone adaptation simulation using combined finite element (FE) and artificial neural network (ANN) computation. Reproduced with permission. Copyright 2011, Elsevier [441]. b ML in predicting multiscale bone regeneration outcome in bone scaffolds. Reproduced with permission. Copyright 2021, Springer Nature [409]

Regarding mechanobiology-driven bone ingrowth in tissue scaffolds, Wu et al. [33] developed an ML-based multiscale computational framework to predict bone ingrowth in bulk scaffolds, as shown in Fig. 11b. In stage I, the in vivo image data were correlated with the ML-based in silico results to inversely determine the subject-specific parameters (R1, R2, R3, K, s) associated with a mechanobiological remodelling algorithm. NN-3 outputs the Pearson correlation coefficients (P1, P2) between the in vivo and in silico data. In stage II, microscopic bone densities within the scaffold’s representative volume element (RVE) were input to NN-2 to evaluate the strain energy density (SED). This SED served as a mechanical stimulus to update bone densities using the Wolff’s law model established with a set of inversely identified algorithmic parameters for properly predicting bone formation. In stage III, homogenisation of the RVE was performed using NN-1 to predict effective mechanical properties. Given the heterogeneous nature of tissue ingrowth within a scaffold, characterised by spatial–temporal variations in mechanical stimuli, the ML techniques were employed at the microscopic level. Here, homogenisation and strain energy density of RVEs were directly derived using the ANN models instead of time-consuming micro-FE analyses (Fig. 11b-ii and b-iii). It is noteworthy that the developed ML-based multiscale framework significantly reduces computational costs and provides new opportunities for both inverse determination of different bone ingrowth parameters and design optimisation studies that might be prohibitive when using the conventional FE² approaches.

Regarding the multiscale modelling of tissue mechanics, Pled et al. [443] proposed a ML-based approach for an inverse problem, in which an ANN model was employed to output the identified effective elastic properties of heterogeneous microstructures, as shown in Fig. 12a-i. In their study, the heterogeneous microstructure with random compliance field ${\varvec{S}}$ was parameterised by four hyperparameters ${H}_{1}, {H}_{2}, {H}_{3}, {H}_{4}$ that represent the dispersion parameter, spatial correlation length, mean bulk modulus and mean shear modulus, respectively (Fig. 12a-ii). These four parameters can recover any random compliance field ${\varvec{S}}$ by a nonlinear mapping (Fig. 12a-iii). The region of interest (ROI) for a given domain was analysed by both the High Fidelity Computational Mechanical Model and Computational Homogenisation Model with nine statistic-dependent parameters (${Q}_{1}$ to ${Q}_{9}$) that were taken as the inputs for the ANN model to output four apparent elastic properties of a given compliance field ${\varvec{S}}$ (Fig. 12a-iv). The developed approach was applied in a numerical example based on the experimental data from real heterogeneous bovine cortical bone, which exhibits promising results in terms of both modelling accuracy and computational efficiency.

Fig. 12

Machine learning (ML) in multiscale modelling of tissue/organ biomechanics. a A statistical inverse problem in multiscale biomechanics. Reproduced with permission. Copyright 2020, Elsevier [443]. b The multiscale modelling of liver using a ML algorithm. Reproduced with permission. Copyright 2019, Springer Nature [444]. c A multiscale data-driven approach for bone tissue biomechanics. Multiscale data-driven results. Top: Macroscopic strain field. Bottom: Microscopic strain field in the RVE for the highlighted point of the macroscale. Left: longitudinal strain component. Right: transversal strain. Reproduced with permission. Copyright 2020, Elsevier [445]

Hashemi et al. [444] proposed a ML-based multiscale computational framework for modelling heterogeneous liver tissue composed of versatile shapes of vessels and surrounding soft tissues with anisotropic properties, as illustrated in Fig. 12b. The geometric size of the liver is usually substantially larger than that of its vascularisation, which hinders proper use of a mono-scale FE model that requires extremely fine mesh in some regions with vasculature. Homogenised models with relatively coarse mesh subject to patient-specific geometry then serve as practical solutions, where the homogenised hyperelastic properties of arbitrary heterogeneous microstructures could be determined by a FE framework [444]. Nevertheless, the tedious conventional FE framework may need to be established for every patient-specific model at each ROI, which severely limits its use. To reduce the computational cost and improve the generality, an ANN model trained by the observed data was employed to directly determine the parameters in the Holzapfel-Gasser-Ogden model for anisotropic hyperelastic material, where the inputs were the spatial orientation and diameters of vessels in ROIs. The vascularised liver tissue was discretised into segments, and the geometric parameters of these segments were input to an ANN model to output the homogenised material properties for macro-FE modelling. Compared to the conventional FE² framework, the error of ML-based results is at an acceptable level but with a substantially lower computational cost.

Homogenisation of microstructures normally relies on the assumption of certain material constitutive models (e.g., linear elastic, hyperelastic, viscoelastic). Nevertheless, even a highly sophisticated constitutive model may fail or not be accurate enough to describe the mechanical properties of a heterogenous segment at the microscopic level. To deal with this issue, Mora-Macias et al. [445] developed a data-driven multiscale approach for the mechanical modelling of heterogenous bone, as shown in Fig. 12c. In the proposed algorithm, a biaxial compressive test was carried out on a cortical bone sample. A digital image correlation (DIC) system was used to record the strain field in the course of loading. For a given microscopic ROI as a RVE, the homogenised macro strain ${{\varvec{\upvarepsilon}}}^{M}$ can be obtained using the micro strain ${{\varvec{\upvarepsilon}}}^{m}$ measuring by the DIC. As a result, the experimentally observed dataset contains a pair of macro strain and marco stress (${{\varvec{\upvarepsilon}}}^{M}({{\varvec{\upvarepsilon}}}^{m}), {{\varvec{\upsigma}}}^{M}$), in which the macro strain ${{\varvec{\upvarepsilon}}}^{M}({{\varvec{\upvarepsilon}}}^{m})$ is composed of the micro strain field information ${{\varvec{\upvarepsilon}}}^{m}$. As only a limited number of data could be obtained through the experimental tests, a data-completion technique was proposed to enrich the dataset (${{\varvec{\upvarepsilon}}}^{M}({{\varvec{\upvarepsilon}}}^{m}), {{\varvec{\upsigma}}}^{M}$) at both the macroscopic and microscopic levels. A data-driven modelling approach as an extension of the algorithm presented by Kirchdoerfer and Ortiz [446, 447] was then performed by searching for the closest stress–strain pair (${{\varvec{\upvarepsilon}}}^{M*}, {{\varvec{\upsigma}}}^{M*})$ in the enriched dataset (${{\varvec{\upvarepsilon}}}^{M}({{\varvec{\upvarepsilon}}}^{m}), {{\varvec{\upsigma}}}^{M}$). In the proposed data-driven approach, no constitutive model at the microscopic level was pre-assumed. The relationship between the micro strain and the macro strain was directly obtained from an experimental dataset, thereby avoiding the time-consuming homogenisation analyses and thus improving the accuracy of multiscale results at the same time. In contrast to the conventional linear orthotropic material behaviour of cortical bone tissue, they identified the non-smooth patterns of macro stress and macro strain using the proposed data-driven algorithm, demonstrating a potential improvement of a pre-assumed, well-defined model by a data-driven approach.

5 Machine Learning in Biofabrication

Additive manufacturing (AM) technologies pave a relatively new and solid way for novel biofabrication. The advent of ML techniques has generated a substantial impact on biomedical engineering without the exception in biofabrication due to their distinguished benefits and exceptional flexibility for patient-specific strategies [448,449,450,451,452]. This section aims to comprehensively review the ML techniques involved in biofabrication, focusing on the four crucial aspects: structural design, metamaterial development, optimisation of processing parameters, and in situ monitoring of manufacturing. As general AM techniques have been well developed, readers who are interested in their other generic applications than the biomedical fields can refer to some more comprehensive review articles [53, 453,454,455,456]. The relevant studies discussed in this section were identified using keywords such as “machine learning” or “data-driven,” combined with structural optimisation, topology optimisation, metamaterial design, processing parameters, and in situ monitoring of AM in the Web of Science Core Collection by 2023.

5.1 Structural Design

Additive manufacturing offers a new technological paradigm and exhibits remarkable advantages over conventional fabrication processes for producing geometrically sophisticated products with desired structural characteristics and functions. This capability bridges the gap between novel design and effective realisation [457, 458]. Structural design signifies a crucial step in the workflow of biofabrication, often involving iterative trial-and-error processes and various experimental tests that may not be available with ease [459]. As a result, the so-called rational design has drawn particular interest from the research community and industry sector [460, 461], in which one needs to know how the structural change can affect desired functionalities so as to reasonably tune structural design with an acceptable cost. Nevertheless, the largely improved design freedom offered by AM may increase the cost of conventional rational designs. To this end, ML techniques have been introduced to shed new light on the conventional design workflow [462,463,464].

5.1.1 Parametric Optimisation

One of the most commonly used rational design methods is parametric optimisation [465, 466]. In contrast to trial-and-error approaches, desired structural performances are treated as objectives and/or constraints with respect to design variables that parameterise the structural configuration, materials and dimensions in an explicit form. Taking design of orthopaedic devices as an example, different types of cellular structures have been comprehensively investigated, such as strut-based lattices [467,468,469], triply periodic minimal surface (TPMS)-based lattices [470], bio-inspired lattices [471,472,473,474], auxetic structures [475], honeycomb structures [476], and origami-inspired structures [477] (as shown in Fig. 13a). After generation of these parameterised cellular structures, computational modelling techniques can be involved to calculate the responses of objectives and constraints, where the ML techniques, as reviewed in Sect. 4, have substantial potential to play active roles, e.g., prediction of bone remodelling [33], interactions with the host environment [389, 402], etc.

Fig. 13

Machine learning (ML) in parametric optimisation. a Different types of cellular structures, including strut-based lattices (Reproduced with permission. Copyright 2019, Elsevier [468]), TPMS-based lattices (Reproduced with permission. Copyright 2018, American Chemical Society [470]), bio-inspired structures (Reproduced with permission. Copyright 2020, Elsevier [472]), auxetic structures (Reproduced with permission. Copyright 2019, Authors [475]), Honeycomb-like structures (Reproduced with permission. Copyright 2014, John Wiley and Sons [476]), and Origami-inspired structures (Reproduced with permission. Copyright 2-16, Elsevier [477]). b ML design of implants targeting desired strain pattern. Reproduced with permission. Copyright 2019, John Wiley and Sons [480]. c ML-based design of patient-specific dental implants. Reproduced with permission. Copyright 2018, Elsevier [481]

In parametric optimisation, surrogate models [478] are often employed to approximate the responses of objectives and constraints with respect to design parameters. In this regard, supervised ML techniques show great benefits in parametric optimisation, which vary from the conventional surrogate techniques, such as the response surface model, Kriging model, and radial basis function model [478], to more prevailing ML regression approaches. In literature, there have been several studies [479,480,481] employed NNs as surrogate models to predict the micro strain on bone-implant interfaces, in which the GA was used to optimise the input variables for tweaking the shape, size, and porosity of implants, thereby achieving the desired micro strain to avoid loosening of implants as illustrated in Fig. 13b and c.

Figure 13b-i depicts the internal hollowness of the femoral stems [480]. The ANN model outputs the strain difference, and the GA tunes the input parameters to achieve desired performances and outcomes, including maximum composite desirability (Fig. 13b-iii) and optimum average roof thickness values under different bone conditions (Fig. 13b-iv). In Fig. 13c, the FE analyses were performed to obtain bone-implant interface micro strain and implant stress at different diameters, lengths, and porosities of the porous dental implant for various bone conditions, serving as independent inputs to two ANN models [482]. The desirability function was used as an index to obtain desired micro strain, and the GA optimised these parameters subject to an implant stress constraint.

5.1.2 Topology Optimisation

For rational design of biomedical devices, another widely employed approach is topology optimisation [34, 38, 483]. This technique allows materials to be freely distributed in design domains, facilitating the creation of novel and sophisticated configurations. Topology optimisation enables the exploration of material potential for desired performances by significantly altering structures that notably differ from their initial designs. While intricate geometries generated by topology optimisation were once a bottleneck for fabrication, recent advances in AM technologies have relieved this obstacle, thus largely promoting topological design in real-life applications [484].

In the field of biomedical engineering, topology optimisation has been extensively applied to the design of various implantable devices, including tissue scaffolds [34, 378, 379, 485,486,487,488,489], dental implants [483, 490,491,492,493,494], arterial stents [495,496,497,498], bone fixation plates [38, 499, 500], artificial hips [501, 502], and spinal cages [503, 504]. Conventional topology optimisation methods typically require analytical/numerical sensitivity of objectives and constraints with respect to the design variables (e.g., density-based methods [505,506,507,508,509,510,511] or shape functions (level-set method [512, 513], moving morphable component (MMC) method [514]) to drive topological changes. However, the iterative optimisation process involving repeated FE and sensitivity analyses may not be ideal for achieving real-time responses. To this end, recent studies have coupled ML techniques with conventional topology optimisation techniques, where conventional topological configuration results were used to train ML models for obtaining real-time responses of topology optimisation, as summarised in Table 8.

Table 8 Data-driven and machine learning (ML) techniques for topology optimisation

For example, Yu et al. [515] utilised a CNN-based encoder-decoder network and a conditional generative adversarial network (cGAN) to achieve real-time topology optimisation without any iteration. In this approach, the CNN encoder-decoder predicts some optimal structures subject to different load conditions at low resolution, and then the cGAN takes low-resolution results as input to predict their high-resolution counterparts, as shown in Fig. 14a. Nie et al. [516] employed a generative adversarial network (GAN) to output optimal structures in a real-time fashion, using initial boundary conditions, load magnitude, and desired volume fraction as input images to the GAN model.

Fig. 14

Machine learning (ML) in topology optimisation. a Real-time topology optimisation using a convolutional neural network (CNN) and a conditional generative adversarial network (cGAN). Reproduced with permission. Copyright 2018, Springer Nature [515]. b Topology optimisation using a neural network (NN) model. Reproduced with permission. Copyright 2020, Springer Nature [517]. c Multiscale topology optimisation using ANN as a surrogate. Reproduced with permission. Copyright 2019, Elsevier [518]

In addition to achieving real-time topology optimisation, Chandrasekhar et al. [517] used a NN model to parameterise design variables. In this case, a density function in terms of a conventional solid isotropic material with penalisation (SIMP) interpolation model is directly parameterised by the weights and bias associated with the NN model. Thus, the conventional optimisation procedure was modified to train the NN model in terms of the loss function from FE analyses. Once the NN training is finished, the optimisation problem can be solved straightforwardly, as illustrated in Fig. 14b.

Another significant application of ML techniques in topology optimisation is for design of multiscale structures. Many studies have been devoted to various schemes, as outlined in Table 8. Notably, White et al. [518] employed an ANN model as a surrogate to predict the elastic response of microscale unit cells. At a microscale level, the analytical sensitivity of elastic response with respect to the design parameters controlling micro-unit cells was used to train the ANN model, thus enabling the topology optimisation at a macro-scale to use the ANN model for both the elastic responses and sensitivity information, thereby driving the topology optimisation of every single unit cells (Fig. 14c). Note that multiscale topology optimisation can be extensively useful for metamaterial designs that have broad applications in implantable devices.

5.1.3 Manufacturing Constraints

Although AM techniques have demonstrated substantial benefits for fabricating intricate products, the integration of new manufacturing constraints poses significant challenges for real-life structural designs. Notably, the necessity of support structures for large overhang designs in AM [569] and the requirement to avoid self-enclosed cavities in powder-based AM techniques for the removal of residual powder after fabrication [570] are some critical considerations. In the context of metal printing, the impact of thermal residual stress becomes pivotal, as it can lead to crack-induced failure in the fabricated parts [569]. Consequently, the emerging field of design for additive manufacturing, which systematically accounts for these manufacturing constraints, has garnered considerable attention in research communities [571, 572]. Table 9 provides a summary of some noteworthy studies in topology optimisation design for AM, taking into consideration various manufacturing constraints.

Table 9 Examples of additive manufacturing (AM) constraints in topology optimisation

To address manufacturing constraints in ML-based topology optimisation, Tan et al. [587] proposed a framework utilising deep learning for design of microstructures. In their approach, a deep learning based Generative Adversarial Network (GAN) model is trained to directly learn geometry constraints from a database. The architecture of the combined model for inverse design is depicted in Fig. 15, where the Generator of Deep Convolutional GAN and CNN are represented by a simple neural network structure for clarity. Figure 15 also shows a flowchart of the inverse design process using the combined model, represented as a simplified version in the grey-coloured box for clarity. In conventional topology optimisation, geometry-related manufacturing constraints such as overhang/self-enclosed holes are typically described by certain numerical models, which may be difficult to use for other geometries generally. In this aspect, their study shed new light on coupling arbitrary geometric constraints by directly training the ML models to learn the key features in an unsupervised fashion, which can be extended to other geometry-related manufacturing constraints with ease.

Fig. 15

Machine learning (ML) in topology optimisation coupling with manufacturing constraints. Reproduced with permission. Copyright 2019, Springer Nature [587]

Recently, Weiss et al. [588] proposed a data-driven topology optimisation approach for considering the AM constraints, in which a single fixed minimum feature size and a maximum overhang angle predicted by a data-driven constraint function were integrated with the MMC-based topology optimisation framework. The procedural steps include: (i) setting up the problem with design domain, load, boundary conditions, and an building direction of AM as the inputs, (ii) obtaining a SIMP solution with fixed minimum feature size, (iii) converting the density field into a set of connected morphable components, (iv) adjusting the component endpoints and thicknesses using the MMC algorithm to optimise the objective, (v) assessing the minimum manufacturable thickness for each component using the constraint function, (vi) smoothly reducing density from fully dense to void, projecting each component to the new density field, and (vii) performing FE analysis and sensitivity calculations, with the optimiser updating the decision variables.

5.1.4 Manufacturing Uncertainty

Apart from these manufacturing constraints, AM-induced material and geometric uncertainties are also some crucial parameters to be considered. Material uncertainty may impact the performance of as-built parts, while geometric uncertainty may drastically deviate the geometries of as-built parts from their as-designed counterparts, resulting in considerable variation in functional performance, as reported for development of porous structures [569]. Geometric uncertainty in AM stems from various factors, including: (1) thermal residual stress [589], (2) material shrinkage [590, 591], (3) distortion [592, 593], and (4) manufacturing imperfection [594]. In literature, significant efforts have been dedicated to addressing such critical issues by either minimising geometric uncertainty or simulating the induced sources so as to take into account them in design stage, thereby minimising their impact on their final performance, or ensuring reliability of the built structural systems [580, 595,596,597,598,599,600]. Table 10 summarises some typical studies considering AM-induced uncertainties in topology optimisation.

Table 10 Design optimisation involving AM-induced uncertainties

Nevertheless, the application of ML techniques is still evolving to address these challenges [601,602,603,604]. For example, Ferreira et al. [605] proposed a compensation scheme to reduce deviations between as-built and as-designed parts using ML techniques, in which an automated NN-based modelling method enabled to accurately predict the deviations during AM processes. Huang et al. [606] introduced a Shape Deviation Generator (SDG) as an engineering-informed ML framework that learned from the AM data to control the shape deviations in AM processes.

5.2 Metamaterial Design

In vivo tissue exhibits inhomogeneous structures with notably intricate features ranging from macro to nanoscale. Implantable devices, such as orthopaedic implants, are expected to share similar structural characteristics and material properties with the surrounding host tissues. For instance, an appropriate effective stiffness is crucial for resisting external loads while avoiding severe stress shielding; and an adequate effective permeability ensures cell transformation and nutrition/metabolism transportation. Given these complex and often competing design requirements, metamaterials fabricated using AM techniques are particularly favoured in the design of implantable biomedical devices [621,622,623,624].

Recent studies have introduced innovative approaches to topology optimisation for single-unit cell or periodic structures using data-driven and ML techniques. These approaches offer novel computational tools for designing porous implants with functionally graded microstructures [518, 532, 625,626,627,628,629,630,631]. For example, Wang et al. [626] proposed a multi-response latent-variable Gaussian process (MP-LVGP) for creating microstructural libraries of metamaterials with different classes and sizes. The MP-LVGP model was integrated with multiscale topology optimisation for structures composed of multiple classes of microstructures, which are generally demanding for conventional topology optimisation approaches.

In literature, ML for metamaterial design, combined with AM, has been employed to mimic soft tissue. Chen et al. [632], for example, conducted ML-based design of printable polymers to replicate the mechanical responses of soft tissue under various stress–strain curves. In their study, the functional principal component decomposition approach, coupled with Gaussian process modelling, served as a surrogate model to predict the mechanical responses (stress–strain curves) of simulated metamaterials efficiently. This approach enabled the parametric optimisation for controlling metamaterial structures towards some exceptional material properties. Table 11 summarises the studies using data-driven and ML approaches for metamaterial design, and the structures/morphologies of metamaterials in each study are illustrated in Fig. 16 for clarity and better insights.

Table 11 A summary of data-driven and machine learning (ML) studies on metamaterial design

Fig. 16

Data-driven and machine learning based studies on metamaterial design associated with the index for different structures in Table 11. Reproduced with permission. Copyright 2021, Authors [633]. Reproduced with permission. Copyright 2021, Springer Nature [634]. Reproduced with permission. Copyright 2020,  John Wiley and Sons [635]. Reproduced with permission. Copyright 2020, Springer Nature [627]. Reproduced with permission. Copyright 2020, Elsevier [628]. Reproduced with permission. Copyright 2020, Springer Nature [536]. Reproduced with permission. Copyright 2019, John Wiley and Sons [637]. Reproduced with permission. Copyright 2018, American Chemical Society [638]. Reproduced with permission. Copyright 2021, Authors [639]. Reproduced with permission. Copyright 2020, Authors [630]. Reproduced with permission. Copyright 2018, Elsevier [632]. Reproduced with permission. Copyright 2022, Elsevier [640]. Reproduced with permission. Copyright 2020, Authors [642]. Reproduced with permission. Copyright 2019, Authors [643]. Reproduced with permission. Copyright 2023, Authors [645]. Reproduced with permission. Copyright 2023, Elsevier [647]

5.3 Optimisation of Processing Parameters

The processing parameters in AM can significantly impact the properties of as-built parts, particularly when new materials or new AM techniques are employed [453]. While trial-and-error experiments are a common approach to address this issue, they can be inefficient and costly. For this reason, researchers have turned to physics-based modelling to uncover the intricate relationship between processing parameters and the outcome of as-built parts [649,650,651]. Nevertheless, establishing suitable physics-based models for the complex nonlinear relationships involved can be rather demanding as per conventional modelling techniques [454].

To tackle these challenges, ML techniques have been introduced to discern and optimise the relationship between processing parameters and the performance of as-built parts based on specific requirements. The applications of ML techniques in optimising process parameters generally fall into two categories. Firstly, ML techniques developed for data clustering can be utilised to identify qualitative relationships between the processing parameters and as-built outcome/performance, subsequently determining the most crucial parameters for optimisation [651,652,653]. The dataset for this approach can be sourced from existing physics-based models or experimental tests. Secondly, given the intrinsic nonlinear nature of these relationships, regression ML models exhibit significant potential for explicitly quantifying them without relying on physics-based models, enabling the optimisation of process parameters for desired performances. This flexibility allows coverage of different AM techniques, each with its unique set of process parameters [654, 655]. Table 12 provides a summary of typical studies utilising ML approaches to establish the relationships between various processing parameters and critical as-built structural characteristics and properties with different AM techniques.

Table 12 A summary of machine learning (ML) approaches for building relationships between processing parameters and properties of as-built parts

In the realm of 3D bioprinting, which involves the use of bioink containing live cells for tissue engineering, the significance of processing parameters becomes even more pronounced, affecting both printing accuracy [660] and cell viability [658]. The demand for effective solutions to enhance the stability and precision of cell injection, while simultaneously reducing cell damage, is imperative to the outcome. Take 3D extrusion-based bioprinting (EBB) as an example; here, cell viability is notably influenced by shear stress generated within printing nozzles. This shear stress is, in turn, dependent on such factors as pressure drop and the shape of the nozzles [656]. To tackle this challenge, various ML regression models have been harnessed to predict cell viability, providing valuable guidance for selection of optimal processing parameters [659, 663], as illustrated in Fig. 17a. For inkjet-based bioprinting, a multiobjective optimisation framework has been introduced to address the complexities associated with this technique. In this framework, ANNs play a pivotal role in modelling satellite formation concerning different droplet diameters and speeds [656, 700], as shown in Fig. 17b.

Fig. 17

Machine learning (ML) in optimisation of biofabrication processing parameters. a Key components within the Stereolithography-based bioprinting system as well as the 2D patterns of a four-branch vascular structure under printing. Reproduced with permission. Copyright 2020, Springer Nature [659]. b ML-based optimisation of processing parameters in ink-jet-based bioprinting. Four factors (applied voltage, bioink viscosity, surface tension, and nozzle diameter) determine the droplet size and state. Reproduced with permission. Copyright 2019, Authors [700]

5.4 In Situ Monitoring

In situ monitoring of the AM process involves the analysis of various data from multiple tools, such as cameras, X-rays, images, and sensors, to detect and eliminate potential manufacturing defects or undesired properties (e.g., deformation, missing or excess materials, micro-cracks) [701, 702]. In situ monitoring for AM process holds significant promise for automatically analysing real-time signals without laborious human intervention, which enables to provide instantaneous feedback to the AM process, thereby forming a closed-loop control [703].

Data in the AM process is recorded either in a time-series fashion or stored as images [704, 705]. ML techniques for processing time-series signals or computer vision have exhibited considerable potential and superior performances in identifying abnormal changes across various types of information. In this context, many researchers have developed computer vision systems with cameras to acquire image data during the AM process. Trained Convolutional Neural Networks (CNNs) are then utilised to extract features from observed images, such as melt pool, plume, spatter, and droplet patterns [706,707,708,709], as shown in Fig. 18. For example, Fig. 18b outlines the steps to produce a time-integrated image. Each time series of radiographs is segmented and labelled with time, then flattened into a time-integrated image. The extracted features are classified by the CNN models trained with labelled data in different classifications for in situ monitoring of the AM process.

Fig. 18

In situ monitor of the additive manufacturing process using machine learning techniques. a In situ monitoring using high-speed and high-energy X-ray imaging techniques in the laser powder bed fusion process. Reproduced with permission Copyright 2018, Elsevier [706]. b In situ X-ray imaging detection of defects. Reproduced with permission. Copyright 2018, Authors [707]. c In situ droplet monitor for liquid metal jet printing. Reproduced with permission. Copyright 2018, Elsevier [708]. d In situ monitor of melt pool in powder-based fusion processes using support vector machine and convolutional neural network models for processing images. Reproduced with permission. Copyright 2018, Elsevier [709]

To form the closed-loop control, ML models can establish relationships between extracted features and real-time printing behaviour (e.g., temperature, speed, voltage), as reviewed in Sect. 5.3. The differences between real-time and desired behaviours can be evaluated, and proper control strategies can automatically adjust processing parameters, forming positive feedback on real-time printing outcomes. Given these promising results, more advanced deep learning frameworks are anticipated to enable in situ monitoring of specific issues occurring in the biofabrication process, thereby enhancing bioprinting to be more robust, reliable, and accurate. Table 13 summarises some further studies on ML techniques for the in situ monitoring of the AM processes, which include their inspection objectives, ML algorithms, AM techniques, and data collection approaches.

Table 13 A summary of in situ monitoring of AM process using machine learning (ML) techniques

6 Applications

6.1 Bone Tissue Scaffolds

Bone loss resulting from trauma, tumours, infections, or injuries poses a significant healthcare challenge, necessitating either temporary or permanent replacement with a suitable functional alternative. Traditional treatment approaches, such as allograft and autograft transplantations, as well as Masquelet procedures, exhibit notable drawbacks, including infection risks, disease transmission, donor site morbidity, and restricted tissue supply [33]. To overcome these limitations, there has been growing interest in synthetic bone scaffolds as a potential solution for addressing bone loss in both research communities and clinical settings (Fig. 19a). These implantable scaffolds are specifically designed to replace bony tissues in vivo, requiring not only sufficient mechanical support but also biologically/chemically inert material properties and the ability to facilitate the transport of nutrients and metabolism crucial for tissue regeneration [34].

Fig. 19

Applications of biomedical implants. a Bone scaffold. Reproduced with permission. Copyright 2019, John Wiley and Sons [784]. b Hip implants. Reproduced with permission. Copyright 2017, Authors [752]. c Dental implants. Reproduced with permission. Copyright 2021, Authors [763]. d Coronary stents. Reproduced with permission. Copyright 2016, Elsevier [41]

Table 14 provides a summary of some typical ML-based applications in bone tissue engineering. For example, Entekhabi et al. [743] developed a ML model to predict the degradation rate of a biodegradable scaffold. In their study, the experimental tests were conducted on different samples with varying material constituents. The experimental data were then utilised to train an ANN model for predicting the degradation rate with a fairly low mean squared error (2.68%).

Table 14 Representative machine learning (ML)-based applications in implantable devices

To achieve optimal bone formation in tissue scaffolds, structural scrutiny aligned with subject-specific defect sites is imperative. Consequently, there is a growing demand to efficiently predict bone formation within tissue scaffolds through use of computational modelling techniques, mitigating the need for costly trial-and-error in vivo experimental tests. In this regard, Barrera et al. [744] employed the ML techniques for design of scaffolds, in which a CNN model was employed to directly predict the mechanical properties of innovative scaffolds without experimental tests or numerical models, thereby enabling rapid optimisation of scaffolds for desired biomechanical properties. Moreover, ML techniques have also been applied to guide the bioprinting of bone scaffolds [662, 745, 746].

6.2 Orthopaedic Implants

Hip fractures persist as a significant health concern, particularly in the context of an increasingly ageing population. Consequently, hip replacements utilising artificial implants have become a golden standard for revision surgeries worldwide (Fig. 19b). This widespread adoption underscores the urgency of addressing the challenges associated with such procedures. To this end, several ML-based applications in the realm of hip implants are delineated in Table 14. The introduction of hip implants presents a transformative mechanical environment to be experienced by the host bony tissue. This alteration raises the spectre of possible stress shielding issues, prompting the necessity for patient-specific design of hip implants. Addressing this concern, Cilla et al. [752] proposed a ML-based framework for optimising hip implants. Their approach involved the development of a parametric FE model, quantifying stress shielding effects by assessing the disparity in maximum principal strain between implanted and intact bone models. Subsequently, an artificial neural network (ANN) model, trained from the FE dataset, provided quantified stress shielding values for various parametric models. Such information was then integrated with the GA to determine the optimal parameters conducive to reduction of stress shielding.

Beyond stress shielding, the longevity of hip implants is intricately linked to polyethene wear, a pivotal factor in determining their overall performance. Addressing this concern, Borjali et al. [753] adeptly predicted the polyethene wear rate through the ML models applied to pin-on-disc (PoD) wear experiments. Their innovative approach paved a new avenue for investigating this critical issue by observing diverse operating parameters, potentially mitigating complications such as osteolysis, implant loosening, and mechanical instability.

In clinical applications, ML techniques have found notable utility in the identification of hip implants from plain radiography images owing to their robust performance in imaging analysis [754,755,756,757,758]. This highlights the versatility of ML methodologies in enhancing clinical diagnostics and underscores their potential in augmenting traditional imaging analysis techniques.

6.3 Dental Implants

The prevalence of tooth loss, a consequential issue in oral health, is exacerbated by the ageing population. Apart from impairing masticatory function, missing teeth can significantly compromise dental bone and surrounding tissues. Dental implantation treatment (Fig. 19c), a leading prosthetic technology, has witnessed rapid development over the past five decades and stands as a primary recourse when the application of dental bridges is precluded by adjacent teeth. A multitude of studies in the literature have leveraged ML techniques to explore dental implants comprehensively [772,773,774,775,776,777,778,779,780,781], as catalogued in Table 14.

The failure of dental implants is subject to a myriad of complex factors, encompassing patient-specific variables, implant positioning, surrounding bony tissue condition, fixture characteristics, surgical procedures, and implant timing. Conventional statistical methods encounter limitations due to the diverse types of data, whereas physics-based models addressing these intricate factors are often impractical. Consequently, researchers have turned to ML-based regression models, constituting a dynamic domain in dental implant research [762, 782, 783]. Notably, fracture emerges as a common failure mode for dental implants. Lee et al. [763] utilised a convolutional neural network (CNN) model to detect and classify fractured dental implants through radiograph images, presenting a potential real-time clinical application.

In order to address another critical issue that peri-implant bone loss leads to implant loosening, Cha et al. [764] employed a CNN model to measure peri-implant bone loss from radiographs, offering an in situ assessment of marginal bone loss severity. Additionally, Zhang et al. [765] identified trabeculae microstructure parameters as effective indicators for marginal bone loss. Comparative studies employing various regression models, including SVM, ANN, logistic regression (LR), and RF, revealed the superior accuracy of SVM in predicting marginal bone loss.

ML approaches have also found applications in the patient-specific design of dental implants. For instance, Hsu et al. [168] utilised the deep learning U-net neural networks and an ANN model for mechanobiological design, considering peri-implant bone healing, remodelling, and cell proliferation to optimise designs and prevent potential failures due to bone loss.

6.4 Arterial Stents

Stent treatment stands as a favoured therapeutic strategy for numerous cardiovascular patients seeking to restore blood vessel circulation. These miniature mesh-like mechanical devices, known as stents (Fig. 19d), compress plaque against vessel walls, opening obstructed arteries and offering substantial benefits by minimising surgical risks and reducing hospitalisation periods. Several studies have investigated the applications of ML techniques in arterial stents, as outlined in Table 14. Typically crafted from biomaterials such as stainless steel, Ni–Ti alloy, cobalt-chromium, titanium, and its alloys, stents are intricately shaped through laser cutting techniques. Maudes et al. [766] developed a ML-based model to establish the highly nonlinear relationship between processing parameters and geometrical characteristics during the manufacturing process. This approach holds promise for reducing the high costs associated with experimental tests.

Stent expansion in arteries is pivotal for ensuring clinical outcomes, where inadequate expansion and malposition can lead to chronic complications such as restenosis and thrombosis. Dong et al. [767] integrated ML models with FE methods to predict stent expansion in a calcified coronary artery. Patient-specific optical coherence tomography (OCT) images were employed to reconstruct the FE models, in which the cross-sectional images of pre- and post-stenting were used as a training dataset. Eight different features extracted from pre-stenting images served as inputs for the support vector regression (SVR) model, predicting lumen area from post-stenting images.

7 Challenges and Perspectives

ML techniques present unprecedented opportunities for exploring novel biomaterials, modelling biomechanics and mechanobiology, and designing and controlling biofabrication processes due to their robust capabilities in handling significantly large and complex datasets. The integration of ML approaches in the biomedical engineering field holds significant promise for the entire framework, encompassing biomaterials design, in silico biomechanical or mechanobiological modelling, and the fabrication of real-life products, thereby facilitating the development of novel patient-specific treatments with minimal side effects for clinical applications. However, several key challenges and perspectives in integrating ML approaches for biomedical engineering issues need to be addressed:

• (1) Data collection and preparation: The availability of useful and comprehensive datasets is paramount for training ML models. While training data can be sourced from either experimental tests or computational simulations, experimental tests are often expensive, and simulations for novel materials based on universal physical laws can often be demanding. Moreover, data labelling for supervised learning may incur significant costs. Therefore, the collection and preparation of reliable data without sacrificing crucial information are essential for the effective implementation of ML techniques.

• (2) ML-based design approaches: Conventional approaches for biomaterials design often rely on physical/chemical intuition. In contrast, ML-based design approaches can learn from data, unravelling the relationship between material structures and mechanical/biological behaviours. This offers an efficient method enabling brute force design, which is often prohibitive in conventional approaches due to excessive computational costs.

• (3) Data-driven modelling for Biomechanics and Mechanobiology: Data-driven and ML-based modelling for biomechanics and mechanobiology create new opportunities for the development of digital twins. These twins can precisely replicate in vitro and/or in vivo behaviours of biological systems in silico, offering a supplementary yet important approach to in vitro and/or in vivo tests or guidelines for practical clinics.

• (4) Integration of physics laws in ML models: Embedding physics laws in ML models could enhance the learning process from data, especially in mechanics-related fields. Conversely, ML approaches are expected to discover new physical laws behind data and integrate them into conventional frameworks for more reliable and more realistic solutions.

• (5) ML-based approaches in bioprinting: The design for bioprinting is still in its early stages. ML-based approaches illuminate the design optimisation of biomedical devices, potentially overcoming challenges associated with conventional optimisation methods. Additionally, ML-based techniques provide a feasible way to establish a closed-loop fabrication process with minimal human intervention.

• (6) Interdisciplinary knowledge in biomedical engineering: Biomedical engineering involves complex multidisciplinary knowledge and methodologies, commonly posing great challenges and high cost for the development and implementation of novel treatments for critical healthcare issues. Advanced ML-based methods are expected to create a comprehensive framework in futuristic studies—from the design of novel biomaterials to modelling biomechanical and mechanobiological behaviours, to the fabrication of real-life products.

8 Conclusion

This paper provides an overview of the state-of-the-art of ML approaches in the biomedical engineering field. It begins with a brief review of various ML approaches, followed by discussions on their applications in biomaterials, biomechanics, mechanobiology, and biofabrication, respectively. The review emphasises their advantages, such as superior data processing and data mining capabilities, development of digital twins, and innovative design of biomaterials. The exploration extends from hard tissue to soft tissue, monoscale to multiscale perspectives. The current status of ML techniques in biofabrication is also reviewed, shedding light on structural and metamaterial design, process optimisation, and in situ monitoring for AM processes. The paper concludes by exemplifying typical biomedical applications using ML-based approaches, broadening the horizon for future work, and addressing challenges and perspectives. This review aims to provide valuable information and lighten key perspectives for researchers, engineers, and clinicians, navigating this rapidly emerging multidisciplinary field of ML in biomedical engineering.