An efficient moving morphable component (MMC)-based approach for multi-resolution topology optimization

Abstract

In the present work, a highly efficient moving morphable component (MMC)-based approach for multi-resolution topology optimization is proposed. In this approach, high-resolution optimization results can be obtained with a smaller number of design variables and a relatively low degree of freedoms (DOFs). This is achieved by taking the advantage that the topology optimization model and the finite element analysis model are totally decoupled in the MMC-based problem formulation. A coarse mesh is used for structural response analysis and a design domain partitioning strategy is introduced to preserve the topological complexity of the optimized structures. Numerical examples are then provided so as to demonstrate that with the use of the proposed approach, computational efforts can be saved substantially for large-scale topology optimization problems.

Appendix

The process of generating TDF locally can be elaborated as follows:

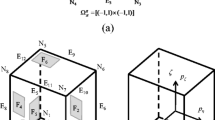
• 1) Generating a rectangle ${\Omega}_i^{\mathrm{ext}}$ (pink region), with the use of the parameters (o_i, θ_i, l_i, t_i), as shown in Fig. A1b. Here the symbol o_i = (x_i0, y_i0)^⊤ denotes the vector of the coordinates of the central point of the i-th component, θ_i is the corresponding inclined angle, while ${l}_i=2{a}_i\sqrt[6]{\left(1+\epsilon \right)}$ and ${t}_i=\max \left(2{t}_i^1,2{t}_i^2\right)\sqrt[6]{\left(1+\epsilon \right)}$ are the length and width of ${\Omega}_i^{\mathrm{ext}}$, respectively. Note that ${\Omega}_i^{\mathrm{ext}}\supset {\Omega}_i^{\prime }=\left\{\boldsymbol{x}|\boldsymbol{x}\in \mathrm{D},{\phi}_i\left(\boldsymbol{x}\right)\ge -\epsilon \right\}$ (yellow region in Fig. A1b);

• 2) From the vertexes (which can be found analytically) of ${\Omega}_i^{\mathrm{ext}}$, generating another rectangle ${\Omega}_i^{\mathrm{rec}}$ (light blue region in Fig. A1b);

• 3) Generating the TDF associated with ${\Omega}_i^{\mathrm{rec}}$;

• 4) Finding the TDF values in ${\Omega}_i^{\mathrm{rec}}$ such that −ϵ ≤ ϕ_i(x) ≤ ϵ, and only storing these values by sparse matrix for subsequent treatment.

The above treatment guarantees that only local values of ϕ_i(x) are evaluated in the corresponding manipulations, which reduce the computational effort substantially.

Fig. 28

A schematical illustration of generating the TDF locally