Abstract
A review of solar cycle prediction methods and their performance is given, including early forecasts for Cycle 25. The review focuses on those aspects of the solar cycle prediction problem that have a bearing on dynamo theory. The scope of the review is further restricted to the issue of predicting the amplitude (and optionally the epoch) of an upcoming solar maximum no later than right after the start of the given cycle. Prediction methods form three main groups. Precursor methods rely on the value of some measure of solar activity or magnetism at a specified time to predict the amplitude of the following solar maximum. The choice of a good precursor often implies considerable physical insight: indeed, it has become increasingly clear that the transition from purely empirical precursors to model-based methods is continuous. Model-based approaches can be further divided into two groups: predictions based on surface flux transport models and on consistent dynamo models. The implicit assumption of precursor methods is that each numbered solar cycle is a consistent unit in itself, while solar activity seems to consist of a series of much less tightly intercorrelated individual cycles. Extrapolation methods, in contrast, are based on the premise that the physical process giving rise to the sunspot number record is statistically homogeneous, i.e., the mathematical regularities underlying its variations are the same at any point of time, and therefore it lends itself to analysis and forecasting by time series methods. In their overall performance during the course of the last few solar cycles, precursor methods have clearly been superior to extrapolation methods. One method that has yielded predictions consistently in the right range during the past few solar cycles is the polar field precursor. Nevertheless, some extrapolation methods may still be worth further study. Model based forecasts are quickly coming into their own, and, despite not having a long proven record, their predictions are received with increasing confidence by the community.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Solar cycle prediction is an extremely extensive topic, covering a very wide variety of proposed prediction methods and prediction attempts on many different timescales, ranging from short term (month–year) forecasts of the runoff of the ongoing solar cycle to predictions of long term changes in solar activity on centennial or even millennial scales. As early as 1963, Vitinsky published a whole monograph on the subject, later updated and extended (Vitinsky 1963, 1973). More recent overviews of the field or aspects of it include Hathaway (2009), Kane (2001), Pesnell (2008), and the first edition of this review (Petrovay 2010b). In order to narrow down the scope of the review, we constrain our field of interest in two important respects.
Firstly, instead of attempting to give a general review of all prediction methods suggested or citing all the papers with forecasts, here we will focus on those aspects of the solar cycle prediction problem that have a bearing on dynamo theory. We will thus discuss in more detail empirical methods that, independently of their success rate, have the potential of shedding some light on the physical mechanism underlying the solar cycle, as well as the prediction attempts based on solar dynamo models.
Secondly, we will here only be concerned with the issue of predicting the amplitude (and optionally the epoch) of an upcoming solar maximum no later than right after the start of the given cycle. This emphasis is also motivated by the present surge of interest in precisely this topic, prompted by the unusually long and deep recent solar minimum and by sharply conflicting forecasts for the maximum of the incipient solar Cycle 24.
As we will see, significant doubts arise both from the theoretical and observational side as to what extent such a prediction is possible at all (especially before the time of the minimum has become known). Nevertheless, no matter how shaky their theoretical and empirical backgrounds may be, forecasts must be attempted. Making verifiable or falsifiable predictions is obviously the core of the scientific method in general; but there is also a more imperative urge in the case of solar cycle prediction. Being the prime determinant of space weather and space climate, solar activity clearly has enormous technical, scientific, and financial impact on activities ranging from space exploration to civil aviation and everyday communication. Political and economic decision makers expect the solar community to provide them with forecasts on which feasibility and profitability calculations can be based. Acknowledging this need, around the time of solar minimum the Space Weather Prediction Center of the US National Weather Service does present annually or semiannually updated “official” predictions of the upcoming sunspot maximum, emitted by a Solar Cycle Prediction Panel of experts. The unusual lack of consensus in the early meetings of this panel during the previous minimum (SWPC 2009), as well as the concurrent, more frequently updated but wildly varying predictions of a NASA MSFC team (MSFC 2017) made evident the deficiencies of prediction techniques available at the time. In view of this, Cycle 24 provided us with some crucial new insights into the physical mechanisms underlying cyclic solar activity. In preparation to convene the Solar Cycle 25 Prediction Panel a new call for predictions was issued in January 2019 (Biesecker and Upton 2019).
While a number of indicators of solar activity exist, by far the most commonly employed is still the smoothed relative sunspot number \(R\); the “Holy Grail” of sunspot cycle prediction attempts is to get \(R\) right for the next maximum. We, therefore, start by briefly introducing the sunspot number and inspecting its known record. Then, in Sects. 2–4 we discuss the most widely employed methods of cycle predictions. Section 5 presents a summary evaluation of the past performance of different forecasting methods, while Sect. 6 finally collects some early forecasts for Cycle 25 derived by various approaches.
1.1 What’s new in this edition?
For readers familiar with the 1st edition of this review, who would prefer to go through the “new stuff” only, here I briefly list the new or thoroughly rewritten sections.
The revision of the sunspot number series that took place in 2015 is one topic that had to be discussed in detail. The new Sect. 1.2.2 is devoted to this subject but other parts of Sects. 1.2 and 1.3 have also been subjected to a major revision.
For reasons explained in Sect. 1.5, the overall structure of the review has been given a major overhaul: the section on extrapolation methods has now been placed after the section on model-based approaches.
Researches into the origins of the sudden change in the behaviour of our Sun from Cycle 23–24 led to important, although still poorly understood realizations, now discussed in a dedicated subsection (Sect. 2.2). And the stellar rise in popularity of the polar precursor led to such an amount of exciting new research that Sect. 2.3, discussing this method, had to be completely rewritten and expanded; furthermore, it gave rise to another section on “The quest for a precursor of the polar precursor” (Sect. 2.5), containing mostly new or thoroughly updated material.
The section on model-based predictions now includes a presentation of the approach based on surface flux transport models (Sect. 3.1). In the field of dynamo-based cycle prediction the major novelty in this decade was the development of nonaxisymmetric models capable to account for the emergence of individual active regions: a new subsection is now devoted to this topic (Sect. 3.4.2).
Finally, the updated summary evaluation and the overview of early predictions for Cycle 25 obviously cover mostly new results (Sects. 5, 6).
1.2 The sunspot number (SSN)
Despite its somewhat arbitrary construction, the series of relative sunspot numbers constitutes the longest homogeneous global indicator of solar activity determined by direct solar observations and by methods that were, until recently, perceived to be carefully controlled. For this reason, their use is still predominant in studies of solar activity variation.
As aptly noted by Clette et al. (2014), until recently the sunspot number series was “assumed to be carved in stone, i.e., it was considered largely as a homogeneous, well-understood and thus immutable data set. This feeling was probably reinforced by the stately process through which it was produced by a single expert center at the Zürich Observatory during 131 years.”
This perception has now been shattered by the major revision of the official sunspot number series that took place in 2015, and opened the way to further periodic revisions.
In what follows, the original series, the revision, and transformed versions of the series will be discussed in turn.
1.2.1 Version 1.0
As defined originally by Wolf (1850), the relative sunspot number is
where g is the number of sunspot groups (including solitary spots), f is the total number of all spots visible on the solar disc, while k is a correction factor depending on a variety of circumstances, such as instrument parameters, observatory location, and details of the counting method. Wolf, who decided to count each spot only once and did not count the smallest spots, used \(k=1\). He also introduced a hierarchical system for the determination of \(R_Z\) where data from a list of auxiliary observers were used for days when the primary observer (Zürich) could not provide a value.
The counting system employed in Zürich was changed by Wolf’s successors to count even the smallest spots, attributing a higher weight (i.e., \(f>1\)) to spots with a penumbra, depending on their size and umbral structure. (The exact details and timing of these changes are incompletely documented and controversial, see discussion in the next subsection.) As the changes in the counting and the regular use of a larger telescope naturally resulted in higher values, the Zürich correction factor was set to \(k=0.6\) for subsequent determinations of \(R_Z\) to ensure continuity with Wolf’s work. (Waldmeier 1961; see also Izenman 1983; Kopecký et al. 1980; Hoyt and Schatten 1998; Friedli 2016 for further discussions on the determination of \(R_Z\)).
In addition to introducing the relative sunspot number, Wolf (1861) also used earlier observational records available to him to reconstruct its monthly mean values since 1749. In this way, he reconstructed 11-year sunspot cycles back to that date: hence, the now universally used numbering of solar cycles starts with the first complete cycle in the monthly \(R_Z\) series. In a later work he also determined annual mean values for each calendar year going back to 1700. This reconstruction and calibration work took place in several steps, so the \(R_Z\) record was very much a project in the making until the end of the nineteenth century (see Clette et al. 2014). It was only from the early twentieth century that the series came to be regarded as “carved in stone”.
In 1981, the observatory responsible for the official determination of the sunspot number changed from Zürich to the Royal Observatory of Belgium in Brussels. The website of the SIDCFootnote 1 (originally Sunspot Index Data Center, recently renamed Solar Influences Data Analysis Center) is now the most authoritative source of archive sunspot number data. The department of SIDC formally responsible for the sunspot number series is WDC-SILSO (World Data Centre for Sunspot Index and Long-term Solar Observations). It has become customary to denote the original Zürich series with \(R_Z\) (“the Zürich sunspot number”), and its continuation by the SIDC from 1981 to 2015 with \(R_i\) (International Sunspot Number, ISN). The new, revised series is conventionally denoted by \(S_N\).
It must be kept in mind that since the middle of the twentieth century, the sunspot number is also regularly determined by other institutions: the most widely used such variants are informally known as the American sunspot number (collected by AAVSO and available from the National Geophysical Data CenterFootnote 2) and the Kislovodsk Sunspot Number (available from the web page of the Kislovodsk Mountain Astronomical Station of Pulkovo ObservatoryFootnote 3).
Given that \(R_Z\) is subject to large fluctuations on a time scale of days to months, it has become customary to use annual mean values for the study of longer term activity changes. To get rid of the arbitrariness of calendar years, the standard practiceFootnote 4 is to use 13-month boxcar averages of the monthly averaged sunspot numbers, wherein the first and last months are given half the weight of other months:
\(R_{{\mathrm {m}},i}\) being the mean monthly value of the daily sunspot number values for ith calendar month counted from the present month. It is this running mean \(R\) that we will simply call “the sunspot number” throughout this review and what forms the basis of most discussions of solar cycle variations and their predictions.
In what follows, \(R_{{\mathrm {max}}}^{(n)}\) and \(R_{{\mathrm {min}}}^{(n)}\) will refer to the maximum and minimum value of \(R\) in cycle n (the minimum being the one that starts the cycle). Similarly, \(t_{{\mathrm {max}}}^{(n)}\) and \(t_{{\mathrm {min}}}^{(n)}\) will denote the epochs when \(R\) takes these extrema.
1.2.2 Revision
The process that led to the 2015 revision was started by Leif Svalgaard (Stanford) who pointed out a number of inhomogeneities in the series, rooted in changes in the base data and processing techniques. Starting from 2011, at Svalgaard’s initiative, a series of four workshops on the sunspot number were held by the community involved. The 2015 revision is the result of this process. The motivation for and the detailed process of the revision was described by Clette et al. (2014) and Clette and Lefèvre (2016) and discussed in a number of papers in a topical issue of Solar Physics (vol. 291, issue 9–10; Clette et al. 2016a).
The revision included dropping the \(k=0.6\) scaling factor traditionally applied to the Zürich data, so all values increased by a factor of \(\textstyle \frac{5}{3}\). In addition to this trivial rescaling and some other minor changes, three major corrections were implemented.
-
(a)
The Locarno drift after 1981. The determination of the International Sunspot Number \(R_i\) by the SIDC did not follow Wolf’s hierarchical system, taking into account observations from all network stations and only dropping outliers. Nevertheless, in order to ensure continuity, the Locarno solar observatory (Zürich’s successor) still had a special role as a pilot station, all other observers being calibrated to Locarno’s scale. A slow time-varying drift in the Locarno data came to light during the revision process and has been corrected in the new series. This change is apparently uncontroversial and was made with the full consensus of all actors involved (Clette et al. 2016b).
-
(b)
The “Waldmeier jump” from 1947. Plotting the original Zürich sunspot numbers against other sunspot-related indices such as sunspot areas or group numbers, or even against non-weighted sunspot numbers determined by non-Zürich observers, a jump was discovered which was suggested to originate in the introduction of a new weighting method (in use in Locarno until the present day) by the new Zürich director, Max Waldmeier and his largely new staff. Under current solar conditions the weighting results in a 15–20% inflation of the sunspot numbers (Svalgaard et al. 2017). This assumed inflation of the series has now been corrected.
-
(c)
The Schwabe–Wolf transition (1849–1864) The upward correction of 14% applied in this period relies primarily on a comparison of the original sunspot number series with group sunspot numbers (the result being apparently insensitive to which group number series is used). The presumed cause of the discrepancy is that in this period the sunspot number was determined by Wolf using small portable telescopes, while Schwabe also continued his observations. For days not covered by his own observations Wolf used Schwabe’s data without marking these out. It was only in 1861 that, upon cross-correlating their data Wolf determined a correction factor \(k=1.25\) for Schwabe, which he also applied retrospectively to the pre-1849 observations of Schwabe (and, by inference, of earlier observers calibrated to Schwabe). However, the correction factor was apparently not considered for his own observations (mixed with Schwabe’s) in the period before the early 1860s.
The revised series, introduced from 1 July 2015, is now considered version 2.0 of the sunspot number series. Further corrections, with proper version tracking, are expected as early data may contain other inconsistencies, and the corrections applied in v2.0 were somewhat crude. In particular, recomputation of the whole series from observational data, wherever available, is planned. The process has now been placed under the ægis of the IAU, with a dedicated Working Group “Coordination of Synoptic Observations of the Sun” focusing on the validation and accreditation process of new SSN versions.
A further possible bias in the series that remains to be corrected may concern the counting of sunspot groups. While in earlier parts of the series physical closeness of spots was considered a sufficient criterion, since the mid-twentieth century evolutionary information is also taken into account, sometimes resulting in the division into several groups of what would have been considered as a single group by early observers. Svalgaard et al. (2017) estimate that this effect may have inflated Waldmeier’s sunspot numbers by 4–5% relative to earlier counts, while the effect on the late eighteenth century sunspot reconstruction of the SSN by Wolf based on the drawings of Staudacher may be even larger, reaching 25% (Svalgaard 2017). On the other hand, Izenman (1983) notes that Waldmeier’s authoritative 1965 edition of the \(R_Z\) series does contain slight corrections also to the data published previously, in 1925 by Wolfer. (One might also consider this as a surreptitious earlier minor “revision” of the SSN.) This shows that Waldmeier himself was very much concerned with the long-term homogeneity of the data, already taking some measures to homogenize the data processing.
Amidst all the revision fervour, some caveats may still be in order. On the one hand, for the current generation of solar physicists it is abundantly clear that our Sun is capable of rather sudden unexpected changes and that a varying ratio between different activity indices (even just those related to sunspots) can be a real, physical feature (Georgieva et al. 2017; see also Sect. 2.2 below). Suggestions for revisions based purely on variations or jumps in the ratio of the sunspot number to other indices are therefore to be treated with strong caution as it may potentially bias understanding of the physical processes involved. Second, having superior instruments does not entitle us to think we are smarter than our predecessors were, or that we know their data better than they themselves did. Information lost and unknown considerations may well explain practices that, in retrospect, seem incorrect to us. Even in the case of the already implemented corrections (b) and (c) some nagging questions do remain and need further exploration (Clette and Lefèvre 2016).
The significant disagreements between determinations of the SSN by various observatories, observers and methods are even more pronounced in the case of historical data, especially prior to the mid-nineteenth century. In particular, the controversial suggestion that a whole solar cycle may have been missed in the official sunspot number series at the end of the eighteenth century is taken by some as glaring evidence for the unreliability of early observations. Note, however, that independently of whether the claim for a missing cycle is well founded or not, there is clear evidence that this controversy is mostly due to the very atypical behaviour of the Sun itself in the given period of time, rather than to the low quality and coverage of contemporary observations. These issues will be discussed further in Sect. 4.2.2.
1.2.3 Alternating series and nonlinear transforms
Instead of the “raw” sunspot number series R(t) many researchers prefer to base their studies on some transformed index \(R'\). The motivation behind this is twofold.
-
(a)
The strongly peaked and asymmetrical sunspot cycle profiles strongly deviate from a sinusoidal profile; also the statistical distribution of sunspot numbers is strongly at odds with a Gaussian distribution. This can constitute a problem as many common methods of data analysis rely on the assumption of an approximately normal distribution of errors or nearly sinusoidal profiles of spectral components. So transformations of \(R\) (and, optionally, t) that reduce these deviations can obviously be helpful during the analysis. In this vein, e.g., Max Waldmeier often based his studies of the solar cycle on the use of logarithmic sunspot numbers \(R'=\log R\); many other researchers use \(R'=R^\alpha\) with \(0.5\le \alpha <1\), the most common value being \(\alpha =0.5\).
-
(b)
As the sunspot number is a rather arbitrary construct, there may be an underlying more physical parameter related to it in some nonlinear fashion, such as the toroidal magnetic field strength B, or the magnetic energy, proportional to \(B^2\). It should be emphasized that, contrary to some claims, our current understanding of the solar dynamo does not make it possible to guess what the underlying parameter is, with any reasonable degree of certainty. In particular, the often used assumption that it is the magnetic energy, lacks any sound foundation. If anything, on the basis of our current best understanding of flux emergence we might expect that the amount of toroidal flux emerging from the tachocline should be \(\int |B-B_0|\,dA\) where \(B_0\) is some minimal threshold field strength for Parker instability and the surface integral goes across a latitudinal cross section of the tachocline (cf. Ruzmaikin 1997; indeed, a generalized linear R–B link involving a threshold field strength has now also been used in the dynamo models of Pipin and Sokoloff 2011 and Pipin et al. 2012). As, however, the lifetime of any given sunspot group is finite and proportional to its size (Petrovay and van Driel-Gesztelyi 1997; Henwood et al. 2010), instantaneous values of \(R\) or the total sunspot area should also depend on details of the probability distribution function of B in the tachocline. This just serves to illustrate the difficulty of identifying a single physical governing parameter behind \(R\).
One transformation that may still be well motivated from the physical point of view is to attribute an alternating sign to even and odd Schwabe cycles: this results in the the alternating sunspot number series \(R_\pm\). The idea is based on Hale’s well known polarity rules, implying that the period of the solar cycle is actually 22 years rather than 11 years, the polarity of magnetic fields changing sign from one 11-year Schwabe cycle to the next. In this representation, first suggested by Bracewell (1953), usually odd cycles are attributed a negative sign. This leads to slight jumps at the minima of the Schwabe cycle, as a consequence of the fact that for a 1–2 year period around the minimum, spots belonging to both cycles are present, so the value of \(R\) never reaches zero; in certain applications, further twists are introduced into the transformation to avoid this phenomenon.
After first introducing the alternating series, in a later work Bracewell (1988) demonstrated that introducing an underlying “physical” variable \(R_B\) such that
(i.e., \(\alpha =2/3\) in the power law mentioned in item (a) above) significantly simplifies the cycle profile. Indeed, upon introducing a “rectified” phase variableFootnote 5\(\phi\) in each cycle to compensate for the asymmetry of the cycle profile, \(R_B\) is a nearly sinusoidal function of \(\phi\). The empirically found 3/2 law is interpreted as the relation between the time-integrated area of a typical sunspot group vs. its peak area (or peak \(R_Z\) value), i.e., the steeper than linear growth of \(R\) with the underlying physical parameter \(R_B\) would be due to the larger sunspot groups being observed longer, and therefore giving a disproportionately larger contribution to the annual mean sunspot numbers. If this interpretation is correct, as suggested by Bracewell’s analysis, then \(R_B\) should be considered proportional to the total toroidal magnetic flux emerging into the photosphere in a given interval. (But the possibility must be kept in mind that the same toroidal flux bundle may emerge repeatedly or at different heliographic longitudes, giving rise to several active regions.)
1.3 Other indicators of solar activity
1.3.1 Group sunspot number (GSN)
Reconstructions of \(R\) prior to the early nineteenth century are increasingly uncertain. In order to tackle problems related to sporadic and often unreliable observations, Hoyt and Schatten (1998) introduced the Group Sunspot Number (GSN) as an alternative indicator of solar activity. In contrast to the SSN, the GSN only relies on counts of sunspot groups as a more robust indicator, disregarding the number of spots in each group. Furthermore, while \(R_Z\) was determined for any given day from a single observer’s measurements (a hierarchy of auxiliary observers was defined for the case if data from the primary observer were unavailable), the GSN uses a weighted average of all observations available for a given day. A further advantage is that, in addition to the published series, all the raw data upon which it is based are made public.
The GSN series published by Hoyt and Schatten (1998) remained unchanged until the 2010s when it was taken under revision in concert with the SSN revision discussed above. As in the case of the GSN there is no generally accepted responsible organization, i.e., no “official” series, revisions were undertaken by several teams, leading to conflicting results.Footnote 6
The common denominator of all efforts to reconstruct the GSN is (or should be) the common set of observations upon which the construction of the series is based. This observational data set has been greatly extended in the past two decades thanks to the discovery and/or publication of many previously inaccessible historical sources. An update of the database providing a good basis for subsequent efforts to construct a GSN series was compiled by Vaquero et al. (2016). This archive is now available from the SILSO site and from the Historical Archive of Sunspot Observations (HASO)Footnote 7. (In principle, a regular upgrade is planned, with version numbers, v1.0 referring to Hoyt and Schatten, but the project is currently stuck at version 1.12 dated May 2016.)
The original method of Hoyt and Schatten (1998) was subject to a random drift of the mean group number over long timescales. While consistent use of the Greenwich Photoheliograph Results, available from 1874, helped to avoid such a drift in the twentieth century, a drift already appears from the late nineteenth century back, owing to the still evolving techniques of photography used at Greenwich. As a result, group numbers before this period may be systematically lower than what the SSN would suggest. This was the main issue motivating a revision of the GSN series.
New GSN series were compiled by Svalgaard and Schatten (2016) and by Usoskin et al. (2016) using two alternative methods: the backbone method and a method based on active day fraction (ADF) statistics. The backbone method resulted in significantly elevated GSN values before about 1900, while the ADF method resulted in a series closer to the original Hoyt & Schatten values. Both of these methods have been subject to criticisms (Cliver 2016; Willamo et al. 2017, 2018). Finally, Chatzistergos et al. (2017) came up with a variety of the backbone method with an improved methodology for the fitting of successive backbones, resulting in an intermediate series. At the time of writing, this “ultimate backbone” GSN series (Fig. 1), available at CDS,Footnote 8 seems to be the most recommendable version for further analysis.
Annual means of the group sunspot number reconstructed by Chatzistergos et al. (2017) (solid red curve). Values before 1749 (dashed black) were taken from the reconstruction by Svalgaard and Schatten (2016), multiplied by a fiducial factor 0.85 to align the two curves in 1750 and to bring the GSN and SSN (dash-dotted green) into better agreement in the early eighteenth century
The GSN series has been reproduced for the whole period since 1611 and it is generally agreed that for the period 1611–1818 it is a more reliable reconstruction of solar activity than the relative sunspot number. Yet there have been relatively few attempts to date to use this data series for solar cycle prediction.
1.3.2 Other sunspot data
The classic source of sunspot area and position data is the Greenwich Photoheliographic Results (GPR) catalogue,Footnote 9 covering the period 1874–1976. The official continuation of the GPR is the Debrecen Photoheliographic Data (DPD) catalogue,Footnote 10 commissioned by the IAU and containing data from 1973 (Baranyi et al. 2016; Győri et al. 2017). The Debrecen database also includes a revised/enriched version of the GPR in the same format as the DPD. Another GPR extension, with USAF/NOAA data, covering the period 1874–2019 is available from a website maintained by NASA MSFC staff.Footnote 11 Sunspot data from many other observatories are also available at the NGDC site.
Recent years have seen a surge in the digitization and processing of sunspot drawings made before the photographic era. A major role in this work has been played by a team in Potsdam led by Rainer Arlt (Arlt 2008; Arlt et al. 2013; Diercke et al. 2015). As a result sunspot positions (butterfly diagrams) have now been reconstructed for the period 1826–1880 from drawings by Schwabe and Spörer (Leussu et al. 2016, 2017); for the period 1749–1796 from drawings by Staudacher (Arlt 2009); for the period 1670–1711 from scattered information (Vaquero et al. 2015b; Neuhäuser et al. 2018); and for the period 1611–1631 from drawings by Scheiner and Galileo (Arlt et al. 2016; Vokhmyanin and Zolotova 2018).
Instead of the sunspot number, the total area of all spots observed on the solar disk might seem to be a less arbitrary measure of solar activity. However, these data have been available since 1874 only, covering a much shorter period of time than the sunspot number data. In addition, the determination of sunspot areas, especially farther from disk center, is not as trivial as it may seem, resulting in significant random and systematic errors in the area determinations. Area measurements performed in two different observatories often show discrepancies reaching \(\sim\) 30% for smaller spots (cf. the figure and discussion in Appendix A of Petrovay et al. 1999). Despite these difficulties, attempts at reconstructing sunpot areas have also been made (Carrasco et al. 2016; Senthamizh Pavai et al. 2015), and Muraközy et al. (2016) recently proposed a new activity index based on a calibration of the emerged magnetic flux to sunspot areas.
1.3.3 Other activity indices
A number of other direct indicators of solar activity have become available from the twentieth century (see Ermolli et al. 2014 for a recent review). These include, e.g., various plage indices or the 10.7 cm solar radio flux—the latter is considered a particularly good and simple to measure indicator of global activity (see Fig. 2). As, however, these data sets only cover a few solar cycles, their impact on solar cycle prediction has been minimal. A promising exception from this is the nearly three centuries long record of the solar EUV flux, recently reconstructed from the diurnal variation of the geomagnetic field by Svalgaard (2016).
Monthly values of the 10.7 cm radio flux in solar flux units for the period 1947–2017. The solar flux unit is defined as \(10^{-22}\) W/m\(^2\) Hz. The dashed green curve shows the monthly mean relative sunspot number \(R_{{\mathrm {m}}}\) for comparison. Data are from the NRC Canada (Ottawa/Penticton)
Of more importance are proxy indicators such as geomagnetic indices (the most widely used of which is the aa index), the occurrence frequency of aurorae or the abundances of cosmogenic radionuclides such as \(^{14}\)C and \(^{10}\)Be in natural archives. For solar cycle prediction uses such data sets need to have a sufficiently high temporal resolution to reflect individual 11-year cycles. For the geomagnetic indices such data have been available since 1868, while an annual \(^{10}\)Be series covering 600 years has been published by Berggren et al. (2009). Attempts have been made to reconstruct the epochs and even amplitudes of solar maxima during the past two millennia from oriental naked eye sunspot records and from auroral observations (Stephenson and Wolfendale 1988; Nagovitsyn 1997), but these reconstructions are currently subject to too many uncertainties to serve as a basis for predictions. Isotopic data with lower temporal resolution are now available for up to 50 000 years in the past; while such data do not show individual Schwabe cycles, they are still useful for the study of long term variations in cycle amplitude. Inferring solar activity parameters from such proxy data is generally not straightforward. (See review by Usoskin 2017.)
1.4 The solar cycle and its variation
The series of \(R\) values determined as described in Sect. 1.2 is plotted in Fig. 3. It is evident that the sunspot cycle is rather irregular. The mean length of a cycle (defined as lasting from minimum to minimum) is 11.0 years (median 10.9 years), with a standard deviation of 1.16 years; actual cycle lengths scatter in the range 9.0–13.6 years. Note that cycle lengths measured between successive maxima show a wider scatter, in the range 7.3 and 16.9 years. This is partly due to the fact that many cycles show a double maximum, the two sub-peaks being separated by 1–2 years. The mean cycle amplitude in terms of R is 179 (median 183),Footnote 12 with a standard deviation of 57. It is this wide variation that makes the prediction of the next cycle maximum such an interesting and vexing issue.
1.4.1 Secular activity variations
Inspecting Fig. 3 one can discern an obvious long term variation. For the study of such long term variations, the series of cycle parameters is often smoothed on time scales significantly longer than a solar cycle: this procedure is known as secular smoothing. One popular method is the so-called Gleissberg filter or 12221 filter (Gleissberg 1967). For instance, the Gleissberg filtered amplitude of cycle n is given by
Amplitudes of the sunspot cycles (dotted) and their Gleissberg filtered values (blue solid), plotted against cycle number. The shaded area marks a \(\pm 2\sigma\) band around the mean amplitude for cycles 17–23 comprising the Modern Maximum. For comparison, Gleissberg filtered cycle amplitudes are also shown for unrevised [v1.0] SSN data (blue dashed) and for two GSN reconstructions (red solid: Chatzistergos et al. 2017; red dashed: Svalgaard and Schatten 2016). (In the case of the two GSN series, amplitudes and dates for cycle maxima were determined from the 121 filtered annual data.)
The Gleissberg filtered series of solar cycles is plotted in Fig. 4. The most obvious feature of the variation is a cyclic modulation of the cycle amplitudes on a timescale of \(\sim\) 9–10 solar cycles. This so-called Gleissberg cycle will be discussed further in Sect. 4.2.3. The first minimum of this cycle plotted in Fig. 4, known as the “Dalton Minimum”, is formed by the unusually weak cycles 5, 6, and 7. The second secular minimum consists of a rather long series of moderately weak cycles 12–16, occasionally referred to as the [last] “Gleissberg Minimum”—but note that most of these cycles are less than \(1\,\sigma\) below the long-term average value given at the start of Sect. 1.4.
Finally the last secular maximum of the cycle comprises the series of strong cycles 17–23 in the second half of the twentieth century: the “Modern Maximum”. In addition to this cyclic modulation there is a tendency for an overall secular increase of solar activity in the figure: the Modern Maximum is clearly stronger than previous maxima. However, the strength of this secular increase in the activity level as well as the amount by which the Modern Maximum exceeds previous maxima of the Gleissberg cycle clearly depends on the reconstruction of the measure of activity chosen. The revision of the sunspot numbers has greatly reduced the amount of secular increase compared to Version 1.0, in agreement with the GSN reconstruction by Svalgaard and Schatten (2016). On the other hand the most recent GSN reconstruction (Chatzistergos et al. 2017) shows a marked long-term increasing trend again. The cosmogenic record rather unequivocally indicates that the persistently high level of solar activity characterizing the second half of the twentieth century had no precedent for thousands of years in the history of solar activity (cf. Table 3 in Usoskin 2017). The currently hotly debated problem of the strength of the Modern Maximum has important implications, e.g., for the understanding of the role of solar forcing in global warming (Lean and Rind 2008; Chylek et al. 2014; Nagy et al. 2017b; Owens et al. 2017). In this context it is important to stress that a secular increase in solar activity from the late nineteenth century (beginning of terrestrial global temperature record) to the mid-twentieth century is unquestionably present in all solar activity reconstructions. The decreasing trend displayed in the last few decades in the smoothed cycle amplitude series is also potentially important in this respect.
While the Dalton and Gleissberg minima are just local minima in the ever changing Gleissberg filtered SSN series, the conspicuous lack of sunspots in the period 1640–1705, known as the Maunder Minimum (Fig. 1) quite obviously represents a qualitatively different state of solar activity. Such extended periods of low activity are usually referred to as grand minima. Ever since the rediscovery of the Maunder Minimum in the late nineteenth century (Maunder 1894; Eddy 1976) its reality and significance has time to time been brought into question. Recent studies have shown that the 11/22-year solar cycle persisted during the Maunder Minimum, but at a greatly suppressed level (Usoskin et al. 2015; Vaquero et al. 2015a; Asvestari et al. 2017). A number of possibilities have been proposed to explain the phenomenon of grand minima, including chaotic behaviour of the nonlinear solar dynamo (Weiss et al. 1984), stochastic fluctuations in dynamo parameters (Moss et al. 2008; Usoskin et al. 2009b); a bimodal dynamo with stochastically induced alternation between two stationary states (Petrovay 2007) or stochastic effects like fluctuations in AR tilt (Karak and Miesch 2018) or “rogue” sunspots (Petrovay and Nagy 2018).
The analysis of long-term proxy data, extending over several millennia further showed that there exist systematic long-term statistical trends and periods such as the so called secular and supersecular cycles (see Sect. 4.2).
1.4.2 Does the Sun have a long term memory?
The existence of long lasting grand minima and maxima suggests that the sunspot number record may have a long-term memory extending over several consecutive cycles. Indeed, elementary combinatorical calculations show that the occurrence of phenomena like the Dalton minimum (3 of the 4 lowest maxima occurring in a row) in a random series of 24 recorded solar maxima has a rather low probability (5%). This conclusion is supported by the analysis of long-term proxy data, extending over several millennia, which showed that the occurrence of grand minima and (perhaps) grand maxima is more common than what would follow from Gaussian statistics (Usoskin et al. 2007; Wu et al. 2018).
It could be objected that for sustained grand minima or maxima a memory extending only from one cycle to the next would suffice. This intercycle memory explanation of persistent secular activity minima and maxima, however, would imply a good correlation between the amplitudes of subsequent cycles, which is not the case (cf. Sect. 2.1). With the known poor cycle-to-cycle correlation, strong deviations from the long-term mean would be expected to be damped on time scales short compared to, e.g., the length of the Maunder minimum. This suggests that the persistent states of low or high activity may be due to truly long term memory effects extending over several cycles.
In an analysis of the GSN series for the period 1799–2011 Love and Rigler (2012) found that the sequence of cycle maxima (and also of time-integrated activity in each cycle), including the Modern Maximum, would not be an unlikely result of the accumulation of multiple random-walk steps in a lognormal random walk of cycle amplitudes where \(\ln R\) performs a Gaussian random walk with mean stepsize 0.39 (or 0.28 for the integrated activity). This analysis, however, does not extend to the Maunder Minimum; and in any case, such a random walk should ultimately take the values of R up to arbitrarily high values in sufficiently long time, whereas the cosmogenic record clearly shows that the level of activity is bounded from above.
Further evidence for a long-term memory in solar activity comes from the persistence analysis of activity indicators. The parameter determined in such studies is the Hurst exponent \(0<H<1\). Essentially, H is the steepness of the growth of the total range \(\mathcal R\) of measured values plotted against the number n of data in a time series, on a logarithmic plot: \(\mathcal{R}\propto n^H\). For a Markovian random process with no memory \(H=0.5\). Processes with \(H>0.5\) are persistent (they tend to stay in a stronger-than-average or weaker-than-average state longer), while those with \(H<0.5\) are anti-persistent (their fluctuations will change sign more often).
Hurst exponents for solar activity indices have been derived using rescaled range analysis by many authors (Mandelbrot and Wallis 1969; Ruzmaikin et al. 1994; Komm 1995; Oliver and Ballester 1996; Kilcik et al. 2009; Rypdal and Rypdal 2012). All studies coherently yield a value \(H=0.85{-}0.88\) for time scales exceeding a year or so, and somewhat lower values (\(H\sim 0.75\)) on shorter time scales. Some doubts regarding the significance of this result for a finite series have been raised by Oliver and Ballester (1998); however, Qian and Rasheed (2004) have shown using Monte Carlo experiments that for time series of a length comparable to the sunspot record, H values exceeding 0.7 are statistically significant.
A complementary method, essentially equivalent to rescaled range analysis is detrended fluctuation analysis. Its application to solar data (Ogurtsov 2004) has yielded results in accordance with the H values quoted above.
The overwhelming evidence for the persistent character of solar activity and for the intermittent appearance of secular cyclicities, however, is not much help when it comes to cycle-to-cycle prediction. It is certainly reassuring to know that forecasting is not a completely idle enterprise (which would be the case for a purely Markovian process), and the long-term persistence and trends may make our predictions statistically somewhat different from just the long-term average. There are, however, large decadal scale fluctuations superposed on the long term trends, so the associated errors will still be so large as to make the forecast of little use for individual cycles.
1.4.3 Waldmeier effect and amplitude–frequency correlation
Greater activity on the Sun goes with shorter periods, and less with longer periods. I believe this law to be one of the most important relations among the Solar actions yet discovered.
(Wolf 1861)
It is apparent from Fig. 3 that the profile of sunspot cycles is asymmetrical, the rise being steeper than the decay. Solar activity maxima occur 3 to 4 years after the minimum, while it takes another 7–8 years to reach the next minimum. It can also be noticed that the degree of this asymmetry correlates with the amplitude of the cycle: to be more specific, the length of the rise phase anticorrelates with the maximal value of \(R\) (Fig. 5), while the length of the decay phase shows weak or no such correlation.Footnote 13
Historically, the relation was first formulated by Waldmeier (1935) as an inverse correlation between the rise time and the cycle amplitude; however, as shown by Tritakis (1982), the total rise time is a weak (inverse logarithmic) function of the rise rate, so this representation makes the correlation appear less robust. (Indeed, when formulated with the rise time it is not even present in some activity indicators, such as sunspot areas—cf. Dikpati et al. 2008; Ogurtsov and Lindholm 2011.) As pointed out by Cameron and Schüssler (2008), the weak link between rise time and slope is due to the fact that subsequent cycle are known to overlap by 1–2 years, so in steeper rising cycles the minimum will occur earlier, thus partially compensating for the shortening due to a higher rise rate. The effect is indeed more clearly seen when the rate of the rise is used instead of the rise time (Lantos 2000; Cameron and Schüssler 2008) or if the rise time is redefined as the time spent from 20 to 80% of the maximal amplitude (Karak and Choudhuri 2011).
Monthly smoothed sunspot number \(R\) at cycle maximum plotted against the rise time to maximum (left) and against cycle length (right). Cycles are labeled with their numbers. In the plots the red dashed lines are linear regressions to all the data, while the blue solid lines are fits to all data except outliers. Cycle 19 is considered an outlier on both plots, Cycle 4 on the right hand plot only. The corresponding correlation coefficients are shown
Nevertheless, when coupled with the nearly nonexistent correlation between the decay time and the cycle amplitude, even the weaker link between the rise time and the maximum amplitude is sufficient to forge a weak inverse correlation between the total cycle length and the cycle amplitude (Fig. 5). This inverse relationship was first noticed by Wolf (1861).
A stronger inverse correlation was found between the cycle amplitude and the length of the previous cycle by Hathaway et al. (1994). This correlation is also readily explained as a consequence of the Waldmeier effect, as demonstrated in a simple model by Cameron and Schüssler (2007); the same probably holds for the correlations reported by Hazra et al. (2015). Note that in a more detailed study Solanki et al. (2002) found that the correlation coefficient of this relationship has steadily decreased during the course of the historical sunspot number record, while the correlation between cycle amplitude and the length of the third preceding cycle has steadily increased. The physical significance (if any) of this latter result is unclear.
In what follows, the relationships found by Wolf (1861), Hathaway et al. (1994), and Solanki et al. (2002), discussed above, will be referred to as “\(R_{{\mathrm {max}}}-t_{{\mathrm {cycle}},n}\) correlations” with \(n = 0, {-}\,1\) or \({-}\) 3, respectively.
Modern time series analysis methods offer several ways to define an instantaneous frequency f in a quasiperiodic series. One simple approach was discussed in the context of Bracewell’s transform, Eq. (3), above. Mininni et al. (2000) discussed several more sophisticated methods to do this, concluding that Gábor’s analytic signal approach yields the best performance. This technique was first applied to the sunspot record by Paluš and Novotná (1999), who found a significant long term correlation between the smoothed instantaneous frequency and amplitude of the signal. On time scales shorter than the cycle length, however, the frequency–amplitude correlation has not been convincingly proven, and the fact that the correlation coefficient is close to the one reported in the right hand panel of Fig. 5 indicates that all the fashionable gadgetry of nonlinear dynamics could achieve was to recover the effect already known to Wolf. It is clear from this that the “frequency–amplitude correlation” is but a secondary consequence of the Waldmeier effect.
Indeed, an anticorrelation between cycle length and amplitude is characteristic of a class of stochastically forced nonlinear oscillators and it may also be reproduced by introducing a stochastic forcing in dynamo models (Stix 1972; Ossendrijver et al. 1996; Charbonneau and Dikpati 2000). In some such models the characteristic asymmetric profile of the cycle is also well reproduced (Mininni et al. 2000, 2002). The predicted amplitude–frequency relation has the form
where \(f\sim \left( t_{{\mathrm {min}}}^{(n+1)}-t_{{\mathrm {min}}}^{(n)}\right) ^{-1}\) is the frequency.
Nonlinear dynamo models including some form of \(\alpha\)-quenching also have the potential to reproduce the effects described by Wolf and Waldmeier without recourse to stochastic driving. In a dynamo with a Kleeorin–Ruzmaikin type feedback on \(\alpha\), Kitiashvili and Kosovichev (2009) are able to qualitatively reproduce the Waldmeier effect. Assuming that the sunspot number is related to the toroidal field strength according to the Bracewell transform, Eq. (3), they find a strong link between rise time and amplitude, while the correlations with fall time and cycle length are much weaker, just as the observations suggest. They also find that the form of the growth time–amplitude relationship differs in the regular (multiperiodic) and chaotic regimes. In the regular regime the plotted relationship suggests
while in the chaotic case
The linear relationship (6) was also reproduced in some stochastically forced nonlinear dynamo models (Pipin and Sokoloff 2011; Pipin and Kosovichev 2011; Pipin et al. 2012).
Note that based on the actual sunspot number series Waldmeier originally proposed
while according to Dmitrieva et al. (2000) the relation takes the form
At first glance, these logarithmic empirical relationships seem to be more compatible with the relation (5) predicted by the stochastic models. These, on the other hand, do not actually reproduce the Waldmeier effect, just a general asymmetric profile and an amplitude–frequency correlation. At the same time, inspection of the the left hand panel in Fig. 5 shows that the data is actually not incompatible with a linear or inverse rise time–amplitude relation, especially if the anomalous Cycle 19 is ignored as an outlier. (Indeed, a logarithmic representation is found not to improve the correlation coefficient—its only advantage is that Cycle 19 ceases to be an outlier.) All this indicates that nonlinear dynamo models may have the potential to provide a satisfactory quantitative explanation of the Waldmeier effect, but more extensive comparisons will need to be done, using various models and various representations of the relation. In one such exploratory study for instance Nagy and Petrovay (2013) found that solar-like parameter correlations can be obtained in a stochastically forced van der Pol oscillator but only if the perturbations are applied to the nonlinearity parameter rather than to the damping. In another study Karak and Choudhuri (2011) found that in a stochastically forced flux transport dynamo perturbing the poloidal field amplitude is not sufficient to induce solar-like parameter correlations, and perturbations to the meridional flow speed are also needed.
1.5 Approaches to solar cycle prediction
As the SSN series is a time series it is only natural that time series analysis methods have been widely applied in order to predict its future variations, including the amplitude of an upcoming cycle. As a group, however, time series methods have not been particularly successful in attaining this goal. In addition, time series analysis is a purely mathematical tool offering little physical insight into the processes driving cycle-to-cycle variations. In view of this, time series methods (or extrapolation methods) have been relegated to a later section of this review, after dealing with the currently much more lively field of the physically more insightful and more successful alternative approaches: precursor schemes and model-based forecasts.
In the 1st edition of this review the model-based approach, then still very new, was discussed well separated from precursor methods, in a section following the discussion of the time series approach. In the time elapsed since the 1st edition, however, a major surge of activity in surface flux transport (SFT) modelling, new developments in dynamo models and in empirical precursors have made it harder to draw a clear line between the precursor and model based approaches. Indeed, there seem to be at least “five shades of grey” arching between archetypical examples of these two categories:
-
(a)
Internal empirical precursors (relying only on the SSN series)
-
(b)
External empirical precursors (relying on other activity indicators)
-
(c)
Physical[ly motivated] precursors
-
(d)
Forecasts based on SFT models
-
(e)
Forecasts based on dynamo models
Accordingly, the present edition has been reorganized so the section discussing model-based predictions immediately follows the section on precursors: the two topics have been separated, somewhat arbitrarily, between the classes (c) and (d) above, i.e., the term “model-based” is reserved for methods employing detailed quantitative models rather than empirical or semiempirical correlations based on qualitative physical ideas.
2 Precursor methods
Jeder Fleckenzyklus muß als ein abgeschlossenes Ganzes, als ein Phänomen für sich, aufgefaßt werden, und es reiht sich einfach Zyklus an Zyklus.
(Gleissberg 1952)
In the most general sense, precursor methods rely on the value of some measure of solar activity or magnetism at a specified time to predict the amplitude of the following solar maximum. The precursor may be any proxy of solar activity or other indicator of solar and interplanetary magnetism. Specifically, the precursor may also be the value of the sunspot number at a given time.
In principle, precursors might also herald the activity level at other phases of the sunspot cycle, in particular the minimum. Yet the fact that practically all the good precursors found need to be evaluated at around the time of the minimum and refer to the next maximum is not simply due to the obvious greater interest in predicting maxima than predicting minima. Correlations between minimum parameters and previous values of solar indices have been looked for, but the results were overwhelmingly negative (e.g., Tlatov 2009). This indicates that the sunspot number series is not homogeneous and Rudolf Wolf’s instinctive choice to start new cycles with the minimum rather than the maximum in his numbering system is not arbitrary—for which even more obvious evidence is provided by the butterfly diagram. Each numbered solar cycle is a consistent unit in itself, while solar activity seems to consist of a series of much less tightly intercorrelated individual cycles, as suggested by Wolfgang Gleissberg in the motto of this section.
In Sect. 1.4.2 we have seen that there may be some evidence for a long-term memory underlying solar activity. In addition to the evidence reviewed there, systematic long-term statistical trends and periods of solar activity, such as the secular and supersecular cycles (to be discussed in Sect. 4.2), also attest to a secular mechanism underlying solar activity variations and ensuring some degree of long-term coherence in activity indicators. However, as we noted, this long-term memory is of limited importance for cycle prediction due to the large, apparently haphazard decadal variations superimposed on it. What the precursor methods promise is just to find a system in those haphazard decadal variations—which clearly implies a different type of memory. As we already mentioned in Sect. 1.4.2, there is obvious evidence for an intracycle memory operating within a single cycle, so that forecasting of activity in an ongoing cycle is currently a much more successful enterprise than cycle-to-cycle forecasting. As we will see, this intracycle memory is one candidate mechanism upon which precursor techniques may be founded, via the Waldmeier effect.
The controversial issue is whether, in addition to the intracycle memory, there is also an intercycle memory at work, i.e., whether behind the apparent stochasticity of the cycle-to-cycle variations there is some predictable pattern, whether some imprint of these variations is somehow inherited from one cycle to the next, or individual cycles are essentially independent. The latter is known as the “outburst hypothesis”: consecutive cycles would then represent a series of “outbursts” of activity with stochastically fluctuating amplitudes (Halm 1901; Waldmeier 1935; Vitinsky 1973; see also de Meyer 1981 who calls this “impulse model”). Note that cycle-to-cycle predictions in the strict temporal sense may be possible even in the outburst case, as solar cycles are known to overlap. Active regions belonging to the old and new cycles may coexist for up to three years or so around sunspot minima; and high latitude ephemeral active regions oriented according to the next cycle appear as early as 2–3 years after the maximum (Tlatov et al. 2010—the so-called extended solar cycle).
In any case, it is undeniable that for cycle-to-cycle predictions, which are our main concern here, the precursor approach seems to have been the relatively most successful, so its inherent basic assumption must contain an element of truth—whether its predictive skill is due to a “real” cycle-to-cycle memory (intercycle memory) or just to the overlap effect (intracycle memory).
The two precursor types that have received most attention are polar field precursors and geomagnetic precursors. A link between these two categories is forged by a third group, characterizing the interplanetary magnetic field strength or “open flux”. In terms of the classification outlined in Sect. 1.5 above, all these belong to the category (c) of physically motivated precursors. But before considering these approaches, we start by discussing categories (a) and (b): the empirical precursors based on the chance discovery of correlations between certain solar parameters and cycle amplitudes. These parameters involved may also be external to the SSN series (b); but first of all we will focus on the most obvious precursor type: internal empirical precursors (a) —the level of solar activity at some epoch before the next maximum.
2.1 Cycle parameters as precursors and the Waldmeier effect
The simplest weather forecast method is saying that “tomorrow the weather will be just like today” (works in about 2/3 of the cases). Similarly, a simple approach of sunspot cycle prediction is correlating the amplitudes of consecutive cycles. There is indeed a marginal correlation, but the correlation coefficient is quite low (0.35). The existence of the correlation is related to secular variations in solar activity, while its weakness is due to the significant cycle-to-cycle variations.
A significantly better correlation exists between the minimum activity level and the amplitude of the next maximum (Fig. 6). The relation is linear (Brown 1976), with a correlation coefficient of 0.68 (if the anomalous cycle 19 is ignored—Brajša et al. 2009; see also Pishkalo 2008). The best fit is
Monthly smoothed sunspot number \(R\) at cycle maximum plotted against the values of \(R\) at the previous minimum (left) and 3 years before the minimum (right). Cycles are labeled with their numbers. Blue solid lines are linear regressions to the data. In the left-hand plot Cycle 19 was treated as an outlier and omitted from the regression. The corresponding correlation coefficients are also displayed
Cameron and Schüssler (2007) pointed out that the activity level three years before the minimum is an even better predictor of the next maximum. The exact value of the time shift producing optimal results may somewhat vary depending on the base period considered: in the Version 2 SSN series for the whole series of cycles 1–24 the highest correlation results for a time shift of 39 months while considering only cycles 8–24, for which data are sometimes considered more reliable, the best correlation is found at 32 months. Here in the right hand panel of Fig. 6 we simply use the round value of of 3 years (36 months) as originally proposed. The linear regression is
This method, to be referred to as as “minimax3” for brevity, can only provide an upper estimate for the expected amplitude of Cycle 25 as the minimum has not been reached at the time of writing. As the minimum will take place no earlier than May 2019, the value of the predictor is not higher than 44.8, which would result in a cycle amplitude of 147. This already gives an indication that the upcoming cycle will be weaker than the climatological average.
As the epoch of the minimum of \(R\) cannot be known with certainty until about a year after the minimum, the practical use of these methods is rather limited: a prediction will only become available 2–3 years before the maximum, and even then with the rather low reliability reflected in the correlation coefficients quoted above. In addition, as convincingly demonstrated by Cameron and Schüssler (2007) in a Monte Carlo simulation, these methods do not constitute real cycle-to-cycle prediction in the physical sense: instead, they are due to a combination of the overlap of solar cycles with the Waldmeier effect. As stronger cycles are characterized by a steeper rise phase, the minimum before such cycles will take place earlier, when the activity from the previous cycle has not yet reached very low levels.
The same overlap readily explains the \(R_{{\mathrm {max}}}-t_{{\mathrm {cycle}},n}\) correlations discussed in Sect. 1.4.3. These relationships may also be used for solar cycle prediction purposes (e.g., Kane 2008) but they lack robustness. The forecast is not only sensitive to the value of n used but also to the data set (relative or group sunspot numbers) (Vaquero and Trigo 2008). Similar correlations between the properties of subsequent cycles were used by Li et al. (2015) to give a prediction for Cycle 25.

Image reproduced with permission from Howe et al. (2017), copyright by the authors
Portents of changes to come 1: solar oscillations. Averaged frequency shifts (symbols with error bars) in the indicated frequency bands as a function of time. Renormalized data on the 10.7-cm radio flux (RF), Ca K index, Kitt Peak global magnetic field strength index (\(B_{\mathrm KP}\)) and SSN v1 are plotted for comparison as shown in the legend. Vertical dotted lines mark cycle minima.
2.2 External empirical precursors
Cycle 24 peaked at an amplitude 35% lower than Cycle 23. This was the 4th largest intercycle drop in solar activity in the monthly SSN record. The last such occurrence was rather different, following the single anomalously strong cycle 19, while in the case of the drop after Cycle 23 a series of 7 strong cycles was ended. This is illustrated in Fig. 4 where the shaded area marks a \(\pm 2\sigma\) band around the mean amplitude of cycles 17–23 comprising the Modern Maximum. Cycle 24 clearly deviates downwards from the Modern Maximum cycles by over \(2\sigma\) on the low side.
The first two occurrences of similar intercycle drops in activity (following cycles 4 and 11) are closer analogues of the recent events. These heralded the two previous Gleissberg minima centuries ago. The circumstance that a new Gleissberg minimum was already overdue suggests that this is indeed what we are witnessing. This is in line with current indications that solar activity will remain at Cycle 24 levels also in Cycle 25 (cf. Sect. 5). Yet no work predating 2005 predicted this drop which mostly caught solar physicists by surprise.
This unexpected drop in the level of solar activity from Cycle 23 to 24 has spurred efforts to find previously overlooked earlier signs of the coming change in solar data. A number of such “portents” were indeed identified, as first reviewed and correlated by Balogh et al. (2014).
A “seismic portent” was identified by Basu et al. (2012). High-frequency solar oscillations, sampling the top of the solar convective zone, have long been known to display frequency variations correlated with the solar cycle. The analysis of Basu et al. (2012) showed that for [relatively] lower frequencies the amplitude of the frequency variation was strongly suppressed in Cycle 23, compared with Cycle 22 or with the variation in higher frequency modes (Fig. 7). This suggests that the (presumably magnetically modulated) variations in the sound speed were limited to the upper 3 Mm of the convective zone in Cycle 23, whereas in the previous cycle they extended to deeper layers. Revisiting the issue, Howe et al. (2017) confirmed a change in the frequency response to activity during Solar Cycle 23, with a lower correlation of the low-frequency shifts with activity in the last two cycles compared to Cycle 22.
A similar disproportionately strong suppression of Cycle 23 relative to Cycle 22 is seen in the occurrence rate of flares, especially of class X and M (Fig. 8), and also in the variation of the H\(_\alpha\) flare index. The suppression is rarely commented on yet clearly seen in the plots of Ataç and Özgüç (2001), Ataç and Özgüç (2006), Hudson et al. (2014), or Gao and Zhong (2016).Footnote 14 It may be worth noting that the relationship between the SSN and the soft X-ray background was also found to differ for different solar cycles by Winter et al. (2016).
This “eruptivity portent” is also manifested in the variation of the coronal index (green coronal line emissivity), as seen in the plots of Ataç and Özgüç (2006). A curious disagreement is seen regarding the suppression of the number of C class flares in Cycle 23: while the data of Hudson et al. (2014) suggest a significant suppression of the number of these flares, only slightly less than for M and X class flares, Gao and Zhong (2016) found a much less strong suppression for C flares compared to M and X type flares. This is puzzling as both works are based on the same NOAA data, the only apparent difference being the exclusion of flares close to the limb by Hudson et al. (2014).
The stronger suppression of larger flares might be interpereted as a relative lack of large active regions harbouring sufficient magnetic energy to produce such flares. Based on the expectation that the magnetic “roots” of larger ARs reach deeper, this would also agree with the seismic portent. Indeed, Howe et al. (2017) explicitly speculate that the observed suppression of the low frequency modulation in Cycle 23 is “perhaps because a greater proportion of activity is composed of weaker or more ephemeral regions”.
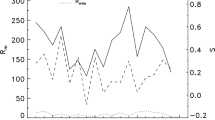
Apparently in line with the above reasoning, de Toma et al. (2013b) reported a strong suppression of the number of very large (\(>700\) msh) sunspots and sunspot groups in Cycle 23. But the situation is not so simple as Kilcik et al. (2011), Lefèvre and Clette (2011) and Kilcik et al. (2014) found an apparently opposite trend: a strong suppression in the number of very small (\({<}\,17\) msh) spots or of sunspot groups of Zürich type A and B (pores/pore pairs) while the number of larger, more complex spots/groups is largely unaffected, or even slightly enhanced (Fig. 9). As the contribution to plage areas, radio flux, TSI or disk-integrated magnetic flux density is dominated by these large ARs, no significant suppression of Cycle 23 is detected in these proxies either (Göker et al. 2017).
These perplexing findings may also be linked to the apparent decrease of the sunspot magnetic field strengths throughout Cycle 23 (Livingston et al. 2012; Nagovitsyn et al. 2016). There is, however, as yet no consensus regarding the reality of this trend (de Toma et al. 2013a; Watson et al. 2014) or regarding to what extent they are cycle related or due to secular trends (Norton et al. 2013; Rezaei et al. 2012, 2015; Nagovitsyn et al. 2017).
Studies pointing to possible interrelationships between the various portents discussed above include Kilcik et al. (2018) where a stronger decrease in sunspot count in flaring AR was reported compared to non-flaring regions. While local subsurface flow properties in AR, in particular vorticity, have also been found to correlate with flare productivity (Mason et al. 2006; Komm et al. 2011, 2015), the apparently only study of the relationship between local disturbances of seismic properties (such as sound speed) in AR and flare index led to inconclusive results (Lin 2014).
2.3 Polar precursor
The polar precursor method, as first suggested by Schatten et al. (1978), is based on the correlation between the amplitude of a sunspot maximum with a measure of the amplitude of the magnetic field near the Sun’s poles at the preceding cycle minimum. Its physical background is the plausible causal relationship between the toroidal flux and the poloidal flux that serves as a seed for the generation of toroidal fields by the winding up of field lines in a differentially rotating convective zone.
It is now widely agreed that, beside internal empirical precursor methods based on the Waldmeier rule, the polar precursor method is currently the most reliable way to forecast an upcoming solar cycle. As the first revision of this review concluded, the polar precursor method “has consistently proven its skill in all cycles.” It is now also widely agreed that the polar precursor stands behind the apparent predicting skill of several other forecasting methods, including geomagnetic precursors.
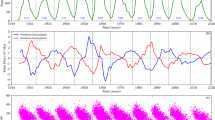
The hemispherically averaged polar field amplitude from the WSO data set (black) and the overall dipole amplitude (cyan) as a function of time. The sunspot number series (green dotted) is shown for comparison, with an arbitrary rescaling. All curves were smoothed with a 13-month sliding window. Times of sunspot minima are marked by the dashed vertical lines. Global dipole amplitudes were obtained by courtesy of Jie Jiang and represent the average of values computed for all available data sets out of a maximum of five (WSO, NSO, MWO, MDI, HMI) at the given time
2.3.1 Polar magnetic field data
Observational data on magnetic fields near the Sun’s poles were reviewed by Petrie (2015). Solar magnetograms have been available on a regular basis from Mt. Wilson Observatory since 1974, from Wilcox Solar Observatory (WSO) since 1976, and from Kitt Peak since 1976 (with a major change in the instrument from KPVT to SOLIS in 2003). The most widely used set of direct measurements of the magnetic field in the polar areas of the Sun is from the WSO series (Svalgaard et al. 1978; Hoeksema 1995). While these magnetograms have the lowest resolution of the three sets, from the point of view of the characterization of the polar fields this is not necessarily a disadvantage, as integrating over a larger aperture suppresses random fluctuations and improves the S/N ratio. As a result of the low resolution, the WSO polar field value is a weighted average of the line-of-sight field in a polar cap extending down to \(\sim \, 55^\circ\) latitude on average (with significant annual variations due to the \(7^\circ\) tilt of the solar axis).
The classic reference on the processing and analysis of WSO polar field data is Svalgaard et al. (1978). The inference from their analysis was that assuming a form \(B=B_0 f(\theta )\) with \(f(\theta )=\cos ^n(\theta )\) for the actual mean magnetic field profile (\(\theta\) is colatitude) inside the polar cap around minimum, \(n=8\pm 1\) while \(B_0\) was around 10 G for Cycle 21 and the next two cycles, being reduced to about half that value in Cycle 24. While one later study (Petrie and Patrikeeva 2009) points to a possibility that the value of n may be even higher, up to 10, the “canonical” value \(n=8\) seems quite satisfactory in most cases (e.g., Fig. 2 in Whitbread et al. 2017).
Figure 10 shows the variation of the smoothed amplitude of the WSO polar field, averaged over the two poles. (The presence of undamped residual fluctuations on short time scales illustrates the unsatisfactory nature of the 13-month smoothing, applied here for consistency with the rest of this review. A regularly updated plot of the WSO polar field with a more optimal smoothing (low-pass filter) is available from the WSO web siteFootnote 15.)
Also shown is an alternative measure of the amplitude of the poloidal field component, the axial dipole coefficient, i.e., the amplitude of the coefficient of the \(Y_1^0\) term in a spherical harmonic expansion of the distribution of the radial magnetic field strength over the solar disk:
where \(\overline{B}\) denotes the azimuthally averaged radial magnetic field.
This formula assumes the use of the Schmidt quasi-normalization in the definition of the spherical harmonics, widely used in solar physics and geomagnetism (see, e.g., Winch et al. 2005). For direct comparison of the amplitudes of harmonics of different degree, a full normalization is sometimes preferred (e.g., in DeRosa et al. 2012): this results in a normalized dipole coefficient \(\hat{D}=(4\pi /3)^{1/2}D\). While (12) or even (13) are often loosely referred to as the “solar dipole moment”, it should also be kept in mind that the magnetic [dipole] moment, as normally defined in physics, is related to D as \((2\pi R_\odot ^3/\mu _0) D\) where \(R_\odot\) is the solar radius and \(\mu _0\) is the vacuum permeability.
The two curves in Fig. 10 are quite similar even in many of their details: the polar field amplitude follows the variations of the dipole coefficient with a phase lag of about a year. This is hardly surprising as the hemispherically averaged polar field amplitude \(|B_N-B_S|/2\) is clearly proportional to the contribution to D coming from the polar caps:
As the polar field is formed by the poleward transport of magnetic fields at lower latitudes, it is only to be expected that the variation of the polar cap contribution will follow that of the overall dipole with some time delay.
Indeed, based on the good agreement of the two curves in Fig. 10, \((B_N-B_S)/2\) may simply be used as a simple measure of the amplitude of the dipole (on an arbitrary scale); on similar grounds, \((B_N+B_S)/2\) may be considered a measure of the quadrupole component (e.g., Svalgaard et al. 2005; Muñoz-Jaramillo et al. 2013a).
We note that the dipole moment in our figure is an average of all available values from different magnetogram data sets for a given date; however, there is a quite good overall agreement among the values from different data sets (see Fig. 9 in Jiang et al. 2018).Footnote 16
The behaviour of the curves in Fig. 10 further shows that the times of dipole reversal are usually rather sharply defined. Based on the 4 reversals seen in the plot, the overall dipole is found to reverse \(3.44 \pm 0.18\) years after the minimum, while the polar contribution to the dipole reverses after \(4.33 \pm 0.36\) years. (The formal errors given are \(1\sigma\).) The low scatter in these values suggests that the cycle phase of dipole reversal may be a sensitive test of SFT and dynamo models.
In contrast to reversal times, maxima of the dipole amplitude are much less well defined (occurring \(7.27 \pm 1.38\) and \(8.33 \pm 1.08\) years after minimum for the two curves). The curves display broad, slightly slanting plateaus covering 3 to 5 years (Iijima et al. 2017); the dipole amplitude at the time of solar minimum is still typically \(84\pm 12\%\) (global dipole) and \(90\pm 6\%\) (polar fields) of its maximal value, reached years earlier. This kind of slanting profile is actually good news for cycle prediction as it opens the way to guess the dipole amplitude at the time of minimum, used as a predictor, years ahead. For example, using the rather flat and low preceding maximum in polar field strength, Svalgaard et al. (2005) were able to predict a relatively weak Cycle 24 (predicted Version 1 peak SSN value \(75\pm 8\) vs. 67 observed) as early as 4 years before the sunspot minimum took place in December 2008!
The potential use of the dipole amplitude as a precursor is borne out by the comparison with the sunspot number curve in Fig. 10. After our arbitrary rescaling of the SSN, its maxima in each cycle are roughly at level with the preceding plateaus of the solid curves. This certainly seems to indicate that the suggested physical link between the precursor and the cycle amplitude is real.
The flatness of the maxima of the polar field imply that the precursor normally cannot be strongly affected by the exact time when it is evaluated. The cycle overlap effect combined with the Waldmeier relation, affecting the timing of the minimum, is therefore unlikely to explain the predictive skill of the polar precursor: we are here dealing with a real physical precursor (as also argued by Charbonneau and Barlet 2011).
The “polar precursor” may thus be interpreted in four different ways. The precursor may be the value of the global dipole moment or of the contribution of polar fields to this dipole moment only (i.e., the WSO field); and either of these may be evaluated at cycle minimum, or a few years earlier when they reach their respective maxima. Table 1 lists these precursor values for individual solar cycles, compared with the actual cycle amplitude. A homogeneous linear fit with one free parameter to the precursor–cycle amplitude relation yields the fit coefficient values given in the lower part of the table. The nominal random scatter is also indicated. Precursor values for Cycle 25 have been evaluated in late 2018; as it is not yet clear whether the maximum of the dipole moment has passed or when the minimum will take place, the forecasts based on these values are to be interpreted as lower/upper estimates, respectively. Taking into account the given values of the scatter, a combination of these results implies that Cycle 25 should peak in the range 102–133 with a nominal probability of \(\sim \, 70\)%, i.e. the next cycle should have an amplitude similar to Cycle 24.
Temporal variation of hemispherically averaged polar magnetic fluxes resulting from the Mt.Wilson polar facular counts (black), WSO polar flux (magenta), rescaled Mitaka polar facular counts (red), and rescaled Kodaikanal polar network index (yellow). The sunspot number series (green dotted) is shown for comparison, with an arbitrary rescaling. Flux values are based on the calibration in Muñoz-Jaramillo et al. (2012). All data refer to the area poleward of \(70^\circ\) latitude. All curves were smoothed with a 13-month sliding window except the annually sampled Mt.Wilson and Kodaikanal data where a 121 filter was applied. Times of sunspot minima are marked by the dashed vertical lines
2.3.2 Proxy reconstructions of the polar magnetic field
Despite the plausibility of a physical link between polar magnetic fields and cycle amplitude, the shortness of the available direct measurement series represents a difficulty when it comes to finding a convincing statistical link between these quantities. A way to circumvent this difficulty is offered by the availability of proxy data for polar magnetism spanning much longer time scales. Indeed, Schatten’s original suggestion of a polar field precursor (Schatten et al. 1978) on a generic physical basis was supported by such proxy studies. It is remarkable that despite the very limited available experience, proxy-based forecasts using the polar field method proved to be consistently in the right range for Cycles 21, 22, and 23 (Schatten and Sofia 1987; Schatten et al. 1996).
The types of proxies of solar polar magnetism were reviewed by Petrie et al. (2014). In the present subsection we focus on polar faculae, which are currently considered the best photospheric proxy data for the reconstruction of polar magnetic field/flux. The interplanetary and geomagnetic precursors discussed in the following sections, however, may also be interpreted as indirect proxies of the solar polar magnetic field.
High resolution observations by the Hinode space observatory confirm that, like all other magnetic fields in the solar photosphere, polar fields are highly intermittent, nearly all of the flux being concentrated in isolated strong magnetic field concentrations (Tsuneta et al. 2008). These magnetic elements are observed as bright facular points in white light and in some spectral lines. The number density of these polar faculae is then related to the intensity of the polar magnetic field, while their total number above a certain latitude is related to the total magnetic flux (Sheeley 1964). This conclusion was indeed confirmed by Li et al. (2002) and, more recently, by Tlatov (2009).
Perhaps the most carefully analyzed polar facular data set is the series of observations in the Mt. Wilson Observatory. These data were validated against MDI observations and then calibrated to WSO and MDI magnetic measurements by Muñoz-Jaramillo et al. (2012). This resulted in a time series of the solar polar magnetic flux (poleward of \(70^\circ\) latitude) for each hemisphere, covering the period 1906–2014. Owing to the varying tilt of the solar axis, the data are available with an annual cadence and with a time shift of 0.5 year between the hemispheres. This reconstructed polar flux was subsequently correlated with cycle amplitudes, confirming the usefulness of the polar precursor method (Muñoz-Jaramillo et al. 2013a, b). Hemispherically averaged data show a highly significant correlation, albeit with a large scatter (\(r=0.69\) at 96%). This imperfect correlation is reflected in Fig. 11 in the wildly varying ratio between the maxima of the black curve and the subsequent maxima of the green dotted curve.
The poor correlation can be improved by separating the hemispheres, but some outlier points appear, apparently obeying an alternative relationship. Arguing that outliers correspond to cycles where the hemispheric asymmetry of polar fields exceeds a threshold, Muñoz-Jaramillo et al. (2013a) finally arrived at four (two for each hemisphere) linear empirical relationships between the reconstructed polar magnetic flux at minimum and the amplitude of the next cycle. The suggested relation correctly reproduced the observed amplitude of Cycle 24 (predicted Version 1 SSN \(77\pm 16\) vs. 67 observed).
Another relevant data set is the polar facular counts recorded in the National Astronomical Observatory of Japan (NAOJ) at Mitaka Observatory during the period 1954–1996 (Li et al. 2002). A third series of polar facular data, originating from Kodaikanal Observatory Ca K spectroheliograms, was compiled by Priyal et al. (2014). (As these are chromospheric features, the authors prefer to call their index a polar network index.) Major disagreements between these data sets are seen in Fig. 11 indicating that the use of polar facular proxies is still not on very firm grounds. This is further shown by a comparison of the deducted MWO polar flux with polar magnetic fluxes computed from WSO polar field data using the calibration formula derived in Muñoz-Jaramillo et al. (2012) (magenta curve in the plot). It is apparent that prior to the calibration period 1996–2006 the reconstructed MWO polar fluxes are systematically higher than the measured WSO fluxes, suggesting problems with these calibrations. In particular, while WSO polar field strengths peak at roughly the same amplitude in cycles 21, 22 and 23, in agreement with the comparable amplitudes of the subsequent sunspot cycles, the different polar facular counts indicate greatly different amplitudes for these minima, and they are also mutually incompatible.
Polar faculae are not the only long-term data base relevant for the study of high-latitude magnetic fields. \({\mathrm {H}}_\alpha\) synoptic charts are available from various observatories from as early as 1870. As \({\mathrm {H}}_\alpha\) filaments and filament channels lie on the magnetic neutral lines, these maps can be used to reconstruct the overall topology, if not the detailed map, of the large-scale solar magnetic field. While in between the neutral lines only the polarity of the field can be considered known, the variation of the global dipole moment may be tolerably well estimated even by fixing the field amplitude at a constant value. As higher order multipoles decay rapidly with distance, a potential field model fitted to the given synoptic map will then yield an acceptable representation of the polar field at the source surface. With this approach Makarov et al. (2001) computed the multipole coefficients of the solar magnetic field, reconstructing the polar field strength at the source surface back to 1915. They also introduced the so-called dipole-octupole index (aka A-index): the sum of the axial dipole and octupole magnetic moments as a simple measure of the polar field amplitude. The method was later applied by Obridko and Shelting (2008) to predict the amplitude of Cycle 24: their forecast proved to be within 10% of the actual value. In turn, Tlatov (2009) has shown that several indices of the polar magnetic field during the activity minimum, determined from these charts, correlate well with the amplitude of the incipient cycle.
2.3.3 Extending the range of the polar precursor: early forecasts for Cycle 25
The polar precursor is customarily evaluated at the cycle minimum, offering a prediction over a time span of 3–4 years, comparable to the rise time of the next cycle. Table 1, however, shows that using the maximal value of the global dipole moment results in a somewhat lower scatter around the mean relationship. This opens the possibility of making a prediction several years before the minimum.
The forecasting potential of the global dipole may also provide the ground for the findings of Hawkes and Berger (2018) who proposed the “helicity flux” as a cycle precursor. Perhaps more aptly called helicity input rate by the differential rotation, their helicity flux is defined by a weighted hemispheric surface integral of (a functional of) the radial magnetic field, where the weight function is fixed by the differential rotation profile. In such an integral, which is not unlike Eq. (12), the dipole component will naturally give a dominant contribution as the higher order terms change sign over each hemisphere, which largely cancels their effect. The authors found that the helicity input rate anticipates the sunspot numbers with a time shift of 4.5–6.9 years (depending on the cycle considered). This seems to be in line with the variable time delays between maxima of the global dipole moment and the next cycle maximum (Fig. 10). Their prediction for the amplitude of Cycle 25 is 117—similar or slightly stronger than Cycle 24.
Similarly, using the brightness temperature of the 17 GHz microwave emission as a proxy for the field strength, Gopalswamy et al. (2018) found that the correlation between this proxy and the sunspot number is maximal for time shifts of \(\sim \, 4\)–6 years (depending on cycle and hemisphere). Their forecast for Cycle 25 is a smoothed SSN of 89 for the S hemisphere and 59 for the N hemisphere (the latter being a lower bound as the proxy had not reached its maximum at the time of publication). These values are again comparable to or slightly higher than the amplitudes for Cycle 24.
In this context it is interesting to note that Makarov et al. (1989) and Makarov and Makarova (1996) found that the number of polar faculae observed at Kislovodsk anticipates the next sunspot cycle with a time lag of 5–6 years on average in cycles 20–22; even short term annual variations or “surges” of sunspot activity were claimed to be discernible in the polar facular record. An apparently conflicting result was obtained by Li et al. (2002), who found using the Mitaka data base that the best autocorrelation results with a time shift of about 4 years only. The discrepancy may perhaps be related to the cycle dependence of these time shifts, as partly different periods were considered.
In theory it is conceivable that successful forecasts might be attempted even earlier. After all, the polar field starts to build up at the time of polar reversal, about 5–6 years before the next minimum. Petrovay et al. (2018) explored this possibility in a study of the coronal green lime emission at high latitudes. They tried to correlate various features of the characteristic “rush to the poles” (RTTP) feature of this emission around the polar reversal with properties of the following sunspot cycle and found a significant correlation between the speed of the RTTP and the time from the reversal to the next maximum. From this they predict that Cycle 25 will most likely peak in late 2024. Combining this date with the minimax3 method discussed in Sect. 2.1 above, the cycle is amplitude is estimated as 130, and the minimum is expected for 2019.
It is worth noting here that, in addition to the start of the increase of the polar field 5–6 years before the minimum, early precursors at high latitudes may be expected also on completely different grounds. The concept of the extended solar cycle implies that small ephemeral bipoles belonging to an upcoming solar cycle appear at high latitudes and start to migrate equatorward years before the first spots of the new cycle are observed. Thus, early signs of the equatorward propagating toroidal flux ring at high latitudes may give hints on the amplitude of an upcoming cycle (cf. also Badalyan et al. 2001). (From a formal point of view this would be then an internal cycle precursor, related to the one based on the Waldmeier rule.)
It is not impossible that some of the very early precursors suggested above, if real, may be partly explained by this effect. For example, Makarov and Makarova (1996) considered all faculae poleward of \(50^\circ\) latitude. Bona fide polar faculae, seen on Hinode images to be knots of the unipolar field around the poles, are limited to higher latitudes, so the wider sample may consist of a mix of such “real” polar faculae and small bipolar ephemeral active regions. These latter are known to obey an extended butterfly diagram, as confirmed by Tlatov et al. (2010): the first bipoles of the new cycle appear at higher latitudes about 4 years after the activity maximum.
In interpreting high-latitude migration patterns it should, however, be taken into account that it is not yet clear how far the wings of the butterfly diagram can actually extended backwards, i.e., to what extent a high latitude equatorward propagating branch is contiguous with the low latitude branch or is an unrelated phomenon (cf. the discussion in Cliver 2014 and Petrie et al. 2014).
The high-latitude torsional oscillation pattern is usually considered the most pregnant manifestation of the extended solar cycle. This pattern has been unusually week during Solar Cycle 24, apparently suggesting significant further weakening of solar activity (Howe et al. 2013). However, later observations (Howe et al. 2018; Komm et al. 2018) indicate that the low-latitude equatorward branch of the torsional oscillation is actually stronger in Cycle 24 than it was in Cycle 23, if measured against the same background flow.
In order to obtain a precursor that varies smoothly enough to be useful also between successive minima, Schatten and Pesnell (1993) introduced a new activity index, the “Solar Dynamo Amplitude” (SoDA) index, combining the polar field strength with a traditional activity indicator (the 10.7 cm radio flux F10.7). Around minimum, SoDA is basically proportional to the polar precursor and its value yields the prediction for F10.7 at the next maximum; however, it was constructed so that its 11-year modulation is minimized, so theoretically it should be rather stable, making predictions possible well before the minimum. It remains to be seen whether SoDA actually improves the predictive skill of the polar precursor, to which it is more or less equivalent in those late phases of the solar cycle when forecasts start to become reliable. Using the SoDA index Pesnell and Schatten (2018) predicted Cycle 25 to peak at \(R=134\pm 25\) in 2025.
2.4 Geomagnetic and interplanetary precursors
Relations between the cycle related variations of geomagnetic indices and solar activity were noted long ago. It is, however, important to realize that the overall correlation between geomagnetic indices and solar activity, even after 13-month smoothing, is generally far from perfect. This is due to the fact that the Sun can generate geomagnetic disturbances in two ways:
-
(a)
By material ejections (such as CMEs or flare particles) hitting the terrestrial magnetosphere. This effect is obviously well correlated with solar activity, with no time delay, so this contribution to geomagnetic disturbances peaks near, or a few years after, sunspot maximum. (Note that the occurrence of the largest flares and CMEs is known to peak some years after the sunspot maximum—see Fig. 16 in Hathaway 2015.)
-
(b)
By a variation of the strength of the general interplanetary magnetic field and of solar wind speed. Geomagnetic disturbances may be triggered by the alternation of the Earth’s crossing of interplanetary sector boundaries (slow solar wind regime) and its crossing of high speed solar wind streams while well within a sector. The amplitude of such disturbances will clearly be higher for stronger magnetic fields. The overall strength of the interplanetary magnetic field, in turn, depends mainly on the total flux present in coronal holes, as calculated from potential field source surface models of the coronal magnetic field. At times of low solar activity the dominant contribution to this flux comes from the two extended polar coronal holes, hence, in a simplistic formulation this interplanetary contribution may be considered linked to the polar magnetic fields of the Sun, which in turn is a plausible precursor candidate as we have seen in the previous subsection. As the polar field reverses shortly after sunspot maximum, this second contribution often introduces a characteristic secondary minimum in the cycle variation of geomagnetic indices (cf. Fig. 12, somewhere around the maximum of the curve.
Illustration of Ohl’s method in cycles 20–23. Shown is the variation of the daily geomagnetic aa index (solid black) and the monthly SSN (dotted green), both smoothed with a 13-month sliding window. Horizontal blue lines mark the value of the predictor in each cycle. Times of sunspot minima are marked by the dashed vertical lines
The component (a) of the geomagnetic variations actually follows sunspot activity with a variable time delay. Thus a geomagnetic precursor based on features of the cycle dominated by this component has relatively little practical utility. This would seem to be the case, e.g., with the forecast method first proposed by Ohl (1966), who noticed that the minimum amplitudes of the smoothed geomagnetic aa index are correlated to the amplitude of the next sunspot cycle (see also Du et al. 2009, Du 2012). This is clearly just a secondary consequence of the previously discussed correlations between solar indices at cycle minimum (occurring somewhat earlier than the minimum in aa, see Fig. 12) and the amplitude of the next maximum. While the polar precursor is more directly relevant and is available sooner, the amplitude of the aa index at minimum is still useful as a proxy as these data have been available since 1868.
An indication that the total geomagnetic activity, resulting from both mechanisms does contain useful information on the expected amplitude of the next solar cycle was given by Thompson (1993), who found that the total number of disturbed days in the geomagnetic field in cycle n is related to the sum of the amplitudes of cycles n and \(n+1\) (see also Dabas et al. 2008).
A method for separating component (b) was proposed by Feynman (1982) who correlated the annual aa index with the annual mean sunspot number and found a linear relationship between \(R\) and the minimal value of aa for years with such \(R\) values. She interpreted this linear relationship as representing the component (a) discussed above, while the amount by which aa in a given year actually exceeds the value predicted by the linear relation would be the contribution of type (b) (the “interplanetary component”). The interplanetary component usually peaks well ahead of the sunspot minimum and the amplitude of the peak seemed to be a good predictor of the next sunspot maximum. However, it is to be noted that the assumption that the “surplus” contribution to aa originates from the interplanetary component only is likely to be erroneous, especially for stronger cycles. It is known that the number of large solar eruptions shows no unique relation to \(R\): in particular, for \(R\) > 100 their frequency may vary by a factor of 3 (see Fig. 18 in Hathaway 2015), so in some years they may well yield a contribution to aa that greatly exceeds the minimum contribution. A case in point was the “Halloween events” of 2003, that very likely resulted in a large false contribution to the derived “interplanetary” aa index (Hathaway 2010). As a result, the geomagnetic precursor method based on the separation of the interplanetary component predicted an unusually strong Cycle 24 (\(R_m\sim 150\)), in contrast to most other methods, including Ohl’s method and the polar field precursor, which suggested a weaker than average cycle (\(R_m\sim 80{-}90\)).
An alternative method for the separation of the interplanetary component, based on the use of the use of the \(F_{10.7}\) index to model the variation of the activity-related component, was proposed by Pesnell (2014).
In addition to the problem of neatly separating the interplanetary contribution to geomagnetic disturbances, it is also wrong to assume that this interplanetary contribution is dominated by the effect of polar magnetic fields at all times during the cycle. Indeed, Wang and Sheeley (2009) pointed out that the interplanetary magnetic field amplitude at the Ecliptic is related to the equatorial dipole moment of the Sun that does not survive into the next cycle, so despite its more limited practical use, Ohl’s original method, based on the minima of the aa index is physically better founded, as the polar dipole dominates around the minimum. (Cf. also Ng 2016.) The total amount of open interplanetary flux, more closely linked to polar fields, could still be determined from geomagnetic activity if the interplanetary contribution to it is further split into:
-
(b1)
A contribution due to the varying solar wind speed (or to the interplanetary magnetic field strength anticorrelated with it), which in turn reflects the strength of the equatorial dipole.
-
(b2)
Another contribution due to the overall interplanetary field strength or open magnetic flux, which ultimately reflects the axial dipole.
Clearly, if the solar wind speed contribution (b1) could also be subtracted, a physically better founded prediction method should result. While in situ spacecraft measurements for the solar wind speed and the interplanetary magnetic field strength do not have the necessary time coverage, Svalgaard and Cliver (2005, 2007) and Rouillard et al. (2007) devised a method to reconstruct the variations of both variables from geomagnetic measurements alone. Building on their results, Wang and Sheeley (2009) arrived at a prediction for the maximum amplitude of solar Cycle 24 which agreed well with that of Bhatt et al. (2009), who applied a modified form of Ohl’s method. Both forecasts proved to be somewhat too high (by \(\sim \, 20\)–25%, a little over \(1\sigma\)).
The open magnetic flux can also be derived from the extrapolation of solar magnetograms using a potential field source surface model. The magnetograms applied for this purpose may be actual observations or the output from surface flux transport models, using the sunspot distribution (butterfly diagram) and the meridional flow as input. Such models indicate that the observed latitude independence of the interplanetary field strength (“split monopole” structure) is only reproduced if the source surface is far enough (\(>10\,R_\odot\)) and the potential field model is modified to take into account the heliospheric current sheet (current sheet source surface model, Schüssler and Baumann 2006; Jiang et al. 2010a). The extrapolations are generally found to agree well with in situ measurements where these are available. A comprehensive review of this topic is given in Lockwood (2013).
2.5 The quest for a precursor of the polar precursor
Just as the suggestion of a polar precursor was based on a qualitative physical understanding of the process generating the strong toroidal magnetic field that gives rise the observed active regions, an extension of the temporal range of our forecasting capability would clearly benefit from a similar qualitative physical understanding of how the strong polar fields prevalent around sunspot minimum are formed.
Magnetograph observations rather clearly indicate that the polar field is built up as a result of the the poleward transport of trailing polarity flux from active regions, while much of the leading polarity flux cancels with its counterpart on the other hemisphere by cross-equatorial diffusion. In the currently widely popular Babcock–Leighton scenario the poleward transport is interpreted as a combination of turbulent diffusion and advection by a poleward meridional flow.Footnote 17 This suggests that the buildup of the polar field may be controlled by either of two effects:
-
(a)
variations of the poleward flow speed
-
(b)
variations in the tilt angles and/or latitudinal distribution of bipolar active regions which ultimately determine the net flux imbalance in the meridional direction.
In the following subsections these two influencing factors are considered in turn.
2.5.1 Photospheric flow variations
Considering the effect of meridional flow variations on intercycle variations is a delicate task as such changes are also associated with the normal course of the solar activity cycle, the overall flow at mid-latitudes being slower before and during maxima and faster during the decay phase. Therefore, it is just the cycle-to-cycle variation in this normal pattern that may be associated with the activity variations between cycles. In this respect it is of interest to note that the poleward flow in the late phases of Cycle 23 seems to have had an excess speed relative to the previous cycle (Hathaway and Rightmire 2010). If this were a latitude-independent amplitude modulation of the flow, then most flux transport dynamo models (e.g., Belucz et al. 2015) would predict a stronger than average polar field at the minimum, contrary to observations. On the other hand, in the surface flux transport model of Wang et al. (2009) an increased poleward flow actually results in weaker polar fields, as it lets less leading polarity flux to diffuse across the equator and cancel there. As the analysis by Muñoz-Jaramillo et al. (2010) has shown, the discrepancy resulted from the form of the Babcock–Leighton source term in flux transport dynamo models, and it can be remedied by substituting a pair of opposite polarity flux rings representing each individual AR as source term instead of the \(\alpha\)-term. With this correction, 2D flux transport dynamos and surface flux transport models agree in predicting a weaker polar field for faster meridional flow.
It is known from helioseismology and magnetic correlation tracking that meridional flow speed fluctuations follow a characteristic latitudinal pattern associated with torsional oscillations and the butterfly diagram, consisting of a pair of axisymmetric bands of latitudinal flows converging towards the activity belts, migrating towards the equator, and accompanied by similar high-latitude poleward branches (Snodgrass and Dailey 1996; Chou and Dai 2001; Beck et al. 2002; Liang et al. 2018; Lin and Chou 2018). This suggests interpreting the unusual meridional flow speeds observed during Cycle 23 as an increased amplitude of this migrating modulation, rather than a change in the large-scale flow speed (Cameron and Schüssler 2010). In this case, the flows converging on the activity belts tend to inhibit the transport of following polarities to the poles, resulting in a lower polar field (Jiang et al. 2010b; note, however, that Švanda et al. 2007 find no change in the flux transport in areas with increased flows). It is interesting to note that the torsional oscillation pattern, and thus presumably the associated meridional flow modulation pattern, was shown to be fairly well reproduced by a microquenching mechanism due to magnetic flux emerging in the active belts (Petrovay and Forgács-Dajka 2002). Alternatively, the modulation pattern may also be thermally induced (Spruit 2003) or it may result from large-scale magnetic field torques (Passos et al. 2017; Hazra and Choudhuri 2017; Ruždjak et al. 2017). This suggests that stronger cycles may be associated with a stronger modulation pattern, introducing a nonlinearity into the flux transport dynamo model (Jiang et al. 2010b; Cameron and Schüssler 2012; Karak and Choudhuri 2012). The relationship between activity level and flow modulation, however, seems more complex than a simple proportionality (Komm et al. 2017). In particular, the modulation signal in the Cycle 24 activity belt seems to be too strong in comparison with the low amplitude of the sunspot cycle.
In addition to a variation in the amplitude of migrating flow modulations, their migration speed may also influence the cycle. Howe et al. (2009) pointed out that in the minimum of Cycle 24 the equatorward drift of the torsional oscillation shear belt corresponding to the active latitude of the cycle was slower than in the previous minimum. They suggested that this slowing may explain the belated start of Cycle 24.
Under the assumption that meridional flow modulations are the main factor controlling the buildup of the poloidal field from AR sources, Hung et al. (2015), Hung et al. (2017) suggest an inverse approach to derive flow variations from magnetic data. As, however, we will see in the next subsection, the validity of the underlying assumption is open to question.
In summary: while magnetically induced modulations of the meridional flow and their effect on flux transport may be a potentially important nonlinear feedback mechanism controlling intercycle activity variations, the limited observational record and the apparent complexities of the interplay have as yet not permitted their use as a precursor.
2.5.2 Active region tilts
As luck would have it, soon after the first version of this review was finished, a paper was published that prompted a flurry of activity in a completely new field. In the paper Dasi-Espuig et al. (2010) analysed sunspot group catalogues extracted from the Mt.Wilson and Kodaikanal photoheliograms for solar cycles 15–21, focusing on the distribution of tilt angles of the longitudinal axis of bipolar active regions to the azimuthal direction. Area-weighted averages of the tilt angles of sunspot groups were calculated in latitudinal bins, then normalized by the latitude to yield a tilt parameter. Two effects emerged from the analysis:
-
1.
Tilt quenching (TQ): an anticorrelation between the amplitude of a solar cycle and its mean tilt parameter.
-
2.
Tilt precursor (TP): the product of the amplitude of a sunspot cycle with its mean tilt parameter turned out to be a good predictor of the amplitude of the subsequent cycle. Muñoz-Jaramillo et al. (2013b) further demonstrated that this product is also a good predictor of the polar magnetic flux at minimum (as reconstructed from polar facular counts), suggesting that the predictive potential of this method is based on the role of tilt angles in controlling the amount of net flux transported towards the poles.
The combination of TP with a TQ relationship upon which random fluctuations in the tilt are superposed implies that intercycle variations in solar activity will be controlled by a nonlinear feedback mechanism, into which a stochastic element is incorporated. This realization prompted intense activity in the development of model-based cycle prediction, to be discussed in the following section.
Ironically, in parallel with the major impact of the Dasi-Espuig et al. (2010) paper on theoretical work, it was soon subjected to criticism on observational grounds. Ivanov (2012) repeated the analysis, now including the Pulkovo sunspot group catalogue (covering a shorter period, cycles 18–21). The TQ effect in the Mt.Wilson data set was found to depend crucially on the low value of the mean tilt for the anomalous strong cycle 19. In the Kodaikanal data the effect appeared more robustly but it still seems to depend on high tilt values in cycles 15 and 16, for which the Mt.Wilson set yields lower values. The Pulkovo data are consistent with the Kodaikanal series but they only start with Cycle 18, so no definitive conclusion was drawn from them.
In their hemispherically separated analysis of the Mt.Wilson data McClintock and Norton (2013) found that in Cycle 19 a strong suppression of the tilt was only present in the Southern hemisphere. Accordingly, the TQ effect is only seen in the South.
Kitchatinov and Olemskoy (2011) analysed the Pulkovo data set, focusing on the TP effect. Instead of considering average tilts, they evaluated the area-weighted latitude difference between leading and trailing subgroups and averaged this quantity for each cycle in their data set. While data were available for 3 cycles only, they confirmed the good correlation between this predictor and a measure (the dipole–octupole index) of the amplitude of the polar magnetic field in the next minimum.
A fourth tilt database was compiled by Baranyi (2015) based on the Debrecen sunspot catalogues, while a fifth set of tilts was measured by Işık et al. (2018) from solar drawings made at Kandilli Observatory for cycles 19–24. Overall, the results for these cycles seem to compare well for the Kodaikanal, Pulkovo, Debrecen and Kandilli data, but as cycles 15 and 16 are only covered by the Kodaikanal data, it is no surprise that the TQ effect is not clearly seen in the shorter Debrecen and Kandilli data sets.
All the previously considered data sets were based on sunspot positions alone, without magnetic polarity information. Tilts of active regions taking into account the magnetic polarities of spots were determined by Li and Ulrich (2012) from Mt.Wilson and MDI magnetograms. McClintock et al. (2014) compared these measurements with the Debrecen tilt data, focusing on anti-Hale regions which are the major reason for the discrepancies. The occurrence rate of anti-Hale regions was found to be 8.5%. Tilts of active regions taking into account the magnetic polarities of spots were recently also determined by Tlatova et al. (2018) from the archive of solar drawings at Mt.Wilson Observatory: these drawings include polarity information since 1917. Their results concerning cycle dependence of tilts are inconclusive.
In summary, the suspected tilt quenching and tilt precursor effects have opened new directions in sunspot cycle forecasting, but the evidence is still controversial, especially for TQ. These inconclusive results underline the importance of obtaining more data and, especially, longer data sets. Contributions towards this goal like that of Senthamizh Pavai et al. (2015), who determined tilts for cycles 7–10 from sunspot drawings by Schwabe, are therefore highly valuable and may be key for a later clarification of these issues.
In view of the doubts regarding the reality of TQ, attention has recently started to turn towards alternatives. One such alternative, proposed by J. Jiang, might be latitude quenching: the mean latitude of active regions in a given cycle was found to be positively correlated with cycle amplitudes (Jiang et al. 2011a). From higher latitudes a lower fraction of leading flux will manage to diffuse across the equator, leaving less trailing flux to contribute to the polar fields. Therefore, the correlation found represents a negative feedback effect—hence the name latitude quenching.
2.5.3 Alternatives to tilt quenching: inflows and latitude quenching
In view of the doubts regarding the reality of TQ, attention has recently started to turn towards alternatives.
The tilts of active regions are usually attributed to the effect of Coriolis force on the rising magnetic flux loops (Schmidt 1968; D’Silva and Choudhuri 1993; Fisher et al. 1995; Pevtsov et al. 2014;). The tilt angle varies inversely with the initial field strength, making the suggested tilt quenching effect quite plausible: stronger toroidal fields should simply come with weaker tilt. (Note that the tilt also depends on the entropy of the rising loop: a cycle-dependent variation in thermal properties of the layer where toroidal flux is stored may therefore also explain TQ, as shown by Işık 2015.)
An alternative explanation for tilt quenching was put forward by Jiang et al. (2010b) and Cameron and Schüssler (2012) who pointed out that the meridional inflows directed towards the activity belts, discussed in Sect. 2.5.1 will tend to reduce the AR tilts.
On the other hand, the activity-related meridional flow pattern may partly originate from the superposition of more localized circular inflows towards individual active regions (Haber et al. 2004; Švanda et al. 2008; Löptien et al. 2017). It is unclear whether such concentric flows can exert a torque on the flux loops that may reduce their tilt; however this may not even be necessary: simulations by Martin-Belda and Cameron (2017) suggested that the hindering effect on the inflows on the separation of leading and trailing polarity fluxes is sufficient to significantly reduce the amplitude of the dipolar seed field being built up for the next cycle. This inflow effect might then even completely substitute TQ as the main nonlinearity mechanism controlling intercycle variations
Another alternative to TQ, proposed by J. Jiang, might be latitude quenching: the mean latitude of active regions in a given cycle was found to be positively correlated with cycle amplitudes (Jiang et al. 2011a). From higher latitudes a lower fraction of leading flux will manage to diffuse across the equator, leaving less trailing flux to contribute to the polar fields. Therefore, the correlation found represents a negative feedback effect—hence the name latitude quenching.
3 Model-based predictions
3.1 Surface flux transport models
Surface flux transport (SFT) models describe the transport of magnetic flux across the solar surface, modelling it as an advective-diffusive transport:
where \(\theta\) and \(\phi\) are colatitude and longitude, B is the radial component of the magnetic flux density, \(\eta\) is the turbulent magnetic diffusivity, \(v\) is the speed of the meridional flow, and \(\varOmega (\theta )\) is the differential rotation profile.
Equation (14) can be interpreted as the radial component of the induction equation where the neglected radial terms have been replaced by the source term S describing flux emergence and the heuristic decay term \(B/\tau\), supposed to represent vertical diffusion. The latter term is only occasionally used, to improve agreement with observations.
SFT models were first developed in the 1980s for the interpretation of the then newly available synoptic magnetogram record. This “age of enlightenment”, to use the expression of Sheeley’s (2005) historical review, was followed by less intense activity in the field until, from about 2010, a renaissance of SFT modelling ensued. The revival was prompted by the increasing acceptance of the polar precursor as the most reliable physical precursor technique: SFT models offered a way to “predict the predictor”, promising to increase the temporal scope of forecasts.
For detailed discussions of the advance made in SFT modelling we refer the reader to the reviews by Jiang et al. (2014b) and Wang (2017). Here we only present brief highlights of the main results from the past decade.
3.1.1 Parameter optimization
For an application of the method, the parameters in Eq. (14) such as \(\eta\), \(v(\theta )\) or \(\tau\) need to be specified. This problem has reopened the issue of parameter optimization (Lemerle et al. 2015; Virtanen et al. 2017; Whitbread et al. 2017). Choosing the right parameters is a nontrivial task as the outcome depends on the data used for calibration and on the choice of the merit function for the optimization.
Recently Petrovay and Talafha (2019) presented the results of a large-scale systematic study of the parameter space in an SFT model where the source term representing the net effect of tilted flux emergence was chosen to represent a typical, average solar cycle as described by observations, comparing the results with observational constraints on the spatiotemporal variation of the polar magnetic field. It was found that without a significant decay term in the SFT equation (i.e., for \(\tau >10\) years) the global dipole moment reverses too late in the cycle for all flow profiles and parameters, providing independent supporting evidence for the need of a decay term, even in the case of identical cycles. An allowed domain is found to exist for \(\tau\) values in the 5–10 years range for all flow profiles considered. Generally higher values of \(\eta\) (500–800) are preferred though some solutions with lower \(\eta\) are still allowed.
3.1.2 Nonlinear feedback effects
Nonlinear feedback mechanisms such as TQ (Cameron et al. 2010), a variable modulation of the meridional flow in the form of inflow belts flanking the active latitudes (Jiang et al. 2010b, Cameron and Schüssler 2012), concentric inflows around individual AR (Martin-Belda and Cameron 2016, 2017) or latitude quenching (Jiang et al. 2011b) have been considered in many studies. With the right parameterization, feedback was found to allow magnetic field reversals even when a stronger cycle is followed by a considerably weaker cycle. [A difficulty in obtaining reversal in such situations was a main motivation for the introduction of the decay term in Eq. (14).]
It is a curious circumstance that TQ currently has stronger support from models than from observations. Indeed, Cameron et al. (2010) found that a combination of TQ with an SFT model results in polar field strengths that approximately correctly predict the amplitude of the next cycle for Cycles 15/16–21/22. The same holds also if the TQ results in the model as a consequence of meridional inflow belts (Cameron and Schüssler 2012).
3.1.3 Extending the polar precursor
Sunspot observations are available for several centuries, while proxy indicators of the polar field strength start from the late nineteenth century only. Using sunspot records to reconstruct the source term in SFT models, the polar field may also be reconstructed for cycles where no polar field proxies are known. Such a programme was carried out by Jiang et al. (2011a) who reconstructed the butterfly diagram from the sunspot number record for the period since 1700; properties of the butterfly “wings” were correlated with the amplitudes and lengths of solar cycles based on the GPR sunspot catalogue, then these correlations were used for reconstruction in earlier times. In a subsequent work (Jiang et al. 2011b), the same authors used this butterfly diagram as a source in an SFT model to determine polar fields. The derived polar field values were found to correlate rather well with the amplitude of the subsequent cycle, thereby extending the period of time for which we have evidence for the polar precursor.
A deficiency of the source reconstruction based on sunspot catalogues is the lack of information on magnetic polarities and on the distribution of weaker plage fields. A promising new method based on the use of Ca ii K synoptic maps combined with available sunspot magnetic field measurements was recently successfully tested by Virtanen et al. (2019).
3.1.4 The importance of fluctuations: rogue active regions
The nonlinear feedback effects discussed above define an essentially deterministic mechanism of intercycle variations. While on the level of the spatiotemporal distribution of individual active regions there may be numerous different realizations of a sunspot cycle with a given sunspot number profile, one might expect that the variation of at least the statistical average taken over all realizations can be reliably predicted.
Starting from 2013, however, it was gradually realized that the behaviour of an individual realization (like the real Sun) can strongly deviate from the statistical expectations. The magnetic flux of the largest ARs in a solar cycle is comparable to the flux in the polar caps where the polar magnetic field is concentrated around the minimum. The amplitude of the polar field built up during a cycle is therefore highly sensitive to the exact balance of leading vs. trailing polarity flux transported to the poles and cancelled by cross-equator diffusion. Major plumes on the observational magnetic butterfly diagram were identified by Cameron et al. (2013) as originating from large cross-equatorial AR where cancellation between the two polarities is minimal due to their advection in opposite directions by the meridional flow diverging on the equator. Such cross-equatorial plumes were incorporated into an SFT model by Cameron et al. (2014).
The role of random scatter in active region properties was further investigated by Jiang et al. (2014a) who showed that the dipole contribution of a single active region drops quite fast with heliographic latitudes. For those low-latitude active regions with an unusually large contribution to the global dipole Nagy et al. (2017a) introduced the name “rogue” AR. Representing an active region as a simple bipole with tilt angle \(\alpha\) relative to the azimuthal direction, it is straightforward to show from Eq. (12) that its contribution to the axial dipole is
where F is the magnetic flux and d is the angular separation of the two polarities. Large values of F, d and/or \(\alpha\) are therefore conditions for a significant “dynamo effectivity” of an AR, i.e., a significant contribution to the polar field built up in the cycle. However, Eq. (15) only gives the initial contribution to the dipole moment. For AR further from the equator cross-equatorial cancellation of the leading polarity will be less efficient, fluxes of both polarities will be largely transferred to the pole and their net effect will mostly cancel: this is the reason why the final dipole contributions and therefore the dynamo effectivity of AR also drops quite fast with heliographic latitude.
3.1.5 Explaining the end of the modern maximum
Beside the general investigations discussed, a special objective of SFT modelling efforts was to correctly “hindcast” the unusually weak polar fields in the minimum of Cycle 24 that brought the Modern Maximum to an end. Initial efforts (Yeates 2014; Upton and Hathaway 2014a) encountered difficulties in reproducing the polar field, until Jiang et al. (2015) were finally able to correctly reproduce the evolution of the polar field by incorporating in their source term individual observed active regions (modelled as idealized bipoles, but with tilt values, fluxes and separations derived from observations). After carefully excluding recurrent ARs from the source term they found that the chief responsibility for the deviation of the polar flux from its expected value lies with a low number of large low-latitude rogue AR with non-Hale or non-Joy orientations.
In a similar research Upton and Hathaway (2014b) focused on the predictability of the evolution of the axial dipole moment. From some selected instant onwards, they substitute actual ARs with the ARs of another solar cycle of similar amplitude, and they find that the dipole evolution can be well predicted over \(\sim \, 3\) years. It should be noted, however, that this study does not cover the period 2003–2006 which seems to have been crucial in the development of an anomalously low dipole moment at the end of Cycle 23. Predictability was also considered by Whitbread et al. (2018) who addressed the issue how many AR need to be taken into account to reproduce the dipole moment at the end of a cycle. Ordering active regions by decreasing dipole moment contribution they found that, despite the fact that the polar magnetic flux is comparable to the flux a single large AR, the dipole moment at the end of a cycle cannot be reproduced without accounting for the net contribution from hundreds of active regions during the cycle.
The tilt of active regions is a manifestation of the writhe of the underlying flux loop, and writhe is one form of helicity (cf. Petrovay et al. 2006), while nonzero helicity is a condition for free magnetic energy available for eruptions. On this ground Petrovay and Nagy (2018) tentatively suggested that there may be a large overlap between rogue AR and flare/CME-productive AR. A relevant study was recently undertaken by Jiang et al. (2019) who found that flare productivity and dynamo effectivity of ARs are governed by different parameters. Flare productivity primarily depends on the structural complexity of ARs, large flares being much more common \(\delta\)-spots, while the dipole moment contribution of an AR, which ultimately determines its effect on the dynamo, is determined by the latitudinal separation of polarities. So while there is indeed a large overlap between the flare-productive ARs and “rogue” or exceptional ARs, the two characteristics do not necessarily go hand in hand.
3.1.6 Forecasting Cycle 25
The buildup of the polar dipole moment during the ongoing Cycle 24 has been followed with keen attention. Researchers analysed a number of important episodes (e.g., Petrie and Ettinger 2017). Yeates et al. (2015) examined the origin of a prominent poleward surge in the magnetic butterfly diagram in 2010–11 by a combination of analysis of observational data and SFT simulations, concluding that the episode is not expected to have a major imact of the dipole buildup. Sun et al. (2015) presented an observational analysis of the polar reversal process in Cycle 24. This is of particular interest owing to the ill-defined nature of polarity reversal in the N hemisphere: the field strength here lingered around zero for well over two years until it finally started to increase towards the end of 2014. (It may be worth noting that this was correctly predicted in the SFT simulation of Upton and Hathaway 2014b.) As a result, the phase shift between the hemispheres has changed sign: while activity peaked first on the N hemisphere in the last few cycles, indications are that in Cycle 25 activity will first peak in the South (cf. also Labonville et al. 2019). The phase shift was the consequence of a few surges of opposite polarity that hindered the growth of flux in the N polar region.
Going further than focusing on selected events, a number of researchers attempted to predict Cycle 25 by incorporationg all ARs of Cycle 24 in the source term of an SFT simulation and modelling further evolution under some more or less plausible assumptions.
Allowing a random scatter in AR tilts and also in the time-dependent meridional flow Hathaway and Upton (2016) and Upton and Hathaway (2018) arrived at a prediction similar to or marginally lower than Cycle 24. A similar conclusion (Cycle 25 somewhat weaker than Cycle 24) was reached by Iijima et al. (2017) who, based on the plateau-like nature of the dipole moment maximum discussed in Sect. 2.3 above, assume no further contributions to the dipole moment.
Considering 50 different random realizations drawn from a statistical ensemble of ARs Cameron et al. (2016) predict that Cycle 25 will be similar or slightly stronger than Cycle 24. In a similar later study with improved technical details Jiang et al. (2018) arrived at the prediction that Cycle 25 will peak in the range 93 to 159 (see also Jiang and Cao 2018).
3.2 The solar dynamo: a brief summary of current models
While attempts to predict future solar cycles on the basis of the empirical sunspot number record have a century-old history, predictions based on physical models of solar activity only started one solar cycle ago. The background of this new trend is, however, not some significant improvement in our understanding of the solar dynamo. Rather, it is the availability of increasingly fast new computers that made it possible to fine-tune the parameters of certain dynamo models to reproduce the available sunspot record to a good degree of accuracy and to apply data assimilation methods (such as those used in terrestrial weather prediction) to these models. This is not without perils. On the one hand, the capability of multiparametric models to fit a multitude of observational data does not prove the conceptual correctness of the underlying model. On the other hand, in chaotic or stochastic systems such as the solar dynamo, fitting a model to existing data will not lead to a good prediction beyond a certain time span, the extent of which can only be objectively assessed by “postdiction” tests, i.e., checking the models predictive skill by trying to “predict” previous solar cycles and comparing those predictions to available data. Apparently successful postdiction tests have led some groups to claim a breakthrough in solar cycle prediction owing to the model-based approach (Dikpati and Gilman 2006; Kitiashvili and Kosovichev 2008). Yet, as we will see in the following discussion, a closer inspection of these claims raises many questions regarding the role that the reliance on a particular physical dynamo model plays in the success of their predictions.
Extensive summaries of the current standing of solar dynamo theory are given in the reviews by Petrovay (2000), Ossendrijver (2003), Solanki et al. (2006), Charbonneau (2010) and Cameron et al. (2017). As explained in detail in those reviews, all current models claiming to acceptably represent the solar dynamo are based on the mean-field theory approach wherein a coupled system of partial differential equations governs the evolution of the toroidal and poloidal components of the large-scale magnetic field. Until recently, the large-scale field was assumed to be axially symmetric in practically all models. In some nonlinear models the averaged equation of motion, governing large-scale flows is also coupled into the system.
In the simplest case of homogeneous and isotropic turbulence, where the scale l of turbulence is small compared to the scale L of the mean variables (scale separation hypothesis), the dynamo equations have the form
Here \({\mathbf {B}}\) and \({\mathbf {U}}\) are the large-scale mean magnetic field and flow speed, respectively; \(\eta _T\) is the magnetic diffusivity (dominated by the turbulent contribution for the highly conductive solar plasma), while \(\alpha\) is a parameter related to the non-mirror symmetric character of the magnetized plasma flow.
In the case of axial symmetry the mean flow \({\mathbf {U}}\) may be split into a meridional circulation \({\mathbf {U}}_c\) and a differential rotation characterized by the angular velocity profile \(\varOmega _0(r,\theta )\):
where r, \(\theta\), \(\phi\) are spherical coordinates and \({\mathbf {e}}_\phi\) is the azimuthal unit vector. Now introducing the shear
assuming \(\alpha \ll \varOmega L\) and ignoring spatial derivatives of \(\alpha\) and \(\eta _T\), Eq. (16) simplifies to the pair
where B and A are the toroidal (azimuthal) components of the magnetic field and of the vector potential, respectively, and \(\frac{\partial A}{\partial x}\) is to be evaluated in the direction \(90^{\circ }\) clockwards of \(\mathbf {\varOmega }\) (along the isorotation surface) in the meridional plane. These are the classic \(\alpha \varOmega\) dynamo equations, including a meridional flow.
In the more mainstream solar dynamo models the strong toroidal field is now generally thought to reside near the bottom of the solar convective zone. Indeed, it is known that a variety of flux transport mechanisms such as pumping (Petrovay 1994) remove magnetic flux from the solar convective zone on a timescale short compared to the solar cycle. Following earlier simpler numerical experiments, MHD numerical simulations have indeed demonstrated this pumping of large scale magnetic flux from the convective zone into the tachocline below, where it forms strong coherent toroidal fields (Browning et al. 2006; Fan and Fang 2014; Warnecke et al. 2018). As this layer is also where rotational shear is maximal, it is plausible that the strong toroidal fields are not just stored but also generated here, by the winding up of poloidal field.Footnote 18 The two main groups of dynamo models, interface dynamos and flux transport dynamos, differ mainly in their assumptions about the site and mechanism of the \(\alpha\)-effect responsible for the generation of a new poloidal field from the toroidal field.
In interface dynamos \(\alpha\) is assumed to be concentrated near the bottom of the convective zone, in a region adjacent to the tachocline, so that the dynamo operates as a wave propagating along the interface between these two layers. While these models may be roughly consistent and convincing from the physical point of view, they have only had limited success in reproducing the observed characteristics of the solar cycle, such as the butterfly diagram.
Flux transport dynamos, in contrast, rely on the Babcock–Leighton mechanism for \(\alpha\), arising due to the action of the Coriolis force on emerging flux loops, and they assume that the corresponding \(\alpha\)-effect is concentrated near the surface. They keep this surface layer incommunicado with the tachocline by introducing some arbitrary unphysical assumptions (such as very low diffusivities in the bulk of the convective zone). The poloidal fields generated by this surface \(\alpha\)-effect are then advected to the poles and there down to the tachocline by the meridional circulation—which, accordingly, has key importance in these models. The equatorward deep return flow of the meridional circulation is assumed to have a significant overlap with the tachocline (another controversial point), and it keeps transporting the toroidal field generated by the rotational shear towards the equator. By the time it reaches lower latitudes, it is amplified sufficiently for the flux emergence process to start, resulting in the formation of active regions and, as a result of the Babcock–Leighton mechanism, in the reconstruction of a poloidal field near the surface with a polarity opposed to that in the previous 11-year cycle. While flux transport models may be questionable from the point of view of their physical consistency, they can be readily fine-tuned to reproduce the observed butterfly diagram quite well. This ready adaptability made flux transport dynamos hugely popular in the research community (Charbonneau 2007; Karak et al. 2014). In flux transport dynamos the \(\alpha\) term is usually nonlocal (generating poloidal field at the surface out of toroidal field at the bottom of the convective zone).
It should be noted that while the terms “interface dynamo” and “flux transport dynamo” are now very widely used to describe the two main approaches, the more generic terms “advection-dominated” and “diffusion-dominated” would be preferable in several respects. This classification allows for a continuous spectrum of models depending on the numerical ratio of advective and diffusive timescales (for communication between surface and tachocline). In addition, even at the two extremes, classic interface dynamos and circulation-driven dynamos are just particular examples of advection or diffusion dominated systems with different geometrical structures.
3.3 Is model-based cycle prediction feasible?
As it can be seen even from the very brief and sketchy presentation given above, all current solar dynamo models are based on a number of quite arbitrary assumptions and depend on a number of free parameters, the functional form and amplitude of which is far from being well constrained. For this reason, Bushby and Tobias (2007) rightfully say that all current solar dynamo models are only of “an illustrative nature”. This would suggest that as far as solar cycle prediction is concerned, the best we should expect from dynamo models is also an “illustrative” reproduction of a series of solar cycles with the same kind of long-term variations (qualitatively and, in the statistical sense, quantitatively) as seen in solar data. Indeed, Bushby and Tobias (2007) demonstrated that even a minuscule stochastic variation in the parameters of a particular flux transport model can lead to large, unpredictable variations in the cycle amplitudes. And even in the absence of stochastic effects, the chaotic nature of nonlinear dynamo solutions seriously limits the possibilities of prediction, as the authors find in a particular interface dynamo model: even if the very same model is used to reproduce the results of one particular run, the impossibility of setting initial conditions exactly representing the system implies that predictions are impossible even for the next cycle. Somewhat better results are achieved by an alternative method, based on the phase space reconstruction of the attractor of the nonlinear system—this is, however, a purely empirical time series analysis technique for which no knowledge of the detailed underlying physics is needed. (Cf. Sect. 4.3 above.)
Despite these very legitimate doubts regarding the feasibility of model-based prediction of solar cycles, in recent years several groups have claimed to be able to predict upcoming solar cycles on the basis of dynamo models with a high confidence. So let us consider these claims.
3.4 Explicit models
3.4.1 Axisymmetric models
The first attempt at model-based solar cycle prediction was the work of the solar dynamo group in Boulder (Dikpati et al. 2006; Dikpati and Gilman 2006). Their model is a flux transport dynamo, advection-dominated to the extreme. The strong suppression of diffusive effects is assured by the very low value (less than 20 \({\hbox {km}}^2/{\hbox {s}}\)) assumed for the turbulent magnetic diffusivity in the bulk of the convective zone. As a result, the poloidal fields generated near the surface by the Babcock–Leighton mechanism are only transported to the tachocline on the very long, decadal time scale of meridional circulation. The strong toroidal flux residing in the low-latitude tachocline, producing solar activity in a given cycle is thus the product of the shear amplification of poloidal fields formed near the surface about 2–3 solar cycles earlier, i.e., the model has a “memory” extending to several cycles. The mechanism responsible for cycle-to-cycle variation is assumed to be the stochastic nature of the flux emergence process. In order to represent this variability realistically, the model drops the surface \(\alpha\)-term completely (a separate, smaller \(\alpha\) term is retained in the tachocline); instead, the generation of poloidal field near the surface is represented by a source term, the amplitude of which is based on the sunspot record, while its detailed functional form remains fixed.
Dikpati and Gilman (2006) found that, starting off their calculation by fixing the source term amplitudes of sunspot cycles 12 to 15, they could predict the amplitudes of each subsequent cycle with a reasonable accuracy, provided that the relation between the relative sunspot numbers and the toroidal flux in the tachocline is linear, and that the observed amplitudes of all previous cycles are incorporated in the source term for the prediction of any given cycle. For Cycle 24 the model predicted peak smoothed annual relative sunspot numbers of 150 (v1) or more. Elaborating on their model, they proceeded to apply it separately to the northern and southern hemispheres, to find that the model can also be used to correctly forecast the hemispheric asymmetry of solar activity (Dikpati et al. 2007).
Even though, ultimately, the prediction proved to be off by about a factor of 2, the extraordinary claims of this pioneering research prompted a hot debate in the dynamo community. Besides the more general, fundamental doubt regarding the feasibility of model-based predictions (see Sect. 4.2 above), more technical concerns arose. In order to understand the origin of the predictive skill of the Boulder model, Cameron and Schüssler (2007) studied a version of the model simplified to an axially symmetric SFT model, wherein only the equation for the radial field component is solved as a function of time and latitude. The equation includes a source term similar to the one used in the Boulder model. As the toroidal flux does not figure in this simple model, the authors use the cross-equatorial flux \(\varPhi\) (the amount of magnetic flux crossing the equator in a given time) as a proxy, arguing that this may be more closely linked to the amplitude of the toroidal field in the upcoming cycle than the polar field. They find that \(\varPhi\) indeed correlates quite well (correlation coefficients \(r\sim 0.8--0.9\), depending on model details) with the amplitude of the next cycle, as long as the form of the latitude dependence of the source term is prescribed and only its amplitude is modulated with the observed sunspot number series (“idealized model”). But surprisingly, the predictive skill of the model is completely lost if the prescribed form of the source function is dropped and the actually observed latitude distribution of sunspots is used instead (“realistic model”). Cameron and Schüssler (2007) interpreted this by pointing out that \(\varPhi\) is mainly determined by the amount of very low latitude flux emergence, which in turn occurs mainly in the last few years of the cycle in the idealized model, while it has a wider temporal distribution in the realistic model. The conclusion is that the root of the apparently good predictive skill of the truncated model (and, by inference, of the Boulder model it is purported to represent) is actually just the good empirical correlation between late-phase activity and the amplitude of the next cycle, discussed in Sect. 2.1 above. This correlation is implicitly “imported” into the idealized flux transport model by assuming that the late-phase activity is concentrated at low latitudes, and therefore gives rise to cross-equatorial flux which then serves as a seed for the toroidal field in the next cycle. So if Cameron and Schüssler (2007) are correct, the predictive skill of the Boulder model is due to an empirical precursor and is thus ultimately explained by the good old Waldmeier effect (cf. Sect. 1.4.3) In view of the fact that no version of the Boulder model with a modified source function incorporating the realistic latitudinal distribution of sunspots in each cycle was ever presented, this explanation seems to be correct, despite the fact that the effective diffusivity represented by the sink term in the reduced model is significantly higher than in the Boulder model, and consequently, the reduced model will have a more limited memory, cf. Yeates et al. (2008).
Another flux transport dynamo code, the Surya code, originally developed by A. Choudhuri and coworkers in Bangalore, has also been utilized for prediction purposes. The crucial difference between the two models is in the value of the turbulent diffusivity assumed in the convective zone: in the Bangalore model this value is 240 \({\hbox {km}}^2/{\hbox {s}}\), 1–2 orders of magnitude higher than in the Boulder model, and within the physically plausible range (Chatterjee et al. 2004). As a result of the shorter diffusive timescale, the model has a shorter memory, not exceeding one solar cycle. As a consequence of this relatively rapid diffusive communication between surface and tachocline, the poloidal fields forming near the surface at low latitudes due to the Babcock–Leighton mechanism diffuse down to the tachocline in about the same time as they reach the poles due to the advection by the meridional circulation. In these models, then, polar magnetic fields are not a true physical precursor of the low-latitude toroidal flux, and their correlation is just due to their common source. In the version of the code adapted for cycle prediction (Choudhuri et al. 2007; Jiang et al. 2007), the “surface” poloidal field (i.e., the poloidal field throughout the outer half of the convection zone) is rescaled at each minimum by a factor reflecting the observed amplitude of the Sun’s dipole field. The model showed reasonable predictive skill for the last three cycles for which data are available, and could even tackle hemispheric asymmetry (Goel and Choudhuri 2009). For Cycle 24, the predicted amplitude was 30–35% lower than Cycle 23.
In retrospect, these first attempts at model-based solar cycle prediction are now generally seen as precursor methods in disguise. Cameron and Schüssler (2007) convincingly argued that the apparent predictive (postdictive) skill of the Boulder model was related to the “minimax” family of internal precursors, based on the Waldmeier law combined with the overlap of consecutive cycles (see Sect. 2.1). The predictive skill of the Surya model, on the other hand, is based on the polar precursor: essentially, the polar field amplitude at minimum is set to its observed value, and the model simply mechanically winds up the poloidal field into a toroidal field, ensuring a proportionality.
A more sophisticated approach to dynamo based predictions was spurred by the realization of the importance of nonlinearities like TQ and stochastic effects in SFT models. In particular, the significance of the effect of individual active regions in the buildup of poloidal fields gave an impetus to the development of non-axisymmetric models where individual AR can be treated. Nevertheless, Kitchatinov et al. (2018) recently constructed an axisymmetric flux transport dynamo where stochastic effects were still retained as fluctuations of the \(\alpha\) parameter. It was found that with a correlation time on the order of a month the model is able to mimick the effects of rogue AR such as intercycle variations and even the triggering of grand minima, as in the model of Nagy et al. (2017a).
3.4.2 Nonaxisymmetric models
The first dynamo model to explicitly deal with individual AR was constructed by Yeates and Muñoz-Jaramillo (2013). Emerging flux loops in this model were created by imposed upflows with properties calibrated to reproduce observed AR characteristics. Another 3D code capable of dealing with individual AR, the STABLE code was developed in Boulder (Miesch and Dikpati 2014; Miesch and Teweldebirhan 2016).
The third such code is the \(2\times 2\)D code of the Montreal group (Lemerle et al. 2015; Lemerle and Charbonneau 2017). This latter code ingenuously combines an axially symmetric flux transport dynamo code with a 2D SFT code. The dynamo code couples to the SFT code by an emergence function specifying the locations and properties of the randomly created bipolar source regions for the SFT, based on the distribution of the toroidal field. The azimuthally averaged magnetic field resulting from the SFT component, in turn, provides the upper boundary condition for the flux transport model. The model is computationally highly efficient, optimizable, and it was carefully calibrated to reproduce the observed statistics of active regions in Cycle 21. It can be run for hundreds or thousands of cycles, thereby providing a data base for analysis that far exceeds the observational record of solar cycles. While the model’s behaviour also displays some differences relative to the real Sun (esp. in the phase relationship of the poloidal and toroidal fields), intercycle variations comparable to those seen in the real Sun are displayed by the solutions, including Dalton-like minima and grand minima (Lemerle and Charbonneau 2017; Nagy et al. 2017a).
Investigations in close analogy with this were also undertaken using the STABLE model. Karak and Miesch (2017) considered the effect of tilt quenching and tilt scatter, and found that the scatter can be a main factor behind long-term activity variations, while even a subtle tilt quenching effect is sufficient to limit the growth of the dynamo. Karak and Miesch (2018) found that fluctuations in AR tilt can be responsible for both the onset of and recovery from grand minima. While these results are in general agreement with those obtained with other codes, in another work based on the STABLE model Hazra et al. (2017) reported that the dynamo effectivity of individual ARs increases with heliographic latitude, in contradiction to other results and to expectations based on the importance of cross-equatorial diffusion for the removal of leading polarity flux. It may be that diffusion of weak magnetic flux through the surface might be responsible for these results—an effect that, by construction, is avoided in the \(2\times 2\)D model and which can also be suppressed by introducing downwards pumping of the magnetic field (Karak and Cameron 2016).
Model ensemble predictions from the \(2\times 2\)D dynamo model, driven by observational data up to November 2017, after Labonville et al. (2019). The time variation of the total magnetic flux in the Northern (top) and Southern (bottom) hemisphere are shown in units of \(10^{21}\) Mx
These nonaxisymmetric dynamo models have now reached a level where actual physics-based prediction is within reach. A new generation of dynamo-based cycle predictions is heralded by the work of Labonville et al. (2019) who used data assimilation in the \(2\times 2\)D to arrive to a state closely mimicking the current state of the solar dynamo, then run the code further to see its future development. Repeating these runs with many different random realizations of the AR emergences the authors generated an ensemble of future solar dynamo models (Fig. 13). This enabled them to give both a mean forecast and to attribute meaningful errors to their forecast. They predicted a peak R value of \(89^{+29}_{-14}\) for cycle 25, the maximum occurring in \(2025.3^{+0.89}_{-1.05}\). The forecast is also broken down to hemispheres: activity in the North is predicted to peak 6 months later but at a 20% higher level than in the South.
3.5 Truncated models
The “illustrative” nature of current solar dynamo models is nowhere more clearly on display than in truncated or reduced models where some or all of the detailed spatial structure of the system is completely disregarded, and only temporal variations are explicitly considered. This is sometimes rationalised as a truncation or spatial integration of the equations of a more realistic inhomogenous system; in other cases, no such rationalisation is provided, representing the solar dynamo by an infinite, homogeneous or periodic turbulent medium where the amplitude of the periodic large-scale magnetic field varies with time only.
In the present subsection we deal with models that do keep one spatial variable (typically, the latitude), so growing wave solutions are still possible—these models, then, are still dynamos even though their spatial structure is not in a good correspondence with that of the solar dynamo.
This approach in fact goes back to the classic migratory dynamo model of Parker (1955) who radially truncated (i.e., integrated) his equations to simplify the problem. Parker seems to have been the first to employ a heuristic relaxation term of the form \(-B_r/\tau _d\) in the poloidal field equation to represent the effect of radial diffusion; here, \(\tau _d=d^2/\eta _T\) is the diffusive timescale across the thickness d of the convective zone. His model was generalized by Moss et al. (2008) and Usoskin et al. (2009b) to the case when the \(\alpha\)-effect includes an additive stochastic noise, and nonlinear saturation of the dynamo is achieved by \(\alpha\)-quenching. These authors do not make an attempt to predict solar activity with their model but they can reasonably well reproduce some features of the very long term solar activity record, as seen from cosmogenic isotope studies.
The other classic reduced dynamo model is that of Leighton (1969), the first mathematical formulation of the flux transport dynamo concept. An updated version of this dynamo, recently developed by Cameron and Schüssler (2017a) is a very promising, simple and versatile tool to reproduce many of the observed features of the solar dynamo with simple parameterizations. While it has not yet been utilized for cycle prediction, it has already proved to be useful in understanding long-term activity variations such as the dominant periods in hemispheric asymmetry (Schüssler and Cameron 2018).
Another radially truncated model, this time formulated in a Cartesian system, is that of Kitiashvili and Kosovichev (2009). In this model stochastic effects are not considered and, in addition to using an \(\alpha\)-quenching recipe, further nonlinearity is introduced by coupling in the Kleeorin–Ruzmaikin equation (Zeldovich et al. 1984) governing the evolution of magnetic helicity, which in the hydromagnetic case contributes to \(\alpha\). Converting the toroidal field strength to relative sunspot number using the Bracewell transform, Eq. (3), the solutions reproduce the asymmetric profile of the sunspot number cycle. For sufficiently high dynamo numbers the solutions become chaotic, cycle amplitudes show an irregular variation. Cycle amplitudes and minimum–maximum time delays are found to be related in a way reminiscent of the Waldmeier relation.
Building on these results, Kitiashvili and Kosovichev (2008) attempted to predict solar cycles using a data assimilation method. The approach used was the so-called Ensemble Kalman Filter method. Applying the model for a “postdiction” of the last 8 solar cycles yielded astonishingly good results, considering the truncated and arbitrary nature of the model and the fundamental obstacles in the way of reliable prediction discussed above. The question may arise whether the actual physics of the model considered has any significant role in this prediction, or we are dealing with something like the phase space reconstruction approach discussed in Sect. 4.3 where basically any model with an attractor that looks reasonably similar to that of the actual solar dynamo would do. Either way, the method is remarkable. Its prediction for Cycle 24 essentially proved to be correct. An early prediction for Cycle 25 (Kitiashvili 2016) yielded a maximum occurring in 2023/24 at a level \(R=90\pm 15\) (v2 values), with the cycle starting in 2019/20. It is noteworthy that a forecast considering observational data up to the previous minimum (2008) already yielded quite similar results for the amplitude, although the timing of the maximum would have been expected earlier. Understanding the origin of this impressive apparent predictive skill certainly deserves more in-depth research.
3.6 The Sun as an oscillator
An even more radical simplification of the solar dynamo problem ignores any spatial dependence in the solutions completely, concentrating on the time dependence only. Spatial derivatives appearing in Eqs. (17) and (18) are estimated as \(\nabla \sim 1/L\) and the resulting terms \(U_c/L\) and \(\eta _T/L^2\) as \(1/\tau\) where \(\tau\) is a characteristic time scale. This results in the pair
which can be combined to yield
where \(D=\alpha \varOmega \tau ^2/L\) is the dynamo number. For \(D<1\), Eq. (21) clearly describes a damped linear oscillator. For \(D>1\), solutions have a non-oscillatory character. The system described by Eq. (21), then, is not only not a true dynamo (missing the spatial dependence) but it does not even display growing oscillatory solutions that would be the closest counterpart of dynamo-like behaviour in such a system. Nevertheless, there are a number of ways to extend the oscillator model to allow for persistent oscillatory solutions, i.e., to turn it into a relaxation oscillator:
-
1.
The most straightforward approach is to add a forcing term \(+\sin (\omega _0t)\) to the r.h.s. of Eq. (21). Damping would cause the system to relax to the driving period \(2\pi /\omega _0\) if there were no stochastic disturbances to this equilibrium. Hiremath (2006) fitted the parameters of the forced and damped oscillator model to each observed solar cycle individually; then in a later work (Hiremath 2008) he applied linear regression to the resulting series to provide a forecast (see Sect. 4.1 above).
-
2.
Another trick is to account for the \(\pi /2\) phase difference between poloidal and toroidal field components in a dynamo wave by introducing a phase factor i into the first term on the r.h.s. of Eq. (20). This can also be given a more formal derivation as equations of this form result from the substitution of solutions of the form \(A\propto e^{ikx}\), \(B\propto e^{i(kx+\pi /2)}\) into the 1D dynamo equations. This route, combined with a nonlinearity due to magnetic modulation of differential rotation described by a coupled third equation, was taken by Weiss et al. (1984). Their model displayed chaotic behaviour with intermittent episodes of low activity similar to grand minima. The generic normal form model recently introduced by Cameron and Schüssler (2017b) is also loosely related to this approach.
-
3.
Wilmot-Smith et al. (2006) showed that another case where dynamo-like behaviour can be found in an equation like (21) is if the missing effects of finite communication time between parts of a spatially extended system are reintroduced by using a time delay \(\varDelta t\), evaluating the first term on the r.h.s. at time \(t-\varDelta t\) to get the value for the l.h.s. at time t. This time-delay approach has been further developed by Hazra et al. (2014) and Turner and Ladde (2018).
-
4.
Yet another possibility is to introduce a nonlinearity into the model by assuming \(D=D_0[1-f(B)]\) where \(f(B=0)=0\) and \(f\ge 0\) everywhere. (Note that any arbitrary form of \(\alpha\)- or \(\varOmega\)-quenching can be cast in the above form by series expansion.) The governing equation then becomes one of a nonlinear oscillator:
$$\begin{aligned} \ddot{B}=\frac{D_0-1}{\tau ^2} B -\frac{2}{\tau }\dot{B}-\frac{D_0-1}{\tau ^2} B f(B). \end{aligned}$$(22)
In the most commonly assumed quenching mechanisms the leading term in f(B) is quadratic; in this case Eq. (22) describes a Duffing oscillator (Kanamaru 2008). For large positive dynamo numbers, \(D_0\gg 1\), then, the large nonlinear term dominates for high values of B, its negative sign imposing oscillatory behaviour; yet the origin is a repeller so the oscillation will never be damped out. The Duffing oscillator was first considered in the solar context by Paluš and Novotná (1999).
More generally, a complete spatial truncation of the nonlinear \(\alpha \varOmega\) dynamo equations with a dimensional analysis of some of the terms (see review by Lopes et al. 2014) can be shown to give rise to a nonlinear oscillator equation of the form
where B is the amplitude of the toroidal magnetic field, and the parameters \(\mu\), \(\xi\) and \(\gamma\) may be expressed by the dynamo parameters (dynamo number, meridional flow amplitude, nonlinearity parameters). This is a combination of the van der Pol and Duffing oscillators, the two most widely studied nonlinear oscillator problems. Under certain conditions on the parameters, it is reduced to a van der Pol oscillator (Adomian 1989; Mininni et al. 2001; Kanamaru 2007):
with \(\mu >0\). From this form it is evident that the problem is equivalent to that of an oscillator with a damping that increases with amplitude; in fact, for small amplitudes the damping is negative, i.e., the oscillation is self-excited.
These simple nonlinear oscillators were among the first physical systems where chaotic behaviour was detected (when a periodic forcing was added). Yet, curiously, they first emerged in the solar context precisely as an alternative to chaotic behaviour. Considering the mapping of the solar cycle in the differential phase space \(\{B, dB/dt\}\), Mininni et al. (2000) got the impression that, rather than showing signs of a strange attractor, the SSN series is adequately modelled by a van der Pol oscillator with stochastic fluctuations. This concept was further developed by Lopes and Passos (2009) who fitted the parameters of the oscillator to each individual sunspot cycle. Subsequently, this parameter fitting was also exploited for cycle prediction purposes (Passos 2012). The parameter \(\mu\) is related to the meridional flow speed and the fit indicates that a slower meridional flow may have been responsible for the Dalton minimum. This was also corroborated in an explicit dynamo model (the Surya code) —however, as we discussed in Sect. 2.5.1, this result of flux transport dynamo models is spurious and the actual effect of a slower meridional flow is likely to be opposite to that suggested by the van der Pol oscillator model.
In an alternative approach to the problem, Nagovitsyn (1997) attempted to constrain the properties of the solar oscillator from its amplitude–frequency diagram, suggesting a Duffing oscillator driven at two secular periods. While his empirical reconstruction of the amplitude–frequency plot may be subject to many uncertainties, the basic idea is certainly noteworthy.
A further twist to the oscillator representation of the solar cycle is to consider a system of two coupled nonlinear oscillators (Kuramoto model). This approach has been taken in a series of papers by Blanter et al. (2014; 2016). The two variables were taken to represent the sunspot numbers and the geomagnetic aa index, considered to be proxies for the toriodal and poloidal field amplitudes, respectively. In a later work (Blanter et al. 2017) a coupled oscillator model was employed to account for the time variation of hemispheric asymmetries of solar activity, as known from observations (Norton and Gallagher 2010; Norton et al. 2014).
In summary: despite its simplicity, the oscillator representation of the solar cycle is a relatively new development in dynamo theory, and its obvious potential for forecasting purposes is yet to be fully exploited.
4 Extrapolation methods
In contrast to precursor methods, extrapolation methods only use the time series of sunspot numbers (or whichever solar activity indicator is considered) but they generally rely on more than one previous point to identify trends that can be used to extrapolate the data into the future. They are therefore also known as time series analysis or, for historic reasons, regression methods.
A cornerstone of time series analysis is the assumption that the time series is homogeneous, i.e., the mathematical regularities underlying its variations are the same at any point of time. This implies that a forecast for, say, three years ahead has equal chance of success in the rising or decaying phase of the sunspot cycle, across the maximum or, in particular, across the minimum. In this case, distinguishing intracycle and intercycle memory effects, as we did in Sects. 1.4.2 and 2, would be meaningless. This concept of solar activity variations as a continuous process stands in contrast to that underlying precursor methods, where solar cycles are thought of as individual units lasting essentially from minimum to minimum, correlations within a cycle being considerably stronger than from one cycle to the next. While, as we have seen, there is significant empirical evidence for the latter view, the possibility of time homogeneity cannot be discarded out of hand. Firstly, if we consider the time series of global parameters (e.g., amplitudes) of cycles, homogeneity may indeed be assumed fairly safely. This approach has rarely been used for the directly observed solar cycles as their number is probably too low for meaningful inferences—but the long data sets from cosmogenic radionuclides are excellent candidates for time series analysis.
In addition, there may be good reasons to consider the option of homogeneity of solar activity data even on the scale of the solar cycle. Indeed, in dynamo models the solar magnetic field simply oscillates between (weak) poloidal and (strong) toroidal configuration: there is nothing inherently special about either of the two, i.e., there is no a priori reason to attribute a special significance to solar minimum. While at first glance the butterfly diagram suggests that starting a new cycle at the minimum is the only meaningful way to do it, there may be equally good arguments for starting a new cycle at the time of polar reversal. And even though SFT and dynamo models strongly suggest that spatial information regarding, e.g., the latitudinal distributions of sunspots may well be essential for cycle prediction, some studies point to a possibility to reconstruct this spatial information from time series alone (Jiang et al. 2011a; Mandal et al. 2017). There is, therefore, plenty of motivation to try and apply standard methods of time series analysis to sunspot data.
Indeed, as the sunspot number series is a uniquely homogeneous and long data set, collected over centuries and generated in what has long been perceived to be a fairly carefully controlled manner, it has become a favorite testbed of time series analysis methods and is routinely used in textbooks and monographs for illustration purposes (Udny Yule 1927; Box and Jenkins 2008; Wei 2005; Tong 1993). This section will summarize the various approaches, proceeding, by and large, from the simplest towards the most complex.
4.1 Linear regression
Linear (auto)regression means representing the value of a time series at time t by a linear combination of values at times \(t-\varDelta t\), \(t-2\varDelta t, \ldots , t-p\varDelta t\). Admitting some random error \(\epsilon _n\), the value of \(R\) in point n is
where p is the order of the autoregression and the \(c_i\)’s are weight parameters. A further twist on the model admits a propagation of errors from the previous q points:
This is known as the ARMA (AutoRegressive Moving Average) model.
Linear regression techniques have been widely used for solar activity prediction during the course of an ongoing cycle. Their application for cycle-to-cycle prediction has been less common and successful (Lomb and Andersen 1980; Box and Jenkins 2008; Wei 2005).
Brajša et al. (2009) applied an ARMA model to the series of annual values of \(R\). A successful fit was found for \(p=6\), \(q=6\). Using this fit, the next solar maximum was predicted to take place around 2012.0 with an amplitude \(90 \pm 27\), and the following minimum occurring in 2017.
Instead of applying an autoregression model directly to SSN data, Hiremath (2008) applied it to a forced and damped harmonic oscillator model claimed to well represent the SSN series. This resulted in a predicted amplitude of \(110 \pm 10\) for Solar Cycle 24, with the cycle starting in mid-2008 and lasting 9.34 years.
4.2 Spectral methods
...the use of any mathematical algorithm to derive hidden periodicities from the data always entails the question as to whether the resulting cycles are not introduced either by the particular numerical method used or by the time interval analyzed.
(de Meyer 1981)
Spectral analysis of the sunspot number record is used for prediction under the assumption that the main reason of variability in the solar cycle is a long-term modulation due to one or more periods.
The usual approach to the problem is the purely formal one of representing the sunspot record with the superposition of eigenfunctions forming an orthogonal basis. From a technical point of view, spectral methods are a complicated form of linear regression. The analysis can be performed by any of the widely used means of harmonic analysis:
-
1.
Least squares (LS) frequency analysis (sometimes called “Lomb–Scargle periodogram”) consists in finding by trial and error the best fitting sine curve to the data using the least squares method, subtracting it (“prewhitening”), then repeating the procedure until the residuals become indistinguishable from white noise. The first serious attempt at sunspot cycle prediction, due to Kimura (1913), belonged to this group. The analysis resulted in a large number of peaks with dubious physical significance. The prediction given for the upcoming Cycle 15 failed, the forecasted amplitude being \(\sim\) 60 while the cycle actually peaked at 105 (SSN v1 values). However, it is interesting to note that Kimura correctly predicted the long term strengthening of solar activity during the first half of the twentieth century! LS frequency analysis on sunspot data was also performed by Lomb and Andersen (1980), with similar results for the spectrum.
-
2.
Fourier analysis is probably the most commonly used method of spectral decomposition in science. It has been applied to sunspot data from the beginning of the twentieth century (Turner 1913c, b; Michelson 1913). Vitinsky (1973) judges Fourier-based forecasts even less reliable than LS periodogram methods. Indeed, for instance Cole (1973) predicted Cycle 21 to have a peak amplitude of 60, while the real value proved to be nearly twice that.
-
3.
The maximum entropy method (MEM) relies on the Wiener–Khinchin theorem that the power spectrum is the Fourier transform of the autocorrelation function. Calculating the autocorrelation of a time series for \(M\ll N\) points and extrapolating it further in time in a particular way to ensure maximal entropy can yield a spectrum that extends to arbitrarily low frequencies despite the shortness of the data segment considered, and also has the property of being able to reproduce sharp spectral features (if such are present in the data in the first place). A good description of the method is given by Ables (1974), accompanied with some propaganda for it—see Press et al. (1992) for a more balanced account of its pros and cons. The use of MEM for sunspot number prediction was pioneered by Currie (1973). Using maximum entropy method combined with multiple regression analysis (MRA) to estimate the amplitudes and phases, Kane (2007) arrived at a prediction of 80 to 101 for the maximum amplitude of Cycle 24 (v1 values). It should be noted that the same method yielded a prediction (Kane 1999) for Cycle 23 that was far off the mark.
-
4.
Singular spectrum analysis (SSA) is a relatively novel method for the orthogonal decomposition of a time series. While in the methods discussed above the base was fixed (the trigonometric functions), SSA allows for the identification of a set of othogonal eigenfunctions that are most suitable for the problem. This is done by a principal component analysis of the covariance matrix \(r_{ik}=\langle R_i R_{i+k}\rangle\). SSA was first applied to the sunspot record by Rangarajan (1998) who only used this method for pre-filtering before the application of MEM. Loskutov et al. (2001) who also give a good description of the method, already made a prediction for Cycle 24: a peak amplitude of 117 (v1 value).The forecast was later corrected slightly downwards to 106 (Kuzanyan et al. 2008).
The dismal performance of spectral predictions with the methods (1)–(3) indicates that the sunpot number series cannot be well represented by the superposition of a limited number of fixed periodic components. Instead,
-
the periods may be time dependent,
-
the system may be quasiperiodic, with a significant finite width of the periodic peaks (esp. the 11-year peak),
-
there may be non-periodic (i.e., chaotic or stochastic) components in the behaviour of the system, manifested as a continuous background in the spectrum.
In practice, all three effects suggested above may play some part. The first mentioned effect, time dependence, may in fact be studied within the framework of spectral analysis. MEM and SSA are intrinsically capable of detecting or representing time dependence in the spectrum, while LS and Fourier analysis can study time dependence by sliding an appropriate data window across the period covered by observations. If the window is Gaussian with a width proportional to the frequency we arrive at the popular wavelet analysis. This method was applied to the sunspot number series by Ochadlick et al. (1993), Vigouroux and Delachie (1994), Frick et al. (1997), Fligge et al. (1999), and Li et al. (2005) who could confirm the existence and slight variation of the 11-year cycle and the Gleissberg-cycle. Recently, Kolláth and Oláh (2009) called attention to a variety of other generalized time dependent spectral analysis methods, of which the pseudo-Wigner transform yields especially clear details (see Fig. 15). The time varying character of the basic periods makes it difficult to use these results for prediction purposes but they are able to shed some light on the variation as well as the presistent or intermittent nature of the periods determining solar activity.
In summary, it is fair to say that forecasts based on harmonic analysis are notoriously unreliable. The secular variation of the basic periods, obeying as yet unknown rules, would render harmonic analysis practically useless for the prediction of solar cycles even if solar activity could indeed be described by a superposition of periodic functions. Although they may be potentially useful for very long term prediction (on centennial scales)Footnote 19, when it comes to cycle-to-cycle forecasts the best we can hope from spectral studies is apparently an indirect contribution, by constraining dynamo models with the inambiguously detected periodicities.
In what remains from this subsection, we briefly review what these apparently physically real periods are and what impact they may have on solar cycle prediction.
4.2.1 The 11-year cycle and its harmonics
As an example of the period spectrum obtained by these methods, in Fig. 14 we present the FFT based power spectrum estimate of the smoothed sunspot number record. Three main features are immediately noticed:
-
The dominant 11-year peak, with its sidelobes and its 5.5-year harmonic.
-
The 22-year subharmonic, representing the even–odd rule.
-
The significant power present at periods longer than 50 years, associated with the Gleissberg cycle.
The dominant peak in the power spectrum is at \(\sim\) 11 years. Significant power is also present at the first harmonic of this period, at 5.5 years. This is hardly surprising as the sunspot number cycles, as presented in Fig. 3, have a markedly asymmetrical profile. It is a characteristic of Fourier decomposition that in any periodic series of cycles where the profiles of individual cycles are non-sinusoidal, all harmonics of the base period will appear in the spectrum.
Indeed, were it not for the 13-month smoothing, higher harmonics could also be expected to appear in the power spectrum. It has been proposed (Krivova and Solanki 2002) that these harmonics are detected in the sunspot record and that they may be related to the periodicities of \(\sim\) 1.3 years intermittently observed in solar wind speed (Richardson et al. 1994; Paularena et al. 1995; Szabo et al. 1995; Mursula and Zieger 2000; Lockwood 2001) and in the internal rotation velocity of the Sun (Howe 2009, Sect. 10.1). An analoguous intermittent 2.5 year variation in the solar neutrino flux (Shirai 2004) may also belong to this group of phenomena. It may be worth noting that, from the other end of the period spectrum, the 154-day Rieger period in solar flare occurrence (Rieger et al. 1984; Bai and Cliver 1990) has also been tentatively linked to the 1.3-year periodicity. Unusually strong excitation of such high harmonics of the Schwabe cycle may possibly be explained by excitation due to unstable Rossby waves in the tachocline (Zaqarashvili et al. 2010).
The 11-year peak in the power spectrum has substantial width, related to the rather wide variation in cycle lengths in the range 9–13 years. Yet Fig. 14 seems to suggest the presence of a well detached second peak in the spectrum at a period of \(\sim\) 14 years. The presence of a distinct peak at the first harmonic and even at the subharmonic of this period seems to support its reality. Indeed, peaks at around 14 and 7 years were already found by other researchers (e.g., Kimura 1913; Currie 1973) who suggested that these may be real secondary periods of sunspot activity.
The situation is, however, more prosaic. Constraining the time interval considered to data more recent than 1850, from which time the sunspot number series is considered to be more reliable, the 14.5-year secondary peak and its harmonics completely disappear. On the other hand, the power spectrum for the years 1783–1835 indicates that the appearance of the 14.5-year secondary peak in the complete series is almost entirely due to the strong predominance of this period (and its harmonic) in that interval. This interval covers the unusually long Cycle 4 and the Dalton minimum, consisting of three consecutive unusually weak cycles, when the “normal” 11-year mode of operation was completely suppressed.
As pointed out by Petrovay (2010a), this probably does not imply that the Sun was operating in a different mode during the Dalton minimum, the cycle length being 14.5 years instead of the usual 11 years. Instead, the effect may be explained by the well known inverse correlation between cycle length and amplitude, which in turn is the consequence of the strong inverse correlation between rise rate and cycle amplitude (Waldmeier effect), combined with a much weaker or nonexistent correlation between decay rate and amplitude (see Sect. 1.4.3). The cycles around the Dalton minimum, then, seem to lie at the low amplitude (or long period) end of a continuum representing the well known cycle length–amplitude relation, ultimately explained by the Waldmeier effect.
Pseudo-Wigner power distribution in the sunspot number record, with time on the abscissa and frequency on the ordinate. The three horizontal bands of high power correspond, from bottom to top, to the Gleissberg cycle, the 11-year cycle and its first harmonic. The sunspot number curve is shown on top for guidance (figure courtesy of Z. Kolláth)
A major consequence of this is that the detailed distribution of peaks varies significantly depending on the interval of time considered. Indeed, Kolláth and Oláh (2009) recently applied time dependent harmonic analysis to the sunspot number series and found that the dominant periods have shown systematic secular changes during the past 300 years (Fig. 15). For instance, the basic period seems to have shortened from 11 years to 10 years between 1850 and 1950, with some moderate increase in the last 50 years. (This is consistent with the known anticorrelation between cycle length and amplitude, cf. Sect. 1.4.3.)
4.2.2 The even–odd (a.k.a. Gnevyshev–Ohl) rule
A cursory look at Fig. 3 shows that solar cycles often follow an alternating pattern of higher and lower maxima. In this apparent pattern, already noticed by the early observers (e.g, Turner 1913a), odd cycles have been typically stronger than even cycles in the last two centuries.
This even–odd rule can be given two interpretations: a “weak” one of a general tendency of alternation between even and odd cycles in amplitude, or a “strong” one of a specific numerical relation between the amplitudes of consecutive cycles.
Let us first consider the rule in its weak interpretation. At first sight the rule admits many exceptions, but the amplitude of solar cycles depends on the particular measuring method used. Exceptions from the even–odd alternation rule become less common if a long term trend (calculated by applying a 12221 or 121 filter, see Sect. 1.4.1) is subtracted from the data (Charbonneau 2001), or if integrated cycle amplitudes (sums of annual mean sunspot numbers during the cycle) are used (Gnevyshev and Ohl 1948).
In fact, as evident from, e.g., the work of Mursula et al. (2001) where cycle amplitudes are based on group sunspot numbers and the amplitude of a cycle is defined as the sum of the annual GSN value over the course of the cycle, the odd–even alternation may be considered as strictly valid with only four exceptions:
-
In the pairs 7–8 and 17–18, odd cycles are followed by stronger even cycles at the end of Dalton minimum and at the beginning of the Modern Maximum. These exceptions could be made to disappear by the subtraction of the long term trend as suggested by Charbonneau (2001).
-
The pair 22–23 represents another apparent break of the weak even–odd rule which is not easily explained away, even though the relative difference is smaller if the Kislovodsk sunspot number series is used (Nagovitsyn et al. 2009). The possibility is obviously there that the subtraction of the long term trend may resolve the problem but we have no way to tell in the near future.
-
Prior to Cycle 5, the phase of the alternation was opposite, even cycles being stronger than odd cycles. As Cycle 4 is known to have been anomalously long anyway (the so-called “phase catastrophe” in the solar cycle, Vitinsky et al. 1986) and its decaying phase is not well covered by observations (Vaquero 2007), this gave rise to the suggestion of a “lost solar cycle” between cycles 4 and 5 (Usoskin et al. 2001). This cycle, however, would have been even more anomalous than cycle 4 and despite intensive searches in historic data the evidence is still not quite conclusive (Krivova et al. 2002; see, however, Usoskin et al. 2009a).
The issue whether the even–odd rule can go through phase jumps or not is important with respect to its possible origin. One plausible possibility is that the alternation is due to the superposition of a steady primordial magnetic field component on the oscillatory magnetic field generated by the dynamo (Levy and Boyer 1982). In this case, any phase jump in the Gnevyshev–Ohl rule should imply a phase jump in Hale’s polarity rules, too. Alternatively, persistent even–odd alternation may also arise in nonlinear dynamos as a period–2 limit cycle (Durney 2000); with a stochastic forcing occasional phase jumps are also possible (Charbonneau 2001; Charbonneau et al. 2007).
While we have no information on this from the eighteenth century phase jump, we can be certain that there was no such phase jump in polarities in the last two decades, even though the even–odd rule seems to have been broken again. It will be interesting to see when (and if) the even–odd rule settles in again, whether it will have done so with a phase jump or not. For instance, if Cycle 25 will again exceed Cycle 24 it would seem that no phase jump occurred and both theoretical options are still open. But if Cycle 25 will represent a further weakening from Cycle 24, followed by a stronger Cycle 26, a phase jump will have occurred, which may exclude the primordial field origin of the rule if Hale’s polarity rules remain unchanged.
Let us now discuss the stronger interpretation of the even–odd rule. In the first quantitative study of the relative amplitudes of consecutive cycles, Gnevyshev and Ohl (1948) found a rather tight correlation between the time integrated amplitudes of even and subsequent odd cycles, while the correlation between odd cycles and subsequent even cycles was found to be much less strong. This gave rise to the notion that solar cycles come in “two-packs” as even–odd pairs. Nagovitsyn et al. (2009) confirmed this puzzling finding on the basis of data covering the whole period of telescopic observations (and renumbering cycles before 1790 in accordance with the lost cycle hypothesis); they also argue that cycle pair 22–23 does not deviate strongly from the even–odd correlation curve so it should not be considered a “real” exception to the even–odd rule. Javaraiah (2012) analyzed the validity of the rule considering large and small sunspot groups separately, and found that while for large groups the rule holds with a few exceptions, for small groups a ‘reverse G-O rule’ holds where odd numbered cycles are consistently stronger than the preceding, rather than the following even numbered cycle.
Shortly after its formulation by Gnevyshev and Ohl (1948), the (strong) even–odd rule was used by Kopecký (1950) to successfully predict the unusually strong Cycle 19. This made this rule quite popular for forecast purposes. However, forecasts based on the even–odd rule completely failed for Cycle 23, overpredicting the amplitude by > 50% (see review by Li et al. 2001). Taken together with the implausibility of the suggested two-pack system, this shows that it is probably wiser to take the position that “extraordinary claims need extraordinary evidence”—which is yet to be provided in the case of the “strong” even–odd rule.
Finally, in the context of the even–odd rule, it is also worth mentioning the three-cycle regularity proposed by Ahluwalia (1998). Even though the evidence presented for the alleged triadic pattern is not overwhelming, this method resulted in one of the few successful predictions for the amplitude of Cycle 23.
4.2.3 The Gleissberg cycle
Besides the changes in the length of the 11-year cycle related to the amplitude–cycle length correlation, even more significant are the variations in the period of the so-called Gleissberg cycle (Gleissberg 1939). This “cycle”, corresponding to the 60–120 year “plateau” in Fig. 14 was actually first noticed by Wolf, who placed it in the range 55–80 years (see Richard 2004 for a discussion of the history of the studies of the Gleissberg cycle). Researchers in the middle of the twentieth century characterized it as an 80–100 year variation. Figure 15 explains why so widely differing periods were found in different studies: the period has in fact shown a secular increase in the past 300 years, from about 50 years in the early eighteenth century, to a current value exceeding 140 years. This increased length of the Gleissberg cycle also agrees with the results of Forgács-Dajka and Borkovits (2007).
The detection of \(\sim\) 100 year periods in a data set of 300 years is of course always questionable, especially if the period is even claimed to be varying. However, the very clear and, most importantly, nearly linear secular trend seen in Fig. 15 argues convincingly for the reality of the period in question. This clear appearance of the period is due to the carefully optimized choice of the kernel function in the time–frequency analysis, a method resulting in a so-called pseudo-Wigner distribution (PWD). In addition, in their study Kolláth and Oláh (2009) presented a conscientious test of the reliability of their methods, effectively proving that the most salient features in their PWD are not artefacts. (The method was subsequently also applied to stellar activity, Oláh et al. 2009.) This is the most compelling evidence for the reality of the Gleissberg cycle since 1750 yet presented. Further evidence was more recently presented by Le Mouël et al. (2017) using singular spectrum analysis.
4.2.4 Supersecular cycles
For the 210-year Suess (known also as de Vries) cycle, McCracken and Beer (2008) presented further evidence for the temporally intermittent nature of this marked peak in the spectrum of solar proxies. The Suess cycle seems to have a role in regulating the recurrence rate of grand minima. Grand minima, in turn, only seem to occur during \(<1\) kiloyear intervals (“Spörer events”) around the minima of the \(\sim\) 2400-year Hallstatt cycle.
For further discussion of long term variations in solar activity we refer the reader to the reviews by Beer et al. (2006) and Usoskin (2017).
4.3 Nonlinear methods
...every complicated question has a simple answer which is wrong. Analyzing a time series with a nonlinear approach is definitely a complicated problem. Simple answers have been repeatedly offered in the literature, quoting numerical values for attractor dimensions for any conceivable system.
(Hegger et al. 1999)
The nonlinearities in the dynamo equations readily give rise to chaotic behaviour of the solutions. The long term behaviour of solar activity, with phenomena like grand minima and grand maxima, is also suggestive of a chaotic system. While chaotic systems are inherently unpredictable on long enough time scales, their deterministic nature does admit forecast within a limited range. It is therefore natural to explore this possibility from the point of view of solar cycle prediction.
4.3.1 Attractor analysis and phase space reconstruction: the pros ...
Assuming that the previous \((M-1)\) values of the sunspot number do in some way determine the current expected value, our problem becomes restricted to an M-dimensional phase space, the dimensions being the current value and the \((M-1)\) previous values. With a time series of length N, we have \(N-M+1\) points fixed in the phase space, consecutive points being connected by a line. This phase space trajectory is a sampling of the attractor of the physical system underlying the solar cycle (with some random noise added to it). The attractor represents a mapping in phase space which maps each point into the one the system occupies in the next time step: if this mapping is known to a good degree of precision, it can be used to extend the trajectory towards the future.
For the mapping to be known, M needs to be high enough to avoid self-crossings in the phase space trajectory (otherwise the mapping is not unique) but low enough so that the trajectory still yields a good sampling of the attractor. The lowest integer dimension satisfying these conditions is the embedding dimension D of the attractor (which may have a fractal dimension itself).
Once the attractor has been identified, its mathematical description may be done in three ways.
-
1.
Parametric fitting of the attractor mapping in phase space. The simplest method is the piecewise linear fit suggested by Farmer and Sidorowich (1987) and applied in several solar prediction attempts, e.g., Kurths and Ruzmaikin (1990). Using a method belonging to this group, Kilcik et al. (2009) gave a correct prediction for Cycle 24. Alternatively, a global nonlinear fit can also be used: this is the method applied by Serre and Nesme-Ribes (2000) as the first step in their global flow reconstruction (GFR) approach.
-
2.
Nonparametric fitting. The simplest nonparametric fit is to find the closest known attractor point to ours (in the \((M-1)\)-dimensional subspace excluding the last value) and then using this for a prediction, as done by Jensen (1993). (This resulted in so large random forecast errors that it is practically unsuitable for prediction.) A more refined approach is simplex projection analysis, recently applied by Singh and Bhargawa (2017) for the problem of solar cycle prediction. (See also Sarp et al. 2018.) A most remarkable extension of these methods was presented by Covas (2017) who, instead of focusing on the time series of SSN only, considered the problem of extending the whole spatiotemporal data set of sunspot positions (butterfly diagram) into the future. Neural networks, discussed in more detail in Sect. 4.3.4 below, are a much more sophisticated nonparametric fitting device. (3) Indirectly, one may try to find a set of differential equations describing a system that gives rise to an attractor with properties similar to the observed. In this case there is no guarantee that the derived equations will be unique, as an alternative, completely different set may also give rise to a very similar attractor. This arbitrariness of the choice is not necessarily a problem from the point of view of prediction as it is only the mapping (the attractor structure) that matters. Such phase space reconstruction by a set of governing equations was performed, e.g., by Serre and Nesme-Ribes (2000) or Aguirre et al. (2008). On the other hand, instead of putting up with any arbitrary set of equations correctly reproducing the phase space, one might make an effort to find a set with a structure reasonably similar to the dynamo equations so they can be given a meaningful physical interpretation. Methods following this latter approach were discussed in Sects. 3.5 and 3.6.
4.3.2 ...the cons ...
Finding the embedding dimension and the attractor structure is not a trivial task, as shown by the widely diverging results different researchers arrived at. One way to find the correct embedding dimension is the false nearest neighbours method (Kennel et al. 1992), essentially designed to identify self-crossings in the phase space trajectory, in which case the dimension M needs to be increased. But self-crossings are to some extent inevitable, due to the stochastic component superimposed on the deterministic skeleton of the system.
As a result, the determination of the minimal necessary embedding dimension is usually done indirectly. One indirect method fairly popular in the solar community is the approach proposed by Sugihara and May (1990) where the correct dimension is basically figured out on the basis of how successfully the model, fit to the first part of the data set, can “predict” the second part (using a piecewise linear mapping).
Another widely used approach, due to Grassberger and Procaccia (1983), starts by determining the correlation dimension of the attractor, by simply counting how the number of neighbours in an embedding space of dimension \(M\gg 1\) increases with the distance from a point. If the attractor is a lower dimensional manifold in the embedding space and it is sufficiently densely sampled by our data then the logarithmic steepness d of this function should be constant over a considerable stretch of the curve: this is the correlation dimension d. Now, we can increase M gradually and see at what value d saturates: that value determines the attractor dimension, while the value of M where saturation is reached yields the embedding dimension.
The first nonlinear time series studies of solar activity indicators suggested a time series spacing of 2–5 years, an attractor dimension \(\sim\) 2–3 and an embedding dimension of 3–4 (Kurths and Ruzmaikin 1990; Gizzatullina et al. 1990). Other researchers, however, were unable to confirm these results, either reporting very different values or not finding any evidence for a low dimensional attractor at all (Calvo et al. 1995; Price et al. 1992; Carbonell et al. 1994; Kilcik et al. 2009; Hanslmeier and Brajša 2010). In particular, I would like to call attention to the paper by Jensen (1993), which, according to ADS and WoS, has received a grand total of zero citations up to 2010, yet it displays an exemplary no-nonsense approach to the problem of sunspot number prediction by nonlinear time series methods. Unlike so many other researchers, the author of that paper does not enforce a linear fit on the logarithmic correlation integral curve (his Fig. 4); instead, he demonstrates on a simple example that the actual curve can be perfectly well reproduced by a simple stochastic process.
These contradictory results obviously do not imply that the mechanism generating solar activity is not chaotic. For a reliable determination a long time series is desirable to ensure a sufficiently large number of neighbours in a phase space volume small enough compared to the global scale of the attractor. Solar data sets (even the cosmogenic radionuclide proxies extending over millennia but providing only a decadal sampling) are typically too short and sparse for this. In addition, clearly distinguishing between the phase space fingerprints of chaotic and stochastic processes is an unsolved problem of nonlinear dynamics which is not unique to solar physics. A number of methods have been suggested to identify chaos unambiguously in a time series but none of them has been generally accepted and this topic is currently a subject of ongoing research—see, e.g., the work of Freitas et al. (2009) which demonstrates that the method of “noise titration”, somewhat akin to the Sugihara–May algorithm, is uncapable of distinguishing superimposed coloured noise from intrinsically chaotic systems.
4.3.3 ...and the upshot
Starting from the 1980s, many researchers jumped on the chaos bandwagon, applying nonlinear time series methods designed for the study of chaotic systems to a wide variety of empirical data, including solar activity parameters. From the 1990s, however, especially after the publication of the influential book by Kantz and Schreiber (1997), it was increasingly realized that the applicability of these nonlinear algorithms does not in itself prove the predominantly chaotic nature of the system considered. In particular, stochastic noise superposed on a simple, regular, deterministic skeleton can also give rise to phase space characteristics that are hard to tell from low dimensional chaos, especially if strong smoothing is applied to the data. As a result, the pendulum has swung in the opposite direction and currently the prevailing view is that there is no clear cut evidence for chaos in solar activity data (Panchev and Tsekov 2007).
One might take the position that any forecast based on attractor analysis is only as good as the underlying assumption of a chaotic system is: if that assumption is unverifiable from the data, prediction attempts are pointless. This, however, is probably a too hasty judgment. The potentially most useful product of phase space reconstruction attempts is the inferences they allow regarding the nature of the underlying physical system (chaotic or not), even offering a chance to constrain the form of the dynamo equations relevant for the Sun. As discussed in the previous section, such truncated models may be used for forecast directly, or alternatively, the insight they yield into the mechanisms of the dynamo may be used to construct more sophisticated dynamo models.
4.3.4 Neural networks
Neural networks are algorithms built up from a large number of small interconnected units (“neurons” or “threshold logic units”), each of which is only capable of performing a simple nonlinear operation on an input signal, essentially described by a step function or its generalized (rounded) version, a sigmoid function. To identify the optimal values of thresholds and weights parameterizing the sigmoid functions of each neuron, an algorithm called “back propagation rule” is employed which minimizes (with or without human guidance) the error between the predicted and observed values in a process called “training” of the network. Once the network has been correctly trained, it is capable of further predictions.
The point is that any arbitrary multidimensional nonlinear mapping may be approximated by a combination of stepfunctions to a good degree—so, as mentioned in Sect. 4.3.1 above, the neural network can be used to find the nonlinear mapping corresponding to the attractor of the given time series.
More detailed introductions to the method are given by Blais and Mertz (2001), Conway (1998), and by Calvo et al. (1995); the latter authors were also the first to apply a neural network for sunspot number prediction. Unfortunately, despite their claim of being able to “predict” (i.e., postdict) some earlier cycles correctly, their prediction for Cycle 23 was off by a wide margin (predicted peak amplitude of 166 [v1] as opposed to 121 observed). One of the neural network forecasts for Cycle 24 (Maris and Oncica 2006) was equally far off, while another one (Uwamahoro et al. 2009) yielded a more conservative value. A prediction for Cycle 25 based on a version of the neural networks approach was given by Attia et al. (2013), resulting in a cycle amplitude slightly below that of cycle 24.
5 Summary evaluation
The performance of various forecast methods in Cycles 21–23 was discussed by Li et al. (2001) and Kane (2001). Predictions for Cycle 24 were presented in Petrovay (2010b) (Table 1), Pesnell (2008) and Pesnell (2012); the experiences gained in this cycle were discussed in Pesnell (2016).
Precursor methods generally stand out with their internally consistent forecasts which for Cycles 21 and 22 proved to be correct. For Cycle 23, these methods were still internally consistent in their prediction, mostly scattering in a narrow range betweenFootnote 20 150 and 170; however, the cycle amplitude proved to be considerably lower (\(R_{{\mathrm {max}}}=121\)). It should be noted, however, that one precursor based prediction, that of Schatten et al. (1996) was significantly lower than the rest (\(138 \pm 30\)) and within \(0.6\,\sigma\) of the actual value. For Cycle 24 most precursor methods again consistently indicated a lower-than-average cycle amplitude in the range 70–100, except Feynman’s geomagnetic precursor method which mistakenly resulted in a very high value of 150. (The likely reasons were discussed in Sect. 2.4 above.) The closest hit at the actual peak value of 67 [v1] or 116 [v2] was produced by the Minimax3 and the polar field precursor methods (Petrovay 2010b; Svalgaard et al. 2005). Indeed, the polar precursor method of Schatten and Sofia (1987) and Schatten et al. (1996), has consistently proven its skill in all cycles. As discussed in Sect. 2.3, this method is essentially based on the polar magnetic field strength as precursor.
Model based methods are a new development that have only had limited occasion to prove their skill. For Cycle 24 only three conceptually different such predictions were made, all of which were based on dynamo models. The pioneering attempt by Dikpati and Gilman (2006) proved to be way too high (see Sect. 3.4.1 for a discussion of the possible reasons). The flux transport dynamo based predictions of Choudhuri et al. (2007) and Jiang et al. (2007) were close hits; however, as already mentioned, these employed a technique (adjusting the dipole moment at the minimum to observations) which renders them essentially a polar field precursor method in disguise. Another correct model-based forecast was given by Kitiashvili and Kosovichev (2008); the good performance of this dynamo model, seemingly rather far removed from physical reality, still needs to be understood and it may possibly be equivalent to a phase space reconstruction method, as in item (3) of Sect. 4.3.1.
Extrapolation methods as a whole have shown a much less impressive performance. Overall, the statistical distribution of maximum amplitude values predicted by “real” forecasts made using these methods (i.e., forecasts made at or before the minimum epoch) for any given cycle does not seem to significantly differ from the long term climatological average of the solar cycle quoted in Sect. 1.4 above. It would of course be a hasty judgement to dismiss each of the widely differing individual approaches comprised in this class simply due to the poor overall performance of the group. In particular, some novel methods introduced in the last decades, such as SSA, phase space reconstruction or neural networks have hardly had a chance to debut, so their further performance will be worth monitoring in upcoming cycles.
The effect of the sunspot number revision on solar cycle prediction methods is limited to numerical corrections of minor importance.
6 Forecasts for Cycle 25
Table 2 presents a collection of forecasts for the amplitude of Cycle 25, without claiming completeness. The objective was to include one or two representative forecasts from each category. As the time of the minimum starting Cycle 25 is yet to be established, all these forecast qualify as “early”, in the sense that the most well-established methods, relying on precursor values evaluated at the time of minimum, cannot yet be applied.
It is clear also from this table that the issue of cycle prediction is less contentious for Cycle 25 than it was for Cycle 24. The overwhelming majority of forecasts agree that the amplitude of Cycle 25 is most likely to lie within \(\pm 20\%\) of Cycle 24, i.e., no major change in the level of solar activity is expected. The remaining controversy mostly concerns where in this range the cycle will peak. Dynamo based predictions indicate that Cycle 25 will peak at somewhat lower values than Cycle 24, while precursor techniques and SFT modelling suggest a cycle amplitude comparable to or slightly higher than the previous cycle. Two recent neural network based forecasts yield a weak cycle peaking quite early.
Following the development of the sunspot number during the next few years will be most interesting in the light of these predictions, and it may shed more light on the strong and weak points in our understanding of the roots of solar activity variations.
Notes
The more precise condition defining \(\phi\) is that \(\phi =\pm \,\pi /2\) at each maximum and \(\phi\) is quadratically related to the time since the last minimum.
Note that Hoyt and Schatten (1998) included a coefficient of 12.08 in the definition of their GSN in order to bring it the same scale as the SSN; this coefficient has been omitted in the more recent reconstructions, sometimes leading to some confusion regarding the scale applied.
http://vizier.cfa.harvard.edu/viz-bin/VizieR?-source=J/A+A/602/A69 (or via the paper’s ADS link).
Here and in the rest of this paper R will normally refer to Version 2 values, unless explicitly noted.
Note that Osipova and Nagovitsyn (2017) recently constructed two separate group number series for small and large sunspot groups and they found that the Waldmeier effect applies better to large spots.
Hudson et al. (2014) also called attention to the unusal temporal distribution of active region flare productivity during Cycle 23: in the first half of the cycle the number of flares produced by a flaring AR remained at an all-time low, then from the 2003 Halloween events it suddenly rose.
With the exception of NSO data (not shown in that plot), which in Cycle 21 significantly deviate from the others.
Some doubts concerning this deep-seated storage of toroidal flux recently arose as in at least one MHD simulation (Nelson et al. 2013) the toroidal flux was found to be floating in a wreath-like structure in the middle of the convective envelope.
But even here care is needed not to read more into the data than they contain, as discussed by Usoskin (2018).
Version 1 sunspot numbers are used throughout this section, unless otherwise indicated.
References
Ables JG (1974) Maximum entropy spectral analysis. Astron Astrophys Suppl 15:383–393
Adomian G (1989) Nonlinear stochastic systems theory and applications to physics. Kluwer Academic, Dordrecht
Aguirre LA, Letellier C, Maquet J (2008) Forecasting the time series of sunspot numbers. Sol Phys 249:103–120. https://doi.org/10.1007/s11207-008-9160-5
Ahluwalia HS (1998) The predicted size of cycle 23 based on the inferred three-cycle quasi-periodicity of the planetary index \(A_p\). J Geophys Res 103:12103–12109. https://doi.org/10.1029/98JA00960
Arlt R (2008) Digitization of sunspot drawings by Staudacher in 1749–1796. Sol Phys 247:399–410. https://doi.org/10.1007/s11207-007-9113-4
Arlt R (2009) The butterfly diagram in the eighteenth century. Sol Phys 255:143–153. https://doi.org/10.1007/s11207-008-9306-5. arXiv:0812.2233
Arlt R, Leussu R, Giese N, Mursula K, Usoskin IG (2013) Sunspot positions and sizes for 1825–1867 from the observations by Samuel Heinrich Schwabe. Mon Not R Astron Soc 433:3165–3172. https://doi.org/10.1093/mnras/stt961. arXiv:1305.7400
Arlt R, Senthamizh Pavai V, Schmiel C, Spada F (2016) Sunspot positions, areas, and group tilt angles for 1611–1631 from observations by Christoph Scheiner. Astron Astrophys 595:A104. https://doi.org/10.1051/0004-6361/201629000. arXiv:1608.07172
Asvestari E, Usoskin IG, Kovaltsov GA, Owens MJ, Krivova NA, Rubinetti S, Taricco C (2017) Assessment of different sunspot number series using the cosmogenic isotope \(^{44}\)Ti in meteorites. Mon Not R Astron Soc 467:1608–1613. https://doi.org/10.1093/mnras/stx190
Ataç T, Özgüç A (2001) Flare index during the rising phase of solar cycle 23. Sol Phys 198:399–407. https://doi.org/10.1023/A:1005218315298
Ataç T, Özgüç A (2006) Overview of the solar activity during solar cycle 23. Sol Phys 233:139–153. https://doi.org/10.1007/s11207-006-1112-3
Attia AF, Ismail HA, Basurah HM (2013) A neuro-fuzzy modeling for prediction of solar cycles 24 and 25. Ap&SS 344:5–11. https://doi.org/10.1007/s10509-012-1300-6
Badalyan OG, Obridko VN, Sýkora J (2001) Brightness of the coronal green line and prediction for activity cycles 23 and 24. Sol Phys 199:421–435. https://doi.org/10.1023/A:1010343520424
Bai T, Cliver EW (1990) A 154 day periodicity in the occurrence rate of proton flares. Astrophys J 363:299–309. https://doi.org/10.1086/169342
Balogh A, Hudson HS, Petrovay K, von Steiger R (2014) Introduction to the solar activity cycle: overview of causes and consequences. Space Sci Rev 186:1–15. https://doi.org/10.1007/s11214-014-0125-8
Baranyi T (2015) Comparison of Debrecen and Mount Wilson/Kodaikanal sunspot group tilt angles and the Joy’s law. Mon Not R Astron Soc 447:1857–1865. https://doi.org/10.1093/mnras/stu2572. arXiv:1412.1355
Baranyi T, Győri L, Ludmány A (2016) On-line tools for solar data compiled at the Debrecen observatory and their extensions with the Greenwich sunspot data. Sol Phys 291:3081–3102. https://doi.org/10.1007/s11207-016-0930-1. arXiv:1606.00669
Basu S, Broomhall AM, Chaplin WJ, Elsworth Y (2012) Thinning of the Sun’s magnetic layer: the peculiar solar minimum could have been predicted. Astrophys J 758:43. https://doi.org/10.1088/0004-637X/758/1/43. arXiv:1208.5493
Beck JG, Gizon L, Duvall TL Jr (2002) A new component of solar dynamics: north–south diverging flows migrating toward the equator with an 11 year period. Astrophys J Lett 575:L47–L50. https://doi.org/10.1086/342636
Beer J, Vonmoos M, Muscheler R (2006) Solar variability over the past several millennia. Space Sci Rev 125:67–79. https://doi.org/10.1007/s11214-006-9047-4
Belucz B, Dikpati M, Forgács-Dajka E (2015) A Babcock–Leighton solar dynamo model with multi-cellular meridional circulation in advection- and diffusion-dominated regimes. Astrophys J 806:169. https://doi.org/10.1088/0004-637X/806/2/169. arXiv:1504.00420
Berggren A, Beer J, Possnert G, Aldahan A, Kubik P, Christl M, Johnsen SJ, Abreu J, Vinther BM (2009) A 600-year annual \(^{10}\)Be record from the NGRIP ice core, greenland. Geophys Res Lett 36:11801. https://doi.org/10.1029/2009GL038004
Bhatt NJ, Jain R, Aggarwal M (2009) Prediction of the maximum amplitude and timing of sunspot cycle 24. Sol Phys 260:225–232. https://doi.org/10.1007/s11207-009-9439-1
Biesecker D, Upton L (2019) Solar cycle 25—call for predictions. Solar News 2019/1:1. https://www.nso.edu/solarnews/solar-cycle-25-call-for-predictions/
Blais A, Mertz D (2001) An introduction to neural networks. IBM Developer. http://www.ibm.com/developerworks/library/l-neural/
Blanter EM, Le Mouël JL, Shnirman MG, Courtillot V (2014) Kuramoto model of nonlinear coupled oscillators as a way for understanding phase synchronization: application to solar and geomagnetic indices. Sol Phys 289:4309–4333. https://doi.org/10.1007/s11207-014-0568-9
Blanter E, Le Mouël JL, Shnirman M, Courtillot V (2016) Kuramoto model with non-symmetric coupling reconstructs variations of the solar-cycle period. Sol Phys 291:1003–1023. https://doi.org/10.1007/s11207-016-0867-4
Blanter E, Le Mouël JL, Shnirman M, Courtillot V (2017) Reconstruction of the north–south solar asymmetry with a Kuramoto model. Sol Phys 292:54. https://doi.org/10.1007/s11207-017-1078-3
Box GEP, Jenkins GM (2008) Time series analysis: forecasting and control, 2nd edn. Wiley, Hoboken
Bracewell RN (1953) The sunspot number series. Nature 171:649–650. https://doi.org/10.1038/171649a0
Bracewell RN (1988) Three-halves law in sunspot cycle shape. Mon Not R Astron Soc 230:535–550. https://doi.org/10.1093/mnras/230.4.535
Brajša R, Wöhl H, Hanslmeier A, Verbanac G, Ruždjak D, Cliver E, Svalgaard L, Roth M (2009) On solar cycle predictions and reconstructions. Astron Astrophys 496:855–861. https://doi.org/10.1051/0004-6361:200810862
Brown GM (1976) What determines sunspot maximum. Mon Not R Astron Soc 174:185–189. https://doi.org/10.1093/mnras/174.1.185
Browning MK, Miesch MS, Brun AS, Toomre J (2006) Dynamo action in the solar convection zone and tachocline: pumping and organization of toroidal fields. Astrophys J Lett 648:L157–L160. https://doi.org/10.1086/507869. arXiv:astro-ph/0609153
Bushby PJ, Tobias SM (2007) On predicting the solar cycle using mean-field models. Astrophys J 661:1289–1296. https://doi.org/10.1086/516628. arXiv:0704.2345
Calvo RA, Ceccato HA, Piacentini RD (1995) Neural network prediction of solar activity. Astrophys J 444:916–921. https://doi.org/10.1086/175661
Cameron R, Schüssler M (2007) Solar cycle prediction using precursors and flux transport models. Astrophys J 659:801–811. https://doi.org/10.1086/512049. arXiv:astro-ph/0612693
Cameron R, Schüssler M (2008) A robust correlation between growth rate and amplitude of solar cycles: consequences for prediction methods. Astrophys J 685:1291–1296. https://doi.org/10.1086/591079
Cameron RH, Schüssler M (2010) Changes of the solar meridional velocity profile during cycle 23 explained by flows toward the activity belts. Astrophys J 720:1030–1032. https://doi.org/10.1088/0004-637X/720/2/1030. arXiv:1007.2548
Cameron RH, Schüssler M (2012) Are the strengths of solar cycles determined by converging flows towards the activity belts? Astron Astrophys 548:A57. https://doi.org/10.1051/0004-6361/201219914. arXiv:1210.7644
Cameron RH, Schüssler M (2017a) An update of Leighton’s solar dynamo model. Astron Astrophys 599:A52. https://doi.org/10.1051/0004-6361/201629746. arXiv:1611.09111
Cameron RH, Schüssler M (2017b) Understanding solar cycle variability. Astrophys J 843:111. https://doi.org/10.3847/1538-4357/aa767a. arXiv:1705.10746
Cameron RH, Jiang J, Schmitt D, Schüssler M (2010) Surface flux transport modeling for solar cycles 15–21: effects of cycle-dependent tilt angles of sunspot groups. Astrophys J 719:264–270. https://doi.org/10.1088/0004-637X/719/1/264. arXiv:1006.3061
Cameron RH, Dasi-Espuig M, Jiang J, Işık E, Schmitt D, Schüssler M (2013) Limits to solar cycle predictability: cross-equatorial flux plumes. Astron Astrophys 557:A141. https://doi.org/10.1051/0004-6361/201321981. arXiv:1308.2827
Cameron RH, Jiang J, Schüssler M, Gizon L (2014) Physical causes of solar cycle amplitude variability. J Geophys Res 119:680–688. https://doi.org/10.1002/2013JA019498
Cameron RH, Jiang J, Schüssler M (2016) Solar cycle 25: Another moderate cycle? Astrophys J Lett 823:L22. https://doi.org/10.3847/2041-8205/823/2/L22. arXiv:1604.05405
Cameron RH, Dikpati M, Brandenburg A (2017) The global solar dynamo. Space Sci Rev 210:367–395. https://doi.org/10.1007/s11214-015-0230-3. arXiv:1602.01754
Carbonell M, Oliver R, Ballester JL (1994) A search for chaotic behaviour in solar activity. Astron Astrophys 290:983–994
Carrasco VMS, Vaquero JM, Gallego MC, Sánchez-Bajo F (2016) A normalized sunspot-area series starting in 1832: an update. Sol Phys 291:2931–2940. https://doi.org/10.1007/s11207-016-0943-9. arXiv:1606.04280
Charbonneau P (2001) Multiperiodicity, chaos, and intermittency in a reduced model of the solar cycle. Sol Phys 199:385–404
Charbonneau P (2007) Flux transport dynamos. Scholarpedia 2(9):3440. https://doi.org/10.4249/scholarpedia.3440. http://www.scholarpedia.org/article/Flux_transport_dynamos
Charbonneau P (2010) Dynamo models of the solar cycle. Living Rev Sol Phys 7:3. https://doi.org/10.12942/lrsp-2010-3
Charbonneau P, Barlet G (2011) The dynamo basis of solar cycle precursor schemes. J Atmos Sol-Terr Phys 73:198–206. https://doi.org/10.1016/j.jastp.2009.12.020
Charbonneau P, Dikpati M (2000) Stochastic fluctuations in a Babcock–Leighton model of the solar cycle. Astrophys J 543:1027–1043. https://doi.org/10.1086/317142
Charbonneau P, Beaubien G, St-Jean C (2007) Fluctuations in Babcock–Leighton dynamos. II. Revisiting the Gnevyshev–Ohl rule. Astrophys J 658:657–662. https://doi.org/10.1086/511177
Chatterjee P, Nandy D, Choudhuri AR (2004) Full-sphere simulations of a circulation-dominated solar dynamo: exploring the parity issue. Astron Astrophys 427:1019–1030. https://doi.org/10.1051/0004-6361:20041199
Chatzistergos T, Usoskin IG, Kovaltsov GA, Krivova NA, Solanki SK (2017) New reconstruction of the sunspot group numbers since 1739 using direct calibration and “backbone” methods. Astron Astrophys 602:A69. https://doi.org/10.1051/0004-6361/201630045. arXiv:1702.06183
Chou DY, Dai DC (2001) Solar cycle variations of subsurface meridional flows in the sun. Astrophys J Lett 559:L175–L178. https://doi.org/10.1086/323724
Choudhuri AR, Chatterjee P, Jiang J (2007) Predicting solar cycle 24 with a solar dynamo model. Phys Rev Lett 98(13):131103. https://doi.org/10.1103/PhysRevLett.98.131103. arXiv:astro-ph/0701527
Chylek P, Klett JD, Lesins G, Dubey MK, Hengartner N (2014) The Atlantic Multidecadal Oscillation as a dominant factor of oceanic influence on climate. Geophys Res Lett 41:1689–1697. https://doi.org/10.1002/2014GL059274
Clette F, Lefèvre L (2016) The new sunspot number: assembling all corrections. Sol Phys 291:2629–2651. https://doi.org/10.1007/s11207-016-1014-y
Clette F, Svalgaard L, Vaquero JM, Cliver EW (2014) Revisiting the sunspot number. A 400-year perspective on the solar cycle. Space Sci Rev 186:35–103. https://doi.org/10.1007/s11214-014-0074-2. arXiv:1407.3231
Clette F, Cliver EW, Lefèvre L, Svalgaard L, Vaquero JM, Leibacher JW (2016a) Preface to topical issue: recalibration of the sunspot number. Sol Phys 291:2479–2486. https://doi.org/10.1007/s11207-016-1017-8
Clette F, Lefèvre L, Cagnotti M, Cortesi S, Bulling A (2016b) The revised Brussels–Locarno sunspot number (1981–2015). Sol Phys 291:2733–2761. https://doi.org/10.1007/s11207-016-0875-4. arXiv:1507.07803
Cliver EW (2014) The extended cycle of solar activity and the Sun’s 22-year magnetic cycle. Space Sci Rev 186:169–189. https://doi.org/10.1007/s11214-014-0093-z
Cliver EW (2016) Comparison of new and old sunspot number time series. Sol Phys 291:2891–2916. https://doi.org/10.1007/s11207-016-0929-7
Cole TW (1973) Periodicities in solar activity. Sol Phys 30:103–110. https://doi.org/10.1007/BF00156178
Conway AJ (1998) Time series, neural networks and the future of the Sun. New Astron Rev 42:343–394. https://doi.org/10.1016/S1387-6473(98)00041-4
Covas E (2017) Spatial–temporal forecasting the sunspot diagram. Astron Astrophys 605:A44. https://doi.org/10.1051/0004-6361/201629130. arXiv:1709.02796
Covas E, Peixinho N, Fernandes J (2019) Neural network forecast of the sunspot butterfly diagram. Sol Phys 294(3):24. https://doi.org/10.1007/s11207-019-1412-z. arXiv:1801.04435
Currie RG (1973) Fine structure in the sunspot spectrum—2 to 70 years. Astrophys Space Sci 20:509–518. https://doi.org/10.1007/BF00642220
Dabas RS, Sharma K, Das RM, Pillai KGM, Chopra P, Sethi NK (2008) A prediction of solar cycle 24 using a modified precursor method. Sol Phys 250:171–181. https://doi.org/10.1007/s11207-008-9200-1
Dasi-Espuig M, Solanki SK, Krivova NA, Cameron R, Peñuela T (2010) Sunspot group tilt angles and the strength of the solar cycle. Astron Astrophys 518:A7. https://doi.org/10.1051/0004-6361/201014301. arXiv:1005.1774
de Meyer F (1981) Mathematical modelling of the sunspot cycle. Sol Phys 70:259–272. https://doi.org/10.1007/BF00151333
de Toma G, Chapman GA, Cookson AM, Preminger D (2013a) Temporal stability of sunspot umbral intensities: 1986–2012. Astrophys J Lett 771:L22. https://doi.org/10.1088/2041-8205/771/2/L22
de Toma G, Chapman GA, Preminger DG, Cookson AM (2013b) Analysis of sunspot area over two solar cycles. Astrophys J 770:89. https://doi.org/10.1088/0004-637X/770/2/89
DeRosa ML, Brun AS, Hoeksema JT (2012) Solar magnetic field reversals and the role of dynamo families. Astrophys J 757:96. https://doi.org/10.1088/0004-637X/757/1/96. arXiv:1208.1768
Diercke A, Arlt R, Denker C (2015) Digitization of sunspot drawings by Spörer made in 1861–1894. Astron Nachr 336:53. https://doi.org/10.1002/asna.201412138. arXiv:1411.7790
Dikpati M, Gilman PA (2006) Simulating and predicting solar cycles using a flux-transport dynamo. Astrophys J 649:498–514. https://doi.org/10.1086/506314
Dikpati M, de Toma G, Gilman PA (2006) Predicting the strength of solar cycle 24 using a flux-transport dynamo-based tool. Geophys Res Lett 33:5102. https://doi.org/10.1029/2005GL025221
Dikpati M, Gilman PA, de Toma G, Ghosh SS (2007) Simulating solar cycles in northern and southern hemispheres by assimilating magnetic data into a calibrated flux-transport dynamo. Sol Phys 245:1–17. https://doi.org/10.1007/s11207-007-9016-4
Dikpati M, Gilman PA, de Toma G (2008) The Waldmeier effect: An artifact of the definition of Wolf sunspot number? Astrophys J Lett 673:L99–L101. https://doi.org/10.1086/527360
Dmitrieva IV, Kuzanyan KM, Obridko VN (2000) Amplitude and period of the dynamo wave and prediction of the solar cycle. Sol Phys 195:209–218. https://doi.org/10.1023/A:1005207828577
D’Silva S, Choudhuri AR (1993) A theoretical model for tilts of bipolar magnetic regions. Astron Astrophys 272:621
Du ZL (2012) The solar cycle: a new prediction technique based on logarithmic values. Astrophys Space Sci 338:9–13. https://doi.org/10.1007/s10509-011-0906-4. arXiv:1110.5973
Du ZL, Li R, Wang HN (2009) The predictive power of Ohl’s precursor method. Astron J 138:1998–2001. https://doi.org/10.1088/0004-6256/138/6/1998
Durney BR (2000) On the differences between odd and even solar cycles. Sol Phys 196:421–426. https://doi.org/10.1023/A:1005285315323
Eddy JA (1976) The Maunder minimum. Science 192(4245):1189–1202. https://doi.org/10.1126/science.192.4245.1189
Ermolli I, Shibasaki K, Tlatov A, van Driel-Gesztelyi L (2014) Solar cycle indices from the photosphere to the corona: measurements and underlying physics. Space Sci Rev 186:105–135. https://doi.org/10.1007/s11214-014-0089-8. arXiv:1705.07054
Fan Y, Fang F (2014) A simulation of convective dynamo in the solar convective envelope: maintenance of the solar-like differential rotation and emerging flux. Astrophys J 789:35. https://doi.org/10.1088/0004-637X/789/1/35. arXiv:1405.3926
Farmer JD, Sidorowich JJ (1987) Predicting chaotic time series. Phys Rev Lett 59:845–848. https://doi.org/10.1103/PhysRevLett.59.845
Feynman J (1982) Geomagnetic and solar wind cycles, 1900–1975. J Geophys Res 87:6153–6162. https://doi.org/10.1029/JA087iA08p06153
Fisher GH, Fan Y, Howard RF (1995) Comparisons between theory and observation of active region tilts. Astrophys J 438:463. https://doi.org/10.1086/175090
Fligge M, Solanki SK, Beer J (1999) Determination of solar cycle length variations using the continuous wavelet transform. Astron Astrophys 346:313–321
Forgács-Dajka E, Borkovits T (2007) Searching for mid-term variations in different aspects of solar activity—looking for probable common origins and studying temporal variations of magnetic polarities. Mon Not R Astron Soc 374:282–291. https://doi.org/10.1111/j.1365-2966.2006.11167.x
Freitas US, Letellier C, Aguirre LA (2009) Failure in distinguishing colored noise from chaos using the “noise titration” technique. Phys Rev E 79(3):035201. https://doi.org/10.1103/PhysRevE.79.035201
Frick P, Galyagin D, Hoyt DV, Nesme-Ribes E, Schatten KH, Sokoloff D, Zakharov V (1997) Wavelet analysis of solar activity recorded by sunspot groups. Astron Astrophys 328:670–681
Friedli TK (2016) Sunspot observations of Rudolf Wolf from 1849–1893. Sol Phys 291:2505–2517. https://doi.org/10.1007/s11207-016-0907-0
Gao PX, Zhong J (2016) The curious temporal behavior of the frequency of different class flares. New Astron 43:91–94. https://doi.org/10.1016/j.newast.2015.08.004
Georgieva K, Kilçik A, Nagovitsyn Y, Kirov B (2017) The ratio between the number of sunspot and the number of sunspot groups. Geomagn Aeron 57:776–782. https://doi.org/10.1134/S001679321707009X. arXiv:1710.01775
Gizzatullina SM, Rukavishnikov VD, Ruzmaikin AA, Tavastsherna KS (1990) Radiocarbon evidence of the global stochasticity of solar activity. Sol Phys 127:281–288. https://doi.org/10.1007/BF00152167
Gleissberg W (1939) A long-periodic fluctuation of the sun-spot numbers. Observatory 62:158–159
Gleissberg W (1952) Die Häufigkeit der Sonnenflecken. Akademie-Verlag, Berlin
Gleissberg W (1967) Secularly smoothed data on the minima and maxima of sunspot frequency. Sol Phys 2:231–233. https://doi.org/10.1007/BF00155925
Gnevyshev MN, Ohl AI (1948) On the 22-year cycle of solar activity. Astron Zh 25:18–20
Goel A, Choudhuri AR (2009) The hemispheric asymmetry of solar activity during the last century and the solar dynamo. Res Astron Astrophys 9:115–126. https://doi.org/10.1088/1674-4527/9/1/010. arXiv:0712.3988
Göker ÜD, Singh J, Nutku F, Priyal M (2017) Temporal variations of different solar activity indices through the solar cycles 21–23. Serbian Astron J 195:59–70. https://doi.org/10.2298/SAJ1795059G
Gopalswamy N, Mäkelä P, Yashiro S, Akiyama S (2018) Long-term solar activity studies using microwave imaging observations and prediction for cycle 25. J Atmos Sol-Terr Phys 176:26–33. https://doi.org/10.1016/j.jastp.2018.04.005. arXiv:1804.02544
Grassberger P, Procaccia I (1983) Characterization of strange attractors. Phys Rev Lett 50:346–349. https://doi.org/10.1103/PhysRevLett.50.346
Győri L, Ludmány A, Baranyi T (2017) Comparative analysis of Debrecen sunspot catalogues. Mon Not R Astron Soc 465:1259–1273. https://doi.org/10.1093/mnras/stw2667. arXiv:1612.03274
Haber DA, Hindman BW, Toomre J, Thompson MJ (2004) Organized subsurface flows near active regions. Sol Phys 220:371–380. https://doi.org/10.1023/B:SOLA.0000031405.52911.08
Halm J (1901) Über eine neue theorie zur erklärung der periodicität der solaren erscheinungen. Astron Nachr 156:33–50. https://doi.org/10.1002/asna.19011560302
Hanslmeier A, Brajša R (2010) The chaotic solar cycle. I. Analysis of cosmogenic \(^{14}\)C-data. Astron Astrophys 509:A5. https://doi.org/10.1051/0004-6361/200913095
Hathaway DH (2009) Solar cycle forecasting. Space Sci Rev 144:401–412. https://doi.org/10.1007/s11214-008-9430-4
Hathaway DH (2010) Does the current minimum validate (or invalidate) cycle prediction methods? In: Cranmer SR, Hoeksema JT, Kohl JL (eds) SOHO-23: understanding a peculiar solar minimum, ASP conference series, vol 428. Astronomical Society of the Pacific, San Francisco, p 307. arXiv:1003.4208
Hathaway DH (2015) The solar cycle. Living Rev Sol Phys 12:4. https://doi.org/10.1007/lrsp-2015-4. arXiv:1502.07020
Hathaway DH, Rightmire L (2010) Variations in the Sun’s meridional flow over a solar cycle. Science 327:1350. https://doi.org/10.1126/science.1181990
Hathaway DH, Upton LA (2016) Predicting the amplitude and hemispheric asymmetry of solar cycle 25 with surface flux transport. J Geophys Res 121(A10):10. https://doi.org/10.1002/2016JA023190. arXiv:1611.05106
Hathaway DH, Wilson RM, Reichmann EJ (1994) The shape of the sunspot cycle. Sol Phys 151:177–190. https://doi.org/10.1007/BF00654090
Hawkes G, Berger MA (2018) Magnetic helicity as a predictor of the solar cycle. Sol Phys 293:109. https://doi.org/10.1007/s11207-018-1332-3
Hazra G, Choudhuri AR (2017) A theoretical model of the variation of the meridional circulation with the solar cycle. Mon Not R Astron Soc 472:2728–2741. https://doi.org/10.1093/mnras/stx2152. arXiv:1708.05204
Hazra S, Passos D, Nandy D (2014) A stochastically forced time delay solar dynamo model: self-consistent recovery from a Maunder-like grand minimum necessitates a mean-field alpha effect. Astrophys J 789:5. https://doi.org/10.1088/0004-637X/789/1/5. arXiv:1307.5751
Hazra G, Karak BB, Banerjee D, Choudhuri AR (2015) Correlation between decay rate and amplitude of solar cycles as revealed from observations and dynamo theory. Sol Phys 290:1851–1870. https://doi.org/10.1007/s11207-015-0718-8. arXiv:1410.8641
Hazra G, Choudhuri AR, Miesch MS (2017) A theoretical study of the build-up of the Sun’s polar magnetic field by using a 3D kinematic dynamo model. Astrophys J 835:39. https://doi.org/10.3847/1538-4357/835/1/39. arXiv:1610.02726
Hegger R, Kantz H, Schreiber T (1999) Practical implementation of nonlinear time series methods: the TISEAN package. Chaos 9:413. https://doi.org/10.1063/1.166424
Henwood R, Chapman SC, Willis DM (2010) Increasing lifetime of recurrent sunspot groups within the greenwich photoheliographic results. Sol Phys 262:299–313. https://doi.org/10.1007/s11207-009-9419-5. arXiv:0907.4274
Hiremath KM (2006) The solar cycle as a forced and damped harmonic oscillator: long-term variations of the amplitudes, frequencies and phases. Astron Astrophys 452:591–595. https://doi.org/10.1051/0004-6361:20042619
Hiremath KM (2008) Prediction of solar cycle 24 and beyond. Astrophys Space Sci 314:45–49. https://doi.org/10.1007/s10509-007-9728-9
Hoeksema JT (1995) The large-scale structure of the heliospheric current sheet during the ulysses epoch. Space Sci Rev 72:137–148. https://doi.org/10.1007/BF00768770
Howe R (2009) Solar interior rotation and its variation. Living Rev Sol Phys 6:1. https://doi.org/10.12942/lrsp-2009-1. arXiv:0902.2406
Howe R, Christensen-Dalsgaard J, Hill F, Komm R, Schou J, Thompson MJ (2009) A note on the torsional oscillation at solar minimum. Astrophys J Lett 701:L87–L90. https://doi.org/10.1088/0004-637X/701/2/L87. arXiv:0907.2965
Howe R, Christensen-Dalsgaard J, Hill F, Komm R, Larson TP, Rempel M, Schou J, Thompson MJ (2013) The high-latitude branch of the solar torsional oscillation in the rising phase of cycle 24. Astrophys J Lett 767:L20. https://doi.org/10.1088/2041-8205/767/1/L20
Howe R, Davies GR, Chaplin WJ, Elsworth Y, Basu S, Hale SJ, Ball WH, Komm RW (2017) The Sun in transition? Persistence of near-surface structural changes through Cycle 24. Mon Not R Astron Soc 470:1935–1942. https://doi.org/10.1093/mnras/stx1318. arXiv:1705.09099
Howe R, Hill F, Komm R, Chaplin WJ, Elsworth Y, Davies GR, Schou J, Thompson MJ (2018) Signatures of solar cycle 25 in subsurface zonal flows. Astrophys J Lett 862:L5. https://doi.org/10.3847/2041-8213/aad1ed. arXiv:1807.02398
Hoyt DV, Schatten KH (1998) Group sunspot numbers: a new solar activity reconstruction. Sol Phys 181:491–512
Hudson H, Fletcher L, McTiernan J (2014) Cycle 23 variation in solar flare productivity. Sol Phys 289:1341–1347. https://doi.org/10.1007/s11207-013-0384-7. arXiv:1401.6474
Hung CP, Jouve L, Brun AS, Fournier A, Talagrand O (2015) Estimating the deep solar meridional circulation using magnetic observations and a dynamo model: a variational approach. Astrophys J 814:151. https://doi.org/10.1088/0004-637X/814/2/151. arXiv:1710.02084
Hung CP, Brun AS, Fournier A, Jouve L, Talagrand O, Zakari M (2017) Variational estimation of the large-scale time-dependent meridional circulation in the Sun: proofs of concept with a solar mean field dynamo model. Astrophys J 849:160. https://doi.org/10.3847/1538-4357/aa91d1. arXiv:1710.02114
Iijima H, Hotta H, Imada S, Kusano K, Shiota D (2017) Improvement of solar-cycle prediction: plateau of solar axial dipole moment. Astron Astrophys 607:L2. https://doi.org/10.1051/0004-6361/201731813. arXiv:1710.06528
Işık E (2015) A mechanism for the dependence of sunspot group tilt angles on cycle strength. Astrophys J Lett 813:L13. https://doi.org/10.1088/2041-8205/813/1/L13. arXiv:1510.04323
Işık E, Işık S, Kabasakal BB (2018) Sunspot group tilt angles from drawings for cycles 19–24. In: Banerjee D, Jiang J, Kusano K, Solanki S (eds) Long-term datasets for the understanding of solar and stellar magnetic cycles. IAU symposium, vol 340. Cambridge University Press, Cambridge, pp 133–146. https://doi.org/10.1017/S1743921318001461. arXiv:1804.10479
Ivanov VG (2012) Joy’s law and its features according to the data of three sunspot catalogs. Geomagn Aeron 52:999–1004. https://doi.org/10.1134/S0016793212080130
Izenman AJ (1983) J. R. Wolf and H. A. Wolfer: an historical note on the Zurich sunspot relative numbers. J R Stat Soc A 146:311–318. https://doi.org/10.2307/2981658. http://www.jstor.org/pss/2981658
Javaraiah J (2012) The G–O rule and Waldmeier effect in the variations of the numbers of large and small sunspot groups. Sol Phys 281:827–837. https://doi.org/10.1007/s11207-012-0106-6. arXiv:1208.2862
Jensen JL (1993) Comments on nonparametric predictions of sunspot numbers. Astron J 105:350–352. https://doi.org/10.1086/116433
Jiang J, Cao J (2018) Predicting solar surface large-scale magnetic field of cycle 24. J Atmos Sol-Terr Phys 176:34–41. https://doi.org/10.1016/j.jastp.2017.06.019. arXiv:1707.00268
Jiang J, Chatterjee P, Choudhuri AR (2007) Solar activity forecast with a dynamo model. Mon Not R Astron Soc 381:1527–1542. https://doi.org/10.1111/j.1365-2966.2007.12267.x. arXiv:0707.2258
Jiang J, Cameron R, Schmitt D, Schüssler M (2010a) Modeling the Sun’s open magnetic flux and the heliospheric current sheet. Astrophys J 709:301–307. https://doi.org/10.1088/0004-637X/709/1/301. arXiv:0912.0108
Jiang J, Işik E, Cameron RH, Schmitt D, Schüssler M (2010b) The effect of activity-related meridional flow modulation on the strength of the solar polar magnetic field. Astrophys J 717:597–602. https://doi.org/10.1088/0004-637X/717/1/597. arXiv:1005.5317
Jiang J, Cameron RH, Schmitt D, Schüssler M (2011a) The solar magnetic field since 1700. I. Characteristics of sunspot group emergence and reconstruction of the butterfly diagram. Astron Astrophys 528:A82. https://doi.org/10.1051/0004-6361/201016167. arXiv:1102.1266
Jiang J, Cameron RH, Schmitt D, Schüssler M (2011b) The solar magnetic field since 1700. II. Physical reconstruction of total, polar and open flux. Astron Astrophys 528:A83. https://doi.org/10.1051/0004-6361/201016168. arXiv:1102.1270
Jiang J, Cameron RH, Schüssler M (2014a) Effects of the scatter in sunspot group tilt angles on the large-scale magnetic field at the solar surface. Astrophys J 791:5. https://doi.org/10.1088/0004-637X/791/1/5. arXiv:1406.5564
Jiang J, Hathaway DH, Cameron RH, Solanki SK, Gizon L, Upton L (2014b) Magnetic flux transport at the solar surface. Space Sci Rev 186:491–523. https://doi.org/10.1007/s11214-014-0083-1. arXiv:1408.3186
Jiang J, Cameron RH, Schüssler M (2015) The cause of the weak solar cycle 24. Astrophys J Lett 808:L28. https://doi.org/10.1088/2041-8205/808/1/L28. arXiv:1507.01764
Jiang J, Wang JX, Jiao QR, Cao JB (2018) Predictability of the solar cycle over one cycle. Astrophys J 863:159. https://doi.org/10.3847/1538-4357/aad197. arXiv:1807.01543
Jiang J, Song Q, Wang JX, Baranyi T (2019) Different contributions to space weather and space climate from different big solar active regions. Astrophys J 871:16. https://doi.org/10.3847/1538-4357/aaf64a. arXiv:1901.00116
Kanamaru T (2007) Van der Pol oscillator. Scholarpedia 2(1):2202. https://doi.org/10.4249/scholarpedia.2202. http://www.scholarpedia.org/article/Van_der_Pol_oscillator
Kanamaru T (2008) Duffing oscillator. Scholarpedia 3(3):6327. https://doi.org/10.4249/scholarpedia.6327. http://www.scholarpedia.org/article/Duffing_oscillator
Kane RP (1999) Prediction of the sunspot maximum of solar cycle 23 by extrapolation of spectral components. Sol Phys 189:217–224. https://doi.org/10.1023/A:1005298313886
Kane RP (2001) Did predictions of the maximum sunspot number for solar cycle 23 come true? Sol Phys 202:395–406
Kane RP (2007) Solar cycle predictions based on extrapolation of spectral components: an update. Sol Phys 246:487–493. https://doi.org/10.1007/s11207-007-9059-6
Kane RP (2008) Prediction of solar cycle maximum using solar cycle lengths. Sol Phys 248:203–209. https://doi.org/10.1007/s11207-008-9125-8
Kantz H, Schreiber T (1997) Nonlinear time series analysis. Cambridge University Press, Cambridge
Karak BB, Cameron R (2016) Babcock–Leighton solar dynamo: the role of downward pumping and the equatorward propagation of activity. Astrophys J 832:94. https://doi.org/10.3847/0004-637X/832/1/94. arXiv:1605.06224
Karak BB, Choudhuri AR (2011) The Waldmeier effect and the flux transport solar dynamo. Mon Not R Astron Soc 410:1503–1512. https://doi.org/10.1111/j.1365-2966.2010.17531.x. arXiv:1008.0824
Karak BB, Choudhuri AR (2012) Quenching of meridional circulation in flux transport dynamo models. Sol Phys 278:137–148. https://doi.org/10.1007/s11207-012-9928-5. arXiv:1111.1540
Karak BB, Miesch M (2017) Solar cycle variability induced by tilt angle scatter in a Babcock–Leighton solar dynamo model. Astrophys J 847:69. https://doi.org/10.3847/1538-4357/aa8636. arXiv:1706.08933
Karak BB, Miesch M (2018) Recovery from Maunder-like grand minima in a Babcock–Leighton solar dynamo model. Astrophys J Lett 860:L26. https://doi.org/10.3847/2041-8213/aaca97. arXiv:1712.10130
Karak BB, Jiang J, Miesch MS, Charbonneau P, Choudhuri AR (2014) Flux transport dynamos: from kinematics to dynamics. Space Sci Rev 186:561–602. https://doi.org/10.1007/s11214-014-0099-6
Kennel MB, Brown R, Abarbanel HDI (1992) Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys Rev A 45:3403
Kilcik A, Anderson CNK, Rozelot JP, Ye H, Sugihara G, Ozguc A (2009) Nonlinear prediction of solar cycle 24. Astrophys J 693:1173–1177. https://doi.org/10.1088/0004-637X/693/2/1173. arXiv:0811.1708
Kilcik A, Yurchyshyn VB, Abramenko V, Goode PR, Ozguc A, Rozelot JP, Cao W (2011) Time distributions of large and small sunspot groups over four solar cycles. Astrophys J 731:30. https://doi.org/10.1088/0004-637X/731/1/30. arXiv:1111.3999
Kilcik A, Yurchyshyn VB, Ozguc A, Rozelot JP (2014) Solar cycle 24: curious changes in the relative numbers of sunspot group types. Astrophys J Lett 794:L2. https://doi.org/10.1088/2041-8205/794/1/L2
Kilcik A, Yurchyshyn V, Donmez B, Obridko VN, Ozguc A, Rozelot JP (2018) Temporal and periodic variations of sunspot counts in flaring and non-flaring active regions. Sol Phys 293:63. https://doi.org/10.1007/s11207-018-1285-6. arXiv:1705.09065
Kimura H (1913) Sun-spots and faculæ, on the harmonic analysis of sun-spot relative numbers. Mon Not R Astron Soc 73:543–548B. https://doi.org/10.1093/mnras/73.7.543
Kitchatinov LL, Olemskoy SV (2011) Does the Babcock–Leighton mechanism operate on the Sun? Astron Lett 37:656–658. https://doi.org/10.1134/S0320010811080031. arXiv:1109.1351
Kitchatinov LL, Mordvinov AV, Nepomnyashchikh AA (2018) Modelling variability of solar activity cycles. Astron Astrophys 615:A38. https://doi.org/10.1051/0004-6361/201732549. arXiv:1804.02833
Kitiashvili IN (2016) Data assimilation approach for forecast of solar activity cycles. Astrophys J 831:15. https://doi.org/10.3847/0004-637X/831/1/15
Kitiashvili IN, Kosovichev AG (2008) Application of data assimilation method for predicting solar cycles. Astrophys J Lett 688:L49–L52. https://doi.org/10.1086/594999. arXiv:0807.3284
Kitiashvili IN, Kosovichev AG (2009) Nonlinear dynamical modeling of solar cycles using dynamo formulation with turbulent magnetic helicity. Geophys Astrophys Fluid Dyn 103:53–68. https://doi.org/10.1080/03091920802396518. arXiv:0807.3192
Kolláth Z, Oláh K (2009) Multiple and changing cycles of active stars. I. Methods of analysis and application to the solar cycles. Astron Astrophys 501:695–702. https://doi.org/10.1051/0004-6361/200811303. arXiv:0904.1725
Komm RW (1995) Hurst analysis of Mt. Wilson rotation measurements. Sol Phys 156:17–28. https://doi.org/10.1007/BF00669572
Komm R, Ferguson R, Hill F, Barnes G, Leka KD (2011) Subsurface vorticity of flaring versus flare-quiet active regions. Sol Phys 268:389–406. https://doi.org/10.1007/s11207-010-9552-1
Komm R, De Moortel I, Fan Y, Ilonidis S, Steiner O (2015) Sub-photosphere to solar atmosphere connection. Space Sci Rev 196:167–199. https://doi.org/10.1007/s11214-013-0023-5
Komm R, Howe R, Hill F (2017) Solar-cycle variation of subsurface-flow divergence: A proxy of magnetic activity? Sol Phys 292:122. https://doi.org/10.1007/s11207-017-1142-z
Komm R, Howe R, Hill F (2018) Subsurface zonal and meridional flow during cycles 23 and 24. Sol Phys 293:145. https://doi.org/10.1007/s11207-018-1365-7
Kopecký M (1950) Cycle de 22 ans de l’activité solaire. Bull Astron Inst Czech 2:14
Kopecký M, Ruzickova-Topolova B, Kuklin GV (1980) On the relative inhomogeneity of long-term series of sunspot indices. Bull Astron Inst Czech 31:267–283
Krivova NA, Solanki SK (2002) The 1.3-year and 156-day periodicities in sunspot data: wavelet analysis suggests a common origin. Astron Astrophys 394:701–706. https://doi.org/10.1051/0004-6361:20021063
Krivova NA, Solanki SK, Beer J (2002) Was one sunspot cycle in the 18th century really lost? Astron Astrophys 396:235–242. https://doi.org/10.1051/0004-6361:20021340
Kurths J, Ruzmaikin AA (1990) On forecasting the sunspot numbers. Sol Phys 126:407–410. https://doi.org/10.1007/BF00153060
Kuzanyan K, Obridko VN, Kotlyarov OL, Loskutov AY, Istomin IA (2008) Predictions of the magnitude of the forthcoming solar cycles using knowledge on the solar dynamo and singular spectrum analysis. In: Peter H (ed) 12th European solar physics meeting (ESPM-12). KIS, Freiburg, pp 2–69
Labonville F, Charbonneau P, Lemerle A (2019) A dynamo-based forecast of solar cycle 25. Sol Phys 294(6):82. https://doi.org/10.1007/s11207-019-1480-0
Lantos P (2000) Prediction of the maximum amplitude of solar cycles using the ascending inflexion point. Sol Phys 196:221–225. https://doi.org/10.1023/A:1005219818200
Le Mouël JL, Lopes F, Courtillot V (2017) Identification of Gleissberg cycles and a rising trend in a 315-year-long series of sunspot numbers. Sol Phys 292:43. https://doi.org/10.1007/s11207-017-1067-6
Lean JL, Rind DH (2008) How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys Res Lett 35:L18701. https://doi.org/10.1029/2008GL034864
Lefèvre L, Clette F (2011) A global small sunspot deficit at the base of the index anomalies of solar cycle 23. Astron Astrophys 536:L11. https://doi.org/10.1051/0004-6361/201118034
Leighton RB (1969) A magneto-kinematic model of the solar cycle. Astrophys J 156:1. https://doi.org/10.1086/149943
Lemerle A, Charbonneau P (2017) A coupled 2 \(\times\) 2D Babcock–Leighton solar dynamo model. II. Reference dynamo solutions. Astrophys J 834:133. https://doi.org/10.3847/1538-4357/834/2/133. arXiv:1606.07375
Lemerle A, Charbonneau P, Carignan-Dugas A (2015) A coupled \(2\times 2\)D Babcock–Leighton solar dynamo model. I. Surface magnetic flux evolution. Astrophys J 810:78. https://doi.org/10.1088/0004-637X/810/1/78. arXiv:1511.08548
Leussu R, Usoskin IG, Arlt R, Mursula K (2016) Properties of sunspot cycles and hemispheric wings since the 19th century. Astron Astrophys 592:A160. https://doi.org/10.1051/0004-6361/201628335
Leussu R, Usoskin IG, Senthamizh Pavai V, Diercke A, Arlt R, Denker C, Mursula K (2017) Wings of the butterfly: sunspot groups for 1826–2015. Astron Astrophys 599:A131. https://doi.org/10.1051/0004-6361/201629533
Levy EH, Boyer D (1982) Oscillating dynamo in the presence of a fossil magnetic field—the solar cycle. Astrophys J Lett 254:L19–L22. https://doi.org/10.1086/183748
Li J, Ulrich RK (2012) Long-term measurements of sunspot magnetic tilt angles. Astrophys J 758:115. https://doi.org/10.1088/0004-637X/758/2/115. arXiv:1209.1642
Li KJ, Yun HS, Gu XM (2001) On long-term predictions of the maximum sunspot numbers of solar cycles 21 to 23. Astron Astrophys 368:285–291. https://doi.org/10.1051/0004-6361:20000547
Li KJ, Irie M, Wang J, Xiong S, Yun H, Liang H, Zhan L, Zhao H (2002) Activity cycle of polar faculae. Publ Astron Soc Japan 54:787–792. https://doi.org/10.1093/pasj/54.5.787
Li KJ, Gao PX, Su TW (2005) The Schwabe and Gleissberg periods in the Wolf sunspot numbers and the group sunspot numbers. Sol Phys 229:181–198. https://doi.org/10.1007/s11207-005-5001-y
Li KJ, Feng W, Li FY (2015) Predicting the maximum amplitude of solar cycle 25 and its timing. J Atmos Sol-Terr Phys 135:72–76. https://doi.org/10.1016/j.jastp.2015.09.010
Liang ZC, Gizon L, Birch AC, Duvall TL, Rajaguru SP (2018) Solar meridional circulation from twenty-one years of SOHO/MDI and SDO/HMI observations. Helioseismic travel times and forward modeling in the ray approximation. Astron Astrophys 619:A99. https://doi.org/10.1051/0004-6361/201833673. arXiv:1808.08874
Lin CH (2014) A statistical study of the subsurface structure and eruptivity of solar active regions. Astrophys Space Sci 352:361–371. https://doi.org/10.1007/s10509-014-1931-x. arXiv:1512.07007
Lin CH, Chou DY (2018) Solar-cycle variations of meridional flows in the solar convection zone using helioseismic methods. Astrophys J 860:48. https://doi.org/10.3847/1538-4357/aac026
Livingston W, Penn MJ, Svalgaard L (2012) Decreasing sunspot magnetic fields explain unique 10.7 cm radio flux. Astrophys J Lett 757:L8. https://doi.org/10.1088/2041-8205/757/1/L8
Lockwood M (2001) Long-term variations in the magnetic fields of the Sun and the heliosphere: their origin, effects, and implications. J Geophys Res 106:16021–16038. https://doi.org/10.1029/2000JA000115
Lockwood M (2013) Reconstruction and prediction of variations in the open solar magnetic flux and interplanetary conditions. Living Rev Sol Phys 10:4. https://doi.org/10.12942/lrsp-2013-4
Lomb NR, Andersen AP (1980) The analysis and forecasting of the Wolf sunspot numbers. Mon Not R Astron Soc 190:723–732. https://doi.org/10.1093/mnras/190.4.723
Lopes I, Passos D (2009) Solar variability induced in a dynamo code by realistic meridional circulation variations. Sol Phys 257:1–12. https://doi.org/10.1007/s11207-009-9372-3
Lopes I, Passos D, Nagy M, Petrovay K (2014) Oscillator models of the solar cycle. Towards the development of inversion methods. Space Sci Rev 186:535–559. https://doi.org/10.1007/s11214-014-0066-2. arXiv:1407.4918
Löptien B, Birch AC, Duvall TL, Gizon L, Proxauf B, Schou J (2017) Measuring solar active region inflows with local correlation tracking of granulation. Astron Astrophys 606:A28. https://doi.org/10.1051/0004-6361/201731064. arXiv:1705.08833
Loskutov AY, Istomin IA, Kotlyarov OL, Kuzanyan KM (2001) A study of the regularities in solar magnetic activity by singular spectral analysis. Astron Lett 27:745–753. https://doi.org/10.1134/1.1415865
Love JJ, Rigler EJ (2012) Sunspot random walk and 22-year variation. Geophys Res Lett 39:L10103. https://doi.org/10.1029/2012GL051818
Makarov VI, Makarova VV (1996) Polar faculae and sunspot cycles. Sol Phys 163:267–289. https://doi.org/10.1007/BF00148001
Makarov VI, Makarova VV, Sivaraman KR (1989) Do polar faculae on the Sun predict a sunspot cycle? Sol Phys 119:45–54. https://doi.org/10.1007/BF00146211
Makarov VI, Tlatov AG, Callebaut DK, Obridko VN, Shelting BD (2001) Large-scale magnetic field and sunspot cycles. Sol Phys 198:409–421. https://doi.org/10.1023/A:1005249531228
Mandal S, Karak BB, Banerjee D (2017) Latitude distribution of sunspots: analysis using sunspot data and a dynamo model. Astrophys J 851:70. https://doi.org/10.3847/1538-4357/aa97dc. arXiv:1711.00222
Mandelbrot BB, Wallis JR (1969) On forecasting the sunspot numbers. Water Resour Res 5:321–340. https://doi.org/10.1029/WR005i002p00321
Maris G, Oncica A (2006) Solar cycle 24 forecasts. Sun and Geosphere 1(1):8–11
Martin-Belda D, Cameron RH (2016) Surface flux transport simulations: effect of inflows toward active regions and random velocities on the evolution of the Sun’s large-scale magnetic field. Astron Astrophys 586:A73. https://doi.org/10.1051/0004-6361/201527213. arXiv:1512.02541
Martin-Belda D, Cameron RH (2017) Inflows towards active regions and the modulation of the solar cycle: a parameter study. Astron Astrophys 597:A21. https://doi.org/10.1051/0004-6361/201629061. arXiv:1609.01199
Mason D, Komm R, Hill F, Howe R, Haber D, Hindman BW (2006) Flares, magnetic fields, and subsurface vorticity: a survey of GONG and MDI data. Astrophys J 645:1543–1553. https://doi.org/10.1086/503761
Maunder EW (1894) A prolonged sunspot minimum. Knowl Illus Mag Sci 17:173–176
McClintock BH, Norton AA (2013) Recovering Joy’s law as a function of solar cycle, hemisphere, and longitude. Sol Phys 287:215–227. https://doi.org/10.1007/s11207-013-0338-0. arXiv:1305.3205
McClintock BH, Norton AA, Li J (2014) Re-examining sunspot tilt angle to include anti-Hale statistics. Astrophys J 797:130. https://doi.org/10.1088/0004-637X/797/2/130. arXiv:1412.5094
McCracken KG, Beer J (2008) The 2300 year modulation in the galactic cosmic radiation. In: Caballero R et al (eds) Proceedings of the 30th international cosmic ray conference, vol 1. UNAM, Mexico City, pp 549–552
Michelson AA (1913) Determination of periodicities by the harmonic analyzer with an application to the sun-spot cycle. Astrophys J 38:268. https://doi.org/10.1086/142033
Miesch MS, Dikpati M (2014) A three-dimensional Babcock–Leighton solar dynamo model. Astrophys J Lett 785:L8. https://doi.org/10.1088/2041-8205/785/1/L8. arXiv:1401.6557
Miesch MS, Teweldebirhan K (2016) A three-dimensional Babcock–Leighton solar dynamo model: initial results with axisymmetric flows. Adv Space Res 58:1571–1588. https://doi.org/10.1016/j.asr.2016.02.018. arXiv:1511.03613
Mininni PD, Gómez DO, Mindlin GB (2000) Stochastic relaxation oscillator model for the solar cycle. Phys Rev Lett 85:5476–5479. https://doi.org/10.1103/PhysRevLett.85.5476
Mininni PD, Gomez DO, Mindlin GB (2001) Simple model of a stochastically excited solar dynamo. Sol Phys 201:203–223. https://doi.org/10.1023/A:1017515709106
Mininni PD, Gomez DO, Mindlin GB (2002) Instantaneous phase and amplitude correlation in the solar cycle. Sol Phys 208:167–179. https://doi.org/10.1023/A:1019658530185
Moss D, Sokoloff D, Usoskin I, Tutubalin V (2008) Solar grand minima and random fluctuations in dynamo parameters. Sol Phys 250:221–234. https://doi.org/10.1007/s11207-008-9202-z. arXiv:0806.3331
MSFC (2017) Solar cycle 24 prediction. http://solarscience.msfc.nasa.gov/predict.shtml
Muñoz-Jaramillo A, Nandy D, Martens PCH, Yeates AR (2010) A double-ring algorithm for modeling solar active regions: unifying kinematic dynamo models and surface flux-transport simulations. Astrophys J Lett 720:L20–L25. https://doi.org/10.1088/2041-8205/720/1/L20. arXiv:1007.1262
Muñoz-Jaramillo A, Sheeley NR, Zhang J, DeLuca EE (2012) Calibrating 100 years of polar faculae measurements: implications for the evolution of the heliospheric magnetic field. Astrophys J 753:146. https://doi.org/10.1088/0004-637X/753/2/146. arXiv:1303.0345
Muñoz-Jaramillo A, Balmaceda LA, DeLuca EE (2013a) Using the dipolar and quadrupolar moments to improve solar-cycle predictions based on the polar magnetic fields. Phys Rev Lett 111(4):041106. https://doi.org/10.1103/PhysRevLett.111.041106. arXiv:1308.2038
Muñoz-Jaramillo A, Dasi-Espuig M, Balmaceda LA, DeLuca EE (2013b) Solar cycle propagation, memory, and prediction: insights from a century of magnetic proxies. Astrophys J Lett 767:L25. https://doi.org/10.1088/2041-8205/767/2/L25. arXiv:1304.3151
Muraközy J, Baranyi T, Ludmány A (2016) An alternative measure of solar activity from detailed sunspot datasets. Sol Phys 291:2941–2950. https://doi.org/10.1007/s11207-016-0898-x. arXiv:1603.05870
Mursula K, Zieger B (2000) The 1.3-year variation in solar wind speed and geomagnetic activity. Adv Space Res 25:1939–1942. https://doi.org/10.1016/S0273-1177(99)00608-0
Mursula K, Usoskin IG, Kovaltsov GA (2001) Persistent 22-year cycle in sunspot activity: evidence for a relic solar magnetic field. Sol Phys 198:51–56. https://doi.org/10.1023/A:1005218414790
Nagovitsyn YA (1997) A nonlinear mathematical model for the solar cyclicity and prospects for reconstructing the solar activity in the past. Astron Lett 23:742–748
Nagovitsyn YA, Nagovitsyna EY, Makarova VV (2009) The Gnevyshev–Ohl rule for physical parameters of the solar magnetic field: the 400-year interval. Astron Lett 35:564–571. https://doi.org/10.1134/S1063773709080064
Nagovitsyn YA, Pevtsov AA, Osipova AA, Tlatov AG, Miletskii EV, Nagovitsyna EY (2016) Two populations of sunspots and secular variations of their characteristics. Astron Lett 42:703–712. https://doi.org/10.1134/S1063773716090048
Nagovitsyn YA, Pevtsov AA, Osipova AA (2017) Long-term variations in sunspot magnetic field-area relation. Astron Nachr 338:26–34. https://doi.org/10.1002/asna.201613035. arXiv:1608.01132
Nagy M, Petrovay K (2013) Oscillator models of the solar cycle and the Waldmeier effect. Astron Nachr 334:964. https://doi.org/10.1002/asna.201211971. arXiv:1404.3668
Nagy M, Lemerle A, Labonville F, Petrovay K, Charbonneau P (2017a) The effect of “rogue” active regions on the solar cycle. Sol Phys 292:167. https://doi.org/10.1007/s11207-017-1194-0. arXiv:1712.02185
Nagy M, Petrovay K, Erdélyi R (2017b) The Atlanto-Pacific multidecadal oscillation and its imprint on the global temperature record. Climate Dyn 48:1883–1891. https://doi.org/10.1007/s00382-016-3179-3
Nelson NJ, Brown BP, Brun AS, Miesch MS, Toomre J (2013) Magnetic wreaths and cycles in convective dynamos. Astrophys J 762:73. https://doi.org/10.1088/0004-637X/762/2/73. arXiv:1211.3129
Neuhäuser R, Arlt R, Richter S (2018) Reconstructed sunspot positions in the Maunder minimum based on the correspondence of Gottfried Kirch. Astron Nachr 339:219–267. https://doi.org/10.1002/asna.201813481. arXiv:1807.10241
Ng KK (2016) Prediction methods in solar sunspots cycles. Sci Rep 6:21028. https://doi.org/10.1038/srep21028
Norton AA, Gallagher JC (2010) Solar-cycle characteristics examined in separate hemispheres: phase, Gnevyshev gap, and length of minimum. Sol Phys 261:193–207. https://doi.org/10.1007/s11207-009-9479-6. arXiv:1001.3186
Norton AA, Jones EH, Liu Y (2013) How do the magnetic field strengths and intensities of sunspots vary over the solar cycle? J Phys: Conf Ser 440:012038. https://doi.org/10.1088/1742-6596/440/1/012038
Norton AA, Charbonneau P, Passos D (2014) Hemispheric coupling: comparing dynamo simulations and observations. Space Sci Rev 186:251–283. https://doi.org/10.1007/s11214-014-0100-4. arXiv:1411.7052
Obridko VN, Shelting BD (2008) On prediction of the strength of the 11-year solar cycle no. 24. Sol Phys 248:191–202. https://doi.org/10.1007/s11207-008-9138-3
Ochadlick AR Jr, Kritikos HN, Giegengack R (1993) Variations in the period of the sunspot cycle. Geophys Res Lett 20:1471–1474. https://doi.org/10.1029/93GL01593
Ogurtsov MG (2004) New evidence for long-term persistence in the Sun’s activity. Sol Phys 220:93–105. https://doi.org/10.1023/B:sola.0000023439.59453.e5
Ogurtsov MG, Lindholm M (2011) Statistical effects in the solar activity cycles during AD 1823–1996. ISRN Astron Astrophys 2011:640817. https://doi.org/10.5402/2011/640817
Ohl AI (1966) Forecast of sunspot maximum number of cycle 20. Soln Dannye 12:84
Oláh K, Kolláth Z, Granzer T, Strassmeier KG, Lanza AF, Järvinen S, Korhonen H, Baliunas SL, Soon W, Messina S, Cutispoto G (2009) Multiple and changing cycles of active stars. II. results. Astron Astrophys 501:703–713. https://doi.org/10.1051/0004-6361/200811304. arXiv:0904.1747
Oliver R, Ballester JL (1996) Rescaled range analysis of the asymmetry of solar activity. Sol Phys 169:215–224. https://doi.org/10.1007/BF00153842
Oliver R, Ballester JL (1998) Is there memory in solar activity? Phys Rev E 58:5650–5654. https://doi.org/10.1103/PhysRevE.58.5650
Osipova AA, Nagovitsyn YA (2017) The Waldmeier effect for two sunspot populations. Geomagn Aeron 57:1092–1100. https://doi.org/10.1134/S0016793217080199
Ossendrijver M (2003) The solar dynamo. Astron Astrophys Rev 11:287–367. https://doi.org/10.1007/s00159-003-0019-3
Ossendrijver AJH, Hoyng P, Schmitt D (1996) Stochastic excitation and memory of the solar dynamo. Astron Astrophys 313:938–948
Owens MJ, Lockwood M, Hawkins E, Usoskin I, Jones GS, Barnard L, Schurer A, Fasullo J (2017) The Maunder minimum and the Little Ice Age: an update from recent reconstructions and climate simulations. J Space Weather Space Clim 7(27):A33. https://doi.org/10.1051/swsc/2017034
Paluš M, Novotná D (1999) Sunspot cycle: A driven nonlinear oscillator? Phys Rev Lett 83:3406–3409. https://doi.org/10.1103/PhysRevLett.83.3406
Panchev S, Tsekov M (2007) Empirical evidences of persistence and dynamical chaos in solar terrestrial phenomena. J Atmos Sol-Terr Phys 69:2391–2404. https://doi.org/10.1016/j.jastp.2007.07.011
Parker EN (1955) Hydromagnetic dynamo models. Astrophys J 122:293–314. https://doi.org/10.1086/146087
Passos D (2012) Evolution of solar parameters since 1750 based on a truncated dynamo model. Astrophys J 744:172. https://doi.org/10.1088/0004-637X/744/2/172
Passos D, Miesch M, Guerrero G, Charbonneau P (2017) Meridional circulation dynamics in a cyclic convective dynamo. Astron Astrophys 607:A120. https://doi.org/10.1051/0004-6361/201730568. arXiv:1702.02421
Paularena KI, Szabo A, Richardson JD (1995) Coincident 1.3-year periodicities in the \(ap\) geomagnetic index and the solar wind. Geophys Res Lett 22:3001–3004. https://doi.org/10.1029/95GL02802
Pesnell WD (2008) Predictions of solar cycle 24. Sol Phys 252:209–220. https://doi.org/10.1007/s11207-008-9252-2
Pesnell WD (2012) Solar cycle predictions (invited review). Sol Phys 281:507–532. https://doi.org/10.1007/s11207-012-9997-5
Pesnell WD (2014) Predicting solar cycle 24 using a geomagnetic precursor pair. Sol Phys 289:2317–2331. https://doi.org/10.1007/s11207-013-0470-x
Pesnell WD (2016) Predictions of solar cycle 24: How are we doing? Space Weather 14:10–21. https://doi.org/10.1002/2015SW001304
Pesnell WD, Schatten KH (2018) An early prediction of the amplitude of solar cycle 25. Sol Phys 293:112. https://doi.org/10.1007/s11207-018-1330-5
Petrie GJD (2015) Solar magnetism in the polar regions. Living Rev Sol Phys 12:5. https://doi.org/10.1007/lrsp-2015-5
Petrie GJD, Ettinger S (2017) Polar field reversals and active region decay. Space Sci Rev 210:77–108. https://doi.org/10.1007/s11214-015-0189-0
Petrie GJD, Patrikeeva I (2009) A comparative study of magnetic fields in the solar photosphere and chromosphere at equatorial and polar latitudes. Astrophys J 699:871–884. https://doi.org/10.1088/0004-637X/699/1/871. arXiv:1010.6041
Petrie GJD, Petrovay K, Schatten K (2014) Solar polar fields and the 22-year activity cycle: observations and models. Space Sci Rev 186:325–357. https://doi.org/10.1007/s11214-014-0064-4
Petrovay K (1994) Theory of passive magnetic field transport. In: Rutten RJ, Schrijver CJ (eds) Solar surface magnetism, NATO ASI Series C, vol 433. Kluwer, Dordrecht, pp 415–440
Petrovay K (2000) What makes the Sun tick? The origin of the solar cycle. In: Wilson A (ed) The solar cycle and terrestrial climate, solar and space weather. ESA Special Publication, vol SP-463. ESA Publications Division, Noordwijk, p 3. arXiv:astro-ph/0010096
Petrovay K (2007) On the possibility of a bimodal solar dynamo. Astron Nachr 328:777–780. https://doi.org/10.1002/asna.200710804. arXiv:0708.2131
Petrovay K (2010a) Harmonic analysis approach to solar cycle prediction and the Waldmeier effect. In: Kosovichev A, Andrei A, Rozelot JP (eds) Solar and stellar variability: impact on earth and planets, IAU symposium, vol 264. Cambridge University Press, Cambridge, pp 150–154. https://doi.org/10.1017/S1743921309992560
Petrovay K (2010) Solar cycle prediction. Living Rev Sol Phys 7:6. https://doi.org/10.12942/lrsp-2010-6. arXiv:1012.5513
Petrovay K, Forgács-Dajka E (2002) The role of active regions in the generation of torsional oscillations. Sol Phys 205:39–52. https://doi.org/10.1023/A:1013833709489
Petrovay K, van Driel-Gesztelyi L (1997) Making sense of sunspot decay. I. Parabolic decay law and Gnevyshev–Waldmeier relation. Sol Phys 176:249–266. https://doi.org/10.1023/A:1004988123265
Petrovay K, Nagy M (2018) Rogue active regions and the inherent unpredictability of the solar dynamo. In: Banerjee D, Jiang J, Kusano K, Solanki S (eds) Long-term datasets for the understanding of solar and stellar magnetic cycles. IAU symposium, vol 340. Cambridge University Press, Cambridge, pp 307–312. https://doi.org/10.1017/S1743921318001254. arXiv:1804.03427
Petrovay K, Talafha M (2019) Optimization of surface flux transport models for the solar polar magnetic field. Astron Astrophys 632:A87. https://doi.org/10.1051/0004-6361/201936099. arXiv:1909.06125
Petrovay K, Martínez Pillet V, van Driel-Gesztelyi L (1999) Making sense of sunspot decay. II. Deviations from the mean law and plage effects. Sol Phys 188:315–330 arXiv:astro-ph/9906258
Petrovay K, Chaterjee P, Choudhuri A (2006) Helical magnetic fields in solar active regions: theory vs. observations. Publ Astron Dep Eotvos Lorand Univ 17:5
Petrovay K, Nagy M, Gerják T, Juhász L (2018) Precursors of an upcoming solar cycle at high latitudes from coronal green line data. J Atmos Sol-Terr Phys 176:15–20. https://doi.org/10.1016/j.jastp.2017.12.011. arXiv:1802.05628
Pevtsov AA, Berger MA, Nindos A, Norton AA, van Driel-Gesztelyi L (2014) Magnetic helicity, tilt, and twist. Space Sci Rev 186:285–324. https://doi.org/10.1007/s11214-014-0082-2
Pipin VV, Kosovichev AG (2011) The asymmetry of sunspot cycles and Waldmeier relations as a result of nonlinear surface-shear shaped dynamo. Astrophys J 741:1. https://doi.org/10.1088/0004-637X/741/1/1. arXiv:1105.1828
Pipin VV, Sokoloff DD (2011) The fluctuating \(\alpha\)-effect and Waldmeier relations in the nonlinear dynamo models. Phys Scripta 84(6):065903. https://doi.org/10.1088/0031-8949/84/06/065903. arXiv:1110.2255
Pipin VV, Sokoloff DD, Usoskin IG (2012) Variations of the solar cycle profile in a solar dynamo with fluctuating dynamo governing parameters. Astron Astrophys 542:A26. https://doi.org/10.1051/0004-6361/201118733. arXiv:1112.6218
Pishkalo MI (2008) Preliminary prediction of solar cycles 24 and 25 based on the correlation between cycle parameters. Kinemat Phys Celest Bodies 24:242–247. https://doi.org/10.3103/S0884591308050036
Podladchikova T, Van der Linden R, Veronig AM (2017) Sunspot number second differences as a precursor of the following 11-year sunspot cycle. Astrophys J 850:81. https://doi.org/10.3847/1538-4357/aa93ef. arXiv:1712.05782
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. Cambridge University Press, Cambridge
Price CP, Prichard D, Hogenson EA (1992) Do the sunspot numbers form a ‘chaotic’ set? J Geophys Res 97:19113. https://doi.org/10.1029/92JA01459
Priyal M, Banerjee D, Karak BB, Muñoz-Jaramillo A, Ravindra B, Choudhuri AR, Singh J (2014) Polar network index as a magnetic proxy for the solar cycle studies. Astrophys J Lett 793:L4. https://doi.org/10.1088/2041-8205/793/1/L4. arXiv:1407.4944
Qian B, Rasheed K (2004) Hurst exponent and financial market predictability. In: Hamza MH (ed) Financial engineering and applications (FEA 2004). Acta Press, pp 203–209
Racine É, Charbonneau P, Ghizaru M, Bouchat A, Smolarkiewicz PK (2011) On the mode of dynamo action in a global large-eddy simulation of solar convection. Astrophys J 735:46. https://doi.org/10.1088/0004-637X/735/1/46
Rangarajan GK (1998) Sunspot variability and an attempt to predict solar cycle 23 by adaptive filtering. Earth Planets Space 50:91–100. https://doi.org/10.1186/BF03352090
Rezaei R, Beck C, Schmidt W (2012) Variation in sunspot properties between 1999 and 2011 as observed with the Tenerife Infrared Polarimeter. Astron Astrophys 541:A60. https://doi.org/10.1051/0004-6361/201118635. arXiv:1203.1444
Rezaei R, Beck C, Lagg A, Borrero JM, Schmidt W, Collados M (2015) Variation in sunspot properties between 1999 and 2014. Astron Astrophys 578:A43. https://doi.org/10.1051/0004-6361/201425557
Richard JG (2004) The eight-Schwabe-cycle pulsation. Sol Phys 223:319–333. https://doi.org/10.1007/s11207-004-1165-0
Richardson JD, Paularena KI, Belcher JW, Lazarus AJ (1994) Solar wind oscillations with a 1.3 year period. Geophys Res Lett 21:1559–1560. https://doi.org/10.1029/94GL01076
Rieger E, Kanbach G, Reppin C, Share GH, Forrest DJ, Chupp EL (1984) A 154-day periodicity in the occurrence of hard solar flares? Nature 312:623–625. https://doi.org/10.1038/312623a0
Rigozo NR, Souza Echer MP, Evangelista H, Nordemann DJR, Echer E (2011) Prediction of sunspot number amplitude and solar cycle length for cycles 24 and 25. J Atmos Sol-Terr Phys 73(11–12):1294–1299. https://doi.org/10.1016/j.jastp.2010.09.005
Rouillard AP, Lockwood M, Finch I (2007) Centennial changes in the solar wind speed and in the open solar flux. J Geophys Res 112(A11):5103. https://doi.org/10.1029/2006JA012130
Ruždjak D, Brajša R, Sudar D, Skokić I, Poljančić Beljan I (2017) A relationship between the solar rotation and activity analysed by tracing sunspot groups. Sol Phys 292:179. https://doi.org/10.1007/s11207-017-1199-8. arXiv:1711.03723
Ruzmaikin A (1997) On the origin of sunspots. Astron Astrophys 319:L13–L16
Ruzmaikin A, Feynman J, Robinson P (1994) Long-term persistence of solar activity. Sol Phys 149:395–403. https://doi.org/10.1007/BF00690625
Rypdal M, Rypdal K (2012) Is there long-range memory in solar activity on timescales shorter than the sunspot period? J Geophys Res 117:A04103. https://doi.org/10.1029/2011JA017283. arXiv:1111.4787
Sarp V, Kilcik A, Yurchyshyn V, Rozelot JP, Ozguc A (2018) Prediction of solar cycle 25: a non-linear approach. Mon Not R Astron Soc 481:2981–2985. https://doi.org/10.1093/mnras/sty2470
Schatten KH, Pesnell WD (1993) An early solar dynamo prediction: cycle 23 is approximately cycle 22. Geophys Res Lett 20:2275–2278. https://doi.org/10.1029/93GL02431
Schatten KH, Sofia S (1987) Forecast of an exceptionally large even-numbered solar cycle. Geophys Res Lett 14:632–635. https://doi.org/10.1029/GL014i006p00632
Schatten KH, Scherrer PH, Svalgaard L, Wilcox JM (1978) Using dynamo theory to predict the sunspot number during solar cycle 21. Geophys Res Lett 5:411–414. https://doi.org/10.1029/GL005i005p00411
Schatten KH, Myers DJ, Sofia S (1996) Solar activity forecast for solar cycle 23. Geophys Res Lett 23:605–608. https://doi.org/10.1029/96GL00451
Schmidt HU (1968) Magnetohydrodynamics of an active region. In: Kiepenheuer KO (ed) Structure and development of solar active regions, IAU symposium, vol 35. Cambridge University Press, Cambridge, pp 93–107. https://doi.org/10.1017/S0074180900021379
Schüssler M, Baumann I (2006) Modeling the Sun’s open magnetic flux. Astron Astrophys 459:945–953. https://doi.org/10.1051/0004-6361:20065871
Schüssler M, Cameron RH (2018) Origin of the hemispheric asymmetry of solar activity. Astron Astrophys 618:A89. https://doi.org/10.1051/0004-6361/201833532. arXiv:1807.10061
Senthamizh Pavai V, Arlt R, Dasi-Espuig M, Krivova NA, Solanki SK (2015) Sunspot areas and tilt angles for solar cycles 7–10. Astron Astrophys 584:A73. https://doi.org/10.1051/0004-6361/201527080. arXiv:1508.07849
Serre T, Nesme-Ribes E (2000) Nonlinear analysis of solar cycles. Astron Astrophys 360:319–330
Sheeley NR Jr (1964) Polar faculae during the sunspot cycle. Astrophys J 140:731. https://doi.org/10.1086/147966
Sheeley NR Jr (2005) Surface evolution of the Sun’s magnetic field: a historical review of the flux-transport mechanism. Living Rev Sol Phys 2:5. https://doi.org/10.12942/lrsp-2005-5
Shirai T (2004) Time variation of the solar neutrino fluxes from Super-Kamiokande data. Sol Phys 222:199–201. https://doi.org/10.1023/B:SOLA.0000043565.83411.ec
Simard C, Charbonneau P, Dubé C (2016) Characterisation of the turbulent electromotive force and its magnetically-mediated quenching in a global EULAG-MHD simulation of solar convection. Adv Space Res 58:1522–1537. https://doi.org/10.1016/j.asr.2016.03.041. arXiv:1604.01533
Singh AK, Bhargawa A (2017) An early prediction of 25th solar cycle using Hurst exponent. Astrophys Space Sci 362:199. https://doi.org/10.1007/s10509-017-3180-2
Snodgrass HB, Dailey SB (1996) Meridional motions of magnetic features in the solar photosphere. Sol Phys 163:21–42. https://doi.org/10.1007/BF00165454
Solanki SK, Krivova NA, Schüssler M, Fligge M (2002) Search for a relationship between solar cycle amplitude and length. Astron Astrophys 396:1029–1035. https://doi.org/10.1051/0004-6361:20021436
Solanki S, Inhester B, Schüssler M (2006) The solar magnetic field. Rep Prog Phys 69:563–668. https://doi.org/10.1088/0034-4885/69/3/R02
Spruit HC (2003) Origin of the torsional oscillation pattern of solar rotation. Sol Phys 213:1–21. https://doi.org/10.1023/A:1023202605379. arXiv:astro-ph/0209146
Stephenson FR, Wolfendale AW (eds) (1988) Secular solar and geomagnetic variations in the last 10,000 years. NATO ASI Series C, vol 236. Kluwer, Dordrecht. https://doi.org/10.1007/978-94-009-3011-7
Stix M (1972) Non-linear dynamo waves. Astron Astrophys 20:9
Sugihara G, May RM (1990) Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 344:734–741. https://doi.org/10.1038/344734a0
Sun X, Hoeksema JT, Liu Y, Zhao J (2015) On polar magnetic field reversal and surface flux transport during solar cycle 24. Astrophys J 798:114. https://doi.org/10.1088/0004-637X/798/2/114. arXiv:1410.8867
Svalgaard L (2016) Reconstruction of solar extreme ultraviolet flux 1740–2015. Sol Phys 291:2981–3010. https://doi.org/10.1007/s11207-016-0921-2. arXiv:1506.04408
Svalgaard L (2017) A recount of sunspot groups on Staudach’s drawings. Sol Phys 292:4. https://doi.org/10.1007/s11207-016-1023-x
Svalgaard L, Cliver EW (2005) The IDV index: its derivation and use in inferring long-term variations of the interplanetary magnetic field strength. J Geophys Res 110(A9):12103. https://doi.org/10.1029/2005JA011203
Svalgaard L, Cliver EW (2007) Interhourly variability index of geomagnetic activity and its use in deriving the long-term variation of solar wind speed. J Geophys Res 112(A11):10111. https://doi.org/10.1029/2007JA012437. arXiv:0706.0961
Svalgaard L, Schatten KH (2016) Reconstruction of the sunspot group number: the backbone method. Sol Phys 291:2653–2684. https://doi.org/10.1007/s11207-015-0815-8. arXiv:1506.00755
Svalgaard L, Duvall TL Jr, Scherrer PH (1978) The strength of the Sun’s polar fields. Sol Phys 58:225–239. https://doi.org/10.1007/BF00157268
Svalgaard L, Cliver EW, Kamide Y (2005) Sunspot cycle 24: Smallest cycle in 100 years? Geophys Res Lett 32:1104. https://doi.org/10.1029/2004GL021664
Svalgaard L, Cagnotti M, Cortesi S (2017) The effect of sunspot weighting. Sol Phys 292:34. https://doi.org/10.1007/s11207-016-1024-9
Švanda M, Kosovichev AG, Zhao J (2007) Speed of meridional flows and magnetic flux transport on the Sun. Astrophys J Lett 670:L69–L72. https://doi.org/10.1086/524059. arXiv:0710.0590
Švanda M, Kosovichev AG, Zhao J (2008) Effects of solar active regions on meridional flows. Astrophys J Lett 680:L161. https://doi.org/10.1086/589997. arXiv:0805.1789
SWPC (2009) Solar cycle 24 prediction. https://www.swpc.noaa.gov/content/solar-cycle-24-prediction-updated-may-2009
Szabo A, Lepping RP, King JH (1995) Magnetic field observations of the 1.3-year solar wind oscillations. Geophys Res Lett 22:1845–1848. https://doi.org/10.1029/95GL01737
Thompson RJ (1993) A technique for predicting the amplitude of the solar cycle. Sol Phys 148:383–388. https://doi.org/10.1007/BF00645097
Tlatov AG (2009) The minimum activity epoch as a precursor of the solar activity. Sol Phys 260:465–477. https://doi.org/10.1007/s11207-009-9451-5
Tlatov AG, Vasil’eva VV, Pevtsov AA (2010) Distribution of magnetic bipoles on the Sun over three solar cycles. Astrophys J 717:357–362. https://doi.org/10.1088/0004-637X/717/1/357
Tlatova K, Tlatov A, Pevtsov A, Mursula K, Vasil’eva V, Heikkinen E, Bertello L, Pevtsov A, Virtanen I, Karachik N (2018) Tilt of sunspot bipoles in solar cycles 15 to 24. Sol Phys 293:118. https://doi.org/10.1007/s11207-018-1337-y. arXiv:1807.07913
Tong H (1993) Non-linear time series: a dynamical system approach. Oxford University Press, Oxford
Tritakis BP (1982) Evidence of interdependence within 22-year solar cycles. Astrophys Space Sci 82:463–471. https://doi.org/10.1007/BF00651452
Tsuneta S, Ichimoto K, Katsukawa Y, Lites BW, Matsuzaki K, Nagata S, Orozco Suárez D, Shimizu T, Shimojo M, Shine RA, Suematsu Y, Suzuki TK, Tarbell TD, Title AM (2008) The magnetic landscape of the Sun’s polar region. Astrophys J 688:1374–1381. https://doi.org/10.1086/592226. arXiv:0807.4631
Turner HH (1913a) On a simple method of detecting discontinuities in a series of recorded observations, with an application to sun-spots, suggesting that they are caused by a meteor swarm. Mon Not R Astron Soc 74:82–109. https://doi.org/10.1093/mnras/74.2.82
Turner HH (1913b) Sun-spots and faculæ, on the expression of sun-spot periodicity as a Fourier sequence, in similar problems. Mon Not R Astron Soc 73:714–732. https://doi.org/10.1093/mnras/73.9.714
Turner HH (1913c) Sun-spots and faculæ, on the harmonic analysis of Wolf’s sun-spot numbers, with special reference to Mr. Kimura’s paper. Mon Not R Astron Soc 73:549–552. https://doi.org/10.1093/mnras/73.7.549
Turner DC, Ladde GS (2018) Stochastic modelling, analysis, and simulations of the solar cycle dynamic process. Astrophys J 855:108. https://doi.org/10.3847/1538-4357/aaaf1c
Udny Yule G (1927) On a Method of Investigating Periodicities in Disturbed Series, with Special Reference to Wolfer’s Sunspot Numbers. Philos Trans R Soc London, Ser A 226:267–298
Upton L, Hathaway DH (2014a) Effects of meridional flow variations on solar cycles 23 and 24. Astrophys J 792:142. https://doi.org/10.1088/0004-637X/792/2/142. arXiv:1408.0035
Upton L, Hathaway DH (2014b) Predicting the Sun’s polar magnetic fields with a surface flux transport model. Astrophys J 780:5. https://doi.org/10.1088/0004-637X/780/1/5. arXiv:1311.0844
Upton LA, Hathaway DH (2018) An updated solar cycle 25 prediction with AFT: the modern minimum. Geophys Res Lett 45:8091–8095. https://doi.org/10.1029/2018GL078387. arXiv:1808.04868
Usoskin IG (2017) A history of solar activity over millennia. Living Rev Sol Phys 14:3. https://doi.org/10.1007/s41116-017-0006-9
Usoskin IG (2018) Comment on the paper by Popova, et al. On a role of quadruple component of magnetic field in defining solar activity in grand cycles. J Atmos Sol-Terr Phys 176:69–71. https://doi.org/10.1016/j.jastp.2017.09.018. arXiv:1710.05203
Usoskin IG, Mursula K, Kovaltsov GA (2001) Was one sunspot cycle lost in late xviii century? Astron Astrophys 370:L31–L34. https://doi.org/10.1051/0004-6361:20010319
Usoskin IG, Solanki SK, Kovaltsov GA (2007) Grand minima and maxima of solar activity: new observational constraints. Astron Astrophys 471:301–309. https://doi.org/10.1051/0004-6361:20077704. arXiv:0706.0385
Usoskin IG, Mursula K, Arlt R, Kovaltsov GA (2009a) A solar cycle lost in 1793–1800: early sunspot observations resolve the old mystery. Astrophys J Lett 700:L154–L157. https://doi.org/10.1088/0004-637X/700/2/L154. arXiv:0907.0063
Usoskin IG, Sokoloff D, Moss D (2009b) Grand minima of solar activity and the mean-field dynamo. Sol Phys 254:345–355. https://doi.org/10.1007/s11207-008-9293-6
Usoskin IG, Arlt R, Asvestari E, Hawkins E, Käpylä M, Kovaltsov GA, Krivova N, Lockwood M, Mursula K, O’Reilly J, Owens M, Scott CJ, Sokoloff DD, Solanki SK, Soon W, Vaquero JM (2015) The Maunder minimum (1645–1715) was indeed a grand minimum: a reassessment of multiple datasets. Astron Astrophys 581:A95. https://doi.org/10.1051/0004-6361/201526652. arXiv:1507.05191
Usoskin IG, Kovaltsov GA, Lockwood M, Mursula K, Owens M, Solanki SK (2016) A new calibrated sunspot group series since 1749: statistics of active day fractions. Sol Phys 291:2685–2708. https://doi.org/10.1007/s11207-015-0838-1. arXiv:1512.06421
Uwamahoro J, McKinnell L, Cilliers PJ (2009) Forecasting solar cycle 24 using neural networks. J Atmos Sol-Terr Phys 71:569–574. https://doi.org/10.1016/j.jastp.2008.12.003
Vaquero JM (2007) Historical sunspot observations: a review. Adv Space Res 40:929–941. https://doi.org/10.1016/j.asr.2007.01.087. arXiv:astro-ph/0702068
Vaquero JM, Trigo RM (2008) Can the solar cycle amplitude be predicted using the preceding solar cycle length? Sol Phys 250:199–206. https://doi.org/10.1007/s11207-008-9211-y
Vaquero JM, Kovaltsov GA, Usoskin IG, Carrasco VMS, Gallego MC (2015a) Level and length of cyclic solar activity during the Maunder minimum as deduced from the active-day statistics. Astron Astrophys 577:A71. https://doi.org/10.1051/0004-6361/201525962. arXiv:1503.07664
Vaquero JM, Nogales JM, Sánchez-Bajo F (2015b) Sunspot latitudes during the Maunder minimum: a machine-readable catalogue from previous studies. Adv Space Res 55:1546–1552. https://doi.org/10.1016/j.asr.2015.01.006. arXiv:1501.05989
Vaquero JM, Svalgaard L, Carrasco VMS, Clette F, Lefèvre L, Gallego MC, Arlt R, Aparicio AJP, Richard JG, Howe R (2016) A revised collection of sunspot group numbers. Sol Phys 291:3061–3074. https://doi.org/10.1007/s11207-016-0982-2. arXiv:1609.04882
Vigouroux A, Delachie P (1994) Sunspot numbers uncertainties and parametric representations of solar activity variations. Sol Phys 152:267–274. https://doi.org/10.1007/BF01473214
Virtanen IOI, Virtanen II, Pevtsov AA, Yeates A, Mursula K (2017) Reconstructing solar magnetic fields from historical observations. II. Testing the surface flux transport model. Astron Astrophys 604:A8. https://doi.org/10.1051/0004-6361/201730415
Virtanen IOI, Virtanen II, Pevtsov AA, Bertello L, Yeates A, Mursula K (2019) Reconstructing solar magnetic fields from historical observations. V. Testing the reconstruction method. Astron Astrophys 627:A11
Vitinsky YI (1963) Prognozi solnechnoi aktivnosti. Nauka, Leningrad
Vitinsky YI (1973) Tsiklichnost i prognozi solnechnoi aktivnosti. Nauka, Leningrad
Vitinsky YI, Kopecký M, Kuklin GV (1986) Statistika Pyatnoobrazovatel’noy Deyatel’nosti Solntsa. Nauka, Moscow
Vokhmyanin MV, Zolotova NV (2018) Sunspot positions and areas from observations by Galileo Galilei. Sol Phys 293:31. https://doi.org/10.1007/s11207-018-1245-1
Waldmeier M (1935) Neue Eigenschaften der Sonnenfleckenkurve. Astr Mitt Zürich 14:105–130
Waldmeier M (1961) The sunspot activity in the years 1610–1960. Schultheiss & Co., Zürich
Wang YM (2017) Surface flux transport and the evolution of the Sun’s polar fields. Space Sci Rev 210:351–365. https://doi.org/10.1007/s11214-016-0257-0
Wang YM, Sheeley NR (2009) Understanding the geomagnetic precursor of the solar cycle. Astrophys J Lett 694:L11–L15. https://doi.org/10.1088/0004-637X/694/1/L11
Wang YM, Robbrecht E, Sheeley NR (2009) On the weakening of the polar magnetic fields during solar cycle 23. Astrophys J 707:1372–1386. https://doi.org/10.1088/0004-637X/707/2/1372
Warnecke J, Rheinhardt M, Tuomisto S, Käpylä PJ, Käpylä MJ, Brandenburg A (2018) Turbulent transport coefficients in spherical wedge dynamo simulations of solar-like stars. Astron Astrophys 609:A51. https://doi.org/10.1051/0004-6361/201628136. arXiv:1601.03730
Watson FT, Penn MJ, Livingston W (2014) A multi-instrument analysis of sunspot umbrae. Astrophys J 787:22. https://doi.org/10.1088/0004-637X/787/1/22. arXiv:1511.07300
Wei WWS (2005) Time series analysis: univariate and multivariate methods, 2nd edn. Addison Wesley, Reading
Weiss NO, Cattaneo F, Jones CA (1984) Periodic and aperiodic dynamo waves. Geophys Astrophys Fluid Dyn 30:305–341. https://doi.org/10.1080/03091928408219262
Whitbread T, Yeates AR, Muñoz-Jaramillo A, Petrie GJD (2017) Parameter optimization for surface flux transport models. Astron Astrophys 607:A76. https://doi.org/10.1051/0004-6361/201730689. arXiv:1708.01098
Whitbread T, Yeates AR, Muñoz-Jaramillo A (2018) How many active regions are necessary to predict the solar dipole moment? Astrophys J 863:116. https://doi.org/10.3847/1538-4357/aad17e. arXiv:1807.01617
Willamo T, Usoskin IG, Kovaltsov GA (2017) Updated sunspot group number reconstruction for 1749–1996 using the active day fraction method. Astron Astrophys 601:A109. https://doi.org/10.1051/0004-6361/201629839. arXiv:1705.05109
Willamo T, Usoskin IG, Kovaltsov GA (2018) A test of the active-day fraction method of sunspot group number calibration: dependence on the level of solar activity. Sol Phys 293:69. https://doi.org/10.1007/s11207-018-1292-7. arXiv:1803.10501
Wilmot-Smith AL, Nandy D, Hornig G, Martens PCH (2006) A time delay model for solar and stellar dynamos. Astrophys J 652:696–708. https://doi.org/10.1086/508013
Winch DE, Ivers DJ, Turner JPR, Stening RJ (2005) Geomagnetism and Schmidt quasi-normalization. Geophys J Int 160:487–504. https://doi.org/10.1111/j.1365-246X.2004.02472.x
Winter LM, Pernak RL, Balasubramaniam KS (2016) Comparing SSN index to X-ray flare and coronal mass ejection rates from solar cycles 22–24. Sol Phys 291(9–10):3011–3023. https://doi.org/10.1007/s11207-016-0901-6. arXiv:1605.00503
Wolf R (1850) Mittheilungen über die Sonnenflecken I. Astr Mitt Zürich 1:3–13
Wolf R (1861) Abstract of his latest results. Mon Not R Astron Soc 21:77. https://doi.org/10.1093/mnras/21.3.77
Wu CJ, Usoskin IG, Krivova N, Kovaltsov GA, Baroni M, Bard E, Solanki SK (2018) Solar activity over nine millennia: a consistent multi-proxy reconstruction. Astron Astrophys 615:A93. https://doi.org/10.1051/0004-6361/201731892. arXiv:1804.01302
Yeates AR (2014) Coronal magnetic field evolution from 1996 to 2012: continuous non-potential simulations. Sol Phys 289:631–648. https://doi.org/10.1007/s11207-013-0301-0. arXiv:1304.0609
Yeates AR, Muñoz-Jaramillo A (2013) Kinematic active region formation in a three-dimensional solar dynamo model. Mon Not R Astron Soc 436:3366–3379. https://doi.org/10.1093/mnras/stt1818. arXiv:1309.6342
Yeates AR, Nandy D, Mackay DH (2008) Exploring the physical basis of solar cycle predictions: flux transport dynamics and persistence of memory in advection- versus diffusion-dominated solar convection zones. Astrophys J 673:544–556. https://doi.org/10.1086/524352. arXiv:0709.1046
Yeates AR, Baker D, van Driel-Gesztelyi L (2015) Source of a prominent poleward surge during solar cycle 24. Sol Phys 290:3189–3201. https://doi.org/10.1007/s11207-015-0660-9. arXiv:1502.04854
Zaqarashvili TV, Carbonell M, Oliver R, Ballester JL (2010) Magnetic Rossby waves in the solar tachocline and Rieger-type periodicities. Astrophys J 709:749–758. https://doi.org/10.1088/0004-637X/709/2/749. arXiv:0911.4591
Zeldovich YB, Ruzmaikin AA, Sokoloff DD (1984) Magnetic fields in astrophysics. Gordon & Breach, New York
Acknowledgements
This work was supported by the Hungarian National Research, Development and Innovation Fund (Grant No. NKFI K-128384) and by the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 739500. Some figures (or their input data) have been provided by J. Jiang, A. Kilcik and P. Charbonneau, as noted in the captions. Source for International Sunspot Numbers: WDC-SILSO, Royal Observatory of Belgium, Brussels. Wilcox Solar Observatory data used in this study was obtained via the web site http://wso.stanford.edu, courtesy of J. T. Hoeksema. The Wilcox Solar Observatory is currently supported by NASA.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Petrovay, K. Solar cycle prediction. Living Rev Sol Phys 17, 2 (2020). https://doi.org/10.1007/s41116-020-0022-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41116-020-0022-z
Keywords
Article history
Latest
Solar cycle prediction- Published:
- 23 March 2020
- Received:
- 02 July 2019
- Accepted:
- 17 January 2020
DOI: https://doi.org/10.1007/s41116-020-0022-z
Original
Solar Cycle Prediction- Published:
- 01 December 2010
DOI: https://doi.org/10.12942/lrsp-2010-6