Introduction

Clean and safe water is essential for human consumption, hygiene, and sanitation. Contaminated water harbors harmful microorganisms, pathogens, and pollutants that cause waterborne diseases, such as diarrhea, cholera, typhoid, and hepatitis (Nemčić-Jurec et al. 2022). Water quality plays a crucial role in maintaining the health of aquatic ecosystems, including rivers, lakes, wetlands, and oceans. Aquatic organisms, including fish, plants, and other wildlife, depend on clean water to survive and thrive. Polluted water, containing chemicals, toxins, or excessive nutrients, leads to habitat degradation, species loss, and disruptions in the ecological balance (Bhat et al. 2022). Water quality is critical for agriculture and food production. Contaminated water used for irrigation negatively impacts crop health and productivity. It also leads to the accumulation of harmful substances in food, posing risks to human health. Maintaining good water quality in irrigation systems is essential for sustainable agriculture and safe food production (Mensah-Akutteh et al. 2022). Water quality is crucial for human health, ecosystem functioning, sustainable development, and various economic activities. It is essential to monitor, manage, and maintain water quality to safeguard human well-being, protect the environment, and ensure the sustainable use of this precious resource (Giri et al. 2022).

Electrical conductivity (EC) is an important parameter used to assess and monitor water quality. It is a measure of the ability of water to conduct an electric current and is influenced by the concentration of dissolved ions in the water (Naiel et al. 2022). Electrical conductivity provides an estimate of the TDS concentration in water. TDS refers to the total concentration of inorganic and organic substances dissolved in water, including salts, minerals, metals, and other dissolved solids. High EC values generally indicate higher TDS levels, which can affect the taste, odor, and overall palatability of water (Ezea et al. 2022). Electrical conductivity is commonly used as a measure of salinity in water bodies. Salinity refers to the concentration of salts, particularly sodium chloride, in water. High EC values indicate higher salinity levels, which have adverse effects on aquatic life, irrigation practices, and the suitability of water for various uses (Liu et al. 2023). Changes in electrical conductivity indicates the presence of pollutants or contaminants in water. Elevated EC levels may suggest the presence of dissolved substances like heavy metals, industrial chemicals, agricultural runoff, or sewage contamination. Monitoring EC can help identify potential pollution sources and assess the overall water quality (Lakrout et al. 2022). Electrical conductivity is also used in agriculture to assess soil and irrigation water quality. High EC in irrigation water leads to increased soil salinity, negatively affecting soil fertility and crop growth. Monitoring EC helps farmers and agricultural professionals make informed decisions about irrigation practices and nutrient management to maintain soil health and crop productivity (Gomaa 2020). Electrical conductivity plays a significant role in assessing water quality by providing information about TDS concentration, salinity, pollution levels, and suitability for various uses. Monitoring EC helps identify potential issues, implement appropriate water management practices, and ensure compliance with regulatory standards to protect both human health and the environment.

EC measurement is primarily sensitive to the presence of ions in the water. It may not detect non-ionic substances or organic contaminants that do not significantly contribute to the electrical conductivity. Therefore, EC measurements alone may not provide a comprehensive assessment of water quality in terms of organic pollutants or certain non-ionic substances (Igboama et al. 2022). EC is influenced by temperature variations. Changes in temperature affects the accuracy of EC measurements. To overcome this limitation, temperature compensation techniques or standardized temperature conditions are often employed, but variations in temperature still introduce uncertainties in the measurement (Ghorbani et al. 2017). EC measurements are typically point measurements taken at a specific location in the water body. This limited spatial resolution may not capture the spatial heterogeneity of water quality parameters, especially in large or complex water systems. To obtain a more comprehensive understanding of water quality, additional sampling points or continuous monitoring techniques may be required (Mahanta et al. 2022). While changes in EC indicates the presence of contaminants, it does not provide information on the specific sources or types of contaminants. Additional testing and analysis are often needed to identify and quantify specific pollutants in the water (Maansi et al. 2022). It is important to consider these limitations when interpreting EC measurements and to complement them with other water quality parameters and analyses to obtain a more comprehensive understanding of water quality conditions and potential pollutant sources. The accurate measurements of EC in laboratory with considering these limitation is very difficult, time consuming, require large amount of assets, require high skill man power and also need large amount of economy. The limitations of electrical conductivity (EC) measurements pose challenges in obtaining accurate and efficient results, especially when considering factors like time, cost, and expertise. Machine learning algorithms offer a promising approach to address these challenges and enhance the accuracy and efficiency of EC prediction (Taşan 2023). By training machine learning models using historical data that includes both EC measurements and associated water quality parameters, it is possible to establish relationships and patterns that are used to predict EC values in the future. Machine learning models have the potential to capture complex relationships and nonlinear dependencies between EC and other water quality parameters, allowing for more accurate predictions (Boubakri et al. 2023). Using machine learning algorithms also helps overcome the limitations of EC measurements by incorporating additional variables and parameters that may contribute to water quality. By considering a wider range of inputs, such as temperature, pH, dissolved oxygen, and specific ion concentrations, machine learning models provides a more comprehensive understanding of water quality conditions and potential pollutant sources. Additionally, machine learning models automate the prediction process, reducing the need for extensive manual labor and time-consuming laboratory measurements. Once the model is trained, it quickly processes new data and provides near real-time predictions of EC, making it a more efficient and cost-effective solution compared to traditional laboratory measurements.

The issue of water saltiness is especially vital in arid and semiarid, mostly waterfront zones, where overuse of groundwater to cover intemperate crop water needs, particularly in summer, may prompt ocean water interruption, in this manner falling apart irrigation water quality, lastly, bringing about the supposed optional soil salinization (Szabolcs 1986). High salt concentrations in waste effluents can build up the saltiness of the water, which may result in unfriendly natural impacts on amphibian biota (Dunlop et al. 2005). Electrical conductivity can be utilized for evaluating the impact of various particles on chemical balance, physiological consequences for plants or creatures, and erosion rates (Kisi and Ay 2014). Environmentalists and ecologists are applying electrical conductivity to follow the movement of the water system in order to foresee and take care of issues with marine life (Chapman 1996). An effective investigation of salinity and irrigation water quality needs electrical conductivity data, which is measured only at specific stations of the central water commission in India. The large number of relationships developed with other water quality parameters for estimating the electrical conductivity of water. However, no forecasting model was developed for the prediction of the electrical conductivity of water.

In recently years, the large quantity of research was completed based on machine-learning in several fields such as hydrology (Mirbagheri et al. 2010; Noori et al. 2011; Kisi and Shiri 2012; Atieh et al. 2015; Singh et al. 2016a, b, 2017, 2018a, b, 2022a, b; Kumar et al. 2019; Esfahani and Keshavarzi 2020; Elbeltagi et al. 2022, 2023a, b, c; Markuna et al. 2023; Achite et al. 2023; Saroughi et al. 2023; Mirzania et al. 2023), ground water level forecasting (Samantaray et al. 2022; Saroughi et al. 2023), soil permeability and hydraulic conductivity (Sihag et al. 2019a, b; Singh et al. 2022b), soil moisture (Gu et al. 2021), sprinkler irrigation’s wind drift and evaporation losses (Al-Ghobari et al. 2018; Mattar et al. 2022), soil temperature (Tabari et al. 2011; Napagoda and Tilakaratne 2012; Singh et al. 2018b), evapotranspiration (Mattar 2018; Roy et al. 2022), irrigation water infiltration rate (Mattar et al. 2017), meteorological droughts and standardized precipitation index (SPI) (Bouaziz et al. 2021; Elbeltagi et al. 2023b), global solar radiation (Hassan et al. 2017; Voyant et al. 2017; Cornejo-Bueno et al. 2019; Feng et al. 2019; Ağbulut et al. 2021), water quality (Maier et al. 2010; Barzegar et al. 2018; Deng et al. 2021; Singha et al. 2021), medical (Chen et al. 2015; Venkatesan and Velmurugan 2015; Podolsky et al. 2016). Tutmez et al. (2006) applied the adaptive neuro-fuzzy inference system (ANFIS) algorithm to predict the EC of groundwater using ions present in the water. The performance of the ANFIS algorithm was better than that of traditional approaches. Wen et al. (2013) applied artificial intelligence techniques to develop a reliable prediction model for the dissolved oxygen (DO) of surface water in the Heihe River. Also, most input variables influence on output was examined by sensitivity analysis. Nemati et al. (2015) investigated the usability of machine learning and regression algorithms in the simulation of the DO. It is the most effective physical properties of quality water to study aquatic subsidies, health care, water quality, and aquatic ecosystems. Eight different physiochemical parameters were used for the prediction of DO in two different rivers. Ghorbani et al. (2017) forecasted the EC concentration of surface water in the Asi River based on a machine learning algorithm to assess the water quality based on physiochemical parameters of surface water. In addition, outcomes were compared with regression-based techniques. Khadr and Elshemy (2017) studied the abilities of the ANFIS model for forecasting different water quality factors based on electrical conductivity, turbidity, discharge, water temperature, dissolved oxygen, total suspended solids, total dissolved solids, and pH. Najah Ahmed et al. (2019) applied different artificial intelligence algorithms for the prediction of suspended solids, ammoniacal nitrogen, and pH of surface water in the Johor River Basin. The results of all algorithms were found satisfactory. Ekemen Keskin et al. (2020) used machine learning and regression-based techniques to predict groundwater EC. Various hydro-chemical parameters were applied as input variables, which affect the EC. Mokhtar et al. (2022) demonstrated the potential of using multiple regression models and the developed machine learning methods for predicting the irrigation water quality index. The models were served as rapid decision tools for modeling irrigation water quality, assisting in water resource management strategies. Masoudi et al. (2023) demonstrated that the RF model outperformed the other models, albeit with only a slight difference in accuracy. Additionally, the analysis of relative importance highlighted that the sodium adsorption ratio (SAR) and pH had the most significant impact in explaining groundwater quality classes.

After reviewing the importance of fresh water, the role of electrical conductivity for the assessment of water quality, limitations during measurement of electrical conductivity, potential and accuracy of machine learning, and its wide range of applications in different fields. The authors applied four different machine learning algorithms namely decision tree (DT), multilayer perceptron (MLP), random forest (RF), and co-adaptive neuro-fuzzy inference system (CANFIS) for the prediction of the electrical conductivity of surface water in the Upper Ganga basin. The study aimed to investigate the optimal input–output arrangements and the length of training and testing datasets using cross-correlation and gamma testing. Additionally, the researchers aimed to develop an efficient machine learning model for multi-ahead forecasting of electrical conductivity in the Upper Ganga basin and compare the performance of the DT, MLP, RF, and CANFIS algorithms for electrical conductivity prediction.

Materials and methods

Data collection and study area

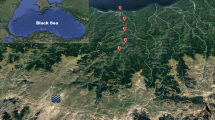
The Ganga River originates in the Uttarakhand state of India, beginning with the Gangrotri glacier. The present study was concentrated on Varanasi and Prayagraj sites switched in the main branch of the Upper Ganga basin, as presented in Fig. 1. The total area of 87,787 km2 is covered by the Upper Ganga Basin. The high-altitude difference present in the Upper Ganga basin ranges from 7500 m in the upper mountain region to 100 m in the lower plains. The study site is presented in the lower plane of the Upper Ganga basin. The yearly normal precipitation varies from 550 to 2500 mm in mountainous to plain areas of the Upper Ganga basin. The monthly water sample was picked up from Prayagraj and Varanasi sites of the Upper Ganga River basin and analyzed by the Central Water Commission (CWC), New Delhi, India. The water sample was collected in the first week of the month. The total of 37 years from 1980 to 2016 of water quality data was acquired from the divisional office of the Central Water Commission, Lucknow, Uttar Pradesh, India. The total data was divided into two different sets: the training data set (362), used for the development of the model, and the testing data set (82) used for multi-ahead validation of the model.

Fig. 1
figure 1

Location information about the present study area of Upper Ganga basin

Full size image

Machine learning algorithms

Multilayer perceptron (MLP) algorithm

MLP is a system architecture of ANN that consists of one or more hidden layers between the independent vectors (input vectors) and dependent vector (output vector). The independent layer nodes obtain signal permits to depended layer by hidden layer (Singh et al. 2018a). The independent vectors are multiplied over and done with the initial weight value; then, produce every neuron input vector of the next layer. Then, acquire dependent of hidden (dependent vector) layer neurons through activation function. The neurons in each node were found through a large number of trails. The literature on MPL can be found in Fu (1994); Srinivasulu and Jain (2006); Rezaeianzadeh et al. (2014).

Co-adaptive neuro-fuzzy inference system (CANFIS) algorithm

A standout among the most prominent incorporated frameworks is CANFIS, which has indicated promising outcomes in displaying nonlinear arrangements. In CANFIS, a Takagi–Sugeno-type fuzzy induction framework is utilized. The independent yield of each standard can be a direct composite of independent input vectors in addition to a consistent term. The data space of CANFIS is disconnected into three one-of-a-kind parts to store the data (Malik and Kumar 2015; Singh et al. 2016b; Gholami et al. 2021). The methodologies are named scatter, grid, and art. Fragmentary examination is normally utilized as a piece of control world in light of its rightness (Aytek 2009). Fuzzy inference frameworks are also refreshing as they relate the illustrative idea of tenets (membership function) with the direction of “black-box” neural systems. The optimal parameters of CANFIS algorithms were defined by a large number of trails. The elementary information about CANFIS algorithms was found in Mizutani and Jang (1995); Aytek (2009); Tahmasebi and Hezarkhani (2011).

Random forest (RF) regression algorithm

The RF algorithm is a characterization and regression strategy consisting of a mix of tree indicators, where each tree is produced utilizing an arbitrary vector examined freely from the information vector. In regression, the RF regression algorithm is a troupe strategy fit for performing both relapse and order undertakings with the utilization of different choice (decision) trees and a method called Bootstrap and Aggregation, ordinarily known as bagging (Breiman 1999, 2001). The essential thought behind this is to join numerous choice trees in deciding the last yield as opposed to depending on singular choice trees (Hastie et al. 2001; Karimi et al. 2018). The RF algorithm has numerous choice trees as base learning models. We arbitrarily perform line examining and highlight inspecting from the dataset, shaping example datasets for each model. This part is called Bootstrap (Pal and Mather 2003; Chen et al. 2017). Bootstrap alludes to irregular inspection with substitution. Bootstrap permits us to more likely comprehend the predisposition and the difference in the dataset. Bootstrap includes the arbitrary examination of a small subset of information from the dataset. It is a general strategy that can be utilized to lessen the fluctuation for those calculations that have high differences, commonly called choice trees. Sacking makes each model run freely and afterward totals the yields toward the end without inclination to any model (Quinlan 1992; Adams and Sterling 1992).

Decision tree (DT) algorithm

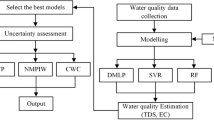
The DT algorithm is one of the outstanding classification strategies. DT constructs relapse or characterization models as a tree structure. It separates a dataset into smaller and smaller subsets while simultaneously a related DT is gradually evolved. The conclusive outcome is a tree with choice (decision) hubs and leaf hubs (Fakhari and Moghadam 2013). A choice hub (e.g., Outlook) has at least two branches, each speaking to values for the property tried (Nasridinov et al. 2013; Nagalla et al. 2017). The leaf hub speaks to a choice on the numerical objective. The highest-choice hub in a tree, which compares to the best indicator called the root hub. Choice trees can deal with both all-out and numerical information (Lee et al. 2013; Loh 2014). The facts of the DT algorithm can be assessed from (Harb et al. 2009; Fakhari and Moghadam 2013; Czajkowski and Kretowski 2016). The flow diagram of methodology is presented in Fig. 2.

Fig. 2
figure 2

Flowchart of complete process

Full size image

Performance evaluation

It is very important to clearly identify the criteria that are used to judge the performance of the model in order to evaluate its effectiveness. Throughout the literature, it has been clearly mentioned that the performance of the model in this study was measured according to a set of criteria. All of the aforementioned decision tree (DT), multilayer perceptron (MLP), random forest (RF), and co-adaptive neuro-fuzzy inference system (CANFIS) models were evaluated on the basis of a variety of measures of goodness of fit in order to assess their predictive power. A variety of statistical indices were used in this analysis, including Percent Bias (PBIAS), Root Mean Square Error (RMSE), Correlation Coefficient (R), Coefficient of Efficiency (CE), Index of Agreement (PI), Willmott’s Index (WI) and Legate-McCabe Index (LMI). The following equations were used to calculate these indices (Vishwakarma et al. 2018; Kumar et al. 2022; Singh et al. 2022a, b; Khatti and Grover 2023):

$$\mathrm{PBIAS }(\mathrm{\%})=\frac{\sum_{t=1}^{N}\left({EC}_{p}-{EC}_{t}\right)}{\sum_{i=1}^{N}{EC}_{t}}\times 100$$
(1)
$$\mathrm{RMSE}=\sqrt{\frac{{\sum }_{i=1}^{n}{({EC}_{t}-{EC}_{p})}^{2}}{n}}$$
(2)
$$R=\left[\frac{{\sum }_{i=1}^{n}\left\{({EC}_{t}-{\overline{EC} }_{t})({EC}_{p}-{\overline{EC} }_{p})\right\}}{\sqrt{{\sum }_{i=1}^{n}{({EC}_{t}-{\overline{EC} }_{t})}^{2}}\sqrt{{\sum }_{i=1}^{n}{({EC}_{p}-{\overline{EC} }_{p})}^{2}}}\right]$$
(3)
$$\mathrm{CE}=1-\frac{\sum_{i=1}^{n}{\left({EC}_{t}-{EC}_{p}\right)}^{2}}{\sum_{i=1}^{n}{\left({EC}_{t}-{\overline{EC} }_{t}\right)}^{2}}$$
(4)
$$\mathrm{PI}=1-\frac{{\sum }_{i=1}^{n}{({EC}_{\mathrm{t}}-{EC}_{p})}^{2}}{\sum_{i=1}^{n}{\left(\left|{EC}_{p}-{\overline{EC} }_{t}\right|+\left|{EC}_{t}-{\overline{EC} }_{t}\right|\right)}^{2}}$$
(5)
$$\mathrm{WI}=1-\frac{\sum_{i=1}^{n}{\left({EC}_{t}-{EC}_{p}\right)}^{2}}{\sum_{i=1}^{n}{\left(\left|{EC}_{p}-{\overline{EC} }_{t}\right|+\left|{EC}_{t}-{\overline{EC} }_{t}\right|\right)}^{2}}$$
(6)
$$\mathrm{LMI}=1-\left[\frac{\sum_{i=1}^{n}\left|{EC}_{p}-{\overline{EC} }_{p}\right|}{\sum_{i=1}^{n}\left|{EC}_{t}-{\overline{EC} }_{t}\right|}\right]$$
(7)

where ECt is measured electrical conductivity data series, ECp is modeled electrical conductivity data series, n is number of observations.\({\overline{EC} }_{t}\) is average of the measured electrical conductivity data series and \({\overline{EC} }_{p}\) is average of modeled electrical conductivity data series.

R measures how well the model fits the data, but RMSE measures how well the model fits the data in an absolute sense, and a lower value of RMSE indicates that the model fits better. The index of agreement (d) was developed by Willmott (1981) as a standardized measure of the degree of model prediction error and varies between 0 and 1. A value of 1 indicates a perfect match, and 0 indicates no agreement at all. The model that has the highest index of agreement (d), r, and R2, and the least error (RSME), will be the best model (Kushwaha et al. 2021; Vishwakarma et al. 2022a, b).

In addition to the statistical parameters stated in Eqs. (1–7), the correctness of the investigated models was validated using a scatter plot, Violin diagram, a discrepancy ratio (DR), and a Taylor diagram (TD) (Taylor 2001), among other. A simplified definition of the Taylor diagram is a thorough depiction of the observed and expected data (Taylor 2001). Taylor delivered a single demonstration demonstrating how to simultaneously show several assessment metrics in real-time. Correlation coefficients and standard deviation values between expected and observed values might be shown in this diagram to aid in the detection of changes between the two values (Taylor 2001; Elbeltagi et al. 2023b; Saroughi et al. 2023; Vishwakarma et al. 2023).

Results

In this study, the capability of four different modeling algorithms for forecasting the electrical conductivity of surface water was evaluated based on performance evaluation criteria (PBIAS, RMSE, R, CE, PI, WI and LMI) obtained from observed and modeled datasets during training (calibration) and testing periods. The obtained outcomes from four various algorithms were presented in terms of a scatter diagram and a time series diagram between measured and modeled electrical conductivity of surface water for the duration of testing. Four different algorithms, specifically MLP, RF, CANFIS, and DT, were applied for the prediction of the EC of surface water in the Upper Ganga basin at Varanasi and Prayagraj sites and developed models to compare with each other. Table 1 illustrates the parameters of these four different algorithms applied for prediction. The modeling capability of MLP, RF, CANFIS, and DT algorithms is influenced by their parameters. The optimal parameters of different algorithms were defined through a large number of trials and compared with different performance indices. Similarly, Table 2 illustrates the performance of the developed model during the training and testing periods at the Varanasi and Prayagraj sites. The CANFIS and MLP algorithm-based electrical conductivity forecasting models were established via NeuroSolution 5.0 and the R Studio 3.5.1 version used for the establishment of RF and DT models.

Table 1 Input and outputs combinations for EC prediction
Full size table
Table 2 Performance of different machine learning algorithms at Varanasi.
Full size table

Input vector selection based on gamma test

Gamma test has a decent capability of selecting appropriate input vectors from a large number of input vectors (Stefánsson et al. 1997; Shukla et al. 2021; Markuna et al. 2023). A large number of input vectors has a high probability of overfitting the model and increases its complexity (Bajirao et al. 2021a, b). In the present study, we analyzed the twenty-one biological, chemical, and physical parameters of surface water at Varanasi and Prayagraj stations of the Upper Ganga basin using a correlation chord diagram, which is presented in Fig. 3. It shows from the correlation diagram that calcium (Ca), magnesium (Mg), sodium (Na), total hardness (TH), chloride (Cl), and hardness due to MgCO3 parameters of water quality were correlated with the EC of surface water at both stations. Therefore, these parameters were applied to develop the input–output arrangement of the model based on the gamma test, which is presented in Table 1. Eight different combinations were explored to determine the most efficient input–output arrangements based on the minimum values of gamma and standard error. It was therefore the gamma test applied for electing relevant input and output arrangements. After analyzing the results of the gamma test, it was finalized that total hardness (TH), magnesium (Mg), and chloride (Cl) inputs combinations have a minimum value of gamma (0.0154) and standard error (0.0345) for Varanasi station; gamma (0.0148) and standard error (0.0245) for Prayagraj station. The basic literature can be assessed in several articles (Stefánsson et al. 1997; Kakaei Lafdani et al. 2013; Czajkowski and Kretowski 2016). Singh et al. (2018a) compared the potential of gamma test and correlation function for sorting appropriate input–output combination. The gamma test was found to be effective in capturing both linear and nonlinear relationships between input and output variables. By comparing its performance across several datasets, Markuna et al. (2023) evaluated the gamma test’s robustness and generalization capacity. It was determined that the machine learning model with the greatest potential and efficiency for long-term rainfall was obtained at minimal values for gamma, SE, and V-ratio. According to Kumar et al. (2022), the gamma test (GT) examines the relationship between the information vector, which consists of the days of anthesis, days of silking, days to senescence, plant height, ear length, number of kernels, and gross yield per plant, and the yield vector, represented by the drought-tolerance index (DTI) and stress-tolerance index (STI), and both. The goal of the research was to determine the configuration that produced the lowest gradient, standard error (SE), and gamma values. While the SE offers a way to gauge the degree of uncertainty surrounding the predicted gradient, the gradient indicates the rate of change in the yield vector with respect to the information vector. The information and yield vectors have a strong link, which is indicated by the gamma value. Singh et al. (2020) investigated 22 models and chose the best inputs (sand, silt, clay, and OC) as the model’s input variables. The best input variables were chosen based on the lowest gamma and SE values, which show a strong and consistent relationship between the chosen input factors and soil permeability. When we sorted the optimal input/output combination, we also discovered a similar outcome.

Fig. 3
figure 3

Correlation chord diagram of parameters in Varanasi (a) and Prayagraj stations (b)

Full size image

Comparison of different machine learning algorithms

The results of the developed models are presented in Tables 2 and 3. The MLP model was developed using the Tan hyperbolic (Tanh) transfer function and the Levenberg Marquard (LM) learning rule. The processing element (neuron) and hidden layer were defined based on trial-and-error technique. The neuron was varied from 1 to 50 with a single hidden layer during the development of the model and also compared for each model based on error value during the training and testing periods. The best architectures of the MLP model for Varanasi and Prayagraj stations were obtained (3–29–1) and (3–11–1), respectively, among all other models. The values of PBIAS (0.11), RMSE (360.42), R (0.956), CE (0.932), PI (0.083), WI (0.908) and LMI (0.085) were found during the training period, and PBIAS (− 0.46), RMSE (26.57), R (0.929), CE (0.915), PI (0.033), WI (0.965) and LMI (-0.028) during testing at Varanasi station. In addition, the performance index values of PBIAS (0.50), RMSE (368.3), R (0.909), CE (0.872), PI (0.015), WI (0.921) and LMI (0.083) at the Prayagraj site were estimated during training time. Similarly, values of PBIAS (− 0.06), RMSE (24.1), R (0.903), CE (0.878), PI (0.035), WI (0.960) and LMI (− 0.038) were found during the testing period. The CANFIS model was prepared by applying the Bell membership function (MFs) and Takagi–Sugeno-Kang (TSK) fuzzy model. In the CANFIS model, membership functions (MFs) per input were defined based on the trial-and-error technique and vary only from 2 to 7 because of the complexity of the model and available computer facilities. The membership function (4) per input was found in the best model among all developed models. The result of the CANFIS model originated in terms of PBIAS (0.24), RMSE (419.13), R (0.799), CE (0.0.638), PI (0.096), WI (0.865) and LMI (0.109 during the training period and PBIAS (-7.90), RMSE (54.19), R (0.708), CE (0.738), PI (0.082), WI (0.791) and LMI (0.060) during testing time at the Varanasi site.

Table 3 Performance of different machine learning algorithms at Prayagraj.
Full size table

Moreover, For MLP model, the values of PBIAS = 1.55, RMSE = 372.39, r = 0.932, CE = 0.867, PI = 0.102, WI = 0.964, LMI = 0.055 during training and PBIAS = − 10.77, RMSE = 48.02, r = 0.744, CE = 0.876, PI = 0.081, WI = 0.605, LMI = 0.305, respectively, during the testing period in Varanasi site. In the RF model, the number of trees was decided based on the error rate. The out-of-bag (OOB) was initially dropped, then became more and less constant at 300 trees. The number of mtry in the model was definite based on OOB error. The value of OOB was at its minimum (1.81) at 7 mtry in the developed model. After comparing the results of the developed RF model, the values of PBIAS = 0.11, RMSE = 360.42, r = 0.956, CE = 0.932, PI = 0.083, WI = 0.908, LMI = 0.083 were obtained during training and PBIAS = − 0.46, RMSE = 26.57, r = 0.929, CE = 0.915, PI = 0.033, WI = 0.965, LMI = − 0.028, respectively, during the testing period in Varanasi. Correspondingly, values of PBIAS = 0.50, RMSE = 368.3, R = 0.909, CE = 0.872, PI = 0.015, WI = 0.921, LMI = 0.083 during training and PBIAS = − 0.06, RMSE = 24.1, R = 0.903, CE = 0.878, PI = 0.035, WI = 0.960, LMI = − 0.038, respectively, during the testing period in Prayagraj. In the DT model, the size of the tree was defined based on the cross validation and pruning of the model. The appropriate size of the tree was eight based on the cross validation and pruning of the tree. The size of the tree (6) in the developed DT model was obtained after cross validation and pruning of the tree. The results obtained from the DT model showed the values of PBIAS = 0.12, RMSE = 376.15, r = 0.842, CE = 0.709, PI = 0.086, WI = 0.896, LMI = 0.083 in the training period and PBIAS = − 1.38, RMSE = 35.23, r = 0.890, CE = 0.858, PI = 0.044, WI = 0.946, LMI = − 0.093, respectively, in the testing period at Varanasi. Likewise, the values of PBIAS = − 1.63, RMSE = 399.8, R = 0.882, CE = 0.854, PI = 0.104, WI = 0.925, LMI = 0.074 in the training period were PBIAS = 1.68, RMSE = 35.2, R = 0.856, CE = 0.867, PI = 0.054, WI = 0.940, LMI = − 0.175in the testing at Prayagraj.

Similarly, MLP model Violin graph (Figs. 4 and 5) demonstrate the deviation between observed and modeled values of electrical conductivity (EC) using MLP, CANFIS, RF, and DT models. The MLP and CANFIS models had a high deviation between the observed and predicted model values of EC in Varanasi and Prayagraj, respectively. It was demonstrated from these graphs that the electrical conductivity of surface water has good prediction accuracy through the RF model, and other models have good arrangements between the observed and modeled EC of surface water. Similarly, the scatter diagram (Figs. 6 and 7) indicated that MLP and CANFIS models were over-predicted at Varanasi and under-predicted in Prayagraj. Also, RF model had good agreement with observed EC at both stations. The scatter diagram of the discrepancy ratio (DR) is illustrated in Figs. 8 and 9. The discrepancy ratio (DR) is defined as the logarithm of the ratio of modeled data to observed data (Singh et al. 2018a). The DR values were near zero, which means the model was highly accurate. It was shown from the scatter diagram of DR values of different algorithms that the DR of the RF algorithm was plotted on about a zero line in both stations as compared to the MLP, CANFIS, and DT algorithms. After comparing all the results of four different algorithms, it was found that all models performed well for the prediction of the electrical conductivity of surface water. Also, the RF model has obtained the best results during training and testing periods in both sites as compared to the DT, CANFIS, and MLP models. The prediction capability of the DT model was also good as compared to the CANFIS and MLP models. The prediction ability of the RF and DT models was found to be better than that of the CANFIS and MLP models, and the reason for this phenomenon may be overfitting and the complexity of the model. In addition, using RF and DT models can avoid the overfitting of large and complex data sets.

Fig. 4
figure 4

Violin plot of between observed and different predicted machine learning models at Varanasi site

Full size image
Fig. 5
figure 5

Violin plot of between observed and different predicted machine learning models at Prayagraj site

Full size image
Fig. 6
figure 6

Scatter diagram of different machine learning models at Varanasi Site

Full size image
Fig. 7
figure 7

Scatter diagram of different machine learning models at Prayagraj Site

Full size image
Fig. 8
figure 8

Discrepancy ratio (DR) values of MPL, CANFIS, RF and DT model in Varanasi

Full size image
Fig. 9
figure 9

Discrepancy ratio (DR) values of MPL, CANFIS, RF and DT model in Prayagraj

Full size image

Multi-ahead electrical conductivity forecasting

In multi-ahead forecasting of electrical conductivity, current-month total hardness (TH), magnesium (Mg), and chloride (Cl) parameters were used as input variables for forecasting multi-ahead electrical conductivity (ECt+1, ECt+2, ECt+3). The same architecture of MLP, CANFIS, RF, and DT algorithms was used for the forecasting of multi-ahead electrical conductivity, which was developed during the prediction of current electrical conductivity (ECt). The results of multi-ahead models are presented in Tables 2 and 3, respectively, for Varanasi and Prayagraj stations. The performance of multi-ahead electrical conductivity forecasting models was assessed using statistical indices PBIAS, RMSE, R,CE, PI, WI, and LMI, while the comparative assessment was done based on the Violin plot (Figs. 4 and 5) and the Taylor diagram (Figs. 12 and 13).

Radar plot is platform that show multi-indices in single diagram. Radar plot (Figs. 10 and 11) illustrates the comparative assessment of MLP, CANFIS, RF, and DT models. The radar plot of RF and DT models represented a good aggregate with observed EC of surface water as compared to CANFIS and MLP models and had low error as compared to CANFIS and MLP models. Also, RF and DT models had high correlation and efficiency as compared to CANFIS and MLP models. It also observed that RF model had good aggregate, low error, high correlation and high potential for forecasting multi-ahead electrical conductivity (ECt+1, ECt+2, ECt+3) at both stations. The Taylor diagram is a single stand that provides three different statistical indices platforms to compare multiple models in a single diagram. RMSE, correlation coefficient, and standard deviation indices were used in the Taylor diagram. It was observed from the results of multi-ahead forecasting models, which are presented in Tables 2 and 3, that the potential of developed models was reduced as compared to current-month electrical conductivity forecasting models. It was concluded that the applicability of MLP, CANFIS RF, and DT algorithms was satisfactory for multi-ahead electrical forecasting at both Varanasi and Prayagraj stations of the Upper Ganga basin.

Fig. 10
figure 10

Radar Plot of different indices for current and multi-ahead electrical conductivity at Varanasi site

Full size image
Fig. 11
figure 11

Radar plot of different indices for current (ECn) and multi-ahead electrical conductivity at Prayagraj site

Full size image

Discussion

The focus of the present study is to compare the performances of MLP, CANFIS RF, and DT models by using the observed and simulated electrical conductivity plots based on the training and testing periods data sets. The forecasting accuracy of MLP, CANFIS RF, and DT algorithms deteriorated when the lead time of electrical conductivity was increased. This finding is in agreement with Nanda et al. (2019). The capability of MLP and CANFIS algorithms for electrical conductivity prediction was lower as compared to RF and DT models. Similar results were found in the prediction of soil permeability by Singh et al. (2020). It was shown from the Taylor diagram in Figs. 12 and 13 that the RMSE of MLP, CANFIS RF, and DT algorithms increased with increasing electrical conductivity, whereas the correlation coefficient of the RMSE of MLP, CANFIS RF, and DT algorithms decreased with increasing electrical conductivity at Varanasi and Prayagraj stations. It was also concluded based on statistical indices and the Taylor diagram that the regression-based random forest model was the best performing model for prediction of multi-ahead electrical conductivity at both Varanasi and Prayagraj stations of the Upper Ganga basin. It was determined that current moth total hardness (TH), magnesium (Mg), and chloride (Cl) parameters can be used as input variables for forecasting multi-ahead electrical conductivity (ECt+1, ECt+2, and ECt+3) in the future study in the Upper Ganga basin. It seemed that RF and DT models had better performance as compared to MLP and CANFIS models. RF and DT models can be used for multi-ahead forecasting of monthly electrical conductivity at both Varanasi and Prayagraj stations of the Upper Ganga basin.

Fig. 12
figure 12

Taylor diagram of present month ECt (A), one month ahead ECt+1 (B), two month ahead ECt+2 (C) and ahead three-month ECt+3 (D) during testing period at Varanasi station

Full size image
Fig. 13
figure 13

Taylor diagram of present month ECt (A), one month ahead ECt+1 (B), two month ahead ECt+2 (C) and ahead three—month ECt+3 (D) during testing period at Prayagraj station

Full size image

Similar results also found by researchers, Ravansalar and Rajaee (2015) studied the effectiveness of the hybrid WANN model for predicting monthly EC. The integration of wavelet analysis and neural networks improves the prediction accuracy compared to using ANN alone, making it a valuable tool for assessing water quality in similar environmental systems. Ahmadianfar et al. (2020) compared various standalone approaches, including locally weighted linear regression (LWLR), support vector regression (SVR), wavelet support vector regression (W-SVR), autoregressive integrated moving average (ARIMA), wavelet ARIMA (W-ARIMA), multivariate linear regression (MLR), and wavelet MLR (W-MLR), for predicting the monthly electrical conductivity (EC) values. The W-LWLR method demonstrated the highest correlation coefficient among the compared methods. A higher correlation coefficient indicates a stronger linear relationship between the predicted and observed EC values. Therefore, the W-LWLR method exhibited superior performance in capturing the EC variations. Ahmadianfar et al. (2022) compared the performance of several models: standalone ANFIS, least-square support vector machine (LSSVM), multivariate adaptive regression spline (MARS), generalized regression neural network (GRNN), wavelet-LSSVM (WLSSVM), wavelet-MARS (W-MARS), wavelet-ANFIS (W-ANFIS), and wavelet-GRNN (W-GRNN). The results indicated that the W-ANFIS model significantly improves the prediction certainty of EC, outperforming the other models with the Dmey mother wavelet in terms of EC prediction. Melesse et al. (2020) also compared the conventional random forest and hybrid random forest. It was found that hybridization of machine learning methods significantly improves the model performance in capturing maximum EC values, which is crucial for effective water resource management. Abba et al. (2023) studied the direct modeling of electrical conductivity (EC) in a sandstone groundwater (GW) aquifer in Southern Saudi Arabia. The research explores the application of hydrogeochemical and physical variables to predict EC using an adaptive neuro-fuzzy inference system (ANFIS)-based method. ANFIS method was outperforming model for predicting EC of ground water.

Conclusions

In this work, the electrical conductivity of surface water was predicted in the upper Ganga basin of India based on different machine learning algorithms, including multilayer perceptron (MLP), co-adaptive neuro-fuzzy inference system (CANFIS), random forest (RF), and decision tree (DT), and also examined the capabilities of the models. It was suggested based on the gamma test that current-month total hardness (TH), magnesium (Mg), and chloride (Cl) parameters were established as the best suitable independent vector combination for forecasting current-month electrical conductivity (ECt) as well as multi-ahead electrical conductivity (ECt+1, ECt+2, and ECt+3). The results indicate, based on statistical indices and visual interpretation, that the random forest algorithm demonstrated the best performance for forecasting the current month’s electrical conductivity of surface water among MLP, CANFIS and decision tree algorithms while decision tree algorithms perform better than the multilayer perceptron, co-adaptive neuro-fuzzy inference system. The obtainable results of multilayer perceptron, co-adaptive neuro-fuzzy inference system, random forest, and decision tree algorithms for prediction of the current month electrical conductivity (ECt) as well as multi-ahead electrical conductivity (ECt+1, ECt+2, and ECt+3) were satisfactory at both Varanasi and Prayagraj stations of Upper Ganga basin. Moreover, the different machine learning algorithms and the results presented now provide an orientation line on the upcoming investigation of the upper Ganga basin, and it was also suggested that policies of irrigation and drinking water quality deterrence should be applied continuously for proper supervision along the upper Ganga basin.

There is still work to be done to improve the situation, though, due to various restrictions. The following issues should be researched more in the future.

  1. 1.

    Temporal prediction is the subject of the current prediction outcomes. Future work will examine the performance of our model in multi-head predictions of electrical conductivity using both spatial and temporal prediction.

  2. 2.

    Only the indications of water quality itself are taken into account in the current projection; however, additional variables like location, precipitation, and temperature may also have an impact. We shall keep these things in mind going forward to better enhance the forecasting outcomes.

  3. 3.

    In the future, we want to experiment with the multi objective optimization approach to create hybrid algorithms for machine learning (HMLA) and evaluate their performance against traditional models.

  4. 4.

    Other climatic factors also impact water quality, however in this particular study, only the quality of the water data is considered. We will use these variables as inputs in the future for long-term forecasting.