1 Introduction

Water is vital for all life forms. It is not only used for drinking, but also for industry, agriculture and global trade in maritime and interoceanic regions (Abuzir & Abuzir, 2022). Surface water resources, which directly affect the daily activities of humanity, are one of the most important types of water. Among these water supplies, freshwaters (river, lake etc.) are significant social resources that benefit society in a variety of ways, such as ecological habitat, fisheries, farming, and recreational assets (Mutlu et al., 2018; Nacar et al., 2020). However, nowadays freshwater ecosystems are suffering from a variety of threats, including over-exploitation, global warming, and man-made pollution (Brack et al., 2017).

The River Water Quality (RWQ) is a highly sensitive and essential topic in many countries. Similarly, a greater appreciation and definition of the implications of RWQ for daily use, cosystem, farming and industrial uses is badly needed (Gupta & Gupta, 2021). This is because rivers play an important role in creating habitat for many organisms and providing water for human activities. Anthropogenic activities are primarily responsible for the degradation and pollution of natural surface waters and surface sediments (Akkan & Mutlu, 2022; Mutlu et al., 2020; Withanachchi et al., 2018). In addition, rapid industrialization and population growth have increased water quality concerns (Bhattarai et al., 2021). It seems clear that quality monitoring in urban water bodies has become an increasingly important area of research for water scientists around the world over the past 20 years. The qualitative study of river water quality based on physical, chemical and biological parameters includes many water quality characteristics and analysis of a complex data matrix (Said & Khan, 2021).

The WQI is A mathematical tool and composite indicator. This index allows the water quality information to be converted from a single unit to smaller values, depending on the selected variables (Kadam et al., 2019). WQI is well-suited to the assessment of the suitability of RWQ in a range of applications, including agriculture, aquaculture and domestic use (Naubi et al., 2016). The use of water quality indices (WQIs) in the assessment of river water quality has been used since the 1960s. WQI has the potential to transform chosen WQ variables into a dimensionless number, which could enable for easy and clear visualisation of changes in river water character within a specific locality and period of time (Sutadian et al., 2016). Many different indices for WQ assessment based on different parameters are commonly utilized in research (Gad et al., 2022; Pan et al., 2022; Prasad & Sangita, 2008; Sobhan Ardakani et al., 2016). Determining water quality using conventional methods is often time consuming and expensive, especially in developing countries, as multiple parameters need to be determined (Dimple et al., 2022; Ragi et al., 2019). The increasing significance of water quality on a global scale is driving extensive research and the development of innovative and intelligent monitoring solutions. The traditional approach—known as the laboratory method—involves collecting samples from water resorces for analysis in a laboratory setting. While this approach has its merits, it is not without its limitations. It is costly, time-consuming, and a waste of human effort. Furthermore, it may not be the most cost-effective solution. Therefore, innovative methods are used to solve this problem, such as artificial neural network (ANN). This method eliminates the need for the chemical method to assess water quality parameters and is also cost-effective (Ragi et al., 2019).

ANN methodology is a configuration architecture that simulates the human brain and the biological organisation of the nervous system. The underlying technical components of this architecture need a high accuracy. For this reason, the raw data input is normalized and optimized in this simulated system. This is imperative for enhancing the computational speed and precision of ANN performance. They are automatically trained using the optimization algorithm of their designers and generate the outputs, such as WQ (Kadam et al., 2019). Successful estimation of RWQ has attracted the attention of various government agencies and environmental agencies worldwide because it is useful in determining watershed health, biodiversity, ecology, and suitability of drinking water needs of river basins (Satish et al., 2022). Some researchers have statistically correlated WQI results using regression analysis (Chauhan & Trivedi, 2022; Fernández del Castillo et al., 2022; Khan et al., 2022; Yıldız & Karakuş, 2020). Regression modelling is a valuable and powerful instrument for assessing time series. It allows the effect of influencing variables to be modelled, and it is particularly effective in dealing with outliers, lacking observations and disordered measurement models (Abaurrea et al., 2011). Recently, ANN modeling is often used to quantify the severity of WQ problems due to the fast training progress and its intuitive capability for handling both complex linear and nonlinear problems (Nathan et al., 2017). Moreover, novel leakage detection and water loss management methods are being used for the urban water management using very efficient methods (Geng et al., 2019; Hu et al., 2021). The utilisation of forecasting methods are beneficial in a multitude of disciplines, including economics, hydrology and meteorology. In the majority of cases, time series in the rational world offer decision-makers highly accurate forecasts (Cansu et al., 2024; Eğrioğlu & Bas, 2023; Egrioglu et al., 2024; Egrioglu et al., 2019). The importance of these innovative methods that are highly accurate, cost-effective, and adaptable to global changes is increasing in the sustainable management of water resources.

Over recent years, machine learning (ML) algorithms have become a valuable instrument for the effective resolution of numerous environmental issues, including the assessment of water quality (Akkan et al., 2022; Lap et al., 2023). However, because of the incompatibility of current WQI methods, many scientists started to use machine learning to minimize model fuzziness and estimate WQIs at an accurate level (Hassan et al., 2021; Kouadri et al., 2021).

One of the weaknesses of ANN models is that they are developed based on previous data and thus cannot be used if limited data is available (Nhantumbo et al., 2018). The Levenberg–Marquardt algorithm has some limitations: it is used for networks with only one source element, the algorithm requires a large amount of memory proportional to the square of the neural network, so it is not recommended for large networks (Kostiuk et al., 2022). However, the search for a structured method for selecting the suitable network structure to best predict water quality parameters has attracted attention (Ahmed et al., 2019). The single prediction models cannot cope with complex conditions in datasets, easily decrease to local optima and become liable to overfitting (Dong et al., 2023; Xu et al., 2017). The ANN faces some limitations due to the nonlinear and non-stationary properties of some time series (Dong et al., 2023; Yang et al., 2021). Deficiencies in ANN models are identified with the results obtained from different studies. Therefore, the most optimum models have to be developed through these studies. The obvious utilization of ANN to optimize the projection model for WQI forecasting for the currently surveyed regions is an application that has not yet been studied. The present paper is motivated by three objectives: (1) to conduct a preliminary assessment of RWQ for drinking and irrigation water by computing WQIs; (2) to apply ANN and MLR models for the prediction of WQI; and (3) to contrast ANN and MLR models to determine the exact values of WQIs for sustainable management of aquatic supplies.

2 Materials and method

2.1 Study area

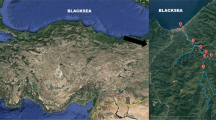
The Aksu Creek flows into the Black Sea at the borders of Giresun Province, the central district of the eastern Black Sea region (Fig. 1). It rises in the Giresun Karagol region at an altitude of 3107 m, is fed by many streams in the Kızıltaş, Sarıyakup, Pınarlar and Gudul regions, and empties into the Black Sea after a distance of 60 km on the eastern border of the central district. Mount Kılıç (3107 m) in the south of the Aksu Basin is the highest area. In addition to the rather large altitude difference, the inclination values of the basin vary between 0° and 90°. The area of the basin that collects the water of the Aksu Creek is 731 km2, its circumference is 129.4 km, the main waterway is 58.8 km long and has a slope of 4.5%. Moreover, the median value of the basin is 2102.3 m, the river grade is 4, the drainage density is 0.48 km−1, and the channel frequency is 0.16 waterways/km2. The main tributaries of Aksu Creek are Soğucaksu, Kargilimacun, Tehnelli, Karpuz, Kuçukaksu, Kırkgeçit, Bafadan, Tatlıçay, Çobanozu, Eğrioz, Hayıtlı, Karganlı, Asar, Naneli, Kuzgun creeks (Anli, 2003). The water area of Aksu Creek is 250 ha and its flow rate is 562.0 hm3/year.

Fig. 1
figure 1

Sampling area (Google Earth)

Full size image

2.2 Collection of surface water samples

To evaluate the physicochemical variables, the sample containers used for the study were washed in a bath of weak acid or distilled water 1 day before being used in the field. Then, the sample vessels rinsed with distilled water were dried in an oven and made ready for use. The water sample was taken with a Nansen bottle according to the relevant guideline of TS EN ISO 5667 and brought to the laboratory without losing time in the cold chainn. In this paper, data were collected from five different stations for this dataset for 1 year. In other studies, similar to our study, water samples were taken for a year as a data set to determine the quality of aquatic resources (Huang & Yang, 2019; Krtolica et al., 2021; Najah Ahmed et al., 2019; Ucun Ozel et al., 2020).

2.3 Analysis of water samples

Analyzes of surface water samples from Aksu Creek were conducted in two phases, under field and laboratory conditions. During field studies, water temperature, pH, dissolved oxygen, salinity, electrical conductivity, total dissolved solids, and oxidation potential of water samples were measured using YSI 556 MPS and turbidimeters WTW-355 IR. Nutrients, which must be measured immediately under field conditions, were also analyzed using the YSI 9300 photometer and appropriate commercial kits. During the field studies, measurement calibrations of all variables were performed each month using standard calibration solutions and the instruments were made ready for use.

2.4 Water quality indexes assessment

A first basic step in the calculation of water quality indices is the selection of the variables, the determination of the value of the partial index, the creation of the weights, and the use of the aggregation processes of the partial indices to obtain the value of the final index that can be used to comment on water quality. In this study, the basic water quality variables and their weights were obtained from literature studies (Gupta & Gupta, 2021; Khalid and others 2019; Pan et al., 2022; Qi et al., 2022). In accordance with the expert opinion, the weights calculated with different equations were used to eliminate the possible differences that may result from the conventional weighting processes. WHO (2011; 2017), CCME (2007), and FAO (1994) were used for the default values used in the WQI assessment.

WQI: the weighted arithmetic water quality index method, uses the most frequently measured water quality variables to classify water quality according to quality levels. For this purpose, it was calculated and evaluated using the following equation to evaluate the WQ adequacy of Aksu Creek (Brown et al., 1972, Table 1).

$${\text{W}}_{{\text{i}}} = \frac{{{\text{w}}_{{\text{i}}} }}{{\sum\limits_{{\text{i}}}^{{\text{n}}} {{\text{w}}_{{\text{i}}} } }}$$
(1)
$$\text{Qi}=\frac{{\text{E}}_{\text{m}-}{\text{E}}_{\text{id}}}{{\text{E}}_{\text{s}-}{\text{E}}_{\text{id}}}\times 100$$
(2)
$${\text{SI}} = {\text {W}}_{\dot{\text {I}}} \times {\text{ Q}}_ {\dot{\text {I}}}$$
(3)
Table 1 WQI rating scale
Full size table
$${\text{WQI}}=\sum_{\text{i}=1}^{\text{n}}\text{SI}$$
(4)

In equality

\({\text{W}}_{\text{i}}\): weight of each variable, \({\text{w}}_{\text{i}}\): relative weight of each variable, \({\text{E}}_{\text{m}}\): element measured value, \({\text{E}}_{\text{id}}\): element ideal value, \({\text{E}}_{\text{s}}\): element standard value, \({\text{Q}}_{\text{i}}\): rating value, SI: the sub-index value represents.

Evaluation

The nutrient pollution index (NPI) was determined and evaulated by Isiuku and Enyoh, (2020):

$$NPI = {\raise0.7ex\hbox{${C_{{NO3}} }$} \!\mathord{\left/ {\vphantom {{C_{{NO3}} } {MAC_{{NO3}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${MAC_{{NO3}} }$}} + {\raise0.7ex\hbox{${C_{{TP}} }$} \!\mathord{\left/ {\vphantom {{C_{{TP}} } {MAC_{{TP}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${MAC_{{TP}} }$}}$$
(5)

In equality

Cx: NO3-N and TP (average concentration), MACx: Maximum permitted level (Turkish Surface Water Quality Regulation, 2016).

2.5 Statistical calculations

The normality test, analysis of variance, multiple comparison tests, correlation analysis, cluster analysis, factor analysis, and principal component analysis used to specifically test the data obtained in this work were analyzed using the statistical program SPSS 17.0. MATLAB deep statistics and machine learning toolbox was used to estimate the WOI.

2.6 Machine learning (ML) models

Machine learning (ML) is a key element of artificial intelligence (AI)—it allows a system automatically to learn and evolve from its experience, without the need for a specific programme (Sun & Scanlon, 2019). The term machine learning describes an artificial intelligence (AI) and computer science technique that uses data and algorithms to model and progressively improve the accuracy of the human intelligence process. Additionally, in water management applications, it is used to evaluate real-time data, enhance water quality monitoring, as well as assess and forecast present and predicted water quality caused by various factors like acidity, turbidity, salts, nutrients and pollutants (Jafar et al., 2023).

In order to ascertain the most accurate prediction model for water quality, five machine learning (ML) algorithms were employed: support vector machine (SVM), neural network/multilayer perceptron (MLP), ensemble, Gaussian process regression (GPR), and decision tree. The efficacy of each algorithm was evaluated through comparison of their respective accuracy, with the aim of identifying the most suitable prediction model. The performance evaluation of the ML models in question revealed that Gaussian Process Regression (GPR) exhibited the lowest training error and provided the most accurate prediction of the WQI input dataset.

2.6.1 Gaussian process regression

Machine learning is a crucial aspect of the programming domain. The primary benefit of GPR is its capacity to discern that the learning sample adheres to the prior probabilities of a Gaussian process regression (Elbeltagi et al., 2021). Gaussian process regression (GPR) is kernel machine learning methodology that does not require the specification of a parametric model. This method has gained considerable attention in the literature over the past few years (Sharifzadeh et al., 2019). The Gaussian process regression (GPR) technique is concerned with the conditioning and bounding via the use a priori knowledge of a Gaussian fit in regression-based fields (Ali et al., 2022). The application of GPR in the fields of aquatic sciences encompasses a number of diverse areas, including the forecasting of water flow, the estimation of pipe bursting rates in water distribution systems and the monitoring of groundwater quality (Zare Farjoudi & Alizadeh, 2021).

2.7 Multiple linear regression (MLR) based WQI model

MLR is widely used for water quality estimation in different parts of the world (Egbueri & Agbasi, 2022). Two water quality indices were estimated using MLR. In the context of (MLR, the estimators are unknown variables that are estimated from two or more known variables. In other words, multiple regression analysis helps to estimate the value Y for given values X1, X2, …, Xk. The commonly known multiple regression equation of X1, X2, …, Xk and Y (the dependent variable) is Said and Khan, (2021):

$${\text{Y}} = {\text{b}}_{0} + {\text{b}}_{{1}} {\text{X}}_{{1}} + {\text{b}}_{{2}} {\text{X}}_{{2}} + \cdots + {\text{b}}_{{\text{k}}} {\text{X}}_{{\text{k}}}$$
(6)

The assumption of independence of variable components in MLR, as a parametric statistical model, may deviate from the real situation (Golfinopoulos & Arhonditsis, 2002). Multiple linear regression (MLR) analysis was performed using the stepwise method. This methodology entails the utilisation of variables that exert a considerable influence on the dependent variable. In this technique, the WQI was calculated as the independent variable and the factors affecting this factor were accepted as independent variables.

2.8 Artificial neural networks

The ANN model is based on the human brain (Choden et al., 2022). ANNs represents a form of artificial intelligence that attempts to emulate—in both structure and function—the biological architecture of the human neurosystem and nervous system (Malinova & Guo, 2004). ANNs are suitable for use in nonlinear mapping and exhibit advanced fault tolerance, self-adaptation, self-regulation, and self-learning capabilities, in addition to other beneficial attributes. The suitability of ANNs for high-dimensional and non-linear system problems has been idenitified (Bas et al., 2022; Che & Wan, 2022). The ANNs activates each neuron's inputs (WQ variables) to produce an output signal through (WQI) the application of an activation function (Jain et al., 2022).

2.9 Application of artificial neural network (ANN) based WQI model (MLP-ANN)

ANN adapted to MATLAB software was used as a computational tool to check the correlation between input and output variables and to make a prediction regression of the obtained data (Adeogun et al., 2021; Igwegbe et al., 2019). The computational tool ANN, adapted to MATLAB software, was employed to assess the correlation between input and output variables Furthermore, a regression analysis was conducted to predict the outcomes of the obtained data (Adeogun et al., 2021; Igwegbe et al., 2019). The predicted results by the ANN were comparing with the WQI outcomes by using nntool to train the dataset.

The architecture structure of ANN includes three layers: input, hidden and output, and these layers consist of one or more simple artificial neural cells, called neurons or processing elements. For this study, 14 parameters correspond to neurons in the input layer, which is the number of parameters examined. A trial-and-error approach was used to estimate neurons in the hidden layer. For that purpose, initially a network is trained and tested using a minimum set of networks (2 nodes of the hidden layer). Afterwards, the number of hidden layer nodes was gradually increased (up to 5) to measure the overall performance during training and testing. To build an ANN model, all datasets were divided into training (70%), validation (15%) and testing (15%), respectively. The training input set is employed to compute gradients and update the weights at layers of the network. In contrast, the validation dataset is utilised to make decisions, complete training, and avoid overfitting the network. Levenberg Marquardt (trainlm) technique was used to test the function of the network. The proposed structure of the ANN model is shown in Fig. 2.

Fig. 2
figure 2

General scheme for the Levenberg Marquardt (trainlm) technique

Full size image

The MLP characterized by its adaptability to any application of the learning procedure applying the enormously widespread back-propagation algorithm technique. Nonetheless, convergence is not without limitations. These include a tendency to be slow, unstable, and to remain at local minima. Thus, the Levenberg–Marquardt algorithm, which has been enhanced, provides a solution to these shortcomings (Toha & Tokhi, 2008). The Levenberg–Marquardt algorithm is sufficiently adequate for use with hundreds of weights in models. The problems of approximating functions that demand precision in formation often profit by utilizing it (Bekas et al., 2021).

2.10 Determining the accuracy of the model

The models were evaluated by means of coefficient of determination (R2), root mean squared error (RMSE) and mean absolute percentage error (MAPE). RMSE, MAPE, and R2 were calculated using Eqs. (7), (8), and (9), respectively. The coefficient of determination (R2) range is 0 to 1, and it idenifies the degree of correlation between the observed and predicted values. The 1 represents an excellent correlation within the observed values and the line drawn through them, and 0 represents there is no statistical correlation within the observed and forecasted data (Barzegar et al., 2016).

The majority of the aforementioned tasks were completed using MATLAB, which included model training, statistical analysis of parameters, calculation of correlation coefficients, error analysis, and so forth.

$$RMSE=\sqrt{\frac{1}{n}\sum_{t=1}^{n}{\left({output}_{t}-{target}_{t}\right)}^{2}}$$
(7)
$$MAPE=\frac{1}{n}{\sum }_{t=1}^{n}\left|\frac{{output}_{t}-{target}_{t}}{{target}_{t}}\right|$$
(8)
$$R^{2} = 1 - (\mathop \sum \limits_{t = 1}^{n} (output_{t} - target_{t} )^{2} /(output_{t} - target_{t} )^{2}$$
(9)

3 Discussion and conclusion

3.1 Statistical analysis results

Multivariate statistical methods, such as correlation analysis, principal component analysis, factor analysis, and cluster analysis, are frequently employed to identify the key variables that influence water and sediment quality, as well as to ascertain the dominant factors that affect water and sediment quality. These methods are also used to investigate the sources of these factors and to determine the long-distance relationship between them (Al-Ani et al., 2019; Basatnia et al., 2018).

According to the results of Pearson correlation of the variables observed in the surface water samples of Aksu Stream, the significant correlation pairs are respectively: pH/Turb, pH/DO, Alk/EC, Alk/TDS, Hard/EC, Hard/TDS, Hard/Alk, TAN/DO, TAN/Alk, TAN/Hard, NO3/EC, NO3/TDS, NO3/DO, SO4/EC, SO4/EC, SO4/Hard, Na/NO3 were observed (Fig. 3).

Fig. 3
figure 3

Pearson correlation graph of water variables

Full size image

According to the results of factor analysis, 5 factors explained 78.585 of the total variance in this study (Table 2). In the first factor, the variance explained is 29.629. A strong positive weight and a positive weight of alkalinity and hardness were found in the variables EC and TDS. The variance value of the second factor explained 14.648. NO3 and DO were strongly positive and TAN was determined with positive weight. Based on these factors, we can say that there are climatic, agricultural input and erosion factors on water quality of Aksu Creek. The variance value of the third factor explains 13.807. Na and K have strong positive weights. The variance value of the fourth factor explains 10.537. TP has a negative weight and NO2 has a medium positive weight. The variance value of the fifth factor explains 9.965. pH has a medium positive weight and turbidity is weighted toward a positive weight. Using these factors, we can show the impact of anthropogenic influences on the water quality of Aksu Creek, especially heavy metals released by mining activities and inputs from erosion.

Table 2 Varimax rotated factor matrix of water variables
Full size table

In order to determine the variable factors affecting water quality in the Aksu Stream, a total of 14 variables were studied from the physicochemical parameters determined in the water. As criteria for evaluating the principal components, values with eigenvalues greater than one were determined as sources of variance to be explained from the data used. The diagram expressing the eigenvalues of the principal components is shown in Fig. 4.

Fig. 4
figure 4

Scree Plot diagram of water variables

Full size image

The three-dimensional representation of the rotated factor matrix, which shows which factor the variables are in relationship with, is given in Fig. 5.

Fig. 5
figure 5

Component plot, R-mode factor analysis plot of the physicochemical parameters in the studied

Full size image

3.2 Water quality index results

WQI comprehensively represents the quality of groundwater and surface aquaticresources as a combination of various WQ parameters (Acharya et al., 2018; Deshmukh & Aher, 2016; Gupta & Gupta, 2021; Khalid and others 2019). In the Yellow River (China), the highest and lowest WQI values were calculated as 92.1 & 52.6 and 95.3 & 57, respectively, where water quality was "good" and "moderate" (Pan et al., 2022), WQ assessment in the Yihe River (China) were reported to vary from upstream to downstream, with average WQI values ranging from 78.54 to 83.67, with the highest WQI values (82.43) (Qi et al., 2022). In our study, it was found that the WQI values of Aksu Creek ranged from 103 to 141, with an average value of 113.6, which can be expressed as "not suitable for drinking water use" (Fig. 6). The highest value was obtained at the discharge point of Aksu Creek, which is expressed as the 5th station. This can be explained by the fact that downstream stations receive more pollutants from upstream stations due to runoff after rainfall and runoff from high altitude is a possible additional source of pollutants in these regions (Singh et al., 2015). Similarly, NPI is frequently applied to evaluate nutrient contamination effects at surface water bodies. In a practical application, it is calculated according to the NO3 and TP concentrations and shows the quality of the water (Isiuku & Enyoh, 2020). The NPI values were higher at Station 3. The NPI results showed that station S4 was “considerable polluted”, and other stations were “very high polluted” in Aksu Creek. This undesired condition may be reflection from anthropogenic effects.

Fig. 6
figure 6

WQI and NPI results in water samples

Full size image

3.3 Machine learning (ML) algorithms results for WQI prediction

Various performance criteria were used to compare different algorithms to determine the best model. After the evaluation of the machine learning algorithms, as shown in Table 3, the results of linear gaussian process regression; RMSE of 0.00362, MSE of 0.00001, R2 of 0.99999, MAE of 0.00256 were found to be the best algorithm.

Table 3 Various performance criteria were used to determine the best model after the evaluation of the machine learning algorithms
Full size table

Figure 7 shows that the Gaussian Process Regression model of the points representing the calculated WQI values and the prediction points with the Gaussian Process Regression model showed an overall 1:1 perfect line match. It is evident that this model is the most suitable for forecasting the water quality parameter values.

Fig. 7
figure 7

Gaussian process regression model of the points representing the calculated WQI values

Full size image

3.4 MLR and MLP-ANN application results for WQI prediction

In this study, water quality variables were measured from surface water stations and used to predict water quality using MLR methods. This approach is essentially a basic least squares technique. Due to its realistic return, the MLR technique is relatively straightforward and requires less time (Sahoo & Jha, 2013). The MLR is a method modelled to reveal linear relationships between two random vectors, X and Y. Among the reasons why multivariate regression is generally preferred are (1) predicting Y with respect to X, (2) testing assumptions about the relationship between X and Y, and (3) the adaptability of Y to forecasted time series or spatial patterns (DelSole & Tippett, 2022). The R2 (R-squared) metric is the ratio of the regression model to the independent variables and means how much of the variance of the dependent variable it measures. The R2 value takes a range from 0 to 1. The high R2 shows that the model explains a large amount of the variance in the dependent variable and a good model is achieved. However, the R2 metric can lead to the problem of over-fitting; in other terms, the R2 value can be high in overly complex models, but this weakens the generalisability of the model (Akdağ, 2023). A non-linear model may not be preferred unless a linear relationship is expected to be present in the data set or the model is required to be complex. Linear models are simpler to interpret and are quite adequate for predicting complex biological systems (Heil et al., 2023). Furthermore, linear models can be combined with artificial neural networks (ANNs) by constructing a linear model of the data and then using an ANN to model the residuals. In this way, a good model performances can be achieved while preserving the interpretations obtained from the linear part of the model (Laarne et al., 2022). The high R2 value of the water parameters used in our study, which may be due to a linear relationship, may indicate an overfitting problem. This result can be interpreted as the model is too specific to the data. It provides an advantage in the sustainable policy-making of a specific area in water resources management, such as a basin, wetland, and water reservoir etc. In order to overcome this situation, analyses can be performed using various adjustment techniques or different model options. In addition, it would be more advantageous to use MLR when there is a linear relationship between the variables in the data set. The reasons why linear regression is a better method for small sample sizes and low-dimensional data have been discussed and data have been presented that it is a good method (Kipruto & Sauerbrei, 2022; Santana et al., 2021; Wang & Yao, 2020; Yan & Wang, 2022).

R2 was employed to assess the robustness of the MLR models presented in this paper. Water variables of Aksu Creek such as pH, EC, TDS, DO, turbidity, alkalinity, hardness, TP, TAN, NO2, NO3, SO4, Na and K were used in the study. Furthermore, an artificial neural network (ANN) structure is employed, comprising a number of neurons in the input layer, which correlate with the aforementioned water variables, and a single output variable. By this process, MLR modeling demonstrated high prediction performance with R2 = 1.0, RMSE = 0.0025 and MAPE = 0.0296 accuracy values. A summary The MLR estimates and performances are presented in Table 4. It is sufficient to mention an MLR as a very useful tool for estimating the WQI.

Table 4 The performance results for modelling
Full size table

ANN modeling utilized for the present paper also showed high prediction performance. Figure 8 shows the parity plots and regression models related to MLP-ANN estimation of WOIs. To ascertain the degree of error within the MLP-ANNs, the sum of squared errors was determined. Generally, there is obtained lower modeling inaccuracies obtained in all MLP-ANN methods. The present investigation shows that MLP-ANNs provide precise and reliable estimates for the WQ output variables of Aksu Creek.

Fig. 8
figure 8

The regression plot of the ANN model of a Training, b Validation, c Testing, and d All

Full size image

Figure 8 also shows the data regression both individually and as a whole. The dotted line function in these plots is the objective function, i.e., the best mode determined by the neural network. At that, the correlation coefficient is equal to 1 (R = 1), or else it is less than 1. The function represents the function along the vertical axis whose line fits the data points using a neural network. This figure shows all three different datasets, including training, validation, and testing. In addition, the regression of each data category was found to be above 0.97 in all figures. A plot of the calculated WQI values compared to those predicted by ANN can be found in Fig. 8.

From Fig. 8, the predicted outcomes of the proposed ANN model is in good accordance with the computed results. ANN was observed as a powerful technique for WQI modeling with strong [R2 = training (0.99)], testing (0.97) and validation (0.98).

The ANN implementation was performed utilizing an algorithm introduced in the MATLAB platform to select the minimum number of principal components to be utilized as input and the number of neurons in the hidden layer, resulting in the most suitable ANN model. Figure 9 is illustrates the proposed structure of the ANN.

Fig. 9
figure 9

Optimal multilayer perceptron neural network for WQI

Full size image

An ANN-based validation evaluation (RMSE, MAPE and R2) of the WQI from surface water in Aksu Stream (RMSE, MAPE, and R2) is also given (Table 5). The error difference with the simulated outcome and the observed data set is utilized to assess the efficiency of algorithm. The number of hidden neurons was determined to be 2, 3, 4, and 5, but the model ANN with 2 hidden neurons showed the best performance. Therefore, 2 hidden neurons were selected in the study. The selected model 14-2–1-1 proved to be the most reliable in terms of R2.

Table 5 Performance statistics of the model in training, validation and testing for MLP-ANN (Levenberg-marudt)
Full size table

3.5 Comparative performance of water quality prediction models

The results of the study show that both MLR and MLP-ANN modeling are accurate and reliable options for calculating the WQI values of the RWQ. The R2 values of both models ranged from 0.970 to 1.000. Moreover, the 70/15/15 partitioning of the dataset, comprising training, validation, and testing subsets, has been demonstrated to be an effective approach for estimating the WQI with the Levenberg–Marquardt algorithm (LMA). The optimum hidden neurons number was determined to be 2, 3, 4, or 5. The model ANN with 2 hidden neurons demonstrated the best performance. Therefore, 2 hidden neurons were chosen in the study. However, the MLR model outperformed the ANN used to estimate the WQI of the RWQ.

It is high that the WQI values estimated by MLR model are consistent with the observed values and therefore provide successful results in estimating WQI values. The results of present paper indicate that the MLR model is suitable according to the MLP-ANN model. With this process, MLR modeling showed high prediction performance with R2 = 1.0, RMSE = 0.0025 and MAPE = 0.0296 (Table 6).

Table 6 Comparative performance of water quality prediction models
Full size table

The MLR technique, which has a significant realistic success, functions as much simpler and less time-consuming (Sahoo & Jha, 2013), and our findings have been supported in the literature (Egbueri & Agbasi, 2022). In addition, a low RMSE value indicates that the model is performing well. The MAPE value is the set aside value used for a model to execute the forecast. The value of the smallest MAPE shows the good performance of the model (Olyaie et al., 2015).

Root mean square error (RMSE), mean square error (MSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) are used in this research to interpret the model performance because these criteria have been considered in most studies (Asadollah et al., 2021; Uddin et al., 2023; Zaghloul & Achari, 2022). The application of multiple regression algorithms has significantly demonstrated its efficacy and reliability in accurately predicting the WQI (Ahmed et al., 2019).

4 Conclusion

The main objective of present paper is identify the WQI to assess the availability of river water for sustainable management for drinking and irrigation purposes. The WQI results demonstrate that 80% of the analyzed river water samples exhibited satisfactory quality for public use, whereas 20% exhibited poor quality and were unsuitable for public consumption. In a similar viewpoint, the NPI classified the aforementioned option as being highly unsuitable. Nevertheless, the river water was limitedly suitable for irrigation purposes. Therefore, the majority of the river water resources within the basin is suitable for both human consumption and household usage. Pearson correlation analysis and principal component analysis were used to effectively rule out possible sources of contamination. It was determined that the water chemistry and quality of Aksu Creek were affected by a confluence of geogenic and anthropogenic factors.

As a further objective of present paper, ANN, ML and MLR models were comparisons to identify the precision of WQI for WQ prediction in the future. WQI values estimation was verified using ANN and MLR models. However, the MLR model outperformed the ANN and ML used to estimate the WQI of the surface water of Aksu Creek. Based on presented findings, multiple regression and ANN methods for estimating parameters used in determining RWQ and WQI, which is an important quality index, can be used. In this way, errors caused by factors such as expert opinions in WQIs will be eliminated, and purer results will be achieved.

The results of this study will contribute to the sustainable monitoring, assessment, and management of surface water resources, as this is the first estimation in this region. In addition, the knowledge gained here will make an important contribution to the diversification and growth of the global literature on WQ prediction. This fundamental study will shape similar studies. Finally, the information contained herein will provide important information to water managers, policy makers, and water researchers, particularly locally and globally, and will promote relative evaluation of models.