1 Introduction

The automation of bioanalytical assay panels has been a paramount objective of microfluidic technologies since their debut in the early 1990s (Manz et al. 1990; Auroux et al. 2002; Reyes et al. 2002; Whitesides 2006; Janasek et al. 2006). In the meantime, these Lab-on-a-Chip devices have pervaded manifold application spaces, primarily in biomedical point-of-care and global diagnostics, liquid handling automation for the life sciences, process analytical techniques and cell line development for biopharma, as well as monitoring the environment, infrastructure, industrial processes and agrifood (Gijs et al. 2010; Nge et al. 2013; Liu et al. 2014; Mauk et al. 2017; Yuan and Oleschuk 2018; Olanrewaju et al. 2018). Compliance with the relevant workflows, infrastructure, operator skill and competitive cost of ownership/per test are vital for their deployment in locations outside sophisticated medical infrastructure.

Various miniaturized liquid handling platforms have been introduced, which may be distinguished by their pumping scheme; among them are pressure sources, capillary force, electrokinetics, electrowetting on dielectric, bulk and surface-acoustic waves. Throughout the last about 30 years, centrifugal microfluidic platforms have been at the center of commercial and academic endeavors. Driven by a rugged spindle motor, these low-complexity “Lab-on-a-Disc” (LoaD) systems (Schembri et al. 1992, 1995; Abaxis (Piccolo Express) 2021; Andersson et al. 2007; Inganas et al. 2005; Gyros Protein Technologies 2021; Madou and Kellogg 1998; Shea 2003; Smith et al. 2016a; Kong et al. 2016a; Maguire et al. 2018; Gorkin et al. 2010a; Burger et al. 2016; Aeinehvand et al. 2018; Sciuto et al. 2020; Ducrée 2021a; Ramachandraiah et al. 2013; Thompson et al. 2016a; Krauss et al. 2019; Abi-Samra et al. 2011a; Thompson et al. 2016b; Watts et al. 2007; Kim et al. 2013; Moschou et al. 2006) excel through their high-performance centrifugal sample preparation, and their modular setup featuring an instrument ("player”) spinning a microfluidic disc carrying the sample and reagents.

Mostly operating in batch-mode, biosamples are preconditioned through a series of centrifugally implemented Laboratory Unit Operations (LUOs), such as metering (Mark et al. 2008; Keller et al. 2015), mixing (Grumann et al. 2005; Ducrée et al. 2006a, b; Burger et al. 2020), incubation, purification/concentration/extraction (Strohmeier et al. 2015a; Brassard et al. 2019), homogenization (Karle et al. 2009; Kido et al. 2007), particle filtering (Haeberle et al. 2006; Steigert et al. 2007; Kinahan et al. 2016a; Dimov et al. 2014; Gaughran et al. 2016; Zehnle et al. 2017), and droplet generation (Haeberle et al. 2007; Schuler et al. 2015, 2016), while transiently held back in each step by a downstream valve. Note that some assay steps may also be realized by transferring functionalized magnetic particles between reagent chambers (Czilwik et al. 2015; Grumann et al. 2004).

Akin to the pick-up heads familiar with digital data storage technologies like CD, DVD or Blu-ray, most read-out schemes for LoaD systems are based on optical detection (Maguire et al. 2018; Gorkin et al. 2010a; Burger et al. 2016; Ducrée et al. 2007; Lutz et al. 2011; Tang et al. 2016; Duffy et al. 1999; Azimi-Boulali et al. 2020; Strohmeier et al. 2015b; Kong et al. 2016b; Aeinehvand et al. 2017, 2019; Hess et al. 2019; Nguyen et al. 2019; Rombach et al. 2020; Homann et al. 2021; Madadelahi et al. 2020; Miyazaki et al. 2020; Brennan et al. 2017; Delgado et al. 2016). While the radially directed, outwards pointing centrifugal field is independent of the outer contours of the microfluidic chip, a disc shape complies with the rotational symmetry and supports mechanical balance, layout, and mold flow in common mass manufacturing schemes such as (compression-)injection molding; yet, deviations from the common 12-cm diameter and 1.2-mm thick CD format are quite common, e.g., smaller “mini-discs”, disc segments, tubes (Kloke et al. 2014; Mark et al. 2009a; Haeberle et al. 2008), or rectangular, e.g., microscope slides (Morais et al. 2006). Furthermore, the alignment of the inlet ports, outlets and detection chambers may also be important for seamless interfacing with standard well-plate formats, liquid handling robotics, and associated equipment like readers. For simplicity, we refer to all these LoaD variants as “discs” in the following.

Liquid volumes concurrently residing on a rotor experience the same spin rate, and are thus simultaneously driven by the rotationally induced centrifugal field, which further depends on their individual radial locations. Hence, and other than for most conventional Lab-on-a-Chip systems, valving represents a key ingredient for automating sequential liquid handling protocols of the LoaD. In principle, the disc could be halted for valve opening, for instance, by a manual or instrument-based, e.g., mechanical, thermal or radiation-based actuator (Mishra et al. 2017; Kinahan et al. 2016b; SpinX Technologies 2021; Abi-Samra et al. 2011b; Kong et al. 2015; Al-Faqheri et al. 2013; García-Cordero et al. 2009, 2010; Torres Delgado et al. 2018). However, it is often preferrable to keep the disc-based liquid volumes at bay through, at least moderate, centrifugation; such suppression of flow during spinning involves co-rotating power sources, e.g., pneumatic pumps (Clime et al. 2015, 2019) or electro-thermal or radiative units for melting sacrificial barriers film (Torres Delgado et al. 2018; Kinahan et al. 2018; Delgado et al. 2018).

However, this work focuses on rotationally controlled valving concepts, which have been chosen by many researchers by virtue of to their smooth alignment with the low overall complexity of the LoaD platform (Ducrée 2021b). In these passive valves, the centrifugal pressure head propelling liquid segments towards the perimeter of the disc is combined with other pressure contributions that are independent of external power. In their high-pass variants, the centrifugal driving force is, for instance, opposed by a capillary barrier, while low-pass siphon valves typically feature hydrophilic coatings in their inbound sections, or pneumatic effects, so that valving is ushered in by reducing the spin rate below a critical threshold. In addition, various centrifugo- or thermo-pneumatic flow control mechanisms (Godino et al. 2013; Schwemmer et al. 2015a, 2015b; Zhao et al. 2015; Zehnle et al. 2015; Henderson et al. 2021; Gorkin et al. 2012; Kinahan et al. 2014, 2015; Mishra et al. 2015) have been engineered for creating forward or reverse pressure differentials.

To provide full-fledged sample-to-answer automation for conforming with the needs of point-of-care applications, the disc has to be pre-loaded with liquid or dry reagents; this way the user only needs to introduce the sample while being relieved from dealing with the logistics and loading of reagents from separate stocks. In addition to the capabilities of many techniques conceived for temporarily retaining liquid volumes while carrying out LUOs along with assay protocols, valves for longer-term storage also need to impede evaporation, diffusion into the bulk material, or exposure to ambient contaminants and humidity over shelf lives of many months, sometimes even years, and possibly even harsh ambient conditions and rough handling during transport.

In addition to (dry) storage within matrices (Zhang et al. 2016; Hin et al. 2018; Eker et al. 2014; Rombach et al. 2014; Tijero et al. 2015), liquid buffers and reagents have been retained by physical barriers (Deng and Jiang 2019), like flexible membranes (Baier et al. 2009; Margell et al. 2008; Czurratis et al. 2015; Kazemzadeh et al. 2019), blisters/pouches (Smith et al. 2016b), ampoules (Krauss et al. 2019; Hoffmann et al. 2010), cartridges (Kloke et al. 2014; Li et al. 2020), or wax plugs (Abi-Samra et al. 2011b; Kong et al. 2015; Al-Faqheri et al. 2013; Wang et al. 2019); similar to the previously discussed active valves, these containers may be opened by stimuli such as mechanical piercing, illumination by a high-power laser, or by local heating. Further performance criteria of suitable reagent storage valves are their compatibility with manufacture and assembly, the suppression of possible leaching of chemicals from solids during extended periods of phase contact. Last but not least, the fluidic performance needs to be assured in terms of the reliability of the release mechanism, and the recovery ratio, accuracy, and precision of the delivered liquid volume.

Dovetailing the centrifugal microfluidics covered in this work, also directly rotationally induced opening is, at least theoretically, possible. Yet, for existing mechanisms, it needs to be considered that, e.g., for limited motor power and safety, there is an upper limit for practically achievable spin rates, and the reservoir might have to be placed centrally, which would severely restrict obtainable pressure heads to fractions of common atmospheric pressures. Thus, the valve controlling the reagent reservoir has to yield at rather small pressure heads. Reliability is additionally impaired as the mechanical strength of a required designated mechanical weak or yield point is hard to define, thus smearing out the associated spin frequency threshold for triggering liquid release. Critical operational robustness hence demands setting a high rotational speed for opening, which tends to counteract the options for fluidic multiplexing of concurrently loaded liquids (Ducrée 2021a, c).

This paper focuses on a novel type of rotationally actuated valve; during storage of an aqueous reagent, a (water) dissolvable film (DF) presents a diffusion barrier which is initially protected by an oleophilic, ancillary liquid having a certain, specific density (Gaughran et al. 2016; Mishra et al. 2015, 2017, 2020; Ducrée 2021d; Lu et al. 2020). Upon spinning, a centrifugo-hydrostatic equilibrium is reached, in which the interface between the two immiscible liquids contacts and thus dissolves the DF. In an idealized model, the reagent will be issued at any finite spin rate situated within its practical limits imposed by motor power, operational robustness and safety.

In addition to the general prerequisites for on-board storage of liquid (and potentially also for protecting dry / lyophilized) reagents, such valves need to meet further specifications. During logistics and manual handling, acceleration due to shaking and terrestrial gravity act on the liquid volumes, while the meniscus between the immiscible fluids needs to stay near its default rest position to prevent premature opening. Moreover, manufacturing and dispensing precision, evaporation rates, and structural fidelity affect the release mechanism, and potentially enclosed or emerging gas bubbles need to be tolerated.

This work first elaborates the operational principles for rotationally controlled on-board storage and release valving enabled by an immiscible ancillary liquid. In the initial section, strategic features of the basic layout are introduced, and first motivated in a mostly qualitative manner. Next, design objectives are quantified in terms of key performance indicators. The individual or collective optimization of these “KPIs” is implemented based on a “digital twin” (Digital Twin 2021; Marr 2017; Grieves et al. 2017), which constitutes a virtual representation of a real-world physical system derived on the underlying functional model. The digital twin method allows virtualizing the optimization of the novel reagent storage technology, thus substantially reducing cost and time scales for product development.

2 Working principle

Figure 1 illustrates the fundamental mechanism underpinning storage and release of liquid reagents described in this work. In the portrayed, exemplary fluidic structure, which is referred in the following to as \(\Gamma\), two reservoirs of upper and lower cross sections \(A\) and \(a\), and heights \(H\) and \(h\) on the left, and \(A^{\prime }\) and \(a^{\prime }\), and \(H^{\prime }\) and \(h^{\prime }\) on the right, hold the aqueous reagent and the immiscible ancillary liquid of densities \(\varrho\) and \({\varrho }^\prime\), respectively. These containers are interconnected by an isoradial channel placed at an (inner) radial position \(R\) of axial length \(\mathcal{L}\), radial height \(\mathcal{H}\), and of cross section \(\mathcal{A}\), which accommodates a water-dissolvable film (DF) of axial extension \(\delta Z\) at the (mean) position on the \(z\)-axis.

Fig. 1
figure 1

Basic storage and release mechanism (linearized, 2-dimensional display of cylindrical coordinates, dimensions not to scale). The two-pronged structure, referred to as \(\Gamma\), is divided into upper and lower radial sections of cross sections \(A\) and \(A^{\prime }\), and \(a\) and \(a^{\prime }\), and heights of \(H,H^{\prime } ,h\) and \(h^{\prime }\), respectively. An isoradial channel at an inner radial position \(R\) possesses an axial length \(\mathcal{L}\), a radial extension \(\mathcal{H}\) and cross section \(\mathcal{A}\); a section of radial height \(\fancyscript{h}\), cross section \(\fancyscript{a}\) and length is centered at to provide a further degree of freedom. (Left) In a first step at rest (\(\omega =0\)), the aqueous reagent and an immiscible ancillary liquid of volumes \(U\) and \(U^{\prime }\), densities \(\varrho\) and \(\varrho^{\prime }\), and viscosities \(\eta\) and \(\eta^{\prime }\), are loaded to the left and right reservoirs with initial meniscus positions \(r_{0}\) and \(r_{0}^{\prime }\) of their liquid distributions \({\Lambda }\left( \omega \right)\) and \(\Lambda^{\prime } \left( \omega \right)\), respectively; their phase interface \(z\) is targeted to be located within the center of the -segment of axial length and centered at in the isoradial channel, or at least . These compartments are then isolated at pneumatic pressures \({p}_{V}(\omega =0)={p}_{V}^{\prime}(\omega =0)={p}_{0}\) (9) from the ambient pressure at \({p}_{0}\approx {p}_{\mathrm{std}}=1013.25 \, \mathrm{hPa}\). (Right) Before its (default) on-site usage, both seals are removed from the disc. During rotation at (theoretically any) \(\omega >0\), the initial difference \(\Delta {p}_{\omega }\left(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma ,\omega ,z\right)={p}_{\omega }\left(\varrho ,U,R,\Gamma ,\omega ,z\right)-{p}_{\omega }\left({\varrho }^{\prime},{U}^{\prime},R,\Gamma ,\omega ,z\right)>0\) resulting from the pressure heads \({p}_{\omega }\) (4) drives the liquid distributions \({\Lambda }\left( \omega \right)\) and \(\Lambda^{\prime } \left( \omega \right)\) towards hydrostatic equilibrium \(\Delta {p}_{\omega }\left(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma ,\omega ,z\right)=0\) (4), and consequently to new inner meniscus positions \(r>{r}_{0}\) and \({r}^{\prime}<{r}_{0}^{\prime}\). For triggering the reagent release through an outlet, e.g., located in a lower disc layer connected by a vertical via, the liquid–liquid interface at \(z=z(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma ,\omega )\) in hydrostatic equilibrium needs to cover the DF at , which features an axial extension , that was so far protected by the ancillary liquid, i.e., . Note that the geometry \(\Gamma\) is deliberately composed of cuboid segments to facilitate calculations. The default values for the parameters indicated are compiled in Table 1. Evidently, by suitably adjusting the dissolution characteristics of the DF, also non-aqueous liquids may be stored and released with the same mechanism

Full size image

For the duration of storage and transport (\(\omega =0\)), the phase interface between the immiscible liquids must reside within a (coaxial) segment of a cross section \(\fancyscript{a}\) of axial length , at a target position , or at least . For activation and release in hydrostatic equilibrium at an angular spin rate \(\omega =2\pi \cdot \nu >0\), the meniscus needs to move beyond the location of the DF at .

The conservation of liquid volumes is generally expressed as

$$ U\left( {{\check{r}},\hat{r}} \right) = \mathop \smallint \nolimits_{\check{r}}^{{\hat{r}}} A\left( {\fancyscript{r}} \right)d{\fancyscript{r}} $$
(1)

for general geometries \(\Gamma\) by the integral over the function \(A(\fancyscript{r})\) representing the dependence of the (compartmentalized) cross section \(A\) on the radial coordinate \(\fancyscript{r}\) between the inner and outer radial confinements of the liquid distributions \(\Lambda\) or \({\Lambda }^{\prime}\); this liquid volume \(U\) (1) spans between its inner and other radial confinements \({\check{r}}\) and \(\hat{r}\), respectively.

To simplify the math without compromising the outcomes of this work, we consider a structure \(\Gamma\) composed of cuboidal segments in Fig. 1, with \(\check{r} = r_{0}\) or \(r\) (and \(r_{0}^{\prime }\) and \(r^{\prime }\) for the ancillary liquid), and \(\hat{r}=R+\fancyscript{h}\) (for both arms). Instead of having to (numerically) solve the possibly complex integral \(U\left({{\check{r}}},{\hat{r}}\right)\) in (1), the liquid volumes can then be expressed (assuming \(R-h-H\le r\le R-h\)) by the algebraic formulas

$$ U =A\cdot \left(R-h-r\right)+a\cdot h+\mathcal{A}\cdot z\Rightarrow r=r(U,R,\Gamma ,z)$$
(2)

for the aqueous reagent and (assuming \(R-{h}^{\prime}-{H}^{\prime}\le {r}^{\prime}\le R-{h}^{\prime}\))

$${U}^{\prime}={A}^{\prime}\cdot \left(R-{h}^{\prime}-{r}^{\prime}\right)+{a}^{\prime}\cdot {h}^{\prime}+\mathcal{A}\cdot \left(L-z\right)\Rightarrow {r}^{\prime}\left({U}^{\prime},R,\Gamma ,z\right)$$
(3)

for the ancillary liquid. Equations (2) and (3) link the loaded liquid volumes \(U\) and \(U^{\prime }\) to the radial position \(R\) of \({\Gamma }\), their structural parameters \(A,A^{ \prime},a,a^{ \prime},h,h^{ \prime},\) and \(\mathcal{L}\) as represented by \(\Gamma\), their liquid levels \(r\) and \(r^{\prime }\), and their phase interface at \(0<z<\mathcal{L}\); the liquid levels at rest can therefore be expressed as \(r=r(U,R,\Gamma )\) in (2) and \(r^{\prime } \left( {U^{\prime } ,R,\Gamma } \right)\) in (3).

2.1 Loading, storage and transport

Following a suitable, well-reproducible, possibly closed-loop controlled experimental loading procedure at \(\omega =0\), the two liquids are introduced at ambient pressure \({p}_{0}\) (typically \({p}_{0}\approx {p}_{\mathrm{std}}\) with the standard atmospheric pressure \({p}_{\mathrm{std}}=1013.25 \, \mathrm{hPa}\)) to place the phase interface at \(z\) within the center of the isoradial segment at . For a starting position of the initial interface after properly loading \(U\) and \(U^{\prime }\) at \(\omega =0\), the conservation of mass (1) trivially yields the initial filling levels \(r_{0} = r_{0} \left( {U,{\Gamma },{\rm Z}} \right)\) and \(r_{0}^{\prime } = r_{0}^{\prime } \left( {U^{\prime } ,\Gamma ,{\rm Z}} \right)\). To suppress evaporation and contamination during subsequent storage, transport and handling, each reservoir is then isolated from ambient by a membrane exhibiting good barrier properties.

2.2 Liquid release

In response to spinning at a finite spin speed \(\omega > 0\), the centrifugal pressure heads

$$p_{\omega } = \varrho \cdot \overline{r}\Delta r \cdot \omega^{2} \,{\text{and}}\, p_{\omega }^{\prime } = \varrho ^\prime \cdot \overline{r}{^ \prime } \Delta r^{\prime} \cdot \omega^{2}$$
(4)

are induced to move and reshape the liquid distributions \(\Lambda\) and \({\Lambda }^{\prime}\), which are then confined by their (inner) menisci at the radially inner \(r,{r}^{\prime}\) and common outer positions \(R\), respectively. (Note that \(\mathcal{H}/R\ll 1\) and \(\fancyscript{h}/R\ll 1\) are assumed throughout.) The products \(\overline{r}{\Delta }r\) and \(\overline{r}^{\,}{^ \prime } \Delta r^{\prime }\) in (4) are composed of the mean radial positions \(\overline{r} = 0.5 \cdot \left( {R + r} \right)\) and \(\overline{r}^{\,}{^ \prime } = 0.5 \cdot \left( {R + r^{\prime } } \right)\), and the liquid level differences \({\Delta }r = R - r\) and \({\Delta }r^{\prime} = R - r^{\prime}\).

In default actuation mode, the pneumatic seals are removed from the disc prior to launching the centrifugal assay protocol \(\omega (t)\). While rotating at sufficiently high \(\omega\), so that \({p}_{\omega }\propto {\omega }^{2}\) (4) overcomes unfavorable stiction and capillary effects occurring in real-world systems, a hydrostatic equilibrium

$$\Delta {p}_{\omega }={p}_{\omega }-{p}_{\omega }^{\prime}$$
(5)

establishes which can be rewritten

$$\varrho \cdot \left(R+r\right)\cdot \left(R-r\right)={\varrho }^{\prime}\cdot \left(R+{r}^{\prime}\right)\cdot \left(R-{r}^{\prime}\right)$$
(6)

and therefore only relates the two liquid levels \(r = r\left( {\varrho ,\varrho ^{\prime},U,U^{\prime},R,{\Gamma }} \right)\) and \(r^{\prime} = r^{\prime}\left( {\varrho ,\varrho ^{\prime},U,U^{\prime},R,{\Gamma }} \right)\) to the radial position \(R\) of \(\Gamma\), the loaded liquid volumes \(U\) and \({U}^{\prime}\), and their densities \(\varrho\) and \(\varrho ^{\prime }\), but not to \(\omega\). The new, centrifugally stabilized position of the phase interface is defined by \(\Delta {p}_{\omega }(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma ,z)=0\) (5), and hence directly obtained from \(r\) and \(\Gamma\), i.e., \(z=z(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma )\).

Consequently, the centrifugally triggered release through the DF at comes down to , which predicates on \(\Delta {p}_{\omega }(z)>0\) (5) during the transition of the meniscus at \(z\) all along the way from the position during storage at to the DF at . This condition implies that a minimum reagent volume

(7)

(for ) needs to be displaced for valve opening, and the shift of the left liquid level from \({r}_{0}\) to \(r>{r}_{0}\), while the meniscus of the ancillary liquid moves radially inbound from \({r}_{0}^{\prime}\) to \({r}^{\prime}<{r}_{0}^{\prime}\). Given that all meniscus positions \({r}_{0},r,{r}_{0}^{\prime}\) and \({r}^{\prime}\) remain in their respective inner compartments of cross sections \(A\) and \({A}^{\prime}\) during this reconfiguration of the liquid segments towards centrifugo-hydrostatic equilibrium from to , we obtain and .

2.3 Reliability

In practical applications, tolerances, mainly in the geometrical dimensions, as quantified by the standard deviations here collectively referred to as \(\mathrm{\Delta \Gamma }\), and in the liquid volumes \(\Delta U\) and \(\Delta {U}^{\prime}\) after pipetting, impact the spread \(\Delta z\) of the interface \(z\) from their target positions and at \(\omega =0\) and \(\omega >0\), respectively. Using (5), (2) and (3) for the meniscus position \(z=z(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma )\), its standard deviation

$${\Delta }z\left( {\left\{ {\frac{\partial z}{{\partial \gamma_{k} }}} \right\},\left\{ {{\Delta }\gamma_{k} } \right\}} \right) = \sqrt {\left( {\mathop \sum \limits_{k} \frac{{\partial z\left( {\varrho ,{\varrho }^{\prime} ,U,{U}^{\prime} ,R,{\Gamma }} \right)}}{{\partial \gamma_{k} }} \cdot {\Delta }\gamma_{k} } \right)^{2} }$$
(8)

depends on the partial derivatives \(\partial z/\partial {\gamma }_{k}\) with \({\gamma }_{k}\in \{\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma \}\), and the standard deviations \(\Delta {\gamma }_{k}\in \{\Delta \varrho ,\Delta {\varrho }^{\prime},\Delta U,\Delta {U}^{\prime},\Delta R,\mathrm{\Delta \Gamma }\}\), evaluated at the critical positions and , respectively. Note that strictly speaking, Eq. (8) only holds for small deviations \(\{\Delta {\gamma }_{k}\)}. Alternatively, as used for robustness analysis further below, Monte-Carlo methods (see Fig. 7 below) can be employed to compute \(\Delta z\) at the two target positions and .

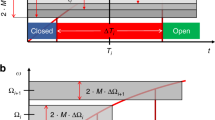
According to this functional model, operational robustness during storage, transport and rotation caused by statistical variations \(\{\Delta {\gamma }_{k}\}\) is tightly linked to squeezing the interval of the actual interface positions \(z\pm 0.5\cdot M\cdot\Delta z\) (8) within the narrow segment after loading at rest, i.e., , and for reliable release at \(\omega >0\), . The factor \(M\) quantifies the targeted degree of operational robustness, with \(68\%,95\%,99.7\%,99.99\%,\dots\) for \(M\in \left\{\mathrm{1,2},\mathrm{3,4},\dots \right\}.\)

3 Design characterization and optimization

The digital twin (Ducrée 2021b; Digital Twin 2021; Marr 2017) developed here allows to configure the free experimental parameters \(\{{\gamma }_{k}\}\) for achieving key performance goals, while staying commensurate with design-for-manufacture and scale-up of fabrication (Ducrée 2019). Such design optimization is facilitated by the multi-segmented structure \(\Gamma\) (Fig. 1) featuring cross sections \(A,a,{A}^{\prime},{a}^{\prime},\mathcal{A}\) and \(\fancyscript{a}\) with respect to the axial direction (and their respective axial heights / lengths and \(\mathcal{L}\)). The core motivation of this draft layout is now briefly outlined on a qualitative, heuristic manner; note that due to the huge variety of possible application cases in the multi-dimensional parameter space \(\{\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma \}\), only computational optimization towards well-defined target metrics is likely to lead to good-quality results.

The liquid volumes \(U\) and \({U}^{\prime}\) are chosen to settle the menisci \(r\) and \({r}^{\prime}\) in the inner (wider) region of their reservoirs with cross sections \(A\) and \({A}^{\prime}\), so that effects of volume deviations, whether related to systematic loss by evaporation or dispenser precision \(\Delta U\) and \(\Delta {U}^{\prime}\), on the initial liquid levels \({r}_{0}\), and \({r}_{0}^{\prime}\), and thus the centrifugal equilibrium (5) determining \(z\) at \(\omega >0\), are largely mitigated. For given volumes \(U\) and \({U}^{\prime}\), the lower radial segments of the reservoirs display smaller cross sections \(a\) and \({a}^{\prime}\); for instance, \(a<A\) amplifies \(\Delta r={r}^{\prime}-r\), and thus the net pressure \({p}_{\omega }\propto\Delta r\) (4) for pumping the minimum volume fraction \({U}_{\Delta }\) (7) of \(U\) to reach , as required for prompting disintegration of the DF.

The additional segment centered at in the isoradial channel featuring a cross section \(\fancyscript{a}\) over an axial extension has been introduced for supporting the definition of the liquid–liquid interface, and to suppress the shift of the meniscus by a high flow resistance scaling with during storage and transport. Evidently, it is critical that the actual position of the meniscus at \(\tilde{z }\), when factoring in experimental tolerances in \(\{\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma ,\}\), remains between the edges, i.e., (while avoiding enclosure of gas between the liquid phases). A large extension is desirable for improving the tolerance to discrepancies in the loading procedure of the two liquids.

3.1 Loading

The reservoirs are filled at the factory (while \(\omega =0\)) with the two immiscible liquids, in the main exemplary case considered here with water and FC-72 (3 M™ Fluorinert™ Electronic Liquid FC-72), of target volumes \(U\) and \({U}^{\prime}\) and densities \(\varrho\) and \(\varrho^{\prime }\) through their designated inlet ports. The loading procedure should be highly reproducible, and ideally be monitored until the actual meniscus location \(\tilde{z }\) matches , or at least settles sufficiently central in their designated channel section around , i.e., . For the low contact angles that are often observed between an oil-based ancillary liquid and the polymer surface, it is advisable to first load the aqueous phase or to coat the wall with a suitable agent.

3.2 Transport

When taken out of its storage, a LoaD may experience various accelerations \(\beta\), e.g., repetitively during manual handling, walking or in a moving vehicle, or punctually and more forcefully when its full weight hits solid ground, e.g., after falling from a height. The directions of the resulting, usually unintended forces tend to be oriented randomly but may possess components parallel to the designated radial axis during spinning. The unknown number, magnitude, orientation and duration of such arbitrary inertial effects make it impossible to exactly quantify their impact on the deviation of the actual meniscus position \(\tilde{z }\) from its target value . As successive accelerations might point in opposite directions, and thus somewhat neutralize their effect on the meniscus position, it is mostly likely that a single hard impact aligned in \(\fancyscript{r}\)-direction will compromise the liquid distributions \(\Lambda\) and \({\Lambda }^{\prime}\). We consider here two main mechanisms for pinning the phase interface during transport.

3.2.1 Pneumatic stabilization

Air-tight membranes seal the inlet ports of the reservoirs after loading the reagent and ancillary liquid to prevent evaporation. In addition, these fluid barriers also pneumatically stabilize \(\Lambda\) and \({\Lambda }^{\prime }\) by virtue of Boyle’s law

$$p_{V} = p_{0} \cdot \frac{{V_{0} }}{V}$$
(9)

stating that a change of an originally confined gas volume \({V}_{0}\) at \({p}_{0}\) to \(V\) alters the pressure to \({p}_{V}\ne {p}_{0}\) (9). So, for instance, according to the conservation of liquid volume \(dU/dt=0\) (1), transport-related disruption may induce a shift of the liquid level \(r\) on the (left) aqueous side towards the center of rotation, which ensues a peripheral displacement of the liquid level \(r^{\prime }\) of the ancillary fluid (right) towards \(R\) (Fig. 1).

The resultant changes in the gas volumes \(V\) and \({V}^{\prime}\) lead to an increase in \({p}_{V}\) and a reduction of \({p}_{V}^{\prime}\), thus seeking to restore . The driving pressure (difference)

$$\begin{aligned} \Delta p_{V} \left( z \right) & = ~p_{V}^{\prime } \left( z \right) - p_{V} \left( z \right) = p_{0} \cdot \left[ {\frac{{V_{0}^{\prime } }}{{{V}^{\prime} \left( z \right)}} - \frac{{V_{0} }}{{V\left( z \right)}}} \right] \\ & = p_{0} \cdot \left[ {\frac{{V_{0}^{\prime } }}{{V_{0}^{\prime } - U_{\Delta } \left( z \right)}} - \frac{{V_{0} }}{{V_{0} + U_{\Delta } \left( z \right)}}} \right] \\ \end{aligned}$$
(10)

should consequently be maximized through adjusting the \(z\)-dependent, displaced liquid volume \({U}_{\Delta }(z)\) in (7), and the initial gas volumes \({V}_{0}\) and \({V}_{0}^{\prime}\) underneath the seal for steadying the interface position near during transport. Figure 2(left) illustrates the dependency of the effective counter pressure \(\Delta {p}_{V}\) (10) in response to (left) a shift \(z\) from the default Figure 2(right) reveals that the restoring pressure \(\Delta {p}_{V}<0\) (10), evaluated at the downstream boundary of the -segment , approaches 0 towards scaling the initially enclosed gas volumes \({V}_{0}\) and \({V}_{0}^{\prime}\) by the (same) factor \(\xi\).

Fig. 2
figure 2

Net pneumatic (counter-)pressure \({\Delta p}_{V}\) (10) as a function of (left) the axial coordinate \(z\) with the equilibrium \(\Delta {p}_{V}=0\) at , and (right) scaling the initial volumes \({V}_{0}\) and \({V}_{0}^{\prime}\) by applying a factor \(\xi\) to their heights while pinning the meniscus position at the end of the -section . Reducing the initial gas volumes \({V}_{0}\) and \({V}_{0}^{\prime}\) hence stabilizes the actual meniscus position \(\tilde{z }\) in the vicinity of during transport. Default values (Table 1) are used in this example

Full size image

3.2.2 Geometrical factors

It would be disastrous from an operational point of view if the full volume in (7) was displaced so that the aqueous reagent already reaches to open the DF during storage, transport and handling. This fatal event would happen in case the liquid distributions \(\Lambda\) and \({\Lambda }^{\prime}\) experienced an acceleration \(\beta\) with a strong component parallel to the radial \(\fancyscript{r}\)-direction of the centrifugal field (Fig. 1) for a sufficiently long duty cycle \(\tau\). Note that even though not discussed here for the sake of clarity, the interface may also leave the designated isoradial region, i.e., , under the impact of \(\beta\) to disrupt the phase interface.

In response to an acceleration \(\beta\) with a major component parallel to the radial \(\fancyscript{r}\)-axis, the liquid distributions \(\Lambda\) and \({\Lambda }^{\prime}\) seek hydrostatic equilibrium (5). The resulting flow is driven by the pressure differential

$${p}_{\beta }\approx \beta \cdot \left[\varrho \cdot\Delta r-{\varrho }^{\prime}\cdot\Delta {r}^{\prime}\right]$$
(11)

(initially) applying along the axial \(z\)-axis towards , and throttled by the aggregate hydrodynamic resistance

$$\mathcal{R}=\sum_{q}{\mathcal{R}}_{q}=\sum_{q}{c}_{q}\cdot \frac{{\eta }_{q}\cdot {l}_{q}}{{A}_{q}^{2}}$$
(12)

of the structural segments indexed by \(q\), possessing a cross section \({A}_{q}\), and filled over an axial length \({l}_{q}\) with the reagent and ancillary liquid with viscosities \(\eta\) or \({\eta }^{\prime}\), respectively. The numerical coefficients \({c}_{q}\) amount to \(8\pi\) for round cross sections. This law of Hagen-Poiseuille delivers a volume flow rate

$${\dot{U}}_{V}=\frac{dU}{dt}=\frac{{p}_{\beta }}{\mathcal{R}}\approx \frac{\beta \cdot \left[\varrho \cdot\Delta r-{\varrho }^{\prime}\cdot\Delta {r}^{\prime}\right]}{\sum_{q}{c}_{q}\cdot {\eta }_{q}\cdot {l}_{q}/{A}_{q}^{2}}$$
(13)

which is governed by \({p}_{\beta }\) (11) and {\({\mathcal{R}}_{q}\}\) (12). As the outlet opens for \({\dot{U}}_{V}\cdot \tau \ge {U}_{\Delta }(z)\) in (7), the duty cycle \({\tau =U}_{\Delta }/{\dot{U}}_{V}\) ought to be maximized to best suppress operationally disastrous premature release of reagent during transport. However, since \(\beta\) is unknown, we define a resilience (evaluated for )

expressed in units of \({\mathrm{s}}^{3}\cdot {\mathrm{m}}^{-1}\), to be maximized by adjusting to the structure \(\Gamma\) (Fig. 1) for mitigating unfavorable effects owing to transport conditions.

This design goal of maximizing \({\tau }_{\beta }\) (14) translates into enlarging the dead volumes (7) of the isoradial channel extending between on the left, and on the right, which turns out to be mostly determined via the part having the (larger) cross section \(\mathcal{A}\). Furthermore, the flow rate \({\dot{U}}_{V}\) (13) should stay small; this means that the (initial) liquid level difference \({r}^{\prime}-r\) should be minimized, e.g., by adjusting the cross sections or the reservoirs \(A,a,A^{\prime }\) and \(a^{\prime}\), while the dominant flow resistance \(\mathcal{R}\) (12), as imposed by the isoradial segment of length and cross section \({A}_{q}=\fancyscript{a}\), and scaling with the geometrical ratio , should be large. As the properties of the reagent are usually prescribed by the assay, an ancillary liquid possessing a high viscosity \({\eta }^{\prime}\) would also be beneficial to increase \({\tau }_{\beta }\) (14). Figure 3 shows the dependency of the resilience \({\tau }_{\beta }\) (14) on (left) the length , and (right) the cross section \(\fancyscript{a}\) of the -segment, which accounts for the biggest impact on the flow resistance \(\mathcal{R}\) (12) through .

Fig. 3
figure 3

Resilience quantified by \({\tau }_{\beta }\) (14) of the liquid distributions \(\Lambda\) and \({\Lambda }^{\prime}\) contained in the structure \(\Gamma\) as a function of (left) the length of the isoradial segmented centered at , and (right) its cross section \({a}_{q}=\fancyscript{a}\). As inferred from its definition (14), the resilience \({\tau }_{\beta }\) steeply increases towards high flow resistance \(\mathcal{R}\) (12), i.e., with \({l}_{q}/{\fancyscript{a}}_{q}^{2}\). The gridlines mark the values when inserting default parameters (Table 1)

Full size image

3.2.3 Design optimized for transport

By maximizing the quantities \(\Delta {p}_{V}\) (10) and \({\tau }_{\beta }\) (14) within the practical ranges of their input parameters \(\{{\gamma }_{k}\}\) and their tolerances {\(\Delta {\gamma }_{k}\)}, the parametrized structure \(\Gamma\) can be algorithmically optimized to accomplish these design goals. Figure 4 shows (left) the layouts for the highest restoring pressure \(\Delta {p}_{V}\) (10), (center) the resilience \({\tau }_{\beta }\) (14), and (right) their product \(\Delta {p}_{V}\cdot {\tau }_{\beta }\).

Fig. 4
figure 4

Algorithmically optimized layouts \(\Gamma\) obtained with given design metrics for stabilizing the liquid–liquid interface at during transport. (Left) Pneumatic \(\Delta {p}_{V}\) (10): Both ports closed, (Center), Resilience \({\tau }_{\beta }\) (14): Both ports open, and (Right) Combination of stabilization of pneumatics and resilience \(\Delta {p}_{V}\cdot {\tau }_{\beta }\) with both ports closed, which finds the right balance between partially contradictory design guidelines

Full size image

While the reasoning behind these designs is rather complicated, we point out some key characteristics of the optimization in Fig. 4. The left, pneumatically stabilized design shows a minimized gas volume above the reagent to raise the \({p}_{V}\) (9) at the initial position (Fig. 1), thus preventing advancement of the phase interface during storage towards the DF. To still enable rotational actuation within the allowed frequency envelope, the gas volume above the ancillary liquid is kept noticeably larger. The resilience \({\tau }_{\beta }\) (14) in the central layout displaying open reservoirs is improved with the high flow resistance \(\mathcal{R}\) (12), as imposed by the narrow section in the horizontal channel. The compromise design on the right-hand side of Fig. 4 features a tiny outer part of the radial channel on the reagent side to maintain a large \(\Delta r\), and thus \(\Delta {p}_{\omega }\) (4), so the counter pressure required for opening the DF at (Fig. 1) can still be provided.

4 Actuation

4.1 Pneumatic modes

In the case of the default scenario portrayed in Fig. 1, the inlets of the reservoirs for the aqueous reagent and the ancillary liquid are vented during rotation \((\omega >0\)), which can be interpreted as \({V}_{0}\mapsto \infty\) and \({V}_{0}^{\prime}\mapsto \infty\) in (10), and thus \(\Delta {p}_{V}\mapsto 0\) (10). So, as long as the centrifugally induced pressure head remains positive, i.e., \(\Delta {p}_{\omega }>0\) (5) for , the meniscus will reach , and thus wet and open the DF at the outlet. However, for centrifugo-pneumatic actuation, a critical spin rate

$$\Omega =\sqrt{\frac{{p}_{V}^{\prime}-{p}_{V}}{\varrho \overline{r }\Delta r-{\varrho }^{\prime}{\overline{r} }^{\mathrm{^{\prime}}}\Delta {r}^{\prime}}}$$
(15)

first needs to be surpassed, i.e., \(\omega >\Omega\), before trigging reagent release. Here, the ambient pressure \({p}_{0}\) applies to open, and \({p}_{V}\) and \({p}_{V}^{\prime}\) (9) to sealed ports. Such a finite \(\Omega >0\) (15) proves especially advantageous for multiplexed flow control (Ducrée 2021b, c).

As the default experimental parameters \(\varrho ,\varrho^{\prime},U,U^{\prime},R\) and \(\Gamma\) (Table 1) are geared to result in \(\Delta {p}_{\omega }=0\) (5) at , and thus \(\Omega \mapsto \infty\), centrifugo-pneumatic actuation requires adjusting a subset of these variables. In general, the digital twin allows to calculate the changes required within the rather intricate correlation between the parameters \(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R,\Gamma\) and \(\Omega\) in order realize certain design targets, e.g., a release threshold \(\Omega\) (15) that is commensurate with a rotationally automated, multiplexed assay protocol. The example portrayed in Fig. 5 shows the scaling of the critical spin rate \(\Omega /2\pi\) (15) with the ancillary volume \(\chi \cdot {U}^{\prime}\). Spindle speeds \(\Omega /2\pi\) (15) within the experimentally feasible range smaller than \(100\, \mathrm{Hz}\) only emerge below \(\chi \approx 0.55\). It follows that, to make sure that the isoradial channel is always filled with the ancillary liquid, the cross sections \(\mathcal{A}\) and \(\fancyscript{a}\) are both reduced by a factor of 3 with respect to the values in Table 1.

Fig. 5
figure 5

Burst frequency \(\Omega /2\pi\) required to establish when both inlet ports remain sealed during rotation when reducing the ancillary volume \(U^{\prime }\) by a factor of \(\chi\). Towards \(\chi \mapsto 1\), \(\Omega\) reaches values that are way beyond the capabilities pf typical LoaD instruments, thus effectively preventing release. Yet, spin rates below the practical upper limit \(\omega /2\pi \approx 100\, \mathrm{Hz}\) can be achieved below \(\chi \approx 0.55\). Default parameters (Table 1) are employed, except that the cross sections \(\mathcal{A}\) and \(\fancyscript{a}\) of the isoradial channel have been reduced by a factor of 3 to still assure its complete filling

Full size image

Note that Eq. (10) also discloses \(\Delta {p}_{V}\propto {p}_{0}\). This scaling with the atmospheric pressure \({p}_{0}\) only affects the overall magnitude of \(\Delta {p}_{V}\), but not the direction and ratio of the pneumatic pressures. We therefore refer to previous work on centrifugo-pneumatic valving where the impact and possible compensation of variation in the atmospheric pressure by weather, and particularly local altitude, have been examined in more detail (Ducrée 2021a, b, c, d).

The critical spin rate \(\Omega\) (15), furthermore, determines the maximum (density) of the centrifugal field \({f}_{\omega }={\varrho }_{\mathrm{part}}\cdot {R}_{\mathrm{LUO}}\cdot {\Omega }^{2}\) that can be sustained by the reagent valve, e.g., while an LUO, for instance, plasma extraction, is simultaneously processed to separate blood cells of (relative) density \({\varrho }_{\mathrm{part}}\) at \(\omega <\Omega \pm M\cdot \mathrm{\Delta \Omega }\).

4.2 Systematic volume losses

Due to evaporation or absorption at rates \(\dot{U}\) and \({\dot{U}}^{\prime}\), liquid volumes \(U\) and \({U}^{\prime}\) may appreciably decline during storage over time periods \(T\), typically lasting months up to a few years, by \(\delta U=\dot{U}\cdot T\) and \(\delta {U}^{\prime}=\dot{{U}^{\prime}}\cdot T\). Even for open inlet ports during rotation, the reduced volumes \(U-\delta U\) and \({U}^{\prime}-\delta {U}^{\prime}\) may lead to (5), and thus cause valve malfunction by failure to dissolve the DF at . (In addition, these volume losses \(\delta U\) and \(\delta {U}^{\prime}\) may also affect the outcome of quantitative bioassays.)

The main influence of the lost liquid volumes \(\delta U\) and \(\delta {U}^{\prime}\) on the density-weighted radial products \(\overline{r }\Delta r\) and \({\overline{r} }^{\, \prime}\Delta {r}^{\prime}\) in the centrifugal equilibrium (6) manifests through \({\Delta }r = R - r\) and \({\Delta }r^{\prime} = R - r^{\prime}\) via \(r\left( {U,\delta U,A} \right) = (U - \dot{U} \cdot T)/A\) and \(r^\prime \left( {U^\prime ,\delta U^\prime ,A^\prime } \right) = (U^{\prime } - \dot{U}^{\prime } \cdot T)/A^\prime\). Enlarged cross sections \(A\) and \(A^{\prime }\) thus reduce the effect of evaporation or other losses \(\delta U\) and \(\delta {U}^{\prime}\) of the reagent and ancillary phases at \(\dot{U}\) and \(\dot{U}^{\prime }\). Figure 6 shows that the prerequisite \(\Delta {p}_{\omega }>0\) for is assured for nearly 2.5 years at exemplary annual evaporation losses of 5% and 1% for the reagent and the ancillary liquid, respectively. This condition of a positive centrifugal pressure differential \(\Delta {p}_{\omega }\) (10) also entails that sufficient liquid volumes \(U\) and \({U}^{\prime}\) remain available along all locations of the interface , to eventually displace \({U}_{\Delta }\) (7) from the reagent side through the isoradial segment towards the ancillary reservoir.

Fig. 6
figure 6

Systematic reductions \(\delta U=\dot{U}\cdot T\) and \(\delta {U}^{\prime}=\dot{{U}^{\prime}}\cdot T\) of the originally loaded liquid volumes \(U\) and \({U}^{\prime}\) at rates \(\dot{U}\) and \({\dot{U}}^{\prime}\), thus changing the centrifugal pressure balance \({p}_{\omega }/{\omega }^{2}\) (6) over a time period \(T\). In this example, annual loss rates of \(\dot{U}\) and \({\dot{U}}^{\prime}\) of 5% and 1% are assumed, and \(\dot{U} > \dot{U}^{\prime}\) is compensated by loading 10% more reagent volume \(U\). The curve uncovers that the opening condition \({\Delta p}_{\omega }/{\omega }^{2}>0\) at is assured beyond a typical minimum storage period of 24 months

Full size image

If evaporation through the DF membrane turns out to be unacceptably high, its formulation ought to be altered, a coating applied, or its thickness enlarged. Note also that leaks in the assembly or permeation through the bulk material should be investigated. Moreover, even if the reagent valve still properly opens, the forwarded liquid volume might still be insufficient to actuate subsequent valves, e.g., by failing to generate enough centrifugal pressure head \({p}_{\omega }\) (4) for overcoming a critical frequency threshold, such as \(\Omega\) (15).

4.3 Statistical tolerances

Consistent reagent release hinges upon in hydrostatic equilibrium (5) at \(\omega >0.\) The standard deviation \(\Delta z\) (8) is affected by the unavoidable spreads {\(\Delta {\gamma }_{k}\)} of the experimental input parameters {\({\gamma }_{k}\)}, mainly within the geometrical dimensions \(\mathrm{\Delta \Gamma }\) and \(\Delta U\) delineating the structure \(\Gamma\), and the loaded liquid volumes \(U\) and \({U}^{\prime}\), respectively.

The histogram in Fig. 7 displays the distribution of \(\tilde{z }\) with a mean \(\overline{z }=19.97 \, \mathrm{mm}\) close to and a standard deviation \(\Delta z=4.02 \, \mathrm{mm}\) (8) as acquired from a Monte-Carlo simulation with 1000 runs using the default values and realistic tolerances \(\Delta d\) and \(\Delta w\) in vertical and lateral machining, and pipetting the liquid volumes \(\Delta U\) and \(\Delta {U}^{\prime}\), as listed in Table 1. This digital-twin based Monte-Carlo method may be regarded as a virtualized manufacture and testing, which is very useful in view of the common paucity of physical devices throughout prototyping.

Fig. 7
figure 7

Monte-Carlo simulation of the distribution of actual meniscus position \(\tilde{z }\) when targeting at centrifugal equilibrium \(\Delta {p}_{\omega }=0\) found for the default parameters \(\varrho ,{\varrho }^{\prime},U,{U}^{\prime},R\) and \(\Gamma\) while factoring in their respective tolerances \(\Delta U,\Delta {U}^{\prime}\) and \(\mathrm{\Delta \Gamma }\) (Table 1). After 1000 (time consuming) runs, the histogram features a mean position \(\overline{z }=19.99 \, \mathrm{mm}\) with a standard deviation \(\Delta z=0.387 \, \mathrm{ mm}\). The vertical lines indicate (magenta) the default center and limits of the DF at and , respectively, and (red shades) with \(M=\{\mathrm{1,2},3\}\) with the standard deviation \(\Delta z\) (8) of the \(\tilde{z }\)-distribution

Full size image

4.4 Gas enclosure

During priming or storage, bubbles may emerge from or between the two liquids, e.g., driven by the vapor pressure of the ancillary phase. For developing a semi-quantitative understanding of their influence on valving, we consider the case of a gas volume \({V}_{\mathrm{g},0}\) entrapped, after loading, at ambient pressure \({p}_{0}\) in the center of the isoradial -segment. Upon reaching hydrostatic equilibrium during spinning at \(\omega >0\), its original volume \({V}_{\mathrm{g},0}\) is compressed to

$${V}_{\mathrm{g}}(\omega )={V}_{\mathrm{g},0}\cdot \frac{{p}_{0}}{{p}_{0}+{p}_{\omega }}={V}_{\mathrm{g},0}\cdot \frac{{p}_{0}}{{p}_{0}+\varrho \cdot \overline{r}\Delta r\cdot {\omega }^{2}}$$
(16)

while now residing near . To still open the DF in presence of the entrapped gas, the liquid volumes \(U\) and \({U}^{\prime}\) need to be sized so that the meniscus at \(z\) was to shift by a further \(0.5\cdot {V}_{\mathrm{g}}(\omega )/\mathcal{A}\) (16) in the isoradial \(z\)-axis, compared to the absence of the bubble. (Alternatively, the position of the DF at can be appropriately adjusted to provide bubble tolerance.)

Assuming symmetrical displacement into each lateral reservoir (which is, strictly speaking, only the case for \(\varrho ={\varrho }^{\prime}\)), the liquid levels \(r\) and \({r}^{\prime}\) in hydrostatic equilibrium (5) are lifted by about \(0.5\cdot {V}_{\mathrm{g}}(\omega )/A\) and \(0.5\cdot {V}_{\mathrm{g}}(\omega )/{A}^{\prime}\) towards the center of rotation, respectively. The impact of such an entrapped gas bubble is assessed here in a back-of-the-envelope calculation; for this, we assume \({V}_{0}=1 \, \upmu \mathrm{l}\), \({p}_{0}={p}_{\mathrm{std}}\), \(\nu =\omega /2\pi =25 \, \mathrm{Hz}\) and default values for the other parameters (Table 1), to arrive at \(V\approx 0.9 {V}_{\mathrm{g},0}\) and \(\delta r\approx \delta {r}^{\prime}\approx 1 \, \mathrm{mm}\).

5 Refinements

To illustrate the very concept and potential of a digital twin for optimizing the long-term storage and release mechanism towards strategic design goals, we introduced a basic structure \(\Gamma\) (Fig. 1); this way, engineering objectives could be quantified and expressed by algebraic formulas without obfuscating the underlying mechanisms; moreover, these equations can be solved on reasonable time scales by commonly available computing resources.

Pegging the forward meniscus of the first introduced liquid by a minor capillary barrier, occasionally referred to as phase guide, at , is amongst many possible improvements. Trapping of an interstitial bubble after filling the second liquid may be prevented by an (initially) gas-permeable membrane, located near , or a local outlet to be sealed after priming has been completed. Stiction of the progressing meniscus, e.g., caused by capillary pinning owing to manufacturing-related artefacts or dust, may be overcome by choosing a sufficiently elevated spin rate \(\omega \gg 0\) for reaching hydrostatic equilibrium (5) at .

In our own, naturally limited set of similar assay implementations (Lu et al. 2020; Mishra et al. 2020), we did not observe any adverse effect of the ancillary liquid on the bioanalytical performance. Yet, a general, blanket guarantee cannot be issued a priori. To avoid possible interference with the assay protocol, the immiscible ancillary liquid can be cleanly removed under prevalent laminar flow conditions through an additional, radially outer side pocket. Through centrifugal stratification, this reservoir can be designed to retain the entire volume of the higher-density ancillary liquid, while the released liquid reagent overflows towards the next stage. A corresponding structure has been proposed in the context of high-quality centrifugal separation of the plasma phase (Haeberle et al. 2006) (Czugala et al. 2013; Yao et al. 2021) or bands (Kinahan et al. 2016a) from whole blood.

Specific configurations of the reagent storage technique have been tested for premature opening upon possibly adverse conditions during storage, manual handling and transport. The valve proved to be stable, the main impact was evaporation, which was therefore included in the digital twin simulation (Fig. 6) (Lu et al. 2020; Mishra et al. 2020). It is assumed that a malicious, brute force approach would be required for inducing valve opening by deformation of the disc.

The permanently gas-filled parts of reservoirs may be placed at distal locations, as long as they are still pneumatically connected through conduits, e.g., to make efficient use of precious disc real estate required for multiplexed assay panels. The pneumatic seals may also be removed through a secondary mechanism, e.g., akin to venting procedures implemented for centrifugo-pneumatic valves based on mechanical (Kinahan et al. 2016b), laser- (García-Cordero et al. 2010; Mishra et al. 2018) or pneumatic (Keller et al. 2015; Hess et al. 2019; Kinahan et al. 2016c, 2018; Godino et al. 2012, 2013; Schwemmer et al. 2015a; Zhao et al. 2015; Zehnle et al. 2015; Ducrée 2021c; Mishra et al. 2018; Gorkin et al. 2010b, 2011; Mark et al. 2008, 2009b) principles.

6 Summary and outlook

6.1 Summary

A novel technology has been introduced for Lab-on-a-Disc systems, which offers a physical evaporation barrier and stabilization of liquid distributions during long-term storage, transport, and handling. Initially protected by an immiscible ancillary liquid, the aqueous reagent contacts a dissolvable film by centrifugal displacement. The convoluted interdependencies governing the operational principle over its multiparameter space have been modelled to characterize system robustness and behavior in silico. The resulting digital twin further enables computational design optimization towards given performance objectives within practically achievable regimes of the experimental input parameters and their tolerances. In addition, systematic volume losses, e.g., through evaporation during storage, artefacts such as enclosed gas bubbles, and statistical deviations in the governing parameters can be factored in, thus permitting algorithmic enhancement the operational robustness of the valving mechanism.

6.2 Outlook

Evidently, the work presented only represents a blueprint for setting up digital twins to efficiently characterize and improve other functional elements of (centrifugal) microfluidic Lab-on-a-Disc systems. Its simplified representation of the valving structure by cuboidal elements can be significantly refined to optimize flow, e.g., by curved contours of the compartments, their inclination with respect to the radial orientation, and fins to guide the relocation of liquids and gases. Similar to the entrapped bubble, further parasitic effects observed during experimental testing, and additional elements of the layout can be included in the digital twin. Such enhancements will require a more complex computational fluid dynamic (CFD) simulation, which should also include inertia of the liquid and elastic components, like the sealing membranes, which may bend or even yield under pressure.

It is well known that tests with real systems will show effects that are not included in the digital-twin modelling. So, it is well expected that experimental validation will remain a substantial tool for arriving at a product. Nevertheless, in particular during the early stage of development where manufacturing and testing are mostly manual, only smaller numbers of fluidic chips are available, which usually precludes collecting sufficient statistics for proper device performance and reliability analysis. Extensive experimental validation of a wide spectrum of use cases, and sophistication of the rudimentary digital twin model, by the scientific community is highly encouraged.

The digital twin presented in this work can then markedly expedite the design iteration of microfluidic systems by providing virtual prototyping and testing. Such a tool hence empowers failure mode and effects analysis (FMEA) regarding unavoidable tolerances, and in silico optimization of the layout for given design targets. Adding similar programs for simulating manufacturing and biochemical processes would also be desirable to combine with the digital twin for fluidics presented here.

On the bigger picture, the digital twin approach can boost microfluidic industries by standardization (Heeren 2012; Stavis 2012; Reyes et al. 2021), interpreted in a way that validated boundary conditions issued by foundries can be incorporated in computational design software to guarantee manufacturability, reliability and targetted performance within given cost limits. Moreover, the digital twin modelling published here, in tandem with simultaneously evolving, exponential technologies such as artificial intelligence (AI) and digital manufacture in an increasingly virtualized “metaverse” (Metaverse 2021; Meta 2021), lends itself for open platform concepts which can leverage crowdsourcing of brains, hands, infrastructure and equipment, e.g., coordinated by the rapidly emerging, decentralized blockchain technology (Ducrée et al. 2020a, b, 2021; Ducrée 2020, 2021e).