Space–Time Variational Multiscale Isogeometric Analysis of a tsunami-shelter vertical-axis wind turbine

Abstract

We present computational flow analysis of a vertical-axis wind turbine (VAWT) that has been proposed to also serve as a tsunami shelter. In addition to the three-blade rotor, the turbine has four support columns at the periphery. The columns support the turbine rotor and the shelter. Computational challenges encountered in flow analysis of wind turbines in general include accurate representation of the turbine geometry, multiscale unsteady flow, and moving-boundary flow associated with the rotor motion. The tsunami-shelter VAWT, because of its rather high geometric complexity, poses the additional challenge of reaching high accuracy in turbine-geometry representation and flow solution when the geometry is so complex. We address the challenges with a space–time (ST) computational method that integrates three special ST methods around the core, ST Variational Multiscale (ST-VMS) method, and mesh generation and improvement methods. The three special methods are the ST Slip Interface (ST-SI) method, ST Isogeometric Analysis (ST-IGA), and the ST/NURBS Mesh Update Method (STNMUM). The ST-discretization feature of the integrated method provides higher-order accuracy compared to standard discretization methods. The VMS feature addresses the computational challenges associated with the multiscale nature of the unsteady flow. The moving-mesh feature of the ST framework enables high-resolution computation near the blades. The ST-SI enables moving-mesh computation of the spinning rotor. The mesh covering the rotor spins with it, and the SI between the spinning mesh and the rest of the mesh accurately connects the two sides of the solution. The ST-IGA enables more accurate representation of the blade and other turbine geometries and increased accuracy in the flow solution. The STNMUM enables exact representation of the mesh rotation. A general-purpose NURBS mesh generation method makes it easier to deal with the complex turbine geometry. The quality of the mesh generated with this method is improved with a mesh relaxation method based on fiber-reinforced hyperelasticity and optimized zero-stress state. We present computations for the 2D and 3D cases. The computations show the effectiveness of our ST and mesh generation and relaxation methods in flow analysis of the tsunami-shelter VAWT.

1 Introduction

We address the computational challenges encountered in and present results from flow analysis of a vertical-axis wind turbine (VAWT) that has been proposed to also serve as a tsunami shelter. The VAWT model is based on “Life tower” [1]. In addition to the three-blade rotor, the turbine has four support columns at the periphery. The columns support the turbine rotor and the shelter. The challenges encountered in computational flow analysis of wind turbines in general include accurate representation of the turbine geometry, multiscale unsteady flow, and moving-boundary flow associated with the rotor motion. The tsunami-shelter VAWT, because of its rather high geometric complexity, poses the additional challenge of reaching high accuracy in turbine-geometry representation and flow solution when the geometry is so complex.

The computational challenges encountered in flow analysis of turbines in a more general context have been addressed also by other researchers. The approaches are quite diverse, such as using a single blade with spatially-periodic boundary conditions (see, e.g., [2,3,4,5,6,7,8,9]), which is more traditional, and “sliding interfaces” (see, e.g., [10,11,12,13,14,15]), which is more recent.

We address the challenges with a space–time (ST) computational method that integrates three special ST methods around a core ST method and mesh-related methods. The core method is the ST Variational Multiscale (ST-VMS) method [16,17,18], which subsumes its precursor “ST-SUPS” (see Sect. 1.1). The three special methods are the ST Slip Interface (ST-SI) method [19, 20], ST Isogeometric Analysis (ST-IGA) [16, 21, 22], and the ST/NURBS Mesh Update Method (STNMUM) [21, 23,24,25]. The mesh-related methods are a general-purpose NURBS mesh generation method [26, 27] and a mesh relaxation method [28] based on fiber-reinforced hyperelasticity and optimized zero-stress state (ZSS).

The ST-discretization feature of the integrated method provides higher-order accuracy compared to standard discretization methods. The VMS feature addresses the computational challenges associated with the multiscale nature of the unsteady flow. The moving-mesh feature of the ST framework enables high-resolution computation near the blades. The ST-SI enables moving-mesh computation of the spinning rotor. The mesh covering the rotor spins with it, and the SI between the spinning mesh and the rest of the mesh accurately connects the two sides of the solution. The ST-IGA enables more accurate representation of the blade and other turbine geometries and increased accuracy in the flow solution. The STNMUM enables exact representation of the mesh rotation. The general-purpose NURBS mesh generation method makes it easier to deal with the complex turbine geometry. The quality of the mesh generated with this method is improved with the mesh relaxation method.

The first flow computations for the tsunami-shelter VAWT were presented in [19], in the context of finite element discretization, as test computations with 2D and 3D models to show how the ST-SI method, introduced in the paper, worked. Preliminary test computations with isogeometric discretization were presented in [29] for the 2D model and in [30] for both the 2D and 3D models.

1.1 ST-VMS and ST-SUPS

The Deforming-Spatial-Domain/Stabilized ST (DSD/SST) method [31,32,33] was introduced for computation of flows with moving boundaries and interfaces (MBI), including fluid–structure interaction (FSI). In MBI computations the DSD/SST functions as a moving-mesh method. Moving the fluid mechanics mesh to follow an interface enables mesh resolution control near the interface and, consequently, high-resolution boundary-layer representation near fluid–solid interfaces. Because the stabilization components of the original DSD/SST are the Streamline-Upwind/Petrov-Galerkin (SUPG) [34] and Pressure-Stabilizing/Petrov-Galerkin (PSPG) [31] stabilizations, it is now called “ST-SUPS.” The ST-VMS is the VMS version of the DSD/SST. The VMS components of the ST-VMS are from the residual-based VMS (RBVMS) method [35,36,37,38]. The ST-VMS has two more stabilization terms beyond those in the ST-SUPS, and the additional terms give the method better turbulence modeling features. The ST-SUPS and ST-VMS, because of the higher-order accuracy of the ST framework (see [16, 17]), are desirable also in computations without MBI.

As a moving-mesh method, the DSD/SST is an alternative to the Arbitrary Lagrangian–Eulerian (ALE) method, which is older (see, for example, [39]) and more commonly used. The ALE-VMS method [40,41,42,43,44,45,46] is the VMS version of the ALE. It succeeded the ST-SUPS and ALE-SUPS [47] and preceded the ST-VMS. To increase their scope and accuracy, the ALE-VMS and RBVMS are often supplemented with special methods, such as those for weakly-enforced Dirichlet boundary conditions [48,49,50], “sliding interfaces” [51, 52], and backflow stabilization [53]. The ALE-SUPS, RBVMS and ALE-VMS have been applied to many classes of FSI, MBI and fluid mechanics problems. The classes of problems include ram-air parachute FSI [47], wind-turbine aerodynamics and FSI [10,11,12,13,14,15, 54,55,56,57,58,59,60], more specifically, VAWTs [12, 13, 61, 62], floating wind turbines [63], wind turbines in atmospheric boundary layers [12, 13, 29, 30, 60, 64], and fatigue damage in wind-turbine blades [65], patient-specific cardiovascular fluid mechanics and FSI [40, 66,67,68,69,70,71], biomedical-device FSI [72,73,74,75,76,77,78,79], ship hydrodynamics with free-surface flow and fluid–object interaction [80, 81], hydrodynamics and FSI of a hydraulic arresting gear [82, 83], hydrodynamics of tidal-stream turbines with free-surface flow [84], passive-morphing FSI in turbomachinery [8], bioinspired FSI for marine propulsion [85, 86], bridge aerodynamics and fluid–object interaction [87,88,89], and mixed ALE-VMS/Immersogeometric computations [75,76,77, 90, 91] in the framework of the Fluid–Solid Interface-Tracking/Interface-Capturing Technique [92]. Recent advances in stabilized and multiscale methods may be found for stratified incompressible flows in [93], for divergence-conforming discretizations of incompressible flows in [94], and for compressible flows with emphasis on gas-turbine modeling in [95].

The ST-SUPS and ST-VMS have also been applied to many classes of FSI, MBI and fluid mechanics problems (see [96] for a comprehensive summary of the work prior to July 2018). The classes of problems include spacecraft parachute analysis for the landing-stage parachutes [43, 97,98,99,100], cover-separation parachutes [101] and the drogue parachutes [102,103,104], wind-turbine aerodynamics for horizontal-axis wind-turbine (HAWT) rotors [10, 43, 105, 106], full HAWTs [11, 25, 107, 108] and VAWTs [12,13,14,15, 19], flapping-wing aerodynamics for an actual locust [21, 23, 43, 109], bioinspired MAVs [24, 107, 108, 110] and wing-clapping [111, 112], blood flow analysis of cerebral aneurysms [107, 113], stent-blocked aneurysms [113,114,115], aortas [78, 79, 116,117,118,119,120], heart valves [78, 79, 108, 111, 118, 120,121,122,123,124,125] and coronary arteries in motion [126], spacecraft aerodynamics [101, 127], thermo-fluid analysis of ground vehicles and their tires [18, 29, 30, 122], thermo-fluid analysis of disk brakes [20], flow-driven string dynamics in turbomachinery [14, 15, 128,129,130], flow analysis of turbocharger turbines [22, 26, 27, 131, 132], flow around tires with road contact and deformation [122, 133,134,135,136], fluid films [136, 137], ram-air parachutes [29, 30, 138], and compressible-flow spacecraft parachute aerodynamics [139, 140].

The ST-SUPS, ALE-SUPS, RBVMS, ALE-VMS and ST-VMS all have some embedded stabilization parameters that play a significant role (see [43]). These parameters involve a measure of the local length scale (also known as “element length”) and other parameters such as the element Reynolds and Courant numbers. There are many ways of defining the stabilization parameters. Some of the newer options for the stabilization parameters used with the SUPS and VMS can be found in [18, 19, 21, 25, 106, 135, 141,142,143,144,145]. Some of the earlier stabilization parameters used with the SUPS and VMS were also used in computations with other SUPG-like methods, such as the computations reported in [2, 3, 5, 7,8,9, 146,147,148,149,150,151,152,153]. We will specify which ones we use here in Appendix A.1 and when we describe the computations in Sect. 4.

1.2 ST-SI

The ST-SI was introduced in [19], in the context of incompressible-flow equations, to retain the desirable moving-mesh features of the ST-VMS and ST-SUPS in computations involving spinning solid surfaces, such as a turbine rotor. The mesh covering the spinning surface spins with it, retaining the high-resolution representation of the boundary layers, while the mesh on the other side of the SI remains unaffected. This is accomplished by adding to the ST-VMS formulation interface terms similar to those in the ALE-SI [51, 52]. The interface terms account for the compatibility conditions for the velocity and stress at the SI, accurately connecting the two sides of the solution. An ST-SI version where the SI is between fluid and solid domains was also presented in [19]. The SI in that case is a “fluid–solid SI” rather than a standard “fluid–fluid SI” and enables weak enforcement of the Dirichlet boundary conditions for the fluid. The ST-SI introduced in [20] for the coupled incompressible-flow and thermal-transport equations retains the high-resolution representation of the thermo-fluid boundary layers near spinning solid surfaces. These ST-SI methods have been applied to aerodynamic analysis of VAWTs [12,13,14,15, 19], thermo-fluid analysis of disk brakes [20], flow-driven string dynamics in turbomachinery [14, 15, 128,129,130], flow analysis of turbocharger turbines [22, 26, 27, 131, 132], flow around tires with road contact and deformation [122, 133,134,135,136], fluid films [136, 137], aerodynamic analysis of ram-air parachutes [29, 30, 138], and flow analysis of heart valves [78, 79, 118, 123,124,125] and ventricle-valve-aorta sequences [120].

In the ST-SI version presented in [19] the SI is between a thin porous structure and the fluid on its two sides. This enables dealing with the porosity in a fashion consistent with how the standard fluid–fluid SIs are dealt with and how the Dirichlet conditions are enforced weakly with fluid–solid SIs. This version also enables handling thin structures that have T-junctions. This method has been applied to incompressible-flow aerodynamic analysis of ram-air parachutes with fabric porosity [29, 30, 138]. The compressible-flow ST-SI methods were introduced in [139], including the version where the SI is between a thin porous structure and the fluid on its two sides. Compressible-flow porosity models were also introduced in [139]. These, together with the compressible-flow ST SUPG method [154], extended the ST computational analysis range to compressible-flow aerodynamics of parachutes with fabric and geometric porosities. That enabled ST computational flow analysis of the Orion spacecraft drogue parachute in the compressible-flow regime [139, 140].

1.3 ST-IGA and STNMUM

The success with IGA basis functions in space [40, 51, 66, 155] motivated the integration of the ST methods with isogeometric discretization, which is broadly called “ST-IGA.” The ST-IGA was introduced in [16]. Computations with the ST-VMS and ST-IGA were first reported in [16] in a 2D context, with IGA basis functions in space for flow past an airfoil, and in both space and time for the advection equation. Using higher-order basis functions in time enables deriving full benefit from using higher-order basis functions in space. This was demonstrated with the stability and accuracy analysis given in [16] for the advection equation.

The ST-IGA with IGA basis functions in time enables a more accurate representation of the motion of the solid surfaces and a mesh motion consistent with that. This was pointed out in [16, 17] and demonstrated in [21, 23, 24]. It also enables more efficient temporal representation of the motion and deformation of the volume meshes, and more efficient remeshing. These motivated the development of the STNMUM [21, 23, 24], with the name coined in [25]. The STNMUM has a wide scope that includes spinning solid surfaces. With the spinning motion represented by quadratic NURBS in time, and with sufficient number of temporal patches for a full rotation, the circular paths are represented exactly. A “secondary mapping” [16, 17, 21, 43] enables also specifying a constant angular velocity for invariant speeds along the circular paths. The ST framework and NURBS in time also enable, with the “ST-C” method, extracting a continuous representation from the computed data and, in large-scale computations, efficient data compression [18, 20, 122, 128,129,130, 156]. The STNMUM and the ST-IGA with IGA basis functions in time have been used in many 3D computations. The classes of problems solved are flapping-wing aerodynamics for an actual locust [21, 23, 43, 109], bioinspired MAVs [24, 107, 108, 110] and wing-clapping [111, 112], separation aerodynamics of spacecraft [101], aerodynamics of horizontal-axis [11, 25, 107, 108] and vertical-axis [12,13,14,15, 19] wind-turbines, thermo-fluid analysis of ground vehicles and their tires [18, 29, 122], thermo-fluid analysis of disk brakes [20], flow-driven string dynamics in turbomachinery [14, 15, 128,129,130], flow analysis of turbocharger turbines [22, 26, 27, 131, 132], and flow analysis of coronary arteries in motion [126].

The ST-IGA with IGA basis functions in space enables more accurate representation of the geometry and increased accuracy in the flow solution. It accomplishes that with fewer control points, and consequently with larger effective element sizes. That in turn enables using larger time-step sizes while keeping the Courant number at a desirable level for good accuracy. It has been used in ST computational flow analysis of turbocharger turbines [22, 26, 27, 131, 132], flow-driven string dynamics in turbomachinery [14, 15, 129, 130], ram-air parachutes [29, 30, 138], spacecraft parachutes [140], aortas [78, 118, 119], heart valves [78, 79, 118, 123,124,125], ventricle-valve-aorta sequences [120], coronary arteries in motion [126], tires with road contact and deformation [134,135,136], and fluid films [136, 137]. The image-based arterial geometries used in patient-specific arterial FSI computations do not come from the ZSS of the artery. A number of methods [41, 43, 157,158,159,160,161,162,163,164,165,166] have been proposed for estimating the ZSS required in the computations. Using IGA basis functions in space is now a key part of some of the newest ZSS estimation methods [78, 164,165,166,167] and related shell analysis [168]. The IGA has also been successfully applied to the structural analysis of wind turbine blades [169,170,171,172,173]

1.4 General-purpose NURBS mesh generation method

To make the ST-IGA use, and in a wider context the IGA use, even more practical in computational flow analysis with complex geometries, NURBS volume mesh generation needs to be easier and more automated. To that end, a general-purpose NURBS mesh generation method was introduced in [26]. The method is based on multi-block-structured mesh generation with existing techniques, projection of that mesh to a NURBS mesh made of patches that correspond to the blocks, and recovery of the original model surfaces. The recovery of the original surfaces is to the extent they are suitable for accurate and robust fluid mechanics computations. The method is expected to retain the refinement distribution and element quality of the multi-block-structured mesh that we start with. Because there are ample good techniques and software for generating multi-block-structured meshes, the method makes general-purpose mesh generation relatively easy. Mesh-quality performance studies for 2D and 3D meshes, including those for complex models, were presented in [27]. A test computation for a turbocharger turbine and exhaust manifold was also presented in [27], with a more detailed computation in [131], and with additional computational analysis in [132]. The mesh generation method was used also in the pump-flow analysis part of the flow-driven string dynamics presented in [14, 15, 130]. The performance studies and test computations demonstrated that the general-purpose NURBS mesh generation method makes the IGA use in fluid mechanics computations even more practical.

1.5 ST-SI-IGA

An SI provides mesh generation flexibility in a general context by accurately connecting the two sides of the solution computed over nonmatching meshes. This type of mesh generation flexibility is especially valuable in complex-geometry flow computations with isogeometric discretization, removing the matching requirement between the NURBS patches without loss of accuracy. This feature was used in the flow analysis of heart valves [78, 79, 118, 123,124,125], ventricle-valve-aorta sequences [120], turbocharger turbines [22, 26, 27, 131, 132], spacecraft parachute compressible-flow analysis [140], and flow around tires with road contact and deformation [135, 136]. It is used also in the VAWT flow analysis presented here.

1.6 Mesh relaxation based on fiber-reinforced hyperelasticity and optimized ZSS

Mesh relaxation and mesh moving methods based on fiber-reinforced hyperelasticity and optimized ZSS were introduced in [28]. The methods have been developed targeting isogeometric discretization but are also applicable to finite element discretization. The objective of the mesh relaxation is to improve the quality of the mesh after its initial creation and to have an equilibrium state with the optimized ZSS, boundary conditions and the constitutive law. The constitutive models and parameters can be defined individually for the elements or mesh regions. For more on the method, see [28].

1.7 Computations presented

We present computations for the 2D and 3D cases. In the 2D case, we present computations for three different meshes, two different time-step sizes, and two different tip-speed ratios. In the 3D case, we compute with one of the combinations of the 2D case and compare the 2D and 3D results.

1.8 Outline of the remaining sections

In Sect. 2, for completeness, we describe the ST-VMS and ST-SI. The tsunami-shelter VAWT model is described in Sect. 3. We present the computations in Sect. 4, and give the concluding remarks in Sect. 5. The stabilization parameters used in the ST-VMS and ST-SI are given in Appendix A.

2 ST-VMS and ST-SI

For completeness, we include, mostly from [19, 133], the ST-VMS and ST-SI methods.

2.1 ST-VMS

The ST-VMS is given as

$$\begin{aligned}&\int _{Q_n} \mathbf {w}^h \cdot \rho \left( \frac{\partial \mathbf {u}^h}{\partial t} + \mathbf {u}^h \cdot \pmb {\nabla }\mathbf {u}^h - \mathbf {f}^h \right) \mathrm {d}Q \nonumber \\&\quad + \int _{Q_n} \pmb {\varepsilon }(\mathbf {w}^h) : \pmb {\sigma }^h \mathrm {d}Q-\int _{\left( P_n\right) _\mathrm {h}} \mathbf {w}^h \cdot {\mathbf {h}}^h \mathrm {d}P\nonumber \\&\quad +\int _{Q_n} q^h \pmb {\nabla }\cdot \mathbf {u}^h \mathrm {d}Q+ \int _{\Omega _n} (\mathbf {w}^h)_{n}^{+} \cdot \rho \left( (\mathbf {u}^h)_{n}^+ - (\mathbf {u}^h)_{n}^- \right) \mathrm {d}\Omega \nonumber \\&\quad + \sum _{e=1}^{(n_{\mathrm {el}})_n} \int _{Q_n^e} \frac{\tau _{\mathrm {SUPS}}}{\rho } \left( \rho \left( \frac{\partial \mathbf {w}^h}{\partial t} + \mathbf {u}^h \cdot \pmb {\nabla }\mathbf {w}^h \right) +\pmb {\nabla }q^h \right) \cdot \mathbf {r}_{\mathrm {M}}^h \mathrm {d}Q\nonumber \\&\quad + \sum _{e=1}^{(n_{\mathrm {el}})_n} \int _{Q_n^e} \nu _{\mathrm {LSIC}}\pmb {\nabla }\cdot \mathbf {w}^h \rho {r}_{\mathrm {C}}^h \mathrm {d}Q\nonumber \\&\quad -\sum _{e=1}^{(n_{\mathrm {el}})_n} \int _{Q_n^e} \tau _{\mathrm {SUPS}}\mathbf {w}^h \cdot \left( \mathbf {r}_{\mathrm {M}}^h \cdot \pmb {\nabla }\mathbf {u}^h \right) \mathrm {d}Q\nonumber \\&\quad -\sum _{e=1}^{(n_{\mathrm {el}})_n} \int _{Q_n^e} \frac{\tau _{\mathrm {SUPS}}^2}{\rho } \mathbf {r}_{\mathrm {M}}^h \cdot \left( \pmb {\nabla }\mathbf {w}^h\right) \cdot \mathbf {r}_{\mathrm {M}}^h \mathrm {d}Q\nonumber \\&= 0, \end{aligned}$$

(1)

where

$$\begin{aligned} \mathbf {r}_{\mathrm {M}}^h&= \rho \left( \frac{\partial \mathbf {u}^h}{\partial t} + \mathbf {u}^h \cdot \pmb {\nabla }\mathbf {u}^h - \mathbf {f}^h \right) - \pmb {\nabla }\cdot \pmb {\sigma }^h, \end{aligned}$$

(2)

$$\begin{aligned} {r}_{\mathrm {C}}^h&= \pmb {\nabla }\cdot \mathbf {u}^h \end{aligned}$$

(3)

are the residuals of the momentum equation and incompressibility constraint. Here, $\rho$, $\mathbf {u}$, $p$, $\mathbf {f}$, and $\mathbf {h}$ are the density, velocity, pressure, body force, and the stress specified at the boundary. The stress tensor is defined as $\pmb {\sigma }= - p\mathbf {I}+ 2 \mu \pmb {\varepsilon }(\mathbf {u})$, where $\mathbf {I}$ is the identity tensor, $\mu = \rho \nu$ is the viscosity, $\nu$ is the kinematic viscosity, and $\pmb {\varepsilon }\left( \mathbf {u}\right) = \left( \left( \pmb {\nabla }\mathbf {u}\right) +\left( \pmb {\nabla }\mathbf {u}\right) ^T\right) /2$ is the strain-rate tensor. The test functions associated with the $\mathbf {u}$ and $p$ are $\mathbf {w}$ and $q$. A superscript “h” indicates that the function is coming from a finite-dimensional space. The symbol $Q_n$ represents the ST slice between time levels n and $n+1$, $\left( P_n\right) _\mathrm {h}$ is the part of the slice lateral boundary associated with the boundary condition $\mathbf {h}$, and $\Omega _n$ is the spatial domain at time level n. The superscript “e” is the ST element counter, and $n_{\mathrm {el}}$ is the number of ST elements. The functions are discontinuous in time at each time level, and the superscripts “−” and “$+$” indicate the values of the functions just below and above the time level.

Remark 1

The ST-SUPS can be obtained from the ST-VMS by dropping the eighth and ninth integrations.

The stabilization parameters, $\tau _{\mathrm {SUPS}}$ and $\nu _{\mathrm {LSIC}}$, will be given in Appendix A.1.

2.2 ST-SI

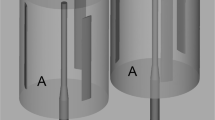
In describing the ST-SI, labels “Side A” and “Side B” will represent the two sides of the SI. The ST-SI version of the formulation given by Eq. (1) includes added boundary terms corresponding to the SI. The boundary terms for the two sides are first added separately, using the test functions ${\mathbf {w}}_\mathrm {A}^h$ and ${q}_\mathrm {A}^h$ and ${\mathbf {w}}_\mathrm {B}^h$ and ${q}_\mathrm {B}^h$. Then, putting together the terms added to each side, the complete set of terms added becomes

$$\begin{aligned}&- \int _{\left( P_n\right) _\mathrm {SI}} \left( {q}_\mathrm {B}^h {\mathbf {n}}_\mathrm {B} - {q}_\mathrm {A}^h {\mathbf {n}}_\mathrm {A} \right) \cdot \frac{1}{2} \left( {\mathbf {u}}_\mathrm {B}^h - {\mathbf {u}}_\mathrm {A}^h \right) \mathrm {d}P \nonumber \\&- \int _{\left( P_n\right) _\mathrm {SI}} \rho {\mathbf {w}}_\mathrm {B}^h \cdot \frac{1}{2} \left( \left( {\mathcal {F}}_\mathrm {B}^h - \left| {\mathcal {F}}_\mathrm {B}^h \right| \right) {\mathbf {u}}_\mathrm {B}^h - \left( {\mathcal {F}}_\mathrm {B}^h - \left| {\mathcal {F}}_\mathrm {B}^h \right| \right) {\mathbf {u}}_\mathrm {A}^h \right) \mathrm {d}P \nonumber \\&- \int _{\left( P_n\right) _\mathrm {SI}} \rho {\mathbf {w}}_\mathrm {A}^h \cdot \frac{1}{2} \left( \left( {\mathcal {F}}_\mathrm {A}^h - \left| {\mathcal {F}}_\mathrm {A}^h \right| \right) {\mathbf {u}}_\mathrm {A}^h - \left( {\mathcal {F}}_\mathrm {A}^h - \left| {\mathcal {F}}_\mathrm {A}^h \right| \right) {\mathbf {u}}_\mathrm {B}^h \right) \mathrm {d}P \nonumber \\&+ \int _{\left( P_n\right) _\mathrm {SI}} \left( {\mathbf {n}}_\mathrm {B} \cdot {\mathbf {w}}_\mathrm {B}^h + {\mathbf {n}}_\mathrm {A} \cdot {\mathbf {w}}_\mathrm {A}^h \right) \frac{1}{2} \left( {p}_\mathrm {B}^h + {p}_\mathrm {A}^h \right) \mathrm {d}P \nonumber \\&- \int _{\left( P_n\right) _\mathrm {SI}} \left( {\mathbf {w}}_\mathrm {B}^h - {\mathbf {w}}_\mathrm {A}^h \right) \cdot \left( {\hat{\mathbf {n}}}_\mathrm {B} \cdot \mu \left( \pmb {\varepsilon }({\mathbf {u}}_\mathrm {B}^h) + \pmb {\varepsilon }({\mathbf {u}}_\mathrm {A}^h) \right) \right) \mathrm {d}P \nonumber \\&- \gamma \int _{\left( P_n\right) _\mathrm {SI}} {\hat{\mathbf {n}}}_\mathrm {B} \cdot \mu \left( \pmb {\varepsilon }\left( {\mathbf {w}}_\mathrm {B}^h \right) + \pmb {\varepsilon }\left( {\mathbf {w}}_\mathrm {A}^h \right) \right) \cdot \left( {\mathbf {u}}_\mathrm {B}^h - {\mathbf {u}}_\mathrm {A}^h \right) \mathrm {d}P \nonumber \\&+ \int _{\left( P_n\right) _\mathrm {SI}} \frac{\mu C}{h} \left( {\mathbf {w}}_\mathrm {B}^h - {\mathbf {w}}_\mathrm {A}^h \right) \cdot \left( {\mathbf {u}}_\mathrm {B}^h - {\mathbf {u}}_\mathrm {A}^h \right) \mathrm {d}P, \end{aligned}$$

(4)

where

$$\begin{aligned} {\mathcal {F}}_\mathrm {B}^h&= {\mathbf {n}}_\mathrm {B} \cdot \left( {\mathbf {u}}_\mathrm {B}^h - {\mathbf {v}}_\mathrm {B}^h \right) , \end{aligned}$$

(5)

$$\begin{aligned} {\mathcal {F}}_\mathrm {A}^h&= {\mathbf {n}}_\mathrm {A} \cdot \left( {\mathbf {u}}_\mathrm {A}^h - {\mathbf {v}}_\mathrm {A}^h \right) , \end{aligned}$$

(6)

$$\begin{aligned} {\hat{\mathbf {n}}}_\mathrm {B}&= \frac{ {\mathbf {n}}_\mathrm {B} - {\mathbf {n}}_\mathrm {A} }{ \left\| {\mathbf {n}}_\mathrm {B} - {\mathbf {n}}_\mathrm {A} \right\| } . \end{aligned}$$

(7)

Here, $\left( P_n\right) _\mathrm {SI}$ is the SI in the ST domain, $\mathbf {n}$ is the unit normal vector, $\mathbf {v}$ is the mesh velocity, $\gamma =1$, and C is a nondimensional constant. The element length h will be defined in Appendix A.2.

Fig. 1

Tsunami-shelter VAWT model. The disk-shaped structure just below the rotor is the shelter. The four columns at the periphery support the turbine rotor and the shelter

3 Tsunami-shelter VAWT model

Figure 1 shows the VAWT model, which has four support columns at the periphery. The model is based on “Life tower” [1]. The rotor diameter is 16 m, and the machine height is 45 m. The three blades are based on the NACA0015 airfoil, and the chord length and the blade height are 1.5 m and 18 m. There are two connecting rods from the hub to each blade, and the blades are supported without any tilt with respect to the tangent of the rotation path. The four support columns are cylindrical with circular cross-section, and they provide enough strength to support the rotor, which is estimated to weigh 3 t, and the shelter.

We carry out the computations at a constant free-stream velocity $U_\infty$ and with prescribed rotor motion at constant angular velocity. The rotation is clockwise viewed from the top. The air density and kinematic viscosity are 1.205 kg/m$^3$ and 1.511$\times$10$^{-5}$ m$^2$/s. We extract from the computations the instantaneous power coefficient $C_\mathrm {POW}$, defined as

$$\begin{aligned} C_\mathrm {POW} = \frac{P}{\frac{1}{2}\rho U_\infty ^3 A}, \end{aligned}$$

(8)

where A and P are the projected area of the wind turbine and the power generated. We report the power coefficient as a function of the blade orientation as represented by the angle $\phi$ seen in Fig. 2. With that orientation, the flow speed seen by a blade can be calculated as

Fig. 2

Blade orientation as represented by the angle $\phi$

$$\begin{aligned} V&= U_\infty \sqrt{1 - 2 \lambda \sin \phi + \lambda ^2}, \end{aligned}$$

(9)

where $\lambda$ is the tip-speed ratio (TSR). The symbol T will denote the rotation cycle.

4 Computations

We present computations for the 2D and 3D cases. The computational-domain size in the wind direction is 62.5 times the rotor diameter, with a distance of 18.75 times the rotor diameter between the upstream boundary and the rotor center. In the cross-wind direction, the domain size is 37.5 times the rotor diameter. In the 3D case, the domain height is 10 times the rotor diameter. The mesh position is represented by quadratic NURBS in time. There are three patches that are 120$^\circ$ each, and the secondary mapping introduced in [21] is used to achieve the constant angular velocity. We set $U_\infty =12.56~\mathrm {m/s}$.

Fig. 3

2D case. Model geometry and SI

Fig. 4

2D case. Mesh 3 (control mesh)

In the 2D case, the time-step sizes used correspond to $\varDelta \phi = 1^{\circ }$ and $2^{\circ }$. In the 3D case, we use only one time-step size, and that corresponds to $\varDelta \phi = 1^{\circ }$. The number of nonlinear iterations per time step is 4, and the number of GMRES iterations per nonlinear iteration is 200. The first two nonlinear iterations are based on the ST-SUPS, and the last two the ST-VMS. The stabilization parameters are those given by Eqs. (10)–(12) and (21)–(22). In the ST-SI (see Eq. (4)), we set $C=2$.

Table 1 2D case. Number of control points (nc) and elements (ne)

Fig. 5

2D case. $C_\mathrm {POW}$, for $\varDelta \phi =2^\circ$ (top) and $1^\circ$ (bottom), averaged over the three blades in the last three rotations

4.1 2D case

We first compute with TSR = 2. The model geometry and the SI are shown in Fig. 3. The boundary conditions are $U_\infty$ at the inflow, zero stress at the outflow, slip at the lateral boundaries, and no-slip on the rotor and support column surfaces. The prescribed velocities are evaluated at the time integration points, with the values extracted from the NURBS representation of the prescribed motion.

We use three different meshes. We start with Mesh 1, and obtain the other two meshes by knot insertion. We halve the knot spacing to get Mesh 2, and halve it again to get Mesh 3. Figure 4 shows Mesh 3. The number of control points and elements are shown in Table 1. We compute for 10 rotations. Figure 5 shows, for $\varDelta \phi = 2^\circ$ and $1^\circ$, $C_\mathrm {POW}$, averaged over the three blades in the last three rotations. The results from different combinations of spatial and temporal resolutions are mostly in agreement. The cases with the lower spatial resolution and highest Courant number show some differences in parts of the rotation cycle. Figures 6 and 7 show, for Mesh 1 with $\varDelta \phi = 1^{\circ }$ and Mesh 2 with $\varDelta \phi = 2^{\circ }$, the velocity magnitude in the wake of the support columns located at $\phi = 180^{\circ }$ and $\phi = 90^{\circ }$. Mesh 1, with even $\varDelta \phi = 1^{\circ }$, is not able to capture the wake as well as Mesh 2 does even with $\varDelta \phi = 2^{\circ }$. This indicates that a reasonable level of mesh refinement is needed. Table 2 shows $C_\mathrm {POW}$ averaged over the three blades in the last three rotations and the standard deviation ($\sigma _{\mathrm {CPOW}}$) associated with that, both averaged over the rotation cycle. We believe the higher $\sigma _{\mathrm {CPOW}}$ values we see at higher Courant numbers are caused by strong vortices, which we do not believe to be representative of what actually happens in 3D.

Fig. 6

2D case. Velocity magnitude ($\mathrm {m/s}$) for Mesh 1 with $\varDelta \phi = 1^{\circ }$ in the wake of the support columns located at $\phi = 180^{\circ }$ (left) and $90^{\circ }$ (right), in the last rotation, for t/T ranging from 0.2 to 1

Fig. 7

2D case. Velocity magnitude ($\mathrm {m/s}$) for Mesh 2 with $\varDelta \phi = 2^{\circ }$ in the wake of the support columns located at $\phi = 180^{\circ }$ (left) and $90^{\circ }$ (right), in the last rotation, for t/T ranging from 0.2 to 1

Table 2 2D case. $C_\mathrm {POW}$ averaged over the three blades in the last three rotations and the standard deviation associated with that, both averaged over the rotation cycle

Fig. 8

2D case. $C_\mathrm {POW}$ for TSR = 2 and 3, computed with Mesh 3 and $\varDelta \phi = 1^\circ$, averaged over the three blades in the last three rotations

Fig. 9

3D case. Initial mesh (control mesh)

Fig. 10

3D case. The three SIs, marked in color, with an actual slip. 3D view (left) and vertical cut plane (right)

Fig. 11

3D case. The four SIs, marked in color, that are for mesh generation purposes and in the rotating mesh. 3D view (left) and vertical cut plane (right)

Fig. 12

3D case. The two SIs, marked in color, that are for mesh generation purposes and in the stationary mesh. 3D view (left) and vertical cut plane (right)

Fig. 13

3D case. Horizontal cut plane. Initial mesh (top) and mesh after the relaxation (bottom)

Fig. 14

3D case. Vertical cut plane. Initial mesh (left) and mesh after the relaxation (right)

We also compute with TSR = 3. We use Mesh 3 with $\varDelta \phi = 1^\circ$. Figure 8 shows $C_\mathrm {POW}$, averaged over the three blades in the last three rotations, for TSR = 3 and 2. Rotation-cycle-averaged value of $C_\mathrm {POW}$ is 0.18, which is significantly larger than what we have for TSR = 2, translates to a total $C_\mathrm {POW}$ value of 0.54.

4.2 3D case

We compute with TSR = 3. The boundary conditions are no-slip on all turbine surfaces and the bottom boundary, $U_\infty$ at the inflow, zero stress at the outflow, and slip at the lateral and top boundaries. All prescribed velocities are evaluated at the time integration points with the values extracted from the NURBS representation of the prescribed motion.

Figure 9 shows the initial mesh, generated with the method in [26]. There are 1,544,460 control points and 955,477 quadratic NURBS elements. There are total nine SIs in the mesh. Figure 10 shows the SIs with an actual slip. Figures 11 and 12 show the SIs that are just for mesh generation purposes.

To improve the mesh quality, we use the mesh relaxation method introduced in [28], which is based on fiber-reinforced hyperelasticity and optimized ZSS. The hyperelasticity model is the one given by Eqs. (48), (39), (50) and (51) in [28], with $\kappa =0$. The material properties are $\kappa _{\mathrm {B}} = 10^{-2}$, $\beta _{\mathrm {B}}=2$, $\mu = 1$, $C_{1} = 100$, and $C_{2} = 10^{-2}$. We ramp-up to the optimized ZSS in 10 equal increments. For the numerical integration, $4{\times }4{\times }4$ quadrature points are used. Figures 13 and 14 show the initial mesh and the mesh after the relaxation. We clearly see the improvement in the mesh-line orthogonality, without much change in the element aspect ratio or the local resolution.

We compute for two rotations and report the solution from the last rotation. Figure 15 shows the isosurfaces of the second invariant of the velocity gradient tensor near a blade, at different positions of the blade. Figure 16 shows $C_\mathrm {POW}$. The total $C_\mathrm {POW}$ averaged over the rotation cycle is about 0.56. Figure 17 shows $C_\mathrm {POW}$ from the 2D and 3D computations, averaged over the three blades. They are in reasonably good agreement, considering that the space dimensions are not the same. The 3D value is slightly higher in an average sense. Because the shelter and the upper part of the frame divert some of the flow to the rotor, the blades see more flow than what corresponds to the projected area calculated using the blade height.

Fig. 15

3D case. Isosurfaces corresponding to a positive value of the second invariant of the velocity gradient tensor, colored by the velocity magnitude (m/s), at $\phi =90^\circ$, $180^\circ$, $270^\circ$ and $360^\circ$ (from left to right and top to bottom) in the last rotation

Fig. 16

3D case. $C_\mathrm {POW}$ for the three blades (red, blue, green) and the total $C_\mathrm {POW}$, in the last rotation, at instants defined by the position of the red blade

Fig. 17

$C_\mathrm {POW}$ from the 2D and 3D computations, averaged over the three blades, in the last three rotations for the 2D case and in the last rotation for the 3D case

5 Concluding remarks

We have presented computational flow analysis of a VAWT that has been proposed to also serve as a tsunami shelter. The turbine has, in addition to the three-blade rotor, four support columns at the periphery, which support the turbine rotor and the shelter. The computational challenges encountered in flow analysis of the tsunami-shelter VAWT include those encountered in flow analysis of wind turbines in general, such as accurate representation of the turbine geometry, multiscale unsteady flow, and moving-boundary flow associated with the rotor motion. Beyond those, because of its rather high geometric complexity, the tsunami-shelter VAWT poses the challenge of reaching high accuracy in turbine-geometry representation and flow solution when the geometry is so complex.

We address the challenges with an ST computational method that integrates three special ST methods around a core ST method and mesh-related methods. The core method is the ST-VMS, which subsumes its precursor ST-SUPS. The three special methods are the ST-SI, ST-IGA, and the STNMUM. The mesh-related methods are a general-purpose NURBS mesh generation method and a mesh relaxation method based on fiber-reinforced hyperelasticity and optimized ZSS.

The ST-discretization feature of the integrated method provides higher-order accuracy compared to standard discretization methods. The VMS feature addresses the computational challenges associated with the multiscale nature of the unsteady flow. The moving-mesh feature of the ST framework enables high-resolution computation near the blades. The ST-SI enables moving-mesh computation of the spinning rotor. The mesh covering the rotor spins with it, and the SI between the spinning mesh and the rest of the mesh accurately connects the two sides of the solution. The ST-IGA enables more accurate representation of the blade and other turbine geometries and increased accuracy in the flow solution. The STNMUM enables exact representation of the mesh rotation. The general-purpose NURBS mesh generation method makes it easier to deal with the complex turbine geometry. The quality of the mesh generated with this method is improved with the mesh relaxation method.

We have presented computations for the 2D and 3D cases. In the 2D case, we have presented computations for three different meshes, two different time-step sizes, and two different tip-speed ratios. In the 3D case, we computed with one of the combinations of the 2D case and compared the 2D and 3D results. The computations show the effectiveness of our ST and mesh generation and relaxation methods in flow analysis of the tsunami-shelter VAWT.

Stabilization parameters

1.1 ST-VMS

There are various ways of defining the stabilization parameters $\tau _{\mathrm {SUPS}}$ and $\nu _{\mathrm {LSIC}}$. Here, $\tau _{\mathrm {SUPS}}$ is mostly from [142]:

$$\begin{aligned} \tau _{\mathrm {SUPS}}&= \left( \tau _{\mathrm {SUGN12}}^{-2} + \tau _{\mathrm {SUGN3}}^{-2} + \tau _{\mathrm {SUGN4}}^{-2}\right) ^{-\frac{1}{2}}. \end{aligned}$$

(10)

The first and second components are given as

$$\begin{aligned} \tau _{\mathrm {SUGN12}}^{-2}&= \begin{bmatrix} 1 \\ \mathbf {u}\\ \end{bmatrix} \begin{bmatrix} 1 \\ \mathbf {u}\\ \end{bmatrix} : \mathbf {G}^\mathrm {ST} \end{aligned}$$

(11)

and

$$\begin{aligned} \tau _{\mathrm {SUGN3}}^{-1}&= \nu \mathbf {r}\mathbf {r}:\mathbf {G}, \end{aligned}$$

(12)

where $\mathbf {r}$ is the solution-gradient direction:

$$\begin{aligned} \mathbf {r}&= \frac{\pmb {\nabla }\left\| \mathbf {u}\right\| }{\left\| \pmb {\nabla }\left\| \mathbf {u}\right\| \right\| }. \end{aligned}$$

(13)

Here $\mathbf {G}^\mathrm {ST}$ and $\mathbf {G}$ are the ST and space-only element metric tensors:

$$\begin{aligned} \mathbf {G}^\mathrm {ST}&= \left( \hat{\mathbf {Q}}^\mathrm {ST}\right) ^{-T} \cdot \left( \hat{\mathbf {Q}}^\mathrm {ST}\right) ^{-1}, \end{aligned}$$

(14)

$$\begin{aligned} \mathbf {G}&= \hat{\mathbf {Q}}^{-T} \cdot \hat{\mathbf {Q}}^{-1}, \end{aligned}$$

(15)

where

$$\begin{aligned} \hat{\mathbf {Q}}^\mathrm {ST}&= \mathbf {Q}^\mathrm {ST} \cdot \left( \mathbf {D}^\mathrm {ST}\right) ^{-1}, \end{aligned}$$

(16)

$$\begin{aligned} \hat{\mathbf {Q}}&= \mathbf {Q} \cdot \mathbf {D}^{-1}. \end{aligned}$$

(17)

The ST and space-only Jacobian tensors are

$$\begin{aligned} \mathbf {Q}^\mathrm {ST}&= \begin{bmatrix} \frac{\partial t}{\partial \theta } &{} \frac{\partial t}{\partial \pmb {\xi }} \\ \frac{\partial \mathbf {x}}{\partial \theta } &{} \mathbf {Q} \\ \end{bmatrix} \end{aligned}$$

(18)

and

$$\begin{aligned} \mathbf {Q} = \frac{\partial \mathbf {x}}{\partial \pmb {\xi }}, \end{aligned}$$

(19)

where $\theta$ and $\pmb {\xi }$ are the temporal and spatial parametric coordinates. The transformation tensor $\mathbf {D}^\mathrm {ST}$ is defined as

$$\begin{aligned} \mathbf {D}^\mathrm {ST}&= \begin{bmatrix} D_\theta &{} \mathbf {0}^T \\ \mathbf {0}&{} \mathbf {D} \\ \end{bmatrix}. \end{aligned}$$

(20)

The definitions used for $D_\theta$ and $\mathbf {D}$ play an important role, especially for higher-order isogeometric discretization [142, 144] and simplex elements [143].

In this article, we set $D_\theta =1$ and set $\mathbf {D}$ to its “RQD-MAX” version [144].

The third component, originating from [18], is defined as

$$\begin{aligned} \tau _{\mathrm {SUGN4}}&= \left\| \pmb {\nabla }\mathbf {u}^h\right\| _F^{-1} , \end{aligned}$$

(21)

where $\Vert \cdot \Vert _F$ represents the Frobenius norm.

The stabilization parameter $\nu _{\mathrm {LSIC}}$ is from [25]:

$$\begin{aligned} \nu _{\mathrm {LSIC}}&= \frac{h^2_\mathrm {LSIC}}{\tau _{\mathrm {SUPS}}}, \end{aligned}$$

(22)

where $h_\mathrm {LSIC}$ is set equal to the minimum element length $h_\mathrm {MIN}$:

$$\begin{aligned} h_\mathrm {MIN}&= 2 \left( \max _{\mathbf {r}} \left( \mathbf {r} \mathbf {r} : \mathbf {G} \right) \right) ^{-\frac{1}{2}} . \end{aligned}$$

(23)

For more ways of calculating the stabilization parameters in flow computations, see [2, 3, 5, 7,8,9, 141, 146,147,148,149,150,151,152].

1.2 ST-SI

The element length used in the ST-SI is given as

$$\begin{aligned} h&= \left( \frac{{h}_\mathrm {B}^{-2}+ {h}_\mathrm {A}^{-2}}{2}\right) ^{-\frac{1}{2}}, \end{aligned}$$

(24)

$$\begin{aligned} {h}_\mathrm {B}&= 2 \left( {\mathbf {n}}_\mathrm {B} {\mathbf {n}}_\mathrm {B} : \mathbf {G} \right) ^{-\frac{1}{2}}&\text {(for Side B)}, \end{aligned}$$

(25)

$$\begin{aligned} {h}_\mathrm {A}&= 2 \left( {\mathbf {n}}_\mathrm {A} {\mathbf {n}}_\mathrm {A} : \mathbf {G} \right) ^{-\frac{1}{2}}&\text {(for Side A)}, \end{aligned}$$

(26)

$$\begin{aligned} {\hat{\mathbf {n}}}_\mathrm {B}&= \frac{ {\mathbf {n}}_\mathrm {B} - {\mathbf {n}}_\mathrm {A} }{ \left\| {\mathbf {n}}_\mathrm {B} - {\mathbf {n}}_\mathrm {A} \right\| }. \end{aligned}$$

(27)

Remark 2

We note that the expression for h given by Eq. (24) is slightly different from its original form introduced in [131]:

$$\begin{aligned} h&= \left( \frac{{h}_\mathrm {B}^{-1}+ {h}_\mathrm {A}^{-1}}{2}\right) ^{-1}. \end{aligned}$$

(28)

The modification, which has only minor effect, is for consistency with how the stabilization parameters are calculated from their components and for implementation convenience.