Abstract
We utilize the recent LHC-13 TeV data to study the lower mass bound on the top-squark (stop) in natural supersymmetry. We recast the LHC sparticle inclusive search of  1)
1) with \(\alpha _T\) variable, the direct stop pair search (1-lepton channel and all-hadronic channel) and the monojet analyses. We find that these searches are complementary depending on stop and higgsino masses: for a heavy stop the all-hadronic stop pair search provides the strongest bound, for an intermediate stop the inclusive SUSY analysis with \(\alpha _T\) variable is most efficient, while for a compressed stop–higgsino scenario the monojet search plays the key role. Finally, the lower mass bound on a stop is: (1) 320 GeV for compressed stop–higgsino scenario (mass splitting less than 20 GeV); (2) 765 (860) GeV for higgsinos lighter than 300 (100) GeV.
with \(\alpha _T\) variable, the direct stop pair search (1-lepton channel and all-hadronic channel) and the monojet analyses. We find that these searches are complementary depending on stop and higgsino masses: for a heavy stop the all-hadronic stop pair search provides the strongest bound, for an intermediate stop the inclusive SUSY analysis with \(\alpha _T\) variable is most efficient, while for a compressed stop–higgsino scenario the monojet search plays the key role. Finally, the lower mass bound on a stop is: (1) 320 GeV for compressed stop–higgsino scenario (mass splitting less than 20 GeV); (2) 765 (860) GeV for higgsinos lighter than 300 (100) GeV.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The discovery of the Higgs boson is a great triumph for the Standard Model (SM). However, the SM Higgs mass is quadratically sensitive to the cutoff scale \(\Lambda \) (usually taken as GUT or Planck scale) via radiative corrections because of the lack of symmetry protection. This renders the SM with \(m_h \sim 125~\mathrm{GeV} \ll \Lambda \) rather unnatural. A well-known theory for solving such a naturalness problem is supersymmetry.
Among various supersymmetric models, natural supersymmetry (NSUSY) is a well-motivated framework [1,2,3], which consists of a small set of sparticles that closely relate to the naturalness, such as higgsinos, stop, and gluino. This can be understood by the minimization of the Higgs potential [4],
where \(\mu \) is the higgsino mass parameter in the superpotential and contributes to \(M_Z\) at tree level, \(\tan \beta \equiv v_u/v_d \gg 1\) is assumed in the last approximate equality, \(m^2_{H_d}\) and \(m^2_{H_u}\) denote the soft SUSY breaking masses of the Higgs fields at weak scale, and \(\Sigma _{u}\) and \(\Sigma _{d}\) arise from the radiative corrections to the Higgs potential. Due to the large top Yukawa couplings, \(\Sigma _{u}\) is dominated by the stop at 1-loop level, while the gluino contributes to \(\Sigma _{u}\) via the corrections to the stop mass. Other contributions from the first two generation squarks and sleptons to \(M_Z\) are negligibly small. Therefore, the requirement of getting the correct value of \(M_Z\) without fine-tuning will give upper bounds on the masses of higgsinos, stops, and gluino [5, 6]. In the past few years, much work has been devoted to the searches for the stop at the LHC in NSUSY [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].
With the recent \(\sim \)15 fb\(^{-1}\) dataset at the LHC run-2, the stop and gluino masses are respectively excluded up to \(\sim \)1 TeV [23] and 1.8 TeV [24], while the electroweakinos below 0.4–1 TeV can also be covered for different decay channels [25]. But these limits are obtained in the simplified models [26,27,28] and sensitively depend on the assumptions of the nature of the lighest supersymmetric partner (LSP), the branching ratios of heavier sparticles and the mass splitting between heavier sparticles and the LSP. Therefore, it is necessary to examine the current LHC run-2 coverage of NSUSY and assess the fine-tuning extent. In this work, we utilize the recent results of the LHC run-2 inclusive sparticle searches and direct stop pair searches to constrain the stop mass in NSUSY. We compare their sensitivities and find that they are complementary in probing NSUSY. We will also evaluate the electroweak fine-tuning measure in the allowed parameter space of NSUSY and comment on the prospect for covering the low fine-tuning parameter space of NSUSY at HL-LHC.
2 Constraints on stop in NSUSY
In MSSM, the stop mass matrix in the weak-basis \((\tilde{t}_L, \tilde{t}_R)\) is given by
with
Here \(m_{\tilde{Q}_{3L}}^2\) and \(m_{\tilde{U}_{3R}}^2\) are the soft-breaking mass parameters for the third generation left-handed squark doublet \(\tilde{Q}_{3L}\) and the right-handed stop \(\tilde{U}_{3R}\), respectively. \(A_t\) is the stop soft-breaking trilinear parameter. The weak eigenstates \(\tilde{t}_{L,R}\) can be rotated to the mass eigenstates \(\tilde{t}_{1,2}\) by a unitary transformation,
After diagonalizing the mass matrix, see Eq. (2), we can have the stop masses \(m_{\tilde{t}_{1,2}}\) and the mixing angle \(\theta _{\tilde{t}}\) (\(-\pi /2 \le \theta _{\tilde{t}} \le \pi /2\)),
The decays of stop are determined by the interactions between stop and neutralinos/charginos, which are given by
where \(P_{L/R}=(1\mp \gamma _5)/2\) and
with \(y_t=\sqrt{2}m_t/(v\sin \beta )\) and \(y_b=\sqrt{2}m_b/(v\cos \beta )\) being the Yukawa couplings of top and bottom quarks. The mixing matrices of the neutralinos \(N_{ij}\) and charginos \(U_{ij}\), \(V_{ij}\) are defined in [29]. In NSUSY, \(M_{1,2}\gg \mu \), one has \(V_{11}, U_{11}, N_{11,12,21,22} \sim 0\), \(V_{12} \sim \mathrm{sgn}(\mu )\), \(U_{12} \sim 1\) and \(N_{13,14,23}=-N_{24} \sim 1/\sqrt{2}\). So, \(\tilde{\chi }^{\pm }_{1}\) and \(\tilde{\chi }^0_{1,2}\) are higgsino-like and nearly degenerate.Footnote 1 The left-handed stop will mainly decay to \(t \tilde{\chi }^{0}_{1,2}\) when the phase space is accessible and \(\tan \beta \) is small. The couplings of the right-handed stop with \(\tilde{\chi }^0_{1,2}\) and \(\tilde{\chi }^\pm _{1}\) are proportional to \(y_t\), and the branching ratios of \(\tilde{t}_{1} \rightarrow t \tilde{\chi }^{0}_{1,2}\) and \(\tilde{t}_1 \rightarrow b \tilde{\chi }^+_1\) are about 25 and 50%, respectively.
To address the lower mass limit of the stop in NSUSY, we can focus on a right-handed stop. This is because the left-handed stop is linked with the left-handed sbottom by the SU(2) symmetry. Then the left-handed sbottom decay channel \(\tilde{b}_1 \rightarrow t \tilde{\chi }^-_1\) can mimics the left-handed stop signals \(\tilde{t}_{1} \rightarrow t \tilde{\chi }^{0}_{1,2}\) since \(\tilde{\chi }^0_{1,2}\) and \(\tilde{\chi }^+_{1}\) are higgsino-like and degenerate in NSUSY. This enhances the LHC limit on a left-handed stop, which is stronger than the limit on a right-handed stop [15, 20].
Now we examine the constraints on the NSUSY scenario that consists of a right-handed stop and higgsinos. We scan the parameter space in the ranges
The lower limit on the higgsino mass is motivated by the LEP searches for electroweakinos. We require the stop mixing angle \(|\sin \theta _{\tilde{t}}|^2>0.5\) to obtain a right-handed stop \(\tilde{t}_1\). Since the gluino contributes to the naturalness measure in Eq. (15) at 2-loop level, a low fine-tuning allows the gluino with a mass up to several TeV, which is possibly beyond the reach of LHC. So we assume the gluino mass parameter to be \(M_3=2\) TeV in our scan. Since the electroweak gauginos, heavy Higgs bosons, the sleptons, the first two generations of squarks and the right-handed sbottom are not strongly related to the naturalness, we decouple their contributions by fixing \(M_1=M_2=m_A=m_{\tilde{\ell }}=m_{\tilde{q}_{1,2}}=m_{\tilde{D}_{R}}=2\) TeV at the weak scale.
In our scan, we impose the following indirect constraints:
-
Higgs mass We require that the lighter CP-even Higgs boson be the SM-like Higgs boson with a mass in the range of \(125\pm 2\) GeV, which is calculated by the package FeynHiggs-2.11.2 [35, 36].Footnote 2
-
Vacuum stability We impose the constraint of metastability of the vacuum state by requiring \(|A_t| \lesssim 2.67\sqrt{M^2_{\tilde{Q}_{3L}}+M^2_{\tilde{t}_R}+M^2_A \cos ^2\beta }\) [38], because the large trilinear parameter \(A_t\) can potentially lead to a global vacuum where charge and color are broken [38,39,40].
-
Low-energy observables We require our samples to satisfy the bound of \(B\rightarrow X_s\gamma \) at 2\(\sigma \) range, which is implemented by the package of SuperIso v3.3 [41, 42].
-
Dark matter detection We require the thermal relic density of the neutralino dark matter \(\Omega h^2\) to be below the 2\(\sigma \) upper limit of 2015 Planck value [43]Footnote 3 and the LUX WS2014-16 [47]. The results for the spin-independent neutralino–proton scattering cross section \(\sigma ^{SI}_p\) is rescaled by a factor of \(\Omega h^2/\Omega _{PL} h^2\). We use the package of MicrOmega v2.4 [48] to calculate \(\Omega h^2\) and \(\sigma ^{SI}_p\).
Besides, the LHC run-2 experiments have covered a wide parameter space of the MSSM. We list the relevant LHC experimental analyses for our scenario:
-
From ATLAS,
-
From CMS,
-
Inclusive, 0 lepton + \(\geqslant 1\) jets +
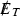 + \(\alpha _T\), 12.9 fb\(^{-1}\) [54]
+ \(\alpha _T\), 12.9 fb\(^{-1}\) [54] -
Inclusive, 0 lepton + \(\geqslant 1\) jets +
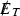 + \(M_{T_2}\), 12.9 fb\(^{-1}\) [55]
+ \(M_{T_2}\), 12.9 fb\(^{-1}\) [55] -
Inclusive, 0 lepton + \(\geqslant 1\) jets +
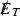 + \(H^\mathrm{miss}_T\), 12.9 fb\(^{-1}\) [56]
+ \(H^\mathrm{miss}_T\), 12.9 fb\(^{-1}\) [56] -
Stop, 0 lepton + (b)jets +
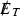 , 12.9 fb\(^{-1}\) [23],
, 12.9 fb\(^{-1}\) [23], -
Stop, 1 lepton + (b)jets +
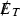 , 12.9 fb\(^{-1}\) [57],
, 12.9 fb\(^{-1}\) [57], -
Compressed Spectrum, 1 jet + soft lepton pair +
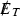 , 12.9 fb\(^{-1}\) [58].
, 12.9 fb\(^{-1}\) [58].
-
It should be mentioned that the higgsinos \(\tilde{\chi }^{\pm }_{1}\) and \(\tilde{\chi }^{0}_{2}\) have the small mass difference with the LSP \(\tilde{\chi }^0_{1}\) in NSUSY. Then the decay products of \(\tilde{\chi }^{\pm }_{1}\) and \(\tilde{\chi }^0_{2}\) are too soft to be tagged at the LHC. So, the stop decays can be categorized into two topologies:  and
and  . Among the current ATLAS searches for the stop, the all-hadronic final state channel has a better sensitivity than those with leptons in the high stop mass region (\(m_{\tilde{t}_1} > 800\) GeV) because of the application of boosted top technique. Similar results are obtained by the CMS Collaboration. With the decrease of the mass splitting \(\Delta m_{\tilde{t}_1-\tilde{\chi }^0_1}\), the sensitivity of the conventional stop searches for the energetic top quark in the final states become poor. In particular, if \(\Delta m_{\tilde{t}_1-\tilde{\chi }^0_1} \ll m_t\), the stop decay will be dominated by the four-body channel \(\tilde{t}_1 \rightarrow bf'\bar{f}\tilde{\chi }^0_1\) [59, 60] or the two-body loop channel \(\tilde{t}_1 \rightarrow c \tilde{\chi }^0_1\) [61,62,63,64,65]. Then the decay products of the stop are usually very soft so that a high \(p_T\) hard jet from the ISR/FSR is needed to tag these compressed stop events, such as the ATLAS monojet analysis listed above. Note that the very recent CMS monojet with the soft lepton pair analysis of the compressed electroweakinos can exclude the wino-like chargino mass \(m_{\tilde{\chi }^\pm _{1}}\) up to 175 GeV for a mass difference of 7.5 GeV with respect to the LSP. However, this limit is not applicable to our scenario because the cross section of the higgsino pair production is 1/4 of the wino pair. On the other hand, both ATLAS and CMS experiments have performed the inclusive SUSY searches for final states with (generally untagged) jets and a large amount of
. Among the current ATLAS searches for the stop, the all-hadronic final state channel has a better sensitivity than those with leptons in the high stop mass region (\(m_{\tilde{t}_1} > 800\) GeV) because of the application of boosted top technique. Similar results are obtained by the CMS Collaboration. With the decrease of the mass splitting \(\Delta m_{\tilde{t}_1-\tilde{\chi }^0_1}\), the sensitivity of the conventional stop searches for the energetic top quark in the final states become poor. In particular, if \(\Delta m_{\tilde{t}_1-\tilde{\chi }^0_1} \ll m_t\), the stop decay will be dominated by the four-body channel \(\tilde{t}_1 \rightarrow bf'\bar{f}\tilde{\chi }^0_1\) [59, 60] or the two-body loop channel \(\tilde{t}_1 \rightarrow c \tilde{\chi }^0_1\) [61,62,63,64,65]. Then the decay products of the stop are usually very soft so that a high \(p_T\) hard jet from the ISR/FSR is needed to tag these compressed stop events, such as the ATLAS monojet analysis listed above. Note that the very recent CMS monojet with the soft lepton pair analysis of the compressed electroweakinos can exclude the wino-like chargino mass \(m_{\tilde{\chi }^\pm _{1}}\) up to 175 GeV for a mass difference of 7.5 GeV with respect to the LSP. However, this limit is not applicable to our scenario because the cross section of the higgsino pair production is 1/4 of the wino pair. On the other hand, both ATLAS and CMS experiments have performed the inclusive SUSY searches for final states with (generally untagged) jets and a large amount of  , which can also be used to derive limits on the parameter space in various simplified models. In our study, we reinterpret the recent CMS analysis of
, which can also be used to derive limits on the parameter space in various simplified models. In our study, we reinterpret the recent CMS analysis of  1)
1) . This strategy is built around the use of the kinematic variable \(\alpha _T\), which is constructed from jet-based quantities to provide strong discriminating power between sources of genuine and misreconstructed \(\vec {p}^\mathrm{miss}_T\). Such a variable can highly suppress multijet background, and is suitable for early searches at 13 TeV LHC. Based on the above considerations, we use four LHC experimental analyses to constrain the parameter space of NSUSY, which are listed in Table 1.
. This strategy is built around the use of the kinematic variable \(\alpha _T\), which is constructed from jet-based quantities to provide strong discriminating power between sources of genuine and misreconstructed \(\vec {p}^\mathrm{miss}_T\). Such a variable can highly suppress multijet background, and is suitable for early searches at 13 TeV LHC. Based on the above considerations, we use four LHC experimental analyses to constrain the parameter space of NSUSY, which are listed in Table 1.
In our Monte Carlo simulations, we use MadGraph5_a MC@NLO [66] to generate the parton level signal events, which are showered and hadronized by the package PYTHIA [67]. The detector simulation effects are implemented with the package Delphes [68]. The jets are clustered with the anti-\(k_t\) algorithm [69] by the package FastJet [70]. The cross section of the stop pair production at 13 TeV LHC are calculated by NLL-fast package [71,72,73,74,75] with the CTEQ6.6M PDFs [76]. We impose the ATLAS monojet constraint with MadAnalysis 5-1.1.12 [77,78,79]. The ATLAS 1-lepton stop and the CMS 0-lepton stop analyses are implemented within the CheckMATE framework [80, 81]. But as mentioned above, we only focus on the heavy stop mass range (\(m_{\tilde{t}_1}>500\) GeV) for the CMS 0-lepton analyses because of the improved sensitivity by application of the top tagging technique. Besides, the higgsinos \(\tilde{\chi }^{\pm }_{1}\) and \(\tilde{\chi }^0_{1,2}\) are nearly degenerate in NSUSY. The stop decay \(\tilde{t} \rightarrow b \tilde{\chi }^+_1\) gives the same topology as the sbottom decay \(\tilde{b} \rightarrow b \tilde{\chi }^0_1\). So we can determine the exclusion limit on the stop by using the cross section upper limit of the sbottom pair production reported from the CMS inclusive search with \(\alpha _T\).
Scatter plots on the plane of \(m_{\tilde{t}_1}\) versus \(m_{\tilde{\chi }^0_1}\). All samples satisfy the constraints of the Higgs mass, vacuum stability, \(B \rightarrow X_s\gamma \), and dark matter detections. The exclusion limits of the LHC SUSY searches in Table 1 are recast. The triangles (gray), squares (cyan) and bullets (red) represent the samples that have the electroweak fine-tuning \(\Delta _\mathrm{EW}<10\), \(10<\Delta _\mathrm{EW}<30\) and \(30<\Delta _\mathrm{EW}<300\), respectively
In Fig. 1, we project the samples allowed by the Higgs mass, vacuum stability, \(B \rightarrow X_s\gamma \) and dark matter detections on the plane of \(m_{\tilde{t}_1}\) versus \(m_{\tilde{\chi }^0_1}\). To quantitatively evaluate the naturalness, we use the electroweak fine-tuning measure \(\Delta _\mathrm{EW}\) Footnote 4 [82]; we have
where \(C_\mu =-\mu ^2\), \(C_{H_u}=-m^2_{H_u}\tan ^2\beta /(\tan ^2\beta -1)\), \(C_{H_d}=m^2_{H_d}/(\tan ^2\beta -1)\), \(C_{\Sigma _u(i)}=-\Sigma _u(i)(\tan ^2\beta )/(\tan ^\beta -1)\), and \(C_{\Sigma _d(i)}=\Sigma _d(i)/(\tan ^\beta -1)\) with i labeling the various loop contributions by \(\Sigma _u\) and \(\Sigma _d\). The one-loop stop contributions \(\Sigma _u (\tilde{t}_{1,2})\) are given by [83].
where the form factor \(F(m^2)= m^2\left( \log \frac{m^2}{Q^2}-1\right) \) with the optimized scale \(Q^2 =m_{\tilde{t}_1}m_{\tilde{t}_2}\), \(y_t\) is the top quark Yukawa coupling and \(\Delta _t=(m_{\tilde{t}_L}^2-m_{\tilde{t}_R}^2)/2+M_Z^2\cos 2\beta (\frac{1}{4}- \frac{2}{3}x_W)\), \(x_W\equiv \sin ^2\theta _W\). In this figure the triangles, squares, and bullets represent the samples that have the electroweak fine-tuning \(4<\Delta _\mathrm{EW}<10\), \(10<\Delta _\mathrm{EW}<30\) and \(30<\Delta _\mathrm{EW}<300\), respectively. In our parameter space, the low fine-tuning \(4<\Delta _\mathrm{EW}<10\) requires the higgsino mass \(\mu \lesssim 200\) GeV and the stop mass \(0.4~\mathrm{TeV} \lesssim m_{\tilde{t}_1} \lesssim 1.3\) TeV. It can be seen that 70% of such a parameter space can be covered by the current LHC Run-2 SUSY searches. A lighter stop mass (\(m_{\tilde{t}_1} \lesssim 0.4~\mathrm{TeV}\)) requires a large trilinear parameter \(A_t\) to satisfy the Higgs mass constraint, which leads to a large value of \(\Delta _\mathrm{EW}\).
Besides, from Fig. 1 it can be seen that the ATLAS monojet search produces a strong exclusion limit in the low stop mass region, which excludes the stop mass up to 320 GeV for \(m_{\tilde{\chi }^0_1}=300\) GeV. This is because when the stop mass is close to the LSP mass, the b-jets from the stop decay \(\tilde{t}_1 \rightarrow b \tilde{\chi }^+_1/b f\bar{f'}\tilde{\chi }^0_{1,2}\) or c-jets from \(\tilde{t}_1 \rightarrow c \tilde{\chi }^0_{1,2}\) are too soft to be identified. Then the monojet search is very sensitive in the low stop region.
In the moderate or heavy stop region, the stop dominantly decays to \(b \tilde{\chi }^+_1\) and \(t\tilde{\chi }^0_{1,2}\), which produce \(2b+E^\mathrm{miss}_T\) and \(t\bar{t}+E^\mathrm{miss}_T\) signatures, respectively. The CMS inclusive search with \(\alpha _T\) shows a better sensitivity than the 0/1-lepton stop searches in most of parameter space. But we also note that the exclusion limit of the CMS 0-lepton stop search is slightly stronger than the CMS inclusive search because of the application of top tagging technique in ATLAS analysis. Finally, we conclude that the stop mass can be excluded up to 765 (850) GeV for \(m_{\tilde{\chi }^0_1} < 300\) (\(m_{\tilde{\chi }^0_1} = 100\)) GeV by the current LHC Run-2 experiments. Such limits are much stronger than the LHC run-1 limits on NSUSY, which excluded a stop below 600 GeV [15, 16, 18, 20].
It should be mention that when the stop and LSP mass splitting \(\Delta m_{\tilde{t}_1-\tilde{\chi }^0_1} \simeq m_t\), the kinematics of the top quarks from stop decay are similar to those in the top pair production so that the above LHC searches for stop pair have the poor sensitivity. With the help of an additional high momentum jet recoiling against stop pair system, one can utilize the observable  to extend the reach of stop to about 800 GeV at 13 TeV LHC with \(\mathcal{L}=3000\) fb\(^{-1}\) [84]. Besides, the VBF production of the stop pair was also proposed to detect such a compressed stop region, which can cover the stop mass to about 300 GeV because of the large systematical uncertainty [85]. In NSUSY, when both decay channels \(\tilde{t}_1 \rightarrow t \tilde{\chi }^0_1\) and \(\tilde{t}_1 \rightarrow b \tilde{\chi }^+_1\) are allowed, search for the asymmetric final states \(\tilde{t}(\rightarrow t \tilde{\chi }^0_1)\tilde{t}^\dagger (\rightarrow b\tilde{\chi }^-_1)\) can provide a complementary way to probing stop at the LHC. With the variable topness to suppress \(t\bar{t}\) background, such an asymmetric stop search has a comparable sensitivity with the symmetric stop searches at the HL-LHC [86]. Therefore, together with conventional LHC search strategies, we can expect that the future high luminosity LHC is able to probe the stop and higgsino mass up to 1.5 and 0.6 TeV, respectively [87]. At that time, most of the NSUSY parameter space with \(\Delta _\mathrm{EW}<30\) can be covered [87, 88].
to extend the reach of stop to about 800 GeV at 13 TeV LHC with \(\mathcal{L}=3000\) fb\(^{-1}\) [84]. Besides, the VBF production of the stop pair was also proposed to detect such a compressed stop region, which can cover the stop mass to about 300 GeV because of the large systematical uncertainty [85]. In NSUSY, when both decay channels \(\tilde{t}_1 \rightarrow t \tilde{\chi }^0_1\) and \(\tilde{t}_1 \rightarrow b \tilde{\chi }^+_1\) are allowed, search for the asymmetric final states \(\tilde{t}(\rightarrow t \tilde{\chi }^0_1)\tilde{t}^\dagger (\rightarrow b\tilde{\chi }^-_1)\) can provide a complementary way to probing stop at the LHC. With the variable topness to suppress \(t\bar{t}\) background, such an asymmetric stop search has a comparable sensitivity with the symmetric stop searches at the HL-LHC [86]. Therefore, together with conventional LHC search strategies, we can expect that the future high luminosity LHC is able to probe the stop and higgsino mass up to 1.5 and 0.6 TeV, respectively [87]. At that time, most of the NSUSY parameter space with \(\Delta _\mathrm{EW}<30\) can be covered [87, 88].
3 Conclusions
In this paper, we examined the lower mass limit of the stop in natural supersymmetry (NSUSY) by using the recent LHC-13 TeV data. We recast the LHC SUSY inclusive search for  1)
1) events with \(\alpha _T\) variable, the direct stop pair searches (1-lepton channel and all-hadronic channel) and the monojet analyses. We found that the inclusive SUSY analysis with \(\alpha _T\) is complementary to the direct stop pair analyses in probing NSUSY. The current LHC data can exclude the stop up to 765 (860) GeV for \(m_{\tilde{\chi }^0_1} < 300\) (\(m_{\tilde{\chi }^0_1} = 100\)) GeV. While in the compressed region (\(\Delta m_{\tilde{t}_1-\tilde{\chi }^0_1} \simeq 20\) GeV), the stop mass can be still light as 320 GeV. About 70% of the NSUSY parameter space with \(\Delta _\mathrm{EW}<10\) can be covered by the current LHC Run-2 data. The future HL-LHC is expected to push the lower mass limits of the stop and higgsino up to 1.5 and 0.6 TeV, respectively, and cover most NSUSY parameter space with \(\Delta _\mathrm{EW}<30\).
events with \(\alpha _T\) variable, the direct stop pair searches (1-lepton channel and all-hadronic channel) and the monojet analyses. We found that the inclusive SUSY analysis with \(\alpha _T\) is complementary to the direct stop pair analyses in probing NSUSY. The current LHC data can exclude the stop up to 765 (860) GeV for \(m_{\tilde{\chi }^0_1} < 300\) (\(m_{\tilde{\chi }^0_1} = 100\)) GeV. While in the compressed region (\(\Delta m_{\tilde{t}_1-\tilde{\chi }^0_1} \simeq 20\) GeV), the stop mass can be still light as 320 GeV. About 70% of the NSUSY parameter space with \(\Delta _\mathrm{EW}<10\) can be covered by the current LHC Run-2 data. The future HL-LHC is expected to push the lower mass limits of the stop and higgsino up to 1.5 and 0.6 TeV, respectively, and cover most NSUSY parameter space with \(\Delta _\mathrm{EW}<30\).
Notes
The prediction of the SM-like Higgs mass depends on the spectrum generators. The differences arise from the choice of the renormalization scheme and the higher order correction calculations. These effects often lead to a few GeV uncertainty for the SM-like Higgs mass in the MSSM [37].
The thermal relic density of the light higgsino-like neutralino dark matter is typically low as a result of the large annihilation rate in the early Universe. One possible way to produce the correct relic density is introducing the mixed axion–higgsino dark matter [44, 45]. However, if the naturalness requirement is relaxed, the heavy higgsino-like neutralino with a mass \(\sim \)1–2 TeV can solely produce the correct relic density in the MSSM [46].
References
L.J. Hall, D. Pinner, J.T. Ruderman, JHEP 1204, 131 (2012)
M. Papucci, J.T. Ruderman, A. Weiler, JHEP 1209, 035 (2012)
C. Brust, A. Katz, S. Lawrence, R. Sundrum, JHEP 1203, 103 (2012)
R. Arnowitt, P. Nath, Phys. Rev. D 46, 3981 (1992)
R. Barbieri, G.F. Giudice, Nucl. Phys. B 306, 63 (1988)
H. Baer, V. Barger, M. Savoy, Phys. Rev. D 93(3), 035016 (2016)
H. Baer, V. Barger, P. Huang, A. Mustafayev, X. Tata, Phys. Rev. Lett. 109, 161802 (2012)
H. Abe, T. Kobayashi, Y. Omura, Phys. Rev. D 76, 015002 (2007). doi:10.1103/PhysRevD.76.015002. arXiv:hep-ph/0703044 [HEP-PH]
H. Baer, V. Barger, D. Mickelson, M. Padeffke-Kirkland, Phys. Rev. D 89(11), 115019 (2014)
H. Baer, V. Barger, P. Huang, D. Mickelson, A. Mustafayev, W. Sreethawong, X. Tata, JHEP 1312, 013 (2013). (Erratum: [JHEP 1506, 053 (2015)])
Z. Kang, J. Li, T. Li, JHEP 1211, 024 (2012)
H. Baer, V. Barger, P. Huang, X. Tata, JHEP 1205, 109 (2012)
J. Cao, C. Han, L. Wu, J.M. Yang, Y. Zhang, JHEP 1211, 039 (2012)
G.D. Kribs, A. Martin, A. Menon, Phys. Rev. D 88, 035025 (2013)
C. Han, K. Hikasa, L. Wu, J.M. Yang, Y. Zhang, JHEP 1310, 216 (2013)
K. Kowalska, E.M. Sessolo, Phys. Rev. D 88(7), 075001 (2013)
G. Belanger, D. Ghosh, R. Godbole, S. Kulkarni, JHEP 1509, 214 (2015)
A. Kobakhidze, N. Liu, L. Wu, J.M. Yang, M. Zhang, Phys. Lett. B 755, 76 (2016)
K. Hikasa, J. Li, L. Wu, J.M. Yang, Phys. Rev. D 93(3), 035003 (2016)
M. Drees, J.S. Kim, Phys. Rev. D 93(9), 095005 (2016)
D. Goncalves, K. Sakurai, M. Takeuchi. arXiv:1604.03938 [hep-ph]
G.H. Duan, K.I. Hikasa, L. Wu, J.M. Yang, M. Zhang. arXiv:1611.05211 [hep-ph]
The CMS collaboration, CMS-PAS-SUS-16-029
The ATLAS collaboration, ATLAS-CONF-2015-067
The CMS collaboration, CMS-PAS-SUS-16-024
J. Fan, R. Krall, D. Pinner, M. Reece, J.T. Ruderman, JHEP 1607, 016 (2016)
K. Kowalska. arXiv:1608.02489 [hep-ph]
A. Barr, J. Liu. arXiv:1605.09502 [hep-ph]
J.F. Gunion, H.E. Haber, Nucl. Phys. B 272, 1 (1986)
G.F. Giudice, A. Pomarol, Phys. Lett. B 372, 253 (1996)
H. Baer, V. Barger, P. Huang, JHEP 1111, 031 (2011)
C. Han, A. Kobakhidze, N. Liu, A. Saavedra, L. Wu, J.M. Yang, JHEP 1402, 049 (2014)
Z. Han, G.D. Kribs, A. Martin, A. Menon, Phys. Rev. D 89, 075007 (2014)
C. Han, D. Kim, S. Munir, M. Park, JHEP 1504, 132 (2015)
S. Heinemeyer, W. Hollik, G. Weiglein, Comput. Phys. Commun. 124, 76 (2000)
S. Heinemeyer, W. Hollik, G. Weiglein, Eur. Phys. J. C 9, 343 (1999)
J.P. Vega, G. Villadoro, JHEP 1507, 159 (2015). doi:10.1007/JHEP07(2015)159
D. Chowdhury, R.M. Godbole, K.A. Mohan, S.K. Vempati, JHEP 1402, 110 (2014)
J.E. Camargo-Molina, B. Garbrecht, B. O’Leary, W. Porod, F. Staub, Phys. Lett. B 737, 156 (2014)
U. Chattopadhyay, A. Dey, JHEP 1411, 161 (2014)
F. Mahmoudi, Comput. Phys. Commun. 180, 1579 (2009)
F. Mahmoudi, Comput. Phys. Commun. 178, 745 (2008)
P.A.R. Ade et al. [Planck Collaboration]. arXiv:1303.5076 [astro-ph.CO]
H. Baer, A. Lessa, S. Rajagopalan, W. Sreethawong, JCAP 1106, 031 (2011)
H. Baer, A. Lessa, W. Sreethawong, JCAP 1201, 036 (2012)
N. Arkani-Hamed, A. Delgado, G.F. Giudice, Nucl. Phys. B 741, 108 (2006)
D.S. Akerib et al. arXiv:1608.07648 [astro-ph.CO]
G. Belanger et al., Comput. Phys. Commun. 182, 842 (2011)
The ATLAS collaboration, ATLAS-CONF-2016-077
The ATLAS collaboration, ATLAS-CONF-2016-050
The ATLAS collaboration, ATLAS-CONF-2016-076
M. Aaboud et al. [ATLAS Collaboration]. arXiv:1606.08772 [hep-ex]
M. Aaboud et al. [ATLAS Collaboration], Phys. Rev. D 94(3), 032005 (2016)
The CMS collaboration, CMS-PAS-SUS-16-016
The CMS collaboration, CMS-PAS-SUS-16-015
The CMS collaboration, CMS-PAS-SUS-16-014
The CMS collaboration, CMS-PAS-SUS-16-028
The CMS collaboration, CMS-PAS-SUS-16-025
A. Djouadi, Y. Mambrini, Phys. Rev. D 63, 115005 (2001)
C. Boehm, A. Djouadi, Y. Mambrini, Phys. Rev. D 61, 095006 (2000)
K. Hikasa, M. Kobayashi, Phys. Rev. D 36, 724 (1987)
T. Han, K. Hikasa, J.M. Yang, X. Zhang, Phys. Rev. D 70, 055001 (2004)
M. Muhlleitner, E. Popenda, JHEP 1104, 095 (2011)
R. Grober, M. Muhlleitner, E. Popenda, A. Wlotzka, Phys. Lett. B 747, 144 (2015)
J. Aebischer, A. Crivellin, C. Greub, Phys. Rev. D 91(3), 035010 (2015). arXiv:1410.8459 [hep-ph]
J. Alwall et al., JHEP 1407, 079 (2014)
T. Sjostrand, S. Mrenna, P.Z. Skands, JHEP 0605, 026 (2006)
J. de Favereau et al. [DELPHES 3 Collaboration], JHEP 1402, 057 (2014)
M. Cacciari, G.P. Salam, G. Soyez, JHEP 0804, 063 (2008)
M. Cacciari, G.P. Salam, G. Soyez, Eur. Phys. J. C 72, 1896 (2012)
W. Beenakker et al., Int. J. Mod. Phys. A 26, 2637 (2011)
A. Kulesza, L. Motyka, Phys. Rev. D 80, 095004 (2009)
W. Beenakker et al., JHEP 0912, 041 (2009)
A. Kulesza, L. Motyka, Phys. Rev. Lett. 102, 111802 (2009)
W. Beenakker, R. Hopker, M. Spira, P.M. Zerwas, Nucl. Phys. B 492, 51 (1997)
D. Stump et al., JHEP 0310, 046 (2003). arXiv:hep-ph/0303013
E. Conte, B. Dumont, B. Fuks, C. Wymant, Eur. Phys. J. C 74(10), 3103 (2014)
B. Dumont et al., Eur. Phys. J. C 75(2), 56 (2015)
D. Sengupta. doi:10.7484/INSPIREHEP.DATA.GTH3.RN26
M. Drees et al., Comput. Phys. Commun. 187, 227 (2014)
J.S. Kim et al. arXiv:1503.01123 [hep-ph]
H. Baer, V. Barger, D. Mickelson, Phys. Rev. D 88(9), 095013 (2013)
H. Baer, V. Barger, P. Huang, D. Mickelson, A. Mustafayev, X. Tata, Phys. Rev. D 87(11), 115028 (2013)
H. An, L.T. Wang, Phys. Rev. Lett. 115, 181602 (2015). doi:10.1103/PhysRevLett.115.181602. arXiv:1506.00653 [hep-ph]
B. Dutta et al., Phys. Rev. D 90(9), 095022 (2014). doi:10.1103/PhysRevD.90.095022. arXiv:1312.1348 [hep-ph]
M. L. Graesser, J. Shelton, Phys. Rev. Lett. 111(12), 121802 (2013). doi:10.1103/PhysRevLett.111.121802. arXiv:1212.4495 [hep-ph]
J.S. Kim, K. Rolbiecki, R. Ruiz, J. Tattersall, T. Weber. arXiv:1606.06738 [hep-ph]
H. Baer, V. Barger, M. Savoy, X. Tata, Phys. Rev. D 94(3), 035025 (2016)
Acknowledgements
This work is partly supported by the Australian Research Council, by the CAS Center for Excellence in Particle Physics (CCEPP), by the National Natural Science Foundation of China (NNSFC) under Grants Nos. 11275057, 11305049, 11375001, 11405047, 11135003, 11275245, by Specialised Research Fund for the Doctoral Program of Higher Education under Grant No. 20134104120002. CCH is supported by World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan. MCZ is supported by Institute for Basic Science (IBS-R018-D1).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Han, C., Ren, J., Wu, L. et al. Top-squark in natural SUSY under current LHC run-2 data. Eur. Phys. J. C 77, 93 (2017). https://doi.org/10.1140/epjc/s10052-017-4662-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-4662-7




 , 13.3 fb
, 13.3 fb , stop, 13.3 fb
, stop, 13.3 fb , stop, 13.3 fb
, stop, 13.3 fb , 3.2 fb
, 3.2 fb , 3.2 fb
, 3.2 fb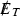 +
+ 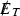 +
+ 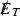 +
+ 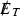 , 12.9 fb
, 12.9 fb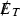 , 12.9 fb
, 12.9 fb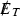 , 12.9 fb
, 12.9 fb