1 Introduction

Einstein’s general relativity is able to describe the dynamics of our solar system well enough. In addition, this theory predicted the existence of gravitational waves, which recently were observed by the LIGO and Virgo collaborations [1]. It is notable that observations of the LIGO collaboration could be employed to test the validation of Einstein theory of the gravity or the necessity of modified theories of gravity [2–7]. The Einstein theory of gravity may have some problems in describing gravity accurately at all scales. One of the problems that general relativity faced was that it could not describe the accelerated expansion of the universe accurately [8–10]. Also, it is consistent with neither Mach’s principle nor Dirac’s large number hypothesis [11, 12]. Thus, cosmologists explored various alternatives for gravitational fields [13–22]. The pioneering studies of scalar–tensor theory were done by Brans and Dicke [23]. This theory accommodates both Mach’s principle and Dirac’s large number hypothesis [11, 12]. Scientists have investigated various aspects of black holes and gravitational collapse in Brans–Dicke (BD) theory due to their importance in both classical and quantum aspects of gravity [24–27]. It has been shown that the stationary and vacuum BD solution in four dimensions is just the Kerr solution with a trivial scalar field everywhere [28]. Cai and Myung showed that in four dimensions the BD-Maxwell (BDM) solution is just the Reissner–Nordström (RN) solution with a constant scalar field [29–32]. However, in higher dimensions, due to the fact that the action of Maxwell field is not invariant under a conformal transformation and the stress energy tensor of the Maxwell field is not traceless, the solution of BDM is an RN solution with a non-trivial scalar field.

On the other hand, black hole thermodynamics has been a field of interest for many researchers since the work of Hawking [33]. Recently, in most treatments of black hole thermodynamics, physicists have considered the cosmological constant \((\Lambda )\) as a dynamical variable [34–36]. Furthermore, some authors suggested to treat \( \Lambda \) as a thermodynamic variable [37, 38], such as thermodynamical pressure [39–56]. One of the interesting aspects of black hole thermodynamics is its stability. In order to have a black hole in thermal stability, its heat capacity must be positive. In other words, positivity of the heat capacity guarantees thermal stability of the black holes. This approach of studying the stability is in the context of the canonical ensemble. Studying the heat capacity of a system also provides a mechanism to study the phase transitions of that system. There are two distinctive points: in one point, changing the sign of the heat capacity is called a physical limitation point and therefore, the root of the heat capacity is a border between non-physical and physical black hole solutions. Other characterized points are related to the divergencies of the heat capacity. We identify these points as second order phase transitions [57].

In the past few decades, applying the thermodynamical geometry for studying the phase transition of black holes has gained a lot of attention. These studies were pioneered by Weinhold [58, 59] and Ruppeiner [60, 61]. Weinhold introduced a metric on the space of equilibrium state and defined the metric tensor as the second derivative of the internal energy with respect to entropy and other extensive quantities. On the other hand, the metric that Ruppeiner introduced was defined as the minus second derivatives of entropy with respect to internal energy and other extensive quantities, which was conformal to Weinhold’s metric [62]. However, applying these treatments to the study of black hole thermodynamics caused some puzzling anomalies. Neither Weinhold nor Ruppeiner metrics were invariant under a Legendre transformation. A few years ago, Quevedo [63–66] proposed an approach to obtain a metric which was Legendre invariant in the space of equilibrium state. His work was based on the observation that standard thermodynamics was invariant with respect to a Legendre transformation. The formalism of geometrothermodynamics (GTD) indicates that a phase transition occurs at points where the thermodynamics curvature is singular, and as a consequence, the curvature can be interpreted as a measure of thermodynamics interaction. After Quevedo, interesting studies were performed by some authors [67–71]. Recently, it was pointed out that using the mentioned approaches toward GTD may sometimes confront with some problems. In order to overcome these problems, a new approach was introduced in Refs. [72–75].

The outline of the paper is as follows; in Sect. 2, we review the charged BD black holes and their thermodynamical quantities. In Sect. 3, we introduce the approaches for studying phase transitions of these black holes in the context of the heat capacity and geometrical thermodynamics. Then we investigate the existence of the phase transitions in the context of the two approaches mentioned and compare them with each other. We also investigate the effect of the BD parameter. In addition, we study the free energy of BD black holes. The last section is devoted to closing remarks.

2 Black holes solutions in BDM gravity

Regarding \((n+1)\)-dimensional BDM theory, one finds the related action [29–32]

$$\begin{aligned} I_{G}= & {} -\frac{1}{16\pi }\int _{\mathcal {M}}d^{n+1}x\sqrt{-g}\nonumber \\&\times \left( \Phi \mathcal {R}-\frac{\omega }{\Phi }(\nabla \Phi )^{2}-V(\Phi )-F_{\mu \nu }F^{\mu \nu }\right) , \end{aligned}$$
(1)

where \(\Phi \) and \(V(\Phi )\) are, respectively, a scalar field and its self-interacting potential. Besides, the factor \(\omega \) is the coupling constant, \(\mathcal {R}\) is the scalar curvature, \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) is the electromagnetic tensor field, and \(A_{\mu }\) is the electromagnetic potential. The equations of motion can be obtained with the following explicit forms by varying the action (1) with respect to the gravitational field \(g_{\mu \nu }\), the scalar field \(\Phi \), and the gauge field \(A_{\mu }\) [29–32]:

$$\begin{aligned} G_{\mu \nu }= & {} \frac{\omega }{\Phi ^{2}}\left( \nabla _{\mu }\Phi \nabla _{\nu }\Phi -\frac{1}{2}g_{\mu \nu }(\nabla \Phi )^{2}\right) \nonumber \\&-\frac{V(\Phi ) }{2\Phi }g_{\mu \nu }+\frac{1}{\Phi }\left( \nabla _{\mu }\nabla _{\nu }\Phi -g_{\mu \nu }\nabla ^{2}\Phi \right) \nonumber \\&+\frac{2}{\Phi }\left( F_{\mu \lambda }F_{\nu }^{\lambda }-\frac{1}{4} F_{\rho \sigma }F^{\rho \sigma }g_{\mu \nu }\right) , \end{aligned}$$
(2)
$$\begin{aligned} \nabla ^{2}\Phi= & {} -\frac{n-3}{2\left[ \left( n-1\right) \omega +n\right] } F^{2}+\frac{1}{2\left[ \left( n-1\right) \omega +n)\right] }\nonumber \\&\times \left[ (n-1)\Phi \frac{dV(\Phi )}{d\Phi }-\left( n+1\right) V(\Phi )\right] , \end{aligned}$$
(3)
$$\begin{aligned} \nabla _{\mu }F^{\mu \nu }=0, \end{aligned}$$
(4)

where \(G_{\mu \nu }\) and \(\nabla _{\mu }\) are, respectively, the Einstein tensor and covariant derivative of manifold \(\mathcal {M}\) with metric \( g_{\mu \nu }\). Due to the appearance of inverse powers of the scalar field on the right hand side of (2), solving the field equations (2)–(4) directly is a non-trivial task. This difficulty can be removed, by using a suitable conformal transformation [29–32]. Indeed, via the conformal transformation the BDM theory can be transformed into the Einstein–Maxwell theory with a minimally coupled scalar dilaton field. A suitable conformal transformation can be shown as [29–32]

$$\begin{aligned}&\bar{g}_{\mu \nu } =\Phi ^{2/(n-1)}g_{\mu \nu }, \end{aligned}$$
(5)
$$\begin{aligned}&\bar{\Phi } =\frac{n-3}{4\alpha }\ln \Phi , \end{aligned}$$
(6)

where

$$\begin{aligned} \alpha =(n-3)/\sqrt{4(n-1)\omega +4n}. \end{aligned}$$
(7)

It is worth mentioning that all functions and quantities in Jordan frame (\({g }_{\mu \nu }\), \({\Phi }\), and \({F}_{\mu \nu }\)) can be transformed into Einstein frame (\(\bar{g}_{\mu \nu }\), \(\bar{\Phi }\) and \(\bar{F}_{\mu \nu }\) ). Applying the mentioned conformal transformation on the BD action (1), one finds the action of dilaton gravity,

$$\begin{aligned} \bar{I}_{G}= & {} -\frac{1}{16\pi }\int _{\mathcal {M}}d^{n+1}x\sqrt{-\bar{g}} \left\{ \bar{\mathcal {R}}-\frac{4}{n-1}(\bar{\nabla }\bar{\Phi })^{2}\right. \nonumber \\&\left. -\bar{V}( \bar{\Phi })-\exp \left( -\frac{4\alpha \bar{\Phi }}{(n-1)}\right) \bar{F} _{\mu \nu }\bar{F}^{\mu \nu }\right\} , \end{aligned}$$
(8)

where \(\bar{\nabla }\) and \(\overline{\mathcal {R}}\) are, respectively, the covariant derivative and Ricci scalar corresponding to the metric \(\bar{g} _{\mu \nu }\), and \(\bar{V}(\bar{\Phi })\) is

$$\begin{aligned} \bar{V}(\bar{\Phi })=\Phi ^{-(n+1)/(n-1)}V(\Phi ). \end{aligned}$$
(9)

Regarding the \((n+1)\)-dimensional Einstein–Maxwell-dilaton action (8), \(\alpha \) is an arbitrary constant that governs the strength of coupling between the dilaton and Maxwell fields. One can obtain the equations of motion by varying this action (8) with respect to \(\bar{g}_{\mu \nu }\), \(\bar{\Phi }\), and \(\bar{F}_{\mu \nu }\)

$$\begin{aligned}&\bar{\mathcal {R}}_{\mu \nu }=\frac{4}{n-1}\left( \bar{\nabla }_{\mu }\bar{\Phi }\bar{\nabla }_{\nu }\bar{\Phi }+\frac{1}{4}\bar{V}\bar{g}_{\mu \nu }\right) \nonumber \\&\quad +2e^{-4\alpha \bar{\Phi }/(n-1)}\left( \bar{F}_{\mu \lambda }\bar{F}_{\nu }^{\lambda }-\frac{1}{2(n-1)}\bar{F}_{\rho \sigma }\bar{F}^{\rho \sigma } \bar{g}_{\mu \nu }\right) ,\end{aligned}$$
(10)
$$\begin{aligned}&\bar{\nabla }^{2}\bar{\Phi }=\frac{n-1}{8}\frac{\partial \bar{V}}{\partial \bar{\Phi }}-\frac{\alpha }{2}e^{-4\alpha \bar{\Phi }/(n-1)}\bar{F}_{\rho \sigma }\bar{F}^{\rho \sigma },\end{aligned}$$
(11)
$$\begin{aligned}&\partial _{\mu }\left[ \sqrt{-\bar{g}}e^{-4\alpha \bar{\Phi }/(n-1)}\bar{F} ^{\mu \nu }\right] =0. \end{aligned}$$
(12)

Assuming the \(\left( \bar{g}_{\mu \nu },\bar{F}_{\mu \nu },\bar{\Phi }\right) \) as solutions of Eqs. (10)–(12) with the potential \(\bar{V }\left( \bar{\Phi }\right) \) and comparing Eqs. (2)–(4 ) with Eqs. (10)–(12), the solutions of Eqs. (2)–(4) with the potential \(V(\Phi )\) can be written as

$$\begin{aligned} \left[ g_{\mu \nu },F_{\mu \nu },\Phi \right]= & {} \left[ \exp \left( -\frac{ 8\alpha \bar{\Phi }}{\left( n-1\right) (n-3)}\right) \right. \nonumber \\&\left. \times \bar{g}_{\mu \nu },\bar{F }_{\mu \nu },\exp \left( \frac{4\alpha \bar{\Phi }}{n-3}\right) \right] . \end{aligned}$$
(13)

As a consequence, we can solve Eqs. (10)–(12) with a suitable potential, instead of solving Eqs. (2)–(4). Assume an \((n+1)\)-dimensional static and spherically symmetric metric,

$$\begin{aligned} \mathrm{d}\bar{s}^{2}=-f(r)\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{f(r)}+r^{2}R^{2}(r)\mathrm{d}\Omega _{n-1}^{2}, \end{aligned}$$
(14)

where \(\mathrm{d}\Omega _{n-1}^{2}\) is the metric of a unit \((n-1)\)-sphere, and f(r) and R(r) are metric functions. By integrating the Maxwell equation (12), we can obtain the nonzero electric field \(\bar{F}_{tr}\) as

$$\begin{aligned} \bar{F}_{tr}=\frac{q}{(rR)^{n-1}}\exp \left( \frac{4\alpha \bar{\Phi }}{n-1} \right) , \end{aligned}$$
(15)

where q is an integration constant related to electric charge. Now, we regard the following Liouville-type potential to solve the field equations:

$$\begin{aligned} \bar{V}(\bar{\Phi })=2\Lambda \exp \left( \frac{4\alpha \bar{\Phi }}{n-1} \right) +\frac{(n-1)(n-2)\alpha ^{2}}{c^{2}\left( \alpha ^{2}-1\right) }e^{ \frac{4\bar{\Phi }}{(n-1)\alpha }}. \end{aligned}$$
(16)

Taking into account the metric (14) with the Maxwell field (15) and potential (16), the consistent solutions of Eqs. (10) and (11) are [56]

$$\begin{aligned} f(r)= & {} -\frac{\left( n-2\right) \left( \alpha ^{2}+1\right) ^{2}c^{-2\gamma }r^{2\gamma }}{\left( \alpha ^{2}+n-2\right) \left( \alpha ^{2}-1\right) }\nonumber \\&+ \frac{2\Lambda (\alpha ^{2}+1)^{2}c^{2\gamma }}{(n-1)(\alpha ^{2}-n)} r^{2(1-\gamma )}-\frac{m}{r^{(n-2)}}r^{(n-1)\gamma } \nonumber \\&+\frac{2q^{2}(\alpha ^{2}+1)^{2}c^{-2(n-2)\gamma }}{(n-1)(\alpha ^{2}+n-2)r^{2(n-2)(1-\gamma )}}, \end{aligned}$$
(17)
$$\begin{aligned} R(r)= & {} \exp \left( \frac{2\alpha \bar{\Phi }}{n-1} \right) =\left( \frac{c}{r}\right) ^{\gamma }, \end{aligned}$$
(18)
$$\begin{aligned} \bar{\Phi }(r)= & {} \frac{(n-1)\alpha }{2(1+\alpha ^{2})}\ln \left( \frac{c}{r} \right) , \end{aligned}$$
(19)

where m is an integration constant which is related to the total mass, c is another arbitrary constant related to the scalar field and \(\gamma =\alpha ^{2}/(1+\alpha ^{2})\).

Now, using the conformal transformation, we are able to obtain the solutions of Eqs. (2)–(4). Considering the following spherically symmetric metric:

$$\begin{aligned} \mathrm{d}s^{2}=-U(r)\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{V(r)}+r^{2}H^{2}(r)\mathrm{d}\Omega _{n-1}^{2}, \end{aligned}$$
(20)

with Eqs. (2)–(4), we find that the functions U(r) and V(r) are [56]

$$\begin{aligned} U(r)= & {} \frac{2\Lambda (\alpha ^{2}+1)^{2}c^{2\gamma (\frac{n-5}{n-3})}}{ (n-1)(\alpha ^{2}-n)}r^{2(1-\frac{\gamma \left( n-5\right) }{n-3})}\nonumber \\&-\frac{ mc^{(\frac{-4\gamma }{n-3})}}{r^{(n-2)}}r^{\gamma (n-1+\frac{4}{n-3})} \nonumber \\&+\frac{2q^{2}(\alpha ^{2}+1)^{2}c^{-2\gamma (n-2+\frac{2}{n-3})}}{ (n-1)(\alpha ^{2}+n-2)r^{2[(n-2)(1-\gamma )-\frac{2\gamma }{n-3}]}}\nonumber \\&-\frac{ \left( n-2\right) \left( \alpha ^{2}+1\right) ^{2}}{\left( \alpha ^{2}+n-2\right) \left( \alpha ^{2}-1\right) }\left( \frac{c}{r}\right) ^{-2\gamma \left( \frac{n-1}{n-3}\right) }, \end{aligned}$$
(21)
$$\begin{aligned} V(r)= & {} \frac{2\Lambda (\alpha ^{2}+1)^{2}c^{2\gamma (\frac{n-1}{n-3})}}{ (n-1)(\alpha ^{2}-n)}r^{2(1-\frac{\gamma \left( n-1\right) }{n-3})}\nonumber \\&-\frac{ mc^{(\frac{4\gamma }{n-3})}}{r^{(n-2)}}r^{\gamma (n-1-\frac{4}{n-3})} \nonumber \\&+\frac{2q^{2}(\alpha ^{2}+1)^{2}c^{-2\gamma (n-2-\frac{2}{n-3})}}{ (n-1)(\alpha ^{2}+n-2)r^{2[(n-2)(1-\gamma )+\frac{2\gamma }{n-3}]}} \nonumber \\&-\frac{ \left( n-2\right) \left( \alpha ^{2}+1\right) ^{2}}{\left( \alpha ^{2}+n-2\right) \left( \alpha ^{2}-1\right) }\left( \frac{c}{r}\right) ^{-2\gamma \left( \frac{n-5}{n-3}\right) }, \end{aligned}$$
(22)

where we used the conformal transformation of Eq. (16) with the following explicit form:

$$\begin{aligned} V(\Phi )= & {} 2\Lambda \Phi ^{2}+\frac{(n-1)(n-2)\alpha ^{2}}{c^{2}\left( \alpha ^{2}-1\right) }\nonumber \\&\times \Phi ^{[(n+1)(1+\alpha ^{2})-4]/[(n-1)\alpha ^{2}]}. \end{aligned}$$
(23)

In addition, one can use the conformal transformation to obtain a consistent electromagnetic field as

$$\begin{aligned} F_{tr}=\frac{qc^{(3-n)\gamma }}{r^{(n-3)(1-\gamma )+2}}. \end{aligned}$$
(24)

As one can see, the electromagnetic field becomes zero as \(r\longrightarrow \infty \). It is evident that as \(\omega \longrightarrow \infty \), the obtained solutions are just the charged solutions of Einstein gravity (RN AdS black hole).

Using the Euclidean action, the finite mass and the entropy of the black hole can be obtained [29–32],

$$\begin{aligned}&M =\frac{c^{(n-1)\gamma }}{16\pi }\left( \frac{n-1}{1+\alpha ^{2}}\right) m, \end{aligned}$$
(25)
$$\begin{aligned}&S =\frac{c^{(n-1)\gamma }}{4}r_{+}^{(n-1)\left( 1-\gamma \right) }. \end{aligned}$$
(26)

By considering the flux of electric field at infinity, one can find the total charge of this configuration,

$$\begin{aligned} Q=\frac{q}{4\pi }. \end{aligned}$$
(27)

Calculations show that the Hawking temperature of a BD black hole on the outer horizon \(r_{+}\) is

$$\begin{aligned} T=\frac{\kappa }{2\pi }=\left. \frac{1}{4\pi }\sqrt{\frac{V}{U}}\left( \frac{ \mathrm{d}U}{\mathrm{d}r}\right) \right| _{r=r_{+}}, \end{aligned}$$
(28)

where \(\kappa \) is the surface gravity. After some simplifications, we obtain [56]

$$\begin{aligned} T= & {} -\frac{2(1+\alpha ^{2})}{4\pi (n-1)}\left( \Lambda c^{2\gamma }r_{+}^{1-2\gamma }+\frac{q^{2}c^{-2(n-2)\gamma }}{{r_{+}}^{\gamma }}{r_{+}} ^{(2n-3)(\gamma -1)}\right) \nonumber \\&+\frac{\left[ \gamma \left( n-3\right) -n+2\right] \left( 1-n\right) \left( n-2\right) }{{2r}_{+}\left( \alpha ^{2}+n-2\right) \left( \alpha ^{2}-1\right) }\left( \frac{c}{r_{+}}\right) ^{-2\gamma }. \end{aligned}$$
(29)

3 Stability, phase transition, and geometrical thermodynamics

In this section, first, we study the stability and phase transition of the solutions in the context of the heat capacity. Next, we consider the geometrical approach for studying phase transition. We investigate the effect of the BD parameter and compare the results of both approaches.

There are several approaches for studying the stability of black holes. One of these approaches is related to studying the perturbed black holes and see if and how they acquire stable state and will be in equilibrium. This approach is known as dynamical stability of black holes. In this paper, we are not interested in the dynamical stability of black holes. We focus our studies on the thermal stability of charged black hole solutions in the context of BD theory through the canonical ensemble. To do so, we calculate the heat capacity and study its behavior.

Black holes should have a positive heat capacity in order to be thermally stable. In other words, the positivity of the heat capacity guarantees the local thermal stability of the black holes. One can use the following relation for the heat capacity:

$$\begin{aligned} C_{Q}=T\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}^{-1}=T\left( \frac{\partial S}{\partial T}\right) _{Q}=T\left( \frac{\partial S}{\partial r_{+}}\right) _{Q}\left( \frac{\partial T}{\partial r_{+}}\right) _{Q}^{-1}. \end{aligned}$$
(30)

On the other hand, it is possible to employ the heat capacity for studying the phase transitions of black holes. In the context of black holes, it is argued that the root of the heat capacity (\(C_{Q}=T=0\)) is representing a border line between physical (\(T>0\)) and non-physical (\(T<0\)) black holes. We call it a physical limitation point. The system in the case of this physical limitation point has a change in sign of the heat capacity. In addition, it is believed that the divergencies of the heat capacity represent phase transitions of black holes. These phase transitions are known as second order phase transition [57]. Therefore, the phase transition and limitation points of the black holes in the context of the heat capacity are calculated with the following relations:

$$\begin{aligned} \left\{ \begin{array}{cc} T=\left( \frac{\partial M}{\partial S}\right) _{Q}=0, &{} \mathrm{physical}\, \mathrm{limitation}\,\mathrm{point}, \\ &{} \\ \left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}=0, &{} \mathrm{second}\, \mathrm{order}\ \mathrm{phase}\,\mathrm{transition}. \end{array} \right. \end{aligned}$$
(31)

Regarding Eq. (31) and in order to find the physical limitation point, one should solve the following equation for the entropy:

$$\begin{aligned} \left( \frac{\partial M}{\partial S}\right) _{Q}= & {} 7\frac{\pi ^{2}\Lambda \left( n-9-4\omega \right) A_{1}c^{\left( n+1\right) j_{1}}}{4}\nonumber \\&+\frac{\left( n-2\right) \pi ^{2}\left[ \left( n-1\right) \omega +n\right] A_{2}c^{\left( n-3\right) j_{1}}}{2} \nonumber \\&+\frac{\left( n-9-4\omega \right) Q^{2}}{c^{\left( n-3\right) j_{1}}A_{2}} =0, \end{aligned}$$
(32)
Fig. 1
figure 1

For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \( \omega =1\), \(c=1\), and \(q=0.1\). (Upper diagrams \(d=5\) and lower diagrams \(d=6\))

Full size image

while for the second order phase transition points (divergence points of the heat capacity), we obtain the following relation:

$$\begin{aligned} \left( \frac{\partial T}{\partial S}\right) _{Q}= & {} \frac{\pi ^{2}\Lambda \left( n-9-4\omega \right) A_{1}c^{\left( n+1\right) j_{1}}}{32}\nonumber \\&-\frac{ \left( n-2\right) \pi ^{2}\left[ \left( n-1\right) \omega +n\right] A_{2}c^{\left( n-3\right) j_{1}}}{16} \nonumber \\&+\frac{\left[ \left( n-12\right) \omega +9\left( n-1\right) \right] Q^{2}}{ 8A_{2}c^{\left( n-3\right) j_{1}}}=0, \end{aligned}$$
(33)

where

$$\begin{aligned}&A_{1}=\left( c^{-\frac{\left( n-3\right) ^{2}}{\left( 4n-4\right) \omega +4n}}\left( 4S\right) ^{\frac{n^{2}+\left( 4\omega -2\right) n+9-4\omega }{4 \left[ \left( \omega +1\right) n-\omega \right] \left( n-1\right) }}\right) ^{j_{2}},\\&A_{2}=\left( c^{-\frac{\left( n-3\right) ^{2}}{\left( 4n-4\right) \omega +4n}}\left( 4S\right) ^{\frac{n^{2}+\left( 4\omega -2\right) n+9-4\omega }{4 \left[ \left( \omega +1\right) n-\omega \right] \left( n-1\right) }}\right) ^{j_{3}},\\&j_{1}=\zeta \left( n-3\right) ^{2},\\&j_{2}=\zeta \left[ 4n\omega \left( n-1\right) +3n\left( n+1\right) +3n-9 \right] , \\&j_{3}=\zeta \left( n-1\right) \left[ \left( 4n-8\right) \omega +5n-9\right] , \\&\zeta =\left[ \left( n-1\right) ^{2}+4\left( n-1\right) \omega +8\right] ^{-1}. \end{aligned}$$

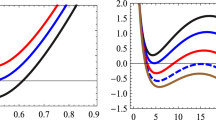
It is worthwhile to mention that for the case of a physical limitation point, numerical evaluation shows that there is only one root for this case which will be seen by plotting graphs for the heat capacity. In the case of a phase transition point, interestingly, numerical evaluation shows that two cases might occur: in one of these cases, there is no real root for Eq. (33), hence there is no phase transition for the black holes; whereas in the other case, due to the structure of Eq. (33), there will be two roots for this equation, which indicates the existence of two divergence points, and therefore, could be interpreted as phase transitions for these black holes. This will be seen in the plotted graphs (Figs. 1, 2, 3, 4, and 5) in more detail.

Fig. 2
figure 2

For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line), and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \( \omega =1\), \(c=1\), and \(q=1\). (Left diagram \(d=5\) and middle, and right diagrams \(d=6\))

Full size image
Fig. 3
figure 3

For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \( \omega =1\), \(c=1\), and \(q=2\). (Left diagram \(d=5\) and middle, and right diagrams \(d=6\))

Full size image
Fig. 4
figure 4

For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \(q=1\), \(c=1\), and \(\omega =0.1\). (Up diagrams \(d=5\) and lower diagrams \(d=6\))

Full size image
Fig. 5
figure 5

For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \(q=1\), \(c=1\), and \(\omega =3\). (Left diagram \(d=5\) and middle and right diagrams \(d=6\))

Full size image

Another approach for studying the phase transition of black holes is through geometrical thermodynamics. There are several metrics that one can employ in order to build a geometrical phase space by thermodynamical quantities. The well-known ones are the Ruppeiner, Weinhold, and Quevedo cases. It was previously argued that these metrics may not provide us with a completely flawless mechanism for studying the geometrical thermodynamics of specific types of black holes [72–75]. In this paper, we will show that the method of geometrical thermodynamics reported in [76] is not suitable in the presence of a scalar field. Recently, a new metric (HPEM metric) was proposed in order to solve the problems that other metrics may confront with [72–75].

According to Ref. [63], it is possible to derive, in principle, an infinite number of Legendre invariant metrics. In addition, it was shown that one of the simplest ways for obtaining the Legendre invariant metrics is to apply a conformal transformation. Comparing HPEM metric with Quevedo’s one, we find that they are the same up to a conformal factor. In addition, despite Weinhold and Ruppeiner, the HPEM and Quevedo metrics enjoy the same (\(- + + + \cdots \)) signature. Regarding the same signature with a difference in the conformal factor, it is expected that HPEM enjoys Legendre invariance with a different Legendre multiplier.

On the other hand, we should mention an unavoidable feature related to Legendre invariance. Although it was thought that the Legendre invariance guarantees a unique description of thermodynamical metrics, it was shown that such an invariance alone is not sufficient for the mentioned guaranty in terms of thermodynamical curvatures [77]. However, it was proven that in addition to Legendre invariance, we need to require curvature invariance in various representations. Therefore, both Legendre and curvature invariances should be checked. In addition, there are two issues with a fundamental relation between them; (I) agreement of thermodynamical curvature results with usual thermodynamical approaches (such as the heat capacity); (II) curvature invariance in addition to the Legendre invariance. It is important to probe the fundamentals of cases (I) and (II) for discovering which case may lead to satisfaction of another one. Although the former case has been investigated for special cases [77], the latter one has been remained unanalyzed yet. One may address them in an independent work in the future.

The Weinhold, Ruppeiner, and Quevedo thermodynamical metrics are given by

$$\begin{aligned}&\mathrm{d}s_{W}^{2}=Mg_{ab}^{W}\mathrm{d}X^{a}\mathrm{d}X^{b}, \end{aligned}$$
(34)
$$\begin{aligned}&\mathrm{d}s_{R}^{2}=-MTg_{ab}^{W}\mathrm{d}X^{a}\mathrm{d}X^{b}, \end{aligned}$$
(35)
$$\begin{aligned}&\mathrm{d}s_{Q}^{2}=\left( SM_{S}+QM_{Q}\right) \left( -M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}\right) , \end{aligned}$$
(36)

where \(g_{ab}^{W}=\partial ^{2}M\left( X^{c}\right) /\partial X^{a}\partial X^{b}\) and also \(X^{a}\equiv X^{a}\left( S,N^{i}\right) \), in which \(N^{i}\) denotes other extensive variables of the system. The HPEM metric, with two extensive parameters (entropy and electric charge), is

$$\begin{aligned} \mathrm{d}s_\mathrm{HPEM}^{2}=\frac{SM_{S}}{M_{QQ}^{3}}\left( -M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}\right) , \end{aligned}$$
(37)

where \(M_{X}=\left( \frac{\partial M}{\partial X}\right) \) and \(M_{XX}=\left( \frac{\partial ^{2}M}{\partial X^{2}}\right) \). Calculations show that the numerator and denominator of HPEM method for this type of thermodynamical system are given by [72–75]

$$\begin{aligned}&\mathrm{num}(\mathcal {R}_\mathrm{HPEM}) =6S^{2}M_{S}^{2}M_{QQ}M_{SS}^{2}M_{QQQQ}\nonumber \\&-6SM_{S}^{2}M_{QQ}^{2}M_{SS}M_{SSQQ}+2SM_{SQQ}^{2}M_{S}^{2}M_{QQ}M_{SS} \nonumber \\&+2\left[ SM_{S}M_{SSS}-\frac{1}{2}M_{SS}\left( SM_{SS}-M_{S}\right) \right] SM_{QQ}^{2}M_{S}M_{SQQ}\nonumber \\&-9S^{2}M_{QQQ}^{2}M_{S}^{2}M_{SS}^{2}\nonumber \\&+4\left[ \frac{1}{4}M_{SQ}M_{SS}+M_{S}M_{SSQ}\right] S^{2}M_{QQ}M_{S}M_{QQQ}\nonumber \\&+\left[ S^{2}M_{S}^{2}M_{SSQ}-S^{2}M_{SQ}M_{SS}M_{S}M_{SSQ}\right. \nonumber \\&\times \left. SM_{QQ}M_{S}\left( SM_{SS}-M_{S}\right) M_{SS}-2\left( S^{2}M_{SS}^{3}+M_{S}^{2}M_{SS}\right) \right. \nonumber \\&\times \left. M_{QQ}+2S^{2}M_{SQ}^{2}M_{SS}^{2} \right] M_{QQ}^{2} \end{aligned}$$
(38)

and

$$\begin{aligned} \mathrm{denom}(\mathcal {R}_\mathrm{HPEM})=S^{3}M_{S}^{3}M_{SS}^{2}. \end{aligned}$$
(39)

It is obvious that, in general, the roots of the numerator and denominator of this Ricci scalar do not coincide. This means that the case where the divergency of the Ricci scalar could be canceled by its root does not occur. The denominator of the Ricci scalar of the HPEM metric contains numerator and denominator of the heat capacity. In other words, divergence points of the Ricci scalar of the HPEM metric coincide with both roots and phase transition points of the heat capacity. Therefore, all the phase transition and limitation points are included in the divergencies of the Ricci scalar of this metric.

In the following, we study the stability and phase transition of charged BD black holes in the context of the canonical ensemble by calculating heat capacity. Then we study geometrical thermodynamics of these black holes by using the HPEM thermodynamical metric. Before conducting the research in the context of HPEM method, we will show that the Weinhold, Ruppeiner, and Quevedo metrics fail to provide effective results.

First of all, one should take the fact into consideration that the sign of temperature puts a restriction on the system as to it being physical or non-physical. In other words, the negativity of temperature denotes a non-physical system which in our case is a black hole. It is evident that there is a critical horizon radius, say \(r_{c}\), in which for \(r_{+}<r_{c}\) the temperature of the system is negative. Therefore, in this region solutions are non-physical. Since for \(r_{+}>r_{c}\) the system has a positive temperature, the horizon radius of physical black holes is placed in this region.

In the case of five-dimensional black holes, for sufficiently small values of the electric charge (Fig. 1 top) and BD coupling constant (Fig. 4 top), these black holes have three characteristic points. One is related to the root of heat capacity and the others are related to its divergencies (\( r_{Div1}\) and \(r_{Div2}\), in which \(r_{Div1}<r_{Div2}\)). It is clear that the root of heat capacity and \(r_{c}\) are the same and for the case \(r_{+}<r_{c}\) the heat capacity is negative but due to the negativity of temperature, the system is not physical. On the other hand, for the region \( r_{c}<r_{+}<r_{Div1}\), the heat capacity is positive definite. Therefore, in this region, the system is in a stable state. As for the case \( r_{Div1}<r_{+}<r_{Div2}\) the heat capacity has a negative value, which is called an instability of the black holes. In other words, in the case of \( r_{+}=r_{Div1}\) the system may undergo a phase transition from a large and unstable black hole to a smaller and stable one. In the case of \(r_{+}=r_{Div2}\) the system will have another phase transition and its stability will change from an unstable to a stable one. In other words, for \(r_{+}>r_{Div2}\) the heat capacity has a positive value and the black hole is stable. It is notable that for sufficiently large values of q (Figs. 2, 3 left), \(\omega \) (Fig. 5 left), the divergencies of the heat capacity vanish and the black hole is thermally stable for \(r_{+}>r_{c}\), without any phase transition.

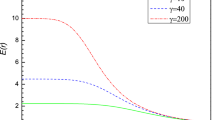
In the case of six-dimensional charged BD black holes, we find the following results. It is clear that in the six-dimensional case, using the values considered in the case of five-dimensional solutions, in all cases one root and two divergence points for the heat capacity are observed. In these cases, the heat capacity and phase transitions have similar behavior to that observed in five dimensions for charged BD black holes. \(r_{Div1}\) is an increasing function of the electric charge (Figs. 2, 3 middle) while \(r_{Div2}\) is a decreasing function of the BD coupling constant (Figs. 2, 5 right). We should note that the effects of variation of q on the second divergence point are small (Figs. 2, 3 right).

Fig. 6
figure 6

Left panel Weinhold, right panel Ruppeiner; \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \(\omega =1\), \(c=1\), and \(q=0.1\). (Upper diagrams \(d=5\) and lower diagrams \(d=6\))

Full size image

Next, by employing the metrics that were defined, Eqs. (34)–(37), we construct a thermodynamical spacetime with mass as the thermodynamical potential. Using Eqs. (25)–(27) one can write the total mass of the black holes as a function of extensive parameters. By employing Eqs. (34)–(37) the phase space will be constructed. Next, we calculate the curvature scalar of the mentioned thermodynamical metrics. Analytical calculation of the curvature scalar is too large and, therefore, we leave out the analytical result for reasons of economy.

Studying Fig. 6 shows that using the Weinhold and Ruppeiner cases leads to a mismatch between the divergency of the Ricci scalar of these two metrics and the divergency of the heat capacity. In other words, the phase transitions of the Ruppeiner and Weinhold metrics do not coincide with phase transitions of the canonical ensemble, and hence the heat capacity. Next, we present the behavior of the results obtained for the HPEM method in the plotted graphs (Figs. 1, 2, 3, 4, and 5). These figures show that divergencies of thermodynamical Ricci scalar coincide with the root and divergence points of the heat capacity. As for the Quevedo metric, we will follow another approach to show that it fails to produce suitable results. It is a matter of calculation to show that using the Quevedo metric (36), one can find the following denominator for its Ricci scalar:

$$\begin{aligned} \mathrm{denom}(\mathcal {R}_{Q})=\left( SM_{S}+QM_{Q}\right) ^{3}M_{SS}^{2}M_{QQ}^{2}. \end{aligned}$$
(40)

Here, three terms contribute to divergencies of the Ricci scalar of the Quevedo metric. \(M_{SS}\) ensures that phase transitions of the heat capacity and some of the divergencies of the Ricci scalar of this metric coincide, where the other two terms will result in extra divergencies that do not coincidence with any phase transition. In other words, the results of using this metric are not consistent with the results of heat capacity. Therefore, if one uses this metric independent of the heat capacity, due to being plugged with extra divergencies, it is not possible to make acceptable statements regarding the physical properties of the system. For further clarification, we give an example. For \(d=5\) and \(\Lambda =\omega =c=1\), one can find the following relation for the Ricci scalar of Quevedo metric:

$$\begin{aligned}&R=\frac{-104799744 \pi ^{2}\;r_{+}^{\frac{228}{29}}}{841\;\Gamma _{1}^{2}\;\Gamma _{2}^{3}}\left\{ 11981115\;r_{+}^{\frac{390}{29} }-8575308\;r_{+}^{\frac{336}{29}}\right. \nonumber \\&\qquad \left. -83387808\;r_{+}^{\frac{282}{29} }+116784640\;r_{+}^{\frac{228}{29}}\right. \nonumber \\&\qquad \left. -5880114\;r_{+}^{\frac{222}{29}}+33781860\;r_{+}^{\frac{168}{29} }+343570752\;r_{+}^{\frac{114}{29}}\right. \nonumber \\&\qquad \left. -123023853\;r_{+}^{\frac{54}{29} }-133929936\right\} , \end{aligned}$$
(41)

where the \(\Gamma _{1}\) term,

$$\begin{aligned} \Gamma _{1}=9\;r_{+}^{\frac{168}{29}}+28\;r_{+}^{\frac{114}{29}}-47, \end{aligned}$$
(42)

in the denominator, ensures that all the divergencies of the heat capacity coincide with some of the divergencies of the Ricci scalar, whereas the \(\Gamma _{2}\) term,

$$\begin{aligned} \Gamma _{2}=171\;r_{+}^{\frac{168}{29}}-532\;r_{+}^{\frac{114}{29}}-333, \end{aligned}$$
(43)

provides extra divergencies, which are not matched with any phase transition point. It is worthwhile to mention that the root of the numerator does not cancel extra divergencies of the Ricci scalar. Therefore, this simple example shows that the Quevedo metric is plugged with extra divergencies which are not consistent with phase transition points.

Therefore, the HPEM metric provides a successful mechanism for studying the places of the root and phase transition points of these black holes in the context of the canonical ensemble. It is worthwhile to mention that the behavior of the thermodynamical Ricci scalar is different around the root and divergence points of the heat capacity. In other words, in the case of a divergency of the Ricci scalar coinciding with the root of heat capacity, the behavior of the diagrams differs from the case in which the divergency of the Ricci scalar coincides with the divergencies of heat capacity. Therefore, considering the HPEM method, we find that the root and phase transitions are distinguishable from one another. In order to recognize the physical limitation point (\(r_{c}\)) from phase transition points, one can extract the following information from the figures. In the case of the root of the heat capacity (\(S=S_{0}\)), hence, a physical limitation point, there is a change in sign of the Ricci scalar from \(+\infty \) to \(-\infty \); whereas for the case of the divergence points of the heat capacity, hence, second order phase transitions, the sign of the Ricci scalar stays fixed. Therefore, this change/non-change in sign is a characteristic that enables one to distinguish the root of the heat capacity from phase transition points. We summarize the mentioned information in Table 1.

Table 1 Comparison of root with phase transition points
Full size table
Fig. 7
figure 7

For different scales: \(C_{Q}\) versus \(r_{+}\) for \(\Lambda =-1\), \( c=1 \), \(d=5\), \(q=1\), and \(\omega =0.01\) (continuous line), \(\omega =0.1\) (dotted line) and \(\omega =1\) (dashed line)

Full size image
Fig. 8
figure 8

For different scales: \(C_{Q}\) versus \(r_{+}\) for \(\Lambda =-1\), \( c=1 \), \(d=6\), \(q=1\), and \(\omega =0.01\) (continuous line), \(\omega =0.1\) (dotted line) and \(\omega =1\) (dashed line)

Full size image

Regarding \(C_{Q}\) versus entropy, numerical calculations and also the figures show that the heat capacity has a real positive root (\(S_{0}\)) for all values of parameters (q, \(\omega \), \(\Lambda \), c). For the case of divergence points of the heat capacity, there are two cases. In the first case and for special choices of parameters, the heat capacity does not diverge, while for the second case, one can set the free parameters in such a way that \(C_{Q}\) has two real positive divergence points (\(S_{1c}\) and \(S_{2c}\)).

In order to emphasize the effects of the Brans–Dicke gravity, we have plotted Figs. 7 and 8 for the variation of \(\omega \). It is evident that the variation of the Brans–Dicke parameter modifies the number of the divergencies and roots and their corresponding places. These modifications lead to changes in the stability conditions (regions of the stability) as well as phase transitions of the black holes. This shows that in the presence of modified gravity (Brans–Dicke gravity), the thermodynamical structure of the black holes will be modified and acquires a different structure compared to the absence of Brans–Dicke gravity.

According to the pioneering work of Davies [57], regarding phase transitions in black holes, the divergencies of the heat capacity are second order phase transitions. In his work, he showed that these divergencies of the heat capacity have the characteristics of the second order phase transition. In addition, the studies that are conducted in extended phase space proved that the divergencies of the heat capacity and the second order phase transition in phase diagrams coincide with each other [78–82]. In other words, second order phase transition points that are observed in Gibbs free energy versus temperature, pressure versus horizon radius, and temperature versus horizon radius are matched with divergencies of the heat capacity. Therefore, the divergencies of the heat capacity are second order phase transitions. For more clarification, we will study the corresponding free energy versus horizon radius as well.

The free energy for these black holes is given by

$$\begin{aligned} F=M-TS, \end{aligned}$$

in which by using Eqs. (25), (26), and (29), one can find the free energy as

$$\begin{aligned} F= & {} \frac{\zeta \left[ n\left( n-2\right) +4\omega \left( n-1\right) \right] }{4\pi j_{3}}\nonumber \\&\times \left\{ \frac{q^{2}\left[ n\left( \omega +\frac{9}{8}\right) - \frac{3}{2}\omega -\frac{9}{8}\right] }{\left[ \omega \left( n-1\right) +n \right] c^{j_{1}}r^{j_{3}}}+\frac{\left( n-2\right) c^{j_{1}}r^{j_{3}}}{4} \right. \nonumber \\&\nonumber \\&\left. -\frac{\Lambda \left( n-4\omega -9\right) \left[ n\left( \omega + \frac{5}{4}\right) -2\omega -\frac{9}{4}\right] c^{(n+1)j_{1}}r^{\zeta \left( n-1\right) \left[ 3\left( 3n+1\right) +4n\omega \right] }}{2\left[ \omega \left( n-1\right) +n\right] \left[ n\left( 3+4\omega \right) +9\right] }\right\} .\nonumber \\ \end{aligned}$$
(44)

Now, by employing this relation and specific choices of the different parameters in the plotted diagrams, we plot Figs. 9, 10, and 11.

Fig. 9
figure 9

For different scales: F (continuous line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \(c=1\), and \(d=5\). (Left diagram \(\omega =1\) and \(q=0.1\) and right diagram \(q=1\) and \(\omega =0.1\))

Full size image
Fig. 10
figure 10

For different scales: F (continuous line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \(c=1\), \(d=6\), and \(\omega =1\). (Left diagram \(q=0.1\), middle diagram \(q=1\), and right diagram \(q=2\))

Full size image
Fig. 11
figure 11

For different scales: F (continuous line) and T (dashed line) versus \(r_{+}\) for \(\Lambda =-1\), \(c=1\), \(d=6\), and \(q=1\). (Left diagram \(\omega =0.1\) and right diagram \(\omega =3\))

Full size image

Thermodynamically speaking, in free energy diagrams, the second order phase transition takes place when the free energy acquires an extremum. Here, we see for these specific choices of the different parameters, that the free energy has two extrema. These extrema are located exactly where the temperature has extrema as well. The existence of extrema in the temperature is observed as divergencies in the heat capacity. Therefore, the extrema of free energy, where a second order phase transition takes place, coincide with the divergencies of the heat capacity. This leads to the conclusion that the divergencies that are observed in the heat capacity are where black holes undergo a second order phase transition.

Furthermore, we calculate the critical horizon radius and temperature by \(\left( \frac{\partial T}{\partial r_{+}}\right) \) and present the results in Table 2. In order to compare the results of heat capacity with those of \(T-r_{+}\) diagram and HPEM approach for calculating the critical horizon radius, we combine all results in Table 2. It is evident from the values obtained for the critical horizon radius and their corresponding critical temperatures that they coincide with the extrema in the free energy and divergencies of the heat capacity as well. This shows that phase transition points which are second order ones are consistent for free energy, temperature, and the heat capacity. Therefore, the divergencies of the heat capacity in fact are at places in which second order phase transitions take place.

Table 2 Critical horizon radius and temperature for \(\Lambda =-1\) and \(c=1\)
Full size table

4 Closing remarks

In this paper, we have studied the thermal stability and phase transitions of charged BD black holes in the context of the canonical ensemble by calculating the heat capacity. We showed that there is a lower bound for the horizon radius of physical charged BD black holes. This restriction originated from the sign of the temperature of these black holes. We found that the regions of the physical and non-physical black holes were functions of the electric charge and BD coupling constant.

Regarding the phase transition of the black holes, we found that black holes in the context of BD enjoy the existence of second order phase transitions. In other words, the heat capacity of these black holes diverged in two points and it had a real valued positive root. It was pointed out that the existence of the divergence points and their places were functions of q and \(\omega \). It is worthwhile to mention that the effect of variation of the electric charge on a larger divergence point was relatively small. This small effect indicates that the existence of the larger divergence point is due to the contribution of the BD gravity. It was also seen that the dimensions changed the existence of the divergence points of the heat capacity and also the places of the root and divergencies of it. It is notable that these black holes have three characteristic points, which are related to a positive temperature and the thermal (in)stability of these black holes.

In the context of thermal stability, it was pointed out that there are four regions with different conditions. These regions are specified by the root and two divergencies of the heat capacity. In the case of the root of the heat capacity, there was a limitation point between non-physical black holes and physical ones. Between two divergencies, it was an unstable state and after the larger divergency it acquired a stable state. In other words, in a smaller divergency black hole may undergo a phase transition from an unstable state with larger horizon radius to a smaller stable black hole, whereas in the case of a larger divergency, the system would undergo another phase transition and was stabilized with a larger horizon radius.

Finally, we used the geometrical thermodynamics for studying the phase transitions of the system. It was shown that the divergencies of the curvature scalar of the HPEM metric exactly coincide with both physical limitation point and phase transitions of the heat capacity. In other words, the divergencies of the heat capacity and its root are matched with the divergencies of the Ricci scalar. It was also shown that, unlike RN-AdS black holes [76] (in the absence of dilaton field), employing the Weinhold, Ruppeiner, and Quevedo metrics failed to provide effective results for BD black hole solutions. It is notable that the behavior of the Ricci scalar around its divergence points for root and phase transitions was different. It means that there were characteristic behaviors that enable one to recognize the divergence point of the Ricci scalar related to the root of the heat capacity from the divergence points of \(\mathcal {R}\) related to the divergencies of \(C_{Q}\). Therefore, one is able to point out that a physical limitation point and phase transitions occurred in the divergencies of the thermodynamical Ricci scalar of the HPEM metric with different distinctive behaviors.

In addition, the free energy of these black holes has been investigated. It was shown that the free energy enjoys extrema in its diagrams versus horizon radius. These extrema were located exactly where the temperature acquires extrema and the heat capacity diverges. It was pointed out that the divergencies that are observed in the heat capacity are places where black holes undergo a second order phase transition.