Introduction

Brans–Dicke (BD) theory of gravity [1] is the simplest modification of general relativity in which gravity is described by a metric \(g_{\mu \nu }\) and a scalar \(\Psi\) whose inverse plays the role of Newtonian constant of gravity. In addition, there is a parameter denoted by \(\omega\), which represents the strength of scalar–tensor coupling. The BD theory passed a large value of experimental and theoretical tests successfully and can be used to explain some physical phenomena such as inflation [2], the cosmological constant problem [3] and dark energy [4]. The first black hole solutions of BD theory have been obtained by Brans in 1962 [5]. These solutions were four-dimensional and presented in four classes. Because of the coupling between scalar field and curvature, higher-dimensional BD field equations are too difficult to be solved directly. Fortunately, as it is shown by many authors, there is a conformal transformation which transforms the BD Lagrangian to that of Einstein-dilaton theory. The Conformal transformation is an interesting characteristic of the scalar–tensor theories such as BD theory [6]. Using conformal transformation enables us to solve BD field equations in a simpler. For instance, we obtained charged rotating black branes in Brans–Dicke–Born–Infeld (BDBI) theory by applying a conformal transformation [7].

The appearance of an infinite self-energy for a point-like charge at the charge position is one of the main problems of the classical Maxwell theory. Although this divergence can be removed in quantum electrodynamics, it still is a problem in the classical electrodynamics. Born and Infeld introduced a new Lagrangian to overcome this problem [8]. In addition to the Born–Infeld nonlinear electrodynamics, other types of nonlinear electrodynamic fields such as the logarithmic, the exponential, and the power law Maxwell field have received more attention [9,10,11,12]. These theories are richer than linear electrodynamics and can reduce to linear Maxwell theory. In addition, several authors have studied cosmological models, including nonlinear electrodynamic fields [13,14,15,16,17,18]. Some authors have found charged black hole and black brane solutions coupled to nonlinear electrodynamics [19,20,21,22,23,24,25,26]. The thermal stability of the black hole solutions in the presence of the linear and nonlinear electrodynamics have been analyzed in [27,28,29,30,31]. So far, exact charged spherical solutions of BD theory coupled to Born–Infeld field have not been obtained. In the present paper firstly, we introduce the action of BD theory with the nonlinear Born–Infeld field and find the field equations. Then, we construct charged black hole solutions in higher-dimensional BD theory with the nonlinear Born–Infeld field and investigate their properties.

The outline of this paper is as follows: The basic field equations and conformal transformations between the Einstein-dilaton theory and the BD theory are presented in Sect. 2. Spherically symmetric higher-dimensional exact solutions to the BDBI theory are obtained in Sect. 3. The physical properties of the obtained solutions are investigated in Sect. 4. Thermodynamics of the BD black hole solution is studied in Sect. 5 and validity of the first law of black hole thermodynamics is investigated. A thermal stability analysis or phase transition is performed in Sect. 6. Conclusions are presented in the last section.

Basic equations and conformal transformation

The action of the \((n+1)\)-dimensional BD gravitational theory in the presence of nonlinear electrodynamics can be written as

$$\begin{aligned} I_{{\rm BD}}=-\frac{1}{16\pi }\int d^{n+1}x\sqrt{-g}\left( \Psi R-U(\Psi )-\frac{ \omega }{\Psi }g^{\mu \nu }\nabla _{\mu }\Psi \nabla _{\nu }\Psi +L(F)\right), \end{aligned}$$
(1)

where R is the Ricci scalar, \(\Psi\) denotes the BD scalar field, and \(U(\Psi )\) is a potential for the scalar field \(\Psi\). The parameter \(\omega\) is the scalar–tensor coupling constant. L(F) is the Born–Infeld nonlinear electrodynamics and is given by

$$\begin{aligned} L(F)=2\gamma \left( 1-\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{\gamma }} \right). \end{aligned}$$
(2)

Here, \(F_{\mu \nu }\) denotes the electromagnetic tensor and \(\gamma\) is the parameter of nonlinearity. It is well known that for large values of \(\gamma \rightarrow \infty\), L(F) reduces to Maxwell’s theory of electrodynamics and in the limit \(\gamma \rightarrow 0\), \(L(F)\rightarrow 0\). By varying the action (1) with respect to the gravitational, scalar and the gauge fields, we get the following coupled field equations as

$$\begin{aligned}R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R &=\frac{\omega }{\Psi ^{2}}\left( \nabla _{\mu }\Psi \nabla _{\nu }\Psi \right. \nonumber \\&\left. \quad -\,\frac{1}{2}g_{\mu \nu }(\nabla \Psi )^{2}\right) -\frac{U(\Psi )}{2\Psi }g_{\mu \nu }+\frac{1}{\Psi }\left( \nabla _{\mu }\nabla _{\nu }\Psi -g_{\mu \nu }\nabla ^{2}\Psi \right) \nonumber \\&\quad +\frac{2}{\Psi }\left[ \frac{1}{4}g_{\mu \nu }\left( 1-\sqrt{1+\frac{ F_{\mu \nu }F^{\mu \nu }}{\gamma }}\right) +\frac{F_{\mu \lambda }F_{\nu }^{\lambda }}{\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{\gamma }}}\right], \end{aligned}$$
(3)
$$\begin{aligned}\nabla ^{2}\Psi &=\frac{2}{\left[ \left( n-1\right) \omega +n\right] }\frac{ F_{\mu \nu }F^{\mu \nu }}{\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{\gamma }}}+ \frac{\left( n+1\right) }{\left[ \left( n-1\right) \omega +n\right] }\left( 1-\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{\gamma }}\right) \nonumber \\&\quad +\,\frac{1}{2\left[ \left( n-1\right) \omega +n)\right] }\left[ (n-1)\Phi \frac{dU(\Psi )}{d\Psi }-\left( n+1\right) U(\Psi )\right], \end{aligned}$$
(4)
$$\begin{aligned}&\nabla _{\mu }\left[ \frac{F^{\mu \nu }}{\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{\gamma }}}\right] =0, \end{aligned}$$
(5)

The appearance of the second order derivatives in the Eq. (3) makes the field equations too difficult to be solved, directly. Therefore, we propose the following conformal transformations

$$\begin{aligned} g_{\mu \nu }&= {} \Omega ^{2}{\tilde{g}}_{\mu \nu }, \nonumber \\ {\tilde{\Psi}}&= {} \frac{\sqrt{n(\omega +1)-\omega }}{2}\ln \Psi, \nonumber \\ \gamma&= {} {\tilde{\gamma}}\exp \left(\frac{8\alpha {\tilde{\Psi}}}{n-3}\right), \end{aligned}$$
(6)

with \(\Omega =\Psi ^{-\frac{1}{n-1}}\) in the BD action (1). By using these conformal transformations, the action (1) transforms to the following action

$$\begin{aligned} {\tilde{I}}_{{\rm ED}}=-\frac{1}{16\pi }\int d^{n+1}x\sqrt{-{\tilde{g}}}\left({\tilde{R}}-{\tilde{U}}({\tilde{\Psi}})-\frac{4}{n-1}{\tilde{g}}^{\mu \nu }{\widetilde{\nabla}} _{\mu }{\tilde{\Psi}}{\widetilde{\nabla}}_{\nu }{\tilde{\Psi}}+{\tilde{L}}({\tilde{F}}, {\tilde{\Psi}})\right), \end{aligned}$$
(7)

which is the action of Einstein-dilaton gravity with the Born–Infeld electrodynamic field [32], provided that the following relation are fulfilled

$$\begin{aligned} \omega =\frac{1}{n-1}\left( \frac{(n-3)^{2}}{4\alpha ^{2}}-n\right), \end{aligned}$$
(8)

In action (7) \({\tilde{R}}\) is the Ricci scalar and \({\widetilde{\nabla}}\) is the covariant differentiation with respect to the metric \({\tilde{g}}_{\mu \nu }\). The parameter \(\alpha\) is the coupling constant between the scalar and electromagnetic field. The transformed nonlinear field \({\tilde{L}}({\tilde{ F}},{\tilde{\Psi}})\) and \({\tilde{U}}({\tilde{\Psi}})\) are given by

$$\begin{aligned} {\tilde{L}}({\tilde{F}},{\tilde{\Psi}})&= {} 2{\tilde{\gamma}}e^{4\alpha {\tilde{\Psi}} /(n-1)}\left( 1-\sqrt{1+\frac{e^{-8\alpha {\tilde{\Psi}}/(n-1)}{\tilde{F}}_{\mu \nu }{\tilde{F}}^{\mu \nu }}{{\tilde{\gamma}}}}\right), \end{aligned}$$
(9)
$$\begin{aligned} {\tilde{U}}({\tilde{\Psi}})&= {} U(\Psi )\Psi ^{-\left( \frac{n+1}{n-1}\right) }. \end{aligned}$$
(10)

By varying the action (7) with respect to \({\tilde{g}}_{\mu \nu }\), \({\tilde{\Psi}}\), and \({\tilde{A}}_{\mu }\), we get the following coupled field equations as

$$\begin{aligned}{\tilde{R}}_{\mu \nu } &=\frac{4}{n-1}\left( {\widetilde{\nabla}}_{\mu }{\tilde{\Psi}} {\widetilde{\nabla}}_{\nu }{\tilde{\Psi}}+\frac{1}{4}{\tilde{U}}{\tilde{g}}_{\mu \nu }\right) \nonumber \\&\quad +\,2e^{-4\alpha {\tilde{\Psi}}/(n-1)}\left( 1+\frac{e^{-8\alpha {\tilde{ \Psi}}/(n-1)}{\tilde{F}}_{\mu \nu }{\tilde{F}}^{\mu \nu }}{{\tilde{\gamma}}}\right) ^{-1/2}{\tilde{F}}_{\mu \eta }{\tilde{F}}_{\nu }^{\eta } \nonumber \\&\quad +\,\frac{2\gamma }{n-1}e^{4\alpha {\tilde{\Psi}}/(n-1)}\left[ \left( 1+\frac{ e^{-8\alpha {\tilde{\Psi}}/(n-1)}{\tilde{F}}_{\mu \nu }{\tilde{F}}^{\mu \nu }}{ {\tilde{\gamma}}}\right) ^{-1/2}-1\right] {\tilde{g}}_{\mu \nu }, \end{aligned}$$
(11)
$$\begin{aligned}&{\widetilde{\nabla}}^{2}{\tilde{\Psi}}=\frac{n-1}{8}\frac{\partial {\tilde{U}}}{ \partial {\tilde{\Psi}}}+{\tilde{\gamma}}\alpha e^{4\alpha {\tilde{\Psi}}/(n-1)} \left[ \left( 1+\frac{e^{-8\alpha {\tilde{\Psi}}/(n-1)}{\tilde{F}}_{\mu \nu } {\tilde{F}}^{\mu \nu }}{{\tilde{\gamma}}}\right) ^{-1/2}-1\right], \end{aligned}$$
(12)
$$\begin{aligned}&{\widetilde{\nabla}}_{\mu }\left[ \frac{e^{-4\alpha {\tilde{\Psi}}/(n-1)}{\tilde{F}} ^{\mu \nu }}{\sqrt{1+\frac{e^{-8\alpha {\tilde{\Psi }}/(n-1)}{\tilde{F}}_{\mu \nu }{\tilde{F}}^{\mu \nu }}{{\tilde{\gamma}}}}}\right] =0. \end{aligned}$$
(13)

Here, we are interested on the charged spherically symmetric solutions of Eqs. (3)–(5). Since the field Eq. (11) does not contain second order derivatives of scalar field \(\Psi\), the field Eqs. (11)–(13) can be solved in a simpler way. These solutions are obtained in [33]. In the next section first, we review these solutions then by using the conformal transformations (6) the solutions of Eqs. (3)–(5) are obtained.

Spherically symmetric solutions in (\(n+1)\)-dimensions

As we mentioned before, we cannot obtain the solutions of BDBI gravity directly. In order to find the spherically symmetric solutions of BDBI gravity in \((n+1)\)-dimensions, we use the conformal transformations introduced in Eq. (6). To do so, we should obtain the conformal solutions of BDBI, the so-called Einstein-dilaton–Born–Infeld solutions. Such solutions have been presented in Ref. [33] and we shall give a brief review, here. The general form of a \((n+1)\)-dimensional spherically symmetric metric can be written as

$$\begin{aligned} {\rm d}{\tilde{s}}^{2}=-W(r){\rm d}t^{2}+{\frac{{\rm d}r^{2}}{W(r)}}+r^{2}{\tilde{H}} ^{2}(r){\rm d}\Omega _{n-1}^{2}, \end{aligned}$$
(14)

where \({\rm d}\Omega _{n-1}^{2}\) is the metric of a unit \((n-1)\) sphere. In [33], a Liouville-type potential as the solution to the scalar field Eq. (12) has been introduced in the following form

$$\begin{aligned} {\tilde{U}}({\tilde{\Psi}})=2\Lambda e^{2\eta {\tilde{\Psi}}}+\frac{ (n-1)(n-2)\alpha ^{2}}{c^{2}(\alpha ^{2}-1)}e^{2\eta _{0}{\tilde{\Psi}}}, \end{aligned}$$
(15)

with

$$\begin{aligned} \eta _{0}=\frac{2}{(n-1)\alpha },\qquad \eta =\frac{2\alpha }{(n-1)}. \end{aligned}$$
(16)

Also, this type of potential was studied in Einstein–Maxwell-dilaton gravity, previously [34, 35] and Born–Infeld–Dilaton black holes [36]. The solutions for the field Eqs. (11) and (12) are [33]

$$\begin{aligned}W(r) &=-{\frac{\left( n-2\right) \left( {\alpha }^{2}+1\right) ^{2}}{\left( {\alpha }^{2}-1\right) \left( n+{\alpha }^{2}-2\right) }}\left( \frac{r}{c} \right) ^{2\beta }-\frac{m}{r^{(n-1)(1-\beta )-1}} \nonumber \\&\quad +\frac{2(\Lambda -{\tilde{\gamma}})\left( {\alpha }^{2}+1\right) ^{2}{c}^{2} }{(n-1)(\alpha ^{2}-n)}\left( \frac{c}{r}\right) ^{2\beta -2}-\frac{2{\tilde{ \gamma}}(\alpha ^{2}+1)^{2}c^{2}}{(n-1)(\alpha ^{2}-n)}\left( \frac{c}{r} \right) ^{2\beta -2} \nonumber \\&\quad \times {}_{2}F_{1}\left( -\frac{1}{2},\left[ {\frac{{\alpha }^{2}{ -1}}{{2(n-1)}}-}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)} }+}\frac{1}{2}\right] ;\frac{-2q^{2}}{{\tilde{\gamma}}c^{2(n-1)}}\left( \frac{r }{c}\right) ^{2(n-1)(\beta -1)}\right), \end{aligned}$$
(17)
$$\begin{aligned}&{\tilde{\Psi}}(r)=\frac{(n-1)\beta }{2\alpha }\ln \left( \frac{c}{r}\right), \end{aligned}$$
(18)
$$\begin{aligned}&{\tilde{H}}(r)=\left(\frac{c}{r}\right)^{\beta }, \end{aligned}$$
(19)
$$\begin{aligned}&{\tilde{F}}_{{\rm tr}}=\frac{qe^{\frac{4\alpha {\tilde{\Psi}}}{n-1}}}{\sqrt{\left( r {\tilde{H}}(r)\right) ^{2n-2}+{\frac{2q^{2}}{{\tilde{\gamma}}}}}}, \end{aligned}$$
(20)

where q and m are two integration constants and \(\beta =\alpha ^{2}/(\alpha ^{2}+1)\). It is notable to mention that these solutions are ill-defined for \(\alpha =1,\sqrt{n}\). Using the mentioned conformal transformation (6) and Eq. (8), the (\(n+1\))-dimensional charged spherical solutions of BDBI gravity for \((n\ge 4)\) can be obtained as

$$\begin{aligned} {\rm d}s^{2}=\Omega ^{2}{\rm d}{\tilde{s}}^{2}=-A(r){\rm d}t^{2}+{\frac{{\rm d}r^{2}}{B(r)}} +r^{2}H^{2}(r){\rm d}\Omega _{n-1}^{2}, \end{aligned}$$
(21)

where A(r), B(r), \(\Psi (r)\), and H(r) are

$$\begin{aligned}A(r) &=\left( \frac{c}{r}\right) ^{-\Upsilon }W(r) \nonumber \\&=-{\frac{\left( n-2\right) \left( {\alpha }^{2}+1\right) ^{2}}{\left( { \alpha }^{2}-1\right) \left( n+{\alpha }^{2}-2\right) }}\left( \frac{r}{c} \right) ^{2\beta +\Upsilon }-\frac{m{c}^{-\Upsilon }}{r^{-\Upsilon +(n-1)(1-\beta )-1}} \nonumber \\&\quad +\,\frac{2\Lambda c^{2}\left( {\alpha }^{2}+1\right) ^{2}}{(n-1)(\alpha ^{2}-n)}\left( \frac{r}{c}\right) ^{2(1-\beta )+\Upsilon }+\frac{2\gamma (\alpha ^{2}+1)^{2}}{(n-1)(\alpha ^{2}-n)}\left( \frac{r}{c}\right) ^{2(1-\beta )+n\Upsilon } \nonumber \\&\quad \times\,\left( 1-_{2}F_{1}\left( -\frac{1}{2},\left[ \frac{\alpha ^{2}-n}{ 2n-2}\right],\left[ \frac{\alpha ^{2}+n-2}{2n-2}\right] ;-\zeta \right) \right), \end{aligned}$$
(22)
$$\begin{aligned}B(r) &=\left( \frac{c}{r}\right) ^{\Upsilon }W(r) \nonumber \\& =-{\frac{\left( n-2\right) \left( {\alpha }^{2}+1\right) ^{2}}{\left( { \alpha }^{2}-1\right) \left( n+{\alpha }^{2}-2\right) }\left( \frac{r}{c} \right) ^{2\beta -\Upsilon }-}\frac{m{c}^{\Upsilon }}{r^{\Upsilon +(n-1)(1-\beta )-1}} \nonumber \\&\quad +\,\frac{2\Lambda c^{2}(\alpha ^{2}+1)^{2}}{(n-1)(\alpha ^{2}-n)}\left( \frac{r}{c}\right) ^{2(1-\beta )-\Upsilon }+\frac{2\gamma (\alpha ^{2}+1)^{2} }{(n-1)(\alpha ^{2}-n)}\left( \frac{r}{c}\right) ^{2(1-\beta )+(n-2)\Upsilon } \nonumber \\&\quad \times\,\left( 1-{}_{2}F_{1}\left( -\frac{1}{2},\left[ \frac{ \alpha ^{2}-n}{2n-2}\right],\left[ \frac{\alpha ^{2}+n-2}{2n-2}\right] ;-\zeta \right) \right), \end{aligned}$$
(23)
$$\begin{aligned}&\Psi (r)=\left( \frac{c}{r}\right) ^{(n-1)\Upsilon /2}, \end{aligned}$$
(24)
$$\begin{aligned}&H(r)=\left( \frac{c}{r}\right) ^{\beta -\Upsilon /2}, \end{aligned}$$
(25)

where \(\Upsilon =4\beta /(n-3)\) and

$$\begin{aligned} \zeta =\frac{2q^{2}}{\gamma r^{2(n-1)}}\left( \frac{r}{c}\right) ^{\left( n-1\right) \left( 2\beta -\Upsilon \right) }. \end{aligned}$$
(26)

Under the conformal transformations (6), the electric field (20) and the scalar potential (15) become

$$\begin{aligned} F_{{\rm tr}}&= {} \frac{qc^{(3-n)\beta }}{r^{(n-3)(1-\beta )+2}\sqrt{1+{\frac{ 2q^{2}c^{2(3-n)\beta }}{\gamma r^{2((n-3)(1-\beta )+2)}}}}}, \end{aligned}$$
(27)
$$\begin{aligned} U(\Psi )&= {} 2\Lambda \Psi ^{2}+\frac{(n-1)(n-2)}{c^{2}}\left(\frac{\alpha ^{2}}{ \alpha ^{2}-1}\right)\Psi ^{\frac{(n+1)+(n-3)\alpha ^{2}}{n-1}}. \end{aligned}$$
(28)

It is worth to note that these solutions are valid only for the space times with dimensions equal or more than five (i.e., \(n\ge 4\)) and do not exist for \(\alpha =1,\sqrt{n}\). One may note that as \(\gamma\) goes to infinity, these solutions reduce to the solutions of Brans–Dicke–Maxwell gravity [37].

Physical properties of the solutions

In order to investigate the physical properties of the solutions, we first study the behavior of the electric field. The behavior of the electric field versus r for different values of the parameter \(\gamma\) has plotted in Fig. 1. From this figure, it is clear that the electric field goes to zero for large r irrespective of the other parameters q, c and \(\beta\) and has a finite value at \(r=0\) in contrast to Maxwell electrodynamics. We also notice that with increasing \(\gamma\), the electric field increases as \(r\rightarrow 0\). This result can be expected because for large \(\gamma\) our theory reduces to the Brans–Dicke–Maxwell theory [37].

Fig. 1
figure 1

E(r) versus r for \(n=4\), \(\alpha =0.4\), \(c=1\) and \(q=2\)

Full size image

Next, we look for the curvature singularities. After some calculation, we find that the Ricci scalar, R, and the Kretschmann scalar \(R_{\mu \nu \lambda \eta }R^{\mu \nu \lambda \eta }\), are finite for \(r\ne 0\) and diverge at \(r=0\)

$$\begin{aligned} \lim _{r\rightarrow 0^{+}}R=\infty,\quad \lim _{r\rightarrow 0^{+}}R_{\mu \nu \lambda \eta }R^{\mu \nu \lambda \eta }=\infty. \end{aligned}$$
(29)

These indicate that the spacetime has an essential singularity located at \(r=0\). In order to have a better understanding of the behavior of our solutions, we expand the metric function (22) for large\(\ r\). We find

$$\begin{aligned} \lim _{r\rightarrow \infty }A(r)&= {} -{\frac{\left( n-2\right) \left( {\alpha } ^{2}+1\right) ^{2}}{\left( {\alpha }^{2}-1\right) \left( n+{\alpha } ^{2}-2\right) }}\left( \frac{r}{c}\right) ^{2\beta +\Upsilon } \nonumber \\& \quad +\,\frac{2\Lambda c^{2}(\alpha ^{2}+1)^{2}}{(n-1)(\alpha ^{2}-n)}\left( \frac{r}{c}\right) ^{2(1-\beta )-\Upsilon }. \end{aligned}$$
(30)

It is notable that as \(\omega \rightarrow \infty\) \((\alpha =\beta =0)\) and \(\gamma \rightarrow \infty\), solutions (22) and (23) reduce to

$$\begin{aligned} A(r)=B(r)=1-\frac{m}{r^{n-2}}-\frac{2\Lambda r^{2}}{n(n-1)}+\frac{2q^{2}}{ (n-1)(n-2)r^{2(n-2)}}, \end{aligned}$$
(31)

which has the form of static and spherically symmetric Reissner–Nordstrom black hole in (A)dS spacetime. In the absence of scalar field as r goes to infinity, the metric function (31) takes the following form

$$\begin{aligned} \lim _{r\rightarrow \infty }A(r)=1-\frac{2\Lambda r^{2}}{n(n-1)}, \end{aligned}$$
(32)

which describes an asymptotically flat, dS or AdS spacetimes for \(\Lambda =0\), \(\Lambda >0\) and \(\Lambda <0\), respectively. Nevertheless, as one can notice from Eq. (30), in the presence of the scalar field, our solutions are neither asymptotically flat nor (A)dS. For example, taking \(\alpha =\sqrt{3}\), \(n=5\), and \(c=1\), we obtain

$$\begin{aligned} \lim _{r\rightarrow \infty }A(r)=-\frac{16}{5}r^{9/2}-\frac{32\Lambda }{15} r^{7/2}, \end{aligned}$$
(33)

which indicates that the metric function (22) is neither asymptotically flat nor dS or AdS. After calculation of the Ricci scalar in \((n+1)\) dimensions for large values of r, we obtain

$$\begin{aligned} R\propto \Lambda \left( \frac{c}{r}\right) ^{\beta \left( \frac{n+2}{n-2}\right) }, \end{aligned}$$
(34)

which does not have the same form of the Ricci scalar for asymptotically dS or AdS spacetime. The horizons of spacetime can be obtained by solving the relation \(B(r_{+})=0\),

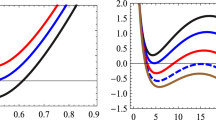
$$\begin{aligned}&-{\frac{\left( n-2\right) \left( {\alpha }^{2}+1\right) ^{2}}{\left( { \alpha }^{2}-1\right) \left( n+{\alpha }^{2}-2\right) }\left( \frac{r_{+}}{c} \right) ^{2\beta -\Upsilon }-}\frac{m{c}^{\Upsilon }}{r_{+}^{\Upsilon +(n-1)(1-\beta )-1}} \nonumber \\&\quad +\,\frac{2\Lambda c^{2}(\alpha ^{2}+1)^{2}}{(n-1)(\alpha ^{2}-n)}\left( \frac{r_{+}}{c}\right) ^{2(1-\beta )-\Upsilon }+\frac{2\gamma (\alpha ^{2}+1)^{2}}{(n-1)(\alpha ^{2}-n)}\left( \frac{r_{+}}{c}\right) ^{2(1-\beta )+(n-2)\Upsilon } \nonumber \\&\quad \times\,\left( 1-{}_{2}F_{1}\left( -\frac{1}{2},\left[ \frac{ \alpha ^{2}-n}{2n-2}\right],\left[ \frac{\alpha ^{2}+n-2}{2n-2}\right] ;-\zeta _{+}\right) \right) =0, \end{aligned}$$
(35)

unfortunately, Eq. (23) is more complicated to be solved for an arbitrary value of \(\alpha\). Thus, we have plotted the function of B(r) versus r in Figs. 2, 3 and 4. For simplicity, the other metric parameters \(\alpha\), \(\gamma\), c and q have kept fixed. As it is clear from Fig. 4, we notice that the number of horizons decreases with increasing the value of \(\alpha\). In fact, in the case of \(\alpha <\sqrt{n}\), one encounters with two horizons, extreme black holes and naked singularities depending on the values of the parameters such as \(\alpha\), \(\gamma\), m and q.

Fig. 2
figure 2

B(r) versus r for \(n=4\), \(\alpha =0.5\), \(c=1\), \(\Lambda =-\,6\) and \(q=1\)

Full size image
Fig. 3
figure 3

B(r) versus r for \(n=4\), \(\alpha =0.5\), \(c=1\), \(\Lambda =-\,6\) and \(m=1\)

Full size image
Fig. 4
figure 4

B(r) versus r for \(n=4\), \(q=1\), \(c=1\), \(\Lambda =-\,6\) and \(m=1\)

Full size image

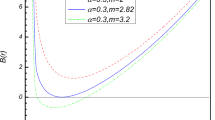
Some information can be obtained by calculating of the mass parameter m as a function of the horizon radius \(r_{h}\)

$$\begin{aligned} m(r_{h})&= {} -{\frac{\left( n-2\right) \left( {\alpha }^{2}+1\right) ^{2}{c} ^{-2\beta }}{\left( {\alpha }^{2}-1\right) \left( n+{\alpha }^{2}-2\right) }} {r}_{h}^{\beta (3-n)+n-2}+\frac{2\Lambda \left( {\alpha }^{2}+1\right) ^{2}{c }^{2\beta }}{(n-1)(\alpha ^{2}-n)}r_{h}^{n-\beta (n+1)} \nonumber \\&\quad +\,\frac{2\gamma (\alpha ^{2}+1)^{2}c^{-2\beta \left( \frac{n+1}{n-3}\right) }}{(n-1)(\alpha ^{2}-n)}r_{h}^{n-\beta (n+1)-4\beta \left( \frac{n-1}{n-3} \right) } \nonumber \\&\quad\times\,\left( 1-_{2}F_{1}\left( -\frac{1}{2},\left[ {\frac{{\alpha }^{2}{-1 }}{{2(n-1)}}-}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+ }\frac{1}{2}\right] ;-\zeta _{h}\right) \right), \end{aligned}$$
(36)

which comes from this fact that \(B(r_{h})=0\). We plot in Figs. 5 and 6 the mass parameter m versus \(r_{h}\) for a fixed value of other parameters. These figures show that the intersections of the curve \(m(r_{h})\) with the line \(m=\) constant determines the number of black hole horizons. For some certain value of the mass parameter m, there are two inner and outer horizons (\(r_{-}\) and \(r_{+}\)). There is also a minimum value \(m_{\mathrm {{\rm ext}}}\) in which the two horizons meet. It is the solution of \(B(r)=B^{^{\prime }}(r)=0\)

$$\begin{aligned} m_{\mathrm {{\rm ext}}}&= {} \frac{2(n-2)(\alpha ^{2}+1)^{2}c^{-2\beta }}{(n-\alpha ^{2})(n+\alpha ^{2}-2)}r_{\mathrm {{\rm ext}}}^{(n-2)(1-\beta )+\beta }+\frac{ 4q^{2}(\alpha ^{2}+1)^{2}c^{2(2-n)\beta }}{(n-\alpha ^{2})(n+\alpha ^{2}-2)} r_{\mathrm {{\rm ext}}}^{(n-3)(\beta -1)-1} \nonumber \\&\quad \times\, {}_{2}F_{1}\left( {\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{-1 }}{{2(n-1)}}+}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+ }\frac{3}{2}\right],-\zeta _{\mathrm {{\rm ext}}}\right). \end{aligned}$$
(37)

Depending on the value of m, there are three cases to consider separately. In the first case where \(m>m_{\mathrm{{\rm ext}}}\), the metric of (21) has two inner and outer horizons \((r_{-}\) and \(r_{+})\). In the case of \(m=m_{\mathrm {{\rm ext}}}\), we have an extreme black hole and a naked singularity provided \(m<m_{\mathrm {ext}}\).

Fig. 5
figure 5

The mass parameter m versus r for \(n=4\), \(\gamma =2\), \(c=1\), \(\Lambda =-\,6\) and \(q=1\)

Full size image
Fig. 6
figure 6

The mass parameter m versus r for \(n=4\), \(\alpha =0.4\), \(c=1\), \(\Lambda =-\,6\) and \(\gamma =1\)

Full size image

Thermodynamics of Brans–Dicke black holes

In this section, we want to calculate the conserved and thermodynamic quantities of the BD black hole solutions with Born–Infeld field we just found. At first, it must be noted that the Hawking temperature on the outer horizon \(r=r_{+}\), is defined in terms of the surface gravity,

$$\begin{aligned} T=\frac{\kappa }{2\pi }, \end{aligned}$$
(38)

where the surface gravity \(\kappa\) is given by

$$\begin{aligned} \kappa =\sqrt{-\frac{1}{2}\left( \nabla _{\mu }\chi _{\nu }\right) \left( \nabla ^{\mu }\chi ^{\nu }\right) }, \end{aligned}$$
(39)

here \(\chi =\partial _{t}\) is the null Killing vector of the horizon. In the Einstein-dilaton frame (14), we have \(\chi ^{\nu }=(1,0,0,\dots)\) and \(\chi _{\nu }=(-W(r),0,0,\dots)\). So, the Hawking temperature of the Einstein-dilaton–Born–Infeld gravity becomes

$$\begin{aligned} {\tilde{T}}=\frac{\kappa }{2\pi }=\frac{1}{2\pi }\sqrt{-\frac{1}{2}(\nabla _{\mu }\chi _{\nu })(\nabla ^{\mu }\chi ^{\nu })}=\frac{1}{4\pi }\frac{{\rm d}W(r) }{{\rm d}r}|_{r=r_{+}}. \end{aligned}$$
(40)

In the BD frame (21), by applying conformal transformation, the Hawking temperature is given by [38]

$$\begin{aligned} T=\frac{(\Omega ^{2}W(r_{+}))^{^{\prime }}}{4\pi \Omega ^{2}}, \end{aligned}$$
(41)

using the fact that \(W(r_{+})=0\), it is a matter of calculation to show that

$$\begin{aligned} T&= {} {\tilde{T}}=\frac{W^{\prime }(r_{+})}{4\pi } \nonumber \\&= {} -\frac{(n-2)(\alpha ^{2}+1)}{4\pi (\alpha ^{2}-1)c}(\frac{r_{+}}{c} )^{2\beta -1}-\frac{(\Lambda -\gamma )(\alpha ^{2}+1)c}{2\pi (n-1)}\left(\frac{c}{ r_{+}}\right)^{2\beta -1} \nonumber \\&\quad -\,\frac{(\alpha ^{2}+1)\gamma c}{2\pi (n-1)}(\frac{c}{r_{+}})^{2\beta -1}\times {}_{2}F_{1}\left( -{\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{ -1}}{{2(n-1)}}-}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)} }+}\frac{1}{2}\right] ;-\zeta _{+}\right) \nonumber \\&\quad-\,\frac{q^{2}(\alpha ^{2}+1)}{\pi (\alpha ^{2}+n-2)c^{2n-3}}(\frac{r_{+}}{c} )^{2(n-2)(\beta -1)-1} \nonumber \\&\quad\times\,{}_{2}F_{1}\left( {\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{-1 }}{{2(n-1)}}+}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+ }\frac{3}{2}\right] ;-\zeta _{+}\right). \end{aligned}$$
(42)

The mass of the black holes can be calculated through the use of Brown and York method [39, 40]. Thus, the mass of the solution per volume of the unit \((n-1)\) sphere \(\Omega _{n-1}\) can be obtained as [33, 41]

$$\begin{aligned} M=\frac{(n-1)c^{(n-1)\beta }m}{16\pi (1+\alpha ^{2})}. \end{aligned}$$
(43)

Black hole entropy follows the area law which states that the black hole entropy is one-quarter of the event horizon area. In BD theory, where we have a scalar field, the entropy is not one-quarter of the event horizon area and is defined by [42]

$$\begin{aligned} S=\frac{A\Psi }{4}=\frac{{\tilde{A}}}{4}, \end{aligned}$$
(44)

where A and \({\tilde{A}}\) are the horizon area in the BD and Einstein-dilaton theory respectively. Therefore, the entropy per unit volume of the hypersurface boundary can be obtained as

$$\begin{aligned} S=\frac{c^{(n-1)\beta }}{4}r_{+}^{(n-1)(1-\beta )}. \end{aligned}$$
(45)

The electric charge of the solutions, Q, can be calculated through the Gauss theorem, obtaining

$$\begin{aligned} Q=\frac{1}{4\pi }\int _{r\rightarrow \infty }d^{n-1}x\sqrt{-g}\frac{F_{\mu \nu }}{\sqrt{1+\frac{F_{\mu \nu }F^{\mu \nu }}{\gamma }}}=\frac{q}{4\pi } \Omega _{n-1}. \end{aligned}$$
(46)

The gauge potential \(A_{t}\) corresponding to the electric field (20) can be easily calculated through the relation \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\). Since we deal with static solution, we have \(\partial _{t}A_{r}=0\), and hence the gauge potential \(A_{t}\) can be derived as

$$\begin{aligned} A_{t}=-\int F_{{\rm tr}}{\rm d}r=\frac{qc^{(3-n)\beta }}{\Delta r_{+}^{\Delta }}\ \ _{2}F_{1}\left( {\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+} \frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+}\frac{3}{2} \right] ;-\zeta \right), \end{aligned}$$
(47)

where \(\Delta =\frac{n-3}{\alpha ^{2}+1}+1\). The black hole’s electric potential \(\Phi\) on the horizon, measured at the reference point, is defined by [43, 44]

$$\begin{aligned} \Phi =A_{\mu }\chi ^{\mu }\left| _{r\rightarrow \infty }-A_{\mu }\chi ^{\mu }\right| _{r=r_{+}}, \end{aligned}$$
(48)

where \(\chi =\partial _{t}\) is the null generators of the horizon. Therefore, the electric potential may be derived as

$$\begin{aligned} \Phi =\frac{qc^{(3-n)\beta }}{\Delta r_{+}^{\Delta }}\ \ _{2}F_{1}\left( { \frac{1}{2},}\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+}\frac{1}{2}\right], \left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+}\frac{3}{2}\right] ;-\zeta _{+}\right). \end{aligned}$$
(49)

Finally, we check the first law of thermodynamics for the black hole. For this purpose, we obtain the mass M as a function of extensive quantities S and Q. Combining equations for mass, the entropy and the charge given in (43), (45) and (46) and by using the fact that \(B(r_{+})=0\), we can obtain a Smarr-type formula as

$$\begin{aligned} M(S,Q)&= {} -\frac{(n-1)(n-2)(\alpha ^{2}+1)c^{-\beta (\alpha ^{2}+1)}}{16\pi (\alpha ^{2}-1)(\alpha ^{2}+n-2)}(4S)^{\frac{n+\alpha ^{2}-2}{n-1}} \nonumber \\&\quad +\,\frac{(\alpha ^{2}+1)\Lambda c^{\beta (\alpha ^{2}+1)}}{8\pi (\alpha ^{2}-n)}(4S)^{\frac{n-\alpha ^{2}}{n-1}}-\frac{(\alpha ^{2}+1)\gamma c^{\beta (\alpha ^{2}+1)}}{8\pi (\alpha ^{2}-n)}(4S)^{\frac{n-\alpha ^{2}}{ n-1}} \nonumber \\&\quad \times\, \left( 1-_{2}F_{1}\left( -{\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{ -1}}{{2(n-1)}}-}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)} }+}\frac{1}{2}\right] ;-\frac{2\pi ^{2}Q^{2}}{\gamma S^{2}}\right) \right), \end{aligned}$$
(50)

making use of Eq. (50), we can calculate the intensive parameters \(\Phi\) and T as the extensive parameters conjugate to the black hole charge and entropy, respectively. After some algebraic calculations, we obtain

$$\begin{aligned} \left( \frac{\partial M}{\partial S}\right) _{Q}&= {} -\frac{(n-2)(\alpha ^{2}+1)c^{-\beta (\alpha ^{2}+1)}}{16\pi (\alpha ^{2}-1)S}(4S)^{\frac{ n+\alpha ^{2}-2}{n-1}}-\frac{(\alpha ^{2}+1)\Lambda c^{\beta (\alpha ^{2}+1)} }{8\pi (n-1)S}(4S)^{\frac{n-\alpha ^{2}}{n-1}} \nonumber \\&\quad+\,\frac{(\alpha ^{2}+1)\gamma c^{\beta (\alpha ^{2}+1)}}{8\pi (n-1)S}(4S)^{ \frac{n-\alpha ^{2}}{n-1}} \nonumber \\&\quad \times\, \left( 1-_{2}F_{1}\left( -{\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{ -1}}{{2(n-1)}}-}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)} }+}\frac{1}{2}\right] ;-\frac{2\pi ^{2}Q^{2}}{\gamma S^{2}}\right) \right) \nonumber \\&\quad-\,\frac{(\alpha ^{2}+1)\pi Q^{2}c^{\beta (\alpha ^{2}+1)}}{4(\alpha ^{2}+n-2)S^{3}}(4S)^{\frac{n-\alpha ^{2}}{n-1}} \nonumber \\&\quad \times\,_{2}F_{1}\left( {\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{-1}}{{ 2(n-1)}}+}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+} \frac{3}{2}\right] ;-\frac{2\pi ^{2}Q^{2}}{\gamma S^{2}}\right), \end{aligned}$$
(51)
$$\begin{aligned} \left( \frac{\partial M}{\partial Q}\right) _{S}&= {} \frac{\pi Q(\alpha ^{2}+1)c^{\beta (\alpha ^{2}+1)}}{4(\alpha ^{2}+n-2)S^{2}}(4S)^{\frac{ n-\alpha ^{2}}{n-1}}\nonumber \\&\quad \times\,_{2}F_{1}\left( {\frac{1}{2},}\left[ {\frac{{ \alpha }^{2}{-1}}{{2(n-1)}}+}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{ -1}}{{2(n-1)}}+}\frac{3}{2}\right] ;-\frac{2\pi ^{2}Q^{2}}{\gamma S^{2}} \right). \end{aligned}$$
(52)

Note that in obtaining these equations the following relation has been used

$$\begin{aligned} \frac{\partial _{2}F_{1}\left( a,b;c;z\right) }{\partial z}=\frac{ab}{c} _{2}F_{1}\left( a+1,b+1;c+1;z\right), \end{aligned}$$
(53)

regarding Eqs. (45) and (46), it is easy to show

$$\begin{aligned} \left( \frac{\partial M}{\partial S}\right) _{Q}&= {} T, \end{aligned}$$
(54)
$$\begin{aligned} \left( \frac{\partial M}{\partial Q}\right) _{S}&= {} \Phi. \end{aligned}$$
(55)

Thus, these quantities satisfy the first law of black hole thermodynamics,

$$\begin{aligned} {\rm d}M(S,Q)=\left( \frac{\partial M}{\partial S}\right) _{Q}{\rm d}S+\left( \frac{ \partial M}{\partial Q}\right) _{S}{\rm d}Q. \end{aligned}$$
(56)

It is worthwhile to note that the thermodynamic quantities of our solutions coincide with the thermodynamic quantities of Einstein-dilaton theory in the presence of the Born–Infeld field. This coincidence shows that these thermodynamic quantities are invariant under the conformal transformations. Thus, the satisfaction of the first law for BD black holes in the presence of Born–Infeld field is expected. It is also notable that for large values of the Born–Infeld parameter (\(\gamma \rightarrow \infty\)), our conserved and thermodynamic quantities reduce to those of Brans–Dicke-Maxwell theory [37].

Stability analysis in the canonical ensemble

Here, we are interested in the investigation of the thermal stability or phase transition of the new BD black holes solutions, we just obtained. To do so, we need to calculate black hole heat capacity with the black hole charge as a constant. It is defined as

$$\begin{aligned} C_{Q}=T\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}^{-1}, \end{aligned}$$
(57)

it is well known that the black hole with positive heat capacity is thermodynamically stable. Unstable black hole undergoes phase transition to be stabilized. The points at which black hole heat capacity vanishes are known as the points of type one phase transition. The divergent point of heat capacity or the points at which the denominator of the black hole heat capacity vanishes are the points of type two phase transition [31, 45]. Regarding the mentioned points, we proceed to analyze the stability or Phase transition of the new BD black holes introduced in this work. For this purpose, we need to calculate the denominator of the black hole heat capacity. That is

$$\begin{aligned} \left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}&= {} -\frac{ (n-2)(\alpha ^{2}+1)c^{-\beta (\alpha ^{2}+1)}}{16\pi (n-1)S^{2}}(4S)^{\frac{ n+\alpha ^{2}-2}{n-1}}+\frac{(\alpha ^{4}-1)\Lambda c^{\beta (\alpha ^{2}+1)} }{8\pi (n-1)^{2}S^{2}}(4S)^{\frac{n-\alpha ^{2}}{n-1}} \nonumber \\&\quad -\,\frac{(\alpha ^{4}-1)\gamma c^{\beta (\alpha ^{2}+1)}}{8\pi (n-1)^{2}S^{2} }(4S)^{\frac{n-\alpha ^{2}}{n-1}} \nonumber \\&\quad \times\,\left( 1-_{2}F_{1}\left( -{\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{ -1}}{{2(n-1)}}-}\frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)} }+}\frac{1}{2}\right] ;-\frac{2\pi ^{2}Q^{2}}{\gamma S^{2}}\right) \right) \nonumber \\&\quad +\,\frac{(\alpha ^{2}+1)c^{\beta (\alpha ^{2}+1)}}{8\pi (n-1)(\alpha ^{2}+n-2)S^{3}}\left[ (\alpha ^{2}-n)+\frac{2\pi ^{2}Q^{2}(\alpha ^{2}+2n-3) }{S}\right] (4S)^{\frac{n-\alpha ^{2}}{n-1}} \nonumber \\&\quad_{2}F_{1}\left( {\frac{1}{2},}\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+} \frac{1}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+}\frac{3}{2} \right] ;-\frac{2\pi ^{2}Q^{2}}{\gamma S^{2}}\right) \nonumber \\&\quad-\,\frac{(\alpha ^{2}+1)\pi ^{3}Q^{4}c^{\beta (\alpha ^{2}+1)}}{2(\alpha ^{2}+3n-4)S^{6}}(4S)^{\frac{n-\alpha ^{2}}{n-1}} \nonumber \\&\quad\times\,_{2}F_{1}\left( {\frac{3}{2},}\left[ {\frac{{\alpha }^{2}{-1}}{{ 2(n-1)}}+}\frac{3}{2}\right],\left[ {\frac{{\alpha }^{2}{-1}}{{2(n-1)}}+} \frac{5}{2}\right] ;-\frac{2\pi ^{2}Q^{2}}{\gamma S^{2}}\right). \end{aligned}$$
(58)

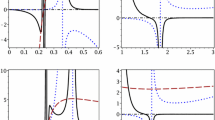
The real roots of \(\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}=0\), which we label by \(r_{0}\) are the points of type two phase transition. Because of the complexity of the statement given in (58), it can not be solved, analytically. Therefore, we have plotted it in Figs. 7, 8 and (9). The nominator of the black hole heat capacity is the black hole temperature which has been shown in (42). Thus, the real root(s) of the equation, \(T=0\) is the vanishing point(s) of black hole heat capacity at which type one phase transition takes place. The plots of T versus \(r_{+}\) are shown in Figs. 7, 8 and 9, too. Thermodynamically speaking, the black hole having positive temperature are physically reasonable, and those with negative temperature are known as the physical black holes. Therefore, the physical black holes with \(\left( \frac{ \partial ^{2}M}{\partial S^{2}}\right) _{Q}>0\) are locally stable.

Fig. 7
figure 7

T (continuous line) and \(0.6\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}\) (dashed line) versus \(r_{+}\) for \(n=4\), \(c=1\), \(\Lambda =-\,6\), \(\gamma =10\), \(\alpha =0.27\) and \(q=2\)

Full size image
Fig. 8
figure 8

T (continuous line) and \(0.6\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}\) (dashed line) versus \(r_{+}\) for \(n=4\), \(c=1\), \(\Lambda =-\,6\), \(\gamma =10\), \(\alpha =0.27\) and \(q=0.6\)

Full size image
Fig. 9
figure 9

T (continuous line) and \(0.6\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}\) (dashed line) versus \(r_{+}\) for \(n=4\), \(c=1\), \(\Lambda =-\,6\), \(\gamma =10\), \(\alpha =0.27\) and \(q=0.4\)

Full size image

As it is shown in Figs. 7, 8 and 9, three following cases are distinguishable:

  1. 1.

    \(T=0\) has two real roots labeled by \(r_{1{\rm ext}}\) and \(r_{2{\rm ext}}\) and \(\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}=0\) has only one real root denoted by \(r_{0}\). In this case, the black holes are stable if \(r_{+}>r_{2{\rm ext}}>r_{1{\rm ext}}\). Type two phase transition takes place at point \(r=r_{+}\), where the black hole heat capacity diverges. The black holes undergo type one phase transition at the point \(r_{+}=r_{1{\rm ext}}\) and \(r_{+}=r_{2{\rm ext}}\) (Fig. 7).

  2. 2.

    \(T=0\) has only one real root located at \(r=r_{{\rm ext}}\) and \(\left( \frac{ \partial ^{2}M}{\partial S^{2}}\right) _{Q}\) vanishes at \(r_{0}\). In this case, type one phase transition occurs at \(r_{+}=r_{{\rm ext}}\) and black holes with \(r_{+}=r_{0}\) undergo type two phase transition to be stabilized. Also, black holes with \(r_{+}>r_{0}\) are locally stable (Fig. 8).

  3. 3.

    \(T=0\) does not has any real roots and \(\left( \frac{\partial ^{2}M}{ \partial S^{2}}\right) _{Q}\) has a real root located at \(r_{+}=r_{0}\). In this case, no type one phase transition occurs. The black holes with \(r_{+}=r_{0}\) undergo type two phase transition. Also the black holes with \(r_{+}>r_{0}\) have positive heat capacity and are thermodynamically stable (Fig. 9).

Conclusions

In this paper, we presented the \((n+1)\)-dimensional BDBI action and obtained the coupled field equations by varying this action with respect to the gravitational field \(g_{\mu \nu }\), the dilaton field \(\Psi\), and the gauge field \(A_{\mu }\). Because of the coupling between the scalar field \(\Psi\) and curvature R, solving the field equations is complicated. For this purpose, new conformal transformations are presented to transform the Einstein-dilaton–Born–Infeld gravity Lagrangian to the BDBI gravity Lagrangian. Then, by using these conformal transformations, we constructed a new class of charged black hole solutions in \((n+1)\)-dimensional BDBI theory in the presence of the generalized Liouville-type potential. These solutions are neither asymptotically flat \((\Lambda =0)\) nor (A)dS. In addition, our solutions can describe black holes with two horizons, an extreme black hole or naked singularity depending on the value of the solution parameters in theory. In the limiting case \(\gamma \rightarrow \infty\), our solutions are reduced to Brans–Dicke-Maxwell black hole solutions, which are presented in [37]. We also obtained charge and thermodynamic quantities and found that these quantities satisfy the first law of black hole thermodynamics. We also found out that the conserved and thermodynamic quantities are invariant under conformal transformations. Finally, we performed a thermal stability analysis making use of the black hole heat capacity with the black hole charge as a constant. We showed that black holes with \(r_{+}=r_{0}\) undergo type two phase transition and those these with \(r_{+}=r_{1{\rm ext}}\) or \(r_{+}=r_{2{\rm ext}}\) undergo type one phase transition. Also, the black holes with \(r_{+}>r_{2{\rm ext}}>r_{1{\rm ext}}\) are locally stable (Fig. 7). We showed that, for properly fixed parameters, \(T=0\) has only one real root located at \(r_{{\rm ext}}\). In this case, \(r_{{\rm ext}}\) is a point of type one phase transition, \(r_{0}\) is a type two phase transition point, and black holes with \(r_{+}>r_{0}>r_{{\rm ext}}\) are locally stable (Fig. 7). It is possible to fix the parameters such that the black hole temperature be positive everywhere. In such a case there is no type one phase transition. The black holes with \(r_{+}=r_{0}\) undergo type two phase transition and the black hole with \(r_{+}>r_{0}\) are thermodynamically stable (Fig. 8). As for future work, it would be interesting to study the rotating black hole solutions. In addition, one may consider other types of nonlinear electrodynamic fields such as the logarithmic or exponential field [46, 47].