Abstract
Motivated by a thermodynamic analogy of black holes and Van der Waals liquid/gas systems, in this paper, we study P–V criticality of both dilatonic Born–Infeld black holes and their conformal solutions, Brans–Dicke–Born–Infeld solutions. Due to the conformal constraint, we have to neglect the old Lagrangian of dilatonic Born–Infeld theory and its black hole solutions, and introduce a new one. We obtain spherically symmetric nonlinearly charged black hole solutions in both Einstein and Jordan frames and then we calculate the related conserved and thermodynamic quantities. After that, we extend the phase space by considering the proportionality of the cosmological constant and thermodynamical pressure. We obtain critical values of the thermodynamic coordinates through numerical methods and plot the relevant P–V and G–T diagrams. Investigation of the mentioned diagrams helps us to study the thermodynamical phase transition. We also analyze the effects of varying different parameters on the phase transition of black holes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In 1872 James Clerk Maxwell combined the electricity and magnetism laws in a unified theory. In Maxwell’s formulation of electromagnetism, the electric field of a point-like charge is singular at its position, which leads to an infinite self-energy. In 1934 Max Born and Leopold Infeld [1, 2] introduced a new theory with an upper bound of the electric field in order to obtain a finite value for the self-energy of point-like charges in classical electrodynamics.
In theoretical physics, the Born–Infeld (BI) model is known as an example of interesting and valuable nonlinear version of electrodynamics [1, 2]. The BI action has obtained vast attention for many reasons. For example, in the context of superstring theory, the low-energy dynamics of D-branes is handled by the BI action [3]. In addition, loop correction analysis of quantum field theory leads to a BI type action [4–6]. BI electrodynamics also exhibits some physical properties regarding wave propagation like the absence of shock waves [7, 8]. This theory is very close to Einstein’s idea of introducing a nonsymmetrical metric with an antisymmetric part as the electromagnetic field and a symmetric part as the usual metric. It can also be regarded as a covariant generalization of Mie’s theory [9]. Einstein–BI theory has led to some interesting observable predictions in the context of solar interior dynamics, big bang nucleosynthesis, neutron stars [10, 11], the nonsingular cosmological models, and alternatives to inflation [12]. The supersymmetric version of the BI Lagrangian is constructed in Refs. [13, 14], while in Refs. [15–17] it was identified as an invariant action of the Goldstone multiplet in \(N=2\) supersymmetric theory which is spontaneously broken to \(N=1\). The results of Ref. [16] have been generalized to the case of n vector multiplets in \(N=2\) supersymmetry [18, 19] with explicit solution for \(n=2\) and \(n=3\). Moreover, the scalar perturbation at the pre-inflationary stage driven by a massive scalar field in Eddington-inspired BI gravity was investigated in Ref. [20].
One of the main reasons for considering scalar-tensor theory is that it may give a clue to interpret the acceleration expansion of the universe [21]. In addition, inflation may be explained based on the scalar-tensor theory of gravitation. Such an inflationary model is known as the hyper-extended inflation [22]. From the cosmological point of view, inflation can be naturally accommodated in the (low-energy limit of) string theory, since it contains a fundamental scalar field which acts as inflation. In addition, at high-energy regimes it seems that gravity cannot be described by the Einstein theory, but it may be modified by the superstring terms. Such modified superstring terms contain a dilaton field.
On the other hand, the theory of Brans–Dicke (BD) is one of the modified theories of general relativity that gets convenient data of several cosmological problems like inflation, early and late behavior of the universe, the coincidence problem, and cosmic acceleration [23, 24]. It was shown that BD theory can be used for dark energy modeling [23, 25]. This theory has been probed to be a possible explanation for the accelerated expansion of our universe [26–28].
The BD theory is a modified form of general relativity that is made by coupling a scalar field with a gravitational tensor field. It has a free constant, known as the coupling parameter \(\omega \) (a tunable parameter), which can be adjusted according to the suitable observational evidence. The four dimensional action of BD theory has the following form [29]:
This theory is compatible with the weak equivalence principle, Mach’s principle, and Dirac’s large number hypothesis [30]. In addition, it is in agreement with solar system experimental observations for a specific domain of \(\omega \) [31]. BD theory has been considered in various branches of gravitation and cosmology. Instability analysis of the Schwarzschild black hole in BD gravity is discussed in Ref. [32]. The analytical and numerical features of static spherically symmetric solutions in the context of BD-like cosmological model have been explored [29]. Thermodynamical properties of higher dimensional charged rotating black brane solutions in BD-BI gravity are presented in Ref. [33]. The cosmological perturbation equations of BD-BI have been investigated in Ref. [34]. The interaction between two test objects and the anomalous acceleration of Pioneer 10 and Pioneer 11 spacecraft [35, 36] have been studied in the BD-BI context [37]. Higher dimensional BI-dilaton black hole solutions with nonabelian Yang–Mills field and its stability against linear radial perturbations have been examined in [38].
There are several reasons for considering the cases in which the scalar field is non-minimally coupled to the BI field. Here we present some of them. A non-minimal coupling between a scalar field and a nonlinear U(1) gauge field emerges naturally in supergravity and in the low-energy effective action of string theory. Following the work of Refs. [4, 39, 40], it was shown that the BI action coupled to a dilaton field appears in the low-energy limit of open superstring theory. In other words, considering the coupling of gravity to other gauge fields, the presence of the dilaton field cannot be ignored. Therefore from the electrodynamic point of view, one remains with Einstein–BI-dilaton gravity or its conformal transformation, BD-BI theory. In addition, asymptotically adS (nonlinearly) charged dilaton black hole solutions may be known as the family of four-charge black holes in \(N = 8\) four dimensional gauged supergravity [41]. Furthermore, the thermodynamical phase structure of dilatonic (BI) black objects is more interesting with respect to Reissner–Nordström solutions [33, 42–44]. Also, in the holographic perspective, (nonlinearly) charged dilatonic black holes have shown a rather rich and interesting phenomenology [42, 45–51]. Moreover, regarding gauge/gravity duality, nonlinearly charged black holes with a non-minimal coupling to a scalar field are good candidates for the gravitational side as regards duality to Lifshitz-like theories [46, 52, 53].
Regarding black hole thermodynamics as an important connection between quantum gravity and the classical nature of general relativity [54], one may be motivated to consider thermal phase transitions. The behavior of a thermodynamic system can be explained with physical temperature and entropy [55, 56]. On the other hand, by considering the extended phase space of a black hole, we may treat the cosmological constant proportional to a typical dynamical pressure [57–70]. Considering the thermodynamics of black holes, we should note that a phase transition plays an important role in describing critical phenomena from the thermodynamics and quantum points of view. The thermodynamic behavior of charged black hole solutions in BD theory and the analogy of these solutions with the Van der Waals liquid–gas system in the extended phase space was investigated in Ref. [71]. In this paper, we study the P–V criticality and phase transition of charged black holes in BD-BI theory and compare it with Einstein–BI-dilaton solutions. At first we consider the Lagrangian of Einstein–BI-dilaton gravity and investigate its thermodynamical properties. Then we present a brief discussion regarding the conformal inconsistency of this Lagrangian and introduce a new well-defined Lagrangian of Einstein–BI-dilaton theory. We obtain its exact solutions and analyze the thermodynamic behavior of black holes. We also use the conformal transformation to obtain correct BD-BI black hole solutions. Finally, we discuss P–V criticality of the black holes in both Einstein and Jordan frames.
2 Part A: old Lagrangian
2.1 Black hole solutions in Einstein–BI-dilaton gravity
The well-known action of \((n+1)\)- dimensional BI-dilaton gravity is
where \(\mathcal {R}\) is the Ricci scalar, \(V(\Phi )\) is a self-interacting potential for the scalar field \(\Phi \), and \(L(\mathcal {F},\Phi )\) is the coupled Lagrangian of BI-dilaton theory [72],
In Eq. (2), the constants \(\alpha \) and \(\beta \) are, respectively, the dilaton and BI parameters, \(\mathcal {F}=F_{{\mu \nu }}F^{\mu \nu }\) is the Maxwell invariant, in which \(F_{\mu \nu }=\partial _{[\mu }A_{\nu ]}\) and \(A_{\mu }\) is the gauge potential. In the limit of \(\beta \rightarrow \infty \), \(L\left( \mathcal {F},\Phi \right) \) reduces to the standard Maxwell Lagrangian coupled to a dilaton field,
Variation of the action (1) with respect to \(g_{\mu \nu }\), \(\Phi \), and \(F_{{\mu \nu }}\) leads to the following field equations [72]:
where we have used the following notations:
In order to obtain static solutions, one can assume the following metric:
where
indicates the Euclidean metric of an \((n-1)\)-dimensional hypersurface with constant curvature \((n-1)(n-2)k\) and volume \(\varpi _{n-1}\). It has been shown that the following functions satisfy all of the field equations simultaneously [72]:
where \(\gamma =\alpha ^{2}/(1+\alpha ^{2})\), \(\Delta =\frac{q^{2}}{\beta ^{2}r^{2(n-1)}}\left( \frac{r}{b}\right) ^{2\gamma (n-1)}\), m is an integration constant which is related to the total mass, and b is another arbitrary constant related to the scalar field. In addition, one should consider the following suitable Liouville-type potential [72]:
to obtain consistent solutions. Calculation of curvature scalars shows that there is a curvature divergency at the origin and all curvature invariants are finite for \(r\ne 0\) [72]. It means that there is a physical singularity located at \(r=0\) which can be covered with an event horizon, and therefore, one can interpret it as a black hole. In the next section we study thermodynamics and P–V criticality of the mentioned solutions.
2.1.1 Extended phase space and P-V criticality of the solutions
The thermodynamic properties of the mentioned solutions were discussed before [72]. In this section, we study the P–V criticality in the extended phase space. First of all, we calculate the Hawking temperature by using the surface gravity interpretation (\(\kappa \)),
where \(\chi =\partial /\partial t\) is the null Killing vector of the event horizon \(r_{+}\). Calculations lead to the following explicit relation [72]:
where \(\Delta _{+}=\frac{q^{2}\left( \frac{r_{+}}{b}\right) ^{2\gamma \left( n-1\right) }}{\beta ^{2}r_{+}^{2(n-1)}}\). The entropy and the finite mass of the black hole can be obtained with the following forms [72]:
where m is the (geometrical) mass parameter of the black hole which can be expressed in terms of the event horizon radius,
Now, we extend the phase space by defining a thermodynamical pressure proportional to cosmological constant and its corresponding conjugate quantity as the volume. Using the concept of the energy-momentum tensor, one can find the generalized definition for the pressure in the presence of a dilaton field [71]
where in the absence of the dilaton field (\(\alpha =\gamma =0\)), the well-known relation \(P=\frac{-\Lambda }{8\pi }\) is recovered.
By regarding the relation between cosmological constant and thermodynamical pressure, one may interpret the mass as enthalpy. Hence we can calculate the generalized volume as
where in the absence of dilaton field, one obtains \(V=\frac{\varpi _{n-1}r_{+}^{n}}{n}\), as expected.
Now, we are in a position to study the phase transition through the P–V and G–T diagrams. The equation of state of the black hole can be written, using Eqs. (12) and (16), in the following form:
Due to the relation between the volume and radius of the black hole, we use the horizon radius (specific volume) in order to investigate the critical behavior of these systems [64–66]. Considering the mentioned equation of state, one can investigate the inflection point of P–\(r_{+}\) diagram to obtain the phase transition point. The inflection point of isothermal curves in P–\(r_{+}\) diagram has the following properties:
One can use Eqs. (19) and (20) with the equation of state (18) to calculate the critical values for temperature, pressure, and volume. In addition, we can study the phase transition through calculation of the Gibbs free energy. Since we are working in the extended first law of black hole thermodynamics, M (the finite mass of the black hole) will be interpreted as the enthalpy instead of the internal energy, and therefore, the Gibbs free energy of the black hole can be written as
where, after some manipulations, we obtain the following Gibbs free energy per unit volume \(\varpi _{n-1}\):
We should note that the characteristic swallow-tail behavior in G–T diagrams guarantees the existence of the phase transition.
2.2 Black hole solutions in BD-BI gravity
In this section, we discuss the possibility of BD-BI solutions which are conformally related to the obtained BI-dilaton black holes. To do so, one should find a suitable conformal transformation to obtain BD-BI counterpart of action (1). In the action of BD theory, the dilaton field should be decoupled from matter field (electrodynamics) and be coupled with gravity. In other words, one should find a suitable conformal transformation in which it transforms the action (1) to the following well-known BD-BI action [73]:
where \(\mathcal {L}(\mathcal {F})\) is the Lagrangian of the BI theory [33],
In Eq. (23) \(\mathcal {R}\) is the Ricci scalar, \(\omega \) is the coupling constant, \(\Phi \) denotes the BD scalar field, and \(V(\Phi )\) is a self-interaction potential for \(\Phi \). It is notable that in the limit of \(\beta \rightarrow \infty \), \(\mathcal {L}(\mathcal {F})\) reduces to the standard Maxwell form \(\mathcal {L}(\mathcal {F})=-\mathcal {F}\), as it should.
It is a matter of calculation to show that there is no consistent conformal transformation between the actions (1) and (23) [74]. In other words, although the action (1) leads to the well-known action of Maxwell-dilaton gravity for \(\beta \rightarrow \infty \), it is not conformally related to the BD-BI action, and therefore, Eq. (1) is not a suitable and consistent action. Considering the conformally ill-defined action (1), in the next section, we follow the method of Ref. [74] to obtain a conformally well-defined action of BI-dilaton gravity.
3 Part B: new Lagrangian: field equations and conformal transformations
The action of \((n+1)\)-dimensional BD-BI theory with a scalar field \(\Phi \) and a self-interacting potential \(V(\Phi )\) can be written as Eq. (23). Variation of this action with respect to \(g_{\mu \nu }\), \(\Phi \) and \(F_{{\mu \nu }}\) leads to [73]
Due to the appearance of the scalar field in the denominator of field equation (25), solving Eqs. (25)–(27), directly, is a non-trivial task. In order to remove this difficulty, one can use the traditional approach; the conformal transformation. Indeed, using the conformal transformation [73], the BD-BI theory will be transformed into the Einstein–BI-dilaton gravity. The suitable conformal transformation is as follows:
where
Applying the mentioned conformal transformation, one finds that the action of BD-BI and its related field equations change to the well-known dilaton gravity with the following explicit forms:
where \(\overline{\mathcal {R}}\) and \(\overline{\nabla }\) are, respectively, the Ricci scalar and covariant differentiation related to the metric \(\overline{g}_{\mu \nu }\). In addition, the potential \(\overline{V}\left( \overline{\Phi }\right) \) and the BI-dilaton coupling Lagrangian \(\overline{L}\left( \overline{F}, \overline{\Phi }\right) \) are, respectively [74],
and
It is easy to find that \(\overline{L}\left( \overline{\mathcal {F}},\overline{\Phi } \right) \rightarrow 0\) as \(\beta \rightarrow 0\), and on the other side, it reduces to the following standard Maxwell-dilaton Lagrangian in the limit of \(\beta \rightarrow \infty \):
In other words, comparing both Lagrangians of BI-dilaton theory [Eqs. (2) and (36)], one finds that although both Lagrangians lead to the Maxwell-dilaton Lagrangian for the weak nonlinearity strength (\(\beta \rightarrow \infty \)), only the new Lagrangian [Eq. (36)] is the correct and consistent one with a conformal transformation.
It is notable that we used the following notations for writing the field equations (32)–(34):
where
Taking into account the conformal relation of BD-BI theory and BI-dilaton gravity, one can find that if \(\left( \overline{g}_{\mu \nu },\overline{F} _{\mu \nu },\overline{\Phi }\right) \) is the solution of Eqs. (32)–(34) with the potential \(\overline{V}(\overline{\Phi }) \), then
is the solution of BD-BI field equations [Eqs. (25)–(27)] with potential \(V(\Phi )\).
4 Part C: new Lagrangian: exact solutions
4.1 Black hole solutions in Einstein–BI-dilaton gravity and BD-BI theory
4.1.1 Einstein frame
In this section, first we obtain the solutions of dilaton gravity in the Einstein frame and then we use the conformal transformation to obtain the solutions of the BD-BI theory.
We assume the following metric:
where \(\mathrm{d}\Omega _{k}^{2}\) was presented in Eq. (7). We obtain the consistent dilaton field as well as metric functions. To do this, we should consider a potential \(\mathbf {\overline{V}}(\overline{\Phi })\). It was shown that a suitable potential is the Liouville-type potential with BI correction [74],
which reduces to \(2\Lambda \) in the absence of the dilaton field. In other words, the first two terms of Eq. (43) come from Maxwell-dilaton gravity [71], while the third term appears because of the nonlinearity of electrodynamics (BI effect). Now, considering the potential (43) with Eqs. (32)–(34), one finds
where m and b are integration constants related to the mass and scalar field, respectively, and
It is notable that for \(\beta \rightarrow \infty \), the last term of Eq. (43) vanishes and the resultant relations reduce to dilatonic Maxwell solutions [71]. Calculations show that the curvature scalars diverge at the origin and they are finite for \(r\ne 0\). In other words, since the metric function Z(r) has real positive root(s), one can interpret the singularity as a black hole.
In the next section, we use the conformal transformation to obtain BD-BI black hole solutions.
4.1.2 Jordan frame
Now, we are going to obtain charged black hole solutions of BD-BI theory. Using the conformal transformation (35), the potential \(\mathbf {V}(\Phi )\) in the Jordan frame is
Taking into account the solutions in an Einstein frame with the mentioned conformal transformation, we can obtain the solutions of Eqs. (25)–(27). Considering the following \((n+1)\)-dimensional metric:
we find that the functions A(r) and B(r) are
Since the curvature scalars of the mentioned metric diverge at \(r=0\), it is easy to show that the corresponding solution can be interpreted as a black hole and it can be covered by an event horizon which is the largest real root of Z(r). Since it was shown that for \(k=0,-1\) there is no phase transition [71]; hereafter, we choose the positive curvature constant boundary (\(k=1\)) to investigate the phase transition.
4.2 Thermodynamic properties and P–V criticality: dilatonic-BI vs. BD-BI black holes
4.2.1 Thermodynamic properties
In this section, we focus on the conserved and thermodynamic quantities of the black hole solutions in both Einstein and Jordan frames. In order to calculate the Hawking temperature, one can use the surface gravity interpretation,

It is easy to show that the Hawking temperature in an Einstein frame is exactly equal to that in a Jordan frame, with the following form:

where
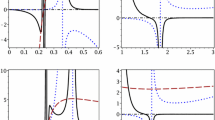
BD-BI: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \(n=4\), \( q=1\), \(\beta =0.5\) and \(\omega =100\). P–\(r_{+}\) diagram, from bottom to up \(T=0.1T_{c}\), \(T=T_{c}\) and \(T=2T_{c}\), respectively. G–T diagram, from bottom to up \(P=0.5P_{c}\), \(P=P_{c}\) and \(P=1.5P_{c}\), respectively
BI-dilaton: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \( n=4 \), \(q=1\), \(\beta =0.5\) and \(\omega =100\). P–\(r_{+}\) diagram, from bottom to up \(T=0.1T_{c}\), \(T=T_{c}\) and \(T=2T_{c}\), respectively. G–T diagram, from bottom to up \(P=0.5P_{c}\), \(P=P_{c}\) and \(P=1.5P_{c}\), respectively
BD-BI: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \(n=6 \), \( q=1\), \(\beta =0.5\) and \(\omega =100\). P–\(r_{+}\) diagram, from bottom to up \(T=0.1T_{c}\) and \(T=T_{c}\), \(T=2T_{c}\), respectively. G–T diagram, from bottom to up \(P=0.5P_{c}\), \(P=P_{c}\) and \(P=1.5P_{c}\), respectively
BI-dilaton: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \( n=6 \), \(q=1\), \(\beta =0.5\) and \(\omega =100\). P–\(r_{+}\) diagram, from bottom to up \(T=0.1T_{c}\), \(T=T_{c}\) and \(T=2T_{c}\), respectively. G–T diagram, from bottom to up \(P=0.5P_{c}\), \(P=P_{c}\) and \(P=1.5P_{c}\), respectively
BD-BI: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \(\omega =100\), \(\beta =0.5\), \(q=1\). P–\(r_{+}\) diagram, for \(T=T_{c}\), \(n=4\) (solid line), \(n=5\) (dotted line) and \(n=6\) (dashed line). G–T diagram, for \(P=0.5P_{c}\), \(n=4\) (solid line), \(n=5\) (dotted line), and \(n=6\) (dashed line)
BI-dilaton: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \( \omega =100\), \(\beta =0.5\), \(q=1\). P–\(r_{+}\) diagram, for \(T=T_{c}\), \(n=4\) (solid line), \(n=5\) (dotted line), and \(n=6\) (dashed line). G–T diagram, for \(P=0.5P_{c}\), \(n=4\) (solid line), \(n=5\) (dotted line), and \(n=6\) (dashed line)
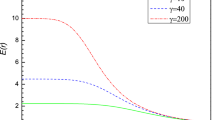
BD-BI: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \(n=4 \), \( \beta =0.5\) and \(q=1\). P–\(r_{+}\) diagram, for \(T=T_{c}\), \(\omega =50\) (solid line), \( \omega =100\) (dotted line), and \(\omega =300\) (dashed line). G–T diagram, for \(P=0.9P_{c}\), \(\omega =50\) (solid line), \(\omega =100\) (dotted line), and \(\omega =300\) (dashed line)
BI-dilaton: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \( n=4 \), \(\beta =0.5\) and \(q=1\). P–\(r_{+}\) diagram, for \(T=T_{c}\), \(\omega =50\) (solid line), \( \omega =100\) (dotted line), and \(\omega =300\) (dashed line). G–T diagram, for \(P=0.9P_{c}\), \(\omega =50\) (solid line), \(\omega =100\) (dotted line), and \(\omega =300\) (dashed line)
BD-BI: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \(n=4\), \( \omega =100\), \(q=1\). P–\(r_{+}\) diagram, for \(T=T_{c}\), \(\beta =0.5\) (solid line), \(\beta =0.8\) (dotted line), and \(\beta =5\) (dashed line). G–T diagram, for \(P=0.5P_{c}\) and \(\beta =0.5\) (solid line), \( \beta =0.8\) (dotted line), and \(\beta =5\) (dashed line)
BI-dilaton: P–\(r_{+}\) (left), G–T (right) diagrams for \(b=1\), \( n=4 \), \(\omega =100\), \(q=1\). P–\(r_{+}\) diagram, for \(T=T_{c}\), \(\beta =0.5\) (solid line), \(\beta =0.8\) (dotted line), and \(\beta =5\) (dashed line). G–T diagram, for \(P=0.5P_{c}\) and \(\beta =0.5\) (solid line), \( \beta =0.8\) (dotted line), and \(\beta =5\) (dashed line)
Since the conformal transformation is a regular smooth function at the horizon, this equality is expected. In addition, the finite mass and the entropy of the black hole for both frames can be obtained with the following forms:
Using the Gauss law, the electric charge would have the following form:
which is valid for both frames.
Now, we extend the phase space by defining a thermodynamical pressure proportional to the cosmological constant and its corresponding conjugate quantity as the volume. Following the method of [71], one finds the generalized definition for the pressure in the presence of a dilaton field as
We should note that in the absence of a dilaton field (\(\alpha =\gamma =0\)), the well-known relation \(P=\frac{-\Lambda }{8\pi }\) is recovered. In order to calculate the volume, we should obtain the enthalpy. Following the previous interpretation of mass and enthalpy, we can calculate the generalized volume as
where, for \(\alpha \rightarrow 0\), we obtain \(V=\frac{\varpi _{n-1}r_{+}^{n}}{ n}\), as expected. It is worthwhile to mention that although P and V are different for the Einstein and Jordan frames, both frames have the same multiplication of “\(P \times V\)”.
4.2.2 P–V criticality of dilatonic BI vs. BD-BI
Now, we are in a position to study the phase transition through the P–V and G–T diagrams. The equation of state of the black hole can be written, using Eqs. (54), (61), and (62), in the following form:
where
Now, one can consider the mentioned equation of state to obtain critical quantities through the properties of the inflection point of the P–\(r_{+}\) diagram [Eqs. (19) and (20)]. In addition, we can use Eq. (21) to obtain the Gibbs free energy of the black holes. After some manipulations, we obtain the Gibbs free energy per unit volume \(\varpi _{n-1}\) as
where
As we mentioned before, the existence of the characteristic swallow-tail behavior in G–T diagrams helps us to obtain the thermal phase transition (for further details, see the G–T diagrams and their related text). Since analytical investigation of the critical behavior is not possible, we use numerical analysis instead. We present various tables and figures to study such behavior.
4.3 Discussion on the results of diagrams
In Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, we show the critical behavior of the system in both BI-dilaton and BD-BI theories. In addition, we present six tables to investigate the critical points more clearly. As we know, the phase transition occurs at the critical point, which demonstrates the critical pressure, horizon radius, and temperature. Studying the G–T diagrams of the Einstein and Jordan frames with related tables shows that by increasing the BD coupling constant (\(\omega \)) (decreasing dilatonic coupling constant \(\alpha \) in Einstein frame), the critical values of temperature and horizon radius increase
(decrease) in the Jordan (Einstein) frame. Regarding the P–\(r_{+}\) diagrams and related tables, we find that by increasing \(\omega \), the critical pressure and also the ratio \(\frac{P_{c}r_{c}}{T_{c}}\) increase in both BD-BI gravity and its conformally related BI-dilaton gravity. Comparing the right panels of Figs. 7 and 8 with Tables 1 and 2, we find an interesting result. According to the tables, one finds increasing \(\omega \) leads to increasing (decreasing) \(T_{c}\) in BD-BI (BI-dilaton) gravity. While regarding the right panels of Figs. 7 and 8, we find that for \(P<P_{c}\), the phase transition temperature is a decreasing function in both frames.
We can also examine the effects of dimensionality on the critical values and phase transition of the system in Figs. 5 and 6 and the related Tables 3 and 4. By considering the G–T and P–\(r_{+}\) plots of Figs. 5 and 6, we can find that when n increases, the critical values of temperature and pressure, and the size of the swallow tail and the ratio \(\frac{P_{c}r_{c}}{T_{c}}\) increase, while the critical horizon radius decreases.
In addition, by studying Tables 5 and 6, we can find when the nonlinearity parameter increases, the critical horizon radius and the ratio \(\frac{P_{c}r_{c}}{T_{c}}\) increase, but the critical values of temperature and pressure decrease in both frames. One can confirm this behavior in Figs. 9 and 10.
To sum up, we can say that by increasing \(\omega \), we have an increment in critical value of pressure in both theories and a reduction in the critical values of horizon radius and temperature in dilaton gravity, but in BD-BI gravity they increase. On the other hand, we can see that increasing the dimension leads to a reduction in horizon radius and an increment in critical values of the pressure and temperature. In addition, by increasing \(\beta \), we have an increment in critical value of horizon radius and a reduction in the critical values of pressure and temperature in both frames. Furthermore regarding G–T diagrams, it is clear that although increasing \(\beta \) leads to increasing G, the Gibbs free energy decreases when we increase n and \(\omega \). It is also notable that when we increase \(\omega \), n, and \(\beta \), the ratio \(\frac{P_{c}r_{c}}{T_{c}}\) increases too. Furthermore, we should note that although the related figures of both frames are very similar, they are not completely a match to each other (see Fig. 11 for more clarifications). As a final comment, we should note that for \(\omega \rightarrow \infty \) (\(\alpha \rightarrow 0\)) and \(\beta \rightarrow \infty \), the solutions of BD-BI reduce to Reissner–Nordström black hole solutions. As a result, in order to have sensible effects for the BD and BI parameters, we should regard small values.
5 Conclusions
In this paper, the main goal was studying the properties of BD-BI black hole solutions. At first, we have given a brief discussion regarding to the old Lagrangian of BI-dilaton gravity. Since this Lagrangian was not consistent with the well-known BD-BI gravity, we had to define a new Lagrangian. This new BI-dilaton Lagrangian emanates from conformal transformation and it is a well-behaved Lagrangian for \(\beta \rightarrow \infty \). We have obtained new field equations and calculated exact black hole solutions of field equations in both Einstein and Jordan frames.
We have considered both BD-BI and BI-dilaton theories with spherically symmetric horizon and studied their phase structure. By considering cosmological constant proportional to thermodynamical pressure and its conjugate variable as volume, we have investigated the extended phase space and used the interpretation of the total mass of a black hole as the enthalpy.
Studying calculated critical values through two different types of phase diagrams (related to both frames) resulted in a phase transition taking place in the critical values. Studying P–\(r_{+}\) and G–T diagrams we presented a similar Van der Waals behavior near the critical point. We have also shown that both scalar field and nonlinearity parameter of the electromagnetic field have considerable effects on the critical quantities. We have examined the effects of the BD coupling constant, the nonlinearity parameter, and the dimensionality on the critical quantities. We have found that an increasing BD coupling constant leads to an increment in all critical quantities in a Jordan frame. In addition, for both frames, increasing dimensionality leads to increasing critical values of temperature and pressure, but decreasing the critical horizon radius. Also, regarding the effects of \(\beta \), we have found that its reduction leads to reduction (increment) of the critical pressure (critical temperature and horizon radius). It is notable that although changing \(\omega \) does not have the same effects on some values of the critical quantities in both frames, variations of n and \(\beta \) have the same effects for both the Einstein and the Jordan frames. In addition, we should note that increasing \(\omega \), n, and \(\beta \) leads to increasing the ratio \(\frac{P_{c}r_{c}}{T_{c}}\), regardless of \(P_{c}\), \(r_{c}\) and \(T_{c}\) behaviors (for both Einstein and Jordan frames).
Another interesting result of this paper is based on comparing the consequences of both frames. Comparing the figures of BD-BI with BI-dilaton branches, we have found that the total behavior of the figures are very similar to each other. This is due to the fact that the conformal factor is a regular smooth function at the horizon and most of the thermodynamic quantities are the same for both frames. But as we have found in some figures (specially Fig. 11) and related tables, the critical quantities are not exactly the same in both frames.
Following the same adapted approach, the extended phase space and P–V criticality conditions of other models of nonlinear electrodynamics are under investigation. In addition, the phase transition of such solutions can be studied through geometrical thermodynamics. This issue will be addressed in future work.
References
M. Born, Proc. R. Soc. Lond. A 143, 410 (1934)
M. Born, L. Infeld, Proc. R. Soc. Lond. A 144, 425 (1934)
R. Leigh, Mod. Phys. Lett. A 4, 2767 (1989)
E. Fradkin, A.A. Tseytlin, Phys. Lett. B 163, 123 (1985)
G.W. Gibbons, Rev. Mex. Fis. 49S1, 19 (2003). arXiv:hep-th/0106059
A. A. Tseytlin, arXiv:hep-th/9908105
G. Boillat, J. Math. Phys. 11, 941 (1970)
G. Boillat, J. Math. Phys. 11, 1482 (1970)
M. Najafikhah, S.R. Hejazi, arXiv:1009.5490
I.L.J. Casanellas, P. Pani, V. Cardoso, Astrophys. J. 745, 15 (2012)
J.H.C. Scargill, M. Banados, P.G. Ferreira, Phys. Rev. D 86, 103533 (2012)
P.P. Avelino, R.Z. Ferreira, Phys. Rev. D 86, 041501 (2012)
M.K. Gaillard, B. Zumino, Nucl. Phys. B 193, 221 (1981)
S. Deser, R. Puzalowski, J. Phys. A 13, 2501 (1980)
R. Casalbuoni, S. De Curtis, D. Dominic, F. Feruglio, R. Gatto, Phys. Lett. B 220, 569 (1989)
J. Bagger, A. Galperin, Phys. Rev. D 55, 1091 (1997)
Z. Komargodski, N. Seiberg, JHEP 09, 066 (2009)
S. Ferrara, M. Porrati, A. Sagnotti, JHEP 12, 065 (2014)
S. Ferrara, M. Porrati, A. Sagnotti, R. Stora, A. Yeranyan, Fortsch. Phys. 63, 189 (2015)
I. Cho, N.K. Singh, Eur. Phys. J. C 75, 240 (2015)
A.G. Riess et al., Supernova Search Team Collaboration. Astrophys. J. 607, 665 (2004)
P.J. Steinhardt, F.S. Accetta, Phys. Rev. Lett. 64, 2740 (1990)
N. Banerjee, D. Pavon, Phys. Rev. D 63, 043504 (2001)
M. Sharif, S. Waheed, Eur. Phys. J. C 72, 1876 (2012)
M.K. Mak, T. Harko, Europhys. Lett. 60, 155 (2002)
S. Sen, T.R. Seshadri, Int. J. Mod. Phys. D 12, 445 (2003)
D.F. Torres, Phys. Rev. D 66, 043522 (2002)
N. Banerjee, D. Pavon, Class. Quantum Gravity 18, 593 (2001)
D.A. Treyakova, B.N. Latosh, S.O. Alexeyev, Class. Quantum Gravity 32, 185002 (2015)
P.A.M. Dirac, Proc. R. Soc. Lond. A 165, 199 (1938)
A.D. Felice, Phys. Rev. D 74, 103005 (2006)
O.J. Kwon, Phys. Rev. D 34, 333 (1986)
S.H. Hendi, J. Math. Phys. 49, 082501 (2008)
L. Amendola, arXiv:hep-th/0409224
J.D. Anderson, P.A. Laing, E.L. Lau, A.S. Liu, M.M. Nieto, S.G. Turyshev, Phys. Rev. D 65, 082004 (2002)
V.T. Toth, S.G. Turyshev, Can. J. Phys. 84, 1063 (2006)
M.N. Smolyakov, arXiv:0907.3744
S.H. Mazharimousavi, M. Halilsoy, Z. Amirabi, arXiv:0802.3990
R.R. Metsaev, M.A. Rakhmanov, A.A. Tseytlin, Phys. Lett. B 193, 207 (1987)
E. Bergshoeff, E. Sezgin, C. Pope, P. Townsend, Phys. Lett. B 188, 70 (1987)
M.J. Duff, J.T. Liu, Nucl. Phys. B 554, 237 (1999)
M. Cadoni, G. D’Appollonio, P. Pani, JHEP 03, 100 (2010)
C. Charmousis, B. Gouteraux, B.S. Kim, E. Kiritsis, R. Meyer, JHEP 11, 151 (2010)
D.D. Doneva, S.S. Yazadjiev, K.D. Kokkotas, I.Z. Stefanov, M.D. Todorov, Phys. Rev. D 81, 104030 (2010)
S.S. Gubser, F.D. Rocha, Phys. Rev. D 81, 046001 (2010)
K. Goldstein, S. Kachru, S. Prakash, S.P. Trivedi, JHEP 08, 078 (2010)
K. Goldstein et al., JHEP 10, 027 (2010)
C.M. Chen, D.W. Pang, JHEP 06, 093 (2010)
B.H. Lee, D.W. Pang, C. Park, JHEP 07, 057 (2010)
Y. Liu, Y.W. Sun, JHEP 07, 099 (2010)
B.H. Lee, D.W. Pang, C. Park, JHEP 11, 120 (2010)
G. Bertoldi, B.A. Burrington, A.W. Peet, Phys. Rev. D 82, 106013 (2010)
E. Perlmutter, JHEP 02, 013 (2011)
R.A. Hennigar, W.G. Brenna, R.B. Mann, JHEP 07, 077 (2015)
S.W. Hawking, Phys. Rev. Lett. 26, 1344 (1971)
J.D. Bekenstein, Phys, Rev. D 7, 2333 (1973)
J. Creighton, R.B. Mann, Phys. Rev. D 52, 4569 (1995)
M.M. Caldarelli, G. Cognola, D. Klemm, Class. Quantum Gravity 17, 399 (2000)
D. Kastor, S. Ray, J. Traschen, Class. Quantum Gravity 26, 195011 (2009)
B.P. Dolan, Phys. Rev. D 84, 127503 (2011)
B.P. Dolan, Class. Quantum Gravity 28, 235017 (2011)
B.P. Dolan, arXiv:1209.1272
M. Cvetic, G.W. Gibbons, D. Kubiznak, C.N. Pope, Phys. Rev. D 84, 024037 (2010)
D. Kubiznak, R.B. Mann, JHEP 07, 033 (2012)
S. Gunasekaran, D. Kubiznak, R.B. Mann, JHEP 11, 110 (2012)
S.H. Hendi, M.H. Vahidinia, Phys. Rev. D 88, 084045 (2013)
S.H. Hendi, S. Panahiyan, R. Mamasani, Gen. Relativ. Gravity 47, 91 (2015)
R.G. Cai, L.M. Cao, L. Li, R.Q. Yang, JHEP 09, 005 (2013)
S.H. Hendi, S. Panahiyan, B. Eslam Panah, Prog. Theor. Exp. Phys. 2015, 103E01 (2015)
S.H. Hendi, S. Panahiyan, B. Eslam, Panah. Int. J. Mod. Phys. D 25, 1650010 (2016)
S.H. Hendi, Z. Armanfard, Gen. Relativ. Gravity 47, 125 (2015)
A. Sheykhi, N. Riazi, Phys. Rev. D 75, 24021 (2007)
R.G. Cai, Y.S. Myung, Phys. Rev. D 56, 3466 (1997)
S.H. Hendi, M.S. Talezadeh, arXiv:1605.00456
Acknowledgments
We would like to thank the anonymous referee for valuable suggestions. We also acknowledge A. Poostforush and S. Panahiyan for reading the manuscript. We thank the Research Council of Shiraz University. This work has been supported financially by the Research Institute for Astronomy and Astrophysics of Maragha (RIAAM), Iran.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Hendi, S.H., Tad, R.M., Armanfard, Z. et al. Extended phase space thermodynamics and P–V criticality: Brans–Dicke–Born–Infeld vs. Einstein–Born–Infeld-dilaton black holes. Eur. Phys. J. C 76, 263 (2016). https://doi.org/10.1140/epjc/s10052-016-4106-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4106-9