Dynamo models of the solar cycle

Abstract

This paper reviews recent advances and current debates in modeling the solar cycle as a hydromagnetic dynamo process. Emphasis is placed on (relatively) simple dynamo models that are nonetheless detailed enough to be comparable to solar cycle observations. After a brief overview of the dynamo problem and of key observational constraints, I begin by reviewing the various magnetic field regeneration mechanisms that have been proposed in the solar context. I move on to a presentation and critical discussion of extant solar cycle models based on these mechanisms, followed by a discussion of recent magnetohydrodynamical simulations of solar convection generating solar-like large-scale magnetic cycles. I then turn to the origin and consequences of fluctuations in these models and simulations, including amplitude and parity modulation, chaotic behavior, and intermittency. The paper concludes with a discussion of our current state of ignorance regarding various key questions relating to the explanatory framework offered by dynamo models of the solar cycle.

Introduction

Scope of review

The cyclic regeneration of the Sun’s large-scale magnetic field is at the root of all phenomena collectively known as “solar activity”. A near-consensus now exists to the effect that this magnetic cycle is to be ascribed to the inductive action of fluid motions pervading the solar interior. However, at this writing nothing resembling consensus exists regarding the detailed nature and relative importance of various possible inductive flow contributions.

My assigned task, to review “dynamo models of the solar cycle”, is daunting. I will therefore interpret this task as narrowly as I can get away with. This review will not discuss in any detail solar magnetic field observations, the physics of magnetic flux tubes and ropes, the generation of small-scale magnetic field in the Sun’s near-surface layers, solar cycle prediction, or magnetic field generation in stars other than the Sun. These topics do have a lot to bear on “dynamo models of the solar cycle”, but a line needs to be drawn somewhere, and moreover many of these topics are the subject of full length reviews in this journal: Hathaway (2015) and Usoskin (2017) on characteristics of the observed and reconstructed solar cycle, Stein (2012) on photospheric magnetoconvection, Brun and Browning (2017) on stellar magnetism and cycles, Fan (2009) and Cheung and Isobe (2014) on magnetic flux emergence, and Petrovay (2020) on solar cycle predictions.

This review thus focuses on the cyclic regeneration of the large-scale solar magnetic field through the inductive action of fluid flows, as described by various approximations and simplifications of the partial differential equations of magnetohydrodynamics. Most current dynamo models of the solar cycle rely heavily on numerical solutions of these equations, and this computational emphasis is reflected throughout the following pages.

Many of the mathematical and physical intricacies associated with the generation of magnetic fields in electrically conducting astrophysical fluids are well covered in a few existing reviews and textbooks (see Ossendrijver 2003; Brandenburg and Subramanian 2005; Charbonneau 2013; Schrijver and Siscoe 2009; Moffatt and Dormy 2019), and will not be addressed at depth in what follows. The focus is on models of the solar cycle, seeking primarily to describe the observed spatio-temporal variations of the Sun’s large-scale magnetic field.

What is a “model”?

The review’s very title demands an explanation of what is to be understood by “model”. A model is a theoretical construct used as thinking aid in the study of some physical system too complex to be understood by direct inferences from observed data. A model is usually designed with some specific scientific questions in mind, and asking different questions about a given physical system will, in all legitimacy, lead to distinct model designs. A well-designed model should be as complex as it needs to be to answer the questions having motivated its inception, but not more. Throwing everything into a model—usually in the name of “physical realism”—is likely to produce results as complicated as the data coming from the original physical system under study. Such model results are doubly damned, as they are usually as opaque as the original physical data, and, in addition, are not even real-world systems!

Nearly all of the solar dynamo models discussed in this review rely on severe geometrical and/or dynamical simplifications of the set of equations known to govern the dynamics of the Sun’s turbulent, magnetized fluid interior. Yet all of them are bona fide models, as defined here. Global magnetohydrodynamical simulations of convection and dynamo action are also models, but in a different sense; while geometrically and dynamically correct on all resolved scales, they typically operate in physical parameter regimes far removed from solar interior conditions. Moreover, computational limitations usually force truncation, sometimes severe, of the spatial and temporal scales captured by these simulations.

A brief historical survey

While regular observations of sunspots go back to the early seventeenth century, and discovery of the sunspot cycle to 1843, it is the landmark work of George Ellery Hale and collaborators that, in the opening decades of the twentieth century, demonstrated the magnetic nature of sunspots and of the solar activity cycle. In particular, Hale’s celebrated polarity laws established the existence of a well-organized magnetic flux system, residing somewhere in the solar interior, as the source of sunspots. In 1919, Joseph Larmor suggested the inductive action of fluid motions as one of a few possible explanations for the origin of this magnetic field, thus opening the path to contemporary solar cycle modelling. Larmor’s suggestion fitted nicely with Hale’s polarity laws, in that the inferred equatorial antisymmetry of the solar internal toroidal fields is precisely what one would expect from the shearing of a large-scale poloidal magnetic field by an axisymmetric and equatorially symmetric differential rotation pervading the solar interior. However, two decades later Thomas S. Cowling placed a major hurdle in Larmor’s path—so to speak—by demonstrating that even the most general purely axisymmetric flows could not, in themselves, sustain an axisymmetric magnetic field against Ohmic dissipation. This result became known as Cowling’s antidynamo theorem.

A viable way out of this quandary was only discovered in the mid-1950s, when Eugene N. Parker pointed out that the Coriolis force could impart a systematic cyclonic twist to rising turbulent fluid elements in the solar convection zone, and in doing so provide the break of axisymmetry needed to circumvent Cowling’s theorem. This groundbreaking idea was put on firm quantitative footing by the subsequent development of mean-field electrodynamics in the 1960s, which rapidly became the theory of choice for solar dynamo modelling. By the late 1970s, concensus had almost emerged as to the fundamental nature of the solar dynamo, and the $\alpha$-effect of mean-field electrodynamics was at the heart of it.

Serious trouble soon appeared on the horizon, however, and from no less than three distinct directions. First, it was realized that because of buoyancy effects, magnetic fields strong enough to produce sunspots could not be stored in the solar convection zone for sufficient lengths of time to ensure adequate amplification. Second, the ability of the $\alpha$-effect and turbulent magnetic diffusivity to operate as assumed in mean-field electrodynamics was also called into question by theoretical calculations and numerical simulations. Third, and perhaps most decisive, the nascent field of helioseismology succeeded in providing the first determinations of the solar internal differential rotation, which turned out markedly different from those needed to produce solar-like dynamo solutions in the context of mean-field electrodynamics.

It is fair to say that even at this writing solar dynamo modelling has not yet recovered from this three-way punch, in that nothing resembling concensus currently exists as to the mode of operation of the solar dynamo. As with all major scientific crises, this situation provided impetus not only to drastically redesign existing models based on mean-field electrodynamics, but also to explore new physical mechanisms for magnetic field generation, and resuscitate older ideas that had fallen by the wayside in the wake of the $\alpha$-effect—perhaps most notably the so-called Babcock–Leighton mechanism, dating back to the early 1960s and relying on photospheric dispersal of magnetic flux from decaying active regions. These post-helioseismic developments, beginning in the mid to late 1980s, are the primary focus of this review.

Sunspots and the butterfly diagram

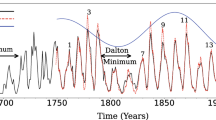
The sunspot cycle is arguably the best known manifestation of the solar magnetic cycle. Figure 1 shows time series for three declinations of the international sunspot numbers (SSN): monthly average (orange), 13-month smoothed monthly average (red), and prior to 1749, yearly average. The average sunspot cycle period is 11 years, but Hale’s polarity Laws reveal an underlying magnetic cycle of twice that period. Reproducing the polarity reversals and decadal period of the solar magnetic cycle is the first order of business for any dynamo model of the solar cycle.

Fig. 1

a The time series of the Version 2.0 international sunspot number (SSN), plotted here as monthly averages (orange), 13-month smoothed monthly average (red), and yearly average for 1700–1749 (red dots). The Group Sunspot Number of Hoyt and Schatten (1998), scaled to match the yearly average SSN in 1700–1749, is also shown in blue, allowing to extend the record back to 1610 (see also Chatzistergos et al. 2017). Panel b focuses on the last four sunspot cycles, and includes time series for the smoothed monthly hemispheric sunspot number, as color coded. Sunspot cycle numbering conventionally begins at one with the 1755–1766 cycle. Data source: WDC-SILSO, Royal Observatory of Belgium, Brussels

Next to cyclic polarity reversal, the sunspot butterfly diagram has provided the most stringent observational constraints on solar dynamo models (see Fig. 2). In addition to the obvious cyclic pattern, three features of the diagram are particularly noteworthy:

• Sunspots are restricted to latitudinal bands some $\simeq 30^\circ$ wide, symmetric about the equator.

• Sunspots emerge closer and closer to the equator in the course of a cycle, peaking in coverage at about $\pm \,15^{\circ }$ of latitude.

• Spatiotemporal variations of sunspot coverage are well synchronized across the two solar hemispheres

Sunspots appear when deep-seated toroidal flux ropes rise through the convective envelope and emerge at the photosphere (Parker 1955, 1975). Assuming that they rise radially and are formed where the magnetic field is the strongest, the sunspot butterfly diagram can be interpreted as a spatio-temporal “map” of the Sun’s internal, large-scale toroidal magnetic field component. This interpretation is not unique, however, since the aforementioned assumptions may be questioned. In particular, we still lack quantitative understanding of the process through which the diffuse, large-scale solar magnetic field produces the concentrated toroidal flux ropes that will later, upon buoyant destabilisation, give rise to sunspots. This remains perhaps the most severe missing link between dynamo models and solar magnetic field observations. On the other hand, the stability and rise of toroidal flux ropes is now fairly well-understood (see, e.g., Fan 2009, and references therein).

Fig. 2

The sunspot “butterfly diagram”, showing the fractional coverage of sunspots as a function of solar latitude and time (courtesy of D. Hathaway, Solar Cycle Science; see http://www.solarcyclescience.com/solarcycle.html)

Magnetographic mapping of the Sun’s surface magnetic field (see Fig. 3) has also revealed that the Sun’s poloidal magnetic component undergoes cyclic variations, reversing polarity at times of sunspot maximum. Note on Fig. 3 the poleward drift of the surface fields, away from sunspot latitudes. This pattern is believed to originate from the transport of magnetic flux released by the decay of sunspots at low latitudes (see Petrovay and Szakály 1999; Ulrich and Tran 2013, for alternate viewpoints).

Fig. 3

Zonally-averaged time–latitude magnetogram of the radial component of the solar surface magnetic field. The low-latitude component is associated with sunspots. Note the polarity reversal of the high-latitude magnetic field, occurring approximately at time of sunspot maximum (courtesy of D. Hathaway, Solar Cycle Science; see http://www.solarcyclescience.com/solarcycle.html)

The surface polar cap flux amounts to about $10^{22}$ Mx, while the total unsigned flux emerging in active regions in the course of a typical cycle adds up to a few $10^{25}$ Mx; this is usually taken to indicate that on large spatial scales the solar internal magnetic field is dominated by its toroidal (zonal) component.

Organization of review

The remainder of this review is organized in seven sections. In Sect. 2 the mathematical formulation of the solar dynamo problem is laid out in some detail, together with the various simplifications that are commonly used in modelling. Section 3 details various pertinent physical mechanisms of magnetic field generation. In Sect. 4, a selection of representative models relying on turbulent induction are presented and critically discussed, with abundant references to the technical literature. Section 5 focuses on models based on the Babcock–Leighton mechanism of polar field reversal, while Sect. 6 covers global magnetohydrodynamical simulations, with emphasis on simulations producing large-scale magnetic cycles. Section 7 surveys the various physical mechanisms that can lead to fluctuations in the characteristics of magnetic cycles, with pointers to illustrative model results and reviewing the recent literature on the topic. The concluding Sect. 8 offers a somewhat more personal discussion of current challenges and trends in solar dynamo modelling.

A great many review papers have been and continue to be written on dynamo models of the solar cycle, and the solar dynamo is discussed in most recent solar physics textbooks, notably Stix (2004), Foukal (2004) and Schrijver and Siscoe (2009). The series of review articles published in Balogh et al. (2014) are also essential reading for more in-depth coverage of some of the topics covered here. Among older review papers, Petrovay (2000), Rüdiger and Arlt (2003), Ossendrijver (2003) and Brandenburg and Subramanian (2005) offer (in my opinion) particularly noteworthy alternate and/or complementary viewpoints to those expressed here.

Making a solar dynamo model

Magnetized fluids and the MHD induction equation

In the interiors of the Sun and most stars, the collisional mean-free path of microscopic constituents is much shorter than competing plasma length scales, fluid motions are non-relativistic, and the plasma is electrically neutral and non-degenerate. Under these physical conditions, Ohm’s law holds, and so does Ampère’s law in its pre-Maxwellian form. Maxwell’s equations can then be combined into a single evolution equation for the magnetic field ${\varvec{B}}$, known as the magnetohydrodynamical (MHD) induction equation (see, e.g., Davidson 2001):

$$\begin{aligned} {\partial {{\varvec{B}}}\over \partial {t}}= \nabla \times ({\varvec{u\times B}}-\eta \nabla \times {\varvec{B}}), \end{aligned}$$

(1)

where $\eta =c^2/4\pi \sigma _{\rm e}$ is the magnetic diffusivity ($\sigma _{\rm e}$ being the electrical conductivity), in general only a function of depth for spherically symmetric solar/stellar structural models. The magnetic field must satisfy $\nabla \cdot {\varvec{B}}=0$, and an evolution equation for the flow field ${\varvec{u}}$ must also be provided. This is the Navier–Stokes equations, augmented by the Lorentz force:

$$\begin{aligned} {\partial {{\varvec{u}}}\over \partial {t}}+({\varvec{u}}\cdot \nabla ){\varvec{u}}= -{1\over \rho }\nabla p+{\varvec{g}}+{1\over 4\pi \rho }(\nabla \times {\varvec{B}})\times {\varvec{B}}- 2{{\varvec{\varOmega \times }}}{\varvec{u}}+ {1\over \rho }\nabla \cdot {{\varvec{\tau }}}, \end{aligned}$$

(2)

where ${{\varvec{\tau }}}$ is the viscous stress tensor, and other symbols have their usual meaning.¹ In the most general circumstances, Eqs. (1) and (2) must be complemented by suitable equations expressing conservation of mass and energy, as well as an equation of state. The resulting set of equations defines magnetohydrodynamics, quite literally the dynamics of magnetized fluids.

Even though Eq. (1) looks (misleadingly) linear in ${\varvec{B}}$, the dynamo process is fundamentally nonlinear. Upon taking the scalar product of Eq. (1) with ${\varvec{B}}$ and integrating over the volume V within which the dynamo is operating, one can arrive at the following evolution equation for the total magnetic energy within the system:

$$\begin{aligned} {\mathrm{d}\over \mathrm{d}{t}} \int _V {{{\varvec{B}}}^2\over 8\pi } \, \mathrm {d}V =-\oint _{\partial V} {\varvec{S}}\cdot {\varvec{n}}\,\mathrm {d}A -{1\over \sigma _{\rm e}}\int _V {\varvec{J}}^2\,\mathrm {d}V -{1\over c}\int _V {\varvec{u}}\cdot ({\varvec{J}}\times {\varvec{B}})\,\mathrm {d}V \end{aligned}$$

(3)

where ${\varvec{S}}$ is the Poynting flux; the associated first term on the RHS vanishes for isolated systems (such as a star imbedded in vaccum) and is of no further concern here. The second captures Ohmic dissipation of the electrical currents supporting the magnetic field, and will always decrease magnetic energy except in the ideal MHD limit $\sigma _{\rm e}\rightarrow \infty$. The third term on the RHS is where dynamo action resides. With the flow ${\varvec{u}}$ looked upon as the displacement of a fluid element per unit time, this term indicates that an increase of magnetic energy can only occur if the flow does work against the Lorentz force. This conversion of mechanical energy into electromagnetic energy is the very essence of any dynamo mechanism, from Faraday’s simple homopolar generator to astrophysical dynamos.

The dynamo problem

The first term on right hand side of Eq. (1) represents the inductive action of the flow field ${\varvec{u}}$, and it can act as a source term for ${\varvec{B}}$; the second term, on the other hand, describes the resistive dissipation of the current systems supporting the magnetic field, and is thus always a global sink for ${\varvec{B}}$. The relative importances of these two terms is measured by the magnetic Reynolds number

$$\begin{aligned} \mathrm {Rm}={uL\over \eta } , \end{aligned}$$

(4)

obtained by dimensional analysis of Eq. (1). Here $\eta$, u, and L are “typical” numerical values for the magnetic diffusivity, flow speed, and length scale over which ${\varvec{B}}$ varies significantly. The latter, in particular, is not easy to estimate a priori, as even laminar MHD flows have a nasty habit of generating their own magnetic length scales (usually $\propto \mathrm {Rm}^{-1/2}$ at high Rm). Nonetheless, on length scales comparable to the sun itself, Rm is immense, and so is the usual viscous Reynolds number $\mathrm {Re}=uL/\nu$. This implies that energy dissipation will occur on length scales very much smaller than the solar radius.

The dynamo problem consists in finding/producing a (dynamically consistent) flow field ${\varvec{u}}$ that has inductive properties capable of sustaining ${\varvec{B}}$ against Ohmic dissipation. Ultimately, the amplification of ${\varvec{B}}$ occurs by shearing, compression, and transport of the pre-existing magnetic field by the flow. This is readily seen upon rewriting the inductive term in Eq. (1) as

$$\begin{aligned} \nabla \times ({\varvec{u\times B}})= \underbrace{({\varvec{B}}\cdot \nabla ){\varvec{u}}}_{\mathrm{shearing}} -\underbrace{{\varvec{B}}(\nabla \cdot {\varvec{u}})}_\mathrm{compression} -\underbrace{({\varvec{u}}\cdot \nabla ){\varvec{B}}}_{\mathrm{transport}} \end{aligned}$$

(5)

In itself, the first term on the right hand side of this expression can obviously lead to exponential amplification of the magnetic field, at a rate proportional to the local flow gradient.

In the solar cycle context, the dynamo problem is reformulated towards identifying the circumstances under which the flow fields observed and/or inferred in the Sun can sustain the cyclic regeneration of the magnetic field associated with the observed solar cycle. This involves more than merely sustaining the field. A model of the solar dynamo should also reproduce

• cyclic polarity reversals with a decadal half-period,

• equatorward migration of the sunspot-generating deep toroidal field and its inferred strength,

• poleward migration of the diffuse surface field,

• observed $\pi /2$ phase lag between poloidal and toroidal components,

• polar field strength,

• observed antisymmetric equatorial parity,

• predominantly negative (positive) magnetic helicity in the Northern (Southern) solar hemisphere.

At the next level of “sophistication”, a solar dynamo model should also be able to exhibit amplitude fluctuations, and reproduce (at least qualitatively) the empirical patterns and correlations extracted from the sunspot and proxy records, including the so-called Grand Minima, during which the cycle amplitude –and perhaps the cycle itself– is strongly suppressed over many cycle periods (more on this in Sect. 7 below). One should finally add to the list torsional oscillations in the convective envelope, with proper amplitude and phasing with respect to the magnetic cycle. This is a very tall order by any standard.

Because of the great disparity of time- and length scales involved, and the fact that the outer 30% in radius of the Sun are the seat of vigorous, thermally-driven turbulent convective fluid motions, the solar dynamo problem is very hard to tackle as a direct numerical simulation of the full set of MHD equations (but do see Sect. 6 below). Most solar dynamo modelling work has thus relied on simplification—usually drastic—of the MHD equations, as well as assumptions on the structure of the Sun’s magnetic field and internal flows.

Kinematic models

A first drastic simplification of the MHD system of equations consists in dropping Eq. (2) altogether by specifying a priori the form of the flow field ${\varvec{u}}$. This kinematic regime remained until relatively recently the workhorse of solar dynamo modelling. Note that with ${\varvec{u}}$ given, the MHD induction equation becomes truly linear in ${\varvec{B}}$. Helioseismology (Christensen-Dalsgaard 2002) has now pinned down with good accuracy two important solar large-scale flow components, namely differential rotation throughout the interior, and meridional circulation in the outer half of the solar convection zone (for reviews, see Gizon 2004; Howe 2009). Given the low amplitude of observed torsional oscillations in the solar convective envelope, the kinematic approximation is perhaps not as bad a working assumption as one may have thought, at least for the differential rotation contribution to the mean flow ${\varvec{u}}$.

Axisymmetric formulation

The sunspot butterfly diagram, Hale’s polarity law, synoptic magnetograms, and the shape of the solar corona at and around solar activity minimum jointly suggest that, to a tolerably good first approximation, the large-scale solar magnetic field is axisymmetric about the Sun’s rotation axis, as well as antisymmetric about the equatorial plane. Under these circumstances it is convenient to express the large-scale field as the sum of a toroidal (i.e., longitudinal) component and a poloidal component (i.e., contained in meridional planes), the latter being expressed in terms of a toroidal vector potential. Working in spherical polar coordinates $(r,\theta ,\phi )$, one writes

$$\begin{aligned} {\varvec{B}}(r,\theta ,t)=\nabla \times (A(r,\theta ,t)\hat{{\varvec{e}}}_{\phi })+ B(r,\theta ,t)\hat{{\varvec{e}}}_{\phi }. \end{aligned}$$

(6)

Such a decomposition automatically satisfies ${\nabla \cdot {\varvec{B}}}=0$. Likewise, the (steady) large-scale flow field ${\varvec{u}}$ is written as the sum of an axisymmetric azimuthal component (differential rotation), and an axisymmetric “poloidal” component ${\varvec{u}}_{\rm p}$ ($\equiv u_r(r,\theta )\hat{{\varvec{e}}}_{r}+u_\theta (r,\theta )\hat{{\varvec{e}}}_{\theta }$), i.e., a flow confined to meridional planes:

$$\begin{aligned} {\varvec{u}}(r,\theta )={\varvec{u}}_{\rm p}(r,\theta )+ \varpi \varOmega (r,\theta )\hat{{\varvec{e}}}_{\phi } , \end{aligned}$$

(7)

where $\varpi =r\sin \theta$ and $\varOmega$ is the angular velocity ($\mathrm {rad\ s}^{-1}$). Substitution of (6) and (7) into the MHD induction equation (1) yields two separate (but coupled) evolution equations for A and B:

$${\partial {A}\over \partial {t}} = \underbrace{\eta \left( \nabla ^2-{1\over \varpi ^2}\right) A}_{{\rm resistive}\,{\rm decay}}- \underbrace{{{\varvec{u}}_{\rm p}\over \varpi }\cdot \nabla (\varpi A)}_{\rm transport}, $$

(8)

$$\begin{aligned} {\partial {B}\over \partial {t}}& {} = \underbrace{ \eta \left( \nabla ^2-{1\over \varpi ^2}\right) B+ {1\over \varpi }{\partial {(\varpi B)}\over \partial {r}}{\partial {\eta }\over \partial {r}} }_{{\rm resistive}\,{\rm decay}}- \,\underbrace{\varpi {\varvec{u}}_{\rm p}\cdot \nabla \left( {B\over \varpi }\right) }_{\rm transport} \nonumber \\&\quad - \underbrace{B\nabla \cdot {\varvec{u}}_{\rm p}}_{\rm compression}+ \underbrace{\varpi (\nabla \times (A\hat{{\varvec{e}}}_{\phi }))\cdot \nabla \varOmega }_{\rm shearing}. \end{aligned}$$

(9)

where in anticipation of later developments, the magnetic diffusivity may depend on radius inside the Sun.

Augmented with suitable additional source terms, Eqs. (8)–(9) will become our model axisymmetric dynamo equations. They are to be solved in a meridional plane, i.e., $R_{\rm i}\le r\le R_\odot$ and $0\le \theta \le \pi$, with regularity of the solutions requiring that $A=0$ and $B=0$ on the symmetry axis. It is usually assumed that the deep radiative interior can be treated as a perfect conductor, so that one sets $A=0$ and $\partial (rB)/\partial r=0$ at some depth $R_{\rm i}$ chosen deeper than the lowest extent of the region where dynamo action is taking place. It is usually assumed that the Sun/star is surrounded by a vacuum, in which no electrical currents can flow, i.e., $\nabla \times {\varvec{B}}=0$; such an axisymmetric potential field, expressed via Eq. (6), then requires

$$\begin{aligned}\left( \nabla ^2-{1\over \varpi ^2}\right) A=0, \quad B=0, \quad r/R_\odot > 1, \end{aligned}$$

(10)

Formulated in this manner, the dynamo solution spontaneously “picks” its own parity, i.e., its symmetry with respect to the equatorial plane. Alternately, one may solve only in a meridional quadrant ($0\le \theta \le \pi /2$) and impose equatorial parity via the boundary condition at the equatorial plane ($\theta =\pi /2$):

$$\begin{aligned}&{\partial {A}\over \partial {\theta }}=0, \quad \, B=0 \quad \rightarrow \,\mathrm {antisymmetric}, \end{aligned}$$

(11)

$$\begin{aligned}&A=0, \quad \displaystyle {\partial {B}\over \partial {\theta }}=0 \quad \rightarrow \,\mathrm {symmetric}. \end{aligned}$$

(12)

Mechanisms of magnetic field generation

The Sun’s poloidal magnetic component, as measured on photospheric magnetograms, reverses polarity near sunspot cycle maximum, which (presumably) corresponds to the epoch of peak internal toroidal field T. The poloidal component P, in turn, peaks at time of sunspot minimum. The cyclic regeneration of the Sun’s full large-scale field can thus be thought of as a temporal sequence of the form

$$\begin{aligned} P(+) \rightarrow T(-) \rightarrow P(-) \rightarrow T(+) \rightarrow P(+) \rightarrow \dots , \end{aligned}$$

(13)

where the $(+)$ and $(-)$ refer to the signs of the poloidal and toroidal components, as established observationally. A full magnetic cycle of period $\simeq 22\,{\hbox {years}}$ thus consists of two successive sunspot cycles, each of duration $\sim 11\,{\hbox {years}}$. The dynamo problem can thus be broken into two sub-problems: generating a toroidal field from a pre-existing poloidal component ($P\rightarrow T$), and a poloidal field from a pre-existing toroidal component ($T\rightarrow P$). In the solar case, the former turns out to be straightforward, but the latter is not.

Poloidal to toroidal: $P\rightarrow T$

Consider the various terms on the RHS of Eq. (9); transport neither creates nor destroys magnetic flux, and resistive decay destroys magnetic flux. The compression term does not contribute significantly for strongly subsonic flows, for which $\nabla \cdot {\varvec{u}}\simeq 0$.² The shearing term in Eq. (9), however, is a true source term, as it amounts to converting rotational kinetic energy into magnetic energy. This is the needed $P\rightarrow T$ production mechanism, and it plays a major role in very nearly all extant dynamo models of the solar cycle.

Neglecting resistive decay and meridional flows, the $\phi$-component of the induction equation (9) integrates to yield a linear growth of the toroidal magnetic component B in response to (kinematic) shearing of a pre-existing poloidal magnetic field ${\varvec{B}}_{\mathrm{p}}$ ($\equiv \nabla \times (A\hat{{\varvec{e}}}_{\phi })$) by differential rotation:

$$\begin{aligned} B(r,\theta ,t)= \underbrace{\left( {\varvec{B}}_\mathrm{p}\cdot \nabla \varOmega \right) }_{\mathrm{shearing}}t . \end{aligned}$$

(14)

It is easily verified that over a $\sim 10\,{\hbox {years}}$ time span a solar-like differential rotation can shear a $\sim 10\,{\hbox {G}}$ dipole into $\sim 1\,{\hbox {kG}}$ toroidal field, antisymmetric about the equatorial plane, in agreement with Hale’s Laws. However, there is no comparable source term on the RHS of Eq. (8); this becomes clearer upon rewriting this expression in the equivalent form:

$$\begin{aligned} \left( {\partial \over \partial {t}} + {\varvec{u}}_p\cdot \nabla \right) (\varpi A) =\underbrace{\eta \left( \nabla ^2-{1\over \varpi ^2}\right) A .}_{{\rm resistive}\,{\rm decay}} \end{aligned}$$

(15)

The LHS is the Lagrangian derivative of $\varpi A$, and described the variation of this quantity as a fluid element is followed in the meridional flow ${\varvec{u}}_p$. The RHS is again dissipation. Therefore, no matter what the toroidal component does and how A is advected around by the meridional flow, A will inexorably decay. Going back now to Eq. (9), notice now that once A is gone, the shearing term vanishes, which means that B will in turn inexorably decay. This is the essence of Cowling’s theorem: an axisymmetric flow cannot sustain an axisymmetric magnetic field against resistive decay.³

Toroidal to poloidal: $T\rightarrow P$

In view of Cowling’s theorem, we have no choice but to look for some fundamentally non-axisymmetric process to provide an additional source term in Eq. (8). It turns out that under solar interior conditions, there exist various mechanisms that can power an azimuthally-oriented electromotive force (hereafter emf), and thus act as a source of poloidal magnetic field. In what follows we introduce and briefly describe the three classes of such mechanisms that appear most promising, but defer discussion of their implementation in dynamo models to Sects. 4 and 5, where illustrative solutions are also presented.

Turbulence and mean-field electrodynamics

The outer $\sim$ 30% of the Sun are in a state of thermally-driven turbulent convection. This turbulence is anisotropic because of the stratification imposed by gravity, and lacks reflectional symmetry due to the influence of the Coriolis force. Since we are primarily interested in the evolution of the large-scale magnetic field (and perhaps also the large-scale flow), mean-field electrodynamics offers a tractable alternative to 3D turbulent MHD. The idea is to express the total flow and field as the sum of mean components, $\left\langle {\varvec{u}}\right\rangle$ and $\left\langle {\varvec{B}}\right\rangle$, and small-scale fluctuating components ${\varvec{u}}^\prime$, ${\varvec{B}}^\prime$. This is not a linearization procedure, in that we are not assuming that $|{\varvec{u}}^\prime |/|\left\langle {\varvec{u}}\right\rangle |\ll 1$ or $|{\varvec{B}}^\prime |/|\left\langle {\varvec{B}}\right\rangle |\ll 1$. In the context of the axisymmetric models to be described below, the averaging (“〈 〉”) is most naturally interpreted as a longitudinal average, with the fluctuating flow and field components vanishing when so averaged, i.e., $\left\langle {\varvec{u}}^\prime \right\rangle =0$ and $\left\langle {\varvec{B}}^\prime \right\rangle =0$. The mean field $\left\langle {\varvec{B}}\right\rangle$ is then interpreted as the large-scale, axisymmetric magnetic field usually associated with the solar cycle. Upon this separation and averaging procedure, the MHD induction equation for the mean component becomes

$$\begin{aligned} {\partial {\left\langle {\varvec{B}}\right\rangle }\over \partial {t}}= \nabla \times (\left\langle {\varvec{u}}\right\rangle \times \left\langle {\varvec{B}}\right\rangle + \varvec{\mathcal {E}}-\eta \nabla \times \left\langle {\varvec{B}}\right\rangle ), \end{aligned}$$

(16)

with

$$\begin{aligned} \varvec{\mathcal {E}}=\left\langle {\varvec{u}}^\prime \times {\varvec{B}}^\prime \right\rangle \end{aligned}$$

(17)

being the mean turbulent electromotive force induced by the fluctuating flow and field components. Its appearance in Eq. (16) is the only novelty, as compared the original MHD induction Eq. (1). It arises here because the cross product ${\varvec{u}}^\prime \times {\varvec{B}}^\prime$ in general will not vanish upon averaging, even though ${\varvec{u}}^\prime$ and ${\varvec{B}}^\prime$ do so individually.

The reader versed in fluid dynamics will have recognized in the turbulent electromotive force the equivalent of Reynolds stresses appearing in mean-field versions of the Navier–Stokes equations, and will have anticipated that the next (crucial!) step is to relate $\varvec{\mathcal {E}}$ to the mean field $\left\langle {\varvec{B}}\right\rangle$ in order to achieve closure. This is carried out by expressing $\varvec{\mathcal {E}}$ as a truncated series expansion in $\left\langle {\varvec{B}}\right\rangle$ and its derivatives. Retaining the first two terms yields, in component notation:

$$\begin{aligned} \mathcal{E}_i=a_{ij}\left\langle B\right\rangle _j+b_{ijk}{\partial {\left\langle B\right\rangle _j}\over \partial {x_k}}+\cdots \end{aligned}$$

(18)

where truncation is warranted if a good separation of scales exists between $\left\langle {\varvec{B}}\right\rangle$ and ${\varvec{B}}^\prime$. In such an expansion the tensors components $a_{ij}$ and $b_{ijk}$ may depend on properties of the flow, but not on $\left\langle {\varvec{B}}\right\rangle$. For the purposes of the foregoing construction of dynamo models, it is useful and instructive to separate the symmetric and antisymmetric parts of these tensors and rewrite (18) in the form:

$$\begin{aligned} {\varvec{\mathcal{E}}}= {\varvec{\alpha }}\cdot \left\langle {\varvec{B}}\right\rangle +{\varvec{\gamma }}\times \left\langle {\varvec{B}}\right\rangle -{\varvec{\beta }}\cdot (\nabla \times \left\langle {\varvec{B}}\right\rangle ) +\ldots \end{aligned}$$

(19)

where the tensor ${\varvec{\alpha }}$ is the symmetric part of ${\varvec{a}}$, the vector ${\varvec{\gamma }}$ collects the three independent components of the antisymmetric part of ${\varvec{a}}$, and the rank-2 tensor ${\varvec{\beta }}$ collects the antisymmetric part of ${\varvec{b}}$ (see Krause and Rädler 1980; Schrinner et al. 2007, for further details).

Calculating the components of these various tensors requires a turbulence model, and is no trivial task. We defer discussion of specific formulations to Sect. 4.2, but note already the following:

• Even if $\left\langle {\varvec{B}}\right\rangle$ is axisymmetric, the ${\varvec{\alpha }}$-term in Eq. (18) will effectively introduce source terms for A and B in both Eqs. (8) and (9), so that Cowling’s theorem can be circumvented.

• The helical twisting of toroidal fieldlines by the Coriolis force, as originally proposed by Parker (1955), corresponds to a specific functional form for ${\varvec{\alpha }}$, and so finds formal quantitative expression in mean-field electrodynamics.

• The isotropic part of the ${\varvec{\beta }}$ tensor directly adds to $\eta$ in Eq. (16); it corresponds to a turbulent diffusivity, and will thus enhance the dissipation of the large-scale magnetic component $\left\langle {\varvec{B}}\right\rangle$.

The crucial ${\varvec{\alpha }}\cdot \left\langle {\varvec{B}}\right\rangle$ term on the RHS of Eq. (19) is called the $\alpha$-effect; it acts as a source term for both A and B, and thus offers a viable $T\rightarrow P$ mechanism; but there is no free lunch here: there cannot be an ${\varvec{\alpha }}$-term without an associated turbulent diffusivity, as both are parts of the turbulent electromotive force $\varvec{\mathcal {E}}$.

The Babcock–Leighton mechanism

The larger sunspot pairs (“bipolar magnetic regions”, hereafter BMR) often emerge with a systematic tilt with respect to the E–W direction, in that on average, the leading sunspot (with respect to the direction of solar rotation) is located at a lower latitude than the trailing sunspot, the more so the higher the latitude of the emerging BMR (see, e.g., Stenflo and Kosovichev 2012; McClintock and Norton 2013). This pattern is known as “Joy’s law”. The tilt of the magnetic axis of a BMR implies a non-zero projection along the N–S direction, which amounts to a dipole moment. The decay of BMRs and subsequent dispersal of their magnetic flux by surface flows can release a fraction of this dipole moment and contribute to the global dipole.

This process is clearly observed in synoptic magnetograms such as Fig. 3, and is well reproduced by surface flux transport simulations (more on these in Sect. 5.2 below). The net effect of the emergence and decay of many such BMRs is thus to take a formerly toroidal internal magnetic field and convert a fraction of its associated flux into a net surface dipole moment, i.e., $T\rightarrow P$. This is known as the Babcock–Leighton mechanism, after Babcock (1961) and Leighton (1964). Together with shearing by differential rotation, it can in principle yield a working dynamo loop.

The solar polar cap magnetic flux adds up to $\sim 10^{22}\,$Mx, which is equivalent to the unsigned flux contained in one large bipolar active regions. About $10^{25}\,$Mx of (unsigned) magnetic flux emerge in bipolar active regions in the course of a typical activity cycle, so the toroidal-to-poloidal flux conversion efficiency required of the Babcock–Leighton mechanim is quite low. As per Eq. (14), the poloidal flux so produced would in itself be sufficient to account for the magnetic flux emerging in all active regions in a cycle, considering the amplitude of the observed differential rotation (on this point see also Cameron and Schüssler 2015).

Hydrodynamical and magnetohydrodynamical instabilities

The tachocline is the rotational shear layer uncovered by helioseismology immediately beneath the Sun’s convective envelope, providing a smooth match between the latitudinal differential rotation of the envelope, and the rigidly rotating radiative core (see, e.g., Spiegel and Zahn 1992; Brown et al. 1989; Tomczyk et al. 1995; Gough and McIntyre 1998; Charbonneau et al. 1999, and references therein). A number of magnetofluid instabilities can be excited within the tachocline, and the associated flow perturbations can develop a net helicity under the action of the Coriolis force. A systematic twist can then be imparted to an ambient mean toroidal field (or magnetic flux rope). This can drive an azimuthal mean electromotive force, and act as a $T\rightarrow P$ source for the poloidal component in a manner qualitatively similar to the $\alpha$-effect. Operating in in conjunction with rotational shearing of the poloidal field, such instabilities can potentially lead to a working dynamo loop. Instabilities investigated in this context include horizontal hydrodynamical and MHD shear instabilities (Dikpati and Gilman 2001; Arlt et al. 2007b; Cally et al. 2008; Dikpati et al. 2009), helical wave instabilities along magnetic flux ropes (Schüssler 1996; Schüssler and Ferriz-Mas 2003; Ferriz-Mas et al. 1994) and the buoyancy-drive or shear-driven breakup of thin magnetized fluid layers (Matthews et al. 1995; Thelen 2000a; Chatterjee et al. 2011).

A selection of representative mean-field models

Each and every one of the $T\rightarrow P$ mechanisms described in Sect. 3.2 relies on fundamentally non-axisymmetric physical effects, yet these must be “forced” into axisymmetric dynamo equations for the mean magnetic field. There are a great many different ways of doing so, which explains the wide variety of dynamo models of the solar cycle to be found in the recent literature. The aim of this and the following section is to provide representative examples of various classes of models, to highlight their similarities and differences, and illustrate their successes and failings. In all cases, the model equations are to be understood as describing the evolution of the mean field $\left\langle {\varvec{B}}\right\rangle$, namely the large-scale, slowly varying, axisymmetric component of the total solar magnetic field. For those wishing to code up their own versions of these (relatively) simple models, Jouve et al. (2008) have set up a suite of benchmark calculations against which numerical dynamo solutions can be validated.

Common model ingredients

All kinematic solar dynamo models have some basic “ingredients” in common, most importantly (i) a solar structural model, (ii) a differential rotation profile, and (iii) a magnetic diffusivity profile (possibly depth-dependent).

Helioseismology has pinned down with great accuracy the internal solar structure, including the exact location of the core–envelope interface (Basu 2016), as well as the internal differential rotation (Howe 2009). Unless noted otherwise, all illustrative models discussed in this section are computed using the following analytic formulae for the angular velocity $\varOmega (r,\theta )$ and magnetic diffusivity $\eta (r)$:

$$\begin{aligned} {\varOmega (r,\theta )\over \varOmega _{\rm E}}=\varOmega _{\rm C}+ {\varOmega _{\rm S}(\theta )-\varOmega _{\rm C}\over 2} \left[ 1+{{\,\mathrm{erf}\,}}\left( {r-r_{\rm c}\over w}\right) \right] , \end{aligned}$$

(20)

with

$$\begin{aligned} \varOmega _{\rm S}(\theta )=1-a_2\cos ^2\theta -a_4\cos ^4\theta , \end{aligned}$$

(21)

and

$$\begin{aligned} {\eta (r)\over \eta _{\rm T}}= \varDelta \eta +{1-\varDelta \eta \over 2} \left[ 1+{{\,\mathrm{erf}\,}}\left( {r-r_{\rm c}\over w}\right) \right] . \end{aligned}$$

(22)

With appropriately chosen parameter values, Eq. (20) describes a solar-like differential rotation profile, namely a purely latitudinal differential rotation in the convective envelope, with equatorial acceleration and smoothly matching a core rotating rigidly at the angular speed of the surface mid-latitudes.⁴ This rotational transition takes place across a spherical shear layer of half-thickness w coinciding with the core–envelope interface at $r_{\rm c}/R_\odot =0.7$ (see Fig. 4b, with parameter values listed in caption). As per Eq. (22), a similar transition takes place with the net diffusivity, falling from some large, “turbulent” value $\eta _{\rm T}$ in the envelope to a much smaller diffusivity $\eta _{\rm c}$ in the convection-free radiative core, the diffusivity contrast being given by $\varDelta \eta =\eta _{\rm c}/\eta _{\rm T}$. Given helioseismic constraints, these represent minimal yet reasonably realistic choices.⁵

Such a solar-like differential rotation profile is quite complex, in that it is characterized by three partially overlapping shear regions: a strong positive radial shear in the equatorial regions of the tachocline, an even stronger negative radial shear in its the polar regions, and a significant latitudinal shear throughout the convective envelope and extending partway into the tachocline. For a tachocline of half-thickness $w/R_\odot =0.05$, the mid-latitude latitudinal shear at $r/R_\odot =0.7$ is comparable in magnitude to the equatorial radial shear; its potential contribution to dynamo action should not be casually dismissed.

Fig. 4

Common ingredients to the mean-field and mean-field-like dynamo models discussed in this and the following section. Panel b shows the run of net magnetic diffusivity (blue) with depth, as described by Eq. (22), with parameter values $r_c/R_\odot =0.7$ and $w/R_\odot =0.05$. The red and green profiles refer to the depth dependency of the poloidal source terms introduced in Sects. 4.2.10 and 5.4.2, respectively. Panel b shows isocontours of angular velocity normalized to the surface equatorial value, as generated by Eq. (20) with parameter values $\varOmega _{\rm C}=0.8752$, $a_2=0.1264$, $a_4=0.1591$. The radial shear changes sign at colatitude $\theta =55^\circ$ at the core–envelope interface (dotted line on all panels). Panel c depicts streamlines of the meridional flow, from the model of van Ballegooijen and Choudhuri (1988), with parameter values $m=0.5$, $p=0.25$, $q=0$, and $r_{\rm b}=0.675$

$\alpha \varOmega$ mean-field models

Calculating the $\alpha$-effect and turbulent diffusivity

Mean-field electrodynamics is a subject well worth its own full-length review, so the foregoing discussion will be limited to the bare essentials. Detailed discussion of the topic can be found in Krause and Rädler (1980), Moffatt (1978), Rüdiger and Hollerbach (2004), chapter 3 in Schrijver and Siscoe (2009), and in the recent review articles by Ossendrijver (2003) and Hoyng (2003).

The task at hand is to calculate the components of the ${\varvec{\alpha }}$ and ${\varvec{\beta }}$ tensor in terms of the statistical properties of the underlying turbulence. A particularly simple case is that of homogeneous, weakly anisotropic turbulence, which reduces the ${\varvec{\alpha }}$ and ${\varvec{\beta }}$ tensor to simple scalars, so that the mean electromotive force becomes

$$\begin{aligned} \varvec{\mathcal {E}}=\alpha \left\langle {\varvec{B}}\right\rangle -\beta \nabla \times \left\langle {\varvec{B}}\right\rangle . \end{aligned}$$

(23)

This is the form commonly used in solar dynamo modelling, even though turbulence in the solar interior is most likely inhomogeneous and anisotropic. There are three (kinematic) regimes in which simple closed form expressions for $\alpha$ and $\beta$ can be obtained in terms of the small-scale flow ${\varvec{u}}^\prime$, all ultimately amounting to the large-scale field $\left\langle {\varvec{B}}\right\rangle$ suffering little deformation by the turbulent flow ${\varvec{u}}^\prime$:

• 1. weak turbulent magnetic fields, in the sense $|{\varvec{B}}^\prime | \ll |\left\langle {\varvec{B}}\right\rangle |$,

• 2. low ($<1$) magnetic Reynolds number $\mathrm {Rm}=v\ell /\eta$,

• 3. short coherence time turbulence, in the sense that the lifetime of turbulent eddies $\tau _{\rm c}$ is smaller than their turnover time $\ell /v$, i.e., the Strouhal Number $\mathrm {St}=\tau _c v/\ell <1$.

With mixing length theory of convection suggesting $v\sim 10^4 \,{\text{cm s}}^{-1}$ and $\ell \sim 10^9 \,\mathrm {cm}$ as characteristic velocities and length scales for the dominant turbulent eddies, and $\eta \sim 10^4 \,\mathrm {cm}^2\,\mathrm {s}^{-1}$, one finds $\mathrm {Rm}=v\ell /\eta \sim 10^9$; mixing length convection also implicitly assumes $\mathrm {St}\simeq 1$, and high-$\mathrm {Rm}$ MHD turbulence simulations suggest that $|{\varvec{B}}^\prime | \gg |\left\langle {\varvec{B}}\right\rangle |$ if a mean-field is present at all. Equation (23) should be dubious already. Nonetheless, if either of the three conditions above is satisfied, it can be shown that in the kinematic regime (i.e., $\alpha$ and $\beta$ are not affected by either $\left\langle {\varvec{B}}\right\rangle$ or ${\varvec{B}}^\prime$):

$$ \alpha\sim - {\tau _{\rm c}\over 3} \left\langle {\varvec{u}}^\prime \cdot \nabla \times {\varvec{u}}^\prime \right\rangle , $$

(24)

$$ \beta\sim {\tau _{\rm c}\over 3} \left\langle ({\varvec{u}}^\prime )^2\right\rangle . $$

(25)

Order-of-magnitude estimates of the scalar coefficients yield $\alpha \sim \varOmega \ell$ and $\beta \sim v\ell$, where $\varOmega$ is the solar angular velocity. At the base of the solar convection zone, one then finds $\alpha \sim 10^3 \,{\text{cm s}}^{-1}$ and $\beta \sim 10^{12} \,\mathrm {cm}^2\,\mathrm {s}^{-1}$, these being understood as very rough estimates. Because the kinetic helicity may well change sign along the longitudinal (averaging) direction, thus leading to cancellation, the resulting value of $\alpha$ may be much smaller than its r.m.s. deviation about the longitudinal mean. In contrast the quantity being averaged on the right hand side of Eq. (25) is positive definite, so one would expect a more “stable” mean value (see Hoyng 1993; Ossendrijver et al. 2001, for further discussion). Equations (24)–(25) certainly indicate that one cannot have an $\alpha$-effect without turbulent diffusivity being also present, but that the converse is possible, e.g. for non-helical flows. At any rate, difficulties in computing $\alpha$ and $\beta$ from first principle (whether as scalars or tensors) have led to these quantities often being treated as free parameters of mean-field dynamo models, to be adjusted (within reasonable bounds) to yield the best possible fit to observed solar cycle characteristics, most importantly the cycle period. One finds in the literature numerical values in the approximate ranges $10{-}10^3 \,{\text{cm s}}^{-1}$ for $\alpha$ and $10^{10}{-}10^{13} \,\mathrm {cm}^2\,\mathrm {s}^{-1}$ for $\beta$.

The cyclonic character of the $\alpha$-effect also indicates that it is equatorially antisymmetric and positive in the Northern solar hemisphere, except perhaps at the base of the convective envelope, where the horizontal divergence of downflows can lead to a sign change. These expectations have been confirmed in a general sense by theory and numerical simulations (see, e.g., Rüdiger and Kitchatinov 1993; Brandenburg et al. 1990; Ossendrijver et al. 2001; Käpylä et al. 2006a, also Sect. 6 herein).

In cases where the turbulence is more strongly inhomogeneous, an additional effect comes into play: turbulent pumping. Mathematically it is associated with the antisymmetric part to the $\alpha$-tensor in Eq. (19), whose three independent components can be recast as a velocity-like vector field ${\varvec{\gamma }}$ that acts as an additional (and non-solenoidal) contribution to the mean flow:

$$\begin{aligned} {\varvec{\mathcal{E}}}= \alpha \left\langle {\varvec{B}}\right\rangle +{\varvec{\gamma }}\times \left\langle {\varvec{B}}\right\rangle +\beta \nabla \times \left\langle {\varvec{B}}\right\rangle . \end{aligned}$$

(26)

with

$$\begin{aligned} {\varvec{\gamma }}\sim -{1\over 6}\tau _c\nabla \left\langle ({\varvec{u}}^\prime )^2\right\rangle , \end{aligned}$$

(27)

in the same kinematic physical regimes in which Eqs. (24)–(25) hold.

Algebraic $\alpha$-quenching

Assuming the dynamo-generated magnetic field grows in time, magnetic tension will increasingly resist deformation by the small-scale turbulent fluid motions. Something is bound to happen when the growing dynamo-generated mean magnetic field reaches a magnitude such that its energy per unit volume is comparable to the kinetic energy of the underlying turbulent fluid motions:

$$\begin{aligned} {\left\langle {\varvec{B}}\right\rangle ^2\over 8\pi }={1\over 2}\rho ({\varvec{u}}^\prime )^2 . \end{aligned}$$

(28)

Denoting the corresponding equipartition field strength by $B_{\rm eq}$, one often introduces an ad hoc nonlinear dependency of $\alpha$ directly on the mean-field $\left\langle {\varvec{B}}\right\rangle$ by writing:

$$\begin{aligned} \alpha \rightarrow \alpha (\left\langle {\varvec{B}}\right\rangle )={\alpha _0\over 1+(\left\langle {\varvec{B}}\right\rangle /B_{\rm eq})^2} . \end{aligned}$$

(29)

This expression “does the right thing”, in that $\alpha \rightarrow 0$ as $\left\langle {\varvec{B}}\right\rangle$ starts to exceed $B_{\rm eq}$. It remains an extreme oversimplification of the complex interaction between flow and field that characterizes MHD turbulence,⁶ but its wide usage in solar dynamo modeling makes it a nonlinearity of choice for the illustrative purpose of this section.

Dynamical $\alpha$-quenching

The nonlinear feedback of the small-scale magnetic field ${\varvec{B}}^\prime$ on small-scale cyclonic turbulence can be also understood in terms of magnetic helicity conservation. Magnetic helicity ($\mathcal{H}$) is a topological measure of linkage between magnetic flux systems linking a volume of fluid (Berger 1999). It is mathematically defined as

$$\begin{aligned} \mathcal{H}_B= \int _V {\varvec{A}}\cdot {\varvec{B}}\mathrm{d}V, \end{aligned}$$

(30)

where ${\varvec{B}}=\nabla \times {\varvec{A}}$. In a closed system, i.e. without helicity flux through its boundaries, magnetic helicity can be shown to evolve according to:

$$\begin{aligned} {\mathrm{d}\over \mathrm{d}{t}}\int {\varvec{A}}\cdot {\varvec{ B}}\mathrm{d}V = -{8\pi \eta \over c}\int {\varvec{J}}\cdot {\varvec{B}}\mathrm{d}V . \end{aligned}$$

(31)

In the ideal limit $\eta \rightarrow 0$, which is the relevant limit for dynamo action in the interior of the sun and stars, the RHS vanishes and Eq. (31) then indicates that total helicity must be conserved, or at best vary on the (long) diffusive timescale. Conservation of magnetic helicity thus puts a strong constraint on the high-$\mathrm {Rm}$ amplification of any magnetic field that carries a net helicity, which is certainly the case with the large-scale solar magnetic field.

Following the scale separation logic introduced in Sect. 3.2.1, and because both the current density ${\varvec{J}}$ and vector potential ${\varvec{A}}$ are linearly related to ${\varvec{B}}$, the total vector potential and electric current density can be written as ${\varvec{A}}=\left\langle {\varvec{A}}\right\rangle +{\varvec{A}}^\prime$ and ${\varvec{J}}=\left\langle {\varvec{J}}\right\rangle +{\varvec{J}}^\prime$, with again $\left\langle {\varvec{A}}^\prime \right\rangle =0$ and $\left\langle {\varvec{J}}^\prime \right\rangle =0$. Substituting into Eq. (31) and averaging leads to an evolution equation for the mean helicity of the large-scale field:

$$\begin{aligned} {\mathrm{d}\over \mathrm{d}{t}}\int \left\langle {\varvec{A}}\right\rangle \cdot \left\langle {\varvec{B}}\right\rangle \mathrm{d}V = +2\int \varvec{\mathcal {E}}\cdot \left\langle {\varvec{B}}\right\rangle \mathrm{d}V -{8\pi \eta \over c}\int \left\langle {\varvec{J}}\right\rangle \cdot \left\langle {\varvec{B}}\right\rangle \mathrm{d}V , \end{aligned}$$

(32)

where $\varvec{\mathcal {E}}=\left\langle {\varvec{u}}^\prime \times {\varvec{B}}^\prime \right\rangle$ is the usual turbulent emf (see, e.g., Sect. 3.4.7 in Schrijver and Siscoe 2009). Subtracting Eq. (32) from the unaveraged form of (31) yields a companion equation for the evolution of small-scale magnetic helicity:

$$\begin{aligned} {\mathrm{d}\over \mathrm{d}{t}}\int \left\langle {\varvec{A}}^\prime \cdot {\varvec{B}}^\prime \right\rangle \mathrm{d}V = -2\int \varvec{\mathcal {E}}\cdot \left\langle {\varvec{B}}\right\rangle \mathrm{d}V -{8\pi \eta \over c}\int \left\langle {\varvec{J}}^\prime \cdot {\varvec{B}}^\prime \right\rangle \mathrm{d}V . \end{aligned}$$

(33)

Because the first terms on the RHS of Eqs. (32) and (33) are identical but for their sign, the total helicity given by the sum of Eqs. (32) and (33) is still conserved in the ideal limit $\eta \rightarrow 0$. But these expressions also indicate that the turbulent emf leads to the buildup of helicity of opposite signs at large and small spatial scales. This corresponds to a dual helicity cascade away from the scale at which the emf is operating (Brandenburg 2001). Buildup of a helical large-scale magnetic field is only possible in the $\mathrm {Rm}\rightarrow \infty$ regime because an equal amount of oppositely-signed magnetic helicity is cascading down to dissipative scales. In this way $\left\langle {\varvec{B}}\right\rangle$ can be amplified by the turbulent electromotive force $\varvec{\mathcal {E}}$, with its growth rate ultimately determined by the rate at which helicity can be transported and dissipated at small scales, or evacuated from the region where dynamo action is taking place (Pipin et al. 2013; Blackman 2015).

Following Pouquet et al. (1976), the total (isotropic) $\alpha$-effect is often written as the sum of a two contributions, proportional respectively to the kinetic and magnetic (current) helicities:

$$\begin{aligned} \alpha =\alpha _K+\alpha _M = - {\tau _{\rm c}\over 3}\left( \left\langle {\varvec{u}}^\prime \cdot \nabla \times {\varvec{u}}^\prime \right\rangle - {1\over \rho } \left\langle {\varvec{B}}^\prime \cdot \nabla \times {\varvec{B}}^\prime \right\rangle \right) . \end{aligned}$$

(34)

A key finding of Pouquet et al. (1976) is that these two contributions have opposite signs, i.e, the magnetic helicity contribution to the total $\alpha$-effect opposes that of kinetic helicity. This forms the basis of the various dynamical $\alpha$-quenching formulations that have been proposed in the literature (e.g., Kleeorin et al. 1995; Blackman and Brandenburg 2002, and references therein). For example, Brandenburg et al. (2009) take $\alpha _K$ to be temporally steady and given by Eq. (24), and the evolution of the magnetic contribution to be described by:

$$\begin{aligned} {\partial {\alpha _M}\over \partial {t}}=-2\eta k_f^2 \left( {\varvec{\mathcal {E}}\cdot \left\langle {\varvec{B}}\right\rangle \over B_{\rm eq}^2}+{\alpha _M\over \mathrm {Rm}}\right) , \end{aligned}$$

(35)

in the absence of helicity fluxes in or out of the dynamo region. The quantity $k_f$ is a scale factor relating current to magnetic helicity. Stable cycles amplitudes can be obtained by quenching the $\alpha$-effect in this manner (see also Schmalz and Stix 1991; Chatterjee et al. 2011; Pipin et al. 2012). Indeed, the quenching can even become “catastrophic”, in the sense that it sets in long before the mean-field reaches significant strength (see Brandenburg and Subramanian 2005).

An interesting situation can arise if the growth of $\alpha _M$ is such that $|\alpha _M|>|\alpha _K|$ over a substantial fraction of the magnetic cycle. The resulting sign change in the total $\alpha$-effect can then lead to a reversal in the direction of dynamo wave propagation (viz. Sect. 4.2.9 below). The effect has been observed in the mean-field model of Chatterjee et al. (2011), and may also be at play in some of the MHD simulations discussed in Sect. 6 further below.

Diffusivity quenching

The same small-scale magnetic field that quenches the $\alpha$-effect can in principle also reduce the turbulent diffusivity $\beta$ (Sect. 4.2.1). This effect has been included in some mean-field and mean-field-like solar cycle models, sometimes via a simple algebraic parametrization similar to Eq. (29) (e.g., Tobias 1996; Guerrero et al. 2009), sometimes in a more elaborate manner through specific turbulence models (e.g., Rüdiger et al. 1994; Rüdiger and Arlt 1996), and sometimes through a dynamical equation for $\beta$ in the spirit of dynamical $\alpha$-quenching (e.g., Muñoz-Jaramillo et al. 2011). The nature and magnitude of the consequent impact on cyclic amplitude and period are highly model-dependent. A noteworthy effect of magnetic diffusivity quenching is the possibility to produce super-equipartition magnetic fields in the tachocline (Tobias 1996; Gilman and Rempel 2005). On the other hand, the stability analyses of Arlt et al. (2007a, b) suggests that there exist a lower limit to the magnetic diffusivity, below which equipartition-strength toroidal magnetic field beneath the core–envelope interface become unstable.

Backreaction on large-scale flows

The backreaction of the growing magnetic field on the large-scale flows contributing to induction and transport can also quench the growth of the dynamo. In the context of solar cycle models, one could expect the Lorentz force to reduce the amplitude of differential rotation, gradually decreasing its inductive effect until the magnetic field amplitude stabilizes, as it does under $\alpha$-quenching. In the mean-field literature it has become costumary to distinguish two classes of (related) amplitude-limiting mechanisms:

• The Malkus–Proctor effect (after the groudbreaking numerical investigations of Malkus and Proctor 1975): this is the Lorentz force associated with the mean magnetic field directly affecting the large-scale flow $\left\langle {\varvec{u}}\right\rangle$.

• $\varLambda$-quenching (e.g., Kitchatinov and Rüdiger 1993; Kitchatinov et al. 1994): this is the Lorentz force impacting small-scale turbulence and the associated Reynolds stresses powering large-scale flows.

An efficient approach to model the Malkus–Proctor effect consists in simply dividing the large-scale flow into two components, the first (${\varvec{U}}$) corresponding to some prescribed, steady profile, and the second (${\varvec{U}}^\prime$) to a time-dependent flow field driven by the Lorentz force (see, e.g., Tobias 1997; Beer et al. 1998; Moss and Brooke 2000; Thelen 2000b; Covas et al. 2001; Brooke et al. 2002; Bushby 2006; Simard and Charbonneau 2020):

$$\begin{aligned} {\varvec{u}}={\varvec{U}}({\varvec{x}})+{\varvec{U}}^\prime ({\varvec{x}},t,\left\langle {\varvec{B}}\right\rangle ), \end{aligned}$$

(36)

with the (non-dimensional) governing equation for ${\varvec{U}}^\prime$ including only the Lorentz force and a viscous dissipation term on its right hand side:

$$\begin{aligned} {\partial {{\varvec{U}}^\prime }\over \partial {t}}= {\varLambda \over 4\pi \rho }(\nabla \times \left\langle {\varvec{B}}\right\rangle )\times \left\langle {\varvec{B}}\right\rangle + \mathrm {Pm}\nabla ^2{\varvec{U}}, \end{aligned}$$

(37)

where time has been scaled according to the magnetic diffusion time $\tau =R_\odot ^2/\eta _{\rm T}$. Two dimensionless parameters appear in Eq. (37). The first ($\varLambda$) is a numerical parameter setting the absolute scale of the magnetic field, and can be set to unity without loss of generality (cf. Tobias 1997; Phillips et al. 2002). The second, $\mathrm {Pm}=\nu /\eta$, is the magnetic Prandtl number. It measures the relative importance of viscous and Ohmic dissipation. An additional, long timescale is thus introduced in the system, associated with the evolution of the magnetically-driven flow; the smaller $\mathrm {Pm}$, the longer that timescale.

Incorporating $\varLambda$-quenching in mean-field or mean-field-like dynamo models requires a turbulence model allowing to calculate Reynolds stresses and their quenching by the magnetic field. Various such prescriptions have been developed (see Kitchatinov et al. 1994), and, upon being inserted in dynamo models, can lead to stable magnetic cycles (Küker et al. 1996; Rempel 2006a).

Nonlinear magnetic backreaction, whether through $\varLambda$ quenching or the Malkus–Proctor effect, can lead to strong modulation of the cycle amplitude and large-scale flow unfolding on timescales much longer than the primary cycle if the Prandlt number is significantly smaller than unity (see Brooke et al. 1998; Küker et al. 1999; Pipin 1999; Rempel 2006a); more on this in Sect. 7.2.3 further below.

Flux loss through magnetic buoyancy

Another amplitude-limiting mechanism is the loss of magnetic flux through magnetic buoyancy. Magnetic fields concentrations are buoyantly unstable in the convective envelope, and so should rise to the surface on time scales much shorter than the cycle period (see, e.g., Parker 1975; Schüssler 1977; Moreno-Insertis 1983, 1986). This is often incorporated on the right-hand-side of the dynamo equations by the introduction of an ad hoc loss term of the general form $-f(\left\langle {\varvec{B}}\right\rangle )\left\langle {\varvec{B}}\right\rangle$; the function f measures the rate of flux loss, and is often chosen proportional to the magnetic pressure $\left\langle {\varvec{B}}\right\rangle ^2$, thus yielding a cubic damping nonlinearity in the mean-field.

The degree to which flux emergence actually depletes the internal toroidal flux is not trivial to estimate quantitatively, as it hinges critically on the longitudinal extend of the buoyantly destabilized loop and on the manner in which the emerging flux disconnects from the underlying axisymmetric toroidal magnetic flux system; see Sect. 2.3 in Miesch and Teweldebirhan (2016) for an insightful discussion of this issue. In addition to regulating cycle amplitude in dynamo models, (see, e.g., Schmitt and Schüssler 1989; Moss et al. 1990), magnetic flux loss can also have a large impact on the cycle period (Kitchatinov et al. 2000).

The $\alpha \varOmega$ dynamo equations

Adding the mean-electromotive force given by Eq. (23) to the MHD induction equation leads to the following form for the axisymmetric mean-field dynamo equations:

$$ {\partial {\left\langle A\right\rangle }\over \partial {t}}= \underbrace{(\eta +\beta ) \left( \nabla ^2-{1\over \varpi ^2}\right) \left\langle A\right\rangle }_{{\rm turbulent}\,{\rm diffusion}}- {{\varvec{u}}_{\rm p}\over \varpi }\cdot \nabla (\varpi \left\langle A\right\rangle )+ {\underbrace{\alpha \left\langle B\right\rangle }_{{\rm MFE}\,{\rm source}}}, $$

(38)

$$\begin{aligned} {\partial {\left\langle B\right\rangle }\over \partial {t}}& {} = \underbrace{(\eta +\beta ) \left( \nabla ^2-{1\over \varpi ^2}\right) \left\langle B\right\rangle + {1\over \varpi }{\partial {\varpi \left\langle B\right\rangle }\over \partial {r}} {\partial {(\eta +\beta )}\over \partial {r}}}_{\mathrm {turbulent}\,{\rm diffusion}}- \varpi {\varvec{u}}_{\rm p}\cdot \nabla \left( {\left\langle B\right\rangle \over \varpi }\right) - \left\langle B\right\rangle \nabla \cdot {\varvec{u}}_{\rm p} \nonumber \\&\quad +\underbrace{\varpi (\nabla \times (\left\langle A\right\rangle \hat{{\varvec{e}}}_{\phi }))\cdot \nabla \varOmega }_{\rm shearing}+ \underbrace{\nabla \times [\alpha \nabla \times (\left\langle A\right\rangle \hat{{\varvec{e}}}_{\phi })]}_{{\rm MFE}\,{\rm source}}, \end{aligned}$$

(39)

[compare to Eqs. (8)–(9)]. There are now source terms on both right hand sides, so that dynamo action becomes possible at least in principle. For solar-like convective turbulence one expects $\beta \gg \eta$, and in what follows the total magnetic diffusivity is denoted $\eta _{\rm T}=\eta +\beta$ ($\simeq \beta$ in the turbulent fluid layers). The relative importance of the $\alpha$-effect and shearing terms in Eq. (39) is measured by the ratio of the two dimensionless dynamo numbers

$$\begin{aligned} C_\alpha ={\alpha _0 R_\odot \over \eta _0}, \quad C_\varOmega ={(\varDelta \varOmega )_0R_\odot ^2\over \eta _0}, \end{aligned}$$

(40)

where in the spirit of dimensional analysis, $\alpha _0$, $\eta _0$, and $(\varDelta \varOmega )_0$ are “typical” values for the $\alpha$-effect, turbulent diffusivity, and angular velocity contrast. These quantities arise naturally in the non-dimensional formulation of the mean-field dynamo equations, when time is expressed in units of the magnetic diffusion time $\tau$ based on the envelope (turbulent) diffusivity:

$$\begin{aligned} \tau ={R_\odot ^2\over \eta _0}. \end{aligned}$$

(41)

In the solar case, it is usually estimated that $C_\alpha \ll C_\varOmega$, so that the $\alpha$-term is neglected in Eq. (39); this results in the class of dynamo models known as $\alpha \varOmega$ dynamos, which will be the only ones discussed in the remainder of this section. Models retaining both $\alpha$-terms are dubbed $\alpha ^2\varOmega$ dynamos, and may be relevant to the solar case even in the $C_\alpha \ll C_\varOmega$ regime, in particular if the latter operates in a very thin layer, e.g. the tachocline (see, e.g., DeLuca and Gilman 1988; Gilman et al. 1989; Choudhuri 1990).⁷

Eigenvalue problems and initial value problems

With the large-scale flows, turbulent diffusivity and $\alpha$-effect considered given, Eqs. (38, 39) become truly linear in A and B. It becomes possible to seek eigensolutions in the form

$$\begin{aligned} \left\langle A\right\rangle (r,\theta ,t)= a(r,\theta )\exp (s t), \quad \left\langle B\right\rangle (r,\theta ,t)= b(r,\theta )\exp (s t), \end{aligned}$$

(42)

with $s=\sigma +i\omega$. Substitution of these expressions into Eqs. (38, 39) yields an eigenvalue problem for s and associated eigenfunction $\{a,b\}$. The real part $\sigma$ of the eigenvalue is then a growth rate, and the imaginary part $\omega$ an oscillation frequency. One typically finds that $\sigma <0$ until the total dynano number

$$\begin{aligned} D=C_\alpha \times C_\varOmega , \end{aligned}$$

(43)

exceeds a critical value $D_{\rm crit}$ beyond which $\sigma >0$, corresponding to a growing solutions. Such solutions are said to be supercritical, while the solution with $\sigma =0$ is critical. A dynamo solution is considered weakly supercritical if its dynamo number only slightly exceeds $D_{\rm crit}$; cyclic solution exhibiting polarity reversals require $\omega \not =0$. In the weakly supercritical regime such cyclic solutions typically have $\sigma \ll \omega$, while $\sigma \gg \omega$ in the strongly supercritical regime.

With any amplitude-limiting nonlinearity included, the dynamo equations are usually solved as an initial-value problem, with some arbitrary low-amplitude seed field used as initial condition. Equations (38, 39) are then integrated forward in time using some appropriate time-stepping scheme. A useful quantity to monitor in order to ascertain saturation is the magnetic energy within the computational domain:

$$\begin{aligned} \mathcal{E}_B={1\over 8\pi }\int _V \left\langle {\varvec{B}}\right\rangle ^2 \, \mathrm {d}V. \end{aligned}$$

(44)

Figure 5 shows time series of this quantity in a sequence of $\alpha$-quenched kinematic $\alpha \varOmega$ mean-field dynamo solutions. The four solutions have increasing values for the dynamo number D, and all start from the same initial condition of very weak magnetic field.

Fig. 5

Time series of total magnetic energy in an $\alpha$-quenched kinematic axisymmetric $\alpha \varOmega$ mean-field dynamo model, for increasing values of the dynamo number scaled to its critical value ($D/D_{\rm crit}$), as labeled. Magnetic energy is scaled to the corresponding equipartition field strength $B_{\rm eq}$ in Eq. (29), via Eq. (44). All solutions are initialized with a purely toroidal magnetic field of very low amplitude. The gray lines indicate the linear phase, during which the magnetic amplitude grows exponentially at a rate increasing with the dynamo number. In the nonlinearly saturated phase that is eventually established, the overall magnetic cycle amplitude increases with increasing value of the dynamo number

The linear phase of exponential growth (gray lines), at rates increasing with D, is followed by saturation at an energy level also increasing with D; these are behaviors typical of $\alpha$-quenched mean-field and mean-field-like dynamo models operating not too far in the supercritical regime. Here $\alpha$-quenching has the desired effect, namely stabilizing the cycle amplitude at field strengths corresponding to a significant fraction of the equipartition value $B_{\rm eq}$ introduced in the quenching parametrization (29). Dynamo models achieving amplitude saturation through backreaction on large-scale flows (viz. Sect. 4.2.5) behave similarly, provided the magnetic Prandtl number is not much smaller than unity.

Dynamo waves and cycle period

One of the most remarkable property of the (linear) $\alpha \varOmega$ dynamo equations is that they support travelling wave solutions. This was first demonstrated in Cartesian geometry by Parker (1955), who proposed that a latitudinally-travelling “dynamo wave” was at the origin of the observed equatorward drift of sunspot emergences in the course of the cycle. This finding was subsequently shown to hold in spherical geometry, as well as for non-linear models (Yoshimura 1975; Stix 1976). Dynamo waves⁸ travel in a direction ${\varvec{s}}$ given by

$$\begin{aligned} {\varvec{s}}=\alpha \nabla \varOmega \times \hat{{\varvec{e}}}_{\phi }, \end{aligned}$$

(45)

a result now known as the “Parker–Yoshimura sign rule”. Dynamo waves also materialize in $\alpha ^2\varOmega$ mean-field dynamos (Choudhuri 1990), as long as the ratio $C_\alpha /C_\varOmega$ is not too high (see, e.g., Charbonneau and MacGregor 2001).

Recalling the rather complex form of the helioseismically inferred solar internal differential rotation (cf. Fig. 4b), even an $\alpha$-effect of uniform sign in each hemisphere can produce complex migratory patterns, as will be apparent in the illustrative $\alpha \varOmega$ dynamo solutions to be discussed presently. If the seat of the dynamo is to be identified with the low-latitude portion of the tachocline, and if the (positive) radial shear therein dominates over the latitudinal shear, then equatorward migration of dynamo waves will require a negative $\alpha$-effect in the low latitudes of the Northern solar hemisphere.

In linear $\alpha \varOmega$ mean-field models without a significant meridional flow, the cycle frequency increases with the total dynamo number D (viz. Eq. 43). In nonlinearly saturated models, the cycle frequency shows reduced sensitivity to D and becomes equal to some approximately fixed fraction of the magnetic diffusion time (41). The primary determinant of the (dimensional) period then becomes the adopted value for the turbulent diffusivity. Although model dependent to some extent, decadal periods typically require a few $10^{11}$ to $10^{12}\,\hbox {cm}^2\,\hbox {s}^{-1}$, roughly consistent with estimates from mixing length models of convective energy transport; values lower by a factors of $\sim 10$ are required for dynamos contained in radially thin layers, because the smaller radial length scale enhances dissipation. Similarly low values are also possible (and in fact expected) in the upper tachocline, where residual turbulent diffusivity presumably results from convective overshoot. The ratio of poloidal-to-toroidal field strength, in turn, is found to scale as some power (usually close to 1/2) of the ratio $C_\alpha /C_\varOmega$, at a fixed value of the product $C_\alpha \times C_\varOmega$.

Representative results

We first consider $\alpha \varOmega$ models without meridional circulation [${\varvec{u}}_{\rm p}=0$ in Eqs. (38, 39)], with the $\alpha$-term omitted in Eq. (39), and using the magnetic diffusivity and angular velocity profiles of Fig. 4. We investigate the behavior of $\alpha \varOmega$ models, with the $\alpha$-effect concentrated just above the core–envelope interface (green line on Fig. 4a). We also consider two latitudinal dependencies, namely $\alpha \propto \cos \theta$, which is the “minimal” possible latitudinal dependency compatible with the required equatorial antisymmetry of the Coriolis force, and an $\alpha$-effect concentrated towards the equator⁹ via an assumed latitudinal dependency $\alpha \propto \sin ^2\theta \cos \theta$. Unless otherwise noted all models have $C_\varOmega =25{,}000$, $|C_\alpha |=10$, $\eta _{\rm T}/\eta _{\rm c}=10$, and $\eta _{\rm T}=5\times 10^{11} \,\mathrm {cm}^2\,\mathrm {s}^{-1}$, which leads to $\tau \simeq 300\,{\text {years}}$. To facilitate comparison between solutions, here antisymmetric parity is imposed via the boundary condition at the equator (via Eq. 11). Algebraic $\alpha$-quenching, in the form of Eq. (29), is chosen as the amplitude-limiting nonlinearity.

Figures 6 and 7 show a selection of such dynamo solutions, in the form of animations in meridional planes and time–latitude diagrams of the toroidal field extracted at the core–envelope interface, here $r_{\rm c}/R_\odot =0.7$. If sunspot-producing toroidal flux ropes form in regions of peak toroidal field strength, and if those ropes rise radially to the surface, then such diagrams are directly comparable to the sunspot butterfly diagram of Fig. 2.

Fig. 6

Stills from meridional plane animations of various $\alpha \varOmega$ dynamo solutions using different latitudinal profiles and sign for the $\alpha$-effect, as labeled. The polar axis coincides with the left quadrant boundary. The toroidal field is plotted as filled contours (constant increments, green to blue for negative B, yellow to red for positive B), on which poloidal fieldlines are superimposed (blue for clockwise-oriented fieldlines, orange for counter-clockwise orientation). The dashed line is the core–envelope interface at $r_c/R=0.7$. Time–latitude “butterfly” diagrams for these three solutions are plotted in Fig. 7. For accompanying movies, see the supplementary material section below

Fig. 7

Northern hemisphere time–latitude (“butterfly”) diagrams for the three $\alpha \varOmega$ dynamo solutions of Fig. 6, constructed at the depth $r_{\rm c}/R_\odot =0.7$ corresponding to the core–envelope interface. Isocontours of toroidal field are normalized to their peak amplitudes, and plotted for increments $\varDelta B/\max (B)=0.2$, with yellow-to-red (green-to-blue) contours corresponding to $B>0$ ($<0$). The assumed latitudinal dependency of the $\alpha$-effect is given above each panel. Other model ingredients as in Fig. 4. Note the co-existence of two distinct cycle periods in the solution shown in Panel b

Examination of these animations reveals that the dynamo is concentrated in the vicinity of the core–envelope interface, where the adopted radial profile for the $\alpha$-effect is maximal (cf. Fig. 4a). In conjunction with a fairly thin tachocline, the radial shear therein then dominates the induction of the toroidal magnetic component. With an eye on Fig. 4b, notice also how the dynamo waves propagates along isocontours of angular velocity, in agreement with the Parker–Yoshimura sign rule (cf. Sect. 4.2.9). Note that even for an equatorially-concentrated $\alpha$-effect (Panels b and c), a strong polar branch is nonetheless apparent in the butterfly diagrams, a direct consequence of the stronger radial shear present at high latitudes in the tachocline (see also corresponding animations). Models using an $\alpha$-effect operating throughout the whole convective envelope, on the other hand, would feed primarily on the latitudinal shear therein, so that for positive $C_\alpha$ the dynamo mode would propagate radially upward in the envelope (see Lerche and Parker 1972).

It is noteworthy that co-existing dynamo branches, as in Panel b of Fig. 7, can have distinct dynamo periods (on this see also Belvedere et al. 2000), which in nonlinearly saturated solutions leads to long-term amplitude modulation. This is typically not expected in dynamo models where the only nonlinearity present is a simple algebraic quenching formula such as Eq. (29). This does not occur for the $C_\alpha <0$ solution, where both branches propagate away from each other, but share a common latitude of origin and so are phased-locked at the onset (cf. Panel c of Fig. 7).

The models discussed above are based on rather minimalistics and partly ad hoc assumptions on the form of the $\alpha$-effect. More elaborate models have been proposed, relying on calculations of the full $\alpha$-tensor based on an underlying turbulence model (see, e.g., Kitchatinov and Rüdiger 1993). While this approach usually displaces the ad hoc assumptions into the turbulence model, it has the definite merit of offering an internally consistent approach to the calculation of turbulent diffusivities and large-scale flows. Rüdiger and Brandenburg (1995) and Rempel (2006b) remain a good example of the current state-of-the-art in this area; see also Rüdiger and Arlt (2003), Inceoglu et al. (2017), and references therein.

Critical assessment

From a practical point of view, the outstanding success of the mean-field $\alpha \varOmega$ model remains its robust explanation of the observed equatorward drift of toroidal field-tracing sunspots in the course of the cycle in terms of a dynamo wave. On the theoretical front, the model is also buttressed by mean-field electrodynamics which, in principle, offers a physically sound theory from which to compute the (critical) $\alpha$-effect and magnetic diffusivity. The models’ primary uncertainties turn out to lie at that level, in that the application of the theory to the Sun in a tractable manner requires additional assumptions that are most likely not met under solar interior conditions. Those uncertainties are exponentiated when taking the theory into the nonlinear regime, to calculate the dependence of the $\alpha$-effect and diffusivity on the magnetic field strength. This latter problem remains very much open at this writing.

Interface dynamos

Strong $\alpha$-quenching and the saturation problem

The $\alpha$-quenching expression (29) used in the preceding section amounts to saying that dynamo action saturates once the mean, dynamo-generated field reaches an energy density comparable to that of the driving turbulent fluid motions [viz. Eq. (28)]. At the base of the solar convective envelope, one finds $B_{\rm eq}\simeq 8 \,\mathrm {kG}$, for $v\simeq 5\times 10^3 \,{\text{cm s}}^{-1}$, according to mixing length theory of convection. However, various calculations and numerical simulations have indicated that long before the mean field $\left\langle {\varvec{B}}\right\rangle$ reaches this strength, the helical turbulence reaches equipartition with the small-scale, turbulent component of the magnetic field (e.g., Cattaneo and Hughes 1996, and references therein), ultimately as a consequence of the constraint posed by magnetic helicity conservation (viz. Sect. 4.2.3 herein; see also Brandenburg and Subramanian 2005). Such calculations also indicate that the ratio between the small-scale and mean magnetic components should itself scale as $\mathrm {Rm}^{1/2}$, where $\mathrm {Rm}=v\ell /\eta$ is a magnetic Reynolds number based on the microscopic magnetic diffusivity. This then leads to the alternate algebraic quenching expression

$$\begin{aligned} \alpha \rightarrow \alpha (\left\langle {\varvec{B}}\right\rangle )={\alpha _0\over 1+\mathrm {Rm}(\left\langle {\varvec{B}}\right\rangle /B_{\rm eq})^2}, \end{aligned}$$

(46)

known in the literature as strong $\alpha$-quenching or catastrophic quenching. Since $\mathrm {Rm}\sim 10^{9}$ in the solar convection zone, this leads to quenching of the $\alpha$-effect for very low amplitudes for the mean magnetic field, of order $10^{-1}$ G. Even though significant field amplification is likely in the formation of a toroidal flux rope from the dynamo-generated magnetic field, we are now a very long way from the 10–100 kG demanded by simulations of buoyantly rising magnetic flux ropes (see Fan 2009).

A beautifully simple way out of this difficulty was proposed by Parker (1993), in the form of interface dynamos. In a situation where a radial shear and $\alpha$-effect are segregated on either side of a discontinuity in magnetic diffusivity (taken to coincide with the core–envelope interface), the $\alpha \varOmega$ dynamo equations support solutions in the form of travelling surface waves localized on the discontinuity in diffusivity. The key aspect of Parker’s solution is that for supercritical dynamo waves, the ratio of peak toroidal field strength on either side of the discontinuity surface is found to scale with the diffusivity ratio as

$$\begin{aligned} {\max (B_2)\over \max (B_1)} \sim \left( {\eta _2\over \eta _1} \right) ^{-1/2}, \end{aligned}$$

(47)

where the subscript “1” refers to the low-$\eta$ region below the core–envelope interface, and “2” to the high-$\eta$ region above. If one assumes that the envelope diffusivity $\eta _2$ is of turbulent origin then $\eta _2\sim \ell v$, so that the toroidal field strength ratio then scales as $\sim (v\ell /\eta _1)^{1/2}\equiv \mathrm {Rm}^{1/2}$. This is precisely the factor needed to bypass strong $\alpha$-quenching (Charbonneau and MacGregor 1996). Somewhat more realistic variations on Parker’s basic model were later elaborated (MacGregor and Charbonneau 1997; Zhang et al. 2004), and, while differing in important details, nonetheless confirmed Parker’s overall picture.  Tobias (1996) discusses in detail a related Cartesian model bounded in both horizontal and vertical direction, but with constant magnetic diffusivity $\eta$ throughout the domain. Like Parker’s original interface configuration, his model includes an $\alpha$-effect residing in the upper half of the domain, with a purely radial shear in the bottom half. The introduction of diffusivity quenching then reduces the diffusivity in the shear region, “naturally” turning the model into a bona fide interface dynamo, supporting once again oscillatory solutions in the form of dynamo waves travelling in the “latitudinal” x-direction. This basic model was later generalized by various authors (Tobias 1997; Phillips et al. 2002) to include the nonlinear backreaction of the dynamo-generated magnetic field on the differential rotation (as described in Sect. 4.2.5).

Representative results

The next obvious step is to construct an interface dynamo in spherical geometry, using a solar-like differential rotation profile. Such numerical models can be constructed as a variation on the $\alpha \varOmega$ models considered earlier, introducing a continuous but rapidly varying diffusivity profile at the core–envelope interface, an $\alpha$-effect concentrated at the base of the envelope, and the radial shear immediately below, but without significant overlap between these two source regions (see Panel b of Fig. 8).

In spherical geometry, and especially in conjunction with a solar-like differential rotation profile, making a working interface dynamo model is markedly trickier than if only a radial shear is operating, as in the Cartesian models discussed earlier (see Charbonneau and MacGregor 1997; Markiel and Thomas 1999; Zhang et al. 2003a). Panel a of Fig. 8 shows a butterfly diagram for a numerical interface solution with $C_\varOmega =2.5\times 10^5$, $C_\alpha =+10$, and a core-to-envelope diffusivity contrast $\varDelta \eta =10^{-2}$. The poleward propagating equatorial branch is what one would expect from the combination of positive radial shear and positive $\alpha$-effect according to the Parker–Yoshimura sign rule.¹⁰ Here the $\alpha$-effect is (artificially) concentrated towards the equator, by imposing a latitudinal dependency $\alpha \sim \sin (4\theta )$ for $\pi /4\le \theta \le 3\pi /4$, and zero otherwise.

Fig. 8

A representative interface dynamo model in spherical geometry. This solution has $C_\varOmega =2.5\times 10^5$, $C_\alpha =+10$, and a core-to-envelope diffusivity contrast of $10^{-2}$. Panel a shows a sunspot butterfly diagram, and Panel b a series of radial cuts of the toroidal field at latitude $15^\circ$. The (normalized) radial profiles of magnetic diffusivity, $\alpha$-effect, and radial shear are also shown, again at latitude $15^\circ$. The core–envelope interface is again at $r/R_\odot =0.7$ (dotted line), where the magnetic diffusivity varies near-discontinuously. Panels c and d show the variations of the core-to-envelope peak toroidal field strength and dynamo period with the diffusivity contrast, for a sequence of otherwise identical dynamo solutions

The model does achieve the kind of toroidal field amplification one would like to see in interface dynamos. This can be seen in Panel b of Fig. 8, which shows radial cuts of the toroidal field taken at latitude $\pi /8$, and spanning half a cycle. Notice how the toroidal field peaks below the core–envelope interface (vertical dotted line), well below the $\alpha$-effect region and near the peak in radial shear. Panel c of Fig. 8 shows how the ratio of peak toroidal field below and above $r_{\rm c}$ varies with the imposed diffusivity contrast $\varDelta \eta$. The dashed line is the dependency expected from Eq. (47). For relatively low diffusivity contrast, $-1.5\le \log (\varDelta \eta ) \lesssim 0$, both the toroidal field ratio and dynamo period increase as $\sim (\varDelta \eta )^{-1/2}$. Below $\log (\varDelta \eta )\sim -1.5$, the $\max (B)$-ratio increases more slowly, and the cycle period falls, contrary to expectations for interface dynamos (see, e.g., MacGregor and Charbonneau 1997). This is basically an electromagnetic skin-depth effect; the cycle period is such that the poloidal field cannot diffuse as deep as the peak in radial shear in the course of a half cycle. The dynamo then runs on a weaker shear, thus yielding a smaller field strength ratio and weaker overall cycle.

Critical assessment

The great success of interface dynamos remains their ability to evade $\alpha$-quenching even in its “strong” formulation, and so produce equipartition or perhaps even super-equipartition mean toroidal magnetic fields immediately beneath the core–envelope interface. They represent the only variety of dynamo models formally based on mean-field electrodynamics that can achieve this without additional physical effects introduced into the model. All of the uncertainties regarding the calculations of the $\alpha$-effect and magnetic diffusivity carry over from $\alpha \varOmega$ to interface models, with diffusivity quenching becoming a particularly sensitive issue in the latter class of models (see, e.g., Tobias 1996).

Interface dynamos suffer acutely from “structural fragility”. A given model’s dynamo behavior often end up depending sensitively on what one would normally hope to be minor details of the model’s formulation. For example, the interface solutions of Fig. 8 are found to behave very differently if the $\alpha$-effect region is displaced slightly upwards, or assumes other latitudinal dependencies. Moreover, as exemplified by the calculations of Mason et al. (2008), this sensitivity carries over to models in which the coupling between the two source regions is achieved by transport mechanisms other than diffusion. This sensitivity is exacerbated when a latitudinal shear is present in the differential rotation profile; compare, e.g., the behavior of the $C_\alpha >0$ solutions discussed here to those discussed in Markiel and Thomas (1999). Often in such cases, a mid-latitude $\alpha \varOmega$ dynamo mode, powered by the latitudinal shear within the tachocline and envelope, interferes with and/or overpowers the interface mode [see also Dikpati et al. (2005)]. Because of this structural fragility, interface dynamo solutions also end up being annoyingly sensitive to choice of time-step size, spatial resolution, and other purely numerical details. From a modelling point of view, interface dynamos lack robustness.

Including meridional circulation: flux transport dynamos

Meridional circulation is as unavoidable as differential rotation in turbulent, compressible rotating convective shells (see Featherstone and Miesch 2015, and references therein). Long considered unimportant from the dynamo point of view, meridional circulation has gained popularity in recent years, initially in the Babcock–Leighton context but now also in other classes of models.

Accordingly, we now add a steady meridional circulation to our basic $\alpha \varOmega$ models of Sect. 4.2. The convenient parametric form developed by van Ballegooijen and Choudhuri (1988) is used here and in all later illustrative models including meridional circulation (Sects. 4.5 and 5). This “minimal” parameterization defines a steady quadrupolar circulation pattern, with a single flow cell per quadrant extending from the surface down to a depth $r_{\rm b}$. Circulation streamlines are shown in Fig. 4c; the flow is poleward in the outer convection zone, with an equatorial return flow peaking slightly above the core–envelope interface, and rapidly vanishing below.

The inclusion of meridional circulation in the non-dimensionalized $\alpha \varOmega$ dynamo equations leads to the appearance of a new dimensionless quantity, again a magnetic Reynolds number, but now based on an appropriate measure of the meridional circulation speed $u_0$ and turbulent diffusivity $\eta _{\rm T}$:

$$\begin{aligned} \mathrm {Rm}={u_0R_\odot \over \eta _{\rm T}}. \end{aligned}$$

(48)

Using the value $u_0=1500 \,{\text{cm s}}^{-1}$ from observations of the poleward surface meridional flow leads to $\mathrm {Rm}\simeq 200$, again with $\eta _{\rm T}=5\times 10^{11} \,\mathrm {cm}^2 \,\mathrm {s}^{-1}$. In the solar cycle context, using higher values of Rm thus implies proportionally lower turbulent diffusivities.

Representative results

Meridional circulation can bodily transport the dynamo-generated magnetic field [terms labeled “transport” in Eqs. (8, 9)], and therefore, for a (presumably) solar-like equatorward return flow that is vigorous enough—in the sense of Rm being large enough—overpower the Parker–Yoshimura propagation rule (see, e.g. Choudhuri et al. 1995; Küker et al. 2001; Pipin and Kosovichev 2011a). The behavioral turnover from dynamo wave-like solutions to circulation-dominated magnetic field transport sets in when the circulation speed becomes comparable to the propagation speed of the dynamo wave. In the circulation-dominated regime, the cycle period loses sensitivity to the assumed turbulent diffusivity value, and becomes determined primarily by the circulation’s turnover time. Models achieving equatorward propagation of the deep toroidal magnetic component in this manner are now often called flux-transport dynamos (see Dikpati and Gilman 2009; Karak et al. 2014, and references therein).

With a solar-like differential rotation profile, however, once again the situation is far more complex. Starting from the most basic $\alpha \varOmega$ dynamo solution with $\alpha \sim \cos \theta$ (Fig. 7a), new solutions are now recomputed, this time including meridional circulation. An animation of a typical solution is shown in Fig. 9, and a sequence of time–latitude diagrams for four increasing values of the circulation flow speed, as measured by Rm, are plotted in Fig. 10.

At $\mathrm {Rm}=50$, little difference is seen with the circulation-free solutions (cf. Fig. 7a), except for an increase in the cycle frequency, due to the Doppler shift experienced by the equatorwardly propagating dynamo wave (Roberts and Stix 1972). At $\mathrm {Rm}=100$ (part B), the cycle frequency has further increased and the poloidal component produced in the high-latitude region of the tachocline is now advected to the equatorial regions on a timescale becoming comparable to the cycle period, so that a cyclic activity, albeit with a longer period, becomes apparent at low latitudes. At $\mathrm {Rm}=10^{3}$ (panel c and animation in Fig. 9) the dynamo mode now peaks at mid-latitude, a consequence of the inductive action of the latitudinal shear, favored by the significant stretching experienced by the poloidal fieldlines as they get advected equatorward. At $\mathrm {Rm}=2000$ the original high latitude dynamo mode has all but vanished, and the mid-latitude mode is dominant. The cycle period is now set primarily by the turnover time of the meridional flow; this is the telltale signature of flux-transport dynamos.

Fig. 9

Meridional plane animations for an $\alpha \varOmega$ dynamo solutions including meridional circulation. With $\mathrm {Rm}=10^{3}$, this solution is operating in the advection-dominated regime as a flux-transport dynamo. The corresponding time–latitude “butterfly” diagram is plotted in Fig. 10c below. Color-coding of the toroidal magnetic field and poloidal fieldlines as in Fig. 6. For an accompanying movie, see the supplementary material section below

Fig. 10

Time–latitude “butterfly” diagrams for the $\alpha$-quenched $\alpha \varOmega$ solutions depicted earlier in Panel a of Fig. 7, except that meridional circulation is now included, with a $\mathrm {Rm}=50$, b $\mathrm {Rm}=100$, c $\mathrm {Rm}=1000$, and d $\mathrm {Rm}=2000$. For the turbulent diffusivity value adopted here, $\eta _{\rm T}=5\times 10^{11} \,\mathrm {cm}^2\,\mathrm {s}^{-1}$, $\mathrm {Rm}=200$ would corresponds to a solar-like circulation speed

All this may look straightforward, but it must be emphasized that not all dynamo models with solar-like differential rotation behave in this (relatively) simple manner. For example, the $C_\alpha =-10$ solution with $\alpha \sim \sin ^2\theta \cos \theta$ (Fig. 7c) transits to a steady mode as Rm increases above $\sim 10^2$. Moreover, the sequence of $\alpha \sim \cos \theta$ shown in Fig. 10 actually presents a narrow window around $\mathrm {Rm}\sim 200$ where the dynamo is decaying, due to a form of destructive interference between the high-latitude $\alpha \varOmega$ mode and the mid-latitude advection-dominated dynamo mode that emerges at higher values of Rm. Qualitatively similar results were obtained by Küker et al. (2001) using different prescriptions for the $\alpha$-effect and solar-like differential rotation (see in particular their Fig. 11; also Rüdiger and Elstner 2002; Bonanno et al. 2003).

When transport by turbulent pumping is included (see Käpylä et al. 2006b), $\alpha \varOmega$ models including meridional circulation can provide time–latitude “butterfly” diagrams that are closer to solar-like, even without an equatorward return flow in the deep convection zone (Pipin and Kosovichev 2013).

Even if the meridional flow is too slow—or the turbulent magnetic diffusivity too high—to force the dynamo model in the advection-dominated regime, being much faster at the surface the poleward flow can dominate the spatio-temporal evolution of the radial surface magnetic field. For the dynamo solutions of Fig. 10, at low circulation speeds (${\mathrm {Rm}}\lesssim 50$) the spatiotemporal evolution of the surface radial field is simply a diffused imprint of the equatorward drift of the deep-seated toroidal field. At higher circulation speeds, however, the surface magnetic field is swept instead towards the pole becoming strongly concentrated and amplified there for Rm exceeding a few hundreds.

Critical assessment

From the modelling point-of-view, in the kinematic regime at least the inclusion of meridional circulation yields a much better fit to observed surface magnetic field evolution, as well as a robust setting of the cycle period. Whether it can provide an equally robust equatorward propagation of the deep toroidal field is less clear. The results presented here in the context of mean-field $\alpha \varOmega$ models suggest a rather complex overall picture, and in interface dynamos the cartesian solutions obtained by Petrovay and Kerekes (2004) even suggest that dynamo action can be severely hindered. Yet, in other classes of models discussed below (Sects. 4.5 and 5), circulation does have this desired effect.

On the other hand, dynamo models including meridional circulation tend to produce surface polar field strength largely in excess of observed values, unless magnetic diffusion is significantly enhanced in the surface layers, and/or field submergence takes place very efficiently. This is a direct consequence of magnetic flux conservation in the converging poleward flow. This situation carries over to the other types of models to be discussed in Sects. 4.5 and 5, unless additional modelling assumptions are introduced (e.g., enhanced surface magnetic diffusivity, see Dikpati et al. 2004), or if a counterrotating meridional flow cell is introduced in the high latitude regions (Dikpati et al. 2004; Jiang et al. 2009), a feature that has actually been detected in surface Doppler measurements as well as helioseismically during cycle 22 (Haber et al. 2002; Ulrich and Boyden 2005).

A more fundamental and potential serious difficulty harks back to the kinematic approximation, whereby the form and speed of ${\varvec{u}}_{\rm p}$ is specified a priori. Meridional circulation is a relatively weak flow in the bottom half of the solar convective envelope (see Miesch 2005), and the stochastic fluctuations of the Reynolds stresses powering it are expected to lead to strong spatiotemporal variations, an expectation verified by both analytical models (Rempel 2005) and numerical simulations (Miesch 2005; Passos et al. 2017). The ability of the meridional flow to merrily advect equipartition-strength magnetic fields should not be taken for granted (but do see Rempel 2006a, b).

Before leaving the realm of mean-field dynamo models it is worth noting that many of the conceptual difficulties associated with calculations of the $\alpha$-effect and turbulent diffusivity are not unique to the mean-field approach, and in fact carry over to all models discussed in the following sections. In particular, to operate properly all of the upcoming solar dynamo models require the presence of a strongly enhanced magnetic diffusivity, presumably of turbulent origin, at least in the convective envelope. In this respect, the rather low value of the turbulent magnetic diffusivity needed to achieve high enough $\mathrm {Rm}$ in flux transport dynamos is also somewhat problematic, since the corresponding turbulent diffusivity ends up at least one order of magnitude smaller than the (uncertain) mean-field estimates. However, the model calculations of Muñoz-Jaramillo et al. (2011) indicate that magnetic diffusivity quenching may offer a viable solution to this latter quandary.

Models based on HD and MHD instabilities

The various rotationally-influenced hydrodynamical and magnetohydrodynamical instabilities described in Sect. 3.2.3 have been invoked as $T\rightarrow P$ inductive mechanisms that can, usually acting in conjunction with rotational shear, form the basis of viable solar cycle models. These models are all mean-field-like, in the sense that the axisymmetric mean-field dynamo equations (38)–(39) are solved, usually in their $\alpha \varOmega$ form and sometimes including a meridional flow, with mean-field turbulent diffusivity also implicitly invoked. The inductive action of the chosen instability is parametrized by a source term replacing the $\alpha$-effect (see, e.g., Ferriz-Mas et al. 1994; Dikpati and Gilman 2001; Ossendrijver 2000a).

Hydrodynamical shear instabilities

Perhaps the most thoroughly studied class of instability-based models is that relying on the shear instability of the latitudinal shear within the tachocline (Dikpati and Gilman 2001; Dikpati et al. 2004). The resulting “tachocline $\alpha$-effect” ends up proportional to the longitudinally-averaged kinetic helicity of the hydrodynamical instability planform, the latter computed in the framework of shallow-water theory. The Dikpati and Gilman (2001) dynamo model is of the flux transport variety, with the advective action of the deep meridional flow setting equatorward propagation of the deep toroidal field; it uses a solar-like differential rotation, depth-dependent magnetic diffusivity and meridional circulation pattern much similar to those shown in Fig. 4 herein. The usual ad hoc $\alpha$-quenching formula [cf. Eq. (29)] is introduced as the sole amplitude-limiting nonlinearity.

The model can be adjusted to yield equatorward propagating dominant activity belts, solar-like cycle periods, and correct phasing between the surface polar field and the tachocline toroidal field. These features can be traced primarily to the advective action of the meridional flow. It also yields the correct solution parity, and is self-excited. Its primary weakness, in its present form, is the reliance on a linear stability analysis that altogether ignores the known destabilizing effect of magnetic fields (see, e.g., Gilman and Fox 1997; Zhang et al. 2003b). Progress has been made in studying non-linear development of both the hydrodynamical and MHD versions of the shear instability (see Cally 2001; Cally et al. 2003; Dikpati et al. 2009), so that the needed improvements on the dynamo front are potentially forthcoming.

Instability of sheared magnetic layers

Dynamo models relying on the buoyant instability of sheared magnetized layers have been presented in Thelen (2000b), the layer being identified with the tachocline. Here also the resulting azimuthal electromotive force is parameterized as a mean-field-like $\alpha$-effect, introduced into the standard $\alpha \varOmega$ dynamo equations. The model is nonkinematic, in that it includes the magnetic backreaction on the large-scale, purely radial velocity shear within the layer. The analysis of Thelen (2000a) indicates that the $\alpha$-effect is negative in the upper part of the shear layer. Cyclic solutions are found in substantial regions of parameter space, and the solutions exhibit migratory wave patterns compatible with the Parker–Yoshimura sign rule. These models are not yet at the stage where they can be meaningfully compared with the solar cycle. They do have a number of attractive features, including their ability to operate in the strong field regime (see also Chatterjee et al. 2011).

Buoyant instability of magnetic flux tubes

Dynamo models relying on the non-axisymmetric buoyant instability of toroidal magnetic fields were first proposed by Schmitt (1987), and further developed by Ferriz-Mas et al. (1994); Schmitt et al. (1996) and Ossendrijver (2000a, b) for the case of toroidal flux tubes. Working in the framework of the thin-flux tube approximation (Spruit 1981), it is possible to construct “stability diagrams” taking the form of growth rate contours in a parameter space comprised of flux tube strength, latitudinal location, depth in the overshoot layer, etc. One such diagram, taken from Ferriz-Mas et al. (1994), is reproduced in Fig. 11. Dynamo action is possible when the instability is weak (growth rates $\gtrsim 1 \,\mathrm {year}$). In the case shown in Fig. 11, these regions are restricted to flux tube strengths in the approximate range 60–150 kG. The correlation between the flow and field perturbations is such as to yield a mean azimuthal electromotive force operationally equivalent to a positive $\alpha$-effect in the N-hemisphere (Ferriz-Mas et al. 1994; Brandenburg and Schmitt 1998).

Fig. 11

Stability diagram for toroidal magnetic flux tubes located in the overshoot layer immediately beneath the core–envelope interface. The plot shows contours of growth rates in the latitude-field strength plane. The gray scale encodes the azimuthal wavenumber of the mode with largest growth rate, and regions left in white are stable. Dynamo action is associated with the regions with growth rates $\sim$ 1 year, here labeled I and II (diagram kindly provided by A. Ferriz-Mas)

This dynamo mechanism operates without difficulty in the strong field regime (in fact it requires strong fields to operate). Difficulties include the need of a relatively finely tuned magnetic diffusivity to achieve a solar-like dynamo period, and a finely tuned level of subadiabaticity in the overshoot layer for the instability to turn on at the appropriate toroidal field strengths (compare Figs. 1 and 2 in Ferriz-Mas et al. 1994). Because the instability model predicts a positive $\alpha$-effect-like poloidal source term in the Northern hemisphere, equatorward propagation of the low latitude deep toroidal field would require the addition of a meridional flow, as it does in true mean-field models with positive $\alpha$-effect (cf. Sect. 4.4).

Babcock–Leighton models

Solar cycle models based on what is now called the Babcock–Leighton mechanism were first proposed by Babcock (1961) and further elaborated by Leighton (1964, 1969), yet they were all but eclipsed by the rise of mean-field electrodynamics in the mid- to late 1960s. Their revival was motivated not only by the mounting difficulties with mean-field models alluded to earlier, but also by the fact that synoptic magnetographic monitoring over sunspot cycles 21 and 22 gave strong evidence that the surface polar field reversals are indeed triggered by the decay of active regions (see Wang et al. 1989; Wang and Sheeley 1991; Mackay and Yeates 2012, and references therein).

The tilts of bipolar active regions

Consider a bipolar magnetic region (BMR) of (unsigned) magnetic flux $\varPhi$ emerging at latitude $\lambda$, with angular separation d between the two magnetic poles, and the line joining them making an tilt angle $\alpha$ with respect to the E–W direction. Spherical harmonic decomposition of such a surface magnetic flux distribution includes an axisymetric dipole contribution ($l=1,m=0$) given by:

$$\begin{aligned} \delta D={3d\cos \lambda \over 4\pi R^2}\varPhi \sin \alpha . \end{aligned}$$

(49)

with the sign of $\varPhi$ corresponding to that of the trailing polarity. This expression quantifies the $T\rightarrow P$ process in a Babcock–Leighton dynamo, with the formerly (i.e., prior to destabilisation and emergence) toroidal flux $\varPhi$ in a BMR providing a contribution to the ultimate dipole building up at the end of the cycle that is proportional to its associated $\delta D$. The quantities $\varPhi$, d and $\alpha$ are all accessible observationally from magnetograms. The tilt angle $\alpha$ emerges as a key quantity. Observationally, upon averaging over many BMRs the mean tilt is found to increase with latitude, a relationship known as Joy’s Law. Leighton (1969) parameterized it as:

$$\begin{aligned} \sin \alpha =0.5\sin \lambda , \end{aligned}$$

(50)

but other closely related functional forms have also been proposed (see Wang and Sheeley 1991; McClintock and Norton 2013; Pevtsov et al. 2014; Senthamizh Pavai et al. 2015, and references therein). Substantial scatter exists about this mean relationship, at a level increasing with decreasing magnetic flux of emerging BMRs. This indicates that the Babcock–Leighton mechanism is characterized by high stochastic variability.

The form of Eq. (49) suggests that for fixed $\varPhi$ and d, BMRs emerging at at high latitudes make the highest contribution to the ultimate dipole. This is however not the case, as the latter is also influenced by surface flux transport processes (viz. Fig. 12 and Sect. 5.2 immediately below). Surface flux transport simulations reveal that for solar-like surface meridional flow profiles, BMRs emerging close to the equator contribute the most to the ultimate dipole, because they undergo greater cross-equatorial diffusive cancellation of leading polarity flux (see,e.g., DeVore et al. 1984; Cameron et al. 2013; Jiang et al. 2014).

A robust prediction of numerical simulations of buoyantly rising thin magnetic flux tubes is that at a given emergence latitude, the tilt with respect to the East-West direction they acquire prior to emergence decreases with increasing magnetic strength of the rope (Fan 2009; Weber et al. 2013, and references therein). This occurs because more strongly magnetized flux ropes rise more rapidly through the convection zone, leaving less time for the Coriolis force to act on the secondary flow developing along the axis of the rope and impart to it the twist that, upon emergence, reproduces Joy’s Law (Fan et al. 1993; D’Silva and Choudhuri 1993; Caligari et al. 1995; Weber et al. 2011). Since the contribution to the total dipole moment of an emerging BMR is proportional to this tilt angle (viz. Eq. (49) above), this suggests that the Babcock–Leighton mechanism of poloidal field regeneration becomes quenched beyond field strengths of $\sim 10^5\,{\hbox {G}}$.

A number of studies have attempted to extract trends in tilt angle statistics with the amplitude of the sunspot cycle (e.g., Dasi-Espuig et al. 2010; Stenflo and Kosovichev 2012; Li and Ulrich 2012; McClintock and Norton 2013; Tlatova et al. 2018). Globally, the tilt reduction effect is marginally present, and more pronounced in some cycles and/or hemispheres than others (see Sect. 6 of Pevtsov et al. 2014, for further discussion).

Admittedly, there are many ill-understood physical steps between the diffuse magnetic field produced by the dynamo —of whichever variety—and the magnetic strength $B_0$ and flux $\varPhi$ of BMR-forming toroidal flux ropes. Nonetheless, many kinematic axisymetric models of Babcock–Leighton dynamo incorporate a quenching of their poloidal source terms in Eq. (38) as a function of the internal toroidal field strength B. In fact, the algebraic $\alpha$-quenching parametrization (29) is commonly used even though tilt quenching has nothing to do with the turbulent electromotive force. Again, it is a computationally friendly nonlinearity that simply “does the right thing”.

Thin flux tube simulations also indicate that for flux ropes of strength inferior to a few $10^4$ G, turbulent convection entrains the rising magnetic flux ropes too violently for a systematic Joy’s-Law-like tilt pattern to materialize; the Babcock–Leighton mechanism is thus also subject to a lower operating threshold, so that the associated dynamos are not self-excited, i.e., they cannot amplify an arbitrarily weak seed magnetic field.

Surface magnetic flux transport and the Babcock–Leighton mechanism

The magnetic flux liberated in the photosphere upon the decay of BMRs at low latitudes must find its way to polar regions in order to complete the $T\rightarrow P$ step of the dynamo loop. Surface flux transport (SFT) simulations solve the r-component of the magnetic induction equation (1) on a spherical surface corresponding to the solar photosphere. In the vast majority of SFT implementations (e.g., DeVore et al. 1984; Wang et al. 1989; Baumann et al. 2004; Jiang et al. 2014; Lemerle et al. 2015; Virtanen et al. 2017; Whitbread et al. 2017) the large-scale radial magnetic field component is assumed to be passively advected by the (axisymmetric) surface differential rotation and poleward meridional flow, while undergoing diffusive dispersal by unresolved convective flows (see Schrijver et al. 2002; Upton and Hathaway 2014b, for more realistic approaches to advection by convective flows). With proper parameter tuning, such models can reproduce quite well the observed spatiotemporal evolution of synoptic magnetograms.

Figure 12 shows results of a SFT simulation by Lemerle et al. (2015) of surface magnetic flux evolution throughout activity cycle 21 (1976–1986), using observed active region emergences as input.

Fig. 12

A surface flux transport simulation showing the Babcock–Leighton mechanism in action, in response to emergence of bipolar magnetic regions in the course of activity cycle 21 (1976–1986). The bottom panel shows the corresponding magnetic butterfly diagram, with the vertical lines flagging the five epochs at which the temporal cuts are plotted on the top panel. The grayscale is saturated at $\pm 5\,{\hbox {G}}$ to better emphasize the poleward transport at mid-latitudes. Surface flux evolution simulation taken from Lemerle et al. (2015), using as input the cycle 21 active region emergence database of Wang et al. (1989)

The bottom panel is grayscale rendering of the (zonally-averaged) synoptic magnetogram for the radial magnetic component, the simulated equivalent of the first cycle plotted on Fig. 3. The salt-and-pepper pattern at low latitudes reflects the emergence of bipolar magnetic regions, which do not zonally average out to zero here because of their tilt with respect to the East-West direction. The poleward transport of the trailing polarity shows up as slanded streaks, black (negative $B_r$) in the Northern hemisphere and white (positive $B_r$) in the South. This eventually leads to the reversal of the positive dipole moment of the initial condition, occuring here about 5 years after the beginning of the simulation. This is followed by the buildup of the negative dipole, peaking close to the end of the simulation at polar field strength $\simeq 5\,{\hbox {G}}$.

A different view of the dipole buildup is presented on the top panel of Fig. 12, showing latitudinal cuts of the zonally-averaged surface radial magnetic field spaced 25 months apart, as color-coded. Note the steep cross-equatorial gradient in $B_r$ building up and sustained throughout the rising and maximum phases of the sunspot cycle, the signature of diffusive cancellation of the leading polarity flux.

Magnetic flux transport

An important feature of solar cycle models based on the Babcock–Leighton mechanism is that the two substeps of the dynamo loop are segregated spatially; the $P\rightarrow T$ step is driven by rotational shear somewhere within the solar convection zone, as in the mean-field models considered in Sect. 4; whereas the $T\rightarrow P$ step takes place at photospheric levels. These two source regions must be coupled for a working dynamo loop to ensue. Meridional flows can provide the needed transport mechanism, acting as a “conveyor belt” dragging the surface field to the polar regions, then radially inward, then equatorward at the base of the convective envelope, where rotational shear can generate the strong toroidal fields that will give rise to emerging bipolar active regions in the next cycle. Coupling can also be mediated by magnetic diffusion or turbulent pumping, the latter potentially quite efficient in subsurface layers.

Babcock–Leighton solar cycle models are often characterized as “advection-dominated”, when meridional flow mediates transport, or “diffusion-dominated” when magnetic diffusion dominates transport within the convection zone (Yeates et al. 2008). The distinction hinges on the assumed value for the turbulent diffusivity, which effectively sets the value of the magnetic Reynolds number (see Eq. 48) governing the relative importance of advection by the meridional flow in the mean-field dynamo equations (38)–(39).

Axisymmetric kinematic mean-field-like models

The most straightforward approach in building a Babcock–Leighton solar cycle model is to adopt the $\alpha \varOmega$ form of the kinematic mean-field axisymmetric dynamo equations (38)–(39), and replace $\alpha$-term in (38) by a suitably designed axisymmetric source term designed to capture the $T\rightarrow P$ workings of the Babcock–Leighton mechanism.

Formulation of a poloidal source term

The first post-helioseismic dynamo model based on the Babcock–Leighton mechanism is due to Wang et al. (1991); these authors developed a coupled two-layer model ($2\times$ 1D), where a poloidal source term is introduced in the upper (surface) layer, and made linearly proportional to the toroidal field strength at the corresponding latitude in the bottom layer (on such 2-layer models, see also Cameron and Schüssler 2017a). A similar non-local approach was later used by Dikpati and Charbonneau (1999), Charbonneau et al. (2005), Guerrero and de Gouveia Dal Pino (2008), Hotta and Yokoyama (2010), Kitchatinov and Olemskoy (2012) and Olemskoy and Kitchatinov (2013). These kinematic 2D axisymmetric model implementation all use solar-like differential rotation and meridional flow profiles similar to Fig. 4 herein. The otherwise much similar implementation of Nandy and Choudhuri (2001, 2002), Chatterjee et al. (2004) and Jiang et al. (2007), on the other hand, use a mean-field-like local source term, concentrated in the upper layers of the convective envelope and operating in conjunction with a “buoyancy algorithm” whereby toroidal fields located at the core–envelope interface are locally removed and deposited in the surface layers when their strength exceeds some preset threshold. The implementation developed by Durney (1995) is probably closest to the essence of the Babcock–Leighton mechanism (see also Durney et al. 1993; Durney 1996, 1997; Muñoz-Jaramillo et al. 2010); whenever the deep-seated toroidal field exceeds some preset threshold, an axisymmetric “double ring” of vector potential is deposited in the surface layer, and left to spread latitudinally under the influence of magnetic diffusion. As shown by Muñoz-Jaramillo et al. (2010), this formulation, used in conjunction with the axisymmetric models discussed in what follows, also leads to a good reproduction of the observed synoptic evolution of surface magnetic flux.

In all cases the poloidal source term is concentrated in the outer convective envelope, and, in the language of mean-field electrodynamics, amounts to a positive $\alpha$-effect, in that a positive dipole moment is being produced from a positive deep-seated mean toroidal field. Most aforecited model implementations introduce an algebraic $\alpha$-quenching-like upper operating threshold on the toroidal field strength. The Durney (1995), Nandy and Choudhuri (2001) and Charbonneau et al. (2005) implementations also have a lower operating threshold, as suggested by thin flux tubes simulations.

Representative results

Figure 13 is a meridional plane animation of a representative Babcock–Leighton dynamo solution computed following the model implementation of Charbonneau et al. (2005). The equatorward advection of the deep toroidal field by meridional circulation is here clearly apparent. Note also how the surface poloidal field first builds up at low latitudes, and is subsequently advected poleward and concentrated near the pole.

Fig. 13

Meridional plane animation of a representative Babcock–Leighton dynamo solution from Charbonneau et al. (2005). Color coding of the toroidal field and poloidal fieldlines as in Fig. 6. This solution uses the same differential rotation, magnetic diffusivity, and meridional circulation profile as for the advection-dominated $\alpha \varOmega$ solution of Sect. 4.4, but now with the non-local surface source term (red line on Fig. 4a), as formulated in Charbonneau et al. (2005), and parameter values $C_\alpha =5$, $C_\varOmega =5\times 10^4$, $\varDelta \eta =0.003$, $\mathrm {Rm}=840$. Note again the strong amplification of the surface polar fields, and the latitudinal stretching of poloidal fieldlines by the meridional flow at the core–envelope interface. For an accompanying movie, see the supplementary material section below

Figure 14 shows N-hemisphere time–latitude diagrams for the toroidal magnetic field at the core–envelope interface (Panel a), and the surface radial field (Panel b), for a Babcock–Leighton dynamo solution now computed following the closely similar model implementation of Dikpati and Charbonneau (1999). Note how the polar radial field changes from negative (blue) to positive (red) at just about the time of peak positive toroidal field at the core–envelope interface; this is the phase relationship inferred from synoptic magnetograms (see, e.g., Fig. 3 herein) as well as observations of polar faculae (see Sheeley 1991).

Fig. 14

Time–latitude diagrams of the toroidal field at the core–envelope interface (Panel a), and radial component of the surface magnetic field (Panel b) in a Babcock–Leighton model of the solar cycle. This solution is computed for solar-like differential rotation and meridional circulation, the latter here closing at the core–envelope interface. The core-to-envelope contrast in magnetic diffusivity is $\varDelta \eta =1/300$, the envelope diffusivity $\eta _{\rm T}=2.5\times 10^{11} \,\mathrm {cm}^2 \,\mathrm {s}^{-1}$, and the (poleward) mid-latitude surface meridional flow speed is $u_0=16 \,{\text{m s}}^{-1}$. Figure produced from numerical data kindly provided by M. Dikpati

Although it exhibits the desired equatorward propagation, the toroidal field butterfly diagram in Panel a of Fig. 14 peaks at much higher latitude ($\sim$ 45$^\circ$) than the sunspot butterfly diagram ($\sim$ 15$^\circ$–20$^\circ$, cf. Fig. 2). This occurs because this is a solution with high magnetic diffusivity contrast, where meridional circulation closes at the core–envelope interface, so that the latitudinal component of differential rotation dominates the production of the toroidal field, a situation that persists in models using more realistic differential rotation profiles taken from helioseismic inversions (see Muñoz-Jaramillo et al. 2009). This difficulty can be alleviated by letting the meridional circulation penetrate deeply below the core–envelope interface. Solutions with such flows are presented, e.g., in Nandy and Choudhuri (2001, 2002). These latter authors have argued that this is in fact essential for a solar-like butterfly diagram to materialize, but this conclusion appears to be model-dependent at least to some degree (Guerrero and Muñoz 2004; Guerrero and de Gouveia Dal Pino 2007; Muñoz-Jaramillo et al. 2009). From the hydrodynamical standpoint, the boundary layer analysis of Gilman and Miesch (2004) (see also Rüdiger et al. 2005) indicates no significant penetration below the base of the convective envelope, although this conclusion has not gone unchallenged (see Garaud and Brummell 2008), leaving the whole issue somewhat muddled at this juncture. The present-day observed solar abundances of Lithium and Beryllium restrict the penetration depth to $r/R\simeq 0.62$ (Charbonneau 2007a), which is unfortunately too deep to pose stringent constraints on dynamo models. The final word will likely come from helioseismology, hopefully in the not too distant future.

A noteworthy property of this class of model is the dependency of the cycle period on model parameters; in the advection dominated regime, the meridional flow speed is found to be the primary determinant of the cycle period P. For example, in the Dikpati and Charbonneau (1999) model, this quantity is found to scale as

$$\begin{aligned} P=56.8 \, u_0^{-0.89}s_0^{-0.13}\eta _{\rm T}^{0.22} \,[\mathrm {years}]. \end{aligned}$$

(51)

This behavior arises because, in these models, the two source regions are spatially segregated, and the time required for circulation to carry the poloidal field generated at the surface down to the tachocline is what effectively sets the cycle period. The corresponding time delay introduced in the dynamo process has rich dynamical consequences, to be discussed in Sect. 7.2.4 below. The weak dependency of P on $\eta _{\rm T}$ and on the magnitude $s_0$ of the poloidal source term¹¹ is very much unlike the behavior typically found in mean-field models, where both these parameters usually play a dominant role in setting the cycle period.

Interesting variations on the above model follow from the inclusion of turbulent pumping (Guerrero and de Gouveia Dal Pino 2008; Karak and Nandy 2012; Jiang et al. 2013; Karak et al. 2014; Hazra and Nandy 2016; Karak and Cameron 2016). With the expected downward pumping throughout the bulk of the convective envelope, and with a significant equatorward latitudinal component at low latitudes, the Babcock–Leighton mechanism can lead to dynamo action even if the internal meridional flow is weak and/or constrained to the upper portion of the convective envelope. Downward turbulent pumping then links the two sources regions, and latitudinal pumping provides the needed equatorward concentration of the deep-seated toroidal component. An example taken from Guerrero and de Gouveia Dal Pino (2008) is shown in Fig. 15. In this specific solution the circulation penetrates only down to $r/R=0.8$, and the radial and latitudinal peak pumping speed are $\gamma _{r0}=0.3\,{\text{m s}}^{-1}$ and $\gamma _{\theta 0}=0.9\,{\text{m s}}^{-1}$, respectively.

Fig. 15

Time–latitude diagrams of the toroidal field at the core–envelope interface (Panel a), and radial component of the surface magnetic field (Panel b) in a Babcock–Leighton model of the solar cycle with a meridional flow restricted to the upper half of the convective envelope, and including (parametrized) radial and latitudinal turbulent pumping. This is a solution from Guerrero and de Gouveia Dal Pino (2008) (see their Sect. 3.3 and Fig. 5), but the overall modelling framework is almost identical to that described earlier, and used to generate Fig. 14. The core-to-envelope contrast in magnetic diffusivity is $\varDelta \eta =1/100$, the envelope diffusivity $\eta _{\rm T}=10^{11} \,\mathrm {cm}^2 \,\mathrm {s}^{-1}$, and the (poleward) mid-latitude surface meridional flow speed is $u_0=13 \,{\text{m s}}^{-1}$ (figure produced from numerical data kindly provided by G. Guerrero)

With downward turbulent pumping now the primary mechanism linking the surface and tachocline, the dynamo period loses sensitivity to the meridional flow speeds, and becomes set primary by the radial pumping speed. Indeed the dynamo solutions presented Guerrero and de Gouveia Dal Pino (2008) are found to obey a scaling law of the form

$$\begin{aligned} P=181.2 \, u_0^{-0.12}\gamma _{r0}^{-0.51}\gamma _{\theta 0}^{-0.05} \,[\mathrm {years}], \end{aligned}$$

(52)

over a fairly wide range of parameter values. The radial pumping speed $\gamma _{r0}$ emerges here as the primary determinant of the cycle period. Finally, one can note in Fig. 15 that although in this model strong surface magnetic fields materialize at mid-latitudes, the strong polar fields that usually characterizes Babcock–Leighton dynamo solutions operating in the advection-dominated regime are no longer present (cf. Fig. 14). This can be traced primarily to the efficient downward turbulent pumping that subducts the poloidal field as it is carried poleward by the meridional flow.

Critical assessment

A serious weakness of most Babcock–Leighton models just discussed is their use of a steady (kinematic), single-cell-per-quadrant meridional flow. Although helioseismic inversions of the meridional flow are difficult in view of its low amplitude, many inversions published in the last decade suggest mutiple flow cells in radius (see Schad et al. 2013; Zhao et al. 2013; Jackiewicz et al. 2015; Böning et al. 2017), while others do not (e.g., Rajaguru and Antia 2015; Liang et al. 2018; Mandal et al. 2018). In the advection-dominated regime, multi-cells circulation patterns can lead to markedly different dynamo behavior (Bonanno et al. 2006; Jouve and Brun 2007; Belucz et al. 2015), and can also have a profound impact on the evolution of the surface magnetic field (Dikpati et al. 2004; Jiang et al. 2009). On the other hand, the calculations of Hazra et al. (2014) indicate that as long as diffusion (or, presumably, turbulent pumping) acts sufficiently rapidly to couple adjacent flow cells, a solar-like butterfly diagram still emerges as long as an equatorial return flow is present at the core–envelope interface. Global hydrodynamical and magnetohydrodynamical simulations of solar convection suggest that such a deep equatorward return flow is likely a robust feature (see Passos et al. 2015, more on this in Sect. 6 below).

As with most mean-field models including meridional circulation published to date, mean-field-like Babcock–Leighton dynamo models usually produce excessively strong polar surface magnetic fields. While this difficulty can be alleviated by increasing the magnetic diffusivity in the outermost layers, in the context of the Babcock–Leighton models this leads to a much weaker poloidal field being transported into the interior, which can be problematic from the dynamo point-of-view. On this see Dikpati et al. (2004) for illustrative calculations, and Mason et al. (2002) on the closely related issue of competition between surface and deep-seated $\alpha$-effect. Downward turbulent pumping may be a better option to reduce the strength of the polar field without impeding dynamo action (but see also Jiang et al. 2007).

Because of the strong amplification of the surface poloidal field in the poleward-converging meridional flow, Babcock–Leighton models tend to produce a significant—and often dominant—polar branch in the toroidal field butterfly diagram. Many of the models explored to date tend to produce symmetric–parity solutions when computed pole-to-pole over a full meridional plane (see, e.g., Dikpati and Gilman 2001), but it is not clear how serious a problem this is, as relatively minor changes to the model input ingredients may flip the dominant parity (see Chatterjee et al. 2004; Charbonneau 2007b; Hotta and Yokoyama 2010, for specific examples). Nonetheless, in the advection-dominated regime there is definitely a tendency for the quadrupolar symmetry of the meridional flow to imprint itself on the dynamo solutions. A related difficulty, in models operating in the advection-dominated regime, is the tendency for the dynamo to operate independently in each solar hemisphere, so that cross-hemispheric synchrony is lost (Charbonneau 2005, 2007b; Chatterjee and Choudhuri 2006; Norton et al. 2014). Once again these difficulties are alleviated somewhat by increasing the magnetic diffusivity.

Because the Babcock–Leighton mechanism is characterized by a lower operating threshold, the resulting dynamo models are not self-excited. On the other hand, the Babcock–Leighton mechanism is expected to operate even for toroidal fields exceeding equipartition, the main uncertainties remaining the level of amplification taking place when sunspot-forming toroidal flux ropes form from the dynamo-generated mean magnetic field. The nonlinear behavior of this class of models, at the level of magnetic backreaction on the differential rotation and meridional circulation, remains largely unexplored (but see Hazra and Choudhuri 2017; Inceoglu et al. 2017).

Beyond 2D: non-axisymmetric models

Some recent Babcock–Leighton solar cycle models abandon the axisymmetric approximation, either by solving the problem in three spatial dimensions (Yeates and Muñoz-Jaramillo 2013a; Miesch and Dikpati 2014; Miesch and Teweldebirhan 2016; Hazra et al. 2017; Karak and Miesch 2017; Kumar et al. 2019; Whitbread et al. 2019), or solving a (non-axisymmetric) surface magnetic flux evolution model concurrently with a axisymmetric mean-field-like interior dynamo model (Lemerle and Charbonneau 2017; Nagy et al. 2017). All of these dynamo models are still kinematic (prescribed, time independent differential rotation and meridional flow), and use a mean-field-like turbulent diffusivity. A parameterized prescription is introduced to generate emergence of (tilted) bipolar magnetic regions in the surface layers of the model, as a function of the internal distribution of magnetic fields. In all these models emergences are randomly distributed in longitude, and amplitude saturation is usually achieved by ad hoc algebraic quenching of either the tilt or flux of emerging BMRs with increasing internal or magnetic field strength, thus limiting the buildup of the surface dipole (viz. Eq. 49).

Modelling flux emergence

Moving to three spatial dimensions allows a more realistic representation of the process of magnetic flux emergence. One approach , adopted in the simulations of Miesch and Dikpati (2014) and Miesch and Teweldebirhan (2016), is to replace the axisymmetric flux ring used in some mean-field-like 2D models by a truly 3D magnetic flux ring inserted with an E–W tilt compatible with Joy’s Law. The intersection of this ring with the surface of the simulation domain thus defines a magnetic bipole, as in the conventional SFT simulations discussed in Sect. 5.2. These rings are injected only when the internal toroidal component exceeds some preset threshold.

Alternately, it is also possible to force magnetic flux emergence from the interior to the surface by introducing short-lived and spatially localised vortical upflows whenever and wherever the deep toroidal magnetic field exceeds a set threshold. This is the approach introduced by Yeates and Muñoz-Jaramillo (2013b, see also Kumar et al. 2019; Whitbread et al. 2019). The helicity of their prescribed upflows is set to vary as the sine of latitude, and they adjust the amplitude of its horizontal component so as to reproduce Joy’s Law (see their Fig. 9). Figure 16 illustrates the idea. In (a), two toroidal flux concentrations (white tubes), one in the N-hemisphere and the other at the equator, have been acted upon each by its prescribed vortical upflow for 25 days, at which point the upflows turn off. The N-hemisphere emerging structure shows a E–W tilt consistent with Joy’s Law, a direct consequence of the cyclonicity of the imposed upflow, while that emerging at the equator does not (as expected).

Fig. 16

Magnetic flux emergence in the 3D Babcock–Leighton model of Yeates and Muñoz-Jaramillo (2013b). In a, two toroial flux concentrations (in white) have been undergoing emergence. The red/blue surfaces indicate the sign of the associated radial magnetic component, whose intersection with the photosphere (panel b) generates a bipolar structure akin to a BMR. Panels c and d are equatorial plane slices showing the rise and deformation of the emerging magnetic field, for the equatorial emergence event structure in a. Image reproduced with permission from Yeates and Muñoz-Jaramillo (2013b), copyright by the authors

Here the upflow is acting on the large-scale magnetic field, yet as can be seen on panels (c) and (d) of Fig. 16, something akin to an $\varOmega$-loop is produced and even develops an asymetry between the prograde and retrograde legs, as in thin flux tube simulations. Such an approach also allows to capture with internal self-consistency the (diffusive) disconnection of the rising loop from the underlying toroidal flux system, without having to prescribe a “recipe” for magnetic flux loss in the deep magnetic toroidal field (see Whitbread et al. 2019, for more on this matter).

Representative results

Both modelling approaches to flux emergence described above can lead to viable solar-like 3D kinematic dynamo simulations generating sustained magnetic cycles characterized by regular magnetic polarity reversals and good hemispheric synchrony. Figure 17 shows one example, taken from Karak and Miesch (2017). This simulation run has an internal field strength threshold and latitudinal “mask” to restrict emergences to low latitudes, includes downwards turbulent pumping in subsurface layers, and uses algebraic tilt quenching as the solar amplitude-limiting nonlinearity. The top panel shows the zonally-averaged surface radial field, the middle panel the zonally-averaged toroidal field at $r/R=0.72$, and the bottom panel the polar cap magnetic field in the two hemispheres.

Fig. 17

An extended dynamo run from the 3D Babcock–Leighton model of Karak and Miesch (2017) (their simulation A6). The top panel shows the zonally-averaged surface radial magnetic field, the middle panel the zonally-averaged toroidal magnetic field at $r/R=0.72$, and the bottom panel time series of the polar cap (latitude $>75^\circ$) mean magnetic field in the Northern (red) and Southern (blue) hemispheres. Image reproduced with permission from Karak and Miesch (2017), copyright by AAS

The magnetic cycle generated in this simulation is quite stable and maintains good hemispheric synchrony, yet amplitude fluctuations are also clearly seen. It occurs here because Karak and Miesch (2017) introduce a small random scatter about Joy’s Law to their emerging flux rings. Because the peak polar flux is a small ($\sim 10^{-3}$) fraction of magnetic flux emerging in the course of a typical sunspot cycle, even low variability in active region properties can lead to significant amplitude variations in the surface dipole.

The solar cycle model of Lemerle and Charbonneau (2017) has been used extensively to investigate the impact of variability in active region properties on the magnetic cycle (Nagy et al. 2017; Labonville et al. 2019; Ölçek et al. 2019). This model combines a 2D kinematic surface flux transport simulations with a kinematic axisymmetric 2D dynamo model for the interior; the former provides the upper boundary condition for the latter, and the internal magnetic field distribution of the latter is used to generate active region emergences in the former. Physical characteristics of emerging BMRs are drawn from statistical distributions constructed from observational data (see Lemerle et al. 2015, also Jiang et al. 2011). The probability of emergence per timestep increases with internal toroidal magnetic field strength, and is subjected to a lower threshold below which that probability vanishes. Algebraic tilt quenching is the only amplitude-limiting nonlinearity considered. Model parameters are formally optimized by minimizing the difference between observed and simulated time–latitude “butterfly” patterns of BMR emergences.

Figure 18 displays a segment of a solar cycle simulation generated with this model, and covering 4 activity cycles (two full magnetic cycles). Many observed solar features are reproduced, including the dipole reversal near the time of sunspot cycle maximum, and a strong correlation between surface dipole strength at activity minimum and the amplitude of the subsequent cycle. This specific segment, taken from Nagy et al. (2017), exemplifies an event akin to the cycle 23–24 transition, namely an “average” cycle followed by an extended minimum phase, starting here at $t\simeq 2180\,{\text {years}}$, followed by a weak activity cycle showing strong hemispheric asymetry.

Fig. 18

Segment of a reference solar cycle solution from the Lemerle and Charbonneau (2017) $2\times 2$D solar cycle model. Panel a shows a magnetic butterfly diagram, specifically the longitudinally-averaged surface density of synthetic emergences, color-coded according to trailing magnetic polarity. Panel b is a butterfly diagram of active region emergences, panel c a time series of smoothed pseudo-sunspot number, and panel d a time series of the surface dipole moment. The dashed lines illustrate the evolution of a parallel solution where one large near-equatorial active region emerging at $t\simeq 2176\,{\text {years}}$ (vertical dashed lines) is artificially removed from the simulation (see text). Adapted from Nagy et al. (2017)

This weak cycle can be traced to one large active region emerging near the equator in the preceding cycle, at $t\simeq 2176\,{\text {years}}$, with strong deviation from Joy’s Law: its trailing polarity is closer to the equator than its leading polarity. Artificial removal of this single “rogue” active region leads to the pseudo-SSN time and dipole time series plotted as dashed lines on the bottom two panels. The subsequent cycle is still a bit weaker than average, but dipole reversal takes place sooner, the extended minimum vanishes, and an average cycle amplitude is recovered one cycle later.

Critical assessment

In the kinematic (linear) regime, in terms of modelling the buildup of the dipole from the decay of bipolar magnetic active regions, going to 3D (or $2\times 2$D) is superfluous; all one needs to know, for each emerging active region, is its dipole contribution, as given by Eq. (49), and this can be accomodated into mean-field like 2D axisymmetric model (viz. Sect. 5.4), or even 2-layers 1D models (such as, e.g., Cameron and Schüssler 2017a). However the detailed latitude–longitude representation of the solar surface magnetic field is interesting and useful for reconstruction of the coronal and interplanetary magnetic field (e.g., Pinto et al. 2011; Dikpati et al. 2016), of solar irradiance variability, and for magnetographic data assimilation for cycle prediction (e.g., Upton and Hathaway 2014b). The 3D approach becomes essential when nonlinearities are taken into account, such as surface inflows towards active regions (Cameron and Schüssler 2010; Jiang et al. 2010; Upton and Hathaway 2014a; Martin-Belda and Cameron 2016, 2017, and references therein), or if diffusion is replaced by advection by (non-axisymmetric) convective flows (Hazra and Miesch 2018). “Going nonlinear” is the obvious next modelling step for all existing Babcock–Leighton solar cycle models.

Whether truly 3D or $2\times 2$D, model results published to date share some of the difficulties already encountered with mean-field-like Babcock–Leighton models described in Sect. 5.4. Polar fields tend to be too strong, and emergence at high latitude need to be artificially suppressed.¹² Here again the generalized use of a steady, single cell per quadrant meridional flow profiles has been challenged by some recent helioseismic inferences, although “the jury is still out” on this one. Even in the kinematic regime, 3D solutions of the induction equation (1) are very demanding computationally, making it difficult or impossible in practice to systematically explore parameter space or perform simulation runs spanning centuries or millenia. The $2\times 2{\text{D}}$ model of Lemerle and Charbonneau (2017) is an interesting compromise in this respect. Even there, computation time-related constraints on spatial resolution in the SFT module makes it impossible in practice to accurately reproduce the small size (and complexity) of real emerging active regions.

The surface dipole as precursor

The strength of the solar surface magnetic dipole is known to be a good precursor for the strength of the upcoming solar cycle, and this idea remains at the base of the most succesfull extant “precursor” schemes for solar cycle prediction (Schatten et al. 1978; Svalgaard et al. 2005; Pesnell 2016, see also Sect. 2 in Petrovay 2020). This is sometimes taken to imply that the Sun must be a dynamo of the Babcock–Leighton variety; Fig. 19 demonstrates that this is not necessarily the case. Panel a and b show time series of total magnetic energy (Eq. 44) and polar field strength for two dynamo solutions taken from Charbonneau and Barlet (2011). The first is a bona fide mean-field $\alpha \varOmega$ model including meridional circulation, as described in Sect. 4.4, and the second a mean-field-like Babcock–Leighton, as described in Sect. 5.4. In both cases stochastic forcing is introduced by imposing zero-mean random fluctuations on the dynamo number/source term at the 50% level, with a coherence time much shorter than the cycle period.

Fig. 19

Stochastically-driven cycle fluctuations in a an $\alpha \varOmega$ mean-field model including meridional circulation, and b a mean-field-like Babcock–Leighton model. The red and green lines are, respectively, time series of total magnetic energy and surface polar field strength. Stochastic forcing is imposed through piecewise-continuous zero-mean random variations of the dynamo number $C_\alpha$, with coherence time amounting to a few percent of the mean cycle period in each model. The gray horizontal bars indicate epochs where a Gnevyshev–Ohl-like alternating pattern of cycle amplitude materializes in the energy time series. The bottom panels show c the lack of correlation between the maximum cycle amplitude and the dipole strength of the subsequent minimum, and d the strong positive correlation between dipole strength at minimum and the amplitude of the following cycle

As shown in panel c, in either cases the surface polar field at solar minimum shows no significant correlation with cycle amplitude, as measured by magnetic energy. However, both show a very strong correlation between surface polar field and the amplitude of the next cycle (panel d). What matters for this correlation to materialize is that (1) the primary source of fluctuation resides in the $T\rightarrow P$ part of the dynamo loop, and (2) that the surface polar field feeds back into the dynamo loop. Repeating the same experiment with the meridional flow turned off in the mean-field $\alpha \varOmega$ models erases the precursor value of the surface polar field. See Charbonneau and Barlet (2011) for more details on these and related numerical experiments.

Global MHD numerical simulations

Magnetohydrodynamical (MHD) simulations of solar convection solve numerically the set of coupled nonlinear partial differential equations describing the conservation of mass, momentum, internal energy and magnetic flux in a thick spherical shell of electrically conducting fluid subjected to thermal forcing:

$$\begin{aligned}&{\partial {\rho }\over \partial {t}}+\nabla \cdot (\rho {\varvec{u}})=0 , \end{aligned}$$

(53)

$$\begin{aligned}&{\partial {{\varvec{u}}}\over \partial {t}}+({\varvec{u}}\cdot \nabla ){\varvec{u}}= -{1\over \rho }\nabla p-2{\varvec{\varOmega }}\times {\varvec{ u}}+{\varvec{g}} +{1\over 4\pi \rho }(\nabla \times {\varvec{B}})\times {\varvec{B}} +{1\over \rho }\nabla \cdot {\varvec{\tau }} , \end{aligned}$$

(54)

$$\begin{aligned}&{\partial {e}\over \partial {t}}=(\gamma -1)e\,\nabla \cdot {\varvec{u}}= {1\over \rho }\left[ \nabla \cdot \left( (\chi +\chi _r)\nabla T\right) +\phi _u+\phi _B\right] , \end{aligned}$$

(55)

$$\begin{aligned}&{\partial {{\varvec{B}}}\over \partial {t}}=\nabla \times ({\varvec{u}}\times {\varvec{B}} -\eta \nabla \times {\varvec{B}}) . \end{aligned}$$

(56)

Here $\rho$ is the fluid density, e is internal energy,¹³p is gas pressure, ${\varvec{\tau }}$ is the viscous stress tensor, $\chi$ and $\chi _r$ are the kinetic and radiative thermal conductivities, $\phi _u$ and $\phi _B$ are the viscous and Ohmic dissipation functions, and other symbols have their usual meaning.

In the solar/stellar dynamo context it is customary (although not universal) to solve the MHD equations in a rotating reference frame [angular velocity ${\varvec{\varOmega }}$ in Eq. (54)], with the centrifugal force absorbed in the pressure gradient term so that only the Coriolis force appears on the RHS of Eq. (54). Equations (53)–(56) need to be augmented by an equation of state, usually the perfect gas Law, unless ionization effects are explicitly considered as in simulations reaching close to the photosphere (see, e.g., Hotta et al. 2014). The magnetic field subjected to the solenoidal constraint $\nabla \cdot {\varvec{B}}=0$, and a solar structure model, either a helioseismically-calibrated model or a polytropic approximation thereof, sets the fixed background spherically symmetric stratification $\rho (r)$, T(r), etc. Convection is forced by introducing a heat flux through the radial boundaries, or via a volumetric heating/cooling term representing the the non-zero divergence of the radiative flux, the ultimate energy source powering all inductive flows relevant to the problem. Appropriate boundary conditions complete the mathematical specification of the problem.

In the solar convection context the numerical solution of Eqs. (53)–(56) is quite demanding from the computational point of view, in light of the vast range of scales characterizing fluid turbulence at high viscous and magnetic Reynolds numbers. Starting with pioneering work of Gilman (1983) and Glatzmaier (1984, 1985), and propelled by ever improving compute power and algorithmic design, in the past decade many global MHD simulations have succeeded in generating a large-scale magnetic field, sometimes undergoing polarity reversals in the form of more or less regular cycles; for a representative sample, see: Racine et al. (2011), Masada et al. (2013), Nelson et al. (2013), Fan and Fang (2014), Simitev et al. (2015), Duarte et al. (2016), Guerrero et al. (2016a), Hotta et al. (2016), Käpylä et al. (2017) and Strugarek et al. (2018). These simulations collectively encompass a wide variety of simulation designs, algorithmic implementations, boundary conditions, rotation rates, heat fluxes, and, most importantly perhaps, subgrid treatments of unresolved scales. None is operating even remotely close to the dissipative regime expected to characterize solar interior conditions; in particular, all must run with strongly enhanced dissipation (viscosity, thermal diffusivity, magnetic diffusivity), either explicitly through the introduction of enhanced “eddy” diffusivities (Large Eddy Simulations) or dynamical subgrid models (Dynamical Large Eddy Simulations), or implicitly via the adopted numerical discretisation scheme (Implicit Large Eddy Simulations; including upwind schemes, slope limiters, etc.). However, even as remote analogs of the sun and stars, these simulations do capture self-consistently the dynamical interactions between flow and field at all spatial and temporal scales resolved. Nonetheless important discrepancies remain with regards to observed solar behavior. Arguably the most noteworthy has been dubbed the convective conundrum: helioseismic determinations of the subsurface convective power spectrum show much less power at large scales than typically produced by numerical simulations (see Hanasoge et al. 2012; Lord et al. 2014; Cossette and Rast 2016, and references therein, for further discussion).

The aim of this section is to discuss insight gained from such simulations that are the most relevant to the simpler dynamo models discussed in the preceeding sections. Towards this end the first step is to extract from the simulations an equivalent of the large-scale, mean magnetic field, which is what simpler models typically simulate. Working in spherical polar coordinates $(r,\theta ,\phi )$, zonal averaging is the obvious choice, so that the (axisymmetric) mean flow $\left\langle {\varvec{u}}\right\rangle$ and magnetic field ($\left\langle {\varvec{B}}\right\rangle$) are computed from the simulated flow ${\varvec{u}}$ and field ${\varvec{B}}$ as

$$ \left\langle {\varvec{u}}\right\rangle (r,\theta ,t)= {1\over 2\pi }\int {\varvec{u}}(r,\theta ,\phi ,t)\mathrm{d}\phi , $$

(57)

$$ \left\langle {\varvec{B}}\right\rangle (r,\theta ,t)= {1\over 2\pi }\int {\varvec{B}}(r,\theta ,\phi ,t)\mathrm{d}\phi . $$

(58)

The small-scale (and non-axisymmetric) flow and field are then defined as:

$$ {\varvec{u}}^\prime (r,\theta ,\phi ,t)= {\varvec{u}}(r,\theta ,\phi ,t)-\left\langle {\varvec{u}}\right\rangle (r,\theta ,t) , $$

(59)

$$ {\varvec{B}}^\prime (r,\theta ,\phi ,t)= {\varvec{B}}(r,\theta ,\phi ,t)-\left\langle {\varvec{B}}\right\rangle (r,\theta ,t) .$$

(60)

These can then be used to directly calculate the turbulent electromotive force via Eq. (17). The axisymmetric differential rotation profile is extracted as $\varDelta \varOmega (r,\theta ,t) =\left\langle u_\phi \right\rangle /r\sin \theta$, and the meridional flow components are taken directly as $\left\langle u_r\right\rangle$ and $\left\langle u_\theta \right\rangle$.¹⁴

Convection and large-scale flows

Large-scale flows such as differential rotation and meridional circulation are ultimately driven by turbulent convection and associated thermal gradients (see, e.g., Miesch 2005; Miesch and Toomre 2009; Balbus et al. 2012; Featherstone and Miesch 2015). A key dimensionless parameter for global flow dynamics is the Rossby number, measuring the influence of the Coriolis force on convective flows:

$$\begin{aligned} \mathrm {Ro}\equiv {v\over 2\varOmega \ell } , \end{aligned}$$

(61)

where v and $\ell$ are typical velocity and length scale of the convective eddies.¹⁵ The Rossby number is a diagnostic parameter, in that it is measured a posteriori in simulations. It is ultimately determined by the chosen rotation rate and convective thermal heat flux.

In the rotationally-dominated regime $\mathrm {Ro}<1$, convection organizes itself at low latitudes into a longitudinal stack of latitudinally-elongated “banana cells”, oriented parallel to the rotation axis and extending across equatorial latitudes. Differential rotation is largely steady and characterized by rapidly rotating equatorial regions, with the rotational frequency decreasing smoothly towards polar latitudes. Isocontours of angular velocity show a strong tendency to align parallel to the rotation axis outside of a cylinder tangent to the equatorial base of the convectively unstable fluid layers, a direct consequence of the Taylor–Proundman theorem. In the opposite limit $\mathrm {Ro}>1$, the dynamics is dominated by buoyancy, banana cells are absent, and the equator rotates more slowly than the mid latitudes (often dubbed “anti-solar” differential rotation). The magnitude of latitudinal differential rotation typically increases with rotation rate (see, e.g., Varela et al. 2016, and references therein). With $\mathrm {Ro}\sim 0.1$ at the base of its convection zone, the sun is believed to stand in the rotationally-dominated regime, but barely so (see, e.g., Guerrero et al. 2013; Gastine et al. 2014; Featherstone and Miesch 2015; Käpylä et al. 2014; Mabuchi et al. 2015).

The dynamics of the large-scale meridional flow is strongly coupled to that of differential rotation via centrifugal driving (Kippenhahn 1963; Featherstone and Miesch 2015, and references therein), and also shows a strong dependence on the Rossby number. The $\mathrm {Ro}>1$ regime, characterized by anti-solar differential rotation, tends to generate a single meridional flow cell per meridional quadrant, poleward in the upper convection zone and equatorward below. In the $\mathrm {Ro}<1$ regime, on the other hand, the meridional flow tends to break up into multiple flow cells, particularly at low latitudes. While differential rotation patterns are quasi-steady when averaged over time periods significantly longer than the convective turnover time, the mean meridional flows remain highly time-variable, even when averaged over very long time spans. In simulations including an underlying stable fluid layer, an equatorward return flow is typically produced via momentum deposition by penetrating downflows (see Brun et al. 2011; Passos et al. 2015).

Polarity reversals and large-scale magnetic cycles

One of the most puzzling collective feature of current global MHD simulations of solar convection and dynamo action is that simulations that appear quite similar in terms of the flows they generate, often end up being characterized by widely differing spatiotemporal evolution of their large-scale magnetic fields (see Charbonneau 2014, Sect. 3.2 for a discussion of three specific examples; also Käpylä et al. 2017, appendix). Table 1 lists a selection of recent published simulations, with some key features and dimensionless numbers and the last two columns characterizing the behavior of large-scale magnetic cycles, when present.

Table 1 Parameters and characteristics of a sample of 3D MHD simulations generating large-scale magnetic cycles

Care is warranted in comparing parameters of one simulation to those of another, as definitions and measurements methods often differ.¹⁶ Even with this caveat in mind, one is hard pressed to extract any obvious pattern from Table 1 when it comes to magnetic cycles. While this reflects in part a true sensitivity to physical parameter regimes, it is also clear that algorithmic “details”, in particular the (explicit or implicit) treatment of small scales, also play a major role.

As an example of a simulated large-scale magnetic cycle, consider Fig. 20, showing sample results for a 300-year long segment of the EULAG-MHD 1600-year long “millenium” simulation presented in Passos and Charbonneau (2014).

Fig. 20

Magnetic cycles in the global EULAG-MHD anelastic “millenium” simulation of Passos and Charbonneau (2014), essentially identical to those of Ghizaru et al. (2010) and Racine et al. (2011). This simulation includes a convectively stable fluid layer underlying the convecting layers. Part a shows a snapshot in Mollweide projection of the toroidal (zonal) magnetic component at depth $r/R_\odot =0.718$; part b is a snapshot of the zonally-averaged toroidal field in a meridional plane, taken at the same time as in a. Part c and d show respectively time–latitude and radius-latitude diagrams of the zonally-averaged toroidal field, the former at depth $r/R=0.718$ and the latter at latitude $-50^{\circ }$. The dashed lines in b and d indicate the bottom of the convectively unstable layers. This is a moderate resolution simulation, rotating at the solar rate but convectively subluminous with respect to the sun. For an accompanying movie, see the supplementary material section below

This simulation generates a very regular magnetic cycle, well synchronized across hemispheres and with the magnetic field antisymmetric about the equator, all similar to the sun, but with a full magnetic cycle period of about 80 years, longer than the sun’s by a factor of nearly four. Looking back at Table 1, this is at the upper end of the range of cycle periods produced by other global MHD simulations that produce reasonably regular magnetic cycles. As evidenced on Fig. 20b and d, the magnetic field accumulates and reaches its peak strength in the outer reaches of the convectively stable fluid layer (see also Browning et al. 2006; Masada et al. 2013; Guerrero et al. 2016a, 2019), reaching strengths approaching or exceeding equipartition. This is a common feature in many other simulations as well, with some also managing to produce strongly magnetized structures at low latitudes within the convecting layers (e.g., Brown et al. 2010, 2011; Nelson et al. 2013; Strugarek et al. 2018). Assuming that the sunspot-forming toroidal magnetic flux ropes originate from the base of the convecting fluid layers, panel c becomes the analog of a sunspot butterfly diagram; activity thus peaks at mid- rather than low-latitudes, and shows only a hint of equatorward propagation on the poleward edges of the toroidal field bands; some other simulations fare better in this respect (e.g., Warnecke et al. 2014; Augustson et al. 2015; Duarte et al. 2016; Strugarek et al. 2018). This simulation also generates a strong dipole moment oscillating in phase with the toroidal component, as well as a secondary, lower amplitude and higher frequency cycle in the low-latitude outer convective layers, perhaps analogous to the so-called biennial cycle observed in many solar activity indicators (see Beaudoin et al. 2016, and references therein). Multiple cycles with markely distinct frequencies have been observed in other simulations as well (e.g., Käpylä et al. 2016; Strugarek et al. 2018).

While the simulation of Fig. 20 may look quite encouraging, the regular and hemispherically well-coupled magnetic cycle it generates turns out to materialize only in a restricted portion of the simulation’s parameter space. As alluded to earlier, this sensitivity has multiple origins, both in “physics” and in “algorithmics”. Consider for example the sequence of simulations discussed in Strugarek et al. (2018); these are ILES simulations of the convection zone only, spanning rotation rates going from 0.25 to 5.5 time solar, and peak convective luminosities in the range $0.3<L/L_\odot < 17.5$. The ratio of kinetic energy contained in differential rotation (DRKE) over total kinetic energy (KE) is introduced as a diagnostic for the mode of operation of the large-scale dynamo. Plotting this quantity against Rossby number on Fig. 21 reveals a surprisingly clean partition between steady large-scale magnetic fields ($\mathrm {Ro}\gtrsim 1$, in black), deep-seated solar-like decadal cycles ($0.25\lesssim \mathrm {Ro}\lesssim 1$, in red), and short-period subsurface cycles ($\mathrm {Ro}\gtrsim 0.25$, in blue), with simulations straddling the border between these last two regions showing both decadal and short-period cycles. This simulation set thus exhibits two major dynamo transitions within only an order of magnitude in Rossby number, and these are linked to turnovers in the spatial profile and strength of differential rotation, as diagnosed here by the DRKE/KE ratio.

Fig. 21

A synthetic summary of the simulation runs presented in Strugarek et al. (2018). The ratio of kinetic energy associated with differential rotation (DRKE) to total flow kinetic energy (KE, dominated by turbulent convection) is plotted against Rossby number. Decadal, deep-seated cycles are indicated in red, while “short cycles”, with periods $\sim 10$ times shorter, are concentrated in the upper third of the convective envelope. In a restricted range of Rossby number, $\mathrm {Ro}\simeq 0.2$–0.3, both types of cycles co-exist in the same simulation. For $\mathrm {Ro}$ exceeding unity, the large-scale magnetic fields remains steady. Image reproduced with permission from Strugarek et al. (2018), copyright by AAS

Considering that the Coriolis force is the agent providing the break of mirror symmetry that allows for both Reynolds stresses powering differential rotation and a non-zero turbulent $\alpha$-effect, some sort of dependence of magnetic cycle period on rotation rate is certainly expected. Pioneering modelling effort based on (linear) mean-field dynamo theory suggested that cycle period should decrease with increasing rotation rate, and indeed stellar cycle data available at the time could be tolerably well fit by the relationship $\mathrm {P}_{\rm cyc}\propto \mathrm {Ro}^{5/4}$ (see Noyes et al. 1984). Global MHD simulations of the type discussed here, on the other hand, suggest instead a trend of increasing cycle period $\mathrm {P}_{\rm cyc}$ with increasing rotation rate, as measured by the Rossby number; Strugarek et al. (2018) find $\mathrm {P}_{\rm cyc}/\mathrm {P}_{\rm rot}\sim \mathrm {Ro}^{-1.6\pm 0.14}$ (see their Fig. 7), while  Warnecke (2018) extracts from his simulations a slightly flatter relationship (see his Fig. 7); both relationships yield comparable levels of agreement with extant stellar cycle data; cf. Fig. 2 in  Strugarek et al. (2017) and Fig. 10 in Warnecke (2018).  Augustson et al. (2019) provide additional insight and scaling laws over a broader range of Rossby numbers and underlying convection zone structure.

There is of course much more to cycle periods than the Rossby number. As a case in point consider the two simulations from Käpylä et al. (2017) listed in Table 1; they are identical in all but one input parameter, the magnetic Prandtl number $\mathrm {Pm}$ (the ratio $\nu /\eta$ of viscosity over magnetic diffusivity), which differs only by a factor of two. These two simulations are characterized by nearly identical Rossby and Reynolds numbers, but the periods of their magnetic cycles differ by almost a factor of two.

Magnetic field storage, amplification and instability in the tachocline

With or without magnetism, simulations including an underlying layer of convectively stable fluid tend to develop a tachocline-like shear layer therein (see, e.g., Brun et al. 2011; Racine et al. 2011; Beaudoin et al. 2013; Guerrero et al. 2013, 2016a). The presence of such a stable layer has a drastic impact on magnetic cycles, for reasons that are not yet fully understood. It can act as reservoir for magnetic fields generated in the convection zone and subjected to downward turbulent pumping. Local amplification by differential rotation shear, if sustained in the stable layers, can also contribute to the buildup of magnetic fields therein (see Browning et al. 2006). Whatever the relative importance of local amplification versus pumping from above, the buildup of very strong magnetic fields in the stable layer is observed in all simulations in which such a layer is included (see Ghizaru et al. 2010; Racine et al. 2011; Masada et al. 2013; Guerrero et al. 2016a, 2019; Käpylä et al. 2019; Stejko et al. 2020).

Empirically, magnetic cycles unfold over longer periods in simulations with a stable layer than in its absence. Consider, e.g., the two simulations by Guerrero et al. (2016a) listed in Table 1, identical in all respects but for the presence of a stable fluid layer in RC02 but not in CZ02; The former generates a magnetic cycle with period over ten times that materializing in the latter, with markedly different spatiotemporal evolution of the large-scale magnetic field even within the convection zone.

One intriguing possibility is that the strong magnetic fields building up below the convective layers become susceptible to one or more MHD instability, whose growth and saturation ends up impacting dynamo action within the overlying convecting layers. A proof-of-concept demonstration for the development of the magnetocentrifugal instability is presented in Miesch (2007), for a tachocline-like shear layer with forced differential rotation and toroidal magnetic field. The development of this instability is characterized by a specific phasing pattern between the toroidal magnetic field and non-axisymmetric magnetic field (see Fig. 2 in Miesch 2007). The same phasing pattern was measured by Lawson et al. (2015) (see their Fig. 8) in the EULAG-MHD millenium simulation of Fig. 20, as well as by Guerrero et al. (2019), in similar simulation setups where the buildup differential rotation and toroidal magnetic field occurs self-consistently. On the other hand, Lawson et al. (2015) computed the (resolved) Poynting flux at the interface between their convectively stable and unstable fluid layers, and found it to be downward-directed at all phases of the magnetic cycle (see their Figs. 6 and 7), indicating that dynamo action is driven primarily in the convecting layers, and that the impact of MHD instabilities in the tachocline is indirect, and may take place through alterations of the inductive flows at the base of the convective fluid layers (on this point see also Käpylä et al. 2019).

Turbulent induction and mean-field coefficients

The mathematical machinery of mean-field electrodynamics (Sect. 3.2.1) can be harnessed to provide insight on the nature of turbulent induction in MHD simulations. Various approaches have been developed towards this end. The simplest is to extract ${\varvec{u}}^\prime$ from the simulation output and use Eqs. (24)–(25) and (27) to calculate the isotropic parts of the ${\varvec{\alpha }}$ and ${\varvec{\beta }}$ tensors, and the turbulent pumping speed ${\varvec{\gamma }}$. This will yield physically meaningful results only to the extent that the simulations operate in a regime in which Eqs. (24)–(27) are valid, which is not obvious to establish either a priori or a posteriori. Dubé and Charbonneau (2013) offer one example where an axisymmetric kinematic mean-field $\alpha \varOmega$ model constructed using Eq. (24) and the small-scale flow ${\varvec{u}}^\prime$ extracted from a EULAG simulation via Eq. (59) does generate a large-scale magnetic cycle resembling that materializing in the parent MHD simulation (cf. their Figs. 7 and 8).

Next in line in simplicity is to best-fit, by least-squares minimisation, the reconstructed time series of mean electromotive force to the mean magnetic field time series. This implies first extracting from the simulation output ${\varvec{u}}^\prime$, ${\varvec{B}}^\prime$ and $\left\langle {\varvec{B}}\right\rangle$ via Eqs. (59), (60) and (58) at each time step, then calculating the turbulent mean electromotive force $\varvec{\mathcal {E}}$ via Eq. (17). The tensorial coefficients in Eq. (18), which now depend only on r and $\theta$ (working in spherical polar coordinates), are adjusted so as to minimize the differences between the $\varvec{\mathcal {E}}(t)$ and $\left\langle {\varvec{B}}\right\rangle (t)$ time series (see Brandenburg and Sokoloff 2002; Racine et al. 2011; Simard et al. 2016; Augustson et al. 2015). Experience shows that useful (i.e., statistically significant) results require very long time series and fairly stable cycles.

A more versatile (and complex) approach is the test-field method (Schrinner et al. 2007; Warnecke et al. 2018; Viviani et al. 2019), and is directly anchored in mean-field electrodynamics. Upon subtracting the mean-field induction equation (16) from the unaveraged induction equation, one can obtain an evolution equation for the fluctuating magnetic component ${\varvec{B}}^\prime$:

$$\begin{aligned} {\partial {{\varvec{B}}^\prime }\over \partial {t}}= \nabla \times (\left\langle {\varvec{u}}\right\rangle \times {\varvec{B}}^\prime + {\varvec{u}}^\prime \times \left\langle {\varvec{B}}\right\rangle + {\varvec{u}}^\prime \times {\varvec{B}}^\prime - \varvec{\mathcal {E}}- \eta \nabla \times {\varvec{B}}^\prime ) . \end{aligned}$$

(62)

The test-field method solves this equation kinematically, with the mean and fluctuating flow components $\left\langle {\varvec{u}}\right\rangle$ and ${\varvec{u}}^\prime$ extracted from a simulation snapshot, acting on a set of imposed large-scale test-fields for $\left\langle {\varvec{B}}\right\rangle$ of distinct spatial orientations. This scheme has the advantage of requiring only a snapshot of the flow as input, and therefore allows to calculate the mean-field tensors in both the linear and nonlinearly-saturated phases of the simulation.

Figure 22a–c shows meridional plane representations of the diagonal elements of the ${\varvec{\alpha }}$-tensor, radial and latitudinal turbulent pumping speed in d–e, and in f the isotropic part of the the turbulent diffusivity tensor ${\varvec{\beta }}$, all extracted from the EULAG-MHD millenium simulation of Fig. 20 by Simard et al. (2016) using a least-squares minimization method.

Fig. 22

A selection of mean-field tensor components extracted from the global EULAG-MHD simulation of Fig. 20. a $\alpha _{rr}$; b $\alpha _{\theta \theta }$; c $\alpha _{\phi \phi }$; d radial turbulent pumping speed $\gamma _r$; (e) latitudinal turbulent pumping speed $\gamma _\theta$; f the isotopic part of the ${\varvec{\beta }}$ tensor, in unit of $10^7\,\hbox {m}^2\hbox {s}^{-1}$. In all cases the extraction is carried out independently in each hemisphere, so that the high degree of symmetry/antisymmetry about the equatorial plane is a true feature of the simulation

These show both similarities and differences with the tensor components extracted from the simulations of Augustson et al. (2015) by a similar least-squares-based method, and from the simulation of Warnecke et al. (2018), using the test-field method. Considering that mean-field coefficients are strongly fluctuating quantities, an inevitable consequence of the turbulent nature of MHD convection, it is not clear at this juncture whether the differences reflect true differences in the turbulent electromotive force developing in each of these (algorithmically and physically distinct) numerical simulations, or artefacts introduced by the technique used to extract the tensor components from the simulation output.¹⁷ Focusing on the similarities, the following appear to be robust properties:

• 1. The ${\varvec{\alpha }}$-tensor is full, with off-diagonal components of roughly similar magnitude as diagonal components;

• 2. The largest magnitudes, reaching up to a few tens of m $\hbox {s}^{-1}$, are found in the $\alpha _{rr}$ component, with $\alpha _{\phi \phi }$ taking second place. The simulations of Augustson et al. (2015) is somewhat more balanced in this respect, with the $\alpha _{\theta \theta }$ and off-diagonal components showing magnitudes similar to $\alpha _{rr}$ and $\alpha _{\phi \phi }$.

• 3. $\alpha _{\phi \phi }$ and $\alpha _{\theta \theta }$ are both mostly positive (negative) in the Northern (Southern) hemisphere, but shows a sign change near the base of convecting fluid layer (on this see also Duarte et al. 2016);

• 4. Radial turbulent pumping, associated with the antisymmetric part of the $\mathbf{a}$ tensor in Eq. (18), is downwards in the bulk of the convecting layers.

• 5. Significant equatorward latitudinal turbulent pumping, at speed in the m $\hbox {s}^{-1}$ range, materializes at mid- to low-latitudes in the bulk of the convecting fluid layers.

• 6. The isotropic turbulent diffusivity $\beta$ is high, ranging from a few $10^{11}\,\hbox {cm}^2\,\hbox {s}^{-1}$ on Fig. 22f, approaching $10^{13}\,\hbox {cm}^2\,\hbox {s}^{-1}$ in the more luminous simulations analyzed by Warnecke et al. (2018).

In the EULAG-MHD simulation analyzed by Simard et al. (2016), Eqs. (24)–(25) offer a reasonably good reproduction of the $\alpha _{\phi \phi }$ and isotropic part of the diffusivity tensor ${\varvec{\beta }}$ extracted from the simulation, provided one assumes the coherence time to be smaller than the turnover time by a factor of about 5. Interestingly, short coherence time turbulence is one regime in which these expressions can be expected to hold (Moffatt 1978; Schrijver and Siscoe 2009, Chap. 3). Warnecke et al. (2018) also find a reasonably good fit between the diagonal components of their extracted $\alpha$-tensor and Eqs. (24)–(25), with an amplitude scaling factor ranging from $\simeq 3$ for $\alpha _{rr}$ to $\simeq 10$ for $\alpha _{\theta \theta }$ (see their Fig. 1). Overall, these inferences show no outstanding departures from measurements of the $\alpha$-tensor in MHD numerical simulations of rotating, stratified turbulence in a box (see, e.g., Ossendrijver et al. 2001, 2002; Käpylä et al. 2006a, 2009, and references therein).

Magnetic quenching of the $\alpha$-effect and turbulent diffusivity

Measurements of diffusivity quenching in MHD simulations of mechanically forced turbulence with imposed large-scale magnetic fields have led to a wide variety of results (see Sect. 1 in Karak et al. 2014, and references therein). Analysis of simulations generating a large-scale magnetic component autonomously (Brandenburg et al. 2008; Racine et al. 2011; Simard et al. 2016; Warnecke et al. 2018) indicate that the ${\varvec{\beta }}$ tensor components suffer significantly less quenching by the large-scale magnetic field than do the components of the ${\varvec{\alpha }}$-tensor. Racine et al. (2011), Simard et al. (2016) and Warnecke et al. (2018) all find clear cyclic signals in their ${\varvec{\alpha }}$-tensor components, of period commensurate with the large-scale magnetic cycle. Warnecke et al. (2018) detect a sign change due to the current helicity contribution to the $\alpha$-effect (as per Eq. (34) herein), which in their simulation alters the propagation direction of dynamo waves. In the simulation analyzed by Simard et al. (2016), on the other hand, the contribution magnetic (current) helicity to the $\alpha$-tensor remains too small to lead to a sign change. These latter authors find the strong $\alpha$-quenching formula (46) to provide a tolerable fit to the measured quenching, for magnetic Reynolds number values $\mathrm {Rm}\sim 10$–30, consistent with a posteriori estimates from the simulation output (cf. Table 1).

Cyclic magnetic modulation of large-scale flows

Magnetic fields are a major contributor to zonal dynamics, and typically lead to reduced differential rotation as compared to otherwise identical purely hydrodynamical simulations even in cases where little large-scale magnetic fields are generated. (e.g., Brun et al. 2004; Brown et al. 2011; Beaudoin et al. 2013; Varela et al. 2016). Around $\mathrm {Ro}\sim 0.5$ magnetism can tip differential rotation from anti-solar to solar-like (Fan and Fang 2014; Karak et al. 2015; Mabuchi et al. 2015; Simitev et al. 2015), and also break the constraints imposed by the Taylor–Proudman theorem (Hotta 2018). The presence of magnetic fields also has a significant impact on meridional flow dynamics (see Passos et al. 2015; Guerrero et al. 2016b; Passos et al. 2017, and references therein).

Focusing on differential rotation and following Brun et al. (2004), the force balance is expressed by casting the zonal component of the momentum equation in flux form:

$$\begin{aligned} \rho r\sin \theta {\partial {\left\langle u_\phi \right\rangle }\over \partial {t}}& {} = \nabla \cdot \Big \{ r\sin \theta \Big [{1\over 4\pi }\Big ( \underbrace{ \left\langle B_\phi \right\rangle \left\langle {\varvec{B}}\right\rangle }_{\mathrm{MT}}+ \underbrace{ \left\langle b^\prime _\phi {\varvec{B}}^\prime \right\rangle }_{\mathrm{MS}}\Big )\nonumber \\& \quad - \rho \Big (\underbrace{ (\left\langle u_\phi \right\rangle +\varOmega r\sin \theta )\left\langle {\varvec{u}}\right\rangle }_{\mathrm{MC}}+ \underbrace{ \left\langle u^\prime _\phi {\varvec{u}}^\prime \right\rangle }_{\mathrm{RS}}\Big )\Big ]\nonumber \\&\quad + \underbrace{\rho \nu \Big [r{\partial \over \partial {r}}\left( {\left\langle u_\phi \right\rangle \over r}\right) +{\sin \theta \over r}{\partial \over \partial {\theta }}\left( {\left\langle u_\phi \right\rangle \over \sin \theta }\right) \Big ]\hat{{\varvec{e}}}_{\phi }}_{\mathrm{VF}} \Big \} \end{aligned}$$

(63)

Upon using again Eqs. (57)–(60) to extract the mean and fluctuating flow and field component from the simulation output, it is straightforward to compute the terms on the RHS. In the case of the millenium simulation of of Fig. 20, the analysis of Beaudoin et al. (2013) indicates that the magnetic torques associated with the cycling large-scale magnetic component (labeled MT in Eq. 63) do vary significantly in the course of the magnetic cycle, as expected, but the contributions from Reynolds stresses (RS), Maxwell stresses (MS) and advection by the meridional flow (MC) all vary as well, at overall levels similar to the magnetic torques (see Figs. 7,8 in Beaudoin et al. 2013, also Fig. 5b in Augustson et al. 2015 and Guerrero et al. 2016b). In the language of Sect. 4.2.5, both the Malkus–Proctor and $\varLambda$-quenching mechanism operate in these simulations.

Formation of buoyant magnetic structures

Current thinking places the formation and storage of the sunspot-forming toroidal magnetic flux ropes in the mildly subadiabatic outer reaches of the convectively stable layer underlying the solar convection zone, within the tachocline. Some recent simulations (Nelson et al. 2013; Fan and Fang 2014; Chen et al. 2017) have reopened an interesting alternative, namely that buoyant, super-equipartition-strength magnetic rope-like structures could form within the highly turbulent environment of the convecting layers (see also Jouve et al. 2013). Interestingly, these structures retain the approximate orientation of the larger toroidal structures within which they formed all the way to the top of the simulation, in agreement with Hale’s polarity Laws (Nelson et al. 2014). These authors also show that when they reach the the top of the domain, the ensemble of loops also exhibit a distribution of tilt orientation with respect to the direction of rotation that is similar to Joy’s Law (see their Fig. 8).

Lessons learned

The relatively brief (and perhaps dizzying) tour of global MHD simulation presented in this section is necessarily incomplete and glossed over many delicate computational and physical issues. Nonetheless, to sum up the most salient empirically determined features of simulated large-scale magnetic cycles:

• Regular, solar-like stable cycles with strong hemispheric coupling and synchrony are the exception rather than the rule.

• The presence and period of magnetic cycles depends sensitively on rotation; low $\mathrm {Ro}$ favors magnetic cycles, high $\mathrm {Ro}$ favors steady large-scale magnetic fields. In the solar range of $\mathrm {Ro}$, the cycle period increases with increasing rotation rate.

• Multiple magnetic cycles with significantly different periods can coexist at moderately small Rossby numbers ($0.1\lesssim \mathrm {Ro}\lesssim 1$).

• In mean-field terminology, simulated large-scale magnetic cycles are driven by an $\alpha ^2\varOmega$ dynamo.

• The ${\varvec{\alpha }}$-tensor components extracted from simulations compare surprisingly well to expectations based on the kinematic, near-isotropic and homogeneous turbulence regime of mean-field theory.

• In many (but not all, viz. Viviani et al. 2019) simulations, the spatiotemporal propagation of the large-scale magnetic fields appears consistent with the Parker-Yoshimura rule for dynamo waves.

• Both $\varLambda$-quenching and the Malkus–Proctor mechanism are detected in simulations. A form $\alpha$-quenching is also measured, while quenching of the turbulent diffusivity appears marginal.

• The presence of a stably stratified fluid layer underlying the convecting fluid yields longer period cycles, and the growth of MHD instabilities therein may impact cyclic activity

• Autonomous generation of super-equipartition, buoyant flux ropes-like structures takes place within the turbulent convecting layer. These structures rise to the top of the domain retaining their E–W orientation (Hale’s Laws) and at least in some cases acquire a tilt qualitatively similar to Joy’s Law.

Amplitude fluctuations, multiperiodicity, and Grand Minima

Since the basic physical mechanism(s) underlying the operation of the solar cycle are not yet agreed upon, attempting to understand the origin of the observed fluctuations of the solar cycle may appear to be a futile undertaking. Nonetheless, work along these lines continues at full steam in part because of the high stakes involved; the frequencies of all eruptive phenomena relevant to space weather are strongly modulated by the amplitude of the solar cycle; varying levels of solar activity may contribute significantly to long-term climate change (see Haigh 2007, and references therein); and certain aspects of the observed fluctuations may actually hold important clues as to the physical nature of the dynamo process.

The inductive flows driving the solar magnetic cycle are most certainly impacted by the associated Lorentz force; and the inductive processes themselves are most certainly subjected to stochastic fluctuations, as the solar dynamo operates in a turbulent environment. The solar dynamo is thus both stochastic and nonlinear.

The aim of this section is thus to provide an overview of the pattern of cycle variability that can be produced in the various dynamo models considered in the preceeding sections, in response to stochastic forcing and nonlinear magnetic backreaction. Following a brief overview of relevant observed variability patterns in Sect. 7.1, we first consider in Sect. 7.2 some generic patterns of fluctuating behavior, with pointers to specific representative examples in the published literature. We then focus in Sects. 7.3 and 7.4 on intermittency and thresholded modulation as mechanisms providing explanatory models for Grand Minima in solar activity. The few extant occurences of Grand Minima-like behavior in global MHD numerical simulations are discussed in Sect. 7.5, and Sect. 7.6 covers briefly the possible impact of fossil magnetic fields in the solar interior.

The observational evidence: an overview

 Hathaway (2015) and Usoskin (2017) offer comprehensive reviews of the observational phenomenology of the solar cycle, as viewed through the sunspot number and other activity indicators; what follows is restricted to feature having most direct bearing on dynamo modeling.

First an important caveat is in order. Cycle-to-cycle variations in sunspot number (SSN) are usually taken to indicate a corresponding variation in the amplitude of the Sun’s dynamo-generated internal magnetic field. As reasonable as this may sound, it remains a working assumption; at this writing, the process via which the dynamo-generated mean magnetic field produces sunspot-forming magnetic flux ropes is not understood. One should certainly not take for granted, say, that a difference by a factor of two in SSN indicates a corresponding variation by a factor of two in the strength of the internal magnetic field (or energy).

Nonetheless, the idea a nicely regular sunspot cycle does not hold long; the data (see Fig. 1 herein) indicate large variations in amplitude and to a somewhat lesser extent in duration. These variations are not a sunspot-specific artefact; similar variations are in fact observed in other activity proxies with extended records, most notably the 10.7 cm radio flux (Tapping 1987), polar faculae counts (Sheeley 1991; Muñoz-Jaramillo et al. 2012), and the cosmogenic radioisotopes $^{14}$C and $^{10}$Be (Beer 2000; Beer et al. 2012; Usoskin 2017).

The various incarnations of the sunspot number time series (monthly SSN, 13-month smoothed SSN, yearly SSN, etc.) may well be the most intensely studied time series in astrophysics. Various significant correlations and statistical trends have been sought and found in these datasets. For example, the “Waldmeier Rule” refers to a statistically significant anticorrelation between cycle amplitude and rise time, and the “Gnevyshev–Ohl Rule” refers to a marked tendency for odd (even) numbered sunspot cycles to have amplitudes above (below) their running mean. For more on these (and other) empirical sunspot “Rules”, see Hathaway (2015).

Even more striking is the pronounced dearth of sunspots in the interval 1645–1705 (viz. Fig. 1a). This is not due to lack of observational data but represents instead a phase of strongly suppressed activity now known as the Maunder Minimum (Eddy 1976, 1983). Evidence from cosmogenic radioisotopes indicates that similar periods of suppressed activity have taken place in ca. 1282–1342 (Wolf Minimum) and ca. 1416–1534 (Spörer Minimum), also reveals a period of enhanced activity in ca. 1100–1250 (the Medieval Maximum), and that such episodes have recurred irregularly over the more distant past (Usoskin 2017).

A number of long-timescale modulations have also been extracted from these data, most notably the so-called Gleissberg cycle (period $\simeq 88\,{\text {years}}$), but the length of the sunspot number record is insufficient to firmly establish the reality of these periodicities. Likewise, the search for chaotic modulation in the SSN time series has produced a massive literature but without really yielding firm, statistically convincing conclusions, again due to the insufficient lengths of the datasets. See Letellier et al. (2006) for a good recent entry point into this literature, and Wing et al. (2018) for related approaches based on information theory. Activity reconstructions based on cosmogenic radioisotopes allows a considerable extension back in time, but difficulties in establishing absolute amplitudes of production rates introduce additional uncertainties into what is already a complex endeavour (see Beer 2000; Beer et al. 2012; Usoskin 2017, for more details).

Cycle modulation: generic behaviors

Rather than attempting to exhaustively review the published literature on modelling solar cycle variablity, the purpose of this section is to survey and categorize extant models in term of generic behavior, i.e., behaviors that, at least at a qualitative level, do not depend sensitively on model choices and implementation details.

Going critical and Hopfing along

From a dynamical system point of view, the onset of dynamo action at $D\ge D_{\mathrm{crit}}$ (i.e., positive growth rates in the linear regime) reflects the loss of stability of the fixed-point (trivial) solution ${\varvec{B}}=0$ to a limit cycle, through a Hopf-type bifurcation. This is illustrated schematically on Fig. 23, where the thick line is some appropriate measure of cycle amplitude, plotted versus dynamo number. Once the critical dynamo number is exceeded, the dynamo eventually saturates at a magnetic amplitude that increases with increasing dynamo number (see also Fig. 5 in Sect. 4.2.8).

Fig. 23

Schematic representation of a Hopf bifurcation, describing the transition from a fixed-point ${\varvec{B}}=0$ solution of the dynamo equation losing stability to a cyclic (limit cycle) solution when the dynamo number D exceeds its critical value $D_{\mathrm{crit}}$. Depending how far into the supercritical regime the dynamo is operating, variations in the dynamo number can translate into smaller (green) or larger (red) variations in cycle amplitudes $\delta A$ (see text)

The Hopf bifurcation route to cyclic dynamo action is believed to be a generic feature of nonlinear solar/stellar dynamos (e.g., Tobias et al. 1995; Weiss and Tobias 2016, and references therein). Figure 23 then suggests that any mechanisms, deterministic or stochastic, leading to variations in any source term on the RHS of the dynamo equations (38)–(39) can lead to amplitude variability in cycle properties, irrespective of details of the nonlinearity as long as the dynamo is operating not too far into the supercritical regime.¹⁸ This is illustrated by the two colored boxes on Fig. 23; variations of the effective dynamo number (horizontal) will induce variations in cycle amplitude ($\delta A$, vertical) as the system seeks to recover its equilibrium amplitude on a timescale given by the linear growth rate, and the magnitude of these amplitude variations will be largest close to the bifurcation (red box).

Stochastic forcing and the art of noise

Sources of stochastic fluctuations abound in the solar interior, all ultimately due to the strongly turbulent character of solar convection, the ultimate energy source of all inductive processes contributing to solar dynamo action. Tensor components describing the turbulent electromotive force are expected to be strongly fluctuating quantities, an expectation confirmed by analytical estimates (e.g., Hoyng 1988, 1993) and measurements in numerical simulations (e.g., Otmianowska-Mazur et al. 1997; Ossendrijver et al. 2001; Brandenburg and Sokoloff 2002; Käpylä et al. 2006a; Racine et al. 2011; Simard et al. 2016; Warnecke et al. 2018, and references therein). As for the Babcock–Leighton mechanism, observations of emerging bipolar magnetic active regions reveals large fluctuations in key characteristics for buildup of surface polar fields, notably tilt angle, flux, and pole separation. More generally, all inductive mechanisms considered in Sect. 3.2 arise from a finite number of “events” (cyclonic updrafts, emerging bipolar magnetic region, helical twist on a flux rope, etc.) collectively adding up to a mean azimuthal electromotive force. The large-scale flows contributing to magnetic field induction and transport are also driven by turbulent effects, and are expected to show strong fluctuations about their mean profiles.

As exemplified by the red box on Fig. 23, if the dynamo operates only marginally above criticality even small variations in dynamo number can led to large cycle amplitude variations, persisting over a timescale set by the (inverse) linear growth rate, which can be significantly longer than the cycle period for solutions near criticality. Cameron and Schüssler (2017b) introduced the following simple stochastic differential equation as a toy model to quantify the consequences of such stochastic driving:

$$\begin{aligned} {\mathrm{d}{X}\over {\mathrm{d}}{t}}-(\beta +i\omega _0)X+(\gamma _r+i\gamma _i)|X|^2X=\sigma X {\mathrm{d}{W}\over {\mathrm{d}}{t}} . \end{aligned}$$

(64)

Here X is a measure of the magnetic field, the cubic nonlinearity is meant to capture the effect of flux loss by magnetic buoyancy, and W(t) is a stochastic process of amplitude $\sigma$. Without this stochastic term on the RHS, Eq. (64) would describe a nonlinear limit cycle of amplitude $\sqrt{\beta /\gamma _r}$ and angular frequency $\omega _0-\gamma _i\beta /\gamma _r$. Working in the weakly supercritical regime, the various numerical parameters in Eq. (64) can be adjusted to generate time series whose spectral properties closely resemble those of the sunspot number time series. Barnes et al. (1980) present an even simpler toy model achieving qualitatively similar results.

Turning to spatially-extended models, the effect of stochastic forcing has been investigated in most detail in the context of classical mean-field models (see Choudhuri 1992; Hoyng 1993; Ossendrijver and Hoyng 1996; Ossendrijver et al. 1996; Mininni and Gómez 2002, 2004; Moss et al. 2008; Charbonneau and Barlet 2011). In models not too far from criticality variations of the cycle amplitude on timescales much longer than the cycle period are readily generated, especially when the models include a tachocline-like low-diffusivity layer beneath the nominal convection zone. In the advection-dominated regime, time delay effects also provide a robust mechanism for generating a Gnevyshev–Ohl-like pattern of alternating high/low cycle amplitudes in response to stochastic forcing (see, e.g., Fig. 19 herein).

A particularly interesting consequence of random forced variations of the dynamo number, in mean-field models at or very close to criticality, is the coupling of the cycle’s duration and amplitude (Hoyng 1993; Ossendrijver and Hoyng 1996; Ossendrijver et al. 1996), leading to a pronounced anticorrelation between these two quantities that is reminiscent of the Waldmeier Rule, and hard to produce by purely nonlinear effects (cf. Ossendrijver and Hoyng 1996). However, this behavior does not carry over to the supercritical regime, so it is not clear whether this can indeed be accepted as a robust explanation of the observed amplitude-duration anticorrelation. In the supercritical regime, $\alpha$-quenched mean-field models are less sensitive to stochastic noise (Choudhuri 1992), unless of course they happen to operate close to a bifurcation point, in which case large amplitude and/or parity fluctuations can be produced (see, e.g., Moss et al. 1992).

Mean-field-like implementations of Babcock–Leighton dynamos behave similarly upon introduction of random stochastic forcing in their source term and/or other model components (see e.g. Charbonneau and Dikpati 2000; Charbonneau and Barlet 2011; Choudhuri and Karak 2012; Olemskoy and Kitchatinov 2013; Kitchatinov et al. 2018; Hazra and Nandy 2019). The comparison of the two solutions displayed on Fig. 19 herein is quite telling in this respect. Incorporating observed distributions of active region properties in Babcock–Leighton dynamos including a latitude–longitude representation of the solar surface, as considered in Sect. 5.5, can also lead to very solar-like behavior, as exemplified in Fig. 18 herein (see also Karak and Miesch 2017).

Nonlinear modulation: surfing the wave

Considering the key role played by rotational shear in all dynamo models surveyed in Sects. 4 and 5, the dynamical backreaction of the large-scale magnetic field on differential rotation is an obvious mechanism to consider. Such non-kinematic mean-field and mean-field-like models have been studied extensively, either via the perturbation or $\varLambda$-quenching approaches described in Sect. 4.2.5, and shown to lead to a wide range of variability patterns.

Figure 24a depicts schematically the workings of this amplitude modulation mechanism. Imagine the dynamo to operate in the supercritical regime with amplitude indicated by the dot labeled A. Suppose now that the growing magnetic field leads to a reduction of differential rotation, and thus of the effective dynamo number D. The system will gradually move from point A towards B, to a much lower magnetic amplitude, and thus much reduced Lorentz force.

Fig. 24

Schematic depiction of a amplitude modulation, and b parity modulation in non-kinematic dynamo models near criticality

This will allow differential rotation to recover, moving the system back to A. The dynamo number D is thus moving periodically back and forth within the range indicated by the blue box on Fig. 24a, with attendant gradual waxing and waning of the cycle amplitude, from point A to B and back.

An interesting variation on this pattern, parity modulation, occurs when the lowest order equatorially symmetric (quadrupole-like) and antisymmetric (dipole-like) dynamo modes have comparable critical dynamo numbers and growth rates, as is often the case with many mean-fied and mean-field-like models. This is plotted as two distinct bifurcation curves on Fig. 24b, labeled “D” and “Q”. Consider again a slow decrease of the dynamo number driven by a gradual reduction of differential rotation, pushing now the dominant mode (here D) from A to B, i.e., below its critical dynamo number (left-pointing blue arrow). Once differential rotation begins to recover and the effective dynamo number starts to increase (right-pointing arrow), the system resides temporarily in a regime in which the quadrupole-like symmetric mode has the largest growth rate, before returning to its dipole-like initial state. Once again a periodic modulation of the primary cycle is generated, but this time it is accompanied by a change in equatorial parity. For symmetric and antisymmetric modes having closely similar growth rates and critical dynamo numbers, this type of parity modulation can be mediated by relatively small variation of differential rotation (and also by stochastic forcing; see, e.g., Mininni and Gómez 2004; Olemskoy and Kitchatinov 2013; Hazra and Nandy 2019). Figure 25 shows an example, taken from the non-kinematic $\alpha ^2\varOmega$ mean-field dynamo solutions presented in Simard and Charbonneau (2020). The “perturbation flow” procedure outlined in Sect. 4.2.5 is used to follow magnetically-driven variations in differential rotation. Here, as the magnetic cycle amplitude falls and rises again, the equatorial parity switches from symmetric (quadrupole-like) to antisymmetric (dipole-like).

Fig. 25

Parity modulation in the non-kinematic $\alpha ^2\varOmega$ mean-field model of Simard and Charbonneau (2020). The top panel is a time–latitude diagram of the toroidal field (color scale) in the middle of the convection zone. The bottom row shows snapshot of the toroidal field in meridional planes, extracted at the times indicated by dashed lines on the top panel. Poloidal fieldlines are plotted as solid (dashed) lines for couterclockwise (clockwise) orientation

In the case of amplitude modulation (Fig. 24a), energy is exchanged between magnetic and kinetic reservoirs; while in the parity modulation case it is exchanged (mostly) between two magnetic reservoirs (one per parity). These have been dubbed Type II and Type I modulation (see discussion in Tobias et al. 1995; Knobloch and Landsberg 1996; Knobloch et al. 1998; Weiss and Tobias 2016). Both types of modulation can co-exist, as demonstrated by the magnetic energy time series for non-kinematic $\alpha \varOmega$ mean-field dynamo solutions plotted on Fig. 26. These model runs, taken from Bushby (2006), are again computed using the “perturbation flow” procedure outlined in Sect. 4.2.5.

Fig. 26

Cycle amplitude modulation in the non-kinematic $\alpha \varOmega$ mean-field model of Bushby (2006). Each panel shows time series of magnetic energy (ME, black), kinetic energy of the perturbation flow ${\varvec{U}}^\prime$ (PKE, dashed-blue, cf. Eq. 36), and equatorial parity (dotted-red), scaled between $-1$ (antisymmetric, dipole-like) and $+1$ (symmetric, quadrupole-like) to the vertical extent of each panel. The four panels differ in dynamo number and/or magnetic Prandtl number, as labeled. Note also the different vertical scales from one panel to another. Time is measured in units of the magnetic diffusion time $\tau$ [see Eq. (41)]. Plot generated from numerical data kindly provided by P. Bushby

For a magnetic Prandtl number of unity (not shown), a constant amplitude cycle is produced, of period $\mathrm {P}_{\rm cyc}\sim 10^{-2}\,\tau$ and critical dynamo number $\simeq -1.5\times 10^6$. When $\mathrm {Pm}$ is reduced significantly below unity, there appears a large amplitude modulation of the primary cycle, with modulation period $\sim \mathrm {P}_{\rm cyc}/\mathrm {Pm}$ (Panel a). As the dynamo number is increased this modulation becomes chaotic (panel b). At fixed dynamo number, reducing $\mathrm {Pm}$ also increases the magnitude of the differential rotation perturbation, as measured here by the perturbation kinetic energy (cf. blue lines on panels c and d). These behavior are robust and have been observed in a variety of non-kinematic models (see, e.g., Moss and Brooke 2000; Phillips et al. 2002; Simard and Charbonneau 2020), including models relying on $\varLambda$-quenching (e.g., Küker et al. 1999; Pipin 1999; Inceoglu et al. 2017).

Time delays: lagging behind

The introduction of ad hoc time-delays in dynamo models is long known to lead to pronounced cycle amplitude fluctuations (see, e.g., Yoshimura 1978; Wilmot-Smith et al. 2006; Jouve et al. 2010). However, time-delay effects can arise naturally in dynamo models where the source regions for the poloidal and toroidal magnetic components are spatially segregated, such as solar cycle models based on the Babcock–Leighton mechanism. In these models meridional circulation (or turbulent pumping) usually sets the cycle period (see Sect. 5.4.2 herein). In doing so, it also introduces a long time delay in the dynamo mechanism, “long” in the sense of being comparable to the cycle period. This delay originates with the time required for circulation (or pumping) to transport the surface poloidal field down to the core–envelope interface, where the toroidal component is produced by rotational shear.¹⁹ Durney (2000) and Charbonneau (2001) explored the dynamical consequences of this long time delay, using a simple one-dimensional iterative map. As the dynamo number increases beyond criticality, the system exhibits a classical transition to chaos through successive period doubling bifurcations. A Gnevyshev–Ohl pattern also materializes naturally in response to low amplitude stochastic fluctuations. Counterparts of these behaviors materialize in spatially-extended mean-field-like Babcock–Leighton models of the type considered in Sect. 5.4 (see Charbonneau et al. 2005, 2007, also Wilmot-Smith et al. 2006).

Rattling the conveyor belt

Again because of the crucial role played by magnetic field transport mechanisms in solar cycle models of the flux transport variety, deterministic or stochastic forcing of transport mechanisms can lead to large cycle amplitude variability. Efforts along these lines have mostly focused on forced variations of the meridional flow. For example, (Nandy et al. 2011) have presented model results suggesting that the extended activity minimum between cycles 23 and 24 was caused by a slowdown on meridional circulation during cycle 23. By similar means, Lopes and Passos (2009) could reproduce quite well the observed variations of sunspot cycle amplitudes since 1750 (see Fig. 27), while Karak and Choudhuri (2011) could reproduce the observed anticorrelation between cycle rise time and amplitude.

Fig. 27

Effect of persistent variations in meridional circulation on the amplitude of the solar cycle, as modeled by Lopes and Passos (2009). Panel a shows the signed square root of the sunspot number (gray), here used as a proxy of the solar internal magnetic field. A smoothed version of this time series (black) is fitted, one magnetic cycle at a time (green), with the equilibrium solution of the truncated dynamo model of Passos and Lopes (2008); assuming that variations in the fitting parameters are due to variations in the meridional flow speed ($v_p$), the coarse time series of $v_p$ of panel b (in green) is obtained, scaled to the magnetic cycle 1 value and with error bars from the fitting procedure. Input of this piecewise-constant meridional flow variation (scaled down by a factor of two, in red in panel b) in the 2D Babcock–Leighton dynamo model of Chatterjee et al. (2004) yields the pseudo-SSN time series plotted in Panel c (figure produced from numerical data kindly provided by D. Passos)

In all cases, however, the required coherence time of the forced meridional flow variations is quite long, of the order or even exceeding the cycle period; this is hard to justify physically, even more so since MHD simulations indicate that magnetic variability drives meridional flow variations on timescales of the order of the cycle period (or longer), rather than the other way around (Passos et al. 2017).

Intermittency and Grand Minima/Maxima

The term “intermittency” was originally coined to characterize signals measured in turbulent fluids, but has now come to refer more generally to systems undergoing apparently random, rapid switching from quiescent to bursting behaviors, as measured by the magnitude of some suitable system variable (see, e.g., Platt et al. 1993). Intermittency thus requires at least two distinct dynamical states available to the system, and a means of transiting from one to the other. In the context of solar cycle model, intermittency refers to the existence of quiescent epochs of strongly suppressed activity randomly interspersed within periods of “normal” cyclic activity. Observationally, the Maunder Minimum is usually taken as the exemplar for such quiescent epochs.

Much effort has already been invested in categorizing intermittency-like behavior observed in solar cycle models in terms of the various types of intermittency known to characterize dynamical systems (see Ossendrijver and Covas 2003, and references therein). In what follows, we simply survey the various routes to intermittency uncovered in the various types of solar cycle models discussed earlier, and give pointers to good representative examples in the published literature.

Figure 28a depicts schematically the mode of operation of on–off intermittency, potentially relevant to any of the dynamo models considered previously. Consider any mechanism, whether stochastic or deterministic, that can push the dynamo number below its critical value (red arrow); the cycle amplitude then decays exponentially, until the dynamo number moves back above criticality (green arrow) and the amplitude builds up again; this is fundamentally the same idea as amplitude modulation (Fig. 24a), except that the bifurcation is now crossed. On–off intermittency is easiest to produce when the dynamo is operating close to criticality. In situations where the fastest growing modes of symmetric and antisymmetric equatorial parity have comparable growth rates (viz. Fig. 24b), intermittency can be accompanied by parity modulation. (Sokoloff and Nesme-Ribes 1994).

Fig. 28

Schematic depiction of a on–off intermittency and b in–out intermittency in a generic bifurcation diagram close to criticality. In b the gray shaded area indicates the basin of attraction of the finite amplitude cycle. Outside of this basin the amplitude decays exponentially to zero, even if $D>D_{\rm crit}$ (see text)

Figure 29 shows an example, taken from Olemskoy and Kitchatinov (2013). The simulation segment plotted on the top panel exemplifies a Spörer-like Grand Minimum extending over a century, with residual cyclic activity in the Southern hemisphere and persistent hemispheric asymmetry in the recovery to normal cyclic behavior. The bottom panel shows a extended time series of individual peak cycle amplitudes, smoothed with a running 1-2-2-2-1 filter. The primary decadal cycle is lost on such a representation, leaving the multidecadal modulation amplitude generated by the stochastic forcing. The regions colored in blue and red delineate epochs identified as Grand Minima and Maxima, respectively.

Fig. 29

Grand Minima and Maxima in the stochastically-forced 2D axisymmetric kinematic Babcock–Leighton model of Olemskoy and Kitchatinov (2013). The top panel is a time–latitude diagram of the deep toroidal magnetic component, showing an instance of Grand Minima. Panel b shows a 1-2-2-2-1 smoothed time series of magnetic cycle amplitudes. The threshold defining Grand Minima (blue) and Maxima (red) are set at values that match the fraction of time spent in such phases, as inferred from cosmogenic radioisotopes. Graphics kindly provided by L. Kitchatinov

As with most such models stochastically forced to trigger intermittency, the Grand Minima and Maxima on Fig. 29b recur aperidiocally, with an exponential distribution of inter-event waiting times, indicative of a stationary memoryless random process. This is consistent with the waiting time distribution inferred from the cosmogenic radioisotope record (see Usoskin 2017, and references therein). For other interesting examples of on–off intermittency driven by stochastic noise, see Hoyng (1993), Mininni and Gómez (2002), Moss et al. (2008), Usoskin et al. (2009a), Choudhuri and Karak (2012) and Cameron and Schüssler (2017b). For equally interesting examples driven by deterministic dynamical nonlinearities, see Brooke et al. (1998, 2002) For an example including both noise and nonlinearities, see Passos et al. (2012).

An important distinction must be made between dynamos that are self-excited, in that they can amplify an arbitrarily small magnetic field, and dynamos characterized by a lower operating threshold on magnetic field strength. Turbulent mean-field dynamos relying on the $\alpha$-effect belong to the first category, while models relying, e.g., on the Babcock–Leighton mechanism belong to the second. Now even if $D>D_{\rm crit}$ at all times, the dynamo can only operate in a finite range of magnetic amplitude. In such a case intermittency can occur when variations of the cycle amplitude, again either stochastic or deterministic, push the magnetic cycle amplitude below threshold, as depicted schematically on Fig. 28 (red arrow). The amplitude then decays to zero, and an independent inductive mechanism or source of magnetic field is needed to push the dynamo back into normal operating mode (green arrow). This is known as in–out intermittency. For examples in the context of Babcock–Leighton models, see Charbonneau et al. (2004), Karak and Choudhuri (2013), Passos et al. (2014), Hazra et al. (2014) and Ölçek et al. (2019); in the context of mean-field-like models relying on instabilities of thin flux tubes, see Schmitt et al. (1996) and Ossendrijver (2000b).

Thresholded amplitude modulation and Grand Minima/Maxima

Dearth of sunspots, such as during the Maunder Minimum, does not necessarily mean a halted cycle. The same basic magnetic cycle may well have continued unabated all the way through the Maunder Minimum, but at an amplitude just below the threshold for the formation and buoyant destabilisation of magnetix flux ropes containing sufficient magnetic flux to lead to the formation of sunspots upon emergence at the photosphere. Strictly speaking, thresholding a variable controlled by a single dynamical state subject to amplitude modulation is distinct from true intermittency, although the resulting time series for the variable may well look quite “intermittent”.

Thresholded amplitude modulation has some attractive properties as a Maunder Minimum scenario. First, the strong hemispheric asymmetry in sunspots distributions in the final decades of the Maunder Minimum (Ribes and Nesme-Ribes 1993) can occur naturally via parity modulation (see Fig. 25 herein). Second, because the same cycle is operating at all times, cyclic activity in indicators other than sunspots (such as radioisotopes, see Beer et al. 1998) is explain naturally; the dynamo is still operating and the heliospheric magnetic field is still undergoing polarity reversal, but simply fails to reach the amplitude threshold above which sunspots are produced.

There are also important difficulties with this explanatory scheme. Dynamo solutions in the small $\mathrm {Pm}$ regime are usually characterized by large, non-solar angular velocity fluctuations. In such models, solar-like, low-amplitude torsional oscillations do occur, but only for $\mathrm {Pm}\sim 1$. Unfortunately, in this regime the solutions then lack the separation of timescales needed for Maunder-like Grand Minima episodes. One is stuck here with two conflicting requirements, neither of which easily evaded; but do see Bushby (2006) and Simard and Charbonneau (2020). Another difficulty is that Grand Minima often tend to have similar durations and recur in periodic or quasi-periodic fashion [viz. Fig. 26)], while the sunspot and radioisotope records, taken at face value, suggest a pattern far more irregular (Usoskin 2008), including long periods without Grand Minima. It has been suggested, and demonstrated with (relatively) simple nonlinear models, that this problem may be alleviated by supermodulation (Weiss and Tobias 2016). This refers to a deterministic, very long timescale modulation of the primary modulation envelope of the basic decadal magnetic cycle. Grand Minima then only occur in epochs when supermodulation has not suppressed the primary modulation (Beer et al. 2018).

Grand minima in MHD simulations

Global magnetohydrodynamical simulations (Sect. 6) incorporate self-consistently both stochasticity (through the effect of small-scale turbulence) and nonlinear magnetic backreaction. Identifying in such simulations events akin to Grand Minima is not easy, because in most cases the large-scale magnetic cycles produced are often not very regular to begin with. Simulation K3S of Augustson et al. (2015) present arguably the cleanest example to date. Their basic cycle is fairly regular, with a magnetic cycle period of 6.2 years and clear dominance of antisymmetric (dipole-like) equatorial parity. The cycle interruption episode they observe lasts 5 half-cycles and is accompanied by a $\sim 50$% drop in magnetic energy. It appears to be associated with a form of destructive interference between co-existing dynamo modes of symmetric and antisymmetric equatorial parity, akin to the type I parity modulation mechanism discussed in Sect. 7.2.3. The intermittent interruption of cyclic activity in the more irregular magnetic cycle building up in the extended simulation discussed in Käpylä et al. (2016) is also interpreted as arising from interaction between co-existing dynamo modes.

Also very relevant in this context are the rotating cartesian box MHD simulations presented in Bushby et al. (2018). A regularly cyclic large-scale magnetic field is generated, and in part of their parameter space undergoes intermittently recurring Grand Minima-like episodes. These are associated with a reduction of the large-scale vortical flow present in their simulations (see their Fig. 11), and thus can be interpreted as an instance of type II modulation.

Fossil fields and the 22-years cycle

The presence of a large-scale, quasi-steady magnetic field of fossil origin in the solar interior has long been recognized as a possible explanation of the Gnevyshev–Ohl rule. Such a slowly-decaying internal fossil field being effectively steady on solar cycle timescales, its superposition with the 11-years polarity reversal of the overlying dynamo-generated field will lead to a 22-years modulation, whereby the cycle is stronger when the fossil and dynamo field have the same polarity, and weaker when these polarities are opposite (see, e.g., Boyer and Levy 1984; Boruta 1996). The magnitude of the effect is directly related to the strength of the fossil field, versus that of the dynamo-generated magnetic field. This holds true provided that flows and dynamical processes within the tachocline allows magnetic coupling between the radiative core and convective envelope, which is not at all obvious (see, e.g., Forgács-Dajka and Petrovay 2001; Kitchatinov and Rüdiger 2006; Dikpati et al. 2005; Strugarek et al. 2011; Barnabé et al. 2017).

The fossil field explanation of the Gnevyshev–Ohl rule makes one strong prediction: while the pattern may become occasionally lost due to large cycle amplitude fluctuations of other origin, whenever it is present even-numbered cycles should always be of lower amplitudes and odd-numbered cycles of higher amplitude (under Wolf’s cycle numbering convention). The analysis of Mursula et al. (2001), based on cycle-integrated group sunspot numbers, indicates that the odd/even pattern has reversed between the time periods 1700–1800 and 1850–1990 (see their Figure 1). This would then rule out the fossil field hypothesis unless, as argued by some authors (see Usoskin et al. 2009a, and references therein), a sunspot cycle has been “lost” around 1790, at the onset of the Dalton minimum.

Open questions and current trends

I close this review with the following discussion of a few open questions that, in my opinion, bear particularly heavily on our understanding (or lack thereof) of the solar cycle.

What is the primary poloidal field regeneration mechanism?

Given the amount of effort having gone into building detailed dynamo models of the solar cycle, it is quite sobering to reflect upon the fact that the physical mechanism responsible for the regeneration of the poloidal component of the solar magnetic field ($T\rightarrow P$) has not yet been identified with confidence. As discussed at some length in Sects. 4 and 5, current models relying on distinct mechanisms all have their strengths and weaknesses, in terms of physical underpinning as well as comparison with observations. We actually have too many viable $T\rightarrow P$ mechanisms!

Something akin to the $\alpha$-effect of mean-field electrodynamics has been measured in a number of local and global numerical simulations including rotation and stratification, so this certainly remains a favored magnetic field generation mechanism. Some important caveat remain in order, notably the fact that all such simulations operate in a parameter regime far remote from solar interior conditions, and tend to predict much more power in large convective scales than inferred from helioseismology—the so-called convective conundrum. Such MHD simulations cannot yet incorporate self-consistently surface processes such as the Babcock–Leighton mechanism in the context of simulating global magnetic cycles. On the other hand, modelling of the evolution of the Sun’s surface magnetic flux has abundantly confirmed that the Babcock–Leighton mechanism is operating on the Sun, in the sense that magnetic flux liberated by the decay of tilted bipolar active regions does accumulate in the polar regions, where it triggers polarity reversal of the poloidal component. The key question is whether this is an active component of the dynamo cycle, or a mere side-effect of active region decay. Likewise, the buoyant instability of magnetic flux tubes (Sect. 4.5.3) is, in some sense, unavoidable; here again the question is whether or not the associated azimuthal mean electromotive force contributes significantly to dynamo action in the Sun.

What limits the amplitude of the solar magnetic field?

The amplitude of the dynamo-generated magnetic field is almost certainly restricted by the backreaction of Lorentz forces on the driving fluid motions. However, as outlined in Sect. 4.2, this backreaction can occur in many ways. Here as well we have too many potential amplitude regulation mechanisms, and we currently do not know which physical processes regulate the magnetic amplitude of the solar cycle.

Algebraic quenching of the $\alpha$-effect (or $\alpha$-effect-like source terms) is the mechanism most often incorporated in dynamo models. However, this usually has much more to do with computational convenience than commitment to a specific physical quenching mechanism. There is little doubt that the turbulent $\alpha$-effect will be affected once the mean magnetic field reaches equipartition; the critical question is whether it becomes quenched long before that, for example by the small-scale component of the magnetic field. The issue hinges on helicity conservation and flux through boundaries, and subtleties of flow-field interaction in MHD turbulence.

Analysis of global MHD numerical simulations generating large-scale magnetic cycles (Sect. 6) indicate that something akin to $\alpha$-quenching is indeed operating, but so is $\varLambda$-quenching, buoyant flux loss, as well as direct Lorentz force backrection of the cycling large-scale magnetic field on large-scale flows. Magnetic diffusivity quenching is less certain, with only marginally significant measurements at this juncture. On the observational front, helioseismology has revealed only small variations of the differential rotation profile in the course of the solar cycle. The observed variations amount primarily to an extension in depth of the pattern of low-amplitude torsional oscillations long known from surface Doppler measurements (but see also Basu and Antia 2001; Toomre et al. 2003; Howe 2009). If the solar dynamo is operating close to criticality, this may still be sufficient to saturate the magnetic cycle.

How constraining is the sunspot butterfly diagram?

The shape of the sunspot butterfly diagram (see Fig. 2) continues to play a dominant constraining role in many dynamo models of the solar cycle. Yet caution is in order on this front. Calculations of the stability of toroidal flux ropes stored in the overshoot region immediately beneath the core–envelope interface indicate that instability is much harder to produce at high latitudes, primarily because of the stabilizing effect of the magnetic tension force; thus strong fields at high latitudes may well be there, but not produce sunspots. Likewise, the process of flux rope formation from the dynamo-generated mean magnetic field is currently not understood quantitatively, and its efficiency may well depend on latitude (see Kitchatinov 2020, and references therein). These are all crucial questions from the point of view of comparing results from dynamo models to sunspot data. Until they have been answered, uncertainty remains as to the degree to which the sunspot butterfly diagram can be compared in all details to time–latitude diagrams of the toroidal field, as produced by this or that dynamo model. Autonomous flux rope formation in global MHD numerical simulations (see Sect. 6.7) may shed light on this key problem in the not-too-distant future.

Is the tachocline crucial?

Fifteen years ago, when the first version of this review was written, a near concensus existed to the effect that the solar dynamo resides at least in part in the tachocline, and that it was the location of formation and storage of toroidal magnetic flux ropes which would eventually produce bipolar magnetic regions, upon buoyant destabilisation, rise, and emergence as $\varOmega$-loops through the photosphere. This near-concensus has been seriously shaken since, from a number of directions. First, MHD numerical simulations have demonstrated that reasonably solar-like large-scale decadal magnetic cycles can be generated entirely within the convective layers, even with an impenetrable lower boundary condition; second, a subset of these same MHD simulations have also shown that the formation of equipartition-strength flux-rope-like buoyant magnetic structures is possible within a strongly turbulent convection zone (viz. Sect. 6.7 herein), and that these magnetic structures retain their coherence as they rise to the top of the domain. Third, recent stellar observational analyses indicate that fully convective stars seem to exhibit the same relationship between rotation rate and magnetic activity, as measured through X-ray emission (Wright and Drake 2016, see also Blackman and Thomas 2015). This suggests a fundamental similarity in the underlying dynamo process, and thus raises serious doubts regarding any essential role played by a tachocline-like rotational shear layer.

Is meridional circulation crucial?

The main question regarding meridional circulation is not whether it is there or not, but rather what role it plays in the solar cycle. The answer hinges on the value of the turbulent diffusivity, which is notoriously difficult to estimate with confidence. It is probably essential in mean-field and mean-field-like dynamo models characterized by positive $\alpha$-effects in the Northern hemisphere, in order to ensure equatorward transport of the sunspot-forming, deep-seated toroidal magnetic field (see Sects. 4.4, 4.5, and 5.4), unless the latitudinal turbulent pumping speeds turn out high enough to take on that role. Photospheric observations and surface flux transport simulations (Sect. 5.2) certainly indicate that it plays a important role at least in the evolution of the surface and interplanetary magnetic field in the course of the solar cycle (Wang et al. 2002; Upton and Hathaway 2014a).

Some recent helioseismic measurements of meridional circulation have challenged the steady, single-cell-per-quadrant meridional flow used in most flux transport-type mean-field and mean-field-like solar cycle models, including those based on the Babcock–Leighton mechanism. There is hope that this debate will be settled with upcoming improved helioseismic data and inversions. It is noteworthy that the recent inversions that include a mass conservation constraint tend to recover single-cell internal flows. At the modelling level, the primary unknown at this writing is the degree to which meridional circulation is affected by the Lorentz force associated with the dynamo-generated magnetic field. The few extant calculations (Rempel 2006a, b) suggest that the backreaction is limited to regions of strongest toroidal fields, so that the “conveyor belt” is still operating in the bulk of the convective envelope, but this issue requires further study. Inversion of the deep meridional flow from data assimilation into dynamo simulations (Hung et al. 2017) is also an interesting avenue.

Is the mean solar magnetic field really axisymmetric?

While the large-scale solar magnetic field is axisymmetric about the Sun’s rotation axis to a good first approximation, various lines of observational evidence point to a persistent, low-level non-axisymmetric component; such evidence includes the so-called active longitudes (e.g., Henney and Harvey 2002), rotationally-based periodicity in cycle-related eruptive phenomena (Bai 1987), and the shape of the white-light corona in the descending phase of the cycle (see Dikpati et al. 2016, and references therein).

Various mean-field-based dynamo models are known to support non-axisymmetric modes over a substantial portion of their parameter space (see, e.g., Moss et al. 1991; Moss 1999; Bigazzi and Ruzmaikin 2004, and references therein). At high Rm, strong differential rotation (in the sense that $C_\varOmega \gg C_\alpha$) is known to favor axisymmetric modes, because it efficiently destroys any non-axisymmetric component on a timescale much faster than diffusive ($\propto \mathrm {Rm}^{1/3}$ at high $\mathrm {Rm}$, instead of $\propto \mathrm {Rm}$). Although it is not entirely clear that the Sun’s differential rotation is strong enough to place it in this regime (see, e.g., Rüdiger and Elstner 1994), some 3D kinematic dynamos do show this symmetrizing effect of differential rotation (see, e.g., Zhang et al. 2003a).

Many recent numerical 3D MHD simulations producing large-scale magnetic cycles exhibit significant power in non-axisymmetric modes even through the axisymmetric component may dominate (see, e.g., Racine et al. 2011, Fig. 7). The recent simulations of Viviani et al. (2018) suggest that the non-axisymmetric modes become dominant at rotation rates higher than solar, while the simulation analyzed by Lawson et al. (2015) exhibits a “spontaneous” transition to a non-axisymmetric configuration (see their Fig. 14), for reasons perhaps related to the development of a non-axisymmetric MHD instability in the stable fluid layer present in their modelling setup (see also Dikpati et al. 2016; Guerrero et al. 2019). These types of simulations will probably offer the best handle on this question.

Another potential driver of non-axisymmetric behavior is the development of Rossby-type waves in the tachocline (Zaqarashvili et al. 2010), an idea that has attracted a lot of attention in recent years (see, e.g., Dikpati et al. 2018, and references therein). To what degree such waves could impact a turbulent dynamo operating in the overlying convecting layers remains an open question.

What causes Maunder-type Grand Minima?

At this writing, we still do not know what triggers Grand Minima, or which physical processes control their duration and drive recovery to “normal” cyclic activity.

Historical researches have shown that the Sun climbed out of the Maunder Minimum gradually, and showing strongly asymmetric activity, with nearly all sunspots observed between 1670 and 1715 located in the Southern solar hemisphere (see Ribes and Nesme-Ribes 1993). Some historical reconstructions of the butterfly diagram in the pre-photographic era also suggest the presence of what could be interpreted as a quadrupolar component (Arlt 2009). These are the kind of pattern that can be readily produced by nonlinear parity modulation (cf. Fig. 25 herein; see also Tobias 1996; Beer et al. 1998; Sokoloff and Nesme-Ribes 1994; Usoskin et al. 2009b; Beer et al. 2018). Then again, in the context of an intermittency-based model, it is quite conceivable that one hemisphere can pull out of a quiescent epoch before the other, thus yielding sunspot distributions compatible with the aforecited observations in the late Maunder Minimum. Such scenarios, relying on (relatively) weak cross-hemispheric coupling, have hardly begun to be explored (Charbonneau 2005, 2007b; Chatterjee and Choudhuri 2006; Hazra and Nandy 2019).

Another possible avenue for distinguishing between these various scenarios is the persistence of the primary cycle’s phase through Grand Minima. Generally speaking, models relying on thresholded amplitude modulation (Sect. 7.4) can be expected to exhibit good phase persistence across such minima, because the same basic cycle is operating at all times (cf. Fig. 25). True intermittency, on the other hand, should not necessarily lead to phase persistence, since the active and quiescent phases are governed by distinct dynamics. Careful analysis of cosmogenic radioisotope data may indicate the degree to which the solar cycle’s phase persisted through the Maunder, Spörer, and Wolf Grand Minima, in order to narrow down the range of possibilities.

Where do we go from here?

Recent years have witnessed a number of significant advances in solar cycle modelling. Solar cycle models based on the Babcock–Leighton mechanism of dipole reversal and regeneration through active region decay have undergone spectacular developments in the past decade, and have become the favored framework for cycle forecasting schemes based on dynamo models. In parallel, global magnetohydrodynamical simulations of thermally-driven convection are now generating reasonably solar-like large-scale magnetic cycles, allowing measurements of the mean turbulent electromotive force, of the associated ${\varvec{\alpha }}$-tensor, turbulent diffusivity and turbulent pumping speed. Such simulations are also ideally suited for investigating a number of important issues, such as the mechanism(s) responsible for regulating the amplitude of the solar cycle, the magnetically-driven temporal variations of the large-scale flows important for the solar cycle, and the possible impact of a cycling large-scale magnetic field on convective energy transport, to mention but a few.

Despites continuing advances in computing power, global MHD simulations remain extremely demanding, and proper simultaneous capture of important solar cycle elements—most notably the formation, emergence and surface decay of sunspots and active regions—are certainly not forthcoming (although do see Hotta and Iijima 2020). It appears likely that in the foreseeable future, the simpler, mean-field and mean-field-like solar cycle models reviewed here will remain the workhorses of research on long timescale phenomena such as grand activity minima and maxima, on the evolution of surface magnetic flux, on dynamo-model-based solar cycle prediction, and on the modelling and interpretation of stellar activity cycles.