Observationally Guided Models for the Solar Dynamo and the Role of the Surface Field

Abstract

Theoretical models for the solar dynamo range from simple low-dimensional “toy models” to complex 3D-MHD simulations. Here we mainly discuss appproaches that are motivated and guided by solar (and stellar) observations. We give a brief overview of the evolution of solar dynamo models since 1950s, focussing upon the development of the Babcock–Leighton approach between its introduction in the 1960s and its revival in the 1990s after being long overshadowed by mean-field turbulent dynamo theory. We summarize observations and simple theoretical deliberations that demonstrate the crucial role of the surface fields in the dynamo process and give quantitative analyses of the generation and loss of toroidal flux in the convection zone as well as of the production of poloidal field resulting from flux emergence at the surface. Furthermore, we discuss possible nonlinearities in the dynamo process suggested by observational results and present models for the long-term variability of solar activity motivated by observations of magnetically active stars and the inherent randomness of the dynamo process.

1 Introduction

Studies of solar and stellar dynamos face a problem of utter complexity, i.e., the interaction of turbulent convection with rotation and magnetic field in a highly stratified medium, covering wide ranges of spatial and temporal scales. Attempts to directly attack this problem with numerical 3D-MHD simulations have made significant progress in recent years (e.g., Charbonneau 2020; Käpylä et al. 2023), but are still severely limited in spatial resolution, so that a faithful representation of the solar cycle has not been achieved so far. All other approaches to the dynamo problem resort to simplifications in order to obtain a tractable task. They largely rely on the surprising amount of regularity shown by the solar cycle, e.g., Hale’s polarity rules and the systematic tilt of sunspot groups (Joy’s law), the butterfly diagram, and the regular reversals of the global dipole field (Hathaway 2015). These regularities suggest simplified concepts, such as the generation of azimuthal (toroidal) magnetic flux through winding of meridional (poloidal) magnetic field lines by differential rotation (Cowling 1953) or the formation of bipolar sunspot groups by the emergence of buoyantly rising magnetic flux tubes (Parker 1955b).

A variety of models addressing various aspects of the dynamo problem has been developed. These range from rather ad-hoc “toy models” over sophisticated two-scale approaches, pioneered by the model of Parker (1955a) and by mean-field theory of turbulent MHD flows (see review by Brandenburg et al. 2023) to 2D/3D flux-transport dynamo models including various physical processes considered to be relevant for the dynamo (see reviews by Charbonneau 2020; Hazra et al. 2023).

The simplest “model” in the literature is probably due to Barnes et al. (1980). These authors considered a digital narrow-band filtering of Gaussian white noise, corresponding to a randomly disturbed periodic signal that could be illustrated by a “pendulumn pelted with peas” (Yule 1927). The results of their short computer program (15 lines!) exhibit a very similar kind of variability as shown by the sunspot record, including the occurence of extended periods of low activity (grand minima). The important lesson from this result for models of the solar dynamo is that even a striking similarity of their output with records of solar activity alone does not necessarily imply the validity of a model.

In this paper, we focus upon models of the solar dynamo as well as for the cyclic generation and removal of magnetic flux that are guided by solar (and also stellar) observations. The motivation for such approaches comes from the fact that the very complex interactions in the convection zone can lead to comparably simple results, such as the stable differential rotation in latitude, the meridional circulation, the polarity rules of sunspot groups, or the butterfly diagram of magnetic flux emergence. This might perhaps be compared to the flow of water in a watermill: although the detailed turbulent flow pattern is utterly complex, the general result is simple: water flows down the potential well and faithfully drives the wheel. The paradigm of observationally motivated models is the scenario of Babcock (1961), which was later extended and put in a mathematical form by Leighton (1969). These seminal papers paved the way for what are now generally called Babcock–Leighton-type models of the solar dynamo.

The plan of this paper is as follows. In Sect. 2 we describe the principles of the Babock-Leighton scenario and review the evolution of dynamo models until the end of the 1980s, when mounting empirical evidence led to the renaissance of Babcock–Leighton dynamo models after an extended period of near oblivion. The generation and removal of toroidal and poloidal magnetic flux in the Sun and the crucial role of the observable surface field are discussed in Sect. 3. Nonlinearity of the dynamo process, predictability, and models for the long-term variability of solar activity are considered in Sect. 4. Section 5 gives a brief outlook.

2 The Babcock–Leighton Approach and the Evolution of Models for the Solar Dynamo

The seminal paper of Babcock (1961) lays out a purely observationally based scenario for the 11/22-year solar cycle. In a first step, the poloidal magnetic flux connected to the global dipole field is wound up by latitudinal differential rotation in the convection zone. This generates oppositely directed subsurface belts of toroidal field in both hemispheres. Subsequent instability, buoyant rise, and emergence of toroidal flux at the surface produces bipolar magnetic regions (BMRs) and sunspot groups in accordance with Hale’s polarity rules. These regions are observed to be systematically tilted in the sense that the magnetic polarity leading in the direction of rotation is nearer to the equator than the following polarity. This tilt, together with the dispersal of the BMRs in the course of time, leads to preferred transport of leading-polarity flux over the equator, so that a surplus of the respective following-polarity flux builds up in both hemispheres. Poleward transport of this flux by convection and meridional circulation leads to the reversal of the polar fields and the buildup of an oppositely directed dipole field, a process already suggested by Babcock and Babcock (1955). This entails the generation and emergence of a reversed toroidal field followed by another reversal of the dipole field, thus giving rise to the 22-year magnetic cycle.

Babcock (1961) already noted that the systematic tilt of the sunspot groups could be “... the result of Coriolis forces, which induce a vorticity in the whole of the fluid associated with a BMR when it rises to the surface.” The Coriolis effect is also invoked in the concept of “cyclonic convection” of Parker (1955a) and in the mean-field scheme based on turbulence theory pioneered by Steenbeck and Krause (1966) and Steenbeck et al. (1966). Possibly since both these approaches focus on the collective effect of a small-scale process (in the sense of a two-scale approach), neither Parker nor Steenbeck and coworkers apparently realized that the systematic tilt provides direct observational support for the action of the Coriolis effect as well a quantitative measure.

Leighton (1964) added a key component to Babcock’s scenario in the form of a random-walk model for the quasi-diffusive transport of magnetic flux on the solar surface by supergranular convection. Subsequently, he put the Babcock model in the mathematical form of a one-dimensional dynamo equation (Leighton 1969). It is not obvious why this Babcock–Leighton (BL) model fell into near oblivion for about two decades thereafter. In order to provide some understanding for this development, a brief sketch of the evolution of solar dynamo studies from the early 1970s onward is given in what follows.

Perhaps since the mathematically involved mean-field theory was considered to provide a strong theoretical footing, models for the solar dynamo until the 1990s mostly relied on a mean-field turbulent “$\alpha$-effect” based on correlations between small-scale fields operating within the convection zone. To explain the equatorward-directed migration of the activity belts shown by the butterfly diagram, these models generally required an inwardly increasing rotation rate, $d\Omega /dr<0$, according to the Parker-Yoshimura sign rule (Parker 1955a; Köhler 1973; Yoshimura 1975). The effect of the observed strong latitudinal differential rotation was thought to be of secondary importance. Consequently, both key processes for the turbulent dynamo, radial differential rotation and $\alpha$-effect, were assumed to operate in the solar interior, thus inaccessable to observation at that time. Therefore, the corresponding model parameters were largely unconstrained. The observable evolution of the surface field was seen as a mere epiphenomenon of a dynamo process operating deeply hidden in the convection zone and served solely as an observational constraint for the models.

The foundations of this approach were undermined when helioseismology made it possible to measure the differential rotation in the convection zone. It turned out that (except for a shallow near-surface shear layer) the increase of the rotation rate with depth required by these models is absent in the bulk of the convection zone (see review by Howe 2009). On the other hand, the rotation rate at the bottom of the convection zone showed a steep radial gradient across the “tachocline” (Brown et al. 1989), such that $d\Omega /dr<0$ in solar latitudes $\ge 45$ deg and $d\Omega /dr>0$ in lower latitudes. Some years before, Galloway and Weiss (1981) already had suggested that the solar dynamo should work in a stably stratified layer of overshooting convection below the bottom of the convection zone in order to avoid the rapid buoyant loss of toroidal magnetic flux inferred by Parker (1975). These results led to the concept of turbulent dynamo action within the overshoot layer/tachocline (e.g., Rüdiger and Brandenburg 1995) or near its interface with the convection zone proper (Parker 1993), where a properly chosen combination of the signs of $\alpha$-effect and radial gradient of the rotation rate could provide the correct conditions for equatorward propagating dynamo waves and activity belts (e.g., Tobias 1996; Charbonneau and MacGregor 1997). This approach was complemented by studies of equilibrium, stability, and dynamics of thin magnetic flux tubes starting with Spruit and van Ballegooijen (1982), Choudhuri and Gilman (1987), and Moreno-Insertis et al. (1992). Such studies (see reviews by Fan 2021; Işik et al. 2023) indicated that the toroidal field in the overshoot region must be amplified to about $10^{5}$ G before becoming unstable (Ferriz-Mas and Schüssler 1993, 1995) and rising to the surface to form bipolar magnetic regions within the latitude range shown by the butterfly diagram (Schüssler et al. 1994). Twisting of the rising flux tubes due to the Coriolis force then leads to tilt angles consistent with observation (D’Silva and Choudhuri 1993; Fan et al. 1994; Caligari et al. 1995).

Although the combination of tachocline/overshoot layer dynamos and the dynamics of thin flux tubes offered a comprehensive picture from the generation of magnetic flux up to its emergence at the surface, these models relied on a number of untested assumptions and simplifications, so that their predictive power remained rather limited. In the course of time, a number of theoretical considerations and observational results cast severe doubt upon the validity of this aproach:

• The total energy of a toroidal field of $10^{5}$ Gauss at the bottom of the convection zone would be comparable to the energy in the differential rotation of the tachocline (Rempel 2006). However, a corresponding strong variation of the differential rotation in the lower convection zone and tachocline in the course of the 11-year activity cycle is not observed (Basu and Antia 2019). Moreover, the interface between radiative core and convection zone cannot support much shear stress (Spruit 2011). Consequently, the radial differential rotation in the tachocline (mainly reflecting the transition from latitudinally differential rotation in the convection zone to nearly rigid rotation below) cannot generate a sizeable amount of toroidal magnetic flux unless being maintained by a very powerful downward transport of angular momentum.

• The latitudinal differential rotation is sufficient to create the total toroidal flux covered by the emergence of bipolar magnetic regions and sunspot groups. At the same time, the contribution of the observed radial differential rotation in the convection zone is only a few percent of that of the latitudinal differential rotation (Cameron and Schüssler 2015). Moreover, the radial shear in the tachocline is strong in high latitudes and weak in low latitudes, thus unfavorable for toroidal flux generation in low latitudes.

• Helioseismology indicates that the overshoot layer is much more strongly subadiabatic than assumed in the models for the storage and stability of toroidal flux (Christensen-Dalsgaard et al. 2011). On the other hand, part of the lower convection zone could be subadiabatically stratified (e.g., Spruit 1997; Hotta 2017).

• Observations of magnetically active stars show that partly and fully convective stars follow the same activity-rotation law (Wright and Drake 2016; Reiners et al. 2022), thus questioning the relevance of convective overshoot and the existence of a tachocline for the dynamo process. This is also supported by 3D-MHD simulations of partially and fully convective M dwarfs (Bice and Toomre 2023). Furthermore, even very cool, fully convective dwarfs (beyond spectral type M7) can exhibit activity cycles (Route 2016). Recently, Lu et al. (2023) found that the spin-down rates of M-type stars appear to sharply rise across the transition between partly and fully convective stars, indicating more organized large-scale surface fields of fully convective stars.

• 3D-MHD simulations demonstrate the formation of super-equipartion magnetic flux concentrations and buoyantly rising flux loops within a simulated convection zone without overshoot and tachocline (Fan and Fang 2014; Chen et al. 2017). Nelson et al. (2014) obtained similar results, albeit with a simulation assuming three times the solar rotation rate.

• If emerged magnetic structures were “anchored” near to the bottom of the convection zone, they should show slower rotation than that of the surface plasma below about $\pm 30$ deg latitude according to the helioseismically determined rotation profile. However, magnetic structures are observed rotate faster than the plasma at the surface (e.g., Howard 1996).

A new twist came when observations of a systematic poleward-directed meridional flow at the surface pioneered by Duvall (1979) and Howard (1979) became established during the 1980s (see review by Hanasoge 2022). This led to the suggestion that the associated deep return flow within the convection zone could transport toroidal flux equatorward. Models of flux-transport dynamos (FTDs) that rely upon this concept can provide a butterfly diagram consistent with observations regardless of the sign of the radial gradient of the rotation rate (Wang and Sheeley 1991; Durney 1995; Choudhuri et al. 1995). A recent review of FTD models has been provided by Hazra et al. (2023).

The confirmation of the systematic poleward surface flow also sparked the development of simulation models for the transport of magnetic flux at the solar surface on solar-cycle time scales, pioneered by the NRL group (DeVore et al. 1984; Wang et al. 1989b). Such Surface Flux Transport (SFT) models (see reviews by Mackay and Yeates 2012; Yeates et al. 2023) assume passive transport of vertically (radially) orientated magnetic flux by surface flows. Comparison of SFT simulations with observed synoptic magnetograms shows that the evolution of the surface flux can be faithfully described by flux emergence in systematically tilted bipolar magnetic regions followed by passive flux transport by differential rotation, meridional flow, and supergranular flows (the latter mostly being treated as a diffusion-like random walk, cf. Leighton 1964), and flux cancellation. In particular, the models confirm the buildup of polar fields due to the preferred transport of following-polarity flux toward the poles (Wang et al. 1989a).

The success of the SFT simulations led to the re-appraisal of the BL approach for the (re)generation of the poloidal field in the course of the dynamo process (Giovanelli 1985; Wang and Sheeley 1991), typically in connection with equatorward flux transport by meridional flow in the convection zone as Flux Transport Dynamo (FTD) models (Wang et al. 1991; Charbonneau 2020; Hazra et al. 2023). In the course of time, further lines of evidence for the validity of the BL approach and the crucial role of the surface flux for the solar dynamo became apparent:

• SFT models reproduce the evolution of the surface field, particularly the poleward drift of the following-polarity surface field leading to the buildup of the polar fields and the axial dipole (e.g., Wang et al. 2002; Baumann et al. 2004; Jiang et al. 2014b; Upton and Hathaway 2014; Whitbread et al. 2017).

• The polar field strength around cycle minimum is strongly correlated with the amplitude of the subsequent activity maximum (Legrand and Simon 1981; Wang and Sheeley 2009; Kitchatinov and Olemskoy 2011b; Hathaway and Upton 2016), thus providing a faithful predictor of cycle strength (Schatten et al. 1978; Petrovay 2020; Kumar et al. 2021; Bhowmik et al. 2023). Recent work by Kumar et al. (2022) and Biswas et al. (2023b) suggests that an earlier prediction is possible by considering the rise rate of the polar field a few years before minimum.

• Cameron and Schüssler (2015) showed that the above correlation in fact reflects a causation: the net hemispheric toroidal flux generated during a half cycle results from the action of the latitudinal differential rotation on the poloidal flux connected to the polar fields (see Sect. 3.1 below).

• The observed azimuthal surface field (a proxy for flux emergence) evolves in accordance with an updated BL model (Cameron et al. 2018).

The timescale for the rise of flux loops formed by the toroidal field and the subsequent flux emergence is generally considered to be short compared to the cycle time scale. Therefore, BL dynamo models typically do not explicitely include these processes but rather incorporate a source term near the surface that is related to the deep-seated toroidal field in the convection zone (for a discussion of various approaches, see Choudhuri and Hazra 2016). A few examples of two-dimensional axisymmetric dynamo models with different prescriptions for the BL source term are the studies of Durney (1997), Dikpati and Charbonneau (1999), Nandy and Choudhuri (2001), Chatterjee et al. (2004), and Muñoz-Jaramillo et al. (2010). More complete overviews have been provided by Charbonneau (2020) and Hazra et al. (2023).

FTD/BL models mostly rely on radial differential rotation in the tachocline and often also assume penetration of the meridional flow into the stably stratified interior in order to “store” the toroidal magnetic flux at the bottom of the convection zone (e.g., Nandy and Choudhuri 2002), which seems to be difficult to achieve (cf. Gilman and Miesch 2004). In fact, Muñoz-Jaramillo et al. (2009) showed that no such penetration is necessary for FTD models to reproduce the basic features of the solar cycle. These authors also showed that the helioseismically determined differential rotation in the convection zone leads to a dominant production of toroidal flux by the latitudinal differential rotation (see also Guerrero and de Gouveia Dal Pino 2007). Recently, Zhang and Jiang (2022) presented a comprehensive dynamo model including the helioseismically determined differential rotation (including the near-surface shear layer), a one-cell meridional circulation, radial pumping keeping the surface field vertical and inhibiting diffusive loss of the toroidal field, and a BL source term. The latitudinal propagation of the toroidal flux belts in this model is provided by a combination of flux transport by the equatorward meridional return flow and the latitude dependence of the latitudinal rotational shear generating toroidal magnetic flux, the latter as already envisaged by Babcock (1961). Test cases with removal of the radial shear in the tachocline or putting the numerical boundary above the tachocline does not significantly change the results of the model, thus strongly suggesting that the tachocline shear is indeed largely irrelevant for the dynamo (cf. Spruit 2011; Brandenburg 2005; Cameron and Schüssler 2015).

Typically, FT/BL dynamo models are 2D (axisymmetric) or even 3D and time-dependent. Although they exhibit solar-like solutions for properly chosen values of the parameters (e.g., turbulent diffusivity, geometry and speed of the meridional flow, dynamo excitation, etc.), computational limitations do not permit a complete coverage of the parameter space. In order to systematically investigate the parameter ranges for solar-like solutions, Cameron and Schüssler (2017a) updated the 1D, two-layer model of Leighton (1969). Model quantities are the azimuthally averaged radial field at the surface and the radially integrated toroidal flux, both as a function of latitude. Poleward meridional flow at the surface, an equatorward return flow somewhere in the convection zone, latitudinal differential rotation as well as radial differential rotation in the near-surface shear layer are included. Furthermore, downward convective pumping of the near-surface horizontal field and turbulent diffusion of the radial surface field and the toroidal field are considered. Using the radially integrated magnetic flux has the advantage that the model neither depends on the radial distribution of the toroidal field in the convection zone nor on the depth location of the meridional return flow. The solutions of this linear model depend on four parameters which represent the driving of the dynamo (by emergence of tilted bipolar regions), the effective speed of the meridional return flow, the turbulent diffusivity affecting the toroidal field in the convection zone, and the effective radial shear below the near-surface shear layer. All other parameters (such as meridional flow and diffusivity at the surface) are taken from observations. The simplicity of the model permits the exploration of the full four-dimensional parameter space. Relevant ranges of parameters are identified by requiring that the model results meet observational constraints: positive growth rate, dipole parity, 22-year magnetic period, flux emergence concentrated in low latitudes, and a 90 deg phase difference between the maximum of flux emergence and maximum strength of the polar field. It turns out that these requirements strongly constrain the parameters, yielding about 2 m s⁻¹ for the speed of the return flow, a turbulent diffusivity of about 80 km² s⁻¹, toroidal flux generation dominated by latitudinal differential rotation, and weak dynamo excitation not far above the threshold. A sketch of the model is shown in Fig. 1 and an example of the results in Fig. 2.

Fig. 1

Sketch of the updated Babcock–Leighton model of Cameron and Schüssler (2017a)

Fig. 2

Results from the updated Babcock–Leighton model of Cameron and Schüssler (2017a). Left panels: Radial surface field (upper panel) and depth-integrated toroidal flux (lower panel) as a function of latitude and time for a solution consistent with the properties of the solar cycle. Right panels: Properties of model solutions as functions of the amplitude of the effective speed of the equatorward return flow and of the magnetic diffusivity in the convection zone. Colour shadings indicate the dynamo period (upper panel) and the phase difference between the maximum of the polar field and the maximum rate of flux emergence (lower panel). The regions between the coloured lines indicate “solar-like” models: period in the range 21–23 yr and phase difference between 80 and 100 degrees. These results indicate a rather tight constraint for the speed of the return flow of about 2–3 m s⁻¹

The model results indicate that the solar dynamo most probably is a flux-transport dynamo near marginal excitation, operating in the high-diffusivity regime (see also Yeates et al. 2008). The inferred speed of the equatorward flow transporting the toroidal flux is consistent with the latitudinal drift rate of the activity belts. The relevant values of the magnetic diffusivity affecting the toroidal flux are also consistent with the observed evolution of the solar activity belts (Cameron and Schüssler 2016). Dominance of latitudinal differential rotation entails a natural explanation for the concentration of flux emergence in low latitudes: the latitudinal rotational shear peaks at mid latitudes and the deep meridional return flow transports the generated toroidal flux equatorward. Consequently, it is not necessary to assume a threshold value of the toroidal field for the initiation of flux emergence, e.g., in the sense of a buoyancy instability.

Further development of BL dynamo models was provided through a closer connection between the near-surface evolution and the interior evolution of the magnetic field. Cameron et al. (2012) found that downward convective pumping (leading to predominantly radial field near the surface) is required to bring a 1D SFT model into accordance with the results of a 2D axisymmetric FTD model. Furthermore, FTD dynamos with convective pumping provide “solar-like” results also with high turbulent diffusivity in the convective interior of the order of $10^{12}$ cm² s⁻¹ consistent with mixing-length arguments (e.g., Karak and Cameron 2016; Hazra et al. 2019). Pumping also significantly reduces the loss of magnetic flux through the surface, so that the “restart” of the normal dynamo mode after a grand minimum can be achieved in a BL dynamo with the emergence of a few bipolar regions, without the need of an additional generation process (Karak and Miesch 2018).

Bhowmik and Nandy (2018) used the surface distribution of magnetic flux during activity minima resulting from a data-driven SFT simulation as input for a FTD model. A fully coupled 2D × 2D model was developed by Lemerle et al. (2015) and Lemerle and Charbonneau (2017). These authors connected an observationally calibrated SFT model in latitude and longitude with an axisymmetric FTD model operating in the meridional (radius-latitude) plane. The FTD model provides the source for the SFT model by stochastic flux emergence in tilted bipolar magnetic regions. In turn, the SFT model feeds back upon the FTD model in the form of a BL-like source term near the upper boundary of the dynamo model, resulting in a self-consistent coupling of the two models. Figure 3 illustrates that properly calibrated results from this model are consistent with the characteristic features of the corresponding solar observations. A similar approach was presented by Miesch and Dikpati (2014).

Fig. 3

Example result obtained by Nagy et al. (2017, part of their Fig. 1) using the 2D × 2D dynamo model developed by Lemerle and Charbonneau (2017). Shown are time-latitude diagrams of the radial field at the surface (upper panel) and of the number of flux emergences (butterly diagram, lower panel)

The BL source in such models is typically provided by “deposition” of tilted bipolar regions in the SFT part of the model, non-locally depending on the (latitude-dependent) strength of the deep-seated toroidal field. For the time delay between sunspot emergences, a probability distribution function obtained from sunspot observations can be assumed (e.g., Miesch and Dikpati 2014; Hazra et al. 2017). Such ad-hoc procedures ignore the details of the formation and rise of flux loops through the convection zone, in particular the development of the tilt angle. They also implicitely assumes a dynamical disconnection of the emerged bipolar region from its subsurface roots. Bekki and Cameron (2023) considered the post-emergence evolution of deposited bipolar regions in the framework of a nonlinear 3D simulation in a spherical shell, including the Lorentz force as well as solar-like differential rotation and meridional flow driven by a mean-field prescription. These authors found that the evolution depends sensitively on the initial shape and depth of the injected bipolar regions. When initialized with zero tilt, the Lorentz force in combination with the Coriolis force tends to produce negative tilt angles. The simulated BMRs also develop an systematic asymmetry between the strength of leading and following spots, which is consistent with observations.

Yeates and Muñoz-Jaramillo (2013) suggested a more consistent treatment of flux emergence by assuming helical upflows that transport flux loops through the convection zone, thus capturing aspects of buoyancy and advection by convective flows as well as the connection between the surface and interior field. A similar treatment was proposed by Pipin (2022). The idea of this approach is consistent with the results of detailed observations of the properties of emerging flux, which favor passive flux transport by convective upflows (Birch et al. 2016). On the other hand, comparison with well-calibrated SFT models (Whitbread et al. 2019) shows that after emergence the surface flux needs to be dynamically disconnected from its deep toroidal roots as suggested by Schüssler and Rempel (2005). Moreover, Schunker et al. (2019) and Schunker et al. (2020) showed that the tilt of bipolar magnetic regions develops only after emergence, possibly related to the extended flows converging towards the bipolar magnetic regions (Martin-Belda and Cameron 2016; Gottschling et al. 2021). In view of these results it seems fair to say that the formation of rising flux loops, their transfer through the convection zone, the actual emergence process, and the subsequent early evolution of the emerged magnetic flux are still poorly understood (see also reviews by Fan 2021; Işik et al. 2023), so that these processes cause a significant amount of uncertainty in all FTD/BL models presented so far.

Among the first 3D studies of FTD/BL models for the solar dynamo are the models of Hazra et al. (2017) and Karak and Miesch (2017). While these authors used the deposition approach to represent flux emergence, Kumar et al. (2019) implemented the more consistent recipe of Yeates and Muñoz-Jaramillo (2013) in a kinematic 3D dynamo code. Another step towards a full 3D treatment was taken by Hazra and Miesch (2018), who introduced a 3D, stationary, convection-like flow field in the upper part of the convection zone. This serves to replace the diffusion term in standard SFT models by a more realistic explicit transport process. The assumed flow pattern was based upon an observational power spectrum of the surface flows and a downward extrapolation under the assumption of zero divergence of the mass flux and an imposed radial profile. The kinematic model ran into problems owing to unlimited small-scale dynamo action driven by the imposed stationary flow. Further results obtained with kinematic 3D models of BL dynamos have been reviewed by Hazra (2021). Bekki and Cameron (2023) used their 3D model to perform nonlinear BL dynamo simulations with the near-surface deposition of properly tilted bipolar regions. The Lorentz force provides nonlinear saturation of the dynamo amplitude. This feedback drives non-axisymmetric flows as well as solar-like zonal flows superposed upon the differential rotation and also modifies the meridional circulation. Other nonlinear effects (see also Sect. 4.1 that could lead to dynamo saturation and determine the cycle amplitude have been studied by Jiang (2020), Jiao et al. (2021), and Talafha et al. (2022).

3 Generation and Removal of Magnetic Flux

3.1 Toroidal Flux

Toroidal magnetic field (azimuthal field in the case of an average over longitude) is considered to be generated in the Sun through the action of differential rotation on a poloidal magnetic field. Part of the generated toroidal flux emerges when radial motions carry loops of magnetic flux through the solar surface. Flux emergence leads to the formation of two surface areas with oppositely-directed radial field components. These bipolar magnetic regions (BMRs) have been studied extensively (e.g. Hale et al. 1919; Harvey et al. 1975; Martin and Harvey 1979; Wilson et al. 1988; Harvey 1993; McClintock and Norton 2016; Schunker et al. 2016). A map showing the latitudes at which larger BMRs with sunspots emerge in time (known as the butterfly diagram) is shown in the upper panel of Fig. 4.

Fig. 4

Observationally based time-latitude diagrams of sunspots (top panel, data from Royal Greenwich Observatory/NOAA: http://solarcyclescience.com/AR_Database), longitudinally averaged azimuthal surface field (middle panel, data from Wilcox Solar Observatory, WSO), and longitudinally averaged radial field (lower panel, data from WSO)

BMRs show various systematic properties. One example is Hale’s law (Hale et al. 1919), which states that the leading polarity (with respect to the direction of rotation) of BMRs in each hemisphere has the same sign in most (up to 95%) of the cases during an activity cycle. The leading polarity is opposite in the two hemispheres and switches from cycle to cycle. These properties imply a systematic East-West component of the horizontal field during emergence, which flips sign between each hemisphere and from cycle to cycle. This can be illustrated in a time-latitude map of the longitudinally averaged azimuthal component of the surface field covering four activity cycles, which is shown in the middle panel of Fig. 4 (cf. Cameron et al. 2018; Liu and Scherrer 2022). The latitudes where sunspot groups emerge correspond to locations where the surface azimuthal field is strong. Weaker azimuthal field corresponds to flux emergence of smaller BMRs (ephemeral regions, Martin and Harvey 1979).

Another systematic property of BMRs is Joy’s law (Hale et al. 1919). It refers to the tendency for the leading part of a BMR or sunspot group to be closer to the equator. Because of Hale’s law, the leading parts mostly have the same polarity, so that there is a systematic tendency in both hemispheres that more radial magnetic flux of one polarity appears closer to the equator. The radial field of the leading parts in the other hemisphere has the opposite polarity, and the polarities switch from cycle to cycle. These properties are illustrated in the time-latitude diagram for the longitudinally averaged radial surface field shown in the bottom panel of Fig. 4. The locations of flux emergence can be clearly seen, with the leading polarity dominating on the equatorward side of the “butterfly wings”. Plumes of magnetic field with widths of a few months connect the butterfly wings to the polar regions, where the field switches polarity with the period of the solar cycle.

An important feature of the time-latiude diagram of the toroidal surface field (middle panel of Fig. 4) is that during times of activity maximum (when there are many sunspots) the toroidal field at every latitude in each hemisphere is of the same sign. This suggests to consider the evolution of the net subsurface toroidal flux in each hemisphere. For this we start from the induction equation,

$$ \frac{\partial{\mathbf{B}}}{\partial t}=\nabla \times \left ( {\mathbf{U}} \times {\mathbf{B}} - \eta \nabla \times {\mathbf{B}} \right ), $$

(1)

where ${\mathbf{B}}$ is the magnetic field, ${\mathbf{U}}$ the flow velocity, and $\eta$ the (molecular) magnetic diffusivity. Following Cameron and Schüssler (2015), Cameron and Schüssler (2020), and Jeffers et al. (2022), we now consider the area A that is enclosed by the thick outline in the left panel of Fig. 5 and apply Stokes’ theorem to the induction equation, viz.

$$ \frac{\partial{\iint _{A} {\mathbf{B}} \cdot \mathrm{d}{\mathbf{A}}}}{\partial t}= \oint _{\delta A} \left ( {\mathbf{U}} \times {\mathbf{B}} - \eta \nabla \times {\mathbf{B}} \right ) \cdot \mathrm{d} {\mathbf{l}} \,, $$

(2)

where $\delta A$ indicates the boundary of $A$ and ${\mathrm{d}\mathbf{l}}$ is the corresponding line element. We now take the azimuthal average of Eq. (2) and neglect the diffusive term in the contour integral since the magnetic Reynolds number is very large. This leads to

$$ \frac{\partial{\iint _{A} {\langle {\mathbf{B}} \rangle} \cdot \mathrm{d}{\mathbf{A}}}}{\partial t}= \oint _{\delta A} \left ( \langle{\mathbf{U}}\rangle \times \langle{\mathbf{B}} \rangle + \langle{\mathbf{u}}\times {\mathbf{b}}\rangle \right ) \cdot \mathrm{d} {\mathbf{l}} \,, $$

(3)

where $\langle \dots \rangle$ indicates the azimuthal average. This equation represents the temporal change of net toroidal flux in the Northern hemisphere resulting from the inductive action of the flow field on the magnetic field. The quantities ${\mathbf{b}}={\mathbf{B}}-\langle {\mathbf{B}} \rangle$ and ${\mathbf{u}}={\mathbf{U}}-\langle {\mathbf{U}} \rangle$ denote, respectively, the fluctuating components of magnetic field and flow velocity with respect to the corresponding azimuthal averages.

Fig. 5

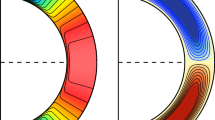
Left panel: Area and contour used for calculating the net axisymmetric toroidal flux in a hemisphere. The bottom part of the contour is placed at a radius $R_{\mathrm{interior}}$, where the penetration of the 22 year cyclic component of the magnetic field is negligible. Right panel: Solar differential rotation along segments of the contour in the left panel. Shown are the radial dependence of $\Omega$ on the equatorial plane (red curve, upper scale) and the (co)latitudinal dependence at the surface (blue curve, lower scale), both relative to the equatorial surface rotation rate. The data for this plot was obtained from Larson and Schou (2018)

Since the Sun’s radial differential rotation in the equatorial plane is small compared to its latitudinal differential rotation (see right panel of Fig. 5) it is convenient to use a frame of reference rotating with the surface equatorial rate. In this frame, we have

$$\begin{aligned} \oint _{\delta A} \left ( \langle{\mathbf{U}}\rangle \times \langle{\mathbf{B}} \rangle \right ) \cdot \mathrm{d} {\mathbf{l}} =& \int _{0}^{\pi /2} \left ( \Omega (R_{\odot},\theta )-\Omega (R_{\odot},\frac{\pi}{2}) \right ) \sin \theta \langle{B_{r}}\rangle R_{\odot}^{2} \mathrm{d} \theta \\ & -\int _{R_{\mathrm{interior}}}^{R_{\odot}} \left (\Omega (r, \frac{\pi}{2})-\Omega (R_{\odot},\frac{\pi}{2})\right ) \langle{B_{ \theta}}\rangle r \mathrm{d}r \,, \end{aligned}$$

(4)

where $\theta$ is the colatitude. Only the surface part of the contour integral (first term on right-hand side) and the part in the equatorial plane (second term) contribute to the contour integral. The bottom part in the interior vanishes since B is zero there and the part along the rotation axis vanishes since we consider azimuthal averages of all quantities. The solenoidality of the magnetic field implies

$$ \int _{0}^{\pi /2} \langle{B_{r}}\rangle R_{\odot}^{2} \sin \theta \mathrm{d} \theta = -\int _{R_{\mathrm{interior}}}^{R_{\odot}} \langle{B_{\theta}}\rangle r \mathrm{d}r, $$

(5)

which means that the net magnetic flux through the equatorial plane beneath the surface is equal in magnitude to the net flux through the solar surface in each hemisphere.

Owing to the weak radial differential rotation in the equatorial plan), the net toroidal flux generation is strongly dominated by the surface part of the contour integral, i.e., the first term on the right-hand side of Eq. (4). This can be directly evaluated from synoptic observations of the radial field on the surface and the Sun’s differential rotation, with a net hemispheric toroidal flux of 5–$8 \times 10^{23}$ Mx per cycle being thus generated. The integrand for the surface part in the contour integral (Eq. (4)) is strongly dominated by the polar caps (see bottom left panel of Fig. 6), so that the flux associated with the polar dipole field represents the relevant poloidal source for the generation of net toroidal flux. Other poloidal flux that is contained in the convection zone and does not cross the surface leads to equal amounts of East-West and West-East orientated toroidal flux in a hemisphere and thus does not contribute to the net toroidal flux required by Hale’s polarity laws.

Fig. 6

Generation and loss of net unsigned toroidal flux in the Northern hemisphere, covering four activity cycles on the basis of synoptic magnetograms from the Wilcox Solar Observatory. The time-latitude diagrams on the left side show the observational input for evaluating the dominating surface part of the contour integral (Eqs. (4) and 6). Toroidal flux is generated proportional to the product of the azimuthally averaged surface radial field and the surface rotation rate relative to the equatorial rate (lower left panel). Toroidal flux is lost through flux emergence at a rate proportional to the product of $\langle B_{\phi }\rangle$ at the surface (upper left panel) and the radial emergence velocity estimated as $v_{\mathrm{em}} = 200$ m s⁻¹ (Centeno 2012). The panel to the right shows a phase plot of the yearly integrated values of the generated and lost toroidal flux indicated by red dots. The connecting line segments with arrows illustrate the change from one year to the next

The term in Eq. (3) involving the fluctuating components, $\oint _{\delta A} \langle{\mathbf{u}}\times {\mathbf{b}}\rangle \cdot \mathrm{d} {\mathbf{l}}$, is dominated by (turbulent) diffusive fluxes across the axis and the equatorial plane. Some of the other terms, such as those owing to the turbulent electromotoric force ($\alpha$-effect), are expected to vanish due to symmetries – along the axis owing to the conservation of helicity and at the equator owing to the expected vanishing of the kinetic helicity, which in its simplest form scales like $\cos \theta$.

Another contribution from the fluctuating terms is the change of the net toroidal flux by flux emergence and submergence through the surface, which is described by

$$ \left (\frac{\mathrm{d} \Phi}{\mathrm{d} t}\right )_{\mathrm{em},\mathrm{subm}} = \int ^{0}_{\pi /2} \langle u_{r} b_{\phi }\rangle \vert _{R_{\odot}} R_{ \odot} \mathrm{d}\theta \,. $$

(6)

Flux loss through the surface was part of the original Babcock–Leighton model (Leighton 1969), but later fell out of favour since it was thought that the emerged flux is mostly retracted back through the surface (e.g., Wallenhorst and Topka 1982). This process can take place in flux cancellation events when loops of emerged flux become sufficiently narrow, so that the tension force dominates. Some retraction of flux is possibly required to account for the amount of flux brought to the surface by repeated emergences in so-called “nests of activity” (e.g., Gaizauskas et al. 1983).

Parker (1984) argued that a net loss of toroidal flux from the Sun would require an organized sequence of reconnection events between narrowly-spaced bipolar regions, thus effectively shedding the mass from the toroidal field lines and allowing them to freely escape with the solar wind. However, observations show that the bipolar regions generally are much too widely spaced for this process to operate on the Sun, so that Parker concluded that in dynamo models the solar photosphere should be approximated by an impenetrable boundary.

Parker’s argument, however, ignores that what is relevant for the dynamo models is the effect of the emergence on the mean (azimuthally averaged) toroidal field. Cameron and Schüssler (2020) showed that the amount of the azimuthally averaged toroidal field lost due to the emergence of a bipolar region is time-independent, irrespective of the further evolution of its magnetic flux. While cancellation/retraction of most of the field may occur, at the same time the remaining surface flux spreads out in longitude (transported by near-surface flows) to eventually fully encircle the Sun. In this way, toroidal field detached from the solar interior is formed which can be carrried away by the solar wind and the same amount of flux is lost from the mean toroidal field in the interior. A quantitative analysis of the net azimuthally averaged toroidal flux lost during a cycle arrives at $3.3 \times 10^{23}$ Mx/hemisphere/cycle (Cameron and Schüssler 2020). A similar estimate of $5\times 10^{23}$ was obtained using in situ measurements of the magnetic field and flows in the solar wind (Bieber and Rust 1995). The observations thus indicate that, integrated over a cycle, the amount of the toroidal magnetic flux generated by the axisymmetric flows and fields ($\oint _{ \delta A} \left ( \langle{\mathbf{U}}\rangle \times \langle{\mathbf{B}}\rangle \right ) \cdot \mathrm{d} {\mathbf{l}}$) is similar to the amount lost through flux emergence ($\oint _{\delta A} \langle{\mathbf{u}}\times {\mathbf{b}} \rangle \cdot \mathrm{d} {\mathbf{l}}$).

The toroidal flux budget shown in Fig. 6 shows the approximate balance between the amount of toroidal magnetic flux lost throughout a cycle due to flux emergence and the amount produced by the winding up of poloidal flux threading the solar surface, both being determined by surface observations of the magnetic field ($B_{\phi}$ and $B_{r}$). In hindsight, this result reinforces the justification for neglecting the radial shear in the tachocline. There is a phase shift between the production rate and loss of about 90^∘, which is consistent with the loss through flux emergence being proportional to the total subsurface toroidal flux. The phase diagram is based on Eqs. (4) and (6), which confirms the concept that the toroidal flux is mainly generated by the action of latitudinal differential rotation on the poloidal flux threading the solar surface in the polar dipole field.

3.2 Poloidal Flux

The previous section has shown that the application of Stokes’ theorem to the induction equation over a properly defined meridional area illuminates the essence of the generation and loss of net toroidal flux during solar activity cycles. A similar procedure can be used to determine the evolution of the net radial flux threading a hemisphere of the Sun (cf. Durrant et al. 2004; Pipin and Kosovichev 2023). To this end, we integrate the radial component of the azimuthally averaged induction equation over the photospheric surface area, $A$, of the Northern hemisphere, NH, and apply Stokes’ theorem, which yields

$$ \frac{\partial \Phi _{\mathrm{pol, NH}}}{\partial t} = \frac{\partial}{\partial t} \oint _{A} B_{r} dA = 2 \pi R_{\odot } \left ( \langle u_{r} b_{\theta }\rangle - \langle u_{\theta }b_{r} \rangle \right ) \,, $$

(7)

where the contour integral is taken over the boundary of $A$, i.e., the equator. The two terms on the r.h.s. correspond to observable quantities. The term $\langle u_{r} b_{\theta }\rangle$ quantifies the effect of flux emerging across the equator. This term is important when large and highly tilted active regions emerge with polarities on either side of the equator (e.g., Cameron et al. 2013). The term $\langle u_{\theta }b_{r} \rangle$ corresponds to convective motions carrying radial flux across the equator and can be approximated by a “turbulent” diffusion term, viz.

$$ \langle u_{\theta }b_{r} \rangle = \eta _{\mathrm{T}} R_{\odot } \frac{\partial B_{r}}{\partial \theta} \,. $$

(8)

There is a systematic component to ${\partial B_{r}}/{\partial \theta}$ corresponding to the systematic tilt angle of bipolar regions (see the time-latitude diagram of the radial magnetic field in Fig. 4). A random component is introduced by large, highly tilted active regions which emerge near to the equator (Cameron et al. 2013), also called “rogue active regions” (Nagy et al. 2017). Such regions, together with “Anti-Hale” active regions with reversed polarity sequence (e.g., Li 2018; Muñoz-Jaramillo et al. 2021) can introduce significant randomness into the net flux in each hemisphere and the axial dipole moment (Cameron et al. 2014; Hazra et al. 2017; Pal et al. 2023). This randomness thus carries over into the production of the toroidal flux emerging in the subsequent cycle. Jiang et al. (2015) and Whitbread et al. (2018) showed that the low amplitude of solar cycle 24 can be understood in terms of rogue active regions that emerged during cycle 23.

Figure 7 illustrates the budget of poloidal surface flux for four activity cycles on the basis of synoptic magnetograms from the Wilcox Solar Observatory. The poloidal flux is determined by integration of the longitudinally averaged radial field over the solar surface, viz.

$$ \Phi _{\mathrm{pol}}= \pi R_{\odot}^{2} \int _{0}^{\pi} \langle{B_{r}} \rangle \mathrm{sign}(\pi /2-\theta ) \sin \theta \mathrm{d}\theta \,, $$

(9)

where the results for the two hemispheres are averaged.

Fig. 7

Systematic part of the generation rate and amount of net poloidal flux in the course of four activity cycles. The left panels illustrate the observational input: the azimuthally averaged radial surface field (upper left panel) determines the total net poloidal surface flux (cf. Eq. (9)) while the azimuthally averaged azimuthal surface field (lower left panel) represents flux emergence in tilted bipolar regions and thus determines the rate of generation of poloidal flux via flux transported over the equator (cf. Eq. (15)). The right panel shows a phase plot of both quantities, with each red dot representing the average value for one year. The line segments with arrows represent the change from one year to the next

The generation term for the poloidal flux results from summing the contributions of all bipolar regions to the amount of magnetic flux which is carried across the equator. The contribution of a single bipolar region ($i$) depends on the magnetic flux of each polarity, $\Phi _{i}$, the angular separation of the two polarities in latitude, $\delta _{\lambda ,i}$, the latitude of emergence, $\lambda _{i}$, and a parameter characterizing the surface evolution of the magnetic flux near the equator, $\lambda _{R}$ (cf. Petrovay et al. 2020). This parameter depends on the latitudinal derivative of the surface meridional flow speed, $V$, at the equator ($\lambda =0$), and the turbulent diffusivity at the surface, $\eta _{\mathrm {T}}$, viz.

$$ \lambda _{R}=\sqrt{ \frac{\eta _{\mathrm {T}}}{R_{\odot }{(\mathrm{d}V}/{\mathrm{d}\lambda})_{\lambda =0}}} \,. $$

(10)

Petrovay et al. (2020) estimated the time-integrated amount of magnetic flux crossing the equator (and thus the contribution of the bipolar region to the buildup of the poloidal field) by the leading term of a Taylor expansion as

$$ \Phi _{{\mathrm{pol}},i} = \frac{\Phi _{i} \delta _{\lambda ,i}}{\sqrt{2\pi}\lambda _{R}} \; { \mathrm {e}}^{-\lambda ^{2}_{i}/ (2 \lambda _{R}^{2})} \,. $$

(11)

During its emergence, the flux tube forming the bipolar region contributes to the longitudinally averaged toroidal surface field, $\langle B_{\phi} \rangle$, by the amount $\langle B_{\phi ,i} \rangle$ according to

$$ \Phi _{i} \frac{\delta _{\phi ,i}}{2\pi}=\langle B_{\phi ,i} \rangle v_{ \mathrm{em}}\, \Delta t \,R_{\odot}\, \Delta \lambda \,, $$

(12)

where $\delta _{\phi ,i}$ is the longitudinal angular extent of the bipolar region, $\Delta t$ is the time over which the emergence takes place, $\Delta \lambda$ is the latitudinal width of the leading polarity of the emerging region, and $v_{\mathrm{em}}$ is the mean emergence speed (assumed to be the same for all emergences). The latitudinal and longitudinal extents are related by $\delta _{\lambda ,i}= \tan (\alpha _{i})\cos (\lambda _{i})\delta _{ \phi ,i}$, where $\alpha _{i}$ is tilt angle. We thus obtain

$$ \Phi _{i} \delta _{\lambda ,i}=\langle B_{\phi ,i} \rangle \, v_{ \mathrm{em}}\, \Delta t \, R_{\odot }\, \Delta \lambda \, 2\pi \tan ( \alpha _{i})\cos (\lambda _{i}) \,. $$

(13)

Inserting this result into Eq. (11), we obtain

$$ \Phi _{{\mathrm{pol}},i} = \frac{\langle B_{\phi ,i} \rangle \, v_{\mathrm{em},i}\, \Delta t \, R_{\odot }\, \Delta \lambda \, \sqrt{2\pi} \, \tan (\alpha _{i}) \, \cos (\lambda _{i})}{\lambda _{R}} \, \mathrm{e}^{-\lambda ^{2}_{i}/ (2 \lambda _{R}^{2})} $$

(14)

For the tilt angle we consider Joy’s law without scatter, so that $\alpha _{i}=\alpha (\lambda _{i})$. We further assume that the emergence velocity is the same for all bipolar regions with a value of $v_{\mathrm{em}}=200$ m s⁻¹ (Centeno 2012). Adding together the contributions of the individual bipolar regions to obtain the rate of generation of poloidal flux then amounts to the latitude integral

$$ \frac{{\mathrm {d}}\Phi _{\mathrm{pol}}}{\mathrm {d} t} = \frac{\sqrt{2\pi}\, v_{\mathrm{em}}}{\lambda _{R}} \int _{-\pi /2}^{ \pi /2} \langle B_{\phi} \rangle R_{\odot }\tan [\alpha (\lambda )] \cos (\lambda )\, {\mathrm {e}}^{-\lambda ^{2}/ (2 \lambda _{R}^{2})} { \mathrm {d}}\lambda $$

(15)

We choose the parameters as in Jiang et al. (2014a) with $\eta _{\mathrm {T}}=250$ km² s⁻¹, surface meridional flow $V(\lambda )= 11\sin (180\lambda /75)$ m s⁻¹, and Joy’s law for a cycle of intermediate strength in the form $\alpha (\lambda )=0.7\times 1.3 \sqrt{\vert \lambda \vert}\, \mathrm{sign}(\lambda )$.

The poloidal flux budget resulting from using the observed longitudinally averaged radial and azimuthal surface fields in Eqs. (9) and (15) is illustrated by the phase diagram on the right side of Fig. 7. It demonstrates that poloidal flux and poloidal flux generation as determined through Eqs. (9) and (15) are consistent with each other. This confirms the basic concept that the poloidal field is being generated by the joint contributions of tilted bipolar regions. Compared to the toroidal flux budget (Fig. 6), the phase diagram is somewhat less smooth. This is a consequence of the significant random component affecting the generation of poloidal flux. This component is only included in the poloidal flux but not in the rate of poloidal flux generation, where we have assumed Joy’s law without scatter.

3.3 Flux Transport

The net toroidal and poloidal flux budgets discussed in the previous sections show that the observable magnetic flux at the surface plays a crucial role in the solar dynamo, highlighting the role of differential rotation, flux emergence, and Joy’s law. This section briefly discusses additional processes which modifiy the spatial distribution of the fluxes. In terms of the poloidal flux, the budget shown in Fig. 7 demonstrates that flux carried across the equator is essential. Furthermore, the toroidal flux budget is dominated by the polar fields, which means that the poleward transport of flux is an important ingredient of the dynamo process: surface flux which crosses the equator is transported to the poles by a combination of the large-scale meridional flow and small-scale flows associated with convection. These processes are captured by the surface flux transport model (Jiang et al. 2014b; Yeates et al. 2023).

The butterfly diagram of flux emergence demonstrates that there is a similar requirement for the equatorward transport of the subsurface toroidal flux from latitudes of about $55^{\circ}$, where the toroidal flux is most efficiently produced (cf. Spruit 2011), towards the equator. Low-latitude flux emergence in accordance with Joy’s law then leads to the cross-equatorial transport of poloidal field. The nature of this transport of toroidal flux is not directly constrained, so that dynamo waves, turbulent pumping, and meridional circulation are all viable candidates. Gizon et al. (2020) showed that the speed of the deep equatorward meridional flow inferred from helioseismology is consistent with the observed migration of the activity belts if the toroidal flux is distributed over the lower half of the convection zone. This lends credibility to the concept of flux transport dynamos (recently reviewed by Hazra et al. 2023).

4 Nonlinearity, Predictability, and Long-Term Variability

4.1 Nonlinear Effects

An excited hydromagnetic dynamo leads to exponential growth of an initially weak magnetic field until further amplification becomes limited by the action of the Lorentz force, which introduces a nonlinearity into the system. The nonlinearity can affect large-scale flows (e.g, differential rotation and meridional flow), modify turbulence effects (e.g., the mean-field $\alpha$-term, turbulent diffusivity, and turbulent pumping), or change the properties of flux emergence. A nonlinearity often invoked in mean-field models is “$\alpha$-quenching” (Steenbeck and Krause 1969; Stix 1972), a parameterization of the decreasing efficiency of turbulence to produce poloidal field from the toroidal field as the field amplitude grows. In the case of a system with a high magnetic Reynolds number, $R_{m}$, such as the Sun, this nonlinearity is potentially catastrophic since the ratio of the small-scale field and the mean field scales as $\sqrt{R_{\mathrm {m}}}$ (Cattaneo and Vainshtein 1991). This causes saturation of the dynamo at field amplitudes many orders of magnitude smaller than observed on the Sun. However, catastrophic quenching may be alleviated by removal of magnetic helicity from the system (Kleeorin et al. 2000; Hubbard and Brandenburg 2012).

In the Babcock–Leighton framework, the poloidal field generation results from the systematic tilt angle of bipolar magnetic regions. While there is observational evidence that the average tilt angle decreases with increasing cycle strength (Dasi-Espuig et al. 2010; McClintock and Norton 2013; Jiao et al. 2021) as well as with increasing maximum field strength of bipolar magnetic regions (Jha et al. 2020), catastrophic quenching is not expected in this case (Kitchatinov and Olemskoy 2011a). Sufficiently strong magnetic field can also reduce the turbulent magnetic diffusivity (e.g., Kleeorin and Rogachevskii 2007; Guerrero et al. 2009). This affects the operation of a Babcock–Leighton dynamo and may, in the case of fluctuating sources, lead to subcritical dynamo action (Vashishth et al. 2021).

Magnetically induced changes of the large-scale differential rotation (zonal flows, cf. Labonte and Howard 1982) and of the meridional circulation (systematic inflows towards active regions, cf. Gizon et al. 2001) have been observed (see also Hathaway et al. 2022). The zonal flows are probably too weak to have a substantial effect on the dynamo mechanism. The inflows towards active regions explain part of the cyclic variation of the meridional flow (Cameron and Schüssler 2012; Mahajan et al. 2023). Their effects have been studied in the framework of surface flux transport and Babcock–Leighton models (Martin-Belda and Cameron 2017; Nagy et al. 2020). It was found that, in principle, the resulting changes to the meridional flow can provide nonlinear saturation of the dynamo.

Another nonlinearity which has been studied in the Babcock–Leighton framework is ‘latitudinal quenching’ (Jiang 2020; Talafha et al. 2022). This effect is related to the observation that the average latitudes of sunspots are located more poleward in strong cycles as compared to weak cycles (Waldmeier 1955; Solanki et al. 2008; Hathaway 2015). Since bipolar regions at higher latitudes contribute less to the flux crossing the equator and thus to the buildup of the poloidal field (Jiang et al. 2014a), this effect provides an amplitude-limiting nonlinearity as demonstrated by (Karak 2020) using a 3D BL dynamo model..

A closer look at the properties of flux emergence depending on cycle strength yields further insight into the nature of latitude quenching. In Fig. 8, we used 13-month smoothed sunspot sunspot numbers (Version 2) between solar cycles 12 and 24 from the SILSO data base (https://www.sidc.be/silso/datafiles) and 12-month averages of observed times, latitudes, and areas of sunspots given in the Royal Greenwich Observatory and USAF/NOAA data bases (downloaded from http://solarcyclescience.com/activeregions.html) to plot the sunspot number, the central latitude, and the full width at half maximum (FWHM) of the sunspot zones (“butterfly wings”), respectively, as functions of time since the start of a cycle. Depending on their peak sunspot number, four cycles each were put into groups of strong, medium, and weak cycles. Central latitude and FWHM of the sunspot zones were determined from Gaussian fits of the sunspot data with unsigned latitudes, thus merging both hemispheres.

Fig. 8

Properties of the sunspot zones as function of time from cycle start, based upon the historical sunspot record. Shown are the sunspot number (top panel), central latitude (middle panel), and full width at half maximum (lower panel) of the sunspot zones. The quantities are averaged over weak cycles ($n=12, 14, 24, 16$, blue lines), intermediate cycles ($n= 15, 20, 17, 23$, green lines), and strong cycles ($n=18, 21, 22, 19$, red lines). Shading indicates the range covered by the $\pm 1$ stderr, calculated using the scatter between the four cycles in each group

Since the solar cycle is not perfectly periodic, comparing the evolution of different cycles requires a definition of a reference time for each cycle. One possibility is to fit the shape of the time evolution of the sunspot number to a given functional relationship. Using such a procedure, Hathaway (2011) found that the central latitude of the sunspot belts propagates equatorward in the same way for all cycles (see also Waldmeier 1939). We thus take the reference time as the instant at which the central latitude is at $19^{\circ}$ and define the start of the cycle to be 4 years before that instant. These particular choices have no significant impact on the analysis and the results.

The figure confirms earlier results of Waldmeier (1955): (i) the activity of stronger cycles rises faster and peaks earlier than that of weaker cycles (often referred to as “Waldmeier effect”) while the declining phase is independent of cycle strength, and (ii) the time profile of the propagation of the sunspot zones towards the equator is independent of cycle strength (see also Hathaway 2011). Furthermore, the full wdth at half maximum of the sunspot zones in the declining phase is also independent of cycle strength (Cameron and Schüssler 2016), while stronger cycles show broader sunspot zones (see also Mandal et al. 2017; Biswas et al. 2022). These properties reveal three aspects of latitude quenching, namely

• 1. The Waldmeier effect has the consequence that flux emergence around cycle maxima on average occurs in higher latitudes for stronger cycles than for weaker cycles, thus being less effective for the buildup of the polar field. This corresponds to a negative feedback.

• 2. The broader wings of the sunspot zones during the maximum phases of stronger cycles have the opposite effect since more flux emerges in lower latitudes.

• 3. The fact that all three properties, sunspot number as well as central latitude and width of the sunspot zones, behave independently of cycle strength in the declining phase of the cycles means that, during this most critical phase for the buildup of the poloidal field, the amount of magnetic flux transferred across the equator is independent of cycle strength, thus corresponding to negative feedback.

These three aspects reveal the action of an underlying nonlinearity connected to flux emergence. It is plausible that the cycle strength reflects the amount of toroidal magnetic flux in the convection zone which is available for flux emergence. In strong cycles, latitudinal differential rotation, which is steepest in mid latitudes, acts upon a stronger poloidal field and thus produces more and stronger toroidal magnetic flux. A nonlinearity matching the cycle properties discussed above could be that flux emergence occurs when a critical field strength of the order of the equipartition field strength is exceeded. While the latitude drift of the sunspot zones is independent of cycle strength (possibly being determined by a deep meridional flow towards the equator, which is largely unaffected by the magnetic field), the critical field strength is reached earlier in strong cycles, meaning that more flux emerges at higher latitudes (point 1 of the list above). At the same time, the critical field strength is exceeded in a broader range of latitudes (point 2). Consequently, stronger cycles have lost a bigger part of their available toroidal flux earlier in the cycle compared to weaker cycles, so that in the later phases flux emergence and width of the sunspot zones become independent of cycle strength. Biswas et al. (2022) confirmed this conjecture using a Babcock–Leighton flux-transport dynamo model. They suggested that, in the declining phase of all cycles, flux emergence compensates the increase of the toroidal field strength due to the pileup of flux near the stagnation point of the equatorward meridional flow. Consequently, the mean field strength remains near to the critical field strength for flux emergence and all cycles decline in the same way.

All mechanisms discussed in this section are plausible explanations for the nonlinearity limiting the amplitude of the solar dynamo. Distinguishing which combination of them acts on the Sun is an open observational challenge.

4.2 Aspects of Long-Term Variability

The sunspot cycle shows variability on a wide range of timescales (see reviews by Usoskin 2023; Biswas et al. 2023a). Panel A of Fig. 9 shows the historical sunspot record from telescopic observations since the beginning of the 17th century. It reveals significant cycle-to-cycle fluctuations of cycle strength together with longer-term variability. Particularly conspicuous is the period of very low sunspot activity between 1645 to 1715 and the period of high average sunspot activity between about 1940 and 2006. Other such “grand minima” and “grand maxima” are found in reconstructions of solar activity during the past millenia (albeit at a coarser time resolution) on the basis of various records of cosmogenic isotopes (e.g., Solanki et al. 2004; Usoskin et al. 2016). An example of such a reconstruction is shown in panel B of Fig. 9.

Fig. 9

Observed and simulated records of solar activity. The historical sunspot record (sunspot group number, panel A) and the level of solar activity reconstructed from cosmogenic isotopes samples (Usoskin et al. 2016) are shown in panels A and B, respectively. Panels C and D in the middle show random realizations of a normal-form model (near a Hopf bifurcation) model with noise, covering the same lengths of time as panels A and B. Panels E and F at the bottom shows realizations from a simple Babcock–Leighton dynamo model. Figure reprinted with permission from Cameron and Schüssler (2017b), copyright by AAS

Observational studies of the rotational evolution (gyrochronology) of solar-type stars (e.g., Metcalfe et al. 2016; van Saders et al. 2016; David et al. 2022; Metcalfe et al. 2022, 2023) indicate that magnetic braking by a stellar wind is significantly reduced for stars near or beyond the solar age, which suggests a decline of their large-scale magnetic fields (for a different view, see Kotorashvili et al. 2023). This indicates that, at its current rotation rate, the Sun could be approaching a transition point where its gobal dynamo switches off, so that at present the excitation of the solar dynamo is only weakly supercritical (or even subcritical, e.g., Karak et al. 2015; Tripathi et al. 2021; Vashishth et al. 2021). Weak excitation of the solar dynamo is also supported by the existence of grand minima as shown by the activity records since highly supercritical dynamos do not exhibit such episodes (e.g., Kitchatinov and Olemskoy 2010; Cameron and Schüssler 2017b; Vashishth et al. 2023).

The observationally well-studied rotation-activity relation for magnetically active stars (e.g., Brun and Browning 2017) suggests the rotation rate as the relevant control parameter for dynamo excitation. For most dynamo models, the transition from decaying field to excited oscillatory dynamo action corresponds to a supercritical Hopf bifurcation (e.g., Tobias et al. 1995), when a fixed point (equilibrium) spawns a limit cycle (oscillatory solution). The behaviour of a weakly excited nonlinear system near a Hopf bifurcation is fully described by a generic normal-form model that is independent of the specific properties of the system, including also the nature of its nonlinearity (e.g., Guckenheimer and Holmes 1983).

Cameron and Schüssler (2017b) applied this concept to the solar dynamo and showed that the observed power spectrum of the solar cycle (from the sunspot record and from the reconstruction based on cosmogenic isotopes) is consistent with a noisy normal-form model whose parameters are completely determined by observations. The noise in the system results from the large scatter in the observed tilt angles of active regions, which is possibly associated with the interaction of magnetic flux and convective motions (Longcope and Fisher 1996). As discussed in Sects. 3.1 and 3.2, the tilt angle scatter leads to randomness in the amount of flux transported across the equator, and hence to randomness in the amount of toroidal field generated for the subsequent cycle.

Panels C and D of Fig. 9 show an example realization of the normal-form model covering 10,000 years. Panel B of Fig. 10 gives the corresponding temporal power spectrum, which is consistent with the observed spectrum shown in panel A of Fig. 10. Moreover, the model also exhibits extended periods of low activity (grand minima) whose statistical properties in terms of the distributions of their lengths and the waiting times between grand minima is consistent with the reconstructed record of solar activity by Usoskin et al. (2016).

Fig. 10

Power specta of empirical solar data and models. (A) Sunspot group number (green), and reconstruction from cosmogenic isotopes (blue), together with the expectation value from 10.000 realizations of the normal form model (black curve) and the corresponding 25% to 75% quartiles (grey shading). (B) One realization of the normal form model. (C) Same as (A), but compared to the expectation value and quartiles from realizations of an updated Babcock–Leighton model (red curve and pink shading). (D) One relization of the updated Babcock–Leighton model. Figure reprinted with permission from Cameron and Schüssler (2017b), copyright by AAS

Likewise, the updated 1D Babcock–Leighton dynamo model of Cameron and Schüssler (2017a) with slightly supercritical excitation and including noise in the source term for the poloidal field also yields time series that are statistically similar to the empirical series (see panels E and F of Fig. 9). The corresponding power spectra in panels C and D of Fig. 10) show a good match to the observed spectra (panel A of Fig. 10). A similar approach was taken by Kitchatinov and Nepomnyashchikh (2017) and Kitchatinov et al. (2018), who studied a more comprehensive dynamo model.

Cameron and Schüssler (2019) carried out a detailed analysis of power pectra obtained with the generic noisy normal-form model (incorporating only the 11/22 year base period) in order to evaluate the statistical significance of periodicities inferred from the record of reconstructed solar activity on the basis of cosmogenic isotopes. They showed that power spectra from realizations covering 10,000 years of simulated time (matching the length of the reconstructed solar data) typically exhibit spectral peaks at various periods that are qualitatively similar to those found in the solar data. Such peaks, which result from the stochastic noise in the dynamo excitation, can reach significance levels of $3\sigma$. These results cast doubt on the proposition that seemingly significant periodicities such as the $~90$-year Gleissberg and the $~210$-year de Vries “cycles” are intrinsic to the solar dynamo and not just statistical fluctuations. In fact, the sharpness of the corresponding peaks in the power spectrum indicates a random origin since spectral peaks representing intrinsic dynamo periodicities tend to be broadened owing to the damping inherent to the dynamo process.

Apart from stochastic forcing as discussed above, long-term variability in the dynamo process can also arise from magnetic feedback on the flow and from time delays in the dynamo process. Comprehensive reviews of models for the long-term variability are provided by Karak (2023) and Biswas et al. (2023a).

Let us finally briefly discuss the operation of the dynamo during grand minima and the recovery from such episodes. In both, the noisy normal form model and dynamo simulations shown in Fig. 9, dynamo excitation is weakly supercritical, so that the system can transition into grand-minimum phases by the observed level of stochastic noise. During such weak-field episodes, the system is essentially kinematic and the dynamo recovers on the kinematic growth time. Such a scenario is supported by cosmogenic isotope data showing continued 11-year periodicity during the main phase of the Maunder minimum between the years 1645 to 1700 (Beer et al. 1998). Alternatively, the dynamo excitation may require a minimum field amplitude. Dynamo action would then switch off once the threshold is fallen below, but can be restarted by sufficiently strong stochastic fluctuations, thus leading to on-off intermittency (e.g., Schmitt et al. 1996).

In the BL framework, both possibilities could arise. If the systematic tilt angle of bipolar magnetic regions (Joy’s law), which is essential for the BL dynamo process, is restricted to active regions with a magnetic flux exceeding, say, $10^{20}$ Mx, this could involve a threshold effect if the underlying flux loops originate from an undular instability of toroidal field stored in the overshoot region. Studies in the framework of the thin-flux-tube approximation (see review by Fan 2021) show that this instability requires that the field strength exceeds a critical value for the formation of buoyantly rising loops. These loops then acquire a systematic tilt by the action of the Coriolis force. This could mean that the BL dynamo switches off when its amplitude falls below a threshold value, because the emergence of tilted active regions then ceases. The dynamo would then not work in the kinematic regime and would need an additional process (e.g., a distributed turbulent $\alpha$-effect) in order to restart (e.g., Hazra et al. 2014).

On the other hand, if the small ephemeral regions, which have a statistical tendency to obey Hale’s law (Martin and Harvey 1979; Harvey 1992), should also have a tendency to obey Joy’s law, then the BL dynamo can operate during grand minima when sunspots and big active regions are absent. In fact, there is an observed phase shift between sunspot activity and cosmogenic isotope concentration during grand minima: the two are in phase except during grand minima when they are out of phase (Beer et al. 1998; Usoskin et al. 2001). Wang and Sheeley (2013) argued that this shift is because the axial dipole moment dominates the signal in cosmogenic isotopes during periods of low activity while the equatorial dipole moment (reflecting low-latitude active region emergences) dominates outside grand minima. This indicates that even during grand minima, the polar fields were behaving in a manner similar that of the BL dynamo, albeit based on ephemeral regions rather than on larger active regions.

4.3 Notes on Predictability

Based on sufficient understanding of the global solar dynamo, the observed state of the solar magnetic field can be used to predict its future evolution (for comprehensive reviews, see Petrovay 2020; Bhowmik et al. 2023). In the Babcock–Leighton model, the cycle-to-cycle variability is directly related to the amount of magnetic flux that gets across the equator. At the end of a cycle, all this flux ends up in the polar regions and the amplitude of the polar field is strongly correlated with the strength of the subsequent cycle (e.g., Kumar et al. 2021). The physical basis for this correlation is explained in Sect. 3.1. Predicting the strength of a cycle thus becomes a matter of predicting the polar field strength at the end of a cycle (Schatten et al. 1978), which is almost equivalent to predicting how much flux is transported across the equator (see Sect. 3.2). This can be achieved by performing surface-flux-transport simulations using the actual observations of latitude, magnetic flux, and tilt angle of each emerging active region. Such simulations rather accurately reproduce the amount of flux in each hemisphere and the resulting axial dipole moment as a predictor for the subsequent cycle (Jiang et al. 2015; Yeates et al. 2023). A prediction for the next cycle during an ongoing cycle (i.e., before all the active regions of the cycle have emerged) can be made by including all active regions which have been observed and performing Monte-Carlo simulations of the effect of the active regions which have not yet emerged, using their average properties (Cameron et al. 2016). The result of this approach is the prediction of the polar field at the end of the cycle with error estimates. These can then be converted into predictions for the strength of the subsequent cycle.

In any case, all predictions are limited by the inherent randomness of the dynamo process (Jiang et al. 2018; Kitchatinov et al. 2018). For instance, individual “rogue active regions” can have a strong effect and may potentially even shut down the large-scale dynamo and initiate a grand minimum episode (Nagy et al. 2017).

5 Outlook

Considering the enormous range of scales and the complexity of physical processes governing the interaction of turbulent convection, differential rotation, and magnetic field in the solar convection zone, it is rather surprising that a comparatively simple approach such as the Babcock–Leighton scenario seems to provide such a successful description of the solar dynamo process. An important factor here is that key ingredients of the model, such as the properties of bipolar magnetic regions (latitude range, tilt, flux distribution, etc.) and surface flows, can be obtained by observations. To a large extent, such observations are not available for other stars, so that basic input is missing for the application of the model. Furthermore, the underlying processes leading to flux emergence, i.e., the roles of convective flows, magnetic buoyancy, and instabilities deep in the convection zone, are largely not understood. In the absence of direct observational evidence, 3D MHD simulations seem to be the only possibility here. Considering the impressive progress that simulations have seen during the last decade (recently reviewed by Käpylä et al. 2023), there is hope that the complexity of these processes will be better understood in the not-too-far future, providing an even better basis for simplified models such as the Babcock–Leighton approach. Still, we need to exercise caution and be aware of the severe limitations of all our efforts to understand the solar dynamo as lucidly expounded by Parker (2009) and Spruit (2011, 2012).