Flare Observations

Solar flares are observed at all wavelengths from decameter radio waves to gamma-rays beyond 1 GeV. This review focuses on recent observations in EUV, soft and hard X-rays, white light, and radio waves. Space missions such as RHESSI, Yohkoh, TRACE, SOHO, and more recently Hinode and SDO have enlarged widely the observational base. They have revealed a number of surprises: Coronal sources appear before the hard X-ray emission in chromospheric footpoints, major flare acceleration sites appear to be independent of coronal mass ejections, electrons, and ions may be accelerated at different sites, there are at least 3 different magnetic topologies, and basic characteristics vary from small to large flares. Recent progress also includes improved insights into the flare energy partition, on the location(s) of energy release, tests of energy release scenarios and particle acceleration. The interplay of observations with theory is important to deduce the geometry and to disentangle the various processes involved. There is increasing evidence supporting magnetic reconnection as the basic cause. While this process has become generally accepted as the trigger, it is still controversial how it converts a considerable fraction of the energy into non-thermal particles. Flare-like processes may be responsible for large-scale restructuring of the magnetic field in the corona as well as for its heating. Large flares influence interplanetary space and substantially affect the Earth’s ionosphere. Flare scenarios have slowly converged over the past decades, but every new observation still reveals major unexpected results, demonstrating that solar flares, after 150 years since their discovery, remain a complex problem of astrophysics including major unsolved questions.

Invited Review: Short-term Variability with the Observations from the Helioseismic and Magnetic Imager (HMI) Onboard the Solar Dynamics Observatory (SDO): Insights into Flare Magnetism

Article Open access 19 May 2022

Energetics of X-Class Flares at the Minima of 22, 23, and 24 Solar Cycles

Article 21 December 2020

Solar Electrons and Protons in Flares with a Pronounced Impulsive Phase

Article 01 August 2021

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

1 Introduction

1.1 Detection and definition

Since September 1, 1859, when R. C. Carrington and R. Hodgson observed the first flare in the continuum of white light, these localized, minute-long brightenings on the Sun have remained an enigma. Local flaring of the Sun has been reported at all wavelengths accessible from the ground and from space. Thus the word “flare” is used in solar physics today in a rather ill-defined way, describing a syndrome of apparently related processes at various wavelengths. The problem is even more acute in other languages, such as German and French, denoting flares with the equivalent to “eruption”, which may be confused with coronal mass ejections (CMEs) that often happen simultaneously at the time of large flares. The general use of the term “flare” today often alludes to an “impulsive release of magnetic energy by reconnection”. However, one has to bear in mind that such a definition represents a specific, although widely accepted, interpretation of observations. It may be used as a guide for novices to distinguish flares from other plasma physical phenomena in the solar atmosphere also associated with brightenings, such as the expulsion of magnetic flux or dissipation of shock waves. Nevertheless, it is better to define the flare phenomenon observationally as a brightening of any emission across the electromagnetic spectrum occurring at a time scale of minutes to hours. Most manifestations seem to be secondary responses to the original energy release process, converting magnetic energy into particle energy, heat, waves, and motion.

1.2 Brief history of flare observations

A few years after Carrington and Hodgson, the Sun was studied extensively in the hydrogen H$\alpha $ line originating in the chromosphere, and the reports of flares became much more frequent, but also bewilderingly complex. Variations of source size, ejections of plasma blobs into interplanetary space, and large-scale chromospheric waves (Moreton 1964) were noted. Meter wave radio emissions, detected serendipitously in 1942 during military radar operations, revealed the presence of non-thermal electrons in the corona (Hey 1983). During a radio burst, the solar irradiance in radio waves may increase by several orders of magnitude. At about the same time, S. E. Forbush noticed ground-level cosmic ray enhancements associated with major solar flares. These discoveries could only mean that the flare phenomena are not confined to thermal plasma, but include high-energy particles and involve the corona. In the late 1950s it became possible to observe the Sun in hard X-rays ($\gtrsim $10 keV) by balloons and rockets. Peterson and Winckler (1959) discovered the first hard X-ray emission during a flare in 1958. Later, the enhancements observed in centimeter^{Footnote 1} radio and hard X-ray emissions have led to the surprising suggestion that the radiating energetic particles may contain a sizeable fraction of the initial flare energy release (Neupert 1968). Hard X-rays are caused by the bremsstrahlung of colliding electrons. The photon distribution in energy exhibits a non-thermal shape, close to a power-law. Some of the broadband radio emissions from about 1 GHz to beyond 100 GHz result from the gyration of mildly relativistic electrons in the magnetic field (termed gyrosynchrotron emission). In 1972 the $\gamma $-ray line emission of heavy nuclei was discovered, excited by MeV protons (Chupp et al. 1973). Finally, thermal millimeter, EUV, and soft X-ray ($\lesssim $10 keV) emissions have shown that the flare energy heats the plasma of coronal loops to temperatures from 1.5 MK to beyond 30 MK. Within minutes, some active-region loops become brilliant soft X-ray emitters, outshining the rest of the corona. Such temperatures and the acceleration of non-thermal particles (implying low collision rates) suggest that the flare is originally a coronal phenomenon. As a consequence, the discovery observations in the white light and later in H$\alpha $ came to seem like secondary phenomena. However, this view could be questioned, based on the relatively large energy emitted in white light (e.g., Emslie et al. 2012). This review will show that present observations get much closer to the heart of flares, but still miss the primary process. On the other hand, this review will also demonstrate that flares are not purely coronal. They couple to the chromosphere in a substantial way and must be understood as processes in which corona and chromosphere form an interactive system (as exemplified in Fig. 1).

1.3 The phases of flares

The timing of the different emissions of the same flare is presented schematically in Fig. 2. In the preflare phase the coronal plasma in the flare region slowly heats up and is visible in soft X-rays and EUV. It must be added, however, that non-thermal emissions sometimes occur and are observed at locations different from later phases. Large numbers of energetic electrons (up to $10^{38}$) and, in some events, ions as well (with similar total energy) are accelerated in the impulsive phase, when most of the energy is released. The appearance of hard X-ray footpoint sources at chromospheric altitude is a characteristic of this phase (Hoyng et al. 1981). Some high-energy particles are trapped and produce intensive emissions in the radio band. The thermal soft X-ray and H$\alpha $ emissions finally reach their maxima after the impulsive phase, when energy is more gently released, manifest in decimetric pulsations, and further distributed. The rapid increase in H$\alpha $ intensity and line width has been termed the flash phase. It coincides largely with the impulsive phase, although H$\alpha $ may peak later. In the decay phase, the coronal plasma returns nearly to its original state, except in the high corona (${>}$1.2 $R_\odot $, where $R_\odot $ is the photospheric radius), where magnetic reconfiguration, plasma ejections and shock waves continue to accelerate particles, causing meter wave radio bursts and interplanetary particle events. Figure 2 illustrates the various phases.

1.4 The big picture

The flare observations may be ordered in a scenario or a sequence of processes in which the flare energy is released in the corona by reconnecting magnetic fields. The process heats the plasma in the reconnection region to temperatures of tens of millions of degrees Kelvin (MK), but also efficiently accelerates electrons to super-thermal energies peaking below some 20 keV and extending sometimes to several tens of MeV. Reconnection is not unique to flares and must take place also in the lower solar atmosphere and in the interior of the Sun. The impulsiveness of flares indicates a slow build up of magnetic energy followed by a “dam breaking” event. In plasmas this can occur with low magnetic diffusion (collisional) prior to the energy release but then a sudden and drastic increase in diffusion rate during the flare. Diffusion may suddenly increase in contracting current sheets when their thickness becomes thinner than the particles’ gyroradius and the particles become decoupled from the magnetic field (Lin 2011). Alternatively, high-frequency (collisionless) wave turbulence may suddenly increase resistivity, expediting the magnetic diffusion (new works by Shimizu et al. 2009), redistributing the current and rearranging the magnetic field (Fuentes-Fernández et al. 2012). Energy storage and impulsive release generally imply small collision rates, i.e., low density. Not surprisingly, impulsive flare reconnection is generally assumed to take place in the corona (Fig. 3).

The energy then propagates from the corona into the dense chromosphere along a magnetic loop by thermal conduction or free-streaming non-thermal particles, depending on the flare and the flare phase. The chromospheric material is heated to tens of million degrees and expands into the corona. The upward motion fills up existing coronal loops, but the motion may continue in an expansion of these loops. In some cases, the flare may be only a minor part of a much larger destabilization of the corona, when the magnetic confinement of a considerable part of the corona is broken up. It expands and is expelled by magnetic forces in a coronal mass ejection (CME, Fig. 4). The shock front associated with this motion is also a site of particle acceleration, particularly of high-energy solar cosmic rays observed near Earth or even at ground level. Note that a CME is not simply the explosive result of a flare, but has its own magnetic driver. A CME is a different plasma physical process and may even lead to the conditions for reconnection, causing a flare.

We cannot close this subsection without reminding the reader that the “big picture” is a scenario, not an established theory. The continuing fascination of solar flares originates in the suspicion that this scenario may be good for future surprises because essential parts of our understanding are still lacking.

1.5 Organization of review

In this review, recent observations by new instrumentation are summarized in view of the basic processes involved in the release of magnetic energy resulting in particle acceleration. The material is ordered along the big questions in flare physics:

Section 2: Flare signatures in the photosphere, chromosphere, and corona (Coupling atmospheric layers).
Section 3: Where is the flare energy released? (Flare geometry).
Section 4: Into what forms is the energy released? (Energy budget).
Section 5: Which emissions are direct signatures of energy release? (Signatures).
Section 6: How are particles accelerated? (Acceleration processes).

The literature reviewing flare observations spans more than a century. Substantial summaries of flares observations related to the RHESSI X-ray mission may be found in Emslie et al. (2011), a short general review in Aschwanden (2002). Reviews in more specialized fields have been published by Bastian et al. (1998), Nindos et al. (2008), and Pick and Vilmer (2008) on radio emissions, Fletcher and Warren (2003) on ultraviolet emissions, Ryan et al. (2000), Schwenn (2006), and Miroshnichenko and Perez-Peraza (2008) on flare effects and energetic flare particles in interplanetary space. Somov (1992), Shibata and Magara (2011), and Priest and Forbes (2000) have reviewed theory. Hudson (2011) focussed on global properties, and Benz and Güdel (2010) on solar flares in the context of stars and stellar objects. Older reviews, such as Sturrock (1980) and Švestka (1976) are still worth reading. The Astrophysics Data System (2015) lists more than 21,700 articles on the keyword “solar flare”. Any review, including this one, can only focus on a small fraction of the accumulated information. Comments and suggestions are welcome.

2 Energy release in a coupled solar atmosphere

2.1 Flares and photospheric field configuration

Flares can occur everywhere on the Sun, in active regions, sunspots and penumbrae, on the boundaries of the magnetic network of the quiet Sun, and even in the network interior (Krucker et al. 1997b; Benz and Krucker 1998; Berghmans et al. 1998). Regular (large) flares, however, have preferred locations. They occur in active regions showing a complex geometry of the 3D magnetic field as revealed in photospheric vector magnetograms (Régnier and Canfield 2006, see Fig. 5). Major flares occur in active regions that exhibit a $\delta $ configuration, defined as showing umbrae with mixed magnetic polarity. Flares of the largest size (X-class) are associated with arcades of loops spanning a line of zero line-of-sight magnetic field on the surface. Hagyard et al. (1990) have shown that the magnetic field in flaring locations is strongly sheared (Fig. 6). Magnetic shear alone, however, is not a sufficient condition. An additional requirement for large flares is the emergence of new magnetic flux from below (Choudhary et al. 1998). Vector magnetograms often show narrow channels of strong horizontal field components near the neutral line at the site of large flares (Zirin and Wang 1993). Such fields may already be sheared when emerging and are still moving when they appear in the photosphere (Georgoulis and LaBonte 2006).

Large-scale shear in the magnetic field can also build up through the slow motion of foot points stretching the length of a loop. This evolution can progress through stable field configurations. Large-scale sheared fields in active regions store huge amounts of free magnetic energy. The emerging flux may then provide the trigger mechanism for impulsive energy release. The energy is unleashed above the photosphere, either in the chromosphere or corona (Moore et al. 2001). The build-up of the unstable configuration for large flares is often well observable in photospheric magnetic fields. Wang et al. (2004) find an increase of the photospheric magnetic field strength during the flare, consistent with the scenario of magnetic flux emerging into the corona. In all of the 15 X-class flares studied by Sudol and Harvey (2005) there was an abrupt, significant, and persistent change in the photospheric magnetic field. A frequent flare site is the separatrix between different magnetic loop systems (Démoulin et al. 1997) forming a current sheet, or in a cusp-shaped coronal structure (Longcope 2005). There is also evidence for flares being related to helical magnetic fields (Low 1996; Pevtsov et al. 1996).

Photospheric observations clearly support the scenario that flare energy originates from free magnetic energy in excess of the potential value (defined by the photospheric boundary) or, equivalently, from electric currents in the corona. For a rapid release, the currents must be concentrated into small regions (e.g., Priest and Forbes 2000). Such currents may be inferred observationally in regions with a tangential discontinuity of the magnetic field direction in the system of rising loops near the base of the corona (Solanki et al. 2003; Musset et al. 2015).

The flare energy resides in the magnetic field that originated in the interior and is convected to the surface. Not much can be observed of the flare processes until the energy appears in the form of accelerated particles and extremely hot plasma. In the next section we switch from the origin and build-up to the first observable signature after the primary energy release.

2.2 Geometry of hard X-ray emissions

An electron that hits another particle in a Coulomb collision emits bremsstrahlung. In fully ionized plasma, this is the physical process also known as free-free radiation of thermal electrons, produced by free electrons scattering off ions without being captured. The change in direction and momentum may cause a particle with some keV energy or greater to emit X-ray photons. Bremsstrahlung (X-ray emissions) of thermal and non-thermal electron populations are shown in Fig. 7.

The cross-section of a single electron for producing an X-ray photon of a certain energy can be described by the quantum-mechanical Bethe-Heitler formalism. The instantaneous emissivity of an electron propagating in a plasma is known as the “thin target approximation”. It does not account for the resulting particle energy change to be considered in further collisions. If the target is deep enough, the incident particle slows down to thermal speed. The total radiation is therefore the integral in time over all emissions starting at the entry into the target until the particle energy is thermalized. If other deceleration processes than Coulomb collisions can be excluded, this is the “collisionally thick target” situation (Brown 1971). The thick-target X-ray spectrum of an electron beam is flatter (usually called harder) than that produced in any thin target it may traverse before, as it includes emission of the decelerating electrons. In an ideal situation including a power-law distribution of electron energies, the power-law index of thin target emission is smaller by 2 than the thick target spectrum.

The emission of hard X-rays with a non-thermal energy distribution was first located by Hoyng et al. (1981) at footpoints of coronal loops. Based on stereoscopic observations, Kane (1983) reported that 95% of the $\gtrsim $150 keV X-ray emission in impulsive flares originates at altitudes $\lesssim $2500 km, that is at the level of the chromosphere. Brown et al. (1983) concluded that this upper limit in altitude satisfies the collisional thick-target model in which precipitating electrons lose their energy in the dense, cold target. The emission presumably originates from flare-accelerated electrons precipitating into the chromosphere. They follow the field line until they reach a density high enough for collisions and emit bremsstrahlung while scattering and slowing down. Footpoint sources are also occasionally found on H$\alpha $ flare ribbons some 30,000 km apart, tracing the base of a magnetic arcade (Masuda et al. 2001). The connecting loops are observed in thermal soft X-ray emission, indicating that the density has greatly increased. Densities of more than $10^{11} \ \mathrm {cm}^{-3}$ are frequently reported (e.g., Švestka 1976; Tsuneta et al. 1997) and agree with the concept of “chromospheric evaporation”. Evaporation is actually a misnomer and refers to the expansion and possible explosion of chromospheric material heated by precipitating particles. Up-streaming plasma filling up a coronal loop has been observed in blue shifted lines (Antonucci et al. 1982; Mariska et al. 1993).

Flare footpoints are usually observed to move, indicating propagation of the energy release site (Krucker et al. 2003). Reconnection in a cusp above the flare ribbons predicts that footpoints move apart. Contrary to expectation, parallel motion along the flare arcade has also been reported by Grigis and Benz (2005a) and Bogachev et al. (2005) (see movie in Fig. 8). Stochastic jumps in the time evolution are frequent (Fletcher et al. 2004; Krucker et al. 2005a). These hard X-ray observations suggests that most of the flare energy at a given site is released in an initial burst. The footpoints move apart perpendicular to the flare ribbon. It is well observed in H$\alpha $, but appears to be the result of a more gentle energy release in a later flare phase (Švestka 1976; Martin 1989).

Hard X-rays have been noted to correlate in time with H$\alpha $ kernels (Vorpahl 1972; Wülser and Marti 1989), indicating that the flare energy reaches the dense part of the chromosphere within less than 10 s. Hard X-ray footpoints coincide spatially with H$\alpha $ kernels (Radziszewski et al. 2007, see Fig. 9).

Hard X-ray footpoints and soft X-ray flare loops are consistent with the standard flare scenario of energy release in the corona, energy transport to the chromosphere and chromospheric evaporation, but where is the energy released? First hints came from a third hard X-ray source above the soft X-ray loop (Masuda et al. 1994). The coronal X-ray emission contains a thermal part, dominating at low energies, and a weak non-thermal part above about 8–10 keV. The non-thermal spectrum of the coronal source is usually soft (Mariska and McTiernan 1999; Petrosian et al. 2002), consistent with the idea of a thin target (Datlowe and Lin 1973). Thus, the accelerated electrons lose only a small fraction of their energy and continue to propagate towards the chromosphere. In the chromosphere they meet a thick target, yielding a harder spectrum (Brown 1971; Hudson 1972). An example showing two footpoints and a coronal source is shown in Fig. 10. In exceptional cases, only the fastest electrons reach the chromosphere (Veronig and Brown 2004). The coronal source often appears before the main flare hard X-ray increase, but is well correlated in time and spectrum with the footpoints (Emslie et al. 2003). These observations suggest strong coupling between corona and chromosphere during flares.

The altitude of coronal hard X-ray sources, some 6000–25,000 km, is compatible with observed time delays of hard X-ray peaks emitted at the footpoints (Aschwanden et al. 1995). Low energy photons are emitted later compared to higher energy photons. Delay-time observations scale with the observed lengths of the soft X-ray loop (Aschwanden et al. 1996), consistent with the interpretation of longer propagation times of lower energy electrons. If only time-of-flight effects are assumed, the propagation path would put the acceleration above the loop-top hard X-ray source. The assumption of simultaneous injection puts strong constraints on the timescales involved on the acceleration process (Brown et al. 1998).

The difference in the spectrum of coronal source and footpoints can be taken as a test for the geometry. Measurements by Petrosian et al. (2002) show that the power-law indices differ by about 1 on the average, contrary to expectations. A possible interpretation for a value less than 2 may be a mixture of thick and thin target emissions, overlapping in the observed resolution element. On the other hand, an analysis based on RHESSI data demonstrates the existence of index differences larger than 2 in 3 out of 9 events (Battaglia and Benz 2007). This discrepancy requires a more complete physical scenario than ballistic particle motion and will be discussed in the following section.

2.3 Return current

It is unlikely that the fluxes of high-energy electrons and ions precipitating to the chromosphere balance out. Thus a beam current results. In a conducting plasma, a beam current cannot induce appreciable magnetic fields within appropriate time, and in static state the electric charge cannot separate along the field line. A return current builds up to conserve charge and current neutrality (Spicer and Sudan 1984; van den Oord 1990; Benz 2002). The current is most likely driven by a dominant electron flux in the precipitating particles. Thus the return current direction is downward in the loop. It can be composed mostly of thermal electrons moving freely upward along field lines.

As the return current consists of slower, if not thermal, particles, collisions play a much bigger role than for the beam particles [see Eq. (8)]. Collisions cause electric resistance. Ohm’s law then requires an electric field in downward direction, slowing down the beam electrons. If the return current exceeds the thermal ion velocity, instabilities enhance the resistivity beyond that by Coulomb collisions (Benz 2002, Sect. 6.1). The return current and its associated electric field are inevitable consequences of the standard flare model.

Some observational features have been interpreted as the effect of a downward pointing electric field slowing down the beam electrons. Figure 11 displays spectra of the two footpoints observed in hard X-rays. They do not show a trace of thermal emission in the RHESSI range of energies. Their non-thermal power-law indices are identically $2.7 \pm 0.1$. The power-law of the coronal non-thermal emission (Fig. 11, right) is $5.6 \pm 0.1$. The difference larger than 2 can be interpreted as an effect of the return current’s electric field flattening the spectra of the footpoints. The return current may also leave an observational signature in the shape of the non-thermal X-ray spectrum in the form of a kink (Zharkova et al. 1995).

Return currents may solve what has been referred to as the flare particle number problem: as the number of precipitating electrons inferred from hard X-rays is very large, the coronal acceleration region would soon be evacuated if not replenished. If only electrons escape from the acceleration region, the return current keeps the electron density constant. If also ions escape, the acceleration region is evacuated. This may be avoided by a pressure driven flow of neutral plasma. None of the observational signatures, however, for both neutral flow and return current are fully established, and their existence still needs corroboration.

2.4 Neupert effect

Neupert (1968) noted that in the rise phase of the soft X-rays their flux corresponds to the time integral of the centimeter radio flux since the start of the flare. As the centimeter flare emission is emitted by relativistic electrons, it is not surprising that the same correlation was later also found between the soft X-ray flux and the cumulative time integral of the hard X-ray flux, i.e.,

$$\begin{aligned} F_{\mathrm {SXR}}(t) \propto \int _{t_0}^{t} F_{\mathrm {HXR}}(t')\, \mathrm {d}t' \,, \end{aligned}$$

(1)

or, equivalently,

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} F_{\mathrm {SXR}}(t) \propto F_{\mathrm {HXR}}(t) \,. \end{aligned}$$

(2)

This empirical relationship is called the “Neupert effect”. An example is presented in Fig. 12. Already Neupert (1968) suggested that there may be a direct causal relation between the energetic electrons and the thermal plasma: the soft X-rays originate from a plasma heated chiefly by the accumulated energy deposited through flare accelerated electrons. It must be remarked here that Eq. (1) is an approximation and disagrees occasionally with observations, for example when cooling (by conduction or radiation) is significant.

2.5 Standard flare scenario

The assumption of a strict causal relation between soft X-ray emission and hard X-ray signatures of energetic electrons has led to a simple scenario. It postulates that flare energy release consists of accelerating particles. The acceleration process is not part of the scenario. Energetic particles then precipitate to the chromosphere, where they heat the plasma to the high temperatures observed in soft X-rays. The hot plasma expands along the loop into the corona, a process termed “evaporation”. This simple scenario can explain several phenomena observed in flares:

Correlation of soft X-ray flux with cumulative hard X-ray flux (Neupert effect)
Hard X-rays (>25 keV) often originate from sources at the footpoints of the loop emitting soft X-rays.
The coronal hard X-ray source, where reconnection releases energy, is occasionally observed to be above the soft X-ray loop, into which energy was release before and which is still emitting soft X-rays (Masuda et al. 1994).
The energy in accelerated electrons tends to be larger than the thermal energy contained in the soft X-ray source (see discussion in Sect. 4).
The hard X-ray spectrum of non-thermal electrons in the coronal source is considerably softer than in the footpoints, suggesting that the latter is a thick target. In thick targets an electron loses all its kinetic energy, and its bremsstrahlung emission is the result of all collisions until the particle comes to full stop.
The emission measure of the soft X-ray source greatly increases during the impulsive phase, indicating that chromospheric material is evaporating during this period. Evaporation has been observed directly, first in blue-shifted lines of hot material, later also in soft X-ray images (see following section).

Henceforth we refer to this scenario as the standard scenario (Fig. 13). It should be noted that it is not a quantitative theory, but a an attempt to order some, but not all observations. The cusp on top suggests that the magnetic reconnection may open up the coronal loop, which happens only for some large flares.

2.6 Evaporation of chromospheric material

When energetic electrons (and possibly ions) precipitate from the coronal acceleration site and lose their energy in the dense underlying chromosphere via Coulomb collisions, the plasma responds dynamically. Note that the same may result also from heat conduction, when thermal particles transport the energy released in the corona. The temperature in the chromosphere increases and the resulting pressure exceeds the ambient chromospheric pressure. If the overpressure builds up sufficiently fast, the heated plasma expands explosively along the magnetic field in both directions. The expansion of this plasma into the corona was first reported by Doschek et al. (1980) and Feldman et al. (1980). It was thoroughly studied in blue-shifted lines of Ca xix by Antonucci et al. (1982), who found plasma at a temperature of 20 MK, moving with 300 to $400\ \mathrm {km}\ \mathrm {s}^{-1}$ and filling up the loop (Fig. 14). More recent observations using Hinode/EUV suggest a temperature-dependent upflow velocity of $\approx $8–18T km $\mathrm {s}^{-1}$ in the temperature range of $T=2$–$16\times 10^6\ \mathrm {K}$ (Milligan and Dennis 2009). Chromospheric evaporation was reviewed by Milligan (2015).

The evaporated hot plasma appears to be the source of most of the soft X-ray emission (Neupert 1968; Silva et al. 1997). Thus, the soft X-ray emitting plasma accumulates a significant fraction of the energy in the precipitating non-thermal electrons. Consequentially, the soft X-ray emission is proportional to the integrated preceding hard X-ray flux. As already noted by Neupert (1968), this may explain the effect named after him. Note that the scenario assumes that the observed soft X-ray plasma is not heated by the primary flare energy release, but is a secondary product when flare energy is transported to the chromosphere. This is an important point to remember in theories assuming that the coronal plasma is heated by flares.

The evaporation scenario predicts a linear relation between instantaneous energy deposition rate by the electron beam and time derivative of the cumulative energy in the thermal plasma, thus a linear relation between hard X-ray flux and derivative of the soft X-ray flux (Fig. 12). This is not always the case (Dennis and Zarro 1993). There are several reasons for this: (i) the spectral index of the hard X-rays changes with time in most flares (Sect. 5.2), (ii) the flare energy may be preferentially transported by heat conduction (particularly in the pre-flare phase), and (iii) ions may contribute to the energy deposition. Some flares, however, fit extremely well and a time lag in the flare thermal energy of only 3 s relative to the energy input as observed in hard X-rays has been reported by Liu et al. (2006).

Evaporation is the result of coupling between corona and chromosphere. Such coupling is expected from the fact that the transition region separating the two layers in the solar atmosphere is relatively small compared to the mean free path length in the corona. The chromosphere is only a few collisions away from the corona for thermal particles in the tail of a plasma at flare temperatures. There must be a constant heat flow through the transition region. In the impulsive phase of a flare, non-thermal particles may well dominate the energy transfer.

The expansion of the heated chromospheric plasma is driven by pressure gradients. Thus, the phenomenon is no phase transition nor the escape of the fastest particles, but is an MHD process and occasionally like an explosion. Wülser et al. (1994) and Milligan and Dennis (2009) report downflowing material in H$\alpha $ at the location of the flare loop footpoints, suggesting a motion opposite to evaporation in the low chromosphere. The upflowing hot plasma and the downflowing chromospheric plasma appear to have equal momenta, as required by the conservation of momentum in a ballistic explosion. Evaporation due to a flare may thus be understood as a sudden heating in the chromosphere, followed by an expansion that may initially be supersonic.

Brosius and Phillips (2004) presented evidence for a much more gentle kind of evaporation during the preflare phase of a flare. The maximum velocity in Ca xix was found to be only $65\ \mathrm {km}\ \mathrm {s}^{-1}$. Such gentle evaporation below the coronal sound speed is interpreted as driven by a non-thermal electron flux below $3 \times 10^{10} \ \mathrm {erg}\ \mathrm {cm}^{-2}\ \mathrm {s}^{-1}$ (Milligan et al. 2006). Zarro and Lemen (1988) found signatures of gentle evaporation in the post flare phase, and Singh et al. (2005) reported signatures of evaporation also in a non-flaring state of a loop, suggesting thermal conduction of a hot coronal loop as the driver. These observations confirm that the evaporative response of the chromosphere depends sensitively on the flux of incident electrons. Fisher and Hawley (1990) have studied evaporation due to thermal energy input into the corona. Evaporation resulting from non-thermal particle precipitation has been simulated by several groups (Sterling et al. 1993; Hori et al. 1998; Reeves et al. 2007). In general, the results of these simulations agree with observed flare emissions quite well, indicating that the standard scenario of solar flares is energetically consistent with observations.

2.7 Deviations from standard flare scenario

A variant of the standard scenario has been proposed for flares without footpoints (Veronig et al. 2002; Veronig and Brown 2004). The flare loop has been found so dense that accelerated electrons have collisions already in the corona and lose a large fraction of their energy to the flare loop (Fig. 15). A preceding flare at the same location may have produced the high density of the loop (Strong et al. 1984; Bone et al. 2007).

There are other indications, that the standard scenario is not sufficient. In about half of the hard X-ray events, the Neupert behavior is violated in terms of relative timing between soft and hard X-ray emissions (Dennis and Zarro 1993; McTiernan et al. 1999; Veronig et al. 2002). This is particularly obvious in flares with soft X-rays preceding the hard X-ray emission. Such preheating is well known and cannot be explained by lacking hard X-ray sensitivity (e.g., Benz et al. 1983; Jiang et al. 2006). Soft X-ray brightenings at footpoints with durations less than a minute have been reported by McTiernan et al. (1993) and Hudson et al. (1994), indicating impulsive heating to some 10 MK or more. However, it has been noted by several authors that the plasma in the coronal source at the top is generally hotter than at the footpoints of the loop.

An alternative to the standard scenario is that the soft X-ray emitting plasma is not heated exclusively by high-energy electrons (e.g., Acton et al. 1992; Dennis and Zarro 1993). A likely amendment to the standard scenario is that some coronal particles get so little energy during flare energy release that they have frequent enough collisions to approximately retain their Maxwellian velocity distribution. Thus their energization corresponds to heating. In a preflare, the heat of the coronal source may reach the chromosphere by thermal conduction. Depending on the rate of the energy release, particles may gain sufficient energy that collisions become infrequent [Eq. (8)]. These particles then are accelerated further, get a non-thermal velocity distribution, and may eventually leave the energy release region in the flare phase.

The standard scenario requires a dense beam of electrons to propagate from the acceleration region to the footpoints. There are observations that cast doubts on this beaming: (i) The required beam density is very high and may be unstable (Krucker et al. 2011). (ii) The hard X-ray emission of the beam is isotropic, contrary to expectations (Dickson and Kontar 2013). (iii) The hard X-ray source is observed at very low height, lower than expected for the energy deposition of a beam (Martínez Oliveros et al. 2012). To avoid the problems with the beam model, Fletcher and Hudson (2008) proposed a different scenario, where the energy released through reconnection is transported by Alfvén waves, which accelerate electrons near the chromospheric footpoints. The simple fact that alternative scenarios are still seriously discussed may remind the gentle reader to mistrust any scenario.

3 Flare geometry

3.1 Geometry of the coronal magnetic field

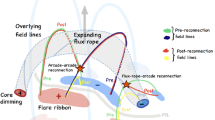
While there is nearly unanimous agreement that sheared or anti-parallel magnetic fields provide the flare energy released in an impulsive reconnection, the geometry of these magnetic fields in the corona at large scale is not clear. The prevalent view is depicted in Figs. 13 and 16 (left), as well as illustrated by a coronagraph image in Fig. 16 (right). The scenario has evolved over the past four decades and is generally credited to Carmichael (1964), Sturrock (1966), Hirayama (1974), and Kopp and Pneuman (1976). So it also named CSHKP scenario after these scientists. It is basically a two-dimensional geometry and an oversimplification in most cases. Its major assumption is a magnetic loop that is pinched at its legs. The loop may be extremely large or moving outward, so that its legs consist of oppositely directed (anti-parallel) fields. As a result of reconnection, the top of the loop is ejected as a plasmoid. The best evidence for this geometry are vertical cusp-shaped structures seen in soft X-rays after the flare (Tsuneta et al. 1997; Shibata 1999; Sui et al. 2006). The cusp grows with time, and higher loops have a higher temperature (Hori et al. 1997), as predicted by continuous reconnection. The observational evidence also includes horizontal inflows of cold material from the side and two sources of hot plasma that move away from the X-point upward and downward. The observations of the former has been reported for a single event by Yokoyama et al. (2001) and Chen et al. (2004). Hot sources being ejected are more frequently observed in soft X-ray (Shibata et al. 1995). They have been noticed to be associated with drifting pulsating structures in decimetric radio emission (Khan et al. 2002) indicating the presence of non-thermal electrons. The reported association with hard X-rays and centimeter radio emission (caused by the synchrotron emission of mildly relativistic electrons) suggests that the plasmoids also include highly energetic particles (Hudson et al. 2001). There is also occasional evidence for the downward reconnection outflow in addition to the observed upward motion of the soft X-ray source (McKenzie and Hudson 1999; Sui et al. 2004). Finally, the existence of two ribbons marking the footpoints of an arcade of loops in H$\alpha $, EUV, and X-ray emissions (Fig. 8) is long-standing evidence for the one-loop model, stretched into a third dimension. It should be noted that these elements specific to the CSHKP scenario are rarely observed, and this kind of flare may occur less frequently than expected from its popularity.

In another also widely proposed geometry, two non-parallel loops meet and reconnect. There are several possibilities or the cause of such interaction. Merging magnetic dipoles (Sweet 1958), collision of an newly emerging loop with a pre-existing loop, proposed by Heyvaerts et al. (1977), or the breakthrough of the emerging loop through the corona (Antiochos 1998). In such a scenario the geometry is closed, i.e., no magnetic field line leads from the energy release site to interplanetary space. Ejecta leaving the Sun are still possible, but not as necessary ingredient of the model. Thus, the two-loop model is often proposed for non-eruptive “compact flares”. The model predicts the existence of 4 footpoints. The number of footpoints in hard X-rays rarely exceeds two. However, radio observations have been presented that complement the number of X-ray footpoints, resulting in the frequent detection of three or more footpoints (Kundu 1984; Hanaoka 1996, 1997). Nishio et al. (1997) find that the two loop considerably differ in size and that the smaller loop usually dominates the X-ray emission. There is also evidence from recent pre-flare EUV observations for multiple-loop interactions (Sui et al. 2006).

One-loop flare models of the CSHKP type predict the presence of plasmoids in interplanetary space, suggesting a detached bubble (i.e., magnetic field lines that close within the solar wind). Such plasmoids are characterized by the lack of suprathermal electrons (few times thermal) because their field lines are disconnected from the Sun. They have indeed been reported (Gosling et al. 1995). More frequently observed are counter-streaming suprathermal electrons, indicating that the field line is closed, i.e., still connected to the Sun on both sides (Crooker et al. 2004). According to these authors, such features in the electron distribution are frequently observed in magnetic clouds associated with CMEs. Nevertheless, they are not associated with the great number of smaller flares.

Furthermore, there is a well-known association of nearly every large flare with type III radio bursts at meter wavelengths, produced by electron beams escaping from the Sun on open field lines connected to interplanetary space. Benz et al. (2005) report that 33% of all RHESSI hard X-ray flares larger than C5 in GOES class are associated with such bursts. This suggests that in a third of all flares at least one of the four ends of reconnecting field lines is open. As type III bursts represent only a small fraction of the flare energy, this may not hold for the major flare energy release site, but only to subsites. We note, furthermore, that type III bursts very often occur also in the absence of reported X-ray flares (Kane et al. 1974). The energy release by an open and a closed field line, termed interchange reconnection, has been proposed some time ago (Heyvaerts et al. 1977; Fisk et al. 1999) and applied more recently to in situ observations in a CME (Crooker and Webb 2006).

In conclusion, there is good evidence for both the one-loop and two-loop scenarios for the geometry of the coronal magnetic field in solar flares. There is no reason to assume that they exclude each other. The combination of both in the same flare at different stages, hybrids of a closed loop reconnecting with an erupting loop, and other scenarios are also conceivable. Thus we do not state a standard geometry for the preflare coronal magnetic field configuration. The magnetic topologies of one loop, interchange and two loop are generally classified as dipolar, tripolar, and quadrupolar, respectively. In addition, 2D and 3D versions can be distinguished (Aschwanden 2002), and various nullpoint geometries have been proposed (Priest and Forbes 2000).

3.2 Coronal hard X-ray sources

In the standard flare scenario, where the flare energy is released in the corona and non-thermal particles are accelerated in the corona, coronal X-ray emission showing a non-thermal photon energy distribution must attract special attention. It is generally assumed that its emission is near or in the acceleration region. This section thus concentrates on flare-related X-ray emissions from well above the chromospheric footpoints.

The ordinary corona has a low density that is not favorable of hard X-ray emission. However, such radiation was discovered as soon as it became technically feasible. Frost and Dennis (1971) reported an extremely energetic event from active region behind the limb. Its origin must have been at an altitude of about 45,000 km above the photosphere. The presence of non-thermal electrons in coronal sources has been inferred by the first observers based on the high energy of the detected photons, exceeding 200 keV and in some cases up to 800 keV (Krucker et al. 2008b). Coronal hard X-ray observations have been studied essentially event-by-event beyond the limb (e.g., Hudson 1978; Kane 1983) until it became possible to image hard X-rays thanks to the RHESSI satellite (Lin et al. 2002). Krucker et al. (2008a) have reviewed the RHESSI results concerning the coronal X-ray sources of flares.

Occasional emission of bremsstrahlung photons by non-thermal electrons in the corona may not be surprising, the observed intensity is. It is so high because of a high density of the background plasma. Estimates of the loop-top density from soft X-rays and EUV lines are typically around $10^{10}$ and can reach up to a few times $10^{12} \ \mathrm {cm}^{-3}$ (Tsuneta et al. 1997; Feldman et al. 1994; Veronig and Brown 2004; Liu et al. 2006; Battaglia and Benz 2006). The reported temperatures are several ten millions of degree (Lin et al. 1981), producing a pressure up to $5\times 10^3 \mathrm {erg}\,\mathrm {cm}^{-3}$. The pressure balance with the magnetic field would require a field strength up to 350 G. The longevity of such structures is enigmatic. What is the origin of this thermal loop-top source?

Thermal loop-top sources have first been interpreted in terms of chromospheric evaporation. Thus one may expect them to follow the Neupert behavior where the soft X-rays are proportional to the hard X-ray flux integrated over prehistory. It is then incomprehensible that thermal coronal sources appear before the start of the hard X-ray emission. In fact, the most prominent feature in the preflare phase (if any) is the early appearance of a thermal source at the loop-top. The material content (emission measure) in these sources greatly exceeds the normal value in the active region corona. Thus it must have evaporated from the chromosphere, although not necessarily from the same footpoints.

A characteristic of the thermal source is the temperature distribution with loop height. The highest looptops usually show Fe xxiv emission, suggesting a temperature of some 20 MK, while at the same time lower-laying loops show emission in the Fe xi and Fe xii lines characteristic for temperatures between 1–3 MK (Warren et al. 1999). The thermal emission must not be confused with the thermal X-ray emission from giant arches observed in the post-flare phase (Švestka 1984).

Masuda et al. (1994) have reported hard X-ray emission from above the thermal X-ray loop. Historically, this has raised great interest as it seemed to confirm the scenario of reconnection in a current sheet in a vertical cusp-shaped structure far above the soft X-ray loops. However, this seems to be rather exceptional. In more recent studies, the large majority of non-thermal sources are nearly cospatial with the thermal source (Krucker et al. 2008a). However, the non-thermal source is often seen a few arcseconds higher, at the location where later the thermal loop appears (e.g., Tomczak 2001; Krucker et al. 2007). This is consistent with the standard model where the sites of reconnection and acceleration acceleration are moving upward.

Stereoscopic observations by two spacecraft (Kane 1983) and recent RHESSI observations find that the non-thermal emission from the corona and the footpoints correlate in time. Even the soft-hard-soft behavior (Sect. 5.2) was detected in the coronal source (Battaglia and Benz 2007). The coronal hard X-ray emission is not always stationary. Upward motions have been reported with velocities of about $1000\ \mathrm {km}\ \mathrm {s}^{-1}$ following the direction of a preceding CME (Hudson et al. 2001; Sui et al. 2004; Liu et al. 2008).

The coronal source has been observed to emit hard X-rays even in the pre-flare phase before footpoints appear. Astonishingly, non-thermal emission at centimeter wavelengths, suggesting the presence of relativistic electrons, has also been reported in such sources (Asai et al. 2006).

3.3 Intermediate thin–thick target coronal sources

The observation of coronal sources suggests a model that consists of four basic elements: a particle accelerator above the top of a magnetic loop (consistently imagined at the peak of a cusp), a coronal source visible in SXR and HXR, collision-less propagation of particles along the magnetic loop and HXR-footpoints in the chromosphere. Wheatland and Melrose (1995) developed a simple model that has been used and investigated further (e.g., Metcalf and Alexander 1999; Fletcher and Martens 1998). The thermal coronal source acts as an intermediate thin–thick target on electrons depending on energy (thick target for lower energetic electrons, thin target on higher energies). This model is known as intermediate thin–thick target, or ITTT model. It features a dense coronal source into which a beam of electrons with a power-law energy distribution is injected. Some high-energy electrons then leave the dense region and precipitate down to the chromosphere. The coronal region acts as a thick target on particles with energy lower than a critical energy $E_c$ and as thin target on electrons with energy $>{\!}E_c$. This results in a characteristic hard X-ray spectrum showing a broken power-law as well as soft X-ray emission due to collisional heating of the coronal region. The altered electron beam reaches the chromosphere, causing thick target emission in the footpoints of the magnetic loop. Battaglia and Benz (2007) have tested the ITTT model in a series of flares using RHESSI data. The results indicate that such a simple model cannot account for all of the observed relations between the non-thermal spectra of coronal and footpoint sources. Including non-collisional energy loss of the electrons in the flare loop due to an electric field can solve most of the inconsistencies.

The simple ITTT model shows that the standard flare geometry is partially consistent with current observations. The remaining inconsistencies concern the coronal source. Its non-thermal component was found less bright than the footpoints would predict according the ITTT model (Battaglia and Benz 2008). A possible remedy is a filling factor smaller than unity for the thermal source and acceleration in the gaps. Jiang et al. (2006) argue that thermal conductivity in the coronal source is reduced by wave turbulence to interpret the soft X-ray emission. Turbulence could also scatter non-thermal particles or even accelerate them.

Coronal sources were intensively observed recently (review by Krucker et al. 2008a), but it is proper to conclude that they are not understood.

3.4 Emissions from above the coronal X-ray source

The standard model (Fig. 13) predicts that magnetic reconnection takes place above the loop emitting thermal X-rays. Relatively little is known about that region apart from the previously mentioned rare above-the-loop-top emissions in hard X-rays. Soft X-rays were reported by Sui and Holman (2003), Sui et al. (2004), and Liu et al. (2008) to extend far beyond the coronal source. In a flare where the loop’s chromospheric footpoints were occulted, thus reducing the dynamic range of the image, various wavelengths show double sources. Nonthermal photons at higher energies were found between the low-energy sources (Fig. 17). In an event observed also by the SUMER spectrometer on SOHO, Wang et al. (2007) reported material flowing away from the coronal source.

Radio emission from the region above the loops may be more frequent, but little imaging information is available. Outward moving radio sources at meter waves are often associated with CMEs (e.g., Pick et al. 2005). At decimeter waves stationary bursts above the flaring region have been observed by Benz et al. (2002). Their centroid positions outline cusp-like structures in decimetric spike events (Battaglia and Benz 2009) and radial structures in the case of pulsations (Benz et al. 2011). Figure 18 shows that the centroid positions of a decimetric pulsation follow a height dependance typical for emission at the local plasma frequency, indicating deceasing density. Surprisingly, the suggested structure is strongly non-radial in this case.

Hard and soft X-rays and radio emissions above the flare loop suggest activity at higher altitude, such as an upward rising current sheet. They do not necessarily prove the standard model as at is not possible to estimate the energy released in these sources. It is clear, however, that the region above the flare loop sometimes takes part in the event.

3.5 Particle acceleration site

Observations of the region above the flare loop cannot locate compellingly the energy release and acceleration region. Accelerated particles precipitate from the acceleration site or are temporarily trapped. On their way spiraling along the magnetic field, they radiate various radio emissions at frequencies depending on the local plasma. As the corona is transparent to radio emission above the plasma frequency, the accelerated particles may outline the geometry of the environment of acceleration and/or the actual site of acceleration.

Gyrosynchrotron radiation is emitted incoherently by relativistic electrons over the whole loop (review by Bastian et al. 1998, Fig. 19). The spectrum at high frequencies is close to a power-law, shaped by the initial power-law energy distribution of accelerated electrons. The loop-top radio spectrum falls off far more steeply at high frequencies than does the footpoint spectrum. Thus the centimeter radio emission confirms the differences between loop-top and footpoints found in X-ray sources. In addition to gyrosynchrotron emission, Wang et al. (1994) and Silva et al. (1996) report thermal loop-top radio emission at a temperature of about 30 MK, in rough agreement with the hot thermal component of the coronal soft X-ray source. These imaging results confirm previous interpretations of thermal flare radiation at centimeter wavelengths, known as “post-burst increase” and “gradual rise and fall” bursts with correlated soft X-ray emission (Kundu 1965).

The most intense flare radio emission at meter and decimeter wavelengths originates not from single particles, but from waves in the plasma, i.e., from coherent radiation processes. Fast-drift radio bursts, or type III bursts, were among the first types of meter wave emissions discovered in the 1940s, and they represent the most frequent incidents of known particle acceleration by the Sun (more than 5000 in an active year). The drift of the radiation to lower frequencies with time was interpreted by Wild (1950) as the signature of an electron beam propagating upward through the corona at a speed of 0.2–0.6c. Later, occasional reverse-drift bursts were discovered (downward-directed beams). The number of electrons in type III driving beams is small and difficult to observe in X-rays. A tentative detection was reported by Krucker et al. (2008c). Summaries of earlier type III observations can be found in Krüger (1979), Suzuki and Dulk (1985), and Pick and van den Oord (1990).

Imaging observations have shown that the type III sources are often not single, but emerge simultaneously into different directions (Fig. 21). Paesold et al. (2001) found double type III sources to diverge from a common source of narrowband spikes around 300 MHz. Figure 21 shows a three-dimensional reconstruction assuming an exponential (constant temperature) model for the density. The spikes observed to be close to the point of divergence suggest the location of the acceleration at an altitude around 90,000 km. Krucker et al. (1995, 1997a) located spike sources at about $5 \times 10^{5} \ \mathrm {km}$ altitude. Klein et al. (1997) found evidence for acceleration of type III electron beams at the height of one solar radius.

Spikes at meter waves have been found to be associated in some cases with impulsive electron events in the interplanetary medium (Fig. 20; Benz et al. 2001). The low energy cut-off of the interplanetary electron distribution defines an upper limit of the density in the acceleration region (Lin et al. 1996). The derived electron density is of the order of $3 \times 10^{8} \ \mathrm {cm}^{-3}$, consistent with the density in the source of metric spikes, assuming second harmonic plasma emission. The difference between acceleration height in hard X-rays, particle events and coherent radio waves suggests different acceleration processes.

3.6 Energetic ions

Gamma-ray lines between 0.8 and 20 MeV are emitted by atomic nuclei excited by impinging ions. Not all flares have gamma-ray lines (Vilmer et al. 2011), yet there is a good correlation between ions accelerated beyond 30 MeV and electrons having energy above 300 keV (Shih et al. 2009).

The neutron-capture line at 2.223 MeV (forming deuterium) is usually the strongest of the many lines (Fig. 22). Protons and other nuclei accelerated from about 10 to $\gtrsim $100 MeV per nucleon collide with the nuclei in the dense chromosphere and produce neutrons. Neutrons thermalize and are captured by an ambient proton to form deuterium (Ramaty and Kozlovsky 1974; Hua and Lingenfelter 1987). Thus images in the 2.223 MeV line indicate the site of high-energy ion precipitation. Comparison of imaged and spatially integrated fluences observed by the RHESSI satellite show that in all cases most of the emission was confined to compact sources within the active region (Hurford et al. 2006). In some events double footpoints were observed. Thus the flare associated gamma-rays are produced by ions accelerated in the flare process and not by a large-scale shock driven by a coronal mass ejection.

Surprisingly, RHESSI found that the footpoints of the 2.223 MeV line—indicating ion precipitation—and the footpoints of the non-thermal continuum emission—produced by precipitating electrons—do not always coincide (Fig. 23). The discrepancy demonstrates that protons and electrons are accelerated differently, or originate, as proposed by Emslie et al. (2004), in large and small loops, respectively.

3.7 Thermal flare

Most of the flare energy is thermalized in the solar atmosphere, some of which is heated to high temperatures. This part is visible in soft X-rays (Fig. 24) and centimeter-wave radiation. Flare loop cooling has been investigated by many authors. In the absence of further energy release the plasma cools by thermal conduction to the chromosphere and by radiating X-rays. Radiative cooling and conduction losses have been found to balance approximately (e.g., Jiang et al. 2006). At high temperature and low density, conductive cooling dominates; radiative cooling is more efficient in the opposite case (Cargill et al. 1995). If conductive cooling leads to evaporation of chromospheric material, the cooling time becomes longer as the energy remains in the loop. In the late phase, radiative cooling usually dominates, but considerable heat input is frequently observed (e.g., Milligan et al. 2005). Note that thermal conduction implies a multi-thermal plasma, observational evidence of which has been presented by Aschwanden (2007).

4 Energy budget

Magnetohydrodynamic models suggest that reconnection releases magnetic energy into ohmic heating and fluid motion in the ratio 40:60 (textbook by Priest and Forbes 2000, p. 133). Using 3-dimensional simulations Birn et al. (2009) specified this partition in relation to the magnetic field strength. Ohmic heating is the result of resistivity in a current loop. At the level of kinetic plasma theory, the resistivity may be greatly enhanced by collisionless wave turbulence. Thus ohmic heating may amount to stochastically accelerating particles, possibly leading to a non-thermal energy distribution. The motion of the reconnection jet may involve waves and shocks, both are also capable of acceleration. Thus a flare releases energy initially into the forms of non-thermal particles, heat, waves, and motion. Non-local transport by the energetically dominant suprathermal particles changes the course of the processes and the energy partition. The energy release may in reality be very different from the MHD prediction.

In the past, the reported partition of energy in flares into the various forms has often changed with new instrumentation. The increase in total solar irradiance provides a good measure of the thermalized flare energy (Milligan et al. 2014). Woods et al. (2004) determined the total flare irradiance to exceed the soft X-ray emission (<27 nm) by a factor of 200 in two well observed, large flares. The total irradiance enhancement is dominated by white light and infra-red emission (77%). UV and soft X-ray emissions <200 nm amount to 23%.

The origin of white-light flare emission is not clear. It was found to correlate excellently in time with hard X-rays (Matthews et al. 2003; Metcalf et al. 2003; Hudson et al. 2006) (Fig. 25). Recent imaging data indicate that white light and hard X-rays (40 keV) also coincide in space within less than an arcsecond (Krucker et al. 2011; Martínez Oliveros et al. 2012). According to these authors, the source region of the white light is in the low chromosphere. Jess et al. (2008) point out that white light flares are not different from others, and that possibly all flares may be observed in white light with sufficient sensitivity.

Not included in the total irradiance is the energy that leaves the corona in coronal mass ejections. Emslie et al. (2012) report on 38 large eruptive flares. The kinetic energy of the CME exceeds the non-thermal electrons’ energy of the associated flare by about an order of magnitude. However, taking into account the flare energy radiated at wavelengths other than X-rays, in particular in white light, brings the flare energy up to nearly the CME energy within a factor of a few (Table 1).

Table 1 Energy budgets as reported by Saint-Hilaire and Benz (2005) for two M-class flares (a) and by Emslie et al. (2005) for two X-class flares (b)

Full size table

4.1 Non-thermal electron energy

Particles accelerated to a non-themal energy distribution are a primary form of flare energy. The energy, $E_{\mathrm {kin}}$, of these electrons is

$$\begin{aligned} E_{\mathrm {kin}} = \int _{\varepsilon _{\min }}^{\varepsilon _{\max }} F(\varepsilon ) \varepsilon \, d\varepsilon , \end{aligned}$$

(3)

where $\varepsilon $ is the electron energy and F is the electron distribution per energy unit. If the accelerated electrons have a power-law distribution with a spectral index of $\delta $, the emitted bremsstrahlung by a thick target is also approximately a power-law in photon energy with index $\gamma = \delta - 1$. As $\delta > 2$ in all observations, the integral in Eq. (3) depends strongly on the low-energy cut-off $\varepsilon _{\min }$. It is difficult to observe as the emission of the non-thermal electrons is usually outshone by the emission of the thermal plasma below about 10 keV. Only with the 1 keV spectral resolution of RHESSI, it has become possible to reconstruct the electrons’ energy distribution at low energies (<20 keV). Structure in the reconstructed electron distribution was reported by Kontar et al. (2002, 2005), indicating that spectral features may indeed be observed. It suggested that the inversion of photon spectra into electron energy distributions is possible (Piana et al. 2003). However, several effects distort the photon spectrum around 10 keV, in particular reflection of X-rays at the chromosphere, termed albedo effect (Kontar et al. 2006; Kašparová et al. 2007), free-bound emission and pulse pile-up in the detectors. Thus the low-energy turn-overs of the electron distribution measured and reported to be at 20–40 keV or below by Saint-Hilaire and Benz (2005) and between 15–50 keV by Sui et al. (2007) may be upper limits, underestimating the energy of accelerated electrons.

4.2 Thermal energy

Electron energy distributions can be inferred from X-ray spectra with high spectral resolution, e.g., Fig. 7. The quasi-thermal part, observed mostly in coronal sources, reaches temperatures of several ten MK. For simplicity, it is often modeled with a single temperature, sometimes with an additional much hotter, but smaller second component. In reality, the distribution of the emission measure with temperature (called differential emission measure, DEM) typically decrease with increasing temperature in the MK range (McTiernan et al. 1999; Chifor et al. 2007; Aschwanden 2007). The quasi-thermal population may be directly heated coronal material or evaporated chromospheric material heated by precipitating particles accelerated by the flare. As the coronal emission measure greatly increases during a flare, most of the thermal flare plasma must originate from the chromosphere. The first X-ray emissions appear to be purely thermal, but already contain more material than expected in the corona of quiescent active regions. Thus the thermal X-ray plasma is generally assumed to be evaporated chromospheric material. The thermal energy $E_{\mathrm {th}}$ of this plasma is thus of flare origin and amounts to

$$\begin{aligned} E_{\mathrm {th}} = \frac{3}{2}\sum _{\alpha }\int n_{\alpha } k_B T_{\alpha }\, \mathrm {d}V, \end{aligned}$$

(4)

where $\alpha $ refers to the plasma species, n, T, and V refer to density, temperature, and volume. Assuming a homogeneous source having equal temperatures among species and approximate equality between electron and ion density,

$$\begin{aligned} E_{\mathrm {th}} = 3 k_B T \sqrt{\mathcal {M}V}, \end{aligned}$$

(5)

where $\mathcal {M}$ is the observed emission measure of soft X-rays. The observations suggest that $E_{\mathrm {kin}}$ is larger by a factor of 0.5–10 than $E_{\mathrm {th}}$ for plasma at $T>10\ \mathrm {MK}$ (Emslie et al. 2012). The factor concurs with the uncertainty in the total energy in electrons due to the low-energy cut-off and with the expectation that heating to coronal temperature is not a loss-free process. The result is also consistent with the observations in white light suggesting that a major part of the precipitated energy is lost to low-temperature plasma not observable in X-rays (Sect. 4.4).

4.3 Energy in waves

The reconnection scenario of magnetic energy release involves flux tubes combining; this launches two reconnection jets that can be viewed as Alfvénic excursions of two waves. The waves cascade to smaller wavelengths until they resonate with electrons or ions (Miller et al. 1997; Petrosian et al. 2006). Thus waves are essential in the currently most popular view of particle acceleration. Reconnection may still be collision-free as found in the terrestrial magnetosphere (Øieroset et al. 2001), involving effects of electron inertia. For solar conditions, involving much larger energies and particle numbers, intense wave turbulence may play a more prominent role.

Waves of all frequencies from large scale MHD waves to high-frequency waves up to whistler waves have been predicted and observed in magnetospheric reconnection (Deng and Matsumoto 2001; Øieroset et al. 2001). Waves can propagate energy across magnetic field lines. Low-frequency Alfvén waves produced by coronal reconnection can move through most of the corona and be partially absorbed at inhomogeneities. Thus they can transport energy even to the high corona and solar wind.

MHD waves related to flares have been inferred from pulsating radio bursts (Roberts et al. 1983) and were more recently reported in high-temperature EUV emission (Aschwanden et al. 1999) and in X-rays (Foullon et al. 2005; Nakariakov et al. 2006). Schrijver et al. (2002) have shown that most larger flares (classes M and X) trigger low-frequency loop oscillations. However, the energy deposited in these oscillations is typically six orders of magnitude smaller compared to the flare energy release (Terradas et al. 2007). Furthermore, the oscillations are observed to damp within a few oscillation periods. From the existing observations it is not clear how far the energy of these oscillations propagates into the corona. Nevertheless, it is obvious that the observed oscillations do not significantly contribute to coronal heating.

Recent acceleration models are based on wave damping (Sect. 6). The relatively small energy in observed MHD waves originating from flares is in striking contrast to expectation from the assumed role they are proposed to play in acceleration.

4.4 Other energies

The energy in the non-thermal ions is less known than for electrons. Ramaty et al. (1995) have argued that the fraction of the available flare energy that is contained in accelerated ions above 1 MeV is similar to that of electrons above 20 keV. This conclusion is supported by the observations that the derived non-thermal energy in protons is occasionally comparable within an order of magnitude to the non-thermal energy in electrons (e.g., Cliver et al. 1994; Miller et al. 1997). On the other hand, there are flares with no signature of accelerated ions within the observational limits. Unfortunately, the total energy content of accelerated ions is difficult to assess, since there are few diagnostics for ions below 1 MeV. The above observations, however, leave doubtful whether the energy in non-thermal electrons and ions add up to the energy of flares observed in total irradiance (see Table 1).

The possibility remains that some energy propagates from the release site to the chromosphere by means of low energy (non-thermal) particles below the current threshold for X-ray detection or by heat conduction (i.e., thermal particles). This is supported by the observation that in a quarter of the events there is clear evidence for the presence of an additional energy transport mechanism other than non-thermal electron beams (Veronig et al. 2002, 2005). Furthermore, the relative contribution to energy transport by non-thermal electrons is found to decrease with the flare importance and in the late phase of flares.

Other forms of energy must also be considered. The reconnection process releases bipolar outflows that may be observed as ejections. Magnetic field and plasma are expelled from the X-point where oppositely directed field lines meet. Reconnection jets may not propagate far and are distinct from CMEs. Saint-Hilaire and Benz (2002) observed a stopped ejection in a flare having an initial kinetic energy of motion of some $10^{29} \ \mathrm {erg}$, about the same as the thermal energy in the soft X-ray plasma, and interpreted it as a reconnection jet (Fig. 26). The thermal energy that such ejections contain was found even an order of magnitude larger, but it was not possible to estimate what fraction of it originated in the flare.

The reconnection outflows also carry magnetic energy. The motion amounts to a Poynting flux that transports magnetic energy (Fletcher and Hudson 2008; Birn et al. 2009). The mode is Alfvénic, thus the energy can be transported without loss and is released where the density or magnetic field are inhomogeneous, resulting in heating and/or acceleration.

If the expansion of the heated flare plasma from chromospheric density to the observed value of the thermal X-ray source were adiabatic, the temperature would drop by many orders of magnitude. This is not observed, the expansion appears to be basically isothermal (McTiernan et al. 1993; Graham and Cauzzi 2015). Thus the thermal plasma of the coronal source contains also the work done by the expansion (enthalpy: Benz and Krucker 2002; Bradshaw and Cargill 2010; Cargill et al. 2012). This expansion in volume by a factor of $10^{3}$ or more at constant temperature, consumes energy that is not accounted for in the thermal energy measurement of X-rays. The expansion energy is released when the material cools and rains back to the chromosphere. A fraction is finally radiated away at temperatures below coronal. The uncertainties in these estimates make it difficult to assess the energy partition of flares and their contribution to coronal heating.

4.5 Energy input into the corona

The predominant heating of the stationary corona is a long-standing debate and is not the issue here. Occasional large flares occurring in active regions during solar maximum are unlikely candidates because their energy is not sufficient for heating and because of their intermittency (Hudson 1991). Hannah et al. (2011) arrived at the same conclusion from the statistics of active region microflares observed by RHESSI. The existence of tiny flares in active region loops unobservable by current instruments (Parker 1988) is an unproven hypothesis, although the evidence is increasing (e.g., Viall and Klimchuk 2015). We note that the theoretical concept of nanoflares is based on the reconnection of twisted magnetic field lines in loops, thus appealing to a scenario different from the standard flare cartoon.

In the quiet Sun the question of flare heating is different. It has come up by observations of extremely small brightenings in low-energy soft X-rays in the quiet corona (Krucker et al. 1997b). Their energies are up to three orders of magnitude smaller than the smallest RHESSI flares in active regions. Some of the larger events have been found to correlate with centimeter radio emission. Similar events have also been reported in high-temperature EUV lines (Benz and Krucker 1998; Berghmans et al. 1998; Krucker and Benz 1998). Figure 27 shows the time profiles of two radio sources at the opposite ends of a small Fe xii loop. In one of them (third panel), the radio source has a negative slope (3.8 cm flux larger than 2 cm flux), indicating gyrosynchrotron emission. The radio peaks occur before the temperature maximum and emission measure peak of the thermal EUV emission, following the Neupert relation between thermal and non-thermal flare emissions. The other source (fourth panel) has an increasing spectrum, indicating optically thick thermal radio emission, coincident with the EUV emission. The events were soon realized to be at least similar to regular flares and thus also termed “nanoflares”. The most relevant difference to regular flares is the order of magnitude lower ratio of synchrotron emission to soft X-rays compared to regular flares (Krucker and Benz 2000). To avoid confusion with Parker’s theoretical concept of nanoflares, we will use here the term “quiet-region microflares”.

The pertinent question is how much the observed flare-like events contribute to the heating of the corona. The largest quiet-region microflares reported contain energies of a few $10^{26} \ \mathrm {erg}$ (Krucker and Benz 1998). This number refers to the thermal energy in the soft X-ray plasma and is identical to the largest individual flare-like quiet-region events inferred from Fe xi/x, and Fe xii lines. Quiet-region microflares differ from coronal bright points, locations in the quiet corona where continuous flaring during many hours is observed. The smallest flares reported given by the TRACE instrumental limit is a few $10^{23} \ \mathrm {erg}$ (Parnell and Jupp 2000). The rate of events larger than few $10^{24} \ \mathrm {erg}$ and lasting about 15 min each, estimated over the whole Sun is 300 per second (Krucker and Benz 1998). Benz and Krucker (2002) have estimated that the total energy measured in quiet-region microflares in the energy range from $5 \times 10^{24} \ \mathrm {erg}$ to $5 \times 10^{26} \ \mathrm {erg}$ observable by EIT/SOHO amounts to about 12% of the energy radiated by the corona in the area in which the quiet-region microflares were observed.

This review of flare observations emphasizes that the thermal energy measured at peak soft X-ray or EUV emission is not equivalent to the total flare energy input into the corona. Most of the thermal flare plasma is just the reaction of the chromosphere on a coronal phenomenon. We may thus end this short subchapter by the conclusion that the hypothesis of coronal heating by flares needs more accurate measurements. Flare heating cannot be quantitatively assessed from observations of one energy receiving channel alone as long as the energy partition of regular flares into waves, direct heating, motion, and particle acceleration is unclear.

5 Signatures of energy release

As explained in Sect. 3, the location of energy release is not well known. Even less understood is its process. Some observational evidence restricting the possible mechanisms is presented in the following.

5.1 Coronal hard X-ray signatures

The coronal hard X-ray source is a thin or thick target for accelerated electrons, but not necessarily identical to the acceleration region. The relation between coronal hard X-rays and acceleration is not clear. The centroid position of the coronal hard X-ray emission has been reported to be higher with increasing photon energy, and to be located above the thermal soft X-ray loop (Masuda et al. 2000). In some cases it has been reported to move out (Shibata et al. 1995). In another case, the speed of the outward motion of several hundred $\ \mathrm {km}\ \mathrm {s}^{-1}$ was correlated with the flux of accelerated electrons (Sui et al. 2004, Fig. 28). The altitude of this source decreases from the start of the hard X-rays until peak time at 23:12 UT, while a source above the loop-top moves upwards at a speed of $23\ \mathrm {km}\ \mathrm {s}^{-1}$. Well contained emission is also seen (e.g., Fig. 26). Elongated tongues stretching out from the loop-top are frequently reported (e.g., Sui et al. 2004).

With higher spectral resolution it became possible to determine also the photon energy distribution. The coronal hard X-rays have been found to be well represented by a power-law in energy (Emslie et al. 2003; Battaglia and Benz 2006), similar to what is well known for footpoint sources. The predominant near power-law distribution of accelerated electron energies is thus a stringent characteristic of the acceleration process, and not the result of propagation.

5.2 Soft-hard-soft behavior in hard X-rays

The hardness of the non-thermal spectrum changes in the course of a flare, starting soft (steep), getting harder at the peak and softening toward the end (Parks and Winckler 1969; Kane and Anderson 1970). A few large flares continue to harden after the peak (Frost and Dennis 1971; Krucker et al. 2005b). These flares were shown to be particularly well associated with solar energetic particle events (Kiplinger 1995), but this relation was recently questioned by Kahler (2012).

The great majority of flares follows a soft-hard-soft behavior (illustrated in Fig. 29). This correlation between (negative) spectral index and flux is generally interpreted as a signature of the acceleration process. A similar relation also holds for peak values of flares, showing that small flares are on the average softer (Battaglia et al. 2005). Both the time variation and the size variation of the spectral index with flux indicate that intense hard X-ray radiation is not a superposition of many small events. High flux means that the acceleration process is driven more forcefully, resulting in a harder spectrum. It is a intrinsic property of the acceleration process, but alas, many acceleration processes show this behavior.

The soft-hard-soft property becomes relevant if it is possible to express the relation between flux and spectral index in a quantitative way that can be compared to models. Grigis and Benz (2004, 2005b) found a power-law relation between the photon spectral index $\gamma $ and the flux density $F(E_0)$ measured at a given energy $E_0$ for SOL2002-11-09 (Fig. 29),

$$\begin{aligned} \gamma = A F(E_0)^{-\alpha } \,, \end{aligned}$$

(6)

where A is constant that varies from flare to flare, and $\alpha $ is $0.121\,{\pm }\,0.009$ in the flare rise phase and $0.172 \pm 0.012$ in the decay phase for $E_0=35\,\hbox {keV}$ (Grigis and Benz 2004). In this quantitative form, the soft-hard-soft behavior becomes a stringent condition for electron acceleration theories.

5.3 Radio emissions from the acceleration region

There are several flare-related processes that emit radio waves. The large variety of radio emissions may be grasped from Fig. 30. Their emission processes must be distinguished as they refer to widely different physical mechanisms. Only few of the radio emissions in Fig. 30, if any, come directly from the acceleration region. Most flare radio emissions, except thermal radiations at millimeter and submillimeter waves (post-burst increases and gradual rise and fall), are interpreted to be caused by non-thermal electrons. Non-thermal emissions come in two kinds: incoherent and coherent. In incoherent emissions, such as the synchrotron process, non-thermal electrons radiate individually. When a wave organizes electrons to emit in phase, the emission becomes coherent. On some cases, radio emission results from coupling two plasma waves (textbooks by Melrose 1980; Benz 2002). Coherent emissions are emitted at the local plasma frequency, upper hybrid frequency, electron gyrofrequency, or their harmonics and carry information on the plasma parameters in the source. As the plasma frequency exceeds the electron gyrofrequency by more than an order of magnitude in most of the corona, the plasma frequency is the lowest frequency observable from outside the solar atmosphere. If the flare energy is released at electron densities between $10^{8}$ and $10^{11} \ \mathrm {cm}^{-3}$, as generally believed, the corresponding emission is at short meter waves and, predominantly, in the decimeter region.

The study of the spatial distribution of the synchrotron emission by mildly relativistic electrons (gyrosynchrotron) has a long history. Both loop-top sources and double sources located close to the conjugate magnetic footpoints were reported (Marsh and Hurford 1982; Kundu et al. 1982; Kawabata et al. 1983). The comparison with theoretical simulations of the gyrosynchrotron brightness distribution along model magnetic loops (see Bastian et al. 1998, for a review) strongly suggests that the distribution of mildly relativistic electrons along an extended flaring loop must be highly inhomogeneous: accelerated electrons are concentrated in the upper part of the loop (Nindos et al. 2000; Melnikov et al. 2002). Some of the centimeter loop-top emissions were observed in the late phase of flares (e.g., Karlický 2004). They are not related to the main energy release, but possibly to high-energy X-rays detected late in flares (Krucker, personal communication) and possibly the end stage of the spectral hardening observed in non-thermal X-rays (see Sect. 5.2). The investigation of the acceleration region using gyrosynchrotron emission has greatly profited from combination with hard X-rays. It may result in the measurement of the magnetic field in loop-tops in future work.

Benz et al. (2007) found some coherent radio emission in all flares larger than C5 class, except near the limb where absorption seems to play a role. While there is good association between coherent radio emission and X-rays, correlation in details of the time profile is less frequent. Thus coherent emissions cannot expected to be reliable tracers of the main flare energy release in general. Emissions at higher frequencies, such as decimetric narrowband spikes, pulsations, and stationary type IV events appear to be more directly related to the acceleration process. The association but loose correlation between HXR and coherent radio emission may be interpreted by multiple reconnection sites connected by common field lines, along which accelerated particles may propagate and serve as a trigger for distant accelerations. Thus coherent radio emissions may be interesting diagnostics in for large-scale flare dynamics.

Correlation of coherent radio emissions with hard X-rays (or gyrosynchrotron emission) has been reported for spikes and pulsations (Slottje 1978; Benz and Kane 1986; Aschwanden et al. 1990; Kliem et al. 2000; Dabrowski and Benz 2009). If these coherent radiations are emitted at the second harmonic of the plasma frequency—the usual assumption—the density of the source region is in the range from $10^{9} \ \mathrm {cm}^{-3}$ to a few times $10^{10} \ \mathrm {cm}^{-3}$. This range is a possible indication for the density in the acceleration region. Although initially interpreted as loss-cone emissions of trapped particles near footpoints, they have been found at high altitudes (Benz et al. 2002; Khan et al. 2002; Kundu et al. 2006). As the emission mechanism of spikes and pulsations is not well understood, the origin of the radiating high-frequency waves is not known.

Best candidates for direct emission from an acceleration region are small clusters of narrowband spikes around 300 MHz, reported to correlate in detail with electron beam emission (type III radio bursts). About 10% of all meter wave type III groups are accompanied with spikes near but slightly above the start frequency (Benz et al. 1982). The spikes are concentrated in the spectrogram on the extrapolation of the type III bursts to higher frequency. More precisely, as suggested by Fig. 21, metric spikes are located on the extension of type III trajectories, supporting a model of energy release in or close to the spike sources (Benz et al. 1996). If this is the case, radio observations can approximately locate the acceleration region for the type III electrons and measure the electron density of the acceleration region (Sect. 3).

Type IV emissions occur late relative to the hard X-ray peak and appear to be connected to some late-phase acceleration (e.g., Švestka et al. 1982; Klein et al. 1983). They may be related to delayed electron releases of interplanetary electron events in the corona (Klein et al. 2005).

Some radio emissions (like type III and V) are due to electrons escaping from the acceleration region. Hard X-ray flares are associated with meter-wave type III bursts in 33% of all cases, and in 4% of them type III bursts are the exclusive radio emission. Type III emission is caused by electron beams becoming unstable towards growing electrostatic plasma waves at the local plasma frequency. These waves are converted into radio waves slightly above the plasma frequency $\omega _{\mathrm {p}}$,

$$\begin{aligned} \omega _{\mathrm {p}} = \sqrt{\frac{4 \pi e^2 n_e}{m_e}}, \end{aligned}$$

(7)

or its harmonic, where $n_e$ is the electron density, e the elementary charge, and $m_e$ the electron mass. Type III emission thus occurs at a frequency that varies with the local density. Observed at many different frequencies, it can be used to trace the path of the electron beam in the corona. Different beams following different trajectories diverging from the acceleration region have been used to locate the acceleration region (Fig. 21). The distance from this region to the start of type III emission depends on the energy spectrum of accelerated electrons (Benz 2002, p. 32). Future interferometers observing at many frequencies will refine this method.

A major constraint by radio emission on particle acceleration is the fact, that in 15% of larger flares (>C5.0 class) there is no coherent radiation except some electron beam emission at very high altitude (Benz et al. 2007). The flare capability to accelerate electrons without emitting coherent radio waves is, therefore, an observable criterion for the validity of acceleration models. The frequent lack of direct radio emission from the acceleration region suggests that the acceleration is “gentle”, excluding significant deviations from a distribution monotonically decreasing with velocity, such as a monoenergetic beam, which would emit observable Type III emission. The deviations only build up after the non-thermal electrons have traveled some distance and the faster particles have outpaced the slower particles, or after a loss-cone results from magnetic trapping. Gentle acceleration favors acceleration by diffusion in velocity space as predicted by stochastic acceleration (Sect. 6).

Another constraint suggested by radio waves is the rarity of shock emission from the termination of the reconnection outflows. Termination shocks are expected from the standard scenario (Fig. 2). Observational indications were presented by Aurass et al. (2002) and Mann et al. (2006), but seem to be rare.

6 Acceleration processes

A remarkable fraction of the total flare energy released first appears as kinetic particle energy in non-thermal electrons and sometimes ions (Sect. 5). White-light observations (Sect. 4) suggest that substantial energy is transported to the chromosphere and photosphere in addition to the particles that are observed in X-rays and gamma-rays (Lin and Hudson 1976). The acceleration process thus is a major issue in flare physics and constitutes the core of the flare enigma. We will briefly review here the major ingredients of the current theories and then present the observational evidence.

The transfer of magnetic energy to kinetic particle energy has been observationally separated into two phases. In the impulsive flare phase, the concept is “bulk energization”, involving an increase of the electron energy by more than two orders of magnitude starting from the coronal thermal energy (some 0.1 keV) within less than 1 s as derived from hard X-ray observations (Kiplinger et al. 1984). The other class of acceleration occurs in a secondary phase, possibly as a result of the first phase such as shock wave initiated by a flare or an associated coronal mass ejection. The second phase may be less efficient in particle acceleration, but is more important for solar energetic particles in interplanetary space.

We will concentrate here on bulk energization, in which the whole particle population gains energy and remains close to a Maxwellian distribution and/or develops a non-thermal tail. The acceleration of a particle to an energy $E_{\mathrm {kin}}$ must occur faster than the collision time $\tau _{\mathrm {coll}}(E_{\mathrm {kin}})$ for energy loss. The energy loss time for an electron with velocity v is

$$\begin{aligned} \tau _{\mathrm {coll}}(E_{\mathrm {kin}}) = 3.1 \times 10^{-20} \frac{v^3}{n_e} = 0.31 \left( \frac{v}{10^{10} \ \mathrm {cm}\ \mathrm {s}^{-1}}\right) ^3 \left( \frac{10^{11} \ \mathrm {cm}^{-3}}{n_e}\right) \ \mathrm{[s]}, \end{aligned}$$

(8)

where $n_e$ is the electron density. Equation (8) yields a collision time requiring acceleration within less than 1 s. Note that densities up to some $10^{12} \ \mathrm {cm}^{-3}$ are reported for coronal sources (Sect. 3.2). Equation (8) excludes efficient particle acceleration at high densities if the process takes a finite time.

6.1 Electron acceleration theories

The free mobility of charged particles in dilute plasma and the difference in inertia between electrons and ions make it likely that electrons are accelerated in every major impulsive process in the corona. Releasable (free) magnetic energy requires the presence of an electric current and an associated electric field before the flare-like process. Waves of various types from MHD to collisionless are expected to be excited by the flare and are also capable to accelerate particles in resonance. From a plasma-physics point of view, acceleration is not surprising; what is controversial is, however, which process dominates.

The conversion of magnetic energy into accelerated particles can be accomplished by several processes. It is likely that more than one occurs during a flare and its secondary effects. The most widely discussed can be grouped into three types (e.g., Melrose 1990; Benz 2002):

stochastic acceleration (e.g., resonant acceleration by waves),
electric field parallel to the magnetic field,
perpendicular and parallel shocks (first and second order Fermi acceleration).

The preferred but not generally accepted acceleration model for solar flares is stochastic acceleration by the magnetic field component of low-frequency waves (Miller et al. 1997; Schlickeiser and Miller 1998; Petrosian et al. 2006). Particles near Cerenkov resonance ($v\approx \omega /k_{\parallel }$) are mirrored by the waves. The process is known as “transit-time damping” of waves. It acts as a diffusion process of the particle distribution $f(\mathbf {p})$ in momentum space, described by the Fokker–Planck equation

$$\begin{aligned} \frac{\partial f(\mathbf {p})}{\partial t} = \left( \frac{1}{2}\sum _{i,j} \frac{\partial }{\partial p_i \partial p_j} D_{ij} - \sum _i \frac{\partial }{\partial p_i} F_{i} \right) f(\mathbf{p}) \,. \end{aligned}$$

(9)

The diffusion coefficients $D_{ij}$ and $ F_{i}$ contain the physics: the action of accelerating waves and decelerating Coulomb collisions (Fig. 31).

6.2 Comparing theories with observations

Flare particle acceleration may occur in connection with magnetic reconnection in low density plasma. The details are still obscure. Current flare observations contain a wealth of information that limits the scenarios for particle acceleration. Concerning the three types mentioned in the previous section, observations exclude more than they confirm. In particular:

High-frequency waves near the plasma frequency (such as Langmuir waves) can be excluded as drivers for stochastic acceleration. They would couple into radio decimeter waves and be present in every flare. On the other hand, acceleration by transit-time damping is compatible with the frequent lack of radio emission because the frequency of the postulated turbulence is far below the plasma frequency and does not cause radio emission.
The number of electrons that can be accelerated in current sheets is limited by the total current, and observed large values are difficult to match with a classic current sheet (Holman 1985; Litvinenko 1996).
Large-scale, stationary electric fields would cause major distortions in velocity space, susceptible to velocity-space instabilities and beam driven high-frequency waves observable as radio waves. Such radio emission should correlate well with hard X-ray emission. Such a tight correlation is not seen in every flare.
Shock acceleration plays an important role in interplanetary space, which is not the issue here. More directly related to flares are shocks possibly produced by the reconnection process. Radio signatures of such shocks have been reported by Aurass et al. (2002); Mann et al. (2006), but are still disputed and, if confirmed, extremely rare. Nevertheless, slow shocks have been predicted at the interface between inflow and outflow regions of reconnection, as well as fast shocks at the bow of the reconnection outflows. High energies could be readily be achieved (100 MeV ions in <1 s, Ellison and Ramaty 1985; Tsuneta and Naito 1998).

The transit-time damping scenario is consistent with present observations, although there is no direct evidence for it. Thus it must be considered as an unproven hypothesis. In fact, there are other viable scenarios such as low-frequency fluctuating electric fields parallel to the magnetic field. Such fields may originate from low-frequency and high-amplitude turbulence, such as kinetic Alfvén waves. They accelerate and decelerate electrons, leading to a net diffusion in energy space (Arzner and Vlahos 2004).

7 Conclusions

Flares may be considered to result from the loss of equilibrium in magnetic configurations. Although reconnection is a general phenomenon, it occurs in an impulsive way only in the corona, where collisions are rare and thus the plasma is highly conductive. Regular flares must be considered as extreme phenomena of the continuous dynamics of the corona. Radio noise storms (type I bursts) and meter wave type III bursts hint at activity in the high corona that is not yet accessible to other wavelengths and is prone to surprises.

Therefore, flares should not be considered exceptional catastrophes that occur rarely and mostly during solar maximum. Flare-like brightenings, known as “quiet-region microflares” or nanoflares, occur in the quiet corona at a rate of at least a few thousand per second. Is the corona heated by flares? Impulsive processes in the coronal plasma can suddenly change the resistivity to an anomalous value that is orders of magnitude higher than normal. They may thus release the energy stored in the magnetic field and be the cause of the corona. We cannot answer this question yet as long as we do not understand how much energy flares deposit into the corona in the various possible ways and how this energy is distributed. Furthermore, the corona below 20,000 km above the photosphere, including the transition region, is not well explored in flare research. It is also the place where most of the coronal heating occurs. It may be added here that the heating of the chromosphere is partly related to the corona and to reconnection, but is even more demanding.

Regular flares are not two of a kind, and each flare has individual features. For this reason, it is not surprising that observations at various wavelengths do not correlate in a simple manner as predicted by a standard scenario. The fact, that every flare appears to be different, must be taken as evidence that coronal dynamics has many degrees of freedom. Nevertheless, recent observations in X-rays and EUV allow identifying the magnetic topologies, confirming the general scenario of reconnection. They have shown that various groups of flares exist and have greatly contributed to our ever growing understanding of coronal phenomena.

Flares consist of a series of processes, starting with energy build-up in the corona and ending by restructuring the magnetic configuration and releasing magnetic energy. The processes include reconnection, instabilities, anomalous resistivity, efficient particle acceleration, particle propagation, coronal and chromospheric heating, evaporation, mass loss, high-frequency waves and MHD oscillations, as well as various emission mechanisms. All these processes are important issues in astrophysics and worth studying for their own. They all have seen significant progress in the past decades and will be addressed by the new observing facilities planned and in construction. The low corona will soon become accessible to white-light imaging and high-temperature line observations. Flare research will also profit from observations from close to the Sun and from imaging decimetric radio emissions. New instrumentation in imaging UV spectroscopy (IRIS) and submillimeter waves (ALMA) are expected to yield new insights in the near future. A major impact can be expected from simultaneous imaging observations in practically all wavelengths. They will greatly contribute to the growing physical understanding of solar flares in the near future.

Notes

The literature often uses the term ‘microwaves’ for frequencies in the range 1–30 GHz, in particular in connection with gyrosynchrotron emission. In the lower wavelength part, microwaves overlap with the decimeter wavelength range. We will thus use strictly the decimal wavelength notation in this review to avoid confusion.

References

Acton LW, Feldman U, Bruner ME, Doschek GA, Hirayama T, Hudson HS, Lemen JR, Ogawara Y, Strong KT, Tsuneta S (1992) The morphology of $20 \times 10^6$ K plasma in large non-impulsive solar flares. Publ Astron Soc Jpn 44:L71–L75
ADS Google Scholar
Antiochos SK (1998) The magnetic topology of solar eruptions. Astrophys J Lett 502:L181–L184. doi:10.1086/311507. arXiv:astro-ph/9806030
Article ADS Google Scholar
Antonucci E, Gabriel AH, Acton LW, Leibacher JW, Culhane JL, Rapley CG, Doyle JG, Machado ME, Orwig LE (1982) Impulsive phase of flares in soft X-ray emission. Solar Phys 78:107–123. doi:10.1007/BF00151147
Article ADS Google Scholar
Arzner K, Vlahos L (2004) Particle acceleration in multiple dissipation regions. Astrophys J Lett 605:L69–L72. doi:10.1086/392506. arXiv:astro-ph/0402605
Article ADS Google Scholar
Asai A, Nakajima H, Shimojo M, White SM, Hudson HS, Lin RP (2006) Preflare nonthermal emission observed in microwaves and hard X-rays. Publ Astron Soc Jpn 58:L1–L5. doi:10.1093/pasj/58.1.L1
Article ADS Google Scholar
Aschwanden MJ (2002) Particle acceleration and kinematics in solar flares: a synthesis of recent observations and theoretical concepts (invited review). Space Sci Rev 101:1–227. doi:10.1023/A:1019712124366
Article ADS Google Scholar
Aschwanden MJ (2007) RHESSI timing studies: multithermal delays. Astrophys J 661:1242–1259. doi:10.1086/516814
Article ADS Google Scholar
Aschwanden MJ, Benz AO, Kane SR (1990) Correlation of solar radio pulsations with hard X-ray emission. Astron Astrophys 229:206–215
ADS Google Scholar
Aschwanden MJ, Schwartz RA, Alt DM (1995) Electron time-of-flight differences in solar flares. Astrophys J 447:923. doi:10.1086/175930
Article ADS Google Scholar
Aschwanden MJ, Kosugi T, Hudson HS, Wills MJ, Schwartz RA (1996) The scaling law between electron time-of-flight distances and loop lengths in solar flares. Astrophys J 470:1198. doi:10.1086/177943
Article ADS Google Scholar
Aschwanden MJ, Fletcher L, Schrijver CJ, Alexander D (1999) Coronal loop oscillations observed with the transition region and coronal explorer. Astrophys J 520:880–894. doi:10.1086/307502
Article ADS Google Scholar
Aurass H, Vršnak B, Mann G (2002) Shock-excited radio burst from reconnection outflow jet? Astron Astrophys 384:273–281. doi:10.1051/0004-6361:20011735
Article ADS Google Scholar
Bastian TS, Benz AO, Gary DE (1998) Radio emission from solar flares. Annu Rev Astron Astrophys 36:131–188. doi:10.1146/annurev.astro.36.1.131
Article ADS Google Scholar
Battaglia M, Benz AO (2006) Relations between concurrent hard X-ray sources in solar flares. Astron Astrophys 456:751–760. doi:10.1051/0004-6361:20065233. arXiv:astro-ph/0606353
Article ADS Google Scholar
Battaglia M, Benz AO (2007) Exploring the connection between coronal and footpoint sources in a thin–thick target solar flare model. Astron Astrophys 466:713–716. doi:10.1051/0004-6361:20077144. arXiv:astro-ph/0702309
Article ADS Google Scholar
Battaglia M, Benz AO (2008) Observational evidence for return currents in solar flare loops. Astron Astrophys 487:337–344. doi:10.1051/0004-6361:200809418. arXiv:0806.1701
Article ADS Google Scholar
Battaglia M, Benz AO (2009) Do solar decimetric spikes originate in coronal X-ray sources? Astron Astrophys 499:L33–L36. doi:10.1051/0004-6361/200912143. arXiv:0904.4146
Article ADS Google Scholar
Battaglia M, Grigis PC, Benz AO (2005) Size dependence of solar X-ray flare properties. Astron Astrophys 439:737–747. doi:10.1051/0004-6361:20053027. arXiv:astro-ph/0505154
Article ADS Google Scholar
Benz AO (2002) Plasma astrophysics: kinetic processes in solar and stellar coronae, astrophysics and space science library, vol 279, 2nd edn. Kluwer, Dordrecht. doi:10.1007/0-306-47719-X
Google Scholar
Benz AO (2004) Decimeter burst emission and particle acceleration. In: Gary DE, Keller CU (eds) Solar and space weather radiophysics: current status and future developments, astrophysics and space science library, vol 314. Kluwer Academic Publishers, Dordrecht, pp 203–222. doi:10.1007/1-4020-2814-8_10
Chapter Google Scholar
Benz AO, Güdel M (2010) Physical processes in magnetically driven flares on the sun, stars, and young stellar objects. Annu Rev Astron Astrophys 48:241–287. doi:10.1146/annurev-astro-082708-101757
Article ADS Google Scholar
Benz AO, Kane SR (1986) Electron acceleration in flares inferred from radio and hard X-ray emissions. Solar Phys 104:179–185. doi:10.1007/BF00159960
Article ADS Google Scholar
Benz AO, Krucker S (1998) Heating events in the quiet solar corona. Solar Phys 182:349–363. doi:10.1023/A:1005046620684
Article ADS Google Scholar
Benz AO, Krucker S (2002) Energy distribution of microevents in the quiet solar corona. Astrophys J 568:413–421. doi:10.1086/338807. arXiv:astro-ph/0109027
Article ADS Google Scholar
Benz AO, Zlobec P, Jaeggi M (1982) Fine structure near the starting frequency of solar type III radio bursts. Astron Astrophys 109:305–313
ADS Google Scholar
Benz AO, Barrow CH, Dennis BR, Pick M, Raoult A, Simnett G (1983) X-ray and radio emissions in the early stages of solar flares. Solar Phys 83:267–283. doi:10.1007/BF00148280
Article ADS Google Scholar
Benz AO, Csillaghy A, Aschwanden MJ (1996) Metric spikes and electron acceleration in the solar corona. Astron Astrophys 309:291–300
ADS Google Scholar
Benz AO, Lin RP, Sheiner OA, Krucker S, Fainberg J (2001) The source regions of impulsive solar electron events. Solar Phys 203:131–144. doi:10.1023/A:1012725610185
Article ADS Google Scholar
Benz AO, Saint-Hilaire P, Vilmer N (2002) Location of narrowband spikes in solar flares. Astron Astrophys 383:678–684. doi:10.1051/0004-6361:20011774. arXiv:astro-ph/0112442
Article ADS Google Scholar
Benz AO, Grigis PC, Csillaghy A, Saint-Hilaire P (2005) Survey on solar X-ray flares and associated coherent radio emissions. Solar Phys 226:121–142. doi:10.1007/s11207-005-5254-5
Article ADS Google Scholar
Benz AO, Brajša R, Magdalenić J (2007) Are there radio-quiet solar flares? Solar Phys 240:263–270. doi:10.1007/s11207-007-0365-9. arXiv:astro-ph/0701570
Article ADS Google Scholar
Benz AO, Battaglia M, Vilmer N (2011) Location of decimetric pulsations in solar flares. Solar Phys 273:363–375. doi:10.1007/s11207-011-9760-3. arXiv:1103.5353
Article ADS Google Scholar
Berghmans D, Clette F, Moses D (1998) Quiet sun EUV transient brightenings and turbulence. A panoramic view by EIT on board SOHO. Astron Astrophys 336:1039–1055
ADS Google Scholar
Birn J, Fletcher L, Hesse M, Neukirch T (2009) Energy release and transfer in solar flares: simulations of three-dimensional reconnection. Astrophys J 695:1151–1162. doi:10.1088/0004-637X/695/2/1151
Article ADS Google Scholar
Bogachev SA, Somov BV, Kosugi T, Sakao T (2005) The motions of the hard X-ray sources in solar flares: images and statistics. Astrophys J 630:561–572. doi:10.1086/431918
Article ADS Google Scholar
Bone L, Brown JC, Fletcher L, Veronig A, White S (2007) Birth and evolution of a dense coronal loop in a complex flare region. Astron Astrophys 466:339–346. doi:10.1051/0004-6361:20065129
Article ADS Google Scholar
Bradshaw SJ, Cargill PJ (2010) A new enthalpy-based approach to the transition region in an impulsively heated corona. Astrophys J Lett 710:L39–L43. doi:10.1088/2041-8205/710/1/L39
Article ADS Google Scholar
Brosius JW, Phillips KJH (2004) Extreme-ultraviolet and X-ray spectroscopy of a solar flare loop observed at high time resolution: a case study in chromospheric evaporation. Astrophys J 613:580–591. doi:10.1086/422873
Article ADS Google Scholar
Brown JC (1971) The deduction of energy spectra of non-thermal electrons in flares from the observed dynamic spectra of hard X-ray bursts. Solar Phys 18:489. doi:10.1007/BF00149070
Article ADS Google Scholar
Brown JC, Carlaw VA, Cromwell D, Kane SR (1983) A comparison of the thick-target model with stereo data on the height structure of solar hard X-ray bursts. Solar Phys 88:281–295. doi:10.1007/BF00196193
Article ADS Google Scholar
Brown JC, Conway AJ, Aschwanden MJ (1998) The electron injection function and energy-dependent delays in thick-target hard X-rays. Astrophys J 509:911–917. doi:10.1086/306522
Article ADS Google Scholar
Cargill PJ, Mariska JT, Antiochos SK (1995) Cooling of solar flares plasmas. 1: theoretical considerations. Astrophys J 439:1034–1043. doi:10.1086/175240
Article ADS Google Scholar
Cargill PJ, Bradshaw SJ, Klimchuk JA (2012) Enthalpy-based thermal evolution of loops. II. Improvements to the model. Astrophys J 752:161. doi:10.1088/0004-637X/752/2/161. arXiv:1204.5960
Article ADS Google Scholar
Carmichael H (1964) A process for flares. In: Hess WN (ed) The physics of solar flares, NASA scientific and technical information division, vol SP-50. NASA special publications, Washington, pp 451–456
Google Scholar
Chen PF, Shibata K, Brooks DH, Isobe H (2004) A reexamination of the evidence for reconnection inflow. Astrophys J Lett 602:L61–L64. doi:10.1086/382479
Article ADS Google Scholar
Chifor C, Del Zanna G, Mason HE, Sylwester J, Sylwester B, Phillips KJH (2007) A benchmark study for CHIANTI based on RESIK solar flare spectra. Astron Astrophys 462:323–330. doi:10.1051/0004-6361:20066261
Article ADS Google Scholar
Choudhary DP, Ambastha A, Ai G (1998) Emerging Flux and X-class flares in NOAA 6555. Solar Phys 179:133–140. doi:10.1023/A:1005063609450
Article ADS Google Scholar
Chupp EL, Forrest DJ, Higbie PR, Suri AN, Tsai C, Dunphy PP (1973) Solar gamma ray lines observed during the solar activity of August 2 to August 11, 1972. Nature 241:333. doi:10.1038/241333a0
Article ADS Google Scholar
Cliver EW, Crosby NB, Dennis BR (1994) Are solar gamma-ray-line flares different from other large flares? Astrophys J 426:767–773. doi:10.1086/174113
Article ADS Google Scholar
Crooker NU, Webb DF (2006) Remote sensing of the solar site of interchange reconnection associated with the May 1997 magnetic cloud. J Geophys Res 111:A08108. doi:10.1029/2006JA011649
Article ADS Google Scholar
Crooker NU, Forsyth R, Rees A, Gosling JT, Kahler SW (2004) Counterstreaming electrons in magnetic clouds near 5 AU. J Geophys Res 109:A06110. doi:10.1029/2004JA010426
ADS Google Scholar
Dabrowski BP, Benz AO (2009) Correlation between decimetric radio emission and hard X-rays in solar flares. Astron Astrophys 504:565–573. doi:10.1051/0004-6361/200811108
Article ADS Google Scholar
Datlowe DW, Lin RP (1973) Evidence for thin-target X-ray emission in a small solar flare on 26 February 1972. Solar Phys 32:459. doi:10.1007/BF00154958
Article ADS Google Scholar
Démoulin P, Bagalá LG, Mandrini CH, Hénoux JC, Rovira MG (1997) Quasi-separatrix layers in solar flares. II. Observed magnetic configurations. Astron Astrophys 325:305–317
ADS Google Scholar
Deng XH, Matsumoto H (2001) Rapid magnetic reconnection in the Earth’s magnetosphere mediated by whistler waves. Nature 410:557–560
Article ADS Google Scholar
Dennis BR, Zarro DM (1993) The Neupert effect: What can it tell us about the impulsive and gradual phases of solar flares? Solar Phys 146:177–190. doi:10.1007/BF00662178
Article ADS Google Scholar
Dickson ECM, Kontar EP (2013) Measurements of electron anisotropy in solar flares using albedo with RHESSI X-ray data. Solar Phys 284:405–425. doi:10.1007/s11207-012-0178-3. arXiv:1210.4757
Article ADS Google Scholar
Doschek GA, Feldman U, Kreplin RW, Cohen L (1980) High-resolution X-ray spectra of solar flares. III. General spectral properties of X1–X5 type flares. Astrophys J 239:725–737. doi:10.1086/158158
Article ADS Google Scholar
Ellison DC, Ramaty R (1985) Shock acceleration of electrons and ions in solar flares. Astrophys J 298:400–408. doi:10.1086/163623
Article ADS Google Scholar
Emslie AG, Kontar EP, Krucker S, Lin RP (2003) RHESSI hard X-ray imaging spectroscopy of the large gamma-ray flare of 2002 July 23. Astrophys J Lett 595:L107–L110. doi:10.1086/378931
Article ADS Google Scholar
Emslie AG, Kucharek H, Dennis BR, Gopalswamy N, Holman GD, Share GH, Vourlidas A, Forbes TG, Gallagher PT, Mason GM, Metcalf TR, Mewaldt RA, Murphy RJ, Schwartz RA, Zurbuchen TH (2004) Energy partition in two solar flare/CME events. J Geophys Res 109:A10104. doi:10.1029/2004JA010571
Article ADS Google Scholar
Emslie AG, Dennis BR, Holman GD, Hudson HS (2005) Refinements to flare energy estimates: a followup to ‘Energy partition in two solar flare/CME events’ by A.G. Emslie et al. J Geophys Res 110:A11103. doi:10.1029/2005JA011305
Article ADS Google Scholar
Emslie AG, Dennis BR, Hudson H, Lin RP (eds) (2011) High-energy aspects of solar flares: a RHESSI-inspired monograph. Space Science Reviews, vol 159. Springer, Berlin. doi:10.1007/s11214-011-9815-7
Emslie AG, Dennis BR, Shih AY, Chamberlin PC, Mewaldt RA, Moore CS, Share GH, Vourlidas A, Welsch BT (2012) Global energetics of thirty-eight large solar eruptive events. Astrophys J 759:71. doi:10.1088/0004-637X/759/1/71. arXiv:1209.2654
Article ADS Google Scholar
Feldman U, Doschek GA, Kreplin RW, Mariska JT (1980) High-resolution X-ray spectra of solar flares. IV. General spectral properties of M type flares. Astrophys J 241:1175–1185. doi:10.1086/158434
Article ADS Google Scholar
Feldman U, Hiei E, Phillips KJH, Brown CM, Lang J (1994) Very impulsive solar flares observed with the YOHKOH spacecraft. Astrophys J 421:843–850. doi:10.1086/173696
Article ADS Google Scholar
Fisher GH, Hawley SL (1990) An equation for the evolution of solar and stellar flare loops. Astrophys J 357:243–258. doi:10.1086/168911
Article ADS Google Scholar
Fisk LA, Schwadron NA, Zurbuchen TH (1999) Acceleration of the fast solar wind by the emergence of new magnetic flux. J Geophys Res 104(A9):19765–19772. doi:10.1029/1999JA900256
Article ADS Google Scholar
Fletcher L, Hudson HS (2008) Impulsive phase flare energy transport by large-scale Alfvén waves and the electron acceleration problem. Astrophys J 675:1645–1655. doi:10.1086/527044. arXiv:0712.3452
Article ADS Google Scholar
Fletcher L, Martens PCH (1998) A model for hard X-ray emission from the top of flaring loops. Astrophys J 505:418–431. doi:10.1086/306137
Article ADS Google Scholar
Fletcher L, Warren HP (2003) The energy release process in solar flares; constraints from TRACE observations. In: Klein KL (ed) Energy conversion and particle acceleration in the solar corona. Lecture notes in physics, vol 612. Springer, Berlin, pp 58–79
Chapter Google Scholar
Fletcher L, Pollock JA, Potts HE (2004) Tracking of TRACE ultraviolet flare footpoints. Solar Phys 222:279–298. doi:10.1023/B:SOLA.0000043580.89730.4d
Article ADS Google Scholar
Foullon C, Verwichte E, Nakariakov VM, Fletcher L (2005) X-ray quasi-periodic pulsations in solar flares as magnetohydrodynamic oscillations. Astron Astrophys 440:L59–L62. doi:10.1051/0004-6361:200500169
Article ADS Google Scholar
Frost KJ, Dennis BR (1971) Evidence from hard X-rays for two-stage particle acceleration in a solar flare. Astrophys J 165:655. doi:10.1086/150932
Article ADS Google Scholar
Fuentes-Fernández J, Parnell CE, Priest ER (2012) The onset of impulsive bursty reconnection at a two-dimensional current layer. Phys Plasmas 19(7):072901. doi:10.1063/1.4729334. arXiv:1205.2120
Article ADS Google Scholar
Georgoulis MK, LaBonte BJ (2006) Reconstruction of an inductive velocity field vector from Doppler motions and a pair of solar vector magnetograms. Astrophys J 636:475–495. doi:10.1086/497978. arXiv:astro-ph/0511447
Article ADS Google Scholar
Gosling JT, Birn J, Hesse M (1995) Three-dimensional magnetic reconnection and the magnetic topology of coronal mass ejection events. Geophys Res Lett 22:869–872. doi:10.1029/95GL00270
Article ADS Google Scholar
Graham DR, Cauzzi G (2015) Temporal evolution of multiple evaporating ribbon sources in a solar flare. Astrophys J Lett 807:L22. doi:10.1088/2041-8205/807/2/L22. arXiv:1506.03465
Article ADS Google Scholar
Grigis PC, Benz AO (2004) The spectral evolution of impulsive solar X-ray flares. Astron Astrophys 426:1093–1101. doi:10.1051/0004-6361:20041367. arXiv:astro-ph/0407431
Article ADS Google Scholar
Grigis PC, Benz AO (2005a) The evolution of reconnection along an arcade of magnetic loops. Astrophys J Lett 625:L143–L146. doi:10.1086/431147. arXiv:astro-ph/0504436
Article ADS Google Scholar
Grigis PC, Benz AO (2005b) The spectral evolution of impulsive solar X-ray flares. II. Comparison of observations with models. Astron Astrophys 434:1173–1181. doi:10.1051/0004-6361:20042265. arXiv:astro-ph/0501431
Article ADS Google Scholar
Grigis PC, Benz AO (2006) Electron acceleration in solar flares: theory of spectral evolution. Astron Astrophys 458:641–651. doi:10.1051/0004-6361:20065809. arXiv:astro-ph/0606339
Article ADS MATH Google Scholar
Hagyard MJ, Venkatakrishnan P, Smith JB Jr (1990) Nonpotential magnetic fields at sites of gamma-ray flares. Astrophys J Suppl Ser 73:159–163. doi:10.1086/191447
Article ADS Google Scholar
Hanaoka Y (1996) Flares and plasma flow caused by interacting coronal loops. Solar Phys 165:275–301. doi:10.1007/BF00149715
Article ADS Google Scholar
Hanaoka Y (1997) Double-loop configuration of solar flares. Solar Phys 173:319–346. doi:10.1023/A:1004953003558
Article ADS Google Scholar
Hannah IG, Hudson HS, Battaglia M, Christe S, Kašparová J, Krucker S, Kundu MR, Veronig A (2011) Microflares and the statistics of X-ray flares. Space Sci Rev 159:263–300. doi:10.1007/s11214-010-9705-4. arXiv:1108.6203
Article ADS Google Scholar
Hey JS (1983) The radio universe, 3rd edn. Pergamon Press, Oxford
Google Scholar
Heyvaerts J, Priest ER, Rust DM (1977) An emerging flux model for the solar flare phenomenon. Astrophys J 216:123–137. doi:10.1086/155453
Article ADS Google Scholar
Hirayama T (1974) Theoretical model of flares and prominences. I: evaporating flare model. Solar Phys 34:323–338. doi:10.1007/BF00153671
Article ADS Google Scholar
Holman GD (1985) Acceleration of runaway electrons and Joule heating in solar flares. Astrophys J 293:584–594. doi:10.1086/163263
Article ADS Google Scholar
Hori K, Yokoyama T, Kosugi T, Shibata K (1997) Pseudo-two-dimensional hydrodynamic modeling of solar flare loops. Astrophys J 489:426–441. doi:10.1086/304754
Article ADS Google Scholar
Hori K, Yokoyama T, Kosugi T, Shibata K (1998) Single and multiple solar flare loops: hydrodynamics and Ca XIX resonance line emission. Astrophys J 500:492–510. doi:10.1086/305725
Article ADS Google Scholar
Hoyng P, Duijveman A, Machado ME, Rust DM, Švestka Z, Boelee A, de Jager C, Frost KT, Lafleur H, Simnett GM, van Beek HF, Woodgate BE (1981) Origin and location of the hard X-ray emission in a two-ribbon flare. Astrophys J Lett 246:L155. doi:10.1086/183574
Article ADS Google Scholar
Hua XM, Lingenfelter RE (1987) Solar flare neutron and accelerated ion angular distributions. Astrophys J 323:779–794. doi:10.1086/165871
Article ADS Google Scholar
Hudson HS (1972) Thick-target processes and white-light flares. Solar Phys 24:414. doi:10.1007/BF00153384
Article ADS Google Scholar
Hudson HS (1978) A purely coronal hard X-ray event. Astrophys J 224:235–240. doi:10.1086/156370
Article ADS Google Scholar
Hudson HS (1991) Solar flares, microflares, nanoflares, and coronal heating. Solar Phys 133:357–369. doi:10.1007/BF00149894
Article ADS Google Scholar
Hudson HS (2011) Global properties of solar flares. Space Sci Rev 158:5–41. doi:10.1007/s11214-010-9721-4. arXiv:1108.3490
Article ADS Google Scholar
Hudson HS, Strong KT, Dennis BR, Zarro D, Inda M, Kosugi T, Sakao T (1994) Impulsive behavior in solar soft X-radiation. Astrophys J Lett 422:L25–L27. doi:10.1086/187203
Article ADS Google Scholar
Hudson HS, Kosugi T, Nitta NV, Shimojo M (2001) Hard X-radiation from a fast coronal ejection. Astrophys J Lett 561:L211–L214. doi:10.1086/324760
Article ADS Google Scholar
Hudson HS, Wolfson CJ, Metcalf TR (2006) White-light flares: a TRACE/RHESSI overview. Solar Phys 234:79–93. doi:10.1007/s11207-006-0056-y
Article ADS Google Scholar
Hurford GJ, Krucker S, Lin RP, Schwartz RA, Share GH, Smith DM (2006) Gamma-ray imaging of the 2003 October/November solar flares. Astrophys J Lett 644:L93–L96. doi:10.1086/505329
Article ADS Google Scholar
Jess DB, Mathioudakis M, Crockett PJ, Keenan FP (2008) Do all flares have white-light emission? Astrophys J Lett 688:L119. doi:10.1086/595588. arXiv:0810.1443
Article ADS Google Scholar
Jiang YW, Liu S, Liu W, Petrosian V (2006) Evolution of the loop-top source of solar flares: heating and cooling processes. Astrophys J 638:1140–1153. doi:10.1086/498863. arXiv:astro-ph/0508532
Article ADS Google Scholar
Kahler SW (2012) Solar energetic particle events and the Kiplinger effect. Astrophys J 747:66. doi:10.1088/0004-637X/747/1/66
Article ADS Google Scholar
Kane SR (1983) Spatial structure of high energy photon sources in solar flares. Solar Phys 86:355–365. doi:10.1007/BF00157209
Article ADS Google Scholar
Kane SR, Anderson KA (1970) Spectral characteristics of impulsive solar-flare X-rays 10 KeV. Astrophys J 162:1003. doi:10.1086/150732
Article ADS Google Scholar
Kane SR, Kreplin RW, Martres MJ, Pick M, Soru-Escaut I (1974) Acceleration of electrons in absence of detectable optical flares deduced from type III radio bursts, H$\alpha $ activity and soft X-ray emission. Solar Phys 38:483–497. doi:10.1007/BF00155083
Article ADS Google Scholar
Karlický M (2004) Loop-top gyro-synchrotron source in post-maximum phase of the August 24, 2002 flare. New Astron 9:383–389. doi:10.1016/j.newast.2004.01.002
Article ADS Google Scholar
Kašparová J, Kontar EP, Brown JC (2007) Hard X-ray spectra and positions of solar flares observed by RHESSI: photospheric albedo, directivity and electron spectra. Astron Astrophys 466:705–712. doi:10.1051/0004-6361:20066689. arXiv:astro-ph/0701871
Article ADS Google Scholar
Kawabata KA, Ogawa H, Suzuki I (1983) A flare model deduced from HINOTORI and millimeter wave interferometer observations. Solar Phys 86:247–251. doi:10.1007/BF00157197
Article ADS Google Scholar
Khan JI, Vilmer N, Saint-Hilaire P, Benz AO (2002) The solar coronal origin of a slowly drifting decimetric-metric pulsation structure. Astron Astrophys 388:363–372. doi:10.1051/0004-6361:20020385
Article ADS Google Scholar
Kiplinger AL (1995) Comparative studies of hard X-ray spectral evolution in solar flares with high-energy proton events observed at earth. Astrophys J 453:973. doi:10.1086/176457
Article ADS Google Scholar
Kiplinger AL, Dennis BR, Frost KJ, Orwig LE (1984) Fast variations in high-energy X-rays from solar flares and their constraints on nonthermal models. Astrophys J Lett 287:L105–L108. doi:10.1086/184408
Article ADS Google Scholar
Klein KL, Aurass H, Soru-Escaut I, Kalman B (1997) Electron acceleration sites in a large-scale coronal structure. Astron Astrophys 320:612–619
ADS Google Scholar
Klein KL, Krucker S, Trottet G, Hoang S (2005) Coronal phenomena at the release of solar energetic electron events. Astron Astrophys 431:1047–1060. doi:10.1051/0004-6361:20041258
Article ADS Google Scholar
Klein L, Pick M, Trottet G, Vilmer N, Anderson K, Kane S (1983) Association between gradual hard X-ray emission and metric continua during large flares. Solar Phys 84:295–310. doi:10.1007/BF00157463
Article ADS Google Scholar
Kliem B, Karlický M, Benz AO (2000) Solar flare radio pulsations as a signature of dynamic magnetic reconnection. Astron Astrophys 360:715–728 arXiv:astro-ph/0006324
ADS Google Scholar
Kontar EP, Brown JC, McArthur GK (2002) Nonuniform target ionization and fitting thick target electron injection spectra to RHESSI data. Solar Phys 210:419–429. doi:10.1023/A:1022494318540
Article ADS Google Scholar
Kontar EP, Emslie AG, Piana M, Massone AM, Brown JC (2005) Determination of electron flux spectra in a solar flare with an augmented regularization method: application to RHESSI data. Solar Phys 226:317–325. doi:10.1007/s11207-005-7150-4. arXiv:astro-ph/0409691
Article ADS Google Scholar
Kontar EP, MacKinnon AL, Schwartz RA, Brown JC (2006) Compton backscattered and primary X-rays from solar flares: angle dependent Green’s function correction for photospheric albedo. Astron Astrophys 446:1157–1163. doi:10.1051/0004-6361:20053672. arXiv:astro-ph/0510167
Article ADS Google Scholar
Kopp RA, Pneuman GW (1976) Magnetic reconnection in the corona and the loop prominence phenomenon. Solar Phys 50:85–98. doi:10.1007/BF00206193
Article ADS Google Scholar
Krucker S, Benz AO (1998) Energy distribution of heating processes in the quiet solar corona. Astrophys J Lett 501:L213–L216. doi:10.1086/311474
Article ADS Google Scholar
Krucker S, Benz AO (2000) Are heating events in the quiet solar corona small flares? Multiwavelength observations of individual events. Solar Phys 191:341–358. doi:10.1023/A:1005255608792. arXiv:astro-ph/9912501
Article ADS Google Scholar
Krucker S, Aschwanden MJ, Bastian TS, Benz AO (1995) First VLA observation of a solar narrowband, millisecond spike event. Astron Astrophys 302:551
ADS Google Scholar
Krucker S, Benz AO, Aschwanden MJ (1997a) YOHKOH observation of the source regions of solar narrowband, millisecond spike events. Astron Astrophys 317:569–579
ADS Google Scholar
Krucker S, Benz AO, Bastian TS, Acton LW (1997b) X-ray network flares of the quiet sun. Astrophys J 488:499. doi:10.1086/304686
Article ADS Google Scholar
Krucker S, Hurford GJ, Lin RP (2003) Hard X-ray source motions in the 2002 July 23 gamma-ray flare. Astrophys J Lett 595:L103–L106. doi:10.1086/378840
Article ADS Google Scholar
Krucker S, Fivian MD, Lin RP (2005) Hard X-ray footpoint motions in solar flares: comparing magnetic reconnection models with observations. Adv Space Res 35:1707–1711. doi:10.1016/j.asr.2005.05.054
Article ADS Google Scholar
Krucker S, Hurford GJ, Lin RP (2005b) RHESSI X-ray and gamma-ray observations of the January 20, 2005 event. Eos Trans AGU 86:SH21A-01, fall Meet. Suppl
Krucker S, Hannah IG, Lin RP (2007) RHESSI and Hinode X-ray observations of a partially occulted solar flare. Astrophys J Lett 671:L193–L196. doi:10.1086/525019
Article ADS Google Scholar
Krucker S, Battaglia M, Cargill PJ, Fletcher L, Hudson HS, MacKinnon AL, Masuda S, Sui L, Tomczak M, Veronig AL, Vlahos L, White SM (2008a) Hard X-ray emission from the solar corona. Astron Astrophys Rev 16:155–208. doi:10.1007/s00159-008-0014-9
Article ADS Google Scholar
Krucker S, Hurford GJ, MacKinnon AL, Shih AY, Lin RP (2008b) Coronal $\gamma $-ray bremsstrahlung from solar flare-accelerated electrons. Astrophys J Lett 678:L63–L66. doi:10.1086/588381
Article ADS Google Scholar
Krucker S, Saint-Hilaire P, Christe S, White SM, Chavier AD, Bale SD, Lin RP (2008c) Coronal hard X-ray emission associated with radio type III bursts. Astrophys J 681:644–649. doi:10.1086/588549
Article ADS Google Scholar
Krucker S, Hudson HS, Jeffrey NLS, Battaglia M, Kontar EP, Benz AO, Csillaghy A, Lin RP (2011) High-resolution imaging of solar flare ribbons and its implication on the thick-target beam model. Astrophys J 739:96. doi:10.1088/0004-637X/739/2/96
Article ADS Google Scholar
Krüger A (1979) Introduction to solar radio astronomy and radio physics. In: Geophysics and astrophysics monographs, vol 16. Reidel, Dordrecht. doi:10.1007/978-94-009-9402-7
Kundu MR (1965) Solar radio astronomy. Interscience Publication, New York
Google Scholar
Kundu MR (1984) Relative positions of microwave and hard X-ray burst sources. Adv Space Res 4:157–162. doi:10.1016/0273-1177(84)90175-3
Article ADS Google Scholar
Kundu MR, Schmahl EJ, Velusamy T (1982) Magnetic structure of a flaring region producing impulsive microwave and hard X-ray bursts. Astrophys J 253:963–974. doi:10.1086/159694
Article ADS Google Scholar
Kundu MR, White SM, Garaimov VI, Subramanian P, Ananthakrishnan S, Janardhan P (2006) The morphology of decimetric emission from solar flares: GMRT observations. Solar Phys 236:369–387. doi:10.1007/s11207-006-0059-8
Article ADS Google Scholar
Lin RP (2011) Energy release and particle acceleration in flares: summary and future prospects. Space Sci Rev 159:421–445. doi:10.1007/s11214-011-9801-0. arXiv:1110.1805
Article ADS Google Scholar
Lin RP, Hudson HS (1976) Non-thermal processes in large solar flares. Solar Phys 50:153–178. doi:10.1007/BF00206199
Article ADS Google Scholar
Lin RP, Schwartz RA, Pelling RM, Hurley KC (1981) A new component of hard X-rays in solar flares. Astrophys J Lett 251:L109–L114. doi:10.1086/183704
Article ADS Google Scholar
Lin RP, Larson D, McFadden J, Carlson CW, Ergun RE, Anderson KA, Ashford S, McCarthy M, Parks GK, Rème H, Bosqued JM, d’Uston C, Sanderson TR, Wenzel KP (1996) Observation of an impulsive solar electron event extending down to $\sim $0.5 keV energy. Geophys Res Lett 23:1211–1214. doi:10.1029/96GL00710
Article ADS Google Scholar
Lin RP, Dennis BR, Hurford GJ, Smith DM, Zehnder A, Harvey PR, Curtis DW, Pankow D, Turin P, Bester M, Csillaghy A, Lewis M, Madden N, van Beek HF, Appleby M, Raudorf T, McTiernan J, Ramaty R, Schmahl E, Schwartz R, Krucker S, Abiad R, Quinn T, Berg P, Hashii M, Sterling R, Jackson R, Pratt R, Campbell RD, Malone D, Landis D, Barrington-Leigh CP, Slassi-Sennou S, Cork C, Clark D, Amato D, Orwig L, Boyle R, Banks IS, Shirey K, Tolbert AK, Zarro D, Snow F, Thomsen K, Henneck R, McHedlishvili A, Ming P, Fivian M, Jordan J, Wanner R, Crubb J, Preble J, Matranga M, Benz AO, Hudson HS, Canfield RC, Holman GD, Crannell C, Kosugi T, Emslie AG, Vilmer N, Brown JC, Johns-Krull CM, Aschwanden MJ, Metcalf TR, Conway A (2002) The Reuven Ramaty high-energy solar spectroscopic imager (RHESSI). Solar Phys 210:3–32. doi:10.1023/A:1022428818870
Article ADS Google Scholar
Lin RP, Krucker S, Hurford GJ, Smith DM, Hudson HS, Holman GD, Schwartz RA, Dennis BR, Share GH, Murphy RJ, Emslie AG, Johns-Krull CM, Vilmer N (2003) RHESSI observations of particle acceleration and energy release in an intense solar gamma-ray line flare. Astrophys J Lett 595:L69–L76. doi:10.1086/378932
Article ADS Google Scholar
Litvinenko YE (1996) Particle acceleration in reconnecting current sheets with a nonzero magnetic field. Astrophys J 462:997. doi:10.1086/177213
Article ADS Google Scholar
Liu W, Liu S, Jiang YW, Petrosian V (2006) RHESSI observation of chromospheric evaporation. Astrophys J 649:1124–1139. doi:10.1086/506268. arXiv:astro-ph/0603510
Article ADS Google Scholar
Liu W, Petrosian V, Dennis BR, Jiang YW (2008) Double coronal hard and soft X-ray source observed by RHESSI: evidence for magnetic reconnection and particle acceleration in solar flares. Astrophys J 676:704–716. doi:10.1086/527538. arXiv:0709.1963
Article ADS Google Scholar
Longcope DW (2005) Topological methods for the analysis of solar magnetic fields. Living Rev Solar Phys 2:lrsp-2005-7. doi:10.12942/lrsp-2005-7. http://www.livingreviews.org/lrsp-2005-7
Low BC (1996) Solar activity and the corona. Solar Phys 167:217–265. doi:10.1007/BF00146338
Article ADS Google Scholar
Mann G, Aurass H, Warmuth A (2006) Electron acceleration by the reconnection outflow shock during solar flares. Astron Astrophys 454:969–974. doi:10.1051/0004-6361:20064990
Article ADS Google Scholar
Mariska JT, McTiernan JM (1999) Hard and soft X-ray observations of occulted and nonocculted solar limb flares. Astrophys J 514:484–492. doi:10.1086/306927
Article ADS Google Scholar
Mariska JT, Doschek GA, Bentley RD (1993) Flare plasma dynamics observed with the YOHKOH Bragg crystal spectrometer. I. Properties of the Ca XIX resonance line. Astrophys J 419:418. doi:10.1086/173494
Article ADS Google Scholar
Marsh KA, Hurford GJ (1982) High spatial resolution solar microwave observations. Annu Rev Astron Astrophys 20:497–516. doi:10.1146/annurev.aa.20.090182.002433
Article ADS Google Scholar
Martin SF (1989) Mass motions associated with solar flares. Solar Phys 121:215–238. doi:10.1007/BF00161697
Article ADS Google Scholar
Martínez Oliveros JC, Hudson HS, Hurford GJ, Krucker S, Lin RP, Lindsey C, Couvidat S, Schou J, Thompson WT (2012) The height of a white-light flare and its hard X-ray sources. Astrophys J Lett 753:L26. doi:10.1088/2041-8205/753/2/L26. arXiv:1206.0497
Article ADS Google Scholar
Masuda S, Kosugi T, Hara H, Tsuneta S, Ogawara Y (1994) A loop-top hard X-ray source in a compact solar flare as evidence for magnetic reconnection. Nature 371:495–497. doi:10.1038/371495a0
Article ADS Google Scholar
Masuda S, Sato J, Kosugi T, Sakao T (2000) Spectral characteristics of above-the-looptop hard X-ray source. Adv Space Res 26:493–496. doi:10.1016/S0273-1177(99)01101-1
Article ADS Google Scholar
Masuda S, Kosugi T, Hudson HS (2001) A hard X-ray two-ribbon flare observed with Yohkoh/HXT. Solar Phys 204:55–67. doi:10.1023/A:1014230629731
Article ADS Google Scholar
Matthews SA, van Driel-Gesztelyi L, Hudson HS, Nitta NV (2003) A catalogue of white-light flares observed by Yohkoh. Astron Astrophys 409:1107–1125. doi:10.1051/0004-6361:20031187
Article ADS Google Scholar
McKenzie DE, Hudson HS (1999) X-ray observations of motions and structure above a solar flare arcade. Astrophys J Lett 519:L93–L96. doi:10.1086/312110
Article ADS Google Scholar
McTiernan JM, Kane SR, Loran JM, Lemen JR, Acton LW, Hara H, Tsuneta S, Kosugi T (1993) Temperature and density structure of the 1991 November 2 flare observed by the YOHKOH soft X-ray telescope and hard X-ray telescope. Astrophys J Lett 416:L91. doi:10.1086/187078
Article ADS Google Scholar
McTiernan JM, Fisher GH, Li P (1999) The solar flare soft X-ray differential emission measure and the Neupert effect at different temperatures. Astrophys J 514:472–483. doi:10.1086/306924
Article ADS Google Scholar
Melnikov VF, Shibasaki K, Reznikova VE (2002) Loop-top nonthermal microwave source in extended solar flaring loops. Astrophys J Lett 580:L185–L188. doi:10.1086/345587
Article ADS Google Scholar
Melrose DB (1980) Plasma astrophysics: nonthermal processes in diffuse magnetized plasmas, vol 2. Gordon and Breach, New York
Google Scholar
Melrose DB (1990) Particle acceleration processes in the solar corona. Aust J Phys 43:703–752. doi:10.1071/PH900703
Article ADS Google Scholar
Metcalf TR, Alexander D (1999) Coronal trapping of energetic flare particles: Yohkoh/HXT observations. Astrophys J 522:1108–1116. doi:10.1086/307679
Article ADS Google Scholar
Metcalf TR, Alexander D, Hudson HS, Longcope DW (2003) TRACE and Yohkoh observations of a white-light flare. Astrophys J 595:483–492. doi:10.1086/377217
Article ADS Google Scholar
Miller JA, Cargill PJ, Emslie AG, Holman GD, Dennis BR, LaRosa TN, Winglee RM, Benka SG, Tsuneta S (1997) Critical issues for understanding particle acceleration in impulsive solar flares. J Geophys Res 102:14631–14660. doi:10.1029/97JA00976
Article ADS Google Scholar
Milligan RO (2015) Extreme ultra-violet spectroscopy of the lower solar atmosphere during solar flares (invited review). Solar Phys 290:3399–3423. doi:10.1007/s11207-015-0748-2. arXiv:1501.04829
Article ADS Google Scholar
Milligan RO, Dennis BR (2009) Velocity characteristics of evaporated plasma using Hinode/EUV imaging spectrometer. Astrophys J 699:968–975. doi:10.1088/0004-637X/699/2/968. arXiv:0905.1669
Article ADS Google Scholar
Milligan RO, Gallagher PT, Mathioudakis M, Keenan FP, Bloomfield DS (2005) Plasma diagnostics of active-region evolution and implications for coronal heating. Mon Not R Astron Soc 363:259–267. doi:10.1111/j.1365-2966.2005.09446.x. arXiv:astro-ph/0509219
Article ADS Google Scholar
Milligan RO, Gallagher PT, Mathioudakis M, Keenan FP (2006) Observational evidence of gentle chromospheric evaporation during the impulsive phase of a solar flare. Astrophys J Lett 642:L169–L171. doi:10.1086/504592. arXiv:astro-ph/0603652
Article ADS Google Scholar
Milligan RO, Kerr GS, Dennis BR, Hudson HS, Fletcher L, Allred JC, Chamberlin PC, Ireland J, Mathioudakis M, Keenan FP (2014) The radiated energy budget of chromospheric plasma in a major solar flare deduced from multi-wavelength observations. Astrophys J 793:70. doi:10.1088/0004-637x/793/2/70. arXiv:1406.7657
Article ADS Google Scholar
Miroshnichenko LI, Perez-Peraza JA (2008) Astrophysical aspects in the studies of solar cosmic rays. Int J Mod Phys A 23:1–141. doi:10.1142/S0217751X08037312
Article ADS Google Scholar
Moore RL, Sterling AC, Hudson HS, Lemen JR (2001) Onset of the magnetic explosion in solar flares and coronal mass ejections. Astrophys J 552:833–848. doi:10.1086/320559
Article ADS Google Scholar
Moreton GF (1964) H$\alpha $ shock wave and winking filaments with the flare of 20 September 1963. Astron J 69:145. doi:10.1086/109375
Article Google Scholar
Musset S, Vilmer N, Bommier V (2015) Hard X-ray emitting energetic electrons and photospheric electric currents. Astron Astrophys 580:A106. doi:10.1051/0004-6361/201424378. arXiv:1506.02724
Article ADS Google Scholar
Nakariakov VM, Foullon C, Verwichte E, Young NP (2006) Quasi-periodic modulation of solar and stellar flaring emission by magnetohydrodynamic oscillations in a nearby loop. Astron Astrophys 452:343–346. doi:10.1051/0004-6361:20054608
Article ADS Google Scholar
Neupert WM (1968) Comparison of solar X-ray line emission with microwave emission during flares. Astrophys J Lett 153:L59. doi:10.1086/180220
Article ADS Google Scholar
Nindos A, White SM, Kundu MR, Gary DE (2000) Observations and models of a flaring loop. Astrophys J 533:1053–1062. doi:10.1086/308705
Article ADS Google Scholar
Nindos A, Aurass H, Klein KL, Trottet G (2008) Radio emission of flares and coronal mass ejections. Invited review. Solar Phys 253:3–41. doi:10.1007/s11207-008-9258-9
Article ADS Google Scholar
Nishio M, Yaji K, Kosugi T, Nakajima H, Sakurai T (1997) Magnetic field configuration in impulsive solar flares inferred from coaligned microwave/X-ray images. Astrophys J 489:976. doi:10.1086/304793
Article ADS Google Scholar
Øieroset M, Phan TD, Fujimoto M, Lin RP, Lepping RP (2001) In situ detection of collisionless reconnection in the Earth’s magnetotail. Nature 412:414–417. doi:10.1038/35086520
Article ADS Google Scholar
Paesold G, Benz AO, Klein KL, Vilmer N (2001) Spatial analysis of solar type III events associated with narrow band spikes at metric wavelengths. Astron Astrophys 371:333–342. doi:10.1051/0004-6361:20010358. arXiv:astro-ph/0103491
Article ADS Google Scholar
Parker EN (1988) Nanoflares and the solar X-ray corona. Astrophys J 330:474–479. doi:10.1086/166485
Article ADS Google Scholar
Parks GK, Winckler JR (1969) Sixteen-second periodic pulsations observed in the correlated microwave and energetic X-ray emission from a solar flare. Astrophys J Lett 155:L117. doi:10.1086/180315
Article ADS Google Scholar
Parnell CE, Jupp PE (2000) Statistical analysis of the energy distribution of nanoflares in the quiet sun. Astrophys J 529:554–569. doi:10.1086/308271
Article ADS Google Scholar
Peterson LE, Winckler JR (1959) Gamma-ray burst from a solar flare. J Geophys Res 64:697. doi:10.1029/JZ064i007p00697
Article ADS Google Scholar
Petrosian V, Donaghy TQ, McTiernan JM (2002) Loop top hard X-ray emission in solar flares: images and statistics. Astrophys J 569:459–473. doi:10.1086/339240. arXiv:astro-ph/0112363
Article ADS Google Scholar
Petrosian V, Yan H, Lazarian A (2006) Damping of magnetohydrodynamic turbulence in solar flares. Astrophys J 644:603–612. doi:10.1086/503378. arXiv:astro-ph/0508567
Article ADS Google Scholar
Pevtsov AA, Canfield RC, Zirin H (1996) Reconnection and helicity in a solar flare. Astrophys J 473:533. doi:10.1086/178164
Article ADS Google Scholar
Piana M, Massone AM, Kontar EP, Emslie AG, Brown JC, Schwartz RA (2003) Regularized electron flux spectra in the 2002 July 23 solar flare. Astrophys J Lett 595:L127–L130. doi:10.1086/378171
Article ADS Google Scholar
Pick M, van den Oord GHJ (1990) Observations of beam propagation. Solar Phys 130:83–99. doi:10.1007/BF00156781
Article ADS Google Scholar
Pick M, Vilmer N (2008) Sixty-five years of solar radioastronomy: flares, coronal mass ejections and Sun Earth connection. Astron Astrophys Rev 16:1–153. doi:10.1007/s00159-008-0013-x
Article ADS Google Scholar
Pick M, Malherbe JM, Kerdraon A, Maia DJF (2005) On the disk H$\alpha $ and radio observations of the 2003 October 28 flare and coronal mass ejection event. Astrophys J Lett 631:L97–L100. doi:10.1086/497137
Article ADS Google Scholar
Priest ER, Forbes T (2000) Magnetic reconnection: MHD theory and applications. Cambridge University Press, Cambridge
Book MATH Google Scholar
Radziszewski K, Rudawy P, Phillips KJH (2007) High time resolution observations of solar H$\alpha $ flares. I. Astron Astrophys 461:303–313. doi:10.1051/0004-6361:20053460
Article ADS Google Scholar
Ramaty R, Kozlovsky B (1974) Deuterium, tritium, and helium-3 production in solar flares. Astrophys J 193:729–740. doi:10.1086/153212
Article ADS Google Scholar
Ramaty R, Mandzhavidze N, Kozlovsky B, Murphy RJ (1995) Solar atmopheric abundances and energy content in flare accelerated ions from gamma-ray spectroscopy. Astrophys J Lett 455:L193. doi:10.1086/309841
Article ADS Google Scholar
Reeves KK, Warren HP, Forbes TG (2007) Theoretical predictions of X-ray and extreme-UV flare emissions using a loss-of-equilibrium model of solar eruptions. Astrophys J 668:1210–1220. doi:10.1086/521291
Article ADS Google Scholar
Régnier S, Canfield RC (2006) Evolution of magnetic fields and energetics of flares in active region 8210. Astron Astrophys 451:319–330. doi:10.1051/0004-6361:20054171
Article ADS Google Scholar
Roberts B, Edwin PM, Benz AO (1983) Fast pulsations in the solar corona. Nature 305:688–690. doi:10.1038/305688a0
Article ADS Google Scholar
Ryan JM, Lockwood JA, Debrunner H (2000) Solar energetic particles. Space Sci Rev 93:35–53
Article ADS Google Scholar
Saint-Hilaire P, Benz AO (2002) Energy budget and imaging spectroscopy of a compact flare. Solar Phys 210:287–306. doi:10.1023/A:1022478300679. arXiv:astro-ph/0210023
Article ADS Google Scholar
Saint-Hilaire P, Benz AO (2005) Thermal and non-thermal energies of solar flares. Astron Astrophys 435:743–752. doi:10.1051/0004-6361:20041918
Article ADS Google Scholar
Schlickeiser R, Miller JA (1998) Quasi-linear theory of cosmic-ray transport and acceleration: the role of oblique magnetohydrodynamic waves and transit-time damping. Astrophys J 492:352. doi:10.1086/305023
Article ADS Google Scholar
Schrijver CJ, Aschwanden MJ, Title AM (2002) Transverse oscillations in coronal loops observed with TRACE—I. An overview of events, movies, and a discussion of common properties and required conditions. Solar Phys 206:69–98. doi:10.1023/A:1014957715396
Article ADS Google Scholar
Schwenn R (2006) Space weather: the solar perspective. Living Rev Solar Phys 3:lrsp-2006-2. doi:10.12942/lrsp-2006-2. http://www.livingreviews.org/lrsp-2006-2
Shibata K (1999) Evidence of magnetic reconnection in solar flares and a unified model of flares. Astrophys Space Sci 264:129–144. doi:10.1007/978-94-011-4780-4_95
Article ADS MATH Google Scholar
Shibata K, Magara T (2011) Solar flares: magnetohydrodynamic processes. Living Rev Solar Phys 8:lrsp-2011-6. doi:10.12942/lrsp-2011-6. http://www.livingreviews.org/lrsp-2011-6
Shibata K, Masuda S, Shimojo M, Hara H, Yokoyama T, Tsuneta S, Kosugi T, Ogawara Y (1995) Hot-plasma ejections associated with compact-loop solar flares. Astrophys J 451:L83–L85. doi:10.1086/309688
Article ADS Google Scholar
Shih AY, Lin RP, Smith DM (2009) RHESSI observations of the proportional acceleration of relativistic $> 0.3$ MeV Electrons and $> 30$ MeV protons in solar flares. Astrophys J lett 698:L152–L157. doi:10.1088/0004-637X/698/2/L152
Article ADS Google Scholar
Shimizu T, Kondo K, Ugai M, Shibata K (2009) Magnetohydrodynamics study of three-dimensional fast magnetic reconnection for intermittent snake-like downflows in solar flares. Astrophys J 707:420–427. doi:10.1088/0004-637X/707/1/420
Article ADS Google Scholar
Silva AVR, White SM, Lin RP, de Pater I, Shibasaki K, Hudson HS, Kundu MR (1996) First images of a solar flare at millimeter wavelengths. Astrophys J Lett 458:L49. doi:10.1086/309918
Article ADS Google Scholar