Abstract
Solar flares are observed at all wavelengths from decameter radio waves to gamma-rays at 100 MeV. This review focuses on recent observations in EUV, soft and hard X-rays, white light, and radio waves. Space missions such as RHESSI, Yohkoh, TRACE, and SOHO have enlarged widely the observational base. They have revealed a number of surprises: Coronal sources appear before the hard X-ray emission in chromospheric footpoints, major flare acceleration sites appear to be independent of coronal mass ejections (CMEs), electrons, and ions may be accelerated at different sites, there are at least 3 different magnetic topologies, and basic characteristics vary from small to large flares. Recent progress also includes improved insights into the flare energy partition, on the location(s) of energy release, tests of energy release scenarios and particle acceleration. The interplay of observations with theory is important to deduce the geometry and to disentangle the various processes involved. There is increasing evidence supporting reconnection of magnetic field lines as the basic cause. While this process has become generally accepted as the trigger, it is still controversial how it converts a considerable fraction of the energy into non-thermal particles. Flare-like processes may be responsible for large-scale restructuring of the magnetic field in the corona as well as for its heating. Large flares influence interplanetary space and substantially affect the Earth’s lower ionosphere. While flare scenarios have slowly converged over the past decades, every new observation still reveals major unexpected results, demonstrating that solar flares, after 150 years since their discovery, remain a complex problem of astrophysics including major unsolved questions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Detection and definition
Since September 1, 1859, when R.C. Carrington and R. Hodgson observed the first flare in the continuum of white light, the localized, minute-long brightenings on the Sun have remained an enigma. Local flaring of the Sun has been reported at all wavelengths accessible from the ground and from space. Thus the word “flare” is used in solar physics today in a rather ill-defined way, describing a syndrome of apparently related processes at various wavelengths. The problem is even more acute in other languages, such as German and French, denoting flares with the equivalent to “eruption”, which may be confused with Coronal Mass Ejections (CMEs) that often happen simultaneously at the time of large flares. The general use of the term “flare” today often alludes to a “sudden release of magnetic energy by reconnection”. However, one has to bear in mind that such a definition represents a specific, although widely accepted, interpretation of observations. It may be used as a guide for novices to distinguish flares from other plasma physical phenomena in the solar atmosphere also associated with brightenings, such as the expulsion of magnetic flux or dissipation of shock waves. Nevertheless, it is better to define the flare phenomenon observationally as a brightening of any emission across the electromagnetic spectrum occurring at a time scale of minutes. Most manifestations seem to be secondary responses to the original energy release process, converting magnetic energy into particle energy, heat, waves, and motion.
1.2 Brief history of flare observations
A few years after Carrington and Hodgson, the Sun was studied extensively in the Hα line originating in the chromosphere, and the reports of flares became much more frequent, but also bewilderingly complex. Variations of source size, ejections of plasma blobs into interplanetary space, and blast waves (Moreton, 1964) were noted. Meter wave radio emissions, detected serendipitously in 1942 during military radar operations, revealed the presence of non-thermal electrons in the corona (Hey, 1983). During a radio burst, the total solar luminosity in radio waves may increase by several orders of magnitude. At about the same time, S.E. Forbush noticed ground-level cosmic ray enhancements associated with major solar flares. These discoveries could only mean that the flare phenomena is not confined to thermal plasma, but includes high-energy particles and involves the corona. In the late 1950s it became possible to observe the Sun in hard X-rays (≳ 10 keV) by balloons and rockets. Peterson and Winckler (1959) discovered the first hard X-ray emission during a flare in 1958. Later, the enhancements observed in centimeterFootnote 1 radio and hard X-ray emissions have led to the surprising suggestion that the radiating energetic particles may contain a sizeable fraction of the initial flare energy release (Brown, 1971). Hard X-rays are caused by the bremsstrahlung of colliding electrons. The photon distribution in energy exhibits a non-thermal shape, close to a power-law. Some of the broadband radio emissions from about 1 GHz to beyond 100 GHz result from the gyration of mildly relativistic electrons in the magnetic field (termed gyrosynchrotron emission). In 1972 the γ-ray line emission of heavy nuclei was discovered, excited by MeV protons (Chupp et al., 1973). Finally, millimeter, EUV, and soft X-ray (≲ 10 keV) emissions have shown that the flare energy heats the plasma of coronal loops to temperatures from 1.5 MK to beyond 30 MK. Within minutes, some active-region loops become brilliant soft X-ray emitters, outshining the rest of the corona. Such temperatures and the existence of non-thermal particles requiring low collision rates suggest that the flare is originally a coronal phenomenon. As a consequence, the discovery observations in the white light and later in Hα turned out to have stumbled upon secondary phenomena. This review will show that present observations get much closer to the heart of flares, but still miss the primary process. On the other hand, this review will also demonstrate that flares are not purely coronal. They couple to the chromosphere in a substantial way and must be understood as processes in which corona and chromosphere form an interactive system (as exemplified in Figure 1).
mpg-Movie (14976.1992188 KB) Still from a movie showing Soft X-rays (red), hard X-rays (blue) and gamma-rays (purple) observed by the RHESSI satellite are overlaid on an optical Hα image. The movie starts in white light zooming into an active region. The color then changes to the Hα line of hydrogen, emitted in the chromosphere. Its brightening indicates the start of the flare. Visualization by RHESSI scientists. (For video see appendix)
1.3 The phases of flares
The timing of the different emissions of the same flare is presented schematically in Figure 2. In the preflare phase the coronal plasma in the flare region slowly heats up and is visible in soft X-rays and EUV. A large number of energetic electrons (up to 1038) and ions (with similar total energy) is accelerated in the impulsive phase, when most of the energy is released. The appearance of hard X-ray footpoint sources at chromospheric altitude is a characteristic of this phase (Hoyng et al., 1981). Some high-energy particles are trapped and produce intensive emissions in the radio band. The thermal soft X-ray and Hα emissions finally reach their maxima after the impulsive phase, when energy is more gently released, manifest in decimetric pulsations, and further distributed. The rapid increase in Hα intensity and line width has been termed flash phase. It coincides largely with the impulsive phase, although Hα may peak later. In the decay phase, the coronal plasma returns nearly to its original state, except in the high corona (> 1.2 R⊙, where R⊙ is the photospheric radius), where magnetic reconfiguration, plasma ejections and shock waves continue to accelerate particles, causing meter wave radio bursts and interplanetary particle events. In Figure 3 the various phases can be recognized.
A schematic profile of the flare intensity at several wavelengths. The various phases indicated at the top vary greatly in duration. In a large event, the preflare phase typically lasts a few minutes, the impulsive phase 3 to 10 minutes, the flash phase 5 to 20 minutes, and the decay one to several hours (from Benz, 2002).
mpg-Movie (15763.2460938 KB) Still from a movie showing Flare observed in the Fe xii line at 195 Å (sensitive to 1.5 MK plasma) by the TRACE satellite. Note the different phases, starting with irregular brightnings in the impulsive phase. The luminosity peaks when a sheet-like structures appears above the initial brightening. The diffuse emission at this time is attributed to the presence of the Fe xxiv (192 Å) line within the TRACE passband, emitted by a plasma of 20 MK. The flare proceeds into a long decay phase with post-flare loops growing in height. (For video see appendix)
1.4 The big picture
The flare observations may be ordered in a scenario or a sequence of processes in which the flare energy is released in the corona by reconnecting magnetic fields. The process heats the plasma in the reconnection region to temperatures of tens of millions of degrees Kelvin (MK), but also efficiently accelerates electrons to super-thermal energies peaking below some 20 keV and extending sometimes to several tens of MeV. Reconnection most likely takes place also in the interior of the Sun and the lower solar atmosphere. The impulsiveness of the flare energy release is possibly caused by a sudden change in resistivity by high-frequency (collisionless) wave turbulence and is probably related to the capability of particle acceleration. Both require long collision times, i.e., low density. Not surprisingly, impulsive flare reconnection is generally assumed to take place in the corona, consistent with observations.
The energy then propagates from the corona into the dense chromosphere along a magnetic loop by thermal conduction or free-streaming non-thermal particles, depending on the flare and the flare phase. The chromospheric material is heated to tens of million degrees and expands into the corona. The upward motion fills up existing coronal loops, but the motion may continue in an expansion of these loops. In some cases, the flare may be only a minor part of a much larger destabilization of the corona, when the magnetic confinement of a considerable part of the corona is broken up. It expands and is expelled by magnetic forces in a coronal mass ejection (CME, Figure 4). The shock front associated with this motion is also a site of particle acceleration, particularly of high-energy solar cosmic rays observed near Earth or at ground level. Note that a CME is not simply the explosive result of a flare, but has its own magnetic driver. A CME is a different plasma physical process and may even lead to the conditions for reconnection, causing a flare.
mpg-Movie (1895.02832031 KB) Still from a movie showing Zoom into an active region where a large flare took place on April 21, 2002. The movie starts in white light observed by the SOHO/MDI instrument, adds the coronal images observed by the SOHO/LASCO coronagraph, then changes to extreme ultraviolet observed by SOHO/EIT and later by the TRACE satellite, and later the RHESSI observations of the flare in soft X-rays (red) and hard X-rays (blue). The focus then goes to the associated coronal mass ejection observed by the coronagraph. The movie ends in a storm of streaks produced by energetic flare particles (mostly protons), hitting the detectors on the Solar and Heliospheric Observatory (SOHO) in space. Visualization by RHESSI scientists. (For video see appendix)
1.5 Organization of review
In this review, recent observations by new instrumentation are summarized in view of the basic processes involved in the release of magnetic energy resulting in particle acceleration. The material is ordered along the big questions in flare physics:
-
Section 2: Flare signatures in the photosphere, chromosphere, and corona (Coupling atmospheric layers).
-
Section 3: Where is the flare energy released? (Flare geometry).
-
Section 4: Into what forms is the energy released? (Energy budget).
-
Section 5: Which emissions are direct signatures of energy release? (Signatures).
-
Section 6: How are particles accelerated? (Acceleration processes).
The literature reviewing flare observations spans more than a century. Substantial summaries of flares observations have been published among others recently by Murdin (2001) and Aschwanden (2002), in more specialized fields by Bastian et al. (1998) on radio emissions, Fletcher and Warren (2003) on ultraviolet emissions, Ryan et al. (2000) and Schwenn (2006) on flare effects and energetic flare particles in interplanetary space. Somov (1992), Tajima and Shibata (1997), and Priest and Forbes (2000) have reviewed theory. Older reviews, such as Sturrock (1980) and Švestka (1976) are still worth reading. The Astrophysics Data System lists more than 14,500 articles on the keyword “solar flare”. Any review, including this one, can only focus on a small fraction of the accumulated information. Comments and suggestions are welcome.
2 Energy Release in a Coupled Solar Atmosphere
2.1 Flares and photospheric field configuration
Flares can occur everywhere on the Sun, in active regions, penumbras, on the boundaries of the magnetic network of the quiet Sun, and even in the network interior (Krucker et al., 1997b; Benz and Krucker, 1998; Berghmans et al., 1998). Regular (large) flares, however, have preferred locations. They occur in large active regions showing a complex geometry of the 3D magnetic field as revealed in photospheric vector magnetograms (Régnier and Canfield, 2006, see Figure 5). Major flares occur in active regions that exhibit a δ configuration, defined as showing umbrae of opposite magnetic polarity. Flares of the largest size (X class) are associated with arcades of loops spanning a line of zero line-of-sight magnetic field on the surface. Hagyard et al. (1990) have shown that the magnetic field in flaring locations is strongly sheared (Figure 6). Magnetic shear alone, however, is not a sufficient condition. An additional requirement for large flares is the emergence of new magnetic flux from below (Choudhary et al., 1998). Vector magnetograms often show narrow channels of strong horizontal field components near the neutral line at the site of large flares (Zirin and Wang, 1993). Such fields may already be sheared when emerging and are still moving when they appear in the photosphere (Georgoulis and LaBonte, 2006).
mpg-Movie (118.463867188 KB) Still from a movie showing Left: White light image of a sunspot taken with SOT on board the Hinode satellite. The resolution is 2″. Visualization by Hinode scientists. Right: Vector magnetogram showing in red the direction of the magnetic field and its strength (length of the bar). The movie shows the evolution in the photospheric fields that has led to an X class flare in the lower part of the active region. Courtesy of NAOJ/NINS. (For video see appendix)
Map of the line-of-sight magnetic field strength measured in a photospheric line by the MSFC magnetograph. Solid curves denote positive field, dashed curves the negative field, and the dotted curve the neutral line. Circles indicate where the transverse field deviates between 70° and 80° from the potential field (perpendicular to the neutral line), and filled squares indicate deviations > 80°. A large flare (X3 class) occurred several hours later at the location of the largest shear (from Hagyard et al., 1990).
Large-scale shear in the magnetic field can also build up through the slow motion of foot points stretching the length of a loop. This evolution can progress through stable field configurations. Large-scale sheared fields in active regions store huge amounts of free magnetic energy. The emerging flux may then provide the trigger mechanism for impulsive energy release. The energy is unleashed above the photosphere, either in the chromosphere or corona (Moore et al., 2001). The build-up of the unstable configuration for large flares is often well observable in photospheric magnetic fields. The flare leaves, however, few if any observable traces in photospheric magnetograms. Wang et al. (2004) find an increase of the photospheric magnetic field strength during the flare, consistent with the scenario of magnetic flux emerging into the corona. A frequent flare site is the separatrix between different magnetic loop systems (Démoulin et al., 1997) forming a current sheet, or in a cusp-shaped coronal structure (Longcope, 2005). There is also evidence for flares being related to helical magnetic fields (Low, 1996; Pevtsov et al., 1996).
Photospheric observations clearly support the scenario that flare energy originates from free magnetic energy in excess of the potential value (defined by the photospheric boundary) or, equivalently, from electric currents in the corona. For a rapid release, the currents must be concentrated into small regions. Such currents may be inferred observationally in regions with a tangential discontinuity of the magnetic field direction in the system of rising loops near the base of the corona (Solanki et al., 2003).
The flare energy resides in the magnetic field that originated in the interior and is convected to the surface. Not much can be observed of the flare processes until the energy appears in the form of accelerated particles and extremely hot plasma. In the next section we switch from the origin and build-up to the first observable signature after the primary energy release.
2.2 Geometry of hard X-ray emissions
When an electron hits another particle in a Coulomb collision, it emits bremsstrahlung. In fully ionized plasma, this is the physical process also known as free-free radiation of thermal electrons. The change in direction and momentum causes a particle with some keV energy or greater to emit X-ray photons. Bremsstrahlung (X-ray emissions) of thermal and non-thermal electron populations are shown in Figure 7.
Typical X-ray spectrum of flare observed by the RHESSI satellite. The soft part is fitted with a thermal component (green) having a temperature of 16.7 MK, and the high-energy part with a power law having two breaks at 12 keV (possibly due to the acceleration process if real) and at 50 keV, of which the origin is unknown (Grigis and Benz, 2004).
The cross-section of a single electron for producing an X-ray photon of a certain energy is given by the quantum mechanical Bethe-Heitler formalism. The instantaneous emissivity of an electron beam propagating in a plasma is named thin target solution. It does not account for the resulting particle energy change to be considered in further collisions. If the target is deep enough, the incident particle slows down to thermal speed. The total radiation is therefore the integral in time over all emissions starting at the entry into the target until the particle energy is thermalized. If other deceleration processes than Coulomb collisions can be excluded, this is the thick target situation (Brown, 1971). The thick target photon spectrum of an electron beam is flatter (usually called harder) than any thin target it may transverse before, as it includes emission of the decelerating electrons. In an ideal situation including a power-law distribution of electron energies, the power-law index of thin target emission is smaller by 2 than the thick target spectrum.
The emission of hard X-rays with a non-thermal energy distribution was first located by Hoyng et al. (1981) at footpoints of coronal loops. Based on stereoscopic observations, Kane (1983) reported that 95% of the ≳ 150 keV X-ray emission in impulsive flares originates at altitudes ≲ 2500 km, that is at the level of the chromosphere. Brown et al. (1983) concluded that this upper limit in altitude satisfies the collisional thick-target model in which precipitating electrons loose their energy in the dense, cold target. The emission presumably originates from flare-accelerated electrons precipitating into the chromosphere. They follow the field line until they reach a density high enough for collisions and emit bremsstrahlung by scattering and slowing down. Footpoint sources are also occasionally found on Hα flare ribbons some 30,000 km apart, tracing the base of a magnetic arcade (Masuda et al., 2001). The connecting loop are observed in thermal soft X-ray emission, indicating that the density has greatly increased. Densities of more than 1011 cm−3 are frequently reported (e.g., Tsuneta et al., 1997) and agree with the concept of chromospheric evaporation. Up-streaming plasma, presumably heated by precipitating particles and filling up a coronal loop, has been observed in blue shifted lines (Antonucci et al., 1982; Mariska et al., 1993).
Flare footpoints are usually observed to move, indicating propagation of the energy release site (Krucker et al., 2003). Reconnection in a cusp above the flare ribbons predicts that footpoints move apart. Contrary to expectation, parallel motion along the flare arcade has also been reported by Grigis and Benz (2005a) and Bogachev et al. (2005) (see movie in Figure 8). Stochastic jumps in the time evolution are frequent (Fletcher et al., 2004; Krucker et al., 2005a). These hard X-ray observations suggests that most of the flare energy at a given site is released in an initial burst. The separation of the footpoints perpendicular to the flare ribbon, well observed in Hα, appears to be the result of a more gentle energy release in a later flare phase (Švestka, 1976; Martin, 1989).
mpg-Movie (1895.02832031 KB) Still from a movie showing Hard X-ray footpoints (with error bars) observed with the RHESSI satellite during the flare of November 9, 2002. Simultaneous footpoints are connected by a line colored sequentially with time. The footpoint information is overlaid on a SOHO/EIT image at 195 Å, indicating enhanced density in the corona. The movie shows two simultaneous footpoints connected by a vertical half-circle. The flux at each footpoint is indicated by the size of the purple circle at logarithmic scale (from Grigis and Benz, 2005a), courtesy of Paolo Grigis. (For video see appendix)
Hard X-rays have been noted to correlate with Hα kernels (Vorpahl, 1972; Wuelser and Marti, 1989), indicating that the flare energy reaches the dense part of the chromosphere within less than 10 seconds. Hard X-ray footpoints coincide spatially with Hα kernels (Radziszewski et al., 2007, see Figure 9).
mpg-Movie (9783.75390625 KB) Still from a movie showing Left: RHESSI flare observations of soft X-rays (red, 8–12 keV) and hard X-rays (blue, 20–50 keV) overlaid on an Hα background. Note the high-energy footpoints moving on the Hα flare ribbons, which moves apart in the very late phase. Visualization by RHESSI scientists. (For video see appendix)
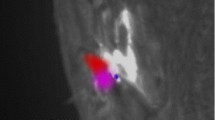
Hard X-ray footpoints and soft X-ray flare loops are consistent with the standard flare scenario of energy release in the corona, energy transport to the chromosphere and chromospheric evaporation, but where is the energy released? First hints came from a third hard X-ray source above the soft X-ray loop (Masuda et al., 1994). The coronal X-ray emission contains a thermal part, dominating a low energies, and a weak non-thermal part above about 8–10 keV. The non-thermal emission in the corona is usually soft (Mariska and McTiernan, 1999; Petrosian et al., 2002), consistent with the idea of a thin target (Datlowe and Lin, 1973). Thus, the accelerated electrons lose only a small fraction of their energy and continue to propagate towards the chromosphere. In the chromosphere they meet a thick target, yielding a harder spectrum (Brown, 1971; Hudson, 1972). An example showing two footpoints and a coronal source is shown in Figure 10. In exceptional cases, only the fastest electrons reach the chromosphere (Veronig and Brown, 2004). The coronal source often appears before the main flare hard X-ray increase, but is well correlated in time and spectrum with the footpoints (Emslie et al., 2003). These observations suggest strong coupling between corona and chromosphere during flares.
Image of a solar flare in hard X-rays observed by the RHESSI satellite. The curved line indicates the limb of the photosphere. The displayed energy range 12–50 keV is dominated by the low energies, where the coronal source (right) prevails. Two footpoints (left) are clearly visible on the disk. The spider like structures are mostly artifacts of image reconstruction (from Battaglia and Benz, 2007).
The altitude of coronal hard X-ray sources, some 6000–25,000 km, is compatible with observed time delays of hard X-ray peaks emitted at the footpoints (Aschwanden et al., 1995). Low energy photons are emitted later compared to higher energy photons. Delay-time observations scale with the observed lengths of the soft X-ray loop (Aschwanden et al., 1996), consistent with the interpretation of longer propagation times of lower energy electrons. If only time-of-flight effects are assumed, the propagation path would put the acceleration above the loop-top hard X-ray source. The assumption of simultaneous injection puts strong constraints on the timescales involved on the acceleration process (Brown et al., 1998).
The difference in the spectrum of coronal source and footpoints can be taken as a test for the geometry. Measurements by Petrosian et al. (2002) show that the power-law indices differ by about 1 on the average, contrary to expectations. A possible interpretation for a value less than 2 may be a mixture of thick and thin target emissions, overlapping in the observed resolution element. On the other hand, an analysis based on RHESSI data demonstrates the existence of index differences larger than two in 3 out of 9 events (Battaglia and Benz, 2007). This discrepancy requires a more complete physical scenario than ballistic particle motion and will be discussed in the following section.
2.3 Return current
It is unlikely that the fluxes of high-energy electrons and ions precipitating to the chromosphere balance out. Thus a beam current results. In a conducting plasma, a beam current cannot induce appreciable magnetic fields, and in static state the electric charge cannot separate along the field line. Thus a return current builds up to conserve charge and current neutrality (Spicer and Sudan, 1984; van den Oord, 1990; Benz, 2002). The current is most likely driven by a dominant electron flux in the precipitating particles. Thus the return current direction is downward in the loop. It is composed mostly of thermal electrons moving freely upward along field lines.
As the return current consist of thermal particles, collisions play a much bigger role than for the beam particles (see Equation 8). Collisions cause electric resistance. Ohm’s law then requires an electric field in downward direction, slowing down the beam electrons. The return current and its associated electric field are inevitable consequences of the standard flare model.
Some observational features have been interpreted as the effect of an upward pointing electric field. Figure 11 displays spectra of the two footpoints observed in hard X-rays. They do not show a trace of thermal emission in the RHESSI range of energies. Their non-thermal power-law indices are identically 2.7±0.1. The power-law of the coronal non-thermal emission (Figure 11, right) is 5.6±0.1. The difference larger than 2 can be interpreted as an effect of the return current’s electric field flattening the spectra of the footpoints. The return current may also leave an observational signature in the shape of the non-thermal X-ray spectrum in the form of a kink (Zharkova et al., 1995).
Spectra of the three sources shown in Figure 10 as observed by RHESSI at peak time. Left and middle: Spectra of footpoints. A power-law was fitted in energy between the dotted lines. Right: Spectrum of the coronal source. A power-law and a thermal population was fit between the dashed lines (from Battaglia and Benz, 2007).
Return currents solves what has been referred to as the flare particle number problem: as the number of precipitating electrons inferred from hard X-rays is very large, the coronal acceleration region would soon be evacuated if not replenished. If only electrons escape from the acceleration region, the return current keeps its density constant. If also ions escape, the acceleration region is evacuated. This may be avoided by a pressure driven flow of neutral plasma. None of the observational signatures, however, for both neutral flow and return current are fully established, and their existence still needs corroboration.
2.4 Neupert effect
Neupert (1968) noted that in the rise phase of the soft X-rays their flux corresponds to the time integral of the centimeter radio flux since the start of the flare. As the centimeter flare emission is emitted by relativistic electrons, it is not surprising that the same correlation was later also found between the soft X-ray flux and the cumulative time integral of the hard X-ray flux, i.e.,
or, equivalently,
This empirical relationship is called the “Neupert effect”. An example is presented in Figure 12. Already Neupert (1968) suggested that there may be a direct causal relation between the energetic electrons and the thermal plasma: the soft X-rays may originate chiefly from a plasma heated by the accumulated energy deposited through flare accelerated electrons. It should be remarked here that Equation 1 is only an approximation and that the correspondence with theory works only if cooling (by conduction or radiation) is negligible.
The derivation of the soft X-ray flux (observation by the GOES satellite) correlates in 80% of the flares with the hard X-ray flux (observation of the RHESSI satellite). This is an example of what is called the Neupert effect (from Dennis and Zarro, 1993).
2.5 Standard flare model
The assumption of a strict causal relation between soft X-ray emission and hard X-ray signatures of energetic electrons has lead to a simple scenario. It postulates that flare energy release consists of accelerating particles. The acceleration process is not part of the model. Energetic particles then precipitate to the chromosphere, where they heat the plasma to the high temperatures observed in soft X-rays. The hot plasma expands along the loop into the corona, a process termed “evaporation”. This simple scenario can explain several phenomena observed in flares:
-
Correlation of soft X-ray flux with cumulative hard X-ray flux (Neupert effect)
-
Hard X-rays (> 25 keV) often originate from sources at the footpoints of the loop emitting soft X-rays.
-
The coronal hard X-ray source, where reconnection releases energy, is occasionally observed to be above the soft X-ray loop, into which energy was release before and which is still emitting soft X-rays (Masuda et al., 1994).
-
The energy in accelerated electrons tends to be larger than the thermal energy contained in the soft X-ray source (see discussion in Section 4).
-
The hard X-ray spectrum of non-thermal electrons in the coronal source is considerably softer than in the footpoints, suggesting that the latter is a thick target. In thick targets the particles lose all their kinetic energy, and their bremsstrahlung emission is the result of all collisions until they come to full stop.
-
The emission measure of the soft X-ray source greatly increases during the impulsive phase, indicating that chromospheric material is evaporating during this period. Evaporation has been observed directly, first in blue-shifted lines of hot material, later also in soft X-ray images (see following section).
Henceforth we refer to this scenario as the standard model (Figure 13).
2.6 Evaporation of chromospheric material
When energetic electrons (and possibly ions) precipitate from the coronal acceleration site and lose their energy in the dense underlying chromosphere via Coulomb collisions, the plasma responds dynamically. Note that the same may result also from heat conduction, when thermal particles transport the energy released in the corona. The temperature in the chromosphere increases and the resulting pressure exceeds the ambient chromospheric pressure. If the overpressure builds up sufficiently fast, the heated plasma expands along the magnetic field in both directions. The expansion of this plasma into the corona was first reported by Doschek et al. (1980) and Feldman et al. (1980). It was thoroughly studied in blue-shifted lines of Ca xix by Antonucci et al. (1982), who found plasma at a temperature of 20 MK, moving with 300 to 400 km s−1 and filling up the loop (Figure 14). A summary can be found in Antonucci (1989). More recent observations from SOHO/CDS suggest an upflow velocity of 230 km s−1 (Milligan et al., 2006).
Averaged density profile along a loop inferred from the separation of X-ray footpoints, moving up the flare loop in a very dense flare. Note the increase in density between the first profile (dashed) and last profile (dotted). The loop fills up in between from the bottom (solid curve) (from Liu et al., 2006).
The evaporated hot plasma appears to be the source of most of the soft X-ray emission (Silva et al., 1997). Thus, the soft X-ray emitting plasma accumulates a significant fraction of the energy in the precipitating non-thermal electrons. Consequentially, the soft X-ray emission is proportional to the integrated preceding hard X-ray flux. As already noted by Neupert (1968), this may explain the effect named after him. Note that the scenario assumes that the observed soft X-ray plasma is not heated by the primary flare energy release, but is a secondary product when flare energy is transported to the chromosphere. This is an important point to remember in theories assuming that the coronal plasma is heated by flares.
The evaporation scenario predicts a linear relation between instantaneous energy deposition rate by the electron beam and time derivative of the cumulative energy in the thermal plasma, thus a linear relation between hard X-ray flux and derivative of the soft X-ray flux (Figure 12). This is not always the case (Dennis and Zarro, 1993). There are several reasons for this: (i) the spectral index of the hard X-rays changes with time in most flares (Section 5.2), (ii) the flare energy may be preferentially transported by heat conduction (particularly in the pre-flare phase), and (iii) ions may contribute to the energy deposition. Some flares, however, fit extremely well and a time lag in the flare thermal energy of only 3 seconds relative to the energy input as observed in hard X-rays has been reported by Liu et al. (2006).
Evaporation is the result of coupling between corona and chromosphere. Such coupling is expected from the fact that the transition region separating the two layers in the solar atmosphere is relatively small compared to the mean free path length in the corona. The chromosphere is only a few collisions away from the corona even for thermal particles. There must be a constant heat flow through the transition region. In the impulsive phase of a flare, non-thermal particles may well dominate the energy transfer.
The expansion of the heated chromospheric plasma is driven by pressure gradients. Thus “evaporation” is a misnomer, as the phenomenon is no phase transition nor the escape of the fastest particles, but is an MHD process and more like an explosion. Wuelser et al. (1994) report downflowing material in Hα at the location of the flare loop footpoints, suggesting a motion opposite to evaporation in the low chromosphere. The upflowing hot plasma and the downflowing chromospheric plasma have equal momenta, as required by the conservation of momentum in a ballistic explosion. Evaporation due to a flare may thus be understood as a sudden heating in the chromosphere, followed by an expansion that is initially supersonic.
Brosius and Phillips (2004) presented evidence of much more gentle kind of evaporation during the preflare phase of a flare. The maximum velocity in Ca xix was found to be only 65 km s−1. Such gentle evaporation below the coronal sound speed is interpreted by a non-thermal electron flux below 3 × 1010 erg cm−2s−1 (Milligan et al., 2006). Zarro and Lemen (1988) found signatures of gentle evaporation in the post flare phase, and Singh et al. (2005) reported signatures of evaporation also in a non-flaring state of a loop, suggesting thermal conduction of a hot coronal loop as the driver. These observations confirm that the evaporative response of the chromosphere depends sensitively on the flux of incident electrons. Fisher and Hawley (1990) have studied evaporation due to thermal energy input into the corona. Evaporation resulting from non-thermal particle precipitation has been simulated by several groups (Sterling et al., 1993; Hori et al., 1998; Reeves et al., 2007). In general, the results of these simulations agree with observed flare emissions quite well, indicating that the standard model of solar flares is energetically consistent with observations.
2.7 Deviations from standard flare model
A variant of the standard model has been proposed for flares without footpoints (Veronig et al., 2002; Veronig and Brown, 2004). The flare loop has been found so dense that accelerated electrons have collisions already in the corona and lose a large fraction of their energy to the flare loop (Figure 15). A preceding flare at the same location may have produced the high density of the loop (Strong et al., 1984; Bone et al., 2007).
RHESSI observations at 6–12 keV (red) and 25–50 keV (blue) of a coronal flare. The high-energy photons have a non-thermal origin and originate near the loop-top without pronounced footpoints (Veronig and Brown, 2004).
There are other indications, that the standard model is not sufficient. In about half of the hard X-ray events, the Neupert behavior is violated in terms of relative timing between soft and hard X-ray emissions (Dennis and Zarro, 1993; McTiernan et al., 1999; Veronig et al., 2002). This is particularly obvious in flares with soft X-rays preceding the hard X-ray emission. Such preheating is well known and cannot be explained by lacking hard X-ray sensitivity (e.g., Benz et al., 1983; Jiang et al., 2006). Also it has been noted by several authors that the plasma in the coronal source at the top is generally hotter than at the footpoints of the loop.
An alternative interpretation to the standard model is that the soft X-ray emitting plasma is not heated exclusively by high-energy electrons, (e.g., Acton et al., 1992; Dennis and Zarro, 1993). A likely amendment to the standard model is that some coronal particles get so little energy during flare energy release that they have frequent enough collisions to approximately retain their Maxwellian velocity distribution. Thus their energization corresponds to heating. In a preflare, the heat of the coronal source may reach the chromosphere by thermal conduction. Depending on the rate of the energy release, other particles may gain so much energy that collisions become infrequent (Equation 8). These particles then are accelerated further, get a non-thermal velocity distribution, and may eventually leave the energy release region.
3 Flare Geometry
3.1 Geometry of the coronal magnetic field
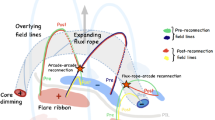
While there is nearly unanimous agreement that sheared or anti-parallel magnetic fields provide the flare energy released in an impulsive reconnection, the geometry of these magnetic fields in the corona at large scale is not clear. The prevalent view is depicted in Figures 13 and 16 (left), as well as illustrated by a coronagraph image in Figure 16 (right). The scenario has evolved over the past four decades and is generally credited to Carmichael (1964), Sturrock (1966), Hirayama (1974), and Kopp and Pneuman (1976). So it also named CSHKP model after these scientists. It is basically a two-dimensional geometry, involving a magnetic loop that is pinched at its legs. The loop may be extremely large or moving outward, so that its legs consist of oppositely directed (anti-parallel) fields. As a result of reconnection, the top of the loop is ejected as a plasmoid. The best evidence for this geometry are vertical cusp-shaped structures seen in soft X-rays after the flare (Tsuneta et al., 1997; Shibata, 1999; Sui et al., 2006). The cusp grows with time, and higher loops have a higher temperature (Hori et al., 1997), as predicted by continuous reconnection. The observational evidence also includes horizontal inflows of cold material from the side and two sources of hot plasma that move away from the X-point upward and downward. The observations of the former has been reported for a single event by Yokoyama et al. (2001) and Chen et al. (2004). Hot sources being ejected are more frequently observed in soft X-ray (Shibata et al., 1995). They have been noticed to be associated with drifting pulsating structures in decimetric radio emission (Khan et al., 2002) indicating the presence of non-thermal electrons. The reported association with hard X-rays and centimeter radio emission (caused by the synchrotron emission of mildly relativistic electrons) suggests that the plasmoids also include highly energetic particles (Hudson et al., 2001). There is also occasional evidence for the downward reconnection jet in addition to the observed upward motion of the soft X-ray source (Sui et al., 2004). Finally, the existence of two ribbons marking the footpoints of an arcade of loops in Hα, EUV, and X-ray emissions (Figure 8) is long-standing evidence for the one-loop model, stretched into a third dimension.
In another also widely proposed geometry, two non-parallel loops meet and reconnect. There are several versions of the cause of interaction. Merging magnetic dipoles (Sweet, 1958), collision of an newly emerging loop with a pre-existing loop, proposed by Heyvaerts et al. (1977), or the breakthrough of the emerging loop through the corona (Antiochos, 1998). In this scenario the geometry is closed, i.e., no magnetic field line leads from the energy release site to interplanetary space. Ejecta leaving the Sun are still possible, but not a necessary ingredient of the model. Thus the two-loop model is often proposed for non-eruptive “compact flares”. The model predicts the existence of 4 footpoints. The number of footpoints in hard X-rays rarely exceeds two. However, radio observations have been presented that complement the number of X-ray footpoints, resulting in the frequent detection of three or more footpoints (Kundu, 1984; Hanaoka, 1996, 1997). Nishio et al. (1997) find that the two loop considerably differ in size and that the smaller loop preferentially emits X-rays. There is also evidence from recent pre-flare EUV observations for multiple-loop interactions (Sui et al., 2006).
One-loop flare models predict the presence of plasmoids in interplanetary space, consisting of hot plasma interwoven with a closed magnetic field (i.e., magnetic field lines that close within the structure). Such plasmoids are characterized by the lack of electron heat flux because their field lines are disconnected from the Sun and have indeed been reported (Gosling et al., 1995). More frequently observed are counterstreaming hot electrons, indicating that the field line is closed, i.e., still connected to the Sun on both sides (Crooker et al., 2004). According to these authors, such features in the electron distribution are frequently observed in magnetic clouds associated with CMEs. Nevertheless, they are not associated with the great number of smaller flares.
Furthermore, there is a well-known association of nearly every large flare with type III radio bursts at meter wavelengths, produced by electron beams escaping from the Sun on open field lines connected to interplanetary space. Benz et al. (2005) report that 33% of all RHESSI hard X-ray flares larger than C5 in GOES class are associated with such bursts. This suggests that in a third of all flares at least one of the four ends of reconnecting field lines is open. As type III bursts represent only a small fraction of the flare energy this may not hold for the major flare energy release site. We note, furthermore, that type III bursts very often occur also in the absence of reported X-ray flares (Kane et al., 1974). The energy release by open and a closed field lines, termed interchange reconnection, has been proposed some time ago (Heyvaerts et al., 1977; Fisk et al., 1999) and applied more recently to in situ observations in a CME (Crooker and Webb, 2006).
In conclusion, there is good evidence for both the one-loop and two-loop scenarios for the geometry of the coronal magnetic field in solar flares. There is no reason to assume that they exclude each other. The combination of both in the same flare, hybrids of a closed loop reconnecting with an open loop, and other scenarios are also conceivable. Thus we do not state a standard geometry for the preflare coronal magnetic field configuration. The magnetic topologies of one loop, interchange and two loop are generally classified as dipolar, tripolar, and quadrupolar, respectively. In addition, 2D and 3D versions can be distinguished (Aschwanden, 2002), and various nullpoint geometries have been proposed (Priest and Forbes, 2000).
3.2 Coronal hard X-ray sources
In the standard flare scenario, where the flare energy is released in the corona and non-thermal particles are accelerated in the corona, coronal X-ray emission showing a power-law photon energy distribution must attract special attention. It is generally assumed that its emission is near or in the acceleration region. This section thus concentrates on flare related X-ray emissions from well above the chromospheric footpoints.
The ordinary corona has a density that is not suggestive of hard X-ray emission. However, such radiation was discovered as soon as it became technically feasible. Frost and Dennis (1971) reported an extremely energetic event from active region behind the limb. Its origin must have been at an altitude of about 45,000 km above the photosphere. The presence of non-thermal electrons in coronal sources has been inferred by the first observers based on the high energy of the detected photons, exceeding 200 keV. Coronal hard X-ray observations have been studied essentially event-by-event beyond the limb (e.g., Kane, 1983) until it became possible to image hard X-rays thanks to the RHESSI satellite (Lin et al., 2002). Krucker et al. (2007) have reviewed the RHESSI results concerning the coronal X-ray sources of flares.
Occasional emission of bremsstrahlung photons by non-thermal electrons in the corona may not be surprising, the observed intensity is. It is so high because of a high density of the background plasma. Estimates of the loop-top density from soft X-rays and EUV lines are typically around 1010 and can reach up to a few times 1012 cm−3 (Tsuneta et al., 1997; Feldman et al., 1994; Veronig and Brown, 2004; Liu et al., 2006; Battaglia and Benz, 2006). The reported temperatures are several ten millions of degree (Lin et al., 1981). The pressure balance of such structures is enigmatic. What is the origin of this thermal loop-top source?
Thermal loop-top sources have first been interpreted in terms of chromospheric evaporation. Thus one may expect them to follow the Neupert behavior where the soft X-rays are proportional to the hard X-ray flux integrated over prehistory. It is then incomprehensible that thermal coronal sources appear before the start of the hard X-ray emission. In fact, the most prominent feature in the preflare phase is the early appearance of a thermal source at the loop-top. The material content (emission measure) in these sources greatly exceeds the normal value in the active region corona. Thus is must have evaporated from the chromosphere. One may speculate that in this early phase the flare energy is not transported by energetic particles, but more gently conducted by thermal particles.
A characteristic of the thermal source is the temperature distribution with loop height. The highest looptops sometimes show Fe xxi emission, suggesting a temperature of 20 MK, while at the same time lower laying loops show emission in the Fe xi and Fe xii lines characteristic for temperatures between 1–3 MK (Warren et al., 1999). The thermal emission must not be confused with the thermal X-ray emission from giant arches observed in the post-flare phase (Švestka, 1984).
Masuda et al. (1994) have reported hard X-ray emission from above the thermal X-ray loop. Historically, this has raised great interest as it seemed to confirm the scenario of reconnection in a current sheet in a vertical cusp-shaped structure above the soft X-ray loops. However, this seems to be rather exceptional. In more recent studies, the large majority of non-thermal sources are cospatial with the thermal source (Battaglia and Benz, 2007). Stereoscopic observations by two spacecraft (Kane, 1983) and recent RHESSI observations find that the non-thermal emission from the corona and the footpoints correlated in time. Even the soft-hard-soft behavior (Section 5.2) has been detected in the coronal source (Battaglia and Benz, 2007). The coronal hard X-ray emission is not always stationary. Upward motions have been reported with velocities of about 1000 km s−1 following the direction of a preceding CME (Hudson et al., 2001).
The coronal source has been observed to emit hard X-rays even in the pre-flare phase before footpoints appear. Even more astonishingly, non-thermal emission at centimeter wavelengths, suggesting the presence of relativistic electrons, has been reported in such sources (Asai et al., 2006).
3.3 Intermediate thin-thick target coronal sources
The observation of Masuda et al. (1994) suggests a model that consists of four basic elements: a particle accelerator above the top of a magnetic loop (consistently imagined at the peak of a cusp), a coronal source visible in SXR and HXR, collision-less propagation of particles along the magnetic loop and HXR-footpoints in the chromosphere. Wheatland and Melrose (1995) developed a simple model that has been used and investigated further (e.g., Metcalf and Alexander, 1999; Fletcher and Martens, 1998). The thermal coronal source acts as an intermediate thin-thick target on electrons depending on energy (thick target for lower energetic electrons, thin target on higher energies). This model is known as intermediate thin-thick target, or ITTT model. The ITTT model features a dense coronal source into which a beam of electrons with a power-law energy distribution is injected. Some high-energy electrons then leave the dense region and precipitate down to the chromosphere. The coronal region acts as a thick target on particles with energy lower than a critical energy Ec and as thin target on electrons with energy > Ec. This results in a characteristic hard X-ray spectrum showing a broken power-law as well as soft X-ray emission due to collisional heating of the coronal region. The altered electron beam reaches the chromosphere, causing thick target emission in the footpoints of the magnetic loop. Battaglia and Benz (2007) have tested the ITTT model in a series of flares using RHESSI data. The results indicate that such a simple model cannot account for all of the observed relations between the non-thermal spectra of coronal and footpoint sources. Including non-collisional energy loss of the electrons in the flare loop due to an electric field can solve most of the inconsistencies.
The simple ITTT model shows that the standard flare geometry is consistent with current observations. The remaining inconsistencies concern the coronal source. Its non-thermal component was found less bright than the footpoints would predict according the ITTT model (Battaglia and Benz, 2008). A possible remedy is acceleration within the thermal coronal source. Jiang et al. (2006) argue that thermal conductivity in the coronal source is reduced by wave turbulence to interpret the soft X-ray emission. Turbulence would also scatter non-thermal particles or even accelerate them.
It is proper to conclude that the coronal X-ray source is not understood.
3.4 Location of particle acceleration
Accelerated particles precipitate from the acceleration site or are temporarily trapped. On their way spiraling along the magnetic field, they radiate various radio emissions at frequencies depending on the local plasma. As the corona is transparent to radio emission above the plasma frequency, the accelerated particles outline the geometry of the environment of acceleration and/or the actual site of acceleration.
Gyrosynchrotron radiation is emitted incoherently by relativistic electrons over the whole loop (review by Bastian et al., 1998, Figure 17). The spectrum at high frequencies is close to a power-law, shaped by the initial power-law energy distribution of accelerated electrons. The loop-top radio spectrum falls off far more steeply at high frequencies than does the footpoint spectrum. Thus the centimeter radio emission confirms the differences between loop-top and footpoints found in X-ray sources. In addition to gyrosynchrotron emission, Wang et al. (1994); Silva et al. (1996) report thermal loop-top emission at a temperature of about 30 MK, in rough agreement with the hot thermal component of the coronal soft X-ray source.
mpg-Movie (264.590820312 KB) Still from a movie showing Thermal emission and a flare observed with the Nobeyama interferometer at 17 GHz. The event has the classic signatures of an event associated with a coronal mass ejection: motion is seen first in the prominence material, then the flare goes off, leaving long-duration soft-X-ray emitting loops around for several hours. Note that the prominence material is at a temperature of less than 10,000 degrees K (shown at top), whereas the flare loops come from material at 10 MK: both cool and hot material show up at this radio frequency. The left panel shows total intensity, and the right panel shows circularly-polarized radio emission. Polarization is only detected during the early phase of the flare, when very energetic electrons fill up the loop and emit intense synchrotron radiation. Courtesy of Stephen White. (For video see appendix)
The most intense flare radio emission at meter and decimeter wavelengths originates not from single particles, but from waves in the plasma, i.e., from coherent radiation processes. Fast drift radio bursts, or type III bursts, were among the first types of meter wave emissions discovered in the 1940s. The drift of the radiation to lower frequencies with time was interpreted by Wild (1950) as the signature of an electron beam propagating upward through the corona at a speed of 0.2–0.6 c. Later, occasional reverse-drift bursts were discovered (downward-directed beams). Summaries of the type III observations can be found in Krüger (1979), Suzuki and Dulk (1985), and Pick and van den Oord (1990). Imaging observations have shown that the type III sources are often not single, but emerge simultaneously into different directions. Paesold et al. (2001) found double type III sources to diverge from a common source of narrowband spikes around 300 MHz (see Figure 18). Figure 19 shows a three-dimensional reconstruction assuming an exponential (constant temperature) model for the density. The spikes observed to be close to the point of divergence suggest the location of the acceleration at an altitude around 90,000 km. Krucker et al. (1995, 1997a) located spike sources at about 5 × 105 km altitude. Klein et al. (1997) found evidence for acceleration of type III electron beams at the height of one solar radius.
Spectrogram of type III radio bursts (drifting structures in the upper right) and meter wave type of narrowband spikes (center) (from Benz et al., 1996).
Reconstructed trajectories of two radio events involving type III bursts and spikes, both of the kind often observed at meter wavelength. Upper right: Positions with error bars observed by the Nancay Radio Heliograph at three frequencies. The symbols represent the observed frequencies: × for 327.0 MHz, ■ for 236.6 MHz, and △ for 164.0 MHz. Bottom left: Position of the radio emissions on the Sun. The small square indicates the size of the image presented in the upper right image. Upper left: Projection of the sources on the meridian plane (as seen by an observer West of the source as seen from Earth). Lower right: The radio sources projected on the equatorial plane, showing the view of an observer North of the Sun). In both graphs the trajectories have been 3-dimensionally spline interpolated to outline the trajectory (Paesold et al., 2001).
Metric spikes have been found to be associated in some cases with impulsive electron events in the interplanetary medium (Benz et al., 2001). The low energy cut-off of the interplanetary electron distribution defines an upper limit of the density in the acceleration region (Lin et al., 1996). The derived electron density is of the order of 3 × 108 cm−3, consistent with the density in the source of metric spikes, assuming second harmonic plasma emission. The difference between acceleration height in hard X-rays, particle events and coherent radio waves suggests different acceleration processes.
3.5 Energetic ions
Gamma-ray lines between 0.8 and 20 MeV are emitted atomic nuclei excited by impinging ions. The neutron-capture line at 2.223 MeV (forming deuterium) is usually the strongest of the many lines (Figure 20). Protons and other nuclei accelerated from about 10 MeV to ≳ 100 MeV per nucleon collide with the nuclei in the dense chromosphere and produce neutrons. Neutrons thermalize and, after traveling less than 1000 km, are captured by an ambient proton to form deuterium (Ramaty and Kozlovsky, 1974; Hua and Lingenfelter, 1987). Thus images in the 2.223 MeV line indicate the site of high-energy ion precipitation. Comparison of imaged and spatially integrated fluences observed by the RHESSI satellite show that in all cases most of the emission was confined to compact sources within the active region (Hurford et al., 2006). In some events double footpoints were observed. Thus the flare associated gamma-rays are produced by ions accelerated in the flare process and not by a large-scale shock driven by a coronal mass ejection.
RHESSI gamma-ray spectrum from 0.3 to 10 MeV integrated over the duration of the flare of July 23, 2002. The lines show the different components of the model used to fit the spectrum (Lin et al., 2003).
Surprisingly, RHESSI found that the footpoints of the 2.223 MeV line — indicating ion precipitation — and the footpoints of the non-thermal continuum emission — produced by precipitating electrons — do not coincide (Figure 21). The discrepancy demonstrates that protons and electrons are accelerated differently, or originate, as proposed by Emslie et al. (2004b), in large and small loops, respectively.
Location of the gamma-ray sources observed by the RHESSI satellite on October 28, 2003. The contours at 50%, 70%, and 90% of the peak value show in blue the deuterium recombination line at 2.223 MeV and red the electron bremsstrahlung at 200–300 keV. The centroid positions of the bremsstrahlung emission at different times are indicated by plus signs. The FWHM angular resolution is 35″, given at bottom left. The RHESSI data are overlaid on the negative of a TRACE 195 ∫ image dominated by the emission of Fe xii (Hurford et al., 2006).
3.6 Thermal flare
Most of the flare energy is thermalized in the solar atmosphere, some of which is heated to high temperatures. This part is visible in soft X-rays (Figure 22). In the absence of further energy release the plasma cools by thermal conduction to the chromosphere and by radiating X-rays. At high temperature and low density, conductive cooling dominates, radiative cooling in the opposite case (Cargill et al., 1995). If conductive cooling leads to evaporation of chromospheric material, the cooling time becomes longer as the energy remains in the loop.
Overlays of RHESSI hard X-ray (orange) and white light difference (thick blue) image contours on a white-light image observed by the TRACE satellite. The thin white contours show white light contours as observed by MDI on SOHO; the accuracy of the pointing can be assessed by comparing the white light background observed by MDI and TRACE (Fletcher et al., 2007).
Flare loop cooling has been investigated by several authors. Radiative cooling and conduction losses have been found to balance approximately (e.g., Jiang et al., 2006). In the late phase, radiative cooling usually dominates, but considerable heat input is frequently observed (e.g., Milligan et al., 2005).
4 Energy Budget
Magnetohydrodynamic models suggest that reconnection releases magnetic energy into ohmic heating and fluid motion in about equal amounts (textbook by Priest and Forbes, 2000). At the level of kinetic plasma theory, ohmic heating may amount to accelerating particles to non-thermal energy distribution. The motion of the reconnection jet may involve waves and shocks, both are also capable of acceleration. Thus a flare releases energy initially into the forms of heat, non-thermal particles, waves, and motion.
In the past, the observed partition of energy in flares into the various forms has often changed with new instrumentation. The most complete estimate of the total flare energy is currently the measured enhancement in total solar irradiance. Woods et al. (2004) determined the total flare irradiance to exceed the soft X-ray emission (< 27 nm) by a factor of 5 in two well observed, large flares. The total irradiance enhancement is dominated by white light and infrared emission (77%). UV and soft X-ray emissions < 200 nm amount to 23%.
Most of the white light originates in the chromosphere and upper photosphere (Neidig, 1989), but the excellent correlation with hard X-rays (Matthews et al., 2003; Metcalf et al., 2003; Hudson et al., 2006) suggests that the energy is deposited in the upper chromosphere and is transported to the deeper layers by radiation. The latter authors also point out that white light flares are not different from others, and that possibly all flares may be observed in white light with sufficient sensitivity. Not included in the total irradiance is the energy that leaves the corona in coronal mass ejections. Emslie et al. (2004a) report that the kinetic energy of the CME exceeded the non-thermal electrons’ energy of the associated flare by about an order of magnitude in two major flares. However, taking into account the flare energy radiated at wavelengths other than X-rays, in particular in white light, brings the flare energy up to the CME energy or beyond (Table 1).
4.1 Non-thermal electron energy
White light and soft X-rays probably do not represent primary forms of energy, but result from kinetic energy, Ekin, transported to the chromosphere by particles:
where ε is the electron energy and F is the electron flux distribution per energy unit impinging on the target. If the accelerated electrons have a power-law distribution with a spectral index of δ, the emitted bremsstrahlung by a thick target is also approximately a power-law in photon energy with index γ = δ − 1. As δ > 2 in all observations, the integral in Equation (3) depends strongly on the low-energy cut-off εmin. It is difficult to observe as the emission of the non-thermal electrons usually outshone by the emission of the thermal plasma around 10 keV. Only recently, with the 1 keV spectral resolution of RHESSI, it has become possible to reconstruct the electrons’ energy distribution at low energies (≈ 10 keV). Structure in the reconstructed electron distribution was reported by Kontar et al. (2002, 2005), indicating that spectral features may indeed be observed. It suggested that the inversion of photon spectra into electron energy distributions is possible (Piana et al., 2003). However, several effects distort the photon spectrum around 10 keV, in particular reflection of X-rays at the chromosphere, termed albedo effect (Kontar et al., 2006; Kašparová et al., 2007), free-bound emission and pulse pile-up in the detectors. Thus the low-energy turnover of the electron distribution measured and reported to be at 20–40 keV or below (Saint-Hilaire and Benz, 2005) is unconfirmed and may be an upper limit.
4.2 Thermal energy
Electron energy distributions can be inferred from X-ray spectra with high spectral resolution, e.g., Figure 7. The quasi-thermal part, observed mostly in coronal sources, reaches temperatures of several ten MK. For simplicity, it is often modeled with a single temperature, sometimes with an additional much hotter, but smaller second component. In reality, the distribution of the emission measure with temperature (called differential emission measure, DEM) can easily exceed a factor two in the temperature range (McTiernan et al., 1999; Chifor et al., 2007; Aschwanden, 2007). The quasi-thermal population may be directly heated coronal material or evaporated chromospheric material heated by precipitating particles accelerated by the flare. As the coronal emission measure greatly increases during a flare, most of the thermal flare plasma must origin from the chromosphere. The first X-ray emissions appear to be purely thermal, but already contain more material than expected in the corona of quiescent active regions. Thus the thermal X-ray plasma is generally assumed to be evaporated chromospheric material. The thermal energy Eth of this plasma is thus of flare origin and amounts to
where α refers to the plasma species, n, T, and V refer to density, temperature, and volume. Assuming a homogeneous source having equal temperatures among species and approximate equality between electron and ion density,
where \({\cal M}\) is the observed emission measure of soft X-rays. The observations suggest that Ekin is larger by a factor of 1–10 than Eth for plasma at T > 10 MK (Emslie et al., 2004a; Saint-Hilaire and Benz, 2005). The factor concurs with the expectation that heating to coronal temperature is not a loss-free process. The result is also consistent with the observations in white light suggesting that a major part of the precipitated energy is lost to low-temperature plasma not observable in X-rays (Section 4.4).
4.3 Energy in waves
The process of magnetic energy release reconnects two magnetic field lines and launches two reconnection jets that can be viewed as Alfvénic excursions of two waves. The waves cascade to smaller wavelengths until they resonate with electrons or ion (Miller et al., 1997; Petrosian et al., 2006). Thus waves are essential in the currently most popular view of particle acceleration. Reconnection may be collision-free as found in the terrestrial magnetosphere (Øieroset et al., 2001) and possibly involve effects of electron inertia. For solar conditions, intense turbulence of collision-free waves causing anomalous resistivity may play a role.
Waves of all frequencies from large scale MHD waves to high-frequency waves up to whistler waves have been predicted and observed in magnetospheric reconnection (Deng and Matsumoto, 2001; Øieroset et al., 2001). Waves can propagate energy across magnetic field lines. Low-frequency Alfvén waves produced by coronal reconnection can move through most of the corona having absorption at inhomogeneities. Thus they can transport energy even to the high corona and solar wind.
MHD waves related to flares have been inferred from pulsating radio bursts (Roberts et al., 1983) and were more recently reported in high-temperature EUV emission (Aschwanden et al., 1999) and in X-rays (Foullon et al., 2005; Nakariakov et al., 2006). Schrijver et al. (2002) have shown that most larger flares (classes M and X) trigger loop oscillations. However, the energy deposited in these oscillations is typically six orders of magnitude smaller compared to the flare energy release (Terradas et al., 2007). Furthermore, the oscillations are observed to damp within a few oscillation periods. From the existing observations it is not clear how far the energy of these oscillations propagates into the corona. Nevertheless, it is obvious that the observed oscillations do not significantly contribute to coronal heating.
Current acceleration models are based on wave damping (Section 6). The energy in observed MHD waves originating from flares is in striking contrast to expectation from the assumed role they play in acceleration.
4.4 Other energies
The energy in the non-thermal ions is less known than for electrons. Ramaty et al. (1995) have argued that the fraction of the available flare energy that is contained in accelerated ions above 1 MeV is similar to that of electrons above 20 keV. This conclusion is supported by the observations that the derived non-thermal energy in protons is comparable within an order of magnitude to the non-thermal energy in electrons (e.g., Cliver et al., 1994; Miller et al., 1997). The above observations, however, leave doubtful whether the energy in non-thermal electrons and ions add up to the energy of flares observed in total irradiance (see Table 1).
The possibility remains that some energy propagates from the release site to the chromosphere by means of low energy (non-thermal) particles below the current threshold for X-ray detection or by heat conduction (i.e., thermal particles). This is supported by the observation that in a quarter of the events there is clear evidence for the presence of an additional energy transport mechanism other than non-thermal electron beams (Veronig et al., 2002, 2005). Furthermore, the relative contribution to energy transport by non-thermal electrons is found to decrease with the flare importance and in the late phase of flares.
Other forms of energy must also be considered. The reconnection process releases bipolar outflows that may be observed as ejections. Magnetic field and plasma are expelled from the X-point where oppositely directed field lines meet. Reconnection jets may not propagate far and are distinct from CMEs. Saint-Hilaire and Benz (2002) observed a stopped ejection in a flare and measured an initial kinetic energy of motion of about 1029 erg, about the same as the thermal energy in the soft X-ray plasma, and interpreted it as a reconnection jet (Figure 24). The thermal energy that such ejections contain was found even an order of magnitude larger, but it was not possible to estimate what fraction of it originated in the flare.
mpg-Movie (3460.421875 KB) Still from a movie showing An overview in Fe xii EUV emission observed by EIT/SOHO, later zooming into the observations by TRACE, both showing thermal coronal emission of a plasma at about 1.5 MK. The 12–25 keV hard X-ray emission observed by RHESSI is shown in red and yellow colors (courtesy of Pascal Saint-Hilaire). (For video see appendix)
A further form of energy is the work done by the expansion of the heated flare plasma from chromospheric density to the observed value of the thermal X-ray source. This expansion in volume by a factor of 103 or more, may consume more energy than its heating (Benz and Krucker, 2002). The expansion energy is released when the material cools and rains back to the chromosphere. A fraction is finally radiated away at temperatures below coronal. Other forms of direct energy release, such direct coronal heating are not yet reliably measurable. The uncertainties in these estimates make it difficult to assess the energy partition of flares and their contribution to coronal heating.
4.5 Energy input into the corona
The heating of the corona is a long standing debate and is not the issue here. We may still ask the question of the resulting energy input into the corona based on the new findings on flares. Obviously, large flares occurring in active regions during solar maximum are unlikely candidates. The existence of tiny flares unobservable by current instruments is a questionable hypothesis.
The question of flare heating has come up again recently by observations of extremely small brightenings in soft X-rays in the quiet corona (Krucker et al., 1997b). Some of the larger events have been found to correlate with centimeter radio emission. Similar events have also been reported in high-temperature EUV lines (Benz and Krucker, 1998; Berghmans et al., 1998; Krucker and Benz, 1998). Figure 25 shows the time profiles of two radio sources at the opposite ends of a small Fe xii loop. In one of them (third panel), the radio source has a negative slope (3.8 cm flux larger than 2 cm flux), indicating gyrosynchrotron emission. The radio peaks occur before the temperature maximum and emission measure peak of the thermal EUV emission, following the Neupert relation between thermal and non-thermal flare emissions. The other source (fourth panel) has an increasing spectrum, indicating optically thick thermal radio emission, coincident with the EUV emission. The events were soon realized to be at least similar to regular flares and thus termed nanoflares. The most relevant difference to regular flares is the order of magnitude lower ratio of synchrotron emission to soft X-rays compared to regular flares (Benz, 2001).
Time profile of nanoflare observed in Fe xi/x, and Fe xii lines at 17.1 nm and 19.5 nm by EIT/SOHO. Top panel: temperature averaged over the area of the event; second panel: the emission measure; third panel: radio flux observed by the VLA at 6 and 3.6 cm wavelength at the location of the 6 cm peak; bottom panel: same at the location of the 3.6 cm peak.
The pertinent question is how much the observed flare-like events contribute to the heating of the corona. The largest nanoflares reported contain energies of a few 1026 erg (Krucker and Benz, 1998). This number refers to the thermal energy in the soft X-rays emitting flare plasma and is identical to the largest individual flare-like events inferred from Fe xi/x, and Fe xii lines. It does not include coronal bright points, locations in the quiet corona where continuous flaring during many hours is observed. The smallest flares reported given by the TRACE instrumental limit is a few 1023 erg (Parnell and Jupp, 2000). The rate of events larger than few 1024 erg and lasting about 15 minutes each, estimated over the whole Sun is 300 per second (Krucker and Benz, 1998). Benz and Krucker (2002) have estimated that the total energy measured in nanoflares in the energy range from 5 × 1024 erg to 5 × 1026 erg observable by EIT/SOHO amounts to about 12% of the radiated energy of the observed coronal area.
This review of flare observations emphasizes that the thermal energy measured at peak soft X-ray or EUV emission is not equivalent to the total flare energy input into the corona. Most of the thermal flare plasma is just the reaction of the chromosphere on a coronal phenomenon. We may thus end this short subchapter by the conclusion that the cause of coronal heating by flares needs more quantitative modeling. Flare heating cannot be quantitatively assessed from observations of one energy receiving channel alone as long as the energy partition of regular flares into waves, direct heating, motion, and particle acceleration is unclear.
5 Signatures of Energy Release
As explained in Section 3, the location of energy release is not well known. Even less understood is its process. Some observational evidence restricting the possible mechanisms is presented in the following.
5.1 Coronal hard X-ray signatures
The coronal hard X-ray source is not necessarily identical to the acceleration region, but a thin or thick target for accelerated electrons. The relation between coronal hard X-rays and acceleration is not clear. The centroid position of the coronal hard X-ray emission has been reported to be higher with increasing photon energy, and to be located above the thermal soft X-ray loop (Masuda et al., 2000). In some cases it has been reported to move out (Shibata et al., 1995). In another case, the speed of the outward motion of several hundred km s−1 was correlated with the flux of accelerated electrons (Sui et al., 2004, Figure 26). The shape of the hard X-ray emission is not always plain circular. Elongated tongues stretching out from the loop-top are frequently reported (e.g., Sui et al., 2004). The altitude of this source decreases from the start of the hard X-rays until peak time at 23:12 UT, while a source above the loop-top moves upwards at speeds of 23 km s−1. Well contained emission is also seen (e.g., Figure 24).
Top: Light curves in two energy bands (upper curve, 6–12 keV; lower curve, 25–50 keV) of the April 15, 2002 flare observed by RHESSI. Bottom: Altitude of the loop-top centroid obtained using the 60% contour for the images in the 6–12 (crosses) and 12–25 keV (diamonds) bands. The triangles show the altitude of the lower source above the flare loop. The horizontal bars on each point represents the integration time of the corresponding image. The lines show linear fits to the altitudes vs. time for two time ranges and two energy bands (from Sui et al., 2004).
With higher spectral resolution it became possible to determine also the shape of the photon energy distribution. The coronal hard X-rays have been found to be well represented by a power-law in energy (Emslie et al., 2003; Battaglia and Benz, 2006), similar to what is well known for footpoint sources. The predominant near power-law distribution of accelerated electron energies is a stringent characteristic of the acceleration process, and not the result of propagation.
5.2 Soft-hard-soft behavior in hard X-rays
The hardness of the non-thermal spectrum changes in the course of a flare, starting soft (steep), getting harder at the peak and softening toward the end (Parks and Winckler, 1969; Kane and Anderson, 1970). A few large flares continue to harden after the peak (Frost and Dennis, 1971; Krucker et al., 2005b). These flares have been shown to be particularly well associated with solar energetic particle events (Kiplinger, 1995).
The great majority of flares follows a soft-hard-soft behavior (illustrated in Figure 27). This correlation between (negative) spectral index and flux is generally interpreted as a signature of the acceleration process. A similar relation also holds for peak values of flares with different size, indicating that small flares are on the average softer (Battaglia et al., 2005). Both the time variation and the size variation of the spectral index with flux indicate that intense hard X-ray radiation is not a superposition of many small events. High flux means that the acceleration process is driven more forcefully, resulting in a harder spectrum. It is stringent property of the acceleration process, but alas, many acceleration processes show this behavior.
Flux density at 35 keV and power-law index as determined from RHESSI observations of the non-thermal component of flare hard X-ray emission. Colors mark individual subpeaks. The close correlation demonstrates soft-hard-soft behavior in the smallest details (from Grigis and Benz, 2004).
The soft-hard-soft property has become more relevant recently when it became possible to express the relation between flux and spectral index in a quantitative way that can be compared to models (Grigis and Benz, 2004, 2005b). The relation appears as a power-law relation between the photon spectral index γ and the flux density F(E0) measured at a given energy E0,
where A is constant that varies from flare to flare, and α is 0.121 ± 0.009 in the flare rise phase and 0.172 ± 0.012 in the decay phase for E0 = 35 keV (Grigis and Benz, 2004). In this quantitative form, the soft-hard-soft behavior becomes a stringent condition for electron acceleration theories.
5.3 Radio emissions from the acceleration region
There are several flare related processes that emit radio waves. The large variety of flare related radio emission may be grasped from Figure 28. Their emission processes must be distinguished as they refer to widely different physical mechanisms. Only few radio emission, if any, come from the acceleration region. Most flare radio emissions, except some thermal radiation at millimeter and submillimeter waves, are interpreted to be caused by non-thermal electrons. They emit two kinds of non-thermal emissions: incoherent and coherent. In incoherent emission, such as synchrotron emission, non-thermal electrons radiate individually. When a wave organizes electrons to emit in phase, the emission becomes coherent. On some cases, radio emission results from mixing two plasma waves (textbooks by Melrose, 1980; Benz, 2002). Coherent emissions are emitted at the local plasma frequency, upper hybrid frequency, electron gyrofrequency, or their harmonics and carry information on the plasma parameters in the source. As the plasma frequency exceeds the electron gyrofrequency by more than an order of magnitude in most of the corona, the plasma frequency is the lowest frequency observable from outside the solar atmosphere. If the flare energy is released at electron densities between 108 and 1011 cm−3, as generally believed, the corresponding emission is at short meter waves and, predominantly, in the decimeter region.
Radio spectrogram observed by the Phoenix-2 spectro-polarimeter operated by ETH Zurich. At low frequencies (top of image), the radio emission is dominated by type III bursts and U bursts emitted by escaping electron beams and trapped electron beams. The brightest feature is a type V event, possibly caused by electrons left behind by unstable beams. At high frequencies (bottom of image) the synchrotron emission of mildly relativistic electrons (gyrosynchrotron) dominates, correlating well with hard X-rays. In the middle of the frequency range at about 800–2000 MHz, narrowband spikes of the decimetric type can be seen.
The study of the spatial distribution of the synchrotron emission by mildly relativistic electrons (gyrosynchrotron) has a long history. Both loop-top sources and double sources located close to the conjugate magnetic footpoints were reported (Marsh and Hurford, 1982; Kundu et al., 1982; Kawabata et al., 1983). The comparison with theoretical simulations of the gyrosynchrotron brightness distribution along model magnetic loops (see Bastian et al., 1998, for a review) strongly suggests that the distribution of mildly relativistic electrons along an extended flaring loop must be highly inhomogeneous: accelerated electrons are concentrated in the upper part of the loop (Nindos et al., 2000; Melnikov et al., 2002). Some of the centimeter loop-top emissions were observed in the late phase of flares (e.g., Karlický, 2004). They are not related to the main energy release, but possibly to high-energy X-rays detected late in flares (Krucker, personal communication) and possibly the end stage of the spectral hardening observed in non-thermal X-rays (see Section 5.2). The investigation of the acceleration region using gyrosynchrotron emission has greatly profited from combination with hard X-rays. It may result in the measurement of the magnetic field in loop-tops in future work.
Benz et al. (2007) found some coherent radio emission in all flares larger than C5 class, except near the limb where absorption seems to play a role. While there is good association between coherent radio emission and X-rays, correlation in details of the time profile is less frequent. Thus coherent emissions cannot expected to be reliable tracers of the main flare energy release in general. Emissions at higher frequencies, such as decimetric narrowband spikes, pulsations, and stationary type IV events appear to be more directly related to the acceleration process. The association but loose correlation between HXR and coherent radio emission may be interpreted by multiple reconnection sites connected by common field lines, along which accelerated particles may propagate and serve as a trigger for distant accelerations. Thus coherent radio emissions may be interesting diagnostics in special cases.
Correlation of coherent radio emissions with hard X-rays (or gyrosynchrotron emission) has been reported for spikes and pulsations (Slottje, 1978; Benz and Kane, 1986; Aschwanden et al., 1990; Kliem et al., 2000). If these coherent radiations are emitted at the second harmonic of the plasma frequency — the usual assumption — the density of the source region is in the range from 109 cm−3 to a few times 1010 cm−3. This range is a possible indication for the density in the acceleration region. Although initially interpreted as loss-cone emissions of trapped particles near footpoints, they have been found at high altitudes, consistent with loop-tops (Benz et al., 2002; Khan et al., 2002; Kundu et al., 2006). As the emission mechanism of spikes and pulsations is not well understood, the origin of the radiating high-frequency waves cannot be further investigated.
Best candidates for direct emission from the acceleration region are small clusters of narrowband spikes around 300 MHz, reported to correlate in detail with electron beam emission (type III radio bursts). About 10% of all meter wave type III groups are accompanied with spikes near but slightly above the start frequency (Benz et al., 1982). The spikes are concentrated in the spectrogram on the extrapolation of the type III bursts to higher frequency. More precisely, as suggested by Figure 19, metric spikes are located on the extension of type III trajectories, supporting a model of energy release in or close to the spike sources (Benz et al., 1996). If this is the case, radio observations can approximately locate the acceleration region for the type III electrons and measure the electron density of the acceleration region (Section 3).
Type IV emissions occur late relative to the hard X-ray peak and appear to be connected to some late-phase acceleration (Švestka et al., 1982; Klein et al., 1983). They may be related to delayed electron releases of interplanetary electron events in the corona (Klein et al., 2005).
Some radio emissions (like type III and V) are due to electrons escaping from the acceleration region. Hard X-ray flares are associated with meter-wave type III bursts in 33% of all cases, and in 4% of them type III bursts are the exclusive radio emission. Type III emission is caused by electron beams becoming unstable towards growing electrostatic plasma waves at the local plasma frequency. These waves are converted into radio waves slightly above the plasma frequency ωp,
or its harmonic, where ne is the electron density, e the elementary charge, and me the electron mass. Type III emission thus occurs at a frequency that varies with the local density. Observed at many different frequencies, it can be used to trace the path of the electron beam in the corona. Different beams following different trajectories diverging from the acceleration region have been used to locate the acceleration region (Figure 19). The distance from this region to the start of type III emission depends on the energy spectrum of accelerated electrons (Benz, 2002, p. 32). Future interferometers observing at many frequencies will refine this method.
A major constraint by radio emission on particle acceleration is the fact, that in 15% of larger flares (> C5.0 class) there is no coherent radio emission except some electron beam emitting at very high altitude (Benz et al., 2007). Whether coherent radio emission is necessarily emitted or not, is therefore an observable criterion for the validity of acceleration models. The frequent lack of direct radio emission from the acceleration region suggests that the acceleration is “gentle”, excluding significant deviations from a Maxwellian velocity distribution, such as a monoenergetic beam. The deviations only build up after the non-thermal electrons have traveled some distance and the faster particles have outpaced the slower particles, or after a loss-cone results from magnetic trapping. Gentle acceleration favors acceleration by diffusion in velocity space as predicted by stochastic acceleration (Section 6).
6 Acceleration Processes
A remarkable fraction of the total flare energy released first appears as kinetic particle energy in non-thermal electrons and ions (Section 5). White light observations (Section 4) suggest that in addition to the particles observed in X-rays and gamma-rays particles at lower energies (about 1 keV for electrons) transport energy to the upper chromosphere and transition region. The acceleration process thus is a major issue in flare physics and constitutes the core of the flare enigma. We will briefly review here the major ingredients of the current theories and then present the observational evidence.
The transfer of magnetic energy to kinetic particle energy has been observationally separated into two phases. In the impulsive flare phase, the concept is “bulk energization”, involving an increase of the electron energy by more than two orders of magnitude starting from the coronal thermal energy (some 0.1 keV) within less than 1 s as derived from hard X-ray observations (Kiplinger et al., 1984). The other class of acceleration occurs in a secondary phase, possibly as a result of the first phase such as shock wave initiated by a flare or an associated coronal mass ejection. The second phase may be less productive in particle acceleration, but is more important for solar energetic particles in interplanetary space.
We will concentrate here on bulk energization, in which the whole particle population gains energy and remains close to a Maxwellian distribution and/or develops a non-thermal tail. The acceleration of a particle to an energy Ekin requires that it occurs faster than the collision time τcoll(Ekin) for energy loss. The energy loss time for an electrons with velocity \(v_{T}^{3}\) is
where ne is the electron density. Note that for densities up to some 1012 cm−3 are reported for coronal sources (Section 3.2). Equation (8) yields a collision time requiring acceleration within less than one second. On the other hand, Equation (8) excludes efficient particle acceleration at high densities if the process takes a finite time.
6.1 Electron acceleration theories
The free mobility of charged particles in dilute plasma and the difference in inertia between electrons and ions make it likely that electrons are accelerated in every major impulsive process in the corona. Convertible (free) magnetic energy requires the presence of an electric current and an associated electric field before the flare-like process. Waves of various types from MHD to collisionless are expected to be excited by the flare and are also capable to accelerate particles in resonance. From a plasma physics point of view, acceleration is not surprising; controversial is, however, which process dominates.
The conversion of magnetic energy into accelerated particles can be accomplished by several processes. It is likely that more than one occurs during a flare and its secondary effects. The most widely discussed can be grouped into 3 types (e.g., Melrose, 1990; Benz, 2002):
-
stochastic acceleration (e.g., resonant acceleration by waves),
-
electric field parallel to the magnetic field,
-
perpendicular and parallel shocks (first and second order Fermi acceleration).
The preferred but not generally accepted acceleration model for solar flares is stochastic acceleration by the magnetic field component of low-frequency waves (Miller et al., 1997; Schlickeiser and Miller, 1998; Petrosian et al., 2006). Particles near Cerenkov resonance (υ ≈ ω/k∥) are mirrored by the waves. The process is known as Transit-Time Damping of waves. It acts as a diffusion process of the particle distribution f(p) in momentum space, described by the Fokker-Planck equation
The diffusion coefficients Dij and Fi contain the physics: the action of accelerating waves and decelerating Coulomb collisions.
mpg-Movie (2078.88867188 KB) Still from a movie showing The particle distribution vs. energy in time (blue) as described by Equation (9). A tail develops out of the thermal distribution (purple). The solution becomes stationary after about one second when acceleration balances particle escape out of the acceleration region. The spectral index resulting from fitting a power-law in the region limited by dashed red lines is also shown (from Grigis and Benz, 2006). (For video see appendix)
6.2 Comparing theories with observations
Flare particle acceleration occurs in the wake of reconnection in low density plasma. The details are still obscure. Current flare observations contain numerous information that limits the scenarios for particle acceleration. Concerning the three types mentioned in the previous section, observations exclude more than they confirm. In particular:
-
High-frequency waves near the plasma frequency can be excluded as drivers for stochastic acceleration. They would couple into radio decimeter waves and be present in every flare. On the other hand, acceleration by Transit-Time Damping is compatible with the frequent lack of radio emission because the frequency of the postulated turbulence is far below the plasma frequency and does not cause radio emission.
-
The number of electrons that can be accelerated in current sheets is limited by the current, and observed values are difficult to match with a classic current sheet (Holman, 1985; Litvinenko, 1996).
-
Large-scale, stationary electric fields would cause major distortions in velocity space, susceptible to velocity space instabilities and beam driven high-frequency waves observable as radio waves. Such radio emission should correlate well with hard X-ray emission, which is not seen in every flare.
-
Shock acceleration plays an important role in interplanetary space, which is not the issue here. More directly related to flares are shocks possibly produced by the reconnection process. Radio signatures of such shocks have been reported by Aurass et al. (2002); Mann et al. (2006), but are still disputed and, if confirmed, extremely rare. Nevertheless, slow shocks have been predicted at the interface between inflow and outflow regions of reconnection, as well as fast shocks at the bow of the reconnection outflows. High energies could be readily be achieved (100 MeV ions in < 1s, Ellison and Ramaty, 1985; Tsuneta and Naito, 1998).
The Transit-Time Damping scenario is consistent with present observations, although there is no direct evidence for it. Thus it must be considered as a still unproven hypothesis. In fact, there are other viable scenarios: as an alternative to acceleration by fluctuating magnetic fields (and also to large-scale quasi-electric fields) low-frequency fluctuating electric fields parallel to the magnetic field have been proposed. Such fields may originate from low-frequency and high-amplitude turbulence, such as kinetic Alfvén waves. They accelerate and decelerate electrons, leading to a net diffusion in energy space (Arzner and Vlahos, 2004).
7 Conclusions
Flares may be considered to result from the loss of equilibrium in magnetic configurations. Although reconnection is a general phenomenon, it occurs in an impulsive way only in the corona, where collisions are rare and thus the plasma is highly conductive. Regular flares must be considered as extreme phenomena of the continuous dynamics of the corona. Radio noise storms (type I bursts) and meter wave type III bursts hint at activity in the high corona that is not yet accessible to other wavelengths and is prone to surprises.
Therefore, flares should not be considered exceptional catastrophes that occur rarely and mostly during solar maximum. Flare-like brightenings, called nanoflares, occur in the quiet corona at a rate of at least a few thousand per second. Is the corona heated by flares? It may well be that the impulsive processes in the coronal plasma related to sudden changes in resistivity are the cause of the corona. We cannot answer this question definitively, however, as long as we do not understand how much energy flares deposit into the corona in the various possible ways. Furthermore, the corona below 20,000 km above the photosphere, including the transition region, is not well explored in flare research. It is also the place where most of the coronal heating occurs. This region will soon become accessible to white light coronagraphs and high-temperature line observations. The future of flare research will also profit from spatial resolution in decimetric radio waves.
Regular flares are not two of a kind, and each flare has individual features. For this reason, it is not surprising that observations at various wavelengths do not correlate in a simple manner as predicted by a simple scenario. The fact, that every flare appears to be different, must be taken as evidence that coronal dynamics has many degrees of freedom. Nevertheless, recent observations in X-rays and EUV allow identifying the magnetic topologies, confirming the general scenario of reconnection. They have shown that various groups of flares exist and have greatly contributed to our ever growing understanding of coronal phenomena.
Flares consist of a series of processes, starting with energy build-up in the corona and ending by restructuring the magnetic configuration and releasing magnetic energy. The processes include reconnection, anomalous resistivity, efficient particle acceleration, particle propagation, coronal and chromospheric heating, evaporation, mass loss, high-frequency waves and MHD oscillations, as well as various emission mechanisms. All these processes are important issues in astrophysics and worth studying for their own. They all have seen significant progress in the past decades and will be addressed by the new observing facilities planned and in construction. A major impact can be expected from simultaneous imaging observations in practically all wavelengths. They will greatly contribute to the growing physical understanding of solar flares in the near future.
Notes
The literature often uses the term ‘microwaves’ for frequencies in the range 1–30 GHz, in particular in connection with gyrosynchrotron emission. In the lower wavelength part, microwaves overlap with the decimeter wavelength range. We will thus use strictly the decimal wavelength notation in this review to avoid confusion.
References
Acton, L.W., Feldman, U., Bruner, M.E., Doschek, G.A., Hirayama, T., Hudson, H.S., Lemen, J.R., Ogawara, Y., Strong, K.T., Tsuneta, S., 1992, “The Morphology of 20 × 106 K Plasma in Large Non-Impulsive Solar Flares”, Publ. Astron. Soc. Japan, 44, L71–L75. ADS: http://adsabs.harvard.edu/abs/1992PASJ...44L..71A
Antiochos, S.K., 1998, “The Magnetic Topology of Solar Eruptions”, Astrophys. J. Lett., 502, L181–L184. ADS: http://adsabs.harvard.edu/abs/1998ApJ...502L.181A
Antonucci, E., 1989, “Solar flare spectral diagnosis — Present and future”, Solar Phys., 121, 31–60. ADS: http://adsabs.harvard.edu/abs/1989SoPh..121...31A
Antonucci, E., Gabriel, A.H., Acton, L.W., Leibacher, J.W., Culhane, J.L., Rapley, C.G., Doyle, J.G., Machado, M.E., Orwig, L.E., 1982, “Impulsive phase of flares in soft X-ray emission”, Solar Phys., 78, 107–123. ADS: http://adsabs.harvard.edu/abs/1982SoPh...78..107A
Arzner, K., Vlahos, L., 2004, “Particle Acceleration in Multiple Dissipation Regions”, Astrophys. J. Lett., 605, L69–L72. ADS: http://adsabs.harvard.edu/abs/2004ApJ...605L..69A
Asai, A., Nakajima, H., Shimojo, M., White, S.M., Hudson, H.S., Lin, R.P., 2006, “Preflare Nonthermal Emission Observed in Microwaves and Hard X-Rays”, Publ. Astron. Soc. Japan, 58, L1–L5. ADS: http://adsabs.harvard.edu/abs/2006PASJ...58L...1A
Aschwanden, M.J., 2002, “Particle acceleration and kinematics in solar flares — A Synthesis of Recent Observations and Theoretical Concepts (Invited Review)”, Space Sci. Rev., 101, 1–227. ADS: http://adsabs.harvard.edu/abs/2002SSRv..101....1A
Aschwanden, M.J., 2007, “RHESSI Timing Studies: Multithermal Delays”, Astrophys. J., 661, 1242–1259. ADS: http://adsabs.harvard.edu/abs/2007ApJ...661.1242A
Aschwanden, M.J., Benz, A.O., Kane, S.R., 1990, “Correlation of solar radio pulsations with hard X-ray emission”, Astron. Astrophys., 229, 206–215. ADS: http://adsabs.harvard.edu/abs/1990A&A...229..206A
Aschwanden, M.J., Schwartz, R.A., Alt, D.M., 1995, “Electron Time-of-Flight Differences in Solar Flares”, Astrophys. J., 447, 923. ADS: http://adsabs.harvard.edu/abs/1995ApJ...447..923A
Aschwanden, M.J., Kosugi, T., Hudson, H.S., Wills, M.J., Schwartz, R.A., 1996, “The Scaling Law between Electron Time-of-Flight Distances and Loop Lengths in Solar Flares”, Astrophys. J., 470, 1198. ADS: http://adsabs.harvard.edu/abs/1996ApJ...470.1198A
Aschwanden, M.J., Fletcher, L., Schrijver, C.J., Alexander, D., 1999, “Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer”, Astrophys. J., 520, 880–894. ADS: http://adsabs.harvard.edu/abs/1999ApJ...520..880A
Aurass, H., Vrsnak, B., Mann, G., 2002, “Shock-excited radio burst from reconnection outflow jet?”, Astron. Astrophys., 384, 273–281. ADS: http://adsabs.harvard.edu/abs/2002A&A...384..273A
Bastian, T.S., Benz, A.O., Gary, D.E., 1998, “Radio Emission from Solar Flares”, Annu. Rev. Astron. Astrophys., 36, 131–188. ADS: http://adsabs.harvard.edu/abs/1998ARA&A..36..131B
Battaglia, M., Benz, A.O., 2006, “Relations between concurrent hard X-ray sources in solar flares”, Astron. Astrophys., 456, 751–760. ADS: http://adsabs.harvard.edu/abs/2006A&A...456..751B
Battaglia, M., Benz, A.O., 2007, “Exploring the connection between coronal and footpoint sources in a thin-thick target solar flare model”, Astron. Astrophys., 466, 713–716. ADS: http://adsabs.harvard.edu/abs/2007A&A...466..713B
Battaglia, M., Benz, A.O., 2008, “Evidence for an electric field in solar flares”, unknown format, in preparation
Battaglia, M., Grigis, P.C., Benz, A.O., 2005, “Size dependence of solar X-ray flare properties”, Astron. Astrophys., 439, 737–747. ADS: http://adsabs.harvard.edu/abs/2005A&A...439..737B
Benz, A.O., 2001, “Astronomy: Brown dwarf is a radio star”, Nature, 410, 310–311. ADS: http://adsabs.harvard.edu/abs/2001Natur.410..310B
Benz, A.O., 2002, Plasma Astrophysics: Kinetic Processes in Solar and Stellar Coronae, vol. 279 of Astrophysics and Space Science Library, Kluwer, Dordrecht, Netherlands; Boston, U.S.A., 2nd edn.
Benz, A.O., Kane, S.R., 1986, “Electron acceleration in flares inferred from radio and hard X-ray emissions”, Solar Phys., 104, 179–185. ADS: http://adsabs.harvard.edu/abs/1986SoPh..104..179B
Benz, A.O., Krucker, S., 1998, “Heating Events in the Quiet Solar Corona”, Solar Phys., 182, 349–363. ADS: http://adsabs.harvard.edu/abs/1998SoPh..182..349B
Benz, A.O., Krucker, S., 2002, “Energy Distribution of Microevents in the Quiet Solar Corona”, Astrophys. J., 568, 413–421. ADS: http://adsabs.harvard.edu/abs/2002ApJ...568..413B
Benz, A.O., Jaeggi, M., Zlobec, P., 1982, “Fine structure near the starting frequency of solar type III radio bursts”, Astron. Astrophys., 109, 305–313. ADS: http://adsabs.harvard.edu/abs/1982A&A...109..305B
Benz, A.O., Barrow, C.H., Dennis, B.R., Pick, M., Raoult, A., Simnett, G., 1983, “X-ray and radio emissions in the early stages of solar flares”, Solar Phys., 83, 267–283. ADS: http://adsabs.harvard.edu/abs/1983SoPh...83..267B
Benz, A.O., Csillaghy, A., Aschwanden, M.J., 1996, “Metric spikes and electron acceleration in the solar corona”, Astron. Astrophys., 309, 291–300. ADS: http://adsabs.harvard.edu/abs/1996A&A...309..291B
Benz, A.O., Lin, R.P., Sheiner, O.A., Krucker, S., Fainberg, J., 2001, “The Source Regions of Impulsive Solar Electron Events”, Solar Phys., 203, 131–144. ADS: http://adsabs.harvard.edu/abs/2001SoPh..203..131B
Benz, A.O., Saint-Hilaire, P., Vilmer, N., 2002, “Location of narrowband spikes in solar flares”, Astron. Astrophys., 383, 678–684. ADS: http://adsabs.harvard.edu/abs/2002A&A...383..678B
Benz, A.O., Grigis, P.C., Csillaghy, A., Saint-Hilaire, P., 2005, “Survey on Solar X-ray Flares and Associated Coherent Radio Emissions”, Solar Phys., 226, 121–142. ADS: http://adsabs.harvard.edu/abs/2005SoPh..226..121B
Benz, A.O., Brajsa, R., Magdalenic, J., 2007, “Are There Radio-quiet Solar Flares?”, Solar Phys., 240, 263–270. ADS: http://adsabs.harvard.edu/abs/2007SoPh..240..263B
Berghmans, D., Clette, F., Moses, D., 1998, “Quiet Sun EUV transient brightenings and turbulence. A panoramic view by EIT on board SOHO”, Astron. Astrophys., 336, 1039–1055. ADS: http://adsabs.harvard.edu/abs/1998A&A...336.1039B
Bogachev, S.A., Somov, B.V., Kosugi, T., Sakao, T., 2005, “The Motions of the Hard X-Ray Sources in Solar Flares: Images and Statistics”, Astrophys. J., 630, 561–572. ADS: http://adsabs.harvard.edu/abs/2005ApJ...630..561B
Bone, L., Brown, J.C., Fletcher, L., Veronig, A., White, S., 2007, “Birth and evolution of a dense coronal loop in a complex flare region”, Astron. Astrophys., 466, 339–346. ADS: http://adsabs.harvard.edu/abs/2007A&A...466..339B
Brosius, J.W., Phillips, K.J.H., 2004, “Extreme-Ultraviolet and X-Ray Spectroscopy of a Solar Flare Loop Observed at High Time Resolution: A Case Study in Chromospheric Evaporation”, Astrophys. J., 613, 580–591. ADS: http://adsabs.harvard.edu/abs/2004ApJ...613..580B
Brown, J.C., 1971, “The Deduction of Energy Spectra of Non-Thermal Electrons in Flares from the Observed Dynamic Spectra of Hard X-Ray Bursts”, Solar Phys., 18, 489. ADS: http://adsabs.harvard.edu/abs/1971SoPh...18..489B
Brown, J.C., Carlaw, V.A., Cromwell, D., Kane, S.R., 1983, “A comparison of the thick-target model with stereo data on the height structure of solar hard X-ray bursts”, Solar Phys., 88, 281–295. ADS: http://adsabs.harvard.edu/abs/1983SoPh...88..281B
Brown, J.C., Conway, A.J., Aschwanden, M.J., 1998, “The Electron Injection Function and Energy-dependent Delays in Thick-Target Hard X-Rays”, Astrophys. J., 509, 911–917. ADS: http://adsabs.harvard.edu/abs/1998ApJ...509..911B
Cargill, P.J., Mariska, J.T., Antiochos, S.K., 1995, “Cooling of solar flares plasmas. 1: Theoretical considerations”, Astrophys. J., 439, 1034–1043. ADS: http://adsabs.harvard.edu/abs/1995ApJ...439.1034C
Carmichael, H., 1964, “A Process for Flares”, in The Physics of Solar Flares, (Ed.) Hess, W.N., Proceedings of the AAS-NASA Symposium held 28–30 October, 1963 at the Goddard Space Flight Center, Greenbelt, MD, p. 451, NASA Science and Technical Information Division, Washington, U.S.A.
Chen, P.F., Shibata, K., Brooks, D.H., Isobe, H., 2004, “A Reexamination of the Evidence for Reconnection Inflow”, Astrophys. J. Lett., 602, L61–L64. ADS: http://adsabs.harvard.edu/abs/2004ApJ...602L..61C
Chifor, C., Del Zanna, G., Mason, H.E., Sylwester, J., Sylwester, B., Phillips, K.J.H., 2007, “A benchmark study for CHIANTI based on RESIK solar flare spectra”, Astron. Astrophys., 462, 323–330. ADS: http://adsabs.harvard.edu/abs/2007A&A...462..323C
Choudhary, D.P., Ambastha, A., Ai, G., 1998, “Emerging Flux and X-class Flares in NOAA 6555”, Solar Phys., 179, 133–140. ADS: http://adsabs.harvard.edu/abs/1998SoPh..179..133C
Chupp, E.L., Forrest, D.J., Higbie, P.R., Suri, A.N., Tsai, C., Dunphy, P.P., 1973, “Solar Gamma Ray Lines observed during the Solar Activity of August 2 to August 11, 1972”, Nature, 241, 333. ADS: http://adsabs.harvard.edu/abs/1973Natur.24L.333C
Cliver, E.W., Crosby, N.B., Dennis, B.R., 1994, “Are solar gamma-ray-line flares different from other large flares?”, Astrophys. J., 426, 767–773. ADS: http://adsabs.harvard.edu/abs/1994ApJ...426..767C
Crooker, N.U., Webb, D.F., 2006, “Remote sensing of the solar site of interchange reconnection associated with the May 1997 magnetic cloud”, J. Geophys. Res., 111, A08108. ADS: http://adsabs.harvard.edu/abs/2006JGRA..11108108C
Crooker, N.U., Forsyth, R., Rees, A., Gosling, J.T., Kahler, S.W., 2004, “Counterstreaming electrons in magnetic clouds near 5 AU”, J. Geophys. Res., 109, A06110. ADS: http://adsabs.harvard.edu/abs/2004JGRA..10906110C
Datlowe, D.W., Lin, R.P., 1973, “Evidence for Thin-Target X-Ray Emission in a Small Solar Flare on 26 February 1972”, Solar Phys., 32, 459. ADS: http://adsabs.harvard.edu/abs/1973SoPh...32..459D
Démoulin, P., Bagalya, L.G., Mandrini, C.H., Hyenoux, J.C., Rovira, M.G., 1997, “Quasi-separatrix layers in solar flares. II. Observed magnetic configurations”, Astron. Astrophys., 325, 305–317. ADS: http://adsabs.harvard.edu/abs/1997A&A...325..305D
Deng, X.H., Matsumoto, H., 2001, “Rapid magnetic reconnection in the Earth’s magnetosphere mediated by whistler waves”, Nature, 410, 557–560. ADS: http://adsabs.harvard.edu/abs/2001Natur.410..557D
Dennis, B.R., Zarro, D.M., 1993, “The Neupert effect — What can it tell us about the impulsive and gradual phases of solar flares?”, Solar Phys., 146, 177–190. ADS: http://adsabs.harvard.edu/abs/1993SoPh..146..177D
Doschek, G.A., Feldman, U., Kreplin, R.W., Cohen, L., 1980, “High-resolution X-ray spectra of solar flares. III — General spectral properties of X1–X5 type flares”, Astrophys. J., 239, 725–737. ADS: http://adsabs.harvard.edu/abs/1980ApJ...239..725D
Ellison, D.C., Ramaty, R., 1985, “Shock acceleration of electrons and ions in solar flares”, Astrophys. J., 298, 400–408. ADS: http://adsabs.harvard.edu/abs/1985ApJ...298..400E
Emslie, A.G., Kontar, E.P., Krucker, S., Lin, R.P., 2003, “RHESSI Hard X-Ray Imaging Spectroscopy of the Large Gamma-Ray Flare of 2002 July 23”, Astrophys. J. Lett., 595, L107–L110. ADS: http://adsabs.harvard.edu/abs/2003ApJ...595L.107E
Emslie, A.G., Kucharek, H., Dennis, B.R., Gopalswamy, N., Holman, G.D., Share, G.H., Vourlidas, A., Forbes, T.G., Gallagher, P.T., Mason, G.M., Metcalf, T.R., Mewaldt, R.A., Murphy, R.J., Schwartz, R.A., Zurbuchen, T.H., 2004a, “Energy partition in two solar flare/CME events”, J. Geophys. Res., 109, A10104. ADS: http://adsabs.harvard.edu/abs/2004JGRA..10910104E
Emslie, A.G., Miller, J.A., Brown, J.C., 2004b, “An Explanation for the Different Locations of Electron and Ion Acceleration in Solar Flares”, Astrophys. J. Lett., 602, L69–L72. ADS: http://adsabs.harvard.edu/abs/2004ApJ...602L..69E
Emslie, A.G., Dennis, B.R., Holman, G.D., Hudson, H.S., 2005, “Refinements to flare energy estimates: A followup to “Energy partition in two solar flare/CME events” by A. G. Emslie et al.”, J. Geophys. Res., 110, A11103. ADS: http://adsabs.harvard.edu/abs/2005JGRA..11011103E
Feldman, U., Doschek, G.A., Kreplin, R.W., Mariska, J.T., 1980, “High-resolution X-ray spectra of solar flares. IV — General spectral properties of M type flares”, Astrophys. J., 241, 1175–1185. ADS: http://adsabs.harvard.edu/abs/1980ApJ...241.1175F
Feldman, U., Hiei, E., Phillips, K.J.H., Brown, C.M., Lang, J., 1994, “Very impulsive solar flares observed with the YOHKOH spacecraft”, Astrophys. J., 421, 843–850. ADS: http://adsabs.harvard.edu/abs/1994ApJ...421..843F
Fisher, G.H., Hawley, S.L., 1990, “An equation for the evolution of solar and stellar flare loops”, Astrophys. J., 357, 243–258. ADS: http://adsabs.harvard.edu/abs/1990ApJ...357..243F
Fisk, L.A., Schwadron, N.A., Zurbuchen, T.H., 1999, “Acceleration of the fast solar wind by the emergence of new magnetic flux”, J. Geophys. Res., 104, 19 765–19 772. ADS: http://adsabs.harvard.edu/abs/1999JGR...10419765F
Fletcher, L., Martens, P.C.H., 1998, “A Model for Hard X-Ray Emission from the Top of Flaring Loops”, Astrophys. J., 505, 418–431. ADS: http://adsabs.harvard.edu/abs/1998ApJ...505..418F
Fletcher, L., Warren, H.P., 2003, “The Energy Release Process in Solar Flares; Constraints from TRACE Observations”, in Energy Conversion and Particle Acceleration in the Solar Corona, (Ed.) Klein, K.-L., Contributions presented at the CESRA Workshop, Ringberg Castle, Germany, 2–6 July 2001, vol. 612 of Lecture Notes in Physics, pp. 58–79, Springer, Berlin, Germany; New York, U.S.A. ADS: http://adsabs.harvard.edu/abs/2003LNP...612...58F
Fletcher, L., Pollock, J.A., Potts, H.E., 2004, “Tracking of TRACE Ultraviolet Flare Footpoints”, Solar Phys., 222, 279–298. ADS: http://adsabs.harvard.edu/abs/2004SoPh..222..279F
Fletcher, L., Hannah, I.G., Hudson, H.S., Metcalf, T.R., 2007, “A TRACE White Light and RHESSI Hard X-Ray Study of Flare Energetics”, Astrophys. J., 656, 1187–1196. ADS: http://adsabs.harvard.edu/abs/2007ApJ...656.1187F
Foullon, C., Verwichte, E., Nakariakov, V.M., Fletcher, L., 2005, “X-ray quasi-periodic pulsations in solar flares as magnetohydrodynamic oscillations”, Astron. Astrophys., 440, L59–L62. ADS: http://adsabs.harvard.edu/abs/2005A&A...440L..59F
Frost, K.J., Dennis, B.R., 1971, “Evidence from Hard X-Rays for Two-Stage Particle Acceleration in a Solar Flare”, Astrophys. J., 165, 655. ADS: http://adsabs.harvard.edu/abs/1971ApJ...165..655F
Georgoulis, M.K., LaBonte, B.J., 2006, “Reconstruction of an Inductive Velocity Field Vector from Doppler Motions and a Pair of Solar Vector Magnetograms”, Astrophys. J., 636, 475–495. ADS: http://adsabs.harvard.edu/abs/2006ApJ...636..475G
Gosling, J.T., Birn, J., Hesse, M., 1995, “Three-dimensional magnetic reconnection and the magnetic topology of coronal mass ejection events”, Geophys. Res. Lett., 22, 869–872. ADS: http://adsabs.harvard.edu/abs/1995GeoRL..22..869G
Grigis, P.C., Benz, A.O., 2004, “The spectral evolution of impulsive solar X-ray flares”, Astron. Astrophys., 426, 1093–1101. ADS: http://adsabs.harvard.edu/abs/2004A&A...426.1093G
Grigis, P.C., Benz, A.O., 2005a, “The Evolution of Reconnection along an Arcade of Magnetic Loops”, Astrophys. J. Lett., 625, L143–L146. ADS: http://adsabs.harvard.edu/abs/2005ApJ...625L.143G
Grigis, P.C., Benz, A.O., 2005b, “The spectral evolution of impulsive solar X-ray flares. II. Comparison of observations with models”, Astron. Astrophys., 434, 1173–1181. ADS: http://adsabs.harvard.edu/abs/2005A&A...434.1173G
Grigis, P.C., Benz, A.O., 2006, “Electron acceleration in solar flares: theory of spectral evolution”, Astron. Astrophys., 458, 641–651. ADS: http://adsabs.harvard.edu/abs/2006A&A...458..641G
Hagyard, M.J., Venkatakrishnan, P., Smith Jr, J.B., 1990, “Nonpotential magnetic fields at sites of gamma-ray flares”, Astrophys. J. Suppl. Ser., 73, 159–163. ADS: http://adsabs.harvard.edu/abs/1990ApJS...73..159H
Hanaoka, Y., 1996, “Flares and Plasma Flow Caused by Interacting Coronal Loops”, Solar Phys., 165, 275–301. ADS: http://adsabs.harvard.edu/abs/1996SoPh..165..275H
Hanaoka, Y., 1997, “Double-Loop Configuration of Solar Flares”, Solar Phys., 173, 319–346. ADS: http://adsabs.harvard.edu/abs/1997SoPh..173..319H
Hey, J.S., 1983, The Radio Universe, Pergamon Press, Oxford, U.K.; New York, U.S.A., 3rd edn.
Heyvaerts, J., Priest, E.R., Rust, D.M., 1977, “An emerging flux model for the solar flare phenomenon”, Astrophys. J., 216, 123–137. ADS: http://adsabs.harvard.edu/abs/1977ApJ...216..123H
Hirayama, T., 1974, “Theoretical Model of Flares and Prominences. I: Evaporating Flare Model”, Solar Phys., 34, 323. ADS: http://adsabs.harvard.edu/abs/1974SoPh...34..323H
Holman, G.D., 1985, “Acceleration of runaway electrons and Joule heating in solar flares”, Astrophys. J., 293, 584–594. ADS: http://adsabs.harvard.edu/abs/1985ApJ...293..584H
Hori, K., Yokoyama, T., Kosugi, T., Shibata, K., 1997, “Pseudo-Two-dimensional Hydrodynamic Modeling of Solar Flare Loops”, Astrophys. J., 489, 426. ADS: http://adsabs.harvard.edu/abs/1997ApJ...489..426H
Hori, K., Yokoyama, T., Kosugi, T., Shibata, K., 1998, “Single and Multiple Solar Flare Loops: Hydrodynamics and Ca XIX Resonance Line Emission”, Astrophys. J., 500, 492–510. ADS: http://adsabs.harvard.edu/abs/1998ApJ...500..492H
Hoyng, P., Duijveman, A., Machado, M.E., Rust, D.M., Švestka, Z., Boelee, A., de Jager, C., Frost, K.T., Lafleur, H., Simnett, G.M., van Beek, H.F., Woodgate, B.E., 1981, “Origin and Location of the Hard X-Ray Emission in a Two-Ribbon Flare”, Astrophys. J. Lett., 246, L155. ADS: http://adsabs.harvard.edu/abs/1981ApJ...246L.155H
Hua, X.-M., Lingenfelter, R.E., 1987, “Solar flare neutron and accelerated ion angular distributions”, Astrophys. J., 323, 779–794. ADS: http://adsabs.harvard.edu/abs/1987ApJ...323..779H
Hudson, H.S., 1972, “Thick-Target Processes and White-Light Flares”, Solar Phys., 24, 414. ADS: http://adsabs.harvard.edu/abs/1972SoPh...24..414H
Hudson, H.S., Kosugi, T., Nitta, N.V., Shimojo, M., 2001, “Hard X-Radiation from a Fast Coronal Ejection”, Astrophys. J. Lett., 561, L211–L214. ADS: http://adsabs.harvard.edu/abs/2001ApJ...561L.211H
Hudson, H.S., Wolfson, C.J., Metcalf, T.R., 2006, “White-Light Flares: A TRACE/RHESSI Overview”, Solar Phys., 234, 79–93. ADS: http://adsabs.harvard.edu/abs/2006SoPh..234...79H
Hurford, G.J., Krucker, S., Lin, R.P., Schwartz, R.A., Share, G.H., Smith, D.M., 2006, “Gamma-Ray Imaging of the 2003 October/November Solar Flares”, Astrophys. J. Lett., 644, L93–L96. ADS: http://adsabs.harvard.edu/abs/2006ApJ...644L..93H
Jiang, Y.W., Liu, S., Liu, W., Petrosian, V., 2006, “Evolution of the Loop-Top Source of Solar Flares: Heating and Cooling Processes”, Astrophys. J., 638, 1140–1153. ADS: http://adsabs.harvard.edu/abs/2006ApJ...638.1140J
Kane, S.R., 1983, “Spatial structure of high energy photon sources in solar flares”, Solar Phys., 86, 355–365. ADS: http://adsabs.harvard.edu/abs/1983SoPh...86..355K
Kane, S.R., Anderson, K.A., 1970, “Spectral Characteristics of Impulsive Solar-Flare X-Rays > 10 KeV”, Astrophys. J., 162, 1003. ADS: http://adsabs.harvard.edu/abs/1970ApJ...162.1003K
Kane, S.R., Kreplin, R.W., Martres, M.-J., Pick, M., Soru-Escaut, I., 1974, “Acceleration of electrons in absence of detectable optical flares deduced from type III radio bursts, H alpha activity and soft X-ray emission”, Solar Phys., 38, 483–497. ADS: http://adsabs.harvard.edu/abs/1974SoPh...38..483K
Karlický, M., 2004, “Loop-top gyro-synchrotron source in post-maximum phase of the August 24, 2002 flare”, New Astronomy, 9, 383–389. ADS: http://adsabs.harvard.edu/abs/2004NewA....9..383K
Kašparová, J., Kontar, E.P., Brown, J.C., 2007, “Hard X-ray spectra and positions of solar flares observed by RHESSI: photospheric albedo, directivity and electron spectra”, Astron. Astrophys., 466, 705–712. ADS: http://adsabs.harvard.edu/abs/2007A&A...466..705K
Kawabata, K.-A., Ogawa, H., Suzuki, I., 1983, “A flare model deduced from HINOTORI and millimeter wave interferometer observations”, Solar Phys., 86, 247–251. ADS: http://adsabs.harvard.edu/abs/1983SoPh...86..247K
Khan, J.I., Vilmer, N., Saint-Hilaire, P., Benz, A.O., 2002, “The solar coronal origin of a slowly drifting decimetric-metric pulsation structure”, Astron. Astrophys., 388, 363–372. ADS: http://adsabs.harvard.edu/abs/2002A&A...388..363K
Kiplinger, A.L., 1995, “Comparative Studies of Hard X-Ray Spectral Evolution in Solar Flares with High-Energy Proton Events Observed at Earth”, Astrophys. J., 453, 973. ADS: http://adsabs.harvard.edu/abs/1995ApJ...453..973K
Kiplinger, A.L., Dennis, B.R., Frost, K.J., Orwig, L.E., 1984, “Fast variations in high-energy X-rays from solar flares and their constraints on nonthermal models”, Astrophys. J. Lett., 287, L105–L108. ADS: http://adsabs.harvard.edu/abs/1984ApJ...287L.105K
Klein, K.-L., Aurass, H., Soru-Escaut, I., Kalman, B., 1997, “Electron acceleration sites in a large-scale coronal structure.”, Astron. Astrophys., 320, 612–619. ADS: http://adsabs.harvard.edu/abs/1997A&A...320..612K
Klein, K.-L., Krucker, S., Trottet, G., Hoang, S., 2005, “Coronal phenomena at the release of solar energetic electron events”, Astron. Astrophys., 431, 1047–1060. ADS: http://adsabs.harvard.edu/abs/2005A&A...431.1047K
Klein, L., Pick, M., Trottet, G., Vilmer, N., Anderson, K., Kane, S., 1983, “Association between gradual hard X-ray emission and metric continua during large flares”, Solar Phys., 84, 295–310. ADS: http://adsabs.harvard.edu/abs/1983SoPh...84..295K
Kliem, B., Karlický, M., Benz, A.O., 2000, “Solar flare radio pulsations as a signature of dynamic magnetic reconnection”, Astron. Astrophys., 360, 715–728. ADS: http://adsabs.harvard.edu/abs/2000A&A...360..715K
Kontar, E.P., Brown, J.C., McArthur, G.K., 2002, “Nonuniform Target Ionization and Fitting Thick Target Electron Injection Spectra to RHESSI Data”, Solar Phys., 210, 419–429. ADS: http://adsabs.harvard.edu/abs/2002SoPh..210..419K
Kontar, E.P., Emslie, A.G., Piana, M., Massone, A.M., Brown, J.C., 2005, “Determination of Electron Flux Spectra in a Solar Flare with an Augmented Regularization Method: Application to Rhessi Data”, Solar Phys., 226, 317–325. ADS: http://adsabs.harvard.edu/abs/2005SoPh..226..317K
Kontar, E.P., MacKinnon, A.L., Schwartz, R.A., Brown, J.C., 2006, “Compton backscattered and primary X-rays from solar flares: angle dependent Green’s function correction for photospheric albedo”, Astron. Astrophys., 446, 1157–1163. ADS: http://adsabs.harvard.edu/abs/2006A&A...446.1157K
Kopp, R.A., Pneuman, G.W., 1976, “Magnetic reconnection in the corona and the loop prominence phenomenon”, Solar Phys., 50, 85–98. ADS: http://adsabs.harvard.edu/abs/1976SoPh...50...85K
Krucker, S., Benz, A.O., 1998, “Energy Distribution of Heating Processes in the Quiet Solar Corona”, Astrophys. J. Lett., 501, L213–L216. ADS: http://adsabs.harvard.edu/abs/1998ApJ...501L.213K
Krucker, S., Aschwanden, M.J., Bastian, T.S., Benz, A.O., 1995, “First VLA observation of a solar narrowband, millisecond spike event.”, Astron. Astrophys., 302, 551. ADS: http://adsabs.harvard.edu/abs/1995A&A...302..551K
Krucker, S., Benz, A.O., Aschwanden, M.J., 1997a, “YOHKOH observation of the source regions of solar narrowband, millisecond spike events”, Astron. Astrophys., 317, 569–579. ADS: http://adsabs.harvard.edu/abs/1997A&A...317..569K
Krucker, S., Benz, A.O., Bastian, T.S., Acton, L.W., 1997b, “X-Ray Network Flares of the Quiet Sun”, Astrophys. J., 488, 499. ADS: http://adsabs.harvard.edu/abs/1997ApJ...488..499K
Krucker, S., Hurford, G.J., Lin, R.P., 2003, “Hard X-Ray Source Motions in the 2002 July 23 Gamma-Ray Flare”, Astrophys. J. Lett., 595, L103–L106. ADS: http://adsabs.harvard.edu/abs/2003ApJ...595L.103K
Krucker, S., Fivian, M.D., Lin, R.P., 2005a, “Hard X-ray footpoint motions in solar flares: Comparing magnetic reconnection models with observations”, Adv. Space Res., 35, 1707–1711. ADS: http://adsabs.harvard.edu/abs/2005AdSpR..35.1707K
Krucker, S., Hurford, G.J., Lin, R.P., 2005b, “RHESSI X-ray and Gamma-ray observations of the January 20, 2005 event”, Eos Trans. AGU, 86, SH21A–01. ADS: http://adsabs.harvard.edu/abs/2005AGUFMSH21A..01K, fall Meet. Suppl.
Krucker, S., Battaglia, M., Cargill, P., Fletcher, L., Hudson, H., MacKinnon, A., Masuda, S., Sui, L., Tomcsak, M., Veronig, A., Vlahos, L., White, S., 2007, “Coronal hard X-ray and γ-ray sources”, unknown format, in preparation
Krüger, A., 1979, Introduction to solar radio astronomy and radio physics, vol. 16 of Geophysics and Astrophysics Monographs, Reidel, Dordrecht, Netherlands; Boston, U.S.A.
Kundu, M.R., 1984, “Relative positions of microwave and hard X-ray burst sources”, Adv. Space Res., 4, 157–162. ADS: http://adsabs.harvard.edu/abs/1984AdSpR...4Q.157K
Kundu, M.R., Schmahl, E.J., Velusamy, T., 1982, “Magnetic structure of a flaring region producing impulsive microwave and hard X-ray bursts”, Astrophys. J., 253, 963–974. ADS: http://adsabs.harvard.edu/abs/1982ApJ...253..963K
Kundu, M.R., White, S.M., Garaimov, V.I., Subramanian, P., Ananthakrishnan, S., Janardhan, P., 2006, “The Morphology of Decimetric Emission from Solar Flares: GMRT Observations”, Solar Phys., 236, 369–387. ADS: http://adsabs.harvard.edu/abs/2006SoPh..236..369K
Lin, R.P., Schwartz, R.A., Pelling, R.M., Hurley, K.C., 1981, “A new component of hard X-rays in solar flares”, Astrophys. J. Lett., 251, L109–L114. ADS: http://adsabs.harvard.edu/abs/1981ApJ...251L.109L
Lin, R.P., Larson, D., McFadden, J., Carlson, C.W., Ergun, R.E., Anderson, K.A., Ashford, S., McCarthy, M., Parks, G.K., Reme, H., Bosqued, J.M., d’Uston, C., Sanderson, T.R., Wenzel, K.P., 1996, “Observation of an impulsive solar electron event extending down to ∼0.5 keV energy”, Geophys. Res. Lett., 23, 1211–1214. ADS: http://adsabs.harvard.edu/abs/1996GeoRL..23.1211L
Lin, R.P., Dennis, B.R., Hurford, G.J., Smith, D.M., Zehnder, A., Harvey, P.R., Curtis, D.W., Pankow, D., Turin, P., Bester, M., Csillaghy, A., Lewis, M., Madden, N., van Beek, H.F., Appleby, M., Raudorf, T., McTiernan, J., Ramaty, R., Schmahl, E., Schwartz, R., Krucker, S., Abiad, R., Quinn, T., Berg, P., Hashii, M., Sterling, R., Jackson, R., Pratt, R., Campbell, R.D., Malone, D., Landis, D., Barrington-Leigh, C.P., Slassi-Sennou, S., Cork, C., Clark, D., Amato, D., Orwig, L., Boyle, R., Banks, I.S., Shirey, K., Tolbert, A.K., Zarro, D., Snow, F., Thomsen, K., Henneck, R., McHedlishvili, A., Ming, P., Fivian, M., Jordan, J., Wanner, R., Crubb, J., Preble, J., Matranga, M., Benz, A.O., Hudson, H., Canfield, R.C., Holman, G.D., Crannell, C., Kosugi, T., Emslie, A.G., Vilmer, N., Brown, J.C., Johns-Krull, C., Aschwanden, M.J., Metcalf, T.R., Conway, A., 2002, “The Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI)”, Solar Phys., 210, 3–32. ADS: http://adsabs.harvard.edu/abs/2002SoPh..210....3L
Lin, R.P., Krucker, S., Hurford, G.J., Smith, D.M., Hudson, H.S., Holman, G.D., Schwartz, R.A., Dennis, B.R., Share, G.H., Murphy, R.J., Emslie, A.G., Johns-Krull, C., Vilmer, N., 2003, “RHESSI Observations of Particle Acceleration and Energy Release in an Intense Solar Gamma-Ray Line Flare”, Astrophys. J. Lett., 595, L69–L76. ADS: http://adsabs.harvard.edu/abs/2003ApJ...595L..69L
Litvinenko, Y.E., 1996, “Particle Acceleration in Reconnecting Current Sheets with a Nonzero Magnetic Field”, Astrophys. J., 462, 997. ADS: http://adsabs.harvard.edu/abs/1996ApJ...462..997L
Liu, W., Liu, S., Jiang, Y.W., Petrosian, V., 2006, “RHESSI Observation of Chromospheric Evaporation”, Astrophys. J., 649, 1124–1139. ADS: http://adsabs.harvard.edu/abs/2006ApJ...649.1124L
Longcope, D.W., 2005, “Topological Methods for the Analysis of Solar Magnetic Fields”, Living Rev. Solar Phys., 2, lrsp-2005-7. URL (cited on 05 June 2007): http://www.livingreviews.org/lrsp-2005-7
Low, B.C., 1996, “Solar Activity and the Corona”, Solar Phys., 167, 217–265. ADS: http://adsabs.harvard.edu/abs/1996SoPh..167..217L
Mann, G., Aurass, H., Warmuth, A., 2006, “Electron acceleration by the reconnection outflow shock during solar flares”, Astron. Astrophys., 454, 969–974. ADS: http://adsabs.harvard.edu/abs/2006A&A...454..969M
Mariska, J.T., McTiernan, J.M., 1999, “Hard and Soft X-Ray Observations of Occulted and Nonocculted Solar Limb Flares”, Astrophys. J., 514, 484–492. ADS: http://adsabs.harvard.edu/abs/1999ApJ...514..484M
Mariska, J.T., Doschek, G.A., Bentley, R.D., 1993, “Flare Plasma Dynamics Observed with the YOHKOH Bragg Crystal Spectrometer. I. Properties of the CA XIX Resonance Line”, Astrophys. J., 419, 418. ADS: http://adsabs.harvard.edu/abs/1993ApJ...419..418M
Marsh, K.A., Hurford, G.J., 1982, “High spatial resolution solar microwave observations”, Annu. Rev. Astron. Astrophys., 20, 497–516. ADS: http://adsabs.harvard.edu/abs/1982ARA&A..20..497M
Martin, S.F., 1989, “Mass motions associated with solar flares”, Solar Phys., 121, 215–238. ADS: http://adsabs.harvard.edu/abs/1989SoPh..121..215M
Masuda, S., Kosugi, T., Hara, H., Tsuneta, S., Ogawara, Y., 1994, “A Loop-Top Hard X-Ray Source in a Compact Solar Flare as Evidence for Magnetic Reconnection”, Nature, 371, 495. ADS: http://adsabs.harvard.edu/abs/1994Natur.371..495M
Masuda, S., Sato, J., Kosugi, T., Sakao, T., 2000, “Spectral Characteristics of Above-the-Looptop Hard X-Ray Source”, Adv. Space Res., 26, 493–496. ADS: http://adsabs.harvard.edu/abs/2000AdSpR..26..493M
Masuda, S., Kosugi, T., Hudson, H.S., 2001, “A Hard X-ray Two-Ribbon Flare Observed with Yohkoh/HXT”, Solar Phys., 204, 55–67. ADS: http://adsabs.harvard.edu/abs/2001SoPh..204...55M
Matthews, S.A., van Driel-Gesztelyi, L., Hudson, H.S., Nitta, N.V., 2003, “A catalogue of white-light flares observed by Yohkoh”, Astron. Astrophys., 409, 1107–1125. ADS: http://adsabs.harvard.edu/abs/2003A&A...409.1107M
McTiernan, J.M., Fisher, G.H., Li, P., 1999, “The Solar Flare Soft X-Ray Differential Emission Measure and the Neupert Effect at Different Temperatures”, Astrophys. J., 514, 472–483. ADS: http://adsabs.harvard.edu/abs/1999ApJ...514..472M
Melnikov, V.F., Shibasaki, K., Reznikova, V.E., 2002, “Loop-Top Nonthermal Microwave Source in Extended Solar Flaring Loops”, Astrophys. J. Lett., 580, L185–L188. ADS: http://adsabs.harvard.edu/abs/2002ApJ...580L.185M
Melrose, D.B., 1980, Plasma astrophysics: Nonthermal processes in diffuse magnetized plasmas, 2 Vols., Gordon and Breach, New York, U.S.A.
Melrose, D.B., 1990, “Particle Acceleration Processes in the Solar Corona”, Aust. J. Phys., 43, 703–752. ADS: http://adsabs.harvard.edu/abs/1990AuJPh..43..703M
Metcalf, T.R., Alexander, D., 1999, “Coronal Trapping of Energetic Flare Particles: Yohkoh/HXT Observations”, Astrophys. J., 522, 1108–1116. ADS: http://adsabs.harvard.edu/abs/1999ApJ...522.1108M
Metcalf, T.R., Alexander, D., Hudson, H.S., Longcope, D.W., 2003, “TRACE and Yohkoh Observations of a White-Light Flare”, Astrophys. J., 595, 483–492. ADS: http://adsabs.harvard.edu/abs/2003ApJ...595..483M
Miller, J.A., Cargill, P.J., Emslie, A.G., Holman, G.D., Dennis, B.R., LaRosa, T.N., Winglee, R.M., Benka, S.G., Tsuneta, S., 1997, “Critical issues for understanding particle acceleration in impulsive solar flares”, J. Geophys. Res., 102, 14 631–14 660. ADS: http://adsabs.harvard.edu/abs/1997JGR...10214631M
Milligan, R.O., Gallagher, P.T., Mathioudakis, M., Keenan, F.P., Bloomfield, D.S., 2005, “Plasma diagnostics of active-region evolution and implications for coronal heating”, Mon. Not. R. Astron. Soc., 363, 259–267. ADS: http://adsabs.harvard.edu/abs/2005MNRAS.363..259M
Milligan, R.O., Gallagher, P.T., Mathioudakis, M., Keenan, F.P., 2006, “Observational Evidence of Gentle Chromospheric Evaporation during the Impulsive Phase of a Solar Flare”, Astrophys. J. Lett., 642, L169–L171. ADS: http://adsabs.harvard.edu/abs/2006ApJ...642L.169M
Moore, R.L., Sterling, A.C., Hudson, H.S., Lemen, J.R., 2001, “Onset of the Magnetic Explosion in Solar Flares and Coronal Mass Ejections”, Astrophys. J., 552, 833–848. ADS: http://adsabs.harvard.edu/abs/2001ApJ...552..833M
Moreton, G.F., 1964, “Hα Shock Wave and Winking Filaments with the Flare of 20 September 1963”, Astron. J., 69, 145. ADS: http://adsabs.harvard.edu/abs/1964AJ.....69Q.145M
Murdin, P. (Ed.), 2001, Encyclopedia of Astronomy and Astrophysics, 4 vols., IOP; Nature, Bristol, U.K.; London, U.K.
Nakariakov, V.M., Foullon, C., Verwichte, E., Young, N.P., 2006, “Quasi-periodic modulation of solar and stellar flaring emission by magnetohydrodynamic oscillations in a nearby loop”, Astron. Astrophys., 452, 343–346. ADS: http://adsabs.harvard.edu/abs/2006A&A...452..343N
Neidig, D.F., 1989, “The importance of solar white-light flares”, Solar Phys., 121, 261–269. ADS: http://adsabs.harvard.edu/abs/1989SoPh..121..261N
Neupert, W.M., 1968, “Comparison of Solar X-Ray Line Emission with Microwave Emission during Flares”, Astrophys. J. Lett., 153, L59. ADS: http://adsabs.harvard.edu/abs/1968ApJ...153L..59N
Nindos, A., White, S.M., Kundu, M.R., Gary, D.E., 2000, “Observations and Models of a Flaring Loop”, Astrophys. J., 533, 1053–1062. ADS: http://adsabs.harvard.edu/abs/2000ApJ...533.1053N
Nishio, M., Yaji, K., Kosugi, T., Nakajima, H., Sakurai, T., 1997, “Magnetic Field Configuration in Impulsive Solar Flares Inferred from Coaligned Microwave/X-Ray Images”, Astrophys. J., 489, 976. ADS: http://adsabs.harvard.edu/abs/1997ApJ...489..976N
Øieroset, M., Phan, T.D., Fujimoto, M., Lin, R.P., Lepping, R.P., 2001, “In situ detection of collisionless reconnection in the Earth’s magnetotail”, Nature, 412, 414–417. ADS: http://adsabs.harvard.edu/abs/2001Natur.412..4140
Paesold, G., Benz, A.O., Klein, K.-L., Vilmer, N., 2001, “Spatial analysis of solar type III events associated with narrow band spikes at metric wavelengths”, Astron. Astrophys., 371, 333–342. ADS: http://adsabs.harvard.edu/abs/2001A&A...371..333P
Parks, G.K., Winckler, J.R., 1969, “Sixteen-Second Periodic Pulsations Observed in the Correlated Microwave and Energetic X-Ray Emission from a Solar Flare”, Astrophys. J. Lett., 155, L117. ADS: http://adsabs.harvard.edu/abs/1969ApJ...155L.117P
Parnell, C.E., Jupp, P.E., 2000, “Statistical Analysis of the Energy Distribution of Nanoflares in the Quiet Sun”, Astrophys. J., 529, 554–569. ADS: http://adsabs.harvard.edu/abs/2000ApJ...529..554P
Peterson, L.E., Winckler, J.R., 1959, “Gamma-Ray Burst from a Solar Flare”, J. Geophys. Res., 64, 697. ADS: http://adsabs.harvard.edu/abs/1959JGR....64..697P
Petrosian, V., Donaghy, T.Q., McTiernan, J.M., 2002, “Loop Top Hard X-Ray Emission in Solar Flares: Images and Statistics”, Astrophys. J., 569, 459–473. ADS: http://adsabs.harvard.edu/abs/2002ApJ...569..459P
Petrosian, V., Yan, H., Lazarian, A., 2006, “Damping of Magnetohydrodynamic Turbulence in Solar Flares”, Astrophys. J., 644, 603–612. ADS: http://adsabs.harvard.edu/abs/2006ApJ...644..603P
Pevtsov, A.A., Canfield, R.C., Zirin, H., 1996, “Reconnection and Helicity in a Solar Flare”, Astrophys. J., 473, 533. ADS: http://adsabs.harvard.edu/abs/1996ApJ...473..533P
Piana, M., Massone, A.M., Kontar, E.P., Emslie, A.G., Brown, J.C., Schwartz, R.A., 2003, “Regularized Electron Flux Spectra in the 2002 July 23 Solar Flare”, Astrophys. J. Lett., 595, L127–L130. ADS: http://adsabs.harvard.edu/abs/2003ApJ...595L.127P
Pick, M., van den Oord, G.H.J., 1990, “Observations of beam propagation”, Solar Phys., 130, 83–99. ADS: http://adsabs.harvard.edu/abs/1990SoPh..130...83P
Priest, E.R., Forbes, T.G., 2000, Magnetic Reconnection: MHD Theory and Applications, Cambridge University Press, Cambridge, U.K.; New York, U.S.A.
Radziszewski, K., Rudawy, P., Phillips, K.J.H., 2007, “High time resolution observations of solar Hα flares. I”, Astron. Astrophys., 461, 303–313. ADS: http://adsabs.harvard.edu/abs/2007A&A...461..303R
Ramaty, R., Kozlovsky, B., 1974, “Deuterium, tritium, and helium-3 production in solar flares”, Astrophys. J., 193, 729–740. ADS: http://adsabs.harvard.edu/abs/1974ApJ...193..729R
Ramaty, R., Mandzhavidze, N., Kozlovsky, B., Murphy, R.J., 1995, “Solar Atmopheric Abundances and Energy Content in Flare Accelerated Ions from Gamma-Ray Spectroscopy”, Astrophys. J. Lett., 455, L193. ADS: http://adsabs.harvard.edu/abs/1995ApJ...455L.193R
Reeves, K.K., Warren, H.P., Forbes, T.G., 2007, “Theoretical Predictions of X-Ray and Extreme-UV Flare Emissions Using a Loss-of-Equilibrium Model of Solar Eruptions”, Astrophys. J., 668, 1210–1220. ADS: http://adsabs.harvard.edu/abs/2007ApJ...668.1210R
Régnier, S., Canfield, R.C., 2006, “Evolution of magnetic fields and energetics of flares in active region 8210”, Astron. Astrophys., 451, 319–330. ADS: http://adsabs.harvard.edu/abs/2006A&A...451..319R
Roberts, B., Edwin, P.M., Benz, A.O., 1983, “Fast pulsations in the solar corona”, Nature, 305, 688–690. ADS: http://adsabs.harvard.edu/abs/1983Natur.305..688R
Ryan, J.M., Lockwood, J.A., Debrunner, H., 2000, “Solar Energetic Particles”, Space Sci. Rev., 93, 35–53. ADS: http://adsabs.harvard.edu/abs/2000SSRv...93...35R
Saint-Hilaire, P., Benz, A.O., 2002, “Energy budget and imaging spectroscopy of a compact flare”, Solar Phys., 210, 287–306. ADS: http://adsabs.harvard.edu/abs/2002SoPh..210..287S
Saint-Hilaire, P., Benz, A.O., 2005, “Thermal and non-thermal energies of solar flares”, Astron. Astrophys., 435, 743–752. ADS: http://adsabs.harvard.edu/abs/2005A&A...435..743S
Schlickeiser, R., Miller, J.A., 1998, “Quasi-linear Theory of Cosmic-Ray Transport and Acceleration: The Role of Oblique Magnetohydrodynamic Waves and Transit-Time Damping”, Astrophys. J., 492, 352. ADS: http://adsabs.harvard.edu/abs/1998ApJ...492..352S
Schrijver, C.J., Aschwanden, M.J., Title, A.M., 2002, “Transverse oscillations in coronal loops observed with TRACE — I. An Overview of Events, Movies, and a Discussion of Common Properties and Required Conditions”, Solar Phys., 206, 69–98. ADS: http://adsabs.harvard.edu/abs/2002SoPh..206...69S
Schwenn, R., 2006, “Space Weather: The Solar Perspective”, Living Rev. Solar Phys., 3, lrsp-2006-2. URL (cited on 05 June 2007): http://www.livingreviews.org/lrsp-2006-2
Shibata, K., 1999, “Evidence of Magnetic Reconnection in Solar Flares and a Unified Model of Flares”, Astrophys. Space Sci., 264, 129–144. ADS: http://adsabs.harvard.edu/abs/1999Ap&SS.264..129S
Shibata, K., Masuda, S., Shimojo, M., Hara, H., Yokoyama, T., Tsuneta, S., Kosugi, T., Ogawara, Y., 1995, “Hot-Plasma Ejections Associated with Compact-Loop Solar Flares”, Astrophys. J. Lett., 451, L83. ADS: http://adsabs.harvard.edu/abs/1995ApJ...451L..83S
Silva, A.V.R., White, S.M., Lin, R.P., de Pater, I., Shibasaki, K., Hudson, H.S., Kundu, M.R., 1996, “First Images of a Solar Flare at Millimeter Wavelengths”, Astrophys. J. Lett., 458, L49. ADS: http://adsabs.harvard.edu/abs/1996ApJ...458L..49S
Silva, A.V.R., Wang, H., Gary, D.E., Nitta, N., Zirin, H., 1997, “Imaging the Chromospheric Evaporation of the 1994 June 30 Solar Flare”, Astrophys. J., 481, 978. ADS: http://adsabs.harvard.edu/abs/1997ApJ...481..978S
Singh, J., Sakurai, T., Ichimoto, K., Suzuki, I., Hagino, M., 2005, “Spectroscopic Studies of Solar Corona VII. Formation of a Coronal Loop by Evaporation”, Solar Phys., 226, 201–221. ADS: http://adsabs.harvard.edu/abs/2005SoPh..226..201S
Slottje, C., 1978, “Millisecond microwave spikes in a solar flare”, Nature, 275, 520. ADS: http://adsabs.harvard.edu/abs/1978Natur.275..520S
Solanki, S.K., Lagg, A., Woch, J., Krupp, N., Collados, M., 2003, “Three-dimensional magnetic field topology in a region of solar coronal heating”, Nature, 425, 692–695. ADS: http://adsabs.harvard.edu/abs/2003Natur.425..692S
Somov, B.V., 1992, Physical Processes in Solar Flares, vol. 172 of Astrophysics and Space Science Library, Kluwer, Dordrecht, Netherlands; Boston, U.S.A. ADS: http://adsabs.harvard.edu/abs/1992QB526.F6S65....
Spicer, D.S., Sudan, R.N., 1984, “Beam-return current systems in solar flares”, Astrophys. J., 280, 448–456. ADS: http://adsabs.harvard.edu/abs/1984ApJ...280..448S
Sterling, A.C., Shibata, K., Mariska, J.T., 1993, “Solar chromospheric and transition region response to energy deposition in the middle and upper chromosphere”, Astrophys. J., 407, 778–789. ADS: http://adsabs.harvard.edu/abs/1993ApJ...407..778S
Strong, K.T., Benz, A.O., Dennis, B.R., Poland, A.I., Leibacher, J.W., Mewe, R., Schrijver, J., Simnett, G., Smith Jr, J.B., Sylwester, J., 1984, “A multiwavelength study of a double impulsive flare”, Solar Phys., 91, 325–344. ADS: http://adsabs.harvard.edu/abs/1984SoPh...91..325S
Sturrock, P.A., 1966, “Model of the High-Energy Phase of Solar Flares”, Nature, 211, 695. ADS: http://adsabs.harvard.edu/abs/1966Natur.211..695S
Sturrock, P.A. (Ed.), 1980, Solar flares: A monograph from SKYLAB Solar Workshop II, Colorado Associated University Press, Boulder, U.S.A. ADS: http://adsabs.harvard.edu/abs/1980sfsl.work.....S
Sui, L., Holman, G.D., Dennis, B.R., 2004, “Evidence for Magnetic Reconnection in Three Homologous Solar Flares Observed by RHESSI”, Astrophys. J., 612, 546–556. ADS: http://adsabs.harvard.edu/abs/2004ApJ...612..546S
Sui, L., Holman, G.D., Dennis, B.R., 2006, “Enigma of a Flare Involving Multiple-Loop Interactions: Emerging, Colliding Loops or Magnetic Breakout?”, Astrophys. J., 646, 605–614. ADS: http://adsabs.harvard.edu/abs/2006ApJ...646..605S
Suzuki, S., Dulk, G.A., 1985, “Bursts of Type III and Type V”, in Solar Radiophysics: Studies of Emission from the Sun at Metre Wavelengths, (Eds.) McLean, D.J., Labrum, N.R., pp. 289–332, Cambridge University Press, Cambridge, U.K.; New York, U.S.A. ADS: http://adsabs.harvard.edu/abs/1985srph.book..289S
Švestka, Z., 1976, Solar Flares, vol. 8 of Geophysics and Astrophysics Monographs, Reidel, Dordrecht, Netherlands; Boston; U.S.A.
Svestka, Z., 1984, “Revivals of a coronal arch”, Solar Phys., 94, 171–192. ADS: http://adsabs.harvard.edu/abs/1984SoPh...94..171S
Švestka, Z., Hoyng, P., van Tend, W., Boelee, A., de Jager, C., Stewart, R.T., Acton, L.W., Bruner, E.C., Gabriel, A.H., Rapley, C.G., de Jager, C., Lafleur, H., Nelson, G., Simnett, G.M., van Beek, H.F., Wagner, W.J., 1982, “Observations of a post-flare radio burst in X-rays”, Solar Phys., 75, 305–329. ADS: http://adsabs.harvard.edu/abs/1982SoPh...75..305S
Sweet, P.A., 1958, “The Neutral Point Theory of Solar Flares”, in Electromagnetic Phenomena in Cosmical Physics, (Ed.) Lehnert, B., Proceedings of IAU Symposium No. 6, pp. 123–134, Cambridge University Press, Cambridge, U.K. ADS: http://adsabs.harvard.edu/abs/1958IAUS....6..123S
Tajima, T., Shibata, K. (Eds.), 1997, Plasma astrophysics, vol. 98 of Frontiers in Physics, Addison-Wesley, Reading, U.S.A. ADS: http://adsabs.harvard.edu/abs/1997plas.conf.....T
Terradas, J., Andries, J., Goossens, M., 2007, “Coronal loop oscillations: energy considerations and initial value problem”, Astron. Astrophys., 469, 1135–1143. ADS: http://adsabs.harvard.edu/abs/2007A&A...469.1135T
Tsuneta, S., Naito, T., 1998, “Fermi Acceleration at the Fast Shock in a Solar Flare and the Impulsive Loop-Top Hard X-Ray Source”, Astrophys. J. Lett., 495, L67–L71. ADS: http://adsabs.harvard.edu/abs/1998ApJ...495L..67T
Tsuneta, S., Masuda, S., Kosugi, T., Sato, J., 1997, “Hot and Superhot Plasmas above an Impulsive Flare Loop”, Astrophys. J., 478, 787. ADS: http://adsabs.harvard.edu/abs/1997ApJ...478..787T
van den Oord, G.H.J., 1990, “The electrodynamics of beam/return current systems in the solar corona”, Astron. Astrophys., 234, 496–518. ADS: http://adsabs.harvard.edu/abs/1990A&A...234..496V
Veronig, A., Vršnak, B., Dennis, B.R., Temmer, M., Hanslmeier, A., Magdalenić, J., 2002, “Investigation of the Neupert effect in solar flares. I. Statistical properties and the evaporation model”, Astron. Astrophys., 392, 699–712. ADS: http://adsabs.harvard.edu/abs/2002A&A...392..699V
Veronig, A.M., Brown, J.C., 2004, “A Coronal Thick-Target Interpretation of Two Hard X-Ray Loop Events”, Astrophys. J. Lett., 603, L117–L120. ADS: http://adsabs.harvard.edu/abs/2004ApJ...603L.117V
Veronig, A.M., Brown, J.C., Dennis, B.R., Schwartz, R.A., Sui, L., Tolbert, A.K., 2005, “Physics of the Neupert Effect: Estimates of the Effects of Source Energy, Mass Transport, and Geometry Using RHESSI and GOES Data”, Astrophys. J., 621, 482–497. ADS: http://adsabs.harvard.edu/abs/2005ApJ...621..482V
Vorpahl, J.A., 1972, “X-Radiation (E > 10 keV), Hα and Microwave Emission During the Impulsive Phase of Solar Flares”, Solar Phys., 26, 397. ADS: http://adsabs.harvard.edu/abs/1972SoPh...26..397V
Wang, H., Gary, D.E., Lim, J., Schwartz, R.A., 1994, “Miocrowave spectral imaging, H-alpha and hard X-ray observations of a solar limb flare”, Astrophys. J., 433, 379–388. ADS: http://adsabs.harvard.edu/abs/1994ApJ...433..379W
Wang, H., Qiu, J., Jing, J., Spirock, T.J., Yurchyshyn, V., Abramenko, V., Ji, H., Goode, P.R., 2004, “Evidence of Rapid Flux Emergence Associated with the M8.7 Flare on 2002 July 26”, Astrophys. J., 605, 931–937. ADS: http://adsabs.harvard.edu/abs/2004ApJ...605..931W
Warren, H.P., Bookbinder, J.A., Forbes, T.G., Golub, L., Hudson, H.S., Reeves, K., Warshall, A., 1999, “TRACE and Yohkoh Observations of High-Temperature Plasma in a Two-Ribbon Limb Flare”, Astrophys. J. Lett., 527, L121–L124. ADS: http://adsabs.harvard.edu/abs/1999ApJ...527L.121W
Wheatland, M.S., Melrose, D.B., 1995, “Interpreting YOHKOH hard and soft X-ray flare observations”, Solar Phys., 158, 283–299. ADS: http://adsabs.harvard.edu/abs/1995SoPh..158..283W
Wild, J.P., 1950, “Observations of the Spectrum of High-Intensity Solar Radiation at Metre Wavelengths. III. Isolated Bursts”, Aust. J. Sci. Res. A, 3, 541. ADS: http://adsabs.harvard.edu/abs/1950AuSRA...3..541W
Woods, T.N., Eparvier, F.G., Fontenla, J., Harder, J., Kopp, G., McClintock, W.E., Rottman, G., Smiley, B., Snow, M., 2004, “Solar irradiance variability during the October 2003 solar storm period”, Geophys. Res. Lett., 31, L10802. ADS: http://adsabs.harvard.edu/abs/2004GeoRL..3110802W
Wuelser, J.-P., Marti, H., 1989, “High time resolution observations of H alpha line profiles during the impulsive phase of a solar flare”, Astrophys. J., 341, 1088–1096. ADS: http://adsabs.harvard.edu/abs/1989ApJ...341.1088W
Wuelser, J.-P., Canfield, R.C., Acton, L.W., Culhane, J.L., Phillips, A., Fludra, A., Sakao, T., Masuda, S., Kosugi, T., Tsuneta, S., 1994, “Multispectral observations of chromospheric evaporation in the 1991 November 15 X-class solar flare”, Astrophys. J., 424, 459–465. ADS: http://adsabs.harvard.edu/abs/1994ApJ...424..459W
Yokoyama, T., Akita, K., Morimoto, T., Inoue, K., Newmark, J., 2001, “Clear Evidence of Reconnection Inflow of a Solar Flare”, Astrophys. J. Lett., 546, L69–L72. ADS: http://adsabs.harvard.edu/abs/2001ApJ...546L..69Y
Zarro, D.M., Lemen, J.R., 1988, “Conduction-driven chromospheric evaporation in a solar flare”, Astrophys. J., 329, 456–463. ADS: http://adsabs.harvard.edu/abs/1988ApJ...329..456Z
Zharkova, V.V., Brown, J.C., Syniavskii, D.V., 1995, “Electron beam dynamics and hard X-ray bremsstrahlung polarization in a flaring loop with return current and converging magnetic field”, Astron. Astrophys., 304, 284. ADS: http://adsabs.harvard.edu/abs/1995A&A...304..284Z
Zirin, H., Wang, H., 1993, “Narrow lanes of transverse magnetic field in sunspots”, Nature, 363, 426–428. ADS: http://adsabs.harvard.edu/abs/1993Natur.363..426Z
Acknowledgements
I thank Paolo Grigis and two anonymous referees for a critical and constructive reading of the manuscript. The flare work at ETH Zurich is supported by the Swiss National Science Foundation (grant nr. 200020-113556). This review has made use of NASA’s Astrophysical Data System Bibliographic Services.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
41116_2015_9174_MOESM1_ESM.mpeg
mpg-Movie (14976.1992188 KB) Still from a movie showing Soft X-rays (red), hard X-rays (blue) and gamma-rays (purple) observed by the RHESSI satellite are overlaid on an optical Hα image. The movie starts in white light zooming into an active region. The color then changes to the Hα line of hydrogen, emitted in the chromosphere. Its brightening indicates the start of the flare. Visualization by RHESSI scientists.
41116_2015_9174_MOESM2_ESM.mpg
mpg-Movie (15763.2460938 KB) Still from a movie showing Flare observed in the Fe xii line at 195 Å (sensitive to 1.5 MK plasma) by the TRACE satellite. Note the different phases, starting with irregular brightnings in the impulsive phase. The luminosity peaks when a sheet-like structures appears above the initial brightening. The diffuse emission at this time is attributed to the presence of the Fe xxiv (192 Å) line within the TRACE passband, emitted by a plasma of 20 MK. The flare proceeds into a long decay phase with post-flare loops growing in height.
41116_2015_9174_MOESM3_ESM.mov
mpg-Movie (15435.8730469 KB) Still from a movie showing Zoom into an active region where a large flare took place on April 21, 2002. The movie starts in white light observed by the SOHO/MDI instrument, adds the coronal images observed by the SOHO/LASCO coronagraph, then changes to extreme ultraviolet observed by SOHO/EIT and later by the TRACE satellite, and later the RHESSI observations of the flare in soft X-rays (red) and hard X-rays (blue). The focus then goes to the associated coronal mass ejection observed by the coronagraph. The movie ends in a storm of streaks produced by energetic flare particles (mostly protons), hitting the detectors on the Solar and Heliospheric Observatory (SOHO) in space. Visualization by RHESSI scientists.
41116_2015_9174_MOESM4_ESM.gif
mpg-Movie (118.463867188 KB) Still from a movie showing Left: White light image of a sunspot taken with SOT on board the Hinode satellite. The resolution is 2″. Visualization by Hinode scientists. Right: Vector magnetogram showing in red the direction of the magnetic field and its strength (length of the bar). The movie shows the evolution in the photospheric fields that has led to an X class flare in the lower part of the active region. Courtesy of NAOJ/NINS.
41116_2015_9174_MOESM5_ESM.mpg
mpg-Movie (1895.02832031 KB) Still from a movie showing Hard X-ray footpoints (with error bars) observed with the RHESSI satellite during the flare of November 9, 2002. Simultaneous footpoints are connected by a line colored sequentially with time. The footpoint information is overlaid on a SOHO/EIT image at 195 Å, indicating enhanced density in the corona. The movie shows two simultaneous footpoints connected by a vertical half-circle. The flux at each footpoint is indicated by the size of the purple circle at logarithmic scale (from Grigis and Benz, 2005a), courtesy of Paolo Grigis.
41116_2015_9174_MOESM6_ESM.mpg
mpg-Movie (9783.75390625 KB) Still from a movie showing Left: RHESSI flare observations of soft X-rays (red, 8–12 keV) and hard X-rays (blue, 20–50 keV) overlaid on an Hα background. Note the high-energy footpoints moving on the Hα flare ribbons, which moves apart in the very late phase. Visualization by RHESSI scientists.
41116_2015_9174_MOESM7_ESM.gif
mpg-Movie (264.590820312 KB) Still from a movie showing Thermal emission and a flare observed with the Nobeyama interferometer at 17 GHz. The event has the classic signatures of an event associated with a coronal mass ejection: motion is seen first in the prominence material, then the flare goes off, leaving long-duration soft-X-ray emitting loops around for several hours. Note that the prominence material is at a temperature of less than 10,000 degrees K (shown at top), whereas the flare loops come from material at 10 MK: both cool and hot material show up at this radio frequency. The left panel shows total intensity, and the right panel shows circularly-polarized radio emission. Polarization is only detected during the early phase of the flare, when very energetic electrons fill up the loop and emit intense synchrotron radiation. Courtesy of Stephen White.
41116_2015_9174_MOESM8_ESM.mpg
mpg-Movie (1139.47753906 KB) Still from a movie showing Soft X-ray images observed by Hinode on April 30, 2007. It shows an active region during two hours. Some small flares or microflares occurred; the largest was of class B2.6 (prepared by A. Savcheva).
41116_2015_9174_MOESM9_ESM.mpg
mpg-Movie (3460.421875 KB) Still from a movie showing An overview in Fe xii EUV emission observed by EIT/SOHO, later zooming into the observations by TRACE, both showing thermal coronal emission of a plasma at about 1.5 MK. The 12–25 keV hard X-ray emission observed by RHESSI is shown in red and yellow colors (courtesy of Pascal Saint-Hilaire).
41116_2015_9174_MOESM10_ESM.mpg
mpg-Movie (2078.88867188 KB) Still from a movie showing The particle distribution vs. energy in time (blue) as described by Equation (9). A tail develops out of the thermal distribution (purple). The solution becomes stationary after about one second when acceleration balances particle escape out of the acceleration region. The spectral index resulting from fitting a power-law in the region limited by dashed red lines is also shown (from Grigis and Benz, 2006).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Benz, A.O. Flare Observations. Living Rev. Sol. Phys. 5, 1 (2008). https://doi.org/10.12942/lrsp-2008-1
Published:
DOI: https://doi.org/10.12942/lrsp-2008-1
Keywords
Article history
Latest
Flare Observations- Published:
- 09 December 2016
DOI: https://doi.org/10.1007/s41116-016-0004-3
Original
Flare Observations- Published:
- 01 December 2008
DOI: https://doi.org/10.12942/lrsp-2008-1