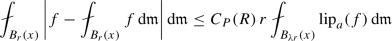On the integration of $L^0$-Banach $L^0$-modules and its applications to vector calculus on $\textsf{RCD}$ spaces

Abstract

A finite-dimensional $\textsf{RCD}$ space can be foliated into sufficiently regular leaves, where a differential calculus can be performed. Two important examples are given by the measure-theoretic boundary of the superlevel set of a function of bounded variation and the needle decomposition associated to a Lipschitz function. The aim of this paper is to connect the vector calculus on the lower dimensional leaves with the one on the base space. In order to achieve this goal, we develop a general theory of integration of $L^0$-Banach $L^0$-modules of independent interest. Roughly speaking, we study how to ‘patch together’ vector fields defined on the leaves that are measurable with respect to the foliation parameter.

1 Introduction

In the setting of metric measure spaces, the theory of $L^0$-normed $L^0$-modules was introduced by Gigli in [27] and later refined in [26]. The goal was to develop a vector calculus in this nonsmooth framework, which could provide effective notions of measurable $1$-forms and vector fields. Indeed, one of the main objects of study in [26, 27] is the cotangent module $L^0(T^*\textrm{X})$ over a metric measure space $(\textrm{X},\textsf{d},\mathfrak {m})$, which is built upon the Sobolev space $W^{1,2}(\textrm{X})$ and comes naturally with a differential operator $\text {d}:W^{1,2}(\textrm{X})\rightarrow L^0(T^*\textrm{X})$. By duality, one then defines the tangent module $L^0(T\textrm{X})$. Both $L^0(T^*\textrm{X})$ and $L^0(T\textrm{X})$ are $L^0(\mathfrak {m})$-Banach $L^0(\mathfrak {m})$-modules, see Definition 2.13. The study of tangent and cotangent modules had remarkable analytic and geometric applications in the field of analysis on metric measure spaces, especially in the fast-developing theory of metric measure spaces verifying synthetic Riemannian Ricci curvature lower bounds, the so-called $\textsf{RCD}$ spaces (see the survey [2] and the references therein indicated). Due to this reason, the technical machinery we develop in this paper is for $L^0$-Banach $L^0$-modules over a $\sigma$-finite measure space. However, the language of $L^0$-normed $L^0$-modules is used in other research fields as well. Let us give a brief historical account about other independent developments on the theory of $L^0$-normed $L^0$-modules. The notion of $L^0(\mathfrak {m})$-normed $L^0(\mathfrak {m})$-module in the sense of Gigli [27] is exactly the notion of a random normed module over $\mathbb {R}$ with base $(X,\Sigma ,\mathfrak {m})$ (RN module in short) that Guo introduced after the previous work on probabilistic metric spaces by Schweizer and Sklar [47]. We refer the reader to Guo’s contributions [31,32,33,34,35,36]. In these series of works as well as in many other papers, Guo and his coauthors studied—in the case of $\sigma$-finite measure spaces—functional properties of RN modules and random inner product spaces. Several topologies on the module structure are studied. The concept of random inner product spaces shares similarities with the functional-analytic machinery developed to study the modules $L^0(T^*\textrm{X})$ and $L^0(T\textrm{X})$ in the infinitesimal Hilbertian setting in [27]. For another independent work see also the work by Haydon, Levy and Raynaud [37]. For the purpose of this paper, since our study is motivated by application to $\textsf{RCD}$ theory and nonsmooth differential geometry, we use the language in [27].

Let us consider a disjoint measure-valued map $q\mapsto \mu _q$ on a measurable space $(\textrm{X},\Sigma )$. Roughly speaking, the measures $\mu _q$ are concentrated on pairwise disjoint measurable subsets of $\textrm{X}$ and vary in a measurable way with respect to the parameter $q\in Q$, where $(Q,{\mathcal {Q}},{\mathfrak {q}})$ is a given measure space; see Definition 2.3. In Definition 3.1 we propose a notion of $L^0$-Banach $L^0$-module bundle $(\{{\mathscr {M}}_q\}_{q\in Q},\Theta ,\Phi )$ consistent with $q\mapsto \mu _q$. Shortly said, each ${\mathscr {M}}_q$ is an $L^0(\mu _q)$-Banach $L^0(\mu _q)$-module, while $\Theta$ and $\Phi$ are families of test sections and test functions, respectively, which are used to declare which sections $Q\ni q\mapsto v_q\in {\mathscr {M}}_q$ are measurable. The space of all measurable sections of $(\{{\mathscr {M}}_q\}_{q\in Q},\Theta ,\Phi )$ is then denoted by $\int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$ and called the integral of $(\{{\mathscr {M}}_q\}_{q\in Q},\Theta ,\Phi )$; see Definition 3.4. The space $\int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$ has a structure of $L^0(\mu )$-Banach $L^0(\mu )$-module, where we define $\mu :=\int \mu _q\,\text {d}{\mathfrak {q}}(q)$. Conversely, it is also possible to disintegrate a given countably-generated $L^0(\mu )$-Banach $L^0(\mu )$-module ${\mathscr {M}}$, thus obtaining an $L^0$-Banach $L^0$-module bundle whose integral is the original space ${\mathscr {M}}$; this claim is proved in Theorem 3.8 (and see also Theorem 3.9).

We now discuss the applications of the above machinery to the vector calculus on metric measure spaces verifying lower Ricci bounds. Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space, where $K\in \mathbb {R}$ and $N\in [1,\infty )$. We focus on two different classes of foliations (of a portion) of $\textrm{X}$: the codimension-one level sets of a function of bounded variation (BV function, for short) and, somehow dually, the one-dimensional needle decomposition induced by a Lipschitz function. More in details:

(a):

The Fleming–Rishel coarea formula proved by Miranda Jr. in [43] states that, given a BV function $f\in BV(\textrm{X})$, the total variation measure $|Df|$ coincides with the ‘superposition’ $\int _\mathbb {R}P(\{f>t\},\cdot )\,\text {d}t$ of the perimeter measures of the superlevel sets $\{f>t\}$; see Theorem 2.22. The fact that the level sets $\{f>t\}$ can be regarded as codimension-one objects is corroborated by the results of [1] (see also [13]). Moreover, as shown in [21], the regularity of $\mathsf RCD$ spaces guarantees that (sufficiently many) vector fields can be ‘traced’ over the essential boundary of a set of finite perimeter $E$, thus obtaining the space $L^0_{P(E,\cdot )}(T\textrm{X})$. In particular, one can define the unit normal $\nu _E\in L^0_{P(E,\cdot )}(T\textrm{X})$ to $E$, as proved in [14]. More generally, one can construct the space of $|Df|$-a.e. defined vector fields $L^0_{|Df|}(T\textrm{X})$ whenever $f\in BV(\textrm{X})$, see [12]. With this said, in Theorem 4.4 we will prove that

$$\begin{aligned} L^0_{|Df|}(T\textrm{X})\cong \int L^0_{P(\{f>t\},\cdot )}(T\textrm{X})\,\text {d}t\quad \text { for every }f\in BV(\textrm{X}), \end{aligned}$$

(1.1)

once the family $\mathbb {R}\ni t\mapsto L^0_{P(\{f>t\},\cdot )}(T\textrm{X})$ is made into an $L^0$-Banach $L^0$-module bundle, in a suitable way. To be precise, (1.1) is not entirely correct as it is written, since the measure-valued map $t\mapsto P(\{f>t\},\cdot )$ is not necessarily disjoint due to the possible presence of the jump part of $|Df|$; this technical subtlety will be dealt with in Proposition 4.3. Notice that one can regard (1.1) as a Fubini-type theorem for measurable vector fields. Similar results, but without integrals of $L^0(\mu )$-Banach $L^0(\mu )$-modules, previously appeared in [9] (for the squared distance functions from a point) and in [12] (for arbitrary BV functions).

(b):

Klartag’s localisation technique [40] has been generalised from the Riemannian setting to metric measure spaces verifying synthetic lower Ricci bounds, see the survey [16] and the references therein. Given a $1$-Lipschitz function $u:\textrm{X}\rightarrow \mathbb {R}$, the so-called transport set ${\mathcal {T}}_u$ can be partitioned (up to $\mathfrak {m}$-null sets) into the images $\textrm{X}_\alpha$ of suitable geodesics $\gamma _\alpha$, which are the gradient flow lines of $-\nabla u$ in a suitable sense. The restriction $\mathfrak {m}|_{{\mathcal {T}}_u}$ of the reference measure $\mathfrak {m}$ to ${\mathcal {T}}_u$ can be disintegrated as $\mathfrak {m}|_{{\mathcal {T}}_u}=\int \mathfrak {m}_\alpha \,\text {d}{\mathfrak {q}}(\alpha )$, where each $\mathfrak {m}_\alpha =h_\alpha {\mathcal {H}}^1$ is a measure concentrated on $\textrm{X}_\alpha$. As proved in [18], the ‘needles’ $(\textrm{X}_\alpha ,\textsf{d},h_\alpha {\mathcal {H}}^1)$ are $\textsf{RCD}(K,N)$ spaces. The intuition suggests that the tangent module $L^0(T\textrm{X}_\alpha )$ is one-dimensional and that a Lipschitz function $f:\textrm{X}\rightarrow \mathbb {R}$ induces a vector field $\partial _\alpha f\in L^0(T\textrm{X}_\alpha )$, which is obtained by differentiating $f\circ \gamma _\alpha$. This is made precise by Theorem 4.5, which says that

$$\begin{aligned} \int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )\cong \langle \nabla u\rangle _{{\mathcal {T}}_u}, \end{aligned}$$

(1.2)

where $\langle \nabla u\rangle _{{\mathcal {T}}_u}\subseteq L^0(T\textrm{X})$ is the $L^0(\mathfrak {m}|_{{\mathcal {T}}_u})$-Banach $L^0(\mathfrak {m}|_{{\mathcal {T}}_u})$-module generated by $\nabla u$, and for any Lipschitz function $f:\textrm{X}\rightarrow \mathbb {R}$ the superposition $\int \partial _\alpha f\,\text {d}{\mathfrak {q}}(\alpha )\in \int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )$ corresponds, via the identification in (1.2), to the element $-\langle \nabla f,\nabla u\rangle \nabla u\in \langle \nabla u\rangle _{{\mathcal {T}}_u}$.

Finally, in Theorem 4.9 we combine the two different foliations of $\textrm{X}$ we described above. Assuming $\mathfrak {m}(\textrm{X})<+\infty$ for simplicity and fixed a $1$-Lipschitz function $u:\textrm{X}\rightarrow \mathbb {R}$ with $\mathfrak {m}(\textrm{X}{\setminus }{\mathcal {T}}_u)=0$, we know from Theorems 4.4 and 4.5 that $\int P(\{u>t\},\cdot )\,\text {d}t\cong L^0(T\textrm{X})$ and $\int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )\cong \langle \nabla u\rangle _\textrm{X}$, respectively. Via these identifications, we can prove that $\int \partial _\alpha u\,\text {d}{\mathfrak {q}}(\alpha )$ corresponds to $-\int \nu _{\{u>t\}}\,\text {d}t$.

2 Preliminaries

Throughout the whole paper, our standing convention (unless otherwise specified) is that

$$\begin{aligned} \textit{all the measures under consideration are }\sigma \textit{-finite.} \end{aligned}$$

Moreover, in this paper a ring $R$ is not assumed to have a multiplicative identity. However, when the identity $1_R$ exists, then we require that each $R$-module $M$ verifies $1_R\cdot v=v$ for every $v\in M$.

Given a collection of non-empty sets $A_\star =\{A_q\}_{q\in Q}$, we define the space of its sections as

$$\begin{aligned} {\mathscr {S}}(A_\star ):=\prod _{q\in Q}A_q. \end{aligned}$$

In the case where each $A_q$ is a ring (resp. a vector space), the product space ${\mathscr {S}}(A_\star )$ is a ring (resp. a vector space) with respect to the componentwise operations.

Remark 2.1

Let $R_\star =\{R_q\}_{q\in Q}$ be a collection of commutative rings. For any $q\in Q$, let $M_q$ be a module over $R_q$. Then ${\mathscr {S}}(M_\star )$ has a natural structure of module over the ring ${\mathscr {S}}(R_\star )$. $\blacksquare$

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space. Let $A_\star =\{A_q\}_{q\in Q}$ be rings (resp. vector spaces). Then

$$\begin{aligned} N_{{\mathfrak {q}}}:=\Big \{v\in {\mathscr {S}}(A_\star )\;\Big |\;\{q\in Q:\,v_q\ne 0\}\subseteq N\text { for some }N\in {\mathcal {Q}}\text { with }{\mathfrak {q}}(N)=0\Big \} \end{aligned}$$

is a two-sided ideal (resp. a vector subspace) of ${\mathscr {S}}(A_\star )$. Therefore, the quotient space

$$\begin{aligned} {\mathscr {S}}_{{\mathfrak {q}}}(A_\star ):={\mathscr {S}}(A_\star )/N_{{\mathfrak {q}}} \end{aligned}$$

is a ring (resp. a vector space). We denote by $\pi _{{\mathfrak {q}}}:{\mathscr {S}}(A_\star )\rightarrow {\mathscr {S}}_{{\mathfrak {q}}}(A_\star )$ the quotient map.

According to this notation, we denote by ${\mathscr {S}}_{{\mathfrak {q}}}(\mathbb {R})$ the set of all the (possibly non-measurable) functions from $Q$ to $\mathbb {R}$, quotiented up to ${\mathfrak {q}}$-a.e. equality.

Remark 2.2

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space and let $R_\star$, $M_\star$ be as in Remark 2.1. Then the vector space ${\mathscr {S}}_{{\mathfrak {q}}}(M_\star )$ inherits a natural structure of module over the ring ${\mathscr {S}}_{{\mathfrak {q}}}(R_\star )$. $\blacksquare$

2.1 Integration and disintegration of measures

Let $(\textrm{X},\Sigma ,\mu )$ be a measure space. Then we denote by $L^0(\mu )$ the space of all real-valued measurable functions on $\textrm{X}$, quotiented up to $\mu$-a.e. identity. The space $L^0(\mu )$ is a Riesz space, where we declare that $f,g\in L^0(\mu )$ satisfy $f\le g$ if and only if $f(x)\le g(x)$ for $\mu$-a.e. $x\in \textrm{X}$. Moreover, $L^0(\mu )$ is Dedekind complete, which means that every order-bounded set $\{f_i\}_{i\in I}\subseteq L^0(\mu )$ admits both a supremum $\bigvee _{i\in I}f_i\in L^0(\mu )$ and an infimum $\bigwedge _{i\in I}f_i\in L^0(\mu )$ (see for instance [24]). We also denote by ${\mathcal {L}}^0(\Sigma )$ the space of all real-valued measurable functions on $\textrm{X}$, while $\pi _\mu$ (or $[\cdot ]_\mu$) stands for the canonical projection map ${\mathcal {L}}^0(\Sigma )\rightarrow L^0(\mu )$. Given any $E\subseteq \textrm{X}$, we denote by $\mathbb {1}_E$ its characteristic function. If $E\in \Sigma$, then we denote $\mathbb {1}^\mu _E:=[\mathbb {1}_E]_\mu$.

The space $L^0(\mu )$ becomes a complete topological vector space and topological ring if endowed with the topology that is induced by the following distance:

$$\begin{aligned} \textsf{d}_{L^0(\mu )}(f,g):=\int |f-g|\wedge 1\,\text {d}{{\tilde{\mu }}}\quad \text { for every }f,g\in L^0(\mu ), \end{aligned}$$

where ${{\tilde{\mu }}}\ge 0$ is some finite measure on $(\textrm{X},\Sigma )$ with $\mu \ll {{\tilde{\mu }}}\le \mu$. When $\mu$ is finite, we take ${{\tilde{\mu }}}=\mu$.

We define a notion of a disjoint measure-valued map, which we will use throughout the paper:

Definition 2.3

(Measure-valued map) Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space and $(\textrm{X},\Sigma )$ a measurable space. Let $\mu _\star =\{\mu _q\}_{q\in Q}$ be a collection of measures on $(\textrm{X},\Sigma )$. Then we say that $q\mapsto \mu _q$ is a (measurable) measure-valued map from $Q$ to $\textrm{X}$ provided the following conditions hold:

$\mathrm i)$:

The function $Q\ni q\mapsto \mu _q(E)\in [0,+\infty ]$ is measurable for every $E\in \Sigma$.

$\mathrm ii)$:

The measure $\mu :=\int \mu _q\,\text {d}{\mathfrak {q}}(q):\Sigma \rightarrow [0,+\infty ]$ is $\sigma$-finite, where we define

$$\begin{aligned} \bigg (\int \mu _q\,\text {d}{\mathfrak {q}}(q)\bigg )(E):=\int \mu _q(E)\,\text {d}{\mathfrak {q}}(q)\quad \text { for every }E\in \Sigma . \end{aligned}$$

We say that $q\mapsto \mu _q$ is a disjoint measure-valued map if there exists a family $\{E_q\}_{q\in Q}\subseteq \Sigma$ of pairwise disjoint sets such that $\mu _q(\textrm{X}{\setminus } E_q)=0$ for every $q\in Q$ and $\bigcup _{q\in A}E_q\in \Sigma$ for every $A\in {\mathcal {Q}}$.

If $f:\textrm{X}\rightarrow [0,+\infty ]$ is measurable, then $Q\ni q\mapsto \int f\,\text {d}\mu _q\in [0,+\infty ]$ is measurable and

$$\begin{aligned} \int f\,\text {d}\mu =\int \bigg (\int f\,\text {d}\mu _q\bigg )\,\text {d}{\mathfrak {q}}(q). \end{aligned}$$

The verification of this claim can be obtained by using the monotone convergence theorem.

Example 2.4

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space. Let us also consider the one-point probability space $(\{\textsf{o}\},\delta _\textsf{o})$. Then $q\mapsto \delta _{(q,\textsf{o})}$ is a disjoint measure-valued map from $Q$ to $Q\times \{\textsf{o}\}$ and

$$\begin{aligned} {\mathfrak {q}}\otimes \delta _\textsf{o}=\int \delta _{(q,\textsf{o})}\,\text {d}{\mathfrak {q}}(q). \end{aligned}$$

Notice also that the measure ${\mathfrak {q}}\otimes \delta _\textsf{o}$ can be canonically identified with ${\mathfrak {q}}$. $\blacksquare$

Remark 2.5

Given any outer measure $\nu$ on $\textrm{X}$, the following implication holds:

$$\begin{aligned} \mu _q\ll \nu \;\text { for }{\mathfrak {q}}\text {-a.e.\ }q\in Q\quad \Longrightarrow \quad \int \mu _q\,\text {d}{\mathfrak {q}}(q)\ll \nu . \end{aligned}$$

(2.1)

Indeed, if $N\in \Sigma$ satisfies $\nu (N)=0$, then trivially $\big (\int \mu _q\,\text {d}{\mathfrak {q}}(q)\big )(N)=\int \mu _q(N)\,\text {d}{\mathfrak {q}}(q)=0$. $\blacksquare$

Definition 2.6

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Then we define $L^0({\mathfrak {q}};L^0(\mu _\star )):=\pi _{{\mathfrak {q}}}\big ({\mathcal {L}}^0({\mathfrak {q}};L^0(\mu _\star ))\big )$, where $L^0(\mu _\star ):=\{L^0(\mu _q)\}_{q \in Q}$ and

$$\begin{aligned} {\mathcal {L}}^0({\mathfrak {q}};L^0(\mu _\star )){:=}\Big \{f\in {\mathscr {S}}(L^0(\mu _\star ))\;\Big |\;\exists F\in {\mathcal {L}}^0(\Sigma ):\,[F]_{\mu _q}{=}f_q\,\text { for }{\mathfrak {q}}\text {-a.e.\ }q\in Q\Big \}. \end{aligned}$$

We have that, letting $\mu :=\int \mu _q\,\text {d}{\mathfrak {q}}(q)$ for brevity, the following identification is in force:

$$\begin{aligned} L^0({\mathfrak {q}};L^0(\mu _\star ))\cong L^0(\mu ). \end{aligned}$$

The following result makes this assertion precise:

Proposition 2.7

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Let us define the mapping $\bar{\textsf{i}}_{{\mathfrak {q}}}:{\mathcal {L}}^0(\Sigma )\rightarrow {\mathcal {L}}^0({\mathfrak {q}};L^0(\mu _\star ))$ as

$$\begin{aligned} \bar{\textsf{i}}_{{\mathfrak {q}}}({\bar{F}})_q:=[{\bar{F}}]_{\mu _q}\quad \text { for every }{\bar{F}}\in {\mathcal {L}}^0(\Sigma )\text { and }q\in Q. \end{aligned}$$

Moreover, letting $\mu :=\int \mu _q\,\text {d}{\mathfrak {q}}(q)$, we define $\textsf{i}_{{\mathfrak {q}}}:L^0(\mu )\rightarrow L^0({\mathfrak {q}};L^0(\mu _\star ))$ as

$$\begin{aligned} \textsf{i}_{{\mathfrak {q}}}(F):=\pi _{{\mathfrak {q}}}\big (\bar{\textsf{i}}_{{\mathfrak {q}}}({\bar{F}})\big ) \quad \text { for every }F\in L^0(\mu )\text { and }{\bar{F}}\in {\mathcal {L}}^0(\Sigma )\text { such that }F=[{\bar{F}}]_\mu . \end{aligned}$$

Then $\textsf{i}_{{\mathfrak {q}}}$ is a linear and ring isomorphism. We denote by $\textsf{j}_{{\mathfrak {q}}}:L^0({\mathfrak {q}};L^0(\mu _\star ))\rightarrow L^0(\mu )$ its inverse.

Proof

The map $\textsf{i}_{{\mathfrak {q}}}$ is well-defined. Indeed, let $\bar{F}_1,\bar{F}_2 \in {\mathcal {L}}^0(\Sigma )$ be such that $[\bar{F}_1]_\mu =[\bar{F}_2]_\mu =F$. In particular, $[\bar{F}_1]_{\mu _q}=[\bar{F}_2]_{\mu _q}$ for $\mathfrak {q}$-a.e. q. Hence, $\pi _{{\mathfrak {q}}}\big (\bar{\textsf{i}}_{{\mathfrak {q}}}({\bar{F}}_1)\big )=\pi _{{\mathfrak {q}}}\big (\bar{\textsf{i}}_{{\mathfrak {q}}}({\bar{F}}_2)\big )$. The fact of being a linear and ring homomorphism follows directly from similar properties for $[\cdot ]_\mu$,$[\cdot ]_{\mu _q}$, $\pi _{{\mathfrak {q}}}$. We check surjectivity. Let $f \in L^0({\mathfrak {q}};L^0(\mu _\star ))$ and let $\bar{f} \in {\mathcal {L}}^0({\mathfrak {q}};L^0(\mu _\star ))$ be such that $f =\pi _{{\mathfrak {q}}}(\bar{f})$. Hence, there exists $\bar{F} \in {\mathcal {L}}^0(\Sigma )$ such that $[\bar{F}]_{\mu _q}=\bar{f}_q$ for $\mathfrak {q}$-a.e. $q\in Q$. Define $F:=[\bar{F}]_{\mu }$. Then, it can be readily checked that $\textsf{i}_{{\mathfrak {q}}}(F)=f$. $\square$

Lemma 2.8

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space and $(\textrm{X},\Sigma )$ a measurable space. Let $q\mapsto \mu _q$ be a disjoint measure-valued map from $Q$ to $\textrm{X}$. Let $(F_n)_{n\in \mathbb {N}}\subseteq {\mathcal {L}}^0(\Sigma )$ and $F\in {\mathcal {L}}^0(\Sigma )$ be given, where we denote $\mu :=\int \mu _q\,\text {d}{\mathfrak {q}}(q)$. Then the following conditions are equivalent:

$\mathrm i)$:

$F(x)=\lim _n F_n(x)$ for $\mu$-a.e. $x\in \textrm{X}$.

$\mathrm ii)$:

For ${\mathfrak {q}}$-a.e. $q\in Q$, it holds that $F(x)=\lim _n F_n(x)$ for $\mu _q$-a.e. $x\in \textrm{X}$.

Proof

First of all, we point out that for any given set $N\in \Sigma$ it holds that

$$\begin{aligned} \mu (N)=0\quad \Longleftrightarrow \quad \mu _q(N)=0\,\text { for }{\mathfrak {q}}\text {-a.e. }q\in Q. \end{aligned}$$

The validity of this claim immediately follows from the identity $\mu (N)=\int \mu _q(N)\,\text {d}{\mathfrak {q}}(q)$. In order to conclude, choose as $N$ the set of all $x\in \textrm{X}$ such that $(F_n(x))_{n\in \mathbb {N}}$ does not converge to $F(x)$. $\square$

Remark 2.9

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, and $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Fix a measurable function $\phi :Q\rightarrow (0,1)$ such that $\int \phi \,\text {d}{\mathfrak {q}}<+\infty$ and define $\tilde{{\mathfrak {q}}}:=\phi \,{\mathfrak {q}}$. Next, fix any $\rho :\textrm{X}\rightarrow (0,1)$ measurable such that $\int \!\!\int \rho \,\text {d}\mu _q\,\text {d}\tilde{{\mathfrak {q}}}(q)<+\infty$. Therefore, letting ${{\tilde{\mu }}}_q:=\rho \mu _q$, we have that $q\mapsto {{\tilde{\mu }}}_q$ is a disjoint measure-valued map and set ${{\tilde{\mu }}}:=\int {{\tilde{\mu }}}_q\,\text {d}\tilde{{\mathfrak {q}}}(q)$. Since (almost) all the measures we marked with a tilde are finite, and we have

$$\begin{aligned} {\mathfrak {q}}\ll \tilde{{\mathfrak {q}}}\le {\mathfrak {q}}, \quad \mu \ll {{\tilde{\mu }}}\le \mu ,\quad \mu _q\ll {{\tilde{\mu }}}_q\le \mu _q \end{aligned}$$

by construction, it will not be restrictive to assume that the measures ${\mathfrak {q}}$, $\mu$, $\mu _q$ are finite. $\blacksquare$

2.2 The theory of $L^0$-Banach ${\mathscr {A}}$-modules

By an algebra we mean an associative, commutative algebra over the real field $\mathbb {R}$ that is not necessarily unital. In particular, an algebra is both a vector space and a ring (possibly without a multiplicative identity). By a subalgebra we mean a subset that is closed under the vector space and ring operations. For example, given any measure space $(\textrm{X},\Sigma ,\mu )$, the space $L^0(\mu )$ is a unital algebra whose multiplicative identity is $\mathbb {1}_\textrm{X}^\mu$. Our choice of this not-so-standard convention, but which is typical in analysis on metric measure spaces (cf. for example [46]), is motivated by the fact that – due to integrability issues when the reference measure is not finite – it is necessary to work with algebras of functions (such as $\textrm{LIP}_{bs}(\textrm{X})$ or $\textrm{Test}(\textrm{X})$) that are not unital (unless the metric space $\textrm{X}$ is bounded).

Observe that if $(\textrm{X},\Sigma ,\mu )$ is a measure space and ${\mathscr {A}}$ is a subalgebra of $L^0(\mu )$, then the space

$$\begin{aligned} {\mathcal {G}}({\mathscr {A}}):=\bigg \{\sum _{n\in \mathbb {N}}\mathbb {1}_{E_n}^\mu f_n\;\bigg |\;(E_n)_{n\in \mathbb {N}}\subseteq \Sigma \text { partition of }\textrm{X},\,(f_n)_{n\in \mathbb {N}}\subseteq {\mathscr {A}}\bigg \} \end{aligned}$$

is a subalgebra of $L^0(\mu )$. Moreover, the space $\hat{{\mathscr {A}}}$ is a subalgebra of $L^0(\mu )$ as well, where we set

$$\begin{aligned} \hat{{\mathscr {A}}}:=\textrm{cl}_{L^0(\mu )}\big ({\mathcal {G}}({\mathscr {A}})\big ). \end{aligned}$$

Remark 2.10

Given any subalgebra ${\mathscr {A}}$ of $L^0(\mu )$, one can easily check that

$$\begin{aligned} \hat{{\mathscr {A}}}\cong L^0(\mu |_{[{\mathscr {A}}]}), \end{aligned}$$

where $[{\mathscr {A}}]\in \Sigma$ is ($\mu$-a.e.) defined as the essential union of $\{f>0\}$ as $f$ varies in ${\mathscr {A}}$. $\blacksquare$

Example 2.11

The field $\mathbb {R}$ is canonically isomorphic to the subalgebra $\mathbb {R}_\mu$ of $L^0(\mu )$ given by

$$\begin{aligned} \mathbb {R}_\mu :=\big \{\lambda \mathbb {1}_\textrm{X}^\mu \in L^0(\mu )\;\big |\;\lambda \in \mathbb {R}\big \}. \end{aligned}$$

Observe also that ${\hat{\mathbb {R}}}_\mu =L^0(\mu )$ thanks to Remark 2.10. $\blacksquare$

Next, let us introduce a notion of $L^0$-normed ${\mathscr {A}}$-module that is a generalization of [26, Definition 2.6] and can be seen as a special case of a RN space in the sense of [32, Definition 3.1] with the additional assumption of module structure over an algebra ${\mathscr {A}} \subseteq L^0(\mu )$.

Definition 2.12

($L^0(\mu )$-normed ${\mathscr {A}}$-module) Let $(\textrm{X},\Sigma ,\mu )$ be a measure space. Let ${\mathscr {A}}\subseteq L^0(\mu )$ be a subalgebra. Let ${\mathscr {M}}$ be both a module over ${\mathscr {A}}$ and a vector space over $\mathbb {R}$ (with the same addition operator). Then we say that a map $|\cdot |:{\mathscr {M}}\rightarrow L^0(\mu )$ is a pointwise norm if

$$\begin{aligned} \begin{aligned}&|v|\ge 0\text { for every }v\in {\mathscr {M}},\text { with equality if and only if }v=0,\\&\quad |v+w|\le |v|+|w|\text { for every }v,w\in {\mathscr {M}},\\&|\lambda v|=|\lambda ||v|\quad \text { for every }\lambda \in \mathbb {R}\text { and }v\in {\mathscr {M}},\\&\quad |f\cdot v|=|f||v|\text { for every }f\in {\mathscr {A}}\text { and }v\in {\mathscr {M}},\\&\quad (\lambda f)\cdot v=\lambda (f\cdot v)\text { for every }\lambda \in \mathbb {R},\,f\in {\mathscr {A}},\text { and }v\in {\mathscr {M}}, \end{aligned} \end{aligned}$$

where all equalities and inequalities are intended in the $\mu$-a.e. sense. Whenever ${\mathscr {M}}$ is endowed with a pointwise norm $|\cdot |$, we say that ${\mathscr {M}}$ is an $L^0(\mu )$-normed ${\mathscr {A}}$-module.

Notice that if $\mathbb {1}_\textrm{X}^\mu \in {\mathscr {A}}$, then $\mathbb {1}_\textrm{X}^\mu \cdot v=v$ for every $v\in {\mathscr {M}}$, whence it follows that

$$\begin{aligned} \lambda v=(\lambda \mathbb {1}_\textrm{X}^\mu )\cdot v\quad \text { for every }\lambda \in \mathbb {R}\text { and }v\in {\mathscr {M}}. \end{aligned}$$

Each pointwise norm $|\cdot |:{\mathscr {M}}\rightarrow L^0(\mu )$ induces a distance $\textsf{d}_{{\mathscr {M}}}$ on ${\mathscr {M}}$, in the following way:

$$\begin{aligned} \textsf{d}_{{\mathscr {M}}}(v,w):=\textsf{d}_{L^0(\mu )}(|v-w|,0)\quad \text { for every }v,w\in {\mathscr {M}}. \end{aligned}$$

(2.2)

We consider ${\mathscr {M}}$ endowed with the distance $\textsf{d}_{{\mathscr {M}}}$ (and the induced topology).

Definition 2.13

($L^0(\mu )$-Banach ${\mathscr {A}}$-module) Let $(\textrm{X},\Sigma ,\mu )$ be a measure space and ${\mathscr {A}}\subseteq L^0(\mu )$ a subalgebra. Then an $L^0(\mu )$-normed ${\mathscr {A}}$-module ${\mathscr {M}}$ is called an $L^0(\mu )$-Banach ${\mathscr {A}}$-module if $\textsf{d}_{{\mathscr {M}}}$ is complete.

Notice that the $L^0(\mu )$-Banach ${\mathscr {A}}$-modules with ${\mathscr {A}}=L^0(\mu )$ are exactly the $L^0(\mu )$-normed $L^0(\mu )$-modules in the sense of [26, Definition 2.6] (indeed, in [26] $L^0(\mu )$-normed $L^0(\mu )$-modules are assumed to be complete). Moreover, the $L^0(\mu )$-Banach $L^0(\mu )$-module in Gigli’s axiomatization is precisely an RN module in the sense of Guo and the topology induced by the metric $\textsf{d}_{\mathscr {M}}$ is precisely the $(\epsilon ,\lambda )$-topology of RN module (see [34]).

Definition 2.14

(Generators) Let $(\textrm{X},\Sigma ,\mu )$ be a measure space and ${\mathscr {M}}$ an $L^0(\mu )$-Banach $L^0(\mu )$-module. Then a vector space $V\subseteq {\mathscr {M}}$ generates ${\mathscr {M}}$ if ${\mathcal {G}}(V)$ is dense in ${\mathscr {M}}$, where we set

$$\begin{aligned} {\mathcal {G}}(V):=\bigg \{\sum _{n\in \mathbb {N}}\mathbb {1}_{E_n}^\mu \cdot v_n\;\bigg |\;(E_n)_{n\in \mathbb {N}}\subseteq \Sigma \text { partition of }\textrm{X}, \,(v_n)_{n\in \mathbb {N}}\subseteq V\bigg \}. \end{aligned}$$

(2.3)

Moreover, we say that ${\mathscr {M}}$ is countably generated if it is generated by a separable subspace.

Example 2.15

Let $(\{\textsf{o}\},\delta _\textsf{o})$ be the one-point probability space. Then we have that

$$\begin{aligned} \big \{L^0(\delta _\textsf{o})\text {-Banach }L^0(\delta _\textsf{o})\text {-modules}\big \}=\{\text {Banach spaces}\}, \end{aligned}$$

in the sense which we are going to explain. First, observe that $L^0(\delta _\textsf{o})=\mathbb {R}_{\delta _\textsf{o}}$ can be canonically identified with $\mathbb {R}$. Given an $L^0(\delta _\textsf{o})$-Banach $L^0(\delta _\textsf{o})$-module ${\mathscr {M}}$, we thus have that the pointwise norm $\Vert \cdot \Vert :=|\cdot |:{\mathscr {M}}\rightarrow L^0(\delta _\textsf{o})\cong \mathbb {R}$ can be regarded as a norm. The resulting normed space ${\mathscr {M}}$ is in fact Banach, as follows from the completeness of the distance $\textsf{d}_{{\mathscr {M}}}(v,w)=\Vert v-w\Vert \wedge 1$. $\blacksquare$

We recall that, given two $L^0(\mu )$-Banach $L^0(\mu )$-modules ${\mathscr {M}}$ and ${\mathscr {N}}$, an isomorphism of $L^0(\mu )$-Banach $L^0(\mu )$-modules is a map $\Phi :{{\mathscr {M}}}\rightarrow {\mathscr {N}}$ that is $L^0(\mu )$-linear, surjective and preserves the pointwise norm, i.e. $|\Phi (v)|=|v|$ as elements of $L^0(\mu )$ for every $v \in {\mathscr {M}}$.

Proposition 2.16

(Completion of an $L^0$-normed ${\mathscr {A}}$-module) Let $(\textrm{X},\Sigma ,\mu )$ be a measure space and ${\mathscr {A}}$ a subalgebra of $L^0(\mu )$ such that $\hat{{\mathscr {A}}}=L^0(\mu )$. Let ${\mathscr {M}}$ be an $L^0(\mu )$-normed ${\mathscr {A}}$-module. Then there exists a unique couple $(\hat{{\mathscr {M}}},\iota )$ having the following properties:

$\mathrm i)$:

$\hat{{\mathscr {M}}}$ is an $L^0(\mu )$-Banach $L^0(\mu )$-module,

$\mathrm ii)$:

$\iota :{\mathscr {M}}\rightarrow \hat{{\mathscr {M}}}$ is a linear map with generating image such that $|\iota (v)|=|v|$ for every $v\in {\mathscr {M}}$.

The couple $(\hat{{\mathscr {M}}},\iota )$ is unique up to a unique isomorphism: given any couple $({\mathscr {N}},{{\tilde{\iota }}})$ with the same properties, there is a unique isomorphism $\Phi :\hat{{\mathscr {M}}}\rightarrow {\mathscr {N}}$ of $L^0(\mu )$-Banach $L^0(\mu )$-modules such that

is a commutative diagram. We say that $\hat{{\mathscr {M}}}$ is the completion of ${\mathscr {M}}$.

Proof

Recall Remark 2.10. The triple $\big (L^0(\mu ),L^0(\mu ),L^0(\mu )\big )$ is a metric $f$-structure in the sense of [42, Definition 2.24]; cf. with [42, Section 4.2.2]. Defining ${\mathscr {V}}:={\mathscr {M}}$ and the map $\psi :{\mathscr {V}}\rightarrow L^0(\mu )^+$ as $\psi (v):=|v|$, we obtain the statement by applying [42, Theorem 3.19] to $({\mathscr {V}},\psi )$. $\square$

Remark 2.17

We point out that, although we consider $L^0(\mu )$-normed ${\mathscr {A}}$-modules, where ${\mathscr {A}} \subseteq L^0(\mu )$ is a subalgebra that does not have a unital element (for example $\textrm{Test}(\textrm{X})$ in Theorem 4.4), this does not happen in the completion. Indeed, if $(\textrm{X},\textsf{d},\mu )$ is an $\textsf{RCD}(K,N)$ space, we have that $\hat{\textrm{Test}(\textrm{X})} = L^0(\mu )$ (see Lemma 2.26 later and the fact that $\mu \ll \textrm{Cap}$). Thus, Proposition 2.16 gives that the completion has a module structure over the algebra $L^0(\mu )$, which has the unital element.

2.2.1 $L^0$-Banach $L^0$-modules with respect to a submodular outer measure

Let $(\textrm{X},\textsf{d})$ be a metric space. We denote by ${\mathscr {B}}(\textrm{X})$ the Borel $\sigma$-algebra of $\textrm{X}$. Fix an outer measure $\nu$ on $\textrm{X}$. Given a Borel function $f:\textrm{X}\rightarrow [0,+\infty ]$ and a set $E\in {\mathscr {B}}(\textrm{X})$, one can define the integral of $f$ on $E$ with respect to $\nu$ via Cavalieri’s formula, i.e.

$$\begin{aligned} \int _E f\,\text {d}\nu :=\int _0^{+\infty }\nu (\{\mathbb {1}_E f\ge t\})\,\text {d}t. \end{aligned}$$

(2.4)

Moreover, we say that:

• $\nu$ is boundedly-finite if $\nu (B)<+\infty$ for every $B\in {\mathscr {B}}(\textrm{X})$ bounded.

• $\nu$ is submodular if $\nu (E\cup F)+\nu (E\cap F)\le \nu (E)+\nu (F)$ for every $E,F\in {\mathscr {B}}(\textrm{X})$.

It holds that the integral defined in (2.4) is subadditive, which means that

$$\begin{aligned} \int _\textrm{X}(f+g)\,\text {d}\nu \le \int _\textrm{X}f\,\,\text {d}\nu +\int _\textrm{X}g\,\text {d}\nu \quad \text { for every }f,g:\textrm{X}\rightarrow [0,+\infty ]\text { Borel,} \end{aligned}$$

if and only if $\nu$ is submodular. See [21] after [22].

Example 2.18

We are concerned with two types of boundedly-finite, submodular outer measures:

$\mathrm i)$:

The outer measure ${\bar{\mu }}$ induced via the Carathéodory construction, i.e.

$$\begin{aligned} {\bar{\mu }}(S):=\inf \big \{\mu (E)\;\big |\;E\in {\mathscr {B}}(\textrm{X}),\,S\subseteq E\big \}\quad \text { for every }S\subseteq \textrm{X}, \end{aligned}$$

by a boundedly-finite Borel measure $\mu \ge 0$ on a metric space $(\textrm{X},\textsf{d})$.

$\mathrm ii)$:

The Sobolev capacity $\mathrm Cap$ on a metric measure space $(\textrm{X},\textsf{d},\mathfrak {m})$.

We will introduce the Sobolev capacity in Sect. 2.3.1. $\blacksquare$

Fix a metric space $(\textrm{X},\textsf{d})$ and a boundedly-finite, submodular outer measure $\nu$ on $\textrm{X}$. Then we denote by $L^0(\nu )$ the space of all Borel functions from $\textrm{X}$ to $\mathbb {R}$, quotiented up to $\nu$-a.e. equality. In order to define a distance on $L^0(\nu )$, fix an increasing sequence $(U_n)_{n\in \mathbb {N}}$ of bounded open subsets of $\textrm{X}$ with the following property: for any bounded set $B\subseteq \textrm{X}$, there exists $n\in \mathbb {N}$ such that $B\subseteq U_n$. In particular, we have that $\textrm{X}=\bigcup _{n\in \mathbb {N}}U_n$. Then we define

$$\begin{aligned} \textsf{d}_{L^0(\nu )}(f,g):=\sum _{n\in \mathbb {N}}\frac{1}{2^n(\nu (U_n)\vee 1)}\int _{U_n}|f-g|\wedge 1\,\text {d}\nu \quad \text { for every }f,g\in L^0(\nu ). \end{aligned}$$

The submodularity of the integration with respect to $\nu$ ensures that $\textsf{d}_{L^0(\nu )}$ is a distance. Even though the distance $\textsf{d}_{L^0(\nu )}$ depends on the chosen sequence $(U_n)_n$, its induced topology does not and makes $L^0(\nu )$ into a topological vector space (see [21, Prop. 2.11]). Given a Borel measure $\mu$ on $\textrm{X}$ such that $\mu \ll \nu$, we denote by $\pi _\mu :L^0(\nu )\rightarrow L^0(\mu )$ the canonical projection map and by $[f]_\mu \in L^0(\mu )$ the equivalence class of a function $f\in L^0(\nu )$. Moreover, in the framework of Example 2.18 i), we have that $L^0({\bar{\mu }})=L^0(\mu )$ as topological vector spaces.

The following definition is adapted from [21, Definition 3.1]:

Definition 2.19

Let $(\textrm{X},\textsf{d})$ be a metric space and $\nu$ a boundedly-finite, submodular outer measure on $\textrm{X}$. Let ${\mathscr {M}}$ be a module over $L^0(\nu )$. Then $|\cdot |:{\mathscr {M}}\rightarrow L^0(\nu )$ is a pointwise norm if

$$\begin{aligned} \begin{aligned}&|v|\ge 0\text { for every }v\in {\mathscr {M}},\text { with equality if and only if }v=0,\\&\quad |v+w|\le |v|+|w|\text { for every }v,w\in {\mathscr {M}},\\&\quad |f\cdot v|=|f||v|\text { for every }f\in L^0(\nu )\text { and }v\in {\mathscr {M}}, \end{aligned} \end{aligned}$$

where all equalities and inequalities are intended in the $\nu$-a.e. sense. Whenever ${\mathscr {M}}$ is endowed with a pointwise norm $|\cdot |$, we say that ${\mathscr {M}}$ is an $L^0(\nu )$-normed $L^0(\nu )$-module. When the distance

$$\begin{aligned} \textsf{d}_{{\mathscr {M}}}(v,w):=\textsf{d}_{L^0(\nu )}(|v-w|,0)\quad \text { for every }v,w\in {\mathscr {M}} \end{aligned}$$

is a complete distance on ${\mathscr {M}}$, we say that ${\mathscr {M}}$ is an $L^0(\nu )$-Banach $L^0(\nu )$-module.

In view of Example 2.18 i), the above notion of a $L^0(\nu )$-normed/Banach $L^0(\nu )$-module generalises Definitions 2.12 and 2.13 with ${\mathscr {A}}=L^0(\mu )$. Generalising Definition 2.14, we say that a vector subspace $V\subseteq {\mathscr {M}}$ generates ${\mathscr {M}}$ if ${\mathcal {G}}(V)$ is dense in ${\mathscr {M}}$, where ${\mathcal {G}}(V)$ is defined as in (2.3) (with $\nu$ in place of $\mu$).

In the case where $\mu \ll \nu$ and ${\mathscr {M}}$ is a given $L^0(\nu )$-Banach $L^0(\nu )$-module, we can ‘quotient ${\mathscr {M}}$ up to $\mu$-a.e. equality’, i.e. there is a natural $L^0(\mu )$-Banach $L^0(\mu )$-module structure on the quotient

$$\begin{aligned} {\mathscr {M}}_\mu :={\mathscr {M}}/\sim _\mu ,\quad \text { where }v\sim _\mu w\text { if and only if }|v-w|=0\text { holds }\mu \text {-a.e.\ on }\textrm{X}.\nonumber \\ \end{aligned}$$

(2.5)

In analogy with (and, in fact, generalising) the notation for the spaces of functions, we denote by $\pi _\mu :{\mathscr {M}}\rightarrow {\mathscr {M}}_\mu$ the canonical projection map and by $[v]_\mu \in {\mathscr {M}}_\mu$ the equivalence class of $v\in {\mathscr {M}}$.

2.3 Calculus on metric measure spaces

By a metric measure space $(\textrm{X},\textsf{d},\mathfrak {m})$ we mean a complete, separable metric space $(\textrm{X},\textsf{d})$ equipped with a boundedly finite Borel measure $\mathfrak {m}\ge 0$. We denote by $\textrm{LIP}(\textrm{X})$ (resp. $\textrm{LIP}_{loc}(\textrm{X})$, resp. $\textrm{LIP}_{bs}(\textrm{X})$) the space of all Lipschitz (resp. locally Lipschitz, resp. boundedly-supported Lipschitz) functions from $\textrm{X}$ to $\mathbb {R}$. The asymptotic slope $\textrm{lip}_a(f):\textrm{X}\rightarrow [0,+\infty )$ of $f\in \textrm{LIP}_{loc}(\textrm{X})$ is defined as

$$\begin{aligned} \textrm{lip}_a(f)(x):=\varlimsup _{y,z\rightarrow x}\frac{|f(y)-f(z)|}{\textsf{d}(y,z)}\quad \text { for every accumulation point }x\in \textrm{X}\end{aligned}$$

The local Lipschitz constant $\textrm{lip}(f):\textrm{X}\rightarrow [0,+\infty )$ of $f\in \textrm{LIP}_{loc}(\textrm{X})$ is defined as

$$\begin{aligned} \textrm{lip}(f)(x):=\varlimsup _{y\rightarrow x}\frac{|f(y)-f(x)|}{\textsf{d}(y,x)}\quad \text { for every accumulation point }x\in \textrm{X}. \end{aligned}$$

In both cases, we use the convention that $\textrm{lip}_a(f)(x):=0$ and $\textrm{lip}(f)(x):=0$ for every isolated point $x\in \textrm{X}$. The Cheeger energy of $(\textrm{X},\textsf{d},\mathfrak {m})$, which was introduced in [4] after [20], is the functional $\textrm{Ch}:L^2(\mathfrak {m})\rightarrow [0,\infty ]$ given by

$$\begin{aligned}{} & {} \textrm{Ch}(f):=\frac{1}{2}\inf \bigg \{\varliminf _{n\rightarrow \infty }\int \textrm{lip}_a^2(f_n)\,\text {d}\mathfrak {m}\; \bigg |\;(f_n)_{n\in \mathbb {N}}\subseteq \textrm{LIP}_{bs}(\textrm{X}),\,\pi _\mathfrak {m}(f_n)\rightarrow f\text { in }L^2(\mathfrak {m})\bigg \} \end{aligned}$$

for every $f\in L^2(\mathfrak {m})$. The Sobolev space $H^{1,2}(\textrm{X})$ is then defined as

$$\begin{aligned} H^{1,2}(\textrm{X}):=\big \{f\in L^2(\mathfrak {m})\;\big |\;\textrm{Ch}(f)<+\infty \big \}. \end{aligned}$$

Given any $f\in H^{1,2}(\textrm{X})$, there exists a unique non-negative function $|Df|\in L^2(\mathfrak {m})$, which is called the minimal relaxed slope of $f$, providing the integral representation

$$\begin{aligned} \textrm{Ch}(f)=\frac{1}{2}\int |Df|^2\,\text {d}\mathfrak {m}. \end{aligned}$$

It holds that $\pi _\mathfrak {m}(\textrm{LIP}_{bs}(\textrm{X}))\subseteq H^{1,2}(\textrm{X})$ and $|Df|\le \textrm{lip}_a(f)$ in the $\mathfrak {m}$-a.e. sense for all $f\in \textrm{LIP}_{bs}(\textrm{X})$. The Sobolev space is a Banach space if endowed with the norm

$$\begin{aligned} \Vert f\Vert _{H^{1,2}(\textrm{X})}:=\big (\Vert f\Vert _{L^2(\mathfrak {m})}^2+\Vert |Df|\Vert _{L^2(\mathfrak {m})}^2\big )^{1/2}\quad \text { for every }f\in H^{1,2}(\textrm{X}). \end{aligned}$$

However, $\big (H^{1,2}(\textrm{X}),\Vert \cdot \Vert _{H^{1,2}(\textrm{X})}\big )$ needs not be a Hilbert space. Following [25], we say that

$$\begin{aligned} (\textrm{X},\textsf{d},\mathfrak {m})\text { is \textit{infinitesimally Hilbertian} if }H^{1,2}(\textrm{X})\text { is a Hilbert space.} \end{aligned}$$

In the infinitesimally Hilbertian setting, the carré du champ operator

$$\begin{aligned}{} & {} H^{1,2}(\textrm{X})\times H^{1,2}(\textrm{X})\ni (f,g)\mapsto \langle \nabla f,\nabla g\rangle \nonumber \\{} & {} \quad :=\frac{|D(f+g)|^2-|Df|^2-|Dg|^2}{2}\in L^1(\mathfrak {m}) \end{aligned}$$

is a bilinear operator. We say that a function $f\in H^{1,2}(\textrm{X})$ has a Laplacian if there exists a (necessarily unique) function $\Delta f\in L^2(\mathfrak {m})$ such that

$$\begin{aligned} \int \langle \nabla f,\nabla g\rangle \,\text {d}\mathfrak {m}=-\int g\,\Delta f\,\text {d}\mathfrak {m}\quad \text { for every }g\in H^{1,2}(\textrm{X}). \end{aligned}$$

We denote by $D(\Delta )$ the space of all those functions $f\in H^{1,2}(\textrm{X})$ having a Laplacian.

The following definition is essentially taken from [26, 27]:

Definition 2.20

(Tangent module) Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an infinitesimally Hilbertian metric measure space. Then there exists a unique (up to a unique isomorphism) couple $(L^0(T\textrm{X}),\nabla )$, where:

$\mathrm i)$:

$L^0(T\textrm{X})$ is an $L^0(\mathfrak {m})$-Banach $L^0(\mathfrak {m})$-module.

$\mathrm ii)$:

$\nabla :H^{1,2}(\textrm{X})\rightarrow L^0(T\textrm{X})$ is a linear operator such that

$$\begin{aligned} \begin{aligned}&|\nabla f|=|Df|\text { for every }f\in H^{1,2}(\textrm{X}),\\&\quad \{\nabla f:\,f\in H^{1,2}(\textrm{X})\}\text { generates }L^0(T\textrm{X}). \end{aligned} \end{aligned}$$

The space $L^0(T\textrm{X})$ is called the tangent module of $(\textrm{X},\textsf{d},\mathfrak {m})$ and $\nabla$ the gradient operator.

Thanks to the locality properties of the minimal relaxed slopes, the gradient operator can be extended to all Lipschitz functions on $\textrm{X}$.

2.3.1 Functions of bounded variation on PI spaces

We recall the notion of function of bounded variation on a metric measure space. The following definition was introduced in [3] after [43].

Definition 2.21

(BV space) Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be a metric measure space and $f\in L^1_{loc}(\textrm{X})$. Given any open set $U\subseteq \textrm{X}$, we define the total variation of $f$ on $U$ as

$$\begin{aligned} |Df|(U){} & {} :=\inf \bigg \{\varliminf _{n\rightarrow \infty }\int _U\textrm{lip}_a(f_n)\,\text {d}\mathfrak {m}\;\bigg |\;(f_n)_{n\in \mathbb {N}}\subseteq \textrm{LIP}_{loc}(U)\cap L^1(U),\,\nonumber \\{} & {} \quad f_n \rightarrow f\text { in }L^1_{loc}(U)\bigg \}. \end{aligned}$$

(2.6)

Then we say that $f$ is of bounded variation if $|Df|(\textrm{X})<+\infty$. We define the space $BV(\textrm{X})$ as

$$\begin{aligned} BV(\textrm{X}):=\big \{f\in L^1(\mathfrak {m})\;\big |\;|Df|(\textrm{X})<+\infty \big \}. \end{aligned}$$

Moreover, we say that $E\subseteq \textrm{X}$ Borel is a set of finite perimeter if $P(E):=|D\mathbb {1}_E|(\textrm{X})<+\infty$.

Given any function $f\in L^1_{loc}(\textrm{X})$ of bounded variation, there exists a unique finite Borel measure on $\textrm{X}$, still denoted by $|Df|$, which extends the set-function on open sets we defined in (2.6). In the case where $f=\mathbb {1}_E$ for some set of finite perimeter $E\subseteq \textrm{X}$, we write $P(E,\cdot ):=|D\mathbb {1}_E|$ and we call $P(E,\cdot )$ the perimeter measure of $E$. The following result is taken from [43]:

Theorem 2.22

(Coarea formula) Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be a metric measure space and let $f\in BV(\textrm{X})$. Then $t\mapsto P(\{f>t\},\cdot )$ is a measurable measure-valued map from $\mathbb {R}$ to $\textrm{X}$. Moreover, it holds that

$$\begin{aligned} |Df|=\int _\mathbb {R}P(\{f>t\},\cdot )\,\text {d}t. \end{aligned}$$

Following [21, Definition 2.6] (which is a variant of [38, formula (7.2.1)]), we define the Sobolev capacity on the space $(\textrm{X},\textsf{d},\mathfrak {m})$ as

$$\begin{aligned} \textrm{Cap}(E):=\inf _f\Vert f\Vert _{H^{1,2}(\textrm{X})}^2\quad \text { for every set }E\subseteq \textrm{X}, \end{aligned}$$

where the infimum is taken over all functions $f\in H^{1,2}(\textrm{X})$ satisfying $f\ge 1$ $\mathfrak {m}$-a.e. on some open neighbourhood of $E$. The Sobolev capacity $\mathrm Cap$ is a boundedly-finite, submodular outer measure on $\textrm{X}$ such that $\mathfrak {m}\ll \textrm{Cap}$. Moreover, it was proved in [12] after [14] that

$$\begin{aligned} |Df|\ll \textrm{Cap}\quad \text { for every }f\in L^1_{loc}(\textrm{X})\text { of bounded variation,} \end{aligned}$$

(2.7)

thus in particular $P(E,\cdot )\ll \textrm{Cap}$ for every set of finite perimeter $E\subseteq \textrm{X}$.

Even though the basic theory of BV functions is meaningful on arbitrary metric measure spaces, a much more refined analysis is available in the setting of PI spaces, which we are going to introduce. We refer e.g. to [10, 38] for a thorough account of this topic.

Definition 2.23

(PI space) Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be a metric measure space. Then:

(i):

We say that $(\textrm{X},\textsf{d},\mathfrak {m})$ is uniformly locally doubling if there exists a non-decreasing function $C_D:(0,+\infty )\rightarrow (0,+\infty )$ such that

$$\begin{aligned} \mathfrak {m}(B_{2r}(x))\le C_D(R)\mathfrak {m}(B_r(x))\quad \text { for every }0<r<R\text { and }x\in \textrm{X}. \end{aligned}$$

(ii):

We say that $(\textrm{X},\textsf{d},\mathfrak {m})$ supports a weak local $(1,1)$-Poincaré inequality if there exist a constant $\lambda \ge 1$ and a non-decreasing function $C_P:(0,+\infty )\rightarrow (0,+\infty )$ such that for any function $f\in \textrm{LIP}(\textrm{X})$ it holds that

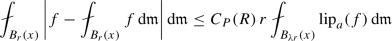
for every $0<r<R$ and $x\in \textrm{X}$.

(iii):

We say that $(\textrm{X},\textsf{d},\mathfrak {m})$ is a PI space if it is uniformly locally doubling and it supports a weak local $(1,1)$-Poincaré inequality.

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be a PI space. The upper density of a Borel set $E\subseteq \textrm{X}$ at a point $x\in \textrm{X}$ is

$$\begin{aligned} \Theta ^*(E,x):=\varlimsup _{r\searrow 0}\frac{\mathfrak {m}(E\cap B_r(x))}{\mathfrak {m}(B_r(x))}\in [0,1]. \end{aligned}$$

The essential boundary of $E$ is defined as the Borel set

$$\begin{aligned} \partial ^*E:=\big \{x\in \textrm{X}\;\big |\;\Theta ^*(E,x),\Theta ^*(\textrm{X}\setminus E,x)>0\big \}. \end{aligned}$$

Following [1], we define the codimension-one Hausdorff measure of a set $E\subseteq \textrm{X}$ as

$$\begin{aligned} {\mathcal {H}}(E):=\lim _{\delta \searrow 0}{\mathcal {H}}_\delta (E), \end{aligned}$$

where for any $\delta >0$ we define

$$\begin{aligned} {\mathcal {H}}_\delta (E):=\inf \bigg \{\sum _{n\in \mathbb {N}}\frac{\mathfrak {m}(B_{r_n}(x_n))}{2r_n}\;\bigg | \;(x_n)_n\subseteq \textrm{X},\,(r_n)_n\subseteq (0,\delta ),\,E\subseteq \bigcup _{n\in \mathbb {N}}B_{r_n}(x_n)\bigg \}. \end{aligned}$$

Both ${\mathcal {H}}_\delta$ and ${\mathcal {H}}$ are Borel regular outer measures on $\textrm{X}$. If $E\subseteq \textrm{X}$ is a set of finite perimeter, then it was proved in [1] (and [6]) that the perimeter measure of $E$ can be written as

$$\begin{aligned} P(E,\cdot )=\theta _E{\mathcal {H}}|_{\partial ^*E}, \end{aligned}$$

for some Borel density function $\theta _E:\textrm{X}\rightarrow [\gamma ,C]$, where the constants $C\ge \gamma >0$ depend exclusively on $C_D(\cdot )$, $C_P(\cdot )$, and $\lambda$. In particular, the perimeter measure $P(E,\cdot )$ is concentrated on $\partial ^*E$.

Definition 2.24

(Precise representative) Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be a PI space. Let $f\in BV(\textrm{X})$ be a given function. Then the approximate lower limit $f^\wedge :\textrm{X}\rightarrow [-\infty ,+\infty ]$ and the approximate upper limit $f^\vee :\textrm{X}\rightarrow [-\infty ,+\infty ]$ of $f$ are defined as

$$\begin{aligned} \begin{aligned} f^\wedge (x)&:=\sup \big \{t\in \mathbb {R}\;\big |\;\Theta ^*(\{f<t\},x)=0\big \},\\ f^\vee (x)&:=\inf \big \{t\in \mathbb {R}\;\big |\;\Theta ^*(\{f>t\},x)=0\big \} \end{aligned} \end{aligned}$$

for every $x\in \textrm{X}$, respectively. We also define the Borel set $\textrm{X}_f\subseteq \textrm{X}$ as

$$\begin{aligned} \textrm{X}_f:=\{f^\wedge >-\infty \}\cap \{f^\vee <+\infty \}. \end{aligned}$$

Finally, the precise representative ${\bar{f}}:\textrm{X}_f\rightarrow \mathbb {R}$ of $f$ is the Borel function given by

$$\begin{aligned} {\bar{f}}(x):=\frac{f^\wedge (x)+f^\vee (x)}{2}\quad \text { for every }x\in \textrm{X}_f. \end{aligned}$$

Remark 2.25

Since $\{f>t\}\subseteq \{f\ge t\}\subseteq \{f>s\}$ for every $s,t\in \mathbb {R}$ with $s<t$, one has that

$$\begin{aligned} \begin{aligned} f^\wedge (x)&=\sup \big \{t\in \mathbb {R}\;\big |\;\Theta ^*(\{f\le t\},x)=0\big \},\\ f^\vee (x)&=\inf \big \{t\in \mathbb {R}\;\big |\;\Theta ^*(\{f\ge t\},x)=0\big \} \end{aligned}\end{aligned}$$

for every $x\in \textrm{X}$. $\blacksquare$

It holds that $\mathfrak {m}(\textrm{X}{\setminus }\textrm{X}_f)=|Df|(\textrm{X}{\setminus }\textrm{X}_f)=0$, so that $|Df||_{\textrm{X}_f}=|Df|$, and that ${\bar{f}}$ is an $\mathfrak {m}$-a.e. representative of $f$. The jump set $J_f\subseteq \textrm{X}_f$ of $f$ is defined as

$$\begin{aligned} J_f:=\big \{x\in \textrm{X}\;\big |\;f^\wedge (x)<f^\vee (x)\big \}. \end{aligned}$$

It holds that $J_f$ is contained in a countable union of essential boundaries of sets of finite perimeter, thus in particular $\mathfrak {m}(J_f)=0$. More precisely, for suitably chosen $(t_n)_n,(s_n)_n\subseteq \mathbb {R}$ with $t_n\ne s_n$,

$$\begin{aligned} J_f=\bigcup _{n\in \mathbb {N}}\partial ^*\{{\bar{f}}>t_n\}\cap \partial ^*\{{\bar{f}}>s_n\}. \end{aligned}$$

Furthermore, there exists a Borel function $\theta _f:\textrm{X}\rightarrow [\gamma ,C]$ such that

$$\begin{aligned} |Df||_{J_f}=(f^\vee -f^\wedge )\theta _f{\mathcal {H}}|_{J_f}. \end{aligned}$$

The following definition has been proposed in [5, Definition 6.1]. We say that the metric measure space $(\textrm{X},\textsf{d},\mathfrak {m})$ is isotropic provided that, given two sets of finite perimeter E and F, it holds that

$$\begin{aligned} \theta _E =\theta _F \quad {\mathcal {H}}\text {-a.e. in }\partial ^* E \cap \partial ^* F. \end{aligned}$$

(2.8)

In the case where $(\textrm{X},\textsf{d},\mathfrak {m})$ is isotropic, we have that for any set $G\subseteq \textrm{X}$ of finite perimeter it holds

$$\begin{aligned} |Df||_{J_f\cap \partial ^*G}=(f^\vee -f^\wedge )P(G,\cdot )|_{J_f}. \end{aligned}$$

(2.9)

We refer to [8, 39] for the proofs of the above claims.

2.4 Calculus on $\textsf{RCD}$ spaces

We assume the reader is familiar with the language of $\textsf{RCD}(K,N)$ spaces. Let us only recall that an $\textsf{RCD}(K,N)$ space $(\textrm{X},\textsf{d},\mathfrak {m})$, with $K\in \mathbb {R}$ and $N\in [1,\infty )$, is an infinitesimally Hilbertian metric measure space whose synthetic Ricci curvature (resp. synthetic dimension) is bounded from below by $K$ (resp. from above by $N$), in the sense of Lott–Sturm–Villani [41, 48]. Each $\textsf{RCD}(K,N)$ space is a PI space (see [48] for the doubling condition and [44] for the Poincaré inequality). Moreover, $\textsf{RCD}(K,N)$ spaces are isotropic. This has been observed in [11, Example 1.29]. For more of this topic, see the survey [2] and the references therein.

Following [27] (after [45]), we consider the distinguished algebra of test functions on $\textrm{X}$:

$$\begin{aligned} \textrm{Test}(\textrm{X}):=\big \{f\in \textrm{LIP}(\textrm{X})\cap D(\Delta )\cap L^\infty (\mathfrak {m})\;\big |\;|Df|\in L^\infty (\mathfrak {m}),\,\Delta f\in H^{1,2}(\textrm{X})\big \}. \end{aligned}$$

The space $\textrm{Test}(\textrm{X})$ is dense in $H^{1,2}(\textrm{X})$. Moreover, the following property holds:

Lemma 2.26

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space. Then $\textrm{Test}(\textrm{X})$ generates $L^0(\textrm{Cap})$.

Proof

In fact, we will prove the following claim, which is a stronger statement, namely that if $f:\textrm{X}\rightarrow \mathbb {R}$ is a Borel function and $\varepsilon >0$ is given, then there exists a Borel partition $(E_n)_n$ of $\textrm{X}$ and $(f_n)_n\subseteq \textrm{Test}(\textrm{X})$ such that

$$\begin{aligned} |f(x)-f_n(x)|\le \varepsilon \quad \text { for every }n\in \mathbb {N}\text { and }x\in E_n. \end{aligned}$$

(2.10)

Indeed, from this claim the statement follows in the following way. Given $F \in L^0(\textrm{Cap})$, let f be Borel such that $[f]_\textrm{Cap}=F$. We fix $\varepsilon >0$ and apply the claim having $E_n$, $f_n$ as above. We define $g:=\sum _{n=1}^\infty \chi _{E_n} f_n$ and we have $|G-F|\le \varepsilon$ $\textrm{Cap}$-a.e. where $G=[g]_\textrm{Cap}$. This gives $\textsf{d}_{L^0(\textrm{Cap})}(|G-F|,0) \le \varepsilon$, proving the statement. Let us now prove the claim. First, we can find a Borel partition $(E_n)_n$ of $\textrm{X}$ into bounded sets and a sequence $(\lambda _n)_n\subseteq \mathbb {R}$ such that $|f-\lambda _n|\le \varepsilon$ on $E_n$. Using the results of [7], for any $n\in \mathbb {N}$ we can find a test cut-off function $f_n\in \textrm{Test}(\textrm{X})$ satisfying $f_n=\lambda _n$ on an open ball containing $E_n$. Property (2.10) follows. $\square$

Given any $f,g\in \textrm{Test}(\textrm{X})$, we have that

$$\begin{aligned} \langle \nabla f,\nabla g\rangle \in H^{1,2}(\textrm{X}). \end{aligned}$$

In particular, we deduce that for any $f\in \textrm{Test}(\textrm{X})$ the function $|Df|$ admits a quasi-continuous representative $\textrm{QCR}(|Df|)\in L^0(\textrm{Cap})$, cf. with [21]. Therefore, the following result, which is taken from [21, Theorem 3.6], is meaningful:

Theorem 2.27

(Capacitary tangent module) Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space. Then there exists a unique (up to a unique isomorphism) couple $(L^0_\textrm{Cap}(T\textrm{X}),{\bar{\nabla }})$, where:

$\mathrm i)$:

$L^0_\textrm{Cap}(T\textrm{X})$ is an $L^0(\textrm{Cap})$-Banach $L^0(\textrm{Cap})$-module.

$\mathrm ii)$:

${\bar{\nabla }}:\textrm{Test}(\textrm{X})\rightarrow L^0_\textrm{Cap}(T\textrm{X})$ is a linear operator such that

$$\begin{aligned} \begin{aligned} |{\bar{\nabla }} f|&=\textrm{QCR}(|Df|)\text { for every }f\in \textrm{Test}(\textrm{X}),\\&\{{\bar{\nabla }} f:\,f\in \textrm{Test}(\textrm{X})\}\text { generates }L^0_\textrm{Cap}(T\textrm{X}). \end{aligned} \end{aligned}$$

The space $L^0_\textrm{Cap}(T\textrm{X})$ is called the capacitary tangent module of $(\textrm{X},\textsf{d},\mathfrak {m})$.

The space $\textrm{Test}(T\textrm{X})\subseteq L^0_\textrm{Cap}(T\textrm{X})$ of test vector fields is then defined as

$$\begin{aligned} \textrm{Test}(T\textrm{X}):=\bigg \{\sum _{i=1}^n g_i{\bar{\nabla }} f_i\;\bigg |\;n\in \mathbb {N},\,(f_i)_{i=1}^n,(g_i)_{i=1}^n\subseteq \textrm{Test}(\textrm{X})\bigg \}. \end{aligned}$$

The space $\textrm{Test}(T\textrm{X})$ generates $L^0_\textrm{Cap}(T\textrm{X})$. Given a Borel measure $\mu$ on $\textrm{X}$ with $\mu \ll \textrm{Cap}$, we set

$$\begin{aligned} L^0_\mu (T\textrm{X}):=L^0_\textrm{Cap}(T\textrm{X})_\mu , \end{aligned}$$

where the right-hand side is defined as in (2.5). One can readily check that

$$\begin{aligned} L^0_\mathfrak {m}(T\textrm{X})\cong L^0(T\textrm{X}),\quad \text { with }\pi _\mathfrak {m}\circ {\bar{\nabla }}=\nabla |_{\textrm{Test}(\textrm{X})}. \end{aligned}$$

Thanks to (2.7), we can consider $L^0_{|Df|}(T\textrm{X})$ whenever $f\in L^1_{loc}(\textrm{X})$ is of bounded variation.

3 Integration of $L^0$-Banach $L^0$-modules

In this section, we introduce a notion of $L^0$-Banach $L^0$-module bundle consistent with a disjoint measure-valued map, which generalises the notion of strong Banach bundle studied in [29].

First, we introduce a useful shorthand notation. Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, and $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Given any collection ${\mathscr {M}}_\star =\{{\mathscr {M}}_q\}_{q\in Q}$, where ${\mathscr {M}}_q$ is an $L^0(\mu _q)$-Banach $L^0(\mu _q)$-module, and for any element $v$ of ${\mathscr {S}}({\mathscr {M}}_\star )$ or of ${\mathscr {S}}_{{\mathfrak {q}}}({\mathscr {M}}_\star )$, we denote by

$$\begin{aligned} |v_\star |\in {\mathscr {S}}_{{\mathfrak {q}}}(L^0(\mu _\star )) \end{aligned}$$

the (${\mathfrak {q}}$-a.e. equivalence class of the) map sending $q\in Q$ to $|v_q|\in L^0(\mu _q)$.

Definition 3.1

($L^0$-Banach $L^0$-module bundle) Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, and $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Let $({\mathscr {M}}_\star ,\Theta ,\Phi )$ be such that:

$\mathrm a)$:

${\mathscr {M}}_\star =\{{\mathscr {M}}_q\}_{q\in Q}$ and each space ${\mathscr {M}}_q$ is an $L^0(\mu _q)$-Banach $L^0(\mu _q)$-module.

$\mathrm b)$:

$\Phi$ is a subalgebra of $L^0({\mathfrak {q}};L^0(\mu _\star ))$ such that the subalgebra ${\mathcal {G}}_{{\mathfrak {q}}}(\Phi )$ is dense in $L^0(\mu )$, where

$$\begin{aligned} {\mathcal {G}}_{{\mathfrak {q}}}(\Phi ):= & {} \bigg \{\sum _{n\in \mathbb {N}}\textsf{j}_{{\mathfrak {q}}}(\mathbb {1}_{S_n}^{{\mathfrak {q}}}f_n)\;\bigg |\;(S_n)_{n\in \mathbb {N}}\subseteq {\mathcal {Q}} \text { partition of }Q,\,(f_n)_{n\in \mathbb {N}}\subseteq \Phi \bigg \}\\\subseteq & {} L^0(\mu ). \end{aligned}$$

In particular, it holds that $\widehat{\textsf{j}_{{\mathfrak {q}}}(\Phi )}=L^0(\mu )$.

$\mathrm c)$:

$\Theta$ is a vector subspace of ${\mathscr {S}}_{{\mathfrak {q}}}({\mathscr {M}}_\star )$ that is also a module over $\textsf{j}_{{\mathfrak {q}}}(\Phi )$ and verifies

$$\begin{aligned} |v_\star |\in L^0({\mathfrak {q}};L^0(\mu _\star ))\quad \text { for every }v\in \Theta . \end{aligned}$$

Then we say that $({\mathscr {M}}_\star ,\Theta ,\Phi )$ is a $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu _q$.

Remark 3.2

Let us clarify why the elements of ${\mathcal {G}}_\mathfrak {q}(\Phi )$ are well-posed. Fix a partition $(S_n)_n\subseteq {\mathcal {Q}}$ of Q and a sequence $(f_n)_n\subseteq \Phi$. Let $F_n\in L^0(\mu )$, with representative ${\bar{F}}_n\in {\mathcal {L}}^0(\Sigma )$ be such that $\textrm{i}_{{\mathfrak {q}}}(F_n)=f_n$. Then $\textsf{i}_\mathfrak {q}(\mathbb {1}_{U_n}^\mu F_n)=\mathbb {1}_{S_n}^\mathfrak {q}f_n\in L^0(\mathfrak {q};L^0(\mu _\star ))$, where $U_n:=\bigcup _{q\in S_n}E_q\in \Sigma$ and $(E_q)_{q\in Q}$ is the family from Definition 2.3. Furthermore, $(U_n)_n$ are pairwise disjoint, $\sum _{n\in \mathbb {N}}\mathbb {1}_{U_n}{\bar{F}}_n\in {\mathcal {L}}^0(\Sigma )$, and $\sum _{n\in \mathbb {N}}\textsf{j}_q(\mathbb {1}_{S_n}^\mathfrak {q}f_n)=\big [\sum _{n\in \mathbb {N}}\mathbb {1}_{U_n}{\bar{F}}_n\big ]_\mu$. $\blacksquare$

One can readily check that the mapping $|\cdot |:\Theta \rightarrow L^0(\mu )$, which we define as

$$\begin{aligned} |v|:=\textsf{j}_{{\mathfrak {q}}}(|v_\star |)\in L^0(\mu )\quad \text { for every }v\in \Theta , \end{aligned}$$

is a pointwise norm on $\Theta$. Therefore, the space $\Theta$ is an $L^0(\mu )$-normed $\textsf{j}_{{\mathfrak {q}}}(\Phi )$-module.

Remark 3.3

Each strong Banach bundle (in the sense of [29]) is in particular an $L^0$-Banach $L^0$-module bundle, in the sense we are going to describe. Given a measure space $(Q,{\mathcal {Q}},{\mathfrak {q}})$ and strong Banach bundle $(\mathbb {B}_\star ,\textrm{T})$ over $(Q,{\mathcal {Q}},{\mathfrak {q}})$, we can regard (thanks to Example 2.15) each space $\mathbb {B}_q$ as an $L^0(\delta _{(q,\textsf{o})})$-Banach $L^0(\delta _{(q,\textsf{o})})$-module, where $(\{\textsf{o}\},\delta _\textsf{o})$ is the one-point probability space. Recall also from Example 2.4 that $q\mapsto \delta _{(q,\textsf{o})}$ is a disjoint measure-valued map from $Q$ to $Q\times \{\textsf{o}\}$ and ${\mathfrak {q}}\otimes \delta _\textsf{o}=\int \delta _{(q,\textsf{o})}\,\text {d}{\mathfrak {q}}(q)$. Moreover, $\mathbb {R}_{{\mathfrak {q}}}\subseteq L^0({\mathfrak {q}})\cong L^0({\mathfrak {q}}\otimes \delta _\textsf{o})\cong L^0({\mathfrak {q}};L^0(\delta _{(\star ,\textsf{o})}))$. Therefore, up to the above identifications, $(\mathbb {B}_\star ,\textrm{T},\mathbb {R}_{{\mathfrak {q}}})$ is a $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \delta _{(q,\textsf{o})}$. $\blacksquare$

Definition 3.4

(Integral of an $L^0$-Banach $L^0$-module bundle) Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, and $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Let $({\mathscr {M}}_\star ,\Theta ,\Phi )$ be a $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu _q$. Then we define $\int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$ as

$$\begin{aligned} \int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q):=\text {completion of the }L^0(\mu )\text {-normed } \textsf{j}_{{\mathfrak {q}}}(\Phi )\text {-module }\Theta . \end{aligned}$$

The $L^0(\mu )$-Banach $L^0(\mu )$-module $\int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$ is referred to as the integral of $({\mathscr {M}}_\star ,\Theta ,\Phi )$. Given an element $v\in \int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$, we will often denote it by $\int v_q\,\text {d}{\mathfrak {q}}(q)$. Whenever we want to make explicit the choice of the classes $\Theta$ and $\Phi$, we write $\Gamma ({\mathscr {M}}_\star ,\Theta ,\Phi )$ instead of $\int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$.

Theorem 3.5

(Identification of the integral) Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, and $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Let $({\mathscr {M}}_\star ,\Theta ,\Phi )$ be an $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu _q$. Let us denote by ${\bar{\Gamma }}({\mathscr {M}}_\star ,\Theta ,\Phi )$ the space of all those elements $v\in {\mathscr {S}}({\mathscr {M}}_\star )$ satisfying the following properties:

$\mathrm i)$:

The element $|v_\star -w_\star |\in {\mathscr {S}}_{{\mathfrak {q}}}(L^0(\mu _\star ))$ belongs to $L^0({\mathfrak {q}};L^0(\mu _\star ))$ for every $w\in \Theta$.

$\mathrm ii)$:

There exists a countable set ${\mathcal {C}}_v\subseteq \Theta$ such that $v_q\in \textrm{cl}_{{\mathscr {M}}_q}(\{w_q\,:\,w\in {\mathcal {C}}_v\})$ for ${\mathfrak {q}}$-a.e. $q\in Q$.

Then $\Theta \subseteq \pi _{{\mathfrak {q}}}({\bar{\Gamma }}({\mathscr {M}}_\star ,\Theta ,\Phi ))$ and $\big (\pi _{{\mathfrak {q}}}({\bar{\Gamma }}({\mathscr {M}}_\star ,\Theta ,\Phi )),|\cdot |\big )$ is (isomorphic to) the integral $\int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$.

Proof

Set $\Gamma :=\pi _{{\mathfrak {q}}}({\bar{\Gamma }}({\mathscr {M}}_\star ,\Theta ,\Phi ))$ for brevity. The inclusion $\Theta \subseteq \Gamma$ is immediate. We define

$$\begin{aligned} {\mathcal {G}}_{{\mathfrak {q}}}(\Theta ):=\bigg \{\sum _{n\in \mathbb {N}}\mathbb {1}_{S_n}^{{\mathfrak {q}}} w^n\;\bigg |\;(S_n)_{n\in \mathbb {N}}\subseteq {\mathcal {Q}} \text { partition of }Q,\,(w^n)_{n\in \mathbb {N}}\subseteq \Theta \bigg \}\subseteq {\mathscr {S}}_{{\mathfrak {q}}}({\mathscr {M}}_\star ), \end{aligned}$$

We have that ${\mathcal {G}}_{{\mathfrak {q}}}(\Theta )$ is a vector subspace of ${\mathscr {S}}_{{\mathfrak {q}}}({\mathscr {M}}_\star )$, a module over ${\mathcal {G}}_{{\mathfrak {q}}}(\Phi )$, and a dense subset of $\Gamma$.

Step 1. Let us verify that ${\mathcal {G}}_\mathfrak {q}(\Theta )\subseteq \Gamma$. Take arbitrary $v=\sum _{n\in \mathbb {N}}\mathbb {1}_{S_n}^\mathfrak {q}w^n\in {\mathcal {G}}_\mathfrak {q}(\Theta )$ and $w^n\in \Theta$. Since $w^n\in \Theta$, for every $n\in {\mathbb {N}}$ it holds that $|w^n_\star -w_\star |\in L^0(\mathfrak {q};L^0(\mu _\star ))$. Hence, there exist ${\bar{F}}_n\in {\mathcal {L}}^0(\Sigma )$, $n\in {\mathbb {N}}$ such that $|w^n_q-w_q|=[{\bar{F}}_n]_{\mu _q}$ $\mathfrak {q}$-a.e. on Q. Further, $\mathfrak {q}$-a.e. on Q it holds that

$$\begin{aligned} \begin{aligned} |v_q-w_q|&=\left| \sum _{n\in \mathbb {N}}\mathbb {1}_{S_n}(q)w^n_q-w_q\right| =\sum _{n\in \mathbb {N}}\mathbb {1}_{S_n}(q)|w^n_q-w_q|\\&\!\! \underset{q\in S_{n_q}}{=}|w_q^{n_q}-w_q|=\left[ \mathbb {1}_{E_q}{\bar{F}}_{n_q}\right] _{\mu _q}=\left[ \sum _{n\in \mathbb {N}}\mathbb {1}_{{ \displaystyle \bigcup _{q\in S_n}E_q}}{\bar{F}}_n\right] _{\mu _q}. \end{aligned}\nonumber \\ \end{aligned}$$

(3.1)

Thanks to the disjointness of measure-valued map $q\mapsto \mu _q$, we have $\sum _{n\in \mathbb {N}}\mathbb {1}_{{\displaystyle \cup _{q\in S_n}E_q}}{\bar{F}}_n\in {\mathcal {L}}^0(\Sigma )$, whence we deduce that $|v_\star -w_\star |\in L^0(\mathfrak {q};L^0(\mu _\star ))$, and thus i) is satisfied. To prove that ii) holds, it is enough to define ${\mathcal {C}}_v=\{w^n\,|\,n\in \mathbb {N}\}$. This concludes the proof that ${\mathcal {G}}_\mathfrak {q}(\Theta )\subseteq \Gamma$. Similarly, one can also readily check that $|v_\star -z_\star |\in L^0({\mathfrak {q}};L^0(\mu _\star ))$ for every $v\in \Gamma$ and $z\in {\mathcal {G}}_{{\mathfrak {q}}}(\Theta )$.

Step 2. We claim that

$$\begin{aligned} \forall v\in \Gamma \quad \exists (z^k)_{k\in \mathbb {N}}\subseteq {\mathcal {G}}_{{\mathfrak {q}}}(\Theta ):\quad \textsf{j}_{{\mathfrak {q}}}(|v_\star -z^k_\star |)\rightarrow 0\,\text { in }L^0(\mu ). \end{aligned}$$

(3.2)

In order to prove it, notice that for any $k\in \mathbb {N}$ we can find a partition $(S^k_n)_{n\in \mathbb {N}}\subseteq {\mathcal {Q}}$ of $Q$ and a sequence $(w^{k,n})_{n\in \mathbb {N}}\subseteq {\mathcal {C}}_v$ such that $z^k:=\sum _{n\in \mathbb {N}}\mathbb {1}_{S^k_n}^{{\mathfrak {q}}}w^{k,n}\in {\mathcal {G}}_{{\mathfrak {q}}}(\Theta )$ satisfies $\textsf{d}_{{\mathscr {M}}_q}(v_q,z^k_q)\le \frac{1}{k}$ for ${\mathfrak {q}}$-a.e. $q\in Q$. Let us explain this in more details. Fix arbitrary $v\in \Gamma$ with ${\mathcal {C}}_v=\{w^n\,|\,n\in \mathbb {N}\}\subseteq \Theta$. For every $k,n\in {\mathbb {N}}$ we define

$$\begin{aligned} {\tilde{S}}_n^k:=\left\{ q\in Q\,|\,\textsf{d}_{{\mathscr {M}}_q}(v_q, w^n_q)\le \frac{1}{k}\right\} . \end{aligned}$$

Thanks to Remark 2.9, we can assume that ${\mathfrak {q}}$ and (almost) all $\mu _q$’s are finite. Therefore, we can deduce that for $\mathfrak {q}$-a.e. $q\in Q$ it holds that

$$\begin{aligned} \textsf{d}_{{\mathscr {M}}_q}(v_q,w^n_q)=\textsf{d}_{L^0(\mu _q)}(|v_q-w^n_q|,0)=\int _\textrm{X}\min \{G^n,1\}\,\text {d}\mu _q, \end{aligned}$$

where $G^n\in {\mathcal {L}}^0(\Sigma )$ are such that $|v_q-w^n_q|=[G^n]_{\mu _q}$ for $\mathfrak {q}$-a.e. $q\in Q$. Since $G^n\in {\mathcal {L}}^0(\Sigma )$, it follows that the map $\gamma _n:Q\ni q\mapsto \int _{\textrm{X}}\min \{G^n,1\}\,\text {d}\mu _q\in [0,+\infty ]$ is measurable. Moreover, for every $n\in \mathbb {N}$ we have that there exists $S_Q^n\in {\mathcal {Q}}$, such that $\mathfrak {q}(S_Q^n)=0$ and $\gamma ^n=\textsf{d}_{{\mathscr {M}}_q}(v_\cdot , w^n_\cdot )$ on $Q\setminus S_Q^n$. Now we conclude that

$$\begin{aligned} {{\tilde{S}}}_n^k=\underset{:=\tilde{{{\tilde{S}}}}_n^{k}=(\gamma ^n)^{-1}([0,1/k]) \in {\mathcal {Q}}}{\underbrace{\left( {{\tilde{S}}}_n^k\cap (Q\setminus S_Q^n)\right) }}\cup \underset{\mathfrak {q}\text {-negligible}}{\underbrace{({{\tilde{S}}}_n^k\cap S_Q^n)}},\quad \text {for every }n,k\in \mathbb {N}. \end{aligned}$$

Let $Q_v\in {\mathcal {Q}}$ be such that $\mathfrak {q}(Q_v)=0$ and for every $q\in Q\setminus Q_v$ it holds that $v_q\in \textrm{cl}(\{w^n_q\,|\,n\in \mathbb {N}\})$. Hence, for every $q\in Q\setminus Q_v$ and every $k\in \mathbb {N}$ there exists $n\in \mathbb {N}$ such that $\textsf{d}_{{\mathscr {M}}_q}(v_q,w^n_q)\le 1/k$. We deduce that for every $k\in \mathbb {N}$ it holds

$$\begin{aligned} Q\setminus \underset{\mathfrak {q}\text {-negligible}}{\underbrace{\left( Q_v\cup \left( \bigcup _{n\in \mathbb {N}}S_Q^n\right) \right) }}=\bigcup _{n\in \mathbb {N}}\left( \tilde{{{\tilde{S}}}}_n^{k}\setminus Q_v\right) . \end{aligned}$$

Further, for every $k\in \mathbb {N}$ set $S_1^k:=\tilde{{{\tilde{S}}}}_1^k\setminus Q_v$, $S_n^k:=\big (\bigcup _{i=1}^n(\tilde{{{\tilde{S}}}}_i^k{\setminus } Q_v)\big ){\setminus } S_{n-1}^k$, $n\ge 2$. In other words, a collection $\{S_n^k\}_{n\in \mathbb {N}}$ is a partition of Q up to $\mathfrak {q}$-negligible set, for every $k\in \mathbb {N}$. Define $z^k:=\sum _{n\in \mathbb {N}}\mathbb {1}_{S_n^k}^\mathfrak {q}w^n$. Obviously $z^k\in {\mathcal {G}}_\mathfrak {q}(\Theta )$, $k\in \mathbb {N}$. Moreover, for every $k\in \mathbb {N}$ it holds that $\textsf{d}_{{\mathscr {M}}_q}(v_q,z_q^k)\le \frac{1}{k}$ for $\mathfrak {q}$-a.e. $q\in Q$. Then

$$\begin{aligned} \textsf{d}_{L^0(\mu )}\big (\textsf{j}_{{\mathfrak {q}}}(|v_\star -z^k_\star |),0\big )= & {} \int \!\!\!\int |v_q-z^k_q|\wedge 1\,\text {d}\mu _q\,\text {d}{\mathfrak {q}}(q)\\= & {} \int \textsf{d}_{{\mathscr {M}}_q}(v_q,z^k_q)\,\text {d}{\mathfrak {q}}(q)\le \frac{{\mathfrak {q}}(Q)}{k}, \end{aligned}$$

whence the validity of (3.2) follows, concluding Step 2.

Having (3.2) at disposal, we can prove the following facts:

• Thanks to $\big ||v_\star |-|z^k_\star |\big |\le |v_\star -z^k_\star |$, we obtain that $|v_\star |\in L^0({\mathfrak {q}};L^0(\mu _\star ))$ for every $v\in \Gamma$.

• If $v,{{\tilde{v}}}\in \Gamma$ are given, then we can find $(z^k)_{k\in \mathbb {N}},({{\tilde{z}}}^k)_{k\in \mathbb {N}}\subseteq {\mathcal {G}}_{{\mathfrak {q}}}(\Theta )$ such that $\textsf{j}_{{\mathfrak {q}}}(|v_\star -z^k_\star |)\rightarrow 0$ and $\textsf{j}_{{\mathfrak {q}}}(|{{\tilde{v}}}_\star -{{\tilde{z}}}^k_\star |)\rightarrow 0$ in $L^0(\mu )$. Since for any $w\in \Theta$ we have $z^k+{{\tilde{z}}}^k-w\in {\mathcal {G}}_{{\mathfrak {q}}}(\Theta )$ and

  $$\begin{aligned} \big ||v_\star +{{\tilde{v}}}_\star -w_\star |-|z^k_\star +{{\tilde{z}}}^k_\star -w_\star |\big |\le & {} \big |(v_\star +{{\tilde{v}}}_\star )-(z^k_\star +{{\tilde{z}}}^k_\star )\big | \\\le & {} |v_\star -z^k_\star |+|{{\tilde{v}}}_\star -{{\tilde{z}}}^k_\star |, \end{aligned}$$

  by letting $k\rightarrow \infty$ we deduce that $|v_\star +{{\tilde{v}}}_\star -w_\star |\in L^0({\mathfrak {q}};L^0(\mu _\star ))$ and $v+{{\tilde{v}}}\in \Gamma$.

• If $v\in \Gamma$ and $f\in L^0(\mu )$ are given, then we can find $(z^k)_{k\in \mathbb {N}}\subseteq {\mathcal {G}}_{{\mathfrak {q}}}(\Theta )$ and $(f_k)_{k\in \mathbb {N}}\subseteq {\mathcal {G}}_{{\mathfrak {q}}}(\Phi )$ such that $\textsf{j}_{{\mathfrak {q}}}(|v_\star -z^k_\star |)\rightarrow 0$ and $f_k\rightarrow f$ in $L^0(\mu )$. Since for any given element $w\in \Theta$ we have that $f_k\cdot z^k-w\in {\mathcal {G}}_{{\mathfrak {q}}}(\Theta )$ and

  $$\begin{aligned} \begin{aligned} \big ||(f\cdot v)_\star -w_\star |-|(f_k\cdot z^k)_\star -w_\star |\big |&\le \big |(f\cdot v)_\star -(f_k\cdot z^k)_\star \big |\\&\le |f-f_k||v_\star |+|f_k||v_\star -z^k_\star |, \end{aligned} \end{aligned}$$

  by letting $k\rightarrow \infty$ we deduce that $|(f\cdot v)_\star -w_\star |\in L^0({\mathfrak {q}};L^0(\mu _\star ))$ and $f\cdot v\in \Gamma$.

From the previous observations, we proved that $\Gamma$ is an $L^0(\mu )$-normed $L^0(\mu )$-module and ${\mathcal {G}}_\mathfrak {q}(\Theta )$ is dense in $\Gamma$. It remains to prove that $\Gamma$ is complete, which we ensure in the next Lemma 3.6. Therefore, by the uniqueness statement in Proposition 2.16, which can be applied since $\Gamma$ verifies both item (i) and (ii) of Proposition 2.16, we conclude that $\Gamma$ is isomorphic to $\int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$ in the sense of $L^0(\mu )$-Banach $L^0(\mu )$-module. $\square$

Lemma 3.6

Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space, $(\textrm{X},\Sigma )$ a measurable space, and $q\mapsto \mu _q$ a disjoint measure-valued map from $Q$ to $\textrm{X}$. Let $({\mathscr {M}}_\star ,\Theta ,\Phi )$ be an $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu _q$. Let us denote ${\mathscr {S}}:=\left\{ v\in {\mathscr {S}}_\mathfrak {q}({\mathscr {M}}_\star )\,:\,|v_\star |\in L^0(\mathfrak {q};L^0(\mu _\star ))\right\}$. Then ${\mathscr {S}}$ is endowed with a structure of an $L^0(\mu )$-Banach $L^0(\mu )$-module. Further, the $L^0(\mu )$-normed $L^0(\mu )$-module $\Gamma$ from Theorem 3.5 is a closed submodule of ${\mathscr {S}}$, whence $\Gamma$ is complete as well.

Proof

It is straightforward to show that ${\mathscr {S}}$ is an $L^0(\mu )$-normed $L^0(\mu )$-module, where we set $|v|:=\textsf{j}_\mathfrak {q}\left( |v_\star |\right) \in L^0(\mu )$, for every $v\in {\mathscr {S}}$. To prove that it is complete we can assume without loss of generality, up to passing to a subsequence, that a Cauchy sequence $(z^k)_{k\in {\mathbb {N}}}$ in ${\mathscr {S}}$ satisfies

$$\begin{aligned} \sum _{k=1}^\infty \int \int \min \{|z^k_q -z^{k+1}_q|, 1\}\,\text {d}\mu _q\,\text {d}\mathfrak {q}(q) <\infty . \end{aligned}$$

Thus, we have that

$$\begin{aligned} \sum _{k=1}^\infty \int \min \{|z^k_q -z^{k+1}_q|, 1\}\,\text {d}\mu _q < \infty \end{aligned}$$

for $\mathfrak {q}$-a.e. q and in particular $(z^k_q)_{k}$ is a Cauchy sequence in $L^0(\mu _q)$ for such q’s. Since ${\mathscr {M}}_q$ is an $L^0(\mu _q)$-Banach $L^0(\mu _q)$-module, we have that there exists $z_q \in {\mathscr {M}}_q$ such that $\int \min \{|z^k_q-z_q|,1\}\,\text {d}\mu _q \rightarrow 0$ for $\mathfrak {q}$-a.e. q. We consider the $\mathfrak {q}$-a.e. defined map z, defined as $Q\ni q\mapsto z_q\in {\mathscr {M}}_q$.

We check that $z \in {\mathscr {S}}$. Since $\int \min \{|z^k_q-z_q|,1\}\,\text {d}\mu _q \rightarrow 0$ for $\mathfrak {q}$-a.e. q, by triangle inequality, we get that $|z^k_q|$ converges to $|z_q|$ in $L^0(\mu _q)$ for $\mathfrak {q}$-a.e. q. Moreover, since $\left| |z^k|-|z^{k+1}|\right| \le |z^k-z^{k+1}|$ holds $\mu$-a.e., it is clear that $(|z^k|)_{k\in {\mathbb {N}}}$ is a Cauchy sequence in $L^0(\mu )$, whence it is convergent. We call its limit $F=[{\bar{F}}]_\mu \in L^0(\mu )$, with $\bar{F}\in {\mathcal {L}}^0(\Sigma )$. This proves, using Lemma 2.8, that $|z_q|=[\bar{F}]_{\mu _q}$ for $\mathfrak {q}$-a.e. q and thus $z \in {\mathscr {S}}$. Moreover, by dominated convergence theorem, we get that $\int \int \min \{|z^k_q-z_q|,1\}\,\text {d}\mu _q\,\text {d}\mathfrak {q}(q) \rightarrow 0$, so $z^k \rightarrow z$ in ${\mathscr {S}}$.

We now prove that $\Gamma$ is a closed submodule of ${\mathscr {S}}$. By Theorem 3.5 it is clear that $\Gamma \subseteq {\mathscr {S}}$. Fix an arbitrary sequence $(v^k)_{k\in {\mathbb {N}}}\subseteq \Gamma$ that converges to $v\in {\mathscr {S}}$. Let us prove that $v\in \Gamma$. Since for any given $w\in \Theta$ we have that $v^k-w\in \Gamma$ and

$$\begin{aligned} \big ||v_\star -w_\star |-|v^k_\star -w_\star |\big |\le |v_\star -v^k_\star |, \end{aligned}$$

by letting $k\rightarrow \infty$ we deduce that $|v_\star -w_\star |\in L^0(\mathfrak {q};L^0(\mu _\star ))$. Thus, v satisfies i). To prove that ii) holds as well, let us denote the sequence $(v^k_n)_{n\in {\mathbb {N}}}\subseteq {\mathcal {G}}_\mathfrak {q}(\Theta )$ which converges to $v^k$, where $v^k_n=\sum _{j=1}^\infty \mathbb {1}^\mathfrak {q}_{S_j^{n,k}} w_j^{n,k}$ and $(w_j^{n,k})_{j\in {\mathbb {N}}}\subseteq \Theta$, $(S_j^{n,k})_{j\in {\mathbb {N}}}\subseteq {\mathcal {Q}}$ for every $k, n\in {\mathbb {N}}$, that can be done by Theorem 3.5. Then we can set $C_v:=\{w_j^{n,k}\,:\,j,n,k\in {\mathbb {N}}\}$, which concludes the proof of the validity of item ii) in the definition of $\Gamma$ in Theorem 3.5 and the proof of the closedness of $\Gamma$. $\square$

Remark 3.7

If ${\mathscr {M}}_\star =L^0(\mu _\star )$ and $\Theta =\Phi =L^0(\mathfrak {q};L^0(\mu _\star ))$, then $L^0(\mathfrak {q};L^0(\mu _\star ))\cong \int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q)$. $\blacksquare$

3.1 Disintegration of a module with respect to a disjoint measure-valued map

The next two theorems assert that, starting from an $L^0(\mu )$-Banach $L^0(\mu )$-module ${\mathscr {M}}$ and a disjoint measure-valued map, we can associate a $L^0$-Banach $L^0$-module bundle such that its integral is isomorphic to ${\mathscr {M}}$. We have to assume something more either on ${\mathscr {M}}$ or on the disjoint measure-valued map. Indeed, in the first theorem ${\mathscr {M}}$ is assumed to be countably-generated, in the second one the measures $\mu _q$’s are all absolutely continuous with respect to a background boundedly-finite, submodular outer measure $\nu$. Regarding the tools involved in the proof of Theorem 3.8, we refer the reader to [23], where the concepts of Banach $\mathbb {B}$-bundle ${{\textbf {E}}}$ and of ${\bar{\Gamma }}({{\textbf {E}}})$ are presented.

Theorem 3.8

(Disintegration of an $L^0$-Banach $L^0$-module) Let $(\textrm{X},\Sigma ,\mu )$ be a $\sigma$-finite measure space and let ${\mathscr {M}}$ be a countably-generated $L^0(\mu )$-Banach $L^0(\mu )$-module. Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space and let $Q\ni q\mapsto \mu _q$ be a disjoint measure-valued map from $Q$ to $\textrm{X}$ such that $\mu =\int \mu _q\,\text {d}{\mathfrak {q}}(q)$. Then there exists an $L^0$-Banach $L^0$-module bundle $({\mathscr {M}}_\star ,\Theta , \Phi )$ consistent with $Q\ni q\mapsto \mu _q$, such that

$$\begin{aligned} {\mathscr {M}}\cong \int {\mathscr {M}}_q\,\text {d}{\mathfrak {q}}(q). \end{aligned}$$

Proof

Let $\mathbb {B}$ be a universal separable Banach space. Then [23, Theorem 4.13] ensures that there exists a separable Banach $\mathbb {B}$-bundle ${\textbf {E}}$, such that $\Gamma _\mu ({{\textbf {E}}})\cong {\mathscr {M}}$, where $\Gamma _\mu ({{\textbf {E}}})$ is the quotient space of the space ${\bar{\Gamma }}({\textbf {E}})$ of all measurable sections of ${\textbf { E}}$, under $\mu$-a.e. equivalence relation. Recall that the elements of ${\bar{\Gamma }}({\textbf {E}})$ are everywhere defined, so that for any $q\in Q$ we can consider an $L^0(\mu _q)$-Banach $L^0(\mu _q)$-module $\Gamma _{\mu _q}({{\textbf {E}}})$. Denote the projections on quotient spaces with $\pi _\mu :{\bar{\Gamma }}({{\textbf {E}}})\rightarrow \Gamma _\mu ({{\textbf {E}}})$ and $\pi _q:{\bar{\Gamma }}({{\textbf {E}}})\rightarrow \Gamma _{\mu _q}({{\textbf {E}}})$, for all $q\in Q$. Define ${\mathscr {M}}_q:=\Gamma _{\mu _q}({{\textbf {E}}})$, $q\in Q$ and

$$\begin{aligned} {\bar{\Theta }}:=\{Q\ni q\mapsto \pi _q({\bar{v}})\in {\mathscr {M}}_{q}\,|\,{\bar{v}}\in {\bar{\Gamma }}({{\textbf {E}}})\},\quad \Theta :=\pi _\mathfrak {q}({\bar{\Theta }}). \end{aligned}$$

Further, let $\Phi :=L^0(\mathfrak {q};L^0(\mu _\star ))$. Then ${\mathcal {G}}_\mathfrak {q}(\Phi )=L^0(\mu )$, $\Theta$ is a vector subspace of ${\mathscr {S}}_\mathfrak {q}({\mathscr {M}}_\star )$ and a module over $\Phi$. Denote with v the $\mathfrak {q}$-a.e. defined equivalence class of the map $q\mapsto \pi _q({\bar{v}})$, then

$$\begin{aligned} |v_\star |=\textsf{i}_\mathfrak {q}\left( |\pi _\mu ({\bar{v}})|\right) \in L^0(\mathfrak {q};L^0(\mu _\star )), \quad \text {for every }{\bar{v}}\in {\bar{\Gamma }}({{\textbf {E}}}), \end{aligned}$$

since $|\pi _\mu ({\bar{v}})|$ and $|\pi _q({\bar{v}})|$ are $\mu$-a.e. and $\mu _q$-a.e. equivalence classes of the map $\textrm{X}\ni x\mapsto \Vert {\bar{v}}(x)\Vert _{\mathbb {B}}\in \mathbb {R}$, respectively. Hence, $({\mathscr {M}}_\star ,\Theta ,\Phi )$ is an $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu _q$. Moreover, we obtained that $\Theta$ is an $L^0(\mu )$-normed $L^0(\mu )$-module. Further, we define

$$\begin{aligned} \textrm{J}(\pi _\mu ({\bar{v}})):=\int \pi _q({\bar{v}})\,\text {d}\mathfrak {q}(q),\quad \text {for every }{\bar{v}}\in {\bar{\Gamma }}({{{\textbf {E}}})}. \end{aligned}$$

The resulting operator $\textrm{J}:\Gamma _\mu ({{\textbf {E}}})\rightarrow \Theta$ is an isomorphism of $L^0(\mu )$-normed $L^0(\mu )$-modules. Let us verify this claim. Take ${\bar{v}},{{\tilde{v}}}\in {\bar{\Gamma }}({{\textbf {E}}})$, such that $\pi _\mu ({\bar{v}})=\pi _\mu ({{\tilde{v}}})$, which means that ${\bar{v}}(x)={{\tilde{v}}}(x)$ $\mu$-a.e. on $\textrm{X}$. Then, since $\mu =\int \mu _q\,\text {d}\mathfrak {q}(q)$, follows that ${\bar{v}}(x)={{\tilde{v}}}(x)$ $\mu _q$-a.e. on $\textrm{X}$ for $\mathfrak {q}$-a.e. $q\in Q$, whence $\pi _q({\bar{v}})=\pi _q({{\tilde{v}}})$ for $\mathfrak {q}$-a.e. $q\in Q$ and $\textrm{J}(\pi _\mu ({\bar{v}}))=\textrm{J}(\pi _\mu ({{\tilde{v}}}))$, so $\textrm{J}$ is well-defined. It is clear that $\mathrm J$ is $L^0(\mu )$-linear and surjective. Furthermore,

$$\begin{aligned} |\textrm{J}(\pi _\mu ({\bar{v}}))|=\textsf{j}_\mathfrak {q}(|\textrm{J}(\pi _\mu ({\bar{v}}))_\star |)=|\pi _\mu ({\bar{v}})|,\quad \text {for every }{\bar{v}}\in {\bar{\Gamma }}({{\textbf {E}}}), \end{aligned}$$

whence $\mathrm J$ preserves pointwise norm and thus it is an isomorphism. Thus, we conclude that $\Theta$ is an $L^0(\mu )$-Banach $L^0(\mu )$ module, which coincides with $\int {\mathscr {M}}_q\,\text {d}\mathfrak {q}(q)$. $\square$

Another result in the same direction, which we will need in Sect. 4.1, is the following:

Theorem 3.9

Let $(\textrm{X},\textsf{d})$ be a complete, separable metric space. Let $\nu$ be a boundedly-finite, submodular outer measure on $\textrm{X}$. Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be a measure space. Let $q\mapsto \mu _q$ be a disjoint measure-valued map from $Q$ to $\textrm{X}$ with $\mu _q\ll \nu$ for every $q\in Q$, and set $\mu :=\int \mu _q\,\text {d}{\mathfrak {q}}(q)\ll \nu$. Let ${\mathscr {M}}$ be an $L^0(\nu )$-Banach $L^0(\nu )$-module. Fix a generating subalgebra ${\mathscr {A}}$ of $L^0(\nu )$, and a vector subspace ${\mathscr {V}}$ of ${\mathscr {M}}$ that is also an ${\mathscr {A}}$-module and generates ${\mathscr {M}}$. Let us define ${\mathscr {M}}_{\mu _\star }:=\{{\mathscr {M}}_{\mu _q}\}_{q\in Q}$,

$$\begin{aligned} \begin{aligned} \Theta&:=\big \{[v]_{\mu _\star }\in {\mathscr {S}}_{{\mathfrak {q}}} ({\mathscr {M}}_{\mu _\star })\;\big |\;v\in {\mathscr {V}}\big \},\\ \Phi&:=\big \{[f]_{\mu _\star }\in L^0({\mathfrak {q}};L^0(\mu _\star ))\;\big |\;f\in {\mathscr {A}}\big \}. \end{aligned} \end{aligned}$$

Then $({\mathscr {M}}_{\mu _\star },\Theta ,\Phi )$ is an $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu _q$. Moreover, it holds that

$$\begin{aligned} {\mathscr {M}}_\mu \cong \int {\mathscr {M}}_{\mu _q}\,\text {d}{\mathfrak {q}}(q), \end{aligned}$$

the canonical isomorphism $\textrm{I}:{\mathscr {M}}_\mu \rightarrow \int {\mathscr {M}}_{\mu _q}\,\text {d}{\mathfrak {q}}(q)$ being the unique homomorphism satisfying

$$\begin{aligned} \textrm{I}([v]_\mu )=\int [v]_{\mu _q}\,\text {d}{\mathfrak {q}}(q)\quad \text { for every }v\in {\mathscr {V}}. \end{aligned}$$

Proof

Since $\pi _\mu ({\mathscr {A}})$ is a generating subalgebra of $L^0(\mu )$ and $\pi _\mu ({\mathscr {A}})\subseteq {\mathcal {G}}_{{\mathfrak {q}}}(\Phi )$, we deduce that ${\mathcal {G}}_{{\mathfrak {q}}}(\Phi )$ is dense in $L^0(\mu )$. Moreover, $\Theta$ is a vector subspace of ${\mathscr {S}}_{{\mathfrak {q}}}({\mathscr {M}}_{\mu _\star })$, is a module over $\Phi$, and

$$\begin{aligned} |[v]_{\mu _\star }|=\textsf{i}_{{\mathfrak {q}}}(|[v]_\mu |)\in L^0({\mathfrak {q}};L^0(\mu _\star ))\quad \text { for every }[v]_{\mu _\star }\in \Theta . \end{aligned}$$

(3.3)

Therefore, $({\mathscr {M}}_{\mu _\star },\Theta ,\Phi )$ is an $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu _q$. Moreover, we define

$$\begin{aligned} \tilde{\textrm{I}}([v]_\mu ):=\int [v]_{\mu _q}\,\text {d}{\mathfrak {q}}(q)=[v]_{\mu _\star }\in \Theta \subseteq \int {\mathscr {M}}_{\mu _q}\,\text {d}{\mathfrak {q}}(q)\quad \text { for every }v\in {\mathscr {V}}. \end{aligned}$$

The resulting operator $\tilde{\textrm{I}}:\pi _\mu ({\mathscr {V}})\rightarrow \Theta$ is well-defined, $\pi _\mu ({\mathscr {A}})$-linear, and satisfying

$$\begin{aligned} |\tilde{\textrm{I}}([v]_\mu )|=\textsf{j}_{{\mathfrak {q}}}(|[v]_{\mu _\star }|)\overset{(3.3)}{=}|[v]_\mu | \quad \text { for every }v\in {\mathscr {V}}. \end{aligned}$$

Since $\pi _\mu ({\mathscr {A}})$ generates $L^0(\mu )$, there exists a unique homomorphism $\textrm{I}:{\mathscr {M}}_\mu \rightarrow \int {\mathscr {M}}_{\mu _q}\,\text {d}{\mathfrak {q}}(q)$ that extends $\tilde{\textrm{I}}$ and preserves the pointwise norm. Given that $\Theta =\tilde{\textrm{I}}(\pi _\mu ({\mathscr {V}}))\subseteq \textrm{I}({\mathscr {M}}_\mu )$ generates $\int {\mathscr {M}}_{\mu _q}\,\text {d}{\mathfrak {q}}(q)$, we can finally conclude that $\textrm{I}$ is an isomorphism, thus the statement is proved. $\square$

4 Applications to vector calculus on $\textsf{RCD}$ spaces

This section deals with applications of the language developed so far to the coarea formula for BV functions and to the 1D-localisation, in both cases in the setting of $\mathsf RCD$ spaces.

4.1 Vector fields on the superlevel sets of a BV function

First, a preliminary lemma:

Lemma 4.1

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be a PI space and $f\in BV(\textrm{X})$. Then, denoting by $\bar{f}$ the precise representative of f (see Definition 2.24) it holds that

$$\begin{aligned} \partial ^*\{{\bar{f}}>t\}\cap (\textrm{X}_f\setminus J_f)\subseteq \{{\bar{f}}=t\}\quad \text { for every }t\in \mathbb {R}. \end{aligned}$$

(4.1)

In particular, $t\mapsto P(\{{\bar{f}}>t\},\cdot )|_{\textrm{X}_f{\setminus } J_f}$ is a disjoint measure-valued map from $\mathbb {R}$ to $\textrm{X}$.

Proof

Let $x\in \partial ^*\{{\bar{f}}>t\}\cap (\textrm{X}_f{\setminus } J_f)$ be given. Since $\Theta ^*(\{{\bar{f}}>t\},x)=\Theta ^*(\{f>t\},x)>0$, we deduce that $t\le f^\vee (x)$. Since $\Theta ^*(\{{\bar{f}}\le t\},x)=\Theta ^*(\{f\le t\},x)=\Theta ^*(\textrm{X}{\setminus }\{f>t\},x)>0$, we deduce that $t\ge f^\wedge (x)$. Since $x\in \textrm{X}_f{\setminus } J_f$ ensures that $f^\vee (x)=f^\wedge (x)={\bar{f}}(x)$, we can conclude that $t={\bar{f}}(x)$, proving (4.1). It follows that

$$\begin{aligned} P(\{{\bar{f}}>t\},\cdot )|_{\textrm{X}_f\setminus J_f}\quad \text { is concentrated on }\{{\bar{f}}=t\}. \end{aligned}$$

(4.2)

Now notice that we have $\{{\bar{f}}=t\}\cap \{{\bar{f}}=s\}=\varnothing$ whenever $t,s\in \mathbb {R}$ and $t\ne s$. This observation, in combination with Theorem 2.22 and (4.2), implies that $t\mapsto P(\{{\bar{f}}>t\},\cdot )|_{\textrm{X}_f{\setminus } J_f}$ is a disjoint measure-valued map. Therefore, the proof is complete. $\square$

Remark 4.2

In the next result, as indexing family we will consider the measure space $(Q,{\mathcal {Q}},{\mathfrak {q}})$ given as follows. We define $Q:=(\mathbb {R}\times \{0\}) \cup (\mathbb {N}\times \{1\})$. We consider the inclusion maps $i_0 :\mathbb {R}\rightarrow Q$ and $i_1 :\mathbb {N}\rightarrow Q$ defined as $i_j(q)=(q,j)$ for $j=0,1$. We define the map $\pi _0:Q \rightarrow \mathbb {R}$ as $\pi _0(q,j):=q$ for $j=\{0,1\}$. We declare that a set $E\subseteq Q$ belongs to ${\mathcal {Q}}$ if and only if $\pi _0(E)$ is a Borel subset of $\mathbb {R}$ (in other words, ${\mathcal {Q}}$ is the pushforward of the Borel $\sigma$-algebra of $\mathbb {R}$ under the map $i_0:\mathbb {R}\hookrightarrow Q$), and

$$\begin{aligned} {\mathfrak {q}}:={i_0}_\#{\mathscr {L}}^1+\sum _{n\in \mathbb {N}}\delta _{(n,1)}, \end{aligned}$$

where ${\mathscr {L}}^1$ stands for the one-dimensional Lebesgue measure on $\mathbb {R}$. $\blacksquare$

Proposition 4.3

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an isotropic PI space and $f\in BV(\textrm{X})$. Fix a countable Borel partition $(\Gamma _n)_n$ of $J_f$ with the following property: for any $n\in \mathbb {N}$, there is $t_n\in \mathbb {R}$ such that $\{{\bar{f}}>t_n\}$ is of finite perimeter and $\Gamma _n\subseteq \partial ^*\{{\bar{f}}>t_n\}$. Let $(Q,{\mathcal {Q}},{\mathfrak {q}})$ be as in Remark 4.2 and define

$$\begin{aligned} \mu ^f_q:=\left\{ \begin{array}{ll} P(\{{\bar{f}}>t\},\cdot )|_{\textrm{X}_f\setminus J_f}\\ (f^\vee -f^\wedge )P(\{{\bar{f}}>t_n\},\cdot )|_{\Gamma _n} \end{array}\quad \begin{array}{ll} \text { if }q=(t,0)\text { for some }t\in \mathbb {R},\\ \text { if }q=(n,1)\text { for some }n\in \mathbb {N}. \end{array}\right. \end{aligned}$$

Then $q\mapsto \mu ^f_q$ is a disjoint measure-valued map from $Q$ to $\textrm{X}$. Moreover, it holds that

$$\begin{aligned} |Df|=\int \mu ^f_q\,\text {d}{\mathfrak {q}}(q). \end{aligned}$$

Proof

It readily follows from Lemma 4.1 that $q\mapsto \mu ^f_q$ is a disjoint measure-valued map from $Q$ to $\textrm{X}$. Moreover, using Theorem 2.22 and (2.9) we see that for any $E\subseteq \textrm{X}$ Borel it holds

$$\begin{aligned} \begin{aligned} |Df|(E)&=|Df|(E\cap (\textrm{X}_f\setminus J_f))+|Df|(E\cap J_f)\\&=\int _{\mathbb {R}} P(\{{\bar{f}}>t\},E\cap (\textrm{X}_f\setminus J_f))\,\text {d}t+\sum _{n\in \mathbb {N}}\int _{E\cap \Gamma _n}(f^\vee -f^\wedge )\,\text {d}P(\{{\bar{f}}>t_n\},\cdot )\\&=\int \mu ^f_{(t,0)}(E)\,\text {d}{\mathscr {L}}^1(t)+\sum _{n\in \mathbb {N}}\mu ^f_{(n,1)}(E)=\int \mu ^f_q(E)\,\text {d}{\mathfrak {q}}(q). \end{aligned} \end{aligned}$$

This proves that $|Df|=\int \mu ^f_q\,\text {d}{\mathfrak {q}}(q)$, thus accordingly the statement is achieved. $\square$

Theorem 4.4

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space, with $K\in \mathbb {R}$ and $N\in [1,\infty )$. Let $f\in BV(\textrm{X})$ be given. Let $q\mapsto \mu ^f_q$ be defined as in Proposition 4.3. Let us also define $\big (L^0_{\mu ^f_\star }(T\textrm{X}),\Theta _f,\Phi _f\big )$ as

$$\begin{aligned} \begin{aligned} L^0_{\mu ^f_\star }(T\textrm{X})&:=\{L^0_{\mu ^f_q}(T\textrm{X})\}_{q\in Q},\\ \Theta _f&:=\big \{[v]_{\mu ^f_\star }\in {\mathscr {S}}_{{\mathfrak {q}}}\big (L^0_{\mu ^f_\star }(T\textrm{X})\big ) \;\big |\;v\in \textrm{Test}(T\textrm{X})\big \},\\ \Phi _f&:=\big \{[f]_{\mu ^f_\star }\in L^0({\mathfrak {q}};L^0(\mu ^f_\star ))\;\big |\;f\in \textrm{Test}(\textrm{X})\big \}. \end{aligned} \end{aligned}$$

Then $\big (L^0_{\mu ^f_\star }(T\textrm{X}),\Theta _f,\Phi _f\big )$ is an $L^0$-Banach $L^0$-module bundle consistent with $q\mapsto \mu ^f_q$. Moreover,

$$\begin{aligned} L^0_{|Df|}(T\textrm{X})\cong \int L^0_{\mu ^f_q}(T\textrm{X})\,\text {d}{\mathfrak {q}}(q), \end{aligned}$$

the isomorphism $\textrm{I}_f:L^0_{|Df|}(T\textrm{X})\rightarrow \int L^0_{\mu ^f_q}(T\textrm{X})\,\text {d}{\mathfrak {q}}(q)$ being the unique homomorphism satisfying

$$\begin{aligned} \textrm{I}_f\big ([v]_{|Df|}\big )=\int [v]_{\mu ^q_f}\,\text {d}{\mathfrak {q}}(q)\quad \text { for every }v\in \textrm{Test}(T\textrm{X}). \end{aligned}$$

Proof

It is enough to show that we are in position to apply Theorem 3.9 with suitable choices of the objects involved. Indeed, with the notation therein let $\nu :=\textrm{Cap}$, $\mu _q:=\mu _q^f$ and notice that $\mu _q^f \ll \textrm{Cap}$, as a consequence of (2.7). Let ${\mathscr {M}}:=L^0_\textrm{Cap}(T\textrm{X})$, ${\mathscr {A}}:=\textrm{Test}(\textrm{X})$, and ${\mathscr {V}}:=\textrm{Test}(T\textrm{X})$. With these choices ${\mathscr {A}}$ is a generating subalgebra of $L^0(\textrm{Cap})$ and ${\mathscr {V}}$ is a vector subspace of ${\mathscr {M}}$ and a module over ${\mathscr {A}}$, which generates the $L^0(\mathrm Cap)$-Banach $L^0(\mathrm Cap)$-module ${\mathscr {M}}$. $\square$

4.2 Vector fields on the integral lines of a gradient

We recall here the theory of 1D-localisation, referring the reader to [15, 17,18,19]. In particular, for the general construction we follow the presentation of [19], where it is not assumed that $\mathfrak {m}(\textrm{X})=1$. Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space, with $K\in \mathbb {R}$ and $N\in [1,\infty )$. Given any $1$-Lipschitz function $u:\textrm{X}\rightarrow \mathbb {R}$, its transport set ${\mathcal {T}}_u$ is defined as the Borel set

$$\begin{aligned} {\mathcal {T}}_u:=\big \{x\in \textrm{X}\;\big |\;|u(x)-u(y)|=\textsf{d}(x,y)\text { for some }y\in \textrm{X}\setminus \{x\}\big \}. \end{aligned}$$

The transport set ${\mathcal {T}}_u$ can be written (up to $\mathfrak {m}$-null sets) as the union of a family $\{\textrm{X}_\alpha \}_{\alpha \in Q}$ of transport rays (see [15, Theorem 5.5]). Each $\textrm{X}_\alpha$ is isometric to a closed real interval $I_\alpha$, i.e. we can find a surjective isometry $\gamma _\alpha :I_\alpha \rightarrow \textrm{X}_\alpha$. Given any $\alpha ,\beta \in Q$ with $\alpha \ne \beta$, we also have that

$$\begin{aligned} \gamma _\alpha ( \overset{\circ }{I_\alpha })\cap \gamma _\beta (\overset{\circ }{I_\beta })=\varnothing . \end{aligned}$$

Moreover, one can find a $\sigma$-algebra ${\mathcal {Q}}$ on $Q$, a finite measure ${\mathfrak {q}}\ge 0$ on $(Q,{\mathcal {Q}})$, and a disjoint measure-valued map $\alpha \mapsto \mathfrak {m}_\alpha$ from $Q$ to $\textrm{X}$ such that $\mathfrak {m}_\alpha (\textrm{X}{\setminus }\textrm{X}_\alpha )=0$ for every $\alpha \in Q$ and

$$\begin{aligned} \mathfrak {m}|_{{\mathcal {T}}_u}=\int \mathfrak {m}_\alpha \,\text {d}{\mathfrak {q}}(\alpha ). \end{aligned}$$

In addition, it holds that $\mathfrak {m}_\alpha =h_\alpha \,{\mathcal {H}}^1|_{\textrm{X}_\alpha }$ for some Borel function $h_\alpha :I_\alpha \rightarrow (0,+\infty )$ (where ${\mathcal {H}}^1$ stands for the one-dimensional Hausdorff measure) and the space $(\textrm{X}_\alpha ,\textsf{d},\mathfrak {m}_\alpha )$ is an $\textsf{RCD}(K,N)$ space (see [18, Theorem 4.2]). In particular, the tangent module $L^0(T\textrm{X}_\alpha )$ can be identified with $L^0(\mathfrak {m}_\alpha )$ via the differential operator $\text {d}\gamma _\alpha :L^0(\mathfrak {m}_\alpha )\rightarrow L^0(T\textrm{X}_\alpha )$ of $\gamma _\alpha$ (in the sense of [30]).

Given any $f:\textrm{X}\rightarrow \mathbb {R}$ Lipschitz and $\alpha \in Q$, we define

$$\begin{aligned} {{\tilde{\partial }}}_\alpha f(x):=\frac{\text {d}}{\text {d}t}(f\circ \gamma _\alpha )(t)\bigg |_{t=\gamma _\alpha ^{-1}(x)} \quad \text { for }{\mathcal {H}}^1\text {-a.e.\ }x\in \textrm{X}_\alpha . \end{aligned}$$

(4.3)

The resulting function ${{\tilde{\partial }}}_\alpha f:\textrm{X}_\alpha \rightarrow \mathbb {R}$ is an element of $L^0(\mathfrak {m}_\alpha )$. We denote by ${{\tilde{\partial }}}_\star f$ the map $Q \ni \alpha \mapsto {{\tilde{\partial }}}_\alpha f \in L^0(\mathfrak {m}_\alpha )$ up to quotient $\mathfrak {q}$-a.e. It also follows from the results of [19, Section 4.1] that ${{\tilde{\partial }}}_\star f\in L^0({\mathfrak {q}};L^0(\mathfrak {m}_\star ))$, and [19, Theorem 4.5] ensures that

$$\begin{aligned} {{\tilde{\partial }}} f:=\textsf{i}_{{\mathfrak {q}}}^{-1}({{\tilde{\partial }}}_\star f)=-\mathbb {1}_{{\mathcal {T}}_u}^\mathfrak {m}\langle \nabla f,\nabla u\rangle \in L^0(\mathfrak {m}|_{{\mathcal {T}}_u}). \end{aligned}$$

(4.4)

Indeed, the infinitesimal Hilbertianity assumption gives $D^-f(-\nabla u)=D^+f(-\nabla u)=-\langle \nabla f,\nabla u\rangle$ (cf. with [25]). From the very definition in (4.3) and the fact that given $t,s \in I_\alpha$ with $s >t$, $u(\gamma _\alpha (t))-u(\gamma _\alpha (s))=|s-t|$, it follows that for $\mathfrak {q}$-a.e. $\alpha$, ${\tilde{\partial }}_\alpha u(x)=1$ for ${\mathcal {H}}^1$-a.e. $x \in \textrm{X}_\alpha$. Thus

$$\begin{aligned} \mathbb {1}_{T_u}^\mathfrak {m}|\nabla u|=|\textsf{i}_{{\mathfrak {q}}}^{-1}({{\tilde{\partial }}}_\star u)|=1 \end{aligned}$$

(4.5)

holds $\mathfrak {m}$-a.e. on ${\mathcal {T}}_u$. We define $L^0(T\textrm{X}_\star ):=\{ L^0(T\textrm{X}_{\alpha })\}_{\alpha \in Q}$ and $\partial _\star f\in {\mathscr {S}}_{{\mathfrak {q}}}(L^0(T\textrm{X}_\star ))$ as

$$\begin{aligned} \partial _\alpha f:=\text {d}\gamma _\alpha ({{\tilde{\partial }}}_\alpha f)\in L^0(T\textrm{X}_\alpha )\quad \text { for }{\mathfrak {q}}\text {-a.e.\ }\alpha \in Q. \end{aligned}$$

Given $v \in L^0(T\textrm{X})$ and a Borel set $A \subseteq \textrm{X}$, we denote the $L^0(\mathfrak {m})$-Banach $L^0(\mathfrak {m})$-module generated by $v$ on $A$ as

$$\begin{aligned} \langle v \rangle _A:=\big \{ \mathbb {1}_A^\mathfrak {m}f\cdot v\;\big |\; f \in L^0(\mathfrak {m}) \big \}. \end{aligned}$$

Theorem 4.5

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space, with $K\in \mathbb {R}$ and $N\in [1,\infty )$. Let $u:\textrm{X}\rightarrow \mathbb {R}$ be a given $1$-Lipschitz function. Let us define $\Theta ^u\subseteq {\mathscr {S}}_{{\mathfrak {q}}}\big (L^0(T\textrm{X}_\star )\big )$ as

$$\begin{aligned} \Theta ^u:=\bigg \{\sum _{n\in \mathbb {N}}\mathbb {1}_{E_n}^{{\mathfrak {q}}}\partial _\star f_n\;\bigg |\; (E_n)_{n\in \mathbb {N}}\subseteq {\mathcal {Q}}\text { partition of }Q,\,(f_n)_{n\in \mathbb {N}}\subseteq \textrm{LIP}(\textrm{X})\bigg \}. \end{aligned}$$

Then $\big (L^0(T\textrm{X}_\star ),\Theta ^u,L^0({\mathfrak {q}};L^0(\mathfrak {m}_\star ))\big )$ is an $L^0$-Banach $L^0$-module bundle consistent with $\alpha \mapsto \mathfrak {m}_\alpha$. Also,

$$\begin{aligned} \int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )\cong \langle \nabla u\rangle _{{\mathcal {T}}_u}\subseteq L^0(T\textrm{X}), \end{aligned}$$

the canonical isomorphism $\textrm{J}_u:\int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )\rightarrow \langle \nabla u\rangle _{{\mathcal {T}}_u}$ being the unique homomorphism with

$$\begin{aligned} \textrm{J}_u\bigg (\int \partial _\alpha f\,\text {d}{\mathfrak {q}}(\alpha )\bigg )=-\mathbb {1}_{{\mathcal {T}}_u}^\mathfrak {m}\langle \nabla f,\nabla u\rangle \nabla u \quad \text { for every }f:\textrm{X}\rightarrow \mathbb {R}\text { Lipschitz.} \end{aligned}$$

Proof

Since $\Theta ^u$ is a module over $L^0({\mathfrak {q}};L^0(\mathfrak {m}_\star ))$ and for any $v_\star =\sum _{n\in \mathbb {N}}\mathbb {1}_{E_n}^{{\mathfrak {q}}}\partial _\star f_n\in \Theta ^u$ we have

$$\begin{aligned} |v_\star |=\sum _{n\in \mathbb {N}}\mathbb {1}_{E_n}^{{\mathfrak {q}}}|\partial _\star f_n|=\sum _{n\in \mathbb {N}}\mathbb {1}_{E_n}^{{\mathfrak {q}}}|{{\tilde{\partial }}}_\star f_n| \overset{(4.4)}{\in }L^0(\mathfrak {m}|_{{\mathcal {T}}_u}), \end{aligned}$$

we obtain that $\big (L^0(T\textrm{X}_\star ),\Theta ^u,L^0({\mathfrak {q}};L^0(\mathfrak {m}_\star ))\big )$ is an $L^0$-Banach $L^0$-module bundle consistent with $\alpha \mapsto \mathfrak {m}_\alpha$. Now let us define the operator $\tilde{\textrm{J}}_u:\{\partial _\star f\;\big |\;f\in \textrm{LIP}(\textrm{X})\}\rightarrow \langle \nabla u\rangle _{{\mathcal {T}}_u}$ as

$$\begin{aligned} \tilde{\textrm{J}}_u(\partial _\star f):=-\mathbb {1}_{{\mathcal {T}}_u}^\mathfrak {m}\langle \nabla f,\nabla u\rangle \nabla u\quad \text { for every }f\in \textrm{LIP}(\textrm{X}). \end{aligned}$$

Since $\{\partial _\star f\,:\,f\in \textrm{LIP}(\textrm{X})\}$ generates $\int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )$ and we can estimate

$$\begin{aligned} |\tilde{\textrm{J}}_u(\partial _\star f)|=\mathbb {1}_{{\mathcal {T}}_u}^\mathfrak {m}|\langle \nabla f,\nabla u\rangle ||\nabla u| \overset{(4.4)}{=}|\partial _\star f|\quad \text { for every }f\in \textrm{LIP}(\textrm{X}), \end{aligned}$$

the map $\tilde{\textrm{J}}_u$ can be uniquely extended to a homomorphism $\textrm{J}_u:\int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )\rightarrow \langle \nabla u\rangle _{{\mathcal {T}}_u}$ that preserves the pointwise norm. Finally, let us check that $\textrm{J}_u$ is surjective. Fix an arbitrary element of $\langle \nabla u\rangle _{{\mathcal {T}}_u}$, which can be written (uniquely) as $h\nabla u$ for some $h\in L^0(\mathfrak {m}|_{{\mathcal {T}}_u})$. Hence, we have that

$$\begin{aligned} \textrm{J}_u(-h\cdot \partial _\star u)=-h\cdot \textrm{J}_u(\partial _\star u)= h\mathbb {1}_{{\mathcal {T}}_u}^\mathfrak {m}\langle \nabla u,\nabla u\rangle \nabla u=h\nabla u, \end{aligned}$$

thus proving the surjectivity of $\textrm{J}_u$. Consequently, the statement is achieved. $\square$

Remark 4.6

We point out that the above results hold in the more general setting of essentially non-branching, infinitesimally Hilbertian $\textsf{MCP}(K,N)$ spaces. $\blacksquare$

4.3 Unit normals and gradient lines

In this conclusive section, we combine the results of Sects. 4.1 and 4.2. First, we recall the following result, which follows from [14, Theorem 2.4]:

Theorem 4.7

(Gauss–Green) Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space. Let $E\subseteq \textrm{X}$ be a set of finite perimeter with $\mathfrak {m}(E)<+\infty$. Then there exists a unique element $\nu _E\in L^0_{P(E,\cdot )}(T\textrm{X})$ such that

$$\begin{aligned} \int _E\textrm{div}(v)\,\text {d}\mathfrak {m}=-\int \langle [v]_{P(E,\cdot )},\nu _E\rangle \,\text {d}P(E,\cdot )\quad \text { for every }v\in \textrm{Test}(T\textrm{X}). \end{aligned}$$

The identity $|\nu _E|=1$ holds $P(E,\cdot )$-a.e. on $\textrm{X}$. Moreover, if $\varphi :\textrm{X}\rightarrow \mathbb {R}$ is bounded Lipschitz, then

$$\begin{aligned} \int _E\textrm{div}(\varphi v)\,\text {d}\mathfrak {m}=-\int \varphi \langle [v]_{P(E,\cdot )},\nu _E\rangle \,\text {d}P(E,\cdot )\quad \text { for every }v\in \textrm{Test}(T\textrm{X}). \end{aligned}$$

Remark 4.8

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space with $\mathfrak {m}(\textrm{X})<+\infty$ and let $u:\textrm{X}\rightarrow \mathbb {R}$ be a Lipschitz function. Then we know from [28, Remark 3.5] that $u\in BV(\textrm{X})$ and $|Du|=\textrm{lip}(u)\mathfrak {m}$. In particular, if ${\mathcal {T}}_u=\textrm{X}$ up to $\mathfrak {m}$-null sets, then $|Du|=\mathfrak {m}$ and thus $\mathfrak {m}=\int _\mathbb {R}P(\{u>t\},\cdot )\,\text {d}t$. Notice also that, since $u$ is continuous, it holds that ${\bar{u}}=u$, so that $\textrm{X}_u=\textrm{X}$ and $J_u=\varnothing$. Therefore, we have that $t\mapsto \mu ^u_t:=P(\{u>t\},\cdot )$ is a disjoint measure-valued map from $\mathbb {R}$ to $\textrm{X}$ and Theorem 4.4 provides an isomorphism of $L^0(\mathfrak {m})$-Banach $L^0(\mathfrak {m})$-modules $\textrm{I}_u:L^0(T\textrm{X})\rightarrow \int L^0_{\mu ^u_t}(T\textrm{X})\,\text {d}t$. $\blacksquare$

Now we are in a position to state and prove the main result of this section:

Theorem 4.9

Let $(\textrm{X},\textsf{d},\mathfrak {m})$ be an $\textsf{RCD}(K,N)$ space with $\mathfrak {m}(\textrm{X})<+\infty$. Fix a $1$-Lipschitz function $u:\textrm{X}\rightarrow [0,+\infty )$ such that ${\mathcal {T}}_u=\textrm{X}$ up to $\mathfrak {m}$-negligible sets. Let $\textrm{I}_u:L^0(T\textrm{X})\rightarrow \int L^0_{\mu ^u_t}(T\textrm{X})\,\text {d}t$ and $\textrm{J}_u:\int L^0(T\textrm{X}_\alpha )\,\text {d}{\mathfrak {q}}(\alpha )\rightarrow \langle \nabla u\rangle _\textrm{X}$ be as in Remark 4.8 and Theorem 4.5, respectively. Then

$$\begin{aligned} (\textrm{I}_u\circ \textrm{J}_u)\bigg (\int \partial _\alpha u\,\text {d}{\mathfrak {q}}(\alpha )\bigg ) =-\int _\mathbb {R}\nu _{\{u>t\}}\,\text {d}t\in \int L^0_{\mu ^u_t}(T\textrm{X})\,\text {d}t. \end{aligned}$$

Proof

For brevity, we denote $\partial _\star u=\int \partial _\alpha u\,\text {d}{\mathfrak {q}}(\alpha )$ and $V:=(\textrm{I}_u\circ \textrm{J}_u)(\partial _\star u)\in \int L^0_{\mu ^u_t}(T\textrm{X})\,\text {d}t$. Fix a countable dense subset ${\mathcal {C}}$ of $\textrm{Test}(\textrm{X})$. Notice that the family ${\mathcal {F}}$ of those elements of $\textrm{Test}(T\textrm{X})$ of the form $\sum _{i=1}^n g_i{\bar{\nabla }} f_i$ for some $f_i,g_i\in {\mathcal {C}}$ generates $L^0_\textrm{Cap}(T\textrm{X})$. If $\varphi \in \textrm{LIP}_{bs}(\mathbb {R})$ and $f,g\in {\mathcal {C}}$, then

$$\begin{aligned}&\int _0^{+\infty }\varphi (t)\int g\langle [\nabla f]_{\mu ^u_t},V_t\rangle \,\text {d}P(\{u>t\},\cdot )\,\text {d}t\\&\quad = \int _0^{+\infty }\!\!\int \big [\langle \varphi \circ u\,g\nabla f,\textrm{J}_u(\partial _\star u)\rangle \big ]_{\mu ^u_t}\,\text {d}P(\{u>t\},\cdot )\,\text {d}t\\&\quad =-\int \langle \varphi \circ u\,g\nabla f,\nabla u\rangle \,\text {d}\mathfrak {m}=\int u\,\textrm{div}(\varphi \circ u\,g\nabla f)\,\text {d}\mathfrak {m}\\&\quad =\int _0^{+\infty }\!\!\int _{\{u>t\}}\textrm{div}(\varphi \circ u\,g\nabla f)\,\text {d}\mathfrak {m}\,\text {d}t\\&\quad =-\int _0^{+\infty }\!\!\int \varphi \circ u\,g\langle [\nabla f]_{\mu ^u_t},\nu _{\{u>t\}}\rangle \,\text {d}P(\{u>t\},\cdot )\,\text {d}t\\&\quad =-\int _0^{+\infty }\varphi (t)\int g\langle [\nabla f]_{\mu ^u_t},\nu _{\{u>t\}}\rangle \,\text {d}P(\{u>t\},\cdot )\,\text {d}t, \end{aligned}$$

where we used Remark 4.8, the layer cake representation formula, Theorem 4.7, and the fact that the measure $\mu ^u_t=P(\{u>t\},\cdot )$ is concentrated on $\partial \{u>t\}\subseteq \{u=t\}$. Thanks to the arbitrariness of $\varphi \in \textrm{LIP}_{bs}(\mathbb {R})$, we deduce that for every $f,g\in {\mathcal {C}}$ it holds that

$$\begin{aligned}{} & {} \int \langle g[\nabla f]_t,V_t\rangle \,\text {d}P(\{u>t\},\cdot )\\{} & {} \quad =-\int \langle g[\nabla f]_t,\nu _{\{u>t\}}\rangle \,\text {d}P(\{u>t\},\cdot ) \quad \text { for }{\mathcal {L}}^1\text {-a.e.\ }t\in \mathbb {R}. \end{aligned}$$

Since ${\mathcal {F}}$ is countable, we can find a ${\mathscr {L}}^1$-null set $N\subseteq \mathbb {R}$ such that $\int \langle w,V_t\rangle \,\text {d}\mu ^u_t=-\int \langle w,\nu _{\{u>t\}}\rangle \,\text {d}\mu ^u_t$ holds for every $t\in \mathbb {R}{\setminus } N$ and $w\in {\mathcal {F}}$. It follows that $V_t=-\nu _{\{u>t\}}$ for ${\mathcal {L}}^1$-a.e. $t\in \mathbb {R}$, so that accordingly $(\textrm{I}_u\circ \textrm{J}_u)(\partial _\star u)=V=-\nu _{\{u>\star \}}$. Therefore, the proof of the statement is complete. $\square$

Observe that Theorem 4.9 applies, for example, to $u:=\textsf{d}(\cdot ,{\bar{x}})$ for any point ${\bar{x}}\in \textrm{X}$.

Remark 4.10

We point out that Theorem 4.4 can be generalised to functions of local bounded variation, thus in turn the finiteness assumption on $\mathfrak {m}$ in Theorem 4.9 can be dropped. However, we do not pursue this goal here, since the results are already quite technically demanding. $\blacksquare$