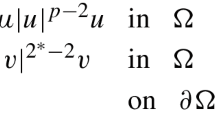Positive Solution for an Elliptic System with Critical Exponent and Logarithmic Terms

Abstract

In this paper, we study the existence and nonexistence of positive solutions for the following coupled elliptic system with critical exponent and logarithmic terms:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u=\lambda _{1}u+ \mu _1|u|^{2}u+\beta |v|^{2}u+\theta _1 u\log u^2, &{} \quad x\in \Omega ,\\ -\Delta v=\lambda _{2}v+ \mu _2|v|^{2}v+\beta |u|^{2}v+\theta _2 v\log v^2, &{}\quad x\in \Omega ,\\ u=v=0, &{}\quad x \in \partial \Omega , \end{array}\right. } \end{aligned}$$

where $\Omega \subset {{\mathbb {R}}}^4$ is a bounded smooth domain, the parameters $\lambda _{1},\lambda _{2},\theta _{1},\theta _{2}\in {{\mathbb {R}}}$, $\mu _{1},\mu _2>0$ and $\beta \ne 0$ is a coupling constant. Note that the logarithmic term $s\log s^2$ has special properties, which makes the problem more complicated. We show that this system has a positive least energy solution for $|\beta |$ small and positive large $\beta$ if $\lambda _{1},\lambda _{2}\in {{\mathbb {R}}}$ and $\theta _{1},\theta _{2}>0$. While the situations for the case $\theta _{1},\theta _{2}<0$ are quite thorny, in this challenging setting we establish the existence result of positive local minimum solutions and nonnegative solutions under various conditions on the parameters. Besides, under some further assumptions, we obtain the nonexistence of positive solutions for both the case where $\theta _{1}$,$\theta _{2}$ are negative and the case where they have opposite signs. Comparing our results with those of Chen and Zou (Arch. Ration. Mech. Anal. 205:515–551, 2012), the logarithmic term $s\log s^2$ introduces some new interesting phenomenon. Moreover, its presence brings major challenges and make it difficult to use the comparison theorem used in the work of Chen and Zou without new ideas and innovative techniques. To the best of our knowledge, our paper is the first to give a rather complete picture for the existence and nonexistence results to the coupled elliptic system with critical exponent and logarithmic terms. Also, we consider the related single equation

$$\begin{aligned} -\Delta u=\lambda u + \mu |u|^{2}u+\theta u\log u^2, ~u\in H_0^1(\Omega ) \end{aligned}$$

with $\mu >0$, $\theta <0$, $\lambda \in {{\mathbb {R}}}$ or $\lambda \in [0,\lambda _{1}(\Omega ))$ and prove the existence of the positive solution under some further suitable assumptions, which is the type of a local minimum or a least energy solution.

Single Equation with \(\theta < 0\)

In this appendix, we consider the following equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u=\lambda u + \mu |u|^{2}u+\theta u\log u^2, &{} \quad x\in \Omega \\ u=0, &{}\quad x \in \partial \Omega , \end{array}\right. } \end{aligned}$$

(A.1)

where $\Omega \subset {\mathbb {R}}^4$ is bounded and $\mu > 0, \theta < 0$. We define the associated modified energy functional

$$\begin{aligned} J(u)=\frac{1}{2} \int _{\Omega }|\nabla u|^2-\frac{\lambda }{2} \int _{\Omega }|u^+|^2-\frac{\mu }{4}\int _{\Omega } |u^+|^4-\frac{\theta }{2} \int _{\Omega } (u^+)^2\left( \log (u^+)^2-1\right) . \end{aligned}$$

Set

$$\begin{aligned}{} & {} \varSigma _3:= \left\{ (\lambda ,\mu ,\theta ): \lambda \in [0,\lambda _{1}(\Omega )), \mu> 0, \theta< 0, \frac{(\lambda _1(\Omega )-\lambda )^2}{\lambda _1(\Omega )^2\mu }S^2 + 2\theta |\Omega |> 0\right\} , \\{} & {} \varSigma _4:= \left\{ (\lambda ,\mu ,\theta ): \lambda \in {\mathbb {R}}, \mu> 0, \theta < 0, \mu ^{-1}S^2 + 2\theta e^{-\frac{\lambda }{\theta }}|\Omega | > 0\right\} . \end{aligned}$$

Lemma A.1

Assume that $(\lambda ,\mu ,\theta ) \in \varSigma _3\cup \varSigma _4$. Then there exist $\delta , \hat{\rho } > 0$ such that $J(u) \ge \delta$ for all $|\nabla u|_2 = \hat{\rho }$.

Proof

The proof can be found in [14], so we omit it. $\square$

Theorem A.1

(Existence of a local minimum) Assume that $(\lambda ,\mu ,\theta ) \in \varSigma _3\cup \varSigma _4$. Define

$$\begin{aligned} \tilde{c}_{\hat{\rho }}:= \inf _{|\nabla u|_2 < \hat{\rho }}J(u), \end{aligned}$$

where $\hat{\rho }$ is given by Lemma A.1. Then equation (A.1) has a positive solution u such that $J(u) = \tilde{c}_{\hat{\rho }}$.

Proof

Similar to Lemma 4.2 we obtain that $-\infty< \tilde{c}_{\hat{\rho }} < 0$. By Lemma A.1, we can take a minimizing sequence $\left\{ u_n\right\}$ for $\tilde{c}_{\hat{\rho }}$ with $|\nabla u_n|_2 < \hat{\rho } - \tau$ and $\tau > 0$ small enough. By Ekeland’s variational principle, we can assume that $J'(u_n) \rightarrow 0$. Similar to Lemma 4.3, we can see that $\left\{ u_n\right\}$ is bounded in $H_0^1(\Omega )$. Hence, we may assume that

$$\begin{aligned} u_n \rightharpoonup u \text { weakly in } H_0^1(\Omega ). \end{aligned}$$

Passing to subsequence, we may also assume that

$$\begin{aligned} \begin{aligned}&u_n \rightharpoonup u \ \text { weakly in } L^4(\Omega ),\\&u_n \rightarrow u \ \text { strongly in } L^p(\Omega ) \text { for } 2\le p<4,\\&u_n \rightarrow u \ \text { almost everywhere in } \Omega . \end{aligned} \end{aligned}$$

By the weak lower semi-continuity of the norm, we see that $|\nabla u|_2 < \hat{\rho }$. Similar to the proof of Theorem 1.1 (1) and (2), we have $J^\prime (u)=0$ and $u \ge 0$. Let $w_n=u_n-u$. Then similar to the proof of Theorem 1.1 (1) and (2) one gets

$$\begin{aligned}{} & {} |\nabla w_n|_2^2=\mu |w_n^+|_4^4+o_n(1). \nonumber \\{} & {} J(u_n)=J(u)+\frac{1}{4}\int _{\Omega }|\nabla w_n|^2+o_n(1). \end{aligned}$$

(A.2)

Passing to subsequence, we may assume that

$$\begin{aligned} \int _{\Omega }|\nabla w_n|^2=k+o_n(1). \end{aligned}$$

Letting $n\rightarrow +\infty$ in (A.2), we have

$$\begin{aligned} \tilde{c}_{\hat{\rho }} \le J(u) \le J(u)+\frac{1}{4}k=\lim _{n\rightarrow \infty } J(u_n) = \tilde{c}_{\hat{\rho }}, \end{aligned}$$

showing that $k=0$. Hence, up to a subsequence we obtain

$$\begin{aligned} u_n \rightarrow u \text { strongly in } H_0^1(\Omega ). \end{aligned}$$

Since $J(u) = \tilde{c}_{\hat{\rho }} < 0$ we have $u \ne 0$. Then by a similar argument as used in the proof of (1)-(2) in Theorem 1.1, we can show that $u>0$ and $u \in C^2(\Omega )$. This completes the proof. $\square$

Theorem A.2

(Existence of the least energy solution) Assume that $(\lambda ,\mu ,\theta ) \in \varSigma _3\cup \varSigma _4$. Define

$$\begin{aligned} \tilde{c}_{\mathcal {K}}:= \inf _{u\in {\mathcal {K}}}J(u) \end{aligned}$$

where

$$\begin{aligned} {\mathcal {K}} = \{u \in H^1_0(\Omega ): J'(u) = 0\}. \end{aligned}$$

Then equation (A.1) has a positive least energy solution u such that $J(u) = \tilde{c}_{\mathcal {K}}$.

Proof

Similar to the case 2 in the proof of Lemma 5.1 we have $-\infty< \tilde{c}_{\mathcal {K}} < 0$. Take a minimizing sequence $\left\{ u_n\right\} \subset {\mathcal {K}}$ for $\tilde{c}_{\mathcal {K}}$. Then $J'(u_n) = 0$. SImilar to Lemma 4.3, we can see that $\left\{ u_n\right\}$ is bounded in $H_0^1(\Omega )$. Hence, we may assume that

$$\begin{aligned} u_n \rightharpoonup u \text { weakly in } H_0^1(\Omega ). \end{aligned}$$

Passing to subsequence, we may also assume that

$$\begin{aligned} \begin{aligned}&u_n \rightharpoonup u \ \text { weakly in } L^4(\Omega ),\\&u_n \rightarrow u \ \text { strongly in } L^p(\Omega ) \text { for } 2\le p<4,\\&u_n \rightarrow u \ \text { almost everywhere in } \Omega . \end{aligned} \end{aligned}$$

Similar to the proof of Theorem 1.1 (1) and (2), we have $J^\prime (u)=0$ and $u \ge 0$. Let $w_n=u_n-u$. Then similar to the proof of Theorem 1.1 (1) and (2) one gets

$$\begin{aligned}{} & {} |\nabla w_n|_2^2=\mu |w_n^+|_4^4+o_n(1). \nonumber \\{} & {} J(u_n)=J(u)+\frac{1}{4}\int _{\Omega }|\nabla w_n|^2+o_n(1). \end{aligned}$$

(A.3)

Passing to subsequence, we may assume that

$$\begin{aligned} \int _{\Omega }|\nabla w_n|^2=k+o_n(1). \end{aligned}$$

Letting $n\rightarrow +\infty$ in (A.3), we have

$$\begin{aligned} \tilde{c}_{\mathcal {K}} \le J(u) \le J(u)+\frac{1}{4}k=\lim _{n\rightarrow \infty } J(u_n) = \tilde{c}_{\mathcal {K}}, \end{aligned}$$

showing that $k = 0$. Hence, up to a subsequence we obtain

$$\begin{aligned} u_n \rightarrow u \text { strongly in } H_0^1(\Omega ). \end{aligned}$$

Since $J(u) = \tilde{c}_{\mathcal {K}} < 0$ we have $u \ne 0$. Then by a similar argument as used in the proof of (1)-(2) in Theorem 1.1, we can show that $u>0$ and $u \in C^2(\Omega )$. This completes the proof. $\square$

Remark A.1

In [14, Theorem 1.3], the authors showed that (A.1) possesses a positive solution when $(\lambda ,\mu ,\theta ) \in \varSigma _3 \cup \varSigma _4$ with $\frac{32e^{\frac{\lambda _i}{\theta _i}}}{\hat{\rho }_{max}^2} < 1$, where

$$\begin{aligned} \hat{\rho }_{max}:= \sup \{r > 0: \exists x \in \Omega \ s.t. \ B(x,r) \subset \Omega \}. \end{aligned}$$

But they don’t know the type of the solution and its energy level. In our Theorems A.1 and A.2, we remove the condition $\frac{32e^{\frac{\lambda _i}{\theta _i}}}{\hat{\rho }_{max}^2} < 1$. Furthermore, we give the type of the positive solution (a local minimum or a least energy solution) and show that its energy level is negative.

It is easy to see that there is a mountain pass geometry since Theorem A.1 shows the existence of a local minimum u and $J(tw) \rightarrow -\infty$ as $t \rightarrow \infty$ when $w^+ \ne 0$. Set

$$\begin{aligned} \tilde{c}_{M} := \inf _{\gamma \in \tilde{\Gamma }}\sup _{t \in [0,1]}J(\gamma (t)), \end{aligned}$$

where

$$\begin{aligned} \tilde{\Gamma }:= \{\gamma \in C([0,1],H_0^1(\Omega )): \gamma (0) = u, J(\gamma (1)) < J(u)\}, \end{aligned}$$

u is the local minimum given by Theorem A.1.

Conjecture 2: Equation (A.1) possesses a positive mountain pass solution at level $\tilde{c}_{M} > 0$.

Remark A.2

If $\tilde{c}_M$ has the following estimate:

$$\begin{aligned} \tilde{c}_M < \tilde{c}_{\mathcal {K}} + \frac{1}{4}\mu ^{-1}S^2, \end{aligned}$$

then Conjecture 2 holds true.