1 Introduction

The vdWm is a challenging problem in the modelling of molecules and materials. Noncovalent vdW or dispersion forces are frequent and have an impact on the structure, dynamics, stability, and function of molecules and materials in biology, chemistry, materials science and physics. The interaction of quantum-mechanical fluctuations in the electronic charge density produces vdW forces (Hermann et al. 2017; Stohr et al. 2019). The science of these interactions is being investigated in order to explore characteristics such as fluctuations in nanostructures (DelRio et al. 2005; Ambrosetti et al. 2016), material design (Woods et al. 2016), thin-film rupture process (Xu et al. 2020), and flow in magnetic systems (Yu et al. 2013). Furthermore, the Van der Waals model (Herminghaus 2005) accurately describes the flow in the granular media.

Granulation is described by the change of primary particles into larger forms as a result of phase separation. Granular matter is a quantity that is made up of separated solids and macrostructure particles. This interaction is explained by the loss of energy in particles as a result of friction caused by particle collision (Bibi et al. 2018). The granular matter is commonly proposed in solid or gas forms, which demonstrate a wide range of industrial applications (Herminghaus 2005; Bibi et al. 2018). There are two types of granulation processes: wet granulation, which uses a liquid, and dry granulation, which does not. The kind of procedure used necessitates a detailed understanding of the drug’s physicochemical characteristics as well as the excipients (Shanmugam 2015). The energy is delivered in fluidized granular materials by continuous injection (Abourabia and Morad 2015). The VdW forces equation is given a non-linear PDE in a normal form, which models the development of fluidized granular materials in nature. Therefore, the VdW equation for the granular medium is given in one dimension as,

$$\begin{aligned} \frac{\partial ^2u}{\partial {t^2}}+\frac{\partial ^2}{\partial {x^2}}\left( \frac{\partial ^2u}{\partial {x^2}} -\eta \frac{\partial {u}}{\partial {t}}-u^3-\varepsilon \,u\right) =0, \end{aligned}$$
(1)

where u represents critical average vertical density function, \(\varepsilon\) shows the bifurcation parameter, \(\eta\) the effective viscosity, and x is the horizontal direction. The term including the highest space derivative in 1 shows the interface tension (Cartes et al. 2004; Clerc and Escaff 2006). Studies to explore the closed-form solutions which exhibit the physical nature of VdW equation (Bibi et al. 2018; Abourabia and Morad 2015; Lu et al. 2017; Zafar et al. 2020) have been contributed analytically.

The study of fractional calculus in nonlinear science has given a new impetus in applications to numerous systems. It has been notably apparent that understanding the dynamical behavior of such systems is a widely studied area with the proper description of non-integer order derivatives such as Riemann–Liouville, conformable, Caputo, truncated-M-derivative (Vanterler et al. 2018; Atangana et al. 2015; Çenesiz et al. 2017; Khan and Khan 2019; Atangana and Gómez-Aguilar 2018). Several applications have been contributed to the models in fractional form by exploring the analytical techniques including the discrete tanh method (Houwe et al. 2020b), the sech–tanh functions expansion (Park et al. 2020), Grunwald Letnikov method (Aminikhah et al. 2017), Sine-Gordon expansion method (Korkmaz et al. 2020; Akbar et al. 2021), generalized Kudryashov method (Korkmaz and Hepson 2018b), ansatz method (Korkmaz and Hepson 2018a) and so on (Sabi’u et al. 2019a, b, 2022; Khan et al. 2022; Sabi’u et al. 2023; Akinyemi et al. 2021a, b; Khater et al. 2020; Qian et al. 2019; Attia et al. 2020; Ghanbari 2021a, b; Ghanbari et al. 2019, 2020). Moreover, to understand the dynamic behaviour of different mathematical and physical models at any given time, the fractional derivatives are one of the best solutions, see Rida et al. (2017), Arafa and Hagag (2019), El-Sayed et al. (2010), Ali et al. (2019), Alquran (2023) and Jaradat and Alquran (2022). For example, the Caputo fractional generalized tumor model (Padder et al. 2023), the numerical comparison of nonlinear Duffing oscillator model with fractional and integer derivative (Qureshi et al. 2023), the optimization of for human immunodeficiency virus with Caputo fractional operator (Jan et al. 2023), the nonlinear Radhakrishnan–Kundu–Lakshmanan equation (Ghanbari and Gómez-Aguilar 2019a), the generalized Schrödinger equation (Ghanbari and Gómez-Aguilar 2019b), the Hirota–Maccari equation (Ghanbari 2019), etc.

In this work, we aim to construct the solutions of VdW equation in fractional form,

$$\begin{aligned} D_{t,M}^{2\alpha ,\beta }u+D_{x,M}^{2\alpha ,\beta }\left( D_{x,M}^{2\alpha ,\beta }u -D_{t,M}^{\alpha ,\beta }u-u^3-\varepsilon \,u\right) =0, \end{aligned}$$
(2)

where \(\alpha \in (0,1],\,\beta >0,\) and the term \(D_{t,M}^{\alpha ,\beta }\) is stated by the truncated M-fractional derivative in time which will be solved analytically by the auxiliary equation method. This method is one of the direct methods which provides effective solutions based on Weierstrass and Jacobi elliptic functions. According to the procedure, the given non-linear PDE is reduced to the ODE by employing a transformation to the model. Recently, studies conducted in Sirendaoreji (2022), Houwe et al. (2020a) and Raheel et al. (n.d.) aimed to propose travelling wave simulations with the present strategy. Another study is employed in Daşcıoğlu and ünal, S. Ç. (2021) to the space-time fractional Kawahara model by using the current strategy. The significance of this study is to derive solitary wave solutions of the time-fractional VdW equation using the auxiliary equation method. To our knowledge, the model equation has not been implemented by the current analytical approach in one dimension. Then, the analytical findings are utilized to examine the physical characteristics of this model graphically. The natural behaviors of the patterns are depicted in two and three-dimensional views.

The following is the structure of this paper: In Sect. 2, the truncated M-fractional description is presented. The methodology of the new algebraic analytical method with the M-fractional derivative is presented in Sect. 3. Section 4 explains the application of the process with graphical visualizations. Finally, Sect. 5 summarizes the concluding remarks and possible extensions of the study.

2 Definition and properties of the truncated M-fractional

For \(u:[0,\infty )\rightarrow {\mathbb {R}},\) the truncated M-fractional derivative of u of order \(\alpha\) is express as

$$\begin{aligned} D_M^{\alpha ,\beta }\{ (u)(t)\} = \mathop {\lim }\limits _{\tau \rightarrow 0} \frac{{u\left( t{\textrm{E}_\beta }\left( \tau {t^{1 - \alpha }}\right) \right) - u(t)}}{\tau }, \quad \,\,\,\forall \,t> 0,\; 0< \alpha < 1,\; \beta > 0, \end{aligned}$$
(3)

where \({\textrm{E}_\beta }(.)\) is a truncated Mittag–Leffler function of one parameter (Vanterler et al. 2018). The main advantage of this fractional operator is that it generalized four different fractional derivatives, for details see Vanterler et al. (2018) and the references therein. The M-fractional derivative supports several properties given below.

Theorem 1

Let \(\alpha \in (0,1]\), \(\beta > 0\), \(a,b \in {\mathbb {R}}\) and u, v \(\alpha\)-differentiable at a point \(t>0.\) Then,

  • \(D_{t,M}^{\alpha ,\beta }\{(au + bv)(t)\}=aD_{t,M}^{\alpha ,\beta }\{u(t)\} +bD_{t,M}^{\alpha ,\beta }\{v(t)\}.\)

  • \(D_{t,M}^{\alpha ,\beta }\{ (u.v)(t)\}=u(t)D_{t,M}^{\alpha ,\beta }\{ v(t)\}+v(t)D_{t,M}^{\alpha ,\beta }\{ u(t)\}.\)

  • \(D_{t,M}^{\alpha ,\beta }\{ (\frac{u}{v})(t)\} = \frac{{v(t)D_{t,M}^{\alpha ,\beta }\{u(t)\}-u(t)D_{t,M}^{\alpha ,\beta }\{v(t)\} }}{{{{[v(t)]}^2}}}.\)

  • \(D_{t,M}^{\alpha ,\beta }(\lambda )=0,\) for constant \(\lambda .\)

  • If u is differentiable, then \(D_{t,M}^{\alpha ,\beta }\{ u(t)\} = \frac{{{t^{1 - \alpha }}}}{{\Gamma (\beta + 1)}}\frac{{du(t)}}{{dt}}\),

for \(\forall a,b\in {\mathbb {R}}\) (Atangana et al. 2015; Çenesiz et al. 2017; Khan and Khan 2019).

Many important characteristics of the M-fractional derivative are supported, including the Laplace transform, exponential function, Gronwall’s inequality, several integration rules, chain rule, and Taylor series expansion (Khan and Khan 2019).

3 Description of the method

This section will describe the proposed methodology for solving Eq. (2) in steps.

Step 1 The procedure starts by reducing the model Eq. (2):

$$\begin{aligned} {P_1}\left( u,D_{t,M}^{\alpha ,\beta }u,D_{x,M}^{\alpha ,\beta }u,D_{t,M}^{2\alpha ,\beta }u,D_{x,M}^{2\alpha ,\beta }u,\ldots \right) = 0, \end{aligned}$$
(4)

to an ODE given as

$$\begin{aligned} P_{2}(U,U^{\prime },U^{\prime \prime },\ldots )=0, \end{aligned}$$
(5)

with the help of a suitable wave transformation

$$\begin{aligned} u(x,t)= U(\xi ),\quad \xi =\frac{{\Gamma (\beta +1)}}{\alpha }(k{x^\alpha }-\varpi {t^\alpha }), \end{aligned}$$
(6)

where k and \(\varpi\) are unknowns to be thought up during the implementation of the method.

Step 2 This step determines the traveling wave solutions to Eq. (6) of the form:

$$\begin{aligned} U(\xi )={A_1}Q(\xi ) \end{aligned}$$
(7)

where \({A_1}\) is an unknown constant, \(Q(\xi )\) provides the following second order auxiliary ODE:

$$\begin{aligned} {Q^{\prime \prime }}(\xi )=c{Q^3}(\xi )-2{a^2}Q(\xi )-3a{Q^\prime }(\xi ). \end{aligned}$$
(8)

Step 3 Moreover, to differentiate this approach from the unified expansion technique, we suggested that the ODE Eq. (8) is an equation whose solutions are:

$$\begin{aligned} Q(\xi )=\left\{ {\begin{array}{*{20}{ll}} \varepsilon \,ae^{-a\xi }ds\left( e^{-a\xi }+ c_2,\frac{\sqrt{2}}{2}\right) ,&{}\quad c=2,\\ \varepsilon \,ae^l{-a\xi }nc\left( \sqrt{2}e^{-a\xi }+c_2,\frac{\sqrt{2}}{2}\right) , &{}\quad c=2,\\ \frac{\varepsilon \,a}{2}\left[ 1-\tanh \left( \frac{a}{2}\xi \right) \right] ,&{}\quad c=2,\\ \frac{\varepsilon \,a}{2}\left[ 1-\coth \left( \frac{a}{2}\xi \right) \right] ,&{}\quad c=2,\\ \varepsilon \,ae^{-a\xi }cn\left( \sqrt{2}e^{-a\xi }+c_3,\frac{\sqrt{2}}{2}\right) ,&{}\quad c=- 2,\\ \frac{\sqrt{2}}{2}\varepsilon \,ae^{-a\xi }sd\left( \sqrt{2}e^{-a\xi }+c_3,\frac{\sqrt{2}}{2}\right) ,&{}\quad c=- 2, \end{array}}\right. \end{aligned}$$
(9)

In solutions Eq. (9), \(\varsigma\) represents the Weirstrass elliptic function, ds, \(nc,\,cn,\) sd are the Jacobi elliptic functions (JEFs), \(\varepsilon =\pm {1}\) and \(a,b,c_1,c_2,c_3\) are constants. By substituting Eq. (7) and Eq. (8) into Eq. (5) and setting the coefficients of like powers of \(Q^i(Q^\prime )^j\) to the zero, we obtain a set of algebraic equations for unknowns \(\eta ,a,\varepsilon ,{A_1},k,\varpi\). The particular goal is to designate the parameters \({A_1},k,\varpi\) in terms of the others. Once the relations between the parameters are arranged, the solution to Eq. (5) can be represented explicitly.

4 Application of the method

Applying wave transformation Eq. (6) into Eq. (1) and integrating twice, the Van der Waals Model can be determined as

$$\begin{aligned} (\varpi ^2-k^2\varepsilon )U(\xi )+{k^4}\frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\xi ^2}}}U( \xi )+{k^2}\eta \varpi \frac{\mathrm{{d}}}{{\mathrm{{d}}\xi }}U(\xi )+k^2U^3(\xi )=0. \end{aligned}$$
(10)

Placing Eq. (7) and solutions of Eq. (8) into Eq. (1)

$$\begin{aligned} A_1\left( {\left( {\varpi ^2-2a^2k^4-\varepsilon \,k^2}\right) Q(\xi )+\left( {{k^2}\eta \varpi -3ak^4}\right) \frac{\mathrm{{d}}}{{\mathrm{{d}}\xi }}Q(\xi )+\left( {c{k^4}+{k^2}{A_1}^2}\right) {{({Q(\xi )})}^3}}\right) =0, \end{aligned}$$
(11)

and equaling the coefficients to zero, we get a set of algebraic equations in terms of \(\eta , a,\varepsilon ,{A_1},k,\varpi\):

$$\begin{aligned} \begin{aligned}&\varpi ^2-2a^2k^4-\varepsilon \,k^2=0,\\&k^2\eta \varpi -3ak^4=0,\\&ck^4+k^2A_1^2=0. \end{aligned} \end{aligned}$$
(12)

Solutions of this algebraic system with respect to \({A_1},k,\varpi\) are

$$\begin{aligned} A_1=\pm \frac{\eta }{a}\sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}},\,\,\,k=\pm \frac{\eta }{a} \sqrt{-\frac{\varepsilon }{2\,\eta ^2-9}},\,\,\,\varpi =-3\frac{\varepsilon \eta }{a(2\eta ^2-9)}. \end{aligned}$$
(13)

for nonzero \(\eta ,\,a\) and \(\varepsilon .\)

Case 1

Using these data and assuming \(Q=\varepsilon \,a{e^{-a\xi }}ds\big (e^{-a\xi }+c_2,\frac{\sqrt{2}}{2}\big ),\) the solution of Eq. (5) can be achieved as:

$$\begin{aligned} {U_{1,2}}(\xi )=\pm \varepsilon \eta \sqrt{\frac{{\varepsilon \,c}}{{2{\eta ^2} -\mathrm{{}}9}}}{e^{-\mathrm{{}}a\xi }}ds\left( {{e^{-\mathrm{{}}a\xi }}+c_2,\frac{\sqrt{2}}{2}}\right) . \end{aligned}$$
(14)

Selecting \(c=2\) and reusing the transformation Eq. (6) to return original variables, the solutions of the vdW Eq. (1) is given as:

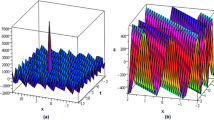
$$\begin{aligned} u_{1,2}(x,t)=\pm \varepsilon \eta \sqrt{\frac{2\varepsilon }{2\eta ^2-9}}e^{ -a\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) }ds\left( e^{ -a\left( \frac{\Gamma (\beta +1)}{\alpha }(kx^{\alpha }-\varpi {t^\alpha })\right) }+c_2,\frac{\sqrt{2}}{2}\right) . \end{aligned}$$
(15)

The solution Eq. (15) are plotted on (a) 3D, (b) contour and (c) 2D for values of \(\eta =0.5\), \(a=2.5\), \(\alpha =0.9\), \(\beta =0.5\), \(\varepsilon =-1\) and \(c_2=0\) in Fig. 1.

Case 2

Using these data and assuming \(Q=\varepsilon \,ae^{-a\xi }nc\left( \sqrt{2}e^{-a\xi }+c_2,\frac{\sqrt{2}}{2}\right) ,\) the solution of Eq. (5) can be achieved as:

$$\begin{aligned} {U_{3,4}}(\xi )=\pm \varepsilon \eta \sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}}e^{-a\xi }nc \left( \sqrt{2}e^{-a\xi }+c_2,\frac{\sqrt{2}}{2}\right) . \end{aligned}$$
(16)

Selecting \(c=2\) and using the transformation Eq. (6) to return original variables, the solutions of the vdW Eq. (1) is given as:

$$\begin{aligned} u_{3,4}(x,t)=\pm \varepsilon \eta \sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}}e^{-a\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) }nc\left( \sqrt{2}e^{-a\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) }+c_2,\frac{\sqrt{2}}{2}\right) . \end{aligned}$$

Case 3

Using these data and assuming \(Q=\frac{\varepsilon \,a}{2}\left[ 1-\tanh \left( \frac{a}{2}\xi \right) \right] ,\) the solution of Eq. (5) can be achieved as:

$$\begin{aligned} U_{5,6}(\xi )=\frac{\varepsilon \eta }{2}\sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}}\left( 1-\tanh \left( \frac{a}{2}\xi \right) \right) . \end{aligned}$$

Selecting \(c=2\) and reusing the transformation Eq. (6) to return original variables, the solutions of the vdW Eq. (1) is given as:

$$\begin{aligned} u_{5,6}(x,t)=\frac{\varepsilon \eta }{2}\sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}}\left( 1 -\tanh \left( \frac{a}{2}\frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) \right) . \end{aligned}$$
(17)

The solution Eq. (17) are plotted on xtu-space for values of \(\eta\), a and \(\varepsilon\) in Figs. 2 and 3.

Fig. 1
figure 1

The hyperbolic exact solution \(\left| {{u_{1,2}}(x,t)} \right|\) with parameters \(\eta =0.5\), \(a=2.5\), \(\alpha =0.9\), \(\beta =0.5\), \(\varepsilon =-1, c_2=0\) and a 3D, b contour, and c 2D plot with respect to t, and d 2D plot with respect \(\alpha\)

Full size image
Fig. 2
figure 2

The Jacobi elliptic function solution plots for Case 3 for \(\eta =1\), \(a=0.5\) and \(\varepsilon =-1.5\) a 3D b contour, c 2D plot with respect to t, and d 2D plot with respect to \(\alpha\)

Full size image
Fig. 3
figure 3

The Jacobi elliptic function solution plots for Case 3 for \(\eta =-1\), \(a=0.5\) and \(\varepsilon =1.5\) a 3D b contour, and c 2D plots with respect to t and, and d 2D plot with respect to \(\alpha\)

Full size image

Case 4

Using these data and assuming \(Q=\frac{\varepsilon \,a}{2}\left[ 1-\coth \left( \frac{a}{2}\xi \right) \right] ,\) the solution of Eq. (5) can be achieved as:

$$\begin{aligned} U_{7,8}(\xi )=\pm \frac{\varepsilon \eta }{2}\sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}}\left[ 1-\coth \left( \frac{a}{2}\xi \right) \right] . \end{aligned}$$
(18)

Selecting \(c=2\) and reusing the transformation Eq. (6) to return original variables, the solutions of the vdW Eq. (1) is given as:

$$\begin{aligned} {u_{7,8}}(x,t)=\pm \frac{\varepsilon \eta }{2}\sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}} \left[ 1-\coth \left( \frac{a}{2}\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) \right) \right] . \end{aligned}$$
(19)

Case 5

Using these data and assuming \(Q=\varepsilon \,ae^{-a\xi }cn\left( sqrt{2}e^{-a\xi }+c_3,\frac{\sqrt{2}}{2}\right) ,\) the solution of Eq. (5) can be achieved as:

$$\begin{aligned} U_{9,10}(\xi )=\pm \varepsilon \eta \sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}}e^{-a\xi }cn \left( \sqrt{2}e^{-a\xi }+c_3,\frac{\sqrt{2}}{2}\right) . \end{aligned}$$
(20)

Selecting \(c=-2\) and reusing the transformation Eq. (6) to return original variables, the solutions of the vdW Eq. (1) is given as:

$$\begin{aligned} u_{9,10}(x,t)=\pm \varepsilon \eta \sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}}e^{-a\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) }cn\left( \sqrt{2}e^{ -a\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) }+c_3,\frac{\sqrt{2}}{2}\right) . \end{aligned}$$
(21)

Case 6

Using these data and assuming \(Q=\frac{\sqrt{2}}{2}\varepsilon \,ae^{-a\xi }sd\left( \sqrt{2}e^{-a\xi }+c_3,\frac{\sqrt{2}}{2}\right) ,\) the solution of Eq. (5) can be achieved as:

$$\begin{aligned} U_{11,12}(\xi )=\pm \frac{\varepsilon \eta }{2}\sqrt{\frac{\varepsilon \,c}{2\eta ^2-9}} e^{-a\xi }sd\left( \sqrt{2}e^{-a\xi }+c_3,\frac{\sqrt{2}}{2}\right) . \end{aligned}$$

Selecting \(c=-2\) and reusing the transformation Eq. (6) to return original variables, the solutions of the vdW Eq. (1) is given as:

$$\begin{aligned} u_{11,12}(x,t)=\pm \frac{\varepsilon \eta }{2}\sqrt{\frac{2\varepsilon \,c}{2\eta ^2-9}}e^{-a\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) }sd\left( \sqrt{2}e^{-a\left( \frac{\Gamma (\beta +1)}{\alpha }(k{x^\alpha }-\varpi {t^\alpha })\right) }+c_3,\frac{\sqrt{2}}{2}\right) . \end{aligned}$$
(22)

4.1 Result discussion

The solutions derived in this article using the auxiliary equation for the M- derivative time fractional vdWm included different Jacobi elliptic functions and hyperbolic function solutions. The solution \(u_{1,2}(x,t)\) is the Jacobi ds function solution, \(u_{3,4}(x,t)\) is the Jacobi nc function solution, \(u_{9,10}(x,t)\) is the Jacobi nc function solution, and \(u_{11,12}(x,t)\) is the Jacobi sd function solution. While the solutions \(u_{5,6}(x,t)\) and \(u_{7,8}(x,t)\) are hyperbolic functions solutions. We applied appropriate values to graph some of these solutions, namely; \(u_{1,2}(x,t)\), and Case 3 in contour, 3D, and 2D plots. Moreover, for Fig. 1, the contour, 3D, and 2D plots are implented with parameters \(\eta =0.5\), \(a=2.5\), \(\alpha =0.9\), \(\beta =0.5\), \(\varepsilon =-1\), \(c_2=0\). Figure 2 is generated with parameters \(\eta =1\), \(a=0.5\) and \(\varepsilon =-1.5\). Lastly, Fig. 3 is adopted with parameters \(\eta =-1\), \(a=0.5\) and \(\varepsilon =1.5\). We set \(t=0.9\) and varied the value of the fractional derivative \(\alpha\) for the subplot (d) in all three figures. This is done because varying values of the fractional derivative are more conducive to comprehending the influence of the conformable derivative \(\alpha\). In addition, the hyperbolic function solution and the Jacobi elliptic function solutions reported in this paper have not been reported to the best of our knowledge for the M- derivative time fractional vdWm in scientific literature. The reported solutions are entirely different from those reported using the extended \(\frac{G'}{G}\)-expansion and \(Exp_a\) function methods (Raheel et al. n.d.).

5 Conclusion

This study investigates the Van der Waals Model using a novel algebraic approach, which results in the achievement of a large number of new exact solutions to the considered problem. Using this method, we first reduced the proposed model to a nonlinear ODE with the help of a complex wave transformation, we then substituted the solution into the resultant ODE and found the relations between the parameters of the equations. The exact solutions are discovered for certain values of \(\eta ,\, a,\,\varepsilon ,\) and other parameters. These solutions for the M- derivative time fractional vdWm included different Jacobi elliptic function solutions such as ds, nc, cn and sd JEFs solutions and hyperbolic function solutions. Then, graphical patterns are presented to show the physical explanation of the model interactions in 2D, contour, and 3D plots. The achieved solutions will be of high significance in the interaction of quantum-mechanical fluctuations, granular matter and other areas of vdWm applications. In conclusion, this approach may be extended to solve the nonlinear ODEs, NPDEs, fractional N0DEs, and fractional NPDEs, in various fields of applied science and engineering.