Introduction

In recent years, renewable energy, in general, and solar energy, in particular, have gained considerable attention owing to their environmental friendliness and effectiveness in generating electrical and thermal energy. Solar energy is usually harnessed using photovoltaic technology or solar collectors (SCs). A SC is preferable owing to its cost efficiency and energy collection capabilities [1]. The suspension of nanoparticles in the base fluid is a major advancement in developing SCs with enhanced efficiency. Choi [2] was the first to observe improved heat transfer using nanoparticles. Over the years, studies investigating nanofluids in parabolic trough solar collectors (PTSCs) have been conducted [3,4,5,6]. Shahzad et al. [7] studied the thermal characterization of a solar-powered ship using Oldroyd hybrid nanofluids in a PTSC. Jamshed et al. [8] performed a thermal examination of renewable solar energy in a PTSC using a Maxwell nanofluid. Jamshed et al. [9] conducted a computational study on implementing renewable solar energy in the presence of a Maxwell nanofluid in a PTSC. Nabwey et al. [10] investigated the effect of resistive and radiative heats on enhanced heat transfer of a PTSC using Maxwell–Oldroyd-B nanofluids.

Many researchers have studied the fractional calculus methods, the effects of convective heat transfer and thermal radiation processes on nanofluid efficiency, and the applications of nanofluids in the presence of oxytactic microorganisms in different engineering problems [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

Currently, binary nanofluids are being studied for various applications as they have better energy transfer than mono nanofluids [29,30,31,32]. Yu [33] employed a decoupled wavelet approach for multiple physical flow fields of binary nanofluids in double-diffusive convection. Lee et al. [34] conducted a theoretical study on the performance comparison of various SCs using binary nanofluids. Reddy et al. [35] studied the effects of viscous dissipation and thermal radiation on electrically conducting Casson–Carreau nanofluid flow using the Cattaneo–Christov heat flux model. Oyelakin et al. [36] investigated the effect of double-diffusion convection on three-dimensional magnetohydrodynamic (MHD) stagnation point flow of a tangent hyperbolic Casson nanofluid. Yousef et al. [37] explored the chemical reaction impact on MHD dissipative Casson–Williamson nanofluid flow over a slippery stretching sheet through a porous medium.

Jamshed and Nisar [38] compared copper/alumina-engine oil Williamson nanofluids in a PTSC. They concluded that copper was considerably better than alumina in terms of heat transfer. Other studies [39,40,41] have also suggested the use of copper rather than other materials owing to its high efficiency to achieve enhanced thermal properties. Notably, the shape of nanoparticles can affect nanofluid heat transfer ability [42, 43].

Based on the literature review, we believe that a direct comparison of binary nanofluids in PTSCs is lacking, and we hope to contribute toward mitigating this lack of knowledge. Notably, the Jeffrey and Casson–Jeffrey nanofluid models have not been investigated in PTSC settings. The other novel aspects of the current study are as follows:

  • The comparison between the Casson–Maxwell, Casson–Jeffrey, and Casson–Oldroyd-B binary nanofluids in PTSCs.

  • The consideration of thermophoretic diffusivity.

  • The consideration of a constant inclined magnetic field.

  • The consideration of different nanoparticle shapes.

The practical significance of this study lies in the use of the considered models in PTSCs [10, 41, 44], solar water pumps [45], and solar-powered ships [7, 8].

Formulation of the problem

Consider the velocity and temperature of a nonuniform stretching insulated sheet as follows [46]:

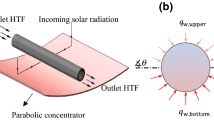
$$U_{{\text{W}}} \left( {x,0} \right) = ax,T_{{\text{W}}} \left( {x,0} \right) = T_{\infty } + a^{*} x$$
(1)

where \(a\), \(a^{*}\), \(T_{{\text{W}}}\), and \(T_{\infty }\) denote the primary stretching rate, thermal discrepancy rate, heat at the wall, and heat at the free stream, respectively. Figure 1 presents a schematic of a PTSC.

Fig. 1
figure 1

Schematic of a parabolic trough solar collector (PTSC). Reprinted with alterations under Creative Common CC BY licence from [52]

Full size image

Stress tensor of binary fluids

Herein, we studied three binary liquids: Casson–Maxwell, Casson–Jeffrey, and Casson–Oldroyd-B.

The rheological equation of state of an incompressible and isotropic flow of a Casson fluid is as follows [47]:

$$\tau_{{{\text{ij}}}} = \left\{ {\begin{array}{*{20}c} {2\left( {\mu_{{\text{B}}} + \frac{{p_{{\text{y}}} }}{{\sqrt {2\pi } }}} \right)e_{{{\text{ij}}}} , \quad \pi > \pi_{{\text{c}}} } \\ {2\left( {\mu_{{\text{B}}} + \frac{{p_{{\text{y}}} }}{{\sqrt {2\pi_{{\text{c}}} } }}} \right)e_{{{\text{ij}}}} , \quad \pi < \pi_{c} } \\ \end{array} } \right.$$
(2)

where \(\tau_{{{\text{ij}}}}\) denotes the stress tensor, \(e_{{{\text{ij}}}}\) denotes the \(\left( {i,j} \right)\)th component of the deformation rate, \(\pi = e_{{{\text{ij}}}} e_{{{\text{ij}}}}\), i.e., the product of the component of deformation with itself, \(\pi_{{\text{c}}}\) denotes a critical value of this product based on the non-Newtonian model, \(\mu_{{\text{B}}}\) denotes the plastic dynamic viscosity of the Casson fluid, and \(p_{{\text{y}}}\) denotes the yield stress of the fluid.

The Maxwell model is a simple linear model with one elastic parameter, which is \(\lambda_{1}\), the fluid relaxation time. This model combines the concepts of fluid viscosity and solid elasticity to arrive at the following relation:

$$\tau + \lambda_{1} \frac{\partial \tau }{{\partial t}} = \mu_{0} \dot{\gamma }$$
(3)

The Jeffrey model extends the Maxwell model by adding a time derivative of the strain rate to yield the following equation:

$$\tau + \lambda_{1} \frac{\partial \tau }{{\partial t}} = \mu_{0} \left( {\dot{\gamma } + \lambda_{3} \frac{{\partial \dot{\gamma }}}{\partial t}} \right)$$
(4)

where \(\lambda_{3}\) denotes the retardation time, which is a measure of the time required by the material to respond to deformation.

The Oldroyd-B model is the nonlinear equivalent of the linear Jeffrey model, because it considers the frame invariance in the nonlinear regime. It can be constructed by replacing the partial time derivatives in the differential form of the Jeffrey model with the upper convective time derivatives to achieve the following form:

$$\tau + \lambda_{1} \tilde{\tau } = \mu_{0} \left( {\dot{\gamma } + \lambda_{3} \widetilde{{\dot{\gamma }}}} \right)$$
(5)

where \(\tilde{\tau }\) and \(\widetilde{{\dot{\gamma }}}\) denote the upper convected derivatives of the stress and strain tensors, respectively, and are expressed as follows:

$$\tilde{\tau } = \frac{\partial \tau }{{\partial t}} + {\mathbf{v}}.\nabla \tau - \left( {\nabla {\mathbf{v}}} \right)^{{\text{T}}} .\tau - \tau .\nabla {\mathbf{v}}$$
(6)
$$\widetilde{{\dot{\gamma }}} = \frac{{\partial \dot{\gamma }}}{\partial t} + {\mathbf{v}}.\nabla \dot{\gamma } - \left( {\nabla {\mathbf{v}}} \right)^{{\text{T}}} .\dot{\gamma } - \dot{\gamma }.\nabla {\mathbf{v}}$$
(7)

For more details about the different aspects of various non-Newtonian fluids we refer the reader to the comprehensive work conducted by Sochi [48].

Governing equations

The principles of conservation of mass, momentum, and energy are applied to two-dimensional, incompressible, laminar, steady flow of binary nanofluids. We also consider the porous medium along with the thermophoresis effect and a constant inclined magnetic field as follows [44, 49]:

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(8)
$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = - \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + 2uv\frac{{\partial^{2} u}}{\partial x\partial y}} \right) + \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} \left( {1 + \lambda_{2} } \right)}}\left( {\left( {1 + \frac{{1{ }}}{\beta }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + \lambda_{3} \left( {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + \frac{\partial u}{{\partial y}}\frac{{\partial^{2} u}}{\partial x\partial y} + v\frac{{\partial^{3} u}}{{\partial y^{3} }} - \frac{\partial u}{{\partial x}}\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)} \right) - \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} k_{{\text{p}}} }}u - \frac{{\sigma_{{{\text{nf}}}} B_{0}^{2} }}{{\rho_{{{\text{nf}}}} }}u {\text{sin}}^{2} \left( \Gamma \right)$$
(9)
$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{{k_{{{\text{nf}}}} }}{{\left( {\rho C_{p} } \right)_{{{\text{nf}}}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{Q_{0} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{nf}}}} }}\left( {T - T_{\infty } } \right) + \frac{{\mu_{{{\text{nf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{nf}}}} }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} - \frac{1}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{nf}}}} }}\frac{{\partial q_{{\text{r}}} }}{\partial y} + \chi \left[ {\frac{{D_{{\text{T}}} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right] + \frac{{\sigma_{{{\text{nf}}}} B_{0}^{2} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{nf}}}} }}u^{2} {\text{sin}}^{2} \left( \Gamma \right)$$
(10)

The suitable boundary constraints are as follows:

$$u = U_{{\text{w}}} + N_{{\text{w}}} \frac{\partial u}{{\partial y}} , v = V_{{\text{w}}} , \kappa_{0} \frac{\partial T}{{\partial y}} = - h_{{\text{f}}} \left( {T_{{\text{W}}} - T} \right) \quad {\text{at}}\quad y = 0$$
(11)
$$u \to 0 , T \to T_{\infty } \quad {\text{as}}\quad y \to \infty$$
(12)

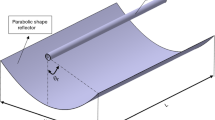
where \(u\) and \(v\) denote the velocity components in the x and y directions, respectively; \(\mu_{{{\text{nf}}}}\), \(\rho_{{{\text{nf}}}}\), \(\sigma_{{{\text{nf}}}}\), \(k_{{{\text{nf}}}}\), and \(C_{{{\text{p}}_{{{\text{nf}}}} }}\) denote the nanofluid viscosity, density, electrical conductivity, thermal conductivity, and specific heat, respectively; \(\lambda_{2}\) denotes the ratio of the relaxation to retardation times; \(\beta\) denotes the Casson parameter; \(k_{{\text{p}}}\) denotes the porosity; \(B_{0}\) denotes the strength of the magnetic field perpendicular to \(\overline{OH}\), and \(\Gamma\) denotes the angle of inclination of the magnetic field; \(T\) denotes the nanofluid temperature; \(Q_{0}\) denotes the heat source; \(q_{{\text{r}}}\) denotes the radiative heat flux; \(\chi\) denotes the ratio of operative heat capability; \(D_{{\text{T}}}\) denotes the thermophoresis diffusion coefficient; \(N_{{\text{w}}}\) denotes the slip length; \(V_{{\text{w}}}\) denotes the surface permeability; \(\kappa_{0}\) denotes the surface thermal conductance; and \(h_{{\text{f}}}\) denotes the heat transfer coefficient. Figure 2 presents the boundary layer flow in a PTSC.

Fig. 2
figure 2

PTSC inner geometry. Reprinted with alterations under Creative Common CC BY licence from [7]

Full size image

The following conditions describe the different case studies:

  1. (1)

    \(\lambda_{1} \ne 0\), \(\lambda_{2} = 0\), \(\lambda_{3} = 0\) represents the Casson–Maxwell model.

  2. (2)

    \(\lambda_{1} = 0\), \(\lambda_{2} \ne 0\), \(\lambda_{3} \ne 0\) represents the Casson–Jeffrey model.

  3. (3)

    \(\lambda_{1} \ne 0\), \(\lambda_{2} = 0\), \(\lambda_{3} \ne 0\) represents the Casson–Oldroyd-B model.

The radiative heat flux under the Rosseland approximation [21, 50] takes the form \(q_{r} = - \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{\partial T}{{\partial y}}\) in which \({\upsigma }^{*}\) is the Stefan–Boltzmann constant and \(k^{*}\) is the mean absorption coefficient.

Table 1 presents the thermophysical aspects of the nanofluids [7, 51], Table 2 specifies the nanoparticle shape factor (m) values for various particle shapes [52, 53], and Table 3 lists the substance properties of engine oil and copper [52].

Table 1 Thermophysical features of nanofluids
Full size table
Table 2 Shape factor values
Full size table
Table 3 Material specifications at 20 °C
Full size table

Solution of the problem

To transform the partial differential equations to ordinary differential equations (ODEs), we introduce the following similarity variables [44]:

$$u = axf^{\prime}\left( \eta \right) , v = - \sqrt {a\nu } f\left( \eta \right) , \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{{\text{W}}} - T_{\infty } }},\eta = y\sqrt {\frac{a}{\nu }}$$
(13)

This transforms Eqs. (9–10) along with boundary conditions (11–12) to the following forms:

$$ff^{\prime \prime} - \beta_{1} \left( {f^{2} f^{\prime \prime \prime}} - 2ff^{\prime} f^{\prime \prime} \right) + \frac{1}{{\varphi_{1} \varphi_{2} \left( {1 + \lambda_{2} } \right)}}\left( {\left( {1 + \frac{1 }{\beta }} \right)f^{\prime \prime \prime} + \beta_{3} \left( {f^{\prime \prime 2} - ff^{\prime \prime \prime \prime } } \right)} \right) - \frac{K}{{\varphi_{1} \varphi_{2} }}f^{\prime} - M\frac{{\varphi_{4} }}{{\varphi_{2} }}f^{\prime} \sin^{2} \left( \Gamma \right) - f^{\prime 2} = 0$$
(14)
$$\left( {\frac{{\varphi_{5} }}{{{\text{Pr}}}} + N_{{\text{r}}} } \right)\theta^{\prime\prime} + \varphi_{3} f\theta^{\prime} + Q\theta + \frac{{{\text{Ec}}}}{{\varphi_{1} }}f^{{\prime\prime}{2}} + N_{{\text{t}}} \varphi_{3} \theta^{{\prime}{2}} + \varphi_{4} M{\text{Ecsin}}^{2} \left( \Gamma \right){ }f^{{\prime}{2}} = 0$$
(15)
$$f^{\prime}\left( 0 \right) = 1 + \Lambda f^{\prime\prime}\left( 0 \right),f\left( 0 \right) = S,\theta^{\prime}\left( 0 \right) = - {\text{Bi}}_{{\text{T}}} \left( {1 - \theta \left( 0 \right)} \right)$$
(16)
$$f^{\prime}\left( \eta \right) \to 0,\;\theta \left( \eta \right) \to 0\quad {\text{as}}\quad \eta \to \infty$$
(17)

where \(\beta_{1} = \lambda_{1} a\) and \(\beta_{3} = \lambda_{3} a\) denote Deborah numbers, \(K = \frac{{\mu_{{\text{f}}} }}{{a{ }\rho_{{\text{f}}} { }k_{{\text{p}}} }}\) denotes the porosity parameter, \(M = \frac{{\sigma_{{\text{f}}} { }B_{0}^{2} { }}}{{a{ }\rho_{{\text{f}}} }}\) denotes the magnetic number, \(\alpha = \frac{{k_{{\text{f}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\) denotes the thermal diffusion rate, \(\nu = \frac{{\mu_{{\text{f}}} }}{{\rho_{{\text{f}}} }}\) denotes the kinematic viscosity, \({\text{Pr}} = \frac{\nu }{\alpha }\) denotes the Prandtl number, \(N_{{\text{r}}} = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \nu \left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\) denotes the thermal radiation parameter, \(Q = \frac{{Q_{0} }}{{a \left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\) denotes the heat source parameter, \({\text{Ec}} = \frac{{U_{{\text{W}}}^{2} }}{{C_{{{\text{p}}_{{\text{f}}} }} \left( {T_{{\text{W}}} - T_{\infty } } \right)}}\) denotes the Eckert number, \(N_{{\text{t}}} = \frac{{\chi D_{{\text{T}}} \left( {T_{{\text{W}}} - T_{\infty } } \right)}}{{\nu T_{\infty } }}\) denotes the thermophoretic parameter, \(\Lambda = N_{{\text{w}}} \sqrt {\frac{a}{\nu }}\) denotes the velocity slip parameter, \(S = - V_{{\text{w}}} \sqrt {\frac{1}{\nu a}}\) denotes the mass transfer parameter, and \({\text{Bi}}_{{\text{T}}} = \frac{{h_{{\text{f}}} }}{{\kappa_{0} }}\sqrt {\frac{\nu }{a}}\) denotes the thermal Biot number.

Physiological concepts of interest

Considerable attention is directed toward the skin friction constant \(C_{{\text{f}}}\), the local Nusselt number \(Nu_{{\text{x}}}\), and the entropy generation equation [45, 46, 52, 54]:

$$C_{{\text{f}}} = \frac{{\tau_{{\text{W}}} }}{{\rho_{{\text{f}}} U_{{\text{W}}}^{2} }},{\text{Nu}}_{{\text{x}}} = \frac{{x q_{{\text{W}}} }}{{k_{{\text{f}}} \left( {T_{{\text{W}}} - T_{\infty } } \right)}}$$
(18)
$$E_{{\text{G}}} = \frac{{k_{{{\text{nf}}}} }}{{T_{\infty }^{2} }}\left( {\left( {\frac{\partial T}{{\partial y}}} \right)^{2} + \frac{16}{3}\frac{{\sigma^{*} T_{\infty }^{3} }}{{k^{*} \nu \left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right) + \frac{{\mu_{{{\text{nf}}}} }}{{T_{\infty } }}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} \left( {1 + \frac{1 }{\beta }} \right) + \frac{{\mu_{{{\text{nf}}}} u^{2} }}{{k_{{\text{p}}} T_{\infty } }} + \frac{{\sigma_{{{\text{nf}}}} B_{0}^{2} }}{{T_{\infty } }}u^{2} {\text{sin}}^{2} \left( \Gamma \right)$$
(19)

where

$$\tau_{{\text{W}}} = \mu_{{{\text{nf}}}} \frac{{\left( {1 + \frac{1 }{\beta }} \right)}}{{\left( {1 + \lambda_{2} } \right)}}\left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0} \quad {\text{and}}\quad q_{{\text{W}}} = - k_{{{\text{nf}}}} \left( {1 + \frac{16}{3}\frac{{\sigma^{*} T_{\infty }^{3} }}{{k^{*} \nu \left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}} \right)\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0}$$
(20)

Using the dimensionless parameters defined in Eq. (13), we get the following:

$$C_{{\text{f}}} {\text{Re}}_{{\text{x}}}^{\frac{1}{2}} = \frac{{\left( {1 + \frac{1 }{\beta }} \right)}}{{\left( {1 + \lambda_{2} } \right)\varphi_{1} }}f^{\prime\prime}\left( 0 \right),\;{\text{Nu}}_{{\text{x}}} {\text{Re}}_{{\text{x}}}^{{ - \frac{1}{2}}} = - \left( {1 + N_{{\text{r}}} } \right)\varphi_{5} \theta^{\prime}\left( 0 \right)$$
(21)
$$N_{{\text{G}}} = {\text{Re}}\left[ {\varphi_{5} \left( {1 + N_{{\text{r}}} } \right)\theta^{{\prime}{2}} + \frac{{B_{{\text{K}}} }}{{\varphi_{1} \Omega }}\left( {\left( {1 + \frac{1 }{\beta }} \right)f^{{\prime\prime}{2}} + Kf^{{\prime}{2}} + M\varphi_{1} \varphi_{4} {\text{sin}}^{2} \left( \Gamma \right){ }f^{{\prime}{2}} } \right)} \right]$$
(22)

where \({\text{Re}}_{{\text{x}}} = \frac{{x U_{{\text{W}}} }}{\nu }\) denotes the local Reynolds number depending on the stretching velocity, \(N_{{\text{G}}} = \frac{{E_{{\text{G}}} T_{\infty }^{2} a^{2} }}{{k_{{\text{f}}} \left( {T_{{\text{W}}} - T_{\infty } } \right)^{2} }}\) denotes the entropy generation dimensionless factor, \({\text{Re}} = \frac{{U_{{\text{W}}} a^{2} }}{\nu x}\) denotes the Reynolds number, \(\Omega = \frac{{\left( {T_{{\text{W}}} - T_{\infty } } \right)}}{{T_{\infty } }}\) denotes difference in temperature parameter, and \(B_{{\text{K}}} = \frac{{\mu_{{\text{f}}} U_{{\text{W}}}^{2} }}{{k_{{\text{f}}} \left( {T_{{\text{W}}} - T_{\infty } } \right)}}\) denotes the Brinkman number.

Numerical solution procedure

Shooting method

Obtaining the exact analytical solutions from highly nonlinear problems is considerably difficult. Thus, the shooting method is employed via bvp4c in MATLAB, which is a finite difference code that implements the three-stage Lobatto–Illa formula, which is fourth-order accurate uniformly in the interval of integration. The mesh selection is based on the residual of the continuous solution. More details on the theoretical and practical backgrounds of bvp4c can be found in [55].

Before using the shooting method, higher-order ODEs must be converted into a set of first-order ODEs. Let

$$f = y\left( 1 \right);\quad f^{\prime } = y\left( 2 \right); \quad f^{\prime \prime } = y\left( 3 \right); \quad f^{\prime \prime \prime } = y\left( 4 \right) \quad f^{{{\prime \prime \prime \prime }}} = yy1; \quad \theta = y\left( 5 \right) \quad \theta^{\prime } = y\left( 6 \right); \quad \theta^{\prime \prime } = yy2.$$
(23)
$$yy1 = \frac{{\varphi_{1} \varphi_{2} \left( {1 + \lambda_{2} } \right)}}{{\beta_{3} y\left( 1 \right)}}\left( { - \beta_{1} \left( {y\left( 1 \right)^{2} y\left( 4 \right) - 2y\left( 1 \right)y\left( 2 \right)y\left( 3 \right)} \right) + \frac{1}{{\varphi_{1} \varphi_{2} \left( {1 + \lambda_{2} } \right)}}\left( {\left( {1 + \frac{1 }{\beta }} \right)y\left( 4 \right) + \beta_{3} y\left( 3 \right)^{2} } \right) - \frac{K}{{\varphi_{1} \varphi_{2} }}y\left( 2 \right) - M\frac{{\varphi_{4} }}{{\varphi_{2} }}{\text{sin}}^{2} \left( \Gamma \right){ }y\left( 2 \right) - { }y\left( 2 \right)^{2} + y\left( 1 \right)y\left( 3 \right)} \right)$$
(24)
$$yy2 = - \frac{1}{{\varphi_{5} \frac{1}{{{\text{Pr}}}} + N_{{\text{r}}} }}\left( {\varphi_{3} y\left( 1 \right)y\left( 6 \right) + Qy\left( 5 \right) + \frac{{{\text{Ec}}}}{{\varphi_{1} }}y\left( 3 \right)^{2} + N_{{\text{t}}} \varphi_{3} y\left( 6 \right)^{2} + \varphi_{4} M{\text{Ec}} {\text{sin}}^{2} \left( \Gamma \right){ }y\left( 2 \right)^{2} } \right)$$
(25)
$$y0\left( 2 \right) = 1 + \Lambda y0\left( 3 \right),\;y0\left( 1 \right) = S,\;y0\left( 6 \right) = - {\text{Bi}}_{{\text{T}}} \left( {1 - y0\left( 5 \right)} \right),\;yinf\left( 2 \right) \to 0,\;yinf\left( 5 \right) \to 0$$
(26)

Validation of the numerical code

To authenticate the current study, the current findings were tested against previous studies [8, 44, 49, 56,57,58,59]; the comparisons are listed in Tables 4 and 5. Overall, the agreement with previous studies provides confidence to proceed with the current study.

Table 4 Comparing the values of \(- f^{\prime\prime} \left( 0 \right)\) with different values of S for \(\varphi = \beta_{1} = \lambda_{2} = \beta_{3} = K = M = \Lambda = 0.\)
Full size table
Table 5 Comparing the values of \(- \theta^{^{\prime}} \left( 0 \right)\) with different values of the Prandtl number for \(\varphi = \beta_{1} = \lambda_{2} = \beta_{3} = K = M = N_{{\text{r}}} = Q = {\text{Ec}} = N_{{\text{t}}} = \Lambda = S = {\text{Bi}}_{{\text{T}}} = 0\)
Full size table

Results and discussion

The effects of the parameters controlling the flow on Casson–Maxwell, Casson–Jeffrey, and Casson–Oldroyd-B copper-engine oil binary nanofluids in a PTSC are presented in Figs. 3–27 and Tables 6, 7. The objectives of this study are to compare the three nanofluids and to determine the parameters that improve the efficiency of the device. The default parameter values are taken as follows: \(\beta = 1; \beta_{1} = \beta_{3} = \lambda_{2} = 0.5;K = 0.6;M = 0.2; \Gamma = \frac{\pi }{2}; S = 0.2,\Lambda = 0.3494; \varphi = 0.2;{\text{Pr}} = 7; N_{{\text{r}}} = {\text{Ec}} = 0.2; Q = 0.1; N_{{\text{t}}} = 0.15; {\text{Bi}}_{{\text{T}}} = 0.1;{\text{Re}} = B_{{\text{K}}} = 5; \;{\text{and}}\;{ }\Omega = 0.5; \;{m = 3}\)

Fig. 3
figure 3

The effect of β on f′

Full size image
Fig. 4
figure 4

The effect of β on θ

Full size image
Fig. 5
figure 5

The effect of β on NG

Full size image
Fig. 6
figure 6

The effect of K on f′

Full size image
Fig. 7
figure 7

The effect of K on θ

Full size image
Fig. 8
figure 8

The effect of K on NG

Full size image
Fig. 9
figure 9

The effect of Λ on f′

Full size image
Fig. 10
figure 10

The effect of Λ on θ

Full size image
Fig. 11
figure 11

The effect of Λ on NG

Full size image
Fig. 12
figure 12

The effect of φ on f′

Full size image
Fig. 13
figure 13

The effect of φ on θ

Full size image
Fig. 14
figure 14

The effect of φ on NG

Full size image
Fig. 15
figure 15

The effect of m on θ

Full size image
Fig. 16
figure 16

The effect of m on NG

Full size image
Fig. 17
figure 17

The effect of M on f′

Full size image
Fig. 18
figure 18

The effect of M on θ

Full size image
Fig. 19
figure 19

The effect of M on NG

Full size image
Fig. 20
figure 20

The effect of Γ on f′

Full size image
Fig. 21
figure 21

The effect of Γ on θ

Full size image
Fig. 22
figure 22

The effect of Γ on NG

Full size image
Fig. 23
figure 23

The effect of BiT on θ

Full size image
Fig. 24
figure 24

The effect of BiT on NG

Full size image
Fig. 25
figure 25

The effect of Nt on θ

Full size image
Fig. 26
figure 26

The effect of Re on NG

Full size image
Fig. 27
figure 27

The effect of BK on NG

Full size image
Table 6 Computing skin friction constant \(C_{{\text{f}}}\) values
Full size table
Table 7 Computing local Nusselt number \({\text{Nu}}_{{\text{x}}}\) values
Full size table

Effect of Casson parameter \(\beta\)

When the Casson parameter \(\beta\) is increased, the resistance to the flow also increases; consequently, a reduction in velocity is presented in Fig. 3. The Casson–Maxwell nanofluid exhibited the greatest resistance among the three binary nanofluids. The decrease in velocity extends the time allowed for the fluid to gain more heat, resulting in improved heat transferability. As presented in Fig. 4, the Casson–Maxwell nanofluid is the most enhanced in terms of heat transfer capabilities of the three binary nanofluids. Figure 5 shows that the entropy generation decreased with the increasing \(\beta\) as the increase in \(\beta\) reduces the rheological features, resulting in a faster shearing along the surface [60, 61]. At the wall, the Casson–Maxwell nanofluid had the highest \(N_{{\text{G}}}\), followed by the Casson–Jeffrey nanofluid, and then the Casson–Oldroyd–B nanofluid, whereas far from the wall, the Casson–Oldroyd–B nanofluid had the highest \(N_{{\text{G}}}\), followed by the Casson–Jeffrey nanofluid, and then the Casson–Maxwell nanofluid.

Effect of the porosity parameter \(K\)

Large values of the porosity parameter contribute against the fluidity, resulting in a reduction in the velocity profile and an increase in both heating and irreversible energy (Figs. 6–8). Physically, the increase in the porosity parameter decreases nanoparticle collision owing to an increase in the size of the flow pore, inhibiting heat generation. The viscous force controls the buoyancy force, thereby decreasing the flow magnitude. The entropy increased owing to existence of considerable temperature gradient at the surface [8, 38]. The most affected of the three nanofluids was the Casson–Jeffrey nanofluid, with the highest heat transfer and an entropy level close to that of the Casson–Maxwell nanofluid. The Casson–Oldroyd-B nanofluid exhibited the lowest heat transfer and highest entropy. The effect of \(K\) on the velocity, temperature, and entropy profiles is the same as that reported by previous studies [8, 38, 45].

Effect of the velocity slip parameter \(\Lambda\)

The friction force between the flow and the surface increases with increasing \(\Lambda\), leading to an increase in viscosity and hence a decrease in velocity (Fig. 9). The decrease in velocity is accompanied by an increase in temperature owing to less heat being transported from one point to another (Fig. 10). Figure 11 clearly shows that the entropy decreases with increasing \(\Lambda\). Generally, no-slip boundary conditions produce large velocity and temperature gradients, causing high entropy values. However, slip boundary conditions as in this study cause reduction in entropy close to the stretching wall [7, 8]. Although the Casson–Jeffrey nanofluid exhibited a substantial heat profile enhancement, the Casson–Oldroyd-B nanofluid continued to exhibit low heat transfer and a high irreversible energy drain. The effect of \(\Lambda\) on the velocity, temperature, and entropy profiles is the same as that reported by previous studies [7, 8, 38, 45, 52].

Effect of the nanoparticle concentration parameter \(\varphi\)

The fluid viscosity increases with increasing \(\varphi\) owing to an increase in nanoparticle concentration and friction escalations, resulting in a decrease in velocity, as shown in Fig. 12. Because fluid velocity is critical for heat transfer, the reduction in velocity causes heat to accumulate, and the temperature profile increases as observed in Fig. 13. It is expected that the entropy increases owing to heat accumulation [7, 8], which is confirmed in Fig. 14. Of the three nanofluids, Casson–Maxwell nanofluid benefited the most, as it underwent the highest improvement in terms of heat transfer. The effect of \(\varphi\) on the velocity, temperature, and entropy profiles is the same as that reported by previous studies [7, 8, 38, 45, 52].

Effect of the nanoparticle shape factor \(m\)

Increasing shape factor values \(m\) by changing the nanoparticle shapes improves heat transferability. Figures 15 and 16 demonstrate that a lamina shape is the most effective in terms of heat transfer while causing a negligible increase in irreversible energy. Among the three nanofluids, the Casson–Maxwell nanofluid exhibited the highest heat transfer after increasing the shape factor. The effect of \(m\) on the temperature and entropy profiles is the same as that reported by a previous study [52].

Effect of the magnetic number \(M\)

Figure 17 shows the effect of \(M\) on the velocity profile. As the strength of the magnetic field increases, the drag force increases, which reduces the velocity of the nanofluid flow. Figure 18 confirms the fact that temperature distribution increases with increasing magnetic field because less heat can be transferred from one point to another with decreasing fluid movement. The lack of heat transfer in the system causes a natural increase in entropy [7], which is seen in Fig. 19. The Casson–Oldroyd-B nanofluid exhibited the lowest heat transfer. The effect of M on the velocity, temperature, and entropy profiles is the same as that reported by a previous study [7].

Effect of the magnetic angle of inclination \(\Gamma\)

As \(\Gamma\) increases from \(\frac{\pi }{6}\) to \(\frac{\pi }{2}\), the normal magnetic forces increase, resulting in a decrease in velocity. The reduced velocity will cause the temperature distribution to increase owing to low heat relocation from the surface toward the flow. The heat accumulation will intensify entropy generation in the system. Heat transferability and entropy are therefore increased, with the Casson–Maxwell nanofluid exhibiting the highest heat transferability as seen in Figs. 20–22. The effect of \(\Gamma\) on the velocity, temperature, and entropy profiles is the same as that reported by a previous study [7].

Effect of the thermal Biot number \({\text{Bi}}_{{\text{T}}}\)

The thermal Biot number describes the ratio between thermal resistances inside the fluid and at the surface. Hence, large values of \({\text{Bi}}_{{\text{T}}}\) amplify the thermal resistance inside the flow, which increases the fluid temperature. The increase in \({\text{Bi}}_{{\text{T}}}\) values leads to an increase in the heat transfer rate and the entropy generated by the system [7], which is illustrated in Figs. 23 and 24. Of the three nanofluids, the Casson–Oldroyd-B nanofluid exhibits the lowest heat transfer. The effect of \({\text{Bi}}_{{\text{T}}}\) on the temperature and entropy profiles is the same as that reported by previous studies [7, 45].

Effect of thermophoretic parameter \(N_{{\text{t}}}\)

Higher values of the thermophoretic parameter indicate larger thermophoretic force, which appears in suspended mixtures of particles and fluids such as nanofluids. This phenomenon is caused by the temperature gradient which leads to a movement of fluid particles in the hot zone toward the cold region. Hence, heat transfer capabilities increase as seen in Fig. 25. The highest heat transfer was observed in the Casson–Maxwell and Casson–Jeffrey nanofluids.

Effects of the Reynolds number Re and the Brinkman number \(B_{{\text{K}}}\)

At high values of Re, the resistive forces replace the viscous forces. Further, the Brinkman number measures the dominant effects responsible for variation in irreversible energy drain. It determines whether heat is transferred or dissipated through conduction at the surface. The increase in \(B_{{\text{K}}}\) values as in this case, causes an increase in entropy generation which indicates the dominant effect of dissipation [7]. Notably, increasing Re or \(B_{{\text{K}}}\) increases the irreversible energy drain, as seen in Figs. 26 and 27. The difference among the three nanofluids was found to be marginal. The effects of Re and \(B_{{\text{K}}}\) on the velocity, temperature, and entropy profiles are the same as that reported by previous studies [7, 8, 38, 45].

Conclusions

The copper-engine oil Casson–Maxwell, Casson–Jeffrey, and Casson–Oldroyd-B binary nanofluids were compared in PTSC settings. Porosity, constant inclined magnetic field, heat source, thermal radiation, viscosity dissipation, and thermophoresis were considered. Analysis was conducted by formulating the continuity, momentum, and energy equations. Subsequently, similarity variables were used to transform the partial differential equations into ODEs, which were then solved using the shooting method. There are various practical applications for the presented models, including solar water pumps, solar-powered ships, solar street lights, solar energy plates, and photovoltaic cells. Overall, an increase in PTSC efficiency can be achieved by decreasing the nanofluid velocity and boosting the nanofluid temperature while maintaining reasonable entropy generation. The key conclusions of this numerical study are as follows:

  • The parameters that reduced the velocity profile are \(\beta\), \(K\), \(\Lambda\), \(\varphi\), \(M\), and \(\Gamma\).

  • The parameters that enhanced heat transfer are \(\beta\), \(K\), \(\Lambda\), \(\varphi\), \(m\), \(M\), \(\Gamma\), \({\text{Bi}}_{{\text{T}}}\), and \(N_{{\text{t}}}\).

  • Entropy generation increased with \(K\), \(\varphi\), \(m\), \(M\), \(\Gamma\), \({\text{Bi}}_{{\text{T}}}\), Re, and \(B_{{\text{K}}}\) but decreased with \(\beta\) and \(\Lambda\).

  • The skin friction values increased with \(\varphi\), \(K\), \(M\), \(\Gamma\), and \(S\) but decreased with \(\beta\) and \(\Lambda\).

  • The local Nusselt number values increased with \(\varphi\), \(\Lambda\), Pr, \(N_{{\text{r}}}\), \(Bi_{{\text{T}}}\), and \(m\) but decreased with \(\beta\), \(K\), \(M\), \(Q\), \(N_{{\text{t}}}\), and \(E_{{\text{c}}}\).

  • The Casson–Oldroyd-B nanofluid consistently exhibited the lowest heat transfer and highest generated entropy.

  • The Casson–Jeffrey and Casson–Maxwell nanofluids responded differently to the change in parameters. Casson–Maxwell had better heat transfer with \(\beta\), \(\varphi\), \(m\), \(M\), \(\Gamma\), \(N_{{\text{t}}}\), and \({\text{Bi}}_{{\text{T}}}\), whereas Casson–Jeffrey had better heat transfer with \(K\) and \(\Lambda\).

  • From the aforementioned discussion, we conclude that the Casson–Maxwell and Casson–Jeffrey nanofluids exhibit similar performance in a PTSC setting, with a slight preference to use the Casson–Maxwell nanofluid.

Limitations and further research

This study is limited to the three binary nanofluids and PTSC settings mentioned herein. As any different nanofluid will have different properties and can lead to different results. Further, different settings will require different assumptions and boundary conditions, which will also lead to different results.

Further research can be directed toward theoretical investigation of different nanofluid models (e.g., Carreau, Walter-B, etc.) in PTSC settings and their comparison. Additionally, the presented model can be generalized by considering the impact of time-dependent flow and temperature-dependent viscosity, conductivity, and porosity on the performance of PTSCs. It is also important to explore the effect of hybrid nanoparticles on the PTSC performance using different binary nanofluid models.