1 Introduction

Ethanol (IUPAC name), also known as ethyl alcohol, has the molecular formula of C2H5OH. Ethanol is an important chemical with numerous uses; it is used as a solvent, in the synthesis of other organic chemicals, as an additive to automotive gasoline, as a renewable transportation fuel, and as an intoxicating ingredient of many alcoholic beverages and distilled spirits. It is also used as a topical agent to prevent skin infections, in pharmaceutical preparations (e.g., lotions, colognes, etc.), in cosmetics, and in perfumes.

In 2013, a new reference correlation for the thermal conductivity of ethanol was presented by Assael et al. [1], covering for the first time a temperature range from the triple point to 600 K and up to 245 MPa. This was made possible following the development of an accurate equation of state for ethanol by Schroeder et al. [2]. This correlation is currently employed in REFPROP 10.0 [3].

The current ethanol viscosity correlation employed in REFPROP 10.0 [3], was developed in 2005 by Kiselev et al. [4], and is based on a generalized SAFT-DFT/DMT model for the thermodynamic, interfacial, and transport properties of associating fluids applied to n-alkanols. Its estimated uncertainty in the liquid phase along the saturation boundary is approximately 3 %, increasing to 10 % at pressures up to 100 MPa, and estimated as 10 % in the vapor phase.

In a series of recent papers, reference correlations for the viscosity of common fluids [1, 5,6,7,8,9,10,11,12,13,14] were developed that cover a wide range of temperature and pressure conditions, including the gas, liquid, and supercritical phases. In this paper, the methodology adopted in the aforementioned papers is extended to developing a new reference correlation for the viscosity of ethanol.

The analysis we use is based on the best available experimental viscosity data. A prerequisite to the analysis is a critical assessment of the experimental data. Here we define two categories of experimental data: primary data, employed in the development of the correlation, and secondary data, used simply for comparison purposes. According to the recommendation adopted by the Subcommittee on Transport Properties (now known as The International Association for Transport Properties) of the International Union of Pure and Applied Chemistry, the primary data are identified by a well-established set of criteria [15]. These criteria have been successfully employed to establish standard reference values for the viscosity and thermal conductivity of fluids over wide ranges of conditions, with uncertainties in the range of 1 %. However, in many cases, such a narrow definition unacceptably limits the range of the data representation. Consequently, within the primary data set, it is also necessary to include results that extend over a wide range of conditions, albeit with a higher uncertainty, provided they are consistent with other lower uncertainty data or with theory. In all cases, the uncertainty claimed for the final recommended data must reflect the estimated uncertainty in the primary information.

2 The Correlation

The viscosity η can be expressed [1, 5,6,7,8,9,10,11,12,13,14] as the sum of four independent contributions, as

$$\eta \left( {\rho ,{T}} \right) = \eta_{0} \left( {T} \right) + \eta_{1}\left( {T} \right)\,\rho + {\Delta }\eta \left( {\rho ,{T}} \right) + {\Delta }\eta_{{\text{c}}} \left( {\rho ,{T}} \right),$$
(1)

where ρ is the density, T is the absolute temperature, and the first term, η0(Τ) = η(0,Τ), is the contribution to the viscosity in the dilute-gas limit, where only two-body molecular interactions occur. The linear-in-density term, η1(Τ) ρ, known as the initial-density dependence term, can be separately established with the use of the Rainwater–Friend theory [16,17,18] for the transport properties of moderately dense gases. The critical enhancement term, Δηc(ρ,Τ), arises from the long-range density fluctuations that occur in a fluid near its critical point, which contribute to divergence of the viscosity at the critical point. This term for viscosity is significant only in the region very near the critical point, as shown in Vesovic et al. [19] and Hendl et al. [20]. For CO2, Vesovic et al. [19] showed that the enhancement contributes greater than 1 % to the viscosity only in the small region bounded by 0.986 < Tr < 1.019 and 0.642 < ρr < 1.283 (where Tr and ρr denote the reduced temperature and density). Since data close to the critical point are unavailable, Δηc(ρ,Τ) will be set to zero in Eq. 1 and not discussed further. Finally, the term Δη(ρ,T), the residual term, represents the contribution of all other effects to the viscosity of the fluid at elevated densities including many-body collisions, molecular-velocity correlations, and collisional transfer.

Identification of these four separate contributions to the viscosity allows one, to some extent, to treat η0(Τ), and η1(Τ) theoretically. In addition, it is possible to derive information about both η0(Τ) and η1(Τ) from experiment. In contrast, there is little theoretical guidance concerning the residual contribution, Δη(ρ,Τ), and its evaluation is usually based entirely on an empirical equation obtained by fitting experimental data.

Table 1 summarizes, to the best of our knowledge, all the available experimental measurements of the viscosity of ethanol reported in the literature. Table 1 displays the experimental technique, purity, uncertainty as reported by the original authors, number of measurements, as well as the range of temperatures and pressures investigated. From the 275 measurement sets shown in total, 14 were performed at pressures above atmospheric, while the remaining 261 were performed at 0.1 MPa (or near saturation pressure), and mostly over a limited temperature range, at about room temperature.

Table 1 Viscosity measurements of ethanol
Full size table

In this particular case, and because of the very large number of measurements at 0.1 MPa, the primary data were separated into two subcategories: (a) primary data above atmopsheric pressure, and (b) primary data at 0.1 MPa.

In the first data set, we included all measurements performed above atmospheric pressure, the only exceptions being the very high-pressure measurements of (a) Yusa et al. [253] performed in a falling-cylinder viscometer in 1977, and (b) the 1926 Bridgman [282] and 1914 Faust [286] measurements performed in a capillary viscometer, as they deviate more than 20 % from the remaining measurements. Therefore, the primary data set at pressures above atmospheric consists of 11 sets.

In relation to the primary data set of measurements at 0.1 MPa presented in Table 1, the following criteria were employed for selection. As already mentioned in the introduction, ethanol is extensively employed in experimental studies on volumetric and viscometric properties of binary and ternary mixtures, phase equilibria studies, or even acoustical studies. In such studies, although the viscosity of pure ethanol is also measured, the emphasis is on the properties of the mixture, the solution, and the effect of the change in concentration. Hence, in recent literature, there are a very large number of papers that include a single measurement of the viscosity of ethanol at room temperature with inadequate assessments of uncertainty. Therefore, we did not include in the primary data set such articles with a single viscosity measurement at room temperature or near it. Furthermore, as water is the only liquid whose viscosity is known to an uncertainty as low as 0.17 % (at the 95 % confidence level) [15], all measurements in which the authors quote uncertainties of less than 0.2 % (e.g., 0.005 %!), characteristic of investigators that do not understand how to assess their measurement uncertainty, have been placed in the secondary data set. Since we are also interested in low-uncertainty measurements, we also did not consider for the primary data set measurements with quoted uncertainty larger than 2 %.

In conclusion, the viscosity measurements in 0.1 MPa, to be included in the primary data set,

  1. 1.

    must not be a single measurement at room temperature,

  2. 2.

    their quoted uncertainty must be between 0.2 % and 2 %, and

  3. 3.

    the purity of the sample and the technique employed must be stated.

Additionally, we included the vapor-measurements of Reid and Belenyessy [94], Titani [95], Vogel [96], Rappenecker [97] and Pedersen [98] as they are the only ones in the vapor phase. Here we note that Uchiyama [272] reported also 4 measurements in the vapor phase, but they were more than 20 % lower than the aforementioned values, so they were not considered as part of the primary dataset.

We also did not include in the primary data set at 0.1 MPa measurements performed by the cone and plate technique as this is an excellent technique for non-Newtonian fluids, but not particularly accurate for Newtonian ones. We also did not include the one set performed in a moving piston viscometer, as this technique is not fully backed by theory. Moreover, we also excluded 9 sets of measurements that, although satisfied the above criteria, showed very large, unexplainable deviations which were higher than the quoted uncertainty, from the remaining sets: Kumari et al. [111] 10 % deviation, Hema et al. [118] 10 %, Zhang et al. [145] 7 %, Gong et al. [153] 5 %, Li et al. [167] 10 %, Domanska and Laskowska [170] 10 %, Awwad et al. [178] 8 %, Romano et al. [208] 5 %, and Das and Jha [235] 48 %.

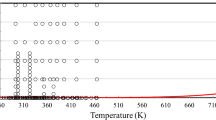
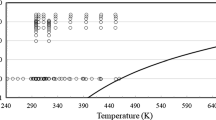
In conclusion, from the 275 sets of measurements shown in Table 1, the primary set is composed of 11 sets under pressure, and 67 sets at 0.1 MPa. Figures 1 and 2 show the ranges of the primary measurements outlined in Table 1, and the phase boundary.

Fig. 1
figure 1

Temperature–pressure ranges of the primary experimental viscosity data for ethanol. (−) saturation curve

Full size image
Fig. 2
figure 2

Temperature–density ranges of the primary experimental viscosity data for ethanol. (−) saturation curve

Full size image

The development of the correlation requires densities; Schroeder et al. [2] in 2014 reviewed the thermodynamic properties of ethanol and developed an accurate, wide-ranging equation of state valid for single-phase and saturation states from 160 K to 650 K at pressures up to 280 MPa, with an uncertainty in density of 0.2 %. We also adopt the values for the critical point and triple point from his equation of state; the critical temperature, Tc, and the critical density, ρc, were taken to be equal to 514.71 K and 273.186 kg·m−3, respectively [2]. The triple point temperature is 159.0 K [2].

2.1 The Dilute-Gas Limit Viscosity Term

The dilute-gas limit viscosity, η0(Τ) is a function only of temperature and can be analyzed independently of all other contributions in Eq. 1. Employing the Chapman-Enskog theory [297], the dilute-gas limit viscosity of a gas of spherical molecules is given as

$$\eta_{0} (T) = 0.02669\frac{{\sqrt {MT} }}{{\sigma^{2} \Omega^{(2,2)} }},$$
(2)

where M (46.0684 g‧mol−1) is the molar mass, the collision diameter σ in nm is the smallest separation distance where the intermolecular potential function is equal to zero, T is the temperature in K, and the resulting viscosity is in μPa·s. Ω(2,2) is a collision integral that depends upon the potential function.

In the case of nonpolar gases, Neufeld et al. [298] developed an empirical correlation for the Lennard–Jones (12-6), Ω(2,2) collision integral, as a function of the dimensionless temperature T* = T/(ε/kB) (where kB is Boltzmann’s constant and ε is the Lennard–Jones energy parameter), as

$$\Omega_{{{\text{LJ}}}}^{(2,2)} (T^*) = 1.16145(T^*)^{ - 0.14874} + 0.52487\,{\text{e}}^{ - 0.7732T^{\ast}} + 2.16178\,{\text{e}}^{ - 2.43787T^{\ast}} - 6.435 \times 10^{ - 4} (T^*)^{0.14874} \sin \left[ {18.0323(T^*)^{ - 0.7683} - 7.27371} \right].$$
(3)

The subscript LJ refers to the Lennard–Jones potential.

For polar gases, it is more appropriate [299] to employ the Stockmayer (12-6-3) potential φSM(r)

$$\varphi_{{{\text{SM}}}} (r) = 4\varepsilon \left[ {\left( {\frac{\sigma }{r}} \right)^{12} - \left( {\frac{\sigma }{r}} \right)^{6} + \delta \left( {\frac{\sigma }{r}} \right)^{3} } \right].$$
(4)

Here, δ, accounts for the anisotropic charge distribution from which the polarity of a particle characterized by its dipole moment μ arises, as well as the angles of inclination of the dipole axis to the line joining the centers of the two molecules and the azimuthal angle between them [299].

Xiang et al. [300] fitted the values for the Stockmayer (12-6-3) collision integral, \(\Omega_{{{\text{SM}}}}^{(2,2)}\), tabulated by Monchick and Mason [301], to an empirical function that reduces to the Lennard–Jones (12-6) form when the dipole moment, μ, is zero and obtained.

$$\Omega_{{{\text{SM}}}}^{(2,2)} = \Omega_{{{\text{LJ}}}}^{(2,2)} \left[ {1\; + \;\frac{{\delta^{2} }}{{1 + a_{1} \delta^{6} }}\Omega_{\delta }^{(2,2)} } \right],$$
(5)
$${\text{with}}\;\Omega_{\delta }^{(2,2)} = a_{2} \left( {T^{\ast} } \right)^{{a_{3} }} + a_{4} \exp \left( {a_{5} T^{\ast} } \right) + a_{6} \exp \left( {a_{7} T^{\ast} } \right),$$
(6)

with coefficients a1 − a7, given in Table 2.

Table 2 Coefficients and parameters for Eqs. 5, 6, 8, and 11
Full size table

In Eq. 5, the parameter δ can be obtained by the expression [301]

$$\delta = \frac{{3.6220\mu^{2} }}{{\sigma^{3} (\varepsilon /k_{{\text{B}}} )}},$$
(7)

where the dipole moment μ is in Debyes, σ in nm, and ε/kB in K.

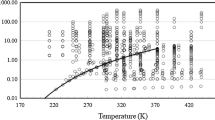
Equations 2, 3, 5 to 7, form a consistent scheme for the calculation of the dilute-gas limit viscosity as a function of the temperature. The only unknowns (as μ = 1.6909 Debyes [302]), are the σ and ε parameters, which can be obtained by fitting all the available experimental vapor viscosity data at very low pressures (Reid and Belenyessy [94], Golubev [31], Titani [95], Vogel [96], Rappenecker [97], Pedersen [98]), and also the vapor-measurements of Khalilov [279] from the secondary set). The values obtained are σ = 0.479 nm and ε/kB = 265 K (also shown in Table 2). Figure 3 shows the gas phase low-pressure data and the calculated results for η0 using Eqs. 2, 3, 5 to 7. The values calculated by the correlation of Kiselev et al. [4], as presented in REFPROP 10 [3], agree very well within the range of the experimental data, but deviate by up to 5 % outside this range—see also Fig. 4). The dilute-gas contribution in the Kiselev et al. [4] correlation was developed by fitting a polynomial to the experimental data. As the range of experimental data is limited, having theoretical guidance provides physically reasonable behavior upon extrapolation outside of the range of data.

Fig. 3
figure 3

Dilute-gas viscosity, η0, as a function of the temperature: Reid and Belenyessy [94] (□), Golubev [31] (●),Titani [95] (O), Vogel [96] (■), Rappenecker [97] (△), Pedersen [98] (×), Khalilov [279] (◊), and correlation of Kiselev et al. [4] (- -), Eqs. 2, 3, 5 to 7 (─)

Full size image
Fig. 4
figure 4

Dilute-gas viscosity deviations from the values obtained by the scheme of Eqs. 2, 3, 5 to 7, as a function of the temperature: Reid and Belenyessy [94] (□), Golubev [31] (●), Titani [95] (O), Vogel [96] (■), Rappenecker [97] (△), Pedersen [98] (×), Touloukian et al. [303] ( +), Khalilov [279] (◊), and values calculated from Eq. 8 (▬), and correlation of Kiselev et al. [4] (- -)

Full size image

For ease of use in calculations, η0 was fitted as:

$$\eta_{0} (T_{{\text{r}}} ) = \frac{{\sum\limits_{i = 0}^{5} {b_{i} T_{{\text{r}}}^{i} } }}{{\sum\limits_{i = 0}^{1} {c_{i} T_{{\text{r}}}^{i} } }},$$
(8)

where the units for η0 are μPa‧s, the reduced temperature is Tr = (T/Tc), and the coefficients bi and ci are in Table 2. Equation 8 reproduces the values calculated by Eqs. 2, 3, 5 to 7 to within 0.05 % up to 1000 K, and thus it will be employed hereafter. Figure 4 shows the deviations of the measurements from the scheme of Eqs. 2, 3, 5 to 7. In the same figure the values obtained by Eq. 8 are shown, as well as the values proposed in 1975 by Touloukian et al. [303]. The values in Touloukian et al. [303] are tabulated recommended values based on analysis of experimental data. The agreement in the range of existing data, is within 2 %.

2.2 The Initial-Density Dependence Viscosity Term

To represent the initial-density dependence of viscosity term, η1ρ, in Eq. 1, we use the model proposed by Vogel et al. [305] which expresses the second viscosity virial coefficient Bη(T) in m3‧kg−1, as

$${B}_{\eta } ({T}) = \frac{{\eta_{1} ({T})}}{{\eta_{0} ({T})}}.$$
(9)

In Eq. 9, when the dilute-gas limit viscosity, η0(Τ), is expressed in μPa·s, the initial-density dependence viscosity term, η1(Τ), has units μPa·s‧m3‧kg−1. The second viscosity virial coefficient can be obtained according to the theory of Rainwater and Friend [16, 17] as a function of a reduced second viscosity virial coefficient, \({B}_{\eta }^{\ast} ({T}^{\ast} )\), as

$${B}_{\eta }^{\ast} ({T}^{\ast} ) = \frac{{{B}_{\eta } ({T})\;M}}{{N_{{\text{A}}} \;\sigma^{3} }},$$
(10)
$${\text{where}}\;\;\;{B}_{\eta }^{\ast} ({T}^{\ast} ) = \sum\limits_{\iota = 0}^{6} {d_{i} (T^{\ast} )^{ - 0.25i} } + d_{7} (T^{\ast} )^{ - 2.5} + d_{8} (T^{\ast} )^{ - 5.5} .$$
(11)

In Eq. 10, M is the molar mass 46.0684 g‧mol−1, the scaled temperature is T* = T/(ε/kB), and NA is the Avogadro constant. The coefficients di from Vogel et al. [304] are given in Table 2.

2.3 The Residual Term

The residual viscosity term, Δη(ρ,T), represents the contribution of all other effects to the viscosity of the fluid at elevated densities including many-body collisions, molecular-velocity correlations, and collisional transfer. An attempt to employ the hard-sphere model proposed by Assael et al. [306] was not very successful, as the present data cover the gas, liquid, and supercritical regions. Hence, it was preferred to evaluate this term almost entirely on experimentally obtained data, as discussed in the next paragraph.

The procedure adopted during this analysis used symbolic regression software [307] to fit all the primary data to the residual viscosity as a function of the reduced temperature, Tr = T/Tc and reduced density, ρr = ρ/ρc. In addition, we adopted a form suggested by the hard-sphere model employed by Assael et al. [306] Δη(ρr,Tr) = (ρr2/3Tr1/2)F(ρr,Tr), where the fitting software was used to determine the functional form for F(ρr,Tr). For this task, the dilute-gas limit and the initial density dependence term were calculated for each experimental point, employing Eqs. 8 to 11, and subtracted from the experimental viscosity to obtain the residual term, Δη(ρr,Tr). The density values were obtained by the Schroeder et al. [2] equation of state. The final equation was

$$\Delta \eta (\rho ,T) = (\rho_{{\text{r}}}^{2/3} T_{{\text{r}}}^{1/2} )\left\{ {8.32575272\rho_{{\text{r}}} + 9.66535242 \times 10^{ - 2} \frac{{\rho_{{\text{r}}}^{8} }}{{T_{{\text{r}}}^{4} (1 + \rho_{{\text{r}}}^{2} ) - T_{{\text{r}}}^{2} }}} \right\},$$
(12)

where Δη is in μPa‧s.

2.4 Comparison with Data

The final correlation model consists of Eqs. 1, and 8 to 12 with the critical enhancement term set to zero. Tables 3 and 4 summarize comparisons of the primary data with the correlation—Table 3 for the primary data under pressure, and Table 4 for the primary data at 0.1 MPa. We define the percent deviation as PCTDEV = 100(ηexp − ηfit)/ηfit, where ηexp is the experimental value of the viscosity and ηfit is the value calculated from the correlation. The average absolute percent deviation (AAD) is found with the expression AAD = (∑|PCTDEV|/n, where the summation is over all n points, the bias percent is found with the expression BIAS = (∑PCTDEV)/n.

Table 3 Evaluation of the ethanol viscosity correlation for the primary data at pressures above atmospheric
Full size table
Table 4 Evaluation of the ethanol viscosity correlation for the primary data at 0.1 MPa
Full size table

The average absolute percentage deviation of the fit for the primary data under pressure is 1.46 %, with a bias of 0.44 %, while for the primary data at 0.1 MPa is 1.12 %, with a bias of 0.07 %, respectively. The estimated uncertainty of the correlation in the temperature range 160 to 620 K and up to 102 MPa is 4.2 % (at the 95 % confidence level). Due to the omission of a critical enhancement term, in the near vicinity of the critical point the uncertainty can be very large since the viscosity becomes infinite at the critical point.

As the primary dataset is composed of 11 sets under pressure and 67 sets at 0.1 MPa, we decided to show only the primary datasets under pressure in figure form. Hence, Fig. 5 shows the relative deviations of the primary viscosity data under pressure, of ethanol from the values calculated by Eqs. 1, 8 to 12, as a function of temperature, while Figs. 6 and 7 show the same deviations but as a function of the pressure and the density. It should be noted that in these three figures we also included the measurements at 0.1 MPa of Komarenko et al. [93] as they are the only ones going down to 160 K.

Fig. 5
figure 5

Relative deviations of primary experimental data under pressure of ethanol from the values calculated by the present model, Eqs. 1, 8 to 12, as a function of temperature. Μendo-Sanchez et al. [21] (△), Zhu et al. [22] (▲), Ono et al. [23] (◊), Ono et al. [24] (◆), Pimentel-Rodas et al. [25] (), Zéberg-Mikkelsen et al. [26] (●), Assael and Polimatidou [27] (O), Papaioannou and Panayiotou [28] (), Papaioannou et al. [29] (), Tanaka et al. [30] (□), Golubev [31] ( ×). The values of Komarenko et al. [93] ( +) at 0.1 MPa are also included

Full size image
Fig. 6
figure 6

Relative deviations of primary experimental data under pressure of ethanol from the values calculated by the present model, Eqs. 1, 8 to 12, as a function of pressure. Μendo-Sanchez et al. [21] (△), Zhu et al. [22] (▲), Ono et al. [23] (◊), Ono et al. [24] (◆), Pimentel-Rodas et al. [25] (), Zéberg-Mikkelsen et al. [26] (●), Assael and Polimatidou [27] (O), Papaioannou and Panayiotou [28] (), Papaioannou et al. [29] (), Tanaka et al. [30] (□), Golubev [31] ( ×). The values of Komarenko et al. [93] ( +) at 0.1 MPa are also included

Full size image
Fig. 7
figure 7

Relative deviations of primary experimental data under pressure of ethanol from the values calculated by the present model, Eqs. 1, 8 to 12, as a function of density. Μendo-Sanchez et al. [21] (△), Zhu et al. [22] (▲), Ono et al. [23] (◊), Ono et al. [24] (◆), Pimentel-Rodas et al. [25] (), Zéberg-Mikkelsen et al. [26] (●), Assael and Polimatidou [27] (O), Papaioannou and Panayiotou [28] (), Papaioannou et al. [29] (), Tanaka et al. [30] (□), Golubev [31] (×). The values of Komarenko et al. [93] ( +) at 0.1 MPa are also included

Full size image

Table 5 shows the average absolute percent deviation (AAD) and the bias for the secondary data. In most cases the agreement is within the uncertainty of the proposed correlation. Finally, Fig. 8 shows a plot of the viscosity of ethanol as a function of the temperature for different pressures. The plot demonstrates the physically reasonable extrapolation behavior at pressures higher than 102 MPa, and at temperatures that exceed the 620 K limit of the current measurements.

Table 5 Evaluation of the ethanol viscosity correlation for the secondary data
Full size table
Fig. 8
figure 8

Viscosity of ethanol as a function of the temperature for different pressures

Full size image

2.5 A Correlation for the Primary Data at 0.1 MPa

As the viscosity of ethanol at 0.1 MPa, η(Τ,0.1 ΜPa), is very often used, the primary data at 0.1 MPa were fitted to the following equation

$$\eta (T,0.1\;{\text{MPa}}) = \exp \left( { - 0.721846\;\theta^{4} + 5.91281\;\theta^{3} - 15.0092\;\theta^{2} + 20.9305\;\theta - 3.62716} \right),$$
(13)

where the viscosity is in (μPa·s) and θ = 273.15/T. The above equation is valid from the triple point (159 K) to the 0.1 MPa boiling temperature of 351.57 K, with an estimated uncertainty of 2.3 % (at the 95 % confidence level). Figure 9 shows the relative deviations of primary experimental data at 0.1 MPa of ethanol from the values calculated by Eq. 13, as a function of temperature.

Fig. 9
figure 9

Relative deviations of primary experimental data at 0.1 MPa of ethanol from the values calculated by Eq. 13, as a function of temperature

Full size image

3 Recommended Values

In Table 6, viscosity values are given along the saturated liquid and vapor curves, calculated from the full correlation given by Eq. 1 and Eqs. 8 to 12 between 160 K and 510 K, while in Table 7 viscosity values are given for temperatures between 180 K and 600 K at selected pressures. Saturation pressure and saturation density values for selected temperatures, as well as the density values for the selected temperature and pressure, are obtained from the equation of state of Schroeder et al. [2]. The calculations in Tables 6 and 7 are performed at the given temperatures and densities. For computer verification of values, the following points may be used for the given T, ρ conditions: T = 300 K, ρ = 0 kg·m−3, η = 8.9893 μPa·s, T = 300 K, ρ = 10.0 kg·m−3, η = 8.9382 μPa·s, T = 300 K, ρ = 850.0 kg·m−3, η = 1682.72 μPa·s.

Table 6 Viscosity values of ethanol along the saturation curve, calculated by the present scheme
Full size table
Table 7 Viscosity values of ethanol at selected temperatures and pressures, calculated by the present scheme
Full size table

4 Conclusions

A new wide-ranging correlation for the viscosity of ethanol was developed based on critically evaluated experimental data and theoretical results. The average absolute percentage deviation of the fit for the primary data under pressure is 1.46 %, with a bias of 0.44 %, while for the primary data at 0.1 MPa is 1.12 %, with a bias of 0.07 %, respectively. The estimated uncertainty of the correlation in the liquid and supercritical regions for the temperature range 160 K to 620 K and up to 102 MPa is 4.2 % (at the 95 % confidence level). The estimated uncertainty in the gas phase at atmospheric pressure is 2 %. Furthermore, for calculating viscosity values at 0.1 MPa, an additional correlation is proposed, valid from the triple point (159 K) to the boiling point (351.57 K), at 0.1 MPa, with an estimated uncertainty of 2.3 % (at the 95 % confidence level).