Abstract
The present paper provides first empirical evidence on the relationship between market size and the number of firms in the healthcare industry for a transition economy. We estimate market-size thresholds required to support different numbers of suppliers (firms) for three occupations in the healthcare industry in a large number of distinct geographic markets in Slovakia, taking into account the spatial interaction between local markets. The empirical analysis is carried out for three time periods (1995, 2001 and 2010) which characterise different stages of the transition process. Our results suggest that the relationship between market size and the number of firms differs both across industries and across periods. In particular, we find that pharmacies, as the only completely liberalised market in our dataset, experience the largest change in competitive behaviour during the transition process. Furthermore, we find evidence for correlation in entry decisions across administrative borders, suggesting that future market analysis should aim to capture these regional effects.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Health systems in OECD countries have seen a steady increase in health spending over the last 50 years. Expenditure in this sector has tended to grow at a faster rate than Gross Domestic Product (GDP). While health spending accounted for less than 4% of GDP on average across OECD countries in 1960, this share increased to 8.9% in 2013 [1]. The health spending share of the GDP grew particularly rapidly in the United States, rising from about 5% in 1960 to 16.4% in 2013. A similar tendency can be seen in Central European countries, where healthcare services today represent one of the most important sectors of the modern economy (with 11.0% of GDP in Germany, 10.1% in Austria, 7.6% in the Slovak Republic and 7.1% in the Czech Republic, for instance). The size of these industries and their long-run trends suggest that understanding their structure, conduct and performance is important not only for the performance of the healthcare industry, but also for understanding the economy as a whole.
The present paper is based on, and extends, an approach pioneered by Bresnahan and Reiss [2]. According to Bresnahan and Reiss [2], the relationship between market structure (i.e., the number of firms) and market size (e.g., population) speaks to the nature and intensity of competition between firms. This approach uses a simple, general entry condition to model market structure. It postulates that if the population (per-firm) required to support a given number of firms in a market grows with the number of firms, then competition must be getting tougher. Intense competition reduces profit margins. A larger population is, thus, necessary for generating sales required to cover entry costs.Footnote 1 Thus, the key data required for applying the Bresnahan–Reiss (entry-threshold) approach are both minimal and commonly available: market structure (i.e., the number of firms) and population in several local markets.
Note, however, that the entry-threshold approach assumes local markets to be fully isolated. The equilibrium in one market must be independent—in terms of demand and competition—of other markets. While this might be a plausible assumption in some sparsely populated (rural) regions,Footnote 2 the high population density in many European countries raises doubts concerning the assumption of perfectly isolated regional markets. Aguirregabiria and Suzuki [4] conclude: ’Focusing on rural areas makes the approach impractical for many interesting retail industries that are predominantly urban’ (p. 26). Spatial spillover effects between different regions might be particularly important for healthcare industries, since the costs of travelling are small relative to the value of the service. Consumers might thus be willing to travel larger distances to patronise a specific service provider. The present paper aims at extending the entry-threshold approach by modelling spatial interaction effects explicitly.
The second novel feature of this paper is that we will provide first empirical evidence on (changes of) market conduct and competition in the healthcare industry of a transition economy (the Slovak Republic). The structure of a planned economy as well as the behaviour of firms (or production units) in this environment differs from the structure and conduct of firms in a market economy in many dimensions [5]. Given the very specific structure of a centrally planned economy, as well as the significant economic and institutional changes during the process of transition, an empirical analysis can provide novel insights into the evolution of market structure and firm conduct in the healthcare industry for a transition economy.
This paper is organised as follows. The next section provides a short overview of the existing empirical literature. This is followed by a section reviewing the relevant changes in the economic environment in Slovakia. Subsequently, the data and empirical framework are presented. The section “Entry threshold analysis” discusses the changes in competitive behaviour across periods. This is followed by a section detailing counterfactual scenarios, both in terms of regulatory frameworks and in terms of overall economic conditions. The paper concludes with a summary of the main findings and proposes possible extensions of the research agenda.
Literature review
Given the increasing significance of the healthcare sector, it is not surprising to find a large number of empirical studies analysing the determinants of market structure (i.e., the location and the number of suppliers in a specific market) as well as the effects of market structure on competition and economic performance.Footnote 3 A substantial share of this literature focuses on the relationship between market size (population) and the number of suppliers (firms) in different local markets.
The relationship between population and market structure (number of suppliers) for the market of physicians was first investigated empirically by Newhouse et al. [7], who found that the size of a town affects the probability of a physician being located there. They also make use of the fact that the number of specialists in the U.S. increased dramatically over the decade of the 1970s. Towns that did not previously have a specialist experienced a larger increase in the number of specialists than those that did.
Rosenthal et al. [8] revisit this issue using data from the 1980s and 1990s. They examine 23 states with low physician to population ratios. The total number of physicians in these states doubled from 1970 to 1999. They find that communities of all sizes gained physicians over this period, but growth rates were larger for smaller communities. A recent paper by Isabel and Paula [9] examines some of these issues using data for Portugal from 1996 and 2007. Over this period, the total number of physicians in Portugal grew by approximately 30% and the number per capita grew by approximately 22%. They estimate a static model using 2007 data and find that population size has a large and significant impact on the number of physicians per capita located in an area. They also test a dynamic model and find that areas that had more physicians per capita in 1996 had lower growth in the number of physicians per capita. This is consistent with the results reported in Newhouse et al. [7]. Brown [10] also confirms this relationship for the Canadian province of Alberta, although the evidence is not overwhelming. A study by Dionne et al. [11] also found this to be true for the province of Quebec, Canada.
A recent paper by Schaumans and Verboven [12] examines the determinants of entry in physician service markets in Belgium. A novel feature of this study is that the authors consider the entry decisions of pharmacies simultaneously with those of other professions. Pharmacies and physician practices provide complementary services. Consequently, each type of firm benefits from the presence of the other. Both prescription drug prices and physician service prices are heavily regulated in Belgium. Therefore, both pharmacies and physician practices engage in non-price competition (convenience, quality of service, quality of care, etc.). While the entry of physicians into local markets is free from restriction, pharmacy entry is regulated: there is a maximum number of pharmacies allowed in an area, based on the local population. Schaumans and Verboven adapt the models of Bresnahan and Reiss [2] and Mazzeo [13] to allow for entry restrictions for pharmacies as well as the fact that products sold by the two types of firms (pharmacies and physicians) may be strategic complements. They find that the population necessary to support a given number of firms increases more or less proportionally with the number of firms. According to Bresnahan and Reiss [2], this implies that entry does not lead to tougher competition. These results suggest that pharmacies and physicians do not engage in more intense price competition as more firms of their own type enter a market. The authors also find that the population necessary to support another physician practice decreases with the number of pharmacies, and vice versa. This supports the hypothesis of strategic complementarities. Schaumans and Verboven then use the parameter estimates from the model to simulate the impacts of policy reform in the pharmacy market. They consider easing entry restrictions by increasing the maximum number of pharmacies allowed in an area, and reducing pharmacies’ regulated markups. They find that simply allowing free entry (no change in markups) would increase the number of pharmacies by 173%. The complementarities between pharmacies and physician practices lead to a 7% increase in the number of physician practices as a result of the entry liberalization for pharmacies.
Abraham et al. [14] specify a static entry model modified from Bresnahan and Reiss [2] to better understand the nature of competition for hospitals. They augment the Bresnahan–Reiss approach by quantity data. Their method allows the separate identification of changes in the fixed costs of entry and changes in the toughness of competition. Their estimates imply that the threshold per-firm population required to support one hospital is approximately 7000, increases to 12,600 to support two hospitals, is approximately 19,000 for three hospitals, and just under 20,000 for four or more hospitals. They also find that a rise in the number of hospitals in the market dramatically increases the number of patients up until there are three hospitals, by 23% with the entry of the second hospital and 15% with the entry of the third hospital. This implies a substantial increase in the toughness of competition with the entry of a second or third firm, but not thereafter. These results point to considerable effects on competition, even from having only a second firm enter the market. However, the magnitude of the effects (23% increase in quantity associated with moving from a monopoly to a duopoly) seems extremely large.
Note that the existing empirical literature considers market structure and competition in developed market economies only. Similar microlevel studies for transition economies are lacking. In view of the series of structural changes inherent in transition process, a close examination of the process is likely to contribute to a better understanding of how healthcare providers react to adjustments in the economic climate (both in terms of changes in demand characteristics, and in terms of remuneration schemes and general regulatory conditions). The following section provides a short description of structural changes in the healthcare sector in Slovakia during the transition period.
Transition of the healthcare system in Slovakia
The transition process in Slovakia has included a number of changes to the regulatory environment of healthcare professions. An overview of the main regulatory changes is provided in Table 1.
SlovakiaFootnote 4 entered the transition from a centrally planned economy to a market economy as a part of Czechoslovakia. Until 1989, the regulatory framework did not allow independent decisions of firms on prices; free entry and exit was impossible, and the entire production process was governed by central and regional governmental units and state-owned institutions. The state was responsible for healthcare coverage and took full responsibility for financing (through general taxation), planning, management and provision of healthcare. Basic services were granted free of charge to all citizens. The pre-1945 social insurance system was abolished. All healthcare providers were nationalised and incorporated into Regional and District Institutes of National Health. Regional Institutes consisted of regional healthcare centers (large hospitals). The District Institutes of National Health consisted of small- or medium-sized hospitals and polyclinics, along with pharmacies, centers of hygiene, emergency, first aid services and nurseries. The centrally planned economy and healthcare system led to inefficiencies and inaccurate resource allocation decisions. The system was not able to deal with the growing incidence of lifestyle diseases and hospitals were equipped with outdated technology. The lack of improvements in technology was compensated for by increasing numbers of health workers and hospital beds, which resulted in a healthcare system with a surplus of ambulatory physicians.
A social insurance system (based on the Bismarck system) was reintroduced after 1989. In 1993, Slovakia gained independence and the National Insurance Fund was established to fund health, social and pension insurance. Social health insurance was legally defined in 1994 by the Act on Health Insurance, which enabled the establishment of other health insurance funds. The reintroduction of social health insurance suffered from problems created during the previous regime and the macroeconomic environment that went along with the transformation process. The Slovak economy was in a deep recession and public finances were seriously constrained. This led to a situation in which the state did not have the capacity to make health insurance contributions for the inactive population. The health system that was based on a new institutional and regulatory framework with privatised healthcare providers was marked by weak budget constraints and corruption, which led to increasing debts and bankruptcies in the health insurance market. Hospitals remained technologically underdeveloped with an oversupply of health personnel and ineffective management. Even though nearly all hospitals were owned by the state (they existed under the control of the Ministry of Health as state contributory organizations) during the 90s, most pharmacies and ambulatory physicians went into private practice. The hierarchical healthcare structure was broken down and the healthcare system became fragmented, with a high number of specialised healthcare providers. The functioning of the healthcare system became unsustainable and required another set of reforms.
The first set of institutional changes was introduced by the new government in the 1999–2002 period as part of a broader set of macroeconomic stabilization measures. However, the major problems were tackled only partially and the structural deformation of the system’s supply deepened. The state lost control of 14 healthcare facilities that were privatised and transformed to non-profit organizations. The management was transferred to regional and local governments in most of the other state-owned healthcare facilities (with the exception of the biggest hospitals and specialised institutions). This restructuring and the migration of doctors and nurses abroad led to a continuous fall in the number of physicians and nurses in relation to the population after 2001.
Key reforms to the healthcare system were introduced in the 2002–2006 period, with major legislative changes taking place in 2004. The health reform was based on a set of structural and functional changes which were supposed to transform the centralised system into a decentralised system; from the state as a provider of healthcare services to the state as a supervisor setting the “rules of the game”; from the hierarchical functional structure to a contractual structure; and from the state as a bearer of risk to a situation in which every player bears the risk (providers, patients, purchasers). The key objective of the reform was to increase the independence and financial responsibility of healthcare providers. During this period, hard budget constraints were introduced; health insurance companies were transformed into joint stock companies; the Health Care Surveillance Authority (HCSA) was established (to split the legislative and control function in the healthcare system); user fees were introduced; flexible prices, contractual relations with selective contracting and flexible basic benefit packages were decentralised to health insurance companies; a flexible healthcare network (with the definition of a minimum network) and drug policy measures accompanied by the liberalization of ownership of pharmacies were implemented. The reform aimed to make the process of entry into the healthcare provision market more transparent and to remove barriers to entry.
After the 2006 elections, some of the pro-market reforms were discarded (selective contracting was restricted, health insurance companies were no longer allowed to make a profit, user fees were scaled down or completely abolished), but key reform acts remained unchanged. A new government in 2010 reversed the trajectory of reforms again and declared plans to continue to bring new market mechanisms into the healthcare system.
As of 2010, the social health insurance system was based on solidarity, provided universal coverage for a broad range of benefits and guaranteed an annual free choice of one of three nationally operating health insurance companies (one of which was state-owned and covered 66% of the insured, and two privately owned). Pharmacies, diagnostic laboratories and almost 90% of outpatient facilities were in private hands. Ambulatory care was provided mostly by privately organised physicians and people were free to choose their general practitioner and specialist. The system was administered by the Ministry of Health, the HCSA and the self-governing regions which, besides other responsibilities, issued permits to healthcare providers. Chambers and professional associations kept registers of health professionals, issued opinions on ethical issues, issued or revoked licences and monitored the management of healthcare facilities.
For providers to enter the Slovak healthcare provision market, several criteria needed to be fulfilled. Healthcare professionals had to obtain a licence from the Slovak Medical Chamber and a permit from the self-governing region or the Ministry of Health (depending on what type of provider it was). Then, providers were supposed to submit a request for a contract with a health insurance company, although providers could also provide services without a contract with a health insurance company. A minimum network of providers was determined by the government which defined the density and structure of healthcare providers across Slovakia. In primary care, general practitioners were entitled to a contract as soon as a patient registered with them. In ambulatory secondary care and in inpatient tertiary care, the minimum network was defined as a minimum number of specialists by type in each region. Health insurance companies then had the option to contract more providers if they had enough resources. Certain state-owned hospitals which were deemed crucial in guaranteeing geographical accessibility of specialised services were required to be contracted even if the quality and price did not match those of their competitors. Exit from the market was usually caused by the lack of contracts with health insurance companies and/or resulting from a negative financial situation.
Dental care was provided either by contracted or non-contracted dentists. But direct payments from patients for dental procedures were necessary in most cases even to contracted dentists, because social health insurance covered only basic dental costs (under the condition of regular preventive dental examination each calendar year).
Besides the described institutional changes, the pharmacy market in Slovakia was influenced by specific regulatory changes. Until 1998, it was regulated by the Act No. 13/1992 on the Slovak Medical Chamber, the Slovak Chamber of Dentists and the Slovak Chamber of Pharmacists. The entry of new pharmacies was not explicitly regulated by demographic or population criteria, but the Slovak Chamber of Pharmacists had the right to comment on the request for establishment of a new pharmacy that had to be approved by the Ministry of Health of the Slovak Republic. A new Act No. 140/1998 from 1998 on drugs and medical facilities gave the Slovak Chamber of Pharmacists an explicit right to approve the request for establishment of new pharmacies in Slovakia. Without its approval, new pharmacies could not enter the market. Later, the Slovak Chamber of Pharmacists approved the directive on Declaration of professional and ethical competencies for the operation of pharmaceutical care in the public pharmacy [16], which explicitly introduced demographic and population criteria for the establishment of new pharmacies. The minimum distance between pharmacies was set to 500 m and the minimum population per pharmacy was regulated to 5000 inhabitants. Based on several decisions of the Antimonopoly Office of the Slovak Republic against the Slovak Chamber of Pharmacists [17,18,19], these restrictions were abolished. The ownership regulation changed in 2004. The revision of the Act on Drugs and medical facilities from 2004 (633/2004) allowed (after fulfilling some specific requirements) any individual or legal entity to own a pharmacy (only pharmacists could own a pharmacy previously). The liberalization of the pharmacy market in 2002 and 2004 led to the entry of new pharmacies thereafter.
Data and empirical framework
Data and descriptive evidence
The empirical analysis is based on data from between 2800 and 2900 regional submarkets in Slovakia.Footnote 5 Data characterizing market conditions for pharmacies, physicians and dentists are collected on a local level for three time periods (1995, 2001, and 2010).
The number of sellers in each town is calculated using data from the “Register of Economic Subjects” of the Slovak Republic, which should cover all relevant firms. We identify firms as belonging to a particular group based on their main economic activity following the NACE Rev. 1 classification of industries. The Register also provides information on the location of the sellers, which allows us to compute the equilibrium number of firms. Large towns may be divided into several submarkets based on ZIP codes. In total, there are 2843 (2897 and 2926) markets in 1995 (2001 and 2010).
Table 2 provides an overview of the observed market structures, as well as their frequency. As markets with more than seven firms are seldom observed, we pool them to increase the precision of the estimates. This approach is in line with previous applications of the methodology.
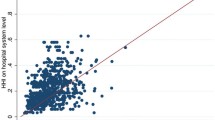
The firm data are merged with market-level information on total population. Demographic variables are available at a highly disaggregated level. As can be seen from Fig. 1, the most common category of towns has a population of fewer than 500 inhabitants. This fine definition of the administrative units allows us to measure variations in local characteristics extremely precisely. The figure also illustrates the close relationship between population and the number of firms, suggesting that the number of inhabitants is a good measure of market size.
To assess the level of market barriers and competitive effects more precisely, it is necessary to build a model which controls for additional municipal specifics, to reflect the fact that consumers differ in their per-capita level of demand. We, therefore, supplement population data with information on the share of young and senior citizens.Footnote 6 These data, as well as the information on the total number of inhabitants, are taken from the “Urban and Municipal Statistics” and as such are provided at the most detailed level. Unfortunately, data on wages and unemployment rates are only available at the district level, as they come from the “Regional Statistics Database” of the Slovak Republic. We provide descriptive statistics for the variables in the Appendix.
Empirical framework
In line with previous work by Bresnahan and Reiss [2] and Schaumans and Verboven [22], we propose that healthcare providers within a given market have identical characteristics. This implies that in a market with N competitors, the level of per-firm per-capita variable profits (v(N)) is the same for all firms. Furthermore, we assume that fixed costs (f) are independent of the number of firms. Per-firm profits are given by \(\pi (N)=v(N)S-f\), where S represents the market size measured by population. In a market with free entry and N firms, revealed preference implies that:
or equivalently:
To estimate \(\ln \frac{v(N)}{f}\), we collect data on market characteristics (summarised in the matrix X), include firm-fixed effects (\(\theta _{N}\)) and allow for random shocks in expected profitability via an unobservable error term \(\varepsilon\).
The model can then be estimated using an ordered probit specification for the number of firms in any given market (y)Footnote 7:
The values of \(\theta _N\) and \(\theta _{N+1}\) measure the changes in the variable profits to fixed costs ratio which can be attributed to market structure. If the two parameters are significantly different from each other, one would conclude that market profitability changes substantially with the entry of the \(N+1\)st competitor.
Note that estimating an ordered probit model on the number of firms in individual markets assumes that these markets are spatially isolated. While the assumption of spatially isolated submarkets might be plausible in Bresnahan and Reiss’ [2] empirical analysis,Footnote 8 the high population density in many Western and Central European countries renders this assumption highly implausible.
A Moran’s I analysis (see Table 3) of our variables of interest also points to the presence of strong spatial autocorrelation both in the number of firms and in the market characteristics.Footnote 9 Particularly for the last two periods, there is correlation in population measures, as certain hubs of economic activity are formed. This shows that similar markets are likely to cluster together and further suggests that unobserved characteristics are also likely to be correlated across space. With this in mind, taking into account not only the level of the latent profitability in a given market, but also in adjacent administrative units, may improve the quality of inference. We therefore follow Lábaj et al. [24] by allowing for spatial autocorrelation across observations. As consumers are likely to demand healthcare services beyond the border of their municipality, we explicitly model interactions across towns and hence implement a model which captures the characteristics of densely populated areas.
Spatial dependence is modelled using a spatial autocorrelated ordered probit model (see [25]), which presumes correlation across latent profitability (\(y^*\)):
We assume that consumers have a strong preference for healthcare providers which are close by and hence use a W matrix with an exponential specification and elements equal to \(w_{ij}=1/\text{dist}_{ij}^2\), where \(\text{dist}_{ij}\) is the distance between regions i and j. For estimation purposes, the matrix is also row-standardised.Footnote 10
In the presence of spatial autocorrelation in the latent profitability measure, the data are assumed to follow a truncated multivariate normal distribution:
Note that the theoretical interpretation of the spillover effects (measured by the parameter \(\rho\)) is ambiguous, since they measure the effect of a one-unit change in the estimated average neighbourhood profitability. This profitability (denoted by \(Wy^*\)) may rise due to two counteracting reasons: (1) if market characteristics improve (in other words \(\mu\) grows) or (2) if more firms have entered the market (since \(y^*_N<y^*_{N+1}\) by construction). Hence, we would expect a positive value of \(\rho\) if practitioners cluster in certain areas (suggesting that demand effects are more important than competitive effects). If the observed values are negative, this would imply that the aim of the regulator is to offer a supply distribution which is uniform. In this scenario, the central planner will try to make sure that firms are not located too closely to each other to increase efficiency and decrease transportation costs in remote areas. In this case, whenever the neighbourhood profitability \(Wy^*\) grows due to entry, the likelihood of a firm establishing itself in the local market will decrease significantly, resulting in a negative sign of \(\rho\).
The Bayesian MCMC procedure used for the estimation is based on Wilhelm and de Matos [26]. Conditional on the observed number of firms and the characteristics of each market, a draw is taken for the latent profitability from the conditional distribution of \(y^*\) via Gibbs sampling. Once these values are obtained, the model can be estimated using standard Bayesian SAR methods.Footnote 11
Once the parameters in Eq. (3) are identified, we can analyse the ease of entry of the first healthcare provider by calculating the so-called monopoly entry threshold (\(S_1\)), which represents the number of consumers necessary to cover the fixed costs of the first entrant:
Changes in the value of \(S_1\) over time would be indicative of changes in the level of entry barriers. A high breakeven population is often a signal for regulatory obstacles to entry, as well as for low expected profitability per capita, even in markets with no additional competitors. By comparing the estimated thresholds across time, it is possible to ascertain to what extent the transition process changed the barriers to entry facing healthcare providers. While the rise in income levels is likely to decrease the threshold for entry by increasing per capita demand, government intervention aimed at raising efficiency may have made it harder for firms in rural areas to remain economically viable. The net effect of these changes is reflected in the estimates of \(S_1\).
Aside from evaluating the ease of entry for providers with a monopoly position, we would also like to access how the competitive pressure exerted by each successive entrant has changed during the transition period. Following Bresnahan and Reiss [2], we focus on the change in per firm breakeven population in order to measure the magnitude of the decrease in profitability attributable to each new firm. If new entrants result in lower markups for incumbent sellers (either through decreasing the price of unregulated services or by increasing costs due to investments in quality), the number of firms will not grow proportionally to population.
We quantify competitive effects by comparing the per-firm break-even population for each market structure:
From these estimates, we construct so-called entry threshold ratios (\(\text{ETR}_N\)):
where \(N^m\) represents the upper limit of the number of firms in a market.Footnote 12
An increase of entry thresholds with the size of the market (\(s_N < s_{N+1}\)) is an indication of intensified competition. Since we assume that in markets with \(N^m\) firms, competition is at its most intense level (this assumption is valid in markets where entry results predominantly in business stealing, rather than market expansion), an estimate of \(s_N\) for which \(s_{N^m}/s_N=1\) would indicate that N entrants are sufficient for a perfectly competitive outcome.
The intuition behind this conclusion is that consumers have the same level of demand per capita across market structures (a presupposition which is reasonable for healthcare services). Abstracting from competitive effects, we would, therefore, expect the number of providers to grow proportionally to market size. If this is not the case and \(s_{N^m}/s_N>1\), then firms in a competitive market (with \(N^m\) firms) need a larger population to break even than those in a market with only N competitors. This would indicate that healthcare providers in more concentrated markets have higher markups, either due to smaller investments in quality or due to stronger government subsidization. As such, the values of \(\text{ETR}_N\) provide valuable information regarding the effects of government policy and strategic firm behaviour.
Entry threshold analysis
Table 4 reports the parameter estimates from the spatial ordered probit model. Population exerts a positive effect on the likelihood of entry across all industries and time periods. Despite the observed variation in the parameter value of \(\alpha\), one would expect an extra consumer to have the same additional value regardless of the number of other patients in the municipality. With this in mind, we constrain \(\alpha\) by dividing all parameters by the estimated value of the population coefficient in order to calculate the break-even population:
Changes in competitive pressure due to entry are measured by the ordered probit parameters \(\theta _N\). All values are significant, suggesting that market structure plays an important role in determining profitability.
Based on these estimates, we calculate the entry threshold population (Table 5) and entry threshold ratios (\(s_7/s_N\)) for all occupations (Table 6). The results are summarised in Fig. 2.
In the values reported below, means are used for the variables capturing market characteristics (\(\bar{X}\)) and the spatial weights matrix W is replaced by a zero matrix to mimic the usual assumption of isolated markets.Footnote 13
Entry barriers
In the market for pharmacy services, entry barriers appear to have fluctuated significantly over time. The estimated monopoly entry threshold (\(S_1\)) in Table 5 suggests that 3845 inhabitants were necessary for a single firm to break even in 1995. This number jumped to 4876 in 2001 and subsequently fell to the initial level of just over 3000.
When analysing this development, it is important to note that the privatization process for pharmacies was concluded in 1994, meaning that the outcome in 1995 is influenced to a large extent by pre-liberalization dynamics and reflects the goal of the government to ensure market coverage by setting extremely low entry barriers for the first potential entrant.
Once the privatization process was complete, the role of regulator was taken up by the Slovak Chamber of Pharmacists, which sought to introduce explicit demographic and population criteria for establishment as a way of improving the performance of its members. The estimated entry threshold of 4876 individuals fits well with the legal limit set by the Chamber, which required that at least 5000 inhabitants should be served by each pharmacy seeking to enter the market. The rise in entry barriers may also be fuelled by the loss of economies of scale which are sometimes present in systems under government control.
The subsequent sharp decrease in entry barriers between 2001 and 2010 can largely be attributed to the decisions of the Antimonopoly Office of the Slovak Republic against the Slovak Chamber of Pharmacists [17,18,19] which removed entry restrictions and liberalised ownership. The more lenient approach to the formation of distribution chains may have allowed firms to reduce operation costs. Furthermore, the income level in the country rose, which naturally depresses the estimates of \(S_1\).
In comparison, the monopoly entry threshold value for physicians and dentists remained stable between 1995 and 2010, a clear indication of the role of administrative decision-making in these industries. Entry into these markets is strongly regulated and the supply of services was reasonably good during the communist regime, leading to very little change during our observation period.
However, it should be pointed out that previous research in Lábaj et al. [24] has shown that in competitive industries the increase in income levels between 1995 and 2010 led to a substantial decrease in entry barriers. As such, the healthcare industry grew more slowly than its more competitive retail counterparts during the transition period. The inability of the industry to generate higher levels of entry may be due to government intervention seeking to sanitise the finances of the healthcare system. In 2004 a “reform package of laws” was adopted to reduce financial inefficiency by limiting consumption [27]. This attempt to improve the efficiency of the providers may have offset the positive effect of rising income levels.
Competitive effects
The changes in entry barriers were also accompanied by changes in the relationship between market structure (the number of firms) and per-capita profitability. However, the estimated entry threshold ratios shown in Fig. 3 and Table 6 point to heterogeneity in the influence of market structure on markups across healthcare markets.
Deregulation on the market for pharmaceutical services had a substantial effect on the relationship between the number of firms and expected profitability. Before the removal of entry barriers, a market with six firms required about 2.32 times the per-firm population of a monopolistic market to break even.Footnote 14 This suggests that regulators were reluctant to introduce new firms into areas where an incumbent was present. The position of monopolists appears to have been most profitable during the brief period of strict self-regulation.Footnote 15 The policy measures introduced in 2004 resulted in a very different relationship between markets in 2010, when a firm with six competitors (in a duopoly) only needed 11% (7%) more consumers than its monopolistic counterparts to break even. This suggests that the abolition of entry restrictions made concentrated markets contestable and led to a decrease in markups (this effect is likely to occur due to an increased investment in quality and hence higher costs, rather than differences in prices).
Changes in regulatory policy also influenced the entry threshold ratios in other healthcare industries. While per-capita profitability in monopoly markets appears to have increased only marginally for physicians and dentists (as reflected by the small changes in \(S_1\)), the profits on competitive markets grew. This is clearly visible from the results in Table 5, which show that entry thresholds for seven firms decreased substantially. This process may explain the fact that ETRs are falling with time. Surprisingly, results for physicians even point to ETRs which are significantly lower than 1. This would indicate that firms on competitive markets experience higher per-capita profits than monopolists. This may be due to the large scope for differentiation in the industry. Especially in the case of large hospitals, which are likely to be situated in densely populated municipalities, the clustering of practitioners may attract more consumers. As such, it cannot be ruled out that entry in these markets does not necessarily lead to more competition for a given number of potential customers. As argued in Schaumans and Verboven [22], entry might also increase product variety and thereby have a positive effect on consumers’ willingness to pay. This countervailing effect of entry reduces entry threshold ratios and could explain ratios smaller than one.
Spatial spillovers
Spatial spillover effects are captured by the parameter \(\rho\) which measures the influence of the spatially weighted (unobserved) measure of neighbourhood profitability (\(Wy^*\)) on the (unobserved) measure of profitability in the local market (\(y^*\)).
Table 4 reports significant and negative spatial correlation effects for all periods and occupations. This suggests that spatial spillovers play an important role in determining profitability. The negative estimates can be interpreted as an indication that the effect of competitive linkages outweighs the demand spillover effects associated with attractive neighboring markets. The presence of a competitor in the neighbourhood (and hence a higher sampled \(Wy^*\)) results in a lower probability of entry. Such an effect could occur on markets where entry is coordinated and professionals seek to avoid direct competition for patients. It is also a likely result if healthcare services are offered in a hierarchical manner with only the most profitable markets hosting a seller, as predicted by models of urban development. As mentioned in Rosenthal et al. [8], the concentration of services in particular areas and their unavailability in adjacent markets implies that health policy should consider the possibility of patients travelling across administrative borders.
Interestingly, this effect wanes over our observation period, with the absolute value of \(\rho\) decreasing with time. This result is especially strong on the pharmacy market. One could interpret the estimates as an indication that with improved infrastructure and increased agglomeration, firms now expect to be patronised by more consumers from neighbouring markets and demand spillovers are starting to outweigh competitive effects. While there are no positive externalities for incumbents when new pharmacies enter in the same region, it may be more attractive for pharmacies to locate in adjacent markets if other industries are clustered in the region and hence attracting commuters and improving the growth prospects of the area. This, coupled with the fact that location decisions are no longer regulated, can lead to a tendency for co-location.
As an additional indication for the rise in co-location can be seen if we calculate transition matrices. Table 7 shows the transition probabilities across market structures. While most markets with a high number of sellers managed to keep the number of firms constant (or even increase this number) over the 15 years of observation, 43% of the monopoly markets lost their only provider of services over the same period. This suggests that once entry was deregulated, certain areas (particularly smaller villages) did not benefit from more entry but rather lost services to larger neighbouring markets. As such, it seems that while deregulation of the sector has had an overall positive effect on entry, the majority of the benefits were reaped by towns and villages where supply levels were already high. This result is also present in the market for dental (medical) services, with 28% (21%) of monopoly markets in 1995 losing their access to a local provider of services (Tables 8, 9).
Counterfactual analysis
Our overall results point to very small changes in firm behaviour on the market for physicians and dentists, and significant changes in the pharmacy market. In order to determine to what extent the results are driven by “behavioural effects” rather than changes in external market conditions (such as demand and cost characteristics or changes in the regulatory framework), we implement two counterfactual scenarios. The first generates predictions for the number of entrants using the parameter estimates from each of the three periods, while holding constant the distribution, income level and demographic structure of the population in each market. As such, this analysis shows how much of the change in the equilibrium number of firms was driven by “behavioural effects” as opposed to adjustments in consumer characteristics. The first part of this section details the predicted entry behaviour in each regime.
The second counterfactual scenario focuses instead on the possibility of changing the regulatory framework. Since our data include a period of self-regulation in the pharmacy industry, we explicitly model the restrictions imposed by the Chamber of Pharmacists and predict how the distribution of firms would have been altered by a reduction in the imposed standards. The results from this analysis are summarised in the second part of this section.
Effect of changes in overall economic conditions
Much of the fluctuation in the number of firms over time is due to changes in market characteristics. To gain more insight into the differences in entry behaviour (“behavioural effects”) while keeping market fundamentals constant, we focus on the dataset from 2010 and predict the number of firms using the parameters estimated by the models in each time period.
We estimate the expected number of firms on each market for period i as:
Tables 10, 11, 12, 13, 14 and 15 show the results of the estimation. In each table, the predicted number of firms in 2010 is compared to the predicted number of firms using parameters from the two prior periods (1995 and 2001). The observations on the diagonal of the matrix represent markets which would be expected to have the same market structure in both periods under investigation. Observations below the diagonal indicate that more firms would be expected to enter in 2010 than in the comparison period. In other words, in the counterfactual based on the earlier regulatory climate, fewer sellers would be on the market. Conversely, observations above the diagonal suggest that entry was less likely on those markets in 2010 than it would have been in previous periods.
The most striking results are visible for pharmacies. Between 1995 and 2010, the predicted number of uncovered markets is estimated to have decreased by 288 due to “behavioural effects” (see Table 10). All 176 markets which are expected to accommodate one firm in 2010, would have remained without coverage in 1995. While the results are clearly indicative of significant changes in firm behaviour, it is important to note that they are driven in part by the fact that wages have a strong negative impact on entry in 1995 (this is the only period and the only industry for which this holds true). Given the wage growth observed during the transition period, the extreme differences in predicted entry behaviour may be due mainly to an unexplained change in the response of firms to overall wage levels. As such, we would be cautious in basing specific policy recommendations on the predicted behaviour of firms in this particular counterfactual simulation.
The predicted entry behaviour based on parameter estimates from the period of self-regulation (2001) and the liberalization thereafter (2010) is summarised in Table 11. The simulation suggests that entry of additional firms on markets with at least one incumbent was significantly harder in 2001 than in 2010. Of the 39 predicted duopoly markets in 2010, 21 would have been a monopoly in 2001. The process is even more severe in more atomistic markets. Of the 27 (22) markets with 3 (4) firms, 25 (16) would see lower entry in 2001. However, it should be noted that the estimates also predict that fewer markets would remain uncovered in 2001. Of the 2605 markets which have a negative monopoly profit in 2010, 28 would have been deemed profitable in 2001. As such, self-regulation seems to encourage entry into rural/less attractive markets.Footnote 16
The results for physicians also show a large difference in expected firm behaviour from 1995 to 2010 (Table 12). In particular, 497 markets which are not expected to be covered in 1995, see entry in 2010. A similar, though less strong effect is visible when comparing 2001 and 2010 (Table 13). Of the 499 monopolies predicted in 2010, 114 would not have been covered in 2001.
On average consumers seem to have benefited from the transition process with regard to the supply of dental services. Table 14 shows that competition intensified in most markets and expected coverage improved. However, it appears that most of the improvement was due to processes occurring before 2001. The results in Table 15 indicate that entry became harder after the initial stages of transition were over. In fact, of the 2411 markets which are expected to remain uncovered in 2010, 152 would have been able to accommodate a monopolist in 2001.
The effects of regulation in the pharmacy sector (2001)
As outlined in Section “Transition of the healthcare system in Slovakia”, the transition process for pharmacies involved a period of self-governance, which encompasses the observations from 2001. During this stage of the transition, general restrictions were passed which required at least 5000 inhabitants per pharmacy and a minimum distance of 500 m between pharmacies.
The licensing process poses a problem for the identification of the competitive effects. In particular, it means that firms may fail to enter in profitable markets due to restrictions placed by the Chamber of Pharmacists. We take this into account by following Schaumans and Verboven [12] and estimating a standard censored ordered probit.
The sample of observations is split into two groups. The first group contains all observations in which the regulation is not binding. For these observations, the likelihood function remains unchanged. We expect to see N firms on the market if:
If we denote the density of the error term \(\varepsilon\) as f(.), the probability of observing N firms is equal to:
The second part of the sample consists of the 284 observations for which the regulation is binding. On those markets, the entry of an additional firm would reduce the number of inhabitants per capita to less than 5000.
We denote the maximum number of firms allowed on the market with \(\bar{N}\). Observing \(\bar{N}\) firms on markets with binding restrictions is less informative than it would be under free entry. We can conclude that the market is profitable for \(\bar{N}\) firms but it may be erroneous to assume that it is unprofitable for \(\bar{N}+1\) firms:
This means that the censored observations provide no information regarding the value of \(\theta _{\bar{N}+1}\). We take this into account by adjusting the likelihood specification on these markets:
The combined likelihood of observing N firms on a given market is formed using a dummy variable d set equal to 1 if the regulation is not binding (\(y<\bar{N}\))Footnote 17:
The results from this estimation are reported in Table 16. With the exception of the first threshold, the results point to significantly lower entry barriers once restrictions are taken into account. This indicates that the regulatory environment played a dominant role in preventing firm entry. However, it should be noted that most markets with incumbent firms are subject to binding restrictions, which means that the estimates from the censored model are based on a likelihood function which is less informative than in the unrestricted model. Of the 220 (38) monopoly (duopoly) markets in our dataset, 214 (32) are censored. This means that only 6 monopoly observations can provide an indication for where the threshold for the second entrant should lie. As such, our ability to estimate the thresholds for more than 1 firm is severely limited. Nevertheless, the conclusion that there is a significant difference in mark-ups across market structures holds true.
Despite the short-comings of the censored model, it can provide some evidence with regard to the effects of self-regulation on the equilibrium number of firms. We conduct a counterfactual analysis in which we examine the effects of reducing restrictions to entry. Following Schaumans and Verboven [12], we define \(\varPhi\) as the factor by which the restrictions are relaxed. If \(\varPhi =1\), then the restriction remains in place and no new pharmacy can enter the market if it reduces the number of inhabitants per incumbent to less than 5000. If \(\varPhi =2\), then the restriction is relaxed and requires only 2500 inhabitants per pharmacy. This is identical to a doubling of the number of firms permitted on the market.
In this framework, the expected number of firms can be defined as:
In Table 17, we show the estimated number of firms using the parameters suggested by the censored model, where the predicted number of firms is rounded to an integer. The predicted distribution of firms under the 2001 legislation does not perfectly coincide with the observed entry behaviour. This is due in part to unobserved market specific sources of profitability, as well as to the fact that the restrictions placed on the market were sometimes violated due to the historical presence of a pharmacy in a given area. Since the regulation only applied to new applicants, we observe pharmacies in markets where in principle the regulatory framework should not allow their entry.
According to the model of restricted entry, 2699 markets are expected to remain uncovered. Allowing for free entry on all markets would lead to entry in 161 of these markets. Additionally, of the 117 markets on which we expect to observe 1 firm under the 2001 legislation, 75 would see an increase in supply by at least one additional firm if the restriction were lifted. Similar processes are observed on more competitive markets as well.
As a next step, we contemplate the effects of a loosening of the legislation (rather than a complete removal). In particular, we set \(\varPhi =2\). The results from this experiment are reported in Table 18. The effects of such an intervention are limited in markets with low predicted profitability. The main change occurs in monopoly markets, of which 29% become a duopoly.
Summary and extensions
The present paper documents the changes in competitive behaviour in markets for professional healthcare services during the transition of Slovakia from a centrally planned to a market economy. An entry model is estimated with a cross section from each stage of the transition (1995, 2001, 2010) to quantify the changes in entry barriers and competitive pressure. The data from 1995 characterise the initial period of transition, which was largely pre-determined by decisions made prior to liberalization. By 2001, the results of the first set of reforms of the sector are visible, especially in those industries where regulation was outsourced from the government to representatives of the profession. The data from 2010 reflect the final outcomes of the transition process.
We find that firm entry became easier during the transition. However, this effect is much smaller than the one estimated for retail industries outside healthcare.Footnote 18 By 2010, approximately 1500 inhabitants were required for the first physician to enter a market and around 2500 (3300) inhabitants were necessary in a local market for the first dentist (pharmacist) to break even. The relatively modest change in entry thresholds may reflect the government’s policy of providing medical services in regional centres where they are accessible to the largest possible number of customers, which biases entry behaviour towards very large towns and therefore results in high monopoly thresholds, even in the context of a growing economy.
The effect of entry differs across professions. For physicians and dentists, the effect of entry has changed very little over time. Furthermore, it seems that new entrants do not depress the per-capita profitability of incumbents (or do so very modestly). As such, one would conclude that on these markets differentiation and regulatory intervention alleviate the effects of market structure.
This is not the case in the pharmaceutical industry, where we find very strong effects of market structure in 1995. The data suggest that monopolists made significantly higher profits directly after the beginning of the transition. This effect becomes more pronounced during the period of self-regulation. The estimates for 2001 show that a monopoly position resulted in even higher profitability in this phase. The sharp decline both in entry barriers and in profit differences across market structures by 2010 seems to suggest that the policy reforms (the decisions of the Antimonopoly Office of the Slovak Republic against the Slovak Chamber of Pharmacists) were effective. The removal of entry restrictions and the liberalization of ownership rights led to a reduction in the break-even population, more entry and an intensification of competition. There does not seem to be a large premium on having a monopoly position in a healthcare profession in the modern Slovak economy.
Further research is necessary to determine the precise channels by which these outcomes were influenced. In particular, information on the actual number of patients and the payments which the practitioners received per-capita would make a more in-depth analysis possible. This information would also allow for a more precise market delineation, as it would provide information on the true distribution of consumers.
This analysis would also benefit from an extension which identifies each individual pharmacy and hence analyses not only the equilibrium outcomes but also the entry and exit decisions upon which they are founded. In this context, it may be important to also take into account complementarities across different types of practitioners, as outlined in Schaumans and Verboven [12].
Notes
For example, if the size of the market needs to triple to add an additional entrant, this suggests that the addition of that firm dramatically reduces firm profits. A discussion of the importance and the effects of competition in the healthcare industries can be found in Barros et al. [3].
Bresnahan and Reiss [2] identify towns or small cities in the continental United States that are at least 20 miles from the nearest town of 1000 people or more to estimate their econometric models.
A comprehensive survey of this literature is available in Gaynor and Town [6].
This section is based on the Health Systems in Transition report for Slovakia by Szalay et al. [15], which provides a detailed description of the healthcare system and of reforms in the Slovak Republic. It was prepared by national experts in collaboration with the European Observatory on Health Systems and Policies.
The fluctuation in the number of observations is due to changes in the definition of administrative units. These alterations are usually the product of towns growing larger and hence splitting into separate administrative units. MISR [20] and SOSR [21] provide additional information regarding the rationale behind these changes. As we expect these administrative decisions to reflect economic phenomena, we accept that split municipalities are likely to represent split markets.
We define young citizens as those who have not yet completed their fifteenth year and the elderly as anyone aged over 60.
In the description of the model below, the parameter of \(\ln S\) is constrained to 1. In the estimation, this parameter is allowed to vary. It is denoted as \(\alpha\) in the reported results (Table 4) and can be interpreted as \(1/\sigma\) (see [22, p. 204]). All parameters are subsequently rescaled in order to arrive at the values relevant for the theoretical model.
The authors study towns which are located at least 100 miles away from a large metropolitan area (with more than 100,000 inhabitants) and are not closer than 20 miles to a town with a population of over 1000 people. In a more complex approach, Seim [23] allows for a more flexible definition of the market by using concentric circles around each seller. However, this increased flexibility is combined with the restriction that the competitive effect of additional entry is the same, regardless of the current number of incumbent firms. Additionally, information on the exact location of each seller is necessary, which is outside the scope of our dataset.
The Moran’s I statistic is calculated as:
$$\begin{aligned} I=\frac{n}{S_0}\frac{\sum _{i=1}^n\sum _{j=1}^nw_{ij}(x_i-\bar{x})(x_j-\bar{x})}{\sum _{i=1}^n(x_i-\bar{x})^2} \end{aligned}$$where \(w_{ij}\) is equal to the inverse distance between town i and town j squared if those are within 30 km of each other and 0 otherwise. \(\bar{x}\) represents the average value of the variable, whereas \(x_i\)(\(x_j\)) measures the variable at a given location i (j). n represents the total number of observations, whereas \(S_0\) counts the number of positive connections between the observations (\(S_0=\sum _{i=1}^n\sum _{j=1}^nw_{ij}\)). The statistic measures the spatial correlation between the observations and compares this to a random distribution.
We set \(w_{ij}=0\) if the towns are more than 30 km apart. This cut-off value corresponds to Bresnahan and Reiss [2], who use a 20-mile threshold. Furthermore, the use of exponential weights means that towns which are further than 30 km away are unlikely to get a high weight. Estimation experiments with alternative cut-off values provide very similar empirical results.
In particular we assume: \(\beta \sim N(0,T)\), where \(T=I_K 10^{12}\) and K is the number of covariates; \(\theta _N \sim U(\theta _{N-1},\theta _{N+1})\) in the interval \([\theta _{N-1},\theta _{N+1})\); \(\rho \sim \beta (1,1)\) in the interval \((-1,1)\). A detailed outline of the assumptions and implementation strategy is available in LeSage and Pace [25], pp. 279–299. For further information on the estimation steps, consult the documentation of the R package spatialprobit.
In the empirical analysis, we follow previous research and set \(N^m = 7\) in order to have sufficient observations to identify each threshold. As additional competitive effects are likely to wane as more firms enter, we believe that the loss of information due to this censoring is likely to be minimal.
To ensure comparability with previous research, we also estimated the model using a non-spatial specification and focusing on rural areas. These results can be found in the Appendix.
A duopolistic market still required 1.36 times the per-firm population of a monopolist to break even (this is not shown in Fig. 3, which takes a competitive market with six firms as a benchmark).
The introduction of entry restrictions by the Slovak Chamber of Pharmacists may have led to censoring in the number of firms. As such, the coefficients estimated in 2001 may include both competitive and regulatory effects. To take this into account, we additionally report the estimates from a censored ordered probit model in Section “Counterfactual analysis”.
It is important to note that in the present analysis, the restrictions imposed through the regulation are not explicitly incorporated into the econometric model. In practice, we observe entry beyond the maximum number of firms which is allowed by the regulation. This is due to the fact that no licenses were revoked by the new legislation. As such, the observed market structure is the result of liberalised entry prior to self-regulation and new firm establishments which were subject to the restrictions. Section “Counterfactual analysis” deals with this issue in detail.
Unlike Schaumans and Verboven [12], we assume that the restrictions are not binding on markets with zero pharmacies. This assumption is based on the text of the legislation, which states that “[t]he committee of the regional chamber shall not issue a certificate to an applicant if he or she is to pursue the occupation of a pharmacist in a pharmacy less than 500 metres from another pharmacy or if the number of inhabitants per public pharmacy in the region goes below 5,000” [16]. While the precise meaning of the text is subject to interpretation, as it could imply that the number of inhabitants for the current incumbents should not be decreased or that the applicant is also taken into account when calculating this number. Since in rural areas the 5000 inhabitants rule is likely to be applied using a wider definition of the market than the village itself, we assume that the regulation is likely to be lenient with the goal of ensuring geographic coverage.
See Lábaj et al. [24] for an overview of entry threshold levels for other industries.
References
OECD: Focus on health spending, p. 2015. Technical report, OECD Health Statistics (2015)
Bresnahan, T.F., Reiss, P.C.: Entry and competition in concentrated markets. J. Polit. Econ. 99(5), 977–1009 (1991)
Barros, P.P., Brouwer, W.B., Thomson, S., Varkevisser, M.: Competition among health care providers: helpful or harmful? Eur. J. Health Econ. 17(3), 229–233 (2016)
Aguirregabiria, V., Suzuki, J.: Empirical games of market entry and spatial competition in retail industries. In: Chapter for the Handbook on the Economics of Retail and Distribution. Edward Elgar Publishers, Northampton (2015)
Estrin, S.: Competition and corporate governance in transition. J. Econ. Perspect. 16(1), 101–124 (2002)
Gaynor M, Town RJ (2011) Competition in health care markets. In: Handbook of health economics. Vol. 2, pp. 499–637 Elsevier
Newhouse, J., Williams, A., Bennett, B., Schwartz, W.: Does the geographical distribution of physicians reflect market failure? Bell J. Econ. 13(2), 493505 (1982)
Rosenthal, M., Zaslavsky, A., Newhouse, J.: The geographic distribution of physicians revisited. Health Serv Res 40(6), 19311952 (2005)
Isabel, C., Paula, V.: Geographic distribution of physicians in Portugal. Eur. J. Health Econ. 11, 383393 (2010)
Brown, M.: Do physicians locate as spatial competition models predict? Evidence from Alberta. Can. Med. Assoc. J. 148(8), 1301–1307 (1993)
Dionne, G., Langlois, A., Lemire, N.: More on the geographical distribution of physicians. J. Health Econ. 6, 365374 (1987)
Schaumans, C., Verboven, F.: Entry and regulation: evidence from health care professions. RAND J Econ 39(4), 949–972 (2008)
Mazzeo, M.: Product choice and oligopoly market structure. RAND J. Econ. 33(2), 221242 (2002)
Abraham, J., Gaynor, M., Vogt, W.: Entry and competition in local hospital markets. J. Ind. Econ. LV(2), 265–288 (2007)
Szalay, T., Pažitný, P., Szalayová, A., Frisová, S., Morvay, K., Petrovič, M., van Ginneken, E.: Slovakia: health system review. Health Syst. Transit. 13(2), 1–200. (2011) http://www.euro.who.int/__data/assets/pdf_file/0004/140593/e94972.pdf?ua=1
SLEK: Declaration of professional and ethical competences for the operation of pharmaceutical care in the public pharmacy. Technical report, Slovak Chamber of Pharmacists (2000)
PMU SR: Decision of the Antimonopoly Office of the Slovak Republic 2001/PO/4/1/271. Technical report, Antimonopoly Office of the Slovak Republic (2001)
PMU SR: Decision of the Antimonopoly Office of the Slovak Republic 2002/PO/4/1/004. Technical report, Antimonopoly Office of the Slovak Republic (2002)
PMU SR: Decision of the Antimonopoly Office of the Slovak Republic 2004/KH/R/2/119. Technical report, Antimonopoly Office of the Slovak Republic (2004)
MISR (2013) Teritorial changes of the municipalities in the Slovak Republic after 1990. Technical report. Ministry of Interior of the Slovak Republic, Bratislava
SOSR: Statistical lexicon of the municipalities in the Slovak Republic 2011. Technical report, Statistical Office of the Slovak Republic, Bratislava (2014)
Schaumans, C., Verboven, F.: Entry and competition in differentiated products markets. Rev. Econ. Stat. 97(1), 195–209 (2015)
Seim, K.: An empirical model of firm entry with endogenous product-type choices. RAND J. Econ. 37(3), 619–640 (2006)
Lábaj, M., Morvay, K., Silanič, P., Weiss, C., Yontcheva, B.: Market structure and competition in transition: results from a spatial analysis. Appl. Econ. 50(15), 1694–1715 (2018)
LeSage, J.P., Pace, R.K.: Introduction to Spatial Econometrics. Chapman and Hall/CRC, Boca Raton (2009)
Wilhelm, S., de Matos, M.G.: Estimating spatial probit models in R. R J. 5(1), 130–143 (2013)
EC: Health in Slovakia. Technical report, European Commission (2013)
Acknowledgements
Open access funding provided by Vienna University of Economics and Business (WU). This article was generously supported by SAIA and OeAD, Action Austria-Slovakia, Cooperation in research and education, project No. 2014-10-15-0005, and by the research project OP Vzdelavanie (OP Education): Increasing the quality of doctoral studies and support of the international research at the FNE, University of Economics in Bratislava (ITMS 26140230005). The project was co-financed by the European Union.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
To assess the importance of spatial effects in more detail, we re-estimate and compare the results of a model using a non-spatial framework (which corresponds to the empirical approach applied in previous studies). We look at two different data samples. The first (step 1) consists of rural areas only, while the second (step 2) includes all towns but does not allow for spatial spillovers.
In the first step, we re-estimate the model of entry using only towns with a population below 15,000 and a density below 800 inhabitants per km\(^{2}\). This is motivated by the conjecture that large cities consist of overlapping markets, whereas rural areas are (more) isolated. Since this results in the removal of all large towns (regardless of their proximity to the observations in the sample), the model is estimated as a standard ordered probit model. The results are reported in Tables 19 and 20.
Several observations are worth mentioning. Firstly, the exclusion of large towns leads to problems with the estimation of the thresholds for markets with many firms, as these are rarely included in the sample. In particular, none of the towns in the sample have more than 4 pharmacies in 2001. This makes it difficult to directly compare the estimates across models. Nevertheless, the general conclusions of the estimation remain the same. In the pharmaceutical industry, entry barriers increase in 2001 but fall in 2010. In the case of physicians we observe a small decrease in the monopoly break-even population. The threshold for dentists appears to stagnate.
Secondly, the estimated thresholds (\(\theta\)) and the resulting break-even population is consistently lower than the ones estimated in the spatial model. This is likely due to the fact that the spatial spillovers (\(\rho\)) are negative. The negative spatial autocorrelation in profitability implies that if a specific local market A is surrounded by towns where entry of the first firm would be unprofitable (i.e. markets with no competitors), then the absence of neighbourhood competition would increase the pay-off of firms in market A. This in turn implies that certain towns with a small population will be able to attract an incumbent due to spillovers from similarly uncovered neighbouring units. Since the standard model cannot capture this effect, it underestimates the profitability of those markets and generates lower threshold levels to accommodate the observed entry behaviour.
The conclusion that non-spatial models result in lower estimated entry thresholds is also confirmed when we use the full sample of towns (step 2). The estimates from these regressions are summarised in Tables 21 and 22. Once the full population of towns is taken into account, the threshold values move closer to those of the spatial model but still tend to be lower. Descriptive statistics detailing the distribution of population in our sample can be found in Table 23.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lábaj, M., Silanič, P., Weiss, C. et al. Market structure and competition in the healthcare industry. Eur J Health Econ 19, 1087–1110 (2018). https://doi.org/10.1007/s10198-018-0959-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10198-018-0959-1