1 Introduction

In this article, we are introducing the Carrier-Domain Method (CDM) for high-resolution computation of time-periodic long-wake flows. The CDM has both the cost-effectives needed to make the computations practical and the accuracy needed in the long-wake computations to correctly represent the vortex patterns far downstream. It is closely related to, and was actually inspired by, the Multidomain Method (MDM) [1], which was introduced 24 years ago, originally intended also for cost-effective computation of long-wake flows and later extended in scope to cover additional classes of flow problems.

In computation of long-wake flows with the MDM, the wake computation alone might be the final objective, or the ultimate objective might the computation of the wake influence on a secondary object placed far downstream. The computation is based on a sequence of subdomains with slight overlap between them. The first one covers the object producing the wake, and that would be the primary object if there is a secondary object downstream. The secondary object would be in the last subdomain. The velocity specified at the inflow boundary of the first subdomain is the free-stream velocity. The inflow velocity for each subsequent subdomain is extracted from the preceding subdomain. If the outflow boundary of a subsequent subdomain is also in the preceding subdomain, for example when the subsequent subdomain is fully inside the preceding subdomain, then the stress at the outflow boundary is also extracted from the preceding subdomain.

The first computations [1] with the MDM were 2D long-wake flow for a circular cylinder, which was a verification study, and 3D wake influence on a wing placed downstream of a larger wing. Other 3D computations conducted soon after that were a cylinder wake extending 300 diameters downstream [2], aerodynamics of a parachute crossing an aircraft wake [3], and fluid–structure interactions (FSI) of that parachute as it is crossing the aircraft wake [4]. The 3D cylinder computation was at Reynolds number 140. The secondary vortex street, appearing far downstream and known from laboratory experiments, was successfully captured. In the parachute computations, the first subdomain was for the aircraft and the near-wake flow. The second subdomain was for the long-wake flow. The third subdomain, which was for the parachute, was translating fully inside the second subdomain.

A different MDM version was used in the thermo-fluids computations reported in [5] for a freight truck and its rear tires. It was a spatially multiscale version with global and local domains. The global domain, as the primary domain, contained the entire truck, including all the tires. The local domain, as the secondary domain, contained the four rear (left) tires. The secondary domain was fully inside the primary domain, with their boundaries on the tire, truck, and road surfaces coinciding. A mesh with reasonable resolution was used in the primary computation. At the inflow boundary, the velocity and temperature were the free-stream values. At the outflow boundary, the stress and the normal component of the heat flux vector were zero. At the top and side computational boundaries, the normal component of the velocity, the tangential stress, and the normal component of the heat flux vector were zero. The computation generated a large amount of time-history data, which was stored with the “ST-C” [6] data compression, to be used in the secondary computation. A mesh with higher resolution was used in the secondary computation. The higher resolution was intended to increase the accuracy of the thermo-fluids analysis and tire heat transfer rates. At the inflow, top, and side computational boundaries, the velocity and temperature were specified, with the values specified at each time step extracted from the primary-computation data stored. The extraction was done by evaluating the temporal NURBS representation of the primary-computation velocity and temperature at the corresponding time. At the outflow boundary, the stress was extracted from the primary-computation data, and the normal component of the heat flux vector was set to zero. Where the primary- and secondary-domain boundaries coincided, the conditions specified for the secondary domain were the same as the conditions specified for the primary domain. The data extraction from the primary-computation data was by the least-squares projection, because, the nodal points of the secondary-domain boundaries cannot be expected to coincide with nodal points in the primary domain.

The MDM version used in the thermo-fluids computations of the freight truck and its tires was also used recently [7] in high-resolution isogeometric analysis of car and tire aerodynamics. The computational model had much of the complexities of the actual car and tire, such as the near-actual tire geometry, road contact, and tire deformation and rotation.The focus was on the tire aerodynamics, with high-resolution in both space and time. The influence of the aerodynamics of the car body was included, in the framework of the MDM, from the global computation with near-actual car body and tire geometries, carried out earlier [8] with a reasonable mesh resolution. The high-resolution local computation was for the left set of tires. It was performed in a nested MDM sequence over three subdomains. The first subdomain was for the front tire, the second for the front-tire wake flow, and the third for the rear tire. The inflow velocities were extracted from the global, first-subdomain, and second-subdomain computations. All remaining boundary conditions for the three subdomains were extracted from the global computation.

In [9, 10], the MDM was used in computation of flow over a complex terrain. The first subdomain was for flow over a flat plate, and the second subdomain for flow over the complex terrain. There was no overlap between the two subdomains. The inflow velocity of the second subdomain was coming, by weak enforcement, from the outflow velocity of the first subdomain.

The MDM in its originally intended way was used in [11] in aerodynamic and FSI analysis of two wind turbines that were placed back to back in an atmospheric boundary layer flow. The two turbines were the primary and secondary objects. There were three subdomains. The first one was for the first turbine and the near-wake flow, the second one for the long-wake flow, and third one for the second turbine. The computations in all subdomains were based on finite element discretization.

The velocity data from a plane located at 10 m downstream of the primary turbine in [11] was used in [12,13,14] as the inflow velocity in the IGA-based two-domain MDM computations of the wind turbine wake. The computational framework, together with a comprehensive set of proof of concept computations of the wake, was presented in [12], studies on spatial and temporal resolution in [13], and studies on spatial-refinement directional preference in [14]. In the MDM version introduced and tested in [12], a subsequent-subdomain computation starts some duration after the preceding-subdomain computation does, thus reducing the computational cost even more. The lag in the start time is from recognizing that there is no flow information for the subsequent-subdomain computation to advect before the preceding-subdomain computation advects the information from its inflow plane to its outflow plane. This version was used in all the studies reported in [13, 14]. The CDM was inspired by this version of the MDM.

Fig. 1
figure 1

The carrier domain (red), the ST domain swept by that (enclosed by the red dashed lines), candidate data extraction instants going back in time one period at a time (black circles with red fillling), and reporting ST domain (shaded blue)

Full size image

In the CDM, the computational domain moves in the free-stream direction, with a velocity that preserves the outflow nature of the downstream computational boundary. As the computational domain is moving, the velocity at the inflow plane is extracted from the velocity computed earlier when the plane’s current position was covered by the moving domain (see Fig. 1). The inflow data needed at an instant is extracted from one or more instants going back in time as many periods. It goes without saying that computing the long-wake flow with a high-resolution moving mesh that has a reasonable length would be far more cost-effective than computing it with a fixed mesh that covers the entire length of the wake. We are also introducing a CDM version where the computational domain moves in a discrete fashion rather than a continuous fashion. We will use the abbreviations “CDM-C” and “CDM-D” to identify the versions with continuous and discrete motion of the computational domain.

To demonstrate how the CDM works, we compute, with the CDM-C, the 2D flow past a circular cylinder at Reynolds number 100. At this Reynolds number, the flow has an easily discernible vortex shedding frequency and widely published lift and drag coefficients and Strouhal number. We compute the wake flow up to 350 diameters downstream of the cylinder, far enough to see the secondary vortex street. The computational platform is made of, in addition to the CDM-C, the Space–Time Variational Multiscale (ST-VMS) method [5, 15, 16], ST Isogeometric Analysis (ST-IGA) [15, 17, 18], and methods for calculating the stabilization parameters and related element lengths targeting IGA discretization [19, 20]. In the ST-IGA, the basis functions are quadratic NURBS in space and linear in time. The ST context of the ST-VMS is bringing higher-order accuracy (see [15, 16]), and the VMS feature is bringing better representation of the multiscale flow patterns. The ST-IGA is bringing higher accuracy in representing the cylinder geometry and flow solution.

1.1 ST-VMS

This subsection, included for completeness, is mostly from [7, 21, 22]. The ST-VMS is the core method used in the wake computations. It can serve as a moving-mesh method in computation of flow problems with FSI and moving boundaries and interfaces (MBI). It originated from and subsumes its precursor the Deforming-Spatial-Domain/Stabilized ST (DSD/SST) method [23,24,25]. The DSD/SST is mostly called “ST-SUPS,” with the abbreviation “SUPS” denoting the stabilization components SUPG and PSPG, which stand for the Streamline-Upwind/Petrov–Galerkin [26] and Pressure-Stabilizing/Petrov–Galerkin [23]. The ST-SUPS, in broader interpretation of the terminology, includes the stabilization component coming from Least-Squares on the Incompressibility Constraint (LSIC), as the DSD/SST in its form in [24] did. The VMS components of the ST-VMS are from the residual-based VMS (RBVMS) method [27,28,29,30]. The increased accuracy associated with the ST framework (see [15, 16, 31]) makes the ST-SUPS and ST-VMS appealing also in flow computations without MBI. Furthermore, the framework, naturally, makes it possible to use IGA basis functions also in time [31].

The arbitrary Lagrangian–Eulerian (ALE) moving-mesh framework is older, though its use in 3D finite element flow computations with modern stabilized methods like the SUPG is somewhat newer compared to the ST-SUPS. The ram-air parachute FSI analysis in [32] was one of the earliest computations with the ALE-SUPS. In the category of moving-mesh methods with the stabilization components coming from the RBVMS, however, the ALE-VMS method [33,34,35,36] precedes the ST-VMS. The ST-SUPS, ALE-SUPS, ALE-VMS, and ST-VMS, as methods, have much in common, and so do the classes of problems computed with them since their inception.

The classes of problems computed with the ALE-SUPS, RBVMS, and ALE-VMS include wind turbines [11, 37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57], turbomachinery [58,59,60,61,62,63,64], stratified flows [9, 65], bridges [66,67,68,69,70], marine applications [71,72,73], free-surface flows [74,75,76,77,78], two-phase flows [79,80,81,82,83,84,85], additive manufacturing [86], aircraft applications [87, 88], hypersonic flows [89], parachutes [32], cardiovascular medicine [33, 90,91,92,93,94,95,96,97,98,99,100,101,102,103], mixed ALE-VMS immersogeometric analysis [100, 104] (ALE-VMS/IMGA) computations [99,100,101, 105,106,107,108,109,110,111,112,113] in the framework of the fluid–solid interface-tracking/interface-capturing technique [114], and IMGA FSI and flow analysis [104, 115,116,117,118].

The classes of problems computed with the ST-SUPS and ST-VMS include those summarized in [119] (all computed in 1993–2018), wind turbines [10, 12,13,14, 35, 50, 52, 53, 120,121,122], turbomachinery [18, 52, 53, 123,124,125,126], ground vehicles and tires [5, 7, 8, 10, 54, 55, 127,128,129,130,131,132], fluid films [130, 132, 133], disk brakes [134], flapping-wing aerodynamics [17, 35, 135,136,137,138,139], spacecraft [140, 141], parachutes [35, 54, 55, 140, 142,143,144,145,146], cardiovascular medicine [22, 102, 103, 137, 147,148,149,150,151,152,153,154,155,156,157,158,159], Taylor–Couette flow [160, 161], U-ducts [162], higher-order temporal IGA discretization [31], and boundary-layer mesh resolution studies [21].

The ST-SUPS, ALE-SUPS, ALE-VMS, and ST-VMS, like all moving-mesh methods, need to be complemented with mesh update methods in FSI and MBI computations. The mesh update most of the time consists of moving the mesh to accommodate the motion of the boundaries and interfaces and to control the mesh resolution near solid surfaces that are moving, and remeshing if the element distortion exceeds an acceptable level. Since the inception of the ST-SUPS, a large number of special- and general-purpose mesh moving methods have been developed for computations with the ST-SUPS and ST-VMS. Some of them have also been used with the ALE-SUPS and ALE-VMS. A recent article [139] on mesh moving methods provides an overview. The general-purpose methods include, as the first one, the linear-elasticity mesh moving method with mesh-Jacobian-based stiffening [160, 163] and, as the most recent ones, the element-based mesh relaxation [142], where the mesh motion is determined by using the large-deformation mechanics equations and an element-based zero-stress state (ZSS) [164,165,166,167,168,169], mesh relaxation and mesh moving methods [170] based on fiber-reinforced hyperelasticity and optimized ZSS, and the linear-elasticity mesh moving method with no cycle-to-cycle accumulated distortion [157, 171].

1.2 ST-IGA

This subsection, included for completeness, is mostly from [7, 21]. The IGA basis functions in space brought major accuracy increases in fluid and solid mechanics computations [33, 90, 172, 173]. That made IGA basis functions appealing for the ST-SUPS and ST-VMS computations and led to the introduction of the ST-IGA, at the same time the ST-VMS was introduced. It is IGA discretization in the ST framework. The terminology “ST-IGA” implies, depending on the context, discretization with IGA basis functions in space or time or both. The test computations reported in [15], which were in 2D, were for flow past an airfoil and for pure advection of a scalar. The flow computation was with IGA basis functions in space, and the advection computations with IGA basis functions in both space and time, accompanied by a stability and accuracy analysis for the pure advection equation. The advection computations and stability and accuracy analysis showed what can naturally be expected, and that is, higher-order basis functions in space will deliver more if they are used together with higher-order basis functions in time. Keeping in mind that the increased accuracy the ST-IGA with IGA basis functions in space brings is attained with fewer control points, the effective element sizes will be larger. With that, larger time steps can be taken while still keeping the Courant number at or below the levels we target for good accuracy.

Using IGA basis functions in time is uniquely offered by the ST framework, and partly because of that the effort was focused on that track in the early years of the ST-IGA computations [15,16,17]. Taking advantage of that opportunity brings higher accuracy in representing the motion of a solid surface, a mesh motion consistent with that surface motion, and better efficiency in representing the mesh motion and in remeshing. The ST/NURBS Mesh Update Method (STNMUM) [17, 120] was built around these positive attributes of the ST-IGA. The ST-C is another example of the good things that come out of the ST-IGA with IGA basis functions in time. The letter “C” in “ST-C” means “continuous.” This is a method for extracting time-continuous data from the computed data, and it can work as a data compression method in dealing with large data volumes [5,6,7, 12,13,14, 52,53,55, 124, 125, 127, 134]. The classes of problems computed by using the ST-IGA with IGA basis functions in time include wind turbines [10, 50, 52, 53, 120,121,122], turbomachinery [18, 52, 53, 123,124,125,126], flapping-wing aerodynamics [17, 35, 135,136,137,138,139], spacecraft cover separation aerodynamics [140], and higher-order temporal IGA discretization [31].

The classes of problems computed by using the ST-IGA with IGA basis functions in space include wind turbines [10, 12,13,14, 52, 53, 122], turbomachinery [18, 52, 53, 123,124,125,126], ground vehicles and tires [7, 8, 10, 128,129,130,131,132], fluid films [130, 132, 133], parachutes [54, 55, 144, 146], cardiovascular medicine [22, 102, 103, 152,153,154,155,156,157,158,159], Taylor–Couette flow [161], U-ducts [161]. higher-order temporal IGA discretization [31], and boundary-layer mesh resolution studies [21]. It was pointed out as early as in 2007 (see [174]) that the image-based geometries used in patient-specific arterial FSI computations are not for the ZSS of the artery and that a ZSS estimation method is needed. The ZSS estimation methods introduced in and after 2016 [102, 166,167,168,169] stand on the IGA basis functions in space, and so does the related hyperelastic shell analysis [175, 176]. The IGA basis functions in space have also been a part of quite a few advanced computational methods targeting design and structural analysis, those reported in [177,178,179,180,181,182,183,184,185,186] are examples of that, and turbine blades and heart valves are among the examples.

1.3 Stabilization parameters and local length scales targeting IGA discretization

This subsection, included for completeness, is mostly from [7, 21, 22]. The stabilization terms of the ST-SUPS, ALE-SUPS, RBVMS, ALE-VMS, ST-VMS, and most stabilized methods have some factors called “stabilization parameters” [35] that multiply the residuals. Some of the parameters have the units of time, and some the units of kinematic viscosity. Those with the units of time are called “\(\tau _{{{\mathrm {SUPG}}}}\)” and “\(\tau _{{{\mathrm {PSPG}}}}\),” and the one with the units of kinematic viscosity is called “\(\nu _{{{\mathrm {LSIC}}}}\)” [187] (see Sect. 1.1 for the abbreviation “LSIC”). That is the terminology used in the context of the ST-SUPS, ALE-SUPS, RBVMS, ALE-VMS, and ST-VMS. The expressions introduced in [188] for stabilization parameters were for separate \(\tau _{{{\mathrm {SUPG}}}}\) and \(\tau _{{{\mathrm {PSPG}}}}\), and test computations with them were successful. Leaving that aside, a single parameter, “\(\tau _{{{\mathrm {SUPS}}}}\)” [15, 35], is used instead of two.

The expressions for the stabilization parameters involve, among other constituents, local lengths scales, also called “element lengths.” Precursors of the element lengths and stabilization parameters used with the SUPG, PSPG, ST-SUPS, ALE-SUPS, RBVMS, ALE-VMS, and ST-VMS can be found in [26, 189,190,191]. Designing good element lengths and stabilization parameters continued as a significant part of the research on residual-based stabilized methods. That generated a good number favorite expressions for the element lengths and stabilization parameters (see, for example, [5, 17, 24, 25, 120, 188, 192,193,194,195,196,197]), and until late 2017 they were all intended for finite element discretization. For about a decade, the element length was a local length scale in the flow direction, which is an advection length scale. A second local length scale, in the solution-gradient direction, was introduced in [194] and was identified as the diffusion length scale in [24]. Element lengths and stabilization parameters in the ST context were introduced in [24, 194], those specific to the VMS stabilization in [5], and those for coupled incompressible-flow and thermal-transport equations in [5]. Direction-dependent element lengths that have node-numbering invariance also for simplex elements were introduced in [197]. All these local length scales and stabilization parameters were intended for finite element discretization but have also been in use in computations with IGA discretization.

Local length scales and stabilization parameters targeting IGA discretization were introduced in 2017 in [19]. They would certainly also be suitable for use in computations with finite element discretization as a special case of IGA discretization. The expression introduced in [19] for the direction-dependent local length scale is from a conceptually simple three-step derivation. In the first step, the direction vector is mapped from the physical element to the parent element; in the second step, the discretization spacing along each of the parametric coordinates is accounted for; in the third step, what has been obtained in the parent element is mapped back to the physical element. Although the derivation steps were in the ST framework, reducing them to space only is straightforward. The stabilization parameters given in [129], which are largely from [19], are the current ones that have been in use in ST-VMS and ST-SUPS computations. In deriving the expressions for the local length scales, we do not have to use the standard integration parametric space. Instead, we can use a preferred parametric space that more effectively serves the purpose, which is obtaining good expressions. This idea was introduced and shown to work well in [20, 197, 198]. The expressions for the local local length scales include a transformation tensor that relates the two parametric spaces. Based on this idea, expressions for the direction-dependent local length scales targeting complex-geometry B-spline meshes were introduced in [20]. We require the local length scales to be invariant with respect to element splitting in B-spline meshes. Without that invariance, the flow solution would be influenced by something that it should not be influenced by. The expressions introduced in [20] meet that requirement, and the proof was given in [198].

The local-length-scale expressions introduced in [19, 20] have been used in computing the following classes of problems: wind turbines [10, 12,13,14, 122], turbomachinery [126], ground vehicles and tires [7, 8, 10, 129,130,131,132], fluid films [130, 132, 133], parachutes [146], cardiovascular medicine [22, 156,157,158,159], Taylor–Couette flow [161], U-ducts [162], higher-order temporal IGA discretization [31], and boundary-layer mesh resolution studies [21]. They have also been used in [63], following a gas turbine flow computation with IGA discretization, to calculate the Courant number from the local flow speed, time-step size, and mesh local length scale in the flow direction.

1.4 Outline of the remaining sections

The CDM is described in Sect. 2, the computations are presented in Sects. 3 and 4, and the concluding remarks are given in Sect. 5.

2 CDM

2.1 MDM and computational cost

Let us consider a time-periodic solution at a plane, with period T, which propagates with the free-stream velocity U. Just for illustration, we use a 1D context, and set the plane location as \(x=0\). This was the case, for example, in the wind turbine computations in [12,13,14]. We set our length scale as \(L = U T\). We assume that we want to know the time-dependent solution for the long domain 0 to kL. The example shown in Fig. 2 is for \(k=4\). We note that k does not have to be an integer. The figure shows how the computation can be carried over two ST domains with slight spatial overlap. This configuration represents the MDM version introduced in [12], where a subsequent-subdomain computation starts some duration after the preceding-subdomain computation does, instead of starting from \(t = 0\). The lag in the start time is from recognizing that there is no flow information for the subsequent-subdomain computation to advect before the preceding-subdomain computation advects the information from its inflow plane to its outflow plane. The total area of the ST subdomains, which is a rough estimate of the computing time, is \(Q = 42 LT = 42 U T^2\) (actually slightly more than that because of the overlap). That represents about 1/4 reduction in the computational cost. Going beyond that, we can reduce the computational cost further by stopping the preceding-subdomain computation at \(t=7T\) (see Fig. 3), and by completing the data set from the later periods of the computed data. That is under the assumption that by then the computed data is time-periodic or nearly time-periodic (see, for example, Fig. 4), from which a time-periodic data can somehow be built. Then, the total area of the ST subdomains is \(Q = 28 U T^2\). That represents about 1/2 reduction in the computational cost.

Fig. 2
figure 2

Two ST subdomains in Configuration 1

Full size image
Fig. 3
figure 3

Two ST subdomains in Configuration 2

Full size image
Fig. 4
figure 4

A fictitious time-periodic solution in the full ST domain. The gray shading is to represent the time-periodicity, which, in general, will not be reached before \(t = x/U\). In this specific example, we consider the solution to have time-periodicity on and above the line \(t = 2 T + x/U\)

Full size image

Generally, if we compute with a full computational domain, we need to compute for a duration of \((k+1)T\), making the area of the ST domain

$$\begin{aligned} Q&= kL (k+1)T \end{aligned}$$
(1)
$$\begin{aligned}&= k(k+1) UT^2. \end{aligned}$$
(2)

Based on the advection speed and the periodicity (see Fig. 4), we can compute over only a portion of the ST domain to obtain the time-periodic solution. Figure 5 shows, as an example, the ideal ST domain portion. Its area is

$$\begin{aligned} Q&= kL T \end{aligned}$$
(3)
$$\begin{aligned}&= k U T^2. \end{aligned}$$
(4)
Fig. 5
figure 5

The ideal ST domain portion to be computed over

Full size image

Remark 1

Comparing Eqs. (2) and (4), the reduction factor for the computational cost is \(\frac{1}{k+1}\).

Remark 2

We define T to be in general the highest time period we expect to see in the wake flow. In our specific case in this article, the relationship between T and the lift period \(T^{{\mathrm {L}}}\) is \(T = 2 T^{{\mathrm {L}}}\) (see Sect. 3.5).

2.2 CDM-C

Let us consider a computational domain with length \(L_{{\mathrm {c}}}\), meant to move with the velocity U (see Fig. 6). That is our “carrier domain.” The computation starts at \(t=2T\), with the carrier domain being stationary at the beginning and at the end. The area of the ST domain swept is \(Q = L \left( T + \frac{k L}{U}\right) = (k+1) U T^2\). In a typical computation, the flow information exists the domain from the outflow boundary. This means that even if the solution near the outflow plane is not as accurate as in the interior, the influence will not accumulate over time. However, in the example of Fig. 6, the flow information will not exit from the outflow plane. Therefore, moving the computational domain with the velocity U would not be practical.

Fig. 6
figure 6

CDM-C. The carrier domain (red) at an instant and the ST domain (enclosed by the red dashed lines) swept by that. In this illustration, \(L_{{\mathrm {c}}} = L\). The red circle with white filling indicates the current position of the inflow plane. The black circle with red filling indicates going back in time one period. The flow information at the left boundary will reach x at \(t = 2T + x/U\), therefore, from \(t=2T\) to 3T we are not showing below that line the solution we have in Fig. 4. (Color figure online)

Full size image

The carrier domain will move with velocity V, satisfying the condition

$$\begin{aligned} V < U. \end{aligned}$$
(5)

We represent it as \(V = \alpha _{{\mathrm {C}}} U\), where \(0< \alpha _{{\mathrm {C}}} < 1\), and the exit speed is \((1-\alpha _{{\mathrm {C}}})U\). To extract the inflow data going back at least one period, the domain length needs to be

$$\begin{aligned} L_{{\mathrm {c}}} \ge V T. \end{aligned}$$
(6)

Based on that, we express \(L_{{\mathrm {c}}}\) as

$$\begin{aligned} L_{{\mathrm {c}}} = \beta _{{\mathrm {C}}} V T, \end{aligned}$$
(7)

where \(\beta _{{\mathrm {C}}} \ge 1\). Figure 7 is for the case \(\beta _{{\mathrm {C}}} = 1\). The area of the ST domain is

$$\begin{aligned} Q&= L_{{\mathrm {c}}} \left( T + \frac{k L}{V}\right) \end{aligned}$$
(8)
$$\begin{aligned}&= (\alpha _{{\mathrm {C}}}+ k) U T^2. \end{aligned}$$
(9)

We examine the extraction of the inflow data further. In the cases like those in Figs. 6 and 7, we can go back only one period, and the extraction would be from the outflow plane of the carrier domain. Because the solution near the outflow plane would not be as accurate as in the interior, \(\beta _{{\mathrm {C}}} = 1\) would not serve our purpose well.

Fig. 7
figure 7

CDM-C. The carrier domain (red) at an instant and the ST domain (enclosed by the red dashed lines) swept by that. This is for the case \(\beta _{{\mathrm {C}}}=1\). As an example, we set \(\alpha _{{\mathrm {C}}} = 0.5\). The red circle with white filling indicates the current position of the inflow plane. The black circle with red filling indicates going back in time one period. The orange dotted line is \(t = 2T + x/U\); we are not showing below that line the solution we have in Fig. 4. (Color figure online)

Full size image

Given the observations above, we now introduce a version of CDM-C that would work without these shortcomings. How far we go back in time to extract the inflow data has to be less than \(L_{{\mathrm {c}}}/V = \beta _{{\mathrm {C}}} T\). To make the data extraction clearer, we split \(\beta _{{\mathrm {C}}}\) as \(\beta _{{\mathrm {C}}} = m + r\), where m is an integer and \(0 < r \le 1\). As an example, for \(\beta _{{\mathrm {C}}} = 2\), we would set \(m=1\) and \(r=1\) instead of \(m=2\) and \(r=0\) to avoid extracting the inflow data from the outflow plane of an earlier computation. Practically, using the smallest r is cost-effective, as long as the solution at rVT upstream of the outflow plane is reliable. In the example in Fig. 8, \(m = 2\) and \(r = 0.4\).

Fig. 8
figure 8

CDM-C. The carrier domain (red) at an instant and the ST domain (enclosed by the red dashed lines) swept by that. In this illustration, \(\alpha _{{\mathrm {C}}} = 0.5\), \(m=2\), and \(r=0.4\), making \(L_{{\mathrm {c}}} = 1.2 L\). The red circle with white filling indicates the current position of the inflow plane. Each black circle with red filling indicates going back in time one period. The orange dotted line is \(t = 2T + x/U\); we are not showing below that line the solution we have in Fig. 4. (Color figure online)

Full size image

To make the inflow-data extraction and time-periodicity of the solution consistent during the entire computation, we compute \((m+r) T\) with the carrier domain being stationary at the beginning and at the end. The area of the ST domain is

$$\begin{aligned} Q_{{\mathrm {C}}}&= L_{{{\mathrm {c}}}} \left( (m+r)T +\frac{kL}{V} \right) , \end{aligned}$$
(10)
$$\begin{aligned}&= (m+r)\left( ( m+r) \alpha _{{\mathrm {C}}} + k \right) U T^2. \end{aligned}$$
(11)

Now, we explain how the inflow boundary condition is extracted. We denote the inflow location at a given time t as \(x_{{\mathrm {inf}}}(t)\), and the computed solutions at t and x as u(x, t). With that, the inflow condition \(g(x_{{\mathrm {inf}}}(t), t)\) is

$$\begin{aligned} g(x_{{\mathrm {inf}}}(t), t)&= u(x_{{\mathrm {inf}}}(t), t-T) , \end{aligned}$$
(12)

if we can go back in time only one period. If we can go back in time m periods, then we set

$$\begin{aligned} g(x_{{\mathrm {inf}}}(t), t)&= \sum _{k=1}^{m} w_k u(x_{{\mathrm {inf}}}(t), t-k T) , \end{aligned}$$
(13)

where \(w_k\) are weights, and \(\sum \limits _{k=1}^m w_k = 1\). We can think of more complicated ways of doing this and enforcing periodicity; we will leave that as future investigation.

Remark 3

Even if \(k/\alpha _{{\mathrm {D}}}\) is an integer, because \(\beta _{{\mathrm {D}}} > 1\), the subdomains will have overlap, and that is how we wanted our method to be.

Remark 4

In reporting the data from the CDM-C computation, we will use the ST domain shown in Fig. 9.

Fig. 9
figure 9

CDM-C. Reporting ST domain (shaded in blue). (Color figure online)

Full size image

Remark 5

An additional good feature of the CDM-C is that the relative velocity with respect to the mesh becomes smaller, making the Courant number smaller. This leads to better accuracy under most flow conditions.

2.3 CDM-D

We are also introducing a CDM version where the computational domain moves in a discrete fashion. Before we describe the method we are actually proposing, like we did for the CDM-C, we go over some basic cases that come to mind first. Similar to what we did in the CDM-C with \(\alpha _{{\mathrm {c}}}=1\) and \(\beta _{{\mathrm {C}}}=1\), we split the domain into k subdomains of length \(L_{{\mathrm {c}}} = U T\). The computation over each is for a duration of 2T (see Fig. 10). The total area of the ST subdomains is \(Q = L (k 2 T) = 2 k U T^2\).

Fig. 10
figure 10

CDM-D. The ST subdomains (red). For this case, \(L_{{\mathrm {c}}} = U T\). The orange dotted line is \(t = 2T + x/U\); we are not showing below that line the solution we have in Fig. 4. (Color figure online)

Full size image

Remark 6

Unless k is an integer, we need to have subdomains with either different sizes or overlap. If there is overlap, Q would be somewhat larger.

Fig. 11
figure 11

CDM-D. The ST subdomains (red). This for the case \(\alpha _{{\mathrm {D}}}<1\). As an example, in this illustration, \(L_{{\mathrm {c}}} = 0.5 U T\). The orange dotted line is \(t = 2T + x/U\); we are not showing below that line the solution we have in Fig. 4. (Color figure online)

Full size image

Similar to what we did in CDM-C with \(\alpha _{{\mathrm {C}}}=0.5\) and \(\beta _{{\mathrm {C}}}=1\), in \(L_{{\mathrm {c}}} = \alpha _{{\mathrm {D}}} L\), we set \(0<\alpha _{{\mathrm {D}}}<1\). There are \(k/\alpha _{{\mathrm {D}}}\) ST subdomains. The computation over each is for a duration of \((1+\alpha _{{\mathrm {D}}})T\) (see Fig. 11). The start time for a subsequent-subdomain computation is arbitrary beyond \(\alpha _{{\mathrm {D}}} T\) because of the periodicity. The total area of the ST subdomains is

$$\begin{aligned} Q&= \alpha _{{\mathrm {D}}} L \left( 1 + \alpha _{{\mathrm {D}}}\right) \frac{k}{\alpha _{{\mathrm {D}}}} T \end{aligned}$$
(14)
$$\begin{aligned}&= \left( 1 + \alpha _{{\mathrm {D}}}\right) k U T^2, \end{aligned}$$
(15)

which implies that \(\alpha _{{\mathrm {D}}} < 1\) is more cost-effective.

Remark 7

If \(k/\alpha _{{\mathrm {D}}}\) is not an integer, Remark 6 for k applies to \(k/\alpha _{{\mathrm {D}}}\).

Neither \(\alpha _{{\mathrm {D}}}=1\) (first basic case) nor \(\alpha _{{\mathrm {D}}} < 1\) would serve our purpose well, because the inflow-data extraction is from the outflow plane of the earlier computation. We extend the length of the computational domain by a factor \(\beta _{{\mathrm {D}}} > 1\) to have overlap between the subdomains. The length becomes \(L_{{\mathrm {c}}} = \alpha _{{\mathrm {D}}} \beta _{{\mathrm {D}}} U T\), with the data extraction from \((\beta _{{\mathrm {D}}} - 1) \alpha _{{\mathrm {D}}} U T\) upstream of the outflow plane of the preceding-subdomain computation.

Fig. 12
figure 12

CDM-D. The ST subdomains (red). In this illustration, \(\alpha _{{\mathrm {D}}} = 0.5\), \(m=2\), \(r=0.2\), and \(\beta _{{\mathrm {D}}} = 1.2\). The blue lines denote the extent of the m periods, which is ending rT above the line \(t=2T+x/U\) (orange dotted line). We are not showing below that line the solution we have in Fig. 4. (Color figure online)

Full size image

To avoid inflow-data extraction on \(t = t_0 + x/U\) (note that \(t_0\) is just an example-dependent starting time, which is \(t_0 = 2 T\) in Fig. 4), we extend the ST domain also in the time direction. We increase it from \((m + \alpha _{{\mathrm {D}}}) T\) to \((m + r + \alpha _{{\mathrm {D}}}) T\). With that, we can extract the inflow data for the full m periods, while avoiding the line \(t = t_0+ x/U\). This was implicitly accounted for in the CDM-C due to the direct relationship between the extraction position and extraction time, which, with the same direct relationship, would have been \((\beta _{{\mathrm {D}}}-1) \alpha _{{\mathrm {D}}} L = U r T\). Figure 12 shows an illustration of the CDM-D, as we are proposing. The total area of the ST subdomains is

$$\begin{aligned} Q_{{\mathrm {D}}}&= \alpha _{{\mathrm {D}}} \beta _{{\mathrm {D}}} L \left( m + r + \alpha _{{\mathrm {D}}}\right) \frac{k}{\alpha _{{\mathrm {D}}}} T \end{aligned}$$
(16)
$$\begin{aligned}&= \beta _{{\mathrm {D}}} \left( m + r + \alpha _{{\mathrm {D}}}\right) k U T^2. \end{aligned}$$
(17)

Remark 8

Even if \(k/\alpha _{{\mathrm {D}}}\) is an integer, because \(\beta _{{\mathrm {D}}} > 1\), the subdomains will have overlap, and that is how we wanted our method to be.

Remark 9

In reporting the data from the CDM-D computation, we will use the ST domain shown in Fig. 13.

Fig. 13
figure 13

CDM-D. Reporting ST domain (shaded in blue). (Color figure online)

Full size image

Remark 10

The inflow-data extraction is easier in the CDM-D than it is in the CDM-C. That is because the extractions are also done in a discrete fashion. We have m periods of the data and there is already a method to build from that an actually time-periodic data (see Section 2.6 in [12]).

Remark 11

We have the freedom to select the starting time for each subdomain on and above the line \(t = t_0 + x/U\), and in the illustration of Fig. 12, we selected that line.

Remark 12

From Eqs. (11) and (17), we get

$$\begin{aligned} \frac{Q_{{\mathrm {D}}}}{Q_{{\mathrm {C}}}}&= \left( 1+ \frac{\alpha _{{\mathrm {D}}}}{m+r} \right) \frac{\beta _{{\mathrm {D}}}}{1 + \frac{m+r}{k} \alpha _{{\mathrm {C}}} } . \end{aligned}$$
(18)

Assuming that \(m \ll k\), \(1 + \frac{m+r}{k} \alpha _{{\mathrm {C}}} \sim 1\) and therefore the cost reduction is higher with the CDM-C than it is with the CDM-D.

3 Cylinder short-wake flow

We first compute the cylinder short-wake flow to establish the wake-flow time period and to generate the source data for the inflow velocity of the long-wake flow.

3.1 Domain and boundary conditions

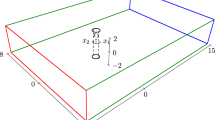
Figure 14 shows the computational domain and boundary conditions. We are working with nondimensional numbers, where the cylinder diameter and uniform inflow velocity are \(D = 1\) and \(U = 1\). The Reynolds number based on U and D is 100. The top and bottom boundaries and slip surfaces, and the outflow boundary is stress-free.

Fig. 14
figure 14

Cylinder short-wake flow. Computational domain and boundary conditions. Uniform-velocity inflow (red), stress-free outflow (blue), slip-surface top and bottom boundaries (green). (Color figure online)

Full size image

3.2 Mesh

Figure 15 shows the quadratic NURBS mesh, which consists of 7292 control points and 6582 elements. There are 14 layers of elements from the cylinder surface, and the first layer thickness is 0.1.

Fig. 15
figure 15

Cylinder short-wake flow. Quadratic NURBS mesh. Full mesh (top) and the layered elements near the cylinder (bottom). The red circles are the control points. The checkerboard pattern is for differentiating between the elements, and the colors are for differentiating between the patches. (Color figure online)

Full size image

3.3 Computational conditions

The flow computation method is the ST-VMS, and the stabilization parameters are those given by Eqs. (4)–(9) in [129]. We use the outflow stabilization given in [199]. The time-step size \(\varDelta t = 0.05\). The number of nonlinear iterations per time step is 4 and the number of GMRES iterations per nonlinear iteration is 300.

3.4 Results

The results are reported after reaching time-periodicity. Figure 16 shows the vorticity. The lift time period is established approximately as \(T^{{\mathrm {L}}} = 116 \varDelta t = 5.8\).

Fig. 16
figure 16

Cylinder short-wake flow. Vorticity at an instant after reaching time-periodicity

Full size image

3.5 Time-periodic data

We use the velocity at \(x_1=2\) as the source data for the inflow velocity of the long-wake flow. The conversion from the source data to time-periodic data is with a method similar to the one described in Section 2.6 of [12]. Figure 17 shows the velocity magnitude at \({\mathbf {x}} = (2,\ 0)\). One of the objectives in our computations is to see the secondary vortex street, which has the time period of \(2 T^{{\mathrm {L}}}\). Therefore, our time-periodic data at the inflow plane has the period \(T = 2 T^{{\mathrm {L}}} = 232 \varDelta t = 11.6.\)

Fig. 17
figure 17

Cylinder short-wake flow. The velocity magnitude at \({\mathbf {x}} = (2,\ 0)\). Source data (\({\mathbf {u}}_{{\mathrm {SRCE}}}\)), time-periodic data (\({\mathbf {u}}_{{\mathrm {PERI}}}\)), and time-periodic data (\({\mathbf {u}}^{{\mathrm {L}}}_{{\mathrm {PERI}}}\)) based on \(T^{{\mathrm {L}}}\)

Full size image

Remark 13

Although, the difference we see in Fig. 17 between \({\mathbf {u}}_{{\mathrm {PERI}}}\) and \({\mathbf {u}}^{{\mathrm {L}}}_{{\mathrm {PERI}}}\) is small, we see a significant difference between what we get from computations with them. We do not see the secondary vortex street in the computation with \({\mathbf {u}}^{{\mathrm {L}}}_{{\mathrm {PERI}}}\). This might be related to the observation in [200] that the secondary vortex street could only be obtained in the 3D computation.

4 Cylinder long-wake flow

Using the time-periodic data from Sect. 3.5, we compute the long-wake flow, first with a single, second subdomain in the framework of the MDM, and then with the CDM-C.

4.1 Wake domains and boundary conditions

Figure 18 shows the single, second subdomain (SD-2), the carrier domain (CD), and the boundary conditions. We note that, in the MDM terminology, the domain used in computation of the cylinder short-wake flow becomes “SD-1.” For both SD-2 and CD, as in Sect. 3.1, the top and bottom boundaries are slip surfaces, and the outflow boundary is stress-free. The inflow velocity for SD-2 is from Sect. 3.5, with the source data coming from the computation with SD-1. With CDM-C, we use \(\alpha _{{\mathrm {C}}} = 0.5\) and \(\beta _{{\mathrm {C}}} = 2.93\), which makes \(L_{{\mathrm {c}}} = 1.465UT\). The inflow velocity for CD is from Sect. 3.5 while it is stationary at its initial position, and from Eq. (12) while it is moving or at its final position.

Fig. 18
figure 18

Cylinder long-wake flow. Top: The single, second subdomain (SD-2) in the framework of the MDM. Bottom: The carrier domain (CD) at its initial and final positions. Boundary conditions: inflow (red), stress-free outflow (blue), and slip-surface top and bottom boundaries (green). The inflow velocity for SD-2 is from Sect. 3.5. The inflow velocity for CD is from Sect. 3.5 while it is stationary at its initial position, and from Eq. (12) while it is moving or at its final position

Full size image

4.2 Meshes

The quadratic NURBS meshes in SD-2 and CD have almost the same resolution as the mesh in SD-1. The number of control points and elements are shown in Table 1.

Table 1 Number of control points (nc) and elements (ne) in the SD-2 and CD meshes, in the product form of the numbers in the \(x_1\) and \(x_2\) directions
Full size table

4.3 Computational conditions

The computational conditions are the same as in Sect. 3.3, except the number of GMRES iterations per nonlinear iteration for the CDM-C computation, which is reduced to 80.

In the MDM computation, the initial condition is U everywhere, except the inflow boundary. We compute for 37T. The inflow velocity is time-periodic, coming from Sect. 3.5.

In the CDM-C computation, CD is stationary for \(0 \le t < 5 T\), a duration longer than \(\beta _{{\mathrm {C}}}T\). For this part of the computation, the initial condition is U everywhere, except the inflow boundary. Then, CD moves with the speed \(V = 0.5U\) for \(5 T \le t \le 62.07 T\), and becomes stationary again for \(62.07 T < t \le 65 T\). For \(0 \le t < 5 T\), the inflow velocity is time-periodic, coming from Sect. 3.5. After that, the inflow velocity is extracted in the framework of the CDM-C, as given by Eq. (12). Although we have data for \(m = 2\), we do not go back in time beyond \(m = 1\). This is because we wanted to reduce the influence of the outflow boundary condition, especially considering that we are computing at such a low Reynolds number.

4.4 Results

4.4.1 MDM computation

Figure 19 shows, for the MDM computation, the vorticity at \(t = 37 T\). The vortices have a vertical pattern in the near wake and gradually change to a horizontal pattern moving downstream. We consider the region from \(x_1 = 89\) to 176 to be the transition to the secondary vortex street. In the region from \(x_1 = 263\) to 350, the secondary vortex street is fully formed. The spacing between the vortices in the secondary vortex street is, as expected, about twice as large compared to the spacing in the first one.

Fig. 19
figure 19

Cylinder long-wake flow. MDM computation. Vorticity at \(t= 37 T\)

Full size image

4.4.2 CDM-C computation

Figures 20, 21, 22 and 23 show, for the CDM-C computation, the vorticity at various instants. We see the effect of the outflow boundary condition, especially when we compare frames with spatial overlap. As we report the data, we will be sufficiently far from the outflow (see Remark 4).

Fig. 20
figure 20

Cylinder long-wake flow. CDM-C computation. Vorticity. The integer-T instants when the inflow plane is in the first quarter

Full size image
Fig. 21
figure 21

Cylinder long-wake flow. CDM-C computation. Vorticity. The integer-T instants when the inflow plane is in the second quarter

Full size image
Fig. 22
figure 22

Cylinder long-wake flow. CDM-C computation. Vorticity. The integer-T instants when the inflow plane is in the third quarter

Full size image
Fig. 23
figure 23

Cylinder long-wake flow. CDM-C computation. Vorticity. The integer-T instants when the inflow plane is in the fourth quarter

Full size image

4.5 Discussion

In Fig. 24, we compare the vorticity from the MDM and CDM-C computations. The MDM data is repetition from Fig. 19. The CDM-C data is from patching together integer-T sections of the reporting ST domain shown in Fig. 9. They are in excellent agreement. The estimated cost reduction based on the ST areas is about 91 %, and the cost multiplier coming from solving the linear equation systems is about 27 %, because of the fewer number of GMRES iterations, and even less because of the smaller system size.

Fig. 24
figure 24

Cylinder long-wake flow. Vorticity from the MDM (top) and CDM-C (bottom) computations. The MDM data is from Fig. 19. The CDM-C data is from patching together integer-T sections of the reporting ST domain shown in Fig. 9

Full size image

5 Concluding remarks

We have introduced the CDM for high-resolution computation of time-periodic long-wake flows. The CDM has both the cost-effectives needed to make the computations practical and the accuracy needed in the long-wake computations to correctly represent the vortex patterns far downstream. It is related to the MDM, which was introduced 24 years ago, with the original version intended also for cost-effective computation of long-wake flows. Some of the later versions of the MDM extended the scope to additional classes of flow problems, and some increased the efficiency in computing the long-wake flows. In the original MDM version, the wake flow is computed over a sequence of subdomains with slight overlap between them. The first one covers the object producing the wake, and that would be the primary object if there is a secondary object downstream. The secondary object would be in the last subdomain. The velocity specified at the inflow boundary of the first subdomain is the free-stream velocity. The inflow velocity for each subsequent subdomain is extracted from the preceding subdomain. In the latest MDM version, which was also intended for long-wake flows, in computing the wake flow over a sequence of subdomains, a subsequent-subdomain computation starts some duration after the preceding-subdomain computation does, thus reducing the computational cost even more. The lag in the start time is from recognizing that there is no flow information for the subsequent-subdomain computation to advect before the preceding-subdomain computation advects the information from its inflow plane to its outflow plane. The CDM was inspired by this version of the MDM.

In the CDM, the computational domain moves in the free-stream direction, with a velocity that preserves the outflow nature of the downstream computational boundary. As the computational domain is moving, the velocity at the inflow plane is extracted from the velocity computed earlier when the plane’s current position was covered by the moving domain. The inflow data needed at an instant is extracted from one or more instants going back in time as many periods. Naturally, computing the long-wake flow with a high-resolution moving mesh that has a reasonable length would be far more cost-effective than computing it with a fixed mesh that covers the entire length of the wake. We have also introduced a CDM version where the computational domain moves in a discrete fashion rather than a continuous fashion. The abbreviations CDM-C and CDM-D identify the versions with continuous and discrete motion of the computational domain.

We demonstrated how the CDM works by computing, with the CDM-C, the 2D flow past a circular cylinder at Reynolds number 100. At this Reynolds number, the flow has an easily discernible vortex shedding frequency and widely published lift and drag coefficients and Strouhal number. We computed the wake flow up to 350 diameters downstream of the cylinder, far enough to see the secondary vortex street. The computational platform was made of, in addition to the CDM-C, the ST-VMS, ST-IGA, and methods for calculating the stabilization parameters and related element lengths targeting IGA discretization. In the ST-IGA, the basis functions were quadratic NURBS in space and linear in time. The ST context of the ST-VMS brought higher-order accuracy, the VMS feature brought better representation of the multiscale flow patterns, and the ST-IGA brought higher accuracy in representing the cylinder geometry and flow solution. The results show the power of the CDM in high-resolution computation of time-periodic long-wake flows.