1 Introduction

Radio telescopes are large technical facilities, that are, among other possible applications such as radio astronomy and astrophysics, deep space tracking or astrometry, used as space geodetic instruments for geodetic very long baseline interferometry (VLBI) observations. Due to various effects, the geometry of these space geodetic instruments can deviate significantly from their ideal geometric representation. These deviations restrict the reliability of the derived geodetic VLBI products, e.g., the estimated station coordinates. For instance, variations of the environmental temperature cause thermal expansion of the telescope structure (e.g., Haas et al. 1999), thus influencing the dimension of the instruments. Automated one-dimensional measuring systems yield seasonal variations of the vertical component of several millimeters caused by changes in temperature (e.g., Johansson et al. 1996; Zernecke 1999). According to Wresnik et al. (2007), the thermal expansion can be modeled, if representative expansion coefficients of the structure are known and the relevant temperature is recorded. Moreover, strategies for continual estimation of the geometrical reference point have been derived (e.g., Lösler 2009; Kallio and Poutanen 2012; Ning et al. 2015; Lösler et al. 2018a) and allow for monitoring the spatial position of the telescope. Mähler et al. (2018) recently report seasonal horizontal variations of about 0.2–0.4 mm. Neidhardt et al. (2010) derived daily variations of the telescope tower caused by the path of the Sun and corresponding unidirectional warming.

Besides external influences, the geometry of the main reflector surface may deform by the reflector’s structural weight. During a geodetic VLBI observation session, a radio telescope points sequentially to several radio sources in different directions. Depending on the pointing direction, different structural loads may occur. For large conventional radio telescopes, variations of the focal length between several millimeters up to the centimeter level have been detected (e.g., Sarti et al. 2009; Nothnagel et al. 2013; Bergstrand et al. 2019). The Global Geodetic Observing System (GGOS) calls for high-accuracy station positions at the millimeter level for deriving a reliable global geodetic reference frame (e.g., Rothacher et al. 2009). Deviations in the signal path affect the accuracy of VLBI and result in systematic biases of the estimated vertical positions of the radio telescopes and, therefore, potentially even affect the estimated scale of derived global geodetic reference frames such as the International Terrestrial Reference Frame (ITRF) (cf. Sarti et al. 2011). To reach the GGOS requirements, these signal path variations (SPV) should be taken into account in the analysis of geodetic VLBI data. For that reason, the VLBI community has been encouraged to include structural gravitational deformation models for VLBI radio telescopes for the upcoming ITRF2020 (cf. Altamimi et al. 2018). Therefore, the International VLBI Service for Geodesy and Astrometry as well as the IERS Working Group on Site Survey and Co-location focus on measuring and modeling gravitational deformations for as many VLBI radio telescopes as possible (cf. Bergstrand 2018; Gross and Herring 2018). An important point in this context is that the telescopes in general show individual deformation behavior (cf. Sarti et al. 2009; Nothnagel et al. 2013; Bergstrand et al. 2019), and thus each type of telescope has to be measured and modeled individually.

In the framework of the VLBI 2010 agenda (Niell et al. 2006), several new radio telescopes have been planned, are under construction, or have already been installed. The goal is to improve the existing network of the International VLBI Service for Geodesy and Astrometry (e.g., Schlüter and Behrend 2007; Nothnagel et al. 2017) and to reach the accuracy requirements that are specified by GGOS. VGOS radio telescopes are new generation VLBI instruments with a more compact design, stiffer mechanical structure, and faster drive systems than conventional radio telescopes. Usually, the diameter of the main reflector is about 12–13 m (e.g., Haas 2013). So far, the deformation of the reflector system and its possible impact on the optical ray path have not yet been investigated, except from finite element analysis performed by the manufacturers. The investigation presented in this manuscript focuses therefore on observations of the deformational behavior of a VGOS-specified radio telescope, exemplified at the Onsala twin telescopes (OTT) project of the Onsala Space Observatory (OSO). The OTT are equipped with ring-focus paraboloids as the main reflectors and rotational-symmetric Gregorian sub-reflectors. Often this kind of telescope type is referred simply to as ring-focus telescope.

Section 2 discusses methods for measuring the main reflector surface of VLBI radio telescopes in terms of spatial restriction, expected uncertainties, and the accuracy requirements that shall be achieved. Moreover, the UAS-based data collection and the data preparation are described. The mathematical model of the ring-focus paraboloid is derived in Sect. 3. Similarities of this model to the simplified rotationally symmetric paraboloid are highlighted. Section 4 introduces the applied SPV model of a ring-focus paraboloid. The data analysis and the results are explained in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Surface measurement methods

The goal in the framework of reverse engineering is to derive model-specific geometric parameters, e.g., dimension, curvature or orientation, by measuring an object. To quantify the parameters of the signal path of VLBI radio telescopes and their possible variations, several measurement methods with various limitations exist. The choice of the measurement method depends on the surrounding conditions, the accuracy requirements, and the size of the expected deformations. The measurement effort increases, if the main reflector is observed in several elevation angles, i.e., from \(0^{\circ }\hbox { to }90^{\circ }\). For instance, the use of tactile observation methods such as theodolite measurement systems or laser trackers is not suitable because of the time-consuming single-point measurement mode. Moreover, a stable platform is needed to carry out measurements in several elevation positions. Close-range photogrammetric methods usually require a crane for mounting coded targets on the reflector surface and for the data acquisition itself (e.g., Shankar et al. 2009; Süß et al. 2012). Furthermore, the spatial restrictions around the radio telescope limit this method, especially if the radio telescope is enclosed by a protecting radome like for the 20 m telescope at Onsala.

As an alternative to close-range photogrammetry, the capability of terrestrial laser scanners as a targetless method was investigated in recent years (e.g., Dutescu et al. 2009; Sarti et al. 2009). Technical innovations and a deeper understanding of instrument-dependent systematic errors were introduced to the measurement and analysis process in order to achieve reliable results (e.g., Lichti 2007, 2010; Holst et al. 2017). The possible mounting points of the laser scanner are limited by the construction parts of the radio telescope. In general, a single position close to the sub-reflector is chosen, which allows observing nearly the full reflector surface and avoiding glancing intersections (cf. Holst et al. 2017; Bergstrand et al. 2019).

The OTT are free-standing radio telescopes designed as ring-focus paraboloids with fixed rotational-symmetric Gregorian sub-reflectors (e.g., Haas 2013). The system focal point is located close to the sub-reflector and enclosed inside the receiver cone where the feed horn and receiver are located. Due to shading effects of this construction, measurements taken from a single position are incomplete. For this reason, in case laser scanning should be performed, several laser scanner positions would be needed to achieve a complete 3D-point cloud that covers the entire surface of the main reflector.

Photogrammetric methods on the other hand are unaffected by such constructional restrictions, because the observed points are derived from a large number of images taken at different camera positions. Advantageous camera positions induce additional reliable intersection conditions during image processing. Moreover, the camera positions vary without changing the radio telescope configuration.

As pointed out before, besides the limiting constructional conditions, there are further aspects, i.e., the accuracy requirements and the expected deformations. To reach the VLBI 2010 goal of 1 mm position accuracy, Petrachenko et al. (2009) advise sub-millimeter for surface accuracy and path length stability for VGOS-specified radio telescopes. If these stability requirements cannot be fulfilled, corresponding correction functions for compensating signal path variations are needed that can be applied in the VLBI data processing. Due to the compact construction of VGOS-specified radio telescopes, i.e., the diameter of the main reflector is about 12–13 m, deformations of about 1 mm are expected. For comparison, the reported SPV of the conventional 100 m radio telescope Effelsberg is about 1 cm (cf. Artz et al. 2014). Following the \(3\sigma \)-rule of thumb in geodesy and metrology, which states that the measurement system should be at least three times better than the expected deformations (cf. Koch 2007, p. 47), the measurement method for VGOS-specified radio telescopes should be on the level of 0.3 mm. Optical methods such as close-range photogrammetry or laser tracker systems fulfill this rule of thumb (e.g., Baars 2007, p. 167f; Luhmann 2018, p. 696f) but need a stable platform or a crane. To overcome the necessity of a crane during the measurement process, we used an unmanned aircraft system (UAS) in this investigation.

2.1 Photogrammetric measurements using UAS

A UAS consists of an unmanned aerial vehicle (UAV) and a ground-based station for remote control. Usually, the UAV is operated in a semiautomatic mode using a predefined flight plan. The flight plan schedules the waypoints to be achieved, the velocities of the UAV, the trigger points for the camera, etc. Several onboard sensors such as an inertial measurement unit (IMU), a global navigation satellite system (GNSS) antenna/receiver, and a magnetometer are used for automated orientation and positioning. Typically, critical flight phases such as take off and landing as well as unforeseen deviations from the flight plan have to be operated manually.

The time of flight of a UAV is restricted by the capacity of its batteries and depends on the weight of the camera. On the one hand, the use of a heavy weight, geometric stabilized and calibrated photogrammetric camera yields more reliable image measurements, but on the other hand, reduces the possible flight time. This reduces the number of images and, therefore, the redundancy of the observations as well as the reliability of the adjusted coordinates. Thus, the possible accuracy benefit of such a calibrated photogrammetric camera has to be balanced with respect to the possible operational time. In this campaign, the use of a lightweight 380 g consumer camera increases the flight time from 10 min to at least 25 min, allowing the acquisition of up to approximately 250 images. The used Sigma DP3 Merrill is equipped with a fixed 50 mm medium-telephoto lens (equivalent to a 75 mm lens on a 35 mm Single Lens Reflex (SLR) camera) and has an APS-C Sensor (\(16\,\hbox {mm} \times 24\,\hbox {mm}\)) based on the Foveon chip (e.g., Greiwe and Gehrke 2013a). This image sensor captures full color information for each pixel in contrast to color filter arrays such as Bayer pattern, where each element of the photodiode array is only sensitive for one waveband. Using a Foveon chip, the full color is observed without interpolations (e.g., Hubel et al. 2004; Verhoeven 2010). Figure 1 depicts the differences in acquired spectral information between a Foveon-based sensor and a color filter array such as the Bayer pattern. As a result of this sensor technique, the images have better micro-contrast compared to Bayer pattern sensors which leads to better image measurements, e.g., target detection (cf. Greiwe and Gehrke 2013b; Meißner et al. 2017).

Fig. 1
figure 1

Differences in spectral information acquirement between Foveon-based sensor (left) and color filter arrays such as Bayer pattern (right) (Verhoeven 2010)

Full size image

Photogrammetric measurement campaigns were carried out two times from elevation \(0^{\circ }\) up to \(90^{\circ }\) using a step-size of \(10^{\circ }\), as well as once at \(34^{\circ }\). The latter was done since the telescope manufacturer adjusted the reflector panels at this elevation. For each elevation angle, the flight path consisted of two centered flight lines crossing the center of the paraboloid and two additional concentric spatial circles around the axis of symmetry of the main reflector. The distance between the geometrical reference point and the flight lines as well as the inner circle is about 20 m. The distance of the outer circle is about 25 m. Both circles have different radii, i.e., \(r_{\mathrm {in}} = 6.5\,\hbox {m}\) and \(r_{\mathrm {out}} = 11.5\,\hbox {m}\). Figure 2 depicts the flight schedule of the UAV for elevation angle \(30^{\circ }\), using the topocentric UTM system. To avoid critical flight phases at lower elevation angles, the altitude of waypoints was limited and, here, the outer circle was planed as shell shape. However, the reflector could be captured even in this configuration by tilting the camera gimbal, since the camera was controlled and triggered remotely by the pilot. The gimbal-mounted camera allowed to point the camera nearly to the diametrical part of the main reflector for each taken image. Thus, the sub-reflector was pictured in every image. Due to the close distance to the telescope, each image contained only a part of the main reflector surface. On average, 40 coded targets were captured per image.

The main reflector was observed in 21 elevation angles by single measurement campaigns. Each campaign was taken during one flight. In total, 21 separate image blocks containing about 200 images were recorded. To avoid varying shading and illumination effects caused by the Sun, the telescope was pointed to the north, sheltering a part of the UAV flight path from wind. Unpredictable wind gusts led to about 25% of the images being blurred, so that for each campaign at least 150 images remained for further processing.

Fig. 2
figure 2

The flight schedule of the UAV for elevation angle \(30^{\circ }\), consisting of two flight lines as well as two concentric circles. The flight lines as well as the circles are parallel to the XY-plane of the defined object coordinate frame. The distance of the inner circle and the flight lines to the reference point is about 20 m. The distance between the reference point and the outer circle is about 25 m. The radii of the inner and the outer circle are about 6.5 m and 11.5 m, respectively

Full size image
Fig. 3
figure 3

ONSA13NE during the UAV measurement campaign. The telescope is equipped with photogrammetric targets, coordination cross at the sub-reflector, and scale-bars located at the sub-reflector, the strut elements, and at the rim of the main reflector. The UAV (HP-TS960) carrying the photogrammetric camera is visible in the upper left corner of the photo

Full size image

Figure 3 depicts ONSA13NE that was equipped with 76 discrete black and white, non-reflecting 12-bit coded targets. The main reflector of ONSA13NE consists of 60 panels mounted in three concentric rings, whereas the outer and the middle rings have 24 panels each, the inner ring consists of 12 panels. Sixty coded targets were glued at the outer parts of the panels, i.e., one target per panel. To improve the distribution of the points, additionally 12 coded targets were glued at the inner part of the panels of the inner ring close to the receiver cone. Four coded targets were attached at the sub-reflector. Moreover, a coordinate cross, which approximately defines the global datum of the resulting point sets by six coded targets, was mounted close to the sub-reflector. As shown in Fig. 2, the origin of the resulting global frame is close to the sub-reflector, the Z-axis points approximately in the direction of the symmetry axis of the main reflector, the X-axis is approximately parallel to the elevation axis, and the Y-axis is perpendicular to X and Z, respectively.

To transform the resulting point sets of the bundle adjustment (see Sect. 2.2) into a metric system (cf. Luhmann 2018, Ch. 7.1.5.2), six scale-bars with coded targets were attached. The scale-bars are made of carbon fiber with a thermal expansion coefficient of about \(\gamma _{\mathrm {c}} = 10^{-7}\,\hbox {K}^{-1}\). Three scale-bars were evenly distributed at the rim of the main reflector, covering the measurement space in the XY-plane of the image–block configuration defined by the coordinate cross. To avoid block deformations in the Z-direction, two scale-bars were mounted on the struts, and one at the sub-reflector. To avoid possible unanticipated time-dependent effects and to decorrelate the campaigns observed by equal elevation angles, no direct repetition was carried out, cf. Table 1. The photogrammetric camera, the Sigma DP3, was carried by the hexacopter HP-TS960 (HEXAPILOTS) and appears in the left upper corner of Fig. 3.

2.2 Data preparation

The well-known collinearity equations yield the functional relation of the planar image coordinates \((\begin{array}{c@{\quad }c} x_i'&y_i' \end{array})^{\mathrm {T}}\) and the corresponding three-dimensional object coordinates \({\mathbf {P}}_i= \left( \begin{array}{c@{\quad }c@{\quad }c} X_i&Y_i&Z_i\end{array}\right) ^{\mathrm {T}}\) by (e.g., Luhmann 2018, Ch. 4.2.2)

$$\begin{aligned} { x_i' = x'_0 -c \frac{ q_{11} \left( X_i-X_0'\right) + q_{21} \left( Y_i-Y_0'\right) + q_{31} \left( Z_i-Z_0'\right) }{q_{13} \left( X_i-X_0'\right) + q_{23} \left( Y_i-Y_0'\right) + q_{33} \left( Z_i-Z_0'\right) } + {{\Delta } x'} , } \nonumber \\\end{aligned}$$
(1a)
$$\begin{aligned} { y_i' = y'_0 -c \frac{ q_{12} \left( X_i-X_0'\right) + q_{22} \left( Y_i-Y_0'\right) + q_{32} \left( Z_i-Z_0'\right) }{q_{13} \left( X_i-X_0'\right) + q_{23} \left( Y_i-Y_0'\right) + q_{33} \left( Z_i-Z_0'\right) } + {{\Delta } y'} . }\nonumber \\ \end{aligned}$$
(1b)

Here, the interior orientation parameters, which are usually constant for all images of a photogrammetric bundle, are the principal distance c, the principal point \(x_0'\), \(y_0'\) and the distortion effect parameters \({{\Delta } x'}\), \({{\Delta } y'}\), which compensate for the radial–symmetric lens distortion and the decentering distortion (e.g., Luhmann 2018, Ch. 3.3.2). The parameters of the exterior orientation refer to the position \((\begin{array}{c@{\quad }c@{\quad }c} X_0'&Y_0'&Z_0' \end{array})^{\mathrm {T}}\) and the orientation \({\mathbf {Q}}\) of the camera w.r.t. the global reference frame. Here, \({\mathbf {Q}}\) is the orthogonal rotation matrix, which fulfills the conditions \(\mathbf {Q^\mathrm {T}}{\mathbf {Q}} = {\mathbf {Q}}{\mathbf {Q}}^\mathrm {T} = {\mathbf {I}}\) and \({\mathbf {Q}}^\mathrm {T} = {\mathbf {Q}}^{-1}\) (e.g., Nitschke and Knickmeyer 2000), having elements \(q_{k,l}\), i.e.,

$$\begin{aligned} {\mathbf {Q}}&= \left( \begin{array}{c@{\quad }c@{\quad }c} q_{11} &{} q_{12} &{} q_{13} \\ q_{21} &{} q_{22} &{} q_{23} \\ q_{31} &{} q_{32} &{} q_{33} \\ \end{array} \right) . \end{aligned}$$

Whereas the coordinates of an object are uniquely mapped on the planar image coordinates by Eq.  (1), the reconstruction of object coordinates from planar image coordinates needs two images picturing the same object. To increase the reliability of the derived object coordinates, usually images are taken from several camera positions and a bundle adjustment is used to solve the resulting over-determined equation system. Figure 4 illustrates the functional relation of the planar image coordinates and corresponding three-dimensional object coordinates of an image–block configuration.

Fig. 4
figure 4

Schematic representation of an image–block configuration consisting of three images which take two object points. The two object points and the three camera positions are depicted by red circles and diamonds, respectively. The six resulting planar coordinates are symbolized by red squares

Full size image

The recorded images of each single campaign were introduced to a bundle adjustment using the AICON 3D Studio software package. Besides the coded targets, natural circular targets at the telescope, e.g., screws, were detected by the software. On average, more than 500 points were used during the adjustment process. These natural targets were introduced only to improve the estimation of the interior and exterior orientations during the bundle adjustment. For further analysis, only coded targets were stored after the bundle adjustment. Figure 5 shows the high number of image measurements per coded target (between 13 and 136). The average value is about 55 images per coded target. The variation in the number of image measurements per coded target results from the environmental conditions (e.g., wind) during the flight of the UAV and the flight configuration (flight lines and circles). Coded targets, which are located closer to the center of the main reflector, were more frequently measured than targets at the rim (circular flights around the telescope). However, each estimated position was derived from highly redundant observations. Thus, a consecutive hypothesis test strategy was applied (e.g., Lehmann and Lösler 2016) to evaluate the reliability of the observed planar image coordinates and to eliminate outliers during the bundle adjustment.

Fig. 5
figure 5

Distribution of the coded targets per image. The number of images is accumulated. The minimum number is colored in dark gray. The average number of images per coded target is given by summing the dark gray and the red bars. Accumulating all bars yields the maximum number of images per coded target. The minimum, maximum and average are pictured by horizontal lines, respectively

Full size image

Consumer cameras such as the Sigma DP3 Merrill are not geometrically stabilized. Turning off the camera after a flight (to exchange the battery of the UAV) may change the interior orientation of the camera. As a result, all images that were acquired in an image–block configuration were taken without turning off the camera, which means they were taken in one flight for each elevation angle. Additionally, the interior orientation of the camera model, including the principal distance, the coordinates of the principal point, the radial–symmetric lens distortion and the decentering distortion, were calibrated in situ, during the bundle adjustment for each single campaign (e.g., Förstner and Wrobel 2016, Ch. 15.5; Luhmann 2018, Ch. 4.4.2).

Each photogrammetric bundle was processed separately as a free-network adjustment. The formal error of the coordinate components of the coded target positions in the global frame was about \(10\,\upmu \hbox {m}\) w.r.t. the datum. However, the formal error does not take into account the limited accuracy of the GNSS sensor, the unpredictable slight wind gusts, or different illumination environments, which all affect the resulting image–block configuration. Moreover, the in situ-derived calibration parameters as well as the telescope temperature may slightly change during the flight campaigns. Based on extensive additional experience with the measurement system, more reliable uncertainties for the coordinate components of the coded target positions were estimated to be between 80 and \(120\,\upmu \hbox {m}\) w.r.t. the datum. These single-point uncertainties are slightly larger than for high-precision photogrammetric cameras (e.g., Subrahmanyan 2005; Baars 2007, p. 167f; Luhmann 2018, p. 696f) but fulfill the requirements for detecting the expected deformations.

The telescope monument, i.e., the base and the mechanical structure of a radio telescope, is made of concrete and metal parts which are affected by temperature changes (e.g., Haas et al. 1999; Nothnagel 2009). In contrast to the thick structural elements of the monument, where the time between a change in the air temperature and the corresponding expansion is delayed by several hours, the construction parts of the main reflector are thinner. Therefore, the time delay between a temperature change and the corresponding expansion has been assumed to be less than 30 min.

Figure 6 depicts the temperatures that were recorded close to the telescope during the measurement period. A representative value for each campaign was derived by averaging the temperature over the time span of the campaign and is plotted as a red dot, see Table 1. The error bars indicate the \(2\sigma \) (standard deviation) interval of the campaign temperature and are derived by assuming a uniform distribution (e.g., JCGM100 2008), i.e.,

$$\begin{aligned} \sigma ^2= & {} \frac{1}{12} \left( b_{\mathrm {max}} - b_{\mathrm {min}}\right) ^2. \end{aligned}$$
(2)

Here, \(b_{\mathrm {min}}\) and \(b_{\mathrm {max}}\) define the two boundaries of the distribution and are selected accordingly to the recorded minimum and maximum campaign temperatures.

Fig. 6
figure 6

Recorded air temperature close to ONSA13NE is plotted in gray color for the measuring period in August 2018. A red dot with error bars (\(2\sigma \)) depicts the average temperature of each campaign. The uncertainties are derived by assuming a uniform distribution of the temperature during each campaign

Full size image

The variation in the campaign temperature is \(<2\,\hbox {K}\) but yields an expansion sensitivity of \(20\,\upmu \hbox {m}\hbox { m}^{-1}\) if \(\gamma _{\mathrm {s}} = 10^{-5}\hbox {K}^{-1}\) is used as the expansion coefficient of steel. In accord with Artz et al. (2014), the estimated point sets of each campaign are scaled uniformly to the reference temperatureFootnote 1\(T_0 = 9\,^{\circ }\hbox {C}\), even if a small delay may exist. In total, 21 point sets were prepared for evaluating possible changes in the ray path of ONSA13NE.

3 Ring-focus paraboloid

The main reflector of most of the conventional radio telescopes is designed as a rotationally symmetric paraboloid (RSP). Depending on the radio telescope type, either the sub-reflector or the receiver, which is located close to the unique focal point of the RSP, will shade the main reflector and result in a field of decreased intensity (cf. Cutler 1947). Depending on the dimension of the main reflector, the shading effect may become significant. The new generation of the so-called VGOS-specified radio telescopes is characterized by drive systems that allow high rotational velocities of about \(12^{\circ }\,\hbox {s}^{-1}\) and \(6^{\circ }\,\hbox {s}^{-1}\) in azimuth and elevation, respectively, and also by a small diameter of about 12–13 m for the main reflector (e.g., Petrachenko et al. 2009). Due to the small diameter of the main reflector, the lower signal strength becomes significant if a RSP is used. For this reason, many of the VGOS-specified radio telescopes are designed as rotationally symmetric ring-focus paraboloids (RSRFP).

Figure 7 depicts a cross-sectional view of a RSRFP with ray paths. Whereas a RSP focuses the rays into a unique focal point, the RSRFP has an infinite number of focal points lying on a spatial circle. Similarly, the unique apex of the RSP becomes a circle in the RSRFP design. If the sub-reflector is located behind the focal-ring, an elliptic torus reflects the ray to the unique system focal point \({\mathbf {F}}_0\) (e.g., Milligan 2005, Ch. 8–16). Such a configuration is known as Gregorian-type radio telescope. The implicit equation of an elliptic torus in canonical form reads

$$\begin{aligned} \frac{\zeta _1^2}{A_1^2} + \frac{\zeta _2^2}{A_2^2}= & {} 1 , \end{aligned}$$
(3)

where

$$\begin{aligned} \zeta _1= & {} \cos {\theta } \left( \sqrt{x_i^2 + y_i^2} - R\right) + \sin {\theta }z_i, \end{aligned}$$
(4)
$$\begin{aligned} \zeta _2= & {} \cos {\theta }z_i - \sin {\theta } \left( \sqrt{x_i^2 + y_i^2} - R\right) . \end{aligned}$$
(5)

Here, R is the distance between the center of the elliptic tube and the center of the torus, \(A_1\) and \(A_2\) are the semi-major and semi-minor axes of the elliptic tube, respectively, and \(\theta \) describes the twist of the tube. The coordinates \({\mathbf {p}}_i^{\mathrm {T}}~=~\left( \begin{array}{c@{\quad }c@{\quad }c}x_i&y_i&z_i \end{array}\right) \) represent a surface point of the elliptic torus.

Fig. 7
figure 7

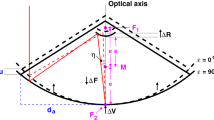
Cross-sectional view of a ring-focus paraboloid with ray paths (right side). On the left side, a ray path is subdivided into segments. Whereas the normal unit vectors \(\hat{\mathbf {z}}\), \(\hat{\mathbf {i}}\), \(\hat{\mathbf {r}}\) are the directions of the path segments, respectively, \(d_1\), \(d_2\), \(d_3\) denote the length of the respective segments. The incidence angle at the system focal point \({\mathbf {F}}_0\) w.r.t. the axis of symmetry of the paraboloid is \(\gamma \). The elliptic torus of the sub-reflector is implied by two gray-dotted ellipses, while the physical parts of the sub-reflector, i.e., the elliptic arcs, are shown in solid black. The focal points of the ellipses are plotted as red dots and denoted by \({\mathbf {F}}_0\) and \({\mathbf {F}}_1\), where \({\mathbf {F}}_0\) is the unique system focal point of the antenna. \(\mathbf {F}_{\bot }\) is the orthogonal projection of \({\mathbf {F}}_1\) onto the (tangent) plane of the apex circle, and \(\mathbf {P}_{0}\) is the circle center, i.e., the system apex

Full size image

The sub-reflector utilizes the geometrical properties of an ellipse, i.e., the summed distances of the focal points \({\mathbf {F}}_0\) and \({\mathbf {F}}_1\) to each point \({{\mathbf {P}}}_i\) lying on the ellipse are equal to the doubled semi-major axis \(A_1\) (e.g., Lösler and Nitschke 2010), i.e.,

$$\begin{aligned} \left| {\mathbf {F}}_0{{\mathbf {P}}}_i \right| + \left| {\mathbf {F}}_1{{\mathbf {P}}}_i \right|= & {} 2A_1. \end{aligned}$$
(6)

3.1 Double-elliptic ring-focus paraboloid

The ring-focus paraboloid results by combining the geometries of a paraboloid and a cylinder. The axis of symmetry of the paraboloid is replaced by an integrated cylinder, so that rays of this area do not participate in the signal. Construction parts inside the cylinder do not disturb the ray path of the signal, i.e., the sub-reflector or the receiver does not shade the main reflector. A closed mathematical description of a common ring-focus paraboloid was recently derived by Lösler et al. (2017, 2018b, c). The canonical form of the double-elliptic ring-focus paraboloid reads

$$\begin{aligned} a_1^2 (x_i - r_i n_{x,i} )^2 + a_2^2 (y_i - r_i n_{y,i} )^2= & {} z_i , \end{aligned}$$
(7)

where

$$\begin{aligned} n_{x,i}= & {} \frac{x_i}{\sqrt{x_i^2 + y_i^2}}, \end{aligned}$$
(8)
$$\begin{aligned} n_{y,i}= & {} \frac{y_i}{\sqrt{x_i^2 + y_i^2}}. \end{aligned}$$
(9)

The parameters of the elliptic paraboloid are \(a_1\) and \(a_2\). The normal unit vector \({\mathbf {n}}_i^{\mathrm {T}} = \left( \begin{array}{c@{\quad }c@{\quad }c}n_{x,i}&n_{y,i}&0 \end{array} \right) \) points in the direction of the axis of symmetry \({\mathbf {n}}_{\mathrm {RF}}\) of the elliptic cylinder, and the coordinate components of the ith surface point \({\mathbf {p}}_i^{\mathrm {T}} = \left( \begin{array}{c@{\quad }c@{\quad }c}x_i&y_i&z_i \end{array} \right) \) are shifted by \(r_i\). The length of the shift is given by (cf. Lösler et al. 2018b)

$$\begin{aligned} r_i= & {} \frac{1}{\sqrt{b_1^2 m_{x,i}^2 + b_2^2 m_{y,i}^2}} , \end{aligned}$$
(10)

where \(b_1\) and \(b_2\) are the inverse semi-major and the inverse semi-minor axes of the elliptic cylinder, respectively, \(\phi \) describes the orientation of the elliptic cylinder w.r.t. to the elliptic paraboloid, and

$$\begin{aligned} m_{x,i}= & {} n_{x,i} \cos {\phi } + n_{y,i} \sin {\phi }, \end{aligned}$$
(11)
$$\begin{aligned} m_{y,i}= & {} n_{y,i} \cos {\phi } - n_{x,i} \sin {\phi }. \end{aligned}$$
(12)

Besides the five datum-invariant parameters, six additional parameters are necessary to parameterize an arbitrarily oriented surface in space, i.e., three translation parameters summarized in vector \({\mathbf {P}}_0\) and three rotation parameters in matrix \({\mathbf {Q}}\). The transformation reads

$$\begin{aligned} {\mathbf {p}}_i= & {} {\mathbf {Q}} \left( {\mathbf {P}}_i - {\mathbf {P}}_0 \right) , \end{aligned}$$
(13)

where \({\mathbf {p}}_i\) and \({\mathbf {P}}_i\) are corresponding points of the canonical representation and the arbitrarily oriented representation of the ring-focus paraboloid, respectively. Usually, \({\mathbf {P}}_i\) is related to the reference frame of the measurement system.

The RSP as well as the RSRFP are two possible sub-models of Eq. (7). The RSRFP design results by introducing the parameter constraints \(a_1 = a_2\) and \(b_1 = b_2\). Moreover, the RSP design is a special type of the RSRFP and results from the further simplification \(r_i = 0\) (cf. Lösler et al. 2017, 2018b).

Due to structural deformations induced by gravity, the focal length F of the radio telescope may change when it rotates around the elevation axis (e.g., Sarti et al. 2009; Nothnagel et al. 2013; Bergstrand et al. 2019). According to Artz et al. (2014), two deformation patterns can exist. The first one describes an unpredictable deformation of the main reflector. This pattern cannot be modeled by quadric surfaces and needs a specific compensation model. The second one describes an affine deformation. Here, the resulting deformations provide surfaces that are similar to each other and can therefore be modeled geometrically. Whereas Artz et al. (2014) assume a homologous deformation, i.e., the focal lengths change while the main reflector maintains its parabolic shape, the use of Eq. (7) extends this homologous deformation pattern to a wider range of applications because Eq. (7) also allows modeling changes in the surface type (Lösler et al. 2018b, c).

Having a discrete set of observed spatial points lying on the paraboloid surface of the ring-focus antenna, the datum-invariant parameters, as well as the isometric parameters, are estimable using an errors-in-variables model. In Sect. 3.2, the sequential quadratic programming (SQP) is proposed for the data analysis.

An elevation-dependent model of the focal lengths \(F(\epsilon )\) can be derived by providing point sets observed in several elevation positions. The focal lengths \(F_1\), \(F_2\) of an elliptic paraboloid depend on the parameter \(a_1\), \(a_2\), respectively, by

$$\begin{aligned} F\left( a\right) = \frac{1}{4a^2} \end{aligned}$$
(14)

and represent the extreme values of the varying focal lengths. In the case of a rotationally symmetric main reflector design, the restriction \(a_1 = a_2\) holds and Eq. (14) results in a single focal length F.

3.2 Parameter estimation

To estimate the parameters of the implicit Eq. (7) of a double-elliptic ring-focus paraboloid, an errors-in-variables (EIV) model is needed. In numerical optimization, a well-known solver that belongs to the class of EIV models is the SQP. The SQP approach is recommended for nonlinear constrained optimization and estimates the unknown parameters \({\mathbf {u}}\) by solving sequences of quadratic sub-problems (cf. Nocedal and Wright 2006, Ch. 18).

Based on the adjusted surface points \({\mathbf {P}}_i\) from the bundle adjustment, the parameters to be estimated for the ring-focus paraboloid are given by

$$\begin{aligned} {\mathbf {u}}^{\mathrm {T}}= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c} {\mathbf {x}}_{\mathrm {SF}}^{\mathrm {T}}&{\mathbf {x}}_{\mathrm {ISO}}^{\mathrm {T}}&{\mathbf {v}}^{\mathrm {T}} \end{array} \right] . \end{aligned}$$
(15)

The vector \({\mathbf {u}}\) is subdivided into the two datum-invariant surface parameters of the elliptic paraboloid as well as the three datum-invariant surface parameters of the elliptic cylinder, i.e., \({\mathbf {x}}_{\mathrm {SF}}^{\mathrm {T}} = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} a_1&a_2&b_1&b_2&\phi \end{array} \right) \), the six datum-dependent isometric parameters concerning \(\mathbf {P}_{0}\) and \({\mathbf {Q}}\) that transform the surface by Eq. (13) into its canonical representation \({\mathbf {x}}_{\mathrm {ISO}}^{\mathrm {T}} = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} X_0&Y_0&Z_0&\xi _x&\xi _y&\xi _z \end{array} \right) \), and the residuals of the coordinate components of the surface points \({\mathbf {v}}^{\mathrm {T}} = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} v_{x_i}&v_{y_i}&v_{z_i}&\ldots \end{array} \right) \). The isometric parameters of the rotation sequence \({\mathbf {Q}}\) in Eq. (13) are denoted by \(\xi _x\), \(\xi _y\), \(\xi _z\), and describe Euler angles of basic rotation matrices (e.g., Nitschke and Knickmeyer 2000).

By minimizing the target function \(\Omega ({\mathbf {u}})\) subject to the constraint function \({\varvec{c}}({\mathbf {u}})\) given by Eqs. (7), (13), the unknown parameters are estimated iteratively. The a priori weight matrix \(\mathbf {W_x}\) of the model parameters \({\mathbf {x}}^{\mathrm {T}} = \left[ \begin{array}{c@{\quad }c} {\mathbf {x}}_{\mathrm {SF}}^{\mathrm {T}}&{\mathbf {x}}_{\mathrm {ISO}}^{\mathrm {T}} \end{array} \right] \) is unknown, i.e., \(\mathbf {W_x} = {\mathbf {0}}\), and the target function \({\Omega }\) becomes, cf. Eq. (46),

$$\begin{aligned} {\Omega }= & {} {\mathbf {v}}^{\mathrm {T}}{\mathbf {W}}_{\mathbf {v}}{\mathbf {v}} . \end{aligned}$$
(16)

Here, \(\mathbf {W}_\mathbf {v}^{{-1}}\) describes the dispersion of the observations and is composed of the derived uncertainties of the estimated points \({\mathbf {P}}_i\) of the bundle adjustment, cf. Sect. 2.2. According to Eq. (43), the normal equation of the SQP approach reads

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c} \nabla _{\mathbf {uu}}^2 {\mathscr {L}} &{} {\mathbf {J}}^{\mathrm {T}} \\ {\mathbf {J}} &{} {\mathbf {0}} \end{array} \right] \left[ \begin{array}{c} \varvec{\Delta } \mathbf {u} \\ {\varvec{\Delta \lambda } } \end{array} \right]= & {} -\left[ \begin{array}{c} \nabla _{{\mathbf {u}}} {\mathscr {L}} \\ {\varvec{c}} \end{array} \right] , \end{aligned}$$
(17)

where \(\nabla _{\mathbf {uu}}^2 {\mathscr {L}}\) and \(\nabla _{{\mathbf {u}}} {\mathscr {L}}\) are the Hessian and the gradient of the Lagrangian w.r.t. the unknown parameters \({\mathbf {u}}\), respectively, cf. Eq. (37). \({\mathbf {J}}\) represents the Jacobian matrix of the constraint equations given by Eq. (45), and \(\varvec{\lambda }\) is the vector of Lagrangian multipliers. A detailed description of the SQP approach, including the derivation of the normal equations system, is presented in “Appendix.”

To avoid an over-parameterization, the number of model parameters should only be expanded to the maximum size if the realized surface type significantly deviates from its ideal surface type. Usually, the surface type is restricted to the designed rotationally symmetric ring-focus paraboloid that yields the seven model parameters to be estimated \({\mathbf {x}}^{\mathrm {T}} = \left( \begin{array}{ccccccc} a&b&X_0&Y_0&Z_0&\xi _x&\xi _y \end{array} \right) \).

The residuals \({\mathbf {v}}\) of the adjustment process depend on the datum of the global frame and are meaningless for the evaluation of the accuracy of the shape. A datum-invariant representation of the observational residuals yields (e.g., Ghilani and Wolf 2006, p. 439)

$$\begin{aligned} \mathbf {v}_{c}= & {} \mathbf {J}_\mathbf {v}{\mathbf {v}} , \end{aligned}$$
(18)

where the Jacobian matrix \(\mathbf {J}_\mathbf {v}\) results from Eq. (45). \(\mathbf {J}_\mathbf {v}\) transforms the residuals \({\mathbf {v}}\) of the coordinate components to the constraint equations space. Due to the datum invariance of the constraint equations of the ring-focus paraboloid \({\varvec{c}}\), the corresponding (equivalent) residuals \(\mathbf {v}_{c}\) must be invariant, too. Thus, the use of \(\mathbf {v}_{c}\) instead of \({\mathbf {v}}\) is recommended to analyze the accuracy of the shape.

3.3 Sub-reflector variations

As a consequence of the variation of the focal length, the sub-reflector position, which is usually mounted by tripod or quadrupod strut elements at the supporting reflector backup structure, may also vary. The changes in the distance \({\Delta }R'(\epsilon )\) between the apex \(\mathbf {F}_{\bot }\) and the sub-reflector \({\mathbf {R}}\) are limited by the length of the struts \(\left| \mathbf {SR}\right| \) and the perpendicular distance from the mounting position of the struts \({\mathbf {S}}\) to the axis of symmetry of the paraboloid \(\left| \mathbf {F}_{\bot }\mathbf {S}_{\bot }\right| \). In general, these variations depend on \(F(\epsilon )\) but have smaller magnitudes than the corresponding focal length variation.

Fig. 8
figure 8

Cross-sectional view of the right paraboloid, see Fig. 7. Displacements of the focal point \({\mathbf {F}}_1\), the sub-reflector position \({\mathbf {R}}\) as well as the mounting position of the strut \({\mathbf {S}}\) as a consequence of reflector deformations. The quantities of the reference state are denoted by an apostrophe and are colored in gray when they change. \({\mathbf {F}_{\bot }}\) and \({\mathbf {S_{\bot }}}\) are the orthogonal projections of \({\mathbf {F}}_1\) and \({\mathbf {S}}_1\), respectively, onto the (tangent) plane of the apex circle. The arc length is denoted by , and \(\left| \cdot \right| \) symbolizes the Euclidean norm

Full size image

The arc length between the apex of the paraboloid and the mounting position of the strut is given by (e.g., Gray 1994, Ch. 1.6)

(19)

where \(q = \sqrt{F^2 + h^2}\) and \(h = \frac{1}{2} \left| \mathbf {F}_{\bot }\mathbf {S}_{\bot }\right| \).

Assuming that \(\left| \mathbf {SR}\right| \) and are invariant quantities w.r.t. the elevation angle \(\epsilon \), changes in \(\left| \mathbf {F}_{\bot }\mathbf {S}_{\bot }\right| \) and, therefore, \(\left| \mathbf {F_{\bot }R}\right| \) depend only on the variations of the focal length \(F(\epsilon )\). By inverting Eq. (19), the elevation-dependent length \(\left| \mathbf {F}_{\bot }\mathbf {S}_{\bot }\right| \) can be derived and introduced to approximate the distance between the apex and the sub-reflector \(\left| \mathbf {F_{\bot }R}\right| \). In canonical form, \({\Delta }R'(\epsilon )\) is given by

$$\begin{aligned} {\Delta }R'\left( \epsilon \right)= & {} \sqrt{ \left| \mathbf {SR} \right| ^2 - \left| \mathbf {F}_{\bot }\mathbf {S}_{\bot }\right| ^2 } + z_{{\mathbf {S}}} - z_{\mathbf {R'}}. \end{aligned}$$
(20)

Figure 8 depicts the counter-moving deformations of the focal point \(\mathbf {F}_{1}\) of the paraboloid and the sub-reflector position \({\mathbf {R}}\). The focal point moves closer to the apex, while the curvature increases. The sub-reflector moves in the opposite direction because the construction and the magnitude of the shifts are unequal to each other. This geometrical behavior is experimentally confirmed by direct measurements of \({\Delta }R'\) (cf. Nothnagel et al. 2013; Bergstrand et al. 2019). It should be mentioned that the struts may be affected by further gravitational effects, e.g., an elevation-dependent bending (e.g., Sarti et al. 2009). Thus, Eq. (20) is only a first-order approximation and can be omitted if local measurements are feasible.

4 Signal path variation

A reliable representation of the signal path variation \({\Delta }L(\epsilon )\) can be described as a weighted sum of three deformation effects, i.e., the focal length variation \({\Delta }F(\epsilon )\), the displacement of the sub-reflector \({\Delta }R(\epsilon )\), and the shift of the vertex \({\Delta }V(\epsilon )\) w.r.t. the elevation axis (Clark and Thomsen 1988). By introducing the corresponding linear weighting coefficients \(\alpha _F\), \(\alpha _R\), and \(\alpha _V\), the SPV reads

$$\begin{aligned} {\Delta }L(\epsilon )= & {} \alpha _F {\Delta }F(\epsilon ) + \alpha _V {\Delta }V(\epsilon ) + \lambda \alpha _R {\Delta }R(\epsilon ) \end{aligned}$$
(21)

where \(\lambda = 1\) for prime focus telescopes and \(\lambda = 2\) for secondary focus telescopes (Abbondanza and Sarti 2010; Artz et al. 2014). Whereas \({\Delta }F\), \({\Delta }V\), and \({\Delta }R\) depend on the underlying geometrical deformation pattern, the weighting coefficients \(\alpha _F\), \(\alpha _R\), and \(\alpha _V\) depend on the geometry of the reflectors and the illumination intensity I (Clark and Thomsen 1988).

Following the line of reasoning worked out by Clark and Thomsen (1988) for prime focus telescopes, and extended by Abbondanza and Sarti (2010) for secondary focus telescopes, the weighting coefficients are linearly dependent on each other, i.e.,

$$\begin{aligned} \alpha _F= & {} \lambda \left( 1 - \alpha _R \right) , \end{aligned}$$
(22a)
$$\begin{aligned} \alpha _V= & {} -1 - \lambda \alpha _R. \end{aligned}$$
(22b)

Integrating the individual ray paths, which are scaled by the telescope-specific normalized illumination function \(I_n\), over the entire reflector \(\Gamma \), yields the parameter to be determined

$$\begin{aligned} \alpha _R= & {} \int \limits _{\Gamma }^{} I_n\left( {\mathbf {P}} \right) h\left( {\mathbf {P}} \right) \hbox {d}\Gamma , \end{aligned}$$
(23)

where the function h describes the changes in the path length w.r.t. the reflector (e.g., Abbondanza and Sarti 2010).

The OTT are secondary focus Gregorian-type radio telescopes, and the fixed sub-reflector is located behind the focal point \(\mathbf {F}_{1}\) of the main reflector, see Fig. 7. The sub-reflector is designed as a rotationally symmetric elliptical torus, cf. Eq. (3), and reflects the signal toward the system focal point \(\mathbf {F}_{0}\). The sub-reflector of ONSA13NE does not provide a movable mounting to adjust the focal length during observations because in geodetic VLBI, the sub-reflector is kept fixed. As shown in Figure 7, the cross section of the rotationally symmetric elliptical torus yields two ellipses, and the ray path can be simply modeled in 2D. However, in contrast to a conventional Gregorian-type radio telescope having an axially parallel ellipse as cross section of the sub-reflector, here, the ellipses of the sub-reflector of the ring-focus telescope are tilted. Thus, the incidence angle \(\gamma \) of the ray at the system focal point \(\mathbf {F}_{0}\) becomes zero if the ray is reflected at the rim of the main reflector.

According to Cha (1987), the resulting path variation caused by a displacement \({\Delta }R\) of the sub-reflector can be approximated by an isosceles triangle, i.e.,

$$\begin{aligned} h\left( {\mathbf {P}} \right) = \left| \mathbf {PK}\right| + \left| \mathbf {PJ}\right| = 2 {\Delta }R \left( -{\hat{\mathbf {z}}^{\mathrm {T}}}{\hat{\mathbf {n}}}\right) \left( {\hat{\mathbf {n}}^{\mathrm {T}}}{\hat{\mathbf {i}}}\right) . \end{aligned}$$
(24)

As shown in Fig. 9, the incident ray is represented by a straight line, defined by the focal point \(\mathbf {F}_{1}\) and the normal unit vector \({\hat{\mathbf {i}}}\). The straight line of the reflected ray is parameterized by the system focal point \(\mathbf {F}_{0}\) and the normal unit vector \({\hat{\mathbf {r}}}\). \({\mathbf {P}}\) is the intersection point of both straight lines, i.e., the point of reflection. The normalized gradient of \(\Gamma \) at \({\mathbf {P}}\) is denoted by \({\hat{\mathbf {n}}}\) and \({\hat{\mathbf {z}}}^{\mathrm {T}}=(\begin{array}{cc} 0&1 \end{array})\). \({\mathbf {K}}\) and \({\mathbf {J}}\) are projections of \(\mathbf {P'}\) onto the incident ray \({\hat{\mathbf {i}}}\) and the reflected ray \({\hat{\mathbf {r}}}\), respectively, and \(\mathbf {P'}\) is the projected point of the shifted position \({\mathbf {P}}_{{\Delta }R}\) onto \({\hat{\mathbf {n}}}\).

Fig. 9
figure 9

The right part of the sub-reflector \(\Gamma \), represented by the arc of the dotted ellipse and defined by the focal points \(\mathbf {F}_{0}\) and \(\mathbf {F}_{1}\), is displaced by gravity and results in the solid plotted elliptical arc. The point of reflection \({\mathbf {P}}\) is shifted by \({\Delta }R\) to \({\mathbf {P}}_{{\Delta }R}\). \(\mathbf {P'}\) is the projected position of \({\mathbf {P}}_{{\Delta }R}\) onto the normalized gradient \({\hat{\mathbf {n}}}\) of \(\Gamma \) at \({\mathbf {P}}\). \({\mathbf {K}}\) and \({\mathbf {J}}\) are projections of \(\mathbf {P'}\) onto the incident ray \({\hat{\mathbf {i}}}\) and the reflected ray \({\hat{\mathbf {r}}}\), respectively. The unshifted ray path \(\left| \mathbf {F}_0\mathbf {P}\right| + \left| \mathbf {F}_1\mathbf {P}\right| \) is denoted by straight lines. The vectors \({\hat{\mathbf {z}}}\), \({\hat{\mathbf {i}}}\), \({\hat{\mathbf {n}}}\) and \({\hat{\mathbf {r}}}\) are normal unit vectors

Full size image

Utilizing the geometric property of an ellipse given by Eq. (6), an alternative approximation is suggested by Artz et al. (2014), i.e.,

$$\begin{aligned} h'\left( {\mathbf {P}} \right) = \left| \mathbf {F}_0''\mathbf {P}''\right| + \left| \mathbf {F}_1\mathbf {P}''\right| - 2A_1 \end{aligned}$$
(25)

where \(\mathbf {P''}\) is the intersection point of the incident ray \({\hat{\mathbf {i}}}\) and the displaced sub-reflector, and \(\mathbf {F}_0''\) is the intersection point of the focal plane and the reflected ray \({\hat{\mathbf {r}}}''\). However, for small quantity \({\Delta }R\) w.r.t. the eccentricity of the ellipse \(\frac{1}{2}\left| {\mathbf {F}}_0{{\mathbf {F}}}_1 \right| \) both approximations are sufficient and \(h({\mathbf {P}}) \approx h'({\mathbf {P}})\) holds. Having Eq. (24) or (25), the change in the path length caused by \({\Delta }R\) is modeled. In Eq. (23), this variation is weighted by the telescope-specific illumination function \(I_n\). The nature of the illumination function is to amplify the entry signals close to the rim and to weaken the entry signals close to the apex. Possible functions to model the illumination intensity are discussed by Abbondanza and Sarti (2010), Artz et al. (2014) and evaluated for several conventional radio telescopes. While for antennas with small subtended angle a cosine-squared illumination function is suitable, see, e.g., Artz et al. (2014), for ring-focus antennas with large subtended angle a Gaussian illumination function is best, see, e.g., Lopez-Fernandez et al. (2014). ONSA13NE provides a large subtended angle, i.e., \(\gamma _a=2\gamma _e=130^{\circ }\), and uses a Gaussian illumination function with a \(-\,16\) dB taper (personal communication, Jonas Flygare 2018), i.e.,

$$\begin{aligned} I_{\mathrm {n}}(\gamma )= & {} k \exp \left( {-2\alpha _e \frac{\gamma ^2}{\gamma _e^2}}\right) , \end{aligned}$$
(26)

where \(\gamma \) is the incidence angle at the system focal point \(\mathbf {F}_{0}\) w.r.t. the axis of symmetry of the paraboloid, \(\alpha _e = 16\,\hbox {dB}\frac{\log {10}}{20}\) parameterizes the maximum edge taper, i.e., \(-\,16\) dB at the maximum angle \(\gamma _e=65^{\circ }\), and k is the normalization factor, which is derived by

$$\begin{aligned} \frac{1}{k}= & {} 2 \pi \int \limits _{\gamma _1}^{\gamma _2} \exp \left( -2\alpha _e \frac{\gamma ^2}{\gamma _e^2 } \right) \hbox {d}\gamma . \end{aligned}$$
(27)

Substituting Eqs. (24) and (26) into Eq. (23) yields the coefficient \(\alpha _R(h) = 0.65\). Using Eq. (25) instead of Eq. (24), the resulting \(\alpha _R\) slightly reduces to \(\alpha _R(h') = 0.62\).

5 Measurement results

To estimate the parameters of the ring-focus paraboloid, the SQP approach described in Sect. 3.2 was applied. All 21 prepared point sets were introduced separately to Eq. (7) and iteratively solved by Eq. (17), applying the parameter constraints \(a_1 = a_2\) and \(b_1 = b_2\) for forcing the RSRFP type. The uncertainties of about \(100\,\upmu \hbox {m}\), derived during the bundle adjustment (see Sect. 2.2), were applied as stochastic model \({\mathbf {W}}_{\mathbf {v}}\), cf. Eq. (47). Preliminary investigations of ONSA13NE showed small systematical deviations which were describable by an elliptic ring-focus paraboloid (Lösler et al. 2017, 2018b, c). However, these deviations were about \(50\,\upmu \hbox {m}\) and could not be detected in the current measurements, since they were below the sensitivity threshold, see Sect. 2.2.

Fig. 10
figure 10

Contour plot of the datum-independent residuals \({\mathbf {v}}_{\mathrm {c}}\) of the main reflector at elevation \(0^\circ \). The residuals vary in a range of about \(\pm \, 0.5\,\hbox {mm}\). The largest residuals can be found at the rim of the main reflector. Coded targets are symbolized by red dots

Full size image

Figure 10 depicts a contour plot of the datum-independent residuals \({\mathbf {v}}_{\mathrm {c}}\) (derived by Eq. (18)) with the main reflector at elevation \(0^{\circ }\). The distance between the iso-lines is 0.1 mm. The largest residuals of about \(\pm \,0.5\,\hbox {mm}\) can be found at the rim of the reflector surface.

Fig. 11
figure 11

Histogram of the datum-independent residuals \({\mathbf {v}}_{\mathrm {c}}\) of the surface points of the estimated ring-focus paraboloid. The histogram is derived from \(n_{{\mathbf {v}}} = 1,491\) residuals of the 21 campaigns. For comparison, the probability density function (PDF) of the normal distribution is plotted by a solid red curve. The estimated sample mean and empirical standard deviation are \({\hat{\mu }} = 7\,\upmu \hbox {m}\) and \({\hat{\sigma }} = 194\,\upmu \hbox {m}\), respectively

Full size image
Table 1 Campaign-wise averaged temperature as well as estimated overall \(\hbox {RMS}(\mathbf {v}_{c})\) w.r.t. different survey elevations \(\epsilon \). During the first ten measurement campaigns, the rotation direction of the telescope was upward, and afterward downward. At \(34^{\circ }\), the telescope was measured only once (rotation direction upward). Horizontal lines indicate the subdivided campaigns. The campaign numbers are in chronological order
Full size table

Due to the small sample size of a single measurement campaign, the 1, 491 datum-independent residuals \({\mathbf {v}}_{\mathrm {c}}\) of all campaigns are combined in a histogram shown in Fig. 11. The number of bins \(n_{\mathrm {b}}\) is derived by (Scott 1979)

$$\begin{aligned} n_{\mathrm {b}}= & {} \frac{ \max {|{\mathbf {v}}_{\mathrm {c}}|} - \min {|{\mathbf {v}}_{\mathrm {c}}|} }{h_\mathrm{b}} , \end{aligned}$$
(28)

where \(h_{\mathrm {b}} = 3.49 {\hat{\sigma }} n_{{\mathbf {v}}}^{-\frac{1}{3}}\), \({\hat{\sigma }}\) is the sample standard deviation and \(n_{{\mathbf {v}}}\) denotes the number of residuals \({\mathbf {v}}_{\mathrm {c}}\). The residuals are unimodal and symmetrically distributed and follow a normal distribution. The maximal residual does not exceed \(\pm \,0.8\,\hbox {mm}\). The resulting sample mean and the empirical standard deviation of the probability density function (PDF) of the normal distribution are \({\hat{\mu }} = 7\,\upmu \hbox {m}\) and \({\hat{\sigma }} = 194\,\upmu \hbox {m}\), respectively.

Table 1 summarizes the campaign-wise estimated RMS values derived by \({\mathbf {v}}_{\mathrm {c}}\). The overall RMS does not exceed \(300\,\upmu \hbox {m}\), but there is a relation between the estimated RMS value and the elevation angle. The smallest values can be found for the elevation angles from \(30^{\circ }\) to \(50^{\circ }\), while the values increase for elevation angles close to \(0^{\circ }\) as well as \(90^{\circ }\). The reflector panels were adjusted at \(34^{\circ }\) elevation during the telescope installation. Thus, smallest deviations can be expected for elevation angles close to \(34^{\circ }\).

Fig. 12
figure 12

Estimated focal length obtained from Eqs. (7), (14). Red upward- and downward-pointing triangles symbolize results which were obtained during increasing and decreasing elevation angles, respectively, cf. Table 1. The error bars indicate the confidence of a single measurement value (\(2\sigma \)), derived by Eqs. (48), (49). For comparison, the estimated result of the panels adjustment process of the main reflector, which was carried out in 2017, is symbolized by a black star (Lösler et al. 2017). Based on the estimated focal lengths, a prediction cosine function was derived and is shown in black together with the resulting confidences in gray (\(2\sigma \)), derived by the law of propagation of uncertainty

Full size image

Figure 12 depicts the estimated variations of the focal length F, derived by Eq. (14). The estimated focal length varies in a range of \(\pm \,1.1\,\hbox {mm}\) and is elevation-dependent. A cosine function was adapted, i.e.,

$$\begin{aligned} f(\epsilon ) = c_0 + c_1 \cos {\epsilon }, \end{aligned}$$
(29)

which predicts the variations quite well. Here, \(c_0\) describes the offset, which is related to \(90^{\circ }\) elevation, and \(c_1\) represents the amplitude of the cosine function. The uncertainties of the derived 21 focal lengths as well as the assumed uncertainties of the elevation angles \(\sigma _{\epsilon } = 0.001^{\circ }\) are taken into account during the adjustment process, cf. “Appendix.” The prediction function is given in black color and dash-dotted style, together with the related confidence interval (\(2\sigma )\). The maximal focal length occurs at \(90^{\circ }\), which confirms the assumption that the main reflector becomes flatter in higher elevation positions. The derived coefficients yield the prediction function

$$\begin{aligned} F(\epsilon )= & {} 3.7017\,\hbox {m} - 2.28\,\hbox {mm} \cos {\epsilon }. \end{aligned}$$
(30)

The uncertainties of the offset and the amplitude are \({\hat{\sigma }}_{c_0} = 0.2\,\hbox {mm}\) and \({\hat{\sigma }}_{c_1} = 0.3\,\hbox {mm}\), respectively.

In 2017, the surface of the main reflector was observed at \(34^{\circ }\) during the panels adjustment. The resulting focal length (cf. Lösler et al. 2017) is symbolized by a black star. The difference of this focal length and the prediction derived by Eq. (30) is \(-\,0.2\,\hbox {mm}\) and confirms the latest results.

During the first ten measurement campaigns, the rotation direction of the telescope was upward, and afterward downward for the repeated measurements. By comparing the derived focal lengths of the upward and the downward configurations, a small, but insignificant hysteresis is visible. The reason might be an unrepresentative temperature compensation. For example, a change of \(2\,\hbox {K}\) yields a corresponding focal length change of about 0.1 mm. However, further investigation, including more than one repetition measurement, is needed to verify this behavior.

To model the ray path to the receiver, the variations of the sub-reflector must be taken into account, see Sect. 3.3. To estimate the distance between the system apex and the sub-reflector, the positions of the four targets mounted at the sub-reflector were combined with the isometric parameters \({\mathbf {x}}_{\mathrm {ISO}}\) of the RSRFP, cf. Eq. (15). The isometric parameters contain the spatial position of the system apex \({\mathbf {P}}_0\) w.r.t. the global frame and the rotation sequence \({\mathbf {Q}}\) which transforms the surface into its canonical form. Using \({\mathbf {P}}_0\) and \({\mathbf {Q}}\), a straight line representing the axis of symmetry of the main reflector \({\mathbf {n}}_{\mathrm {RF}}\) reads

$$\begin{aligned} {\mathbf {P}}\left( t\right)= & {} {\mathbf {P}}_0 + t{\mathbf {n}}_{\mathrm {RF}}, \end{aligned}$$
(31)

where \(\left| {\mathbf {n}}_{\mathrm {RF}}\right| = 1\), \({\mathbf {P}}\left( t\right) \) is a point lying on the straight line, and t describes the distance between \({\mathbf {P}}\left( t\right) \) and \({\mathbf {P}}_0\). Moreover, the best-fit plane, i.e.,

$$\begin{aligned} \mathbf {n_{\mathrm {SR}}}^{\mathrm {T}} {\mathbf {P}}_i= & {} d_{\mathrm {SR}} \end{aligned}$$
(32)

resulting from the four points mounted at the sub-reflector, was adjusted. Here, \({\mathbf {P}}_i\) is an arbitrary point on the plane, \(\mathbf {n}_{\mathrm {SR}}\) is the normal unit vector, and \(d_{\mathrm {SR}}\) is the shortest distance of the plane to the origin. The variations of the sub-reflector were derived from the resulting distances between the system apex \({\mathbf {P}}_0\) and the intersection point of the plane and the axis of symmetry. The uncertainties of each intersection point were derived by the law of propagation of uncertainty (cf. JCGM100 2008; JCGM102 2011). The estimated sub-reflector variations were adjusted by a cosine function, see Eq. (29), using the SQP approach, cf. “Appendix.” Table 2 summarizes the estimated amplitude \(c_1\) of Eq. (29) as well as the derived uncertainties.

To verify the shape of the curve described by the function, the variation \({\Delta }R'(\epsilon )\) was derived independently by Eq. (20). The nominal position of the strut \({\mathbf {S}}\) as well as the nominal length of the strut element \(\left| \mathbf {SR}\right| \) were taken from the mechanical drawings and provide the nominal arc length via Eq. (19), see Fig. 8.

Figure 13 depicts the results of both approaches. Both curves decline with increasing elevation. Thus, the sub-reflector moves closer to the apex and into the opposite direction compared to the focal length, see Fig. 8. Moreover, both approaches result in similar prediction functions. The position of the sub-reflector varies in a range of about \(\pm \,0.3\,\hbox {mm}\). The derived amplitudes of the cosine functions \({\Delta }R(\epsilon )\) and \({\Delta }R'(\epsilon )\) are summarized in Table 2.

Fig. 13
figure 13

Estimated sub-reflector variations \({\Delta }R\) (top) derived by the intersection between the best-fit plane and the axis of symmetry as well as estimated variations \({\Delta }R'\) (bottom) derived by Eq. (20). Red upward- and downward-pointing triangles symbolize results obtained during increasing and decreasing elevation angles, respectively, cf. Table 1. Error bars indicate the related confidence interval (\(2\sigma \)). The curves of the derived cosine functions are shown in black together with the resulting confidences in gray (\(2\sigma \)). Confidences are derived by applying the law of propagation of uncertainty

Full size image
Table 2 Amplitude \(c_1\) of the cosine function, cf. Eq. (29), derived by direct measurements of the sub-reflector variations \({\Delta }R(\epsilon )\) and evaluated by Eq. (20), which uses basic geometrical conditions \({\Delta }R'(\epsilon )\). \({\hat{\sigma }}_{c_1}\) is derived by applying the law of propagation of uncertainty
Full size table

Based on the prediction functions concerning \({\Delta } F\) and \({\Delta } R\), the geometrical ray path to the receiver and its variations w.r.t. the elevation \(\epsilon \) can be parameterized. The surface of the sub-reflector was not observed. Due to the small dimension compared to the main reflector, the sub-reflector is assumed to be stiff. Using the parameters given in Table 3 together with Eq. (6) yields the parameter of the rotationally symmetric elliptic torus representing the sub-reflector surface.

Table 3 Nominal values of the construction components of the Onsala twin telescopes
Full size table

At \(90^{\circ }\), the modeled variations become zero and the ray path length is according to the nominal values. Therefore, \(90^\circ \) is recommended as the reference configuration. As already mentioned, the receiver is not mounted at the sub-reflector, and thus, the sub-reflector variations cannot be transferred to the system focal point.

Fig. 14
figure 14

Map of the geometrical ray path lengths derived by ray tracing at \(0^\circ \)

Full size image

For each elevation, the geometrical ray path is sampled between the boundaries of the paraboloid, i.e., \(\frac{{\tilde{D}}_{\mathrm {c}}}{2}\) and \(\frac{{\tilde{D}}_{\mathrm {m}}}{2}\). Applying the derivations \({\Delta } F(\epsilon )\) and \({\Delta } R(\epsilon )\) yields a geometrical ray path length map of ONSA13NE. Figure 14 illustrates the resulting map for \(0^\circ \). The ray path length varies over a range of about 3 mm. It should be noted that the yellow part of the map is the integrated cylinder of the ring-focus paraboloid and, therefore, is insensitive by definition. However, rays that are reflected close to this cylinder region are affected by rather large variations compared to rays reflected at the rim. Other areas (dark blue) show almost no ray path variation. This latter results from the combination of the reflection at the main reflector and the sub-reflector, respectively, during ray tracing when \({\Delta } F(\epsilon )\) and \({\Delta } R(\epsilon )\) have opposite signs and cancel out for some ranges. In general, Fig. 14 shows clearly that the largest (outer) part of the map covering the area between about 3 and 6.5 m from the center shows very small variation in the ray path, i.e., is stable. These areas are weighted highest by the illumination function Eq. (26), whereas the more central parts showing larger ray path variations are weighted less by the illumination function.

According to Clark and Thomsen (1988), the signal path variation \({\Delta }L\) is composed of the three geometrical deformation patterns, i.e., \({\Delta }F\), \({\Delta }V\), and \({\Delta }R\), and the corresponding weighting coefficients \(\alpha _F\), \(\alpha _R\), and \(\alpha _V\), which depend on the geometry of the reflector and the illumination intensity I, cf. Eq. (21). The shift of the vertex \({\Delta }V\) cannot be derived by the observed photogrammetric point sets because only the main reflector and the sub-reflector were observed. For that reason, \({\Delta }V\) is derived by a finite element method (FEM) carried out by the manufacturer during the design of the VGOS antenna. In total, seven neuralgic FEM sample points were provided from \(0^{\circ }\) to \(100^{\circ }\) (personal communication, Eberhard Sust 2019), which are well adapted by a sine function, i.e.,

$$\begin{aligned} f(\epsilon )= & {} s_0 + s_1 \sin {\epsilon } , \end{aligned}$$
(33)

having coefficients \(s_0 = -0.24\,\hbox {mm}\) and \(s_1 = 0.24\,\hbox {mm}\). Since the prediction function is related to \(90^{\circ }\), both coefficients are identical but have opposite signs. Thus, the maximum shift is \(-\,0.24\,\hbox {mm}\) and corresponds to \(s_0\). In Fig. 15, the FEM sampling points are plotted in red triangles and the derived prediction function is shown in black.

Fig. 15
figure 15

Variation of the vertex w.r.t. the elevation axis. The data shown as red triangles were provided by the antenna manufacturer and were derived by applying a finite element method (FEM). Based on the FEM sampling points, a prediction function was derived and is shown in black. The antenna manufacturer did not provide uncertainties of the FEM, and, therefore, no uncertainties are given in the graph

Full size image

In Sect. 4, the coefficient \(\alpha _R\) was derived by substituting Eqs. (24) and (25) into Eq. (23). The average value reads \(\alpha _R = 0.63\) and yields \(\alpha _F = 0.73\) as well as \(\alpha _V = -2.27\) via Eq. (22). Figure 16 depicts the signal path variation w.r.t. the elevation angle. Whereas the focal length variation and the movement of the sub-reflector are modeled by cosine functions, cf. Figs. 12 and 13, the elevation-dependent shift of the vertex is given by a sine function, cf. Fig. 15. These functions are combined by Eq. (21), i.e., a weighted sum. As a consequence, the resulting signal path variation \({\Delta }L\) in millimeters is well adapted by the combined function

$$\begin{aligned} {\Delta }L(\epsilon )= & {} 0.54 - 0.54 \sin {\epsilon } - 0.91 \cos {\epsilon } , \end{aligned}$$
(34)

which can be applied to correct the signal path.

According to Eq. (34), the minimum of the function can be obtained at \(30.7^{\circ }\), which is close to the \(34^{\circ }\) position of the panels adjustment performed in 2017. The minimum of the function corresponds to the maximum deviation of about \(-\,0.5\,\hbox {mm}\). The corresponding time delay is about

$$\begin{aligned} {\Delta } \tau (30.7^{\circ })= & {} \frac{1}{c} {\Delta }L(30.7^{\circ }) = -1.7\,\hbox {ps} , \end{aligned}$$

where c is the speed of light. To reach the 1 mm goal, a delay measurement precision of about 4 ps is required. The VGOS system is designed to achieve a delay precision of about 2 ps under ideal operating conditions (Petrachenko et al. 2009). The derived maximum signal path variation of about 1.7 ps is on the same level as this expected best possible delay measurement precision of the VGOS system. However, SPV introduces an elevation-dependent systematical error. Therefore, we recommend to correct for the SPV using Eq. (34) in the VLBI data processing.

In Fig. 16, the illustrated uncertainties are derived by Monte Carlo simulation (e.g., JCGM102 2011) starting at the beginning of the data preparing, see Sect. 2.2, and comprising the full analysis process. The SPV approach depends on several input quantities, i.e., the derived point set of the bundle adjustment, the campaign temperature, and the elevation angle of the telescope. The uncertainties of the point set, as well as the uncertainty of the elevation angle, are assumed to be normally distributed. The campaign temperature given in Table 1 is assumed to follow a uniform distribution, cf. Fig. 6.

Besides the input quantities that are related to the metrology part affecting the geometrical deformation pattern in Eq. (21), the uncertainties of \({\Delta }L\) also depend on the weighting coefficients. The weighting coefficient \(\alpha _R\) in Eq. (23) depends on the selected function h as well as \(I_n\). Assuming a uniform distribution of \(\alpha _R\) within the boundaries given by \(\alpha _R(h) = 0.65\) and \(\alpha _R(h') = 0.62\), the uncertainty derived by Eq. (2) reads \(\sigma _{\alpha _R} = 0.01\). The illumination function \(I_n\) is known and, thus, no further uncertainty must be specified.

By applying 100, 000 samples, the uncertainties are evaluated by a Monte Carlo simulation from \(0^{\circ }\) to \(90^{\circ }\) using a step-size of \(1^{\circ }\). The resulting error band regarding only the metrology part is plotted in gray, and the error band, extended by the assumed uncertainties of the weighted coefficients, is colored in red.

Since we are interested in the signal path variations, all values are referred to elevation \(90^{\circ }\). Here, the radio telescope is assumed to be unaffected by gravity deformations and nominal values are valid. Therefore, the uncertainties become smaller and are zero for \(90^{\circ }\). The uncertainties \((2\sigma )\) are about \(200\,\upmu \hbox {m}\) and fulfill the requirements for VGOS-specified radio telescopes (cf. Petrachenko et al. 2009).

Fig. 16
figure 16

Derived signal path variations \({\Delta }L(\epsilon )\) depicted by a solid black line. The confidence intervals \((2\sigma )\) are derived by a Monte Carlo simulation, applied to the entire analysis process. The gray pictured confidence interval results from the metrology part of \({\Delta }L\) and includes the uncertainties of the coded targets, and the campaign temperatures, as well as the telescope angles. Assuming further uncertainties of the \(\alpha \) coefficients in Eq. (21) yields the extended confidence depicted in red

Full size image

6 Conclusion

GGOS aims for 1 mm position accuracy on the global scales for the ITRF. Gravitational deformations of VLBI radio telescopes yield systematic errors and bias the estimated vertical position of the radio telescopes in the geodetic VLBI analysis and, therefore, potentially affect the ITRF scale. For the upcoming ITRF2020, the VLBI community has been encouraged to include gravitational deformation models for VLBI radio telescopes to compensate for the undisputed systematic errors caused by elevation-dependent reflector deformations for as many VLBI radio telescopes as possible. For that reason, mathematical models as well as metrology methods have to validate, to capture, and to model the expected structural deformations.

In this investigation, for the first time, a UAS was used to study the gravitational deformation behavior of a VLBI radio telescope. To our best knowledge, it is also the first time that an observation-based model for the gravitational deformation of a VGOS-specified radio telescope was derived. This model can be easily implemented into VLBI data analysis software packages and used in future VGOS data processing. Several coded targets were mounted at ONSA13NE. The surface of the main reflector and the position of the sub-reflector were measured by photogrammetric methods from elevation \(0^{\circ }\) to \({90}^{\circ }\) using a step-size of \(10^{\circ }\). To increase the reliability, each position was measured twice. In total, 21 measurement campaigns were carried out in August 2018. In contrast to measurement approaches with laser scanners, each target position is highly redundantly observed during a single measurement campaign. This allows for evaluating the quality of the observed points using established statistical methods during the bundle adjustment right at the beginning of the analysis process. The single-point uncertainties of the bundle adjustment are about \(100\,\upmu \hbox {m}\) w.r.t. the datum.

Like many of the VGOS-specified radio telescopes, ONSA13NE makes use of the improved main reflector design and is manufactured as a so-called ring-focus paraboloid. A ring-focus paraboloid results from the combination of two quadric surfaces and, therefore, cannot be modeled as a common paraboloid. The mathematical parameterization of a double-elliptic ring-focus paraboloid was given in detail in this investigation. Similarities of the presented unified model to the simplified rotationally symmetric paraboloid, which has been used in general for modeling the main reflector of conventional VLBI radio telescopes, were mentioned.

Based on the resulting coordinates of the bundle adjustment, the surface parameters of ONSA13NE were estimated using the SQP approach. The focal length varies by about 2 mm. However, the focal length variation itself is a descriptive parameter and does not represent the variation of the optical ray path because the physical position of the sub-reflector also varies. To reconstruct the position variation of the sub-reflector, two approaches were considered. Whereas the first one results from a geometrical modeling of the deformation of the main reflector, the second one is based on direct measurements. Both approaches yield sub-reflector variations of about \(\pm \,0.3\,\hbox {mm}\), which partly counteract the focal length variations. For ONSA13NE, the variations of the focal length and the sub-reflector position can both be expressed by cosine functions.

The model of the main reflector and the model of the sub-reflector are combinations of quadric surfaces, i.e., a ring-focus paraboloid and an elliptic torus, respectively. Considering the geometric properties of both reflectors and the derived deformation pattern, the length of the geometric ray path was derived. As shown in Fig. 14, the length of the geometric ray path depends on the distance from the optical axis and varies over the reflector by about 3 mm at \(0^{\circ }\).

The Gaussian illumination function, which is used by ONSA13NE, was introduced to weight the ray path depending on the incidence angle at the aperture. The resulting amplitude of the modeled signal path variations is about \(-\,0.5\,\hbox {mm}\). For the modeled signal path variations, uncertainties of about \(200\,\upmu \hbox {m}\, (2\sigma )\) were derived by applying a Monte Carlo simulation to the entire analysis process. For VGOS-specified radio telescopes, the requested RMS for modeled path length variations is \(300\,\upmu \hbox {m}\) (Petrachenko et al. 2009). The measurement and analysis concept presented in this investigation fulfill these requirements.

Future work will focus on metrological methods for deriving the shift of the vertex to obtain the SPV independent of the finite element method. Moreover, investigations are needed to verify the possible hysteresis of the focal length variations. Furthermore, the Onsala Space Observatory is in the possibility of having the SPV variation model externally validated by comparing the baseline derived by high-precision terrestrial observations and the baseline obtained by the VLBI data analysis (e.g., Carter et al. 1980). For this purpose, terrestrial measurement campaigns are planed to derive the local baseline vectors between the hosted space geodetic techniques at Onsala.

The OTT are just one type of several different VGOS-type telescopes that have been designed and are currently deployed at various international observatories. To our best knowledge, there are at least three other designs of VGOS-telescopes. We are not aware that any other investigations corresponding to the one presented here have been performed at any of the other VGOS stations. However, a first assumption is that other VGOS-designs also fulfill the VGOS-specifications and will have a similar deformation behavior as the Onsala twin telescopes. Nevertheless, it is strongly advised to derive at least type-specific SPV models for each VGOS telescope type. Regarding the small magnitude of the detected SPV and the small uncertainty of the derived SPV model for the OTT, there are high expectations that VGOS will be able to live up to the challenging GGOS requirements.

In general, the use of a UAS provides a promising and practicable surveying method for free-standing radio telescopes because neither does additional heavy equipment have to be mounted on the radio telescope structure nor is a crane required during the measurement process. This method thus appears very applicable for both VGOS-type and conventional radio telescopes.