A complete VLBI delay model for deforming radio telescopes: the Effelsberg case

Abstract

Deformations of radio telescopes used in geodetic and astrometric very long baseline interferometry (VLBI) observations belong to the class of systematic error sources which require correction in data analysis. In this paper we present a model for all path length variations in the geometrical optics of radio telescopes which are due to gravitational deformation. The Effelsberg 100 m radio telescope of the Max Planck Institute for Radio Astronomy, Bonn, Germany, has been surveyed by various terrestrial methods. Thus, all necessary information that is needed to model the path length variations is available. Additionally, a ray tracing program has been developed which uses as input the parameters of the measured deformations to produce an independent check of the theoretical model. In this program as well as in the theoretical model, the illumination function plays an important role because it serves as the weighting function for the individual path lengths depending on the distance from the optical axis. For the Effelsberg telescope, the biggest contribution to the total path length variations is the bending of the main beam located along the elevation axis which partly carries the weight of the paraboloid at its vertex. The difference in total path length is almost $-$100 mm when comparing observations at 90$^\circ$ and at 0$^\circ$ elevation angle. The impact of the path length corrections is validated in a global VLBI analysis. The application of the correction model leads to a change in the vertical position of $+120$ mm. This is more than the maximum path length, but the effect can be explained by the shape of the correction function.

Appendices

Appendix: Deduction of $\alpha _R''$ coefficient for a Gregorian system

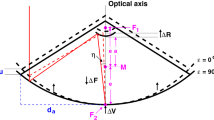
The extra path length which is incurred by a small vertical shift of a Gregorian sub-reflector can be deduced almost in the same way as Abbondanza and Sarti (2010) did for the Cassegrain system. The local reference frame of the following deduction has its origin in the center of the upright ellipsoid, or rather ellipse in the two-dimensional description. In Fig. 11, the signal path that originates from the main reflector (dashed line) goes through $F_1$ and is reflected in $P$ towards the secondary focus $F_2$.

Fig. 11

Ray paths in near-field of Gregorian sub-reflector. The top line (gray) is the original position of the sub-reflector while the lower curve (black, through $P_1$) depicts the shifted position

We assume that the shift $\Delta R$ is small compared to the overall dimensions of the radio telescope. Since the central triangular figure of the extra path length between the two reflecting surfaces of the original and the displaced Gregorian mirror is the same as for the Cassegrain reflector, we can safely apply the approximation for the extra path length

$$\begin{aligned} \Delta L (P) = \overline{PJ} + \overline{PK} \end{aligned}$$

(47)

without any loss of accuracy (Cha 1987).

Abbondanza and Sarti (2010) nicely describe in detail that the extra path length for a single ray through $P$ is

$$\begin{aligned} \Delta L (P) = 2 \Delta R \langle -\hat{z}, \hat{n} \rangle \langle \hat{n}, \hat{i} \rangle \end{aligned}$$

(48)

with the scalar products ($\langle \, \rangle$) of the unit vectors of the vertical displacement $\hat{z}$, of the surface normal $\hat{n}$ and of the incident direction $\hat{i}$. The average total extra path length then results from an integration over the whole effective (unblocked) surface applying the illumination function $I_n$ for the zonal weighting.

$$\begin{aligned} \Delta L = 2\, \alpha _R'' \, \Delta R = 2 \int \limits ^{r_2}_{r_1} I_n \, \langle -\hat{z}, \hat{n} \rangle \langle \hat{n}, \hat{i} \rangle \, \mathrm{d}r \cdot \Delta R \end{aligned}$$

(49)

It now remains to determine the three unit vectors which depend on the geometric function of the reflecting surface. In the Gregorian case it is a “standing“ ellipsoid with the axis connecting the two foci being the vertical ($z$) axis. It is rotationally symmetric reducing the dimensions to two in this deduction, reflected by the parameter $r$

$$\begin{aligned} F: = \frac{r^2}{c^2} + \frac{z^2}{a^2} - 1 = 0 \end{aligned}$$

(50)

with $e = \sqrt{a^2 - c^2}$. The vector $\overline{PF_1}$ is

$$\begin{aligned} \overline{PF_1} = [-r, -(z - e)] = \left[ -r, \, -a \sqrt{1 - \frac{r^2}{c^2}} -e \right] \end{aligned}$$

(51)

The incidence unit vector $\hat{i}$ is

$$\begin{aligned} \hat{i} = \frac{\overline{PF_1}}{\Vert PF_1 \Vert } = \left[ - \frac{r}{\sqrt{r^2 + (z - e )^2}}, \, - \frac{a \sqrt{1 - \frac{r^2}{c^2}} -e}{\sqrt{r^2 + (z - e )^2}} \right] . \end{aligned}$$

(52)

The surface normal, pointing inwards, is

$$\begin{aligned} \hat{n}&= \left[ -\frac{\frac{\partial F}{\partial r}}{\Vert \nabla F \Vert }, \, -\frac{\frac{\partial F}{\partial z}}{\Vert \nabla F \Vert } \right] \nonumber \\&= \left[ - \frac{ar}{\sqrt{c^4 + r^2 \cdot e^2}}, \, -c \sqrt{\frac{c^2 - r^2}{c^4 + r^2 \cdot e^2}} \right] \end{aligned}$$

(53)

and

$$\begin{aligned} - \hat{z} = [ 0, -1] \end{aligned}$$

(54)

The resulting scalar products needed for Eq. 49 are

$$\begin{aligned} \langle -\hat{z}, \hat{n} \rangle = c \sqrt{\frac{c^2 - r^2}{c^4 + r^2 \cdot e^2}} \end{aligned}$$

(55)

and

$$\begin{aligned} \langle \hat{n}, \hat{i} \rangle&= \frac{ar}{\sqrt{c^4 + r^2 \cdot e^2}} \cdot \frac{r}{\sqrt{r^2 + (z - e )^2}}\nonumber \\&\quad +\, c \frac{\sqrt{c^2 - r^2}}{\sqrt{c^4 + r^2 \cdot e^2}} \cdot \frac{z -e}{\sqrt{r^2 + (z - e )^2}}. \end{aligned}$$

(56)

Assuming the $\cos ^2$ law for the illumination function (cf. Eq. 4) and transforming it to decimal units, the coefficient $\alpha _R''$ for Eq. 49 can be evaluated as

$$\begin{aligned} \alpha _R''&= 2 \pi \int \limits ^{r_2}_{r_1} I_n \cdot c \sqrt{\frac{c^2 - r^2}{c^4 + r^2 \cdot e^2}} \nonumber \\&\quad \cdot \left[ \frac{ar}{\sqrt{c^4 + r^2 \cdot e^2}} \cdot \frac{r}{\sqrt{r^2 + (z - e )^2}}\right. \nonumber \\&\quad +\, c \frac{\sqrt{c^2 - r^2}}{\sqrt{c^4 + r^2 \cdot e^2}} \cdot \left. \frac{z -e}{\sqrt{r^2 + (z - e )^2}} \right] \, \mathrm{d}r \end{aligned}$$

(57)

with the normalized illumination function (Eq. 8)

$$\begin{aligned} I_n (\gamma ) = k_c \cdot 10^{\frac{a_0 + a_1 \cdot \cos ^2 \gamma }{10}} \end{aligned}$$

(58)

with $\gamma$ depending on $r$ and the specific construction elements of the radio telescope to be modeled.

Entering all parameters of a telescope in Eq. 57 allows to either determine path length changes of individual rays or as a weighted average when the integral could be solved.

There is, however, a further effect which needs to be taken into account. The deviations of Cha (1987) and Abbondanza and Sarti (2010) assume that the reflected ray $r$ will reach the second focus. As can be explained with Fig. 12, the incoming ray $\mathbf{i}$ hits the non-displaced ellipsoidal sub-reflector at $P$ and the shifted sub-reflector at $P'$. The respective normal vectors $\mathbf{n}$ and $\mathbf{n'}$ are not parallel and the reflected ray $\mathbf{r}$ and $\mathbf{r'}$ are not, either. Rather, $\mathbf{r'}$ hits the focal plane a few centimeters off the focal point. In total, this leads to an even bigger distance factor than that reflected by Eq. 57.

Fig. 12

Ray paths from nominal focus of sub-reflector to reflecting point $P$ on nominal sub-reflector (top gray surface) and for shifted sub-reflector (bottom black surface)

Unfortunately, the additive effect is composed of differences in the position of the reflecting point, in the normal vector and in the reflection vector, and are non-linear practically inhibiting a closed analytical description and formulation.

The intersection of an incoming ray ($Ax + B$) through the original focus with the (vertically) displaced ellipsoidal sub-reflector ($x', y'$) can be computed (in two dimensions) by equating the formulation of a straight line and that of the ellipse:

$$\begin{aligned} A \, x + B = a \sqrt{1- \frac{x^2}{c^2}} + \Delta R. \end{aligned}$$

(59)

The following computations are simplified by setting $B' = B - \Delta R$ yielding

$$\begin{aligned} x' = \frac{\sqrt{a^2 - B'^2 + \frac{(AB')^2}{A + \frac{a^2}{c^2}}} - \frac{AB'}{\sqrt{A^2 + \frac{a^2}{c^2}}}}{\sqrt{A^2 + \frac{a^2}{c^2}}} \end{aligned}$$

(60)

and

$$\begin{aligned} y' = A \, x' + B. \end{aligned}$$

(61)

$A$ can be computed by taking the focus with [0, e] of the ellipse and arbitrary points on the ellipse P($x,y$) starting with [0, a] down to the edge (with e the numerical eccentricity and a the semi-major axis of the ellipse) by

$$\begin{aligned} A = \frac{y - e}{x} \quad \text {and} \quad B = y - Ax . \end{aligned}$$

(62)

The distance between $F_1$ and $P'$ is then

$$\begin{aligned} D_2' = \sqrt{x'^2 + (y' - e)^2} . \end{aligned}$$

(63)

$A$ also provides the direction of $\mathbf{i}$. To compute the reflected ray, the surface normal vector $\mathbf{n}$ is needed and can be taken from Eq. 53. Mirroring $\mathbf{i}$ on $\mathbf{n}$ provides the direction $\mathbf{r}$ from $P'(x'/y')$ to the focal plane. The respective distance $D_3$ is

$$\begin{aligned} D_3 = \frac{-e - y'}{\cos \mathbf{r}} . \end{aligned}$$

(64)

In total, the extra path length due to a shift in the sub-reflector position is then

$$\begin{aligned} \Delta s = D_2' + D_3 - 2a. \end{aligned}$$

(65)

The correct alternative to Eq. 57, although it cannot be integrated analytically, is

$$\begin{aligned} \alpha _R'' = \int \limits ^{r_2}_{r_1} k_c \cdot 10^{\frac{a_0 + a_1 \cdot \cos ^2 \gamma }{10}} \cdot \frac{1}{2}(D_2' + D_3 - 2a) \,\mathrm{d}r . \end{aligned}$$

(66)

The factor 1/2 is introduced to maintain consistency with the definition of $\alpha _R''$ in Abbondanza and Sarti (2010). A solution for the integral can easily be found with a numerical integration.

The Effelsberg case

The Effelsberg 100  m radio telescope has an ellipsoidal sub-reflector with $a$ = 14.3050 m and $c$ = 7.3872 m resulting in $e = \sqrt{a^2 - c^2}$ = 12.25 m. Its diameter is 6.5 m. Taking into account that an inner circle with a radius of 0.29 m is not illuminated by the main reflector through the vertex feed horn cabin, the primary-focus-centered aperture angle of the sub-reflector $\gamma$ ranges 8$^\circ$–80$^\circ$. Assuming a shift of the sub-reflector of 10 mm downwards, the unweighted path length change using Eq. 66 for a ray 8$^\circ$ off the optical axis is $-$20.09 mm while for a ray just skimming the rim, it is $-$21.53 mm. With the coefficients $a_0$ = $-$728.3055 and $a_1$ = 727.3055 for the illumination function in a numerical integration with 1 cm step size, the average path length change is $-$21.23 mm producing a coefficient $\alpha _R''$ of 1.0615.

It should be noted that the size of $\alpha _R''$ is beyond the expected maximum of 1.0. The reason is, that for large telescopes, the divergence of the reflected rays contributes an extra component to the excess path length in addition to the near-field effect represented by Eq. 57. Applying the excess paths derived by Abbondanza and Sarti (2010) produces only an $\alpha _R''$ of 0.894.