A comparative review of peridynamics and phase-field models for engineering fracture mechanics

Abstract

Computational modeling of the initiation and propagation of complex fracture is central to the discipline of engineering fracture mechanics. This review focuses on two promising approaches: phase-field (PF) and peridynamic (PD) models applied to this class of problems. The basic concepts consisting of constitutive models, failure criteria, discretization schemes, and numerical analysis are briefly summarized for both models. Validation against experimental data is essential for all computational methods to demonstrate predictive accuracy. To that end, the Sandia Fracture Challenge and similar experimental data sets where both models could be benchmarked against are showcased. Emphasis is made to converge on common metrics for the evaluation of these two fracture modeling approaches. Both PD and PF models are assessed in terms of their computational effort and predictive capabilities, with their relative advantages and challenges are summarized.

1 Introduction

Fracturing phenomena in natural and engineered systems is studied extensively experimentally, theoretically, and computationally. Here we focus on two promising approaches: phase-field (PF) and peridynamics (PD) for the computational modeling of fractures in materials. Both approaches are distinct from earlier ones as they seek to predict crack path as functions of specimen loading and geometry. Ideally, these approaches attempt the computational predictions after an initial calibration using engineering constants such as Young’s modulus and fracture toughness specific to the material. These ambitious approaches are called free fracture models. This review is intended as a snapshot capturing in broad strokes the modeling details, assumptions, experimental data sets, and numerical simulations necessary for validation. These methods have the potential to address fundamental issues in complex fracturing with minimal introduction of phenomenological modeling assumptions and numerical tuning parameters. However, systematic comparative analysis for these models, together with validation studies on the set of experiments, are rare. In this review, we attempt to initiate such a comparative analysis and, when possible, invoke validation studies from the experimental literature.

As an example of an engineering fracture mechanics application, Hattori et al. (2017) [1] presented a comprehensive comparison of various numerical approaches for the hydraulic fracturing of shale and showed the advantages as well as limitations of many numerical approaches including peridynamics (PD) and phase-field (PF). However, this comparative analysis for various models lacked validation studies on the same set of hydraulic fracturing experiments in order to evaluate predictive capabilities of numerical models. Our review is motivated by the recent workshops on phase-field, peridynamics, and experimental fracture mechanics held at The Banff International Research Station: Hydraulic Fracturing: Modeling, Simulation, and Experiment¹, and the Workshop on Experimental and Computational Fracture Mechanics² [2].

1.1 Other review papers

One of the first overview papers of peridynamic and non-local modeling was written by Du and Lipton³ in the SIAM news, volume 47 (2014). However, this article was quite brief. In 2019, Javili et al. [3] published a review emphasizing the applications of PD. In the same year Diehl et al. [4] published a review with the focus on benchmarking PD against experimental data. In 2021, Isiet et al. [5] published a review on the usage of PD for impact damage. In the same year, Hattori et al. [6] published a review on the usage of PD in reinforced concrete structures. Zhou and Wang [7] published a review on the usage of PD in geomaterials in 2021. To summarize, except for the first PD review in 2019, all reviews focused on some specific topic. Hidayat et al. [8] published a review on the connection of meshfree PD between other meshfree methods in 2021. In addition, the following three books about PD are available [9,10,11].

In what follows, we now list PF review papers and monographs. The first summary on variational modeling of fracture was by the founding authors Bourdin, Francfort and Marigo [12]. Although they explicitly state on page 7 that they are not attempting to review and access existing literature, their work describes on 148 pages the current state-of-the-art in the year 2008. The first review papers (that have explicitly this purpose) with regard to computational/engineering aspects of phase-field (variational) fracture were published by Rabczuk [13] and Ambati, Gerasimov, and De Lorenzis in 2015 [14]. In the latter study, despite review aspects, a new formulation for stress splitting is proposed therein. Due to the ongoing increasing popularity, shortly after, various other reviews, monographs, and news articles appeared. A short SIAM news article about the latest developments and future perspectives was published by Bourdin and Francfort in 2019 [15]. An extensive review paper on theoretical and computational aspects was done by Wu et al. in the year 2020 [16]. The authors also discuss the success or failures of several benchmark problems for quasi-static, dynamic brittle/cohesive fracture. Only considering phase-field (variational) fracture, this review paper certainly exceeds in topics, modeling details and numerical aspects and examples of our current work. In the same year, a monograph on multiphysics phase-field fracture was published by Wick [17]. Therein, the focus is briefly on modeling of classical variational phase-field fracture, error estimation and adaptivity, and including other physics phenomena via volume or interface coupling techniques. Most recently in 2021, one of the original authors, namely, Francfort, published an article entitled with ‘Variational fracture: Twenty years after’ [18].

1.2 Purpose and value of this review paper

In view of existing (recent) reviews on both approaches, we shall explain the purpose and value of the current review paper. First and most importantly, both PD and PF are appearing to be the most prominent approaches for free fracture modeling. Other notable approaches are the displacement-discontinuity method [19], cohesive-zone models [20], boundary elements [21], XFEM/GFEM [22,23,24], and the eigen-erosion framework [25,26,27,28]. A comparative review between XFEM (extended finite elements), mixed FEM, and phase-field models appeared in [29].

The present paper provides for the first time a comparison between both approaches (PD and PF). For this reason, the mathematical descriptions remain rather short while focusing on the key ingredients that allow for comparison of PD and PF. It is through this lens we reference the existing models and numerical methods from the literature. The Sandia Fracture Challenge is chosen for validation against experimental data. The first part of the challenge is to calibrate a free fracture model to simple prototypical problems, e. g. a tensile test, and use this calibration to simulate the crack and fracture phenomena. Thus, the model parameters can not be fitted to the complex scenario and have been instead calibrated using the simple scenario. This additional step of calibration makes the Sandia Fracture Challenge an excellent problem to benchmark phase-field models and peridynamic models to assess their performance on different kinds of crack and fracture phenomena. These numerical, computational, and experimental side-by-side comparisons allow us to identify similarities, common challenges, and specific aspects to each method.

1.3 Outline

The paper is structured as follows: Sect. 2 introduces the two models and provides a basis on which the models can be compared and contrasted. This summary is an adaptation and extension of the review papers and monograph [3, 4, 16, 17]. Section 3 addresses the fracture physics perspective from the macroscale view. Section 4 attempts to compare the predictive accuracy of the two models for validation against the experimental data. To that end, the Sandia Fracture Challenges data sets were analyzed and computed, the $R^2$ correlation of relative errors between the simulations and the experiment are presented. Section 5 compares computational aspects of the two models as well as pointing out challenges and opportunities for development. Finally, Sect. 6 summarizes the modeling capabilities of PD and PF.

Fig. 1

Sketch for the principle of peridynamics where a material point X interacts with its neighbors inside a finite interaction zone $B_\delta (\mathbf {X})$ with the length $\delta$

2 Overview of models and numerical methodology

This section briefly introduces the two methods, peridynamics (PD) and phase field (PF), respectively. A brief overview of the governing equations, material models, discretizations, numerical analysis, and advanced visualization methods is given. We introduce the ingredients for the comparison of these two models and provide references to the extended literature for the interested reader.

2.1 The governing equation of peridynamics

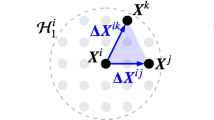
Peridynamics (PD), is a non-local adaptation of classical continuum mechanics (CCM). In PD, each material point $\mathbf {X}$ interacts with its neighbors inside a finite interaction zone $B_\delta (\mathbf {X})$ with the length $\delta$, see Fig. 1. This type of non-local interaction principle is also seen in molecular dynamics (MD) [30] and smoothed particle hydrodynamics (SPH) [31, 32] simulations. The important feature of PD fracture modeling is that the interaction between the intact material and fractured material is modeled implicitly through a non-local field equation that remains the same everywhere in the computational domain. Material damage and fracture phenomena are captured through a force versus strain constitutive model. Because of this, PD is able to capture fracture as an emergent phenomena arising from the non-local equation of motion. This contrasts with classic fracture theory where, off the crack, the elastic interaction is modeled by the equation of elastodynamics and the fracture set is a free boundary with motion coupled to elastodynamics through a physically motivated kinetic relation. Other recently developed non-local models exhibiting emergent behavior include the Cucker Smail equation, where swarming behavior emerges from leaderless flocks of birds [33,34,35,36].

The equation of motion for bond-based peridynamics proposed by Silling [37, 38] reads as

$$\begin{aligned}&\varrho (\mathbf {X})\ddot{\mathbf {u}}(t,\mathbf {X}) =\int \limits _{B_\delta (\mathbf {X})}\mathbf {f}(\mathbf {u}(t,\mathbf {X}')-\mathbf {u}(t,\mathbf {X}),\mathbf {X}'-\mathbf {X}) d\mathbf {X}' + \mathbf {b}(t,\mathbf {X})\text {,} \end{aligned}$$

(1)

where $\varrho \in \mathbb {R}$ is the material density $\ddot{\mathbf {u}}\in \mathbb {R}^n$ is the acceleration at time $t \in \mathbb {R}$ of the material point $\mathbf {X} \in \mathbb {R}^n$, $\mathbf {f} : \mathbb {R}^n \times \mathbb {R}^n \times [0,T] \rightarrow \mathbb {R}^n$ is the pair-wise force function, $\mathbf {b} \in \mathbb {R}^n$ is an external force density, and $\mathbf {u} \in \mathbb {R}^n$ is the state of deformation at a point in space time, $(t,\mathbf {X})$. The constitutive model for the pair-wise force function $\mathbf {f}$ is material dependent and defines how the internal forces react to the displacement $\mathbf {u}$. For the elastic regime the force interaction between a pair of points $\mathbf {X}$ and $\mathbf {X}'$ is a so-called bond and contributes to the name of bond-based PD. The pair-wise interaction leads to a constraint on the Poisson ratio [39, 40].

To overcome the Poisson ratio constraint more general non-local interactions are included in the “state-based” peridynamic model. The generic state-based peridynamic equation of motion introduced by Silling et al. [41] reads as

$$\begin{aligned}&\varrho (\mathbf {X})\ddot{\mathbf {u}}(t,\mathbf {X}) = \int \limits _{B_\delta (\mathbf {X})} (\underline{T}[\mathbf {X},t]\langle \mathbf {X}' - \mathbf {X} \rangle - \underline{T}[\mathbf {X}',t]\langle \mathbf {X} - \mathbf {X}' \rangle ) d\mathbf {X}' + \mathbf {b}(t,\mathbf {X})\text {,} \end{aligned}$$

(2)

where the pair-wise force function $\mathbf {f}$ is exchanged with the so-called peridynamic force state $\underline{T} : \mathbb {R}^n \times \mathbb {R}^n \times [0,T] \rightarrow \mathbb {R}^n$. The usage of PD states lead to the name state-based PD. A peridynamic state relates to second order tensor and they assign each point in a neighborhood a tensorial quantity. However, in general, it is not a linear or continuous function with respect to $\mathbf {X} - \mathbf {X}'$. For more details, we refer to [41, Section 2].

In peridynamics, material damage is part of the constitutive modeling and the material is viewed as damaged when the force state at a point $\mathbf {X}$ no longer influences a material point $\mathbf {X}'$ and vice versa. Damage occurs when the difference between deformation states at each point $\mathbf {X}$ and $\mathbf {X}'$ surpass a threshold. The specifics of how this occurs depends on the material model used. For example, for pairwise force functions $\mathbf {f}$ the force acting between two points is often referred to as a bond. When the pairwise force is zero, it is said that the bond is broken. Bonds can break irreversibly, or alternatively they can heal under the right conditions, this depends upon the material model used.

To fix ideas, we illustrate the constitutive law given by the prototype brittle microelastic (PMB) model introduced in [38]. The deformation of a point $\mathbf {X}$ is $\mathbf {u}(t,\mathbf {X})$ and its position in the deformed configuration is $\mathbf {X} + \mathbf {u}(t,\mathbf {X})$. In this model, the pair-wise force function depends on the strain between two points in the deformed configuration given by

$$\begin{aligned}&S(t,\mathbf {X},\mathbf {X}') \nonumber \\&\quad := \frac{ \Vert (\mathbf {X}' + \mathbf {u}(t,\mathbf {X}')) - (\mathbf {X} + \mathbf {u}(t,\mathbf {X})) \Vert - \Vert \mathbf {X}' - \mathbf {X} \Vert }{\Vert \mathbf {X}' - \mathbf {X} \Vert }. \end{aligned}$$

(3)

The direction vector between two points in the deformed configuration is given by

$$\begin{aligned} \mathbf {e}=\frac{ (\mathbf {X}' + \mathbf {u}(t,\mathbf {X}')) - (\mathbf {X} + \mathbf {u}(t,\mathbf {X})) }{ \Vert (\mathbf {X}' + \mathbf {u}(t,\mathbf {X}')) - (\mathbf {X} + \mathbf {u}(t,\mathbf {X})) \Vert }. \end{aligned}$$

(4)

The force directed between the two points in the deformed configuration is given by the constitutive law

$$\begin{aligned}&\mathbf {f}(\mathbf {u}(t,\mathbf {X}')-\mathbf {u}(t,\mathbf {X}),\mathbf {X}'-\mathbf {X}) := \end{aligned}$$

(5)

$$\begin{aligned}&\mu (t,\mathbf {X},\mathbf {X}')c S(t,\mathbf {X},\mathbf {X}')\mathbf {e}, \end{aligned}$$

(6)

where $c>0$ is the material dependent stiffness constant, and the scalar damage function $\mu$ is given by

$$\begin{aligned} \mu (t,\mathbf {X},\mathbf {X}') := {\left\{ \begin{array}{ll} 1, \quad S(t,\mathbf {X},\mathbf {X}') \le s_c\\ 0, \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(7)

where $s_c>0$ is the material dependent critical bond stretch. Once the force between the two points goes to zero it stays zero. It is noted that there are several other definitions for the damage function $\mu$ using strain-based criteria [38, 42], as well as stress-based [43], or energy-based damage criteria [44, 45], see Fig. 4.

Fig. 2

The classification of the different peridynamic material models visualized as a tree. The material models are classified in two major classes: bond-based and state-based material models, respectively. State-based material models are distinguished as ordinary and non-ordinary models. The following ordinary state-based models are available: elastic-brittle, plasticity, composite, Eulerian fluid, and viscoleastic. For non-ordinary state-based models the Beam\Plate, the correspondence model, and a model for cementitious composites are available. Adapted from [3, 4] and extended for this work

Fig. 3

Schematics of the a bond-based model, b the ordinary state-based model, and c the non-ordinary state-based model. Note that the blue text in the Equations highlights the different assumptions for each model. This figure was adapted from [41]

In numerical implementations crack path evolution is recovered as a post-processing step after simulation. To identify the crack we introduce the damage field $d : [0,T] \times \mathbb {R}^n \rightarrow \mathbb {R}$ given by the density $d(t,\mathbf {X})$ defined by

$$\begin{aligned} d(t,\mathbf {X}) = 1 - \frac{\int \limits _{B_\delta (\mathbf {X})} \mu (t,\mathbf {X},\mathbf {X}')d\mathbf {X}'}{\int \limits _{B_\delta (\mathbf {X})}d\mathbf {X}'} \end{aligned}$$

(8)

where the scalar function $\mu : [0,T] \times \mathbb {R}^n \times \mathbb {R}^n \rightarrow \mathbb {R}$ indicates if the bond between $\mathbf {X}$ and $\mathbf {X}'$ at time t is broken ($\mu =0$) or active ($\mu =1$). Locations where $d=0$ indicate the crack set. The set where $d=0$ is highly localized and indicates the evolving crack path. This damage localization has been demonstrated mathematically by Lipton [46, 47] for peridynamic fracture evolution corresponding to the small deformation bond based models. The method uses Gronwall’s inequality together with methods from the non-local image approximation of the Mumford Shah model [48] introduced by Gobbino [49]. For more theory of peridynamic states, we refer to [41, Section 2]. For additional references, we refer to [9, 10]. For reviews about PD and the comparison with experimental data, we refer to [3, 4].

2.1.1 Material models for PD

Figure 2 shows the tree of different peridynamic material models. The root are state-based material models, with the two subclasses of ordinary state-based and non-ordinary state-based material models. Note that bond-based models [38, 47, 50,51,52,53,54,55,56,57,58,59,60,61,62] are a special case of state-based models. However, the bond-based PD was presented in 2000 and state-based PD in 2007. For ordinary state-based PD, the following material models are available: Elastic brittle [41, 63,64,65], Plasticity [66,67,68,69], Composite [70], Eulerian fluid [71], position-aware linear solid (PALS) [72], and Viscoelastic [73,74,75,76]. For non-ordinary state-based PD the correspondence model [41, 77], the beam/plate model [78], and a model for cementitious composites [79] are available. For more details, we refer to [3].

Figure 3 shows the schematics of the three different models. All of these three models conserve linear momentum. However, only the bond-based model and the ordinary-state-based model conserve angular momentum. For more mathematical details, we refer to [41, Definiton 8.4].

Fig. 4

The classification of different peridynamic damage models visualized as a tree. The majority of the damage models are based on strain, and only a few are based on energy or stress

2.1.2 Discretization methods for PD

Continuous and discontinuous finite element methods [80,81,82], Gauss quadrature [83], and spatial discretization [38, 84, 85] were utilized to discretize the peridynamic equation of motion. However, the most common discretization approach is the EMU nodal discretization, a colocation approach, introduced by Silling in [38]. In this approach, the domain D is discretized with the discrete points $\mathbf {X}=\{ \mathbf {x}_i \in \mathbb {R}^n | i=1,\ldots ,N\}$ with the surrounding volumes $V=\{ v_i \in \mathbb {R} | i=1,\ldots ,N\}$. The following assumptions are made: all the volumes are non-overlapping $v_i \cap v_j \ne \emptyset \text { for } i \ne j$ and the sum of all surrounding volumes is equal to the volume of the reference configuration $\sum v_i \approx V_D$. The discrete interaction zone is defined as $B_\delta (\mathbf {x}_i) := \{ j \vert \, \Vert \mathbf {x}_j - \mathbf {x}_i \Vert \le \delta \}$. The discrete bond-based equation of motion reads as

$$\begin{aligned}&\varrho (\mathbf {x}_i)\ddot{\mathbf {u}}(t,\mathbf {x}_i) \nonumber \\&\quad =\sum \limits _{j \in B_\delta (\mathbf {x}_i)}\mathbf {f}(\mathbf {u}(t,\mathbf {x}_j)-\mathbf {u}(t,\mathbf {x}_i),\mathbf {x}_j-\mathbf {x}_i) dV_j + \mathbf {b}(t,\mathbf {x}_i) \end{aligned}$$

(9)

and the state-based equation of motion reads as

$$\begin{aligned}&\varrho (\mathbf {x}_i)\ddot{\mathbf {u}}(t,\mathbf {x}_i) \nonumber \\&\quad =\sum \limits _{j \in B_\delta (\mathbf {x}_i)} (\underline{T}[\mathbf {x}_i,t]\langle \mathbf {x}_j - \mathbf {x}_i \rangle - \underline{T}[\mathbf {x}_j,t]\langle \mathbf {x}_i - \mathbf {x}_j \rangle ) dV_j \nonumber \\&\qquad + \mathbf {b}(t,\mathbf {x}_i)\text {.} \end{aligned}$$

(10)

The following implementations are available: Peridigm [86, 87] and PDLammps [84] based on the Message Passing Interface (MPI), NonLocal models/PeriHPX [88, 89] based on the C++ standard library for parallelism and concurrency (HPX) [90, 91], PeriPy [92] based on the Python programming langugae, and GPU-based codes [93,94,95]. Four open source implementations of peridynamic PDLammps⁴, Peridigm⁵, PeriPy⁶, and PeriHPX⁷ are available. One commercial code is available. LS-DYNA provides a bond-based peridynamics implementation discretized with the discontinuous Galerkin FEM [96]. Not to forget one of the first peridynamic implementations, EMU by Stewart Silling using FORTRAN 90 [97].

2.1.3 Numerical analysis for PD fracture models

In this section, we summarize the issues that arise in the numerical analysis of PD fracture models and list the numerical results. The following basic questions for PD fracture models are:

• 1. Are peridynamic fracture models well-posed, such that unique solutions exist?

• 2. What is the relation between non-local continuum peridynamic fracture models and their discretizations used in the numerical implementation?

• 3. How do PD solutions to fracture mechanics problems relate to local fracture models with sharp cracks? Particularly, how does PD relate to the more classical Linear Elastic Fracture Mechanics of continuum mechanics?

These are natural questions to ask, and analogous questions have been investigated and answered for several nonlocal and PD models in the absence of fracture, for this case there is now a vast literature; see [98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116]. This work provides the foundation for the numerical analysis of the PD fracture problem and this review concentrates exclusively on the PD fracture problem.

For the case of fracture, the analysis for PD fracture models is still in the initial stages, but meaningful progress has been made, and one can begin to address the three fundamental questions raised in the first paragraph:

First, the answer to question (1) is addressed. The existence and uniqueness of solutions for peridynamic fracture models have been studied for different classes of constitutive laws. For a simple peridynamic model with nonlocal forces that soften beyond a critical strain, the existence and uniqueness of the solution over finite time intervals is demonstrated for bond-based and state-based peridynamics in Lipton [46, 47] and Jha & Lipton [117]. Energy balance is shown to hold for all times of the evolution. This is a simple constitutive model designed for monotonically increasing loads.

Existence and uniqueness is established for more complex material models with the force degradation law determined by both the time and strain rate for strains above a critical value in Emmrich and Puhst [118]. Therein, both existence and uniqueness are established for bond-based peridynamic fracture. The authors Du et al. [119] consider a continuous version of the Prototypical Microelastic Bond (PMB) model introduced by Silling [37]. In this work both existence and uniqueness are shown and the total energy of the system is decreasing with time, see [119]. Existence and uniqueness is established for a state-based model with material degradation law, again determined by both the time and strain rate for strains above a critical load in Lipton et al. [120]. There, the rate form of energy balance is established among energy put into the system the kinetic energy, elastic energy, and energy dissipated due to the damage. The energy dissipation rate due to damage is seen to be positive. This model is suitable for cyclic loads, see [120]. The theme common to all peridynamic models is that both the existence and uniqueness of solutions follow from the Lipschitz continuity of the peridynamic force and the theory of vector-valued ODE on Banach spaces.

Second, the answer to question (2) is addressed. The convergence of finite difference approximations to bond-based and state-based peridynamic field theories with forces that soften is established in Jha & Lipton [121] and [122]. The finite element convergence for bond-based and state-based peridynamic field theories with forces that soften are established by those authors in [123] and [81]. A priori convergent rates are linked to the regularity of continuum PD fracture solutions. Existence and uniqueness of solutions in Hölder spaces, and Sobolev spaces $H^n$, $n=1,2$, are proved for both bond and state based force softening models in [81, 122]. The convergence rates for both bond- and state-based models are found to be linear in the mesh size and time step. However the constants appearing in the convergence estimates grow exponentially as the horizon size tends to zero. Fortunately, dynamic fracture experiments last hundreds of microseconds for brittle materials and linear a priori convergence rates for horizons that are tens of times smaller than the sample size are in force for tens of microseconds. Numerical experiments exhibit much better convergence with respect to mesh size and time step thus driving the need for the development of a posteriori estimates for understanding convergence rates.

Third, the answer to question (3) is addressed. For certain PD models one can theoretically recover a local sharp fracturing evolution. A limiting local evolution is shown to exist for the force softening peridynamic model; see [46, 47]. The limiting local evolution has jump discontinuities in the displacement confined to a set of finite surface areas (more precisely, two-dimensional Hausdorff measure) for almost every time; see [46, 47]. The jump set corresponds to the fracture set in the zero horizon model and the total energy is bounded and given by the classic energy of linear elastic fracture mechanics [46, 47, 124]. It is shown there that the deformation in the limit model satisfies the local balance of linear momentum equation in quiescent zones away from the crack. Recent work explores the zero horizon limit for straight cracks growing continuously with the goal of capturing the explicit interaction between the growing crack and the surrounding elastic material. For this case, it has been found by Lipton et al. [125] that the local model obtained in the zero horizon limit is given by a deformation field, that is, the weak solution of the linear wave equation on the domain with the growing crack satisfies the zero traction condition of the sides of the crack. This is in agreement with Linear Elastic Fracture Mechanics (LEFM). Here, the weak solution of the wave equation outside a time-dependent domain defined by a crack was recently developed in DalMaso and Toader [126]. The convergence of PD to the wave equation in time-dependent domains [125] gives theoretical support backing the recent development of new “asymptotically compatible” methods for fracture modeling given in Trask et al. [127]. Lastly, starting with the PD equation multiplying by the velocity and integrating by parts gives the time rate of change of internal energy surrounding the crack front. Jha & Lipton [128] use applied math arguments to show that on passing to the zero horizon limit, the kinetic relation for crack tip growth given by LEFM is recovered. Here the classic square root singularity in the elastic field at the crack tip is obtained.

Fig. 5

The consistency of non-local models and the limits of the horizon $\delta$ and the nodal spacing h presented in Du et al. [111, 112]. Adapted from [129]

We conclude this section noting that the numerical analysis of PD in the absence of fracture provides compelling heuristics for understanding PD fracture models. Figure 5 illustrates the interplay between horizon length scale and discretization length scale for PD models when local models can be recovered by passing to the small horizon limit in non-local models, see Du et al. [111, 112]. When a numerical scheme can be designed so that the diagonal arrow captures the same limit as obtained by proceeding along the sides of the square problem, a numerical scheme is said to be asymptotically compatible. This is the motivation behind the numerical approach of Trask et al. [127] to capture the coupling between intact material surrounding a growing crack. For example, if one considers elastic problems in the absence of fracture, then for the diagonal transition where the horizon $\delta$ and the nodal spacing h go to zero, it is known that: using piece-wise constant finite elements, the correct local solution is obtained, if the nodal spacing decays faster than the horizon to zero [111]. This is seen for the EMU nodal discretization [97] which converges to the limit $u_{0,0}$ along the diagonal if the nodal spacing decays faster than the horizon in Tian and Du [114].

2.1.4 On the connection between meshfree peridynamics and other meshfree methods

In the absence of fracture, the relation of PD to molecular dynamics (MD) has been shown by Seleson et al. [130]. Along another direction, the relation of PD to smooth-particle hydrodynamics (SPH) is established in Ganzenmüller et al. [110]. With these studies in mind, it is clear that up-scaling MD fracture models to PD and establishing the relation between SPH and PD for fracture would be desirable.

Bessa et al. [131] showed that approximated derivatives of state-based PD are completely equivalent to the approximation received by the reproducing kernel particle method (RKPM) with synchronized derivatives and with a quadratic polynomial basis. Bode et al. [132] introduced the peridynamic Petrov-Galerkin (PPG) method, which is developed based on the PD equation of motion starting from the state-based formulation in [10]. Hillman et al. [133] showed the relation between reproducing kernel (RK) approximation with implicit gradient and peridynamic. Madenci et al. [134] introduced the peridynamic differential operator (PDDO). Shojaei et al. [135] introduced a generalized finite difference method (GDFM) based on PDDO. Table 1 lists all of these connections. Fore more details, we refer to [8].

Table 1 Connection between meshless discrete PD and other meshfree methods. Adapted and extended from [8]

2.1.5 Visualization of PD results

Since most peridynamic simulations are done using a meshless method, information, e.g. stress and strain, are only available on the discrete nodes. Thus, every graphics software, e.g. Paraview [136] or VisIt [137], supporting particles can be used to visualize meshless simulation results. However, to understand the simulation and compare against experimental data, this information is needed on a larger scale. First, peridynamic theory was used for physically-based modeling and rendering. Here, the animation of brittle fracture [138], the animation of fractures in elastoplastic solids [139], and the animation of hyper elastic materials [140] were studied. Second, the visualization of fragmentation [141, 142] and visualization of fracture progression [143] were investigated. For more details, we refer the readers to [4].

2.2 Phase-field models governing equations

Variational models to fracture and damage models were introduced by Francfort & Marigo [144] and Aranson et al. [145]. A numerical approximation of variational fracture models was first introduced by Bourdin et al. [146]. We also refer to [12] and the recent review paper [15].

The principal idea of the variational (phase-field) approach to fracture (here explained for quasi-static fracture in brittle materials) is based on energy minimization in which potential and fracture energies interact. To this end, let $\varOmega \subset \mathbb {R}^n$ be the intact domain and $\varGamma \subset \mathbb {R}^{n-1}$ the fracture set. Let $\mathbf {u}:\varOmega \rightarrow \mathbb {R}^n$ be a displacement field and the total energy be given by

$$\begin{aligned} E(\mathbf {u},\varGamma )&= \underbrace{\int \limits _{\varOmega } \psi _0(\varepsilon (\mathbf {u})) dV - F(\mathbf {u})}_{=: P(\mathbf {u})} + \underbrace{\int \limits _{\varGamma } G_c\, dA}_{=\psi _c(\varGamma )}, \end{aligned}$$

with the potential energy

$$\begin{aligned} P(\mathbf {u}) := \int \limits _{\varOmega } \psi _0(\varepsilon (\mathbf {u})) dV - F(\mathbf {u}), \end{aligned}$$

composed by the bulk energy (first term) with $\psi _0(\varepsilon (\mathbf {u})):= \mathrm {C}\varepsilon (\mathbf {u})\cdot \varepsilon (\mathbf {u})$ being the energy storage function with the stiffness tensor $\mathrm {C}\in \mathbb {R}^{n\times n\times n\times n}$, and the linearized strain tensor $\varepsilon (\mathbf {u}) = \frac{1}{2}(\nabla \mathbf {u} + \nabla \mathbf {u}^T)$. The external potential of volume and surface forces is given by

$$\begin{aligned} F(\mathbf {u}) = \int \limits _\varOmega \mathbf {b}^* \mathbf {u} dV + \int \limits _{\partial \varOmega _t} \mathbf {t}^* \mathbf {u} dA, \end{aligned}$$

(11)

where $\mathbf {b}^*$ is the distributed body force and $\mathbf {t}^*$ are traction forces. The crack surface energy is given by

$$\begin{aligned} \psi _c(\varGamma ) = \int \limits _{\varGamma } G_c\, dA, \end{aligned}$$

(12)

where $G_c>0$ is the critical energy release rate.

Fig. 6

The solid phase-field domain $\varOmega$ with a a sharp crack interface $\varGamma$ and b the approximated crack using the phase-field crack function $\varphi$ resulting in a regularized crack representation $\varOmega _c$

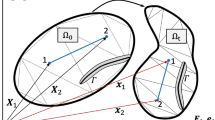
A corresponding configuration is sketched in Fig. 6a. Therein, the domain $\varOmega$ of the solid with a (sharp) crack set $\varGamma$ is considered. For the boundary $\partial \varOmega$ of the domain $\varOmega$ two kinds of boundary conditions along the normal vector $\mathbf {n}$ are considered such that $\partial \varOmega _u \cap \partial \varOmega _t = \emptyset$. On the boundary $\partial \varOmega _u$ Dirichlet displacement conditions are applied, which are built, as usually done, into the governing function spaces. Tractions $\mathbf {t}^*$ are applied to the $\partial \varOmega _t$ boundary. Discussions on boundary conditions can be found for instance in the early work [144, 147, 148].

From mathematical and numerical viewpoints, the sharp fracture representation (12) is challenging because the crack ‘lives’ on a lower-dimensional manifold $\varGamma$. On the one hand, this requires special function spaces (see e.g., [147, 148]), and on the other hand, numerical approximations require specialized discretizations (for instance generalized/extended finite elements [22,23,24] among various other possible techniques).

To handle this challenge one can borrow techniques from image processing. The single-well Modica-Mortola functional is introduced by Ambrosio and Tortorelli [149, 150] in image processing to approximate the the surface area term in the Mumford-Shah functional [48] and is given by

$$\begin{aligned} \int \limits _\varGamma dA \approx \int \limits _{\varOmega _c} \gamma (\varphi ,\nabla \varphi ) dV, \end{aligned}$$

(13)

with

$$\begin{aligned} \gamma (\varphi ,\nabla \varphi )&= \frac{1}{2}\left[ \frac{1}{l_0} (1 - \varphi )^2 + l_0 |\nabla \varphi |^2 \right] . \end{aligned}$$

(14)

Bourdin et al. [146] proposed to use this energy in an appealing approach to regularize the sharp crack defined on $\varGamma$ by a domain integral defined on $\varOmega _c$. In this context it is given by

$$\begin{aligned} \int \limits _\varGamma G_c dA \approx \int \limits _{\varOmega _c} G_c \gamma (\varphi ,\nabla \varphi ) dV, \end{aligned}$$

(15)

with $\gamma (\varphi ,\nabla \varphi )$ is now viewed physically as the crack surface density function as in [151]. Here $l_0>0$ is the so-called length scale (i.e., regularization) parameter and $l_0$ characterizes the width of the regularized domain $\varOmega _c$. Note that there are other formulations for the crack surface density function available [152, 153].

The name ‘phase-field’ was first coined in the year 2008 in the PAMM⁸ proceedings from Kuhn and Müller [154] and in their 2010 follow-up journal paper [155]. In the same year, Miehe et al. [151] used this terminology, which includes the above regularization, but additionally, they justified from a mechanical perspective a thermodynamically consistent framework for the potential and fracture energies. We notice that simultaneous pioneering work in variational gradient damage evolutions was performed by Pham and Marigo [156, 157] for which we also refer the reader to Section 2.2.3.

In other words, within phase-field models the crack is regularized by $\varOmega _c$ around the sharp crack $\varGamma$ using the so-called phase-field crack function $\varphi :\varOmega _c\cup \varOmega \rightarrow [0,1]$, see Fig. 6b. The notation is that $\varphi =0$ indicates damage and $\varphi =1$ means intact material (some authors define it the other way around). Between $\varphi = 0$ and $\varphi = 1$, the function varies smoothly with values $0<\varphi <1$, which is the so-called transition zone.

Figure 6b sketches the situation in which the smoothed region $\varOmega _c$ is shown.

By using the phase-field variable, the bulk strain energy is extended to the entire domain (intact domain plus fractured domain) and we obtain

$$\begin{aligned} \psi _s(\mathbf {u},\varphi ) = \int \limits _{\varOmega \cup \varOmega _c} g(\varphi ) \psi _0(\varepsilon (\mathbf {u})) dV, \end{aligned}$$

(16)

where $\psi _0$ is the so-called non-degraded bulk strain energy and $g(\varphi )$ the so-called degradation function. Usually, $g(\varphi ) = \varphi ^2 + \kappa$ or $g(\varphi ) = (1 - \kappa )\varphi ^2 + \kappa$ with a small $\kappa >0$, which is necessary to ensure regular system matrices within the discretization for quasi-static fracture. Clearly, for $\varphi =0$ (fracture), we have $g(\varphi )=\kappa$. In the non-fractured region, we have $\varphi =1$ and $g(\varphi )=1$. For dynamic fracture (see a discussion in [158]) $\kappa = 0$ is possible, which is obvious because the mass matrix term arising from the discretization of the acceleration term ensures well-posedness of the discrete system. A family of degradation functions and their numerical justification was investigated in [159] and a multidimensional stability analysis with a general degradation function was considered in [160]. The mathematical relation between $l_0$ and $\kappa$ is linked to $\varGamma$ convergence in which $l_0\rightarrow 0$ and $\kappa \rightarrow 0$ with the asymptotic behavior $\kappa = o(l_0)$; see e.g., [161] and again the approximation results in [149, 150].

Summarizing the previous ingredients, the total energy using the regularized crack representation in the entire domain $\varOmega \cup \varOmega _c$ is given by

$$\begin{aligned} E(\mathbf {u},\varphi )&= \int \limits _{\varOmega \cup \varOmega _c} g(\varphi ) \psi _0(\varepsilon (\mathbf {u})) dV - F(\mathbf {u})\nonumber \\&\quad + \int \limits _{\varOmega \cup \varOmega _c} G_c \frac{1}{2}\left[ \frac{1}{l_0} (1 - \varphi )^2 + l_0 |\nabla \varphi |^2 \right] dV \text {.} \end{aligned}$$

(17)

Several general types of $\psi _0$ functions have been proposed, and it was shown that a suitable choice could avoid nonphysical growth of cracks under compressive loading [162]. For more details, we refer to [16, 163].

Moreover, in most studies, as model assumption from a physics perspective, the crack cannot heal, and therefore the above energy functional is subject to a crack irreversibility (an entropy condition), which is mathematically expressed as an inequality constraint in time or quasi-static loading:

$$\begin{aligned} \partial _t \varphi \le 0. \end{aligned}$$

Due to this constraint, we deal with a quasi-static incremental (or time-dependent) nonlinear, coupled variational inequality system. The solution is obtained by minimizing $E(\mathbf {u},\varphi )$ with respect to $\mathbf {u}$ and $\varphi$ by considering $\partial _t \varphi \le 0$. Therein, the bulk and crack energies interact according to the laws outlined in [144] and [151].

2.2.1 Properties of $\varphi$ and crack interface reconstruction

It can be rigorously proven with cut-off arguments that $\varphi \in [0,1]$; see for instance [164], which follows from the definition of the Ambrosio-Tortorelli functional and the regularization of the total energy. When further terms (physics) are added, the property $\varphi \in [0,1]$ may get lost, and one must argue carefully. For instance, in pressurized fractures, the pressure can have positive and negative values and, therefore, further cut-off arguments are necessary in order to establish the bounds for $\varphi$ [165]. As the second topic in this short paragraph, we want to mention the principal idea when the crack interface must be known explicitly. Due to the regularization using $\varphi$, there is some liberty as to when the exact crack interface must be known. In these cases, the phase-field function is interpreted as a level-set function ([166]) and the crack interface is, for instance, chosen as $\varphi _c := \varphi = c_I$ with for example $c_I = 0.2$ [17, 167, 168].

2.2.2 Brief review of some theoretical findings

We briefly list some important well-posedness results. In [169] first existence results for quasi-brittle fracture of the original model by Francfort & Marigo [144] were shown for the antiplane setting for scalar-valued displacements. In [147] the existence and convergence of quasi-static evolutions for the vector-valued case were established. Shortly after, the existence of quasistatic crack growth in nonlinear elasticity was proven [148]. For these settings, in general, uniqueness cannot be established; see also below in Sect. 2.2.3 for discussions and references in the related gradient damage theory. In fact, it is well-known that uniqueness is a general issue in solid mechanics; see e.g. [170].

Regarding uniqueness in phase-field fracture, we deal with two variables, namely $\varphi$ and $\mathbf {u}$, obtained from solving a nonlinear coupled system, and the governing functional to be minimized is not convex, yielding several local minima. Only recently in [171], the issue of non-uniqueness was investigated in detail by using a stochastic approach by computing all solutions with their respective probability in which they may occur.

The existence of solutions for dynamic fracture using Ambrosio-Tortorelli [149, 150] approximations was established in [172]. Since crack initiation is an important topic within phase-field based crack models, we mention theoretical work by Chambolle et al. [173], Goethem/Novotny [174], and recently Kumar et al. [175] and de Lorenzis/Maurini [176]. Some theoretical findings on the crack path were provided in [177]. For mode III dynamic fracture modeled using [172], one can follow a sequence of solutions as $l_0\rightarrow 0$, to obtain existence of a limiting displacement with bounded Linear Elastic Fracture Mechanics energy [47]. The latest review of the original model, in terms of the sharp crack approximation (without phase-field, but nonetheless the ground basis of regularized models such as phase-field) can be founded in recently published article by Francfort [18]. Furthermore, we refer to the SIAM News article [15].

Table 2 Overview of various fracture and damage models available for phase-field modeling. Adapted and extended from [16]

2.2.3 Fracture/damage models for PF

In this section, we first note that phase-field fracture models have a close relationship to damage models. Indeed, due to the regularization in phase-field models yielding a transition zone, and damage mechanics with gradients, similar approaches are obtained. For seminal work in the year 2010, we refer to Pham and Marigo [156, 157] (based on earlier work of Mielke [178]). Therein, the authors propose and investigate local [156] and nonlocal [157] brittle damage laws from a mechanical viewpoint. The evolution is based on three fundamental physical principles: irreversibility of the damage (i.e., fracture) parameter, stability, and an energy balance. The actual relation of gradient damage models with brittle fracture is described in [179]. Further properties of such damage models (and consequently phase-field approaches) are investigated in [180]. Specifically, the stability and uniqueness (in terms of bifurcation) of the evolution of the gradient damage variational formulation is investigated for uniaxial tests, namely the homogeneous response of a bar under an increasing traction loading. The construction of bifurcations for a large class of gradient damage models (i.e., elastic-softening materials) was continued in [181]. Earlier work on stability and bifurcations using energetic variational principles is from Nguyen [182, 183]. Solely bifurcations for a one-dimensional gradient damage model applied to a bar were considered in [184]. Here, the mathematical ill-posedness (aspects of uniqueness and dependencies on the data) is discussed and possible consequences of numerical approximations (in particular mesh sensitivity) is drawn (here, we also point to [171] for uniqueness studies for phase-field fracture). Another, more recent discussion about similarities and differences can be found in [185]. In what follows, we therefore have both fracture and damage models in mind. Table 2 lists the available phase-field fracture and damage models. The following models have been developed within the phase-field framework: brittle fracture [12, 146, 151, 155, 186,187,188], fatigue [189,190,191,192,193,194,195,196], multi-field fracture [152, 197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212], frictional contact [213], plate/shell fracture [214,215,216,217,218,219,220] (where [220] solves some issues with the energy decomposition which were leading in [214, 216] to unphysical results), three-dimensional fracture [151, 202, 221,222,223,224,225,226,227,228], finite deformation/hyperelastic fracture [217, 227, 229,230,231,232,233,234], dynamic fracture [172, 221, 222, 235,236,237,238,239,240,241], cohesive fracture [12, 242,243,244,245,246,247], ductile fracture [199, 225, 248,249,250,251,252,253,254,255,256,257,258], anisotropic surface energy [259,260,261,262,263,264], layered material fracture [215, 244, 265,266,267,268,269,270,271], and polymer composites fracture [272].

Furthermore, we summarize various models for splitting the energy (i.e., strain / stress) into different parts for accounting the fracture growth behavior under tension and compression. To the best of our knowledge, we are aware of Amor et al. [273], Miehe et al. [151], Zhang et al. [274], Strobl/Seelig [275], Steinke/Kaliske [276], Bryant/Sun [277], Freddi/Royer-Carfagni [278], Bilgen/Homberger/Weinberg [279], and Fan et al. [280].

2.2.4 Treating the crack irreversibility constraint

For treating the irreversibility constraint $\partial _t \varphi \le 0$, six fundamental procedures have been proposed:

• 1. Fixing crack nodes by Dirichlet values [146, 155];

• 2. Strain history function [186];

• 3. Penalization: simple and augmented Lagrangian [165, 287,288,289];

• 4. Primal-dual active set methods [290];

• 5. Complementarity system with Lagrange multipliers as unknowns [283];

• 6. Interior-point methods [291].

Comparisons of some of these approaches were performed in [288] and [17].

2.2.5 Discretization, solvers, and software for PF

Classical Lagrange Galerkin finite elements [146], exponential shape functions [292], isogeometric elements [222], discontinuous finite elements [293], or mixed formulations [283] were mostly utilized for the spatial discretization of the fracture/damage models as described in the previous section. Meshless methods for general phase-field were first introduced in [294] and for meshless phase-field fracture, see e.g., [216, 295]. For discretized nonlinear systems, the following solvers are available: alternating minimisation algorithms [146, 153, 187, 237, 273, 296,297,298], alternating minimisation algorithm with path-following strategies [299], staggered scheme [186], stabilized staggered schemes [300,301,302,303], monolithic solvers [17, 151, 290, 304,305,306,307,308], and monolithic solvers with path-following strategies [309, 310].

For solving linear equation systems, most often black-box (direct) solvers have been adopted. Only recently [297] proposed conjugate gradient (CG) solutions with multigrid preconditioning for the decoupled phase-field displacement system. For monolithic solvers, a generalized minimal residual (GMRES) method with parallel algebraic multigrid preconditioning was proposed in [311]. A matrix-free geometric multigrid preconditioner was developed in [307], and its parallelized variant in [312]. Furthermore, we mention the development of a FFT (fast Fourier transform) solver for higher-order phase-field fracture problems [313].

The following proprietary implementations using Matlab [314, 315], COMSOL [316,317,318] using FEAP⁹, and Abaqus [226, 319,320,321,322,323,324] are available. Open source implementations are: [310] using Nutils [243, 325] using JIVE¹⁰, [326] using MOOSE [327, 328] (pfm-cracks¹¹ and [329] using deal.II¹², and [237, 297] using FENICS [330] are available. In addition, a GPU-based implementation [331] and the MEF 90 Fortran implementation [12, 144, 296, 332] are available.

2.2.6 Numerical analysis for PF

A posteriori error estimation For numerical analysis with respect to a posteriori error estimation, a short summary is presented here. First, work on residual-based error estimators goes back to [187, 333]. Extracting error indicators for local mesh refinement based on an a posteriori error estimator for the phase-field variational inequality are presented in [334, 335] The development of goal-oriented mesh adaptivity was undertaken in [17, 336]. The Ambrosio–Tortorelli functional is used to $\varGamma$ approximate each time evolution step in [337]. An additional penalty constraint is enforced for the irreversibility of the fracture as well as the applied displacement field. An a posteriori error estimator driving the anisotropic adaptive procedure is utilized for mesh adaptivity. According to the authors, the main properties of automatically generated meshes are to be very fine and strongly anisotropic in a small neighborhood region of the crack, but only far away from the crack tip, while they show a highly isotropic behavior in a neighborhood of the crack tip instead. The Ambrosio-Tortorelli functional is applied in [187] to two adaptive finite element algorithms for the computation of its (local) minimizers. Two theoretical results demonstrate convergence of the developed algorithms to the local minimizers of the Ambrosio-Tortorelli functional. However, the Ambrosio-Tortorelli functional is for quasi-static simulations and might not apply to dynamic fracture situations. The phase-field parameter itself is used in [158] to refine the mesh. The gradients of the phase-field are high in the near crack region and close to one away from the crack. A threshold is introduced to run the dynamic phase-field simulation for a few time steps, then all elements are refined above the introduced threshold, and the simulation is resumed with the newly refined mesh. This procedure is repeated until the convergence criterion is met.

It is expected that improved error estimates can further advance both PD and PF modeling approaches to pave the path for routine use as predictive simulations for a certain class of fracture problems.

Goal functional evaluations and computational analysis for $l_0 - h$ relationship In [17, 336, 338] a slit domain (a square plate with an initial crack) with displacement discontinuity at the crack and the manufactured displacement field [339, 340] are utilized to study the $l_0 - h$ relationship. Note that the crack in this study is represented by the phase-field damage function $\varphi$. Motivated by [161, 341], various simulations for $l_0=ch^l$ with $l \in (0,1]$ and h as the mesh size are conducted. Three cases of mesh refinement are studied: 1) $c=2.0$ and $l=1.0$, 2) $c=0.5$ and $l=0.5$, and 3) $c=0.5$ and $l=0.25$. First, the influence of $l_0$ on the goal function evaluation is considered. Therefore, the goal function $J(u_\text {FM}):= u_\text {FM}(0.75,-0.75)$ for a displacement point value is utilized, which results in the total error $J(u_\text {FM})-J(u_h)$. The maximal convergence order of $r=\mathcal {O}(l_0)$ was obtained in case 2) where $r=l_0=0.5$. The observed order is $r=l_0=0.25$ for case 3) and $r\approx 0.9 < l_0$ for case 1). These results lead to the assumption that $\vert J(u_\text {FM})-J(u_h) \vert = \mathcal {O}(l_0)$ as presented in [202, 290, 300, 311]. In addition, two phase-field fracture configurations were proposed as prototype models for comparison in the recent benchmark collection [342].

Adaptivity Regarding adaptivity, we distinguish between spatial and temporal mesh refinement and adaptive solution schemes. Spatial mesh refinement goes back to anisotropies introduced by the mesh [343], residual-based adaptive finite elements [187, 333], anisotropic adaptive mesh refinement [337], and pre-refined meshes where the crack path is known a priori [222]. Other computational convergence analyses were undertaken in [344]. For unknown crack paths, a predictor-corrector approach was developed and applied in [202, 290, 345], goal-oriented error-control [336, 338], and mesh refinement in multiscale phase-field methods [346]. A few rigorous studies on temporal error control exist [331, 347]. Apart from classical mesh refinement, an adaptive predictor-corrector non-intrusive global-local (multiscale) approach [315] (see also [348]) was developed based on the approach presented in [349], and was to porous media [350], and extended to multilevel concepts [351].

Solver analyses Using alternating minimization for solving the coupled displacement-phase-field problem, the convergence of the scheme was established in [296] and [187]. A convergence proof for a truncated nonsmooth Newton multigrid method was very recently undertaken in [352]. For further fully-coupled (i.e., monolithic) techniques, no rigorous convergence are available, but significant numerical evidence of the performance of nonlinear solvers [17, 151, 290, 291, 304,305,306,307,308,309,310, 353].

In the following, we discuss some papers in more detail. Zhang et al. [354] used a length scale material parameter to evaluate the accuracy of phase-field modeling of brittle fractures with available experimental data. They observed significant discrepancies between numerical predictions and the experimentally observed load-displacement curves after the critical force, despite a reasonably accurate prediction of crack paths. Zhuang et al. [355] implemented the phase-field method in a staggered scheme to sequentially solve for the displacement, phase-field, and fluid pressure. Asymmetric deflection along material interfaces and penetration of hydraulic fractures in naturally-layered porous media were reported for different layer arrangements based upon their respective stiffness as measured by E and $G_c$. Farrell and Maurini [297] reformulated the alternate minimization algorithm for the variational fracture approach to simulate nucleation and propagation of complex fracture patterns as a nonlinear Gauss-Seidel iteration along with over-relaxation to accelerate its convergence. They showed further reduction in solution time by utilizing the accelerated alternate minimization with Newton’s method. Brun et al. [300] showed an iterative staggered scheme, a two-field variational inequality system with independent phase-field variable and displacement variables. For the convergence using a fix-point argument and a natural condition, the elastic mechanical energy remains bounded and with a sufficiently thick diffusive zone around the crack surface, monotonic convergence is achieved. Noll et al. [356] presented results for ductile fracture with linear isotropic hardening and discussed the computational costs for 3D simulations while analyzing added computations due to mesh refinement. Chukwudozie et al. [357] presented a unified fracture-porous medium hydraulic fracturing model that handled interactions among multiple cracks, as well as the evolution of complex crack paths in 3D simulations using energy minimization without any additional branching criterion, but the location of crack tip and its velocity remains a challenge in complex configurations. Further, detailed linear solver analyses for quasi-monolithic phase-field fracture using a GMRES solver with matrix-free geometric multigrid preconditioning were conducted in [307]. Scalability tests of parallel performance were performed in [311] and [312].

It is evident that further improvements in robust solvers will be the key for both PD and PF approaches to be adopted as the engineering tools of choice to predict fracture phenomena.

3 Macroscale view of crack propagation physics using thermodynamics constraints and constitutive relationships

According to Haslach [358], a maximum dissipation non-equilibrium evolution model can describe the unsteady crack propagation rate for both brittle fracture and for viscoplastic behavior at the crack tip. Ulmer et al. [359] presented a thermodynamically consistent framework for phase-field models of crack propagation in ductile elastic-plastic solids under dynamic loading with an incremental variational principle and validated it against the classical Kalthoff-Winkler experimental results. Mauthe and Miehe [360] used two constitutive functions - free energy and dissipation potential to incorporate fluid flow in cracks during hydraulic fracturing and coupled it to a phase-field approach to fracture within a variational framework. Miehe et al. [361] proposed a gradient damage formulation with two independent length scales to regularize the plastic response and crack discontinuities to ensure that the damage zones of ductile fractures remain inside plastic zones. Roy et al. [362] presented a rephrased phase-field theory of continuum damage in a peridynamics setup and showed promising results of mode II delamination. Farrahi et al. [363] demonstrated that under mode I crack growth and proper calibration of parameters, PFM always agreed with Griffith’s theory. Alessi et al. [364] demonstrated that macroscopic responses assimilable to brittle fractures, cohesive fractures, and a sort of cohesive fracture, including depinning energy contributions by tuning a few key constitutive parameters such as relative yield stresses and softening behaviors of the plasticity and damage criteria. It is duly noted that both PD and PF show promise to visualize and predict complex fracture phenomena without resorting to ad-hoc modeling assumptions.

4 Validation against experimental data

The validation against experimental data is a cornerstone to access the predictive accuracy of any engineering fracture mechanics model. In this section, the experiments used as benchmarks for peridynamic models are compared against the ones used as benchmarks for phase-field models. We limited the focus to the Sandia Fracture Challenge and publications where both models were compared to the same experimental data. For a detailed review about the comparison with experimental data, we refer to [4] for peridynamic models and for phase-field models to [16, Section 2.12]. It is remarked that the experimental data from Jeffery and Bunger [365] may be used in the validation of different numerical simulators for hydraulic fracture propagation.

4.1 Reasons for Sandia Fracture Challenge and outline

Two reasons make the Sandia Fracture Challenge (SFC) an excellent example:

• 1. experimental data is usually not disclosed in the literature [366] whereas all data and experimental designs are made available in the Sandia challenge;

• 2. the Sandia Fracture Challenge has two unique features that together establish the validity of a free fracture model. First, the calibration step requires the free fracture model to be calibrated through a simple prototypical problem, e.g. a tensile test. The subsequent validation step requires the calibrated model to simulate a distinct and more complicated fracture problem. It is the model’s ability to match experimental results for the complex problem that establishes its validity. This prohibits parameter fitting to match a particular experiment.

The outline for the following subsections is as follows: we first provide the methodology for error measurements used to compare the different models. Afterward, the Sandia Fracture Challenge is described in detail, with a focus on the first and third test sets. These descriptions are followed by comparisons of both models, including details on the respective discretizations, numerical cost, and error measurements.

4.2 Error measurements for comparisons

For all compared values, the following error measurements were calculated: For scalar values, the relative error and for a time series the coefficient of determination $R^2$ [367] is computed, when applicable. The coefficient of determination $R^2$ is defined as

$$\begin{aligned} R^2 = 1 - \frac{SSE}{SST} \end{aligned}$$

(18)

for two series of n values $y_1,\ldots ,y_n$, the so-called series of observables and $\hat{y}_1,\ldots ,\hat{y}_n$, the so-called series of predictions. Where the total sum of squares SST reads as

$$\begin{aligned} SST = \sum \limits _1^n (y_i - \overline{y})^2 \quad \text { with } \quad \overline{y} = \frac{1}{n} \sum \limits _1^n y_i \end{aligned}$$

(19)

and the sum of square residuals (or errors) reads as

$$\begin{aligned} SSE = \sum \limits _1^n(y_i - \hat{y}_i)^2\text {.} \end{aligned}$$

(20)

Thus, $R^2$ is a statistical measure in the range of zero to one to indicate how good the series of predictions $\hat{y}_i$ approximates the series of observables $y_i$. Specifically, $R^2=1$ implies that $SSE=0$ and therefore, the series of observables fits the series of predictions perfectly. If $R^2=0$ and therefore $SSE=SST$ then the mean of observables series is as good as any predicted series. For the time series, the WebPlotDigitizer¹³ was used to extract the x and y coordinates of the respective plot from the Sandia report. The scipy.stats.linregress¹⁴ functionality of the python SciPy package [368] was utilized to compute the $R^2$ correlation.

4.3 Sandia Fracture Challenge

The Sandia Fracture Challenge is considered as one of the potential set of benchmarks to showcase the predictive accuracy of the two models for various complex experimental data. There are many other experimental data sets available which could serve as experimental benchmarks as well. However, the SFC addresses some important aspects of calibration vs. validation against experimental results. One essential part of this challenge is to calibrate the free fracture model on simple prototypical problems such as a tensile test, and use this calibration to simulate the crack and fracture phenomena. With this additional step, the model parameters can not be calibrated or fitted to the complex scenario but instead have been calibrated using the simple scenario. This additional step of calibration makes the SFC an excellent problem to benchmark phase-field models and peridynamic models to assess their performance on different kinds of crack and fracture phenomena. For the first and third fracture challenge, we could find the contributions of peridynamic models, see Sect. 4.3.1 and Sect. 4.3.2, respectively. No studies using phase-field models were found for all three fracture challenges. The summary of model accuracy is shown in Table 5.

Fig. 7

First Sandia Fracture Challenge: Simplified geometry of the CT specimen to sketch the experimental quantity of interests which the peridynamic simulation was compared against. Adapted from [369]

4.3.1 First Sandia Fracture Challenge

In the first Sandia Fracture Challenge [369] blind round robin predictions of ductile tearing for an alloy (15-5PH) were studied. The stress-strain curve of a tensile bar was provided to calibrate the model. Experiments on CT specimens were conducted and the extracted quantities of interest are shown in Fig. 7. The geometry has a blunt notch A and three holes B, C, and D, respectively. The two unlabeled holes were used for the load pins to apply the load in force $\pm F$. The following three challenge questions were used for predictive simulations:

• 1. What is the load force and the COD displacement at the time of the crack initiation?

• 2. What is the path of crack propagation?

• 3. At what force and COD displacement does the crack re-initiate out of the first hole, if the crack does propagate to either holes B, C, or D?

The teams had to answers these questions with their respective models. Team 9 from the University of Arizona used a bond-based peridynamic model [37, 38] to answer these questions. The geometry was discretized using hexahedron regions with edge length of $~{0.63}\,\hbox {mm}$ and the horizon was $\delta ={1,5621}\hbox {mm}$. For more details about the simulations, we refer to [369, Section 8.9].

During the ten experiments, the crack path $A-D-C-E$ occurred nine times and the crack path $A-C-E$ occurred one time. Team 9 predicted the second path in their simulations as the answer to the second question. Table 3 shows the answers to the remaining questions. The first row shows the average value for the force (N) and the crack open displacement (COD) ((mm)) for the first crack event and the second crack event. The first value in every column is the value obtained by the load drop, and the second one the visual obtained value. The second row contains the average value obtained by the simulations of team 9. The relative error $\epsilon _{\text {rel}}$ for the 1st crack events are for the force -0.4/-0.28 and for the COD -0.7/-0.7 respectively. The relative error for the 2nd crack events are for the force -0.31/-0.2 and for the COD -0.7/-0.7 respectively.

Using phase-field modeling, recent results were reported in [370]. The discretization is based on tetrahedral elements with locally pre-refined meshes. The authors report force-displacements curves for different numerical models and show contour plots for three different loadings of the crack path, elastic energy, plastic energy, and the coalescence degradation function.

Table 3 The average values of the force (N) and the crack opening displacement (COD) (mm) for the crack path $A-C-E$, see Fig. 7

Fig. 8

Third Sandia Fracture Challenge: Simplified sketch of the geometry to showcase the quantity of interests in the fracture challenge. Adapted from [372]

4.3.2 Third Sandia Fracture Challenge

In the third Sandia Fracture Challenge, the predictions of ductile fracture in additively manufactured metals were studied. The data of tensile tests was provided to calibrate the simulation models. Figure 8 shows a simplified sketch of the geometry to showcase the following challenge questions for predictive simulations:

• 1. What is the force at the displacements 0.25, 0.5, 0.75, and 1.0 mm?

• 2. What is the force and Hencky (logarithmic) strain in the vertical direction of the points P1–P4 on the surface at the following forces: ${75}\%$ and ${90}\%$ of peak load (before peak), at peak load, and ${90}\%$ after the peak load?

• 3. What is the force versus the gauge displacement for the test?

• 4. What is the force and Hencky (logarithmic) strain in the vertical direction of the points P1–P4 on the surface over time?

• 5. What is the force and Hencky (logarithmic) strain in the vertical direction of the lines H1–H4 on the surface at the same forces as in questions 2?

Table 4 Comparison of the measurements and the obtained loads in the simulations for four different displacements

Table 5 Overview of the Sandia Fracture Challenge with contributions of peridynamic models. Two different research groups contributed to the first and second Sandia Fracture Challenge using a peridynamic model. To the best knowledge of the authors, no phase-field model contributed to the Sandia Fracture Challenge. However, phase-field simulations were done using the geometry of the third Sandia Fracture Challenge [374]. To compare with the experimental measurement, the relative error is provided for scalar values, and the $R^2$ correlation for a series of values. For the first Sandia Fracture Challenge, the following quantities were studied: (a) Force (N) 1st crack event, (b) Crack Opening Displacement (COD) (mm) 1st crack event, (c) Force (N) 2nd crack event, and (d) COD (mm) 2nd crack event. For the third Sandia Fracture Challenge, the following quantities were studied: (a–d) Force (kN) at 0.25, 0.5, 0.75, and 1mm displacement; (e) Force vs displacement (time series); (f) Force (kN) at Peak load; and (g) Hencky strain (%) on line H3 at peak load

Team C from the University of Texas Austin used an explicit peridynamic model with bond damage [371]. For the damage evolution, the Johnson-Cook model was used. The geometry was discretized with a nodal spacing of $h={0.14}\hbox {mm}$ resulting in a total of 460.000 nodes. Information of the used horizon were not reported in [372, Table 9]. The answers to question 1 are shown in Table 4. The relative errors are: $-$0.05, $-$0.15, $-$0.47, $-$0.66, respectively. The $R^2$ correlation for question 3, load (kN) vs displacement (mm) is 0.7. For the relative errors with respect to question 2, one can only look at the trend at the peak load, since all other loads were defined relatively to it. For the peak load, a relative error of $-$0.08 was reported. The relative errors for the vertical logarithmic strain (%) for point P2 are 7, 4.8, $-$0.8, and $-$0.8, respectively. The $R^2$ correlation at the peak load for the Hencky strain on lines H3 for question 4 is 0.44. Unfortunately, we had issues extracting the $R^2$ correlations for line H4 with our tools. Note that this was a blind verification, and the same team performed a revisited simulation with more details, receiving better results [373]. However, phase-field simulations were done only qualitatively using the geometry of the third Sandia Fracture Challenge [374].

4.4 Comparison of both models with the same experimental data

First, finite elastic deformation and rupture in rubber-like materials [375] was studied for phase-field models in [376] and for peridynamic models in [377]. In these publications, a rubber sheet with double edge notches was studied on the geometry shown in Fig. 9 (80mm $\times$ 200mm) and a thickness of 3mm. For the experimental setup, the length of the notches a varied from, 12mm, 16mm, 20mm, and 24mm. For the PD simulations, the horizon $\delta =3.015h$ was used. In total, 16000 discrete PD nodes with a surrounding volume of V=1$\hbox {mm}^{2}$ and a nodal spacing of $h=1$mm. For the PF simulations, a quad mesh with a resolution of $h=6.66$mm was used. The applied displacement (mm) vs the reaction force (N) was compared against the experimental observations and the corresponding simulation results. The $R^2$ correlation for PD are: 0.83, 0.99, 0.98, 0.98, 0.98, and 0.78 respectively. The $R^2$ correlation for PF are: 0.78, 0.84, 1, 0.64, and 0.65 respectively.

Second, dynamic brittle fracture in glassy materials was studied in [378, 379]. In this study, a phase-field model [186], a discontinuous-Galerkin implementation of PD [380], and a meshfree discretization of PD [38] are used in the geometry shown in Fig. 10. For the PD simulation, a nodal spacing $h=$0.1mm and a horizon $\delta =$0.5mm were used. For the discontinuous-Galerkin implementation of PD a non-uniform mesh with average element size h of 0.1mm and a horizon $\delta$ of 0.5mm was used. For the phase-field model, the nodal spacing was $h=$0.3mm and the length scale parameter $l_0$ was 0.6mm. Note that the authors did some $\delta$-convergence study in [379], however, we only report the finest resolution here. Fore more details, we refer to [379, Section 5.2]. For all three implementations, the crack angle after branching, the time of crack branching, and position of the crack branching were compared with the experimental results. In this study various discretization parameters were studied, however, we report the discretization parameters corresponding to the best agreement with the experimental data. First, the value for the meshfree discretization is presented, followed by the value for the discontinuous-Galerkin discretization, and the value for the phase-field model last. The relative errors for the crack angle are: -0.21, -0.35, and -0.51, respectively. The relative errors -0.06 for the event of crack branching in time are the same for all simulations. The relative errors for the crack branching position are: 0, -0.12, and 0, respectively.

5 Comparison between peridynamics and phase-field fracture models

In this section, the two approaches PD and PF are compared with respect to their computational aspects, advantages in simulating complex fracture phenomena, and the challenges faced by these numerical methods. For peridynamics, we assume that the presented aspects hold for all three models presented in Fig. 2. If one aspect holds only for specific models, we will mention that explicitly in the text below.

Fig. 9

Geometry of the rubber sheet (80mm $\times$ 200mm) and a thickness of 3mm. The length a of the notches varied from, 12mm, 16mm, 20mm, and 24mm. The radius of the notches is fixed at 1mm

Fig. 10

Sketch of the geometry (100mm $\times$ 150mm) with a thickness of mm. The angle of the cut-off is ${40}^{\circ }$ and the initial crack has a length of 8mm

5.1 Computational aspects

In this section, we focus on the computational aspects of both models from a bird’s eye view and compare the computations on a very high-level. To do so, we define the quantity of a field which can be a vector field $\mathbf {f}=\{f_1,\ldots , f_n \, \vert \, f_i \in \mathbb {R}^3\}$ or a scalar field $f=\{f_1,\ldots , f_n \, \vert \, f_i \in \mathbb {R}\}$. Peridynamics is a single-field model, here one just solves for the displacement field $\mathbf {u}$ and the peridynamic damage field $d(\mathbf {u})$ is obtained from the displacement field using the constitutive law. The displacement field is solved with explicit or implicit time integration [381,382,383,384,385]. The majority of PD simulations utilized bond-based models due to the increased computational costs for the state-based models. Similarly, the majority of simulations utilized explicit time integration due to their lower computational costs.

For phase-field, we have a two field model with the displacement field $\mathbf {u}$ and the damage field ${\varphi }$.

For staggered schemes and alternating minimization [186, 187, 222, 296, 300,301,302, 386] the global system is decoupled, first, one solves for the displacement field $\mathbf {u}$ and second, one solves for the phase-field damage field ${\varphi }$ independently. For the equation of motion, implicit or explicit time integration schemes can be utilized. For the monolithic scheme [151, 155, 236, 304, 306, 307, 319, 353, 387] the displacement field and the phase-field damage field are fully coupled and solved simultaneously. Pham et al. [162] suggested that a suitable choice of fracture process zone corresponding to the intrinsic length scale associated with the phase-field model could provide valid predictions of crack growth in quasi-static brittle fracture.

Classical elasticity parameters can be used to calibrate both models. Both models require a minimal set of parameters for calibration, i.e. Young’s modulus E, Poisson’s ratio $\nu$, and fracture energy $G_c$, which all can be experimentally determined. Thus, both models could use the same elasticity and fracture properties obtained by an experiment to calibrate and validate against the same quantity of interest. Both models depend on length scale parameters; $l_0$ for phase-field models and the horizon $\delta$ for peridynamic models needs to be calibrated. Techniques for calibration that include material strength and flaw size have been shown for PF [388] and PD [55, 115]. On the other hand, when sharp cracks approximations are needed, mathematically $l_0$ should tend to zero (see Sect. 2.2), as confirmed for PF with numerical simulations in [311] using an academic test case in which manufactured solutions for the crack opening displacement and total crack volume were constructed [389]. In the case of PD with bond softening, one sees that the damage is confined to a thin zone about the crack line of thickness controlled by the PD horizon $\delta$, [128]. Here, the thickness is $\delta +2h$ where the mesh diameter h is $h=o(\delta )$. Goswami et al. [390] developed an enhanced physics-informed neural network (PINN) based machine learning (ML) for the fracture growth and propagation problem using PF. Nguyen et al. [391] used ML to develop relationships between the displacements of a material point and the displacements of its neighbors and the applied forces within PD framework. Mandal [392] presented a comparison of PF and PD models and [393] for a tensile impulse traction on the pre-crack faces experiment. Good agreements were reported for crack tip velocities for no-branching case as well as branching for higher stress intensities cases despite the post-processing of PD and PF results using distinct algorithms.

We conclude that there are very few results available where both models are compared against the same experimental data. Confronted with this paucity of information it is difficult to get insights regarding better suitability of a method for specific crack phenomena. With this in mind, the Sandia Fracture Challenge is pointed out in this review for the two main reasons described in Sect. 4.1. This makes the Sandia Fracture Challenge an excellent problem to benchmark phase-field models and peridynamic models in order to assess their performances for different kinds of fracture phenomena. Further, it would be a good exercise for both communities to come together and define a common set of benchmark simulations for experimental validation and model performance assessment.

5.2 Advantages

Several advantages are highlighted for both PD and PF approaches to show why these two methods have been popular approaches to understand fracture phenomena.

• 1. Crack initiation: Growth at the tips of long preexisting cracks are handled by both phase field and peridynamics noting that brittle crack extension is energy based. For short interior cracks and notches quasi-static phase field models have introduced strength based driving forces for to account for crack nucleation Kumar et al. [175]. For peridynamics crack nucleation about defects are manifested as dynamic instabilities Silling et al. [394], for cohesive models see Lipton et al. [47, 124].

• 2. Notion of damage in the model representation: In most other models or computational techniques an additional criteria, e.g. as in Linear Elastic Fracture Mechanics, is needed to describe the growth of cracks. However, in peridynamic and phase-field models the criteria for the crack growth is determined as a part of the solution and no external criteria is needed. The PD correspondence models offer the opportunity to incorporate classic continuum damage models in state based peridynamics see Tupek et al. [395].

• 3. Increasing complexity in multi-field fracture: Both models were extended to multi-field fracture. For peridynamic models: thermal effects [396,397,398,399,400], diffusion [113, 397, 401,402,403], geomechanical fracture [1, 404,405,406,407,408,409,410,411,412,413,414], and corrosion [415,416,417]. For phase-field simulations: hydraulic fracture [168, 201,202,203, 293, 355, 357, 360, 418,419,420,421,422,423,424,425,426,427,428], diffusion [209], thermo-elastic-plastic [199], thermal effects [152, 197, 198, 286, 429], geologic/geo-materials [246, 258, 430], and fluid-structure interaction [17, 347, 431].

5.3 Challenges

The following important issues are identified as challenges in the context of both PD and PF modeling.

5.3.1 Common challenges to PD and PF

• 1. From dynamic to quasi-static evolution A long range goal for fracture modelling will be the ability to recover quasistatic fracture models directly from dynamic fracture models without ad-hoc assumptions. This aspect is largely absent in both PF and PD approaches. To the best of our knowledge such questions have been raised and partially answered only recently for a new local fracture model in the context of the dynamic peeling test in one dimension as described in Freund [432]. In this context the dynamic model is a local model for free de-cohesion developed in Dal Maso et al. [433] and the quasistatic limit is identified in Lazzarioni and Nardini [434]. It is recognized that this is a hard problem and presents a challenge for PD and PF.

• 2. Computational cost: Both PD and PF approaches are computationally expensive. For peridynamics it is the meshless discretization, which is computational intensive, similar to molecular dynamics (MD) and smoothed-particle hydrodynamics (SPH). To accelerate the computations implementations using the Message Passing Interface (MPI) [84, 86, 87], the C++ standard library for parallelism and concurrency (HPX) [88], and GPU accelerated [93,94,95] are available. To speed up the implicit time integration the following methods were proposed: Finite element approaches (FEM) [80, 82, 85], a Galerkin method that exploits the matrix structure [435], using sparse matrices instead of a dense tangent stiffness matrix [436], adaptive dynamic relaxation schemes (ADR) [437,438,439], the Fire algorithm [440, 441], an explicit tangent stiffness matrix [442] using bond softening [46], a convolution based approach [443, 444], and the GMRES algorithm [444, 445] in conjunction with the Arnoldi process [446, 447]. Here, bond-based material models are computationally cheaper than state-based models. Furthermore explicit time integration is computationally cheaper than implicit time integration.

  For phase-field models the length scale parameter $l_0$ tends to become small, thus, requiring small mesh sizes for finite element discretizations. Therefore, the method gets computationally expensive due to the large number of mesh elements. Phase-field models could be accelerated using a staggered schemes instead of a monolithic scheme [226], GPU acceleration [331], and the Message Passing Interface (MPI) based parallelization [237, 311], and matrix-free geometric multigrid methods [307, 312]. Other attempts to reduce the computational costs are model order reduction [448, 449], sympletic time integrators [450], adaptive schemes [187, 202, 290, 331, 333, 336, 337, 451], and global/local (multiscale) approaches [315, 349, 351, 452].

• 3. Lack of detailed three-dimensional simulations: Probably due to their computational expenses, only a few three-dimensional simulations using PF and PD are reviewed here. Following three-dimensional PD simulations are available: hydraulic fracture [410, 453], the Brokenshire torsion experiment [454], polymer chains [455], Kalthoff Winkler [143], pitting corrosion damage [456], 3-point bending [96], impact damage on the glass layered structure [96, 457, 458], penny-shaped crack in a cylindrical bar [459], double edge notch specimen [459], ductile material behavior in a rectangular bar [460], pressurized cylinder [222], and reinforced concrete lap splice [56].

  The following three-dimensional research studies using PF are available: formation and growth of echelon cracks [228], pressure vessel simulation [222], single-edge notched shear test [226], cube with rigid spherical inclusion under tension [221], a block-like geometry [342], Kalthoff Winkler experiment [221], bolted plate compared against experimental results [225], simple shear tests of thoracic aorta with anisotropic failure compared against experimental results [227], random nucleation sites [223], L-shaped specimen [224, 307], tension test of cube with spherical inclusion [151], bending of Hopkinson bar [461], and Sneddon/Lowengrub benchmark [202, 287, 311], and non-isothermal pressurized fractures [462].

  To list some representative three-dimensional simulations, Weinberg et al. [463] showed stress distributions for modes I, II, and III fractures using NURBS-based finite elements in three-dimensional simulations. Heider et al. (2018) compared the hydraulic fracturing simulation results using PF against the experimental data for granite samples from the “Hohenberg” quarry in Germany with good predictive accuracy (within experimental relative errors less than 15%) for the pressure needed to initiate the crack in both 2D and 3D geometries. Another plausible reason for the lack of detailed three-dimensional fracture simulations could also be the associated challenges to perform detailed three-dimensional experimental measurements and provide validation data sets.

• 4. Extraction of crack tip/surfaces: Since both models have a notion of damage, the so-called phase-field crack function $\varphi$ and the peridynamic damage parameter d, the position of the crack tip/surface is not encoded in the model and needs to be approximated. This phenomenon is not limited to phase-field [281] and peridynamic models, e.g. [464, 465], and relates to any other method which does not have explicit crack representation in the model. This could be a source of error for tracking the crack tip and comparing the crack tip velocity against experimental observations in dynamic fracture simulations. Ziaei-Rad et al. (2016) used the non-maximum suppression technique from an image processing field to detect the ridge of the phase-field profile and then applied cubic spline fit to determine the crack path representation with reasonable success to identify crack branching as well as crack tips within the mesh resolution limits. Agrawal and Dayal [466] partially explained the relationship between phase-field and crack opening displacement and irreversibility in the phase-field model. Yoshioka et al. [467] presented two approaches - a line integral and a level-set method, to compute the crack opening displacement that is required in hydraulic fracturing simulations and demonstrated that both approaches computed the crack opening temporal growth accurately. Despite these recent advances, there is still room for improvement to extract the complex multiple interacting crack surfaces from simulations.

• 5. Lack of validation studies against available experimental data: Validation against experimental data for peridynamics is summarized in [4] and for phase-field models in [16, Section 2.12]. However, for an accurate comparison of these two models, the same experiment or a set of experiments should be utilized to gain some insights of both methods on the same problem. Table 6 lists the phase-field and peridynamic models which were compared against the same experimental data. On the other hand, accessing raw experimental data is a different challenge [366], and one of the Sandia Fracture Challenges could be used to validate peridynamics and phase-field models against the same experimental data.

• 6. Unavailability in commercial codes: Most simulations of PF and PD models use their implementations in corresponding scientific code bases. At the time of writing of this review, not many commercial codes implemented either one of the models. LS-DYNA provides a bond-based peridynamics implementation discretized with the discontinuous Galerkin FEM [96].

• 7. Crack nucleation: Although crack propagation and path is autonomously handled by both models, a complete theoretical understanding of nucleation for dynamic and quasistatic fracture is incomplete.

  Recent developments include the introduction of a strength based crack driving force for quasistatic PD [175] based on a realistic phenomenology and comparison with experiments. [162, 468,469,470,471]. As expected it is a very active area of interest both for PF [175, 176, 388, 472] and PD [473,474,475].

• 8. Incompressible hyper elastic material behavior: At the time of completing this review, not many material models or simulations for incompressible hyper elastic material behavior, e.g. a Poisson ratio $\nu = 0.5$, were available for PF [283, 284] and the recent PhD thesis [476], and the application to carbon black filled ethylene propylene diene monomer rubber (EPDM) was done in [285]. For PD we have [140, 477, 478]. Note that modeling of hyper elastic material behavior is challenging for any numerical method since the constitutive material law must reflect material behaviors such as a neo-Hookean [479] or Mooney–Rivlin [480] solids and requires for the well-posedness the inf-sup condition for both the continuous problem formulation and the discretization.

• 9. Microscale view of crack propagation physics using molecular dynamics (MD) simulations:

  Seleson et al. [130] showed that peridynamics (PD) models can recover the same dynamics as the MD model through appropriate selection of the length scale for smooth deformations. Ahadi and Melin [481] investigated accuracy of PD in capturing features emerging from atomistic simulation [482] through calibration of interparticle bond strength and length scale parameters elastic plastic effects. In a similar attempt to connect the phase-field method to MD, Patil et al. [483] derived PFM parameters from the MD atomistic simulations and showed that the theoretical energy release rate G and internal length parameter are consistent with the MD simulation results. It is important to note that the microscale physics of crack nucleation and growth through MD atomistic simulation can provide the information for upscaling [484]. Given the current state of the art, the relation between first principles models and the macroscopic models of PD and PF with crack nucleation and propagation has not been firmly established in the literature.

Table 6 For the two experiments, phase-field and peridynamic models were used for comparison

5.3.2 Specific challenges for peridynamics fracture models

The following challenges are highlighted to show the difficulties in applying boundary conditions, specific material models, and controlling numerical errors in PD.

• 1. Application of boundary conditions: As mentioned in [4] a major challenge within PD is the treatment of boundary conditions in a non-local fashion [485,486,487,488,489,490]. This is seen in nonlocal traction conditions for state based linear peridynamic solids where surface effects appear. For this case techniques to handle nonlocal traction are recently developed [127]. More general non-ordinary state based and correspondence models have yet to be addressed. For local to nonlocal coupling one approach is to couple local and non-local models to enforce boundary conditions in the local region and have the non-local model in the region where cracks and fractures arise. For more details, we refer to the review on non-local coupling approaches [491].

• 2. Constitutive modeling Figure 2 illustrates the plethora of material models proposed for peridynamics. The question of choosing a nonlocal model that is an acceptable representative for a particular material system must be the focus of a coordinated theoretical and experimental effort. This applies to bond based and state based PD models as well as correspondence models Tupek et al. [395] that permit the usage of constitutive models from local theory within the peridynamic formulation. [41, 41, 63,64,65,66,67,68,69,70, 72,73,74,75,76,77,78, 492,493,494]. The possibility for zero energy modes in correspondence models has been acknowledged and methods for stabilization are being developed [492, 493, 495].

• 3. Choice of discretization parameters: As mentioned in [4] the choice of the nodal spacing and the horizon results in diverse convergence scenarios [111, 114]. One challenge is to find the proper ratio between the horizon and mesh size, since the simulations are sensitive [115, 116] with respect of these parameters. One adjustment is to select the ratio such that the PD simulation matches the dispersion curve obtained by the experiment [496]. Another adjustment is to determine the horizon by Griffith’s brittle failure criterion [55]. To determine the discretization parameters from experimental data, the peridynamic formulation of the virtual field method could be applied [497].

• 4. Surface effects and corrections: Most PD models are calibrated under the assumption that a discrete PD node has a full neighborhood. However, points close to the boundary do not have a full neighborhood and their material properties are slightly different from the ones with the full neighborhood. This is the so-called surface effect. Le and Bobaru studied some proposed methods/algorithms to address the surface effect [498]. The following methods/algorithms are available: volume method [9, Section 2], force density method [499], energy density method [10, 499, 500], force normalization method [82], a modified position-aware linear solid constitutive model [72], fictitious node method [397, 501], and correction of the transient heat conduction [502].

• 5. Development of adaptive PD models and methods: There is a lack of adaptive methods developed to handle peridynamic fracture problems for coupling interior dynamics to boundary effects and for coupling inelastic to elastic domains within a simulation. A variable horizon approach is proposed for adaptivity in [503] and [504]. It is well known that nonlocal models are far more expensive to simulate than local models. Additionally they can induce artificial dispersive artifacts in otherwise local elastic regions. These considerations provide motivation for adaptive local-nonlocal models for fracture evolution. Here the fracture set is evolved in terms of bond based PD while FEM methods can be used away from the fracture set [505]. More on this type of numerical modeling and implementation can be found in [491].

• 6. Asymptotically compatible quadrature methods: An additional way to control accuracy of peridynamic methods is through development of asymptotically compatible quadrature methods for state based fracture as in recent approach of [127]. Here, the numerical scheme is designed to recover linear elastic behavior away from the crack set asymptotically as the horizon tends to zero.

• 7. Ductile fracture: As of the time of writing this review, not many material models and simulation for ductile fracture were available [506,507,508,509]. Note that ductile tearing is challenging for any numerical method, due to the choice of an appropriate ductile failure model. This failure model needs to incorporate the failure of hydrostatic stress (or triaxiality of stress) to predict ductile failure. Here, state-based and correspondence models will be beneficial, as bond-based material models are limited to model two point interactions.

• 8. Opportunities for quasistatic PD models: The preponderance of peridynamic simulation has focused on dynamic problems and this provides an opportunity for quasistatic fracture modeling [382, 510,511,512] with suitable PD models. There are plenty of experimental benchmarks for the validation of peridynamic models in the quasistatic regime.

5.3.3 Specific challenges for phase-field fracture models

The following challenges are highlighted regarding the handling of complex geometries, material models, and controlling numerical errors in estimating crack surface geometries in PF.

• 1. Crack path intersecting holes, obstacles, and boundaries: Several issues were reported while obtaining crack paths in agreement with LEFM for problems involving holes [16]. Another study [163] concluded that judgement on if a crack arrests or the method simply does not permit continuation across obstacles, requires expert knowledge. In pressurized fractures, see e.g., [306], the fracture often branches, which raises however whether this is physically reasonable. Moreover, goal functional evaluations are sensitive to boundary conditions and the domain size [311].

• 2. Fast crack propagation under dynamic loading: For some fast crack propagation simulations, e.g. [466], the calculated fracture velocity overestimated the fracture energy dissipation.

• 3. Composite/Concrete fracture: At the time of writing this review, not many fracture/damage models for composites [267, 513, 514] and concrete [515,516,517,518] were available.

• 4. Asymptotic computational understanding of the interaction of regularization, model, and discretization parameters: In terms of numerical and computational convergence analysis, current PF understanding is still incomplete. Ingredients of numerical analysis from image segmentation [519], phase-field in fluid flow [520, 521] are available. Furthermore, computational convergences analyses for phase-field fracture have been undertaken [17, 290] and [522, 523]. Such a rigorous numerical analysis for a phase-field fracture model substantiated with numerical tests is missing to date. However, passing to the limits in the regularization parameters also requires to change the mathematical function spaces, e.g., [147, 148].

• 5. Robust and efficient linear solvers and preconditioners Closely related to the previous aspect is the development of iterative or multigrid linear solvers and preconditioners. Several suggestions exist as we have previously discussed, but a robust preconditioner for variations in the length-scale $l_0$, the regularization parameter $\kappa$, both spatial and temporal discretization parameters, and material parameter limits, for instance, Poisson’s ratio $\nu \rightarrow 0.5$ has not yet been fully understood; first attempts can be found in the PhD theses [524] and [476]. The challenge are spectral-equivalent operators for preconditioning and the multiscale-multidomain character due to the variations of several orders of magnitude of the regularization parameters.

This review paper has highlighted some common challenges and specific challenges for both models. In our opinion, listing these challenges are useful in many ways. First, these challenges can guide young researchers to interesting research topics they might address for their future career. Second, these challenges need to be addressed for rigorous comparison against experiments. Notably in Sect. 5 we point out that there are few comparisons of both methods against the same experiment. Here, more work is needed for comparison of both models’ accuracy for specific crack and fracture phenomena. Another aspect is that both models have not participated in the Sandia Fracture Challenge as consistently as other methods. Third, more rigorous mathematical and numerical analysis of cracks speeds, locations and bifurcations are needed for both methods. Application and calibration of these methods to composite materials should be carried out. We believe that this is necessary for both methods to have a broader acceptance in industry. Presently these methods are being applied by some research and development departments of companies, however, they are not used for validation and certification of products. This is in contrast with the finite element method where it is used in the final structural certification of the the Boeing 777. Here, one could argue that the finite element method was introduced 75 years ago [525,526,527], while free fracture methods were introduced only around 21 years ago. However, addressing these challenges is crucial for a broader adaption of these methods outside the academic setting.

6 Conclusions

A comprehensive review of two numerical modeling approaches - Peridynamics (PD) and Phase-field (PF) is presented with the expectation to highlight their advantages, as well as challenges in modeling fracture initiation, propagation, and predictive capabilities for experimental validation. Both numerical methods can retrieve a consistent microscale physics of crack initiation and propagation. Despite both approaches being computationally challenging, their advantages in capturing multiple fracture interactions with minimal amount of phenomenological assumptions and closures make PD and PF as a good choice to understand engineering fracture mechanics. The following items are listed here for further improvement of both modeling approaches:

• Both PD and PF need to be evaluated against the same experimental benchmark for a reasonable comparison in a blind validation manner. Several experimental datasets are identified as the available community resources.

• Phase-field simulation results for the Sandia Fracture Challenge problems could provide the missing piece of information for a comprehensive and validated comparison among the two modeling approaches.

• There is in general a lack of comparative studies between these two leading modeling approaches for fracture initiation and propagation, even for the same set of simple fracture experiments.¹⁵$^,$¹⁶