Abstract
This paper is the first investigation establishing the link between the meshfree state-based peridynamics method and other meshfree methods, in particular with the moving least squares reproducing kernel particle method (RKPM). It is concluded that the discretization of state-based peridynamics leads directly to an approximation of the derivatives that can be obtained from RKPM. However, state-based peridynamics obtains the same result at a significantly lower computational cost which motivates its use in large-scale computations. In light of the findings of this study, an update to the method is proposed such that the limitations regarding application of boundary conditions and the use of non-uniform grids are corrected by using the reproducing kernel approximation.





Similar content being viewed by others
Notes
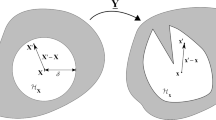
In particular, point \(\mathbf {x}\) can coincide with the specified point \(\mathbf {x}_I\).
Function \(\omega (\mathbf {x}-\mathbf {x}_J)\) can have different names depending on the field of study: weight function, kernel, smoothing function, or influence function. It has the role of defining the radius of influence of the surroundings, and the weight that each point of those surroundings has on the approximation.
The notation used in this article is different from the original articles introducing the peridynamic theory in an effort to facilitate the comparison with different theories that share similar notation, in particular: continuum mechanics, finite difference methods, meshless methods, and finite element methods.
Provided that the distance between that point and any of the boundaries is larger than the horizon \(\delta \), as will be discussed later.
Due to the length of this algebraic procedure, the existence of software that can be used to reach these expressions, and most importantly the straightforward operations involved in these derivations (since these expressions were also determined by hand) it was decided to omit the intermediate expressions, as opposed to what was done in the 1D case previously shown.
References
Silling S, Epton M, Weckner O, Xu J, Askari E (2007) Peridynamic states and constitutive modeling. J Elast 88(2):151. doi:10.1007/s10659-007-9125-1
Silling S, Lehoucq R (2008) Convergence of peridynamics to classical elasticity theory. J Elast 93(1):13. doi:10.1007/s10659-008-9163-3
Silling S (2000) Reformulation of elasticity theory for discontinuities and long-range. J Mech Phys Solids 48(1):175. doi:10.1016/S0022-5096(99)00029-0
Warren TL, Silling SA, Askari A, Weckner O, Epton MA, Xu J (2009) A non-ordinary state-based peridynamic method to model solid material deformation and fracture. Int J Solids Struct 46(5):1186. doi:10.1016/j.ijsolstr.2008.10.029
Foster JT, Silling SA, Chen WW (2010) Viscoplasticity using peridynamics. Int J Numer Methods Eng 81(10):1242. doi:10.1002/nme.2725
Tupek M, Rimoli J, Radovitzky R (2013) An approach for incorporating classical continuum damage models in state-based peridynamics. Comput Methods Appl Mech Eng 263:20. doi:10.1016/j.cma.2013.04.012
Liu WK, Jun S, Zhang YF (1995) Reproducing kernel particle methods. Int J Numer Methods Fluids 20(8–9):1081. doi:10.1002/fld.1650200824
Li S, Liu WK (2002) Meshfree and particle methods and their applications. Appl Mech Rev 55(1):1
Belytschko T, Krongauz Y, Organ D, Fleming M, Krysl P (1996) Meshless methods: an overview and recent developments. Comput Methods Appl Mech Eng 139(1–4):3. doi:10.1016/S0045-7825(96)01078-X
Li S, Liu WK (2004) Meshfree particle methods. Springer, Berlin
Nguyen VP, Rabczuk T, Bordas S, Duflot M (2008) Meshless methods: a review and computer implementation aspects. Math Comput Simul 79(3):763. doi:10.1016/j.matcom.2008.01.003
Nayroles B, Touzot G, Villon P (1992) Generalizing the finite element method: diffuse approximation and diffuse elements. Comput Mech 10(5):307. doi:10.1007/BF00364252
Belytschko T, Lu YY, Gu L (1994) Element-free Galerkin methods. Int J Numer Methods Eng 37(2):229. doi:10.1002/nme.1620370205
Liu WK, Jun S, Li S, Adee J, Belytschko T (1995) Reproducing kernel particle methods for structural dynamics. Int J Numer Methods Eng 38(10):1655. doi:10.1002/nme.1620381005
Liu WK, Li S, Belytschko T (1997) Moving least-square reproducing kernel methods (I) Methodology and convergence. Comput Methods Appl Mech Eng 143(1–2):113. doi:10.1016/S0045-7825(96)01132-2
Liu WK, Chen Y, Uras R, Chang CT (1996) Generalized multiple scale reproducing kernel particle methods. Comput Methods Appl Mech Eng 139(1–4):91. doi:10.1016/S0045-7825(96)01081-X
Liu W, Chen Y, Chang C, Belytschko T (1996) Advances in multiple scale kernel particle methods. Comput Mech 18(2):73. doi:10.1007/BF00350529
Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics-theory and application to non-spherical stars. Mon Notices R Astron Soc 181:375
Oñate E, Idelsohn S, Zienkiewicz OC, Taylor RL (1996) Finite point method in computational mechanics. Applications to convective transport and fluid flow. Int J Numer Methods Eng 39(22):3839
Kim DW, Liu WK (2006) Maximum principle and convergence analysis for the meshfree point collocation method. SIAM J Numer Anal 44(2):515
Hu HY, Chen JS, Hu W (2011) Error analysis of collocation method based on reproducing kernel approximation. Numer Methods Partial Differ Equ 27(3):554. doi:10.1002/num.20539
Li S, Liu WK (1998) Synchronized reproducing kernel interpolant via multiple wavelet expansion. Comput Mech 21(1):28. doi:10.1007/s004660050281
Kim DW, Yoon YC, Liu WK, Belytschko T (2007) Extrinsic meshfree approximation using asymptotic expansion for interfacial discontinuity of derivative. J Comput Phys 221(1):370. doi:10.1016/j.jcp.2006.06.023
Yoon YC, Song JH (2013) Extended particle difference method for weak and strong discontinuity problems: part II. Formulations and applications for various interfacial singularity problems. Comput Mech 13:1–24. doi:10.1007/s00466-013-0951-7
Yoon YC, Song YH (2013) Extended particle difference method for weak and strong discontinuity problems: part I. Derivation of the extended particle derivative approximation for the representation of weak and strong discontinuities. Comput Mech 3:1–17. doi:10.1007/s00466-013-0950-8
Fornberg B (1988) Generation of finite difference formulas on arbitrarily spaced grids. Math Comput 51(184):699
Lanczos C (1956) Applied analysis. Prentice-Hall, Old Tappan
Savitzky A, Golay MJE (1964) Smoothing and differentiation of data by simplified least squares procedures. Anal Chem 36(8):1627. doi:10.1021/ac60214a047
Liu GR, Gu Y (2001) A point interpolation method for two-dimensional solids. Int J Numer Methods Eng 50(4):937
Liu GR (2010) Meshfree methods: moving beyond the finite element method. CRC Press, Boca Raton
Wang JG, Liu GR (2002) A point interpolation meshless method based on radial basis functions. Int J Numer Methods Eng 54(11):1623. doi:10.1002/nme.489
Liu G, Kee BB, Chun L (2006) A stabilized least-squares radial point collocation method (LS-RPCM) for adaptive analysis. Comput Methods Appl Mech Eng 195(37):4843
Hu HY, Chen JS, Hu W (2007) Weighted radial basis collocation method for boundary value problems. Int J Numer Methods Eng 69(13):2736. doi:10.1002/nme.1877
Wang L, Chen JS, Hu HY (2010) Subdomain radial basis collocation method for fracture mechanics. Int J Numer Methods Eng 83(7):851. doi:10.1002/nme.2860
Auricchio F, Veiga LBD, Hughes TJR, Reali A, Sangalli G (2010) Isogeometric collocation methods. Math Models Methods Appl Sci 20(11):2075. doi:10.1142/S0218202510004878
Auricchio F, da Veiga LB, Hughes T, Reali A, Sangalli G (2012) Isogeometric collocation for elastostatics and explicit dynamics. Comput Methods Appl Mech Eng 2:249–252. doi:10.1016/j.cma.2012.03.026
Lehoucq R, Silling S (2008) Force flux and the peridynamic stress tensor. J Mech Phys Solids 56(4):1566. doi:10.1016/j.jmps.2007.08.004
Zhou K, Du Q (2010) Mathematical and numerical analysis of linear peridynamic models with nonlocal boundary conditions. SIAM J Numer Anal 48(5):1759. doi:10.1137/090781267
Silling S, Lehoucq R (2010) Peridynamic theory of solid mechanics. Adv Appl Mech 44:73. doi:10.1016/S0065-2156(10)44002-8
Seleson P, Parks M (2011) On the role of the influence function in the peridynamic theory. Int J Multiscale Comput Eng 9(6):689
Diekema E, Koornwinder TH (2012) Differentiation by integration using orthogonal polynomials, a survey. J Approx Theory 164(5):637. doi:10.1016/j.jat.2012.01.003
Foster J, Silling SA, Chen W (2011) An energy based failure criterion for use with peridynamic states. Int J Multiscale Comput Eng 9(6):675
Zhu T, Atluri S (1998) A modified collocation method and a penalty formulation for enforcing the essential boundary conditions in the element free Galerkin method. Comput Mech 21(3):211
Fernández-Méndez S, Huerta A (2004) Imposing essential boundary conditions in mesh-free methods. Comput Methods Appl Mech Eng 193(12):1257
Tian R (2013) Extra-dof-free and linearly independent enrichments in GFEM. Comput Meth Appl Mech Eng 266:1. doi:10.1016/j.cma.2013.07.005
Chen JS, Hu W, Hu HY (2008) Reproducing kernel enhanced local radial basis collocation method. Int J Numer Methods Eng 75(5):600. doi:10.1002/nme.2269
Chi SW, Chen JS, Luo H, Hu HY, Wang L (2012) Dispersion and stability properties of radial basis collocation method for elastodynamics. Numer Methods Partial Diff Equ 29:818–842. doi:10.1002/num.21732
Hamming RW (1989) Digital filters. Courier Dover Publications, Cambridge
Acknowledgments
This work was funded in part by grants from the United States Air Force Office of Scientific Research grant number W911NF-11-1-0208 and National Energy Technology Laboratory grant number DE-FE0010808.
Author information
Authors and Affiliations
Corresponding author
Appendix: Least squares based meshfree methods
Appendix: Least squares based meshfree methods
The LS approximation is obtained as a special case of Eq. (11) when using the weight function \(\omega =1\), and when considering that point \(\mathbf {x}\) is fixed in space which leads to constant coefficients \(\mathbf {a}(\mathbf {x})\). The fixed points in the domain coincide with the grid points of the discretization \(\mathbf {x} \equiv \mathbf {X}_I\), so for convenience we can drop the prime in the notation of the arbitrary coordinate \(\mathbf {x}' \equiv \mathbf {X}\):
where the constant coefficients \(\mathbf {a}(\mathbf {X}_I)\) are given by Eq. (10) for the particular conditions of a LS approximation:
Then, the approximations to the derivatives of function \(f\) are simple to obtain since the coefficients are constant:
As was already noted in Sect. 2, the above approximation method based on LS can be used to obtain several fundamental methods in numerical analysis: (1) classic and generalized finite difference formulas; (2) discretized Lanczos derivatives; (3) Savitzky-Golay filters for uniform and non-uniform grids.
Finite difference methods
The classic and generalized finite difference formulas for uniform and arbitrarily spaced grids, respectively, are obtained when the number of points \(L\) in the local approximation matches the number of monomials \(m\) in the polynomial basis. The constant coefficients of the polynomial basis \(\mathbf {a}(\mathbf {X}_I)\) can easily be determined according to Eq. (50). Fornberg [26] proposed an algorithm to calculate these coefficients, that are usually called “weights” in the finite differences literature despite being completely different from the weight function \(\omega \) in WLS or MLS/RKPM.
Note that the polynomial approximation that is constructed to obtain the finite difference formulas interpolates every point \(J\) of the domain because the system is fully determined. This is equivalent to finding the approximation function \(f^h\) by overfitting the discretized points using a polynomial approximation, i.e. the polynomial is forced to pass through every discretized point. For this reason, finite difference formulas have a large sensitivity to noise.
Lanczos derivative
Lanczos [27] was perhaps the first to notice that it was possible to approximate the derivatives of a function in a different way:
in what is nowadays called the Lanczos derivative.
Remarkably, Lanczos also proposed a discretized version of the above derivative for the case of having a one-dimensional function \(f(X)\) that is evaluated at uniformly spaced points at a distance \(\varDelta X\) of each other:
with \(X_J = X_0 + J\cdot \varDelta X\), and \(L\) being the odd number of discretization points.
Lanczos used a quadratic polynomial, Eq. (3) with \(k=2\) (or \(m=3\)), and minimized the least squares approximation so that he could obtain the coefficients of that polynomial. This means that he used the simplest version of Eq. (50) to determine those coefficients. Calculating the coefficients and determining the derivatives from Eq. (51), Lanczos found simple formulas for the approximation of the first derivative of function \(f\) due to the use of a uniform grid, as can be seen in Table 1.
These formulas can be generalized for any number of grid points \(L\) as:
Savitzky–Golay filters
After the discovery of the Lanczos derivative, with the seminal contribution of Savitzky and Golay [28], it was possible to generalize this procedure for polynomials of higher degree and for multidimensions by using Eqs. (49) and (50). The impact of this discovery was tremendous, not only in mathematical and statistical analysis but also in many other fields because it gave the ability to extract smooth data from noisy experimental measures. Moreover, it was also found that these derivatives when plotted in frequency space suppress high-frequency signals (noise) which opened the way to the design of digital filters [48]. In digital filters literature the differentiation formulas using \(k=2\) presented in Table 1 are called “low-noise Lanczos differentiators”, and if \(k=4\) they are called “super low-noise Lanczos differentiators”.
From this brief historical perspective it is obvious that subsequent discoveries followed natural steps, as was shown in Sect. 2: (1) generalizing the Savitzky-Golay filters to arbitrarily spaced grids; (2) using WLS; (3) and finally using MLS. Thus, it is not surprising that MLS/RKPM represents the general case that encompasses all the meshfree methods considered in this article.
Rights and permissions
About this article
Cite this article
Bessa, M.A., Foster, J.T., Belytschko, T. et al. A meshfree unification: reproducing kernel peridynamics. Comput Mech 53, 1251–1264 (2014). https://doi.org/10.1007/s00466-013-0969-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-013-0969-x