Continuum-kinematics-based peridynamics and phase-field approximation of non-local dynamic fracture

Abstract

In this work, two non-local approaches to dynamic fracture are investigated: a novel peridynamic formulation and a variational phase-field approach. The chosen continuum-kinematics-based peridynamic model extends the current peridynamic models by introducing surface and volume-based interactions. The phase-field fracture approach optimizes the body’s potential energy and provides a reliable method for predicting fracture in finite element computations. Both methods are able to efficiently compute crack propagation even when the cracks have arbitrary or complex patterns. We discuss the relations of critical fracture parameters in the two methods and show that our novel damage model for the continuum-kinematics-based peridynamics effectively manages fracture under dynamic loading conditions. Numerical examples demonstrate a good agreement between both methods in terms of crack propagation, fracture pattern, and in part, critical loading. We also show the limitations of the methods and discuss possible reasons for deviations.

1 Introduction

In computational mechanics, predicting fracture propagation and material degradation is still challenging. Numerous computational techniques, including damage models, discontinuous finite element discretizations (Xu and Needleman 1994; Ortiz and Pandolfi 1999; Dally et al. 2020), and phase-field fracture simulations (Miehe and Mauthe 2016; Wilson and Landis 2016; Bilgen and Weinberg 2021), have been used to solve fracture problems. The classical continuum mechanics assumption of a homogeneous bulk material forms the basis for these methods.

For the dynamic fracture of brittle materials, several studies have been published using phase-field models for predicting fragmentation. Ren et al. proposed an explicit phase-field model for dynamic brittle fracture that uses sub-stepping to achieve fast convergence (Ren et al. 2019). Geelen et al. expanded a cohesive fracture phase-field/gradient-damage model to the dynamic situation and showed that their model is a reliable and efficient way to simulate the spread of cohesive cracks (Geelen et al. 2019). Mandal et al. reviewed variational phase-field models for dynamic fracture and found that phase-field fracture simulation results are encouraging and similar to other methods (Mandal et al. 2020). Other researchers have proposed spatially adaptive phase-field models and variational eigenerosion approaches for inelastic materials (Phansalkar et al. 2022; Qinami et al. 2020).

Peridynamics is a non-local continuum mechanics formulation that was introduced by Silling (Silling 2000; Silling and Askari 2005). The relative displacements and forces between the continuum’s material points are described by means of integro-differential equations. The original bond-based peridynamics models these interactions with one elastic stiffness parameter and, thus, implies a restriction on the Poisson ratio. In order to account for materials with two varying elastic parameters, state-based formulations, such as ordinary state-based peridynamics and non-ordinary state-based peridynamics, were introduced (Silling and Askari 2005; Silling et al. 2007). Javili et al. recently proposed a novel peridynamic discretization called continuum-kinematics-based peridynamics (CPD), cf. (Javili et al. 2019, 2020, 2021), which uses an analogy to continuum mechanics to derive a non-ordinary state-based peridynamic model.

The CPD starts from the non-local continuum formulation where the interactions of material points (within a certain neighborhood) provide the body’s internal force density. In opposite to the classical peridynamic formulations, the relations in sets of two, three and four material points are now considered. Hereby two points form a bond, three an area, and four a volume element. This discretization introduces two new material parameters, both functions of the one original bond constant, which can be used for elastic models known from finite deformation continuum mechanics where such parameters refer to length-, area-, and volume-related invariants. Recently, correlations between the material parameters of continuum-kinematics-based peridynamics and isotropic linear elasticity were developed for two- and three-dimensional problems (Ekiz et al. 2021, 2022).

The new continuum-based peridynamic approach necessitates a new understanding of damage and fracture. It is no longer sufficient to think of material damage and brittle fracture as a bond-based event because of the three different kinds of interactions (Friebertshäuser et al. 2022, 2023). Thus, we extend the force density of the material, by kinematic variables that account for the loss of load-carrying capability. To the authors’ knowledge, this is the first concept of damage in the continuum-kinematics-based peridynamics paradigm.

The structure of this paper is as follows. First, the terminology and necessary theory is introduced for continuum-kinematics-based peridynamics in Section 2, and dynamic phase-field fracture in Section 3. In Section 4, we discuss the cohesive stress and the critical strain, which provide the crack growth and fracture criteria for both methods. The relations found in Section 4 are investigated in Section 5 with a detailed comparison of load-deflection curves obtained from both methods. Then, numerical examples of brittle fracture follow. Section 6 begins with the well-known dynamic shear test, which is investigated with our novel damage model of continuum-kinematics-based peridynamics and compared to the corresponding phase-field solution. Following that, Section 7 presents the crack initiation caused by propagating and reflecting pressure waves using the example of a curved bar.

2 Theory of continuum-kinematics-based peridynamics

In peridynamics, a body is represented by a set of N points in the Euclidean space $\mathbb {R}^3$, and the dynamics is depicted by the movement of these points. The point position in material configuration is described by $\varvec{X}^i$ and in current configuration as

$$\begin{aligned} \varvec{x}^i = \varvec{X}^i + \varvec{u}(\varvec{X}^i, t) \; , \end{aligned}$$

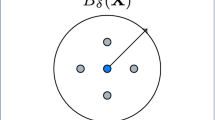
with the displacement vector $\varvec{u}(\varvec{X}^i, t)$ and $i=1,\dots ,N$. Points interact only with other points inside of their specified neighborhood $\mathcal {H}_1^i$, which is defined as the set of points inside the spherical space with the radius $\delta \in \mathbb {R}^+$, also called the horizon $\delta$. Accordingly,

$$\begin{aligned} \mathcal {H}_1^i = \left\{ \varvec{X}^j \in \mathcal {B}_0\; | \; 0 < \left| \varvec{X}^j - \varvec{X}^i\right| \le \delta \right\} \quad \forall \; \varvec{X}^i\in \mathcal {B}_0 \end{aligned}$$

includes all points $\varvec{X}^j$ inside the horizon of point $\varvec{X}^i$ in the reference configuration of the body $\mathcal {B}_0$.

The equation of motion for a point i reads

$$\begin{aligned} \varrho \, \varvec{\ddot{u}}(\varvec{X}^i, t)= & {} \varvec{b}_0^{\textrm{int}}(\varvec{X}^i, t) + \varvec{b}_0^{\textrm{ext}}(\varvec{X}^i, t) \nonumber \\ \forall \; \varvec{X}^i \in \mathcal {B}_0, \; t\ge & {} 0 \end{aligned}$$

(1)

with the density $\varrho$, the point acceleration vector $\varvec{\ddot{u}}$, and the point force density vectors $\varvec{b}_0^{\textrm{int}}$ and $\varvec{b}_0^{\textrm{ext}}$, which denote forces per unit undeformed volume. The external force density $\varvec{b}_0^{\textrm{ext}}$ results from the external forces that are acting on the body and the internal force density $\varvec{b}_0^{\textrm{int}}$ from the interactions between the individual material points. In the following, the notation $\varvec{u}^{i} = \varvec{u}(\varvec{X}^i, t)$ and $\varvec{b}_0^{\textrm{int}, \, i} = \varvec{b}_0^{\textrm{int}}(\varvec{X}^i, t)$ will be used for improved readability.

For calculating the internal force density, different peridynamic formulations are available, and each one is based on the interactions between—typically two— material points. For the CPD the three different interactions, named as one-, two-, and three-neighbor interactions, are considered (see Fig. 1). Correspondingly, $\varvec{b}_0^{\textrm{int}, \, i}$ is the sum of the internal force densities of these three interactions, thus

$$\begin{aligned} \varvec{b}_0^{\textrm{int}, \, i} = \varvec{b}_1^{\textrm{int}, \, i} + \varvec{b}_2^{\textrm{int}, \, i} + \varvec{b}_3^{\textrm{int}, \, i} \; . \end{aligned}$$

(2)

Fig. 1

Illustration of one-, two-, and three-neighbor interactions of point $\varvec{X}^i$

The one-neighbor interaction of point i and j, in standard peridynamics also called the bond, is defined in material and current configuration as

$$\begin{aligned} \varvec{\varDelta X}^{ij}&= \varvec{X}^j - \varvec{X}^i \; , \qquad \varvec{\varDelta x}^{ij} = \varvec{x}^j - \varvec{x}^i \; . \end{aligned}$$

One-neighbor interactions can be interpreted as line elements with the initial length $L^{ij}$ in material notation and the deformed length $l^{ij}$ in current configuration. These so called relative length measures of the one-neighbor interaction are defined as

$$\begin{aligned} L^{ij}&= \left| \varvec{\varDelta X}^{ij}\right| \; ,\qquad l^{ij} = \left| \varvec{\varDelta x}^{ij}\right| \; . \end{aligned}$$

It is assumed, that all one-neighbor interactions of point i contribute equally. Therefore, an effective one-neighbor volume is defined as

$$\begin{aligned} V_1^{i} = \frac{V_{\mathcal {H}}^i}{N_1^i} \; , \end{aligned}$$

with $N_1^i$ being the number of one-neighbor interactions for point i and the neighborhood volume

$$\begin{aligned} V_{\mathcal {H}}^i = \left\{ \begin{array}{ll} \beta ^i \, \frac{4}{3} \, \pi \, \delta ^3 &{} \quad \text {(3D problems)}\\ \beta ^i \, \pi \, \delta ^2 &{} \quad \text {(2D problems)}\\ \beta ^i \, 2 \, \delta &{} \quad \text {(1D problems)} \end{array} \right. \end{aligned}$$

(3)

with the factor $\beta ^i \in [0,1]$ that takes the fullness of the neighborhood into account. As an example, it applies $\beta ^i = 1$ if the neighborhood of point i is completely inside the body $\mathcal {B}_0$. On the other hand, if the neighborhood of point i is partially outside the body $\mathcal {B}_0$, the factor $\beta ^i < 1$ works as a correction factor to the volume $V_{\mathcal {H}}^i$.

The force density due to one-neighbor interactions is defined as

$$\begin{aligned} \varvec{b}_{1}^{\textrm{int}, \, i} = C_1 \int _{\mathcal {H}_1^i} \left( \frac{1}{L^{ij}} - \frac{1}{l^{ij}} \right) \varvec{\varDelta x}^{ij} \; \textrm{d} V_1^i \; , \end{aligned}$$

(4)

with the one-neighbor interaction constant $C_1$. The constant $C_1$ can be interpreted as a resistance against the length change of one-neighbor interactions and is defined as $C_1 = \frac{24 \mu }{\pi \delta ^3}$ for 2D problems (Ekiz et al. 2021) and as $C_1 = \frac{30 \, \mu }{\pi \, \delta ^4}$ for 3D problems (Ekiz et al. 2022). They depend on the first and second Lamé parameters

$$\begin{aligned} \lambda = \frac{E \, \nu }{(1 + \nu )(1-2\nu )}\quad \text { and } \quad \mu = \frac{E}{2(1+\nu )}\,. \end{aligned}$$

(5)

Two-neighbor interactions are area elements, respectively triangles, spanned by the points $\varvec{X}^i$, $\varvec{X}^j$ and $\varvec{X}^k$. They are constructed by two corresponding one-neighbor interactions $\varvec{\varDelta X}^{ij}$ and $\varvec{\varDelta X}^{ik}$ of point i. One important condition is that the distance between the points $\varvec{X}^j$ and $\varvec{X}^k$ needs to be bounded by the horizon $\delta$. Therefore, the set of all corresponding point-sets for two-neighbor interactions of point i is defined as

$$\begin{aligned} \mathcal {H}_2^i{} & {} = \left\{ \big ( \varvec{X}^j,\varvec{X}^k \big ) \in \mathcal {H}_1^i \times \mathcal {H}_1^i \; | \; 0 < \left| \varvec{X}^j - \varvec{X}^k\right| \le \delta \right\} \\{} & {} \quad \forall \; \varvec{X}^i \in \mathcal {B}_0 \; . \end{aligned}$$

The deformation of two-neighbor interactions is mainly described by the relative area measure, in material and current notation defined as

$$\begin{aligned} \varvec{A}^{ijk}&= \varvec{\varDelta X}^{ij} \times \varvec{\varDelta X}^{ik} \; , \qquad \varvec{a}^{ijk} = \varvec{\varDelta x}^{ij} \times \varvec{\varDelta x}^{ik} \; , \end{aligned}$$

and as scalar quantities the areas

$$\begin{aligned} A^{ijk}&= \left| \varvec{A}^{ijk}\right| \; ,\qquad a^{ijk} = \left| \varvec{a}^{ijk}\right| \; . \end{aligned}$$

The force density due to two-neighbor interactions is defined as

$$\begin{aligned} \varvec{b}_{2}^{\textrm{int}, \, i} = 2 \, C_2 \, \int _{\mathcal {H}_2^i} \varvec{\varDelta x}^{ik} \times \left( \frac{1}{A^{ijk}} - \frac{1}{a^{ijk}} \right) \varvec{a}^{ijk} \; \textrm{d} V_2^i \; , \end{aligned}$$

(6)

with the effective two-neighbor volume

$$\begin{aligned} V_2^{i} = \frac{\left( V_{\mathcal {H}}^i\right) ^2}{N_2^i} \; . \end{aligned}$$

The number of two-neighbor interactions of point i is $N_2^i$. The two-neighbor interaction constant $C_2$ can be interpreted as a resistance against the area change and is defined as $C_2 = \frac{27}{8 \pi \delta ^6} (\lambda -\mu )$ for 2D problems (Ekiz et al. 2021) and as $C_2 = 0$ for 3D problems (Ekiz et al. 2022).

Three-neighbor interactions are volume elements, precisely tetrahedrons, spanned by the points $\varvec{X}^i$, $\varvec{X}^j$, $\varvec{X}^k$ and $\varvec{X}^l$. They are constructed by the three corresponding one-neighbor interactions $\varvec{\varDelta X}^{ij}$, $\varvec{\varDelta X}^{ik}$ and $\varvec{\varDelta X}^{il}$ of point i. For a valid three-neighbor interaction, the conditions

$$\begin{aligned}&0< \left| \varvec{X}^j - \varvec{X}^k\right| \le \delta \; ,\qquad 0< \left| \varvec{X}^j - \varvec{X}^l\right| \le \delta \; ,\\&0 < \left| \varvec{X}^k - \varvec{X}^l\right| \le \delta \; , \end{aligned}$$

must be met. Consequently, the set of all corresponding point-sets for three-neighbor interactions of point i is defined as

$$\begin{aligned}&\mathcal {H}_3^i = \left\{ \big ( \varvec{X}^j,\varvec{X}^k,\varvec{X}^l \big ) \in \mathcal {H}_1^i\times \mathcal {H}_1^i\times \mathcal {H}_1^i \; | \; \right. \\&\quad 0< \left| \varvec{X}^j - \varvec{X}^k\right| \le \delta \; , 0< \left| \varvec{X}^j - \varvec{X}^l\right| \le \delta \; ,\\&\quad 0 \left. < \left| \varvec{X}^k - \varvec{X}^l\right| \le \delta \right\} \quad \forall \; \varvec{X}^i \in \mathcal {B}_0 \; . \end{aligned}$$

The deformation of three-neighbor interactions is mainly described by the relative volume measure, in material and current notation defined as

$$\begin{aligned} V^{ijkl}&= \varvec{A}^{ijk} \cdot \varvec{\varDelta X}^{il} \; ,\quad v^{ijkl} = \varvec{a}^{ijk} \cdot \varvec{\varDelta x}^{il} \; . \end{aligned}$$

The force density due to three-neighbor interactions is defined as

$$\begin{aligned} \varvec{b}_{3}^{\textrm{int}, \, i}= & {} 3 \, C_3 \, \int _{\mathcal {H}_3^i} \left( \varvec{\varDelta x}^{ik} \times \varvec{\varDelta x}^{il} \right) \left( \frac{1}{\left| V^{ijkl}\right| } - \frac{1}{\left| v^{ijkl}\right| } \right) \nonumber \\{} & {} \qquad v^{ijkl} \; \textrm{d} V_3^i \;, \end{aligned}$$

(7)

with the effective three-neighbor volume

$$\begin{aligned} V_3^{i} = \frac{\left( V_{\mathcal {H}}^i\right) ^3}{N_3^i} \; . \end{aligned}$$

The number of three-neighbor interactions of point i is $N_3^i$. The three-neighbor interaction constant

$$\begin{aligned} C_3 = \frac{32}{\pi ^4 \, \delta ^{12}} (\lambda -\mu ) \end{aligned}$$

(8)

can be interpreted as a resistance against the volume change (Ekiz et al. 2022). The three types of interaction correspond to the invariants of a general deformation.

With the kinematics at hand we solve the equation of motion 1. Because all of our simulations take place over small time spans, we employ a Velocity-Verlet explicit time integration algorithm, cf. (Littlewood 2015).

In CPD, damage is modeled by the failure of the corresponding one-, two- and three-neighbor interactions. The failure quantity for one-neighbor interactions with a strain-based damage model reads

$$\begin{aligned} d_1^{ij} = \left\{ \begin{array}{ll} 0 &{} \text { if } \varepsilon ^{ij} > \varepsilon _\text {c}\\ 1 &{} \text { else} \end{array} \right. \end{aligned}$$

(9)

with the one-neighbor interaction stretch

$$\begin{aligned} \varepsilon ^{ij} = \frac{l^{ij} - L^{ij}}{L^{ij}} \; , \end{aligned}$$

(10)

and the critical bond strain of fracture $\varepsilon _\text {c}>0$. This critical strain depends on the material’s critical energy release rate $\mathcal {G}_\text {c}$ (Griffith energy) and is related to the horizon $\delta$ of the interacting material points. The pointwise damage quantity $D^i$ incorporates the whole neighborhood, and is defined as

$$\begin{aligned} D^{i} = 1 - \frac{\int _{\mathcal {H}_1^i} d_1^{ij} \; \textrm{d} V_1^i}{\int _{\mathcal {H}_1^i} \textrm{d} V_1^i} \,. \end{aligned}$$

(11)

These equations cannot directly be used to model damage within the continuum-kinematics-based framework, because they do not take two- or three-neighbor interactions into consideration. Applying this damage model alone will not lead to crack paths but to unclear failure zones, because two- or three-neighbor interactions are still active and lead to forces between failed points.

To address this problem, failure quantities for two- and three-neighbor interactions, $d_2^{ijk}$ and $d_3^{ijkl}$, are introduced. Here we propose that two- and three-neighbor interactions fail, if one or more corresponding one-neighbor interactions fail. Therefore, the failure quantity for two-neighbor interactions can be defined as

$$\begin{aligned} d_2^{ijk} = \left\{ \begin{array}{ll} 0 &{} \text { if } d_1^{ij}= 0 \text { or } d_1^{ik} = 0 \; ,\\ 1 &{} \text { else} \; , \end{array} \right. \end{aligned}$$

(12)

and for three-neighbor interactions as

$$\begin{aligned} d_3^{ijkl} = \left\{ \begin{array}{ll} 0 &{} \text { if } d_1^{ij} = 0\text { or } d_1^{ik}= 0\text { or } d_1^{il} = 0 \; ,\\ 1 &{} \text { else} \; . \end{array} \right. \end{aligned}$$

(13)

With these failure quantities, we re-define the internal force density for one-neighbor interactions (4) as

$$\begin{aligned} \varvec{b}_{1}^{\textrm{int}, \, i} = C_1 \int _{\mathcal {H}_1^i} d_1^{ij} \left( \frac{1}{L^{ij}} - \frac{1}{l^{ij}} \right) \varvec{\varDelta x}^{ij} \; \textrm{d} V_1^i \; , \end{aligned}$$

(14)

for two-neighbor interactions (6) as

$$\begin{aligned} \varvec{b}_{2}^{\textrm{int}, \, i} = 2 \, C_2 \int _{\mathcal {H}_2^i} d_2^{ijk} \varvec{\varDelta x}^{ik} \times \left( \frac{1}{A^{ijk}} - \frac{1}{a^{ijk}} \right) \varvec{a}^{ijk} \; \textrm{d} V_2^i \; , \end{aligned}$$

(15)

and for three-neighbor interactions (7) as

$$\begin{aligned}{} & {} \varvec{b}_{3}^{\textrm{int}, \, i} = 3 \, C_3 \int _{\mathcal {H}_3^i} d_3^{ijkl} \left( \varvec{\varDelta x}^{ik} \times \varvec{\varDelta x}^{il} \right) \left( \frac{1}{\left| V^{ijkl}\right| } - \frac{1}{\left| v^{ijkl}\right| } \right) \nonumber \\{} & {} \qquad v^{ijkl} \; \textrm{d} V_3^i \;. \end{aligned}$$

(16)

In such a manner, the failed point interactions do not contribute to the internal material response and their damaging effect is considered.

3 Theory of phase-field fracture

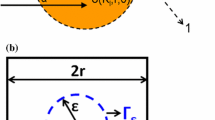
For the phase-field approach to fracture we rely on the classical theory of continuum mechanics, i.e., we consider a solid with domain $\varOmega \subset \mathbb {R}^{d}$ and boundary $\partial \varOmega \equiv \varGamma$ deforming under the action of external forces with density $\varvec{b}_0^\text {ext}$. The internal force density follows from the local stresses $\varvec{\sigma }(\varvec{X}, t)$ as $\varvec{b}_0^\text {int}={\text {div}} \varvec{\sigma }$.

Hence, the solid’s total energy is composed of its kinetic energy, the potential energy with the material’s free Helmholtz energy density $\varPsi ^\text {e}$, and the surface energy contributions from evolving crack boundaries with Griffith energy of fracture $\mathcal {G}_\text {c}$,

$$\begin{aligned} \mathcal {E} = \int _{\varOmega \setminus \varGamma _\text {c}(t)} \left( \frac{1}{2} \varrho |\varvec{v}|^2 + \varPsi ^\text {e} \right) \,\textrm{d}V + \int _{\varGamma _\text {c}(t)} {\mathcal {G}}_\text {c} \,\textrm{d}A \,. \end{aligned}$$

(17)

A phase field $z(\varvec{X},t)$ with $z\in [0,1]$ is introduced to characterize the state of the material; hereby indicates $z=0$ the solid and $z=1$ the broken state. For approximation, the discontinuous set of evolving crack boundaries $\varGamma _\text {c}(t)$ is replaced by a continuous surface-density function $\gamma (z)$ and an approximation of the form $\int _{\varGamma _\text {c}(t)} \,\textrm{d}A \approx \int _{\varOmega } \gamma \,\textrm{d}V$. With the ansatz

$$\begin{aligned} \gamma = \frac{1}{2l_\text {c}}z^2+\frac{l_\text {c}}{2}|\nabla z|^2 \,, \end{aligned}$$

this gives for the solid’s energy the objective

$$\begin{aligned} \mathcal {E}&= \int _{\varOmega } \left( \frac{1}{2} \varrho |\varvec{v} |^2 + \varPsi ^\text {e} + \frac{\mathcal {G}_\text {c}}{2l_\text {c}}z^2+\frac{\mathcal {G}_\text {c}l_\text {c}}{2}|\nabla z|^2 \right) \,\textrm{d}V \nonumber \\&\ \rightarrow \ \text {stationary}. \end{aligned}$$

(18)

By definition, $\gamma (z,\nabla z)$ which is only different from zero along cracks, introduces a length scale parameter $l_\text {c}>0$ in the model.

Fig. 2

Phase-field crack at $x=0$ approximated with a continuous phase field $z \in [0,1]$ and non-local material degradation function g(z)

Assuming a linear relation between the stresses $\varvec{\sigma }$ and the strains $\varvec{\varepsilon }(\varvec{u})= {\text {sym}} (\nabla \varvec{u})$, the material’s energy density is defined as

$$\begin{aligned} \varPsi ^\text {e}(\varvec{\varepsilon }) = \frac{1}{2}\varvec{\varepsilon }:\mathbb {C}^{\star }(z):\varvec{\varepsilon }\,. \end{aligned}$$

(19)

Here $\mathbb {C}^{\star }(z)$ denotes an adapted material tensor of the form

$$\begin{aligned} \mathbb {C}^{\star }(z)&= g(z) \left[ \lambda {\textsf{I}} \otimes {\textsf{I}} +2\mu \, {\text {sym}}\,{\textbf{I}} \right] \nonumber \\ \text {with} \quad g(z)&= (1-z)^2\,, \end{aligned}$$

(20)

where the bracketed term is Hooke’s tensor with ${\textsf{I}}$ and $\textbf{I}$ denoting the second- and four-rank identity tensors, respectively. Function g(z) is a degradation function accounting for the loss of stiffness in the crack, see Fig. 2. The corresponding degraded stresses are

$$\begin{aligned} \varvec{\sigma }= \mathbb {C}^{\star }(z) \varvec{\varepsilon } \,. \end{aligned}$$

(21)

The asymmetry of fracture, i.e., the fact, that only tensile stress states contribute to crack propagation, requires a split of the elastic energy into a tensile and a compressive parts, $\varPsi ^\text {e}(\varvec{\epsilon },z) = g(z)\varPsi ^{\text {e}+} + \varPsi ^{\text {e}-}$. Here this split is based on the spectral decomposition of the strain tensor if necessary, cf. (Bilgen et al. 2018; Bilgen and Weinberg 2019).

A straightforward finite element approximation of (18) results in a discretized version of the second-order Eq. 1. It can be solved for $\varvec{u}(\varvec{X},t)$ with a Newmark-time stepping algorithm. Alternatively, we employ here an approach that has already proven successful in calculating conservation laws. For the computation of wave propagation, the elastic equation of motion is transformed into a coupled system of first-order hyperbolic system,

$$\begin{aligned} \varrho \dot{\varvec{v}} = {\text {div}} \varvec{\sigma }\,,\qquad \dot{\varvec{\sigma }} = \mathbb {C}^{\star }(z) \varvec{\varepsilon }(\varvec{v}) \qquad \text {in }\varOmega \end{aligned}$$

(22)

suitably discretized, and combined with the phase-field evolution to calculate the crack initiation and propagation. In Weinberg and Wieners (2022), the evolution of the phase field is determined by

$$\begin{aligned} \tau _\text {r} \dot{z}&= {\left\{ \begin{array}{ll} Y_\text {el}(\varvec{\sigma }) + M \left( z - l_\text {c}^2\varDelta z \right) &{} z \ge 0 \\ 0 &{} z = 1 \end{array}\right. } \end{aligned}$$

with retardation time $\tau _\text {r}>0$, scaling parameter $M>0$, and the crack driving force $Y_\text {el}(\varvec{\sigma })$ as a stress-based criterion. The force $Y_\text {el}$ is active if the largest eigenvalue of stress tensor $\varvec{\sigma }$, i.e. the maximum principal stress $\sigma _\text {I}$, exceeds the maximum cohesive stress $\sigma _\text {c} > 0$. This yields

$$\begin{aligned} Y_\text {el}(\varvec{\sigma }) = \max \Big \{\displaystyle \frac{\sigma _\text {I}}{\sigma _\text {c}} -1,0\Big \} \,. \end{aligned}$$

(23)

For the algorithmic details of phase-field fracture we refer to Bilgen et al. (2018) for the second-order system and to Weinberg and Wieners (2022) for the first-order system.

4 Maximum cohesive stress and critical strain

Now we study the relation of the maximum stress before decohesion $\sigma _\text {c}$ in the phase-field fracture model and the corresponding critical strain $\varepsilon _\text {c}$ in the peridynamic fracture model for a one-dimensional crack solution, i.e., $\varOmega \subset \mathbb {R}$. We assume a static situation and derive $\sigma _\text {c}$ for a linear-elastic material and a quadratic degradation function $g(z)=(1- z)^2$. The body’s energy (18) is approximated by

$$\begin{aligned} \mathcal {E} = \int _{\varOmega } \left( g( z)\varPsi ^\text {e}_0-\frac{\mathcal {G}_\text {c}}{2 l_\text {c}} z^2\right) \,\textrm{d}V \,,\qquad \varPsi ^\text {e}_0=\frac{1}{2} E\varepsilon ^2 \end{aligned}$$

(24)

(neglection the regularization term $|\nabla z|^2$) and its variation $\delta \mathcal {E} =0$ gives

$$\begin{aligned} (1- z) E\varepsilon ^2-\frac{\mathcal {G}_\text {c}}{l_\text {c}}z&=0 \,. \end{aligned}$$

(25)

With a straightforward calculation we obtain the expression

$$\begin{aligned} 1- z&= \left( \frac{E\varepsilon ^2l_\text {c}}{\mathcal {G}_\text {c}}+1\right) ^{-1} \end{aligned}$$

(26)

which is now inserted in the degraded Hooke’s law (21) such that

$$\begin{aligned} \sigma (\varepsilon ) = \left( \frac{E\varepsilon ^2l_\text {c}}{\mathcal {G}_\text {c}}+1\right) ^{-2} E\varepsilon \end{aligned}$$

(27)

holds true. Based on this equation, the stress maximum is calculated. Minimization with respect to the strain $\varepsilon$ results in

$$\begin{aligned} \frac{\textrm{d}\sigma }{\textrm{d}\varepsilon } = \frac{E-3E^2\frac{l_\text {c}}{\mathcal {G}_\text {c}}\varepsilon ^2}{\left( \frac{E\varepsilon ^2l_\text {c}}{\mathcal {G}_\text {c}}+1\right) ^3} \overset{!}{=}0 \quad \Longrightarrow \quad \varepsilon _\text {c} = \sqrt{\frac{\mathcal {G}_\text {c}}{3l_\text {c}E}} \end{aligned}$$

(28)

and provides an expression for the critical strain $\varepsilon _\text {c}\equiv \varepsilon _\text {c}^\text {PF}$ in phase-field fracture. Inserting it in (27) leads to the degraded stress

$$\begin{aligned} \sigma (\varepsilon _\text {c}^\text {PF}) = g(z)\sigma _\text {c}^\text {PF} = \frac{9}{16}\sqrt{\frac{E\mathcal {G}_\text {c}}{3l_\text {c}}}. \end{aligned}$$

(29)

The maximum cohesive stress $\sigma _\text {c}$ of phase-field fracture is simply obtained from (28) using Hooke’s law

$$\begin{aligned} \sigma _\text {c}^\text {PF} = \sqrt{\frac{E\mathcal {G}_\text {c}}{3l_\text {c}}} \end{aligned}$$

(30)

which in turn determines the critical phase-field value to be $z_\text {c}=\frac{1}{4}$. Both, the maximum cohesive stress $\sigma _\text {c}$ and the critical strain depend on the non-local length scale parameter $l_c$.

In peridynamics the damage model relies on the failure of neighboring bonds once a critical strain $\varepsilon _\text {c}\equiv \varepsilon _\text {c}^\text {PD}$ is reached. The dissipated energy of fracture corresponds to the sum of work necessary to separate all bonds between one material point on the left hand side of the new crack surface to all points on the right hand side of the crack surfaces, within its horizon $\delta$. If this work is referred to the crack surface, then the Griffith energy $\mathcal {G}_\text {c}$ is obtained. Following the procedure outlined in Madenci and Oterkus (2014), we compute the Griffith energy for the one-dimensional case

$$\begin{aligned} \mathcal {G}_\text {c}= \frac{1}{2} c \varepsilon _\text {c}^2 \frac{2 A \delta ^3}{3} \end{aligned}$$

(31)

where A is the cross-sectional area and $C_1=2 E / A\delta ^2$ is the bond parameter of equation 4. Inserting it and solving for the critical strain gives

$$\begin{aligned} \varepsilon _\text {c} = \sqrt{\frac{3 \mathcal {G}_\text {c}}{2 E \delta }} \end{aligned}$$

(32)

and, with Hooke’s law, the corresponding maximum cohesive stress reads

$$\begin{aligned} \sigma _\text {c} = \sqrt{\frac{3 E \mathcal {G}_\text {c}}{2 \delta } } \,. \end{aligned}$$

(33)

This result shows that for an equal cohesive stress state we can relate the non-local parameter of phase-field fracture and peridynamics as

$$\begin{aligned} \delta =4.5 \, l_\text {c} \,. \end{aligned}$$

(34)

5 Comparison of load-deflection curves

To investigate the relationship in equation (34), load–displacement curves of a simple mode-I tension test are compared. Additionally, we evaluate the convergence of CPD and compare it to the solution obtained from the standard phase-field model.

Fig. 3

Geometrical setup and discretizations

The geometrical setup consists of a simple $1 \times 1 \times {0.1}\,\hbox {mm}$ block ($l={1}\,\hbox {mm}$) that contains an initial crack with length $\frac{1}{2}l$ from the left boundary to the center (see Fig. 3). The block is fixed vertically at the lower boundary and loaded at the top edge with the prescribed displacement $\bar{u}$. The mesh used for the phase-field simulations consists of 137 057 tetrahedral elements with an element edge length of ${0.0333}\hbox {mm}$ at the top and the bottom and a refined edge length of ${0.01}\,\hbox {mm}$ in the middle of the model where the crack occurs. For the peridynamics simulations, multiple point clouds with a different number of uniformly distributed points are considered (see Table 1).

All simulations consider a critical energy release rate of $\mathcal {G}_c={2.7}\hbox {N}\,\hbox {mm}^{-1}$ so that, theoretically, the crack propagation should start at the same critical loading. The phase-field results are obtained with the standard phase-field model with $l_\text {c} = {0.015}\, \hbox {mm}$ and all peridynamics simulations with the horizon $\delta = 4.5 l_\text {c} = {0.0675}\,\hbox {mm}$, to consider the relation in equation (34). The results of the quasi-static peridynamics simulations are obtained with the adaptive dynamic relaxation method by Kilic and Madenci (2010).

Table 1 Peridynamics discretizations with total number of one- and three-neighbor interactions and the ratio of horizon and point spacing

Fig. 4

Load-deflection curves for CPD and phase-field simulations of a mode-I tension test with $E={210000}\,\hbox {MPa}$ and $\nu ={0.25}$

Fig. 5

Load-deflection curves for bond-based peridynamics and phase-field simulations of a mode-I tension test with $E={210000}\,\hbox {MPa}$ and $\nu ={0.25}$

In Fig. 4, the load-deflection curve of the phase-field simulation is compared to CPD simulations. The material is modeled with Young’s modulus $E={210\,000}\,\hbox {MPa}$, Poisson ratio $\nu =0.25$, and density $\varrho ={8000}\,{kg/\hbox {m}^{3}}$. These parameters result in $C_1 \approx {3.86 \times 10^{10}}\,\hbox {N} \,\hbox {mm}^{{-6}}$ and $C_2 = C_3 = 0$, therefore only one-neighbor interactions contribute to the peridynamics solution. The simulations differ slightly, but the higher the number of points, the lower the slope of the load–displacement curve. The curve of the finest discretization with $100$ $\times$ $100$ $\times$ $10$ points deviates the most from the phase-field curve. The critical load from which the crack grows is only for the two coarsest discretizations similar to the phase-field solution and slightly lower for the simulations with finer point clouds. However, the slopes of the peridynamics load-deflection curves are lower than the phase-field solution and get flatter with more points and a finer discretization.

One possible reason for these differences is the occurrence of the surface effect since no complete point families do appear because the horizon for all simulations is fixed to $\delta = {0.0675}\,\hbox {mm}$ and the model has a thickness of ${0.1}\,\hbox {mm}$. In CPD, the influence of incomplete point families at the model’s edges is considered by the factor $\beta$ in equation (3). The volume of the points in the initial configuration, e.g., a converted finite element mesh, does not contribute to the calculation. Instead, as seen in equation (10), the effective one-, two- and three-neighbor volumes $V^i_1$, $V^i_2$, and $V^i_3$ are a mean value resulting from the number of points and interactions in the neighborhood.

However, the influence of $\beta$ could not be enough to compensate for the surface effect as a whole. Therefore, additional simulations of bond-based peridynamics (BB) without any correction factors are conducted. Because of $\nu ={0.25}$ and $C_2=C_3=0$, the only difference between the CPD and BB calculation is the previously described correction with the neighborhood volume. As seen in Fig. 5, similar results appear when comparing the BB and CPD calculations for both the maximum load values and the slopes of the load–displacement curves.

Since the surface effect will strongly influence the bond-based calculations, it can be assumed, based on the similarities, that it also contributes to the CPD simulations. The extent to which this is now included in other calculation examples still needs further investigation. It can also be stated that the relationship described in equation (34) cannot be directly proven with the demonstrated numerical calculations.

6 Kalthoff-Winkler experiment

The dynamic shear test, commonly called Kalthoff-Winkler experiment, is a established benchmark problem of fracture mechanics and has been investigated by a series of authors (Kalthoff and Winkler 1988; Kalthoff 2000; Lee and Freund 1988; Batra and Jaber 2001; Silling 2002; Bilgen 2019; Ren et al. 2019). In the following, we will elaborate on how the new damage model of CPD performs regarding the Kalthoff-Winkler experiment.

Fig. 6

Setup and 3D CPD results of the Kalthoff-Winkler experiment

The setup of the Kalthoff-Winkler experiment consists of a rectangular plate of size $100\times 200\times {9}\hbox {mm}$. A cylindrical section with diameter Ø${50}\,\hbox {mm}$ is separated by two ${50}\,\hbox {mm}$ notches in the middle of the plate, see Fig. 6. This cylindrical section is impacted by a projectile. The impact of this projectile is modeled with a velocity boundary condition v(t) on the first 5 point layers on the cylindrical section. For the velocity, it applies

$$\begin{aligned} v(t) = \left\{ \begin{array}{ll} v_0 \, t &{} \quad \text {if } t \le t_0\\ v_0 &{} \quad \text {if } t > t_0\\ \end{array} \right. \; \end{aligned}$$

(35)

with $v_0 ={33}{\hbox {m}/\hbox {s}}$ and $t_0 = 1{\mu \hbox {s}}$. On the side of the sample opposite to the impact, a no-failure-zone for the first three layers of points is applied.

The material is modeled with Young’s modulus of $E={190000}\, \hbox {MPa}$, Poisson ratio of $\nu ={0.3}$ and a density of $\varrho ={8000}\,{\hbox {kg}/\hbox {m}^{3}}$. The peridynamic body is discretized by $88\times 177\times 8$ material points with a point spacing of ${\vartriangle } x={1.125}\,\hbox {mm}$ and a horizon of $\delta = 3.015 {\vartriangle } x$. This results in a total of 12 635 484 one-neighbor and 19 481 512 560 three-neighbor interactions. The simulation was performed on the OMNI-Cluster of University of Siegen (2023) on one node using $\sim {1}\,\hbox {TB}$ RAM on multiple threads for $\sim {8}\,\hbox {h}$. For a simple comparison, a phase-field approximation of the Kalthoff-Winkler experiment in a two-dimensional setup with $256$ $\times$ $256$ B-spline elements is used with a length-scale parameter of $l_\text {c} = {7.8e-4}\,\hbox {m}$ and the same material parameters as for the peridynamics simulation. For additional resources on similar 3D phase-field simulations, see Ren et al. (2019).

In Fig. 7, both simulations are displayed for different states of crack propagation progress. The time $t_\text {c}$ is defined as the time the crack needs to fully propagate to the end of the plate. Note, that the value of $t_\text {c}$ is different for both methods and only chosen to qualitatively compare the results.

The characteristic $\sim {70}^{\circ }$ crack angle of the Kalthoff-Winkler experiment can be found with the phase-field simulation. The peridynamics solution deviates slightly from the expectations with an angle of 64$^{\circ }$. However, the computed crack path agrees well with the phase-field solution and known experimental results. A possible explanation for the slight difference in the starting angle of the crack could be a surface effect due to the large horizon size relative to the thickness of the sample used, cf. Le and Bobaru (2018).

Fig. 7

Different time steps of the Kalthoff-Winkler experiment

Fig. 8

Damage in the 2D curved bar of a) CPD and b) phase-field simulation

Fig. 9

Damage $D^i$ in the 3D curved bar after ${0.5}\,\hbox {ms}$ (top) and ${1.4}\,\hbox {ms}$ (bottom)

7 Curved bar under pressure

In the following section, crack initiation induced by propagating and superposing waves is investigated in two- and three-dimensional discretizations. For this purpose, a model of a curved bar is subjected to pressure waves, which are supposed to superimpose inside the material and eventually lead to crack initiation. Both setups use the material parameters of steel. The material points are spatially distributed along the curve $f(x)=\cos (\frac{\pi }{2} \, x)$ (see Weinberg and Wieners 2022; Friebertshäuser et al. 2022 for more details on the discretizations and the material properties).

On each side of the curved bar, a pressure impulse

$$\begin{aligned} p(t) = \left\{ \begin{array}{ll} - 4 \cdot \frac{p_0}{{t_1}^2} \cdot \left( t - \frac{t_1}{2}\right) ^2 + p_0 &{} \quad t \le t_1 \\ 0 &{} \quad t > t_1\\ \end{array} \right. \end{aligned}$$

with the pressure peak $p_0$ and the impulse duration $t_1$ is applied for one layer of material points in the left and right boundary. The pressure is applied symmetrically via the external body force density $\varvec{b}^{\textrm{ext}, \ i}_0 = p(t) / \varDelta x \, \varvec{n}_{l/r}$ with the normal vector $\varvec{n}_{l/r}$ for the left and right side of the bar. For the two-dimensional setup, a pressure impulse with the peak $p_0 = {4\,\times \,10^{5}}\hbox {N}\,\hbox {m}^{-1}$ and for the three-dimensional setup, $p_0 ={1\,\times \,10^{6}}\hbox {N}\,\hbox {m}^{-2}$ is used. For both setup’s, the pulse has the duration $t_1 = {300}\,\mu \hbox {s}$. Remark that for 2D, the body force density $\varvec{b}^{\textrm{ext}}_0$ has the unit [$\hbox {N}\,\hbox {m}^{-2}$].

Fig. 10

Visualization of the elastic wave interplay for the 3D CPD simulation

In Fig. 8, the damage $D^i$ of the two-dimensional setup is shown and compared with results obtained with a corresponding phase-field calculation (see Weinberg and Wieners 2022). The pressure waves travel through the bar until they get reflected at the free ends, turning them into tensile waves. The peak of these tensile waves then triggers the development of a crack in the middle of the bar, see Fig. 10. Again further cracks develop when the waves continue to propagate and reflect in the model, and a further peak in tension emerges. The two-dimensional model accurately captures this pattern since these secondary cracks appear over time. It is fascinating that this effect occurs very similarly for the peridynamics and the phase-field approach, despite being fundamentally different methods. However, a small difference can be found with the secondary cracks. In the peridynamic calculation, the secondary cracks are wider and slightly branched in the upper edge region, which can be explained by possible surface effects, as already mentioned in Sect. 5, cf. Bobaru and Zhang (2015); Le and Bobaru (2018).

A similar behavior can also be observed with the 3D model (see Fig. 9). One crack starts in the model’s center after the pressure wave’s initial reflection and conversion to tensile waves, see Fig. 10. The stress displayed in Fig. 10 is obtained by calculating the cauchy stress tensor additionally to the CPD simulation with the method of Warren et al. Warren et al. (2009). Additionally, cracking brought on by additional wave superposition can be seen. The location differs from the 2D model, although this could be explained by the several peridynamics-based continuum kinematics influencing aspects, including material characteristics and various discretizations. Further research is required in this case. Because of the much larger computational cost, we could not perform 3D calculations using the phase-field method with the same bar model.

In conclusion, it can be said that CPD can be utilized to map cracking caused by the material’s reaction to wave propagation and compares well to similar results of phase-field computations.

8 Summary

This study presents investigations on the non-local approximation of dynamic fracture with a novel, continuum-kinematics-based peridynamic formulation and an energy-optimizing phase-field approach. We show the relations between the critical crack properties of both methods by deriving the critical cohesive stress $\sigma _c$ and the corresponding critical strain $\varepsilon _c$ for the one-dimensional solution of a non-local crack.

Numerical studies support that the CPD and the phase-field fracture approach are well suited to simulate dynamic fracture. With the proper choice of $\sigma _c$ and $\varepsilon _c$, both methods give almost identical fracture patterns. However, the load-deflection curves of the CPD strongly depend on the discretization, which is presumably attributed to the incomplete neighborhood along the newly formed crack surfaces. These findings underline the crucial role of carefully considering the discretization and the horizon size for peridynamic fracture simulations.

The dynamic shear test of Kalthoff & Winkler was computed to investigate the performance of the new CPD damage model compared to a phase-field simulation. The crack paths show a good agreement with slight deviations. The minor differences between the peridynamics simulation and the expectations could be attributed to the surface effect. Further research is required in this regard. Additionally, curved bar simulations investigate crack initiation induced by propagating and superposing pressure waves. An excellent agreement between the two-dimensional CPD and phase-field simulations can be found here.

Our juxtaposition of continuum-kinematics-based peridynamics and phase-field fracture computations highlights the potential of non-local models in accurately predicting dynamic fracture behavior.