1 Introduction

Initial value problems of fractional order often appear during the modeling of many issues in the major scientific disciplines, leading us to a deeper understanding, quantification capability, and simulation of a particular feature of the real-world problems, including the disciplines of physics, biology, chemistry, engineering, and economics. Unfortunately, it seldom happens that these equations have solutions that can be expressed in closed form, so it is common to seek approximate solutions by means of numerical methods. As a matter of terminology, stiff systems form a class of mathematical problems that appear frequently in the study of many real phenomena. They were first highlighted by Curtiss and Hirschfelder [1]. They are observed in the study of chemical kinetics, aerodynamics, ballistics, electrical circuit theory and other areas of applications [2]. The mathematical stiffness of a problem reflects the fact that various processes in the considered physical models have different rates. It results from the decaying of some of the solution components being more rapidly than other components as they contain the term \(e^{-\lambda t}\), \(\lambda >0\). However, many numerical and analytical techniques have been employed recently for solving stiff systems of ordinary differential equations including the homotopy perturbation method [3], the block method [4], the multistep method [5], and the variational iteration method [6]. Examples of another mathematical models and effective numerical solutions can be found in [7,8,9].

In the last decades, the topic of fractional calculus has attracted the attention of numerous researchers for its considerable importance in many applications such as fluid dynamics, viscoelasticity, physics, entropy theory and vibrations [10,11,12,13,14]. In this regard, many differential equations of integer order were generalized to fractional order, as well as various methods were developed to solve them. Recently, the Atangana-Baleanu fractional concept has been suggested as a novel fractional operator in the Liouville–Caputo sense based on the generalized Mittag-Leffler function; such fractional operator is with a non-singular and non-local kernel that has been introduced in order to better describe complex physical problems that follow at the same time the power and exponential decay law; see for example [15,16,17,18,19]. Thereby, approximate and analytical techniques have been introduced to obtain solutions of fractional stiff systems such as the homotopy analysis method [20], the homotopy perturbation method [21], and the multistage Bernstein polynomial method [22].

For the first time, this paper aims to utilize the residual power series (RPS) algorithm for solving fractional order stiff systems of the following form:

$$ D^{\beta _{i}} u_{i} ( t ) = f_{i} \bigl( t, u_{1} (t), u _{2} (t), \dots , u_{m} (t) \bigr), \quad n-1< \beta _{i} \leq n, n \in \mathbb{N}, $$
(1.1)

subject to the initial condition

$$ u_{i} ( 0 ) = a_{i,0}, $$
(1.2)

where \(t\geq 0\), \(a_{i}\) are real finite constants, \(f_{i}: [0,\infty ) \times \mathbb{R}^{m} \rightarrow \mathbb{R}\), \(i=1,2, \dots ,m\), are continuous real-valued functions on the domain of interest, which can be linear or nonlinear, \(D^{\beta _{i}}\) is the Caputo derivative fractional order \(\beta _{i}\), \(i=1,2, \dots ,m\), \(m \in \mathbb{N}\), and \(u_{i} ( t )\) are unknown analytical functions to be determined. Here, we assume that the fractional stiff systems (1.1) and (1.2) has unique smooth solution for \(t\geq 0\).

The RPS technique has been used in providing approximation numerical solutions for certain class of differential equations under uncertainty [23]. Later, the generalized Lane-Emden equation has been investigated numerically by utilizing the RPS method. Also, the method was applied successfully in solving composite and non-composite fractional DEs, and in predicting and representing multiplicity solutions to fractional boundary value problems [24, 25]. Furthermore, [26,27,28,29] assert that the RPS method is easy and powerful to construct power series solution for strongly linear and nonlinear equations without terms of perturbation, discretization, and linearization. Unlike the classical power series method, the FRPS method distinguishes itself in several important aspects such that it does not require making a comparison between the coefficients of corresponding terms and a recursion relation is not needed and provides a direct way to ensure the rate of convergence for series solution by minimizing the residual error related.

Bearing these ideas in mind, this work is organized as follows. In the next section, some basic definitions and preliminary remarks related to fractional calculus and generalized Taylor’s formula are described. Section 3 is devoted to establishing the FRPS algorithm for obtaining the approximate solutions for a class of stiff system of fractional order. Meanwhile, a description of the proposed method is presented. Stability and convergence analyses are also presented. Several numerical applications are given in Sect. 4 to illustrate the simplicity, accuracy, applicability and reliability of the presented method. Further, a comparison between the numerical results of the FRPS method and another approximate method, namely, the reproducing kernel Hilbert space method, has been given. Finally, a brief conclusion is given in the last section.

2 Fundamentals concepts

The purpose of this section is to present some basic definitions and facts related to fractional calculus and fractional power series, which are used in subsequent sections of this study.

Definition 2.1

([30])

The Riemann–Liouville fractional integral operator of order \(\beta >0\) is defined by

$$ \bigl( J_{a}^{\beta } u \bigr) ( t ) = \frac{1}{ \varGamma (\beta )} \int _{a}^{t} u(\xi ) (t-\xi )^{\beta -1} \,d\xi ,\quad t>0. $$
(2.1)

For \(\beta =0\), it yields \(( J_{a}^{\beta } u ) ( t ) =u(t)\).

Definition 2.2

([30])

For \(n-1<\beta <n\), \(n \in \mathbb{N}\). The Caputo fractional derivative operator of order β is defined by

$$ \bigl( D_{a}^{\beta } u \bigr) ( t ) = \frac{1}{ \varGamma (n-\beta )} \int _{a}^{t} u^{(n)} (\xi ) (t-\xi )^{n-\beta -1} \,d \xi ,\quad t>0. $$
(2.2)

Specially, \(D_{a}^{\beta } u ( t ) = u^{(n)} (t)\) for \(\beta =n\).

The operators \(D_{a}^{\beta }\) and \(J_{a}^{\beta }\) satisfy the following properties:

$$\begin{aligned}& \bullet \quad D_{a}^{\beta } c=0\quad \text{for any constant }c \in \mathbb{R}. \end{aligned}$$
(2.3)
$$\begin{aligned}& \begin{gathered}[b] \bullet \quad D_{a}^{\beta } (t-a)^{q} = \frac{\varGamma (q+1)}{\varGamma (q-\beta +1)} (t-a)^{q-\beta }\quad \text{for }n-1< \beta < n, q>n- 1,\\ \hphantom{\bullet \quad}\text{and is equal to zero otherwise.} \end{gathered} \end{aligned}$$
(2.4)
$$\begin{aligned}& \bullet \quad J_{a}^{\beta } J_{a}^{\alpha } u= J_{a}^{\alpha } J_{a} ^{\beta } u= J_{a}^{\alpha +\beta } u. \end{aligned}$$
(2.5)
$$\begin{aligned}& \bullet \quad J_{a}^{\beta } c= \frac{c}{\varGamma (\beta +1)} (t-a)^{ \beta } \quad \text{for any constant }c \in \mathbb{R}. \end{aligned}$$
(2.6)
$$\begin{aligned}& \begin{gathered}[b] \bullet \quad \bigl( J_{a}^{\beta } D_{a}^{\beta } u \bigr) ( t ) =u ( t ) - \sum_{k=0}^{n-1} \frac{u^{ ( k )} ( a )}{k!} (t-a)^{k}\\ \hphantom{\bullet \quad }\mbox{for $u\in C^{n} [ a,b ]$ and $n-1< \beta \leq n$, with $n \in \mathbb{N}$.} \\ \hphantom{\bullet \quad }\mbox{Moreover, if $\beta \geq 0$, $u\in C [ a,b ]$, then $D^{\beta } J^{\beta } u ( t ) =u(t)$.} \end{gathered} \end{aligned}$$
(2.7)

Definition 2.3

([26])

A power series (PS) expansion at \(t= t_{0}\) of the following form:

$$ \sum_{m=0}^{\infty } a_{m} (t- t_{0} )^{m\beta } = a_{0} + a_{1} ( t- t_{0} )^{\beta } + a_{1} ( t- t_{0} ) ^{2\beta } +\cdots $$

for \(n-1<\beta \leq n\), \(n \in \mathbb{N} \) and \(t\leq t_{0}\), is called the fractional power series (FPS).

Theorem 2.1

([25])

There are only three possibilities for the FPS \(\sum_{m=0}^{\infty } a_{m} (t- t_{0} )^{m\beta }\), which are:

  1. (1)

    The series converges only for \(t= t_{0}\). That is; the radius of convergence equals zero.

  2. (2)

    The series converges for all \(t\geq t_{0}\). That is; the radius of convergence equals ∞.

  3. (3)

    The series converges for \(t\in [ t_{0}, t_{0} +R ) \), for some positive real number R and diverges for \(t> t_{0} +R\). Here, R is the radius of convergence for the FPS.

Theorem 2.2

([25])

Suppose that \(u(t)\) has a FPS representation at \(t= t_{0}\) of the form

$$ u ( t ) = \sum_{m=0}^{\infty } c_{m} ( t- t_{0} ) ^{m\beta }. $$
(2.8)

If \(u(t)\in C[ t_{0}, t_{0} +R)\), and \(D^{m\beta } u ( t ) \in C( t_{0}, t_{0} +R)\), for \(m=0,1,2,\dots \), then the coefficients \(c_{m}\) will be of the form \(c_{m} = \frac{\mathcal{D}_{t}^{m\beta } u ( t_{0} )}{\varGamma ( m\beta +1 )} \), where \(\mathcal{D}^{m\beta } = \mathcal{D}^{\beta } \cdot \mathcal{D}^{\beta } \cdots \mathcal{D}^{\beta }\) (m times).

3 Fractional residual power series method

In this section, we are intending to use the FRPS method for solving a class of stiff systems of fractional order described in (1.1) and (1.2) through substituting the FPS expansions within truncation residual functions will be used. To do so, we assume that the FPS solution of the fractional stiff systems (1.1) and (1.2) at \(t=0\) has the following form:

$$ u_{i} ( t ) = \sum_{n =0}^{\infty } a_{i, n} \frac{t^{n \beta _{i}}}{\varGamma (1+ n \beta _{i} )}. $$
(3.1)

The aim of the FRPS algorithm is obtaining a supportive approximate solution to the proposed model. Thus, by using the initial conditions in Eq. (1.2), \(u_{i} ( 0 ) = a_{i,0}\), as initial iterative approximation of \(u_{i} ( t )\), Eq. (3.1) can be written as

$$ u_{i} ( t ) = a_{i,0} + \sum_{n =1}^{\infty } a_{i, n} \frac{t ^{n \beta _{i}}}{\varGamma (1+ n \beta _{i} )}. $$
(3.2)

Consequently, the suggested solution \(u_{i} ( t )\) can be approximated by the following kth-truncated series:

$$ u_{i, k} ( t ) = a_{i,0} + \sum_{n =1}^{k} a_{i, n} \frac{t ^{n \beta _{i}}}{\varGamma (1+ n \beta _{i} )}. $$
(3.3)

According to the RPS algorithm, the residual function will be defined as

$$ \operatorname{Res} {u_{i}} ( t ) = D^{\beta _{i}} u_{i} ( t ) - f_{i} \bigl( t, u_{1} ( t ), u_{2} ( t ), \dots , u_{m} ( t ) \bigr),\quad i=1,2,\dots ,m,0\leq t< R. $$
(3.4)

Therefore, the kth-residual function \(\operatorname{Res} {u_{i,k}} ( t )\), for \(k=1,2,3,\dots ,n\), can be given by

$$ \operatorname{Res} {u_{i,k}} ( t ) = D^{\beta _{i}} u_{i,k} ( t ) - f_{i} \bigl( t, u_{1,k} ( t ), u_{2,k} ( t ), \dots , u_{m,k} ( t ) \bigr),\quad i=1,2,\dots ,m. $$
(3.5)

As in [25,26,27], we have \(\operatorname{Res} {u_{i}} ( t ) =0\), and \(\lim_{k\rightarrow \infty } \operatorname{Res} {u_{i,k}} ( t ) = \operatorname{Res} {u_{i}} ( t )\), for each \(t\geq 0\). As a matter of fact, this yields \(D^{n\beta _{i}} \operatorname{Res} {u_{i,k}} ( t ) =0\) for \(n=0,1,2,\dots ,k\), \(i=1,2,\dots ,m\), and \(D^{n\beta _{i}} \operatorname{Res} {u_{i}} ( 0 ) = D^{n\beta _{i}} \operatorname{Res} {u_{i,k}} ( 0 ) =0\). As a result, to determine the unknown coefficients of Eq. (3.3), one can seek the solution of the following fractional equation:

$$ D^{(k-1)\beta _{i}} \operatorname{Res} {u_{i,k}} ( 0 ) =0,\quad i=1,2,\dots ,m, k=1,2,3, \dots . $$
(3.6)

To illustrate the basic idea of the FRPS algorithm for finding the first unknown coefficient \(a_{i,1}\), we substitute \(u_{i,1} ( t ) = a_{i,0} + a_{i,1} \frac{t^{\beta _{i}}}{\varGamma (1+ \beta _{i} )}\) in the kth-residual function Eq. (3.5) with \(k=1\), \(\operatorname{Res} {u_{i,1}} ( t )\), to get

$$ \begin{aligned} &\operatorname{Res} {u_{i},1} ( t ) \\ &\quad = D^{\beta _{i}} u_{i,1} ( t ) - f_{i} \bigl( t, u_{1,1} ( t ), u_{2,1} ( t ), \dots , u_{m,1} ( t ) \bigr) \\ &\quad = D^{\beta _{i}} \biggl( a_{i,0} + a_{i,1} \frac{t^{\beta _{i}}}{\varGamma ( 1+ \beta _{i} )} \biggr) \\ &\qquad {} - f_{i} \biggl( t, a_{1,0} + a_{1,1} \frac{t ^{\beta _{i}}}{\varGamma ( 1+ \beta _{i} )}, a_{2,0} + a_{2,1} \frac{t^{\beta _{i}}}{\varGamma ( 1+ \beta _{i} )}, \dots , a _{m,0} + a_{m,1} \frac{t^{\beta _{m}}}{\varGamma ( 1+ \beta _{m} )} \biggr). \end{aligned} $$

Based on Eq. (3.6) and then using the fact \(\operatorname{Res} {u_{i,1}} ( 0 ) =0\), it yields \(a_{i,1} = f_{i} ( 0, a_{1,0}, a_{2,0}, \dots , a_{m,0} )\). Therefore, the first FRPS approximated of IVPs (1.1) and (1.2) will be

$$ u_{i,1} ( t ) = a_{i,0} + f_{i} ( 0, a_{1,0}, a _{2,0}, \dots , a_{m,0} ) \frac{t^{\beta _{i}}}{\varGamma (1+ \beta _{i} )}. $$

Likewise, to obtain the second unknown coefficient \(a_{i,2}\), we substitute \(u_{i,2} ( t ) = a_{i,0} + a_{i,1} \frac{t ^{\beta _{i}}}{\varGamma (1+ \beta _{i} )} + a_{i,2} \frac{t^{2\beta _{i}}}{ \varGamma (1+ 2\beta _{i} )}\) in the kth-residual function Eq. (3.5) with \(k=2\), \(\operatorname{Res} {u_{i,2}} ( t )\), to get

$$ \begin{aligned} \operatorname{Res} {u_{i},2} ( t )& = D^{\beta _{i}} u_{i,2} ( t ) - f_{i} \bigl( t, u_{1,2} ( t ), u_{2,2} ( t ), \dots , u_{m,2} ( t ) \bigr) \\ & = D^{\beta _{i}} \biggl( a_{i,0} + a_{i,1} \frac{t^{\beta _{i}}}{\varGamma ( 1+ \beta _{i} )} + a_{i,2} \frac{t^{2\beta _{i}}}{\varGamma ( 1+ 2\beta _{i} )} \biggr) \\ &\quad {} - f_{i} \biggl( t, a_{1,0} + a_{1,1} \frac{t ^{\beta _{i}}}{\varGamma ( 1+ \beta _{i} )} + a_{1,2} \frac{t ^{2\beta _{i}}}{\varGamma ( 1+ 2\beta _{i} )}, \dots , \\ &\quad {} a_{m,0} + a_{m,1} \frac{t^{\beta _{m}}}{\varGamma ( 1+ \beta _{m} )} + a_{m,2} \frac{t^{2\beta _{i}}}{\varGamma ( 1+ 2\beta _{i} )} \biggr). \end{aligned} $$

Therefore, applying the operator \(D^{\beta _{i}}\) on \(\operatorname{Res} {u_{i},2} ( t )\) will show that

$$ \begin{aligned} D^{\beta _{i}} \operatorname{Res} {u_{i},2} ( t ) &= D^{2\beta _{i}} \biggl( a_{i,0} + a_{i,1} \frac{t^{\beta _{i}}}{\varGamma ( 1+ \beta _{i} )} + a_{i,2} \frac{t ^{2\beta _{i}}}{\varGamma ( 1+ 2\beta _{i} )} \biggr) \\ &\quad {} - D ^{\beta _{i}} \biggl( f_{i} \biggl( t, a_{1,0} + a_{1,1} \frac{t^{\beta _{i}}}{\varGamma ( 1+ \beta _{i} )} + a_{1,2} \frac{t^{2\beta _{i}}}{\varGamma ( 1+ 2\beta _{i} )}, \dots , \\ &\quad a_{m,0} + a _{m,1} \frac{t^{\beta _{m}}}{\varGamma ( 1+ \beta _{m} )} + a _{m,2} \frac{t^{2\beta _{i}}}{\varGamma ( 1+ 2\beta _{i} )} \biggr) \biggr). \end{aligned} $$

Consequently, by using the fact \(D^{\beta _{i}} \operatorname{Res} {u_{i,2}} ( 0 ) =0\), the second unknown coefficient \(u_{i,2}\) will be given by \(u_{i,2} = f_{i} ( 0, a_{1,1}, a_{2,1}, \dots , a_{m,1} )\). Therefore, the second FRPS approximated of IVPs (1.1) and (1.2) will be as

$$ u_{i,1} ( t ) = a_{i,0} + f_{i} ( 0, a_{1,0}, a _{2,0}, \dots , a_{m,0} ) \frac{t^{\beta _{i}}}{\varGamma (1+ \beta _{i} )} + f_{i} ( 0, a_{1,1}, a_{2,1}, \dots , a_{m,1} ) \frac{t^{2\beta _{i}}}{\varGamma ( 1+ 2\beta _{i} )}. $$

By repeating the same routine until arbitrary order, the other unknown coefficients, \(a_{i,k}\), will be obtained [31, 32].

Lemma 3.1

Suppose that \(u ( t ) \in C [t_{0}, t _{0} +R)\), \(R>0\), \(D_{t_{0}}^{j\beta } u(t)\in C( t_{0}, t_{0} +R)\), and \(0<\beta \leq 1\). Then, for any \(j \in \mathbb{N} \), we have

$$ \bigl( J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } u \bigr) ( t ) - \bigl( J_{t_{0}}^{(j+1)\beta } D_{t_{0}}^{(j+1)\beta } u \bigr) ( t ) = \frac{D_{t_{0}}^{j\beta } u( t_{0} )}{ \varGamma (j\beta +1)} (t- t_{0} )^{j\beta }. $$

Proof

Using property (2.5) of the fractional integral operator, we can write

$$\begin{aligned} \bigl( J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } u \bigr) ( t ) - \bigl( J_{t_{0}}^{(j+1)\beta } D_{t_{0}}^{(j+1)\beta } u \bigr) ( t ) &= \bigl( J_{t_{0}}^{j\beta } D_{t_{0}} ^{j\beta } u \bigr) ( t ) - \bigl( J_{t_{0}}^{\beta } J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } D_{t_{0}}^{\beta } u \bigr) ( t ) \\ &= \bigl( J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } u \bigr) ( t ) - \bigl( J_{t_{0}}^{\beta } \bigl( J_{t_{0}}^{j\beta } D_{t_{0}} ^{j\beta } \bigr)D_{t_{0}}^{\beta } u \bigr) ( t ) \\ &= J_{t_{0}}^{j\beta } \bigl[ \bigl( D_{t_{0}}^{j\beta } u \bigr) ( t ) - \bigl( J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } \bigr) \bigl( D_{t_{0}}^{\beta } u \bigr) \bigr] ( t ). \end{aligned}$$

Applying (2.7) for \(( J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } ) ( D_{t_{0}}^{\beta } u ) ( t )\), we get

$$\begin{aligned}& \bigl( J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } u \bigr) ( t ) - \bigl( J_{t_{0}}^{ ( j+1 ) \beta } D_{t_{0}} ^{ ( j+1 ) \beta } u \bigr) ( t ) \\& \quad = J_{t _{0}}^{j\beta } \bigl[ \bigl( D_{t_{0}}^{j\beta } u \bigr) ( t ) - \bigl( D_{t_{0}}^{j\beta } u \bigr) ( t ) + D_{t_{0}}^{j\beta } u ( t_{0} ) \bigr] \\& \quad = J_{t_{0}}^{j\beta } \bigl[ D_{t_{0}}^{j\beta } u ( t_{0} ) \bigr] = \frac{D_{t_{0}}^{j\beta } u ( t_{0} )}{ \varGamma (j\beta +1)} (t- t_{0} )^{j\beta },\quad \mbox{by using (2.6) with } c=D_{t_{0}}^{j\beta } u ( t _{0} ). \end{aligned}$$

 □

Theorem 3.1

Let \(u ( t )\) has the FPS in (2.8) with radius of convergence \(R>0\), and suppose that \(u ( t ) \in C [t_{0}, t_{0} +R)\), \(D_{t_{0}}^{j\beta } u ( t ) \in C ( t_{0}, t_{0} +R )\) for \(j=0,1,2, \dots , N+1\). Then

$$ u ( t ) = u_{N} ( t ) + R_{N} ( \zeta ), $$
(3.7)

where \(u_{N} ( t ) = \sum_{j =0}^{{N}} \frac{D _{t_{0}}^{j\beta } u ( t_{0} )}{\varGamma (j\beta +1)} (t- t _{0} )^{j\beta }\) and \(R_{N} ( \zeta ) = \frac{D_{t_{0}} ^{(N+1)\beta } u ( \zeta )}{\varGamma ((N+1)\beta +1)} (t- t _{0} )^{(N+1)\beta }\), for some \(\zeta \in ( t_{0},t)\).

Proof

First, we notice that

$$ u ( t ) - \bigl( J_{t_{0}}^{ ( N+1 ) \beta } D_{t_{0}}^{ ( N+1 ) \beta } u \bigr) ( t ) = \sum_{j=0}^{N} \bigl[ \bigl( J_{t_{0}}^{j\beta } D_{t_{0}}^{j\beta } u \bigr) ( t ) - \bigl( J_{t_{0}}^{ ( j+1 ) \beta } D_{t_{0}}^{ ( j+1 ) \beta } u \bigr) ( t ) \bigr]. $$

Using Lemma 3.1, we get

$$ u ( t ) - \bigl( J_{t_{0}}^{ ( N+1 ) \beta } D_{t_{0}}^{ ( N+1 ) \beta } u \bigr) ( t ) = \sum_{j =0}^{{N}} \frac{D_{t_{0}}^{j\beta } u ( t_{0} )}{ \varGamma (j\beta +1)} (t- t_{0} )^{j\beta }. $$
(3.8)

So,

$$ u ( t ) = \sum_{j =0}^{{N}} \frac{D_{t_{0}}^{j \beta } u ( t_{0} )}{\varGamma (j\beta +1)} (t- t_{0} )^{j \beta } + \bigl( J_{t_{0}}^{ ( N+1 ) \beta } D_{t_{0}} ^{ ( N+1 ) \beta } u \bigr) ( t ). $$

But

$$\begin{aligned}& \bigl( J_{t_{0}}^{ ( N+1 ) \beta } D_{t_{0}}^{ ( N+1 ) \beta } u \bigr) ( t ) \\& \quad = J_{t_{0}}^{ ( N+1 ) \beta } \bigl( D_{t_{0}}^{ ( N+1 ) \beta } u \bigr) ( t ) \\& \quad = \frac{1}{\varGamma ( ( N+1 ) \beta )} \int _{t_{0}}^{t} D_{t_{0}}^{ ( N+1 ) \beta } u ( \tau ) (t- \tau )^{ ( N+1 ) \beta -1} \,d\tau \\& \quad = \frac{D_{t_{0}}^{ ( N+1 ) \beta } u(\zeta )}{\varGamma ( ( N+1 ) \beta )} \int _{t_{0}}^{t} (t- \tau )^{ ( N+1 ) \beta -1} \,d\tau \quad (\text{by the mean value theorem for integrals}) \\& \quad = \frac{D_{t_{0}}^{ ( N+1 ) \beta } u(\zeta )}{\varGamma ( ( N+1 ) \beta )} \frac{(t- t_{0} )^{(N+1) \beta }}{ ( N+1 ) \beta } \\& \quad = \frac{D_{t_{0}}^{(N+1)\beta } u ( \zeta )}{\varGamma ((N+1) \beta +1)} (t- t_{0} )^{(N+1)\beta }. \end{aligned}$$

Finally, we substitute in (3.8) to get (3.7). □

Remark 1

The formula of \(u_{N} ( t ) \) in the previous theorem gives an approximation of \(u ( t )\), and \(R_{N} ( \zeta )\) is the truncation (the remainder) error that results from approximating \(u ( t ) \) by \(u_{N} ( t ) \). Moreover, if \(\vert D_{t_{0}}^{(N+1) \beta } u ( \zeta ) \vert < M\) on \([ t_{0}, t_{0} +R)\), then the upper bound of the error can be computed by

$$ \bigl\vert R_{N} ( \zeta ) \bigr\vert \leq \biggl\vert \sup _{t\in [ t_{0}, t_{0} +R]} \frac{M (t- t_{0} )^{(N+1)\beta }}{\varGamma ((N+1)\beta +1)} \biggr\vert . $$

Remark 2

For solving stiff system in (1.1) using the FRPS technique, we put

$$ u_{i} ( t ) = \sum_{n =0}^{\infty } a_{i, n} \frac{t^{n \beta _{i}}}{\varGamma (1+ n \beta _{i} )} \quad \forall {i}=1,2,\dots ,m. $$
(3.9)

So, if we assume that each \(u_{i} ( t )\) has the FPS in (3.9) with radius of convergence \(R_{i} >0\), and that \(u_{i} ( t ) \in C [ 0, R_{i} )\), \(D_{0}^{j \beta _{i}} u_{i} ( t ) \in C ( 0, R_{i} )\) for \(j=0,1,2, \dots , N+1\), then \(u_{i} ( t ) = u_{iN} ( t ) + R_{iN} ( \zeta )\), ∀i. The approximate solution \(\boldsymbol{U}_{\boldsymbol{N}} ( t ) = ( u_{1N} ( t ), u_{2N} ( t ),\dots , u _{mN} ( t ) )^{T}\) converges to the exact solution \(\boldsymbol{U} ( t ) = ( u_{1} ( t ), u _{2} ( t ),\dots , u_{m} ( t ) )^{T}\) as \(N\rightarrow \infty \), \(\forall t\in [ 0,R ) \), where \(R= \min \{ R_{1}, R_{2},\dots , R_{m} \}\) and the remainder error equals

$$ R_{N} ( \zeta ) = \max \bigl\{ R_{1N} ( \zeta ), R_{2N} ( \zeta ), \dots , R_{mN} ( \zeta ) \bigr\} . $$

4 Numerical applications

To confirm the high degree of accurateness and efficiency of the proposed FRPS method for solving stiff systems of fractional order, numerical patterns and examples are applied in this section. Also, we make a comparison with another numerical technique, namely, the reproducing kernel Hilbert space method. The reader can find a description and applications for this method in [33,34,35,36]. Computations were performed by using the Mathematica package.

Example 4.1

Consider the following fractional-order stiff system:

$$\begin{aligned}& D_{0}^{\alpha } u ( t ) =-u ( t ) +95v ( t ),\quad 0< \alpha \leq 1, \\& D_{0}^{\alpha } v ( t ) =-u ( t ) -97v ( t ), \end{aligned}$$

subject to the initial conditions

$$ u ( 0 ) =1,\qquad v ( 0 ) =1. $$

The exact solution of this system when \(\alpha =1\) is

$$ u ( t ) = \frac{1}{47} \bigl(95 e^{-2t} -48 e^{-96t} \bigr),\qquad v ( t ) = \frac{1}{47} \bigl(48 e^{-96t} - e^{-2t} \bigr). $$

For \(k=1\), the first truncated power series approximations from Eq. (3.3) have the forms

$$ u_{1} (t)=1+ \frac{c_{1}}{\varGamma (1+\alpha )} t^{\alpha },\qquad v_{1} (t)=1+ \frac{d_{1}}{\varGamma (1+\alpha )} t^{\alpha } $$

and the first residual functions are

$$\begin{aligned}& \begin{aligned} \operatorname{Res} {u_{1}} ( t ) &= D_{0}^{\alpha } u_{1} ( t ) + u_{1} ( t ) -95 v_{1} ( t ) \\ &= D_{0}^{\alpha } \biggl( 1+ \frac{c_{1}}{\varGamma ( 1+\alpha )} t^{\alpha } \biggr) + 1+ \frac{c_{1}}{\varGamma ( 1+\alpha )} t^{\alpha } -95 \biggl(1+ \frac{d _{1}}{\varGamma (1+\alpha )} t^{\alpha } \biggr), \end{aligned} \\& \begin{aligned} \operatorname{Res} {v_{1}} ( t ) &= D_{0}^{\alpha } v_{1} ( t ) + u_{1} ( t ) -95 v_{1} ( t ) \\ &= D_{0}^{\alpha } \biggl( 1+ \frac{d_{1}}{\varGamma ( 1+\alpha )} t^{\alpha } \biggr) + 1+ \frac{c_{1}}{\varGamma ( 1+\alpha )} t^{\alpha } +97 \biggl(1+ \frac{d _{1}}{\varGamma (1+\alpha )} t^{\alpha } \biggr). \end{aligned} \end{aligned}$$

From (3.6), \(\operatorname{Res} {u_{1}} ( 0 ) =0\) and \(\operatorname{Res} {v_{1}} ( 0 ) =0\), which gives \(c_{1} =94 \) and \(d_{1} =-98\). So

$$ u_{1} ( t ) = 1 + \frac{94 t^{\alpha }}{\varGamma [ 1 + \alpha ]}\quad \text{and}\quad v_{1} ( t ) = 1 - \frac{98 t ^{\alpha }}{\varGamma [ 1 + \alpha ]}. $$

For \(k=2\), the second truncated power series approximations have the forms

$$ u_{2} ( t ) =1+ \frac{94}{\varGamma ( 1+\alpha )} t^{\alpha } + \frac{c_{2}}{ \varGamma ( 1+2\alpha )} t^{2\alpha },\qquad v_{2} ( t ) =1- \frac{98}{\varGamma (1+\alpha )} t^{\alpha } + \frac{d_{2}}{ \varGamma ( 1+2\alpha )} t^{2\alpha }, $$

and the second residual functions are

$$\begin{aligned}& \begin{aligned} \operatorname{Res} {u_{2}} ( t ) &= D_{0}^{\alpha } u_{2} ( t ) + u_{2} ( t ) -95 v_{2} ( t ) \\ & = D_{0}^{ \alpha } \biggl( 1+ \frac{94}{\varGamma ( 1+\alpha )} t^{ \alpha } + \frac{c_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \biggr) + 1+ \frac{94}{\varGamma ( 1+\alpha )} t^{\alpha } + \frac{c_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \\ &\quad {}-95 \biggl( 1- \frac{98}{\varGamma ( 1+\alpha )} t^{\alpha } + \frac{d _{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \biggr), \end{aligned} \\& \begin{aligned} \operatorname{Res} {v_{2}} ( t ) &= D_{0}^{\alpha } u_{2} ( t ) + u_{2} ( t ) -95 v_{2} ( t ) \\ & = D_{0}^{ \alpha } \biggl( 1+ \frac{94}{\varGamma ( 1+\alpha )} t^{ \alpha } + \frac{c_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \biggr) + 1+ \frac{94}{\varGamma ( 1+\alpha )} t^{\alpha } + \frac{c_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \\ &\quad {} +97 \biggl(1- \frac{98}{\varGamma (1+\alpha )} t^{\alpha } + \frac{d_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \biggr). \end{aligned} \end{aligned}$$

From (3.6), \(D_{0}^{\alpha } \operatorname{Res} {u_{2}} ( 0 ) =0\) and \(D _{0}^{\alpha } \operatorname{Res} {v_{2}} ( 0 ) =0\), which gives \(c_{2} =-9404\) and \(d_{2} = 9412\). So

$$ \begin{gathered} u_{2} ( t ) = 1 + \frac{94 t^{\alpha }}{\varGamma [ 1 + \alpha ]} - \frac{9404 t^{2\alpha }}{\varGamma [ 1 + 2\alpha ]}\quad \text{and}\\ v_{2} ( t ) = 1 - \frac{98 t^{\alpha }}{ \varGamma [ 1 + \alpha ]} + \frac{9412 t^{2\alpha }}{\varGamma [ 1 + 2 \alpha ]}. \end{gathered} $$

Continuing this process, we get

$$\begin{aligned}& u_{3} ( t ) = 1 + \frac{94 t^{\alpha }}{\varGamma [ 1 + \alpha ]} - \frac{9404 t^{2 \alpha }}{\varGamma [ 1 + 2 \alpha ]} + \frac{903\text{,}544 t^{3 \alpha }}{\varGamma [ 1 + 3 \alpha ]}, \\& v_{3} ( t ) = 1 - \frac{98 t^{\alpha }}{\varGamma [ 1 + \alpha ]} + \frac{9412 t^{2 \alpha }}{\varGamma [ 1 + 2 \alpha ]} - \frac{903\text{,}560 t^{3 \alpha }}{\varGamma [ 1 + 3 \alpha ]}, \\& u_{4} ( t ) = 1 + \frac{94 t^{\alpha }}{\varGamma [ 1 + \alpha ]} - \frac{9404 t^{2 \alpha }}{\varGamma [ 1 + 2 \alpha ]} + \frac{903\text{,}544 t^{3 \alpha }}{\varGamma [ 1 + 3 \alpha ]} - \frac{86\text{,}741\text{,}744 t^{4 \alpha }}{\varGamma [ 1 + 4 \alpha ]}, \\& v_{4} ( t ) = 1 - \frac{98 t^{\alpha }}{\varGamma [ 1 + \alpha ]} + \frac{9412 t^{2 \alpha }}{\varGamma [ 1 + 2 \alpha ]} - \frac{903\text{,}560 t^{3 \alpha }}{\varGamma [ 1 + 3 \alpha ]} + \frac{86\text{,}741\text{,}776 t^{4 \alpha }}{\varGamma [ 1 + 4 \alpha ]}, \\& u_{5} ( t ) = 1 + \frac{94 t^{\alpha }}{\varGamma [ 1 + \alpha ]} - \frac{9404 t^{2 \alpha }}{\varGamma [ 1 + 2 \alpha ]} + \frac{903\text{,}544 t^{3 \alpha }}{\varGamma [ 1 + 3 \alpha ]} - \frac{86\text{,}741\text{,}744 t^{4 \alpha }}{\varGamma [ 1 + 4 \alpha ]} + \frac{8\text{,}327\text{,}210\text{,}464 t^{5 \alpha }}{\varGamma [ 1 + 5 \alpha ]}, \\& v_{5} ( t ) = 1 - \frac{98 t^{\alpha }}{\varGamma [ 1 + \alpha ]} + \frac{9412 t^{2 \alpha }}{\varGamma [ 1 + 2 \alpha ]} - \frac{903\text{,}560 t^{3 \alpha }}{\varGamma [ 1 + 3 \alpha ]} + \frac{86\text{,}741\text{,}776 t^{4 \alpha }}{\varGamma [ 1 + 4 \alpha ]} - \frac{8\text{,}327\text{,}210\text{,}528 t^{5 \alpha }}{\varGamma [ 1 + 5 \alpha ]}. \end{aligned}$$

Some numerical results and tabulated data for \(\alpha =1\) and \(k=200\) are given in Table 1 using the FRPS method. In Table 2, numerical results for the same example using the RKHS method have been given. Figures 1 and 2 show the comparison between the behavior of the exact solution and the approximate solution using the FRPS and the RK methods, respectively, for \(\alpha =1\) with step size 0.2.

Figure 1
figure 1

The behavior of FRPS solution of Example 4.1: __ exact; …. approximated

Full size image
Figure 2
figure 2

The behavior of RK solution of Example 4.1: __ exact; …. approximated

Full size image
Table 1 Numerical results of the FRPS solutions at different values of t of Example 4.1
Full size table
Table 2 Numerical results of the RK solutions at different values of t of Example 4.1
Full size table

Example 4.2

Consider the nonlinear fractional-order stiff system:

$$\begin{aligned}& D_{0}^{\alpha } u ( t ) =-1002u ( t ) +1000 v^{2} ( t ),\quad 0< \alpha \leq 1 \\& D_{0}^{\alpha } v ( t ) =u ( t ) -v ( t ) - v^{2} ( t ),\quad t\in [ 0,2 ], \end{aligned}$$

subject to the initial conditions \(u ( 0 ) =1\), \(v ( 0 ) =1\).

The exact solution of this system when \(\alpha =1\) is \(u ( t ) = e^{-2t}\), \(v ( t ) = e^{-t}\).

For \(k=1\), the first truncated power series approximations have the forms

$$ u_{1} (t)=1+ \frac{c_{1}}{\varGamma (1+\alpha )} t^{\alpha },\qquad v_{1} (t)=1+ \frac{d_{1}}{\varGamma (1+\alpha )} t^{\alpha } $$

and the first residual functions are

$$\begin{aligned} &\operatorname{Res} {u_{1}} ( t ) \\ &\quad = D_{0}^{\alpha } u_{1} ( t ) +1002 u_{1} ( t ) -1000 v_{1}^{2} ( t ) \\ &\quad = D_{0}^{\alpha } \biggl( 1+ \frac{c_{1}}{\varGamma ( 1+\alpha )} t^{\alpha } \biggr) + 1002 \biggl( 1+ \frac{c_{1}}{\varGamma ( 1+\alpha )} t^{ \alpha } \biggr) -1000 \biggl(1+ \frac{d_{1}}{\varGamma (1+\alpha )} t^{ \alpha } \biggr)^{2}, \\ &\operatorname{Res} {v_{1}} ( t ) \\ &\quad = D_{0}^{\alpha } v_{1} ( t ) - u_{1} ( t ) + v_{1} ( t ) + v_{1}^{2} ( t ) \\ &\quad = D_{0}^{\alpha } \biggl( 1+ \frac{d_{1}}{\varGamma ( 1+\alpha )} t^{\alpha } \biggr) - \biggl( 1+ \frac{c_{1}}{\varGamma ( 1+\alpha )} t^{\alpha } \biggr) \\ &\qquad {}+ \biggl( 1+ \frac{d_{1}}{\varGamma ( 1+\alpha )} t^{ \alpha } \biggr)+ \biggl(1+ \frac{d_{1}}{\varGamma (1+\alpha )} t^{\alpha } \biggr)^{2}. \end{aligned}$$

From (3.6), \(\operatorname{Res} {u_{1}} ( 0 ) =0\) and \(\operatorname{Res} {v_{1}} ( 0 ) =0\), which gives \(c_{1} =-2\) and \(d_{1} =-1\). So

$$ u_{1} ( t ) = 1 - \frac{2 t^{\alpha }}{\varGamma [ 1 + \alpha ]}\quad \text{and}\quad v_{1} ( t ) = 1 - \frac{t^{ \alpha }}{\varGamma [ 1 + \alpha ]}. $$

For \(k=2\), the second truncated power series approximations have the forms

$$ u_{2} ( t ) =1- \frac{2}{\varGamma ( 1+\alpha )} t^{\alpha } + \frac{c_{2}}{ \varGamma ( 1+2\alpha )} t^{2\alpha },\qquad v_{2} ( t ) =1- \frac{1}{\varGamma (1+\alpha )} t^{\alpha } + \frac{d_{2}}{ \varGamma ( 1+2\alpha )} t^{2\alpha }, $$

and the second residual functions are

$$\begin{aligned} &\operatorname{Res} {u_{2}} ( t ) \\ &\quad = D_{0}^{\alpha } u_{2} ( t ) +1002 u_{2} ( t ) -1000 v_{2}^{2} ( t ) \\ &\quad = D_{0}^{\alpha } \biggl(1- \frac{2}{\varGamma ( 1+\alpha )} t ^{\alpha } + \frac{c_{2}}{\varGamma ( 1+2\alpha )} t^{2 \alpha } \biggr)+1002 \biggl(1- \frac{2}{\varGamma ( 1+\alpha )} t^{ \alpha } + \frac{c_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \biggr) \\ &\qquad {}-1000 \biggl(1- \frac{1}{\varGamma (1+\alpha )} t^{\alpha } + \frac{d_{2}}{ \varGamma ( 1+2\alpha )} t^{2\alpha } \biggr)^{2}, \\ &\operatorname{Res} {v_{2}} ( t ) \\ &\quad = D_{0}^{\alpha } v_{2} ( t ) - u_{2} ( t ) + v_{2} ( t ) + v_{2}^{2} ( t ) \\ &\quad = D_{0}^{\alpha } \biggl(1- \frac{1}{\varGamma (1+\alpha )} t^{\alpha } + \frac{d _{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \biggr)- \biggl(1- \frac{2}{ \varGamma ( 1+\alpha )} t^{\alpha } + \frac{c_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } \biggr) \\ &\qquad {}+1- \frac{1}{\varGamma (1+ \alpha )} t^{\alpha } + \frac{d_{2}}{\varGamma ( 1+2\alpha )} t^{2\alpha } + \biggl(1- \frac{1}{ \varGamma (1+\alpha )} t^{\alpha } + \frac{d_{2}}{\varGamma ( 1+2 \alpha )} t^{2\alpha } \biggr)^{2}. \end{aligned}$$

From (3.6), \(D_{0}^{\alpha } \operatorname{Res} {u_{2}} ( 0 ) =0\) and \(D _{0}^{\alpha } \operatorname{Res} {v_{2}} ( 0 ) =0\), which gives \(c_{2} = 4\) and \(d_{2} = 1\). So

$$ u_{2} ( t ) = 1- \frac{2 t^{\alpha }}{\varGamma [1+\alpha ]} + \frac{4 t^{2\alpha }}{ \varGamma [1+2\alpha ]}\quad \text{and}\quad v_{2} ( t ) = 1- \frac{t^{ \alpha }}{\varGamma [1+\alpha ]} + \frac{t^{2\alpha }}{\varGamma [1+2\alpha ]}. $$

Continuing this process, we get

$$\begin{aligned}& u_{3} ( t ) = 1 - \frac{2 t^{\alpha }}{\varGamma [ 1 + \alpha ]} + \frac{4 t^{2\alpha }}{\varGamma [ 1 + 2\alpha ]} - \frac{8 t ^{3\alpha } ( 251 \varGamma [ 1 + \alpha ]^{2} - 125 \varGamma [ 1 + 2 \alpha ])}{\varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 3\alpha ]}, \\& v_{3} ( t ) = 1 - \frac{t^{\alpha }}{\varGamma [ 1 + \alpha ]} + \frac{t^{2\alpha }}{\varGamma [ 1 + 2\alpha ]} + \frac{t^{3\alpha } ( \varGamma [ 1 + \alpha ]^{2} - \varGamma [ 1 + 2\alpha ])}{\varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 3\alpha ]}, \\& \begin{aligned} u_{4} ( t ) &= 1 - \frac{2 t^{\alpha }}{\varGamma [ 1 + \alpha ]} + \frac{4 t^{2\alpha }}{\varGamma [ 1 + 2\alpha ]} - \frac{8 t ^{3\alpha } ( 251 \varGamma [ 1 + \alpha ]^{2} - 125 \varGamma [ 1 + 2 \alpha ])}{\varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 3\alpha ]} \\ &\quad {} + \bigl(16 t^{4\alpha } \bigl( 12\text{,}5876 \varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 2\alpha ] \\ &\quad {}- 62\text{,}750 \varGamma [ 1 + 2\alpha ]^{2} - 125 \varGamma [ 1 + \alpha ] \varGamma [ 1 + 3\alpha ]\bigr)\bigr) \\ &\quad {}/\bigl(\varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 2 \alpha ] \varGamma [ 1 + 4\alpha ]\bigr), \end{aligned} \\& \begin{aligned} v_{4} ( t ) &= 1 - \frac{t^{\alpha }}{\varGamma [ 1 + \alpha ]} + \frac{t^{2\alpha }}{\varGamma [ 1 + 2\alpha ]} + \frac{t^{3\alpha } ( \varGamma [ 1 + \alpha ]^{2} - \varGamma [ 1 + 2\alpha ])}{\varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 3\alpha ]} \\ &\quad {} + \frac{t^{4\alpha } (-2011 \varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 2\alpha ]+ 1003 \varGamma [ 1 + 2 \alpha ]^{2} + 2 \varGamma [ 1 + \alpha ] \varGamma [ 1 + 3\alpha ])}{ \varGamma [ 1 + \alpha ]^{2} \varGamma [ 1 + 2\alpha ] \varGamma [ 1 + 4\alpha ]}. \end{aligned} \end{aligned}$$

Some numerical results and tabulated data using the FRPS method for \(\alpha =1\) and \(k=20\) are given in Table 3 and Fig. 3.

Figure 3
figure 3

The FRPS solution behavior of Example 4.2 for \(\alpha =1\) and \(k=20\)

Full size image
Table 3 Numerical results of FRPS method of Example 4.2
Full size table

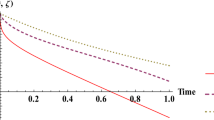
To show the accuracy of this method, the RKHS method for the same example with \(k=1000\) are applied and the results are summarized in Table 4 and Fig. 4. For fractional derivatives, we take \(k=10\) and apply the RPS method for \(\alpha _{i} =0.95+0.005i\), \(i=0, 1, \dots, 9\) as shown in Fig. 5. Figure 6 shows the results for \(\alpha _{i} =0.1+0.1i\), \(i=0, 1, \dots, 9\).

Figure 4
figure 4

The RK solution behavior of Example 4.2 for \(\alpha =1\) and \(k=1000\)

Full size image
Figure 5
figure 5

The solutions behavior of Example 4.2 for \(\alpha _{i} =0.95+0.005i\), \(i=0, 1, \dots, 9\)

Full size image
Figure 6
figure 6

The solutions behavior of Example 4.2 for \(\alpha _{i} =0.1+0.1i\), \(i=0, 1, \dots, 9\)

Full size image
Table 4 Numerical results and approximated RKHS-solutions of Example 4.2
Full size table

5 Conclusion

In this work, we applied an analytical iterative method depending on the residual power series to get an approximate solution to a stiff system of fractional order in the Caputo sense. Numerical examples for both linear and nonlinear fractional stiff systems were given to show the effectiveness of the proposed method. By comparing our results with the exact solutions and results obtained by another numerical method, we observe that the RPS method yields an accurate approximation.