1 Introduction

In recent years fractional calculus has been utilized to find solutions of equations governing the modeling of real materials in engineering and physics. Fractional differential equations model many phenomena in several fields such as fluid mechanics, chemistry [1, 2], biology [3], viscoelasticity [4], engineering, finance, and physics [5–7]. Therefore, the use of fractional calculus has gained the attention of scientists and engineers as, though counter-intuitive, the fractional derivative does arise in physical problems. In this connection there is the work of [8–15]. Due to the difficulty of obtaining exact solutions of equations involving a fractional derivative, approximate and numerical techniques have tended to be used instead. Examples of such approximate and numerical methods are Taylor collocation method followed in [16]; Adomian’s decomposition method followed in [17, 18]; finite difference method followed in [19, 20]; homotopy analysis method and homotopy perturbation methods followed, respectively, in [21–23] and [24].

In addition, there are general papers giving an overview of the field of fractional differential equations [25–28]. Also, numerical methods have been used to find solutions of fractional differential equations [29–37].

Burgers’ equation is the diffusive equation

$$ u_{t}+a u u_{x}-c u_{xx}=0. $$
(1)

Burgers’ equation arises as a model equation for the smoothing of a shock wave by viscosity [38]. In this application c is modeled on the kinematic viscosity in the Navier-Stokes equations. Furthermore, Burgers’ equation has an exact solution via the Cole-Hopf equation which reduces it to the heat equation [37, 38]. Of particular relevance to this work, Burgers’ equation (1) has the front solution [39–41]

$$ u(x,t)=\frac{2 b}{a}-\frac{2 c b}{a} \tanh \bigl[b (x-2 b t) \bigr]. $$
(2)

In this paper we study approximate solutions using VIM for the time and space-time fractional Burgers’ equation. To the best of our knowledge, this is the first study of the space-time fractional Burgers’ equation by VIM. The work of [42, 43] studied only the time fractional Burgers’ equation and the space fractional Burgers’ equation, but did not study the space-time fractional Burgers’ equation.

The present paper is organized as follows. The second and third sections are devoted to the basic ideas of fractional calculus and the standard VIM, respectively. The fourth and fifth sections are devoted to the application of VIM to evaluate solutions of the time and space-time fractional Burgers’ equation, respectively. Conclusions are presented in section seven.

2 Fractional calculus

Definitions of fractional derivatives were given by Riemann, Liouville, Grunwald, Letnikov and Caputo [25–28], and they are based on generalized functions. The most commonly used definitions are those of Riemann [25] and Liouville and Caputo [27]. Here we give some basic definitions and properties of fractional calculus theory.

Definition 2.1

A real function \(f(t)\), \(t>0\), is said to be in the space \(C_{\mu}\), \(\mu\in R\), if there exists a real number \(p>\mu\) such that \(f(t)=t^{p} f_{1} (t)\), where \(f_{1}(t)\in C[0,\infty)\), and it is said to be in the space \(C_{\mu}^{m}\) iff \(f^{m} \in C_{m}\), \(m \in N \).

The Riemann-Liouville fractional integral operator of order \(\alpha> 0\) for a function \(f \in C_{\mu}\), \(\mu\geq-1\), is defined as

$$\begin{aligned} &J_{0}^{\alpha} f(t)= \frac{1}{\Gamma(\alpha)} \int_{0}^{t} (t-\tau )^{\alpha-1} f(\tau) \,d\tau,\quad t>0, \\ &J^{0} f(t)=f(t). \end{aligned}$$

It has the following properties. For \(f\in C_{\mu}\), \(\mu\geq-1\), \(\alpha, \beta\geq0\), and \(\gamma>-1\),

  • \(J^{\alpha} J^{\beta} f(t) = J^{\alpha+\beta} f(t)\),

  • \(J^{\alpha} J^{\beta} f(t) = J^{\beta} J^{\alpha} f(t)\),

  • \(J^{\alpha} t^{\gamma} = \frac{\Gamma(\gamma+1)}{\Gamma (\alpha+\gamma+1)} t^{\alpha+\gamma}\).

Definition 2.2

The fractional derivative of \(f(t)\) in the Caputo sense is defined as

$$ D^{\alpha} f(t) = J^{m-\alpha} D^{m} f(t)= \frac{1}{\Gamma(m-\alpha)} \int_{0}^{t} (t-\tau)^{m-\alpha-1} f^{(m)} (\tau) \,d\tau $$
(3)

for \(m-1 <\alpha\leq m\), \(m\in N\), \(t>0\), \(f \in C_{\mu}^{m}\), \(\mu \geq-1\). Then

$$\begin{aligned} &D^{\alpha} J^{\alpha} f(t)=f(t), \\ &J^{\alpha} D^{\alpha} f(t) = f(t)- \sum_{k=0}^{m-1} f^{k} \bigl(0^{+}\bigr) \frac{t^{k}}{k!}. \end{aligned}$$

3 Basic ideas of VIM

The principles of VIM and its applications to various kinds of differential equations are given in [44–49]. To apply VIM, we consider the differential equation

$$ Lu(x,t)+Nu(x,t)=g(x,t), $$
(4)

where L is a linear operator, N is a nonlinear operator and \(g(x,t)\) is a source term. According to VIM, we construct the correction functional as

$$ u_{n+1}(x,t)=u_{n}(x,t)+ \int_{0}^{t} \lambda \bigl(L u_{n}(x, \tau)+N \tilde{u}_{n}(x,\tau)-g(x,\tau) \bigr) \,d\tau, $$
(5)

where λ is a general Lagrange multiplier [45–47] which can be determined optimally through variational theory. The subscript n denotes the nth order approximation, whereas \(\tilde{u}_{n}(x,t)\) is considered as a restricted variation [45–47], i.e., \(\delta\tilde{u}_{n}(x,t) = 0\). Also new results were obtained in [50, 51] using VIM.

4 The time-fractional Burgers’ equation

In this section, we use VIM to solve the time-fractional Burgers’ equation. To obtain this equation, we replace \(u_{t}\) by \(u_{t}^{\alpha}\) in Burgers’ equation (1), where \(n-1<\alpha\leq n\), \(n\in N\). Hence, we obtain the fractional-time Burgers’ equation

$$ u_{t}^{\alpha}+a u u_{x} -c u_{xx}=0. $$
(6)

Now, we construct the correction functional to solve (6) according to VIM as follows:

$$\begin{aligned} &u_{n+1}(x,t) = u_{n}(x,t)+ J_{t}^{\alpha} \lambda(\tau) \bigl(u_{n,\tau}^{\alpha}+ a \tilde{u}_{n} \tilde{u}_{n,x} -c u_{n,xx} \bigr), \end{aligned}$$
(7)
$$\begin{aligned} & u_{n+1}(x,t) = u_{n}(x,t)+ \frac{1}{\Gamma(\alpha)} \int_{0}^{t} (t-\tau)^{(\alpha-1)}\lambda(\tau) \bigl(u_{n,\tau}^{\alpha}+a \tilde{u}_{n} \tilde{u}_{n,x} -c u_{n,xx} \bigr)\,d\tau, \end{aligned}$$
(8)

where \(\tilde{u}_{n}\), \(\tilde{u}_{n,x}\) and \(\tilde{u}_{n,xx}\) are considered as restricted variations. The correction functional (8) can be approximately expressed as

$$\begin{aligned} u_{n+1}(x,t) = u_{n}(x,t)+ \int_{0}^{t} \lambda(\tau) \bigl(u_{n,\tau}^{m}+a \tilde{u}_{n} \tilde{u}_{n,x} -c \tilde{u}_{n,xx} \bigr) \,d\tau. \end{aligned}$$
(9)

For \(m=1\), we obtain the stationary condition

$$\begin{aligned} &\delta u_{n+1}(x,t)=\delta u_{n}(x,t) \bigl(1+ \lambda(\tau) \bigr)|_{t=\tau}+ \int_{0}^{t} \delta u_{n}(x,\tau) \lambda^{\prime}(\tau) \,d\tau=0, \end{aligned}$$
(10)
$$\begin{aligned} & \lambda^{\prime}(\tau) = 0, \end{aligned}$$
(11)
$$\begin{aligned} & \bigl(1+\lambda(\tau) \bigr)|_{\tau=t}= 0. \end{aligned}$$
(12)

Equation (11) is the Euler-Lagrange equation and (12) is the corresponding natural boundary condition. Thus we have \(\lambda=-1\), and we obtain the variational iteration formula

$$\begin{aligned} u_{n+1}(x,t) = u_{n}(x,t)-\frac{1}{\Gamma(\alpha)} \int_{0}^{t} (t-\tau)^{(\alpha-1)} \bigl(u_{n,\tau}^{\alpha}+a u_{n}u_{n,x} -c u_{n,xx} \bigr)\,d\tau. \end{aligned}$$
(13)

Now, as \(n\rightarrow\infty\), we consider \(u_{n}\) as an approximation of the exact solution. Iteration (13) is started with \(u_{0}(x,t) =u(x,0)\), and we obtain the successive approximations

$$\begin{aligned} &u_{0}(x,t) = \frac{2~( b - b ~c \tanh(b~x))}{a}, \end{aligned}$$
(14)
$$\begin{aligned} & u_{1}(x,t) = \frac{2 b}{a \alpha \Gamma(\alpha)} \bigl(\Gamma(\alpha) \bigl(\alpha-\alpha c \tanh(b x) \bigr)+2 b^{2} c t^{\alpha} \mathrm{sech}^{2}(b x) \bigr), \end{aligned}$$
(15)
$$\begin{aligned} &u_{2}(x,t)=\frac{2 b}{a \Gamma(\alpha)} \biggl( \Gamma(\alpha )+\frac{2 b^{2} c t^{\alpha} \mathrm{sech}^{2}(b x)}{\alpha}+8 b^{4} c t^{2 \alpha} \tanh(b x) \mathrm{sech}^{2}(b x) \\ & \phantom{u_{2}(x,t)=}{}\times \biggl(\frac{\sqrt{\pi} 4^{-\alpha}}{\alpha \Gamma (\alpha+\frac{1}{2} )}+ \frac{4 b^{2} c \Gamma(2 \alpha) t^{\alpha} \mathrm{sech}^{2}(b x)}{\Gamma(\alpha+1) \Gamma(3 \alpha +1)} \biggr) -c \Gamma( \alpha) \tanh(b x) \biggr). \end{aligned}$$
(16)

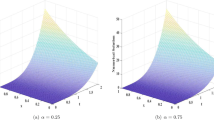
In this manner, we can obtain further approximations \(u_{3}(x,t)\), \(u_{4}(x,t), \ldots \) For brevity, these are not given. Note that if we expand the exact solution (2) in a Taylor series about \(t=0\), we thus obtain VIM solutions at \(\alpha=1\). In Figure 1, we show the surface of the exact solution (2) and the second approximation (16) for \(\alpha=0.7\) in (b) at \(a=1, b=0.01\) and \(c=1\). We note from this figure that the trajectory of the second approximation approaches the exact solution. In Figure 2 we show the absolute error between the exact solution (2) and the second approximation (16) for different values of b. The value of b plays a very important role in the acceleration of convergence. As b deceases, the absolute error becomes very small.

Figure 1
figure 1

Combining the surface exact solution ( 2 ) and the surface approximation ( 16 ) for \(\pmb{\alpha = 0.7}\) , \(\pmb{a=1}\) , \(\pmb{b=0.01}\) , and \(\pmb{c=1}\) . (a) The surface of the exact solution. (b) The surface of the second approximation. (c) Combining (a)-(b).

Full size image
Figure 2
figure 2

Comparison of the second approximation ( 16 ) with the exact solution ( 2 ) for \(\pmb{\alpha=1}\) , \(\pmb{a=1}\) , \(\pmb{c=1}\) with (a)  \(\pmb{b=0.01}\) and (b)  \(\pmb{b=0.001}\) .

Full size image

5 The space-time fractional Burgers’ equation

5.1 Tanh initial condition

In this section we study VIM solutions of the space-time fractional Burgers’ equation. However, before this we expand the exact solution (2) in the basis functions \(e^{-r b (x-2 b t)}\). By definition

$$\begin{aligned} u(x,t)&=\frac{2 b}{a}-\frac{2 c b}{a} \tanh \bigl[b (x-2 b t) \bigr]= \frac{2 b}{a}-\frac{2 c b}{a} \frac{1-e^{-2 (b (x-2 b t) )}}{1+e^{-2 (b (x-2 b t) )}} \\ & = \frac{2 b}{a}-\frac{2 c b}{a} \Biggl(1+ 2 \sum _{r=1}^{\infty} (-1)^{r} e^{-2 r (b (x-2 b t) )} \Biggr) \\ & = h-\frac{4 c b}{a} \Biggl( \sum_{r=1}^{\infty} (-1)^{r} e^{-2 r (b (x-2 b t) )} \Biggr), \quad b (x-2 b t)>0, \end{aligned}$$
(17)

where \(h=\frac{2b}{a}-\frac{2 c b}{a}\). For convenience, we rewrite Burgers’ equation after substituting \(u=v+h\) as

$$ v_{t}+a v v_{x}+a h v_{x}-c v_{xx}=0. $$
(18)

The solution of this equation (18) is

$$ v(x,t)=\frac{-4 c b}{a} \Biggl( \sum _{r=1}^{\infty} (-1)^{r} e^{-2 r (b (x-2 b t) )} \Biggr). $$
(19)

We take the initial condition from (19) on setting \(t=0\)

$$ v(x,0)=\frac{-4 c b}{a} \Biggl( \sum _{r=1}^{\infty} (-1)^{r} e^{-2 r (b x )} \Biggr). $$
(20)

We shall now study VIM for the space-time fractional Burgers’ equation. If we replace \(v_{t}\) by \(v_{t}^{\alpha}\), \(v_{x}\) by \(v_{x}^{\beta}\) and \(v_{xx}\) by \(v_{x}^{2 \beta}\), where \(0<\alpha, \beta\leq1\), in the time fractional Burgers’ equation (18), we obtain

$$ v_{t}^{\alpha}+a (v + h ) v_{x}^{\beta} -c v_{x}^{2\beta}=0. $$
(21)

VIM is given by

$$\begin{aligned} v_{n+1}(x,t) = v_{n}(x,t)-\frac{1}{\Gamma(\alpha)} \int_{0}^{t} (t-\tau)^{(\alpha-1)} \bigl(v_{n,\tau}^{\alpha}+a (v_{n} + h ) v_{n,x}^{\beta} -c v_{n,x}^{2\beta} \bigr)\,d\tau. \end{aligned}$$
(22)

On using this, we can evaluate the successive approximations. We choose \(v_{0}(x,t)=v(x,0)\) and find

$$ v_{0}(x,t)=\frac{-4 c b}{a} \Biggl( \sum _{r=1}^{\infty} (-1)^{r} e^{-2 r (b x )} \Biggr) $$
(23)

and

$$ v_{1}(x,t)= v_{0}(x)-\frac{t^{\alpha}}{\Gamma(1+\alpha)} f_{0}(x). $$
(24)

The second approximation is given by

$$\begin{aligned} & v_{2}(x,t)=v_{1}(x,t)- \biggl( \frac{-t^{\alpha} f_{0}}{\Gamma(1+\alpha)}+a I_{1}-c I_{2} \biggr), \end{aligned}$$
(25)
$$\begin{aligned} &I_{1} = \frac{(h+v_{0})g_{1} }{\Gamma(1+\alpha)} t^{\alpha}- \frac{ (f_{1} g_{1}+ f_{2} h \Gamma (\alpha+1)+f_{2} v_{0}(x))}{\Gamma(2 \alpha+1)}t^{2 \alpha} \\ &\phantom{I_{1} =}{}+\frac{f_{1} f_{2} \Gamma(2 \alpha+1) }{\Gamma(\alpha+1)^{2} \Gamma(3 \alpha+1)}t^{3 \alpha}, \end{aligned}$$
(26)
$$\begin{aligned} & I_{2}=\frac{g_{2} }{\Gamma(\alpha+1)}t^{\alpha}- \frac{ \Gamma(\alpha+1) f_{3}}{\Gamma(2 \alpha+1)}t^{2 \alpha}, \end{aligned}$$
(27)
$$\begin{aligned} & f_{i}(x) = \frac{(-4 b c)^{2}}{a} \sum _{r1=1}^{\infty} \sum_{r=1}^{\infty} \lambda^{\beta} (-1)^{r+r1} (\lambda+\lambda1)^{i \beta} e^{x (\lambda+\lambda1)} \\ &\phantom{f_{i}(x) =}{} -4 h b c \sum_{r=1}^{\infty} (-1)^{r} \lambda^{(i+1) \beta} e^{\lambda x} +\frac{4 b c^{2}}{a} \sum_{r=1}^{\infty} (-1)^{r} \lambda ^{(i+2)\beta} e^{\lambda x},\quad i=0, 1, 2, 3, \end{aligned}$$
(28)
$$\begin{aligned} & g_{i}= -\frac{4 b c}{a} \sum _{r=1}^{\infty} (-1)^{r} \lambda^{i \beta} e^{\lambda x}, \quad i=1, 2, \lambda=-2 b r, \lambda_{1} =-2 b r_{1}. \end{aligned}$$
(29)

In the same manner, we can obtain further approximations \(v_{3}(x,t), \ldots\) Setting \(\beta=1\) in the first approximation (24) and the second approximation (25) and after some simplifications, we obtain the same approximations as (15) and (16) on returning to the original variable. We can obtain VIM solutions of (21) for \(b (x-2 b t)<0\) using the same procedure as for \(b (x-2 b t)>0\). Using Mathematica, we can simplify the first approximation \(v_{1}\) as

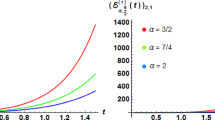
$$\begin{aligned} v_{1}(x,t) ={}& \frac{4 b c}{a (e^{2 b x}+1 )}- \biggl( \frac{4 b c t^{\alpha}}{a \alpha \Gamma (\alpha) (e^{2 b x}+1 )^{3} } \bigl(-4 b^{2} e^{2 b x} \bigl((c+1) e^{2 b x}+3 c+1 \bigr) \bigr) \\ & {} - \bigl(4^{\beta} c (-b)^{2 \beta} \bigl(e^{2 b x}+1 \bigr)^{3} \operatorname{PolyLog} \bigl[-2\beta,-e^{-2 b x} \bigr] \bigl(-e^{-2 b x} \bigr) \bigr) \biggr). \end{aligned}$$
(30)

We now use the first approximation (30), after returning to the original variable, to find VIM solutions. Figure 3 shows VIM solution (30) for different values of α and β. It can be seen from this figure that as \(\alpha\rightarrow1\) and \(\beta\rightarrow1\), VIM solution (30) tends to the exact solution (2). Therefore, VIM is an efficient and accurate method which can be used to find approximate analytical solutions of the space-time fractional Burgers’ equation.

Figure 3
figure 3

VIM solution ( 30 ) in the origin variable u for \(\pmb{a=1}\) , \(\pmb{b=0.01}\) and \(\pmb{c=0.7}\) (a)  \(\pmb{\alpha=0.4}\) , \(\pmb{\beta=0.6}\) , (b)  \(\pmb{\alpha=0.6}\) , \(\pmb{\beta=0.8}\) , (c)  \(\pmb{\alpha=1}\) , \(\pmb{\beta=1}\) and (d) combining (a)-(c).

Full size image

5.2 Polynomial initial condition

In this section we study VIM for the space-time fractional Burgers’ equation for another initial condition. We replace \(u_{t}\) by \(u_{t}^{\alpha}\), \(u_{xx}\) by \(u_{x}^{2 \beta}\) and \(u_{x}\) by \(u_{x}^{ \beta}\), where \(0<\alpha, \beta\leq1\) in Burgers’ equation (1). VIM for (1) is

$$\begin{aligned} u_{n+1}(x,t) = u_{n}(x,t)-\frac{1}{\Gamma(\alpha)} \int_{0}^{t} (t-\tau)^{(\alpha-1)} \bigl(u_{n,\tau}^{\alpha}+a u_{n} u_{n,x}^{\beta} -c u_{n,x}^{2\beta} \bigr)\,d\tau. \end{aligned}$$
(31)

We start the iteration with \(u_{0}(x,t)=u(x,0)=2x\), so that the successive approximations can be derived from (31) as

$$\begin{aligned} & u_{0}(x,t)=2x, \end{aligned}$$
(32)
$$\begin{aligned} & u_{1}(x,t)= \biggl(2 x+ \frac{2 t x^{1-2 \beta}}{\Gamma (\alpha)} \biggl(- \frac{2 a x^{\beta+1}}{\Gamma(2-\beta)} +\frac{c}{\Gamma(2-2 \beta)} \biggr) \biggr), \end{aligned}$$
(33)
$$\begin{aligned} & u_{2}(x,t) =u_{1}(x,t)+ \frac{1}{\Gamma(\alpha)} \biggl(b_{1}-\frac{1}{3} 2 a t (b_{2} +b_{3}) x^{2-3 \beta}+b_{4} \biggr), \end{aligned}$$
(34)
$$\begin{aligned} & b_{1}=\frac{-4 a c t^{2} x^{2-3 \beta}}{\Gamma(\alpha) \Gamma(3-3 \beta)}+\frac{2 a \beta c t^{2} x^{2-3 \beta}}{ \Gamma(\alpha) \Gamma(3-3 \beta)} + \frac{c^{2} t^{2} x^{1-4 \beta}}{\Gamma(\alpha) \Gamma(2-4 \beta)} +\frac{2 c t x^{1-2 \beta}}{\Gamma(2-2 \beta)}, \end{aligned}$$
(35)
$$\begin{aligned} &b_{2}=\frac{3 t (-\frac{2 a x^{\beta+1}-\frac{c \Gamma (2-\beta)}{\Gamma(2-2 \beta)}}{\Gamma(2-\beta)^{2}} +\frac{2 a (\beta-2) x^{\beta+1}}{\Gamma(3-2 \beta)}+\frac {c}{\Gamma(2-3 \beta)} )}{\Gamma(\alpha)} +\frac{6 x^{2 \beta }}{\Gamma(2-\beta)}, \end{aligned}$$
(36)
$$\begin{aligned} & b_{3}=\frac{2 t^{2}}{\Gamma(\alpha)^{2}} \biggl(\frac{-c x^{-2 \beta} (\frac{2 a x^{\beta+1}}{\Gamma(2-\beta)} -\frac{c}{\Gamma(2-2 \beta)} )}{\Gamma(2-3 \beta)} + 2 a \\ &\phantom{b_{3}=}{} \times \biggl(\frac{\frac{a x}{(\beta-1)^{2} \Gamma (-\beta)}+\frac{(\beta-2) c x^{-\beta}}{\Gamma(3-2 \beta)}}{\Gamma(2-2 \beta)}+\frac{4 a x}{\Gamma(3-2 \beta) \Gamma(2-\beta)} \biggr) \biggr), \end{aligned}$$
(37)
$$\begin{aligned} & b_{4}= \frac{2 \sin(\pi \alpha) t^{2-\alpha} x^{1-2 \beta} (2 a \Gamma(2-2 \beta) x^{\beta+1} -c \Gamma(2-\beta) )}{\pi (\alpha-2) (\alpha-1) \Gamma(2-2 \beta ) \Gamma(2-\beta)}, \end{aligned}$$
(38)
$$\begin{aligned} & u_{3}(x,t)= u_{2}(x,t)+ \cdots, \end{aligned}$$
(39)

In a similar manner, we calculate further approximations for (31). When we set \(\alpha=1\) and \(\beta=1\), \(a=1, b=1\) and \(c=1\) in (33)-(39), we obtain

$$\begin{aligned} & u_{1}(x,t)= 2 x (1 - 2 t), \end{aligned}$$
(40)
$$\begin{aligned} &u_{2}(x,t)= 2x \biggl(1-2 t+4 t^{2}- \frac{8 t^{3}}{3} \biggr), \end{aligned}$$
(41)
$$\begin{aligned} &u_{3}(x,t)= 2x \biggl(1 - 2t + 4t^{2} - 8t^{3} + \frac{32}{3}t^{4} - \frac{32}{3}t^{5} + \frac{64}{9}t^{6} - \frac{128}{63}t^{7} \biggr) \cdots. \end{aligned}$$
(42)

Using the fact that

$$\begin{aligned} u(x,t) =& \lim_{n\rightarrow\infty}u_{n}(x,t), \end{aligned}$$
(43)

we obtain an exact solution of Burgers’ equation (1). This solution is the same as that of [42].

Figure 4 shows the surface of the exact solution (43) in (a) and the surface of the second approximation (34) for \(\alpha=0.7\) and \(\beta=0.5\) in (b) at \(a=1\), \(b=1\) and \(c=1\). It can be seen from this figure that the second approximate solution is a good approximation of the exact solution. If we go to higher order approximations, we will obtain better approximations to this exact solution.

Figure 4
figure 4

Combining the surface exact solution ( 43 ) and the surface approximation ( 34 ) for \(\pmb{\alpha = 0.7}\) , \(\pmb{\beta=0.5}\) , \(\pmb{a=1 }\) , \(\pmb{b=1}\) , and \(\pmb{c=1}\) . (a) The surface of the exact solution. (b) The surface of the second approximation. (c) Combining (a)-(b).

Full size image

6 Convergence analysis

In this section the existence of a unique solution is introduced in Theorem 6.2. Furthermore, the convergence of VIM solution (22) is proved in Theorem 6.3. Finally, the maximum absolute truncation error of VIM solution (22) is given in Theorem 6.4. In this section we prove theorems for the space-time fractional Burgers’ equation. This theorem covers the time-fractional Burgers’ equation on setting \(\beta=1\). We define \((C(I), \Vert \cdot \Vert )\) as a Banach space, the space of all continuous functions on \(I=R \times R^{+} \) with the norm \(\Vert v(x,t) \Vert =\max_{(x,t)\in I} \vert {v(x,t)} \vert\).

Lemma 6.1

Suppose that \(v(x,t)\) and their partial derivatives are continuous. Then the derivatives \(D_{t}^{\alpha}v(x,t)\), \(D_{x}^{\beta}v(x,t)\) and \(D_{x}^{2\beta }v(x,t)\) are bounded.

Proof

We prove that \(D_{t}^{\alpha}v(x,t)\) is bounded. From the fractional derivative definition (3) we have

$$\begin{aligned} \bigl\Vert D_{t}^{\alpha}v(x,t) \bigr\Vert &= \biggl\Vert \frac{1}{\Gamma(m-\alpha)} \int_{a}^{b} (t-\tau)^{m-\alpha-1}v^{(m)}(x, \tau) \,d\tau \biggr\Vert \\ &\leq \frac{ \vert b-a \vert }{ \vert (m-\alpha)\Gamma(m-\alpha ) \vert } \bigl\Vert v(x,t) \bigr\Vert =L_{1} \bigl\Vert v(x,t) \bigr\Vert , \end{aligned}$$
(44)

where \(L_{1}=\frac{ \vert b-a \vert }{ \vert (m-\alpha)\Gamma (m-\alpha) \vert }\). In the same manner \(\Vert D_{x}^{\beta}v(x,t) \Vert \leq L_{2} \Vert v(x,t) \Vert \) and \(\Vert D_{x}^{2\beta}v(x,t) \Vert \leq L_{3} \Vert v(x,t) \Vert \). □

Theorem 6.2

Let \(F(v)=-a v v_{x}^{\beta}\) satisfy the Lipschitz condition with the Lipschitz constant  \(L_{4}\). Then problem (21) has the unique solution \(v(x,t)\) whenever \(0 < \gamma<1\).

Proof

Let u and v be two different solutions of the space-time fractional Burgers’ equation (21). For all \(t\in[0,T]\) and \(\tau\in[0,t]\), these solutions are bounded on using Lemma 6.1. Let \(M=\max_{0\leq\tau\leq t, 0\leq t\leq T} \vert (t-\tau)^{\alpha-1} \vert \). Then

$$\begin{aligned} & u-v = J^{\alpha}_{t} \bigl(-ahD_{x}^{\beta}u(x, \tau) + cD_{x}^{2\beta}u(x,\tau) + F(u) \bigr) \\ &\phantom{u-v =}{} -J^{\alpha}_{t} \bigl(-ahD_{x}^{\beta}v(x, \tau)+cD_{x}^{2\beta}v(x,\tau) + F(v) \bigr) \\ &\phantom{u-v }= \frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1} \bigl[-ahD_{x}^{\beta}u(x,\tau) + cD_{x}^{2\beta}u(x, \tau) + F(u) \bigr]\,d\tau \\ &\phantom{u-v =} {}-\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1} \bigl[ -ahD_{x}^{\beta}v(x,\tau) + cD_{x}^{2\beta}v(x, \tau) + F(v) \bigr]\,d\tau, \\ \begin{aligned} &\max\vert u-v \vert= \max \biggl\vert \frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1} \bigl[-ahD_{x}^{\beta}u(x,\tau) + cD_{x}^{2\beta}u(x, \tau) + F(u) \bigr]\,d\tau \\ &\phantom{\max\vert u-v \vert=}{} -\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1} \bigl[- ahD_{x}^{\beta}v(x,\tau) +cD_{x}^{2\beta}v(x, \tau) + F(v) \bigr]\,d\tau\biggr\vert \\ &\phantom{\max\vert u-v \vert}\leq \frac{[ -ahL_{2} + cL_{3} + L_{4}]}{\Gamma(\alpha)}\max \int_{0}^{t}|t - \tau|^{\alpha-1} \vert u - v \vert \,d\tau, \end{aligned} \\ &\Vert u-v \Vert \leq \frac{[ -a h L_{2}+c L_{3} + L_{4}]}{\Gamma(\alpha)}\max \int_{0}^{t}|t - \tau|^{\alpha-1} \vert u - v \vert \,d\tau, \\ &\Vert u-v \Vert \leq \gamma \Vert u-v \Vert , \\ &(1-\gamma) \Vert u-v \Vert \leq 0, \end{aligned}$$
(45)

where \(\gamma= (\frac{[ -a h L_{2} +c L_{3} + L_{4}]M T}{\Gamma (\alpha)} )\). Since \(1-\gamma\neq0\), \(\Vert u-v \Vert = 0\). Therefore, \(u=v\), which completes the proof. □

Theorem 6.3

The sequence \(v_{n}(x,t)\) obtained from VIM iteration (22) converges to the exact solution of problem (21) for \(0<\sigma <1\) and \(0<\gamma_{1}<1\).

Proof

The approximate solution using VIM is given by

$$\begin{aligned} v_{n+1}(x,t) = v_{n}(x,t)-\frac{1}{\Gamma(\alpha)} \int_{0}^{t} (t-\tau)^{(\alpha-1)} \bigl(D_{\tau}^{\alpha}v_{n}+ahD_{x}^{\beta}v_{n} -c D_{x}^{2\beta}v_{n}-F(v_{n}) \bigr)\,d \tau. \end{aligned}$$
(46)

Since v is the exact solution of equation (21), it satisfies VIM formula, i.e.,

$$\begin{aligned} v(x,t) = v(x,t)-\frac{1}{\Gamma(\alpha)} \int_{0}^{t} (t-\tau)^{(\alpha-1)} \bigl(D_{\tau}^{\alpha}v+ahD_{x}^{\beta}v -c D_{x}^{2\beta}v-F(v) \bigr)\,d\tau. \end{aligned}$$
(47)

On subtracting v from \(v_{n+1}\) and recalling that \(E_{n}(x,t)=v_{n}(x,t)-v(x,t)\), we obtain

$$\begin{aligned} & E_{n+1}(x,t) = E_{n}(x,t)- \frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t - \tau)^{\alpha-1} \\ &\phantom{E_{n+1}(x,t) =}{}\times\bigl[D_{t}^{\alpha}(v_{n}-v) + ahD_{x}^{\beta}(v_{n}-v) - cD_{x}^{2\beta}(v_{n}-v) - F(v_{n}-v) \bigr]\,d\tau \end{aligned}$$
(48)
$$\begin{aligned} &\max \bigl\vert E_{n+1}(x,t) \bigr\vert \leq \max \bigl\vert E_{n}(x,t) \bigr\vert -\frac{[L_{1}+ ah L_{2} - c L_{3} - L_{4}] M }{ \Gamma(\alpha)}\max \int_{0}^{t} \bigl\vert E_{n}(x,\tau) \bigr\vert \,d \tau, \end{aligned}$$
(49)
$$\begin{aligned} &\bigl\Vert E_{n+1}(x,t) \bigr\Vert \leq \bigl\Vert E_{n}(x,t) \bigr\Vert -\frac{[L_{1}+ ah L_{2} - c L_{3} - L_{4}] M T}{\Gamma(\alpha)} \bigl\Vert E_{n}(x,t) \bigr\Vert . \end{aligned}$$
(50)

Hence,

$$ \bigl\Vert E_{n+1}(x,t) \bigr\Vert \leq\sigma \bigl\Vert E_{n}(x,t) \bigr\Vert , $$
(51)

where \(\sigma=(1-\gamma_{1})\), \(\gamma_{1}=\frac{[L_{1}+ ah L_{2} - c L_{3} - L_{4}] M T}{\Gamma(\alpha)}\) for all \(n = 0,1,2,\ldots\) Now, if \(n=0\),

$$\begin{aligned} \bigl\Vert E_{1}(x,t) \bigr\Vert \leq \sigma \bigl\Vert E_{0}(x,t) \bigr\Vert , \end{aligned}$$
(52)

while if \(n=1\),

$$\begin{aligned} \bigl\Vert E_{2}(x,t) \bigr\Vert \leq \sigma^{2} \bigl\Vert E_{0}(x,t) \bigr\Vert . \end{aligned}$$
(53)

If \(n=2\), then

$$\begin{aligned} &\bigl\Vert E_{3}(x,t) \bigr\Vert \leq \sigma^{3} \bigl\Vert E_{0}(x,t) \bigr\Vert , \ldots \end{aligned}$$
(54)
$$\begin{aligned} &\bigl\Vert E_{n}(x,t) \bigr\Vert \leq \sigma^{n} \bigl\Vert E_{0}(x,t) \bigr\Vert . \end{aligned}$$
(55)

Since \(0<\sigma<1\), then \(\Vert E_{n}(x,t) \Vert \rightarrow0\) as \(n\rightarrow\infty\), i.e., \(v_{n}\rightarrow v\) and the sequence \(\{v_{n}(x,t) \}_{n=1}^{\infty}\) converges to \(v(x,t)\). □

Theorem 6.4

The maximum absolute truncation error of the approximate solution \({v_{n}(x,t)}\) of the time-space fractional Burgers’ equation (21) can be estimated as \(\Vert E_{n}(x,t) \Vert \leq\frac{\sigma^{n}}{1-\sigma} \Vert v_{1}(x,t) \Vert \).

Proof

$$\begin{aligned} v_{n}(x,t)-v_{n+1}(x,t) &= \bigl(v_{n}(x,t)-v(x,t) \bigr)+ \bigl(v(x,t)-v_{n+1}(x,t) \bigr) \\ &= E_{n}(x,t)-E_{n+1}(x,t). \end{aligned}$$
(56)

Hence,

$$\begin{aligned} \begin{aligned} &E_{n}(x,t) = E_{n+1}(x,t)- \bigl(v_{n+1}(x,t)-v_{n}(x,t) \bigr), \\ &\bigl\Vert E_{n}(x,t) \bigr\Vert = \bigl\Vert E_{n+1}(x,t)- \bigl(v_{n+1}(x,t)-v_{n}(x,t) \bigr) \bigr\Vert \\ &\bigl\Vert E_{n}(x,t) \bigr\Vert \leq \bigl\Vert E_{n+1}(x,t) \bigr\Vert + \bigl\Vert \bigl(v_{n+1}(x,t)-v_{n}(x,t) \bigr) \bigr\Vert \\ &\phantom{\bigl\Vert E_{n}(x,t) \bigr\Vert }\leq \sigma \bigl\Vert E_{n}(x,t) \bigr\Vert + \bigl\Vert \bigl(v_{n+1}(x,t)-v_{n}(x,t) \bigr) \bigr\Vert . \end{aligned} \end{aligned}$$
(57)

Therefore,

$$\begin{aligned} \bigl\Vert E_{n}(x,t) \bigr\Vert &\leq \frac{ \Vert (v_{n+1}(x,t)-v_{n}(x,t)) \Vert }{1-\sigma} \end{aligned}$$
(58)
$$\begin{aligned} &\leq \frac{\sigma^{n}}{1-\sigma} \bigl\Vert v_{1}(x,t) \bigr\Vert . \end{aligned}$$
(59)

 □

7 Conclusions

Approximate solutions of the time and space-time fractional Burgers’ equation have been evaluated using the VIM for different initial conditions by expanding the \(tanh\) initial condition in the basis functions \(e^{-n x}\). The fractional derivative could then be easily calculated. An important point is that many authors avoid this initial condition as there was no direct method to calculate its fractional derivative. In Figure 1, the surface of VIM solutions with the exact solution of Burgers’ equation for \(\alpha=0.7\) was plotted. Also, the absolute error with \(\alpha=1\) for different values for b were displayed in Figure 2. The effect of changes of b was clear through the resulting decrease of the error. As the value of b decreases, the absolute error becomes very small. In Figure 3 the VIM solutions were plotted with different values of α and β. The VIM solutions approach the exact solution as the values of α and β approach 1, as shown in Figure 4. The results were shown to be in very good agreement with both exact solutions and previous approximate solutions. The calculations in this paper were performed using Mathematica 9.