Well-posed conditions on a class of fractional q-differential equations by using the Schauder fixed point theorem

Abstract

In this paper, we propose the conditions on which a class of boundary value problems, presented by fractional q-differential equations, is well-posed. First, under the suitable conditions, we will prove the existence and uniqueness of solution by means of the Schauder fixed point theorem. Then, the stability of solution will be discussed under the perturbations of boundary condition, a function existing in the problem, and the fractional order derivative. Examples involving algorithms and illustrated graphs are presented to demonstrate the validity of our theoretical findings.

1 Introduction

In many applications fractional differential equations present more accurate models of phenomena than the ordinary differential equations. Therefore they have obtained importance due to their applications in science and engineering such as, physics, chemistry, mechanics, fluid dynamic, etc. [1, 2]. Meanwhile, there have appeared many papers dealing with the existence of solutions for different types of fractional boundary value problems; see, for example, [3–19].

The quantum calculus was introduced by Jackson in 1910 [20]. Al-Salam started the fitting of the concept of q-fractional calculus [21]. Then Agarwal continued by studying certain q-fractional integrals and derivatives [22]. After it, some researchers studied q-difference equations (for more details, see [23–36]). There are also many papers dealing with the existence of solutions for q-fractional boundary value problems (see, for example, [37–49]).

Existence of solutions to fractional differential equations has received considerable interest in recent years. There are several papers dealing with the existence and uniqueness of solutions to initial and boundary value problem of fractional order in Caputo or Riemann–Liouville sense (for more details, see [50–52] and the references therein). Some authors have also investigated the existence and uniqueness solutions for a coupled system of multi-term fractional differential equations [53, 54]. However, in general, the study of well-posed conditions for fractional differential equations is less considered in the literature.

In 2015, Houas et al. [55] investigated the existence and uniqueness of solutions for ${}^{c}\mathcal{D}_{q}^{\sigma }[y](t) + w ( y(t), {}^{c} \mathcal{D}_{q}^{\varsigma }[y](t) ) = 0$, for $t \in \overline{J}_{0} :=[0,1]$, where $2 < \sigma \leq 3$, $\varsigma \in J_{0}:=(0,1)$, under the initial conditions $y(0) = y_{0}$, $y'(0)=0$, $y'(1) = \eta \mathcal{I}^{\zeta }y(e)$, where ${}^{c}\mathcal{D}^{\sigma }$ is the Caputo fractional derivative, $e \in J_{0}$, w is a continuous function on $\mathbb{R}^{2}$, and η is a real constant [55]. In [56], authors studied the existence and uniqueness of solution for the fractional differential equation ${}\mathcal{D}^{\sigma }[y](t) = w ( t, y(t), {}\mathcal{D}^{\varsigma }[y](t) )$, where $2 < \sigma < 3$, $\varsigma \in J_{0}$, via sum boundary conditions $y(0) = 0$,

$$ {}\mathcal{D}_{q}^{\sigma }[y](1) = \sum _{i = 1}^{m - 2} a_{i} {} \mathcal{D}_{q}^{\varsigma }[y]( e_{i}), $$

$y''(1) = 0$, where, $a_{i}, e_{i} \in J_{0}$ and ${}\mathcal{D}_{q}^{\sigma }$ is the Caputo fractional derivative. In 2015, Akrami et al. [57] proved the conditions on which the following class of fractional differential equations ${}^{C}\mathcal{D}^{\sigma }[y](t) = w ( y(t), {}\mathcal{D}^{\varsigma }[y](t) )$ for $t \in \overline{J}_{0}$ is well-posed, where $2 < \sigma \leq 3$ and $\varsigma \in J_{0}$, and ${}^{C}\mathcal{D}_{q}^{\sigma }$ is the Caputo fractional derivative subject to the boundary value conditions $y(0) = y'(0)=0$, $y(1) = ay(e)$, where $e \in J_{0}$, $0 \leq a <\frac{1}{e^{2}}$.

In this article, we investigate the conditions on which the fractional q-differential equation

$$ {}^{C}\mathcal{D}_{q}^{\sigma }[y](t) = w \bigl( y(t), {}^{C} \mathcal{D}_{q}^{\varsigma }[y](t) \bigr) $$

(1)

for $t \in \overline{J}_{0}$ is well-posed, where $2 < \sigma \leq 3$, $\varsigma \in J_{0}$, and ${}^{C}\mathcal{D}_{q}^{\sigma }$ is the standard Caputo q-derivative subject to the boundary value conditions

$$ y(0) = y'(0) = 0,\qquad y'(1) = a y (e), $$

(2)

where $e\in \overline{J}_{0}$ with $0 \leq a< \frac{1}{e^{2}}$. We recall that a problem is said to be well-posed if it has a uniqueness solution and this solution depends on a parameter in a continuous way. This parameter, in the classical order differential equations, is dependent on the initial conditions and the function exists in the problem; whereas in the FDEs this dependency and the stability solution with respect to the perturbation of fractional order derivative should be taken into the account too [58].

The rest of the paper is organized as follows. We first prove the existence solution of (1) by means of the Schauder fixed point theorem on the interval $\overline{J}_{0}$ in Sect. 3. Then, we prove the uniqueness by using the Banach contraction map theorem under a suitable condition in Sect. 3. Also, Sect. 3 is devoted to investigating the stability of solutions under the perturbations on boundary condition, the function exists in the problem and the fractional order derivative. Finally, in Sect. 4, we bring some examples to illustrate our results. Let us start with some basic preliminaries in Sect. 2 that we will use in the sequel.

2 Preliminaries and lemmas

This section is devoted to some notations and essential preliminaries that are acting as necessary prerequisites for the results of the subsequent sections. Throughout the context, we shall apply the notations of time scales calculus [59].

In fact, we consider the fractional q-calculus on the specific time scale $\mathbb{T}_{t_{0}} = \{0 \} \cup \{ t: t=t_{0}q^{n} \}$ for $n \in \mathbb{N}$, $t_{0} \in \mathbb{R}$, and $q \in (0,1)$. For brief, we shall denote $\mathbb{T}_{t_{0}}$ by $\mathbb{T}$. Let $a \in \mathbb{R}$. Define $[s]_{q} =(1-q^{s})/(1-q)$ [20]. The q-factorial function $(v-w)_{q}^{(n)}$ with $n \in \mathbb{N}_{0} := \{ 0\} \cup \mathbb{N}$ is defined by $(v-w)_{q}^{(n)}= \prod_{k=0}^{n-1} (v - wq^{k})$, and $( v - w)_{q}^{(0)}=1$, where v, w are real numbers [23]. Also, for $\sigma \in \mathbb{R}$ and $s \neq 0$, we have $(v - w)_{q}^{(\sigma )} = v^{\sigma }\prod_{k=0}^{\infty }(v-wq^{k} )(v -wq^{ -(\sigma + k)})$. In the paper [60], the authors proved $(v -w)_{q}^{(\sigma +\nu )} = (v - w)_{q}^{(\sigma )} (v -q^{\sigma }w)_{q}^{( \nu )}$ and $(sv -sw)_{q}^{(\sigma )} = s^{\sigma }(v - w)_{q}^{(\sigma )}$. If $w=0$, then it is clear that $v^{(\sigma )}= v^{\sigma }$. The q-gamma function is given by $\Gamma _{q} (v) = (1-q)^{1-v} (1-q)_{q}^{(v-1)}$, where $z \in \mathbb{R} \backslash \{\ldots , -2, -1, 0\}$ [20]. Note that $\Gamma _{q} (z+1) = [z]_{q} \Gamma _{q} (z)$ [60, Lemma 1]. For a function $\wp : \mathbb{T} \to \mathbb{R}$, the q-derivative of ℘ is

$$ \mathcal{D}_{q} [\wp ] (v) = \frac{ \wp (v) - \wp (qv)}{(1- q) v} $$

for all $t \in \mathbb{T} \setminus \{0\}$, and $\mathcal{D}_{q} [\wp ](0) = \lim_{v \to 0} \mathcal{D}_{q} \wp (v)$ [23]. Also, the higher order q-derivative of the function ℘ is defined by $\mathcal{D}_{q}^{n} \wp (v) = \mathcal{D}_{q} (\mathcal{D}_{q}^{ n-1} \wp )(v)$ for all $n \geq 1$, where $\mathcal{D}_{q}^{0} \wp (v) = \wp (v)$ [23]. The q-integral of the function ℘ is defined by

$$ \mathcal{I}_{q} \wp (v) = \int _{0}^{v} \wp (\xi ) {\,\mathrm{d}}_{q} \xi = v(1- q) \sum_{k=0}^{\infty } q^{k} \wp \bigl(v q^{k} \bigr) $$

for $0 \leq v \leq b$, provided the series absolutely converges [23]. If v in $[0, b]$, then

$$ \int _{a}^{v} \wp (\xi ) { \,\mathrm{d}}_{q} \xi = \mathcal{I}_{q} \wp (v) - \mathcal{I}_{q} \wp (a) = (1-q) \sum_{k=0}^{\infty } q^{k} \bigl[ v \wp \bigl(v q^{k} \bigr) - a \wp \bigl(a q^{k} \bigr) \bigr], $$

whenever the series exists [61]. The operator $\mathcal{I}_{q}^{n}$ is given by $\mathcal{I}_{q}^{0} \wp (v) = \wp (v)$ and $\mathcal{I}_{q}^{n} \wp (v) = \mathcal{I}_{q} [ \mathcal{I}_{q}^{n-1} \wp ] (v)$ for $n \geq 1$ and $\wp \in C([0, b])$ [23]. It has been proved that $\mathcal{D}_{q} ( \mathcal{I}_{q} \wp )(v) = \wp (v)$, $\mathcal{I}_{q} (\mathcal{D}_{q} \wp )(v) = \wp (v) - \wp (0)$, whenever the function ℘ is continuous at $v=0$ [23]. The fractional Riemann–Liouville type q-integral of the function ℘ is defined by $\mathcal{I}_{q}^{0} \wp (v) = \wp (v)$ and

$$ \mathcal{I}_{q}^{\sigma }\wp (v) = \frac{1}{\Gamma _{q}(\sigma )} \int _{0}^{v} (v- \xi )_{q}^{(\sigma - 1)} \wp (\xi ) \,\mathrm{d}_{q}\xi $$

for $v \in [0, 1]$ and $\sigma >0$ [24, 29]. The Caputo fractional q-derivative of the function ℘ is defined by

$$ {}^{C}\mathcal{D}_{q}^{\sigma }\wp (v) = \mathcal{I}_{q}^{[\sigma ]- \sigma } \bigl[\mathcal{D}_{q}^{[\sigma ]} \wp \bigr] (v) = \frac{1}{\Gamma _{q} ([\sigma ] - \sigma )} \int _{0}^{v} (v- \xi )_{q}^{ ( [\sigma ]-\sigma -1 )} \mathcal{D}_{q}^{[ \sigma ]} \wp (\xi ) {\,\mathrm{d}}_{q} \xi $$

for $v \in [0,1]$ and $\sigma >0$ [29, 62]. It has been proved that $\mathcal{I}_{q}^{ \nu } ( \mathcal{I}_{q}^{\sigma } \wp ) (v) = \mathcal{I}_{q}^{\sigma + \nu } \wp (v)$ and ${}^{c}\mathcal{ D}_{q}^{\sigma } ( \mathcal{I}_{q}^{ \sigma } \wp ) (v)= \wp (v)$, where $\sigma , \nu \geq 0$ [29]. The authors in [61] presented all algorithms and MATLAB lines to simplify q-factorial functions $(v -w)_{q}^{(n)}$, $(v -w)_{q}^{(\sigma )}$, $\Gamma _{q}(v)$, $\mathcal{I}_{q} [\wp ](v)$, and some necessary equations.

Now, we introduce some basic definitions, lemmas, and theorems which are used in the subsequent sections.

Lemma 2.1

([63])

Let $n\in \mathbb{N}$, $n-1<\alpha \leq n$, and $\wp \in AC^{n}[a, b]$. Then one has $\mathcal{I}^{\sigma }({}^{c}\mathcal{ D}_{q}^{\sigma }\wp ) (v)= \wp (v) + \sum_{i=0}^{n-1}c_{i} (v-a)^{i}$, where $c_{0}, c_{1} ,\dots , c_{n-1}\in \mathbb{R}$.

Lemma 2.2

Let $\sigma _{1} > \sigma _{2} > 0$. Then the formula ${}^{C}\mathcal{D}_{q}^{\sigma _{1}} ( \mathcal{I}_{q}^{\sigma _{2}} \wp ) (v) = \mathcal{I}_{q}^{\sigma _{1} - \sigma _{2}} \wp (v)$ holds almost everywhere on $v \in [a,b]$ for $\wp \in L_{1} [a,b]$, and it is valid at any point $v \in [a,b]$ if $\wp \in C([a,b], \mathbb{R})$.

Lemma 2.3

([1])

Let $\sigma > 0$ and $\wp \in C(0,1) \cap L^{1} (0,1)$ with a derivative of order n. Then ${}\mathcal{I}_{q}^{\sigma }( {}^{C}\mathcal{D}_{q}^{\sigma }\wp (v)) = \wp (v) + d_{0} + d_{1}t + d_{2}t^{2} + \cdots + d_{n - 1}t^{ n - 1}$ for $d_{i} \in \mathbb{R}$ with $i = 1, 2, \dots , n-1$, where $n - 1 < \sigma \leq n$.

Definition 2.4

A real function $\wp (v)$, $v > 0$ is said to be in the space $C_{r}$, $r \in \mathbb{R}$, if there exists a real number ν (>r) such that $\wp (v) = v^{\nu }\wp _{1}(v)$, where $\wp _{1}(v) \in C( [0, \infty ), \infty )$.

Theorem 2.5

(Banach contraction principle, [64])

Let $\mathcal{X}$ be a Banach space. If $A : \mathcal{X}\to \mathcal{X}$ is the contraction map, then there exists $x\in \mathcal{X}$ such that $Ax=x$.

3 Main results

First, we consider the following important lemmas in our article.

Lemma 3.1

Let $v\in AC (0,1)$ and $2 < \sigma \leq 3$. The fractional q-differential equation

$$ {}^{C}\mathcal{D}_{q}^{\sigma }[y](t) = v(t) $$

(3)

for $2 < \sigma \leq 3$ under conditions $y(0) = y'(0) = 0$, $y'(1) = a y (e)$, $e \in J_{0}$ with $0 \leq a <\frac{1}{e^{2}}$ has a solution

$$ y(t) = \int _{0}^{1} G_{q}(t, \xi ) v(\xi ) \,\mathrm{d}_{q}\xi + \frac{ a t^{2}}{1 - ae^{2}} \int _{0}^{1} G_{q}(e, \xi ) v(\xi ) \,\mathrm{d}_{q}\xi , $$

(4)

where

$$ G_{q}(t, \xi ) = \textstyle\begin{cases} \frac{ ( t - \xi )_{q}^{ (\sigma - 1)} - t^{2} ( 1 - \xi )_{q}^{( \alpha - 1) }}{ \Gamma _{q} ( \sigma ) },& \xi < t, \\ \frac{- t^{2} ( 1 - \xi )_{q}^{ (\sigma - 1)}}{\Gamma _{q} ( \sigma ) }, & t< \xi , \end{cases} $$

(5)

for all $t, \xi \in \overline{J}_{0}$.

Proof

By Lemma (2.3) the solution of Eq. (3) can be written as

$$ y(t) = \int _{0}^{t} (t - \xi )_{q}^{ (\sigma - 1)} v(\xi ) \,\mathrm{d}_{q}\xi - d_{0} - d_{1}t - d_{2}t^{2}. $$

Since $y(0) = y'(0 ) = 0$, a simple calculation gives $d_{0} - d_{1} = 0$, and from the boundary condition, we get $\mathcal{I}_{q}^{\sigma }[v](1) -d_{2} = a \mathcal{I}_{q}^{\sigma }[v](e) - d_{2} a e^{2}$. Hence,

$$ d_{2} = \frac{1}{1 - a e^{2}} \bigl( \mathcal{I}_{q}^{\sigma }[v](1) - a \mathcal{I}_{q}^{\sigma }[v](e) \bigr). $$

Thus, the solution of boundary value problem (3) is

$$\begin{aligned} y(t) &= \mathcal{I}_{q}^{\sigma }[v](t) - \frac{t^{2}}{1 - a e^{2}} \bigl( \mathcal{I}_{q}^{\sigma }[v](1) - a \mathcal{I}_{q}^{\sigma }[v](e) \bigr) \\ & = \mathcal{I}_{q}^{\sigma }[v](t) - t^{2} \mathcal{I}_{q}^{\sigma }[v](1) - \frac{ae^{2}t^{2}}{1 - a e^{2}} \mathcal{I}_{q}^{\sigma }[v](1) + \frac{at^{2}}{1 - a e^{2}} \mathcal{I}_{q}^{\sigma }[v](e) \\ & = \frac{1}{\Gamma _{q} ( \sigma )} \int _{0}^{t} \bigl( ( t - \xi )_{q}^{ (\sigma - 1)} - t^{2} (1 - \xi )_{q}^{ (\sigma - 1)} \bigr) v(\xi ) \,\mathrm{d}_{q}\xi \\ &\quad {} - \frac{1}{\Gamma _{q} ( \sigma )} \int _{1}^{t} t^{2} (1 - \xi )_{q}^{( \sigma - 1)} v(\xi ) \,\mathrm{d}_{q}\xi \\ &\quad {} + \frac{a t^{2}}{(1 - a e^{2}) \Gamma _{q} ( \sigma ) } \biggl[ \int _{0}^{e} \bigl( (e - \xi )_{q}^{ (\sigma - 1)} - e^{2} (1 - \xi )_{q}^{ (\sigma - 1)} \bigr) v(\xi ) \,\mathrm{d}_{q}\xi \\ &\quad {} - \int _{e}^{t} e^{2} (1 - \xi )_{q}^{ (\sigma - 1)} v(\xi ) \,\mathrm{d}_{q}\xi \biggr] \\ & = \int _{0}^{1} G_{q}(t, \xi ) v(\xi ) \,\mathrm{d}_{q}\xi + \frac{a t^{2}}{1 - a e^{2}} \int _{0}^{1} G_{q}(e, \xi ) v(\xi ) \,\mathrm{d}_{q}\xi , \end{aligned}$$

where $G_{q}(t, \xi )$ is defined in Eq. (5). This completes the proof. □

Now, in order to investigate the existence of solutions, we prove some properties of the function $G_{q}(t, \xi )$.

Lemma 3.2

The functions $G_{q}(t,\cdot)$ and $\frac{\partial }{\partial t} G_{q}(t, \cdot)$ are integrable for each $t \in \overline{J}_{0}$ and have the following properties:

$$ \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi \leq \frac{2}{ \Gamma _{q} ( \sigma + 1)}, \int _{0}^{1} \biggl\vert \frac{ \partial }{\partial t} G_{q}(t, \xi ) \biggr\vert \,\mathrm{d}_{q} \xi \leq \frac{3}{ \Gamma _{q} ( \sigma )}. $$

Proof

Let $t \in \overline{J}_{0}$. Then we have

$$\begin{aligned} \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi &\leq \mathcal{I}_{q}^{\sigma }[I](t) + + t^{2}\mathcal{I}_{q}^{\sigma }[I](1) \\ & \leq \frac{t^{\sigma }}{\Gamma _{q} ( \sigma + 1)} + \frac{t^{2}}{\Gamma _{q} ( \sigma + 1)} \leq \frac{2}{\Gamma _{q} ( \sigma + 1)} \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{1} \biggl\vert \frac{\partial }{ \partial t} G_{q}(t, \xi ) \biggr\vert \,\mathrm{d}_{q}\xi & \leq 2t \mathcal{I}_{q}^{\sigma }[I](1) + + \mathcal{I}_{q}^{\sigma -1}[I](t) \\ & \leq \frac{2t}{\Gamma _{q} ( \sigma + 1)} + \frac{t^{\sigma -1 }}{ \Gamma _{q} ( \sigma ) } \leq \frac{3}{ \Gamma _{q} ( \sigma )}. \end{aligned}$$

Hence, $G_{q}(t, \cdot)$ and $\frac{ \partial }{\partial t} G_{q}(t, \cdot)$ are integrable. □

Let $C^{1} (\overline{J}_{0})$ be the class of all continuous functions. Since ${}^{C}\mathcal{D}_{q}^{\varsigma }[y](t) = \mathcal{I}_{q}^{1 - \varsigma } [y'](t)$ for $\varsigma \in J_{0}$, the operator ${}^{C}\mathcal{D}_{q}^{\varsigma }$ is continuous for any $y \in C^{1} (\overline{J}_{0})$. Now, for $y \in C^{1}(\overline{J}_{0})$, we define the space

$$ \mathcal{A} = \bigl\{ y(t) : y(t) \in C^{1} (\overline{J}_{0}) \bigr\} $$

endowed with the maximum norm

$$ \Vert y \Vert = \max_{t \in \overline{J}_{0} } \bigl\vert y(t) \bigr\vert + \max_{t \in \overline{J}_{0} } \bigl\vert {}^{C}\mathcal{ D}_{q}^{\varsigma }[y](t) \bigr\vert . $$

Lemma 3.3

$(\mathcal{A}, \|\cdot\|)$ is a Banach space.

Proof

Let $\{y_{n} \}_{n=1}^{\infty }$ be a Cauchy sequence in the space $(\mathcal{A}, \|\cdot\|)$. Obviously, $\{y_{n} \}_{n=1}^{\infty }$ and $\{ {}^{C}\mathcal{D}_{q}^{\varsigma }y_{n} \}_{n=1}^{\infty }$ are Cauchy sequences in the space $C (\overline{J}_{0})$. Since $C (\overline{J}_{0})$ is compact, $\{y_{n} \}_{n=1}^{\infty }$ and $\{ {}^{C}\mathcal{D}_{q}^{\varsigma }y_{n} \}_{n=1}^{\infty }$ uniformly converge to some v, $v'$ on $\overline{J}_{0}$. Furthermore, v, $v'$ belong to $C(\overline{J}_{0})$. In the following, we need to show that $v'= {}^{C}\mathcal{D}_{q}^{\varsigma }v$. Now, by the definition of fractional integral,

$$\begin{aligned} \bigl\vert \mathcal{I}_{q}^{\varsigma } \bigl[{}^{C} \mathcal{D}_{q}^{\varsigma }[y_{n}] \bigr](t) - \mathcal{I}_{q}^{\varsigma }v'(t) \bigr\vert & \leq \mathcal{I}_{q}^{\varsigma } \bigl[ \bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }y_{n} - v' \bigr\vert \bigr](t) \\ & \leq \frac{1}{ \Gamma _{q}(\varsigma +1)} \max_{t \in \overline{J}_{0}} \bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }y_{n} - v' \bigr\vert . \end{aligned}$$

Therefore, using the convergence of $\{ {}^{C}\mathcal{D}_{q}^{\varsigma }y_{n} \}_{n=1}^{\infty }$ implies that

$$ \lim_{n \to \infty } \mathcal{I}_{q}^{\varsigma } \bigl[{}^{C}\mathcal{D}_{q}^{\varsigma }[y_{n}] \bigr](t) = \mathcal{I}_{q}^{\varsigma } \bigl[v' \bigr](t) $$

uniformly on $\overline{J}_{0}$. On the other hand, we know $\mathcal{I}_{q}^{\varsigma }[{}^{C}\mathcal{D}_{q}^{\varsigma }[y_{n}]](t) = y_{n}$ for each $t \in \overline{J}_{0}$ and $\varsigma \in J_{0}$. Hence, $\mathcal{I}_{q}^{\varsigma }[v'](t)= v$, and this means $v'={}^{C}\mathcal{D}_{q}^{\varsigma }v$. This completes the proof. □

Remark 3.1

Lemma (2.3) implies that the solution of problem (1) coincides with the fixed point of the operator $\mathcal{O}$ defined as

$$\begin{aligned} \mathcal{O} y(t) & = \int _{0}^{1} G_{q}(t, \xi ) w \bigl( y(t), {}^{C} \mathcal{D}_{q}^{\varsigma }[y](t) \bigr) \,\mathrm{d}_{q}\xi \\ &\quad {} + \frac{a t^{2}}{1 - a e^{2}} \int _{0}^{1} G_{q}(e, \xi ) w \bigl( y(t), {}^{C}\mathcal{D}_{q}^{\varsigma }[y](t) \bigr) \,\mathrm{d}_{q}\xi . \end{aligned}$$

3.1 Existence and uniqueness

According to the Schauder fixed point theorem, the existence result has been stated.

Theorem 3.4

Suppose that $w: \mathbb{R}^{2} \to \mathbb{R}$ is a continuous function and there exist constants $m_{0}, m_{1} \geq 0$, $\beta _{0}, \beta _{1} \in J_{0}$ such that one of the following conditions is satisfied:

• (A1) There exists a nonnegative function $\mu (t) \in \overline{J}_{0}$ such that

  $$ \bigl\vert w(y,z) \bigr\vert \leq \mu (t) + m_{0} \vert y \vert ^{\beta _{0}} + m_{1} \vert z \vert ^{\beta _{1}}. $$

  (6)

• (A2) The function w satisfies

  $$ \bigl\vert w(y,z) \bigr\vert \leq m_{0} \vert y \vert ^{\beta _{0}} + m_{1} \vert z \vert ^{\beta _{1}}. $$

  (7)

Then boundary value problem (1) has at least one solution $y(t)$.

Proof

First, suppose that condition (A1) holds. Define the set $\mathcal{B}$ by

$$ \mathcal{B} = \bigl\{ y(t) : \bigl\Vert y(t) \bigr\Vert \leq \delta , t \in \overline{J}_{0} \bigr\} , $$

where

$$\begin{aligned} &\delta \geq \max \biggl\{ ( 6\Delta m_{0})^{\frac{1}{1 - \beta _{0}} }, (6\Delta m_{1} )^{ \frac{1}{1 - \beta _{1}}}, 6\Delta M_{1}, \biggl( \frac{ 12 \Delta m_{0} }{ \Gamma _{q} (2 - \varsigma )} \biggr)^{ \frac{1}{1 - \beta _{0}} }, \\ &\hphantom{\delta \geq{}} \biggl( \frac{ 12 \Delta m_{1}}{ \Gamma _{q} (2 - \varsigma )} \biggr)^{\frac{1}{1 - \beta _{1}}}, \frac{ 16 a M_{1}}{ \Gamma _{q} (2 - \varsigma )( 1 - a e^{2})}, \frac{ 8 M_{2}}{ \Gamma _{q} (2 - \varsigma ) } \biggr\} , \\ &\Delta = \biggl( 1 + \frac{a}{ 1 - ae^{2}} \biggr) \frac{2}{\Gamma _{q} ( \sigma + 1 )}, \end{aligned}$$

(8)

and

$$\begin{aligned}& M_{1} = \max_{t \in \overline{J}_{0}} \biggl\{ \frac{1}{\Gamma _{q} (\sigma )} \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) \mu ( \xi ) \bigr\vert \,\mathrm{d}_{q}\xi \biggr\} \\& M_{2} = \max_{t \in \overline{J}_{0} } \biggl\{ \frac{1}{\Gamma _{q} (\sigma )} \int _{0}^{1} \biggl\vert \frac{\partial }{\partial t} G_{q}(t, \xi ) \mu (\xi ) \biggr\vert \,\mathrm{d}_{q}\xi \biggr\} . \end{aligned}$$

(9)

It is clear that $\mathcal{B}$ is a closed, bounded, and convex subset of Banach space ${}\mathcal{A}$. Here, we prove that $\mathcal{O} : \mathcal{B} \to \mathcal{B}$. For any $y \in \mathcal{B}$, we obtain

$$\begin{aligned} \bigl\vert \mathcal{O} y(t) \bigr\vert & \leq \int _{0}^{1} \bigl\vert G_{q} (t, \xi ) w \bigl( y(t), {}^{C}\mathcal{D}_{q}^{\varsigma }[y] (t) \bigr) \bigr\vert \,\mathrm{d}_{q}\xi \\ &\quad{} + \frac{a t^{2}}{1 - ae^{2}} \int _{0}^{1} \bigl\vert G_{q}(e, \xi ) w \bigl( y(t), {}^{C}\mathcal{D}_{q}^{\varsigma }[y](t) \bigr) \bigr\vert \,\mathrm{d}_{q}\xi \\ & \leq \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) \mu (\xi ) \bigr\vert \,\mathrm{d}_{q} \xi + \bigl[ m_{0} \delta ^{\beta _{0} } + m_{1} \delta ^{\beta _{1}} \bigr] \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi \\ &\quad{} + \frac{a}{1 - a e^{2}} \biggl[ \int _{0}^{1} \bigl\vert G_{q}(e, \xi ) \mu (\xi ) \bigr\vert \,\mathrm{d}_{q}\xi \\ &\quad{} + \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi \biggr] \\ & \leq \biggl( 1+ \frac{a}{1 - a e^{2}} \biggr) \biggl[ M_{1} + \frac{2}{\Gamma _{q} (\sigma + 1 ) } \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \biggr] \\ & \leq \Delta \bigl[ M_{1} + \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \bigr] \leq \frac{1}{2} \delta . \end{aligned}$$

Thus, for almost all $\varsigma \in J_{0}$, we have

$$\begin{aligned} \bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }[ \mathcal{O}y](t) \bigr\vert & = \bigl\vert \mathcal{I}_{q}^{1 - \varsigma } \bigl[\mathcal{O}y' \bigr](t) \bigr\vert \\ & \leq \frac{1}{\Gamma _{q} ( 1 - \varsigma )} \int _{0}^{t} ( t - \xi )_{q}^{(-\varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{1} \biggl\vert \frac{ \partial }{\partial \xi } G_{q}(\xi , \tau ) w \bigl( \tau , y ( \tau ), {}^{C} \mathcal{ D}_{q}^{\varsigma }[y] (\tau ) \bigr) \biggr\vert \,\mathrm{d}_{q}\tau \\ &\quad{} + \frac{2a \xi }{(1 - a e^{2}) } \int _{0}^{1} \bigl\vert G_{q}(e, \tau ) w \bigl( \tau , y( \tau ), {}^{C}\mathcal{ D}_{q}^{\varsigma }[y] ( \tau ) \bigr) \bigr\vert \,\mathrm{d}_{q} \tau \biggr) \,\mathrm{d}_{q}\xi \\ & \leq \frac{1}{\Gamma _{q} ( 1 - \varsigma ) } \int _{0}^{t} ( t - q \xi )^{(-\varsigma )} \biggl[ \int _{0}^{1} \biggl\vert \frac{\partial }{\partial \xi } G_{q}(\xi , \tau ) \mu (\tau ) \biggr\vert \\ &\quad{} + \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \int _{0}^{1} \biggl\vert \frac{\partial }{\partial \xi } G_{q}(\xi , \tau ) \biggr\vert \,\mathrm{d}_{q}\tau \\ &\quad{} + \frac{2a\xi }{1 - ae^{2}} \biggl( \int _{0}^{1} \bigl\vert G_{q} ( \xi , \tau )\mu (\tau ) \bigr\vert {\,\mathrm{d}}_{q}\tau \\ &\quad{} + \bigl( m_{0} \delta ^{\beta _{0}} + m_{0} \delta ^{\beta _{1}} \bigr) \int _{0}^{1} \bigl\vert G_{q}(e, \tau ) \bigr\vert { \,\mathrm{d}}_{q}\tau \biggr) \biggr] { \,\mathrm{d}}_{q}\xi \\ & \leq \frac{1}{\Gamma _{q} ( 1 - \varsigma ) } \int _{0}^{t} ( t - \xi )_{q}^{(-\varsigma )} \biggl( M_{2} + \frac{3 }{\Gamma _{q} (\sigma )} \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \biggr) \,\mathrm{d}_{q}\xi \\ &\quad{} + \frac{2a}{ (1 - ae^{2}) \Gamma _{q} (1 - \varsigma ) } \int _{0}^{t} \xi (t-\xi )_{q}^{(-\varsigma )} \\ &\quad{} \times \biggl( M_{1} + \frac{2}{\Gamma _{q} (\sigma + 1) } \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \biggr) \,\mathrm{d}_{q}\xi \\ & \leq \frac{1}{\Gamma _{q} ( 1 - \varsigma ) } \biggl( M_{2} + \frac{3 }{\Gamma _{q} (\sigma )} \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \biggr) \frac{t^{1 - \varsigma }}{1 - \varsigma } \\ &\quad{} + \frac{2a}{ (1 - ae^{2}) \Gamma _{q} (1 - \varsigma ) } \biggl( M_{1} + \frac{2}{\Gamma _{q} (\sigma + 1) } \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \biggr) \\ &\quad{} \times \frac{t^{2 - \varsigma }}{(1 - \varsigma ) \Gamma _{q}(2 - \varsigma )} \\ & \leq \frac{1}{\Gamma _{q} ( 2 - \varsigma ) } \biggl( M_{2} + \frac{3 }{\Gamma _{q} (\sigma )} \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \biggr) \\ &\quad{} + \frac{2a}{ (1 - ae^{2}) \Gamma _{q} (3 - \varsigma ) } \biggl( M_{1} + \frac{2}{\Gamma _{q} (\sigma + 1) } \bigl( m_{0} \delta ^{\beta _{0}} + m_{1} \delta ^{\beta _{1}} \bigr) \biggr) \\ & \leq \frac{3 \Delta }{\Gamma _{q} ( 2 - \varsigma )} \bigl( m_{0} \delta ^{\beta _{0}} \bigr) + \frac{2a M_{1} }{(1 - ae^{2})\Gamma _{q} ( 2 - \varsigma ) } + \frac{M_{2}}{\Gamma _{q} ( 2 - \varsigma ) } \\ & \leq \frac{1}{2} \delta . \end{aligned}$$

Clearly, $\mathcal{O}y(t)$ and ${}^{C}\mathcal{D}_{q}^{\varsigma }[\mathcal{O}y](t)$ are continuous in $\overline{J}_{0}$. Therefore $\mathcal{O} : \mathcal{B} \to \mathcal{B}$. In the second case, suppose that condition (A2) holds. Choose

$$ 0 < \delta \leq \min \biggl\{ \biggl( \frac{1}{4\Delta m_{0}} \biggr)^{ \frac{1}{1 - \beta _{0}}}, \biggl( \frac{1}{4\Delta m_{1}} \biggr)^{ \frac{1}{1 - \beta _{1}}}, \biggl( \frac{ \Gamma _{q} (2 - \varsigma ) }{6\Delta m_{0}} \biggr)^{ \frac{1}{1 - \beta _{0}}}, \biggl( \frac{\Gamma _{q} (2 - \varsigma ) }{6\Delta m_{1}} \biggr)^{ \frac{1}{1 - \beta _{1}} } \biggr\} . $$

Again, by a similar way, we get $\| \mathcal{O}y \| \leq \delta$, and therefore, in this case, $\mathcal{O} : \mathcal{B} \to \mathcal{B}$. Here, we need to show that $\mathcal{O}$ is a completely continuous operator. First, the equicontinuity of $\mathcal{O}$ will be shown as follows. Suppose that $s_{1}, s_{2} \in \overline{J}_{0}$ with $s_{1} < s_{2}$ and

$$ N_{0} = 1+\max_{ t \in \overline{J}_{0}} \bigl\{ \bigl\vert w \bigl( t, y(t), {}^{C}\mathcal{D}_{q}^{\varsigma }[y](t) \bigr) \bigr\vert : y \in \mathcal{B} \bigr\} . $$

Then

$$\begin{aligned} &\bigl\vert \mathcal{O}y (s_{1}) - \mathcal{O}y (s_{2}) \bigr\vert \\ &\quad = \biggl\vert \int _{0}^{1} \bigl( G_{q}(s_{2}, \xi ) - G_{q}(s_{1}, \xi ) \bigr) w \bigl( y(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) \,\mathrm{d}_{q}\xi \\ &\quad \quad{} + \frac{a( s_{2}^{2} - s_{1}^{2} ) }{ 1 - ae^{2}} \int _{0}^{1} G_{q}(e, \xi ) w \bigl( y(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad \leq N_{0} \int _{0}^{1} \bigl\vert G_{q}(s_{2}, \xi ) - G_{q}(s_{1}, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi + \frac{2 a N_{0} }{1 - a e^{2}} \bigl( s_{2}^{2} - s_{1}^{2} \bigr) \\ &\quad \leq \frac{2 a N_{0} }{1 - a e^{2}} \bigl( s_{2}^{2} - s_{1}^{2} \bigr) + \frac{N_{0}}{\Gamma _{q} ( \sigma ) } \biggl[ \int _{0}^{s_{1}} \bigl( s_{2}^{2} - s_{1}^{2} \bigr) (1 -\xi )_{q}^{(\sigma - 1)} \\ &\quad \quad{} + (s_{2} - \xi )_{q}^{(\sigma - 1)} + (s_{1} -\xi )_{q}^{( \sigma - 1)} \,\mathrm{d}_{q}\xi \\ &\quad \quad{} + \int _{s_{1}}^{s_{2}} \bigl( s_{2}^{2} - s_{1}^{2} \bigr) (1 - \xi )_{q}^{( \sigma - 1)} + (s_{2} - \xi )_{q}^{(\sigma - 1)} \,\mathrm{d}_{q} \xi \\ &\quad \quad{} + \int _{s_{2}}^{1} \bigl( s_{2}^{2} - s_{1}^{2} \bigr) (1 - \xi )_{q}^{( \sigma - 1)} \,\mathrm{d}_{q}\xi \biggr] \\ &\quad \leq \frac{ 2 a N_{0} }{1 - ae^{2})} \bigl( s_{2}^{2} - s_{1}^{2} \bigr) + \frac{N_{0}}{\Gamma _{q} ( \alpha )} \biggl[ \bigl( s_{2}^{2} - s_{1}^{2} \bigr) \int _{0}^{1} (1 - \xi )_{q}^{(\sigma - 1)} \,\mathrm{d}_{q}\xi \\ &\quad \quad{} + \int _{0}^{s_{2}} \bigl(s_{2}^{2} - \xi \bigr)_{q}^{(\sigma - 1)} \,\mathrm{d}_{q}\xi - \int _{0}^{s_{1}} \bigl(s_{1}^{2} - \xi \bigr)_{q}^{( \sigma - 1)} \,\mathrm{d}_{q}\xi \biggr] \\ & \quad \leq \frac{N_{0}}{\Gamma _{q} ( \alpha + 1)} \biggl[ s_{2}^{2} - s_{1}^{2} + s_{2}^{\sigma }- s_{1}^{\sigma }+ \frac{ 2 a(s_{2}^{2} - s_{1}^{2} )}{1- a e^{2} } \biggr] \\ &\quad \leq N_{0} \biggl[ \Delta \bigl( s_{2}^{2} - s_{1}^{2} \bigr) + \frac{ s_{2}^{\sigma }- s_{1}^{\sigma }}{ \Gamma _{q} ( \sigma + 1) } \biggr], \end{aligned}$$

and

$$\begin{aligned} &\bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }[ \mathcal{O}y](s_{2}) - {}^{C} \mathcal{D}_{q}^{\varsigma }[ \mathcal{O}y ] (s_{2}) \bigr\vert \\ &\quad = \frac{1}{ \Gamma _{q} ( 1 - \varsigma ) } \biggl\vert \int _{0}^{s_{2}} (s_{2} - \xi )_{q}^{(-\varsigma )} \biggl( \int _{0}^{1} \frac{\partial }{ \partial \xi } G_{q}( \xi , \tau ) w \bigl( y (\tau ), {}^{C} \mathcal{D}_{q}^{\varsigma }[y]( \tau ) \bigr) \,\mathrm{d}_{q}\tau \\ &\quad \quad{} + \frac{ 2 a\xi }{1 - ae^{2}} \int _{0}^{1} G_{q}(e, \tau ) w \bigl( y(\tau ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y] (\tau ) \bigr) \biggr) \,\mathrm{d}_{q}\xi \\ &\quad \quad{} - \int _{0}^{s_{1}} (s_{1} - \xi )_{q}^{(-\varsigma )} \biggl( \int _{0}^{1} \frac{\partial }{\partial \xi } G_{q}(\xi , \tau ) w \bigl( y(\tau ), {}^{C} \mathcal{D}_{q}^{\varsigma }[y] (\tau ) \bigr) \,\mathrm{d}_{q}\tau \\ &\quad \quad{} + \frac{ 2 a \xi }{ 1 - ae^{2} } \int _{0}^{1} G_{q}(e, \tau ) w \bigl( y(\tau ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y] ( \tau ) \bigr) \,\mathrm{d}_{q}\tau \biggr) \,\mathrm{d}_{q} \xi \biggr\vert \\ &\quad \leq \frac{3N_{0} }{ \Gamma _{q} ( 1 - \varsigma ) \Gamma _{q} ( \sigma )} \biggl\vert \int _{0}^{s_{2}} (s_{2} - \xi )_{q}^{(-\varsigma )} \,\mathrm{d}_{q}\xi - \int _{0}^{s_{1}} (s_{1} - \xi )_{q}^{(- \varsigma )} \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad \quad{} + \frac{6 a N_{0} }{\Gamma _{q} ( 1 - \varsigma ) \Gamma _{q} ( \sigma ) ( 1 - ae^{2}) } \\ &\quad \quad{} \times \biggl\vert \int _{0}^{s_{2}} \xi (s_{2} - \xi )_{q}^{(- \varsigma )} \,\mathrm{d}_{q}\xi - \int _{0}^{s_{1}} \xi (s_{1} - \xi )_{q}^{(-\varsigma )} \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad \leq \frac{3N_{0}}{\Gamma _{q} ( 1 - \varsigma ) \Gamma _{q} ( \sigma )} \biggl\vert \int _{0}^{s_{1}} \bigl( (s_{2} - \xi )_{q}^{(-\varsigma )} - (s_{1} - \xi )_{q}^{(-\varsigma )} \bigr) \,\mathrm{d}_{q}\xi \\ &\quad \quad{} + \int _{s_{1}}^{s_{2}} (s_{2} - q\xi )^{(-\varsigma )} \,\mathrm{d}_{q}\xi \biggr\vert + \frac{6 aN_{0} }{ \Gamma _{q} ( 1 - \varsigma ) \Gamma _{q} ( \sigma )(1 - ae^{2})} \\ &\quad \quad{} \times \biggl\vert \int _{0}^{s_{1}} \bigl( \xi (s_{2} - \xi )_{q}^{(- \varsigma )} - \xi (S_{1} - \xi )_{q}^{(-\varsigma )} \bigr) \,\mathrm{d}_{q}\xi \\ &\quad \quad{} + \int _{s_{1}}^{s_{2}} \xi ( s_{2} - q\xi )^{(-\varsigma )} \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad \leq \frac{3N_{0} }{\Gamma _{q} ( 1 - \varsigma ) \Gamma _{q} ( \sigma ) } \bigl( s_{2}^{1 - \varsigma } - s_{1}^{ 1 - \varsigma } + 2 ( s_{2} - s_{1} )_{q}^{(1 - \varsigma )} \bigr) \\ &\quad \quad{} + \frac{6 a N_{0} }{ \Gamma _{q} ( \sigma ) ( 1 - ae^{2})} \\ &\quad \quad{} \times \biggl( \frac{ 2 s_{1} ( s_{2} - s_{1} )_{q}^{(1 - \varsigma )} }{ \Gamma _{q} ( 2 - \varsigma )} + \frac{ s_{2}^{2}- s_{1}^{1} }{ \Gamma _{q} ( 3 - \varsigma )} + \frac{2 ( s_{2} - s_{1} )_{q}^{(2 - \varsigma )} }{ \Gamma _{q} ( 3 - \varsigma ) } \biggr). \end{aligned}$$

Since the functions $s_{2}^{2} -s_{1}^{2}$, $d_{2}^{\sigma }- s_{1}^{\sigma }$, $( s_{2} - s_{1} )_{q}^{(2 - \varsigma )}$, and $s_{1} ( s_{2} - s_{1} )^{1 - \varsigma }$ are continuous, we conclude that $\mathcal{O}y$ is an equicontinuous set. Obviously, $\mathcal{O}y$ is uniformly bounded because $\mathcal{O} (\mathcal{B}) \subseteq \mathcal{B}$. By means of the Arzelá–Ascoli theorem, $\mathcal{O}$ is a compact operator. Therefore, from the Schauder fixed point theorem, the operator $\mathcal{O}$ has a fixed point, i.e., the q-fractional boundary value problem (1) has a solution. □

In what follows, we prove the uniqueness of solution for Eq. (1) based on application of the Banach fixed point theorem.

Theorem 3.5

Let $w : \mathbb{R}^{2} \to \mathbb{R}$ be a continuous function and let it fulfill a Lipschitz condition with respect to the first and second variables with Lipschitz constant

$$ 0 < \ell < \frac{\Gamma _{q} ( 2 - \varsigma )}{\Delta [ 3 + \Gamma _{q} ( 2 - \varsigma )] }, $$

(10)

i.e.,

$$ \bigl\vert w(y_{1},z_{1}) - w(y_{2}, z_{2}) \bigr\vert \leq \ell \bigl( \vert y_{1} - y_{2} \vert + \vert z_{1} - z_{2} \vert \bigr). $$

Then problem (1) has a unique solution.

Proof

In Theorem 3.4, we have shown that $\mathcal{O}$ is a continuous operator and $\mathcal{O} : \mathcal{B} \to \mathcal{B}$. Therefore, using the Banach fixed point theorem, it is sufficient to show that $\mathcal{O}$ is a contraction mapping. For any $y_{1}, y_{2} \in \mathcal{A}$,

$$\begin{aligned} &\bigl\vert \mathcal{O}y_{1} (t) - \mathcal{O} y_{2}(t) \bigr\vert \\ &\quad \leq \biggl\vert \int _{0}^{1} G_{q}(t, \xi ) \bigl( w \bigl( y_{1}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y_{1}]( \xi ) \bigr) \\ &\quad \quad{} - w \bigl( y_{2}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y_{2}]( \xi ) \bigr) \bigr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad \quad{} + \frac{at^{2} }{1 - a e^{2}} \biggl\vert \int _{0}^{1} G_{q}(e, \xi ) \bigl( w \bigl( y_{1}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y_{1}]( \xi ) \bigr) \\ &\quad \quad{} - w \bigl( y_{2} (\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y_{2}] (\xi ) \bigr) \bigr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad \leq \ell \Vert y_{1} - y_{2} \Vert \biggl( \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi + \frac{at^{2} }{1 - a e^{2}} \int _{0}^{1} \bigl\vert G_{q}(e, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi \biggr) \\ &\quad \leq \ell \Delta \Vert y_{1} - y_{2} \Vert , \\ &\bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }[ \mathcal{O}y](s_{2}) - {}^{C} \mathcal{D}_{q}^{\varsigma }[ \mathcal{O}y](s_{2}) \bigr\vert \\ &\quad = \biggl\vert \frac{1}{\Gamma _{q} ( 1 - \varsigma ) } \int _{0}^{t} (t - \xi )_{q}^{(-\varsigma )} \bigl( \mathcal{O}'y_{1} ( \xi ) - \mathcal{O}'y_{1} (\xi ) \bigr) \,\mathrm{d}_{q} \xi \biggr\vert \\ &\quad \leq \frac{1}{\Gamma _{q} ( 1 - \varsigma )} \biggl\vert \int _{0}^{t} (t - \xi )_{q}^{(-\varsigma )} \\ &\quad \quad{} \times \biggl( \int _{0}^{1} \frac{ \partial }{ \partial \xi } G_{q} (\xi , \tau ) \bigl( w \bigl( y_{1}(\tau ), {}^{C}\mathcal{D }_{q}^{\varsigma }[y_{1}]( \tau ) \bigr) \\ &\quad \quad{} - w \bigl( y_{2}(\tau ) , {}^{C}\mathcal{D}_{q}^{\varsigma }[y_{2}] (\tau ) \bigr) \bigr) \,\mathrm{d}_{q}\tau \\ &\quad \quad{} + \frac{2a\xi }{1 - a e^{2}} \int _{0}^{1} G_{q}(e, \tau ) \bigl( w \bigl( y_{1}(\tau ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y_{1}]( \tau ) \bigr) \\ &\quad \quad{} - w \bigl( y_{2}(\tau ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y_{2}]( \tau ) \bigr) \bigr) \,\mathrm{d}_{q}\tau \biggr) \,\mathrm{d}_{q} \xi \biggr\vert \\ &\quad \leq \frac{3\ell }{\Gamma _{q} ( 1 - \varsigma )\Gamma _{q} ( \sigma ) } \Vert y_{1} - y_{2} \Vert \\ &\quad \quad{} \times \biggl( \int _{0}^{t} (t - \xi )_{q}^{(-\varsigma )} \,\mathrm{d}_{q}\xi + \frac{2a }{1 - ae^{2}} \int _{0}^{t} \xi (t - \xi )_{q}^{(-\varsigma )} \,\mathrm{d}_{q}\xi \biggr) \\ &\quad \leq \frac{3 \ell \Delta }{\Gamma _{q} ( 2 - \varsigma ) } \Vert y_{1} - y_{2} \Vert . \end{aligned}$$

Therefore

$$ \Vert \mathcal{O}y_{1} - \mathcal{O}y_{2} \Vert \leq \biggl[ \Delta \ell + \frac{3 \ell \Delta }{\Gamma _{q} ( 2 - \varsigma ) } \biggr] \Vert y_{1} - y_{2} \Vert . $$

Hence, by the Banach fixed point theorem, $\mathcal{O}$ has a unique fixed point which is a solution of problem (1). □

3.2 Stability of solution

In this section, we study the stability analysis of problem (1) under various perturbations. Dependence solution on the boundary value condition is discussed in Theorem 3.6. Stability of the solution with respect to the perturbation of w is analyzed in Theorem 3.7. Finally, the perturbation effect of fractional order derivative on the solution is studied in Lemma 3.8 and Theorem 3.9.

Theorem 3.6

Suppose that function w fulfills the conditions of Theorem 3.5, and let $\hat{v}(t)$ be the solution of the following perturbed problem:

$$ {}^{C}\mathcal{D}_{q}^{\sigma }[y](t) = w \bigl( y(t), {}^{C} \mathcal{D}_{q}^{\varsigma }[y](t) \bigr) $$

(11)

for each $2 < \alpha \leq 3$, $\varsigma \in J_{0}$, on the boundary value conditions $y(0) = \epsilon _{1}$, $y'(0) = \epsilon _{2}$, and

$$ y(1) = a y(e) + \epsilon _{3} $$

for $e \in J_{0}$ with $0 \leq a < \frac{1}{e^{2}}$. Then $\| y - \hat{v} \| = O(\epsilon )$, here $\epsilon = \max \{ \epsilon _{1}, \epsilon _{2}, \epsilon _{3}\}$.

Proof

Similar to Lemma 2.3 the solution of problem (11) is

$$\begin{aligned} \hat{v}(t) & = \int _{0}^{1} G_{q}(t, q\xi ) w \bigl( \hat{v}(\xi ), {}^{C} \mathcal{D}_{q}^{\varsigma } \bigl[\hat{v}(\xi ) \bigr] \bigr) \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{at^{2} }{1 - a e^{2}} \int _{0}^{1} G_{q}(e, q\xi ) w \bigl( \hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\xi ) \bigr) \,\mathrm{d}_{q}\xi + h(t), \end{aligned}$$

(12)

where

$$ h(t) = \frac{ t^{2} }{1 - ae^{2}} \bigl( \epsilon _{1} ( a- 1 ) + \epsilon _{2} ( ae - 1 ) \bigr) + \epsilon _{2} t + \epsilon _{1}. $$

Thus,

$$\begin{aligned} \vert y - \hat{v} \vert & \leq \biggl\vert \int _{0}^{1} G_{q}(t, \xi ) \bigl[ w \bigl( y(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) - w \bigl( y(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) \bigr] \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad{} + \frac{ a t^{2} }{1 - ae^{2}} \biggl\vert \int _{0}^{1} G_{q}(e, \xi ) \bigl[ w \bigl( y(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) \\ &\quad{} - w \bigl( \hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\xi ) \bigr) \bigr] \,\mathrm{d}_{q}\xi \biggr\vert + \bigl\vert h(t) \bigr\vert \\ & \leq \ell \Vert y - \hat{v} \Vert \biggl( \int _{0}^{1} G_{q}(t, \xi ) { \,\mathrm{d}}_{q}\xi + \frac{ a t^{2} }{1 - ae^{2}} \int _{0}^{1} G_{q}(t, \xi ) { \,\mathrm{d}}_{q}\xi \biggr) + \bigl\vert h(t) \bigr\vert \\ & \leq \ell \Delta \Vert y - \hat{v} \Vert + \bigl\vert h(t) \bigr\vert , \end{aligned}$$

and

$$\begin{aligned} &\bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }[y](t) - {}^{C}\mathcal{D}_{q}^{\varsigma }[\hat{v}](t) \bigr\vert \\ &\quad = \frac{ 1 }{\Gamma _{q} ( 1 - \varsigma )} \biggl\vert \int _{0}^{t} ( t - \xi )_{q}^{(-\varsigma )} \\ &\qquad {}\times \biggl( \int _{0}^{1} \frac{ \partial }{\partial \xi } G_{q}( \xi , \tau ) \bigl( w \bigl( y(\tau ), {}^{C} \mathcal{D}_{q}^{\varsigma }[y](\tau ) \bigr) - w \bigl( \hat{v}( \tau ), {}^{C} \mathcal{D}_{q}^{\varsigma }[\hat{v}]( \tau ) \bigr) \bigr) \,\mathrm{d}_{q}\tau \\ &\quad \quad{} + \frac{ 2 a\xi }{1 - ae^{2} } \int _{0}^{1} G_{q}(e, \tau ) \bigl( w \bigl( y(\tau ), {}^{C}\mathcal{D }_{q}^{\varsigma }[y]( \tau ) \bigr) \\ &\quad \quad{} - w \bigl( \hat{v}(\tau ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\tau ) \bigr) \bigr) \,\mathrm{d}_{q}\tau \biggr) \,\mathrm{d}_{q}\xi \biggr\vert + \bigl\vert {}^{C} \mathcal{D}_{q}^{\varsigma }[h](t) \bigr\vert \\ &\quad \leq \frac{3 \ell }{ \Gamma _{q} ( 1 - \varsigma )\Gamma _{q} (\sigma )} \Vert y - \hat{v} \Vert \biggl( \int _{0}^{t} ( t - \xi )_{q}^{(-\varsigma )} \,\mathrm{d}_{q}\xi \\ &\quad \quad{} + \frac{ 2 a\xi }{1 - ae^{2} } \int _{0}^{t} \xi ( t - \xi )_{q}^{(- \varsigma )} \,\mathrm{d}_{q}\xi \biggr)+ \bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }[h](t) \bigr\vert \\ &\quad \leq \frac{3 \ell \Delta }{ \Gamma _{q} ( 1 - \varsigma )} \Vert y - \hat{v} \Vert + \bigl\vert {}^{C} \mathcal{D}_{q}^{\varsigma }[h](t) \bigr\vert . \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert y - \hat{v} \Vert & \leq \frac{1}{ 1 - ( \ell \Delta + \frac{3 \ell \Delta }{\Gamma _{q} ( 2 - \varsigma )} ) } \\ &\quad{} \times \biggl( \biggl\vert \frac{ at^{2} }{1 - ae^{2}} \bigl( \epsilon _{1} ( a- 1 ) + \epsilon _{2}( ae - 1 ) \bigr) +\epsilon _{2} t + \epsilon _{1} \biggr\vert \\ &\quad{} + \biggl\vert \frac{2t^{2-\varsigma }}{(1-ae^{2}) \Gamma _{q}(3-\varsigma )} \bigl( \epsilon _{1} ( a- 1 ) + \epsilon _{2}( ae - 1 ) \bigr)+ \frac{ \epsilon _{2}}{\Gamma _{q} ( 2 - \varsigma )} t^{ 1 - \varsigma } \biggr\vert \biggr) \\ & \leq \frac{\epsilon }{1 - (\ell \Delta + \frac{3 \ell \Delta }{\Gamma _{q} ( 2 - \varsigma )} )} \\ &\quad{} \times \biggl\vert \frac{ 1 }{1 - ae^{2}} \biggl[ 1 + \frac{2}{\Gamma _{q} ( 3 - \varsigma )} \biggr] ( a+ 2ae) + 2 + \frac{1}{\Gamma _{q} ( 2 - \varsigma )} \biggr\vert . \end{aligned}$$

This completes the proof. □

Theorem 3.7

Suppose that the conditions of Theorem 3.5hold, and let $\hat{v}(t)$ be the solution of the following perturbed problem on function w:

$$ {}^{C}\mathcal{D}_{q}^{\alpha }[y](t) = w \bigl( y(t), {}^{C} \mathcal{D}_{q}^{\varsigma }[y](t) \bigr) + \epsilon $$

(13)

for $t \in \overline{J}_{0}$, $2 < \alpha \leq 3$, and $\varsigma \in J_{0}$, with the boundary conditions $y_{0} = y'_{0} = 0$, $y_{1} = a y(e)$ for $e \in J_{0}$ with $0 \leq a < \frac{1}{e^{2}}$. Then $\| y - \hat{v} \| = O(\epsilon )$.

Proof

The solution of problem (13) is

$$\begin{aligned} \hat{v} (t)&= \int _{0}^{1} G_{q}(t, \xi ) \bigl( w \bigl( \hat{v}( \xi ), {}^{C}\mathcal{D}_{q}^{\varsigma } \bigr) + \epsilon \bigr) \,\mathrm{d}_{q}\xi \\ &\quad{} + \frac{a t^{2} }{1 - ae^{2}} \int _{0}^{1} G_{q}(e, \xi ) \bigl( w \bigl(\hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\xi ) \bigr) + \epsilon \bigr) \,\mathrm{d}_{q}\xi . \end{aligned}$$

(14)

Then, similar to the proof of the previous theorem

$$\begin{aligned} \vert y - \hat{v} \vert & \leq \ell \Delta \Vert y - \hat{v} \Vert + \epsilon \biggl( \int _{0}^{1} G_{q}(t, \xi ) \,\mathrm{d}_{q}\xi + \frac{ a t^{2} }{1 - ae^{2}} \int _{0}^{1} G_{q}(t, \xi ) \,\mathrm{d}_{q}\xi \biggr) \\ & \leq \Delta \Vert y - \hat{v} \Vert + \epsilon \Delta \end{aligned}$$

and

$$\begin{aligned} \bigl| {}^{C}\mathcal{D}_{q}^{\varsigma }[y](t)- {}^{C}\mathcal{D}_{q}^{\varsigma }[\hat{v}](t)\bigr| &\leq \frac{3\ell \Delta }{\Gamma _{q} ( 2 - \varsigma ) \Gamma _{q} ( \sigma )} \Vert y - \hat{v} \Vert \\ &\quad{} + \epsilon \biggl( \int _{0}^{t} ( t - \xi )_{q}^{(- \varsigma )} \,\mathrm{d}_{q}\xi + \frac{ 2 a}{1 - ae^{2}} \int _{0}^{t} \xi ( t - \xi )_{q}^{(-\varsigma )} \,\mathrm{d}_{q}\xi \biggr) \\ & \leq \frac{3\ell \Delta }{\Gamma _{q} ( 2 - \varsigma )} \Vert y - \hat{v} \Vert + \frac{3 \epsilon \Delta }{\Gamma _{q} ( 2 - \varsigma )}. \end{aligned}$$

Indeed,

$$ \Vert y - \hat{v} \Vert \leq \frac{\epsilon }{1 - (\ell \Delta + \frac{3 \epsilon \Delta }{ \Gamma _{q} ( 2 - \varsigma )} )} \biggl[ \Delta + \frac{3\Delta }{ \Gamma _{q} ( 2 - \varsigma )} \biggr]. $$

This completes the proof. □

For perturbation analysis on the fractional order of the q-derivative, we first state and prove the following lemma and then the main theorem will be discussed.

Lemma 3.8

Let $s,t \in \overline{J}_{0}$ and $2 < \sigma - \epsilon < \sigma$, then

$$ \int _{0}^{t} \biggl\vert \frac{s^{\sigma - 1}}{ \Gamma _{q} (\sigma )} - \frac{s^{ \sigma - \epsilon - 1}}{ \Gamma _{q} (\sigma - \epsilon )} \biggr\vert \,\mathrm{d}_{q}s = O (\epsilon ). $$

Proof

We estimate the integral as follows:

$$\begin{aligned} \int _{0}^{t} \biggl\vert \frac{s^{\sigma - 1}}{ \Gamma _{q} (\sigma ) } - \frac{s^{\sigma - \epsilon - 1} }{ \Gamma _{q} (\sigma - \epsilon )} \biggr\vert \,\mathrm{d}_{q}s &\leq \int _{0}^{t} \biggl\vert \frac{s^{\sigma - 1}}{ \Gamma _{q} (\sigma )} - \frac{ s^{\sigma - \epsilon - 1}}{ \Gamma _{q} (\sigma - \epsilon )} \biggr\vert \,\mathrm{d}_{q}s \\ &\quad{} + \int _{0}^{t} \biggl\vert \frac{s^{\sigma - \epsilon - 1}}{ \Gamma _{q} (\sigma )} - \frac{ s^{\sigma - \epsilon - 1}}{\Gamma _{q} (\sigma - \epsilon )} \biggr\vert \,\mathrm{d}_{q}s \\ & \leq \frac{1}{\Gamma _{q} (\sigma ) } \biggl[ \frac{1}{\sigma } - \frac{1}{ \alpha - \epsilon } \biggr] + \frac{1}{\sigma - \epsilon } \biggl[ \frac{1}{\Gamma _{q}(\sigma )} - \frac{1}{\Gamma _{q}(\sigma - \epsilon ) } \biggr] \\ & \leq \epsilon \biggl[ \frac{1}{ \sigma (\sigma - \epsilon ) \Gamma _{q}(\sigma )} + \frac{ \vert \Gamma _{q}(\alpha ) \vert }{ (\sigma - \epsilon ) \Gamma _{q} (\sigma ) (\sigma - \epsilon )} \biggr], \end{aligned}$$

where $\sigma - \epsilon < \alpha <\sigma$. □

Theorem 3.9

Suppose that the conditions of Theorem 3.5hold, and let $\hat{v}(t)$ be the solution of the following perturbed problem on fractional order derivative σ:

$$ {}^{C}\mathcal{D}_{q}^{\sigma - \epsilon } [y](t) = w \bigl( y(t), {}^{C} \mathcal{D}_{q}^{\varsigma }[y](t) \bigr), $$

(15)

for $t \in \overline{J}_{0}$, $2 < \sigma \leq 3$, $\varsigma \in J_{0}$, under the boundary conditions $y_{0} = y'_{0} = 0$, $y_{1} = a y(e)$, $e \in J_{0}$ with $0 \leq a < \frac{1}{e^{2}}$ and $2 < \sigma - \epsilon < \sigma \leq 3$. Then $\| y - \hat{v} \| = O (\epsilon )$.

Proof

According to the above discussion, the solution of problem (15) is given by

$$\begin{aligned} \hat{v}(t) &= \int _{0}^{1} \hat{G}_{q}( t, \xi ) w \bigl( \hat{v}( \xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\xi ) \bigr) \,\mathrm{d}_{q}\xi \\ &\quad{} + \frac{ a t^{2} }{1 - ae^{2}} \int _{0}^{1} \hat{G}_{q}( t, \xi ) w \bigl( \hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\xi ) \bigr) \,\mathrm{d}_{q}\xi , \end{aligned}$$

(16)

where

$$ \hat{G}_{q}(t, \xi ) = \textstyle\begin{cases} \frac{( t - \xi )_{q}^{( \sigma - \epsilon - 1)} - t^{2} ( 1 - \xi )_{q}^{( \sigma - \epsilon - 1)}}{ \Gamma _{q} (\sigma )}, & \xi < t, \\ \frac{- t^{2} ( 1 - \xi )_{q}^{( \sigma - \epsilon - 1)} }{ \Gamma _{q} ( \sigma )},& t < \xi , \end{cases} $$

(17)

for $t, \xi \in \overline{J}_{0}$. Then

$$\begin{aligned} \vert y - \hat{v} \vert & \leq \biggl\vert \int _{0}^{1} G_{q}(t, \xi ) w \bigl( y( \xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) \,\mathrm{d}_{q}\xi \\ &\quad{} - \int _{0}^{1} \hat{G}_{q}( t, \xi ) w \bigl( \hat{v}(\xi ), {}^{C} \mathcal{D}_{q}^{\varsigma }[ \hat{v}](\varsigma ) \bigr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad{} + \frac{ at^{2} }{1 - ae^{2}} \biggl\vert \int _{0}^{1} G_{q}(e, \xi ) w \bigl( y(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) \,\mathrm{d}_{q}\xi \\ &\quad{} - \int _{0}^{1} \hat{G}_{q}(e, \xi ) w \bigl( \hat{v}(\xi ), {}^{C} \mathcal{D}_{q}^{\varsigma }[ \hat{v}](\xi ) \bigr) \,\mathrm{d}_{q} \xi \biggr\vert \\ & \leq \biggl| \int _{0}^{1} G_{q}(t, \xi ) \bigl( w \bigl( y(\xi ), {}^{C} \mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) - w \bigl( \hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}] \bigr) (\xi ) \bigr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad{} + \biggl\vert \int _{0}^{1} \bigl( G_{q}(e, \xi ) - \hat{G}_{q}( e, \xi ) \bigr) w \bigl(\hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[\hat{v}] (\xi ) \bigr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad{} + \frac{ at^{2} }{1 - ae^{2}} \biggl( \biggl\vert \int _{0}^{1} G_{q}(e, \xi ) \bigl( w \bigl( y(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \xi ) \bigr) \\ &\quad{} - w \bigl( \hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\xi ) \bigr) \bigr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad{} + \biggl\vert \int _{0}^{1} \bigl( G_{q}(e, \xi ) - \hat{G}_{q}(e, \xi ) \bigr) w \bigl( \hat{v}(\xi ), {}^{C}\mathcal{D}_{q}^{\varsigma }[\hat{v}](\xi ) \bigr) \biggr\vert \biggr) \\ & \leq \ell \Vert y - \hat{v} \Vert \int _{0}^{1} | G_{q}(t, \xi ) \,\mathrm{d}_{q}\xi + \Vert w \Vert _{\epsilon } \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) - \hat{G}_{q}( t, \xi ) \bigr\vert \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{a}{1 - ae^{2}} \biggl( \ell \Vert y - \hat{v} \Vert \int _{0}^{1} \bigl\vert G_{q}(e, \xi ) \bigr\vert \,\mathrm{d}_{q}\xi \\ &\quad{} + \Vert w \Vert _{\epsilon } \int _{0}^{1} \bigl\vert G_{q}(e, \xi ) - \hat{G}_{q}( e, \xi ) \bigr\vert \,\mathrm{d}_{q} \xi \biggr) \\ & \leq \ell \Delta \Vert y - \hat{v} \Vert + \Vert w \Vert _{\epsilon } \biggl( \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) - \hat{G}_{q}( t, \xi ) \bigr\vert \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{ a}{1 - ae^{2}} \int _{0}^{1} \bigl\vert G_{q}(e, \xi ) - \hat{G}_{q}( e, \xi ) \bigr\vert \,\mathrm{d}_{q} \xi \biggr), \end{aligned}$$

where

$$ \Vert w \Vert _{\epsilon }= \sup_{ 0 < \epsilon < \sigma - 2} \bigl\vert w \bigl( \hat{v}(t), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}] (t) \bigr) \bigr\vert . $$

Also, we have

$$\begin{aligned} \bigl\vert {}^{C}\mathcal{D}_{q}^{\varsigma }[y](t) - {}^{C} \mathcal{ D}_{q}^{\varsigma }[\hat{v}] (t) \bigr\vert &\leq \frac{1}{\Gamma _{q} ( 1 - \varsigma )} \biggl\vert \int _{0}^{t} ( t - \xi )_{q}^{(-\varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{1} \frac{\partial }{\partial \xi } G_{q}( \xi , \tau ) w \bigl( y(\tau ), {}^{C} \mathcal{D}_{q}^{\varsigma }[y] ( \tau ) \bigr) \\ &\quad{} - \int _{0}^{1} \frac{ \partial }{ \partial \xi } \hat{G}_{q}( \xi , \tau ) w \bigl( \hat{v}(\tau ), {}^{C} \mathcal{D}_{q}^{\varsigma }[\hat{v}](\tau ) \bigr) \,\mathrm{d}_{q}\tau \biggr) \,\mathrm{d}_{q}\xi \biggr\vert \\ &\quad{} + \frac{2 a }{\Gamma _{q}( 1 - \varsigma ) ( 1 - ae^{2})} \biggl\vert \int _{0}^{t} (t - \xi )_{q}^{(-\varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{1} \xi G_{q}(e, \tau ) w \bigl( y( \tau ), {}^{C}\mathcal{D}_{q}^{\varsigma }[y]( \tau ) \bigr) \\ &\quad{} - \int _{0}^{1} \xi \hat{G}(e, \tau ) w \bigl( \hat{v} (\tau ), {}^{C}\mathcal{D}_{q}^{\varsigma }[ \hat{v}](\tau ) \bigr) \,\mathrm{d}_{q}\tau \biggr) \,\mathrm{d}_{q}\xi \biggr\vert \\ & \leq \frac{\ell \Vert y - \hat{v} \Vert }{ \Gamma _{q}( 1 -\varsigma )} \int _{0}^{t} ( t - \xi )_{q}^{(-\varsigma )} \biggl( \int _{0}^{1} \biggl\vert \frac{\partial }{\partial \xi } G_{q}(\xi , \tau ) \biggr\vert \,\mathrm{d}_{q}\tau \biggr) \,\mathrm{d}_{q}\xi \\ &\quad{} + \Vert w \Vert _{\epsilon }\frac{1}{ \Gamma _{q} (1-\varsigma )} \int _{0}^{t} ( t - \xi )_{q}^{(-\varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{1} \biggl\vert \frac{\partial }{\partial \xi } G_{q}(\xi , \tau ) - \frac{ \partial }{\partial \xi } \hat{G}_{q}( \xi , \tau ) \biggr\vert \,\mathrm{d}_{q} \tau \biggr) \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{ 2 a }{\Gamma _{q} ( 1-\varsigma ) ( 1 - ae^{2}) } \biggl[ \ell \Vert y - \hat{v} \Vert \\ &\quad{} \times \int _{0}^{t} \xi ( t - \xi )_{q}^{(-\varsigma )} \biggl( \int _{0}^{1} \bigl\vert G_{q}(e, \tau ) \bigr\vert \,\mathrm{d}_{q}\tau \biggr) \,\mathrm{d}_{q} \xi \\ &\quad{} + \Vert w \Vert _{\epsilon } \int _{0}^{t} \xi (t- \xi )_{q}^{(- \varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{1} \bigl\vert G_{q}(e, \tau ) - \hat{G}_{q}(e, \tau ) \bigr\vert \,\mathrm{d}_{q} \tau \biggr) \,\mathrm{d}_{q}\xi \biggr] \\ & \leq \frac{3 \ell \Delta }{\Gamma _{q} ( 2 - \varsigma )} \Vert y - \hat{v} \Vert + \Vert \ell \Vert _{\epsilon } \frac{1}{\Gamma _{q} ( 1 - \varsigma )} \int _{0}^{t} \xi ( t - \xi )_{q}^{(- \varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{1} \biggl\vert \frac{\partial }{\partial \xi } G_{q}(\xi , \tau ) - \frac{ \partial }{\partial \xi } \hat{G}_{q}( \xi , \tau ) \biggr\vert \,\mathrm{d}_{q} \tau \biggr) \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{2 a}{\Gamma _{q} ( 1 - \varsigma ) ( 1 - ae^{2})} \Vert w \Vert _{\epsilon } \\ &\quad{} \times \int _{0}^{t} \xi ( t - \xi )_{q}^{(-\varsigma )} \biggl( \int _{0}^{1} \bigl\vert G_{q}(e, \tau ) - \hat{G}_{q}(e, \tau ) \bigr\vert \,\mathrm{d}_{q} \tau \biggr) \,\mathrm{d}_{q}\xi . \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert y - \hat{v} \Vert & \leq \frac{1}{1 - (\ell \Delta + \frac{3 \ell \Delta }{\Gamma _{q} ( 2 -\varsigma )} ) } \biggl[ \int _{0}^{t} \bigl\vert G_{q}(t, \xi ) - \hat{G}_{q}(t, \xi ) \bigr\vert \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{a}{1 - a e^{2}} \int _{0}^{1} \bigl\vert G_{q}(e, \xi ) - \hat{G}_{q}(e, \xi ) \bigr\vert \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{1}{\Gamma _{q} ( 1 - \varsigma )} \int _{0}^{t} \xi ( t - q\xi )^{(-\varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{1} \biggl\vert \frac{\partial }{\partial \xi } G_{q}(\xi , \tau ) - \frac{ \partial }{\partial \xi } \hat{G}_{q}( \xi , \tau ) \biggr\vert \,\mathrm{d}_{q} \tau \biggr) \,\mathrm{d}_{q} \xi \\ &\quad{} + \frac{2 a}{\Gamma _{q} ( 1 - \varsigma ) ( 1 - ae^{2})} \int _{0}^{t} \xi ( t - q\xi )^{(-\varsigma )} \\ &\quad{} \times \biggl( \int _{0}^{t} \bigl\vert G_{q}(e, \tau ) - \hat{G}_{q}(e, \tau ) \bigr\vert \,\mathrm{d}_{q} \tau \biggr) \,\mathrm{d}_{q}\xi \biggr]. \end{aligned}$$

According to the structure of $G_{q}(t, \xi )$, we know that every term of $| G_{q}(t, \xi ) - \hat{G}_{q}(t, \xi ) |$ and

$$ \biggl\vert \frac{ \partial }{\partial \xi } G_{q}(t, \xi ) - \frac{\partial }{\partial \xi } \hat{G}_{q}(t, \xi ) \biggr\vert $$

is in the form of Eq. (15). Hence, Lemma 3.8 implies

$$\begin{aligned} & \int _{0}^{1} \bigl\vert G_{q}(t, \xi ) - \hat{G}_{q}(t, \xi ) \bigr\vert \,\mathrm{d}_{q} \xi = O (\epsilon ), \\ & \int _{0}^{1} \biggl\vert \frac{\partial }{\partial \xi } G_{q}(t, \xi ) - \frac{\partial }{\partial \xi } \hat{G}_{q}(t, \xi ) \biggr\vert = O( \epsilon ). \end{aligned}$$

Therefore, $\| y - \hat{v} \| = O (\epsilon )$ and the proof is complete. □

4 Some illustrative examples

Herein, we give some examples to show the validity of the main results. In this way, we give a computational technique for checking problem (1). We need to present a simplified analysis that is able to execute the values of the q-gamma function. For this purpose, we provided a pseudo-code description of the method for calculation of the q-gamma function of order n [61].

Example 4.1

Consider the problem

$$ {}^{D}\mathcal{D}_{q}^{\frac{8}{3}} [y](t) = \frac{4}{7} \bigl( y(t) \bigr)^{ \frac{1}{2} } + \frac{3}{10} \bigl( {}^{C}\mathcal{D}_{q}^{ \frac{1}{2}} [y](t) \bigr)^{\frac{1}{4}} $$

(18)

via boundary conditions $y(0) = y'(0)=0$ and $y(1) =\frac{14}{9} y ( \frac{3}{5} )$. Clearly, $\sigma = \frac{8}{3} \in (2, 3]$, $\varsigma = \frac{1}{2} \in J_{0}$, $e=\frac{3}{5} \in \overline{J}_{0}$, and $a=\frac{14}{9} \in [0, \frac{1}{e^{2}})$. We define $w: \mathbb{R}^{2} \to \mathbb{R}$ by

$$ w(y, z) = \frac{4}{7} \bigl( y(t) \bigr)^{\frac{1}{2}} + \frac{3}{10} \bigl( z(t) \bigr)^{\frac{1}{4}} $$

for $y, z \in \mathbb{R}$. Then we have

$$\begin{aligned} \bigl\vert w \bigl( y(t), {}^{C}\mathcal{D}_{q}^{\frac{1}{2}} [y](t) \bigr) \bigr\vert & = \biggl\vert \frac{4}{7} \bigl( y(t) \bigr)^{\frac{1}{2}} + \frac{3}{10} \bigl( {}^{C} \mathcal{D}_{q}^{\frac{1}{2}} [z](t) \bigr)^{\frac{1}{4}} \biggr\vert \\ & \leq \frac{4}{7} \bigl\vert \bigl( y(t) \bigr)^{\frac{1}{2}} \bigr\vert + \frac{3}{10} \bigl\vert \bigl( {}^{C} \mathcal{D}_{q}^{\frac{1}{2}} [z](t) \bigr)^{ \frac{1}{4}} \bigr\vert \\ & \leq \mu (t) + \frac{4}{7} \bigl\vert \bigl( y(t) \bigr)^{\frac{1}{2}} \bigr\vert + \frac{3}{10} \bigl\vert \bigl( {}^{C}\mathcal{D}_{q}^{\frac{1}{2}} [z](t) \bigr)^{\frac{1}{4}} \bigr\vert , \end{aligned}$$

where $\mu (t) = \exp (t)$. We take $m_{0}=\frac{4}{7}$, $m_{1}= \frac{3}{10}$, $\beta _{0}=\frac{1}{2}$, and $\beta _{1}=\frac{1}{4}$. Also, by using Eq. (8), we obtain

$$\begin{aligned} \Delta &= \frac{2}{\Gamma _{q} ( \sigma + 1 )} \biggl[ 1 + \frac{a}{ 1 - ae^{2}} \biggr] \\ & = \frac{2}{\Gamma _{q} ( \frac{8}{3} + 1 )} \biggl[ 1 + \frac{14}{9 ( 1 - \frac{14}{25} )} \biggr] = \frac{2}{\Gamma _{q} ( \frac{11}{3} ) }\times \frac{449}{99}= \frac{898}{ 99 \Gamma _{q} ( \frac{11}{3} ) } \end{aligned}$$

and

$$\begin{aligned} \delta & \geq \max \biggl\{ ( 6\Delta m_{0})^{\frac{1}{1 - \beta _{0}} }, (6 \Delta m_{1} )^{ \frac{1}{1 - \beta _{1}}}, 6\Delta M_{1}, \biggl( \frac{ 12 \Delta m_{0} }{ \Gamma _{q} (2 - \varsigma )} \biggr)^{ \frac{1}{1 - \beta _{0}} }, \\ &\quad \biggl( \frac{ 12 \Delta m_{1}}{ \Gamma _{q} (2 - \varsigma )} \biggr)^{\frac{1}{1 - \beta _{1}}}, \frac{ 16 a M_{1}}{ \Gamma _{q} (2 - \varsigma )( 1 - a e^{2})}, \frac{ 8 M_{2}}{ \Gamma _{q} (2 - \varsigma ) } \biggr\} \\ & = \max \biggl\{ \biggl( \frac{24}{7}\Delta \biggr)^{2}, \biggl( \frac{9}{5} \Delta \biggr)^{ \frac{4}{3}}, 6\Delta M_{1}, \biggl( \frac{48 \Delta }{7 \Gamma _{q} (\frac{3}{2} ) } \biggr)^{2}, \biggl( \frac{ 18 \Delta }{ 5\Gamma _{q} (\frac{3}{2} ) } \biggr)^{\frac{4}{3} }, \\ &\quad \frac{ 5600 M_{1}}{99 \Gamma _{q} (\frac{3}{2} )}, \frac{ 8 M_{2}}{\Gamma _{q} (\frac{3}{2} ) } \biggr\} . \end{aligned}$$

Table 1 shows $\Delta \cong 6.5573$, 4.2076, 2.6074 for $q=\frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$, respectively. Figure 1 shows 2D graphs of Δ. Therefore, condition (A1) in Theorem 3.4 holds, and hence this problem has a solution.

Figure 1

2D graphs of Δ for $q = \frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$ in Example 4.1

Table 1 Numerical results of $\Gamma _{q}(\sigma +1)$ and Δ for $q = \frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$ in Example 4.1 (Algorithm 1)

Example 4.2

Consider the following problem:

$$ {}^{C}\mathcal{D}_{q}^{\frac{27}{11} } [y](t) = \frac{4}{5} \bigl( y(t) \bigr)^{3} + 3 \bigl( {}^{C}\mathcal{D}_{q}^{\frac{1}{8}} [y](t) \bigr)^{4} $$

(19)

under the boundary conditions $y(0) = y'(0)=0$ and $y(1) = \frac{1}{2} y ( \frac{2}{7} )$. Then

$$ w \bigl( y(t), {}^{C}\mathcal{D}_{q}^{\frac{2}{5}} [y](t) \bigr) \leq 4 \bigl\vert y(t) \bigr\vert ^{3} + 2 \bigl\vert {}^{C} \mathcal{D}_{q}^{\frac{2}{5}} [y](t) \bigr\vert ^{5}. $$

Clearly, $\sigma = \frac{27}{11} \in (2, 3]$, $\varsigma = \frac{1}{8} \in J_{0}$, $e=\frac{2}{7} \in \overline{J}_{0}$, and $a=\frac{19}{4} \in [0, \frac{1}{e^{2}})$. We define $w: \mathbb{R}^{2} \to \mathbb{R}$ by

$$ w(y, z) = \frac{4}{5} \bigl( y(t) \bigr)^{3} + 3 \bigl( z(t) \bigr)^{4} $$

for $y, z \in \mathbb{R}$. Then we have

$$\begin{aligned} \bigl\vert w \bigl( y(t), {}^{C}\mathcal{D}_{q}^{\frac{1}{8}} [y](t) \bigr) \bigr\vert & = \frac{4}{5} \bigl\vert \bigl( y(t) \bigr)^{3} \bigr\vert + 3 \bigl( {}^{C} \mathcal{D}_{q}^{\frac{1}{8}} [y](t) \bigr)^{4} \\ & \leq \frac{4}{5} \bigl\vert y(t) \bigr\vert ^{3} + 3 \bigl\vert {}^{C} \mathcal{D}_{q}^{\frac{1}{8}} [y](t) \bigr\vert ^{4}. \end{aligned}$$

We take $m_{0}=\frac{4}{5}$, $m_{1}= 3$, $\beta _{0}=3$, and $\beta _{1}=4$. Also, by using Eq. (8), we obtain

$$\begin{aligned} \Delta &= \frac{2}{\Gamma _{q} ( \sigma + 1 )} \biggl[ 1 + \frac{a}{ 1 - ae^{2}} \biggr] \\ & = \frac{2}{\Gamma _{q} ( \frac{27}{11} + 1 )} \biggl[ 1 + \frac{19}{4 ( 1 - \frac{19}{49} )} \biggr] \\ & = \frac{2}{\Gamma _{q} ( \frac{38}{11} ) }\times \frac{1051}{120} = \frac{2102}{ 120 \Gamma _{q} ( \frac{38}{11} )}. \end{aligned}$$

Table 2 shows $\Delta \cong 1.3258$, $9.1665\times 10^{1}$, 6.2138 for $q=\frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$, respectively. Figure 2 shows 2D graphs of Δ. Therefore, condition (A2) in Theorem 3.4 holds, and hence this problem has a solution.

Figure 2

2D graphs of Δ for $q = \frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$ in Example 4.2

Table 2 Numerical results of $\Gamma _{q}(\sigma +1)$ and Δ for $q = \frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$ in Example 4.2 (Algorithm 1)

Example 4.3

Consider the problem

$$ {}^{C}\mathcal{D}_{q}^{\frac{12}{5}} [y](t) = \frac{1}{18} \bigl( y(t) \bigr) + \frac{1}{9} \sin \bigl( {}^{C}\mathcal{D}_{q}^{\frac{3}{7}} [y](t) \bigr) $$

(20)

with boundary conditions $y(0) = y'(0)=0$ and $y(1) = \frac{1}{3} y (\frac{8}{11} )$. It is clear that $\sigma = \frac{12}{5} \in (2, 3]$, $\varsigma = \frac{3}{7} \in J_{0}$, $e=\frac{8}{11} \in \overline{J}_{0}$, and $a=\frac{81}{64} \in [0, \frac{1}{e^{2}})$. We define $w: \mathbb{R}^{2} \to \mathbb{R}$ by

$$ w(y, z) = \frac{1}{18} y(t) + \frac{1}{9} \sin \bigl( z(t) \bigr) $$

for $y, z \in \mathbb{R}$. Then we have

$$\begin{aligned} &\bigl\vert w \bigl( y(t), {}^{C}\mathcal{D}_{q}^{\frac{3}{7}} [y](t) \bigr) - w \bigl( z(t), {}^{C}\mathcal{D}_{q}^{ \frac{3}{7}} [z](t) \bigr) \bigr\vert \\ &\quad = \biggl\vert \frac{1}{18} \bigl( y(t) \bigr) + \frac{1}{9} \sin \bigl( {}^{C} \mathcal{D}_{q}^{\frac{3}{7}} [y](t) \bigr) \\ &\quad \quad{} - \biggl( \frac{1}{18} \bigl( z(t) \bigr) + \frac{1}{9} \sin \bigl( {}^{C}\mathcal{D}_{q}^{\frac{3}{7}} [z](t) \bigr) \biggr) \biggr\vert \\ &\quad \leq \frac{1}{18} \bigl\vert y(t) - z(t) \bigr\vert \\ &\quad \quad{} + \frac{1}{9} \bigl\vert \sin \bigl( {}^{C} \mathcal{D}_{q}^{ \frac{3}{7}} [y](t) \bigr) - \sin \bigl( {}^{C}\mathcal{D}_{q}^{ \frac{3}{7}} [z](t) \bigr) \bigr\vert \\ &\quad \leq \frac{1}{18} \bigl\vert y(t) - z(t) \bigr\vert + \frac{1}{9} \bigl\vert {}^{C} \mathcal{D}_{q}^{ \frac{3}{7}} [y](t) - {}^{C}\mathcal{D}_{q}^{ \frac{3}{7}} [z](t) \bigr\vert \\ &\quad \leq \frac{1}{9} \bigl( \bigl\vert y(t) - z(t) \bigr\vert + \bigl\vert {}^{C} \mathcal{D}_{q}^{ \frac{3}{7}} [y](t) - {}^{C}\mathcal{D}_{q}^{ \frac{3}{7}} [z](t) \bigr\vert \bigr). \end{aligned}$$

We take $\ell = \frac{1}{9}$. Table 3 shows that

$$ \frac{\Gamma _{q} ( 2 - \varsigma )}{\Delta [ 3 + \Gamma _{q} ( 2 - \varsigma )] } = 1.3522\times10 ^{-1}, 1.9197 \times10 ^{-1}, 2.7708 \times10 ^{-1} $$

for $q=\frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$, respectively. Also, the results prove that

$$ \ell \leq \frac{\Gamma _{q} ( 2 - \varsigma )}{\Delta [ 3 + \Gamma _{q} ( 2 - \varsigma )] }. $$

Figure 3 shows 2D graphs of

$$ \frac{\Gamma _{q} ( 2 - \varsigma )}{\Delta [ 3 + \Gamma _{q} ( 2 - \varsigma )] }. $$

Also, by using Eq. (8), we obtain

$$\begin{aligned} \Delta &= \frac{2}{\Gamma _{q} ( \sigma + 1 )} \biggl[ 1 + \frac{a}{ 1 - ae^{2}} \biggr] \\ & = \frac{2}{\Gamma _{q} ( \frac{12}{5} + 1 )} \biggl[ 1 + \frac{81}{64 ( 1 - \frac{81}{121} )} \biggr] = \frac{2}{\Gamma _{q} ( \frac{17}{5} ) } \times \frac{12\text{,}361}{2560}= \frac{24\text{,}722}{ 2560 \Gamma _{q} ( \frac{38}{11} )}. \end{aligned}$$

Table 3 shows that $\Delta = 7.3955$, 5.2090, 3.6090 for $q=\frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$, respectively. Figure 4 shows 2D graphs of Δ. Now, by applying Eq. (10), we get

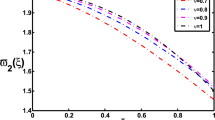
$$ \ell < \frac{\Gamma _{q} ( 2 - \varsigma )}{\Delta [ 3 + \Gamma _{q} ( 2 - \varsigma )] } = \frac{ \Gamma _{q} ( 2 - \frac{3}{7} )}{ \Delta [ 3 + \Gamma _{q} ( 2 - \frac{3}{7} ) ] } = \frac{ \Gamma _{q} ( \frac{11}{7} )}{ \Delta [ 3 + \Gamma _{q} ( \frac{11}{7} ) ] }. $$

Figure 3

2D graphs of $\frac{\Gamma _{q} ( 2 - \varsigma )}{\Delta [ 3 + \Gamma _{q} ( 2 - \varsigma )] }$ for $q = \frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$ in Example 4.3

Figure 4

2D graphs of Δ for $q = \frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$ in Example 4.3

Table 3 Numerical results of $\Gamma _{q}(\sigma +1)$, Δ, and $\ell < \frac{\Gamma _{q} ( 2 - \varsigma )}{\Delta [ 3 + \Gamma _{q} ( 2 - \varsigma )] }$ for $q = \frac{1}{5}$, $\frac{1}{2}$, $\frac{7}{8}$ in Example 4.2 (Algorithm 2)

Since $0 < \ell < \frac{1}{9}< 0.263$, Theorem 3.5 implies that this problem has a unique solution.

5 Conclusion

The Schauder fixed point theorem has been applied in the research study to discuss the well-posed conditions for a class of q-fractional order boundary value problems As a result, we have proved the existence and uniqueness of solution by means of the Schauder fixed point and Banach contraction map theorems on the interval $[0,1]$. We have also studied the perturbation on boundary condition on the function exists in the right-hand side of the problem and on the fractional order. To the leading of our information, the results have never been detailed in other works [11, 12, 61] that consider the problems. In this manner, it is very apparent that the solution of the problem is stable under the small perturbation.

Appendix:  Supporting information

Algorithm 1

MATLAB lines for Examples 4.1 and 4.2

Algorithm 2

MATLAB codes for Example 4.3