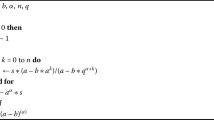Abstract
In this study, we discuss the existence of positive solutions for the system of m-singular sum fractional q-differential equations
with boundary conditions \(x_{i}(0) = x_{i}' (1) = 0\) and \(x_{i}^{(k)}(t) = 0\) whenever \(t=0\), here \(2\leq k \leq n-1\), where \(n= [\alpha_{i}]+ 1\), \(\alpha_{i} \geq2\), \(\gamma_{i} \in(0,1)\), \(D_{q}^{\alpha}\) is the Caputo fractional q-derivative of order α, here \(q \in(0,1)\), function \(g_{i}\) is of Carathéodory type, \(h_{i}\) satisfy the Lipschitz condition and \(g_{i} (t , x_{1}, \ldots, x_{2m})\) is singular at \(t=0\), for \(1 \leq i \leq m\). By means of Krasnoselskii’s fixed point theorem, the Arzelà-Ascoli theorem, Lebesgue dominated theorem and some norms, the existence of positive solutions is obtained. Also, we give an example to illustrate the primary effects.
Similar content being viewed by others
1 Introduction
Fractional calculus and q-calculus belong to the significant branches in mathematical analysis. In 1910, Jackson introduced the subject of q-difference equations [1]. Later, many researchers studied q-difference equations [2–12]. On the other hand, there appeared recently much work on q-differential equations by using different views and fractional derivatives; young researchers could use the main idea in their work (see, for example, [13–30]).
In 2010, the singular Dirichlet problem \(D^{\alpha} x(t) + g(t, x(t), D^{\gamma} x(t) )=0\) under conditions \(x(0) = x(1) = 0\) was investigated by Agarwal et al., where α, γ belong to \((1,2)\), \((0, \alpha- 1 )\), respectively, the function g is of Carathéodory type on \([0,1] \times(0 , \infty) \times\mathbb{R}\) and \(D^{\alpha}\) is the Riemann–Liouville fractional derivative [23]. In 2012, the fractional differential equation \({}^{c}D^{\alpha} y(t) + w(t,y(t))=0\), under boundary conditions \(y(0)=y''(0)=0\) and \(y(1)= \lambda\int_{0}^{1} y(s) \,ds\), was investigated, where \(t, \alpha, \lambda \in(0,1), (2, 3), (0, 2)\), respectively, and the function \(w: J \times[0,\infty) \rightarrow [0,\infty)\) is continuous [24]. Also, in the same year, Ahmad et al., discussed the existence and uniqueness of solutions for the fractional q-difference equations \({}^{c}D_{q}^{\alpha}u(t)= T ( t, u(t) ) \), \(\alpha_{1} u(0) - \beta_{1} D_{q} u(0) = \gamma_{1} u(\eta_{1})\), and \(\alpha_{2} u(1) - \beta_{2} D_{q} u(1) = \gamma_{2} u(\eta_{2})\), for \(t \in I\), where \(\alpha\in(1, 2]\), \(\alpha_{i}, \beta _{i}, \gamma_{i}, \eta_{i} \in\mathbb{R}\), for \(i=1,2\) and \(T \in C([0,1] \times\mathbb{R}, \mathbb{R})\) [6]. In 2013, Zhao et al. reviewed the q-integral problem \((D_{q}^{\alpha}u)(t) + f(t, u(t) )=0\), with conditions \(u(1)\), \(u(0)\) being equal to \(\mu I_{q}^{\beta}u(\eta) \), 0, respectively, for almost all \(t \in(0,1)\), where \(q \in(0,1)\), and α, β, η belong to \((1, 2]\), \((0, 2]\), \((0,1)\), respectively, μ is a positive real number, \(D_{q}^{\alpha}\) is the q-derivative of Riemann–Liouville and we have the real-valued continuous map u defined on \(I \times[0, \infty) \) [10].
In 2014, the singular fractional problem \({}^{c}D_{0^{+}}^{\alpha} x(t)+ f(t , x(t), {}^{c}D_{0^{+}}^{\sigma} x(t))=0\) with boundary conditions \(x(0)=x'(0)=0\) and \(x'(1)= {}^{c}D_{0^{+}}^{\sigma} x(1)\) investigated, where t, α, σ belong to \((0,1)\), \((2, 3)\), \((0, 1)\), respectively, \(f: (0,1] \times\mathbb{R}^{2} \to\mathbb{R} \) is continuous with \(f(t,x,y)\) may be singular at \(t=0\) and \({}^{c}D_{0^{+}}^{\alpha}\) is the Caputo derivative [31]. In 2017, Aydogan et al. and Shabibi et al. studied sum-type singular fractional integro-differential equation with k-point boundary conditions together some properties and sum fractional differential system with some conditions, respectively [21, 22]. Also, in the same year, Zhou et al., provided existence criteria for the solutions of p-Laplacian fractional Langevin differential equations with anti-periodic boundary conditions:
and
for \(t \in[0,1]\), where \(0 < \alpha, \beta\leq1\), λ is larger than or equal to zero, \(1 < \alpha+ \beta<2\), \(q \in(0,1)\), and \(\phi(p) (s) = |s|^{p-2} s\), with \(p \in(1, 2]\) [15]. In 2019, Samei et al., investigated existence of solutions for equations and inclusions of multi-term fractional q-integro-differential equations with non-separated and initial boundary conditions [9].
In this article, motivated by main idea of this work and by these achievements, we are working to address the positive solutions for system of singular sum fractional q-differential equations
under some conditions \(x_{i}(0) = 0\), \(x_{i}' (1) = 0\) and \(\frac{ d^{k} x_{i}(t)}{d t^{k}} |_{t=0} = 0\), for \(i \in N_{m}\) and \(k \in N_{n-1} \setminus\{1\}\), where \(\alpha_{i} \geq2\), \([\alpha_{i}]= n - 1\), \(\gamma_{i} \in J=(0,1)\), \(D_{q}^{\alpha}\) is the Caputo fractional q-derivative of order α, the function \(g_{i}\) is of Carathéodory type, \(h_{i}\) satisfy Lipschitz condition and \(g_{i} (t , x_{1}, \ldots, x_{2m})\) is singular at \(t=0\) for \(i \in N_{m} \), where \(N_{\kappa}= \{1,2, \dots, \kappa\}\).
The rest of the paper is arranged as follows. In Sect. 2, we recall some preliminary concepts and fundamental results of q-calculus. Section 3 is devoted to the main results, while examples illustrating the obtained results and algorithm for the problems are presented in Sect. 4.
2 Preliminaries
First, we point out some of the materials on the fractional q-calculus and fundamental results of it which are needed in the next sections (for more information, refer to [1, 32, 33]). Then, some well-known theorems as regards the fixed point theorem and definitions are presented.
Assume that \(q \in(0,1)\) and \(a \in\mathbb{R}\). Define \([a]_{q}=\frac {1-q^{a}}{1-q}\) [1]. The power function \((x-y)_{q}^{n}\) with \(n \in\mathbb{N}_{0} \) is \((x-y)_{q}^{(n)}= \prod_{k=0}^{n-1} (x - yq^{k})\) and \((x-y)_{q}^{(0)}=1\) where x, y are real numbers and \(\mathbb{N}_{0} := \{ 0\} \cup\mathbb{N}\) [32]. Also, for real number α and \(a \neq0\), we have \((x-y)_{q}^{(\alpha )}= x^{\alpha}\prod_{k=0}^{\infty}(x-yq^{k}) / (x - yq^{\alpha+ k})\). If \(y=0\), then it is clear that \(x^{(\alpha)}= x^{\alpha}\) (Algorithm 1). The q-Gamma function is given by \(\varGamma_{q}(z) = (1-q)^{(z-1)} / (1-q)^{z -1}\), where \(z \in\mathbb{R} \setminus\{0, -1, -2, \ldots\}\) [1]. Note that \(\varGamma_{q} (z+1) = [z]_{q} \varGamma_{q} (z)\). The value of the q-Gamma function, \(\varGamma_{q}(z)\), holds for input values q and z with counting the number of sentences n in summation by simplifying analysis. For this design, we prepare a pseudo-code description of the technique for estimating the q-Gamma function of order n which we show in Algorithm 2. The q-derivative of the function f is defined by \((D_{q} f)(x) = \frac {f(x) - f(qx)}{(1- q)x}\) and \((D_{q} f)(0) = \lim_{x \to0} (D_{q} f)(x)\), which is shown in Algorithm 3 [2]. Also, the higher order q-derivative of a function f is defined by \((D_{q}^{n} f)(x) = D_{q}(D_{q}^{n-1} f)(x)\) for all \(n \geq1\), where \((D_{q}^{0} f)(x) = f(x)\) [2]. The operator
for \(0 \leq x \leq b\), is called the q-integral of a function f, whenever the series is absolutely converges [2]. If a in \([0, b]\), then
whenever the series exists. The operator \(I_{q}^{n}\) is given by \((I_{q}^{0} f)(x) = f(x) \) and
for \(n \geq1\) [2]. It has been proved that \((D_{q} (I_{q} f))(x) = f(x) \) and \((I_{q} (D_{q} f))(x) = f(x) - f(0)\) whenever f is continuous at \(x =0\) [2]. The fractional Riemann–Liouville type q-integral of the function f on \([0,1]\), for \(\alpha\geq0\), is given by \((I_{q}^{0} f)(t) = f(t) \) and
for \(t \in J\) and \(\alpha>0\) [4, 7]. Also, the fractional Caputo type q-derivative of the function f is given by
for \(t \in[0,1]\) and \(\alpha>0\) [4, 7]. It has been proved that \(( I_{q}^{\beta} (I_{q}^{\alpha} f)) (x) = ( I_{q}^{\alpha+ \beta} f) (x)\) and \((D_{q}^{\alpha} (I_{q}^{\alpha} f) ) (x) = f(x)\), where \(\alpha, \beta\geq0\) [7]. By using Algorithm 2, we can calculate \((I_{q}^{\alpha}f)(x)\) which is shown in Algorithm 4. One can find more details of fractional differential and q-differential equations in [34–37].
Now, we present some necessary notions. Throughout this article, we denote \(L^{1}(0,1)\), \(L^{1}[0,1]\), \(C_{\mathbb{R}}(0,1)\), \(C_{\mathbb {R}}[0,1]\), \(C_{\mathbb{R}}^{1}[0,1]\) by \(\mathcal{L}\), \(\overline {\mathcal{L}}\), \(\mathcal{A}\), \(\overline{\mathcal{A}}\), \(\overline {\mathcal{B}}\), respectively. We say that a map \(\theta: \overline{J} \times\mathcal{S} \to\mathbb{R}^{n}\) is of Carathéodory type whenever the function \(t \mapsto\theta( t, r_{1}, \dots, r_{n})\) is measurable for all \((r_{1},\dots, r_{n}) \in\mathcal{S}\) and \((r_{1}, \dots, r_{n})\mapsto\theta(t, r_{1}, \dots, r_{n})\) is continuous for \(t \in \overline{J}\) and for each compact \(C \subseteq\mathcal{S}\) there exists \(\psi_{C} \in\overline{\mathcal{L}}\) such that \(|\theta( t, r_{1}, \dots, r_{n}) |\leq\psi_{C} (t)\) for each \(t \in\overline{J}\) and \((r_{1}, \dots, e_{n}) \in C\), here \(\mathcal{S} = (0,\infty)^{2m}\). At present, we consider four norms which will be used in the sequel: \(\| x \| := \sup\{ |x(t)|: t \in\overline{J}\}\), \(\| x \|_{1} := \int_{0}^{1} |x(t)|\, dt\), \(\| (x_{1}, x_{2}, \dots, x_{n}) \|_{*} := \max\{ \| x_{i} \| : i\in N_{n}\}\) and
The following lemmas can be found in [34, 36–38].
Lemma 1
If \(x \in\overline{\mathcal{A}} \cap\overline{\mathcal{L}}\)with \(D_{q}^{\alpha} x\in\mathcal{A} \cap\mathcal{L}\), then \(I_{q}^{\alpha} D_{q}^{\alpha} x(t) =x(t) + \sum_{i=1}^{n} c_{i} t^{\alpha- i}\), wherenis the smallest integer greater than or equal toαand \(c_{i}\)is some real number.
Lemma 2
Assume that a nonempty subsetCof a Banach space \(\mathcal{X}\)be a closed, convex. Then, there exists \(c \in C\)such that \(c=\mathcal{O}_{1} (c) + \mathcal{O}_{2} (c)\)whenever the operators \(\mathcal{O}_{1}\)and \(\mathcal{O}_{2}\)are compact and continuous, or a contraction, respectively.
Lemma 3
The unique solution for \(D_{q}^{\alpha}x(t) + v(t) = 0\)under conditions \(x'(1)= x(0) =x''(0) = \cdots= x^{n-1}(0) =0\), here \(v \in\overline {\mathcal{L}}\), \(\alpha\in[2, \infty)\)and \(n = [\alpha] +1\), is \(x(t)= \int^{1}_{0} G_{\alpha}(t,qs) v(s) \,d_{q}s\), where
whenever \(t \leq s\)and
whenever \(s \leq t\), for all \(t, s \in\overline{J}\).
Proof
At first, by applying Lemma 1 and the boundary conditions, we conclude that \(x(t)= -I_{q}^{\alpha}v(t) + c_{1} t\) and so \(x'(1) = -I_{q}^{\alpha-1} v(1) + c_{1}\). Since \(x'(1) = 0\), \(c_{1}= I_{q}^{\alpha-1} v(1)\). Thus, \(x(t) = - I_{q}^{ \alpha} v(t) + tI_{q}^{\alpha-1} v(1)\). Hence, we obtain
where
for each \(t, s \in\overline{J}\). □
Remark 1
Consider a q-Green function as in (3). It can be seen that \(G_{\alpha} (t,qs) >0 \) if \(t \leq s\) for each \(t, s \in J\). Also, \(G_{\alpha} (t,qs) >0\) whenever \(s < t\) if and only if \((t -qs)^{(\alpha-1)} < t (\alpha-1) ( t -qs)^{(\alpha-2)}\) for all \(t, s \in J\). In addition
and \(\frac{\partial}{\partial t} G_{\alpha}(t,qs) > 0\) for \(t,s \in J\). Moreover, \(G _{\alpha}\), \(\frac{ \partial}{ \partial t} G_{\alpha} \in C_{\mathbb{R}}(\overline{J} \times\overline{J})\), \(\frac{ \partial}{ \partial t} G_{\alpha}(t,qs) \leq\frac{1}{ \varGamma _{q}( \alpha-1)}\) and \(\int^{1}_{0} \frac{ \partial}{ \partial t} G_{\alpha}(t,s) \geq\frac{1-t^{\alpha-1}}{\varGamma( \alpha)}\), for almost all \(t, s \in\overline{J}\).
Remark 2
Let \(u \in C_{\mathbb{R}}^{1} (\overline{J})\) and \(\gamma\in J\). Since
for all \(t \in\overline{J}\),
and so \(\varGamma_{q}( 2 -\gamma) |D_{q}^{\gamma} u| \leq \Vert u' \Vert \) and \(D_{q}^{\gamma} u \in C_{\mathbb{R}}(\overline{J})\).
3 Main results
Now, we consider the following assumptions for the problem (1):
- (A1)
The maps \(g_{i}\) are Carathéodory functions on \(\overline {J} \times\mathcal{S}\) and there exist positive constants \(\ell_{i}\) such that \(g_{i} ( t, u_{1}, \dots, u_{2m} ) \geq\ell_{i}\) for each \(t \in\overline{J}\) and all \(( u_{1}, \dots, u_{2m}) \in\mathcal {S}\) where \(i \in N_{m}\).
- (A2)
The maps \(h_{i}\) are nonnegative and
$$ \bigl\vert h_{i} ( t, u_{1}, \dots, u_{2m} ) - h_{i} (t, v_{1}, \dots, v_{2m} ) \bigr\vert \leq\sum_{k=1}^{2m} {}_{i}M_{k} \vert u_{k} - v_{k} \vert , $$(6)for each t belonging to J̅ and for almost all \((u_{1}, \dots, u_{2m}), (v_{1}, \dots, v_{2m}) \in\mathcal{S}\), where \({}_{i}M_{j}\) in \([0,\infty)\), for \(i \in N_{m}\) and \(j \in N_{2m}\), are constants such that
$$ \sum_{k=1}^{m} \biggl( {}_{i}M_{k} + \frac{ {}_{i}M_{m + k} }{ \varGamma _{q}(2 - \gamma_{i})} \biggr) < \varGamma_{q}( \alpha_{i} - 1). $$(7) - (A3)
There exist some maps \(\mu_{1}, \dots, \mu_{m} \in\overline {\mathcal{L}}\), some nonincreasing maps \(r_{1}, \dots, r_{m} \in C_{\mathbb {R}}(\mathcal{S})\) with
$$\int_{0}^{1} r_{i} \biggl( L_{1} t^{\alpha_{1}}, \dots, L_{m} t^{ \alpha _{m}}, \frac{ L_{1} (1 - \gamma_{1})}{ 2 } t^{ 1 - \gamma_{1}}, \dots, \frac{ L_{m} (1- \gamma_{m})}{2} t^{1 - \gamma_{m}} \biggr) \, dt < \infty $$and some functions \(w_{1}, \dots, w_{m} \in C_{\mathbb{R}}( \mathcal{S} )\) such that \(w_{i}\) is nondecreasing in all components, \(\lim_{x \to \infty} \frac{ w_{i} (x, \dots, x)}{x} = 0\) and
$$ \begin{aligned}[b] &g_{i} (t, u_{1}, \dots, u_{2m}) + h_{i} (t, u_{1}, \dots, u_{2m} ) \\ &\quad \leq r_{i}( u_{1}, \dots, u_{2m}) + \mu_{i} (t) w_{i} (u_{1}, \dots, u_{2m}), \end{aligned} $$(8)for almost all \(t \in\overline{J}\) and all \(( u_{1}, \dots, u_{2m}) \in \mathcal{S}\) where \(L_{i} \varGamma_{q}(\alpha_{i} + 1) = \ell_{i}(\alpha _{i} - 1)\) for all \(i \in N_{m}\).
Now, we prove the following lemma.
Lemma 4
Suppose that \(\mathcal{P}\)is the set of all \(( u_{1}, \dots, u_{m} ) \)belonging to \(\overline{\mathcal{B}}^{m}\)such that \(u_{i}(t) \)and \(u'_{i}(t) \)are larger than or equal to zero for \(t \in\overline {J}\)and \(i\in\{0\} \cup N_{m}\). Also, for each natural numbernand \(i \in N_{m}\), we define the maps
and
for all \(( u_{1} , \dots, u_{m})\in\mathcal{P}\). Then the self-mapHdefine on \(\mathcal{P}\)is a contraction.
Proof
First, by simple review, we can check that \(H_{i} ( u_{1} , \dots, h_{m}) (t) \geq0\) and
for all \(t \in\overline{J}\), \((u_{1}, \dots, u_{m}) \in\mathcal{P}\) and \(i \in \{0\} \cup N_{m}\). On the other hand,
By using Remark 2, we can conclude that
for \(i \in N_{m} \cup\{0\} \). Hence,
In a similar way, we obtain
Thus, we have
By assumption (A2) and inequality (7), we conclude that H is a contraction mapping. □
At present, for \(i \in N_{m}\) and \(n \in\mathbb{N}\), we take
where \(\chi_{n}(x)=x\) whenever \(x\geq\frac{1}{n}\) and \(\chi_{n} (x) = x\) whenever \(x < \frac{1}{n}\). By simple review, we can check that
\(F_{i,n} (t, u_{1} , \dots, u_{2m} ) \geq\ell_{i}\) and
for all \((u_{1}, \dots, u_{n}) \in\mathcal{S}\), \(i \in N_{m}\) and each \(t \in\overline{J}\).
First, we investigate the system of regular fractional q-differential equations
with the same boundary conditions as in (1).
Lemma 5
Suppose that \(\mathcal{P}\)is the set which is defined in Lemma 4and \(i\in\{0\} \cup N_{m} \). Also, let us, for each natural numbernand \(i \in N_{m}\), define the maps
and
for all \(( u_{1} , \dots, u_{m})\in\mathcal{P}\). Then \(\varOmega_{n}\)is a completely continuous operator on \(\mathcal{P}\)for each natural numbern.
Proof
Assume that \(( u_{1} , \dots, u_{m}) \in\mathcal{P}\). We choose a positive constant \(\ell_{i}\) such that
for almost all \(t \in\overline{J}\). Since \(G_{\alpha_{i}}\) and \(\frac {\partial}{\partial t} G_{\alpha_{i}}\) are nonnegative and continuous on \(\overline{J}^{2}\) for each \(i \in N_{m}\), we conclude that \(T_{i,n} ( u_{1}, \dots, u_{m} )(t) \) and \(( T_{i,n} ( u_{1} , \dots, u_{m} ) )'(t)\) larger than or equal to zero, for all \(t\in\overline{J}\) and \(i \in N_{m}\). Indeed, \(\varOmega_{n}\) maps P into P. Consider a convergent sequence \(\{ ( u_{1,k} , \dots, u_{m,k}) \} \subseteq\mathcal{P}\) with \(\lim_{k \to\infty} ( u_{1,k} , \dots, u_{m,k}) = (u_{1} , \ldots, u_{m})\). In this case, we get \(\lim_{k \to \infty} u_{i,k} = u_{i}\) and \(\lim_{k \to\infty} u'_{i,k} = u'_{i}\) uniformly on J̅ (\(i \in N_{m}\)). But
for each t in J̅ and \(i \in N_{m}\). Hence, \(\lim_{k \to \infty} D^{\mu_{i}} x_{i,k}(t) = D^{\mu_{i}} x_{i}(t)\) uniformly on J̅. Hence,
Since \(F_{i,n} \in C ( \overline{J} \times\mathbb{R}^{2m} )\), the sequence \(\{(u_{1,k} , \dots, u_{m,k}) \} \subseteq \overline{\mathcal{B}}^{m}\) is bounded, there exists a map \(\mu_{i} \in \overline{\mathcal{L}}\) such that
for almost all \(t \in\overline{J}\), \(i \in N_{m}\) and \(k \in\mathbb {N}\). By using the dominated convergence theorem of Lebesgue, we conclude that
and
Hence,
uniformly on J̅ for \(j=0,1\). Thus,
and so \(\varOmega_{n}\) is continuous. Let \(\{ ( u_{1,k} , \dots, u_{m,k}) \} \subseteq\mathcal{P}\) be a bounded sequence. We choose a positive number M such that \(\Vert u_{i,k} \Vert \) and \(\Vert u'_{i,k} \Vert \) are smaller than or equal to M for all \(i \in N_{m}\) and \(k \geq1\). Since \(\Vert D_{q}^{\gamma_{i}} u_{i,k} \Vert \varGamma_{q}( 2 - \gamma_{i}) \leq1\) for each \(i \in N_{m}\), there exists a map \(\mu_{i} \in\overline{\mathcal {L}}\) such that inequality (14) holds for almost all \(t \in \overline{J}\), \(i \in N_{m}\) and \(k \geq1\). On the other hand,
and
for all \(i \in N_{m}\). Hence,
Indeed, \(\{ \varOmega_{n} ( u_{1,k} , \dots, u_{m,k}) \}\) is bounded in \(\overline{\mathcal{B}}^{m}\). Assume that \(t_{1}, t_{2} \in\overline {J}\) such that \(t_{1} \leq t_{2} \) and \(i \in N_{m}\). Then, we have
Since the function \(|t - qs|^{(\alpha_{i} -1)}\) is uniformly continuous on \(\overline{J}^{2} \), there exists \(\delta> 0\) such that \(( t_{2} - qs)^{(\alpha_{i} -1)} - ( t_{1} - qs)^{(\alpha_{i} -1)} < \varepsilon\) for all \(t_{1}, t_{2} \in\overline{J}\) with \(t_{1} \leq t_{2}\), \(t_{2} - t_{1} < \delta\) and \(s \in[0, t_{1}]\), where \(\varepsilon> 0\) be given. Take \(t_{2} - t_{1} < \min\{ \delta, \varepsilon\}\), then we have
Thus,
This implies that \(\{ \varOmega'_{n} ( u_{1,k}, \dots, u_{m,k}) \}\) is equi-continuous on J̅. At present, by using the Arzelà-Ascoli theorem, \(\{ \varOmega_{n} ( u_{1,k} , \dots, u_{m,k}) \}\) is relatively compact. Therefore \(\varOmega_{n}\) is completely continuous. □
Now, we are ready to provide our main results about the problem (1).
Theorem 6
The problem (11) under boundary conditions in (1) has a solution \(( u_{1,n} , \dots, u_{m,n}) \)belongs to \(\mathcal{P}\)such that \(u_{i,n}(t) \varGamma (\alpha_{i} + 1) \geq\ell_{i} t^{\alpha_{i}} (\alpha_{i} -1)\), for all \(t \in\overline{J}\)and \(i \in N_{m}\), whenever assumptions (A1) and (A2) hold.
Proof
The mapping \(H: P \to P\) is a contraction and the operator \(\varOmega_{n} : P \to P\) is completely continuous, by employing Lemma 4 and Lemma 5, respectively. Now, by applying Lemma 2, there exists \(( u_{1,n} , \dots, u_{m,n}) \in\mathcal{P}\) such that \(( u_{1,n} , \dots, u_{m,n}) = \varOmega_{n} ( u_{1,n} , \dots , u_{m,n}) + H ( u_{1,n} , \dots, u_{m,n})\). Therefore, \(u_{i,n}= T_{i,n} ( u_{1,n} , \dots, u_{m,n}) + H_{i} ( u_{1,n} , \dots, u_{m,n})\) for all \(i \in N_{m}\). Hence,
for all \(i \in N_{m}\). By applying the hypothesis, we obtain \(u_{i,n}(t) \varGamma(\alpha_{i} + 1) \geq\ell_{i} t^{\alpha_{i}} (\alpha_{i} -1)\) for all \(t \in\overline{J}\) and \(i \in N_{m} \). By simple review, we can see that the element \(( u_{1,n} , \dots, u_{m,n}) \in\mathcal{P}\) is a solution of the problem (11) under the boundary conditions in (1). □
Lemma 7
Let the element \((u_{1,n} , \dots, u_{m,n}) \)be a solution for the problem (11) under the boundary conditions in (1). Then \(\{ ( u_{1,n} , \dots, u_{m,n} ) \}_{n\geq1}\)is relatively compact in \(\mathcal{P}\)whenever assumptions (A1), (A2) and (A3) hold.
Proof
As we found in Theorem 6,
for all \(n \in\mathbb{N}\), \(t \in\overline{J}\) and \(i \in N_{m}\). Hence,
for \(t \in\overline{J}\) and so,
Thus,
for \(t \in\overline{J}\). Since \(\varGamma_{q}(3- \gamma_{i}) \leq2\), we have \(2 \varGamma_{q}(\alpha_{i}) D_{q}^{\gamma_{i}} u_{i,n} (t) \geq \ell _{i} t^{1-\gamma_{i}}(1 - \gamma_{i})\). Now, put
Therefore, \(u_{i,n} (t) \geq L_{i} t^{\alpha_{i}}\) and \(2 D_{q}^{\gamma _{i}} u_{i,n} (t) \geq L_{i} (1-\gamma_{i}) t^{1-\gamma_{i}}\) for all \(n \geq 1\), \(t \in\overline{J}\) and \(i \in N_{m}\). Indeed,
for \(n \in\mathbb{N}\), \(t \in\overline{J}\) and \(i \in N_{m}\). Hence, we conclude that
for all \(t \in\overline{J}\), \(n\geq1\) and \(i \in N_{m}\). Also, for all \(i \in N_{m}\), we obtain
Assume that \(\lambda_{n} = \Vert ( u_{1,n} , \dots, u_{m,n} ) \Vert _{**}\). Then, for all i and n, we have \(\| u_{i,n} \| \) and \(\Vert u'_{i,n} \Vert \) smaller than or equal to \(\lambda_{n}\). Thus, \(\varGamma_{q}(2 - \gamma _{i}) |D_{q}^{\gamma_{i}} u_{i,n}(t)| \leq \lambda_{n} \) for each \(n \in\mathbb{N}\), \(t \in\overline{J}\) and \(i \in N_{m}\). Hence
and \(0 \leq u_{i,n}(t) = \int^{t}_{0} u'_{i,n}(s) \,ds \) for \(n \in\mathbb {N}\), \(t \in\overline{J}\) and \(i \in N_{m}\). By a similar method, we get
for all i. Since \(\lim_{x \to\infty} \frac{w_{i} (x, \dots, x)}{x} = 0\) for all \(i \in N_{m}\), there exists \(M_{i} > 0\) such that
for all \(\nu_{i}> M_{i}\). We take \(M = \max\{M_{1}, \dots, M_{m}\}\). Then we have
for all \(\nu> M\). Thus,
which implies \(\{ \Vert ( u_{1,n} , \dots, u_{m,n}) \Vert _{**} \} \) is bounded in \(\overline{ \mathcal{B}}_{m}\). Now, take
and
for all i and each \(t\in\overline{J}\). Then, we have \(\varLambda_{i} = \int^{1}_{0} U_{i} (t) \,dt\) and
If \(t_{1} , t_{2} \in\overline{J}\) such that \(t_{1} \leq t_{2}\), then we obtain
Let \(\varepsilon_{i} > 0\) be given. Choose \(\delta( \varepsilon_{i} ) > 0\) such that
for all \(0 \leq t_{1} < t_{2} \leq1\) with \(t_{2} - t_{1} < \delta( \varepsilon_{i} )\) and \(s \in(0, t]\). Take
then \(\varGamma_{q}( \alpha_{i} -1) \vert u'_{i,n} ( t_{2}) - u'_{i,n} (t_{1} ) \vert \leq 3 \varepsilon_{i} ( \varLambda_{i} + C_{i} \Vert \mu _{i} \Vert _{1} )\), for all \(i \in N_{m}\). Hence, \(\{( u_{1,n} , \dots, u_{m,n})' \}\) is equi-continuous. Indeed, \(\{(u_{1,n} , \dots, u_{m,n}) \}_{n \geq1} \subseteq\overline{\mathcal{B}}^{m}\) is relatively compact. □
Theorem 8
The system (1) has a solution \(( u_{1} , \ldots, u_{m}) \in \mathcal{P}\)such that \(2 D_{q}^{ \gamma_{i}} u_{i} (t) \geq L_{i} (1- \gamma_{i}) t^{1 - \gamma_{i}}\)and \(u_{i} (t) \geq L_{i} t^{\alpha _{i}}\)for all \(t \in\overline{J}\)and \(i \in N_{m}\)whenever the assumptions (A1), (A2) and (A3) hold.
Proof
As we found in Theorem 6, for each natural number n the system (11) under the boundary conditions in (1) has a solution \(( u_{1,n} , \dots, u_{m,n} ) \) in \(\mathcal{P}\). By applying Lemma 7, we have \(\{ ( u_{1,n}, \dots, u_{m,n}) \}_{n\geq1}\) is relatively compact in \(\overline{\mathcal{B}}^{m}\). Also, by employing the Arzelá–Ascoli theorem, \(( u_{1} , \dots, u_{m})\) exists such that \(\lim_{n \to\infty} ( u_{1,n} , \dots, u_{m,n}) = ( u_{1} , \dots, u_{m})\). It is obvious that \(( u_{1} , \dots, u_{m})\) satisfies the boundary conditions of the problem (1), \(D_{q}^{\gamma_{i}} u_{i,n} \to D_{q}^{\gamma_{i}} u_{i}\) and
for each t belonging to J̅ and \(i \in N_{m}\). Thus \(( u_{1} , \dots, u_{m}) \in\mathcal{P}\). At present, suppose that \(K = \sup_{n\geq1} \Vert ( u_{1,n} , \dots, u_{m,n}) \Vert _{**}\). Then we have \(\Vert D_{q}^{\gamma_{i}} u_{i,n} \Vert \leq\frac{K}{ \varGamma _{q}(2 - \gamma_{i})}\) for all n and \(i \in N_{m}\). Hence,
for almost all \((t,qs) \in\overline{J}^{2} \), \(n \geq1\) and \(i \in N_{m}\). At present, the dominated theorem of Lebesgue implies that
for all \(i \in N_{m}\) and \(t \in\overline{J}\). This completes the proof. □
4 Example and numerical check technique for the problems
In this part, we give complete computational techniques for illustrating of the problem (1), in Theorems 8, such that it covers all the problems, and present numerical examples which solve the problems perfectly. Foremost, we present a simplified analysis that can be executed to calculate the value of q-Gamma function, \(\varGamma_{q} (x)\), for input values q and x by counting the number of sentences n in summation. To this aim, we consider a pseudo-code description of the method for the calculated q-Gamma function of order n in Algorithm 2 (for more details, see the following link: https://en.wikipedia.org/wiki/Q-gamma_function). Table 1 shows that when q is constant, the q-Gamma function is an increasing function. Also, for smaller values of x, an approximate result is obtained with smaller values of n. It is shown by underlined rows. Table 2 shows that the q-Gamma function for values q close to 1 is obtained with higher values of n in comparison with other columns. They have been underlined in line 8 of the first column, line 17 of the second column and line 29 of third columns of Table 2. Also, Table 3 is the same as Table 2, but x values increase in 3. Similarly, the q-Gamma function for values q near to one is obtained with more values of n in comparison with other columns. Furthermore, we provide Algorithm 3, which calculates \((D_{q}^{\alpha}f) (x)\).
Here, we provide an example to illustrate the results of Theorem 8.
Example 1
Consider the system as (1) with \(m= 2\):
under boundary conditions \(u_{1}(0) = u_{2}(0)= 0\), \(u'_{1}(1) = u'_{2}(1)= 0\) and \(u''_{1}(0) = u''_{2}(0)= 0\), where \(c_{i}, d_{i}\) are positive constants, for \(i=1,2,3,4\). Note that \(\mathcal{S}=(0, \infty)^{4}\). We take the functions
\(\lambda_{1}(t) = \frac{1}{ \sqrt[3]{t^{2}}}\) and \(\lambda_{2}(t)= \frac {1}{\sqrt{t}}\). Put \(m= 2\), \(\alpha_{1} = \frac{5}{2}\), \(\alpha_{2} = \frac{7}{3}\), \(\gamma_{1} = \frac{1}{2}\), \(\gamma_{2} = \frac{1}{3}\),
\(\ell_{1} = 2\) and \(\ell_{2}= 1\). By simple review, we can see that \(g_{1}\) and \(g_{2}\) are Carathéodory functions, \(g_{1} (t, u_{1}, u_{2}, u_{3}, u_{4}) \geq2\), \(g_{2}(t, u_{1}, u_{2}, u_{3}, u_{4}) \geq1\) for all \(( u_{1}, u_{2}, u_{3}, u_{4}) \in\mathcal{S}\) and each \(t \in \overline{J}\), \(h_{1}\) and \(h_{2}\) are nonnegative and \(h_{1}\), \(h_{2}\) satisfy inequality (6):
for \((u_{1}, u_{2}, u_{3}, u_{4}), (v_{1}, v_{2}, v_{3}, v_{4}) \in(0,\infty)^{4}\) and \(t \in\overline{J}\). Also, by putting values in the problem in (7), we have
Tables 4 and 5 show the values of inequalities (16) and (17), respectively. On the other hand, the maps \(r_{1}\) and \(r_{2}\) are nonincreasing with respect to all components. If
then
Also, the functions \(w_{1}\) and \(w_{2}\) are nondecreasing with respect to all components and
Therefore, Theorem 8 implies that the problem (15) has a positive solution.
References
Jackson, F.H.: q-Difference equations. Am. J. Math. 32, 305–314 (1910). https://doi.org/10.2307/2370183
Adams, C.R.: The general theory of a class of linear partial q-difference equations. Trans. Am. Math. Soc. 26, 283–312 (1924)
Adams, C.R.: Note on the integro-q-difference equations. Trans. Am. Math. Soc. 31(4), 861–867 (1929)
Ahmad, B., Etemad, S., Ettefagh, M., Rezapour, S.: On the existence of solutions for fractional q-difference inclusions with q-antiperiodic boundary conditions. Bull. Math. Soc. Sci. Math. Roum. 59(107)(2), 119–134 (2016)
Ahmad, B., Nieto, J.J., Alsaedi, A., Al-Hutami, H.: Existence of solutions for nonlinear fractional q-difference integral equations with two fractional orders and nonlocal four-point boundary conditions. J. Franklin Inst. 351, 2890–2909 (2014). https://doi.org/10.1016/j.jfranklin.2014.01.020
Ahmad, B., Ntouyas, S.K., Purnaras, I.K.: Existence results for nonlocal boundary value problems of nonlinear fractional q-difference equations. Adv. Differ. Equ. 2012, Article ID 140 (2012). https://doi.org/10.1186/1687-1847-2012-140
Ferreira, R.A.C.: Nontrivial solutions for fractional q-difference boundary value problems. Electron. J. Qual. Theory Differ. Equ. 70, Article ID 70 (2010)
Kalvandi, V., Samei, M.E.: New stability results for a sum-type fractional q-integro-differential equation. J. Adv. Math. Stud. 12(2), 201–209 (2019)
Samei, M.E., Ranjbar, G.K., Hedayati, V.: Existence of solutions for equations and inclusions of multi-term fractional q-integro-differential with non-separated and initial boundary conditions. J. Inequal. Appl. 2019, Article ID 273 (2019). https://doi.org/10.1186/s13660-019-2224-2
Zhao, Y., Chen, H., Zhang, Q.: Existence results for fractional q-difference equations with nonlocal q-integral boundary conditions. Adv. Differ. Equ. 2013, Article ID 48 (2013). https://doi.org/10.1186/1687-1847-2013-48
Samei, M.E., Hedayati, V., Rezapour, S.: Existence results for a fraction hybrid differential inclusion with Caputo–Hadamard type fractional derivative. Adv. Differ. Equ. 2019, Article ID 163 (2019). https://doi.org/10.1186/s13662-019-2090-8
Hedayati, V., Samei, M.E.: Positive solutions of fractional differential equation with two pieces in chain interval and simultaneous Dirichlet boundary conditions. Bound. Value Probl. 2019, Article ID 141 (2019). https://doi.org/10.1186/s13661-019-1251-8
Atici, F., Eloe, P.W.: Fractional q-calculus on a time scale. J. Nonlinear Math. Phys. 14(3), 341–352 (2007). https://doi.org/10.2991/jnmp.2007.14.3.4
Baleanu, D., Agarwal, R.P., Mohammadi, H., Rezapour, S.: Some existence results for a nonlinear fractional differential equation on partially ordered Banach spaces. Bound. Value Probl. 2013, Article ID 112 (2013). https://doi.org/10.1186/1687-2770-2013-112
Zhou, H., Alzabut, J., Yang, L.: On fractional Langevin differential equations with anti-periodic boundary conditions. Eur. Phys. J. Spec. Top. 226, 3577–3590 (2017). https://doi.org/10.1140/epjst/e2018-00082-0
Samei, M.E., Khalilzadeh Ranjbar, G.: Some theorems of existence of solutions for fractional hybrid q-difference inclusion. J. Adv. Math. Stud. 12(1), 63–76 (2019)
Ntouyas, S.K., Samei, M.E.: Existence and uniqueness of solutions for multi-term fractional q-integro-differential equations via quantum calculus. Adv. Differ. Equ. 2019, Article ID 475 (2019). https://doi.org/10.1186/s13662-019-2414-8
Samei, M.E., Khalilzadeh Ranjbar, G., Hedayati, V.: Existence of solutions for a class of Caputo fractional q-difference inclusion on multifunctions by computational results. Kragujev. J. Math. 45(4), 543–570 (2021)
Liang, S., Zhang, J.: Existence of three positive solutions of m-point boundary value problems for some nonlinear fractional differential equations on an infinite interval. Comput. Math. Appl. 61, 3343–3354 (2011). https://doi.org/10.1016/j.camwa.2011.04.018
Abdeljawad, T., Alzabut, J.: The q-fractional analogue for Gronwall-type inequality. J. Funct. Spaces Appl. 2013, Article ID 7 (2013). https://doi.org/10.1155/2013/543839
Aydogan, M., Nazemi, S.Z., Rezapour, S.: Positive solutions for a sum-type singular fractional integro-differential equation with m-point boundary conditions. UPB Sci. Bull., Ser. A 79(1), 109–118 (2017)
Shabibi, M., Postolache, M., Rezapour, S.: Positive solutions for a singular sum fractional differential system. Int. J. Anal. Appl. 13(1), 108–118 (2017)
Agarwal, R.P., O’Regan, D., Staněk, S.: Positive solutions for Dirichlet problems of singular nonlinear fractional differential equations. J. Math. Anal. Appl. 371(1), 57–68 (2010). https://doi.org/10.1016/j.jmaa.2010.04.034
Cabada, A., Wang, G.: Positive solution of nonlinear fractional differential equations with integral boundary value conditions. J. Math. Anal. Appl. 389(1), 403–411 (2012). https://doi.org/10.1016/j.jmaa.2011.11.065
Jafari, H., Haghbin, A., Johnston, S.J., Baleanu, D.: A new algorithm for solving dynamic equations on a time scale. J. Comput. Appl. Math. 312, 167–173 (2017). https://doi.org/10.1016/j.cam.2016.02.047
Al-Omari, S.K.Q., Baleanu, D., Purohit, S.D.: Some results for Laplace-type integral operator in quantum calculus. Adv. Differ. Equ. 2018, Article ID 124 (2018). https://doi.org/10.1186/s13662-018-1567-1
Agarwal, R.P., Baleanu, D., Hedayati, V., Rezapour, S.: Two fractional derivative inclusion problems via integral boundary condition. Appl. Math. Comput. 257, 205–212 (2015). https://doi.org/10.1016/j.amc.2014.10.082
Aydogan, S.M., Baleanu, D., Mousalou, A., Rezapour, S.: On high order fractional integro-differential equations including the Caputo–Fabrizio derivative. Bound. Value Probl. 2018, Article ID 90 (2018). https://doi.org/10.1186/s13661-018-1008-9
Baleanu, D., Ghafarnezhad, K., Rezapour, S., Shabibi, M.: On the existence of solutions of a three steps crisis integro-differential equation. Adv. Differ. Equ. 2018, Article ID 135 (2018). https://doi.org/10.1186/s13662-018-1583-1
Baleanu, D., Mohammadi, H., Rezapour, S.: The existence of solutions for a nonlinear mixed problem of singular fractional differential equations. Adv. Differ. Equ. 2013, Article ID 359 (2013). https://doi.org/10.1186/1687-1847-2013-359
Li, R.: Existence of solutions for nonlinear fractional equation with fractional derivative condition. Adv. Differ. Equ. 2014, Article ID 292 (2014). https://doi.org/10.1186/1687-1847-2014-292
Rajković, P.M., Marinković, S.D., Stanković, M.S.: Fractional integrals and derivatives in q-calculus. Appl. Anal. Discrete Math. 1, 311–323 (2007)
Annaby, M.H., Mansour, Z.S.: q-Fractional Calculus and Equations. Springer, Berlin (2012). https://doi.org/10.1007/978-3-642-30898-7
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000). https://doi.org/10.1142/3779
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies. Elsevier, Amsterdam (2006)
Kac, V., Cheung, P.: Quantum Calculus. Universitext. Springer, New York (2002). https://doi.org/10.1007/978-1-4613-0071-7-1
Smart, D.R.: Fixed Point Theorems. Cambridge University Press, New York (1980)
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The author was the only one to contribute to this manuscript and read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The author declares to have no competing interests.
Consent for publication
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Samei, M.E. Existence of solutions for a system of singular sum fractional q-differential equations via quantum calculus. Adv Differ Equ 2020, 23 (2020). https://doi.org/10.1186/s13662-019-2480-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2480-y