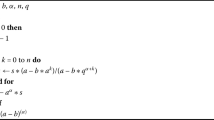Solutions of two fractional q-integro-differential equations under sum and integral boundary value conditions on a time scale

Abstract

In this manuscript, by using the Caputo and Riemann–Liouville type fractional q-derivatives, we consider two fractional q-integro-differential equations of the forms ${}^{c}\mathcal{D}_{q}^{\alpha }[x](t) + w_{1} (t, x(t), \varphi (x(t)) )=0$ and

$$ {}^{c}\mathcal{D}_{q}^{\alpha }[x](t) = w_{2} \biggl( t, x(t), \int _{0}^{t} x(r) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\alpha }[x](t) \biggr) $$

for $t \in [0,l]$ under sum and integral boundary value conditions on a time scale $\mathbb{T}_{t_{0}}= \{ t: t =t_{0}q^{n}\}\cup \{0\}$ for $n\in \mathbb{N}$ where $t_{0} \in \mathbb{R}$ and q in $(0,1)$. By employing the Banach contraction principle, sufficient conditions are established to ensure the existence of solutions for the addressed equations. Examples involving algorithms and illustrated graphs are presented to demonstrate the validity of our theoretical findings.

1 Introduction

It has been recognized that fractional calculus provides a meaningful generalization for the classical integration and differentiation to any order. On the other hand, quantum calculus is equivalent to traditional infinitesimal calculus without the notion of limits. It defines q-calculus where q stands for quantum. Despite the old history of these two theories, the investigation of their properties remains untouched until recent time. Fractional q-calculus, initially proposed by Jackson [1–3], was regarded as the fractional analogue of q-calculus. Soon afterwards, it was further promoted by Al-Salam in [4] and then continued by Agarwal in [5] where many outstanding theoretical results were given. Its emergence and development extended the application of interdisciplinarity and aroused widespread attention of scholars; see [6–28] and the references therein. The existence of solutions for q-fractional boundary value problems has been under consideration by many researchers; see for instance [29–40].

In [41], Ntouyas et al. studied the boundary value problem of first-order fractional differential equations given by

$$\begin{aligned} \textstyle\begin{cases} {}^{c}D_{0^{+}}^{\beta _{1}} [f_{1}](x) = w_{1}(x, f_{1}(x), f_{2}(x)), \\ {}^{c}D_{0^{+}}^{\beta _{2}} [f_{2}](x) = w_{2}(x, f_{1}(x), f_{2}(x)), \end{cases}\displaystyle t \in [0,1], \end{aligned}$$

with Riemann–Liouville integral boundary conditions of different order $f_{1}(0) = c_{1} I^{\alpha _{1}} [f_{1}](a_{1})$ and $f_{2}(0) = c_{2} I^{\alpha _{2}} [f_{2}](a_{2})$ for $0 < a_{1}, a_{2} <1$, $\beta _{i}\in (0, 1]$, $\alpha _{i}, c_{i} \in \mathbb{R}$ where $i=1,2$. In 2015, Zhang et al. through the spectral analysis and fixed point index theorem obtained the existence of positive solutions of the singular nonlinear fractional differential equation $-\mathcal{D}_{t}^{\alpha }u(t) = w(t, u(t), \mathcal{D}_{t}^{\beta }u(t))$ for $0 < t < 1$, with integral boundary value conditions $\mathcal{D}_{t}^{\beta }u(0) =0$ and $\mathcal{D}_{t}^{\beta }u(1) = \int _{0}^{1} \mathcal{D}_{t}^{\beta }u(r) {\,\mathrm{d}}N(r)$, where $\alpha \in (1, 2]$, $\beta \in (0, 1]$, $w(t, u, v)$ may be singular at both $t=0$, 1 and $u=v =0$, $\int _{0}^{1} u(r) {\,\mathrm{d}}N(r)$ denotes the Riemann–Stieltjes integral with a signed measure, in which $N:[0,1] \to \mathbb{R}$ is a function of bounded variation [42]. In 2016, Ahmad et al. investigated the existence of solutions for a q-antiperiodic boundary value problem of fractional q-difference inclusions given by

$$ {}^{c}\mathcal{D}_{q}^{\alpha }[k] (t) \in F \bigl( t, k(t), \mathcal{D}_{q} [k](t), \mathcal{D}_{q}^{2} [k](t) \bigr) $$

for $t \in [0,1]$, $q \in (0,1)$, $2 < \alpha \leq 3$, $0 < \beta \leq 3$, and $k(0) + k(1) =0$, $\mathcal{D}_{q} k(0) + \mathcal{D}_{q} k(1) =0$, $\mathcal{D}_{q}^{2} k(0) + \mathcal{D}_{q}^{2} k(1) =0$, where ${}^{c}\mathcal{D}_{q}^{\alpha }$ denotes Caputo fractional q-derivative of order α and $F: [0,1] \times \mathbb{R}\times \mathbb{R} \times \mathbb{R} \to \mathcal{P}(\mathbb{R})$ is a multivalued map with $\mathcal{P}(\mathbb{R})$ a class of all subsets of $\mathbb{R}$ [15]. In 2019, Ren and Zhai discussed the existence of unique solution and multiple positive solutions for the fractional q-differential equation $\mathcal{D}_{q}^{\alpha }x(t) + w(t, x(t))=0$ for each $t \in [0,1]$ with nonlocal boundary conditions $x(0) = \mathcal{D}_{q}^{\alpha -2} x(0) =0$ and $\mathcal{D}_{q}^{\alpha -1} x(1) = \mu [x] + \int _{0}^{\eta }\phi (r) \mathcal{D}_{q}^{\beta } x(t) {\,\mathrm{d}}_{q}r$, where $\mathcal{D}_{q}^{\alpha }$ is the standard Riemann–Liouville fractional q-derivative of order α, $2 < \alpha \leq 3$, such that $\alpha - 1-\beta >0$, $q \in (0,1)$, $\phi \in L^{1}[0,1]$ is nonnegative, $\mu [x]$ is a linear functional given by $\mu [x] = \int _{0}^{1} x(t) {\,\mathrm{d}}N(t)$ involving the Stieltjes integral with respect to the function $N: [0,1] \to \mathbb{R}$ such that $N(t)$ is right-continuous on $[0,1)$, left-continuous at $t=1$ and, particularly, N is a nondecreasing function with $N(0)=0$ and ${\,\mathrm{d}}N$ is positive Stieltjes measure [40]. The authors in [43] investigated a multi-term nonlinear fractional q-integro-differential equation

$$ {}^{c}D_{q}^{\alpha } [x](t) = w \bigl( t, x(t), ( \varphi _{1} x) (t), ( \varphi _{2} x) (t), {}^{c}D_{q}^{ \beta _{1}} [x](t), {}^{c}D_{q}^{ \beta _{2}} [x](t), \ldots, {}^{c}D_{q}^{ \beta _{n}} [x](t) \bigr) $$

under some boundary conditions. The existence of solutions for the multi-term nonlinear fractional q-integro-differential ${}^{c}D_{q}^{\alpha } [u](t)$ equations in two modes and inclusions of order $\alpha \in (n -1, n]$ with non-separated boundary and initial boundary conditions where natural number n is more than or equal to five was considered in [20]. Recently, some researchers discussed the existence of solutions for some singular fractional differential equations; see the papers [44–47].

Benefiting from the main ideas of the above said papers, we investigate the following two nonlinear fractional q-integro-differential equations in the spaces $\mathcal{A} = C(\overline{J} \times \mathbb{R}^{2}, \mathbb{R})$ and $\mathcal{B}= \{ x: x,{}^{c}\mathcal{D}_{q}^{\beta }[x]\in C^{2}( \overline{J},\mathbb{R}), \overline{J}=[0,l] \}$ with the norms defined by $\|x\| = \sup_{t\in \overline{J}} |x(t)|$ and

$$ \Vert x \Vert _{*}=\sup_{t\in \overline{J}} \bigl\vert x(t) \bigr\vert + \sup_{t\in \overline{J}} \bigl\vert {}^{c} \mathcal{D}_{q}^{\beta }[x](t) \bigr\vert , $$

respectively.

• (P1) First we investigate the nonlinear fractional q-integro-differential equation

  $$ {}^{c}\mathcal{D}_{q}^{\alpha }[x](t) + w_{1} \bigl(t, x(t), \varphi \bigl(x(t)\bigr) \bigr)=0 $$

  (1)

  for $t\in \overline{J}$ under sum and integral boundary value conditions

  $$ x'(a) = -\eta \int _{0}^{1} x( r ) \,\mathrm{d}r,\qquad x'(1) + x(0) = \sum_{i=1}^{m} c_{i} x'(b), $$

  (2)

  where $m \geq 1$, $1 \leq \alpha < 2$, $0 \leq a < b \leq 1$, $\eta \geq 0$, $c_{i} \geq 0$ for each $i=1,2,\ldots, m$ such that $2\varXi > -1$, here $\varXi = \sum_{i=1}^{m} c_{i}$, $\varphi ( x(t)) =\int _{0}^{t} g(r) x(r) \,\mathrm{d}r$ and $w_{1}: \overline{J} \times \mathcal{A}^{2} \to \mathcal{A}$ is a continuous function.

• (P2) Second we consider the nonlinear fractional q-integro-differential equation

  $$ {}^{c}\mathcal{D}_{q}^{\alpha }[x](t) = w_{2} \biggl( t, x(t), \int _{0}^{t} x(r ) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x](t) \biggr) $$

  (3)

  for $t\in \overline{J}$ under the sum boundary conditions

  $$ x(0)=0,\qquad x'(1)=\sum_{i=1}^{m} c_{i} x''(b), $$

  (4)

  where $1 \leq \alpha < 2$, $0 \leq \zeta < 1$, $0< b<1$, $m\geq 1$, $c_{i} \geq 0$ for all $i=1,\dots, m$ and $w_{2}: \overline{J}\times \mathcal{B}^{3} \to \mathcal{B}$ is a continuous function.

This paper is organized as follows: In Sect. 2, we state some useful definitions and lemmas on the fundamental concepts of q-fractional calculus and fixed point theory. In Sect. 3, some main theorems on the solutions of fractional q-integro-differential equations (1)–(2) and (3)–(4) are stated. Section 4 contains some illustrative examples to show the validity and applicability of our results. The paper concludes with some interesting observations.

2 Essential preliminaries

This section is devoted to some notations and essential preliminaries that are acting as necessary prerequisites for the results of the subsequent sections. Throughout this article, we apply the time scales calculus notation [9]. In fact, we consider the fractional q-calculus on the specific time scale $\mathbb{T}= \mathbb{R}$ where $\mathbb{T}_{t_{0}} = \{0 \} \cup \{ t: t=t_{0}q^{n} \}$ for nonnegative integer n, $t_{0} \in \mathbb{R}$ and $q \in (0,1)$. Let $a \in \mathbb{R}$. Define $[a]_{q}=\frac{1-q^{a}}{1-q}$ [2]. The power function $(x-y)_{q}^{n}$ with $n \in \mathbb{N}_{0}$ is defined by

$$ (x-y)_{q}^{(n)}= \prod_{k=0}^{n-1} \bigl(x - yq^{k}\bigr) $$

for $n\geq 1$ and $(x-y)_{q}^{(0)}=1$, where x and y are real numbers and $\mathbb{N}_{0}:= \{ 0\} \cup \mathbb{N}$ [6]. Also, for $\alpha \in \mathbb{R}$ and $a \neq 0$, we have

$$ (x-y)_{q}^{(\alpha )}= x^{\alpha }\prod _{k=0}^{\infty }\frac{x-yq^{k}}{x - yq^{\alpha + k}}. $$

If $y=0$, then it is clear that $x^{(\alpha )}= x^{\alpha }$ [8] (Algorithm 1). The q-gamma function is given by $\varGamma _{q}(z) = (1-q)^{(z-1)} / (1-q)^{z -1}$, where $z \in \mathbb{R} \backslash \{0, -1, -2, \ldots \}$ [2]. Note that $\varGamma _{q} (z+1) = [z]_{q} \varGamma _{q} (z)$. Algorithm 2 shows a pseudo-code description of the technique for estimating q-gamma function of order n. The q-derivative of function f is defined by $\mathcal{D}_{q} [f](x) = \frac{f(x) - f(qx)}{(1- q)x}$ and $\mathcal{D}_{q} [f](0) = \lim_{x \to 0} \mathcal{D}_{q} [f](x)$, which is shown in Algorithm 3 [6, 7]. Furthermore, the higher order q-derivative of a function f is defined by $\mathcal{D}_{q}^{n} [f](x) = \mathcal{D}_{q}[\mathcal{D}_{q}^{n-1} [f]](x)$ for $n \geq 1$, where $\mathcal{D}_{q}^{0} [f](x) = f(x)$ [6, 7]. Tables 1, 2, and 3 show the values $\varGamma _{q} (z)$ for some z and $q \in (0,1)$. The q-integral of a function f is defined on $[0,b]$ by

$$ I_{q} f(x) = \int _{0}^{x} f(s) \,\mathrm{d}_{q} s = x(1- q) \sum_{k=0}^{ \infty } q^{k} f \bigl(x q^{k}\bigr) $$

for $0 \leq x \leq b$, provided the series absolutely converges [6, 7]. If x in $[0, T]$, then

$$ \int _{x}^{T} f(r) \,\mathrm{d}_{q} r = I_{q} [f](T) - I_{q} [f](x) = (1- q) \sum _{k=0}^{\infty } q^{k} \bigl[ T f\bigl(T q^{k}\bigr) - x f\bigl(x q^{k}\bigr) \bigr], $$

whenever the series exists. The operator $I_{q}^{n}$ is given by $I_{q}^{0} [h](x) = h(x)$ and $I_{q}^{n} [h](x) = I_{q} [I_{q}^{n-1} [h]] (x)$ for $n \geq 1$ and $h \in C([0,T])$ [6, 7]. It has been proved that $D_{q} [I_{q} [h]](x) = h(x)$ and $I_{q} [D_{q} [h]](x) = h(x) - h(0)$ whenever h is continuous at $x =0$ [6, 7]. The fractional Riemann–Liouville type q-integral of the function h on $J=(0,1)$ for $\alpha \geq 0$ is defined by $\mathcal{I}_{q}^{0} [h](t) = h(t)$ and

$$\begin{aligned} \mathcal{I}_{q}^{\alpha }[h](t)& = \frac{1}{\varGamma _{q}(\alpha )} \int _{0}^{t} (t- qs)^{(\alpha - 1)} h(s) \, \mathrm{d}_{q}s \\ & = t^{\alpha }(1-q)^{\alpha }\sum_{k=0}^{ \infty } q^{k} \frac{ \prod_{i=1}^{k - 1} (1-q^{\alpha +i } ) }{ \prod_{i=1}^{k - 1} (1 - q^{i +1} ) } h\bigl(t q^{k}\bigr) \end{aligned}$$

(5)

for $t \in J$ [11, 18]. One can use Algorithm 5 for calculating $\mathcal{I}_{q}^{\alpha }[h](t)$ according to Eq. (5). Also, the Caputo fractional q-derivative of a function h is defined by

$$\begin{aligned} {}^{c}\mathcal{D}_{q}^{\alpha }[h](t) & = \mathcal{I}_{q}^{ [\alpha ]-\alpha } \bigl[\mathcal{D}_{q}^{[\alpha ]} [h] \bigr] (t) \\ & = \frac{1}{ \varGamma _{q} ([\alpha ] -\alpha )} \int _{0}^{t} (t- qs)^{ ( [\alpha ] - \alpha - 1 )} \mathcal{D}_{q}^{[ \alpha ]} [h] (s) \,\mathrm{d}_{q}s, \end{aligned}$$

(6)

where $t \in J$ and $\alpha >0$ [18]. It has been proved that $\mathcal{I}_{q}^{\beta } [\mathcal{I}_{q}^{\alpha } [h]] (x) = \mathcal{I}_{q}^{\alpha + \beta } [h] (x)$ and $\mathcal{D}_{q}^{\alpha } [\mathcal{I}_{q}^{\alpha } [h]] (x)= h(x)$, where $\alpha, \beta \geq 0$ [18]. Algorithm 5 shows pseudo-code $\mathcal{I}_{q}^{\alpha }[h](x)$.

Algorithm 1

The proposed method for calculated $(a-b)_{q}^{(\alpha )}$

Algorithm 2

The proposed method for calculated $\varGamma _{q}(x)$

Algorithm 3

The proposed method for calculated $(D_{q} f)(x)$

Table 1 Some numerical results for calculation of $\varGamma _{q}(x)$ with $q=\frac{1}{3}$ that is constant, $x=4.5, 8.4, 12.7$, and $n=1, 2, \ldots, 15$ of Algorithm 2

Table 2 Some numerical results for calculation of $\varGamma _{q}(x)$ with $q=\frac{1}{3}, \frac{1}{2}, \frac{2}{3}$, $x=5$, and $n=1, 2, \ldots, 35$ of Algorithm 2

Table 3 Some numerical results for calculation of $\varGamma _{q}(x)$ with $x=8.4$, $q=\frac{1}{3}, \frac{1}{2}, \frac{2}{3}$, and $n=1, 2, \ldots, 40$ of Algorithm 2

We use $\Vert y \Vert = \max_{t \in \overline{J}} | y(t)|$ as the norm of $A=B= C^{1}(\overline{J})$. Clearly, $(A, \|.\|)$ and $(B, \|.\|)$ are Banach spaces. Also, the product space $(A\times B, \|(y, z)\|)$ is a Banach space where $\|(y, z)\|= \|y\| + \|z\|$. An operator $\mathcal{O}: A \to A$ is called completely continuous if restricted to any bounded set in A is compact.

Lemma 1

(Leray–Schauder alternative [48, p.4])

Let$\mathcal{O}: \mathcal{Y} \to \mathcal{Y}$be completely continuous and$\varOmega (\mathcal{O}) = \{ x \in \mathcal{Y} | x = \lambda \mathcal{O}(x) \}$, where$\lambda \in (0,1)$. Then either the set$\varOmega (\mathcal{O})$is unbounded or$\mathcal{O}$has at least one fixed point.

3 Main results

The main results are presented in this section. To facilitate exposition, we will provide our analysis in two separate folds.

3.1 The nonlinear sum and integral boundary value problem (1)–(2)

First, we provide our key lemma.

Lemma 2

The function$x_{0} \in \mathcal{A}$is a solution for problem (1) under the sum and integral boundary value conditions (2) if and only if$x_{0}$is a solution for the fractionalq-integral equation

$$ x_{0}(t) = \int _{0}^{1} G_{q}(t,r ) w_{1} \bigl(r, x_{0}(r),\varphi \bigl(x_{0}(r) \bigr) \bigr) \,\mathrm{d}_{q}r, $$

where

$$\begin{aligned} G_{q}(t, r)={}& {-}\frac{(t-qr)^{(\alpha -1)}}{ \varGamma _{q} (\alpha )} + \frac{ [ \eta (\frac{1}{2} - t) + 1 ] ( 1 -qr)^{(\alpha -2)}}{ [ \eta (\varXi - \frac{1}{2} ) + 1 ] \varGamma _{q}(\alpha -1)} \\ &{} + \frac{ [ \eta ( \varXi ( t - 1) +\frac{1}{2})- \varXi ] (b -qr )^{(\alpha -2)}}{ [\eta ( \varXi -\frac{1}{2}) + 1 ] \varGamma _{q} (\alpha -1 )} \\ &{} + \frac{ [ \eta ( \varXi - 1+t) ] (1- qr )^{(\alpha )} }{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha +1)} \\ &{} + \frac{ [ \eta \varXi ( \varXi -2)+( \varXi -1+t) ] (a - qr )^{(\alpha -2)}}{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha -1)} \end{aligned}$$

whenever$r \leq a$and$0\leq r \leq t\leq 1$,

$$\begin{aligned} G_{q}(t, r) ={}& {-}\frac{(t-qr)^{(\alpha -1)}}{ \varGamma _{q} (\alpha )} + \frac{ [ \eta (\frac{1}{2} - t) + 1 ] ( 1 -qr)^{(\alpha -2)}}{ [ \eta (\varXi - \frac{1}{2} ) + 1 ] \varGamma _{q}(\alpha -1)} \\ &{} + \frac{ [ \eta ( \varXi ( t - 1) +\frac{1}{2})- \varXi ] (b -qr )^{(\alpha -2)}}{ [\eta ( \varXi -\frac{1}{2}) + 1 ] \varGamma _{q} (\alpha -1 )} \\ &{} + \frac{ [ \eta ( \varXi - 1+t) ] (1-r )^{(\alpha )} }{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha +1)} \end{aligned}$$

whenever$r \leq b$and$0\leq a \leq r \leq t \leq 1$,

$$\begin{aligned} G_{q}(t, r) ={}&{-}\frac{(t-qr)^{(\alpha -1)}}{ \varGamma _{q} (\alpha )} + \frac{ [ \eta (\frac{1}{2} - t) + 1 ] ( 1 -qr)^{(\alpha -2)}}{ [ \eta (\varXi - \frac{1}{2} ) + 1 ] \varGamma _{q}(\alpha -1)} \\ &{} + \frac{ [ \eta ( \varXi - 1+t) ] (1-r )^{(\alpha )} }{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha +1)} \end{aligned}$$

whenever$0\leq a \leq b \leq r \leq t \leq 1$,

$$\begin{aligned} G_{q}(t, r ) = {}&\frac{ [ \eta (\frac{1}{2} - t) + 1 ] ( 1 -qr)^{(\alpha -2)}}{ [ \eta (\varXi - \frac{1}{2} ) + 1 ] \varGamma _{q}(\alpha -1)} \\ &{} + \frac{ [ \eta ( \varXi ( t - 1) +\frac{1}{2})- \varXi ] (b -qr )^{(\alpha -2)}}{ [\eta ( \varXi -\frac{1}{2}) + 1 ] \varGamma _{q} (\alpha -1 )} \\ & {}+ \frac{ [ \eta ( \varXi - 1+t) ] (1- qr )^{(\alpha )} }{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha +1)} \\ &{} + \frac{ [ \eta \varXi ( \varXi -2)+( \varXi -1+t) ] (a - qr )^{(\alpha -2)}}{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha -1)} \end{aligned}$$

whenever$0\leq t \leq r \leq a \leq b \leq 1$,

$$\begin{aligned} G_{q}(t, r ) ={}&\frac{ [ \eta (\frac{1}{2} - t) + 1 ] ( 1 -qr)^{(\alpha -2)}}{ [ \eta (\varXi - \frac{1}{2} ) + 1 ] \varGamma _{q}(\alpha -1)} \\ &{} + \frac{ [ \eta ( \varXi ( t - 1) +\frac{1}{2})- \varXi ] (b -qr )^{(\alpha -2)}}{ [\eta ( \varXi -\frac{1}{2}) + 1 ] \varGamma _{q} (\alpha -1 )} \\ &{} + \frac{ [ \eta ( \varXi - 1+t) ] (1- qr )^{(\alpha )} }{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha +1)} \end{aligned}$$

whenever$a \leq r$and$0\leq t\leq r \leq b \leq 1$, and

$$\begin{aligned} G_{q}(t, r ) = \frac{ [ \eta (\frac{1}{2} - t) + 1 ] ( 1 -qr)^{(\alpha -2)}}{ [ \eta (\varXi - \frac{1}{2} ) + 1 ] \varGamma _{q}(\alpha -1)} + \frac{ [ \eta ( \varXi - 1+t) ] (1- qr )^{(\alpha )} }{ [ \eta ( \varXi -\frac{1}{2})+1 ] \varGamma _{q} (\alpha +1)} \end{aligned}$$

whenever$b \leq r$and$0\leq t\leq r \leq 1$.

Proof

Let $x_{0}$ be a solution for Eq. (1)–(2). Take $v_{0}(t)=w_{1} (t,x_{0}(t), \varphi (x_{0}(t)) )$. Choose $d_{0}, d_{1}\in \mathbb{R}$ such that

$$ x_{0}( t)=- \int _{0}^{t} \frac{( t - qr )^{(\alpha -1)}}{\varGamma _{q} (\alpha )} v_{0}( r ) \,\mathrm{d}_{q}r + d_{0} + d_{1} t. $$

(7)

Thus, we obtain $x'_{0}( t) = - \mathcal{I}_{q}^{\alpha -1} [v_{0}](t ) + d_{1}$. At present, by using the boundary conditions (2), we conclude that $d_{1}= \mathcal{I}_{q}^{\alpha -1} [v_{0}]( a ) - \eta \int _{0}^{1} x_{0}( r ) \,\mathrm{d}r$ and

$$\begin{aligned} d_{0} ={}& \mathcal{I}_{q}^{\alpha -1} [v_{0}](1) - \varXi \mathcal{I}_{q}^{ \alpha -1} [v_{0}](b) + (\varXi -1 ) \mathcal{I}_{q}^{ \alpha -1} [v_{0}]( a) \\ &{} + \eta (1- \varXi ) \int _{0}^{1} x_{0}( r ) \,\mathrm{d}r. \end{aligned}$$

Hence, by substituting $d_{0}$ in Eq. (7), we get

$$\begin{aligned} x_{0}( t) = {}&{-} \mathcal{I}_{q}^{\alpha } [v_{0}](t ) + \mathcal{I}_{q}^{ \alpha -1} [v_{0}](1 ) - \varXi \mathcal{I}_{q}^{\alpha -1} [v_{0}](b) \\ &{} + ( \varXi -1 ) \mathcal{I}_{q}^{\alpha -1} [v_{0}](a )+ \eta ( 1- \varXi ) \int _{0}^{1} x_{0}( r ) \,\mathrm{d}r \\ &{} + t \mathcal{I}_{q}^{\alpha -1} [v_{0}](a ) - \eta t \int _{0}^{1} x_{0}( r ) \,\mathrm{d}r. \end{aligned}$$

(8)

Put $\delta =\int _{0}^{1} x_{0}( r ) \,\mathrm{d}r$. By computing the value of δ and substituting it in (8), we get

$$\begin{aligned} x_{0}( t) ={}& {-}\mathcal{I}_{q}^{\alpha } [v_{0}](t ) + \frac{\eta ( \frac{1}{2}-t ) + 1 }{ \eta ( \varXi -\frac{3}{2} )+1 } \mathcal{I}_{q}^{\alpha -1} [v_{0}](1) \\ &{} + \frac{\eta (\varXi ( t - 1) + \frac{1}{2} )- \varXi }{\eta ( \varXi -\frac{1}{2} ) +1 } \mathcal{I}_{q}^{\alpha -1} [v_{0}](b) \\ & {}+ \frac{\eta ( \varXi -1+t ) }{ \eta ( \varXi -\frac{1}{2} )+1 } \mathcal{I}_{q}^{\alpha +1} [v_{0}](1) \\ & {}+ \frac{\eta \varXi ( \varXi -2) + ( \varXi -1+ t)}{\eta ( \varXi -\frac{1}{2} ) + 1 } \mathcal{I}_{q}^{\alpha -1} [v_{0}](a) \\ ={}& \int _{0}^{1} G_{q}(t, r ) w_{1} \bigl( r, x_{0}( r ), \varphi \bigl(x_{0}( r )\bigr) \bigr) \,\mathrm{d}_{q}r. \end{aligned}$$

Thus, $x_{0}$ is a solution for the fractional q-integral equation (7). It is obvious that $x_{0}$ is a solution for the fractional q-integro-differential equation (1) whenever $x_{0}$ is a solution for the fractional q-integral equation. This completes the proof. □

Theorem 3

Let$g\in C(\overline{J}, \mathbb{R})$be a bounded function with upper bound$L >0$. Assume that for each$t\in \overline{J}$there exist positive continuous functions$m_{1}(t)$and$m_{2}(t)$such that

$$\begin{aligned} &\bigl\Vert w_{1} \bigl( t, x( t), \varphi \bigl(x( t)\bigr) \bigr) - w_{1} \bigl( t , y( t), \varphi \bigl(y( t) \bigr) \bigr) \bigr\Vert \\ &\quad\leq m_{1}(t) \Vert x-y \Vert + L m_{2}(t) \Vert x-y \Vert \end{aligned}$$

for$x, y\in \mathcal{A}$. Also, put

$$ \begin{aligned}& M_{0} = \max \Bigl\{ \sup _{ t \in \overline{J} } \bigl\vert \mathcal{I}_{q}^{\alpha }[m_{1}] (t) \bigr\vert , \sup_{t\in \overline{J}} L \bigl\vert \mathcal{I}_{q}^{\alpha }[m_{2}](t) \bigr\vert \Bigr\} , \\ &M_{1}=\max \Bigl\{ \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{ \alpha +1} [m_{1}] (1) \bigr\vert , \sup_{t\in \overline{J}} L \bigl\vert \mathcal{I}_{q}^{\alpha +1} [m_{2}](1) \bigr\vert \Bigr\} , \end{aligned} $$

(9)

and

$$ M(s) = \max \Bigl\{ \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{ \alpha -1} [m_{1}] (s) \bigr\vert , \sup_{t\in \overline{J}} L \bigl\vert \mathcal{I}_{q}^{\alpha -1} [m_{2}](s) \bigr\vert \Bigr\} $$

(10)

for$s=1$, $s=a$, $s=b$, and

$$\begin{aligned} \Delta = {}&M_{0} + \frac{\eta \varXi }{\eta (\varXi - \frac{1}{2})+1} M_{1} + \frac{\frac{1}{2}\eta +1}{\eta (\varXi -\frac{1}{2} )+1} M(1) \\ &{} + \frac{ \eta \varXi (\varXi -2) +\varXi }{ \eta (\varXi -\frac{1}{2} ) + 1} M(a) + \frac{\frac{1}{2} \eta \varXi - \varXi }{ \eta ( \varXi -\frac{1}{2} )+1 } M(b). \end{aligned}$$

(11)

If$\Delta <1$, then the nonlinear fractionalq-integro-differential equation (1)–(2) has a unique solution.

Proof

We define the operator $\varTheta: C (\overline{J}) \to C (\overline{J})$ by

$$\begin{aligned} (\varTheta y) ( t) = {}&{-} \mathcal{I}_{q}^{\alpha } [w_{1}] \bigl(t, x(t), \varphi \bigl( x(t)\bigr)\bigr) \\ & {}+ \frac{ \eta (\frac{1}{2}-t ) + 1}{ \eta ( \varXi -\frac{1}{2} )+1} \mathcal{I}_{q}^{\alpha -1} [w_{1}]\bigl(1, x(1), \varphi \bigl( x(1)\bigr)\bigr) \\ &{} + \frac{\eta ( \varXi (t-1)+\frac{1}{2} ) - \varXi }{\eta ( \varXi - \frac{1}{2} ) + 1} \mathcal{I}_{q}^{\alpha -1} [w_{1}]\bigl(b, x(b), \varphi \bigl( x(b)\bigr)\bigr) \\ &{} + \frac{\eta ( \varXi -1+t )}{\eta ( \varXi -\frac{1}{2} ) + 1 } \mathcal{I}_{q}^{ \alpha +1} [w_{1}]\bigl(1,x(1), \varphi \bigl(x(1)\bigr)\bigr) \\ &{} + \frac{\eta \varXi ( \varXi -2 ) + ( \varXi -1+ t )}{ \eta ( \varXi -\frac{1}{2} ) + 1} \mathcal{I}_{q}^{\alpha -1} [w_{1}] \bigl(a, x(a), \varphi \bigl( x(a)\bigr)\bigr). \end{aligned}$$

Take $\ell = \sup_{t\in \overline{J}} | w_{1}( t, 0, 0)|$ and choose $r_{0}>0$ such that

$$\begin{aligned} r_{0} \geq{}& \frac{\ell }{1-k} \biggl[ \frac{1}{\varGamma _{q} ( \alpha +1) } + \frac{\frac{1}{2} \eta +1}{ \eta ( \varXi -\frac{1}{2} ) + 1 } \frac{ 1}{ \varGamma _{q} (\alpha ) } + \frac{\frac{1}{2} \eta - \varXi }{\eta ( \varXi -\frac{1}{2} ) + 1} \frac{b^{ (\alpha -1 )}}{ \varGamma _{q} ( \alpha )} \\ &{} + \frac{\eta \varXi }{ \eta ( \varXi -\frac{1}{2} ) + 1} \frac{1}{\varGamma _{q} (\alpha +2 )} + \frac{{\eta \varXi ( \varXi -2 )+ \varXi }}{ \eta ( \varXi -\frac{1}{2} )+1} \frac{\eta ^{ (\alpha -1 )}}{\varGamma _{q} (\alpha )} \biggr]. \end{aligned}$$

Put $B_{r_{0}} = \{ x\in \mathcal{A}: \| x \| \leq r_{0} \}$. Let $x \in B_{r_{0}}$. Then we have

$$\begin{aligned} \bigl\Vert (\varTheta x) ( t) \bigr\Vert \leq{}& \mathcal{I}_{q}^{\alpha } \bigl( \bigl\Vert w_{1}\bigl( t , x(t), \varphi \bigl(x(t)\bigr) \bigr) - w_{1}( t, 0, 0) \bigr\Vert + \bigl\Vert w_{1}( t, 0, 0) \bigr\Vert \bigr) \\ &{} + \frac{ \frac{1}{2} \eta +1}{\eta ( \varXi -\frac{1}{2} ) +1 } \\ & {}\times \mathcal{I}_{q}^{\alpha -1} \bigl( \bigl\Vert w_{1}\bigl( 1, x(1), \varphi \bigl(x(1)\bigr)\bigr) - w_{1}( 1, 0, 0) \bigr\Vert + \bigl\Vert w_{1}( 1, 0, 0) \bigr\Vert \bigr) \\ &{} + \frac{ \frac{1}{2}\eta -\varXi }{\eta ( \varXi -\frac{1}{2} )+1} \\ &{} \times \mathcal{I}_{q}^{\alpha -1} \bigl( \bigl\Vert w_{1}\bigl( b, x(b), \varphi \bigl(x(b)\bigr)\bigr) - w_{1}( b, 0, 0) \bigr\Vert + \bigl\Vert w_{1}( b, 0, 0) \bigr\Vert \bigr) \\ &{} + \frac{\eta \varXi }{\eta ( \varXi - \frac{1}{2} ) +1 } \\ &{} \times \mathcal{I}_{q}^{\alpha +1} \bigl( \bigl\Vert w_{1}\bigl( 1, x(1), \varphi \bigl(x(1)\bigr)\bigr) - w_{1}( 1, 0, 0) \bigr\Vert + \bigl\Vert w_{1}( 1, 0, 0) \bigr\Vert \bigr) \\ &{} + \frac{\eta \varXi (\varXi -2) +\varXi }{\eta ( \varXi -\frac{1}{2} ) + 1} \\ &{} \times \mathcal{I}_{q}^{\alpha -1} \bigl( \bigl\Vert w_{1}\bigl( a, x( a ), \varphi \bigl(x(a)\bigr)\bigr) - w_{1}( a, 0, 0) \bigr\Vert + \bigl\Vert w_{1}( a, 0, 0) \bigr\Vert \bigr) \\ \leq{}& \biggl[M_{0} + \frac{\eta \varXi }{\eta (\varXi - \frac{1}{2})+1} M_{1} + \frac{\frac{1}{2} \eta +1}{\eta (\varXi -\frac{1}{2} )+1} M(1) \\ & {}+ \frac{ \eta \varXi (\varXi -2) +\varXi }{ \eta (\varXi -\frac{1}{2} ) + 1} M(a) + \frac{\frac{1}{2} \eta \varXi - \varXi }{ \eta ( \varXi -\frac{1}{2} )+1 } M(b) \biggr] r_{0} \\ &{} + \biggl[ \frac{1}{\varGamma _{q} (\alpha +1)} + \frac{ \frac{1}{2} \eta +1 }{\eta ( \varXi - \frac{1}{2} ) + 1} \frac{1}{\varGamma _{q} (\alpha )} + \frac{\frac{1}{2}\eta - \varXi }{ \eta ( \varXi -\frac{1}{2} ) + 1 } \frac{b}{ \varGamma _{q} (\alpha )} \\ &{} + \frac{\eta \varXi }{ \eta ( \varXi -\frac{1}{2} ) + 1 } \frac{1}{\varGamma _{q} (\alpha +2)} + \frac{{\eta \varXi ( \varXi -2)+ \varXi }}{\eta ( \varXi -\frac{1}{2} ) +1} \frac{ a^{(\alpha -1)}}{ \varGamma _{q} (\alpha )} \biggr] \ell \\ ={}& \Delta r_{0} + \biggl[ \frac{1}{ \varGamma _{q} (\alpha +1)} + \frac{\frac{1}{2}\eta +1}{\eta ( \varXi -\frac{1}{2} )+1} \frac{1}{\varGamma _{q} (\alpha )} \\ &{} + \frac{\frac{1}{2}\eta - \varXi }{\eta ( \varXi -\frac{1}{2} ) + 1} \frac{b^{(\alpha - 1 ) }}{ \varGamma _{q} (\alpha )} + \frac{\eta \varXi }{\eta ( \varXi - \frac{1}{2} )+1} \frac{1}{\varGamma _{q} (\alpha +2)} \\ & {}+ \frac{{\eta \varXi ( \varXi -2)+ \varXi }}{\eta ( \varXi -\frac{1}{2} )+1 } \frac{\eta ^{(\alpha -1)}}{\varGamma _{q} (\alpha )} \biggr] \ell \leq r_{0}. \end{aligned}$$

Hence, $\varTheta (B_{r_{0}})\subset B_{r_{0}}$. On the other hand, one can write

$$\begin{aligned} &\bigl\Vert (\varTheta x) ( t)- (\varTheta y) ( t) \bigr\Vert \\ &\quad \leq \mathcal{I}_{q}^{\alpha } \bigl( m_{1}(t) \Vert x-y \Vert + m_{2}(t ) \bigl\Vert \varphi (x) -\varphi (y) \bigr\Vert \bigr) \\ &\qquad{} + \frac{\frac{1}{2}\eta +1}{\eta ( \varXi -\frac{1}{2})+1} \mathcal{I}_{q}^{\alpha -1} \bigl( m_{1}(1 ) \Vert x - y \Vert + m_{2}(1 ) \bigl\Vert \varphi (x) - \varphi (y) \bigr\Vert \bigr) \\ &\qquad{} + \frac{\frac{1}{2}\eta -\varXi }{\eta ( \varXi -\frac{1}{2})+1} \mathcal{I}_{q}^{\alpha -1} \bigl( m_{1}(b ) \Vert x-y \Vert + m_{2}(b ) \bigl\Vert \varphi (x) -\varphi (y) \bigr\Vert \bigr) \\ & \qquad{}+ \frac{\eta \varXi }{\eta ( \varXi - \frac{1}{2})+1} \mathcal{I}_{q}^{ \alpha +1} \bigl( m_{1}(1 ) \Vert x - y \Vert + m_{2}(1) \bigl\Vert \varphi (x) - \varphi (y) \bigr\Vert \bigr) \\ &\qquad{} + \frac{\eta \varXi (\varXi -2) +\varXi }{\eta ( \varXi -\frac{1}{2})+1} \mathcal{I}_{q}^{\alpha -1} \bigl( m_{1}(a) \Vert x - y \Vert + m_{2} (a) \bigl\Vert \varphi (x) - \varphi (y) \bigr\Vert \bigr) \\ &\quad \leq \biggl[ M_{0} + \frac{\eta \varXi }{\eta (\varXi - \frac{1}{2})+1} M_{1} + \frac{\frac{1}{2}\eta +1}{\eta (\varXi -\frac{1}{2} )+1} M(1) \\ & \qquad{}+ \frac{ \eta \varXi (\varXi -2) +\varXi }{ \eta (\varXi -\frac{1}{2} ) + 1} M(a) + \frac{\frac{1}{2} \eta \varXi - \varXi }{ \eta ( \varXi -\frac{1}{2} )+1 } M(b) \biggr] \Vert x-y \Vert \\ & \quad= \Delta \Vert x-y \Vert . \end{aligned}$$

Since $\Delta < 1$, Θ is a contraction. Thus, by using the Banach contraction principle, Θ has a unique fixed point $x_{0}$ in $\mathcal{A}$. At present, by using Lemma 2, one can get that ${}^{c}\mathcal{D}_{q}^{\alpha }[x_{0}] \in \mathcal{A}$ and $x_{0}$ is the unique solution for the fractional q-integro-differential equation (1)–(2). □

3.2 The nonlinear boundary value problem (3)–(4)

Lemma 4

Let$w_{2}: \overline{J}\times \mathcal{B}^{3} \to \mathcal{B}$be a continuous function. An element$x_{0}\in \mathcal{B}$is a solution for the fractionalq-integro-differential equation (3) under the sum boundary conditions (4) if and only if$x_{0}$is a solution for the fractional integral equation

$$ y( t)= \mathcal{I}_{q}^{\alpha } [v](t) - t \mathcal{I}_{q}^{\alpha -1} [v](1 ) + t \varXi \mathcal{I}_{q}^{\alpha -2} [v](b). $$

Proof

Put

$$ v_{0}(t) = w_{2} \biggl(t,x_{0}(t), \int _{0}^{t} x_{0} (r) \,\mathrm{d}r, {}^{c}\mathcal{D}_{q}^{\zeta }[x_{0}] (t) \biggr). $$

Let $x_{0}$ be a solution for the fractional q-integro-differential equation (3). Choose $d_{0}, d_{1}\in \mathbb{R}$ such that $x_{0}( t)= \mathcal{I}_{q}^{\alpha } [v_{0}](t) + d_{0}+d_{1} t$ for all $t\in \overline{J}$. Hence, $x'_{0}(t) = \mathcal{I}_{q}^{\alpha -1} [y_{0}](t) + d_{1}$ and $x''_{0}(t)= \mathcal{I}_{q}^{\alpha -2} [v_{0}](t)$. By using the sum boundary conditions (4), we get $d_{0}=0$ and $d_{1}=-\mathcal{I}_{q}^{\alpha -1} [v_{0}](1) + \varXi \mathcal{I}_{q}^{ \alpha -2} [v_{0}](b)$. By substituting $d_{0}$ and $d_{1}$, we obtain

$$ x_{0}( t) = \mathcal{I}_{q}^{\alpha } [v_{0}](t) - t\mathcal{I}_{q}^{ \alpha -1} [v_{0}](1) + t \varXi \mathcal{I}_{q}^{\alpha -2} [y_{0}](b). $$

Thus, $x_{0}$ is a solution for the fractional q-integral equation. It is obvious that $x_{0}$ is a solution for the fractional q-integro-differential equation (3) whenever $x_{0}$ is a solution for the fractional q-integral equation. This completes the proof. □

Theorem 5

Suppose that$w_{2}: \overline{J}\times \mathcal{B}^{3}\to \mathcal{B}$is a continuous map and there exist positive continuous functions$m_{1}$, $m_{2}$, and$m_{3}$such that

$$\begin{aligned} &\biggl\vert w_{2} \biggl(t, x(t), \int _{0}^{t} x(r) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x] (t) \biggr) - w_{2} \biggl(t, y(t), \int _{0}^{t} y(r) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[y](t) \biggr) \biggr\vert \\ &\quad\leq m_{1}(t) \vert x-y \vert + m_{2}(t) \biggl\vert \int _{0}^{t} x(r) \,\mathrm{d}r - \int _{0}^{t} y(r) \,\mathrm{d}r \biggr\vert \\ &\qquad{} + m_{3}(t) \bigl\vert {}^{c}\mathcal{D}_{q}^{\zeta }[x](t) - {}^{c} \mathcal{D}_{q}^{\zeta }[y](t) \bigr\vert \end{aligned}$$

for all$x,y\in \mathcal{B}$and$t\in \overline{J}$. Let

$$\begin{aligned} \begin{aligned} &M_{0} =\max \Bigl\{ \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha }[m_{1}] (t) \bigr\vert , \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha }[m_{2}](t) \bigr\vert , \sup_{t \in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha }[ m_{3}](t) \bigr\vert \Bigr\} , \\ &M(1) =\max \Bigl\{ \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{ \alpha -1} [m_{1}] (1) \bigr\vert , \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha -1} [m_{2}](1) \bigr\vert , \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha -1} [m_{3}](1) \bigr\vert \Bigr\} , \\ &M(b) =\max \Bigl\{ \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{ \alpha -2} [m_{1}] (b) \bigr\vert , \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha -2} [m_{2}](b) \bigr\vert , \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha -2} [m_{3}](b) \bigr\vert \Bigr\} , \end{aligned} \end{aligned}$$

(12)

and

$$ M(t) = \max \Bigl\{ \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{ \alpha -\zeta } [m_{1}] (t) \bigr\vert , \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha - \zeta } [m_{2}](t) \bigr\vert , \sup_{t\in \overline{J}} \bigl\vert \mathcal{I}_{q}^{\alpha -\zeta } [m_{3}](t) \bigr\vert \Bigr\} . $$

(13)

Put

$$ \Delta = M_{0} + M(t) + \frac{\varGamma _{q} (2-\zeta )+ 1 }{ \varGamma _{q} (2-\zeta )} M(1) + \frac{(1+\varGamma _{q} (2-\zeta )) \varXi }{\varGamma _{q} (2-\zeta )} M(b). $$

(14)

If$\Delta < 1$, then the nonlinear fractionalq-integro-differential equation (3)–(4) has a unique solution.

Proof

Define the operator $\varTheta: \mathcal{B} \to \mathcal{B}$ by

$$\begin{aligned} ( \varTheta x) ( t) = \mathcal{I}_{q}^{\alpha } [v](t) - t \mathcal{I}_{q}^{ \alpha -1} [v](1) + t \varXi \mathcal{I}_{q}^{\alpha -2} [v](b), \end{aligned}$$

where

$$ v(t)= w_{2} \biggl(t, x(t), \int _{0}^{t} x(r) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x](t) \biggr). $$

Choose $r>0$ such that

$$\begin{aligned} r \geq {}&\frac{\ell }{1-k} \biggl[ \frac{1}{\varGamma _{q} (\alpha -\zeta +1) } + \frac{1+\alpha }{\varGamma _{q} (\alpha +1)} + \frac{1 }{\varGamma _{q} (2-\zeta )\varGamma _{q} (\alpha )} \\ &{} + \frac{[\varGamma _{q} (2-\zeta )+1] b^{(\alpha -2)} \varXi }{\varGamma _{q} (2-\zeta )\varGamma _{q} (\alpha -1)} \biggr], \end{aligned}$$

where $\ell = \sup_{t\in \overline{J} } | w_{2}( t, 0, 0, 0 ) |$. We show that $\varTheta B_{r_{0}} \subset B_{r_{0}}$, where

$$ B_{r_{0}}=\bigl\{ x\in \mathcal{B}: \Vert x \Vert \leq r_{0} \bigr\} . $$

Let $x \in B_{r_{0}}$. Then

$$\begin{aligned} \bigl\vert (\varTheta x) (t) \bigr\vert \leq{}& \mathcal{I}_{q}^{\alpha } \biggl( \biggl\vert w_{2} \biggl( t, x( t ), \int _{0}^{t} x( r )\,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x]( t ) \biggr) - w_{2} ( t, 0, 0, 0) \biggr\vert \\ &{} + \bigl\vert w_{2}( t, 0, 0, 0 ) \bigr\vert \biggr) \\ & + \mathcal{I}_{q}^{\alpha -1} \biggl( \biggl\vert w_{2} \biggl( 1, x(1), \int _{0}^{1} x( r )\,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x](1) \biggr) - w_{2}( 1, 0, 0, 0) \biggr\vert \\ &{} + \bigl\vert w_{2}( 1, 0, 0, 0 ) \bigr\vert \biggr) \\ &{} + \varXi \mathcal{I}_{q}^{\alpha -2} \biggl( \biggl\vert w_{2} \biggl( b, x(b ), \int _{0}^{b} x( r )\,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x]( b ) \biggr) - w_{2}( b, 0, 0, 0) \biggr\vert \\ &{} + \bigl\vert w_{2}( b, 0, 0, 0 ) \bigr\vert \biggr) \\ \leq{}& M_{0} \bigl\vert x(t) \bigr\vert + \frac{\ell }{ \varGamma _{q} (\alpha +1 )} + M(1) \bigl\vert x(t) \bigr\vert + \frac{\ell }{\varGamma _{q} (\alpha )} \\ &{} + \varXi \bigl(M(b ) \bigl\vert x(t) \bigr\vert \bigr) + \frac{\ell \varXi b^{(\alpha -2)} }{\varGamma _{q} (\alpha -1 )} \\ \leq{}& \bigl( M_{0} + M(1) + \varXi M(b) \bigr) \bigl\vert x(t) \bigr\vert \\ &{} + \ell \biggl[ \frac{ 1 }{\varGamma _{q} (\alpha + 1 )} + \frac{ 1 }{\varGamma _{q} (\alpha )} + \frac{b^{(\alpha -2)} \varXi }{\varGamma _{q} (\alpha -1 )} \biggr]. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \bigl\vert {}^{c}\mathcal{D}^{\zeta }[\varTheta x](t) \bigr\vert \leq{}& M(t) \bigl\vert x(t) \bigr\vert + \frac{\ell }{\varGamma _{q} (\alpha -\zeta +1 )} + \frac{1}{\varGamma _{q}(2-\zeta )} M(1) \bigl\vert x(t) \bigr\vert \\ &{} + \frac{\ell }{ \varGamma _{q}(2-\zeta ) \varGamma _{q}(\alpha )} + \frac{ \varXi }{ \varGamma _{q}(2-\zeta )} \bigl(M(b) \bigl\vert x(t) \bigr\vert \bigr) \\ &{} + \frac{\ell \varXi b^{\alpha -2} }{\varGamma _{q}(2-\zeta )\varGamma _{q}(\alpha -1 )} \\ \leq{}& \biggl[ M(t) + \frac{1}{\varGamma _{q} (2 -\zeta )} M(1) + \frac{ \varXi }{ \varGamma _{q}( 2-\zeta )} M(b) \biggr] \bigl\vert x(t) \bigr\vert \\ &{} + \ell \biggl[ \frac{ 1 }{\varGamma _{q} ( \alpha -\zeta + 1 ) } + \frac{ 1 }{ \varGamma _{q}(2- \zeta ) \varGamma _{q}(\alpha )} + \frac{\varXi b^{\alpha -2} }{\varGamma _{q} (2-\zeta )\varGamma _{q}(\alpha -1 )} \biggr]. \end{aligned}$$

Hence,

$$\begin{aligned} \bigl\vert (\varTheta x) (t) \bigr\vert \leq{}& \Delta r_{0} + \ell \biggl[ \frac{1}{\varGamma _{q}(\alpha - \zeta +1)} + \frac{1+\alpha }{\varGamma _{q} (\alpha +1)} + \frac{1 }{\varGamma _{q}( 2 - \alpha ) \varGamma _{q}(\alpha )} \\ &{} + \frac{ \varXi b^{\alpha -2} [ \varGamma _{q} (2-\zeta )+1] }{\varGamma _{q}(2-\zeta ) \varGamma _{q}(\alpha -1) } \biggr] \leq r_{0} \end{aligned}$$

and so $\varTheta (B_{r_{0}}) \subseteq B_{r_{0}}$. Let $u, v\in X$ and $t\in J$. Then we have

$$\begin{aligned} \bigl\vert (\varTheta x) ( t) - (\varTheta y) ( t) \bigr\vert \leq{}& \mathcal{I}_{q}^{\alpha } \Biggl( \sum _{i=1}^{3} m_{i}(t) \bigl\vert x(t)- y( t) \bigr\vert \Biggr) \\ &{} + \mathcal{I}_{q}^{\alpha - 1} \Biggl( \sum _{i=1}^{3} m_{i}(1) \bigl\vert x(1)- y(1) \bigr\vert \Biggr) \\ &{} + \varXi \mathcal{I}_{q}^{\alpha - 2 } \Biggl( \sum _{i=1}^{3} m_{i}(b) \bigl\vert x(b)- y( b) \bigr\vert \Biggr) \\ \leq {}&\bigl( M_{0} + M(1) + \varXi M(b) \bigr) \vert x -y \vert . \end{aligned}$$

On the other hand,

$$\begin{aligned} &\bigl\vert {}^{c}\mathcal{D}^{\zeta }[\varTheta x](t) - {}^{c} \mathcal{D}^{\zeta }[\varTheta y](t) \bigr\vert \\ &\quad \leq \biggl[ M(t) + \frac{1}{\varGamma _{q}(2-\zeta )}I^{\alpha - 1 } M(1) + \frac{ \varXi }{\varGamma _{q} (2-\zeta )} M(b) \biggr] \vert x-y \vert . \end{aligned}$$

Hence,

$$\begin{aligned} \bigl\Vert (\varTheta x) (t) -(\varTheta y) (t) \bigr\Vert \leq{}& \biggl[ M(t)+ M_{0}+ \frac{\varGamma _{q}(2-\zeta )+1}{\varGamma _{q} (2-\zeta )} M(1) \\ &{} + \frac{ \varXi [1 + \varGamma _{q}(2-\zeta )] }{ \varGamma _{q}(2-\zeta )} M(b) \biggr] \Vert x - y \Vert \\ ={}& \Delta \Vert x-y \Vert . \end{aligned}$$

Since $\Delta < 1$, Θ is a contraction and so, by using the Banach contraction principle, Θ has a unique fixed point. By using Lemma 4, it is clear that the unique fixed point of Θ is the unique solution for the nonlinear fractional integro-differential problem (3)–(4). □

4 Examples, numerical results, and algorithms

Herein, we give an example to show the validity of the main results. In this way, we give a computational technique for checking problems (1)–(2) and (3)–(4). We need to present a simplified analysis that is able to execute the values of the q-gamma function. For this purpose, we provided a pseudo-code description of the method for calculation of the q-gamma function of order n in Algorithms 2, 3, 4, and 5; for more details, follow these addresses https://en.wikipedia.org/wiki/Q-gamma_function and https://www.dm.uniba.it/members/garrappa/software. Tables 1, 2, and 3 show the values $\varGamma _{q} (z)$ for some z and $q \in (0,1)$.

Algorithm 4

The proposed method for calculated $\int _{a}^{b} f(r) d_{q} r$

Algorithm 5

The proposed method for calculated $I_{q}^{\alpha}[x]$

For problems for which the analytical solution is not known, we will use, as reference solution, the numerical approximation obtained with a tiny step h by the implicit trapezoidal PI rule, which, as we will see, usually shows an excellent accuracy [49]. All the experiments are carried out in MATLAB Ver. 8.5.0.197613 (R2015a) on a computer equipped with a CPU AMD Athlon(tm) II X2 245 at 2.90 GHz running under the operating system Windows 7.

Example 1

Consider the fractional q-integro-differential equation similar to problem (1) as follows:

$$ {}^{c}\mathcal{D}^{\frac{3}{2}} [x](t) + \frac{ \vert x(t) \vert }{ 7 ( t^{2} + \frac{7}{4} )^{2} ( 2 + \vert x(t) \vert ) } + \frac{t}{ 1600} \int _{0}^{t} e^{ (- \frac{1}{3} ) } x( r) \,\mathrm{d}r =0, $$

(15)

under sum and integral boundary value conditions $x' ( \frac{1}{4} ) = - \frac{1}{6} \int _{0}^{1} x(r) \,\mathrm{d}r$ and

$$ x'(1) + x(0) = \sum_{i=1}^{5} c_{i} x' \biggl( \frac{3}{4} \biggr). $$

Note that $x' ( \frac{3}{4} )= \frac{\partial }{\partial t} x(t)|_{ \frac{3}{4}}$. Clearly, $\alpha =\frac{3}{2}$, $a = \frac{1}{4}$, $\eta = \frac{1}{6}$, $m=5$, $b = \frac{3}{4}$. Let $c_{1}=\frac{1}{8}$, $c_{2}=\frac{-1}{5}$, $c_{3}=\frac{3}{7}$, $c_{4}= \frac{1}{3}$, and $c_{5}= \frac{1}{6}$. Note that $\varXi = \sum_{i=1}^{5} c_{i} =\frac{239}{280}$ and so $2\varXi > -1$. We define the maps $w_{1}: \overline{J} \times \mathcal{A}^{2} \to \mathcal{A}$ and $g: \overline{J} \to [0,\infty )$ by

$$ w_{1}\bigl( t, x( t), \phi x( t)\bigr) = \frac{ \vert x(t) \vert }{ 7 ( t^{2} +\frac{7}{4} )^{2} ( 2 + \vert x(t) \vert ) } + \frac{t}{1600} \int _{0}^{t} e^{ ( - \frac{1}{3} )} x(r ) \,\mathrm{d}r $$

and $g (r) = \frac{1}{40}$ for all $t\in \overline{J}$, respectively. It is obvious that $g(t) \leq 0.025=L$ for $t \in \overline{J}$. Now, we obtain

$$\begin{aligned} &\bigl\Vert w_{1} \bigl( t, x( t), \varphi \bigl(x( t)\bigr) \bigr) - w_{1} \bigl( t , y( t), \varphi \bigl(y( t) \bigr) \bigr) \bigr\Vert \\ &\quad = \biggl\Vert \frac{ \vert x(t) \vert }{ 7 ( t^{2} +\frac{7}{4} )^{2} ( 2 + \vert x(t) \vert ) } + \frac{t}{1600} \int _{0}^{t} e^{ ( - \frac{1}{2} ) } x(r ) \,\mathrm{d}r \\ &\qquad{} - \biggl[ \frac{ \vert y(t) \vert }{ 7 ( t^{2} + \frac{7}{4} )^{2} ( 2 + \vert y(t) \vert ) } + \frac{t}{1600} \int _{0}^{t} e^{ ( - \frac{1}{2} ) } y(r ) \,\mathrm{d}r \biggr] \biggr\Vert \\ &\quad \leq \biggl\Vert \frac{ \vert x(t) \vert }{ 7 ( t^{2} +\frac{7}{4} )^{2} } - \frac{ \vert y(t) \vert }{ 7 ( t^{2} +\frac{7}{4} )^{2} } \biggr\Vert \\ &\qquad{} + \biggl\Vert \frac{t}{1600} \int _{0}^{t} e^{ ( - \frac{1}{2} ) } \bigl( x(r )- y(r) \bigr) \,\mathrm{d}r \biggr\Vert \\ & \quad\leq \frac{1}{7 (t^{2} + \frac{7}{4})^{2} } \Vert x-y \Vert + \frac{t}{1600} \Vert x-y \Vert . \end{aligned}$$

Thus

$$ \bigl\Vert w_{1} \bigl( t, x( t), \varphi \bigl(x( t)\bigr) \bigr) - w_{1} \bigl( t, y( t), \varphi \bigl(y( t) \bigr) \bigr) \bigr\Vert \leq \biggl[ \frac{1}{7(t^{2}+\frac{7}{4})^{2}} + \frac{t}{1600} \biggr] \Vert x-y \Vert $$

for all $t\in J$, $x, y \in \mathcal{A}$. We define the positive continuous maps $m_{1}(t) = \frac{1}{7 (t^{2} + \frac{7}{4})^{2}}$ and $m_{2}(t) = \frac{t}{40}$. At present, by using Eqs. (9)–(10) and applying Algorithm 5, we calculate $\sup \mathcal{I}_{q}^{\alpha }[m_{1}] (t)$, $\sup L \mathcal{I}_{q}^{\alpha }[m_{2}] (t)$, $\sup \mathcal{I}_{q}^{\alpha +1} [m_{1}] (t)$, $\sup L \mathcal{I}_{q}^{\alpha +1 } [m_{2}] (t)$, $\sup \mathcal{I}_{q}^{\alpha -1} [m_{1}] (t)$, and $\sup L \mathcal{I}_{q}^{\alpha -1} [m_{2}] (t)$ for $t \in (0,1)$ and $q=\frac{1}{8}$, $\frac{1}{2}$, $\frac{6}{7}$. Tables 4 and 5 show these results. Also, Figures 1, 2 and 3 illustrate the numerical results of the tables. Therefore

$$\begin{aligned} &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha }[m_{1}] (t) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{3}{2}} \biggl( \frac{1}{7(t+\frac{7}{4})^{2}} \biggr)= 0.0529, 0.0552, 0.0553, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha +1} [m_{1}] (1)= \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{3}{2}+1} \biggl( \frac{1}{7(1 +\frac{7}{4})^{2}} \biggr)= 0.0466, 0.0346, 0.0258, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -1} [m_{1}] (1) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{3}{2}-1} \biggl( \frac{1}{7(1 +\frac{7}{4})^{2}} \biggr)= 0.0566, 0.0652, 0.0706, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -1} [m_{1}] (a) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{3}{2}-1} \biggl( \frac{1}{7(\frac{1}{16} + \frac{7}{4})^{2}} \biggr)= 0.0409, 0.0432, 0.0447, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -1} [m_{1}] (b) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{3}{2}-1} \biggl( \frac{1}{7(\frac{9}{16} +\frac{7}{4})^{2}} \biggr)= 0.0570, 0.0633, 0.0674 \end{aligned}$$

for $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$, respectively, and

$$\begin{aligned} &\sup_{t \in \overline{J}} L \mathcal{I}_{q}^{\alpha }[m_{2}] (t) = \sup_{t \in \overline{J}} L \mathcal{I}_{q}^{\frac{3}{2}} \biggl( \frac{t}{40} \biggr)= 0.0005, 0.0003, 0.0002, \\ &\sup_{t \in \overline{J}} L \mathcal{I}_{q}^{\alpha +1} [m_{2}] (1)= \sup_{t \in \overline{J}} L \mathcal{I}_{q}^{\frac{3}{2}+1} \biggl( \frac{1}{40} \biggr) = 0.0005, 0.0002, 0.0001, \\ &\sup_{t \in \overline{J}} L \mathcal{I}_{q}^{\alpha -1} [m_{2}] (1) = \sup_{t \in \overline{J}} L \mathcal{I}_{q}^{\frac{3}{2}-1} \biggl( \frac{1}{40} \biggr)= 0.0006, 0.0005, 0.0005, \\ &\sup_{t \in \overline{J}} L \mathcal{I}_{q}^{\alpha -1} [m_{2}] (a) = \sup_{t \in \overline{J}} L\mathcal{I}_{q}^{\frac{3}{2}-1} \biggl( \frac{1}{160} \biggr)= 0.0001, 0.0001, 0.0001, \\ &\sup_{t \in \overline{J}} L\mathcal{I}_{q}^{\alpha }[m_{2}] (b) = \sup_{t \in \overline{J}} L\mathcal{I}_{q}^{\frac{3}{2}-1} \biggl( \frac{3}{160} \biggr)= 0.0004, 0.0003, 0.0003 \end{aligned}$$

for $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$, respectively. Hence, from Eqs. (9)–(10) and the above results in Tables 4 and 5, we obtain $M_{0} = \max \{ 0.0529, 0.0005 \} = 0.0529$, $M_{1} = \max \{ 0.0466, 0.0005 \} = 0.0466$, $M(1) = \max \{ 0.0566, 0.0006 \} = 0.0566$,

$$\begin{aligned} &M(a) = M \biggl(\frac{1}{4} \biggr) = \max \{ 0.0409, 0.0001 \} = 0.0409, \\ &M(b) = M \biggl( \frac{3}{4} \biggr) = \max \{ 0.0570, 0.0004 \} =0.0570 \end{aligned}$$

whenever $q =\frac{1}{8}$, $M_{0} = \max \{ 0.0552, 0.0003 \} = 0.0552$, $M_{1} = \max \{ 0.0346, 0.0002 \} = 0.0346$, $M(1) = \max \{ 0.0652, 0.0005 \} = 0.0652$,

$$\begin{aligned} &M(a)= M \biggl(\frac{1}{4} \biggr) = \max \{ 0.0432, 0.0001 \} = 0.0432, \\ &M(b) = M \biggl( \frac{3}{4} \biggr) = \max \{ 0.0633, 0.0003 \} = 0.0633, \end{aligned}$$

whenever $q=\frac{1}{2}$, $M_{0} = \max \{ 0.0553, 0.0002 \} =0.0553$, $M_{1} = \max \{ 0.0258, 0.0001 \} =0.0258$, $M(1) = \max \{ 0.0706, 0.0005 \} = 0.0706$,

$$\begin{aligned} &M(a) = M \biggl(\frac{1}{4} \biggr) = \max \{ 0.0447, 0.0001 \} = 0.0447, \\ &M(b) = M \biggl( \frac{3}{4} \biggr) = \max \{ 0.0674, 0.0003 \} =0.0674, \end{aligned}$$

whenever $q=\frac{6}{7}$. Also, by using Eq. (11), we can calculate values of Δ. Table 6 shows these results. Thus, by using Eq. (11) we have

$$\begin{aligned} \Delta ={}& M_{0} + \frac{\eta \varXi }{\eta (\varXi - \frac{1}{2})+1} M_{1} + \frac{\frac{1}{2}\eta +1}{\eta (\varXi -\frac{1}{2} )+1} M(1) \\ &{} + \frac{ \eta \varXi (\varXi -2) +\varXi }{ \eta (\varXi -\frac{1}{2} ) + 1} M(a) + \frac{\frac{1}{2} \eta \varXi - \varXi }{ \eta ( \varXi -\frac{1}{2} )+1 } M(b) \\ = {}&0.0529 + \frac{\frac{1}{6}\times \frac{239}{280} }{\frac{1}{6} (\frac{239}{280} - \frac{1}{2})+1} \times 0.0466 + \frac{\frac{1}{2}\times \frac{1}{6} + 1}{\frac{1}{6} (\frac{239}{280} - \frac{1}{2} ) + 1} \times 0.0566 \\ &{} + \frac{ \frac{1}{6} \times \frac{239}{280} (\frac{239}{280} -2 ) + \frac{239}{280}}{ \frac{1}{6} ( \frac{239}{280} -\frac{1}{2} ) + 1} \times 0.0409 + \frac{ \frac{1}{2}\times \frac{1}{6} \times \frac{239}{280} - \frac{239}{280}}{ \frac{1}{6} ( \frac{239}{280} -\frac{1}{2} )+1 } \times 0.0570 \\ = {}&0.1016< 1 \end{aligned}$$

whenever $q=\frac{1}{8}$,

$$\begin{aligned} \Delta ={}& M_{0} + \frac{\eta \varXi }{\eta (\varXi - \frac{1}{2})+1} M_{1} + \frac{\frac{1}{2}\eta +1}{\eta (\varXi -\frac{1}{2} )+1} M(1) \\ & {}+ \frac{ \eta \varXi (\varXi -2) +\varXi }{ \eta (\varXi -\frac{1}{2} ) + 1} M(a) + \frac{\frac{1}{2} \eta \varXi - \varXi }{ \eta ( \varXi -\frac{1}{2} )+1 } M(b) \\ = {}&0.0553 + \frac{\frac{1}{6}\times \frac{239}{280} }{\frac{1}{6} (\frac{239}{280} - \frac{1}{2})+1} \times 0.0346 + \frac{\frac{1}{2}\times \frac{1}{6} + 1}{\frac{1}{6} (\frac{239}{280} - \frac{1}{2} ) + 1} \times 0.0653 \\ &{} + \frac{ \frac{1}{6} \times \frac{239}{280} (\frac{239}{280} -2 ) + \frac{239}{280}}{ \frac{1}{6} ( \frac{239}{280} -\frac{1}{2} ) + 1} \times 0.0432 + \frac{ \frac{1}{2}\times \frac{1}{6} \times \frac{239}{280} - \frac{239}{280}}{ \frac{1}{6} ( \frac{239}{280} -\frac{1}{2} )+1 } \times 0.0634 \\ = {}&0.1081< 1 \end{aligned}$$

whenever $q=\frac{1}{2}$, and

$$\begin{aligned} \Delta = {}&M_{0} + \frac{\eta \varXi }{\eta (\varXi - \frac{1}{2})+1} M_{1} + \frac{\frac{1}{2}\eta +1}{\eta (\varXi -\frac{1}{2} )+1} M(1) \\ & {}+ \frac{ \eta \varXi (\varXi -2) +\varXi }{ \eta (\varXi -\frac{1}{2} ) + 1} M(a) + \frac{\frac{1}{2} \eta \varXi - \varXi }{ \eta ( \varXi -\frac{1}{2} )+1 } M(b) \\ = {}&0.0553 + \frac{\frac{1}{6}\times \frac{239}{280} }{\frac{1}{6} (\frac{239}{280} - \frac{1}{2})+1} \times 0.0258 + \frac{\frac{1}{2}\times \frac{1}{6} + 1}{\frac{1}{6} (\frac{239}{280} - \frac{1}{2} ) + 1} \times 0.0706 \\ & {}+ \frac{ \frac{1}{6} \times \frac{239}{280} (\frac{239}{280} -2 ) + \frac{239}{280}}{ \frac{1}{6} ( \frac{239}{280} -\frac{1}{2} ) + 1} \times 0.0447 + \frac{ \frac{1}{2}\times \frac{1}{6} \times \frac{239}{280} - \frac{239}{280}}{ \frac{1}{6} ( \frac{239}{280} -\frac{1}{2} )+1 } \times 0.0674 \\ = {}&0.1103< 1 \end{aligned}$$

whenever $q=\frac{6}{7}$. Figures 4, 5, and 6 show these results (Algorithm 6). Now, by using Theorem 3, the fractional q-integro-differential equation under sum and integral boundary value conditions (15) has a unique solution.

Figure 1

2D graph of $\mathcal{I}_{q}^{\alpha }[m_{1}] (t)$ and $L\mathcal{I}_{q}^{\alpha }[m_{2}] (t)$ for $t \in \overline{J}$ with $q=\frac{1}{8}$, $\frac{1}{2}$, $\frac{6}{7}$ in Example 1

Figure 2

2D graph of $\mathcal{I}_{q}^{\alpha +1} [m_{1}] (1)$ and $L\mathcal{I}_{q}^{\alpha +1} [m_{2}] (1)$ for $t \in \overline{J}$ with $q=\frac{1}{8}$, $\frac{1}{2}$, $\frac{6}{7}$ in Example 1

Figure 3

2D graph of $\mathcal{I}_{q}^{\alpha -1} [m_{1}] (s)$ and $L\mathcal{I}_{q}^{\alpha -1} [m_{2}] (s)$ for $t \in \overline{J}$ and $s=1, a, b$ with $q=\frac{1}{8}$, $\frac{1}{2}$, $\frac{6}{7}$ in Example 1

Figure 4

2D graphs $M_{0}$, $M_{1}$, $M(1)$, $M(b)$, $M(t)$ on $t \in \overline{J}$ for $q=\frac{1}{8}$ in Example 1

Figure 5

2D graphs $M_{0}$, $M_{1}$, $M(1)$, $M(b)$, $M(t)$ on $t \in \overline{J}$ for $q=\frac{1}{2}$ in Example 1

Figure 6

2D graphs $M_{0}$, $M_{1}$, $M(1)$, $M(b)$, $M(t)$ on $t \in \overline{J}$ for $q=\frac{1}{8}$ in Example 1

Algorithm 6

The MATLAB lines for calculation of all parameters in Example 1

Algorithm 6

(Continued)

Table 4 Some numerical results of $\mathcal{I}_{q}^{\alpha }[m_{1}] (t)$ in Example 1 for $t \in \overline{J}$ and $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$

Table 5 Some numerical results of $\mathcal{I}_{q}^{\alpha }[m_{2}] (t)$ in Example 1 for $t \in \overline{J}$ and $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$

Table 6 Some numerical results for calculation of $M_{0}$, $M_{1}$, $M(1)$, $M(a)$, $M(b)$ and $\Delta < 1$ in Example 1 for $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$

Example 2

Consider the fractional q-integro-differential equation similar to problem (3) as follows:

$$\begin{aligned} {}^{c}\mathcal{D}^{\frac{9}{5}} [x](t) ={}& \frac{ \vert t \vert }{ 35(1+ \vert t \vert )} + \frac{2}{35(4+\sqrt{t})} \bigl\vert x(t) \bigr\vert + \frac{3t}{ 70} \int _{0}^{t} \frac{x(r)}{\sqrt{r}+1} \,\mathrm{d}r \\ &{} + \frac{3t}{35(t^{3}+2)} {}^{c}\mathcal{D}^{\frac{1}{8}} [x](t), \end{aligned}$$

(16)

under the sum boundary value conditions $x' ( 0 ) = 0$ and $x'(1) = \sum_{i=1}^{6} c_{i} x'' ( \frac{7}{9} )$. Clearly, $\alpha =\frac{9}{5}$, $\zeta =\frac{1}{8}$, $b = \frac{7}{9}$, and $m=6$. Let $c_{1} = \frac{7}{12}$, $c_{2}=\frac{9}{8}$, $c_{3}=\frac{9}{5}$, $c_{4}= \frac{2}{3}$, $c_{5}= \frac{5}{6}$, $c_{6}= \frac{11}{10}$, and so $\varXi = \sum_{i=1}^{5} c_{i} =\frac{733}{120}= 6.1083$. We define the map $w_{2}: \overline{J} \times \mathcal{B}^{2} \to \mathcal{B}$ by

$$\begin{aligned} w_{2} \bigl( t, x(t), y(t), z(t) \bigr) ={}& \frac{ \vert t \vert }{ 35(1+ \vert t \vert )} + \frac{2}{35(4+\sqrt{t})} \bigl\vert x(t) \bigr\vert \\ &{} + \frac{3t}{ 70} \int _{0}^{t} \frac{y(r)}{\sqrt{r}+1} \,\mathrm{d}r + \frac{3t}{35(t^{3}+2)} {}^{c}\mathcal{D}^{\frac{1}{8}} [z](t) \end{aligned}$$

for all $t\in \overline{J}$. Now, we get

$$\begin{aligned} &\biggl\vert w_{2} \biggl( t, x(t), \int _{0}^{t} x(r ) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x](t) \biggr) - w_{2} \biggl( t, y(t), \int _{0}^{t} y(r ) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[y](t) \biggr) \biggr\vert \\ & \quad= \biggl\vert \frac{ \vert t \vert }{ 35(1+ \vert t \vert )} + \frac{2}{35(4+\sqrt{t})} \bigl\vert x(t) \bigr\vert + \frac{3t}{ 70} \int _{0}^{t} \frac{x(r)}{\sqrt{r}+1} \,\mathrm{d}r \\ & \qquad{}+ \frac{3t}{35(t^{3}+2)} {}^{c}\mathcal{D}^{\frac{1}{8}} [x](t) - \biggl[\frac{ \vert t \vert }{ 35(1+ \vert t \vert )} + \frac{2}{35(4+\sqrt{t})} \bigl\vert y(t) \bigr\vert \\ & \qquad{}+ \frac{3t}{ 70} \int _{0}^{t} \frac{y(r)}{\sqrt{r}+1} \,\mathrm{d}r + \frac{3t}{35(t^{3}+2)} {}^{c}\mathcal{D}^{\frac{1}{8}} [y](t) \biggr] \biggr\vert \\ &\quad \leq \frac{2}{35(4+\sqrt{t})} \bigl\vert \bigl\vert x(t) \bigr\vert - \bigl\vert y(t) \bigr\vert \bigr\vert + \frac{3t}{ 70} \biggl\vert \int _{0}^{t} \biggl(\frac{x(r)}{\sqrt{r}+1} - \frac{y(r)}{\sqrt{r}+1} \biggr) \,\mathrm{d}r \biggr\vert \\ & \qquad{}+ \frac{3t}{35(t^{3}+2)} \bigl\vert {}^{c}\mathcal{D}^{ \frac{1}{8}} [x](t) - {}^{c}\mathcal{D}^{\frac{1}{8}} [y](t) \bigr\vert \\ &\quad \leq \frac{2}{35(4+\sqrt{t})} \Vert x-y \Vert + \frac{3t}{ 70} \Vert x-y \Vert + \frac{3t}{35(t^{3}+2)} \Vert x-y \Vert . \end{aligned}$$

Thus

$$\begin{aligned} &\biggl\vert w_{2} \biggl( t, x(t), \int _{0}^{t} x(r ) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[x](t) \biggr) - w_{2} \biggl( t, y(t), \int _{0}^{t} y(r ) \,\mathrm{d}r, {}^{c} \mathcal{D}_{q}^{\zeta }[y](t) \biggr) \biggr\vert \\ &\quad \leq \biggl[ \frac{2}{35(4+\sqrt{t})} + \frac{3t}{ 70} + \frac{3t}{35(t^{3}+2)} \biggr] \Vert x-y \Vert \end{aligned}$$

for all $t\in J$, $x, y \in \mathcal{B}$. We define the positive continuous maps $m_{1}(t) = \frac{2}{35(4+\sqrt{t})}$, $m_{2}(t)= \frac{3t}{ 70}$, and $m_{3}(t)= \frac{3t}{35(t^{3}+2)}$. At present, by using Eqs. (12)–(13) and applying Algorithm 5, we calculate $\sup \mathcal{I}_{q}^{\alpha }[m_{i}] (t)$, $\sup \mathcal{I}_{q}^{\alpha -1} [m_{i}] (1)$, $\sup \mathcal{I}_{q}^{\alpha -2} [m_{i}] (b)$, $\sup \mathcal{I}_{q}^{\alpha -\zeta } [m_{i}] (t)$ for $i=1,2,3$. Tables 7, 8, and 9 show these results. Therefore

$$\begin{aligned} &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha }[m_{1}] (t) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}} \biggl( \frac{2}{35(4+\sqrt{t})} \biggr)= 0.0106, 0.0089, 0.0077, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -11} [m_{1}] (1) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}-1} \biggl( \frac{2}{175} \biggr)= 0.0118, 0.0125, 0.0128, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -2} [m_{1}] (b) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}-2} \biggl( \frac{2}{35(4+\sqrt{\frac{7}{9}})} \biggr)= 0.0115, 0.0107, 0.0104, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -\zeta } [m_{1}] (t) =\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}- \frac{1}{8}} \biggl(\frac{2}{35(4+\sqrt{t})} \biggr)= 0.0108, 0.0095, 0.0085 \end{aligned}$$

for $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$, respectively,

$$\begin{aligned} &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha }[m_{2}] (t) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}} \biggl( \frac{3t}{ 70} \biggr)= 0.0343, 0.0184, 0.0109, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -11} [m_{2}] (1)= \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}-1} \biggl( \frac{3}{ 70} \biggr)= 0.0391, 0.0315, 0.0269, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -2} [m_{2}] (b) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}-2} \biggl( \frac{1}{ 30} \biggr)= 0.0357, 0.0367, 0.0374, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -\zeta } [m_{2}] (t) =\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}- \frac{1}{8}} \biggl(\frac{3t}{ 70} \biggr)= 0.0349, 0.0198, 0.0123 \end{aligned}$$

for $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$, respectively, and

$$\begin{aligned} &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha }[m_{3}] (t) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}} \biggl( \frac{3t}{35(t^{3}+2)} \biggr)= 0.0231, 0.0140, 0.0096, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -11} [m_{3}] (1)= \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}-1} \biggl( \frac{1}{35} \biggr)= 0.0262, 0.0230, 0.0215, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -2} [m_{3}] (b) = \sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}-2} \biggl( \frac{7}{105 ( (\frac{7}{9} )^{3} + 2 )} \biggr)= 0.0288, 0.0292, 0.0029, \\ &\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\alpha -\zeta } [m_{3}] (t) =\sup_{t \in \overline{J}} \mathcal{I}_{q}^{\frac{9}{5}- \frac{1}{8}} \biggl(\frac{3t}{35(t^{3}+2)} \biggr)= 0.0234, 0.00150, 0.00108 \end{aligned}$$

for $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$, respectively. Hence, from Eqs. (12)–(13) and the above results in Tables 7, 8, and 9, we obtain $M_{0} = 0.0343$, $M(1)= 0.0391$, $M(b) = 0.0357$, $M(t) = 0.0349$ whenever $q =\frac{1}{8}$, $M_{0} = 0.0184$, $M(1) = 0.0315$, $M(b) = 0.0367$, $M(t) = 0.0198$ whenever $q=\frac{1}{2}$, $M_{0} = 0.0110$, $M(1) =0.0270$, $M(b) = 0.0374$, $M(t) = 0.0125$ whenever $q=\frac{6}{7}$. Also, by using Eq. (14), we can calculate values of Δ. Table 10 shows these results. Thus, by using Eq. (14), we have

$$\begin{aligned} \Delta ={}& M_{0} + M(t) + \frac{\varGamma _{q} (2-\zeta )+ 1 }{ \varGamma _{q} (2-\zeta )} M(1) + \frac{(1+\varGamma _{q} (2-\zeta )) \times 6.1083 }{\varGamma _{q} (2-\zeta )} M(b) \\ ={}& 0.0343 + 0.0349 + \frac{\varGamma _{q} ( 2-\frac{1}{8} )+ 1 }{ \varGamma _{q} ( 2 - \frac{1}{8} ) } \times 0.0391 \\ &{} + \frac{ ( 1 + \varGamma _{q} ( 2 - \frac{1}{8} ) ) \times 6.1083 }{\varGamma _{q} (2-\frac{1}{8} ) } \times 0.0357 = 0.5859< 1 \end{aligned}$$

whenever $q=\frac{1}{8}$,

$$\begin{aligned} \Delta ={}& M_{0} + M(t) + \frac{\varGamma _{q} (2-\zeta )+ 1 }{ \varGamma _{q} (2-\zeta )} M(1) \\ &{}+ \frac{(1+\varGamma _{q} (2-\zeta )) \times 6.1083 }{\varGamma _{q} (2-\zeta )} M(b) \\ = {}&0.0184 + 0.0198 + \frac{\varGamma _{q} ( 2-\frac{1}{8} )+ 1 }{ \varGamma _{q} ( 2 - \frac{1}{8} ) } \times 0.0315 \\ &{} + \frac{ ( 1 + \varGamma _{q} ( 2 - \frac{1}{8} ) ) \times 6.1083 }{\varGamma _{q} (2-\frac{1}{8} ) } \times 0.0367 = 0.5580< 1 \end{aligned}$$

whenever $q=\frac{1}{2}$, and

$$\begin{aligned} \Delta ={}& M_{0} + M(t) + \frac{\varGamma _{q} (2-\zeta )+ 1 }{ \varGamma _{q} (2-\zeta )} M(1) + \frac{(1+\varGamma _{q} (2-\zeta )) \times }{\varGamma _{q} (2-\zeta )} M(b) \\ = {}&0.0110 + 0.0125 + \frac{\varGamma _{q} ( 2-\frac{1}{8} )+ 1 }{ \varGamma _{q} ( 2 - \frac{1}{8} ) } \times 0.0270 \\ &{} + \frac{ ( 1 + \varGamma _{q} ( 2 - \frac{1}{8} ) ) \times 6.1083 }{\varGamma _{q} (2-\frac{1}{8} ) } \times 0.0374 = 0.5458< 1 \end{aligned}$$

whenever $q=\frac{6}{7}$. Figures 7, 8, and 9 show these results (Algorithm 7). Now, by using Theorem 5, the fractional q-integro-differential equation under sum boundary value conditions (16) has a unique solution.

Figure 7

2D graphs of $M_{0}$, $M(1)$, $M(b)$, $M(t)$ on $t \in \overline{J}$ for $q=\frac{1}{8}$ in Example 2

Figure 8

2D graphs of $M_{0}$, $M(1)$, $M(b)$, $M(t)$ on $t \in \overline{J}$ for $q=\frac{1}{2}$ in Example 2

Figure 9

2D graphs of $M_{0}$, $M(1)$, $M(b)$, $M(t)$ on $t \in \overline{J}$ for $q=\frac{6}{7}$ in Example 2

Algorithm 7

The MATLAB lines for calculation of all parameters in Example 2

Algorithm 7

(Continued)

Table 7 Some numerical results of $\mathcal{I}_{q}^{\alpha } [m_{1}] (t)$, $\mathcal{I}_{q}^{\alpha -1} [m_{1}] (1)$, $\mathcal{I}_{q}^{\alpha -2} [m_{1}] (b)$, and $\mathcal{I}_{q}^{\alpha -\zeta } [m_{1}] (t)$ in Example 2 for $t \in \overline{J}$ and $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$

Table 8 Some numerical results of $\mathcal{I}_{q}^{\alpha } [m_{2}] (t)$, $\mathcal{I}_{q}^{\alpha -1} [m_{2}] (1)$, $\mathcal{I}_{q}^{\alpha -2} [m_{2}] (b)$, and $\mathcal{I}_{q}^{\alpha -\zeta } [m_{2}] (t)$ in Example 2 for $t \in \overline{J}$ and $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$

Table 9 Some numerical results of $\mathcal{I}_{q}^{\alpha } [m_{3}] (t)$, $\mathcal{I}_{q}^{\alpha -1} [m_{3}] (1)$, $\mathcal{I}_{q}^{\alpha -2} [m_{3}] (b)$, and $\mathcal{I}_{q}^{\alpha -\zeta } [m_{3}] (t)$ in Example 2 for $t \in \overline{J}$ and $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$

Table 10 Some numerical results for calculation of $M_{0}$, $M(1)$, $M(b)$, $M(t)$, and $\Delta < 1$ in Example 2 for $q=\frac{1}{8}, \frac{1}{2}, \frac{6}{7}$

5 Conclusion

The q-integro-differential boundary equations and their applications represent a matter of high interest in the area of fractional q-calculus and its applications in various areas of science and technology. q-integro-differential boundary value problems occur in the mathematical modeling of a variety of physical operations. The end of this article is to investigate a complicated case by utilizing an appropriate basic theory. In this manner, we prove the existence of a solution for two new q-integro-differential equations under sum and integral boundary conditions (1)–(2) and (3)–(4) on a time scale and show the perfect numerical effects for the problem which confirmed our results.