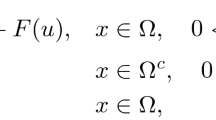Global existence and stability results for a time-fractional diffusion equation with variable exponents

Abstract

This paper aims to study the existence and stability results concerning a fractional partial differential equation with variable exponent source functions. The local existence result for $\alpha \in (0,1)$ is established with the help of the $\alpha$-resolvent kernel and the Schauder-fixed point theorem. The non-continuation theorem is proved by the fixed point technique and accordingly the global existence of solution is achieved. The uniqueness of the solution is obtained using the contraction principle and the stability results are discussed by means of Ulam-Hyers and generalized Ulam-Hyers-Rassias stability concepts via the Picard operator. Examples are provided to illustrate the results.

1 Introduction

The origin of fractional calculus can be dated back to the end of the seventeenth century when Newton and Leibniz developed the cornerstones of integral and differential calculus [13, 23, 32]. Over the past few decades, time-fractional partial differential equations have been used as a tool to open up various perspectives in the study of physical [19] and biological phenomena [21]. Professor Katsuyuki Nishimoto [30] quoted, “the fractional calculus is the calculus of the 21st century”. This fact is acknowledged by the enormous growth and a huge interest in the field of fractional calculus and applications in modeling chaotic dynamics [17], material sciences, economics [40], and control theory [9]. For instance, Tarasov [39] obtained fractional integro-differential equations for electromagnetic waves in a dielectric medium and proved that the electromagnetic fields whose susceptibility follows a fractional power-law dependence in a wide frequency range can be described by time-fractional differential equations. Likewise, K. A. Abro et al. [1] presented a mathematical analysis of plasma diffusion model with three types of fractional integro-differential equations and illustrated a comparative analysis to show their adaptabilites respectively. The memory effect in systems was incorporated into the integro-differential equations used to represent physical and biological phenomena. There are numerous contributions have been made to prove the existence results for the integro-differential systems. In this paper, we use the concept of resolvent operators to achieve our desired result. Zhu et al. [45] investigated the global existence of a nonlinear fractional differential equation by means of contraction principle. They scrutinized the fractional partial differential equation in its abstract form using $\alpha$- resolvent operator [12] and obtained its existence result. The existence of resolvent operators proved by Dos Santos, helps to examine a sort of fractional integro-differential equation [14] in its abstract form under appropriate conditions.

In recent decades, the stability analysis of nonlinear fractional systems were reviewed by many authors. Notably, Li et al. [24] propounded the definition of Mittag-Leffler stability and introduced the fractional Lyapunov direct method with fractional comparison principle. Though the Lyapunov direct method is one of the dominant technique for dealing the stability results, there are some disadvantages in constructing the Lyapunov functionals. The Lyapunov direct approach is merely a sufficient requirement to get the stability results, therefore even if a Lyapunov functional cannot be constructed, stability can still be attained. There are various types of stability technique (we refer [16]) in the literature. Among, Ulam-type stability problems have been scrutinized by many authors (see [6, 22, 37]). Under what conditions one can still say that the result of a theorem holds or is approximately true when altering slightly the assumption?. This question about the stability of functional equations was raised in a talk by Ulam in 1940 in Wisconsin University (for more details, we refer [41]). In 1941, Hyers [20] answerd his question which results in the concept of Ulam-Hyers stability. Further, Rassias [34] developed a generalization of Ulam-Hyers stability concept in 1948 that results in Ulam-Hyers-Rassias stability. The following are some results discussed regarding Ulam-Hyers stability. Abbas et al. [2] studied the stability of partial differential equations via Picard operators. Andras et al. [6] studied Ulam-Hyers stability of first order differential system with non-local condition. Marian et al. [29] provided a stability result for a system of partial differential equation using the Gronwall inequality and the fixed point technique.

Ulam-stability for Caputo fractional differential equations was initiated by Wang et al. [42] and Wei et al. [43]. Recent study of Ulam-stability involves the usage of Picard operators [35] especially the problems interrelated to the fixed point theory. This conceptual approach seems to be very powerful method in studying the existence and uniqueness results of partial differential equations and integral equations. In this study, we consider the following fractional nonlinear reaction-diffusion equation:

$$\begin{aligned} ^C_0D^{\alpha }_t u(x,t)&= \mathbb {D}\displaystyle \frac{\partial ^2 u(x,t)}{\partial x^2}+\displaystyle \int _0^t a(t-s)\displaystyle \frac{\partial ^2 u(x,s)}{\partial x^2}\text {d}s+ f(t,u(x,t)), \hspace{1.1cm}\, x\in \Omega ,\,\,t\geqslant 0, \nonumber \\ u(x,0)&= u_0(x),\quad \quad ~~ \hspace{7.5cm}x\in \Omega ,\nonumber \\ u(x,t)&=0,\quad \quad ~~ \hspace{8.25cm}\! x\in \partial \Omega ,\,\,t\geqslant 0, \end{aligned}$$

(1.1)

where $\Omega =(0,L)$. The operator $^C_0D^{\alpha }_t u$ represents the Caputo fractional derivative with respect to the time variable of order $0<\alpha < 1$ and the function $a(t-s)$ is a positive kernel. The nonlinear source term f(t, u) $=$ $b(x)u^{p(x)}$ or $b(x)\int _{\Omega } u^{p(z)}\textrm{d}z$ which represents a human controlled distribution [28]. The variable coefficient b(x) and the variable exponent $p(x):\Omega \rightarrow (1,\infty )$ is presumed to satisfy the following conditions:

$$\begin{aligned} (H1)&\hspace{0.1cm} 0< b^{-}\leqslant b(x)\leqslant b^{+}<\infty .\\ (H2)&\hspace{0.1cm} 1< p^{-}\leqslant p(x)\leqslant p^{+}<\infty . \end{aligned}$$

Numerous works on problems concerning variable exponent source functions have been developed over the past few decades (for details, we refer [4, 5, 33] and references therein). Problems with source functions similar to (1.1) are found in many branches of applied mathematics and have been utilized to model chemical reactions, heat transfer, and population dynamics. For instance, in the absence of integro-differential term, when $\alpha =1$, Pinasco [31] discussed a parabolic problem and proved the local existence using contraction principle. Also, the author discussed the blow-up phenomena using the differential inequality technique. When $\alpha = 1$, $\mathbb {D}=1$ and without the integro-differential term, the following problem:

$$\begin{aligned} \begin{array}{ll} u_t= \bigtriangleup u+ u^{p(x)} , &{} x\in Q,\,\,t\geqslant 0, \\ u(x,0)= u_0(x),&{}x\in Q, \\ u(x,t)=0,&{} x\in \partial Q,\,\,t\geqslant 0, \end{array} \end{aligned}$$

where Q is a bounded domain in $\mathbb {R}^n$, has been scrutinized by many authors, we refer [15, 44] and references therein for more details. In the sequel, Cao et al. [10] investigated the blow-up phenomena and long term behaviour of solutions for a fractional reaction-diffusion equation with weakly spatial source functions.

The main contribution of this paper is to prove the existence, non-continuation and Ulam stability of solution to a fractional integro-differential equation (1.1) with variable exponent source functions. First, we consider the given problem (1.1) in its abstract form using $\alpha$- resolvent operator and proceed further to prove the existence results using Schauder fixed point theorem. Further, we prove the stability theorem using some known results on Picard operators.

In the absence of variable exponent source functions and for integer order derivative, there are few works in the literature which are mentioned as follows: For $\alpha =1$, an integro-differential equation is discussed in [11] where different types of Ulam-Hyers-Rassias stability results are investigated. Ma et al. [27] analyzed the existence of a Caputo fractional integro-differential equation using a Krasnoselskii fixed point theorem and they developed results on continuous dependance of mild solutions. Further, Akilandeeswari et al. [3] investigated the existence of solution of the fractional diffusion equation with integral kernel using Schauder fixed point theorem and Arzela-Ascoli theorem.

Motivated by the above works, this paper is organized as follows: In Sect. 2, the defintions of fractional operators, concepts of $\alpha$- resolvent operator and its qualitative properties and definitions of Ulam-Hyers stability are presented. In Sect. 3, the local existence of mild solution is established using Schauder fixed point technique. In Sect. 4, the global existence is achieved by proving non-continuation results to the problem (1.1) in its abstract form. In Sect. 5, the uniqueness and stability results via Picard operators are discussed. In Sect. 6, examples are provided to justify our results.

2 Preliminaries

The fundamental definitions of fractional calculus are reviewed in this section. Further, we address the idea of the $\alpha$- resolvent operator [14] for an abstract fractional integro-differential equation and their qualitative properties, which aid in proving the existence and uniqueness of mild solution. Moreover, we recall some definitions and properties of Picard operator that helps to obtain the stability results.

Definition 2.1

[23] The left and right sided Caputo partial fractional derivative of order $\alpha >0$ with respect to the time variable t are defined respectively as follows:

$$\begin{aligned} {^C_0}D_t^{\alpha }u(x,t)&= \displaystyle \frac{1}{\Gamma (n-\alpha )}\displaystyle \int _0^t (t-s)^{n-\alpha -1} \frac{\partial ^n u(x,s)}{\partial s^n}\textrm{d}s,\\ {^C_t}D_T^{\alpha }u(x,t)&= \displaystyle \frac{(-1)^n}{\Gamma (n-\alpha )}\displaystyle \int _t^T (s-t)^{n-\alpha -1} \frac{\partial ^n u(x,s)}{\partial s^n}\textrm{d}s, \end{aligned}$$

where $n-1< \alpha < n$; $n\in \mathbb {N}$ and the function u(x, .) has absolutely continuous derivatives up to order $n-1$.

Definition 2.2

[23] The Riemann-Liouville fractional integral operator of order $\alpha$ with respect to time t of a function u(x, t) is defined by

$$\begin{aligned} I^{\alpha }u(x,t)&= \frac{1}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -n}u(x,s)\textrm{d}s, \end{aligned}$$

where $n-1< \alpha < n$; $n\in \mathbb {N}$ and the function u(x, .) is an integrable function.

Now we define the operators $Au=\mathbb {D}\displaystyle \frac{\partial ^2 u}{\partial x^2}$ and $B(t)u= a(t)\displaystyle \frac{\partial ^2 u}{\partial x^2}$ for $u\in D(A)$ and let $X=L^2(\Omega )$. Further, let $A: \mathscr {D}(A)\subset X\rightarrow X$ and $B(t): \mathscr {D}(A)\subset X\rightarrow X$ are closed linear operators defined on a domain

$$\begin{aligned} \mathscr {D}(A)=\bigg \{u\in X;\,\,\mathbb {D}\displaystyle \frac{\partial ^2 u}{\partial x^2}\in X, u(0)=u(L)=0\bigg \} \end{aligned}$$

which is dense in X. Then according to the results contemplated in [14], the abstract form of the problem (1.1) can be written as follows:

$$\begin{aligned} {^C_0}D_t^{\alpha }u(t)&= Au(t)+ \displaystyle \int _0^t B(t-s)u(s)\textrm{d}s+ f(t,u(t)), t\geqslant 0,\nonumber \\ u(0)&= u_0\in X. \end{aligned}$$

(2.1)

To deal with the abstract problem (2.1), the concept of $\alpha$- resolvent operator for an abstract fractional integro-differential system is presented:

Definition 2.3

[14] An one parameter family of bounded linear operators $(\mathscr {R}_{\alpha }(t))_{t\geqslant 0}$ on X is called an $\alpha$- resolvent operator of (2.1) if the following conditions are satisfied:

• The function $\mathscr {R}_{\alpha }(\cdot ):[0,\infty )\rightarrow \mathscr {L}(X)$ is strongly continuous and $\mathscr {R}_{\alpha }(0)u=u$ for all $u\in X$ and $\alpha \in (0,1)$.

• For $u\in \mathscr {D}(A),$ $\mathscr {R}_{\alpha }(\cdot )u\in C([0,\infty ),\mathscr {D}(A))\cap C^{\alpha }((0,\infty ),X)$ and

  $$\begin{aligned} {^C_0}D_t^{\alpha }\mathscr {R}_{\alpha }(t)u&= A\mathscr {R}_{\alpha }(t)u+\displaystyle \int _0^t B(t-s)\mathscr {R}_{\alpha }(s)u\textrm{d}s\\&= \mathscr {R}_{\alpha }(t)Au+\displaystyle \int _0^t \mathscr {R}_{\alpha }(t-s)B(s)u\textrm{d}s,\,\,\,\,\text {for}\,\, \text {every}\,\, t\geqslant 0. \end{aligned}$$

Here $\mathscr {L}(X)$ denotes the set of all bounded linear operators from X into X. $C^{\alpha }([0,\infty ),X):= \{u\in C([0,\infty ), X); {^C}D_t^{\alpha }u \in C([0,\infty ), X)\}$ and X is a Banach space.

The following are some useful theorems concerning the $\alpha$- resolvent operators that plays a vital role in the proof of the existence results.

Theorem 2.4

[14] The operator $\mathscr {R}_{\alpha }(t)$ is

• (i) exponentially bounded in $\mathscr {L}(X)$;

• (ii) exponentially bounded in $\mathscr {L}([\mathscr {D}(A)])$;

• (iii) strongly continuous on $[0,\infty )$ and uniformly continuous on $(0,\infty )$;

• (iv) strongly continuous on $[0, \infty )$ in $\mathscr {L}([\mathscr {D}](A)).$

Theorem 2.5

[14] The operator function $t\rightarrow t^{\alpha -1}\mathscr {S}_{\alpha }(t)$ is exponentially bounded in $\mathscr {L}(X)$ and uniformly (strongly) continuous on $(0,\infty )$.

Corollary 2.6

[14] Let f $\in$ $L^1_{\text {loc}}(\mathbb {R}_{+},\,X)$, then the convolution $t^{\alpha -1}\mathscr {S}_{\alpha }(t)*f(t)$ $=$ $\displaystyle \int _0^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s)\textrm{d}s$ exists (as a Bochner integral) and defines a continuous function from $\mathbb {R}_+$ into X.

In the sequel, next we recollect the definitions and properties of Picard operator as follows:

Definition 2.7

[2] The operator P :  $X\rightarrow X$ is a Picard operator, if there exists $u_{\star }$ $\in$ X such that:

• (a) $F_P$ $=$ $\{u_{\star }\}$;

• (b) The sequence $\{P^n(u_0)\}_{n\in \mathbb {N}}$ converges to $u_{\star }$ for all $u_0$ $\in$ X.

Here $F_P$ denotes the set of all fixed points of P and X is a Banach space.

Definition 2.8

[2] The operator P :  $X\rightarrow X$ is a weakly Picard operator, if the sequence $\{P^n(u)\}_{n\in \mathbb {N}}$ converges for all $u\in X$, and its limit (may depend on u) is a fixed point of P.

Definition 2.9

[2] If P is a weakly Picard operator, then we consider the operator $P^{\infty }$ defined by

$$\begin{aligned} P^{\infty }: X\rightarrow X;\,\, P^{\infty }(u)\,=\, \lim \limits _{n\rightarrow \infty } P^n(u). \end{aligned}$$

From the above definition, we infer that $F_P$ $=$ $P^{\infty }$. Next, we have the definition of Ulam-Hyers stability of a fixed point equation.

Definition 2.10

[36] Let (X, d) be a metric space and P :  $X\rightarrow X$ be an operator. The fixed point equation u $=$ P(u) is said to be Ulam-Hyers stable, if there exists a real number $c_P$ > 0 such that for each real number $\varepsilon >0$ and each solution $y_{\star }$ of the inequality d(y, Py) $\leqslant$ $\varepsilon$, there exists a solution $u_{\star }$ of the equation u $=$ P(u) such that

$$\begin{aligned} d(y_{\star },u_{\star })\leqslant \varepsilon c_P;\,\,\,\, u\in X. \end{aligned}$$

Lemma 2.11

[36] Let (X, d) be a metric space. If $\mathbb {T}:X\rightarrow X$ is a c-weakly Picard operator, then the fixed point equation $u=\mathbb {T}(u)$ is Ulam-Hyers stable.

Lemma 2.12

[36] Let (X, d) be a metric space. If $\mathbb {T}:X\rightarrow X$ is a contraction with a positive constant $q<1$, then $\mathbb {T}$ is a c-weakly Picard operator with the positive constant $c_{\mathbb {T}}=\frac{1}{1-q}$. Moreover the fixed point equation $u=\mathbb {T}(u)$ is Ulam-Hyers stable.

Lemma 2.13

[8] Let $\chi :[0,T]\rightarrow [0,\infty )$ be a real function and $\zeta (\cdot )$ is a non-negative, locally integrable function on [0, T] and there are positive constants $m>0$ and $0<\beta <1$ such that:

$$\begin{aligned} \chi (t)\leqslant \zeta (t)+m\int _0^t\frac{\chi (s)}{(t-s)^{\beta }}\textrm{d}s. \end{aligned}$$

Then there exists a constant $\mathfrak {M}=\mathfrak {M}(\alpha )$ such that

$$\begin{aligned} \chi (t)\leqslant \zeta (t)+m\mathfrak {M}\int _0^t\frac{\zeta (s)}{(t-s)^{\beta }}\textrm{d}s. \end{aligned}$$

for every $t\in [0,T].$

Lemma 2.14

[25] Let $\textrm{S}$ be a subset of C([0, T]). Then $\textrm{S}$ is precompact if and onlf if the following conditions hold:

• (i) $\{u(t):\,\, u\in \textrm{S}\}$ is uniformly bounded;

• (ii) $\{u(t):\,\, u\in \textrm{S}\}$ is equicontinuous on [0, T].

Lemma 2.15

(Leray-Schauder fixed point theorem) [3] If U is a closed bounded convex subset of a Banach space X and $\mathbb {T}:$ $U\rightarrow U$ is completely continuous, then $\mathbb {T}$ has atleast a fixed point in U.

Corollary 2.16

(Banach fixed point theorem) [13] Suppose that (U, d) is a non-empty complete metric space. Let $0\leqslant a <1$ and the mapping $\mathbb {T}: U\rightarrow U$ satisfy the inequality

$$\begin{aligned} d(\mathbb {T}u, \mathbb {T}v)\leqslant a d(u,v) \end{aligned}$$

for every u, v $\in$ U. Then, $\mathbb {T}$ has uniquely determined fixed point $u^*$. Furthermore, for any $u_0\in U$, the sequence $(\mathbb {T}^ju_0)_{j=1}^{\infty }$ converges to the fixed point $u^*$.

3 Local existence

This section scrutinizes the local existence of mild solution to the problem (1.1) using Lemma 2.14 and Schauder fixed point theorem. The mild solution to the problem (2.1) is represented as follows:

Definition 3.1

A function $u:(0,T)\rightarrow X$ is called a mild solution of problem (2.1) in (0, T) if $u\in C((0,T),X)$ and

$$\begin{aligned} u(t)&= \mathscr {R}_{\alpha }(t)u_0+\displaystyle \int _0^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,u(s))\textrm{d}s \end{aligned}$$

(3.1)

holds for all $t\in (0,T)$, where $T>0$.

The existence of the integral Eq. (3.1) is equivalent to the existence of mild solution to the problem (2.1). In order to prove the existence result, we need the following estimate for the nonlinear function f(t, u). First, we note that, for any fixed $x\in \Omega$, we have [31]

$$\begin{aligned} u^{p(z)}- v^{p(z)}&= p(z)\omega ^{p(z)-1}(u-v), \end{aligned}$$

(3.2)

where $\omega ^{p(z)}$ is a bounded function and $\omega = su+(1-s)v$, $s\in (0,1)$. Thus, we obtain

$$\begin{aligned} f(t,u(t))-f(t,v(t))&= b(x)\displaystyle \int _{\Omega }u^{p(z)}\textrm{d}z- b(x)\displaystyle \int _{\Omega }v^{p(z)}\textrm{d}z\nonumber \\&= b(x)\displaystyle \int _{\Omega }(u^{p(z)}-v^{p(z)})\textrm{d}z\nonumber \\&= b(x)\displaystyle \int _{\Omega }p(z)\omega ^{p(z)-1}(u-v)\textrm{d}z\nonumber \\ \Vert f(t,u(t))-f(t,v(t))\Vert&\leqslant \mathbb {L}\Vert u-v\Vert , \end{aligned}$$

(3.3)

where $\mathbb {L}= |\Omega |c_{\omega }b^+ p^+$ $>0$, where $\Vert \omega ^{p(z)-1}\Vert \leqslant c_w$. Similarly, we can prove the same estimate for the nonlinear function $b(x)u^{p(x)}$.

Theorem 3.2

Suppose that $u_0(x)$ is continuous in $L^2(\Omega )$ and the hypotheses $(H1)-(H2)$ hold. Then there exist atleast one solution $u\in C[0,\tau ]$ for $0<\tau \leqslant T$ to the abstract problem (2.1).

Proof

Let

$$\begin{aligned} U=\bigg \{u\in C[0,T]: \Vert u-u_0\Vert _{C[0,T]}=\sup _{0\leqslant t\leqslant T}|u-u_0|\leqslant r\bigg \}, \end{aligned}$$

where r is a positive constant. Further, we set

$$\begin{aligned} U_{\tau }=\bigg \{u:\,\,u\in C[0,\tau ]: \Vert u-u_0\Vert _{C[0,\tau ]}\leqslant r\bigg \}. \end{aligned}$$

It is important to note that $u(0)\in U_{\tau }$ that means $U_{\tau }$ is non-empty. From the construction, we can say that $U_{\tau }$ is closed and bounded. For $\lambda _1, \lambda _2 \, \geqslant 0$, suppose that $\lambda _1+\lambda _2\,=1$. Then for any $u_1$, $u_2$ $\in$ $U_{\tau }$, we have,

$$\begin{aligned} \Vert \lambda _1u_1+\lambda _2u_2-u(0)\Vert&= \lambda _1\Vert u_1-u_0\Vert +\lambda _2\Vert u_2-u_0\Vert \\&\leqslant \lambda _1 b+\lambda _2 b= b. \end{aligned}$$

Clearly $\lambda _1u_1+\lambda _2u_2$ $\in$ $U_\tau$. Therefore, $U_\tau$ is a non-empty closed convex set. Now we define an operator $\mathbb {T}$ on the set $U_{\tau }$ as follows:

$$\begin{aligned} (\mathbb {T}u)(t)&= \mathscr {R}_{\alpha }(t)u_0+\displaystyle \int _0^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,u(s))\textrm{d}s, \hspace{0.4cm}t\in [0,\tau ]. \end{aligned}$$

(3.4)

It is clear that all solutions of (2.1) are fixed points of (3.4). Let $\Vert u(t)\Vert _{C[0,\tau ]}:= \Vert u(t)\Vert$. In the context of Theorem 2.4 and 2.5, we choose $\tau >0$ such that

$$\begin{aligned} \Vert \mathscr {R}_{\alpha }(t)u_0 - u_0\Vert&\leqslant \displaystyle \frac{r}{2}\end{aligned}$$

(3.5)

$$\begin{aligned} \sup _{0\leqslant t\leqslant h}|\mathscr {S}_{\alpha }(t)|&:=N\end{aligned}$$

(3.6)

$$\begin{aligned} \sup _{0\leqslant t\leqslant h}|f(0,u_0)|&:=M. \end{aligned}$$

(3.7)

For any constant $r>0$, define

$$\begin{aligned} \tau :=\min \bigg \{T, \bigg (\displaystyle \frac{r\alpha }{2N(\mathbb {L}r+M)}\bigg )^{\frac{1}{\alpha }}\bigg \}, \end{aligned}$$

(3.8)

where $\mathbb {L}$, N and M are defined in (3.3), (3.6) and (3.7) respectively. Then by the estimate (3.3) of f(t, u) and using the ansatzes (3.5), (3.6) and (3.7), for any $u\in$ $C[0,\tau ]$, we prove $\mathbb {T}$ maps $U_{\tau }$ into itsef as follows:

$$\begin{aligned} \Vert \mathbb {T}u(t)-\mathbb {T}u(0)\Vert&= \bigg \Vert \mathscr {R}_{\alpha }(t)u_0+\displaystyle \int _0^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,u(s))\textrm{d}s- u_0\bigg \Vert \nonumber \\&\leqslant \displaystyle \frac{r}{2}+N\displaystyle \int _0^t (t-s)^{\alpha -1}\Vert f(s,u(s))-f(0,u(0))+f(0,u(0))\Vert \textrm{d}s\nonumber \\ \Vert \mathbb {T}u(t)-\mathbb {T}u(0)\Vert&\leqslant \displaystyle \frac{r}{2}+ N(\mathbb {L}\Vert u-u_0\Vert +M)\displaystyle \int _0^t (t-s)^{\alpha -1}\textrm{d}s\nonumber \\&= \displaystyle \frac{r}{2}+ N(\mathbb {L}\Vert u-u_0\Vert +M)\displaystyle \frac{t^\alpha }{\alpha }\nonumber \\&\leqslant \displaystyle \frac{r}{2}+ N(\mathbb {L}r+M)\displaystyle \frac{\tau ^\alpha }{\alpha } = r. \end{aligned}$$

(3.9)

This shows that $\mathbb {T}U_{\tau }\subset$ $U_{\tau }$ by the choice of $\tau$. In order to proceed further, we claim that $\mathbb {T}$ is continuous. Let $u_n,$ u $\in$ $U_{\tau }$ and the sequence $\{u_n\}$ is a converging sequence in $U_{\tau }$ to u such that $\Vert u_n-u\Vert _{C[0,\tau ]}\rightarrow 0$ as $n\rightarrow \infty$. Then we have the following estimate using (3.3) and (3.6):

$$\begin{aligned} \Vert \mathbb {T}u_n(t)-\mathbb {T}u(t)\Vert&\leqslant \Vert \mathscr {R}_{\alpha }(t)u_n(0)-\mathscr {R}_{\alpha }(t)u(0)\Vert \\&\quad +\displaystyle \int _0^t (t-s)^{\alpha -1}\Vert \mathscr {S}_{\alpha }(t-s)\Vert \,\,\Vert f(s,u_n(s))-f(s,u(s))\Vert \textrm{d}s.\\ \Vert \mathbb {T}u_n(t)-\mathbb {T}u(t)\Vert&\leqslant \Vert \mathscr {R}_{\alpha }(t)\Vert \Vert u_n(0)-u_0\Vert +N\mathbb {L}\Vert u_n(t)-u(t)\Vert \displaystyle \int _0^t (t-s)^{\alpha -1}\textrm{d}s\\&\leqslant \Vert \mathscr {R}_{\alpha }(t)\Vert \Vert u_n(0)-u_0\Vert +N\mathbb {L}\Vert u_n(t)-u(t)\Vert \displaystyle \frac{\tau ^{\alpha }}{\alpha }. \end{aligned}$$

By Theorem 2.4 and as $n\rightarrow \infty$, we see that $\Vert \mathbb {T}u_n(t)-\mathbb {T}u(t)\Vert$ $\rightarrow$ 0. This implies that the operator $\mathbb {T}$ is continuous. Furthermore, for $u\in U_{\tau }$ and $\forall t\in [0,\tau ]$, we have

$$\begin{aligned} \Vert \mathbb {T}u(t)\Vert&= \Vert \mathbb {T}u(t)-\mathbb {T}u(0)+\mathbb {T}u(0)\Vert \\&\leqslant \Vert \mathbb {T}u(t)-\mathbb {T}u(0)\Vert +\Vert \mathbb {T}u(0)\Vert \leqslant r+ \Vert u_0\Vert . \end{aligned}$$

This shows that $\mathbb {T}U_{\tau }$ is uniformly bounded. Now it remains to prove that $\mathbb {T}$ maps $U_{\tau }$ into an equicontinuous family. Let $u\in U_{\tau }$ and $t_1,\,\,t_2$ $\in$ $[0,\tau ]$. Then, we obtain

$$\begin{aligned} \mathbb {T}u(t_2)-\mathbb {T}u(t_1)&= \mathscr {R}_{\alpha }(t_2)u_0+\displaystyle \int _0^{t_2} (t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s\nonumber \\&\quad -\mathscr {R}_{\alpha }(t_1)u_0-\displaystyle \int _0^{t_1} (t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)f(s,u(s))\textrm{d}s\nonumber \\&=(\mathscr {R}_{\alpha }(t_2)-\mathscr {R}_{\alpha }(t_1))u_0+\displaystyle \int _0^{t_1} (t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s\nonumber \\&\quad +\displaystyle \int _{t_1}^{t_2} (t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s -\displaystyle \int _0^{t_1} (t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)f(s,u(s))\textrm{d}s\nonumber \\&= (\mathscr {R}_{\alpha }(t_2)-\mathscr {R}_{\alpha }(t_1))u_0+\displaystyle \int _{t_1}^{t_2} (t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s\nonumber \\&\quad +\displaystyle \int _0^{t_1}\bigg ((t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)-(t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)\bigg )f(s,u(s))\textrm{d}s\nonumber \\&= (\mathscr {R}_{\alpha }(t_2)-\mathscr {R}_{\alpha }(t_1))u_0+\displaystyle \int _{t_1}^{t_2} (t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)(f(s,u(s))-f(0,u(0)))\textrm{d}s\nonumber \\&\quad +\displaystyle \int _{t_1}^{t_2} (t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(0,u(0))\textrm{d}s\nonumber \\&\quad +\displaystyle \int _0^{t_1}\bigg ((t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)-(t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)\bigg )f(s,u(s))\textrm{d}s. \end{aligned}$$

(3.10)

By the Theorems 2.4 and 2.5 and the Corollary 2.6, the resolvent operators $\mathscr {R}_{\alpha }(\cdot )$ and $\mathscr {S}_{\alpha }(\cdot )$ are bounded and uniformly continuous on $(0,\infty )$ such that for $|t_1-t_2|<\delta$, we have

$$\begin{aligned} \Vert \mathscr {R}_{\alpha }(t_2)-\mathscr {R}_{\alpha }(t_1)\Vert&\leqslant {\varepsilon _1}. \end{aligned}$$

Thus by (3.3) and (3.7), the Eq. (3.10) becomes

$$\begin{aligned} \Vert \mathbb {T}u(t_2)-\mathbb {T}u(t_1)\Vert&\leqslant \varepsilon _1 u_0 + N\mathbb {L}\Vert u-u_0\Vert \displaystyle \frac{(t_2-t_1)^{\alpha }}{\alpha }+MN\displaystyle \frac{(t_2-t_1)^{\alpha }}{\alpha }\\&\quad +\bigg \Vert \displaystyle \int _0^{t_1}\bigg ((t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)-(t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)\bigg )f(s,u(s))\textrm{d}s\bigg \Vert . \end{aligned}$$

For arbitrary small $\varepsilon _1$ and $u_0$ and as $t_1\rightarrow t_2$, we have,

$$\begin{aligned} \Vert \mathbb {T}u(t_2)-\mathbb {T}u(t_1)\Vert&\leqslant \varepsilon _2. \end{aligned}$$

(3.11)

Therefore, the operator $\mathbb {T}$ is equicontinuous. Then by Lemma 2.14, the operator $\mathbb {T}$ is precompact. This implies that $\mathbb {T}$ is completely continuous. Hence by Schauder fixed point theorem, we conclude that $\mathbb {T}$ has a fixed point in $U_{\tau }$ and the problem (2.1) has a local solution in [0, T]. $\square$

4 Global existence

In this section, first we prove a continuation theorem for the abstract problem (2.1) that aids to prove the global existence theorem. For that, first we display the definition of non-continuable solution (we refer [25] and references therein).

Definition 4.1

Let u(t) on $(0,\eta )$ and $\tilde{u}(t)$ on $(0,\tilde{\eta })$ be both solutions of (2.1). If $\eta$ < $\tilde{\eta }$ and u(t) $=$ $\tilde{u}(t)$ for t $\in$ $(0,\eta )$, then we say that $\tilde{u}(t)$ is a continuation of u(t) or u(t) can be continued to $(0,\tilde{\eta })$. A solution u(t) is non-continuable if it has no continuation. The existing interval of the non-continuable solution u(t) is called the maximum existing interval of u(t).

The following results shows that the solution is non-continuable for a certain condition stated as follows:

Theorem 4.2

Let the conditions $(H1)-(H2)$ hold and the nonlinear function f satisfies the Lipschitz condition (3.3). Then u(t), $t\in (0,\eta )$, is non-continuable if and only if for some $\beta$ $\in$ $(0,\frac{\eta }{2})$ and any bounded closed subset D $\subset$ $[\beta ,+\infty )$ $\times$ $\mathbb {R}$, there exists a $\tilde{t}$ $\in$ $[\beta ,\eta )$ such that $(\tilde{t},\, u(\tilde{t}))$ $\notin$ D.

Proof

The proof is divided into two parts. To prove the first, we assume that the latter part of the statement is true and now the case is to prove u(t) is non-continuable. As a contradiction, suppose that u(t) is continuable. Then by Definition 4.1, there exists a solution $\tilde{u}(t)$ of (2.1) defined on $(0,\,\tilde{\eta })$, where $\tilde{\eta }$ > $\eta$ such that u(t) = $\tilde{u}(t)$ for $(0,\eta )$. This implies that $\lim \nolimits _{t\rightarrow {\eta }^{-}}u(t)$ $=$ $\tilde{u}(t)$. Now we define $u(\eta )$ $:=$ $\tilde{u}(\eta )$. Then there exists a set

$$\begin{aligned} S\,= \, \{(t,u(t)):\,\,t\in [\beta ,\eta )\}, \end{aligned}$$

a compact subset of $[\beta ,+\infty )$ $\times$ $\mathbb {R}$. Since u(t) is continuable, there exists no $\tilde{t}$ $\in$ $[\beta ,\eta )$ such that $(\tilde{t},u(\tilde{t}))$ $\notin$ S. This contradiction implies that u(t) is non-continuable. Hence the first part.

To prove the second part, we consider u(t) is non-continuable. Suppose that there exists a subset D $\subset$ $[\beta ,+\infty )$ $\times$ $\mathbb {R}$ such that

$$\begin{aligned} \{(t,u(t)):\,\,t\in [\beta ,\eta )\}\,\,\subset \,\,D. \end{aligned}$$

The compactness of D implies that $\eta$ < $\infty$. The remainder of the proof is given in two steps.

Step 1::

Let $t_1,\, t_2$ $\in$ $[2\beta ,\eta )$ such that $t_1$ < $t_2$. Using the method of contradiction, we now prove that $\lim \limits _{t\rightarrow {\eta }^-} u(t)$ exists. Now consider

$$\begin{aligned} u(t_1)-u(t_2)&= (\mathscr {R}_{\alpha }(t_1)- \mathscr {R}_{\alpha }(t_2))u_0 + \displaystyle \int _0^{t_1}(t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)f(s,u(s))\textrm{d}s \nonumber \\&\quad -\displaystyle \int _0^{t_2}(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s\nonumber \\&= (\mathscr {R}_{\alpha }(t_1)- \mathscr {R}_{\alpha }(t_2))u_0 +\displaystyle \int _0^{\beta }(t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)f(s,u(s))\textrm{d}s\nonumber \\&\quad +\displaystyle \int _{\beta }^{t_1}(t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)f(s,u(s))\textrm{d}s-\displaystyle \int _0^{\beta }(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s\nonumber \\&\quad -\displaystyle \int _{\beta }^{t_1}(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s-\displaystyle \int _{t_1}^{t_2}(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s\nonumber \\&=\displaystyle \int _0^{\beta }\bigg ((t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)-(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)\bigg )f(s,u(s))\textrm{d}s\nonumber \\&\quad +\displaystyle \int _{\beta }^{t_1}\bigg ((t_1-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_1-s)-(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)\bigg )f(s,u(s))\textrm{d}s\nonumber \\&\quad -\displaystyle \int _{t_1}^{t_2}(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s+(\mathscr {R}_{\alpha }(t_1)- \mathscr {R}_{\alpha }(t_2))u_0.\nonumber \\&= I_1+ I_2-\displaystyle \int _{t_1}^{t_2}(t_2-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_2-s)f(s,u(s))\textrm{d}s+(\mathscr {R}_{\alpha }(t_1)- \mathscr {R}_{\alpha }(t_2))u_0. \end{aligned}$$

(4.1)

Theorems 2.4 and 2.5, Corollary 2.6 and the condition (3.3) show that the integrals $I_1$ and $I_2$ are continuous and the operator $\mathscr {R}_{\alpha }(\cdot )$ is bounded and uniformly continuous. Therefore, as $t_1\rightarrow t_2$, we have

$$\begin{aligned} |u(t_1)-u(t_2)|&\leqslant \varepsilon _4+ N\bigg (\mathbb {L}\Vert u-u_0\Vert _{C[0,\beta ]}+M\bigg )\displaystyle \frac{(t_2-t_1)^{\alpha }}{\alpha }+ \varepsilon _1 u_0\leqslant \varepsilon _5, \end{aligned}$$

where $\varepsilon _4+\varepsilon _1 u_0$ $\leqslant$ $\varepsilon _5$, for arbitrary small $u_0$. Hence by Cauchy’s convergence criterion, $\lim \limits _{t\rightarrow \eta ^-}u(t)$ $=$ $u^{\star }$ exists.

Step 2::

Let $u^{\star }$ be the limit point and also we know that D is a closed subset. Hence we can say that $(\eta , u^{\star })$ $\in$ D. Now we define $u(\eta )$ $=$ $u^{\star }$ and the operator

$$\begin{aligned} (Jv)(t)&:= u_1+\displaystyle \int _{\eta }^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,v(s))\textrm{d}s, \end{aligned}$$

where

$$\begin{aligned} u_1 = \mathscr {R}_{\alpha }(t)u_0+\displaystyle \int _{0}^{\eta }(t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,v(s))\textrm{d}s \end{aligned}$$

for v $\in$ $C([\eta ,\, \eta +1])$ and $t\in [\eta ,\,\eta +1]$. Let us suppose the following sets to prove the continuation of solution u.

$$\begin{aligned} V_r= \bigg \{(t,v):\,\, \eta \,\leqslant t\,\leqslant \eta +1,\,\,|v|\,\leqslant \max _{ \eta \leqslant t\leqslant \eta +1}|u_1 +\eta |\bigg \} \end{aligned}$$

and also we set

$$\begin{aligned} V_{\tau }&= \{v\,\in \, C[\eta ,\, \eta +\tau ]\,:\,\, \max _{t\in [\eta ,\eta +\tau ]}|v(t)-u_1(t)|\,\leqslant \, r,\,\, v(\eta )\,=\,u_1(\eta )\}, \end{aligned}$$

where $\tau :=\min \bigg \{1, \bigg (\displaystyle \frac{r\alpha }{2N(\mathbb {L}r+M)}\bigg )^{\frac{1}{\alpha }}\bigg \}.$ Similar to Theorem 3.2, we prove that J is completely continuous. First we prove that J maps $V_{\tau }$ into itself. Thus by Theorems 2.4 and 2.5,

$$\begin{aligned} |(Jv)(t)-(Jv)(0)|&\leqslant |u_1-\mathscr {R}_{\alpha }(0)u_0| +\displaystyle \int _{\eta }^t (t-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t-s)|\,\,|f(s,v(s))|\textrm{d}s\nonumber \\&= |\mathscr {R}_{\alpha }(t)u_0-u_0|+\displaystyle \int _0^t (t-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t-s)|\,\,|f(s,v(s))|\textrm{d}s\nonumber \\ |(Jv)(t)-u_1|&\leqslant \displaystyle \frac{r}{2}+ N(\mathbb {L}\Vert u-u_0\Vert _{C[\eta ,\eta +\tau ]}+M)\displaystyle \frac{\tau ^{\alpha }}{\alpha }. \end{aligned}$$

(4.2)

This shows that $JV_{\tau }$ $\subset$ $V_{\tau }$. Let $\{v_n\}$ $\subset$ $C[\eta ,\,\eta +\tau ]$, then $\Vert v_n-v\Vert _{[\eta ,\eta +\tau ]}\rightarrow 0$ on $V_\tau$ as $n\rightarrow \infty$. To prove continuity of the operator J on $V_{\tau }$, we compute

$$\begin{aligned} |Jv_n(t)-Jv(t)|&\leqslant \displaystyle \int _{\eta }^t (t-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t-s)|\,\,|f(s,v_n(s))-f(s,v(s))|\textrm{d}s\nonumber \\&\leqslant \displaystyle \frac{N\tau ^{\alpha }}{\alpha }\Vert f(s,v_n(s))-f(s,v(s))\Vert _{C[\eta ,\eta +\tau ]}. \end{aligned}$$

(4.3)

By the continuity of v, we see that $\Vert Jv_n(t)-Jv(t)\Vert _{[\eta ,\eta +\tau ]}\rightarrow 0$ as $n\rightarrow \infty$. This shows that the operator J is continuous. Next we claim that J is equicontinuous. Let v $\in$ $V_{\tau }$ and $\eta \leqslant t_1\leqslant t_2 \leqslant \eta +\tau$. Then, we have

$$\begin{aligned} |(Jv)(t_2)-(Jv)(t_1)|&= |u_1(t_2)-u_1(t_1)|+\displaystyle \int _{\eta }^{t_2}(t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|\,\,|f(s,v(s))|\textrm{d}s\\&\quad -\displaystyle \int _{\eta }^{t_1}(t_1-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_1-s)|\,\,|f(s,v(s))|\textrm{d}s\\&=\displaystyle \int _{0}^{\eta }\bigg ((t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|-(t_1-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_1-s)|\bigg )|f(s,v(s))|\textrm{d}s\\&\quad +|\mathscr {R}_{\alpha }(t_2)-\mathscr {R}_{\alpha }(t_1)|u_0+\displaystyle \int _{\eta }^{t_1}(t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|\,\,|f(s,v(s))|\textrm{d}s\\&\quad +\displaystyle \int _{t_1}^{t_2}(t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|\,\,|f(s,v(s))|\textrm{d}s\\&\quad -\displaystyle \int _{\eta }^{t_1}(t_1-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_1-s)|\,\,|f(s,v(s))|\textrm{d}s\\&=\displaystyle \int _{0}^{\eta }\bigg ((t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|-(t_1-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_1-s)|\bigg )|f(s,v(s))|\textrm{d}s\\&\quad +\displaystyle \int _{\eta }^{t_1}\bigg ((t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|-(t_1-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_1-s)|\bigg )|f(s,v(s))|\textrm{d}s\\&\quad +|\mathscr {R}_{\alpha }(t_2)-\mathscr {R}_{\alpha }(t_1)|u_0+\displaystyle \int _{t_1}^{t_2}(t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|\,\,|f(s,v(s))|\textrm{d}s.\\&= I_3+I_4+|\mathscr {R}_{\alpha }(t_2)-\mathscr {R}_{\alpha }(t_1)|u_0+\displaystyle \int _{t_1}^{t_2}(t_2-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_2-s)|\,\,|f(s,v(s))|\textrm{d}s \end{aligned}$$

By the continuity of $I_3$ and $I_4$ and the operator $\mathscr {R}_{\alpha }(\cdot )$ and by the Lipschitz continuity of f, as $t_1\rightarrow t_2$, $\Vert (Jv)(t_2)-(Jv)(t_1)\Vert _{[\eta ,\eta +\tau ]}\rightarrow 0$. Thus the operator J is precompact and this implies that it is completely continuous. By Schauder fixed point theorem, there exists a fixed point $\tilde{u}(t)\in V_{\tau }$. Specifically, we can say that

$$\begin{aligned} \tilde{u}(t)&= u_1+\displaystyle \int _{\eta }^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,v(s))\textrm{d}s,\nonumber \\&= u_0+\displaystyle \int _{0}^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,v(s))\textrm{d}s, \end{aligned}$$

(4.4)

where t $\in$ $[\eta ,\eta +\tau ]$ and we write

$$\begin{aligned} \tilde{u}(t)&= {\left\{ \begin{array}{ll} u(t), &{} t\in (0,\eta ]\\ \tilde{u}(t),&{} t\in [\eta , \eta +\tau ]. \end{array}\right. } \end{aligned}$$

This implies that $\tilde{u}(t)$ $\in$ $C((0,\eta +\tau ])$ and is a solution of (2.1) on $(0,\eta +\tau )$. This contradicts our assumption u(t) is non-continuable. Hence there exists a $\tilde{t}\in [\beta ,\eta )$ so that $(\tilde{t}, u(\tilde{t}))$ $\notin$ D. $\square$

Now we present an another continuation theorem which is more helpful to prove global existence theorem.

Theorem 4.3

Let the conditions $(H1)-(H2)$ hold and the nonlinear function f satisfies the Lipschitz condition (3.3). Then u = u(t), $t\in (0,\eta )$, is non-continuable if and only if

$$\begin{aligned} \lim \limits _{t\rightarrow \eta ^-}\sup |A(t)|=+\infty , \end{aligned}$$

(4.5)

where $A(t)= (t,u(t))$, $\Vert A(t)\Vert =\bigg (u^2+t^2\bigg )^{\frac{1}{2}}$.

Proof

Similar to Theorem 4.2, the proof is divided into two parts. First we assume that (4.5) is true and now the case is to prove u(t) is non-continuable. We prove by the method of contradiction. So we assume that u(t) is continuable. Then by Definition 4.1, there exists a solution $\tilde{u}(t)$ of (2.1) defined on $(0,\,\tilde{\eta })$, where $\tilde{\eta }$ > $\eta$ such that u(t) = $\tilde{u}(t)$ for $(0,\eta )$. This implies that $\lim \nolimits _{t\rightarrow {\eta }^{-}}u(t)$ $=$ $\tilde{u}(t)$. Thus, $|A(t)|\rightarrow |A(\eta )|$ as $t\rightarrow \eta ^-$. This is a contradiction to (4.5). Hence u(t) is non-continuable.

To prove the second part, we assume that u(t) is non-continuable. For the method of contradiction, we suppose that (4.5) is not true. Then there exists a sequence $\{t_l\}$ and a positive constant $m>0$ such that $t_l$ < $t_{l+1}$, for $l\in \mathbb {N}$. Then

$$\begin{aligned} \lim \limits _{l\rightarrow \infty } t_l&= \eta \hspace{0.3cm}\text {and}\hspace{0.3cm} |A(t_l)|\leqslant m, \end{aligned}$$

(4.6)

Hence $t_l^2+u^2(t_l)\leqslant m^2.$ Since ${u(t_l)}$ is bounded, it has a convergent sequence such that we suppose that

$$\begin{aligned} \lim \limits _{l\rightarrow \infty }u(t_l)&= u^*. \end{aligned}$$

(4.7)

Now we claim that

$$\begin{aligned} \lim \limits _{t\rightarrow \eta ^-} u(t)&= u^*. \end{aligned}$$

(4.8)

That is, for given $\varepsilon >0$, there exists a T $\in$ $(0,\eta )$, such that $|u(t)-u^\star |<\varepsilon$, $t\in (T,\eta )$. Now for sufficiently small $\gamma >0$, let

$$\begin{aligned} \mathbb {U}=\bigg \{(t,u): \,\,t\in [\gamma ,\eta ),\,\, |u|\leqslant \sup _{t\in [\gamma ,\eta )}|u(t)|\bigg \} \end{aligned}$$

From (4.6) and (4.7), we see that there exists a $l_0$ such that $t_{l_0}>\gamma$ and for $l\geqslant l_0$, we have

$$\begin{aligned} |u(t_l)-u^*|&\leqslant \frac{\varepsilon }{2}. \end{aligned}$$

(4.9)

If (4.8) is not valid, then there exists a $t_*$ $\in$ $(t_l,\eta )$ such that

$$\begin{aligned} |u(t_*)-u^*|&\geqslant \varepsilon . \end{aligned}$$

(4.10)

Now, we consider

$$\begin{aligned} \varepsilon&\leqslant |u(t_*)-u^*|=|u(t_*)-u^*+u(t_l)-u(t_l)|\\&\leqslant |u(t_l)-u^*|+|u(t_*)-u(t_l)|\\&\leqslant \frac{\varepsilon }{2}+ \bigg |\displaystyle \int _0^{t_*} (t_*-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_*-s)\,\, f(s,u(s))\textrm{d}s- \displaystyle \int _0^{t_l} (t_l-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_l-s)\,\, f(s,u(s))\textrm{d}s\bigg |\\&\leqslant \frac{\varepsilon }{2}+ \displaystyle \int _0^{t_l}\bigg |(t_*-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_*-s)-(t_l-s)^{\alpha -1}\mathscr {S}_{\alpha }(t_l-s)\bigg ||f(s,u(s))|\textrm{d}s\\&\quad + \int _{t_l}^{t_*}(t_*-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t_*-s)|\,\,|f(s,u(s))|\textrm{d}s. \end{aligned}$$

Now by the continuity of $t^{\alpha -1}\mathscr {S}_{\alpha }(t)*f(t)$ and the operator $\mathscr {R}_{\alpha }(t)$ and the condition (3.3), as $t_l\rightarrow t_*$, we have

$$\begin{aligned} \varepsilon&\leqslant \frac{\varepsilon }{2}+ \frac{\varepsilon }{2}=\varepsilon . \end{aligned}$$

This implies that (4.8) exists. This is a contradiction as we suppose that u(t) is non-continuable. Hence (4.5) is valid. $\square$

Before proving the main theorem, we present an auxiliary lemma similar to Theorem 5.1 in [25].

Theorem 4.4

Let the conditions $(H1)-(H2)$ hold and the nonlinear function f satisfies the Lipschitz condition (3.3). Let u(t) be solution of (2.1) on $(0,\eta )$. If u(t) is bounded on $[\gamma ,\eta )$ for some $\gamma \geqslant 0$, then $\eta$ $=$ $+\infty$.

Proof

By Theorems 4.2 and 4.3, we see that if u(t) is continuable on $(0,\eta )$, then $\eta =+\infty$. $\square$

Now we state the main theorem on global existence.

Theorem 4.5

Suppose that the conditions $(H1)-(H2)$ hold and f satisfies the Lipschitz condition (3.3). Then (2.1) has a solution in $C([0,+\infty ))$.

Proof

The existence of local solution is valid by Theorem 2.5. Let the maximum existing interval of the solution u(t) be $(0,\eta )$. Then

$$\begin{aligned} |u(t)|&\leqslant |\mathscr {R}_{\alpha }(t)u_0|+\int _0^t (t-s)^{\alpha -1}|\mathscr {S}_{\alpha }(t-s)|\,\,|f(s,u(s))|\textrm{d}s\\&\leqslant \Vert \mathscr {R}_{\alpha }(t)u_0\Vert _{C[0,\eta ]} + N(\mathbb {L}\Vert u-u_0\Vert _{C[0,\eta ]}+M)\frac{t^{\alpha }}{\alpha }. \end{aligned}$$

This implies that |u(t)| is bounded on $(0,\eta )$ by the boundedness of the operators $\mathscr {R}_{\alpha }(t)$ and $\mathscr {S}_{\alpha }(t)$. Therefore, for any $\gamma \in (0,\eta )$, |u(t)| is bounded in $[\gamma ,\eta )$. Hence by Theorem 4.4, u(t) is a solution on $(0,+\infty )$.

5 Uniqueness and stability

Now we state the four types of Ulam stability of the fixed point equation $u=\mathbb {T}(u)$ in the view of Definition 2.10. Let $\varepsilon$ be a positive real number and $\Psi$ be a continuous function. Then we have:

Definition 5.1

The fixed point equation $u=\mathbb {T}(u)$ is said to be Ulam-Hyers stable if there exists a real number $c_{\mathbb {T}}>0$ such that for each $\varepsilon > 0$ and for each solution $u\in C([0,T])$ of the inequality $\Vert u(t)-(\mathbb {T}u)(t)\Vert \leqslant \varepsilon$, for $t\in [0,T]$, there exists a solution $v\in C([0,T])$ of the equation $u=\mathbb {T}(u)$ with

$$\begin{aligned} \Vert u(t)-v(t)\Vert \leqslant \varepsilon c_{\mathbb {T}};\,\,\,\, t\in [0,T]. \end{aligned}$$

Definition 5.2

The fixed point equation $u=\mathbb {T}(u)$ is said to be generalized Ulam-Hyers stable if there exists $\phi _{\mathbb {T}}$ $\in$ $C([0,\infty ))$, $\phi _{\mathbb {T}}(0)=0$ such that for each $\varepsilon >0$ and for each solution $u\in C([0,T])$ of the inequality $\Vert u(t)-(\mathbb {T}u)(t)\Vert \leqslant \varepsilon$, $t\in J$ , there exists a solution $v\in C([0,T])$ of the equation $u=\mathbb {T}(u)$ with

$$\begin{aligned} \Vert u(t)-v(t)\Vert \leqslant \phi _{\mathbb {T}}(\varepsilon );\,\,\,\, t\in [0,T]. \end{aligned}$$

Definition 5.3

The fixed point equation $u=\mathbb {T}(u)$ is said to be Ulam-Hyers-Rassias stable with respect to an arbitrary function $\Psi$, if there exists a positive real number $c_{\mathbb {T},\Psi }$ such that for each $\varepsilon >0$ and for each solution $u\in C([0,T])$ of the inequality $\Vert u(t)-(\mathbb {T}u)(t)\Vert \leqslant \varepsilon \Psi (t)$; $t\in [0,T]$, there exists a solution $v\in C([0,T])$ of the equation $u=\mathbb {T}(u)$ with

$$\begin{aligned} \Vert u(t)-v(t)\Vert \leqslant \varepsilon c_{\mathbb {T},\Psi }\Psi (t);\,\,\,\, t\in [0,T]. \end{aligned}$$

Definition 5.4

The fixed point equation $u=\mathbb {T}(u)$ is said to be generalized Ulam-Hyers-Rassias stable with respect to $\Psi$, if there exists a positive real number $c_{\mathbb {T},\Psi }$ such that for each $\varepsilon >0$ and for each solution $u\in C([0,T])$ of the inequality $\Vert u(t)-(\mathbb {T}u)(t)\Vert \leqslant \Psi (t)$; $t\in J$, there exists a solution $v\in C([0,T])$ of the equation $u=\mathbb {T}(u)$ with

$$\begin{aligned} \Vert u(t)-v(t)\Vert \leqslant c_{\mathbb {T},\Psi }\Psi (t);\,\,\,\, t\in [0,T]. \end{aligned}$$

Remark 5.5

From the above definitions of stability, it is clear that

• Defintion 5.1 implies Definition 5.2;

• Defintion 5.3 implies Definition 5.4;

• Defintion 5.3 for $\Psi (t)=1$ implies Definition 5.1.

The next theorem states that the solution has atmost one solution.

Theorem 5.6

Let the conditions $(H1)-(H2)$ hold and f satisfies the estimate (3.3). If $0<\mathbb {L}\leqslant \frac{1}{2}$, then (2.1) has a unique mild solution in $C([0,\overline{\tau }])$, where $\overline{\tau }^{\alpha }\leqslant \frac{\alpha }{N}$. Moreover, the operator $\mathbb {T}$ is a c-weakly Picard operator and hence the fixed point equation $u=\mathbb {T}(u)$ is Ulam-Hyers stable.

Proof

The uniqueness of solution to the abstract problem (2.1) is proved using contraction principle. Let u, v $\in$ $U_{\tau }$ be a mild solution of (2.1) with same initial data. Then using ansatzes (3.5), (3.6), (3.7) and the condition (3.3), we have,

$$\begin{aligned} \Vert \mathbb {T}u(t)-\mathbb {T}v(t)\Vert&\leqslant \displaystyle \int _0^t (t-s)^{\alpha -1} \Vert \mathscr {S}_{\alpha }(t-s)\Vert \Vert f(s,u(s))-f(s,v(s))\Vert \textrm{d}s\\ \Vert \mathbb {T}u(t)-\mathbb {T}v(t)\Vert&\leqslant N\mathbb {L}\Vert u-v\Vert \displaystyle \frac{t^{\alpha }}{\alpha }\leqslant \displaystyle \frac{N\mathbb {L}{\overline{\tau }}^{\alpha }}{\alpha }\Vert u-v\Vert \leqslant \mathbb {L}\Vert u-v\Vert . \end{aligned}$$

By the Banach contraction principle, we conclude that there exists a unique fixed point which is the desired mild solution of the problem (1.1). Then by Lemma 2.12, the operator $\mathbb {T}$ is a c-weakly Picard operator with the constant $c_{\mathbb {T}}=\frac{1}{1-q}$, where $q=\mathbb {L}$ and hence the fixed point equation $u=\mathbb {T}(u)$ is Ulam-Hyers stable. $\square$

Next we prove the Ulam-Hyers Rassias stability to the fixed point equation $u=\mathbb {T}(u)$ as follows:

Theorem 5.7

Let the conditions $(H1)-(H2)$ hold and f satisfies (3.3). If u(t) is a solution of the inequality $\Vert u- \mathbb {T}(u)\Vert$ $\leqslant$ $\Psi (t)$ $\in$ $L^1([0,t))$ and there exists $\lambda _{\Psi }>0$ such that for each $t\in [0,\overline{\tau }]$, we have

$$\begin{aligned} I^{\alpha }\Psi (t)&\leqslant \lambda _{\Psi }\Psi (t) \end{aligned}$$

(5.1)

and the operator $\mathbb {T}$ is a contraction, then the fixed point equation $u=\mathbb {T}(u)$ is generalized Ulam-Hyers-Rassias stable such that

$$\begin{aligned} \Vert u(t)-v(t)\Vert \leqslant c_{\Psi }\Psi (t), \end{aligned}$$

where v is the solution of the equation $\mathbb {T}u=u.$

Proof

Let u $\in$ $C([0,\overline{\tau }])$ be a solution of the inequality $\Vert u- \mathbb {T}(u)\Vert$ $\leqslant$ $\Psi (t)$. Then by Theorem 5.6, $\mathbb {T}$ is a contraction and has a unique solution of the fixed point equation $u=\mathbb {T}(u)$. Let v be a solution. Then, we write

$$\begin{aligned} v(t)&=(\mathbb {T}v)(t)\\&= \mathscr {R}_{\alpha }(t)v_0+\int _0^t (t-s)^{\alpha -1}\mathscr {S}_{\alpha }(t-s)f(s,v(s))\textrm{d}s. \end{aligned}$$

Then for each $t\in [0,\overline{\tau }]$, by Lemma 2.13, we obtain

$$\begin{aligned} \Vert u(t)-v(t)\Vert&= \Vert u(t)-\mathbb {T}v(t)\Vert \leqslant \Vert u(t)- \mathbb {T}u(t)\Vert +\Vert \mathbb {T}u(t)-\mathbb {T}v(t)\Vert \nonumber \\&\leqslant \Psi (t)+ \int _0^t (t-s)^{\alpha -1} \Vert \mathscr {S}_{\alpha }(t-s)\Vert \Vert f(s,u(s))-f(s,v(s))\Vert \textrm{d}s\nonumber \\&\leqslant \Psi (t)+ N\mathbb {L}\int _0^t (t-s)^{\alpha -1} \Vert u(s)-v(s)\Vert \textrm{d}s\nonumber \\&\leqslant \Psi (t)+N\mathbb {L}\mathfrak {M}\int _0^t (t-s)^{\alpha -1}\Psi (s)\textrm{d}s\nonumber \\&= \Psi (t)+C I^{\alpha }\Psi (t)\nonumber \\&\leqslant \Psi (t)+\lambda _{\Psi }\Psi (t):= c_{\Psi }\Psi (t), \end{aligned}$$

(5.2)

where $c_{\Psi }$ $=$ $1+\lambda _{\Psi }$. Then by Definition 5.4, the fixed point equation $u=\mathbb {T}(u)$ is generalized Ulam-Hyers-Rassias stable. $\square$

6 Applications

Example 6.1

In problem (1.1), let us consider $a(t-s)=(t-s)^{\beta -1}$, $0<\beta < 1$. Consider the domain $\Omega = [0,2]$ and $t\in [0,1]$. Then the problem (1.1) can be written as

$$\begin{aligned} ^C_0D^{\alpha }_t u(x,t)&= \mathbb {D}\displaystyle \frac{\partial ^2 u(x,t)}{\partial x^2}+\displaystyle \int _0^t (t-s)^{\beta -1}\displaystyle \frac{\partial ^2 u(x,s)}{\partial x^2}\textrm{d}s+ b(x)u^{p(x)}, \hspace{0.2cm} x\in \Omega \end{aligned}$$

(6.1)

with initial and boundary conditions

$$\begin{aligned} u(x,0)&= {\left\{ \begin{array}{ll} 2x, &{} 0\leqslant x \leqslant \frac{1}{2}\\ \frac{4-2x}{3}, &{} \frac{1}{2}< x \leqslant 1\\ \end{array}\right. },\hspace{0.3cm}x\in \Omega \nonumber \\ u(x,t)&=0,\hspace{3cm} x\in \partial \Omega ,\,\,t\geqslant 0. \end{aligned}$$

(6.2)

Let us suppose that p(x) = $x+1$ $>1$ and $b(x)=0.05x^2$. Hence by [14], the problem (6.2) can be written in its abstract form since it satisfies the ansatzes (3.5)–(3.7). Then we define an operator $(\mathbb {T}u)(t)$ similar to (3.4) and we see that the operator $\mathbb {T}$ is a contraction using (3.5)–(3.7). Hence by Theorem 4.3, the problem (6.2) has a unique solution. Moreover, the solution of the fixed point equation $u(t)=(\mathbb {T}u)(t)$ is Ulam-Hyers stable. Now let us assume $\Psi (t):=t+1$. Then from the inequality (5.2), using the substitution method, we obtain

$$\begin{aligned} \Vert u(t)-v(t)\Vert&\leqslant (t+1)+N\mathbb {L}\mathfrak {M}\int _0^t (t-s)^{\beta -1}(s+1)\textrm{d}s\\&= (t+1)+N\mathbb {L}\mathfrak {M}\int _0^t z^{\beta -1}(t-z)\textrm{d}z\\&= (t+1)+N\mathbb {L}\mathfrak {M}t^{\beta +1}\bigg (\frac{1}{\beta }-\frac{1}{\beta +1}\bigg )+\frac{N\mathbb {L}\mathfrak {M}t^{\beta }}{\beta }\\&\leqslant (t+1)+\frac{N\mathbb {L}\mathfrak {M}t^{\beta +1}}{\beta }+\frac{N\mathbb {L}\mathfrak {M}t^{\beta }}{\beta }\\&= (t+1)+\frac{N\mathbb {L}\mathfrak {M}t^{\beta }}{\beta }(t+1)\\ \Vert u(t)-v(t)\Vert&\leqslant \Psi (t)c_{\Psi }, \end{aligned}$$

where $0\leqslant 1+ \lambda _{\Psi }:=c_{\Psi }$, where $\lambda _{\Psi }=1+\frac{N\mathbb {L}\mathfrak {M}t^{\beta }}{\beta }$. Then by Theorem 5.7, the fixed point equation $u=\mathbb {T}u$ is generalized Ulam-Hyer-Rassias stable. To verify numerically, we consider $v=1$. Now

$$\begin{aligned} \bigg \Vert {^C_0}D^{\alpha }_t v -\mathbb {D}\displaystyle \frac{\partial ^2 v}{\partial x^2}-\displaystyle \int _0^t a(t-s)\displaystyle \frac{\partial ^2 v}{\partial x^2}\textrm{d}s-b(x)v^{p(x)}\bigg \Vert&= 0.05x^2\leqslant t+1 . \end{aligned}$$

This implies that v is a solution of the inequality $\Vert \mathbb {T}u-u\Vert \leqslant \Psi (t)$. Then by Theorem 5.7, there exists a solution u that satisfies

$$\begin{aligned} \Vert u-v\Vert&\leqslant c_\Psi \Psi (t). \end{aligned}$$

(6.3)

Fig. 1

Numerical solution of the problem (6.1) for x = 0.5

Fig. 2

$\Vert u-v\Vert \leqslant c_{\Psi }\Psi (t)$ for $\alpha =0.4$ and $\beta =0.5$ to the problem (6.1)

Fig. 3

Numerical solution of the problem (6.4) for x = 0.5

Let us assign values for the parameters: $N=1$, $\mathbb {L}=0.5$ and $\mathfrak {M}=0.5$. We choose $\alpha =0.4$ and $\beta =0.5$. Now using finite difference scheme [18, 26] with time grid size $\bigtriangleup t=0.0001$ and space grid size $\bigtriangleup x=0.25$, one gets Fig. 1 which is the solution u of the problem (6.1). Now using the solution $v=1$ of the inequality $\Vert \mathbb {T}u-u\Vert \leqslant \Psi (t)$, we verify the relation (6.3) by plotting the values of $\Vert u-v\Vert$ and $c_{\Psi }\Psi (t)$. Then at $x=0.5$ and for different values of t, the desired result is presented in the Fig. 2. The tabular values shows that our theoretical results in the Theorem 5.7 are satisfied and hence the solution to the problem (6.1)–(6.2) is generalized Ulam-Hyers Rassias stable.

Example 6.2

Consider the problem (6.1) with $\Omega = [0,1]$ and $t\in [0,1]$:

$$\begin{aligned} ^C_0D^{\alpha }_t u(x,t)&= \mathbb {D}\displaystyle \frac{\partial ^2 u(x,t)}{\partial x^2}+\displaystyle \int _0^t (t-s)^{\beta -1}\displaystyle \frac{\partial ^2 u(x,s)}{\partial x^2}\textrm{d}s+ b(x)u^{p(x)}, \hspace{0.2cm} x\in \Omega \end{aligned}$$

(6.4)

with initial and boundary conditions

$$\begin{aligned} u(x,0)&= x^2,\hspace{3cm}x\in \Omega \nonumber \\ u(x,t)&=0,\hspace{3cm} x\in \partial \Omega ,\,\,t\geqslant 0. \end{aligned}$$

(6.5)

Now we choose $\alpha =0.6$ and $\beta =0.5$ with the assumptions on the parameters $N=1$, $\mathbb {L}=0.5$, $\mathfrak {M}=0.5$, $p(x)= x+1$ and $b(x)=0.05x^2$. Similar to Example (6.1), the problem (6.4)–(6.5) satisfies the ansatzes (3.5)–(3.7). Hence an operator $\mathbb {T}u(t)$ is defined as in (3.4) and see that the operator $\mathbb {T}$ is a contraction using the assumptions (3.5)–(3.7). Hence by Theorem 4.3, the problem (6.4)–(6.5) has a unique solution. This follows that the solution is Ulam-Hyers stable. Now similar to the Example 6.1, we assume $\Psi (t):= t+1$. Then from the similar computation one gets

$$\begin{aligned} \Vert u(t)-v(t)\Vert \leqslant c_{\Psi }\Psi (t). \end{aligned}$$

Hence the solution u to the problem (6.4)–(6.5) is generalized Ulam-Hyers-Rassias stable by Theorem 5.7. To verify numerically, we choose a solution $v=1$ of the inequality

$$\begin{aligned} \bigg \Vert {^C_0}D^{\alpha }_t v -\mathbb {D}\displaystyle \frac{\partial ^2 v}{\partial x^2}-\displaystyle \int _0^t a(t-s)\displaystyle \frac{\partial ^2 v}{\partial x^2}\textrm{d}s-b(x)v^{p(x)}\bigg \Vert&= 0.05x^2\leqslant t+1. \end{aligned}$$

This implies that v is a solution of the inequality $\Vert \mathbb {T}u-u\Vert \leqslant \Psi (t)$. The solution u to the problem (6.4)–(6.5) is obtained using the finite difference scheme [18, 26] and accordingly the Fig. 3 displays the solution at $x=0.5$. The Fig. 4 shows that the relation (6.3) is true for $0<\alpha ,\beta <1$. At $x=0.5$ and for different values of t, the table and the graph is given in Fig. 4. Hence by Theorem 5.7, the solution to the system (6.4)–(6.5) is generalized Ulam-Hyers-Rassias stable.

Fig. 4

$\Vert u-v\Vert \leqslant c_{\Psi }\Psi (t)$ for $\alpha =0.6$ and $\beta =0.5$ to the problem (6.4)

7 Conclusion

The global existence of solution to the problem (1.1) is established by Schauder fixed point theorem and non-continuation principle. The uniqueness of solution is achieved in $(0,\overline{\tau })$ using contraction principle. The Ulam-Hyers and generalized Ulam-Hyers-Rassias stability is discussed using Picard operator in $(0,\overline{\tau })$. The Figs. 2 and 4 shows that our theoretical results are valid for $0<\alpha <1$ and certain conditions on the parameters $\mathbb {L}$, $\mathfrak {M}$ and N. Further, it is planned to investigate the blow-up behaviour of solution to the problem (1.1) in future.