1 Introduction

Fractional integro-differential equations have been studied by many researchers from different points of view during the last decades (see for example, [5, 10] and [15–19]). In 2015, a new fractional derivation without singular kernel was introduced by Caputo and Fabrizio ([8]). Some researchers tried to use it for solving different equations (see, for example, [2, 9] and [14]). Recently, approximate solutions of some fractional differential equations have been reviewed (see, for example, [3, 4, 6, 12, 13] and [7]). Also, one is finding some new applications for fractional derivations (see, for example, [3]).

In this manuscript we consider \(b>0\), \(x\in H^{1}(0,b)\) and \(\alpha\in (0,1)\). The expression of the Caputo–Fabrizio fractional derivative of order α for the function x has the form \({}^{\mathrm{CF}}D^{\alpha}x(t)=\frac{B(\alpha)}{1-\alpha}\int_{0}^{t}\exp(\frac {-\alpha}{1-\alpha}(t-s))x^{\prime}(s)\,ds \), where \(t\geq0\) ([1, 8] and [9]). \(B(\alpha) \) is a normalization constant \((B(1)=B(0)=1)\). The fractional integral of order α for the function x is written as ([14]) \({}^{\mathrm{CF}}I^{\alpha} x(t)=\frac{ 1-\alpha}{B(\alpha)}x(t) +\frac{ \alpha}{B(\alpha)}\int_{0}^{t} x(s) \,ds\), whenever \(0<\alpha<1\). If \(n\geq1\) and \(\alpha\in[0,1]\), then the fractional derivative \({}^{\mathrm{CF}}D^{\alpha+n}\) of order \(n+\alpha\) is defined by \({}^{\mathrm{CF}}D^{\alpha+n}x:= {}^{\mathrm{CF}}D^{\alpha}( D^{n}x(t))\) ([6] and [8]). If the function x is such that \(x^{(k)}=0\) for \(k=1,2,3,\ldots,n\), then \({}^{\mathrm{CF}}D^{\alpha}( D^{n}x(t))=D^{n} ({}^{\mathrm{CF}}D^{\alpha}) x(t)\)([8]). Here, D is the ordinary derivation.

Lemma 1.1

([1] and [14])

Let \(0<\alpha<1\). Then the unique solution for the problem \({}^{\mathrm{CF}}D^{\alpha}x(t)=y(t)\) is given by \(x(t)=x(0)+\frac{ 1-\alpha}{B(\alpha)}y (t) +\frac{ \alpha}{B(\alpha )}\int_{0}^{t} x(s)\,ds\).

Theorem 1.2

([11])

Let \((X,d)\) be a complete metric space and \(F:X\to X\) be a mapping such that \(\varphi (d(Fx,Fy))\leq\varphi(d(x,y))-\phi(d(x,y)) \), for all \(x,y \in X\), where \(\varphi,\phi:[0,1]\to[0,1]\) are continuous non-decreasing maps and \(\varphi(t)=\phi(t)=0\) if and only if \(t=0\). Then F has a unique fixed point.

2 Main result

Let n be a natural number, \(\alpha\in(0,1)\) and \(x^{(n)}\in H^{1}(0,1)\). Then the fractional CFD of order α and n is defined by

$${}^{\mathrm{CF}}D^{\alpha+n}x(t) = {}^{\mathrm{CF}}D^{\alpha } \bigl(D^{n}x(t)\bigr)=\frac{B(\alpha)}{1-\alpha} \int_{0}^{t}\exp\biggl(\frac{-\alpha }{1-\alpha}(t-s) \biggr)x^{(n+1)}(s)\,ds. $$

Also, the fractional DCF of order α and n is defined by

$$\bigl( ^{CF }D^{\alpha}\bigr)^{(n)}x(t) =D^{n}\bigl( {}^{\mathrm{CF}}D^{\alpha }x(t)\bigr)= \frac{B(\alpha)}{1-\alpha}\frac{d^{n}}{dt^{n}} \int_{0}^{t}\exp\biggl(\frac {-\alpha}{1-\alpha}(t-s) \biggr)x^{\prime} ( s)\,ds. $$

Here, D is the ordinary derivative.

Lemma 2.1

Let n be a natural number and \(\alpha\in(0,1)\). Then

$$\bigl( {}^{\mathrm{CF}}D^{\alpha}\bigr)^{(n)}x(t) = {}^{\mathrm{CF}}D^{\alpha +n}x(t) + \exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr) \sigma(\alpha,n,0), $$

where \(\sigma(\alpha,n,t)=\frac{B(\alpha)}{1-\alpha}\sum_{i=1}^{n} (\frac{-\alpha}{1-\alpha})^{n-i}x^{(i)}(t) \).

Proof

For each \(k\geq1\), we have

$$\begin{aligned} \int_{0}^{t}\exp\biggl(\frac{-\alpha}{1-\alpha}(t-s) \biggr)x^{(k)} ( s)\,ds&=x^{(k-1)}(t) -\exp\biggl( \frac{-\alpha}{1-\alpha} t \biggr)x^{(k-1)} (0) \\ &\quad {}+\biggl(\frac{-\alpha}{1-\alpha}\biggr) \int_{0}^{t}\exp\biggl(\frac{-\alpha}{1-\alpha }(t-s) \biggr)x^{(k-1)} ( s)\,ds. \end{aligned} $$

Now by using repetition of the last relation, we get

$$\begin{aligned} {}^{\mathrm{CF}}D^{\alpha+n}x(t) &= {}^{\mathrm{CF}}D^{\alpha} \bigl( D^{n}x(t)\bigr)=\frac{B(\alpha)}{1-\alpha} \int_{0}^{t}\exp\biggl(\frac{-\alpha }{1-\alpha}(t-s) \biggr)x^{(n+1)} ( s)\,ds \\ &=\frac{B(\alpha)}{1-\alpha}\biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n} \int_{0}^{t}\exp \biggl(\frac{-\alpha}{1-\alpha}(t-s) \biggr)x^{\prime} ( s)\,ds\\ &\quad {}+\frac{B(\alpha )}{1-\alpha}\sum_{i=1}^{n} \biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n-i}x^{(i)}(t) \\ &\quad {}-\frac{B(\alpha)}{1-\alpha}\exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr)\sum _{i=1}^{n} \biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n-i}x^{(i)}(0)\\ &=\frac{B(\alpha )}{1-\alpha}\biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n} \int_{0}^{t}\exp\biggl(\frac{-\alpha }{1-\alpha}(t-s) \biggr)x^{\prime}(s)\,ds \\ &\quad {}+\sigma(\alpha,n,t)-\exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr)\sigma( \alpha,n,0)\\ & = \biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n} {}^{\mathrm{CF}}D^{\alpha}x(t)+ \sigma (\alpha,n,t)-\exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr)\sigma(\alpha,n,0). \end{aligned}$$

Also, we have

$$\begin{aligned} \bigl({}^{\mathrm{CF}}D^{\alpha}\bigr)^{(n)}x(t)&= D^{n}\bigl(D^{\alpha}x(t)\bigr)=\biggl(\frac {-\alpha}{1-\alpha} \biggr)^{n} {}^{\mathrm{CF}}D^{\alpha}x(t)+\frac{B(\alpha )}{1-\alpha} \sum_{i=1}^{n} \biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n-i}x^{(i)}(t) \\ &=\frac{B(\alpha)}{1-\alpha}\biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n} \int_{0}^{t}\exp \biggl(\frac{-\alpha}{1-\alpha}(t-s) \biggr)x^{\prime} ( s)\,ds\\ &\quad {}+\frac{B(\alpha )}{1-\alpha}\sum_{i=1}^{n} \biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n-i}x^{(i)}(t) \\ &=\biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n} {}^{\mathrm{CF}}D^{\alpha}x(t)+ \sigma (\alpha,n,t). \end{aligned} $$

Hence \(( {}^{\mathrm{CF}}D^{\alpha})^{(n)}x(t) = {}^{\mathrm{CF}}D^{\alpha+n}x(t) + \exp(\frac{-\alpha}{1-\alpha}t)\sigma(\alpha ,n,0) \). □

By using Lemma 2.1, we conclude that \({}^{\mathrm{CF}}D^{\alpha +n}x(t)=({}^{\mathrm{CF}}D^{\alpha})^{(n)}x(t)\) whenever \(x^{(k)}(0)=0\) for \(0\leq k \leq n\).

Lemma 2.2

Let n be a natural number, \(\alpha\in(0,1)\) and \(y\in H^{1}(0,1)\). Then the solution of the problem \({}^{\mathrm{CF}}D^{{\alpha+n}}x(t)=y(t)\) is given by

$$x(t)=\frac{ 1-\alpha}{B(\alpha)}J^{n}y(t)+\frac{\alpha}{B(\alpha)} J^{n+1}y(t) + x(0)+tx^{\prime}(0)+t^{2} \frac{x^{\prime\prime }(0)}{2!}+\cdots+t^{n}\frac{x^{(n)}(0)}{n!}. $$

Proof

By using Lemma 1.1 for the equation \({}^{\mathrm{CF}} D^{\alpha +n} x(t)= {}^{\mathrm{CF}} D^{\alpha} x^{(n)}(t)=y(t)\), we get \(x^{(n)}(t)= x^{(n)}(0)+\frac{ 1-\alpha}{B(\alpha)} y(t) +\frac{ \alpha}{B(\alpha)} \int_{0}^{t} y(s)\,ds \). By using an integration, we obtain

$$x^{(n-1)}(t)= x^{(n-1)}(0)+tx^{(n)}(0)+\frac{ 1-\alpha}{B(\alpha)} \int _{0}^{t}y(s)\,ds +\frac{ \alpha}{B(\alpha)} \int_{0}^{t} \int_{0}^{s} y(r)\,dr\,ds. $$

By repeating this method, we deduce that

$$\begin{aligned} x^{(n-2)}(t)&= x^{(n-2)}(0)+tx^{(n-1)}(0)+ \frac{t^{2}}{2}x^{(n)}(0) \\ &\quad {}+\frac{ 1-\alpha}{B(\alpha)} \int_{0}^{t} \int_{0}^{s} y(r)\,dr\,ds +\frac{ \alpha}{B(\alpha)} \int_{0}^{t} \int_{0}^{s} \int_{0}^{r} y(k)\,dk\,dr\,ds. \end{aligned} $$

By continuing the process, we conclude that

$$x(t)=\frac{ 1-\alpha}{B(\alpha)}J^{n}y(t)+\frac{ \alpha}{B(\alpha)} J^{n+1}y(t) + x(0)+tx^{\prime}(0)+t^{2} \frac{x^{\prime\prime }(0)}{2!}+\cdots+t^{n}\frac{x^{(n)}(0)}{n!}. $$

On the other hand, by using some calculation, one can find that the given map \(x(t)\) is a solution for the problem \({}^{\mathrm{CF}}D^{{\alpha+n}}x(t)=y(t)\). □

Lemma 2.3

Let n be a natural number, \(\alpha\in(0,1)\) and \(y\in H^{1}(0,1)\). Then the solution of the problem \(({}^{\mathrm{CF}}D^{\alpha})^{(n)}x(t)=y(t)\) is given by

$$\begin{aligned} x(t) &=\frac{ 1-\alpha}{B(\alpha)}J^{n}y(t)+\frac{ \alpha}{B(\alpha)} J^{n+1}y(t) + x(0)+tx^{\prime}(0)+\cdots\\ &\quad {}+t^{n} \frac{x^{(n)}(0)}{n!}- \frac{t^{n}}{n!}\sum_{i=1}^{n} \biggl( \frac{-\alpha}{1-\alpha}\biggr)^{n-i}x^{(i)}(0). \end{aligned} $$

Proof

By using Lemma 2.2 for \(( {}^{\mathrm{CF}}D^{\alpha })^{(n)}x(t)= {}^{\mathrm{CF}}D^{\alpha+n}x(t)+ \exp(\frac{-\alpha }{1-\alpha}t)\sigma(\alpha,n,0)\), we get

$$\begin{aligned} x(t)& =\frac{ 1-\alpha}{B(\alpha)}J^{n}\biggl(y(t)- \exp\biggl( \frac{-\alpha }{1-\alpha}t\biggr)\sigma(\alpha,n,0)\biggr)\\ &\quad {}+\frac{ \alpha}{B(\alpha)} J^{n+1}\biggl(y(t)- \exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr)\sigma( \alpha,n,0)\biggr) \\ &\quad {}+ x(0)+tx^{\prime}(0)+t^{2}\frac{x^{\prime\prime}(0)}{2!}+ \cdots+t^{n}\frac {x^{(n)}(0)}{n!} \end{aligned} $$

or equivalently

$$\begin{aligned} x(t)& =\frac{ 1-\alpha}{B(\alpha)} J^{n}y(t)- \frac{ 1-\alpha}{B(\alpha )}\sigma(\alpha,n,0)J^{n}\exp\biggl(\frac{-\alpha}{1-\alpha}t \biggr)+\frac{ \alpha}{B(\alpha)} J^{n+1}y(t) \\ &\quad {}- \frac{ \alpha}{B(\alpha)}\sigma(\alpha,n,0)J^{n+1}\exp\biggl( \frac{-\alpha }{1-\alpha}t\biggr) + x(0)+tx^{\prime}(0)+t^{2} \frac{x^{\prime\prime }(0)}{2!}+\cdots+t^{n}\frac{x^{(n)}(0)}{n!}\\ & = \frac{ 1-\alpha}{B(\alpha )}J^{n}y(t) +\frac{ \alpha}{B(\alpha)} J^{n+1}y(t)- \sigma(\alpha,n,0)J^{n} \biggl[\frac{ 1-\alpha}{B(\alpha)}\exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr)\\ &\quad {}+ \frac{ \alpha }{B(\alpha)}J^{1}\exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr) \biggr] + x(0)+tx^{\prime }(0)+t^{2}\frac{x^{\prime\prime}(0)}{2!}+\cdots+t^{n}\frac{x^{(n)}(0)}{n!} \\ & =\frac{ 1-\alpha}{B(\alpha )}J^{n}y(t)+ \frac{ \alpha}{B(\alpha)} J^{n+1}y(t)- \sigma(\alpha ,n,0)J^{n}\biggl[ \frac{ 1-\alpha}{B(\alpha)}\exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr) \\ &\quad {}+\frac{ 1-\alpha}{B(\alpha)}\biggl(1- \exp\biggl(\frac{-\alpha}{1-\alpha}t\biggr)\biggr) \biggr] + x(0)+tx^{\prime}(0)+t^{2}\frac{x^{\prime\prime}(0)}{2!}+ \cdots+t^{n}\frac {x^{(n)}(0)}{n!} \\ &=\frac{ 1-\alpha}{B(\alpha)}J^{n}y(t)+\frac{ \alpha}{B(\alpha)} J^{n+1}y(t)+ x(0)+tx^{\prime}(0)+t^{2} \frac {x^{\prime\prime}(0)}{2!}+\cdots+t^{n}\frac{x^{(n)}(0)}{n!} \\ &\quad {}- \frac {t^{n}}{n!} \sum_{i=1}^{n} \biggl(\frac{-\alpha}{1-\alpha}\biggr)^{n-i}x^{(i)}(0). \end{aligned} $$

 □

Lemma 2.4

Let \(\alpha\in(0,1)\), \(2< q=2+\alpha<3\) and \(y\in H^{1}(0,1)\). The fractional differential equation \(^{ {CF}} D^{q} x(t)=y(t)\) with boundary conditions \(x(0)=0\), \(x^{\prime}(1)+ x^{\prime}(0)=0\) and \(x^{\prime \prime}(0) =0\) has the unique solution of the form \(x(t)=\int_{0}^{1} G(t,s)y(s)\,ds\), where \(G(t,s)=\frac{- (1-\alpha)t}{2B(\alpha) }-\frac {\alpha t}{2B(\alpha)}\) whenever \(0< t\leq s<1\) and \(G(t,s)=\frac {1-\alpha}{B(\alpha)}(t-s) + \frac{\alpha}{2B(\alpha)}(t-s)^{2} -\frac {(1-\alpha)t}{2B(\alpha)}- \frac{\alpha t}{2B(\alpha)}(t-s) \) whenever \(0< s\leq t<1\).

Proof

By using Lemma 2.2, we get \(x(t)=\frac{ 1-\alpha}{B(\alpha )}J^{2 }y(t)+\frac{ \alpha}{B(\alpha)} J^{3}y(t) +tx^{\prime}(0)\). Hence, we obtain \(x^{\prime}(t)= \frac{ 1-\alpha}{B(\alpha)}J^{1}y(t)+\frac{ \alpha }{B(\alpha)} J^{2 }y(t) + x^{\prime}(0) \). By using the boundary conditions \(x^{\prime}(1)+ x^{\prime}(0)=0 \) and \(x^{\prime}(1)= \frac{ 1-\alpha}{B(\alpha)}J^{1}y(1)+\frac{ \alpha }{B(\alpha)} J^{2 }y(1) + x^{\prime}(0) \), we have \(x(t)=\frac{ 1-\alpha}{B(\alpha)}J^{2 }y(t)+\frac{ \alpha}{B(\alpha)} J^{3}y(t)-\frac{ (1-\alpha) t}{2B(\alpha) }J^{1}y(1)-\frac{\alpha t}{2B(\alpha) }J^{2 }y(1)\). Thus, \(x(t)= \frac{ 1-\alpha}{B(\alpha)} \int_{0}^{t}y(s)(t-s) \,ds+ \frac{\alpha}{2B(\alpha) }\int_{0}^{t}y(s)(t-s)^{2}\,ds -\frac{ (1-\alpha) t}{2B(\alpha)} \int_{0}^{1}y(s) \,ds-\frac{\alpha t}{2B(\alpha) } \int_{0}^{1}y(s)(t-s) \,ds =\int_{0}^{1} G(t,s)y(s)\,ds \). Note that \({}^{\mathrm{CF}}D^{q}x(t)=0\) if and only if \(x(t)=0 \). This implies that the given map \(x(t)\) is a unique solution. □

Note that \(|G(t,s)|\leq|\frac{ 1-\alpha}{B(\alpha)}|+ |\frac{\alpha }{2B(\alpha) }| +|\frac{-\alpha t}{2B(\alpha) } |+|\frac{-(1-\alpha) t}{2B(\alpha)}|<\frac{3}{2B(\alpha)}\), for \(t \in[0,1]\). Let \(\mu,\mu_{1},\mu_{2}, k_{1},k_{2}\in C^{1}[0,1] \), \(m_{1}\), \(m_{2}\), h and g be bounded continuous functions on \(I:=[0,1]\) with \(M_{1}=\sup_{t\in I}|\mu(t)|<\infty\), \(M_{2}=\sup_{t\in I}|\mu_{1}(t)|<\infty\), \(M_{3}=\sup_{t\in I}|\mu_{2}(t)|<\infty\), \(M_{4}=\sup_{t\in I}|k_{1}(t)|<\infty\), \(M_{5}=\sup_{t\in I}|k_{2}(t)|<\infty\), \(M_{6}=\sup_{t\in I}|m_{1}(t)| <\infty\), \(M_{7}=\sup_{t\in I}|m_{2}(t)| <\infty\), \(M_{8}=\sup_{t\in I}|h(t)| <\infty\), \(M_{9}=\sup_{t\in I}|g (t)| <\infty\), \(N_{1}=\sup_{t\in I}|\mu^{\prime}(t)|<\infty\), \(N_{2}=\sup_{t\in I}|\mu_{1}^{\prime }(t)|<\infty\), \(N_{3}=\sup_{t\in I}|\mu_{2}^{\prime}(t)|<\infty\), \(N_{4}=\sup_{t\in I}|K_{1}^{\prime}(t)|<\infty\) and \(N_{5}=\sup_{t\in I}|K_{2}^{\prime}(t)|<\infty\). Let \(\alpha\in(0,1)\) and \(2< q= 2+\alpha<3\). Now, we investigate the CFD fractional integro-differential problem

$$ \begin{aligned}[b] {}^{\mathrm{CF}}D^{q}x(t)&=\mu(t) x(t)+\mu_{1}(t) x^{\prime}(t)+\mu_{2} (t)x^{\prime\prime}(t)+ k_{1}(t){}^{\mathrm{CF}}D^{\beta_{1}}x(t)+ k_{2}(t){}^{\mathrm{CF}}D^{\beta_{2}}x(t) \\ &\quad{}+ \int_{0}^{t} f \bigl(s,x(s), m _{1}(s) x^{\prime}(s) ,m _{2}(s) x^{\prime \prime}(s), h(s){}^{\mathrm{CF}}D^{ \gamma}x(s) , g(s){}^{\mathrm{CF}}D^{ \nu}x(s) \bigr)\,ds, \end{aligned} $$
(1)

with boundary conditions \(x(0)=0\), \(x^{\prime}(1)+ x^{\prime}(0)=0\) and \(x^{\prime\prime}(0) =0\), where \(1<\beta_{1}< 2<\beta_{2}<3\) and \(1<\gamma< 2<\nu<3\).

Theorem 2.5

Let \(\xi_{1}\), \(\xi_{2}\), \(\xi_{3}\), \(\xi_{4}\) and \(\xi_{5}\) be nonnegative real numbers, \(f:[0,1]\times\Bbb {R}^{5}\to\Bbb{R}\) an integrable function such that

$$\begin{aligned} &\bigl\vert f (t,x,y,z,v,w )-f \bigl(t,x^{\prime},y^{\prime} ,z^{\prime},v^{\prime},w^{\prime} \bigr) \bigr\vert \\ &\quad \leq \xi_{ 1} \bigl\vert x -x^{\prime} \bigr\vert + \xi_{ 2} \bigl\vert y -y^{\prime} \bigr\vert + \xi_{ 3} \bigl\vert z -z^{\prime} \bigr\vert + \xi_{ 4} \bigl\vert v -v^{\prime} \bigr\vert + \xi_{ 5} \bigl\vert v -v^{\prime} \bigr\vert , \end{aligned} $$

for all real numbers x, y, z, v, w, \(x^{\prime}\), \(y^{\prime}\), \(z^{\prime}\), \(v^{\prime} ,w ^{\prime}\in\Bbb{R} \) and \(t \in I\). If \(\Delta<\frac {1}{2}\), then the problem (1) has a unique solution, where \(\Delta :=\max\lbrace\Delta_{1},\Delta_{2},\Delta_{3},\Delta_{4}\rbrace\), \(\Delta_{1}= \frac{3}{2B(\alpha)} [M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta _{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} +\xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu} ] \), \(\Delta_{2}=\frac{3}{2}[ \frac{3+4\alpha}{2B(\alpha)} ] [M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta_{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} +\xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu}] \), \(\Delta_{3}= \frac{1+ \alpha}{B(\alpha)}[M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta_{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} +\xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu} ] \) and \(\Delta_{4}= \frac{\alpha}{B(\alpha)} [M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta_{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} +\xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu} ] +\frac{1-\alpha }{B(\alpha)}[N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3} +B(\beta_{1}-1)[ \frac{ |1-\beta _{1}|M_{4} }{(2-\beta_{1})^{2}} +\frac{ N_{4} +M_{4}}{ 2-\beta_{1} } ] +B(\beta _{2}-2)[\frac{ |2-\beta_{2}|M_{5} }{(3-\beta_{2})^{2}} +\frac{ M_{5}+ N_{5} }{ 3-\beta _{2} } ] + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{M_{ 8}B(\gamma-1)}{ 2-\l\gamma} +\xi_{ 5} \frac{ M_{9}B(\nu-1)}{ 3-\nu}] \).

Proof

Consider the Banach space \(C^{3}_{\mathbb{R}}[0,1]\) equipped with the norm \(\Vert x \Vert= \max_{t\in I}|x(t)|+ \max_{t\in I}| x^{\prime }(t) |+ \max_{t\in I}| x^{\prime\prime}(t) |+ \max_{t\in I}| x^{\prime \prime\prime}(t) | \). Define the map \(F: C^{3}_{\mathbb{R}}[0,1]\to C^{3}_{\mathbb{R}}[0,1]\) by

$$\begin{aligned} Fx(t) &= \int_{0}^{1} G(t,s)R(s)\,ds \\ &= \frac{ 1-\alpha}{B(\alpha)} \int _{0}^{t}R(s) (t-s) \,ds+ \frac{\alpha}{2B(\alpha) } \int_{0}^{t}R(s) (t-s)^{2}\,ds \\ &\quad {}-\frac{ (1-\alpha) t}{2B(\alpha)} \int_{0}^{1}R(s) \,ds-\frac{\alpha t}{2B(\alpha) } \int_{0}^{1}R(s) (t-s) \,ds, \end{aligned} $$

where

$$\begin{aligned} (Rx) (t)&=\mu(t) x(t)+\mu_{1} (t) x^{\prime}(t)+ \mu_{2}(t) x^{\prime\prime }(t)+ k_{1}(t) {}^{\mathrm{CF}}D^{\beta_{1}}x(t)+ k_{2}(t){}^{\mathrm{CF}}D^{\beta_{2}}x(t) \\ &\quad {}+ \int_{0}^{t} f \bigl(s,x(s), m _{1}(s) x^{\prime}(s) ,m _{2}(s) x^{\prime\prime }(s), h(s) {}^{\mathrm{CF}}D^{ \gamma}x(s) , g(s) {}^{\mathrm{CF}}D^{ \nu}x(s) \bigr)\,ds \end{aligned} $$

and

$$\begin{aligned} \bigl(R^{\prime}x\bigr) (t)&=\mu(t) x ^{\prime}(t)+ \mu^{\prime}(t) x (t)+\mu _{1}^{\prime}(t) x^{\prime}(t)+\mu_{1} x^{\prime\prime}(t)\\ &\quad {}+\mu_{2}^{\prime }(t) x^{\prime\prime}(t)+\mu_{2} (t) x^{\prime\prime\prime}(t)+ k_{1}^{\prime}(t) {}^{\mathrm{CF}}D^{\beta_{1}}x(t) \\ &\quad {}+ k_{1}(t)\biggl[\frac{1-\beta_{1}}{2-\beta_{1}} {}^{\mathrm{CF}}D^{\beta _{1}}x(t)+ \frac{B(\beta_{1}-1)}{2-\beta_{1}}x^{\prime\prime}(t)\biggr]\\ &\quad {} + k_{2}(t)\biggl[ \frac{2-\beta_{2}}{3-\beta_{2}} {}^{\mathrm{CF}}D^{\beta_{2}}x(t)+\frac {B(\beta_{2}-2)}{3-\beta_{2}}x^{\prime\prime\prime}(t) \biggr] + k_{2}^{\prime}(t) {}^{\mathrm{CF}}D^{\beta_{2}}x(t) \\ &\quad {}+f \bigl(t,x(t), m _{1}(t) x^{\prime}(t) ,m _{2}(t) x^{\prime\prime}(t), h(t) {}^{\mathrm{CF}}D^{ \gamma}x(t) , g(t) {}^{\mathrm{CF}}D^{ \nu}x(t)\bigr). \end{aligned} $$

By using Lemma 2.4, \(x_{0}\) is a solution for the problem (1) if and only if \(x_{0}\) is a fixed point of the operator F. Note that

$$\begin{aligned} & \bigl\vert (Rx) (t)-(Ry) (t) \bigr\vert \\ &\quad \leq \biggl\vert \mu(t) x(t)+\mu_{1} (t) x^{\prime}(t)+ \mu_{2}(t) x^{\prime\prime}(t)+ k_{1}(t) {}^{\mathrm{CF}}D^{\beta_{1}}x(t)+ k_{2}(t){}^{\mathrm{CF}}D^{\beta _{2}}x(t) \\ &\qquad {}+ \int_{0}^{t} f \bigl(s,x(s), m _{1}(s) x^{\prime}(s) ,m _{2}(s) x^{\prime\prime }(s), h(s) {}^{\mathrm{CF}}D^{ \gamma}x(s) , g(s) {}^{\mathrm{CF}}D^{ \nu}x(s) \bigr)\,ds \\ &\qquad {}- \biggl(\mu(t) y(t)+\mu_{1} (t) y^{\prime}(t)+ \mu_{2}(t) y^{\prime\prime}(t)+ k_{1}(t){}^{\mathrm{CF}}D^{\beta_{1}}y(t)+ k_{2}(t){}^{\mathrm{CF}}D^{\beta _{2}}y (t) \\ &\qquad {}+ \int_{0}^{t} f \bigl(s,y(s), m _{1}(s) y^{\prime}(s) ,m _{2}(s) y^{\prime\prime }(s), h(s) {}^{\mathrm{CF}}D^{ \gamma}y(s) , g(s) {}^{\mathrm{CF}}D^{ \nu}y(s) \bigr)\,ds\biggr) \biggr\vert \\ &\quad \leq \bigl\vert \mu(t) \bigr\vert \bigl\vert x(t)-y(t) \bigr\vert + \bigl\vert \mu_{1}(t) \bigr\vert \bigl\vert x^{\prime}(t)-y^{\prime }(t) \bigr\vert + \bigl\vert \mu_{2}(t) \bigr\vert \bigl\vert x^{\prime\prime }(t)-y^{\prime\prime}(t) \bigr\vert \\ &\qquad {}+ \bigl\vert k_{1}(t) \bigr\vert {}^{\mathrm{CF}}D^{\beta_{1}} \bigl\vert x(t)-y(t) \bigr\vert + \bigl\vert k_{2}(t) \bigr\vert {}^{\mathrm{CF}}D^{\beta_{2}} \bigl\vert x(t)-y(t) \bigr\vert \\ &\qquad {}+ \int_{0}^{t} \bigl\vert f \bigl(s,x(s), m _{1}(s) x^{\prime}(s) ,m _{2}(s) x^{\prime \prime}(s), h(s){}^{\mathrm{CF}}D^{ \gamma}x(s) , g(s){}^{\mathrm{CF}}D^{ \nu}x(s) \bigr)\,ds \\ &\qquad {}- f \bigl(s,y(s), m _{1}(s) y^{\prime}(s) ,m _{2}(s) y^{\prime\prime}(s), h(s) {}^{\mathrm{CF}}D^{ \gamma}y(s) , g(s){}^{\mathrm{CF}}D^{ \nu}y(s) \bigr) \bigr\vert \,ds \\ &\quad \leq M_{1} \Vert x-y \Vert + M_{2} \Vert x-y \Vert + M_{3} \Vert x-y \Vert \\ &\qquad {} + \frac{ M_{4}B(\beta_{1}-1)}{ 2-\beta_{1} } \Vert x-y \Vert + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } \Vert x-y \Vert \\ &\qquad {}+ \biggl[\xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} + \xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu} \biggr] \Vert x-y \Vert \\ &\quad \leq \biggl[M_{1} + M_{2} + M_{3}+ \frac{ M_{4}B(\beta_{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } \\ &\qquad {} + \xi_{ 1} + \xi_{ 2} M_{6}+\xi_{ 3} M_{7}+ \xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} +\xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu} \biggr] \Vert x-y \Vert \end{aligned} $$

and

$$\begin{aligned} &\bigl\vert R^{\prime}x(t)-R^{\prime}y(t) \bigr\vert \\ &\quad \leq \bigl\vert \mu^{\prime}(t) \bigr\vert \bigl\vert x(t)-y (t) \bigr\vert + \bigl\vert \mu(t)+\mu_{1}^{\prime}(t) \bigr\vert \bigl\vert x^{\prime }(t)-y^{\prime}(t) \bigr\vert \\ &\qquad {} + \bigl\vert \mu_{1}(t)+ \mu^{\prime}_{2}(t) \bigr\vert \bigl\vert x^{\prime\prime}(t)-y^{\prime\prime}(t) \bigr\vert + \bigl\vert \mu_{2}(t) \bigr\vert \bigl\vert x^{\prime\prime\prime }(t)-y^{\prime\prime\prime}(t) \bigr\vert \\ &\qquad {} + \biggl\vert \frac{1-\beta _{1}}{2-\beta_{1}} k_{1} (t)+k_{1}^{\prime}(t) \biggr\vert {}^{\mathrm{CF}}D^{\beta_{1}} \bigl\vert x (t)-y (t) \bigr\vert + \frac{ \vert k_{1} (t)B(\beta_{1}-1) \vert }{2-\beta_{1}} \bigl\vert x^{\prime\prime }(t)-y^{\prime\prime}(t) \bigr\vert \\ &\qquad {}+ \biggl\vert \frac{2-\beta_{2}}{3-\beta_{2}} k_{2}(t)+k_{2}^{\prime}(t) \biggr\vert {}^{\mathrm{CF}}D^{\beta_{2}} \bigl\vert x (t)-y (t) \bigr\vert +\frac{ \vert k_{2}^{\prime}(t)B(\beta_{2}-2) \vert }{3-\beta_{2}} \bigl\vert x^{\prime\prime\prime}(t)-y^{\prime\prime\prime}(t) \bigr\vert \\ &\qquad {}+ \bigl\vert f \bigl(t,x(t), m _{1}(t) x^{\prime}(t) ,m _{2}(t) x^{\prime\prime}(t), h(t){}^{\mathrm{CF}}D^{ \gamma}x(t) , g(t){}^{\mathrm{CF}}D^{ \nu}x(t) \bigr) \\ &\qquad {}- f \bigl(t,y(t), m _{1}(t) y^{\prime}(t) ,m _{2}(t) y^{\prime\prime}(t), h(t){}^{\mathrm{CF}}D^{ \gamma}y(t) , g(t){}^{\mathrm{CF}}D^{ \nu}y(t) \bigr) \bigl\vert . \end{aligned} $$

Hence, we get

$$\begin{aligned} &\bigl\vert R^{\prime}x(t)-R^{\prime}y(t) \bigr\vert \\ &\quad \leq \biggl(N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3}+B( \beta_{1}-1)\biggl[ \frac{ \vert 1-\beta_{1} \vert M_{4} }{(2-\beta_{1})^{2}} +\frac{ N_{4} +M_{4}}{ 2-\beta_{1} } \biggr] \\ &\qquad {}+B(\beta_{2}-2)\biggl[\frac{ \vert 2-\beta_{2} \vert M_{5} }{(3-\beta _{2})^{2}} +\frac{ M_{5}+ N_{5} }{ 3-\beta_{2} } \biggr] + \xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}\\ &\qquad {}+\xi_{ 4} \frac{M_{ 8}B(\gamma-1)}{ 2-\l\gamma} + \xi_{ 5} \frac{ M_{9}B(\nu-1)}{ 3-\nu} \biggr) \Vert x-y \Vert . \end{aligned} $$

On the other hand, we have

$$\begin{aligned} \bigl\vert Fx(t)-Fy(t) \bigr\vert &\leq\frac{3}{2B(\alpha)} \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta_{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } \\ &\quad {}+ \xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} + \xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu} \biggr] \Vert x-y \Vert \\ & = \Delta_{1} \Vert x-y \Vert \end{aligned} $$

and

$$\begin{aligned} F^{\prime}x(t)-F^{\prime}y(t)&=\biggl[ \frac{1-\alpha}{B(\alpha)} +\frac{ \alpha }{B(\alpha)} t\biggr] \int_{0}^{t}\bigl(Rx(s)-Ry(s)\bigr)\,ds- \frac{ \alpha}{B(\alpha)} \int _{0}^{t} s\bigl(Rx(s)-Ry(s)\bigr)\,ds \\ &\quad {}-\frac{ (1-\alpha)}{2B(\alpha)} \int_{0}^{1} \bigl(Rx(s)-Ry(s)\bigr)\,ds- \frac{ \alpha t}{B(\alpha)} \int_{0}^{1} \bigl(Rx(s)-Ry(s)\bigr)\,ds\\ &\quad {}+ \frac{ \alpha}{2B(\alpha)} \int _{0}^{1} s\bigl(Rx(s)-Ry(s)\bigr)\,ds \\ & {} \leq\frac{3}{2}\biggl[ \frac{3+4\alpha}{2B(\alpha)} \biggr] \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta_{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta _{2} } \\ &\quad {}+ \xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} + \xi_{ 5}\frac{ M_{9} B(\nu-2)}{ 3-\nu} \biggr] \Vert x-y \Vert \\ & = \Delta_{2} \Vert x-y \Vert \end{aligned} $$

and so \(|F^{\prime}x(t)-F^{\prime}y(t)|\leq \Delta_{2} \Vert x-y \Vert\). Also, we have

$$\begin{aligned} \bigl\vert F^{\prime\prime}x(t)-F^{\prime\prime}y(t) \bigr\vert &\leq \frac{ \alpha}{B(\alpha)} \int_{0}^{t} \bigl\vert Rx(s)-Ry(s) \bigr\vert \,ds+\frac{1-\alpha}{B(\alpha)} \bigl\vert Rx(t)-Ry(t) \bigr\vert \\ &\quad {}+ \frac{ \alpha}{B(\alpha)} \int_{0}^{1} \bigl\vert Rx(s)-Ry(s) \bigr\vert \,ds\\ &\leq \frac{1+\alpha}{B(\alpha)} \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta _{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } \\ &\quad {}+ \xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} + \xi_{ 5}\frac{ M_{9}B(\nu-2)}{ 3-\nu} \biggr]\\ & =\Delta_{3} \Vert x-y \Vert \end{aligned} $$

and

$$\begin{aligned} &\bigl\vert F^{\prime\prime\prime}x(t)-F^{\prime\prime\prime}y(t) \bigr\vert \\ &\quad =\frac{ \alpha}{B(\alpha)} \bigl\vert R x(t)-Ry(t) \bigr\vert + \frac{ 1-\alpha}{B(\alpha)} \bigl\vert R^{\prime}x(t)- R^{\prime}y(t) \bigr\vert \\ &\quad \leq \biggl(\frac{ \alpha}{B(\alpha)} \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta _{1}-1)}{ 2-\beta_{1} } + \frac{ M_{5}B(\beta_{2}-2)}{ 3-\beta_{2} } + \xi_{ 1} + \xi_{ 2} M_{6}+\xi_{ 3} M_{7} \\ &\qquad {}+\xi_{ 4} \frac{ M_{8}B(\gamma-1)}{ 2-\gamma} +\xi_{ 5} \frac{ M_{9}B(\nu -2)}{ 3-\nu} \biggr] +\frac{ 1-\alpha}{B(\alpha)}\biggl[N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3} \\ &\qquad {}+B(\beta_{1}-1)\biggl[ \frac{ \vert 1-\beta_{1} \vert M_{4} }{(2-\beta _{1})^{2}} +\frac{ N_{4} +M_{4}}{ 2-\beta_{1} } \biggr] +B(\beta_{2}-2)\biggl[\frac{ \vert 2-\beta_{2} \vert M_{5} }{(3-\beta_{2})^{2}} +\frac{ M_{5}+ N_{5} }{ 3-\beta _{2} } \biggr] \\ &\qquad {}+ \xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+\xi_{ 4} \frac{M_{ 8}B(\gamma -1)}{ 2-\l\gamma} + \xi_{ 5} \frac{ M_{9}B(\nu-1)}{ 3-\nu} \biggr]\biggr) \Vert x-y \Vert \\ & \quad = \Delta_{4} \Vert x-y \Vert . \end{aligned} $$

Thus, \(\Vert Fx-Fy \Vert \leq\Delta \Vert x-y \Vert\) for all \(x,y\in C^{3}_{\mathbb{R}}[0,1]\). Put \(\varphi(t)=2t\) and \(\phi(t)=t\) for all t. Now by using Theorem 1.2, F has a unique fixed point which is the unique solution for the problem (1). □

Lemma 2.6

Let \(\alpha\in(0,1)\) and \(y\in H^{1}(0,1)\). Then the fractional differential equation \({}^{\mathrm{CF}}D^{\alpha^{(2)}} x(t)=y(t)\) with boundary conditions \(x(0)=0\), \(x^{\prime}(1)+ x^{\prime}(0)=0\) and \(x^{\prime\prime}(0) =0\) has the unique solution \(x(t)=\int_{0}^{1} G(t,s)y(s)\,ds\), where \(G(t,s)=\frac{- (1-\alpha)t}{(2-\alpha)B(\alpha) } +\frac{- \alpha t}{(2-\alpha)B(\alpha) } (t-s)\) whenever \(0< t\leq s<1\) and \(G(t,s)=\frac{1-\alpha}{B(\alpha)}(t-s) + \frac{\alpha}{2B(\alpha) }(t-s)^{2} -\frac{ (1-\alpha) t}{B(\alpha)(2-\alpha)} -\frac{\alpha t}{B(\alpha)(2-\alpha) } (t-s)\) whenever \(0< s\leq t<1\).

Proof

By using Lemma 2.3, we get \(x(t)=\frac{1-\alpha}{B(\alpha)}J^{2 }y(t)+\frac{ \alpha}{B(\alpha)} J^{3}y(t) + x^{\prime}(0)t+\frac{\alpha }{ 1-\alpha} x^{\prime}(0)t\). Hence, \(x^{\prime}(t)= \frac{1-\alpha}{B(\alpha)}J^{1}y(t)+\frac{ \alpha }{B(\alpha)} J^{2 }y(t) + \frac{1}{ 1-\alpha} x^{\prime}(0)\). By using the boundary conditions \(x^{\prime}(1)+ x^{\prime}(0)=0 \) and \(x^{\prime}(1)= \frac{1-\alpha}{B(\alpha)}J^{1}y(1)+\frac{ \alpha }{B(\alpha)} J^{2 }y(1) + \frac{1}{ 1-\alpha} x^{\prime}(0) \), we obtain \(x(t)=\frac{1-\alpha}{B(\alpha)}J^{2 }y(t)+\frac{ \alpha }{B(\alpha)} J^{3}y(t)-\frac{ (1-\alpha) t}{(2-\alpha)B(\alpha) }J^{1}y(1)-\frac{\alpha t}{(2-\alpha)B(\alpha) }J^{2 }y(1)\). Thus, \(x(t)=\frac{1-\alpha}{B(\alpha)} \int_{0}^{t}y(s)(t-s) \,ds+\frac{ \alpha}{2B(\alpha)}\int_{0}^{t}y(s)(t-s)^{2}\,ds -\frac{(1-\alpha)t}{(2-\alpha )B(\alpha)} \int_{0}^{1}y(s) \,ds-\frac{\alpha t}{(2-\alpha)B(\alpha) }\int _{0}^{1}y(s)(t-s) \,ds =\int_{0}^{1} G(t,s)y(s)\,ds\). Note that \(( {}^{\mathrm{CF}} D^{\alpha})^{(2)}x(t)=0\) if and only if \(x(t)=0\). This implies that the given map \(x(t)\) is a unique solution. □

Note that \(|G(t,s)|\leq|\frac{1-\alpha}{B(\alpha)}|+ |\frac{\alpha }{2B(\alpha) }| +|\frac{-\alpha t}{ B(\alpha)} |+|\frac{-(1-\alpha) t}{ B(\alpha)}|<\frac{2}{B(\alpha)}\), for \(t \in[0,1]\). Let \(\alpha,\beta_{1},\beta_{2},\gamma,\nu\in(0,1) \). Now, we investigate the DCF fractional integro-differential problem

$$ \begin{aligned}[b] \bigl( {}^{\mathrm{CF}}D^{\alpha} \bigr)^{(2)}x(t)&=\mu(t) x(t)+\mu_{1}(t) x^{\prime }(t)+ \mu_{2} (t)x^{\prime\prime}(t)\\ &\quad {}+\lambda_{1} k_{1}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{1}}\bigr)^{(1)}x(t)+ \lambda_{2} k_{2}(t) \bigl( {}^{\mathrm{CF}}D^{\beta _{2} } \bigr)^{(2)}x(t) \\ &\quad{}+ \int_{0}^{t} f \bigl(s,x(s), m _{1}(s) x^{\prime}(s) ,m _{2}(s) x^{\prime \prime}(s),\\ &\quad {} h(s) \bigl( {}^{\mathrm{CF}}D^{ \gamma}\bigr)^{(1)}x(s) , g(s) \bigl( {}^{\mathrm{CF}}D^{ \nu}\bigr)^{(2)}x(s) \bigr)\,ds \end{aligned} $$
(2)

with boundary conditions \(x(0)=0\), \(x^{\prime}(1)+ x^{\prime}(0)=0\) and \(x^{\prime\prime}(0)=0\).

Theorem 2.7

Let \(\xi_{1}\), \(\xi_{2}\), \(\xi_{3}\), \(\xi_{4}\), and \(\xi_{5}\) be nonnegative real numbers, \(f :[0,1]\times\Bbb {R}^{5}\to\Bbb{R}\) an integrable function such that

$$\begin{aligned} &\bigl\vert f (t,x,y,z,v,w )-f \bigl(t,x^{\prime},y^{\prime} ,z^{\prime},v^{\prime},w^{\prime} \bigr) \bigr\vert \\ &\quad \leq \xi_{ 1} \bigl\vert x -x^{\prime} \bigr\vert + \xi_{ 2} \bigl\vert y -y^{\prime} \bigr\vert + \xi_{ 3} \bigl\vert z -z^{\prime} \bigr\vert + \xi_{ 4} \bigl\vert v -v^{\prime} \bigr\vert + \xi_{ 5} \bigl\vert v -v^{\prime} \bigr\vert \end{aligned} $$

for all real numbers x, y, z, v, w, \(x^{\prime}\), \(y^{\prime}\), \(z^{\prime}\), \(v^{\prime}\), \(w^{\prime}\) and \(t \in I\). If \(\Delta<\frac{1}{2}\), then the problem (2) has a unique solution, where \(\Delta:=\max\lbrace \Delta_{1},\Delta_{2},\Delta_{3},\Delta_{4}\rbrace\), \(\Delta_{1}=\frac{2}{(2-\alpha)B(\alpha)} [M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}} + \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5} B(\beta _{2})}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac { M_{8} B(\gamma)}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9} B(\nu )}{(1-\nu)^{3}} ] \), \(\Delta_{2}= \frac{3+\alpha }{ B(\alpha)(2-\alpha)} [M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}} + \frac{( \beta_{2}^{2}- \beta _{2}+1)M_{5} B(\beta_{2})}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8} B(\gamma)}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu ^{2}- \nu+1)M_{9} B(\nu)}{(1-\nu)^{3}} ] \), \(\Delta_{3}= \frac{2+\alpha }{B(\alpha)(2-\alpha)} [M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}} + \frac{( \beta_{2}^{2}- \beta _{2}+1)M_{5} B(\beta_{2})}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8} B(\gamma)}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu ^{2}- \nu+1)M_{9} B(\nu)}{(1-\nu)^{3}} ] \) and \(\Delta_{4}=\frac{\alpha}{B(\alpha)}[M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}} + \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5} B(\beta _{2})}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac { M_{8} B(\gamma)}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9} B(\nu )}{(1-\nu)^{3}} ]+\frac{1-\alpha}{B(\alpha )}[N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3}+M_{4}B(\beta_{1}) \frac{ ( \beta_{1}^{2}- \beta _{1}+1)}{(1-\beta_{1})^{3}} +\frac{ B(\beta_{1}) N_{4}}{(1-\beta_{1})^{2}} +M_{5}B(\beta_{2})\frac{ ( 2\beta_{2}^{2}-2 \beta_{2}+1)}{(1-\beta_{2})^{4}} +N_{5}B(\beta_{2}) \frac{ ( \beta_{2}^{2}- \beta_{2}+1)}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\frac{\xi_{ 4} M_{ 8}B(\gamma)}{(1-\l \gamma)^{2}} +\frac{(\nu^{2}- \nu+1)M_{9}B(\nu)}{(1-\nu)^{3}}]\).

Proof

Consider the Banach space \(C^{3}_{\mathbb{R}}[0,1]\) equipped with the norm \(\Vert x \Vert= \max_{t\in I}|x(t)| + \max_{t\in I}| x^{\prime}(t) | + \max_{t\in I}| x^{\prime\prime}(t) |+ \max_{t\in I}| x^{\prime\prime\prime}(t) |\). Define the map \(F: C^{3}_{\mathbb {R}}[0,1]\to C^{3}_{\mathbb{R}}[0,1]\) by

$$\begin{aligned} Fx(t) &= \int_{0}^{1} G(t,s)R(s)\,ds \\ &= \frac{1-\alpha}{B(\alpha)} \int _{0}^{t}R(s) (t-s) \,ds+ \frac{\alpha}{2B(\alpha) } \int_{0}^{t}R(s) (t-s)^{2}\,ds \\ &\quad {}-\frac{ (1-\alpha) t}{B(\alpha)(2-\alpha)} \int_{0}^{1}R(s) \,ds-\frac {\alpha t}{B(\alpha)(2-\alpha) } \int_{0}^{1}R(s) (t-s) \,ds, \end{aligned} $$

where

$$\begin{aligned} (Rx) (t)&=\mu(t) x(t)+\mu_{1}(t) x^{\prime}(t)+ \mu_{2} (t)x^{\prime\prime }(t)\\ &\quad {}+\lambda_{1} k_{1}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{1}}\bigr)^{(1)}x(t)+\lambda _{2} k_{2}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{2} } \bigr)^{(2)}x(t) \\ &\quad {}+ \int_{0}^{t} f \bigl(s,x(s), m _{1}(s) x^{\prime}(s) ,m _{2}(s) x^{\prime\prime }(s), h(s) \bigl( {}^{\mathrm{CF}}D^{ \gamma}\bigr)^{(1)}x(s) , g(s) \bigl( {}^{\mathrm{CF}}D^{ \nu}\bigr)^{(2)}x(s)\bigr)\,ds \end{aligned} $$

and

$$\begin{aligned} \bigl(R^{\prime}x\bigr) (t)&=\mu(t) x ^{\prime}(t)+ \mu^{\prime}(t) x (t)+\mu _{1}^{\prime}(t) x^{\prime}(t)+\mu_{1} x^{\prime\prime}(t) \\ &\quad {}+\mu_{2}^{\prime }(t) x^{\prime\prime}(t)+\mu_{2} (t) x^{\prime\prime\prime}(t) + k_{1}^{\prime}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{1}} \bigr)^{(1)}x(t)\\ &\quad {} + k_{1}(t)B(\beta_{1})\biggl[\biggl( \frac{ -\beta_{1}}{1-\beta_{1}}\biggr)^{2} {}^{\mathrm{CF}}D^{\beta_{1}}x(t) - \frac{\beta_{1}}{(1-\beta_{1})^{2}}x^{\prime}(t) +\frac {1}{ 1-\beta_{1} }x^{\prime\prime}(t) \biggr] \\ &\quad {}+ k_{2}(t)B(\beta_{2})\biggl[\biggl( \frac{ -\beta_{2}}{1-\beta_{2}}\biggr)^{3} {}^{\mathrm{CF}}D^{\beta_{2}}x(t)+ \frac{\beta^{2} _{2}}{(1-\beta_{2})^{3}}x^{\prime}(t)\\ &\quad {} -\frac{\beta_{2}}{( 1-\beta_{2})^{2} }x^{\prime\prime}(t)+ \frac{x^{\prime \prime\prime}(t)}{ 1-\beta_{2} }\biggr] + k_{2}^{\prime}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{2}} \bigr)^{(2)}x(t)\\ &\quad {} +f \bigl(t,x(t), m _{1}(t) x^{\prime}(t) ,m _{2}(t) x^{\prime\prime}(t), h(t) \bigl( {}^{\mathrm{CF}}D^{ \gamma} \bigr)^{(1)}x(t) , g(t) \bigl( {}^{\mathrm{CF}}D^{ \nu} \bigr)^{(2)}x(t)\bigr). \end{aligned} $$

By using Lemma 2.6, \(x_{0}\) is a solution for the problem (2) if and only if \(x_{0}\) is a fixed point of the operator F. Note that

$$\begin{aligned} &(Rx) (t)-(Ry) (t) \\ &\quad \leq\biggl[\mu(t) x(t)+\mu_{1} (t) x^{\prime}(t)+ \mu_{2}(t) x^{\prime\prime }(t)+\lambda_{1} k_{1}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{1}}\bigr)^{(1)}x(t)+ k_{2}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{2}}\bigr)^{(2)}x(t) \\ &\qquad {} + \int_{0}^{t} f \bigl(s,x(s), m _{1}(t) x^{\prime}(s) ,m _{2}(s) x^{\prime\prime }(s), h(s) \bigl( {}^{\mathrm{CF}}D^{ \gamma}\bigr)^{(1)}x(s) , g(s) \bigl( {}^{\mathrm{CF}}D^{ \nu}\bigr)^{(2)}x(s) \bigr)\,ds\biggr] \\ &\qquad {} - \biggl[\mu(t) y(t)+\mu_{1} (t) y^{\prime}(t)+ \mu_{2}(t) y^{\prime\prime}(t)+ k_{1}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{1}}\bigr)^{(1)}y(t)+ k_{2}(t) \bigl( {}^{\mathrm{CF}}D^{\beta_{2}}\bigr)^{(2)}y(t) \\ &\qquad {} + \int_{0}^{t} f \bigl(s,y(s), m _{1}(t) y^{\prime}(s) ,m _{2}(s) y^{\prime\prime }(s), h(s) \bigl( {}^{\mathrm{CF}}D^{ \gamma}\bigr)^{(1)}y(s) , g(s) \bigl( {}^{\mathrm{CF}}D^{ \nu}\bigr)^{(2)}y(s) \bigr)\,ds\biggr] \\ &\quad \leq \bigl\vert \mu(t) \bigr\vert \bigl\vert x(t)-y(t) \bigr\vert + \bigl\vert \mu_{1}(t) \bigr\vert \bigl\vert x^{\prime}(t)-y^{\prime }(t) \bigr\vert + \bigl\vert \mu_{2}(t) \bigr\vert \bigl\vert x^{\prime\prime}(t)-y^{\prime\prime}(t) \bigr\vert \\ &\qquad {} + \bigl\vert k_{1}(t) \bigr\vert \bigl( {}^{\mathrm{CF}}D^{\beta_{1}}\bigr)^{(1)} \bigl\vert x(t)-y(t) \bigr\vert + \bigl\vert k_{2}(t) \bigr\vert \bigl( {}^{\mathrm{CF}}D^{\beta_{2}}\bigr)^{(2)} \bigl\vert x(t)-y(t) \bigr\vert \\ &\qquad {} + \int_{0}^{t} \vert f \bigl(s,x(s), m _{1}(t) x^{\prime}(s) ,m _{2}(s) x^{\prime \prime}(s), h(s) \bigl( {}^{\mathrm{CF}}D^{ \gamma}\bigr)^{(1)}x(s) , g(s) \bigl( {}^{\mathrm{CF}}D^{ \nu}\bigr)^{(2)}x(s) \bigr)\,ds \\ &\qquad {} - f \bigl(s,y(s), m _{1}(t) y^{\prime}(s) ,m _{2}(s) y^{\prime\prime}(s), h(s) \bigl( {}^{\mathrm{CF}}D^{ \gamma} \bigr)^{(1)}y(s) , g(s) \bigl( {}^{\mathrm{CF}}D^{ \nu } \bigr)^{(2)}y(s) \bigr) \vert \,ds \\ & \quad \leq M_{1} \Vert x-y \Vert + M_{2} \Vert x-y \Vert + M_{3} \Vert x-y \Vert \\ &\qquad {} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}} \Vert x-y \Vert + \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5} B(\beta _{2})}{(1-\beta_{2})^{3}} \Vert x-y \Vert \\ &\qquad {} + \biggl[\xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7} +\xi_{ 4} \frac{ M_{8} B(\gamma )}{(1-\gamma)^{2}} + \xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9} B(\nu)}{(1-\nu)^{3}} \biggr] \Vert x-y \Vert \\ &\quad \leq \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta _{1})}{(1-\beta_{1})^{2}}+ \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5} B(\beta_{2})}{(1-\beta_{2})^{3}} \\ &\qquad {} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8} B(\gamma)}{(1-\gamma )^{2}} +\xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9} B(\nu)}{(1-\nu)^{3}} \biggr] \Vert x-y \Vert \end{aligned} $$

and

$$\begin{aligned} &\bigl\vert R^{\prime}x(t)-R^{\prime}y(t) \bigr\vert \\ &\quad \leq \biggl(N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3}+M_{4}B( \beta_{1}) \frac{ ( \beta_{1}^{2}- \beta _{1}+1)}{(1-\beta_{1})^{3}} +\frac{ B(\beta_{1}) N_{4}}{(1-\beta_{1})^{2}} \\ &\qquad{} +M_{5}B(\beta_{2})\frac{ ( 2\beta_{2}^{2}-2 \beta_{2}+1)}{(1-\beta_{2})^{4}} +N_{5}B(\beta_{2}) \frac{ ( \beta_{2}^{2}- \beta_{2}+1)}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7} \\ &\qquad{} + \frac{\xi_{ 4} M_{ 8}B(\gamma)}{(1-\l \gamma)^{2}}+\frac{(\nu^{2}- \nu+1)M_{9}B(\nu)}{(1-\nu)^{3}} \biggr) \Vert x-y \Vert . \end{aligned} $$

Thus,

$$\begin{aligned} \bigl\vert Fx(t)-Fy(t) \bigr\vert &\leq\frac{2}{(2-\alpha)B(\alpha)} \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}} + \frac{( \beta _{2}^{2}- \beta_{2}+1)M_{5} B(\beta_{2})}{(1-\beta_{2})^{3}} \\ &\quad{} + \xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8} B(\gamma )}{(1-\gamma)^{2}} + \xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9} B(\nu)}{(1-\nu)^{3}} \biggr] \Vert x-y \Vert \\ &= \Delta_{1} \Vert x-y \Vert \end{aligned} $$

and

$$\begin{aligned} \bigl\vert F^{\prime}x(t)-F^{\prime}y(t) \bigr\vert &\leq\biggl[ \frac {3+\alpha }{ B(\alpha)(2-\alpha)} \biggr] \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}}+ \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5} B(\beta _{2})}{(1-\beta_{2})^{3}} \\ &\quad{} + \xi_{ 1} +\xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8} B(\gamma )}{(1-\gamma)^{2}} + \xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9} B(\nu)}{(1-\nu)^{3}} \biggr] \Vert x-y \Vert \\ &= \Delta_{2} \Vert x-y \Vert . \end{aligned} $$

Also, we have

$$\begin{aligned} \bigl\vert F^{\prime\prime}x(t)-F^{\prime\prime}y(t) \bigr\vert & \leq \frac{2+\alpha }{B(\alpha)(2-\alpha)} \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4}B(\beta_{1})}{(1-\beta_{1})^{2}} \\ &\quad{} + \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5}B(\beta_{2})}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}\\ &\quad {}+\xi_{ 4} \frac{ M_{8}B(\gamma)}{(1-\gamma )^{2}} +\xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9}B(\nu)}{(1-\nu)^{3}} \biggr]\\ &= \Delta_{3} \Vert x-y \Vert \end{aligned} $$

and

$$\begin{aligned} &\bigl\vert F^{\prime\prime\prime}x(t)-F^{\prime\prime\prime}y(t) \bigr\vert \\ &\quad \leq \frac{\alpha}{B(\alpha)} \bigl\vert R x(t)-Ry(t) \bigr\vert + \frac{1-\alpha}{B(\alpha)} \bigl\vert R^{\prime}x(t)- R^{\prime }y(t) \bigr\vert \\ &\quad \leq\biggl( \frac{\alpha}{B(\alpha)} \biggl[M_{1} + M_{2} + M_{3} + \frac{ M_{4} B(\beta_{1})}{(1-\beta_{1})^{2}} + \frac{( \beta_{2}^{2}- \beta _{2}+1)M_{5} B(\beta_{2})}{(1-\beta_{2})^{3}} \\ &\qquad {}+ \xi_{ 1} + \xi_{ 2} M_{6}+\xi_{ 3} M_{7}+ \xi_{ 4} \frac{ M_{8} B(\gamma)}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu ^{2}- \nu+1)M_{9} B(\nu)}{(1-\nu)^{3}} \biggr] \\ &\qquad{} + \frac{1-\alpha}{B(\alpha)}\biggl[N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3}+M_{4}B( \beta_{1}) \frac { ( \beta_{1}^{2}- \beta_{1}+1)}{(1-\beta_{1})^{3}} \\ &\qquad{} +\frac{ B(\beta_{1}) N_{4}}{(1-\beta_{1})^{2}}+M_{5}B(\beta_{2})\frac{ ( 2\beta_{2}^{2}-2 \beta_{2}+1)}{(1-\beta_{2})^{4}} +N_{5}B(\beta_{2}) \frac{ ( \beta_{2}^{2}- \beta_{2}+1)}{(1-\beta_{2})^{3}} \\ &\qquad{} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+ \frac{\xi_{ 4} M_{ 8}B(\gamma)}{(1-\l \gamma)^{2}}+\frac{(\nu^{2}- \nu+1)M_{9}B(\nu)}{(1-\nu)^{3}} \biggr]\biggr) \Vert x-y \Vert \\ &\quad = \Delta_{4} \Vert x-y \Vert . \end{aligned}$$

Hence, \(\Vert Fx-Fy \Vert \leq\Delta \Vert x-y \Vert\) for all \(x,y\in C^{3}_{\mathbb{R}}[0,1]\). Put \(\varphi(t)=2t\) and \(\phi(t)=t\) for all t. By using Theorem 1.2, F has a unique fixed point, which is the desired solution for the problem. □

Here, we provide three examples to illustrate our main results. Consider the bounded continuous functions \(\mu(t)=\frac{1}{100}\sin (t)\), \(\mu_{1}(t)=\frac{3t-1}{20t+162}\), \(\mu_{2}(t)= \frac {1}{100}e^{-6t}\), \(k_{1}(t)=\frac{1}{300}t^{3}+\frac{1}{100}t+\frac {1}{50}\), \(k_{2}(t)= \frac{1}{800}\cos(t)\), \(m_{1}(t)= e^{2t}\), \(m_{2}(t)=\frac{Ln(t+2)}{20}\), \(h(t)=0\) and \(g(t)=\frac{1}{t-900}\) for all \(t\in I=[0,1]\). Note that \(M_{1}=\sup_{t\in I}|\mu(t)|=\frac {1}{100}\), \(M_{2}=\sup_{t\in I}|\mu_{1}(t)|=\frac{1}{91}\), \(M_{3}=\sup_{t\in I}|\mu_{2}(t)|=\frac{1}{100e^{6}}\), \(M_{4}=\sup_{t\in I}|k_{1}(t)|=\frac{1}{30}\), \(M_{5}=\sup_{t\in I}|k_{2}(t)|=\frac{1}{800}\), \(M_{6}=\sup_{t\in I}|m_{1}(t)| =e^{2}\), \(M_{7}=\sup_{t\in I}|m_{2}(t)|=\frac {Ln(3)}{1200}\), \(M_{8}=\sup_{t\in I}|h(t)| =0\) and \(M_{9}=\sup_{t\in I}|g (t)| = \frac{1}{900 }\). Also, \(N_{1}= \sup_{t\in I}|\mu^{\prime }(t)|=\frac{1}{100}\), \(N_{2}=\sup_{t\in I}|\mu_{1}^{\prime}(t)|=\frac {506}{(162)^{2}}\), \(N_{3}=\sup_{t\in I}|\mu_{2}^{\prime}(t)|=\frac{ 6}{100e^{ 6 }}\), \(N_{4}=\sup_{t\in I}|k_{1}^{\prime}(t)|= \frac{1}{50}\) and \(N_{5}=\sup_{t\in I}|k_{2}^{\prime}(t)|= \frac{1}{800}\). Also, consider the function \(B(\alpha)=1\) for \(\alpha\in(0,1)\).

Example 2.1

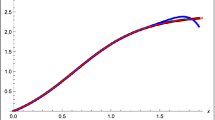
Let \(\alpha\in(0,1)\). By using Lemma 2.4, the fractional differential equation \({}^{\mathrm{CF}}D^{2+\alpha}x_{1}(t)=t\) with boundary conditions \(x_{1}(0)=0\), \(x_{1}^{\prime}(1)+ x_{1}^{\prime}(0)=0\) and \(x_{1}^{\prime\prime}(0) =0\) has the unique solution \(x_{1}(t) \). Also by using Lemma 2.6, the fractional differential equation \(({}^{\mathrm{CF}}D^{ \alpha})^{(2)}x_{2}(t)=t\) with boundary conditions \(x_{2}(0)=0\), \(x_{2}^{\prime}(1)+ x_{2}^{\prime}(0)=0\) and \(x_{2}^{\prime\prime }(0) =0\) has the unique solution \(x_{2}(t) \). For \(\alpha=\frac {1}{100}\), \(\alpha=\frac{1}{10}\), \(\alpha=\frac{1}{5}\), \(\alpha=\frac {1}{2}\), \(\alpha=\frac{4}{5}\) and \(\alpha=\frac{99}{100}\) we compare the solutions \(x_{1}(t)\), \(x_{2}(t)\) and \(X(t)= x_{1}(t)-x_{2}(t)\) in Fig. 1.

Figure 1
figure 1

The solutions of the problem with \(\alpha=\frac{1}{100}\), \(\alpha=\frac{1}{10}\), \(\alpha=\frac{1}{5}\), \(\alpha=\frac{1}{2}\), \(\alpha=\frac{4}{5}\) and \(\alpha=\frac{99}{100}\)

Full size image

Example 2.2

Consider the CFD fractional integro-differential problem

$$ \begin{aligned}[b] {}^{\mathrm{CF}}D^{ \frac{12}{5 }}x(t)&= \frac{\sin(t)}{100}x(t)+\frac {3t-1}{20t+162} x^{\prime}(t)+ \frac{e^{-6t}}{100} x^{\prime\prime }(t)\\ &\quad {}+\biggl( \frac{t^{3}+3t+6}{300} \biggr) {}^{\mathrm{CF}}D^{\frac{3}{2}}x(t) + \frac{\cos(t)}{800} {}^{\mathrm{CF}}D^{\frac{5}{2}}x(t) \\ &\quad{}+ \int_{0}^{t} f \biggl(s,x(s),e^{2t} x^{\prime}(s),\frac{Ln(t+2)}{20} x^{\prime\prime}(s), 0 , \frac{1}{t-900} {}^{\mathrm{CF}}D^{ \frac {8}{3}}x(s) \biggr)\,ds \end{aligned} $$
(3)

with boundary conditions \(x(0)=0\), \(x^{\prime}(1)+ x^{\prime}(0)=0\) and \(x^{\prime\prime}(0) =0\), where \(1<\beta_{1}=\frac{3}{2}< 2<\beta _{2}=\frac{5}{2}<3 \) and \(1<\gamma=\frac{4}{3 }< 2<\nu=\frac{8}{3}<3\). Put \(f(t,x,y,z,v,w)=\frac{2}{91}t+\frac{3}{604 }x+\frac{1}{200}y+\frac {1}{80 }z+\frac{1}{e^{18}}w+2v \). Note that \(\Delta_{1}= \frac{3}{2} [M_{1} + M_{2} + M_{3} + \frac{ M_{4}}{ 2-\beta_{1} } + \frac{ M_{5}}{ 3-\beta_{2} } + \xi_{ 1} + \xi_{ 2} M_{6}+ \xi_{ 3} M_{7}+ \xi _{ 4} \frac{ M_{8}}{ 2-\gamma } +\xi_{ 5}\frac{ M_{9}}{ 3-\nu} ]=0.02 \), \(\Delta_{2}=\frac{3}{2}[ \frac{3+4\alpha}{2} ] [M_{1} + M_{2} + M_{3} + \frac { M_{4}}{ 2-\beta_{1} } + \frac{ M_{5}}{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}}{ 2-\gamma } +\xi_{ 5}\frac{ M_{9}}{ 3-\nu} ]=0.46 \), \(\Delta_{3}= (1+ \alpha) [M_{1} + M_{2} + M_{3} + \frac{ M_{4}}{ 2-\beta_{1} } + \frac{ M_{5}}{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}}{ 2-\gamma } +\xi_{ 5}\frac{ M_{9}}{ 3-\nu} ] =0.3 2 \) and \(\Delta_{4}= \alpha[ M_{1} + M_{2} + M_{3} + \frac{ M_{4}}{ 2-\beta_{1} } + \frac{ M_{5}}{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7} +\xi _{ 4} \frac{ M_{8}}{ 2-\gamma } +\xi_{ 5}\frac{ M_{9}}{ 3-\nu} ] +(1-\alpha)[N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3}+ \frac{ |1-\beta_{1}|M_{4} }{(2-\beta _{1})^{2}} +\frac{ N_{4} +M_{4}}{ 2-\beta_{1} } +\frac{ |2-\beta_{2}|M_{5} }{(3-\beta _{2})^{2}} +\frac{ M_{5}+ N_{5} }{ 3-\beta_{2} } + \xi_{ 1} +\xi_{ 2} M_{6}+\xi _{ 3} M_{7}+\xi_{ 4} \frac{M_{ 8}}{ 2-\l\gamma} +\xi_{ 5} \frac{ M_{6}}{ 3-\nu} ]=0.166 \). By using Theorem 2.5, the problem (3) has a unique solution.

Example 2.3

Consider the DCF fractional integro-differential problem

$$ \begin{aligned}[b] &\bigl( {}^{\mathrm{CF}}D^{\frac{2}{5} }\bigr) ^{(2)}x(t)\\ &\quad =\frac{\sin (t)}{100}x(t)+\frac{3t-1}{20t+162} x^{\prime}(t)+ \frac{e^{-6t}}{100} x^{\prime\prime}(t) \\ &\qquad{}+\biggl( \frac{t^{3}+3t+6}{300} \biggr) \bigl( {}^{\mathrm{CF}}D^{\frac {1}{2}} \bigr)^{(1)}x(t)+ \frac{\cos(t)}{800} \bigl( {}^{\mathrm{CF}}D^{\frac{2}{3} } \bigr)^{(2)}x(t) \\ &\qquad {}+ \int_{0}^{t} f \biggl(s,x(s),e^{-40t} x^{\prime}(s),\frac {Ln(t+2)}{20} x^{\prime\prime}(s), 0 , \frac{1}{t-900}\bigl( {}^{\mathrm{CF}}D^{ \frac{1}{5} }\bigr)^{(2)}x(s) \biggr)\,ds, \end{aligned} $$
(4)

with boundary conditions \(x(0)=0\), \(x^{\prime}(1)+ x^{\prime}(0)=0\) and \(x^{\prime\prime}(0) =0\), where \(\alpha=\frac{2}{5}\), \(\beta_{1}=\frac {1}{2}\), \(\beta_{2}=\frac{2}{3}\), \(\gamma=\frac{1}{3 }\) and \(\nu=\frac {1}{5}\). Put \(f(t,x,y,z,v,w)=\frac{2}{91}t+\frac{3}{604 }x+\frac {1}{200}y+\frac{1}{80 }z+\frac{1}{e^{18}}w+2v \). Note that \(\Delta _{1}=\frac{2}{2-\alpha} [M_{1} + M_{2} + M_{3} + \frac{ M_{4}}{(1-\beta _{1})^{2}} + M_{5}\frac{( \beta_{2}^{2}- \beta_{2}+1)}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}}{(1-\gamma)^{2}} +\xi _{ 5}\frac{( \nu^{2}- \nu+1)M_{9}}{(1-\nu)^{3}} ]<0.391 \), \(\Delta_{2}=[ \frac {3+\alpha }{ 2-\alpha} ] [M_{1} + M_{2} + M_{3} + \frac{ M_{4}}{(1-\beta _{1})^{2}} + \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5}}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9}}{(1-\nu)^{3}}]<0.225\), \(\Delta_{3}= \frac {2+\alpha }{2-\alpha} [M_{1} + M_{2} + M_{3} + \frac{ M_{4}}{(1-\beta_{1})^{2}} + \frac{( \beta_{2}^{2}- \beta_{2}+1)M_{5}}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi_{ 4} \frac{ M_{8}}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu^{2}- \nu+1)M_{9}}{(1-\nu)^{3}} ] <0.132 \) and \(\Delta_{4}=\alpha[M_{1} + M_{2} + M_{3} + \frac{ M_{4}}{(1-\beta_{1})^{2}} + M_{5}\frac{( \beta_{2}^{2}- \beta_{2}+1)}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+\xi _{ 4} \frac{ M_{8}}{(1-\gamma)^{2}} +\xi_{ 5}\frac{( \nu^{2}- \nu +1)M_{9}}{(1-\nu)^{3}} ]+(1-\alpha)[N_{1}+M_{1}+N_{2}+M_{2}+N_{3}+M_{3}+M_{4} \frac{ ( \beta_{1}^{2}- \beta_{1}+1)}{(1-\beta_{1})^{3}} +\frac{ N_{4}}{(1-\beta_{1})^{2}} +M_{5}\frac{ ( 2\beta_{2}^{2}-2 \beta_{2}+1)}{(1-\beta_{2})^{4}} + \frac{ N_{5}( \beta _{2}^{2}- \beta_{2}+1)}{(1-\beta_{2})^{3}} + \xi_{ 1} +\xi_{ 2} M_{6}+\xi_{ 3} M_{7}+ \frac{\xi_{ 4}M_{ 8}}{(1-\l\gamma)^{2}} +\xi_{ 5}\frac{(\nu^{2}- \nu +1)M_{9}}{(1-\nu)^{3}} ] < 0.493 \). By using Theorem 2.7, the problem (4) has a unique solution.

3 Conclusion

It is important that researchers have some methods available enabling them to review some high order fractional integro-differential equations. In this manuscript, we introduce two types of new fractional derivatives entitled CFD and DCF and by using those we investigate the existence of solutions for two high order fractional integro-differential equations of such a type including the new derivatives.