1 Introduction

The fractional calculus theory has recently become an interesting topic of research for mathematicians, scientists, and engineers due to the appearance of this theory in several applications in natural science and engineering and the ability to model many systems and phenomena that have memory effects. For more resources about this theory, we suggest [1–12]. Several new fractional derivatives’ definitions have been proposed in the last decade, and the most common ones are Caputo, Riemann–Liouville, and Hadamard fractional derivatives. Therefore, fractional-order differential equations can be formulated in the form of various fractional differential operators. As a result, several generalized formulations of fractional differential operators have been introduced to effectively combine other operators to avoid the confusion when working with various existing fractional differential operators [13, 14].

Studying the fractional boundary value problems (FcBVPrs) has attracted a special interest of many mathematicians due to the various applications of fractional differential equations in several engineering and scientific fields. Some recent research studies have been conducted on proving the existence and uniqueness of FcBVPrs [15–35]. While there are some studies that have applied various methods depending on the proposed fractional formulation and the selected initial/boundary conditions, some other studies have discussed the FcBVPrs involving p-Laplacian operator such as the investigation of the turbulent flow in a porous medium (refer to [36–41]).

Both Katugampola and Almeida defined and developed new nonlocal notions of fractional derivatives, known as the generalized Caputo fractional (GCpFr) derivative (see [42, 43]). One of the main advantages of the GCpFr derivative is the ability to combine all traditional fractional derivatives, and it satisfies the semigroup property, hence, GCpFr derivative is considered a generalized form of fractional derivatives. There are a number of research studies that have been done in the form of GCpFr derivative [43–45]. However, according to the authors’ knowledge, there are no existing research studies on GCpFr involving p-Laplacian operator.

The authors in [40] proved the solutions’ existence for the following fractional differential equation:

$$ \mathfrak{D}^{\beta }{\varphi }_{p} \bigl( \mathfrak{D}^{\alpha }u ( t ) \bigr) =q \bigl( t,u ( t ) , \mathfrak{D}^{\gamma }u ( t ) \bigr) ,\quad 0\leq t\leq 1, $$

subject to the following p-Laplacian operator and integral boundary conditions:

$$ \textstyle\begin{cases} u ( 0 ) +{\epsilon }_{1}u ( 1 ) ={\lambda }_{1} \int _{0}^{1}{g ( s,u ( s ) ) \,ds}, \\ u' ( 0 ) +{\epsilon }_{2}u' ( 1 ) ={\lambda }_{2}\int _{0}^{1}{h ( s,u ( s ) ) \,ds}, \\ \mathfrak{D}^{\alpha }x ( 0 ) =0,\qquad \mathfrak{D}^{\alpha }u ( 1 ) =\zeta \mathfrak{D}^{\alpha }u ( \zeta ) ,\end{cases}$$
(1)

where q, g, and h are continuous functions. \(\mathfrak{D}^{\alpha }\), \(\mathfrak{D}^{\beta }\) are the Caputo fractional derivatives of orders α, β such that \(\alpha ,\beta \in (1,2]\). ζ, \({\epsilon }_{j}\), \({\lambda }_{j}\) (\(j=1,2\)) are nonnegative parameters.

The following is the integral boundary value problem involving a fractional p-Laplacian equation in the form of mixed fractional derivatives [39]:

$$ \textstyle\begin{cases} \mathfrak{D}_{0^{+}}^{\beta }{\varphi }_{p} ( \mathfrak{D}_{0^{+}}^{ \alpha }u ( t ) ) =q ( t,u ( t ) , \mathfrak{D}^{\gamma }u ( t ) ) ,\quad 0\leq t\leq 1, \\ u ( 0 ) =\epsilon \int _{0}^{1}{u ( s ) \,ds+\nu u(\xi )}, \\ \mathfrak{D}_{0^{+}}^{\alpha }u ( 0 ) =j\mathfrak{D}_{0^{+}}^{ \alpha }u ( \zeta ) ,\end{cases}$$
(2)

where \(q\in C ( [ 0,1 ] \times \mathbb{R} ^{2},\mathbb{R} )\) is a nonlinear function, \(\mathfrak{D}_{0^{+}}^{\beta }\) and \(\mathfrak{D}_{0^{+}}^{\alpha }\) are the Caputo fractional (CapFr) derivatives of orders α, β such that \(\alpha ,\beta \in (0,1]\), \({\varphi }_{p}\) is the p-Laplacian operator, \(p>1\), ϵ, ν, \(j\in \mathbb{R} \), \(\xi ,\zeta \in {}[ 0,1]\).

We study the following fractional differential equation as we got motivated by the above studies:

$$ \textstyle\begin{cases} \frac{d}{dt} ( {\varphi }_{p} ( {{}^{C}\mathfrak{D}}^{ \alpha ,\rho }u ( t ) ) ) =q ( t,u ( t ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( t ) )\quad (0\leq t \leq 1), \\ u ( 0 ) +\mu u ( 1 ) =\theta (u(0),u(1)), \qquad u' ( 1 ) =\nu (u(0),u(1)),\end{cases} $$
(3)

where \({{}^{C}\mathfrak{D}}^{\alpha ,\rho }\) and \({{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( t ) \), \(\alpha \in ( 1,2 ) \), \(\gamma \in (0,1)\), \(\rho >1\), are GCpFr derivatives, \({\varphi }_{p},p>1\) is a p-Laplacian operator, \(\mu \neq -1\), and the nonlinear functions \(q: [ 0,1 ] \times {\mathbb{R}}\times {\mathbb{R}} \rightarrow {\mathbb{R}}\) and \(\theta ,\nu :\mathbb{R}\times \mathbb{R}\rightarrow {\mathbb{R}}\) are given continuous functions. The main goal of this research paper is to prove the existence and uniqueness of equation (3) solutions by applying the Banach and Schauder fixed point theorems. Then, we apply our results by introducing an applicable example to validate all our obtained results. One may observe that the results of this paper are presented in a form which is essentially of high degree of generality. For particular values of ρ, equation (3) can be reduced to (1) and (2). One can find mathematical models of different physical phenomena in the world as simple cases of equation (3), such as blow-up. One can find distinct applications of mathematical models in the literature (see, for example, [46–48]).

2 Basic preliminaries

The following is a review of some important definitions and properties in the theory of fractional differential equations involving the GCpFr derivatives. Note that we have adapted some notations from [3, 49].

Definition 1

(Generalized Caputo fractional integral (GCpFrI))

Assume that \(\alpha \in (m-1,m)\), \(m\in \mathbb{N} \), and \(\rho >0\). The GCpFrI of order α for a given function \(q: [ 0,1 ] \rightarrow \mathbb{R}\) with respect to parameter ρ can be written in the following form:

$$ \mathcal{I}^{\alpha ,\rho }q ( t ) = \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{{ \bigl( t^{\rho }-s^{\rho } \bigr) }^{\alpha -1}s^{ \rho -1}q ( s ) \,ds,} $$
(4)

provided that the integral exists.

The GCpFrI is linear and satisfies the following semigroup/ index property:

  1. (I)

    \(\mathcal{I}^{\alpha ,\rho } ( c_{1}q ( t ) +c_{2}g ( t ) ) =c_{1}\mathcal{I}^{\alpha ,\rho }q ( t ) +c_{2}\mathcal{I}^{\alpha ,\rho }g ( t ) \), \(c_{1},c_{2} \in \mathbb{R}\),

  2. (II)

    \(\mathcal{I}^{\alpha ,\rho } ( \mathcal{I}^{\beta ,\rho }q(t) ) =\mathcal{I}^{\alpha +\beta ,\rho }q ( t ) \), \(\alpha ,\beta >0\).

In addition, if we assume the existence of the first derivative of \(\mathcal{I}^{\alpha ,\rho }f(t)\), we have the following:

$$ \frac{d}{dt}\mathcal{I}^{\alpha ,\rho }q(t)=t^{\rho -1} \mathcal{I}^{ \alpha -1,\rho }q(t). $$
(5)

Definition 2

Assume that \(q: [ 0,1 ] \rightarrow \mathbb{R}\), where \(q\in C^{m} [ 0,1 ] \). The GCpFr derivative of order \(\alpha \in (m-1,m)\) is written as follows:

$$\begin{aligned} {{}^{C}\mathfrak{D}}^{\alpha ,\rho }q ( t ) =& \mathcal{I}^{m- \alpha ,\rho } \bigl( \bigl( {s}^{1-\rho }{q} \bigr) ^{(m)} \bigr) (t) \\ =&\frac{{\rho }^{1-m+\alpha }}{\Gamma ( m-\alpha ) }\int _{0}^{t}{{ \bigl( t^{\rho }-s^{\rho } \bigr) }^{m- \alpha -1}} \bigl( {s}^{1-\rho }{q} \bigr) ^{(m)}{ ( s ) \,ds}. \end{aligned}$$
(6)

Remark 1

Both of the GCpFr derivative and GCpFrI formulated in (4) and (6) generalize the traditional fractional derivative. GCpFr derivative and GCpFrI are forms of the Caputo–Katugampola fractional derivative and integral, respectively. For example, if we assume \(\rho =1\), then the GCpFr derivative and GCpFrI can be reduced to the CapFr derivative and Riemann–Liouville fractional (RIFr) integral, respectively, as follows:

$$ {{}^{C}\mathfrak{D}}^{\alpha }q ( t ) :={{}^{C} \mathfrak{D}}^{ \alpha ,1}q ( t ) =\mathcal{I}^{m-\alpha }q^{ ( m ) } ( t ) = \frac{{1}}{\Gamma ( m-\alpha ) } \int _{0}^{t}{{ ( t-s ) }^{m- \alpha -1}q^{ ( m ) } ( s ) \,ds} $$

and

$$ \mathcal{I}^{\alpha }q(t):=\mathcal{I}^{\alpha ,1}q(t)= \frac{1}{\Gamma ( \alpha ) } \int _{0}^{t}{{ ( t-s ) }^{\alpha -1}q ( s ) \,ds,}\quad \alpha >0. $$

On the contrary, if we let \(\rho \rightarrow 0^{+}\), the GCpFr derivative and GCpFrI can be reduced to the Caputo–Hadamard derivative and Hadamard fractional integral, respectively, as follows:

$$ ^{H}\mathfrak{D}^{\alpha }q(t)= {}^{H} \mathcal{I}^{m-\alpha }q^{(m)}(t) $$

and

$$ {}^{H}\mathcal{I}^{\alpha }q(t)= \frac{1}{\Gamma ( \alpha ) }\int _{0}^{t} {{ \biggl( \ln { \frac{t}{s}} \biggr) }^{\alpha -1} \frac{q(s) }{s}\,ds.} $$

As a result, we can keep the traditional forms of fractional derivatives by selecting particular parameters for the GCpFr derivative.

Lemma 3

The following relations are valid:

  1. (i)

    Let \(0<\gamma <\alpha \), \(q\in C [0,1 ] \), then

    $$ {{}^{C}\mathfrak{D}}^{\gamma ,\rho }\mathcal{I}^{\alpha ,\rho }q ( t ) =\mathcal{I}^{\alpha -\gamma ,\rho }q ( t ) . $$
    (7)
  2. (ii)

    Let \(0<\alpha <\beta \), then

    $$ {{}^{C}\mathfrak{D}}^{\alpha ,\rho }{ \biggl( \frac{t^{\rho }}{\rho } \biggr) }^{\beta -1}=\frac{\Gamma (\beta )}{\Gamma (\beta -\alpha )}{ \biggl( \frac{t^{\rho }}{\rho } \biggr) }^{\beta -\alpha -1}. $$
    (8)

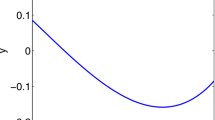
In Figs. 1 and 2, the dynamical behavior of the GCpFr derivative can be observed on four given functions \(u(t) = \frac{t^{4}}{4} \), \(u(t) = \frac{t^{6}}{8} \), \(u(t) = \frac{t^{6}}{9} \), and \(u(t) = \frac{t^{9}}{27} \) for \(\rho = 2\) and \(\rho = 3\), respectively.

Figure 1
figure 1

The GCpFr derivative of \(u(t) = \frac{t^{4}}{4}, \frac{t^{6}}{8}\) for \(\rho =2\)

Full size image
Figure 2
figure 2

The GCpFr derivative of \(u(t) = \frac{t^{6}}{9}, \frac{t^{9}}{27}\) for \(\rho =3\)

Full size image

We discuss the following result due to its importance in finding a solution for the fractional differential equation formulated in the form of GCpFr derivative.

Lemma 4

Assume that \(\alpha \in (m-1,m)\), \(\rho >0\), and \(f\in C^{m} [ 0,1 ]\). Then

$$ \mathcal{I}^{\alpha ,\rho } {}^{C}{\mathfrak{D}^{\alpha ,\rho }}q ( t ) = q(t)+c_{0}+c_{1} \biggl( \frac{t^{\rho }}{\rho } \biggr) +c_{2}{ \biggl( \frac{t^{\rho }}{\rho } \biggr) }^{2} +\cdots +c_{m-1}{ \biggl( \frac{t^{\rho }}{\rho } \biggr) }^{m-1} $$

and \({}^{C}{\mathfrak{D}^{\alpha ,\rho }}\mathcal{I}^{\alpha ,\rho }q(t) =q(t) \) for \(c_{k}\in \mathbb{R}\) and \(k=0,1,\dots ,m-1\).

The following is a review of some important properties of the p-Laplacian operator that will be applied in this research paper in the next sections. For more information about those properties, we refer to [38, 39].

Definition 5

The following p-Laplacian operator is formulated:

$$ {\varphi }_{p} ( u ) ={ \vert u \vert }^{p-2}u=u^{p-1},\quad u\geq 0, p>1, $$

such that \({{\varphi }_{p}}^{-1}={\varphi }_{r}\), where \(\frac{1}{p}+\frac{1}{r}=1\).

Lemma 6

Assume that \({\varphi }_{p} ( u ) , p\geq 2\), is a p-Laplacian operator and \(\vert u \vert , \vert m \vert \leq M\). Then we have the following:

$$ \bigl\vert {\varphi }_{p} ( u ) -{\varphi }_{p} ( m ) \bigr\vert \leq ( p-1 ) M^{p-2} \vert u-m \vert . $$

Our results in this research paper will be based on applying the following Banach and Schauder fixed point theorems.

Theorem 7

(Banach’s fixed point [50])

Assume that \(\mathbb{T}^{*}\) is a contraction mapping from a closed subset \(\mathcal{K}\) of a Banach space \(\mathcal{X}\) into itself. Then there exists unique \(z\in \mathcal{K}\) such that \(\mathbb{T}^{*}(z)=z\).

Theorem 8

(Schauder’s fixed point [50])

Assume that \(\mathbb{D} \) is a nonempty closed convex subset of a Banach space \(\mathcal{U}\). If \(\mathbb{T}^{*} :\mathbb{D}\rightarrow \mathbb{D}\) is a compact operator, then \(\mathbb{T}^{*}\) has at least one fixed point in \(\mathbb{D}\).

3 Main results

By using the fixed point theorems, we study here the existence and uniqueness of solutions for system (3). Let us consider the following linear equation:

$$ \textstyle\begin{cases} \frac{d}{dt} ( {\varphi }_{p} ( {{}^{C}\mathfrak{D}}^{ \alpha ,\rho }u ( t ) ) ) =w ( t )\quad (t \in [0,1]), \\ u ( 0 ) +\mu u ( 1 ) =\theta , \qquad u'(1) = \nu .\end{cases} $$
(9)

Lemma 9

([29])

Suppose that \(w\in C [ 0,1 ] \), \(\alpha \in ( 1,2 ) \), \(\rho >1\), and \(\mu \neq -1\). Then the boundary value problem (BoVaPr) (9) has a solution expressed as follows:

$$\begin{aligned} u ( t ) =&\frac{\theta }{\mu +1}- \frac{\mu \nu }{\rho ( {\mu +1} ) }+\frac{\nu }{\rho }t^{ \rho } \\ &{}+\frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau \\ &{}-\frac{{\rho }^{1-\alpha }t^{\rho }}{\Gamma ( \alpha -1 ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}}{ \varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau \\ &{}-\frac{\mu {\rho }^{1-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau \\ &{}+\frac{\mu {\rho }^{1-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau . \end{aligned}$$
(10)

Proof

By integrating the fractional differential equation in (9), we obtain

$$ {\varphi }_{p} \bigl( {{}^{C}\mathfrak{D}}^{\alpha ,\rho }u ( t ) \bigr) ={\varphi }_{p} \bigl( {{}^{C} \mathfrak{D}}^{\alpha ,\rho }u ( 0 ) \bigr) + \int _{0}^{t}{w ( s ) \,ds}. $$

The definition of generalized Caputo derivative implies that \({{}^{C}\mathfrak{D}}^{\alpha ,\rho }u ( 0 ) =0\), and by using the properties of Laplacian operators, we have

$$ {{}^{C}\mathfrak{D}}^{\alpha ,\rho }u ( t ) ={\varphi }_{r} \biggl( \int _{0}^{t}{w ( s ) \,ds} \biggr) . $$

By applying the generalized Caputo integral \(\mathcal{I}^{\alpha ,\rho }\) to both sides, we deduce the following:

$$ u ( t ) = \mathcal{I}^{\alpha ,\rho }{\varphi }_{r} \biggl( \int _{0}^{t}{w ( s ) \,ds} \biggr) +a_{0}+a_{1}t^{\rho } $$
(11)

for some constants \(a_{0}\) and \(a_{1}\). Accordingly, by using (5), we obtain

$$ u' ( t ) = \frac{{\rho }^{2-\alpha }}{\Gamma ( \alpha -1 ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -2}{ ( t\tau ) }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau +a_{1}\rho t^{ \rho -1}. $$

Then we have

$$ u ( 1 ) = \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{ \rho -1}}{ \varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau +a_{0}+a_{1} $$

and

$$ u' ( 1 ) = \frac{{\rho }^{2-\alpha }}{\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau +a_{1}\rho . $$

It is obvious that \(u ( 0 ) =a_{0}\). Hence, by the boundary conditions, we deduce the following:

$$ a_{1}=\frac{\nu }{\rho }- \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{w ( s ) \,ds} \biggr) \,d\tau $$

and

$$\begin{aligned} a_{0} ={}&\frac{\theta }{\mu +1}- \frac{\mu \nu }{\rho ( {\mu +1} ) } \\ &{}- \frac{\mu {\rho }^{1-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{h ( s ) \,ds} \biggr) \,d\tau \\ &{}+ \frac{\mu {\rho }^{1-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{h ( s ) \,ds} \biggr) \,d\tau . \end{aligned}$$

Substituting \(a_{0}\) and \(a_{1}\) in (11), we get solution (10). This completes the proof. □

Assume that \(\mathfrak{C}:=C ( [ 0,1 ] ,{\mathbb{R}} )\) is the Banach space of all continuous real-valued functions defined on \([0,1]\) endowed with the usual supremum norm defined by \(\Vert u \Vert =\sup_{t\in [ 0,1 ] } \vert {u(t)} \vert \).

Let \(\mathbf{U}= \{ u:u\in \mathfrak{C},{}{{}^{C}\mathfrak{D}}^{ \gamma ,\rho }u\in \mathfrak{C} \} \), then U is a Banach space endowed with the norm

$$ { \Vert u \Vert }_{\mathbf{U}}= \Vert u \Vert + \bigl\Vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }u \bigr\Vert . $$

By virtue of Lemma 9, we deduce that the solution of equation (3) is expressed as follows:

$$\begin{aligned} u ( t ) ={}&\frac{\theta (u(0),u(1))}{\mu +1}- \frac{\mu \nu (u(0),u(1))}{\rho ( {\mu +1} ) }+ \frac{\nu (u(0),u(1))}{\rho }t^{\rho } \\ &{}+\frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \\ &{}- \frac{{\rho }^{2-\alpha }t^{\rho }}{\Gamma ( \alpha -1 ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \\ &{}- \frac{\mu {\rho }^{1-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \\ &{}+ \frac{\mu {\rho }^{2-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{ {}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau . \end{aligned}$$

Let us now pose the following conditions to prove our next result:

  1. (H1)

    The function \(q: [ 0,1 ] \times {\mathbb{R}}\times {\mathbb{R}}\rightarrow {\mathbb{R}}\) is jointly continuous, and there exists a constant \(L_{q}>0\) such that, for \(u_{i},m_{i}\in \mathbb{R}\) (\(i=1,2\)),

    $$ \bigl\vert q(t,u_{1},m_{1})-q(t,u_{2},m_{2}) \bigr\vert \leq L_{q} \bigl( \vert u_{1}-u_{2} \vert + \vert m_{1}-m_{2} \vert \bigr)\quad \bigl(t \in [0,1] \bigr). $$
  2. (H2)

    The functionals \(\theta ,\nu :{\mathbb{R}}\times {\mathbb{R}}\rightarrow {\mathbb{R}}\) have the respective upper bounds \(M_{\theta }\) and \(M_{\nu }\).

  3. (H3)

    There exists a finite solution \(l>0\) of the following inequality:

    $$\begin{aligned} l &\geq \frac{M_{\theta }}{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert M_{\nu }}{\rho \vert \mu +1 \vert }+\frac{M_{\nu }}{\rho }+ \frac{M_{\nu }}{\rho ^{1-\gamma }\Gamma (2-\gamma )} \\ &\quad {}+ \frac{(\alpha \rho +1) ( 2 \vert \mu \vert +1 ) M^{r-1}}{\rho ^{\alpha } \vert \mu +1 \vert \Gamma ( \alpha +1 ) }+ \frac{M^{r-1}}{{\rho }^{\alpha -\gamma }\Gamma ( \alpha -\gamma +1 ) }+ \frac{M^{r-1}}{{\rho }^{\alpha -\gamma -1}\Gamma ( 2-\gamma ) \Gamma ( \alpha ) }, \end{aligned}$$

    where \(M:=L_{q}l+q^{\ast }\) and \(q^{\ast }:=\sup_{t\in {}[ 0,1]}|q(t,0,0)|\).

For the sake of abbreviation, we set

$$\begin{aligned}& \Lambda _{1} := \frac{(r-1)M^{r-2}L_{q} ( 2 \vert \mu \vert +1 ) ( 1+ ( \alpha \rho +1 ) ) \mathbf{B}(\alpha ,\frac{1}{\rho }+1)}{\rho ^{\alpha } \vert \mu +1 \vert \Gamma ( \alpha ) }, \\& \Lambda _{2} :=\frac{(r-1)M^{r-2}L_{q}}{{\rho }^{\alpha -\gamma }} \biggl[ \frac{\mathbf{B}(\alpha -\gamma ,\frac{1}{\rho }+1)}{\Gamma ( \alpha -\gamma ) }+ \frac{\rho \mathbf{B}(\alpha -1,\frac{1}{\rho } +1)}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \biggr] , \end{aligned}$$

where \(\mathbf{B}(\cdot ,\cdot )\) denotes the well-known beta function defined by

$$ \mathbf{B}(m,n)=\frac{\Gamma (m)\Gamma (n)}{\Gamma (m+n)}= \int _{0}^{1}(1-s)^{m-1}s^{n-1}\,ds\quad (m>0,n>0). $$

An operator, denoted by \(\Psi :\mathbf{U}\rightarrow \mathbf{U}\), can be defined as follows:

$$\begin{aligned} \Psi u ( t ) ={}&\frac{\theta (u(0),u(1))}{\mu +1}- \frac{\mu \nu (u(0),u(1))}{\rho ( {\mu +1} ) }+ \frac{\nu (u(0),u(1))}{\rho }t^{\rho } \\ &{} +\frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \\ &{} - \frac{{\rho }^{2-\alpha }t^{\rho }}{\Gamma ( \alpha -1 ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}}{ \varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \\ &{} - \frac{\mu {\rho }^{1-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \\ &{} + \frac{\mu {\rho }^{2-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau . \end{aligned}$$

By virtue of Lemma 3, we deduce

$$\begin{aligned} &{{}^{C}\mathfrak{D}}^{\gamma ,\rho }\Psi u ( t ) \\ &\quad = \frac{\nu (u(0),u(1))}{\rho ^{1-\gamma }\Gamma (2-\gamma )}t^{\rho (1- \gamma )} \\ &\qquad {}+ \frac{{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) }\int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha - \gamma -1}{\tau }^{\rho -1}} \times {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \\ &\qquad {}- \frac{{\rho }^{2-\alpha +\gamma }t^{\rho (1-\gamma )}}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau . \end{aligned}$$

The next result depends on the Banach fixed point theorem.

Theorem 10

Suppose that (H1)–(H3) are valid. If \(\Lambda _{1}+\Lambda _{2}<1\), then the BoVaPr in (3) has a unique solution.

Proof

We consider the set \(B_{l}= \{ u\in \mathbf{U}:{ \Vert u \Vert }_{ \mathbf{U}}\leq l \} \).

For each \(t\in {}[ 0,1]\), \(u\in B_{l}\), we have the following estimation:

$$\begin{aligned} \biggl\vert \int _{0}^{\tau }q \bigl(s,u(s),{{}^{C} \mathfrak{D}}^{\gamma , \rho }u(s) \bigr)\,d\tau \biggr\vert &\leq \int _{0}^{\tau } \bigl\vert q \bigl(s,x(s),{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u(s) \bigr)-q(s,0,0)+q(s,0,0) \bigr\vert \,ds \\ &\leq \int _{0}^{\tau } \bigl( L_{q} \bigl( \bigl\vert u(s) \bigr\vert + \bigl\vert {{}^{C} \mathfrak{D}}^{ \gamma ,\rho }u(s) \bigr\vert \bigr)+ \bigl\vert q(s,0,0) \bigr\vert \bigr) \,ds \\ &\leq \int _{0}^{1} \bigl( L_{q} \bigl( \Vert u \Vert + \bigl\Vert {{}^{C} \mathfrak{D}}^{\gamma ,\rho }u \bigr\Vert \bigr)+q^{\ast } \bigr) \,ds \\ &\leq L_{q}l+q^{\ast }=M. \end{aligned}$$

By Definition 5, we get \({\varphi }_{r}(M)=M^{r-1}\), \(M>0\).

We shall show that \(\Psi B_{l}\subset B_{l}\). For each \(t\in {}[ 0,1]\), \(x\in B_{l}\), and \(r\geq 2\), we have

$$\begin{aligned} \bigl\vert \Psi u(t) \bigr\vert \leq{}& \frac{ \vert \theta (u(0),u(1)) \vert }{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert \vert \nu (u(0),u(1)) \vert }{\rho \vert \mu +1 \vert }+ \frac{ \vert \nu (u(0),u(1)) \vert }{\rho }t^{\rho } \\ &{}+ \biggl\vert \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) }\int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}{ \tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \biggr\vert \\ &{}+ \biggl\vert \frac{{\rho }^{2-\alpha }t^{\rho }}{\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \biggr\vert \\ &{}+ \biggl\vert \frac{\mu {\rho }^{1-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \biggr\vert \\ &{}+ \biggl\vert \frac{\mu {\rho }^{2-\alpha }}{ ( {\mu +1} ) \Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \biggr\vert \\ \leq{}& \frac{ \vert \theta (u(0),u(1)) \vert }{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert \vert \nu (u(0),u(1)) \vert }{\rho \vert \mu +1 \vert }+\frac{ \vert \nu (u(0),u(1)) \vert }{\rho }t^{\rho } \\ &{}+ \frac{M^{r-1}t^{\rho \alpha }}{\rho ^{\alpha }\Gamma ( \alpha +1 ) }+ \frac{M^{r-1}t^{\rho }}{\rho ^{\alpha -1}\Gamma ( \alpha ) }+ \frac{M^{r-1} \vert \mu \vert }{\rho ^{\alpha } \vert \mu +1 \vert \Gamma ( \alpha +1 ) }+ \frac{M^{r-1} \vert \mu \vert }{\rho ^{\alpha -1} \vert \mu +1 \vert \Gamma ( \alpha ) } \\ \leq{}& \frac{M_{\theta }}{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert M_{\nu }}{\rho \vert \mu +1 \vert }+\frac{M_{\nu }}{\rho }+ \frac{(\alpha \rho +1)| ( 2 \vert \mu \vert +1 ) M^{r-1}}{\rho ^{\alpha } \vert \mu +1 \vert \Gamma ( \alpha +1 ) }. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \bigl\vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }\Psi u ( t ) \bigr\vert \leq& \frac{ \vert \nu (u(0),u(1)) \vert }{\rho ^{1-\gamma }\Gamma (2-\gamma )}+ \frac{M^{r-1}{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -\gamma -1}{\tau }^{\rho -1}}\,d\tau \\ &{}+ \frac{M^{r-1}{\rho }^{2-\alpha +\gamma }t^{\rho (1-\gamma )}}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}}\,d\tau \\ \leq& \frac{M_{\nu }}{\rho ^{1-\gamma }\Gamma (2-\gamma )}+ \frac{M^{r-1}}{{\rho }^{\alpha -\gamma }\Gamma ( \alpha -\gamma +1 ) }+ \frac{M^{r-1}}{{\rho }^{\alpha -\gamma -1}\Gamma ( 2-\gamma ) \Gamma ( \alpha ) }. \end{aligned}$$

Thus, we get \(\Vert \Psi u\Vert _{\mathbf{U}}\leq l\), which implies that \(\Psi B_{l}\subset B_{l}\). Now, for each \(t\in {}[ 0,1]\), \(u,m\in B_{l}\), and \(r\geq 2\), we have

$$\begin{aligned} &\bigl\vert \Psi u(t) -\Psi m(t) \bigr\vert \\ &\quad \leq \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{ { \bigl( t^{\rho }-{ \tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{ \rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,m ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m ( s ) \bigr) \,ds} \biggr) \biggr\vert \,d\tau \\ &\qquad {}+ \frac{{\rho }^{2-\alpha }t^{\rho }}{\Gamma ( \alpha -1 ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,m ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m ( s ) \bigr) \,ds} \biggr) \biggr\vert \,d\tau \\ &\qquad {}+ \frac{ \vert \mu \vert {\rho }^{1-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{ \rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,m ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m ( s ) \bigr) \,ds} \biggr) \biggr\vert \,d\tau \\ &\qquad {}+ \frac{ \vert \mu \vert {\rho }^{2-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha -1 ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,m ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m ( s ) \bigr) \,ds} \biggr) \biggr\vert \,d\tau \\ &\quad \leq \frac{(r-1)M^{r-2}L_{q}{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}} \\ &\qquad {}\times \int _{0}^{\tau } \bigl( \bigl\vert u(s)-m(s) \bigr\vert + \bigl\vert {{}^{C} \mathfrak{D}}^{ \gamma ,\rho }u(s)-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m(s) \bigr\vert \bigr) \,ds\,d\tau \\ &\qquad {}+ \frac{(r-1)M^{r-2}L_{q}{\rho }^{2-\alpha }t^{\rho }}{\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} \\ &\qquad {}\times \int _{0}^{\tau } \bigl( \bigl\vert u(s)-m(s) \bigr\vert + \bigl\vert {{}^{C} \mathfrak{D}}^{ \gamma ,\rho }u(s)-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m(s) \bigr\vert \bigr) \,ds\,d\tau \\ &\qquad {}+ \frac{(r-1)M^{r-2}L_{q} \vert \mu \vert {\rho }^{1-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -1}{\tau }^{\rho -1}} \\ &\qquad {}\times \int _{0}^{\tau } \bigl( \bigl\vert u(s)-m(s) \bigr\vert + \bigl\vert {{}^{C} \mathfrak{D}}^{ \gamma ,\rho }u(s)-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m(s) \bigr\vert \bigr) \,ds\,d\tau \\ &\qquad {}+ \frac{(r-1)M^{r-2}L_{q} \vert \mu \vert {\rho }^{2-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -2}{\tau }^{\rho -1}} \\ &\qquad {}\times \int _{0}^{\tau } \bigl( \bigl\vert u(s)-m(s) \bigr\vert + \bigl\vert {{}^{C} \mathfrak{D}}^{ \gamma ,\rho }u(s)-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m(s) \bigr\vert \bigr) \,ds\,d\tau \\ &\quad \leq \frac{(r-1)M^{r-2}L_{q}}{\rho ^{\alpha }} \biggl[ \frac{\mathbf{B}(\alpha ,\frac{1}{\rho } +1)}{\Gamma ( \alpha ) }+ \frac{\rho \mathbf{B}(\alpha -1,\frac{1}{\rho } +1)}{\Gamma ( \alpha -1 ) } \\ &\qquad {} + \frac{ \vert \mu \vert \mathbf{B}(\alpha ,\frac{1}{\rho } +1)}{ \vert \mu +1 \vert \Gamma ( \alpha ) }+ \frac{\rho \vert \mu \vert \mathbf{B}(\alpha -1,\frac{1}{\rho } +1)}{ \vert \mu +1 \vert \Gamma ( \alpha -1 ) } \biggr] \\ &\qquad {}\times \bigl( \Vert u-m \Vert + \bigl\Vert {{}^{C} \mathfrak{D}}^{\gamma , \rho }u-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m \bigr\Vert \bigr) =\Lambda _{1}{ \Vert u-m \Vert }_{ \mathbf{U}}. \end{aligned}$$

Similarly, we have

$$\begin{aligned} \bigl\Vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( t ) -{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m ( t ) \bigr\Vert \leq{}& \frac{(r-1)M^{r-2}{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -\gamma -1}{\tau }^{\rho -1}} \\ &{}\times \int _{0}^{\tau } \bigl\vert {q \bigl( s,u ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) }-{q \bigl( s,m ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }m ( s ) \bigr) } \bigr\vert \,ds \,d\tau \\ &{}+ \frac{(r-1)M^{r-2}{\rho }^{2-\alpha +\gamma }t^{\rho (1-\gamma )}}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} \\ &{}\times \int _{0}^{\tau } \bigl\vert {q \bigl( s,u ( s ) ,{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) }-{q \bigl( s,m ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }m ( s ) \bigr) } \bigr\vert \,ds\,d\tau \\ \leq{}& \frac{(r-1)M^{r-2}L_{q}{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{ \rho } \bigr) }^{\alpha -\gamma -1}{\tau }^{\rho -1}} \\ &{}\times \int _{0}^{\tau } \bigl( \bigl\vert u(s)-m(s) \bigr\vert + \bigl\vert {{}^{C} \mathfrak{D}}^{ \gamma ,\rho }u(s)-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m(s) \bigr\vert \bigr) \,ds\,d\tau \\ &{}+ \frac{(r-1)M^{r-2}L_{q}{\rho }^{2-\alpha +\gamma }t^{\rho (1-\gamma )}}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} \\ &{}\times \int _{0}^{\tau } \bigl( \bigl\vert u(s)-m(s) \bigr\vert + \bigl\vert {{}^{C} \mathfrak{D}}^{ \gamma ,\rho }u(s)-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m(s) \bigr\vert \bigr) \,ds\,d\tau \\ \leq{}& \frac{(r-1)M^{r-2}L_{q}}{{\rho }^{\alpha -\gamma }} \biggl[ \frac{\mathbf{B}(\alpha -\gamma ,\frac{1}{\rho } +1)}{\Gamma ( \alpha -\gamma ) }+ \frac{\rho \mathbf{B}(\alpha -1,\frac{1}{\rho } +1)}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \biggr] \\ &{}\times \bigl( \Vert u-m \Vert + \bigl\Vert {{}^{C} \mathfrak{D}}^{\gamma , \rho }u-{{}^{C} \mathfrak{D}}^{\gamma ,\rho }m \bigr\Vert \bigr) \\ ={}&\Lambda _{2}{ \Vert u-m \Vert }_{\mathbf{U}}. \end{aligned}$$

Therefore, we get

$$ { \Vert \Psi u- \Psi m \Vert }_{\mathbf{U}} \leq (\Lambda _{1}+ \Lambda _{2}){ \Vert u-m \Vert }_{\mathbf{U}}. $$

Since \(\Lambda _{1}+\Lambda _{2}<1\) by the given assumption, then the operator Ψ is a contraction. From the Banach fixed point theorem (Theorem 7), there exists a unique solution for the BoVaPr in (3). This completes the proof. □

We now work on Schauder’s fixed point by assuming the following:

  1. (H4)

    There exist a function \(\omega \in C ( [ 0,1 ] ,{\mathbb{R}^{+}} ) \) and a nondecreasing function \(\Upsilon :\mathbb{R}^{+}\rightarrow \mathbb{R}^{+}\), \(\Upsilon (0)=0\), such that:

    $$ \bigl\vert q(t,u,m) \bigr\vert \leq \omega (t)\Upsilon \bigl( \vert u \vert + \vert m \vert \bigr),\quad \forall t\in {}[ 0,1], u,m \in \mathbb{R}. $$
  2. (H5)

    There exists a finite solution \(l^{{\prime }}>0\) of the following inequality:

    $$\begin{aligned} l^{{\prime }} \geq{}& \frac{M_{\theta }}{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert M_{\nu }}{\rho \vert \mu +1 \vert }+ \frac{M_{\nu }}{\rho }+ \frac{M_{\nu }}{\rho ^{1-\gamma }\Gamma (2-\gamma )}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma }\Gamma ( \alpha -\gamma +1 ) } \\ &{}+ \frac{ ( 2 \vert \mu \vert +1 ) (\alpha \rho +1)( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha } \vert \mu +1 \vert \Gamma ( \alpha +1 ) }+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma -1}\Gamma ( 2-\gamma ) \Gamma ( \alpha ) }. \end{aligned}$$
    (12)

Theorem 11

Assume that (H2), (H4), and (H5) are satisfied. Then the BoVaPr in (3) has at least one solution.

Proof

We transform the BoVaPr in (3) into a fixed point problem. Let us consider the operator \(\Psi :\mathbf{U}\to \mathbf{U}\) defined by (H3), and let \(B_{l^{{\prime }}}= \{ u\in \mathbf{U}:{ \Vert u \Vert }_{\mathbf{U}}\leq l^{{\prime }} \} \). Clearly, \(B_{l^{{\prime }}}\) is a bounded closed convex set in U. Next we shall show that Ψ satisfies everything that is assumed in Theorem 8. Thus, Ψ has a fixed point which is a solution of the BoVaPr in (3). The proof will be given step-by-step.

Step 1. Ψ maps bounded sets into bounded sets in U.

For each \(t\in {}[ 0,1]\), \(u\in B_{l^{{\prime }}}\), we obtain

$$\begin{aligned} \biggl\vert \int _{0}^{\tau }q \bigl(s,u(s),{{}^{C} \mathfrak{D}}^{\gamma , \rho }u(s) \bigr)\,ds \biggr\vert &\leq \int _{0}^{\tau } \bigl\vert q \bigl(s,u(s),{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u(s) \bigr) \bigr\vert \,ds \\ &\leq \int _{0}^{\tau }\omega (s)\Upsilon \bigl( \bigl\vert u(s) \bigr\vert + \bigl\vert {{}^{C}\mathfrak{D}}^{ \gamma ,\rho }u(s) \bigr\vert \bigr)\,ds \\ &\leq \int _{0}^{1} \Vert \omega \Vert \Upsilon \bigl( \Vert u \Vert + \bigl\Vert {{}^{C} \mathfrak{D}}^{\gamma ,\rho }u \bigr\Vert \bigr)\,ds \\ &\leq \Vert \omega \Vert \Upsilon \bigl(l^{{\prime }} \bigr). \end{aligned}$$

By using Definition 5, we obtain the following estimate:

$$\begin{aligned} \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl(s,u(s),{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u(s) \bigr)\,ds \biggr) \biggr\vert &= \biggl\vert \int _{0}^{\tau }q \bigl(s,u(s),{{}^{C} \mathfrak{D}}^{\gamma ,\rho }u(s) \bigr)\,ds \biggr\vert ^{r-1} \\ &\leq \bigl( \Vert \omega \Vert \Upsilon \bigl(l^{{\prime }} \bigr) \bigr)^{r-1}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \bigl\vert \Psi u(t) \bigr\vert \leq{}& \frac{ \vert \theta (u(0),u(1)) \vert }{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert \vert \nu (u(0),u(1)) \vert }{\rho \vert \mu +1 \vert } + \frac{ \vert \nu (u(0),u(1)) \vert }{\rho } \\ &{}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{{ \bigl( t^{ \rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}}\,d\tau \\ &{}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{2-\alpha }t^{\rho }}{\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}}\,d\tau \\ &{}+ \frac{ \vert \mu \vert ( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}}\,d\tau \\ &{}+ \frac{ \vert \mu \vert ( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{2-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}}\,d\tau \\ \leq {}&\frac{M_{\theta }}{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert M_{\nu }}{\rho \vert \mu +1 \vert }+\frac{M_{\nu }}{\rho }+ \frac{ ( 2 \vert \mu \vert +1 ) (\alpha \rho +1)( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha } \vert \mu +1 \vert \Gamma ( \alpha +1 ) }. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \bigl\vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }\Psi u ( t ) \bigr\vert \leq{}& \frac{ \vert \nu (u(0),u(1)) \vert }{\rho ^{1-\gamma }\Gamma (2-\gamma )} + \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -\gamma -1}{\tau }^{ \rho -1}}\,d\tau \\ &{}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{2-\alpha +\gamma }t^{\rho (1-\gamma )}}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{ \alpha -2}{\tau }^{\rho -1}}\,d\tau \\ \leq {}&\frac{M_{\nu }}{\rho ^{1-\gamma }\Gamma (2-\gamma )}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma }\Gamma ( \alpha -\gamma +1 ) }+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma -1}\Gamma ( 2-\gamma ) \Gamma ( \alpha ) }. \end{aligned}$$

Hence, we get

$$\begin{aligned} \Vert \Psi u \Vert _{\mathbf{U}} \leq{}& \frac{M_{\theta }}{ \vert \mu +1 \vert }+ \frac{ \vert \mu \vert M_{\nu }}{\rho \vert \mu +1 \vert }+\frac{M_{\nu }}{\rho }+ \frac{M_{\nu }}{\rho ^{1-\gamma }\Gamma (2-\gamma )}+\frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma }\Gamma ( \alpha -\gamma +1 ) } \\ &{}+ \frac{ ( 2 \vert \mu \vert +1 ) (\alpha \rho +1)( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha } \vert \mu +1 \vert \Gamma ( \alpha +1 ) }+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma -1}\Gamma ( 2-\gamma ) \Gamma ( \alpha ) }. \end{aligned}$$

In view of (H4), we deduce that \(\Psi (B_{l^{{\prime }}})\subset B_{l^{{\prime }}}\).

Step 2. Ψ is continuous.

Assume that \(\{u_{m}\}\) is a sequence where \(u_{m}\rightarrow u\) in U. We have

$$\begin{aligned} &\bigl\vert \Psi u_{m}(t) -\Psi u(t) \bigr\vert \\ &\quad \leq \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t}{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u_{n} ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( s ) \bigr) \,ds \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds \biggr) \biggr\vert \,d\tau \\ &\qquad {}+\frac{{\rho }^{2-\alpha }}{\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u_{m} ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( s ) \bigr) \,ds \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds \biggr) \biggr\vert \,d\tau \\ &\qquad {}+ \frac{ \vert \mu \vert {\rho }^{1-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{ \rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u_{m} ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( s ) \bigr) \,ds \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds \biggr) \biggr\vert \,d\tau \\ &\qquad {}+ \frac{ \vert \mu \vert {\rho }^{2-\alpha }}{ \vert \mu +1 \vert \Gamma ( \alpha -1 ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u_{m} ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( s ) \bigr) \,ds \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds \biggr) \biggr\vert \,d\tau . \end{aligned}$$

Then, by the dominated convergence theorem, for all \(t\in {}[ 0,1]\), we have \(\vert \Psi u_{m}(t)-\Psi u(t) \vert \rightarrow 0\). Further, we have

$$\begin{aligned} &\bigl\vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( t ) - {{}^{C} \mathfrak{D}}^{\gamma ,\rho }u ( t ) \bigr\vert \\ &\quad \leq \frac{{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) } \int _{0}^{t}{{ \bigl( t^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha - \gamma -1}{\tau }^{\rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u_{m} ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( s ) \bigr) \,ds \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds \biggr) \biggr\vert \,d\tau \\ &\qquad {}+ \frac{{\rho }^{2-\alpha +\gamma }}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} \\ &\qquad {}\times \biggl\vert {\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u_{m} ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( s ) \bigr) \,ds \biggr) -{\varphi }_{r} \biggl( \int _{0}^{\tau }q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds \biggr) \biggr\vert \,d\tau . \end{aligned}$$

In view of the dominated convergence theorem, we deduce that \(\vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }u_{m} ( t ) - {{}^{C}\mathfrak{D}}^{\gamma , \rho }u ( t ) \vert \rightarrow 0\). Hence, we conclude that \(\Vert \Psi u_{m}-\Psi u\Vert _{\mathbf{U}}\rightarrow 0\) in U. Hence, Ψ is continuous.

Step 3. \(\{(\Psi u),u\in B_{l^{{\prime }}}\}\) and \(\{{{}^{C}\mathfrak{D}}^{\gamma ,\rho } (\Psi u),u\in B_{l^{{\prime }}}\}\) are equicontinuous.

For \(t_{1}< t_{2}\) with \(t_{1},t_{2}\in {}[ 0,1]\), we have

$$\begin{aligned}& \bigl\vert (\Psi u) (t_{2}) -(\Psi u) (t_{1}) \bigr\vert \\& \quad \leq \biggl\vert \frac{\nu (u(0),u(1))}{\rho } \bigl(t_{2}^{\rho }-t_{1}^{\rho } \bigr) \biggr\vert \\& \qquad {}+ \biggl\vert \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) }\int _{t_{1}}^{t_{2}}{{ \bigl( t_{2}^{\rho }-{ \tau }^{\rho } \bigr) }^{ \alpha -1}{\tau }^{\rho -1}} { \varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \biggr\vert \\& \qquad {}+ \biggl\vert \frac{{\rho }^{1-\alpha }}{\Gamma ( \alpha ) }\int _{0}^{t_{1}} \bigl[ {{ \bigl( t_{2}^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}-{ \bigl( t_{1}^{\rho }-{\tau }^{\rho } \bigr) }^{ \alpha -1}} \bigr] {{\tau }^{\rho -1}} {\varphi }_{r} \\& \qquad {}\times\biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \biggr\vert \,d\tau \\& \qquad {}+ \biggl\vert \frac{{\rho }^{2-\alpha }(t_{2}^{\rho }-t_{1}^{\rho })}{\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}} {\varphi }_{r} \biggl( \int _{0}^{\tau }{q \bigl( s,u ( s ) ,{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u ( s ) \bigr) \,ds} \biggr) \,d\tau \biggr\vert \\& \quad \leq \frac{M_{\upsilon }}{\rho } \bigl(t_{2}^{\rho }-t_{1}^{\rho } \bigr)+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{t_{1}}^{t_{2}}{{ \bigl( t_{2}^{\rho }-{ \tau }^{\rho } \bigr) }^{\alpha -1}{\tau }^{\rho -1}}\,d\tau \\& \qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha }}{\Gamma ( \alpha ) } \int _{0}^{t_{1}} \bigl\vert {{ \bigl( t_{2}^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}-{ \bigl( t_{1}^{ \rho }-{\tau }^{\rho } \bigr) }^{\alpha -1}} \bigr\vert {{\tau }^{\rho -1}}\,d\tau \\& \qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha }(t_{2}^{\rho }-t_{1}^{\rho })}{\Gamma ( \alpha -1 ) }\int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{ \rho -1}}\,d\tau \\& \quad \leq \frac{M_{\upsilon }}{\rho } \bigl(t_{2}^{\rho }-t_{1}^{\rho } \bigr)+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha }\Gamma ( \alpha +1 ) } \bigl[ 2 \bigl(t_{2}^{\rho }-t_{1}^{\rho } \bigr)^{\alpha }+t_{2}^{\rho \alpha }-t_{1}^{ \rho \alpha } \bigr] \\& \qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha }\Gamma ( \alpha ) } \bigl(t_{2}^{\rho }-t_{1}^{\rho } \bigr). \end{aligned}$$

Thus, \(\vert (\Psi u)(t_{2})-(\Psi u)(t_{1}) \vert \rightarrow 0\) as \(t_{2}\rightarrow t_{1}\). In addition, we have the following:

$$\begin{aligned} &\bigl\vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }(\Psi u) ( t_{2} ) -{{}^{C} \mathfrak{D}}^{\gamma ,\rho }( \Psi u) ( t_{1} ) \bigr\vert \\ &\quad \leq \frac{M_{\nu }}{\rho ^{1-\gamma }\Gamma (2-\gamma )} \bigl(t_{2}^{\rho (1- \gamma )}-t_{1}^{\rho (1-\gamma )} \bigr) \\ &\qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) }\int _{t_{1}}^{t_{2}}{{ \bigl( t_{2}^{\rho }-{ \tau }^{\rho } \bigr) }^{ \alpha -\gamma -1}{\tau }^{\rho -1}}\,d\tau \\ &\qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{1-\alpha +\gamma }}{\Gamma ( \alpha -\gamma ) }\int _{0}^{t_{1}} \bigl\vert {{ \bigl( t_{2}^{\rho }-{\tau }^{\rho } \bigr) }^{\alpha -\gamma -1}-{ \bigl( t_{1}^{\rho }-{\tau }^{\rho } \bigr) }^{ \alpha -\gamma -1}} \bigr\vert {{\tau }^{\rho -1}}\,d\tau \\ &\qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}{\rho }^{2-\alpha +\gamma }(t_{2}^{\rho (1-\gamma )}-t_{1}^{\rho (1-\gamma )})}{\Gamma (2-\gamma )\Gamma ( \alpha -1 ) } \int _{0}^{1}{{ \bigl( 1-{\tau }^{\rho } \bigr) }^{\alpha -2}{\tau }^{\rho -1}}\,d\tau \\ &\quad \leq \frac{M_{\nu }}{\rho ^{1-\gamma }\Gamma (2-\gamma )} \bigl(t_{2}^{ \rho (1-\gamma )}-t_{1}^{\rho (1-\gamma )} \bigr) \\ &\qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma }\Gamma ( \alpha -\gamma +1 ) } \bigl[ 2 \bigl(t_{2}^{ \rho }-t_{1}^{\rho } \bigr)^{\alpha -\gamma }+t_{2}^{\rho (\alpha -\gamma )}-t_{1}^{ \rho (\alpha -\gamma )} \bigr] \\ &\qquad {}+ \frac{( \Vert \omega \Vert \Upsilon (l^{{\prime }}))^{r-1}}{{\rho }^{\alpha -\gamma -1}\Gamma (2-\gamma )\Gamma ( \alpha ) } \bigl(t_{2}^{\rho (1-\gamma )}-t_{1}^{\rho (1-\gamma )} \bigr). \end{aligned}$$

Thus, \(\vert {{}^{C}\mathfrak{D}}^{\gamma ,\rho }(\Psi u) ( t_{2} ) -{{}^{C}\mathfrak{D}}^{\gamma ,\rho }(\Psi u) ( t_{1} ) \vert \rightarrow 0\) as \(t_{2}\rightarrow t_{1}\). Hence, \(\{(\Psi u),u\in B_{l^{{\prime }}}\}\) and \(\{{{}^{C}\mathfrak{D}}^{\gamma ,\rho } (\Psi u),u\in B_{l^{{\prime }}} \}\) are equicontinuous and relatively compact according to the Arzelà–Ascoli theorem. Thus, \(\Psi (B_{l^{{\prime }}})\) is a relatively compact subset of U, and the operator Ψ is compact. From Schauder’s fixed point (see Theorem 8), Ψ has a fixed point x which is a solution of the BoVaPr in (3). The proof is completed. □

4 Application

By choosing particular parameters, the following example is provided in this section to apply and validate all obtained results from the previous sections.

We construct an example with specific parameters to expose the applicability of the proposed theoretical results.

Example 1

Consider the following BoVaPr:

$$ \textstyle\begin{cases} \frac{d}{dt} ( {\varphi }_{2} ( {{}^{C}\mathfrak{D}}^{ \frac{3}{2},2}u ( t ) ) ) = \frac{\arctan (t)}{1+\frac{1}{5} \vert u(t) \vert +\frac{1}{5} \vert {{}^{C}\mathfrak{D}}^{\frac{1}{2},2}u(t) \vert }\quad (t\in [0,1]), \\ u ( 0 ) +u ( 1 ) =\sin u(0)\cos u(1), \qquad u' ( 1 ) =\cos u(0)\sin u(1).\end{cases} $$
(13)

Here, \(\alpha =\frac{3}{2}\), \(\gamma =\frac{1}{2}\), \(\rho =2\), \(p=q=2\), \(\mu =M_{\nu }=M_{ \theta }=1\), and q is expressed as

$$ q \bigl(t,u(t),{{}^{C}\mathfrak{D}}^{\gamma ,\rho }u(t) \bigr)= \frac{\arctan (t)}{1+\frac{1}{5} \vert u(t) \vert +\frac{1}{5} \vert {{}^{C}\mathfrak{D}}^{\frac{1}{2},2}u(t) \vert }\quad \bigl(t\in [0,1] \bigr). $$

Clearly, \(q:[0,1]\times \mathbb{R}\times \mathbb{R}\rightarrow \mathbb{R}\) is a continuous function, and we have

$$\begin{aligned} \bigl\vert q(t,u_{1},m_{1})-q(t,u_{2},m_{2}) \bigr\vert &= \biggl\vert \frac{\arctan (t)}{1+\frac{1}{5} \vert u_{1} \vert +\frac{1}{5} \vert m_{1} \vert }- \frac{\arctan (t)}{1+\frac{1}{5} \vert u_{2} \vert +\frac{1}{5} \vert m_{2} \vert } \biggr\vert \\ &\leq \frac{\pi }{20}\bigl( \vert u_{1}-u_{2} \vert + \vert m_{1}-m_{2} \vert \bigr). \end{aligned}$$

Thus, assumption (H1) is satisfied with \(L_{q}=\frac{\pi }{20}\). Also, we have

$$ q^{\ast }=\sup_{t\in {}[ 0,1]} \bigl\vert q(t,0,0) \bigr\vert = \frac{\pi }{4} $$

and

$$ \Lambda _{1}+\Lambda _{2}=0.2091745071+0.235619449=0.4447939561< 1. $$

As a result, all of the assumptions we made in Theorem 10 are satisfied. Hence, the BoVaPr in (13) has a unique solution on \([0,1]\).

Unfortunately, the functions \(\omega (t)=\arctan (t)\) and \(\Upsilon (s)= \frac{1}{1+\frac{1}{5}s}\) do not satisfy assumption (H4). Alternatively, the function

$$ q(t,u,m)=\arctan (t)\frac{ \vert u(t) \vert + \vert m(t) \vert }{1+ \vert u(t) \vert + \vert m(t) \vert }\quad \bigl(t\in [0,1] \bigr), $$

with \(\omega (t)=\arctan (t)\) and \(\Upsilon (s)=\frac{s}{s+1}\) satisfies condition (H4). Moreover, estimate (12) can be simplified as

$$ l^{{\prime }}\geq 2.0479+ \frac{2.6454l^{{\prime }}}{l^{{\prime }}+1}. $$

Hence, any real number \(l^{{\prime }}>4.2\) satisfies assumption (H5). Therefore, everything assumed in Theorem 11 is satisfied, and then there exists a solution of problem (13).

5 Conclusion

The existence and uniqueness of solutions for the proposed p-Laplacian nonperiodic boundary value problem in the sense of generalized Caputo fractional derivative have been successfully investigated in this research paper using the Banach and Schauder fixed point theorems. All the obtained results are supported by an applicable example to apply and validate them. Therefore, this research study sheds the light on this interesting topic of research and motivates all other researchers to work on further investigation of p-Laplacian nonperiodic boundary value problem defined in other fractional derivatives.