1 Introduction

Fractional calculus has been developed and used in different fields of applied science and engineering. Recently, fractional calculus got more importance due to its wide variety of applications in numerous topics, such as wave-like equations, the SIRS-SI malaria disease model, diabetes model, the model of the Ambartsumian equation and the model of Lienard’s equation [17, 19, 22, 23, 42]. Very recently, the fractional calculus with Mittag-Leffler law was widely studied due to its significance and applicability in various fields [20, 21, 24, 41, 43]. During the last decades, FKEs of different models have been successfully applied in describing and explaining numerous problems of physics and astrophysics (see, e.g., [1–3, 5, 13, 16, 18, 28–31, 35–39, 49] and the references therein).

1.1 Fractional kinetic equations

In [15] one determined the fractional differential equation for the rate of change of reaction. The destruction rate and the production rate follow

$$ \frac{d\mathfrak{M}}{dt}=-d (\mathfrak{M}_{t} ) +p ( \mathfrak{M} _{t} ), $$
(1.1)

where \(\mathfrak{M}=\mathfrak{M} ( t ) \) and \(d=d (\mathfrak{M} ) \) the rate of reaction and the rate of destruction, respectively. The rate of production is denoted by \(p=p (\mathfrak{M} ) \) and \(\mathfrak{M}_{t} ( t^{ \ast } ) =\mathfrak{M} (t-t^{\ast } ) \), \(t^{\ast }>0\).

By neglecting the spatial fluctuations or in homogeneities in \(\mathfrak{M} ( t ) \), the particular case of (1.1) is formed as

$$ \frac{d\mathfrak{M}}{dt}=-c_{i}\mathfrak{M}_{i} ( t ), $$
(1.2)

with t \(\mathfrak{M}_{i} ( t=0 ) =\mathfrak{M}_{0}\) is the number of density of species i at time \(t=0\) and \(c_{i}>0\). Integrating the standard kinetic equation (1.2), not considering the index i, we get

$$ \mathfrak{M} ( t ) -\mathfrak{M}_{0}=-c_{0}D_{t}^{-1} \mathfrak{M} ( t ), $$
(1.3)

where \({}_{0}D_{t}^{-1}\) is the particular form of the Riemann–Liouville operator \({}_{0}D_{t}^{-\tau }\) defined by

$$ _{0}D_{t}^{-\tau }f ( t ) =\frac{1}{\varGamma ( \tau ) } \int _{0}^{t} ( t-s ) ^{\tau -1}f ( s )\,ds,\quad t>0,\Re ( \tau ) >0. $$

The fractional generalized form of the standard kinetic equation (1.3) is given in [15] as

$$ \mathfrak{M} ( t )-\mathfrak{M}_{0}=-c_{0}^{\tau }D_{t} ^{-1}\mathfrak{M} ( t ). $$
(1.4)

The solution of (1.4) is

$$ \mathfrak{M} ( t ) =\mathfrak{M}_{0}\sum _{k=0}^{ \infty }\frac{ ( -1 ) ^{k}}{\varGamma ( \tau k+1 ) } ( ct ) ^{\tau k}. $$
(1.5)

Another generalized form of FKE is given in [36] as

$$ \mathfrak{M} ( t )-\mathfrak{M}_{0}f (t ) =-c ^{\tau } \bigl(_{0}D_{t}^{-1}\mathfrak{M} \bigr) ( t ) \quad \bigl( \Re ( \tau ) >0 \bigr), $$
(1.6)

where \(\mathfrak{M}(t)\), \(\mathfrak{M}_{0}=\mathfrak{M} ( 0 ) \) is the same as (1.2), c is a constant and \(f\in L(0, \infty )\). The use of the Laplace transform (LT) to (1.6) (see [36]) gives

$$\begin{aligned} \mathcal{L} \bigl[ \mathfrak{M} ( t ) \bigr] ( p ) &= \mathfrak{M}_{0}\frac{F (p ) }{1+c^{\tau }p ^{-\tau }} \\ &=\mathfrak{M}_{0} \Biggl( \sum_{n=0}^{\infty } \bigl( -c^{\tau } \bigr) ^{n}p^{-n\tau } \Biggr) F ( p ), \end{aligned}$$
(1.7)

where \(n\in \mathfrak{M}_{0}\), \(\vert \frac{c}{p} \vert <1\) and the LT ([44]) is defined by

$$ F ( p ) =\mathcal{L} \bigl[ f(t) \bigr] = \int _{0} ^{\infty }e^{-pt}f ( t ) \,dt\quad \Re ( p ) >0. \vadjust{\goodbreak} $$
(1.8)

To proceed our study, we need the definitions of the Mittag-Leffler (M-L) functions \(E_{\rho } (z )\) (see [27]) and \(E_{\rho ,\lambda } ( x )\) [48]:

$$\begin{aligned}& E_{\tau } ( z ) =\sum_{n=0}^{\infty } \frac{z^{n}}{\varGamma ( \tau n+1 ) }\quad \bigl(z,\tau \in \mathbb{C}; \vert z \vert < 0, \Re ( \tau )>0 \bigr) , \end{aligned}$$
(1.9)
$$\begin{aligned}& E_{\tau ,\eta } ( x ) =\sum_{n=0}^{\infty } \frac{x^{n}}{ \varGamma ( \tau n+\eta ) }\quad \bigl(z,\tau , \eta \in \mathbb{C};\Re ( \tau )>0, \Re ( \eta )>0 \bigr) . \end{aligned}$$
(1.10)

For the details as regards FKEs and solutions, one can refer to [14, 28–31, 35–39, 49].

1.2 Class of functions

A class of functions \(\mathfrak{F}_{\rho }^{\lambda }\) is introduced in [34] and is defined by

$$ \mathfrak{F}_{\rho , \lambda }(x)=\sum _{n=0}^{\infty }\frac{\sigma (n)}{ \varGamma (\rho n+\lambda )}x^{n}, $$
(1.11)

where \(\rho , \lambda \in \mathbb{C}\), \(\Re (\rho )>0\), \(|x|<\mathbb{R}\) and the coefficient \(\sigma (n)\) is a bounded arbitrary sequence of real (or complex) numbers.

1.3 Special cases

  • If we set

    $$\begin{aligned} \sigma (n)=\frac{(\delta )_{\kappa n}}{n!} \end{aligned}$$
    (1.12)

    then (1.11) reduces to the generalized M-L function given by Srivastava and Tomovski [45].

  • If we consider \(\sigma (n)=\frac{(\delta )_{qn}}{n!}\), \(q\in (0,1) \cup \mathbb{N}\) gives \(E_{\rho ,\lambda }^{\delta ,q}(x)\) of [40].

  • By considering \(\sigma (n)=\frac{(\delta )_{k}}{n!}\), (1.11) turns into the generalized Mittag-Leffler function defined in [32].

  • Choosing \(\sigma (n)=1\) we get the well-known generalized M-L function \(E_{\rho ,\lambda }(x)\) [48].

For more details as regards the class of functions and its properties, the interesting reader is referred to [25, 26, 33].

1.4 Sumudu transform

The Sumudu transform is widely used to solve various type of problems in science and engineering and it was introduced by Watugala (see [46, 47]). For the details of Sumudu transforms, properties and its applications the interesting reader is referred to [4, 6–12].

The Sumudu transform over the set functions

$$ A=\bigl\{ f ( t ) \vert \exists ~M,\tau _{1},\tau _{2}>0, \bigl\vert f ( t ) \bigr\vert < Me^{ \vert t \vert / \tau _{j}} ,\text{ if }t\in ( -1 ) ^{j}\times {}[ 0,\infty ) \bigr\} $$

is defined by

$$ G ( u ) =S \bigl[ f ( t ) ;u \bigr] = \int _{0} ^{\infty }f ( ut ) e^{-t}\,dt,\quad u \in ( -\tau _{1},\tau _{2} ). $$
(1.13)

The main aim of this study is to establish the generalized FKEs involving \(\mathfrak{F}_{\rho ,\lambda }(x)\). Here, we consider the Sumudu transform methodology to achieve the results.

2 Solution of generalized fractional kinetic equations involving class of functions

The solution of the generalized fractional kinetic equations involving is given in this section.

Theorem 2.1

If \(d>0\), \(\upsilon >0\), \(\rho ,\lambda , t\in \mathbb{C}\), \(\Re (\rho ) >0\)and \(|x|<\mathbb{R}\). Then the solution of the equation

$$ \mathfrak{N} ( t ) -\mathfrak{N}_{0}\mathfrak{F}_{\rho , \lambda } (t ) =-d^{\upsilon }{ }_{0}D_{t}^{-\upsilon } \mathfrak{N} ( t ) $$
(2.1)

is given by

$$ \mathfrak{N} ( t ) =\mathfrak{N}_{0}\sum _{n=0}^{ \infty }\frac{\sigma {(n)}\varGamma (n+1)}{\varGamma (\rho n+\lambda )}t^{n-1} E_{\upsilon , n} \bigl(-d^{\upsilon }t^{\upsilon } \bigr), $$
(2.2)

where \(E_{v,n} ( . ) \)is the generalized Mittag-Leffler function [27].

Proof

The Sumudu transform of Riemann–Liouville fractional operator is given by

$$ S\bigl[{}_{0}D_{t}^{\upsilon }f(t);u \bigr]=u^{\upsilon }G(u), $$
(2.3)

where \(G(u)\) is defined in (1.13). Applying the Sumudu transform to both sides of (2.1) gives

$$\begin{aligned}& S \bigl[ \mathfrak{N} ( t ) ;u \bigr] =\mathfrak{N}_{0}S \bigl[ \mathfrak{F}_{\rho ,\lambda } (t ) ;u \bigr] -d ^{\upsilon }S \bigl[ _{0}D_{t}^{-\upsilon }\mathfrak{N} (t ) ;u \bigr], \\& \mathfrak{N}^{*} (u ) =\mathfrak{N}_{0} \Biggl( \int _{0} ^{\infty }e^{-t}\sum _{n=0}^{\infty }\frac{\sigma (n)}{\varGamma ( \rho n +\lambda )}(ut)^{n}\,dt \Biggr) -d^{\upsilon }u^{\upsilon } \mathfrak{N}^{*} (u ), \end{aligned}$$

where \(S\{t^{\mu -1}\}=u^{\mu -1}\varGamma (\mu )\). Interchanging integration and summation, we get

$$\begin{aligned} \mathfrak{N}^{*} (u )+d^{\upsilon }u^{\upsilon } \mathfrak{N}^{*} (u ) &=\mathfrak{N}_{0}\sum _{n=0} ^{\infty }\frac{\sigma (n)}{\varGamma (\rho n +\lambda )}(u)^{n} \int _{0} ^{\infty }e^{-t}t^{n}\,dt \\ &=\mathfrak{N}_{0}\sum_{n=0}^{\infty } \frac{\sigma (n)}{ \varGamma (\rho n +\lambda )}(u)^{n}\varGamma (n+1). \end{aligned}$$

This implies that

$$ \mathfrak{N}^{*} (u ) =\mathfrak{N}_{0} \sum_{n=0} ^{\infty }\frac{\sigma (n)}{\varGamma (\rho n +\lambda )} \varGamma (n+1)u ^{n}\sum_{r=0}^{\infty } \bigl[- (du )^{\upsilon } \bigr] ^{r}. $$
(2.4)

Taking the Sumudu inverse of (2.4), and by using

$$ S^{-1} \bigl\{ u^{\upsilon }; t \bigr\} =\frac{t^{\upsilon -1}}{ \varGamma ( \upsilon ) },\quad \Re (\upsilon ) >0, $$

we get

$$\begin{aligned}& S^{-1} \bigl(\mathfrak{N} (t ) \bigr) =\mathfrak{N}_{0} \sum_{n=0}^{\infty }\frac{\sigma (n)\varGamma (n+1)}{\varGamma ( \rho n +\lambda )} S^{-1} \Biggl\{ \sum_{r=0}^{\infty }d^{ \upsilon r}u^{ (n+\upsilon r ) } \Biggr\} , \\& \begin{aligned} \mathfrak{N} ( t ) &=\mathfrak{N}_{0}\sum _{n=0} ^{\infty }\frac{\sigma (n)}{\varGamma (\rho n +\lambda )}\varGamma (n+1) \Biggl\{ \sum_{r=0}^{\infty } ( -1 ) ^{r}d^{\upsilon r}\frac{t^{ (n+\upsilon r )-1}}{\varGamma (n+\upsilon r ) } \Biggr\} \\ &=\mathfrak{N}_{0}\sum_{n=0}^{\infty } \frac{\sigma (n)}{ \varGamma (\rho n +\lambda )}t^{n-1} \Biggl\{ \sum _{r=0}^{\infty } ( -1 ) ^{r}d^{\upsilon r} \frac{t^{\upsilon r}}{\varGamma (n+\upsilon r ) } \Biggr\} . \end{aligned} \end{aligned}$$

In view of Eq. (1.9), we obtain the desired result. □

Theorem 2.2

If \(d>0\), \(\upsilon >0\), \(\rho ,\lambda , t\in \mathbb{C}\), \(\Re (\rho ) >0\)and \(|x|<\mathbb{R}\), then the solution of the equation

$$ \mathfrak{N} ( t ) -\mathfrak{N}_{0}\mathfrak{F}_{\rho , \lambda } \bigl(d^{\upsilon }t^{\upsilon } \bigr) =-d^{\upsilon }{ }_{0}D_{t}^{-\upsilon } \mathfrak{N} ( t ) $$
(2.5)

is given by

$$ \mathfrak{N} ( t ) =\mathfrak{N}_{0}\sum _{n=0}^{ \infty }\frac{\sigma {(n)}\varGamma (n+1)}{\varGamma (\rho n+\lambda )} \bigl(d^{\upsilon }\bigr)t^{\upsilon -1} E_{\upsilon , n} \bigl(-d^{ \upsilon }t^{\upsilon } \bigr). $$
(2.6)

Proof

This theorem can be proved like Theorem 2.1. So the details are omitted. □

Theorem 2.3

If \(d>0\), \(\upsilon >0\), \(\rho ,\lambda , t\in \mathbb{C}\), \(\Re (\rho ) >0\), \(\mathfrak{a} \neq d\)and \(|x|< \mathbb{R}\), then the solution of the equation

$$ \mathfrak{N} ( t ) -\mathfrak{N}_{0}\mathfrak{F}_{\rho , \lambda } \bigl(d^{\upsilon }t^{\upsilon } \bigr) =-{\mathfrak{a}} ^{\upsilon }{ }_{0}D_{t}^{-\upsilon } \mathfrak{N} ( t ) $$
(2.7)

is given by

$$ \mathfrak{N} ( t ) =\mathfrak{N}_{0}\sum _{n=0}^{ \infty }\frac{\sigma {(n)}\varGamma (n+1)}{\varGamma (\rho n+\lambda )} \bigl(d^{\upsilon }\bigr)t^{\upsilon -1} E_{\upsilon , n} \bigl(-{ \mathfrak{a}} ^{\upsilon }t^{\upsilon } \bigr). $$
(2.8)

Proof

Theorem 2.3 can easily be derived from Theorem 2.2, so the details are omitted. □

If we choose \(\sigma (n)=\frac{(\gamma )_{\kappa n}}{\varGamma (n+1)}\) then we get the fractional kinetic equation involving a generalized Mittag-Leffler function [45]

Corollary 2.1

If \(d>0\), \(\upsilon >0\), \(\rho ,\lambda , t\in \mathbb{C}\), \(\Re (\rho ) >0\)and \(|x|<\mathbb{R}\), then the solution of the equation

$$ \mathfrak{N} ( t ) -\mathfrak{N}_{0}E_{\rho ,\lambda }^{ \gamma ,\kappa } (t ) =-d^{\upsilon }{ }_{0}D_{t}^{- \upsilon } \mathfrak{N} ( t ) $$
(2.9)

is given by

$$ \mathfrak{N} ( t ) =\mathfrak{N}_{0}\sum _{n=0}^{ \infty } \frac{(\gamma )_{\kappa n}}{\varGamma (\rho n+\lambda )}t ^{n-1} E_{\upsilon , n} \bigl(-d^{\upsilon }t^{\upsilon } \bigr). $$
(2.10)

If we choose \(\sigma (n)=\frac{(\gamma )_{n,q}}{\varGamma (n+1)}\) then we get the fractional kinetic equation involving the generalized Mittag-Leffler function [40]

Corollary 2.2

If \(d>0\), \(\upsilon >0\), \(\rho ,\lambda , t\in \mathbb{C}\), \(\Re (\rho ) >0\)and \(|x|<\mathbb{R}\), then the solution of the equation

$$ \mathfrak{N} ( t ) -\mathfrak{N}_{0}E_{\rho ,\lambda }^{ \gamma ,q} (t ) =-d^{\upsilon }{ }_{0}D_{t}^{-\upsilon } \mathfrak{N} ( t ) $$
(2.11)

is given by

$$ \mathfrak{N} ( t ) =\mathfrak{N}_{0}\sum _{n=0}^{ \infty }\frac{(\gamma )_{n,q}}{\varGamma (\rho n+\lambda )}t ^{n-1} E_{\upsilon , n} \bigl(-d^{\upsilon }t^{\upsilon } \bigr). $$
(2.12)

If we choose \(\sigma (n)=\frac{(\gamma )_{n}}{\varGamma (n+1)}\) then we get the fractional kinetic equation involving the generalized Mittag-Leffler function [32]

Corollary 2.3

If \(d>0\), \(\upsilon >0\), \(\rho ,\lambda , t\in \mathbb{C}\), \(\Re (\rho ) >0\)and \(|x|<\mathbb{R}\), then the solution of the equation

$$ \mathfrak{N} ( t ) -\mathfrak{N}_{0}E_{\rho ,\lambda }^{ \gamma } (t ) =-d^{\upsilon }{ }_{0}D_{t}^{-\upsilon } \mathfrak{N} ( t ) $$
(2.13)

is given by

$$ \mathfrak{N} ( t ) =\mathfrak{N}_{0}\sum _{n=0}^{ \infty }\frac{(\gamma )_{n}}{\varGamma (\rho n+\lambda )}t ^{n-1} E_{\upsilon , n} \bigl(-d^{\upsilon }t^{\upsilon } \bigr). $$
(2.14)

If we choose \(\sigma (n)=1\) then we get the fractional kinetic equation involving the generalized Mittag-Leffler function [48]

Corollary 2.4

If \(d>0\), \(\upsilon >0\), \(\rho ,\lambda , t\in \mathbb{C}\), \(\Re (\rho ) >0\)and \(|x|<\mathbb{R}\), then the solution of the equation

$$ \mathfrak{N} ( t ) -\mathfrak{N}_{0}E_{\rho ,\lambda } (t ) =-d^{\upsilon }{ }_{0}D_{t}^{-\upsilon } \mathfrak{N} ( t ) $$
(2.15)

is given by

$$ \mathfrak{N} ( t ) =\mathfrak{N}_{0}\sum _{n=0}^{ \infty }\frac{\varGamma (n+1)}{\varGamma (\rho n+\lambda )}t ^{n-1} E_{\upsilon , n} \bigl(-d^{\upsilon }t^{\upsilon } \bigr). $$
(2.16)

Remark 2.1

By choosing different values for \(\sigma (n)\), we can deduce many results from Theorem 2.1. Similarly, from Theorem 2.2 and Theorem 2.3, one can deduce many known and new solutions of the fractional kinetic equation involving a variety of special functions.

3 Graphical results and discussion

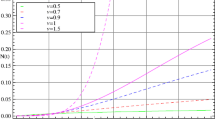
Figures 1 and 2 shows the 2D plots of solutions of (2.2) for \(\lambda = 1\) and \(\lambda = 2\), respectively, with parametric values \(\mathfrak{N_{0}}= 2\), \(\rho =1\), \(d=3\), \(\sigma (n)=1\) and for different values of \(\nu = 1,~0.8,~0.6\). We observe that for \(\lambda =2\) the growth rate is slow as compared to \(\lambda =1\) when ν approaches to 1.

Figure 1
figure 1

Solution of (2.2) for \(\lambda =1\)

Full size image
Figure 2
figure 2

Solution of (2.2) for \(\lambda =2\)

Full size image

In Figs. 3 and 4 3D plots are shown for the time interval \(0.3 < t<1.8\) which give the valid region of convergence of solutions for \(0\leq \nu \leq 1\) and also the time interval \(0.5 < t<3\) gives the valid region of convergence of solutions for \(1.5\leq \nu \leq 2\) of (2.2) for \(\lambda = 1\), respectively. Likewise the valid region of convergence of (2.2) for \(\lambda = 2\) is shown in Figs. 5 and 6.

Figure 3
figure 3

Mesh-plot of (2.2) for \(\lambda = 1\), \(0.3< t<2\)

Full size image
Figure 4
figure 4

Mesh-plot of (2.2) for \(\lambda = 1\), \(0.5< t<3\)

Full size image
Figure 5
figure 5

Mesh-plot of (2.2) for \(\lambda =2\), \(0.4< t<2.4\)

Full size image
Figure 6
figure 6

Mesh-plot of (2.2) for \(\lambda =2\), \(0.6< t<4\)

Full size image

Figures 7 and 8 show the 2D plots of solutions of (2.6) for \(\lambda = 1\) and \(\lambda = 2\), respectively, with parametric values \(\mathfrak{N_{0}}= 2\), \(\rho =1\), \(d=3\), \(\sigma (n)=1\) and for different values of \(\nu = 1,~0.8,~0.6\). We observe that for \(\lambda =1\) the growth rate is slow as compared to \(\lambda =2\) when ν approaches 1.

Figure 7
figure 7

Solution of (2.6) for \(\lambda =1\)

Full size image
Figure 8
figure 8

Solution of (2.6) for \(\lambda =2\)

Full size image

Figures 9 and 10 represent 3D plots where the time interval \(0.3 < t<1.8\) gives the valid region of convergence of solutions for \(0\leq \nu \leq 1\) and the time interval \(0 < t<3\) gives the valid region of convergence of solutions for \(1.3\leq \nu \leq 2\) for \(\lambda = 1\) of (2.6), respectively. Likewise the valid regions of convergence of (2.6) for \(\lambda = 2\) for different values of λ and ν are shown in Figs. 11 and 12. The dark portion in all figures shows the beginning of the divergence of a solution.

Figure 9
figure 9

Mesh-plot of (2.6) for \(\lambda = 1\), \(0.4< t<2\)

Full size image
Figure 10
figure 10

Mesh-plot of (2.6) for \(\lambda = 1\), \(0.5< t<3\)

Full size image
Figure 11
figure 11

Mesh-plot of (2.6) for \(\lambda =2\), \(0.8< t<2\)

Full size image
Figure 12
figure 12

Mesh-plot of (2.6) for \(\lambda =2\), \(0.9< t<4\)

Full size image

The graphical results demonstrate that the region of convergence of solutions depends continuously on the fractional parameter ν as well as on λ. Hence, by examining the behavior of the solutions for different parameters and time intervals it is observed that \(\mathfrak{N} ( t )\) is negative as well as positive.

4 Conclusion

The fractional kinetic equation involving the class of functions is studied using the Sumudu transform technique. The results achieved here are rather general in nature and one can find various new and known solutions of FKEs containing a different type of special function. The behavior of the obtained solutions is studied with the help of graphs.