1 Introduction

The Struve function \(H_{\nu } ( x ) \) introduced by Hermann Struve in 1882, defined for \(\nu \in \mathbb{C}\) by

$$ H_{\nu } ( x ) :=\sum_{r=0}^{\infty } \frac{ ( -1 ) ^{r}}{\Gamma ( r+3/2 ) \Gamma ( r+\nu +\frac{3}{2} ) } \biggl( \frac{x}{2} \biggr) ^{2r+\nu +1}, $$
(1)

is the particular solutions of the non-homogeneous Bessel differential equations, given by

$$ x^{2}y^{{\prime \prime }} ( x ) +xy{^{\prime }} ( x ) + \bigl( x^{2}-{\nu }^{2} \bigr) y ( x ) =\frac{4 ( \frac{x}{2} ) ^{\nu +1}}{\sqrt{\pi }\Gamma ( \nu +1/2 ) }. $$
(2)

The homogeneous version of (2) has Bessel functions of the first kind, denoted as \(J_{\nu }(x)\), for solutions, which are finite at \(x = 0\), when ν is a positive fraction and all integers [1], while they tend to diverge for negative fractions ν. The Struve functions occur in certain areas of physics and applied mathematics, for example, in water-wave and surface-wave problems [2, 3], as well as in problems of unsteady aerodynamics [4]. The Struve functions are also important in particle quantum dynamical studies of spin decoherence [5] and nanotubes [6]. For more details about Struve functions, their generalizations and properties, the esteemed reader is invited to consider the references [7–16]. Recently, Nisar et al. [17] introduced and studied various properties of k-Struve function \(\mathtt{S}_{ \nu ,c}^{\mathtt{k}}\) defined by

$$ \mathtt{S}_{\nu ,c}^{\mathtt{k}}(x):=\sum _{r=0}^{\infty }\frac{(-c)^{r}}{ \Gamma_{\mathtt{k}}(r\mathtt{k}+\nu +\frac{3\mathtt{k}}{2})\Gamma (r+ \frac{3}{2})} \biggl( \frac{x}{2} \biggr) ^{2r+\frac{\nu }{\mathtt{k}}+1}. $$
(3)

The Sumudu transform was introduced by Watugala (see [18, 19]). For more details about the Sumudu transform, see ([1, 20–31]). The Sumudu transform over the set of functions

$$ A= \bigl\{ f( t) \mid \exists ~M,\tau_{1},\tau_{2}>0, \bigl\vert f( t) \bigr\vert < Me^{\vert t\vert /\tau_{j}} ,\text{ if } t\in ( -1) ^{j}\times [0,\infty ) \bigr\} $$

is defined by

$$ G ( u ) =S \bigl[ f ( t ) ;u \bigr] = \int_{0}^{ \infty }f ( ut ) e^{-t}\,dt,\quad u\in ( - \tau_{1},\tau_{2} ) . $$
(4)

The Sumudu transform of k-Struve function is given by

$$\begin{aligned} S \bigl[ \mathtt{S}_{\nu ,c}^{\mathtt{k}}(x) \bigr] &= \int_{0}^{\infty }e ^{-t}\mathtt{S}_{\nu ,c}^{\mathtt{k}}(ut)\,dt \\ &= \int_{0}^{\infty }e^{-t}\sum _{r=0}^{\infty }\frac{(-c)^{r}}{ \Gamma_{\mathtt{k}} ( r\mathtt{k}+\nu +\frac{3\mathtt{k}}{2} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{ut}{2} \biggr) ^{2r+\frac{ \nu }{\mathtt{k}}+1}\,dt \\ &=\sum_{r=0}^{\infty }\frac{(-c)^{r}}{\Gamma_{\mathtt{k}} ( r \mathtt{k}+\nu +\frac{3\mathtt{k}}{2} ) \Gamma ( r+ \frac{3}{2} ) } \int_{0}^{\infty }e^{-t} \biggl( \frac{ut}{2} \biggr) ^{\frac{\nu }{\mathtt{k}}+2r}\,dt \\ &=\sum_{r=0}^{\infty }\frac{(-c)^{r}\Gamma ( \frac{\nu }{ \mathtt{k}}+2r+2 ) }{\Gamma_{\mathtt{k}} ( r\mathtt{k}+\nu +\frac{3 \mathtt{k}}{2} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{u}{2} \biggr) ^{\frac{\nu }{\mathtt{k}}+1+2r}. \end{aligned}$$
(5)

Now, using

$$\begin{aligned} \Gamma_{\mathtt{k}} ( \gamma ) ={\mathtt{k}}^{\frac{\gamma }{ \mathtt{k}}-1}\Gamma \biggl( \frac{\gamma }{\mathtt{k}} \biggr) , \end{aligned}$$
(6)

we have the following:

$$\begin{aligned} S \bigl[ \mathtt{S}_{\nu ,c}^{\mathtt{k}}(x) \bigr] =\sum _{r=0}^{\infty }\frac{(-c)^{r}\Gamma ( \frac{\nu }{\mathtt{k}}+2r+2 ) }{ {\mathtt{k}}^{r+\frac{\nu }{\mathtt{k}}+\frac{1}{2}}\Gamma ( r+\frac{ \nu }{\mathtt{k}}+\frac{3}{2} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{u}{2} \biggr) ^{\frac{\nu }{\mathtt{k}}+1+2r}. \end{aligned}$$
(7)

Denoting the left-hand side by \(G(u)\), we have

$$\begin{aligned} G ( u ) &=S \bigl[ \mathtt{S}_{\nu ,c}^{\mathtt{k}}(t);u \bigr] \\ &= \biggl( \frac{u}{2} \biggr) ^{\frac{\nu }{\mathtt{k}}+1}k^{- \frac{1}{2}-\frac{\nu }{\mathtt{k}}} {}_{2}\Psi_{2}\left [ \textstyle\begin{array}{c} (\frac{\nu }{\mathtt{k}}+2,2),(1,1) \\ (\frac{\nu }{\mathtt{k}}+\frac{3}{2},1),(\frac{3}{2},1) \end{array}\displaystyle \bigg|-\frac{cu^{2}}{4\mathtt{k}} \right ] . \end{aligned}$$
(8)

Now, using the formula

$$ S^{-1} \bigl\{ u^{v};t \bigr\} = \frac{t^{v-1}}{\Gamma (v)}, \qquad \Re (v)>1, $$
(9)

we get the inverse Sumudu transform of k-Struve function as

$$\begin{aligned} S^{-1} \bigl[ \mathtt{S}_{\nu ,c}^{\mathtt{k}}(x) \bigr] &=S^{-1} \Biggl[ \sum_{r=0}^{\infty } \frac{(-c)^{r}}{\Gamma_{\mathtt{k}} ( r\mathtt{k}+ \nu +\frac{3\mathtt{k}}{2} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{u}{2} \biggr) ^{\frac{\nu }{\mathtt{k}}+1+2r} \Biggr] \\ &=\sum_{r=0}^{\infty }\frac{(-c)^{r}}{\Gamma_{\mathtt{k}} ( r \mathtt{k}+\nu +\frac{3\mathtt{k}}{2} ) \Gamma ( r+ \frac{3}{2} ) } \biggl( \frac{1}{2} \biggr) ^{\frac{\nu }{\mathtt{k}}+1+2r}S ^{-1} \bigl[u^{\frac{\nu }{\mathtt{k}}+1+2r} \bigr] \\ &=\sum_{r=0}^{\infty }\frac{(-c)^{r} ( \frac{1}{2} ) ^{\frac{ \nu }{\mathtt{k}}+1+2r}}{\Gamma_{\mathtt{k}} ( r\mathtt{k}+\nu +\frac{3 \mathtt{k}}{2} ) \Gamma ( r+\frac{3}{2} ) } \frac{ ( t ) ^{\frac{\nu }{\mathtt{k}}+2r}}{\Gamma ( \frac{\nu }{\mathtt{k}}+1+2r ) }. \end{aligned}$$
(10)

Applying (6) in (10), we get

$$ S^{-1} \bigl[ \mathtt{S}_{\nu ,c}^{\mathtt{k}}(x) \bigr] = \biggl( \frac{t}{2} \biggr) ^{\frac{\nu }{\mathtt{k}}}k^{-\frac{1}{2}-\frac{\nu }{\mathtt{k}}}{}_{1} \Psi_{3} \left [ \textstyle\begin{array}{c} (1,1) \\ (\frac{\nu }{\mathtt{k}}+\frac{3}{2},1),(\frac{3}{2},1), (\frac{\nu }{\mathtt{k}}, 2) \end{array}\displaystyle \Big|-\frac{ct^{2}}{4\mathtt{k}} \right ] . $$
(11)

In the field of mathematics, many techniques are used to solve various types of problems [32–34]. In this paper, we use the Sumudu transform technique to obtain the solutions of fractional kinetic equations by considering (3). The applications of fractional order calculus are found in many papers (see [35–37]), and it has attracted researchers’ attention in various fields [38–46] because of its importance and efficiency. The fractional differential equation between a chemical reaction or a production scheme (such as in birth-death processes) was established and treated by Haubold and Mathai [47] (also see [21, 38, 48]).

2 Solution of generalized fractional kinetic equations for k-Struve function

Let the arbitrary reaction be described by a time-dependent quantity \(N= ( N_{t} ) \). The rate of change \(\frac{dN}{dt}\) is a balance between the destruction rate \(\mathfrak{d}\) and the production rate \(\mathfrak{p}\) of N, that is, \(\frac{dN}{dt}=-\mathfrak{d}+ \mathfrak{p}\). Generally, destruction and production depend on the quantity N itself, that is,

$$ \frac{dN}{dt}=-\mathfrak{d} ( N_{t} ) +\mathfrak{p} ( N _{t} ) , $$
(12)

where \(N_{t}\) is described by \(N_{t} ( t^{\ast } ) =N ( t-t ^{\ast } ) ,t^{\ast }>0\). Another form of (12) is

$$ \frac{dN_{i}}{dt}=-c_{i}N_{i} ( t ) , $$
(13)

with \(N_{i} ( t=0 ) =N_{0}\), which is the number of density of species i at time \(t=0\) and \(c_{i}>0\). The solution of (13) is

$$ N_{i} ( t ) =N_{0}e^{-c_{i}t}. $$
(14)

Integrating (13) gives

$$ N ( t ) -N_{0}=-c\cdot{}_{0}D_{t}^{-1}N ( t ) , $$
(15)

where \({}_{0}D_{t}^{-1}\) is the particular case of the Riemann-Liouville integral operator and c is a constant. The fractional form of (15) due to [47] is

$$ N ( t ) -N_{0}=-c_{0}^{\upsilon }D_{t}^{-\upsilon }N ( t ) , $$
(16)

where \({}_{0}D_{t}^{-\upsilon }\) is defined as

$$ _{0}D_{t}^{-\upsilon }f ( t ) =\frac{1}{\Gamma ( \upsilon ) } \int _{0}^{t} ( t-s ) ^{\upsilon -1}f ( s )\,ds,\quad \Re ( \upsilon ) >0. $$
(17)

Suppose that \(f(t)\) is a real- or complex-valued function of the (time) variable \(t > 0\) and s is a real or complex parameter. The Laplace transform of \(f(t)\) is defined by

$$ F ( p ) =L \bigl[ f(t):p \bigr] = \int _{0}^{\infty }e ^{-pt}f ( t )\,dt,\quad \Re ( p ) >0. $$
(18)

The Mittag-Leffler functions \(E_{\rho } ( z ) \) (see [49]) and \(E_{\rho ,\lambda } ( x ) \) [50] are defined respectively as follows:

$$ E_{\rho } ( z ) =\sum_{n=0}^{\infty } \frac{z^{n}}{\Gamma ( \rho n+1 ) } \quad \bigl( z,\rho \in \mathbb{C}; \vert z \vert < 0, \Re ( \rho ) >0 \bigr) . $$
(19)
$$ E_{\rho ,\lambda } ( x ) =\sum_{n=0}^{\infty } \frac{x^{n}}{ \Gamma ( \rho n+\lambda ) } \quad \bigl( z,\rho , \lambda \in \mathbb{C};\Re ( \rho ) >0, \Re ( \lambda ) >0 \bigr) . $$
(20)

Theorem 1

If \(d>0,\nu >0, \mu , c, t\in \mathbb{C}\) and \(\mu >-\frac{3}{2} \mathtt{k}\), then the solution of the generalized fractional kinetic equation

$$ N ( t ) =N_{0}~\mathtt{S}_{\mu ,c}^{\mathtt{k}} \bigl( d^{ \nu }t^{\nu } \bigr) -d^{\nu }\text{ }_{0}D_{t}^{-\nu }N ( t ) $$
(21)

is given by the following formula:

$$\begin{aligned} N ( t ) &=N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu ( 2r+\frac{\mu }{\mathtt{k}}+1 ) +1 ] }{ \Gamma_{\mathtt{k}} ( r\mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{d^{\nu }t ^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{\mathtt{k}}+1} \\ &\quad \times E_{\nu ,\nu (2r+\frac{\mu }{\mathtt{k}})+1} \bigl( -d ^{\nu }t^{\nu } \bigr) , \end{aligned}$$
(22)

where \(E_{\nu ,\nu (2r+\frac{\mu }{\mathtt{k}})+1} ( -d^{\nu }t ^{\nu } ) \) is given in (20).

Proof

The Sumudu transform of Riemann-Liouville fractional integral operators is given by

$$\begin{aligned} S \bigl\{ {}_{0}D_{t}^{-\nu }f(t);u \bigr\} =u^{\nu }G(u), \end{aligned}$$
(23)

where \(G(u)\) is defined in (8). Now, applying the Sumudu transform to both sides of (21) and applying the definition of k-Struve function given in (3), we have

$$\begin{aligned} N^{*}(u) &=S \bigl[ N ( t ) ;u \bigr] \\ &=N_{0}S \bigl[ \mathtt{S}_{\mu ,c}^{\mathtt{k}} \bigl( d^{\nu }t^{ \nu } \bigr) ;u \bigr] -d^{\nu }S \bigl[ {}_{0}D_{t}^{-\nu }N ( t ) ;u \bigr] \\ &=N_{0} \Biggl[ \int_{0}^{\infty }e^{-pt}\sum _{r=0}^{\infty }\frac{ ( -c ) ^{r}}{\Gamma_{\mathtt{k}} ( r\mathtt{k}+\mu + \frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{d^{\nu }(ut)^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{ \mathtt{k}}+1}\,dt \Biggr] \\ &\quad {}-d^{\nu }u^{\nu }N^{*} ( u ) , \end{aligned}$$
(24)

where

$$\begin{aligned} S \bigl\{ t^{\mu -1} \bigr\} =u^{\mu -1}\Gamma (\mu ). \end{aligned}$$
(25)

By rearranging terms, we get

$$\begin{aligned} &N^{*} ( u ) +d^{\nu }u^{\nu }N^{*} ( u ) \\ &\quad =N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}}{ \Gamma_{\mathtt{k}} ( r\mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{d^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{\mathtt{k}}+1} \\ &\quad \quad {}\times \int_{0}^{\infty }e^{-t} ( ut ) ^{\nu (2r+\frac{ \mu }{\mathtt{k}}+1)}\,dt \\ &\quad =N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [\nu (2r+\frac{ \mu }{\mathtt{}k}+1)+1]}{\Gamma_{\mathtt{k}} ( r\mathtt{k}+ \mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{u^{\nu }d^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{\mathtt{k}}+1}. \end{aligned}$$

Therefore

$$\begin{aligned} N^{*} ( u ) &=N_{0}\sum _{r=0}^{\infty }\frac{ ( -c ) ^{r}\Gamma [\nu (2r+\frac{\mu }{\mathtt{}k}+1)+1]}{\Gamma_{\mathtt{k}} ( r\mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+ \frac{3}{2} ) } \biggl( \frac{d^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{ \mathtt{k}}+1} \\ &\times \Biggl\{ u^{\nu (2r+\frac{\mu }{\mathtt{k}}+1)}\sum_{n=0}^{ \infty } \bigl[ -(du)^{\nu } \bigr] ^{n} \Biggr\} . \end{aligned}$$
(26)

Taking the inverse Sumudu transform of (26) and by using

$$\begin{aligned} S^{-1} \bigl\{ u^{\nu };t \bigr\} = \frac{t^{\nu -1}}{\Gamma ( \nu ) },\quad \Re ( \nu ) >0, \end{aligned}$$
(27)

we have

$$\begin{aligned} S^{-1} \bigl\{ N^{*} ( u ) \bigr\} &=N_{0}\sum _{r=0}^{\infty }\frac{ ( -c ) ^{r}\Gamma [\nu (2r+\frac{\mu }{\mathtt{}k}+1)+1]}{ \Gamma_{\mathtt{k}} ( r\mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \biggl( \frac{d^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{\mathtt{k}}+1} \\ &\quad \times S^{-1} \Biggl\{ \sum_{n=0}^{\infty }(-1)^{n}(d)^{\nu n}u^{ \nu (2r+\frac{\mu }{\mathtt{k}}+n+1)} \Biggr\} , \end{aligned}$$

which gives

$$\begin{aligned} N(t) &=N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu (2r+\frac{\mu }{\mathtt{k}}+1)+1]}{\Gamma_{\mathtt{k}} ( r \mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+ \frac{3}{2} ) } \biggl( \frac{d^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{ \mathtt{k}}+1} \\ & \quad {}\times \Biggl\{ \sum_{n=0}^{\infty }(-1)^{n}(d)^{\nu n} \frac{t^{ \nu ( 2r+\frac{\mu }{\mathtt{k}}+n+1 ) -1}}{\Gamma [ \nu ( 2r+\frac{\mu }{\mathtt{k}}+n+1 ) ] } \Biggr\} \\ & =N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [\nu (2r+\frac{ \mu }{\mathtt{k}}+1)+1]}{\Gamma_{\mathtt{k}} ( r\mathtt{k}+ \mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{d^{\nu }t^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{ \mathtt{k}}+1} \\ & \quad {}\times \Biggl\{ \sum_{n=0}^{\infty }(-1)^{n}(d)^{\nu n} \frac{t^{ \nu }}{\Gamma [ \nu ( 2r+\frac{\mu }{\mathtt{k}}+n+1 ) ] } \Biggr\} \\ & =N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu ( 2r+\frac{\mu }{\mathtt{k}}+1 ) +1 ] }{\Gamma_{ \mathtt{k}} ( r\mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{d^{\nu }t ^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{\mathtt{k}}+1} \\ &\quad \times E_{\nu ,\nu (2r+\frac{\mu }{\mathtt{k}})+1} \bigl( -d^{\nu }t ^{\nu } \bigr) , \end{aligned}$$

which is the desired result. □

Corollary 1

If we put \(\mathtt{k}=1\) in ( 22 ), then we get the solution of involving the classical Struve function as follows: If \(d>0,\nu >0, \mu , c, t\in \mathbb{C}\) and \(\mu >-\frac{3}{2}\), then the equation

$$ N ( t ) =N_{0}~\mathtt{S}_{\mu ,c}^{1} \bigl( d^{\nu }t^{ \nu } \bigr) -d^{\nu }\text{ }_{0}D_{t}^{-\nu }N ( t ) $$
(28)

has the solution

$$\begin{aligned} N ( t ) &=N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu ( 2r+\mu +1 ) +1 ] }{\Gamma ( r+ \mu +\frac{3}{2} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{d^{\nu }t^{\nu }}{2} \biggr) ^{2r+\mu +1} \\ &\quad {}\times E_{\nu ,\nu (2r+\mu )+1} \bigl( -d^{\nu }t^{\nu } \bigr) . \end{aligned}$$
(29)

Theorem 2

If \(\mathfrak{a}>0, d>0, \nu >0,c,\mu ,t\in \mathbb{C}, \mathfrak{a} \neq d\) and \(\mu >-\frac{3}{2}\mathtt{k}\), then the solution of equation

$$ N ( t ) =N_{0}~\mathtt{S}_{\mu ,c}^{\mathtt{k}} \bigl( {d} ^{\nu }t^{\nu } \bigr) -{\mathfrak{a}}^{\nu }\text{ }_{0}D_{t}^{- \nu }N ( t ) $$
(30)

is given by

$$\begin{aligned} N ( t ) &=N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu ( 2r+\frac{\mu }{\mathtt{k}}+1 ) +1 ] }{ \Gamma_{\mathtt{k}} ( r\mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{d^{\nu }t ^{\nu }}{2} \biggr) ^{2r+\frac{\mu }{\mathtt{k}}+1} \\ &\quad {}\times E_{\nu ,\nu (2r+\frac{\mu }{\mathtt{k}})+1} \bigl( -{\mathfrak{a}} ^{\nu }t^{\nu } \bigr) , \end{aligned}$$
(31)

where \(E_{\nu ,\nu (2r+\frac{\mu }{\mathtt{k}})+1}(\cdot)\) is given in (20).

Proof

Theorem 2 can be proved in parallel with the proof of Theorem 1. So the details of proofs are omitted. □

Corollary 2

By putting \(\mathtt{k}=1\) in Theorem 2, we get the solution of fractional kinetic equation involving classical Struve function: If \(\mathfrak{a}>0, d>0, \nu >0,c,\mu ,t\in \mathbb{C}, \mathfrak{a} \neq d\) and \(\mu >-\frac{3}{2}\), then the equation

$$ N ( t ) =N_{0}~\mathtt{S}_{\mu ,c}^{1} \bigl( {d}^{\nu }t^{ \nu } \bigr) -{\mathfrak{a}}^{\nu }\text{ }_{0}D_{t}^{-\nu }N ( t ) $$
(32)

is given by the following formula:

$$\begin{aligned} N ( t ) &=N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu ( 2r+\mu +1 ) +1 ] }{\Gamma ( r+ \mu +\frac{3}{2} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{d^{\nu }t^{\nu }}{2} \biggr) ^{2r+\mu +1} E_{\nu ,\nu (2r+\mu )+1} \bigl( -{\mathfrak{a}}^{\nu }t^{ \nu } \bigr) . \end{aligned}$$
(33)

Theorem 3

If \(d>0,\nu >0,c,\mu ,t\in \mathbb{C}\) and \(\mu >-\frac{3}{2} \mathtt{k}\), then the solution of

$$ N ( t ) =N_{0}~\mathtt{S}_{\mu ,c}^{\mathtt{k}} \bigl( t^{ \nu } \bigr) -d^{\nu } {}_{0}D_{t}^{-\nu }N ( t ) $$
(34)

is given by

$$\begin{aligned} N ( t ) &=N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu ( 2r+\frac{\mu }{\mathtt{k}}+1 ) +1 ] }{ \Gamma_{\mathtt{k}} ( r\mathtt{k}+\mu +\frac{3}{2}\mathtt{k} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{t}{2} \biggr) ^{2r+\frac{\mu }{\mathtt{k}}+1} \\ &\quad {}\times E_{\nu ,\nu (2r+\frac{\mu }{\mathtt{k}})+1} \bigl( -{{d}}^{ \nu }t^{\nu } \bigr) , \end{aligned}$$
(35)

where \(E_{\nu ,\nu (2r+\frac{\mu }{\mathtt{k}})+1}(\cdot)\) is given in (20).

Proof

The proofs of Theorem 3 would run parallel to those of Theorem 1. □

Corollary 3

If we set \(\mathtt{k}=1\), then (35) is reduced as follows: If \(d>0,\nu >0,c,\mu ,t\in \mathbb{C}\) and \(\mu >-\frac{3}{2}\), then the solution of the following equation

$$ N ( t ) =N_{0}~\mathtt{S}_{\mu ,c}^{1} \bigl( t^{\nu } \bigr) -d ^{\nu } {}_{0}D_{t}^{-\nu }N ( t ) $$
(36)

is given by the formula

$$\begin{aligned} N ( t ) &=N_{0}\sum_{r=0}^{\infty } \frac{ ( -c ) ^{r}\Gamma [ \nu ( 2r+\mu +1 ) +1 ] }{\Gamma ( r+ \mu +\frac{3}{2} ) \Gamma ( r+\frac{3}{2} ) } \frac{1}{t} \biggl( \frac{t}{2} \biggr) ^{2r+\mu +1} \\ &\quad {}\times E_{\nu ,\nu (2r+\mu )+1} \bigl( -{{d}}^{\nu }t^{\nu } \bigr) . \end{aligned}$$
(37)

3 Graphical interpretation

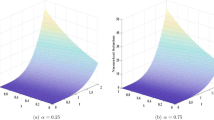
In this section, first we plot the graphs of our solutions of the fractional kinetic equation, which is established in (22). In each graph, we give three solutions of the results on the basis of assigning different values to the parameters. In Figure 1, we take \(\mathtt{k}=1\) and \(\nu =0.5, 0.7, 0.9,1, 1.5\). Similarly, Figures 2, 3 are plotted respectively by taking \(\mathtt{k}=2\) and 3. Figures 4, 5, 6 are plotted by considering the solution given in (35) by taking \(\nu =0.5, 0.7, 0.9, 1, 1.5\) and \(\mathtt{k}=1,2,3\). Other than ν and k, all other parameters are fixed by 1. Observing these figures, we see that \(N{(t)}>0\) for \(t>0\) and the behavior of the solutions for different parameters and time interval can be studied and observed very easily. In this study, we choose first 50 terms of Mittag-Leffler function and first 50 terms of our solutions to plot the graphs. Also, the comparison between solutions of generalized fractional kinetic equations involving generalized Bessel function (solid green line) and k-Struve function (dashed red line) are shown in Figure 7.

Figure 1
figure 1

Solution ( 22 ) for \(\pmb{N(t),\mathtt{k}=1}\) .

Full size image
Figure 2
figure 2

Solution ( 22 ) for \(\pmb{N(t),\mathtt{k}=2}\) .

Full size image
Figure 3
figure 3

Solution ( 22 ) for \(\pmb{N(t),\mathtt{k}=3}\) .

Full size image
Figure 4
figure 4

Solution ( 35 ) for \(\pmb{N(t),\mathtt{k}=1}\) .

Full size image
Figure 5
figure 5

Solution ( 35 ) for \(\pmb{N(t),\mathtt{k}=2}\) .

Full size image
Figure 6
figure 6

Solution ( 35 ) for \(\pmb{N(t),\mathtt{k}=3}\) .

Full size image
Figure 7
figure 7

Comparison between solutions ( 22 ) and (18) of [ 51 ].

Full size image

4 Conclusion

In this work, we have established the solution of fractional kinetic equation involving k-Struve function with the help of the Sumudu transform and provided its graphical interpretations. From the close relationship of the k-Struve function with other special functions, one can easily construct various known and new fractional kinetic equations.