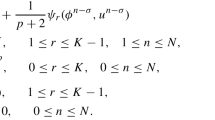Numerical solutions of nonlinear fractional model arising in the appearance of the strip patterns in two-dimensional systems

Abstract

The main aim of this paper is to present a comparative study of modified analytical technique based on auxiliary parameters and residual power series method (RPSM) for Newell–Whitehead–Segel (NWS) equations of arbitrary order. The NWS equation is well defined and a famous nonlinear physical model, which is characterized by the presence of the strip patterns in two-dimensional systems and application in many areas such as mechanics, chemistry, and bioengineering. In this paper, we implement a modified analytical method based on auxiliary parameters and residual power series techniques to obtain quick and accurate solutions of the time-fractional NWS equations. Comparison of the obtained solutions with the present solutions reveal that both powerful analytical techniques are productive, fruitful, and adequate in solving any kind of nonlinear partial differential equations arising in several physical phenomena. We addressed $L_{2}$ and $L_{\infty }$ norms in both cases. Through error analysis and numerical simulation, we have compared approximate solutions obtained by two present aforesaid methods and noted excellent agreement. In this study, we use the fractional operators in Caputo sense.

1 Introduction

Differential equations of nonlinear nature are a practically very useful device for recitation of different physical phenomena, particularly when it is fractional in character. In support of illustration, these equations are gradually more applied to the problems related to diverse branches of engineering [1,2,3,4]. An enormous attempt has been taken throughout the previously years to get healthy and proficient arithmetical and logical methods for solving nonlinear fractional differential equations (FDEs) [5,6,7,8,9,10,11,12,13,14]. This work emphasized that the NSW equation is taken to find the solutions using aforesaid methods. The modified homotopy analysis transform method (MHATM) method is a combination of the Laplace transform and homotopy analysis methods with HP [15,16,17,18]. The RPSM is constructed from the generalized Taylor series, which is a prevailing technique for solving nonlinear FDEs [19,20,21,22,23,24]. The advantage of the RPSM method is that it is not affected by computational round-off errors and also does not require large computer memory and extensive time. Moreover, this method computes the coefficients of the power series by a chain of equations with one or more variables, which indicates a better convergence of the RPSM.

Recently, the NWS equation gained more attention because NWS plays a vital part in nonlinear systems. The NWS equation describes the appearance of the stripe pattern in two-dimensional systems. Moreover, as this is an important model in the field of fluid dynamics, it has numerous applications in fluid dynamics such as traveling wave patterns in binary fluids. A new approach using ADM to evaluate the numerical solution of TFNWS is mentioned in [25]. In [26] the authors analyzed the fractional NWS equation for Riemann fractional space–time, space, and time derivatives. Two methods, Laplace decomposition and finite difference, to solve the numerical approximation of NWS equations are given in [27]. Investigations related to the mathematical biological model in connection with the NWS equation are presented by Korkmaz [28]. Approximate solutions of the NWS using a new iterative method are given in [29]. In [30] the authors gave a comparative study on the reduced transform method and ADM insight of NWS equation, and in [31] a combined form of ADM and Elzaki method is used to solve the NWS equations. Numerous papers studied the solutions of NWS equation by applying different approaches. In [32] the tanh function technique is used to get the exact solution of generalized NWS, and in [33] the HPM is used to solve the nonlinear NWS differential equations. To approximate the solutions of NWS equation from fluid mechanics, Macías-Díaz and Ruiz-Ramírez [34] proposed a method called the finite-difference method. The class of NWS equations with Lie and “nonclassical” symmetry points of view was studied in [35]. Some papers used the variational iteration method (VIM) or modified VIM to solve the NWS equations [36, 37]. Graham [38] studied the two-dimensional NWS equations (also see [39]. Kumar and Sharma [40] combined the HAM and Sumudu transform (ST) to solve the NWS equation. The linear and nonlinear NWS equations are evaluated in [41] with the help of HPM and a hybrid of the Fourier transform and ADM. The NWS amplitude equation and algebraic traveling wave NWS equation were studied in [42] and [43], respectively. For more detail on fractional-order NWS equations in diverse points of view, we refer the interesting readers to the recent papers [44, 45].

We consider the fractional model of NWS equation [30] in the operator form

$$ D^{\lambda }_{t} \xi (\eta , t) = k D ^{2}_{\eta } \xi (\eta , t) + a\xi (\eta ,t)- b \xi ^{c}(\eta , t),\quad 0< \lambda \leq 1, $$

(1.1)

with initial condition

$$ \xi (\eta ,0)= f(\eta ), $$

(1.2)

where c is positive integer, k, a, and $b \in \mathbb{R}$ (real numbers) with $k>0$, and $D^{\lambda }$ is the Caputo derivative of order λ. The first term $D=\frac{\partial \xi }{\partial \eta }$ represents the variation of $\xi (\eta ,t)$ with time and fixed location. The term $D^{2}=\frac{\partial ^{2} \xi }{\partial \eta ^{2}}$ denotes the variation with variable η at a particular time, and the remaining term $a\xi - b \xi ^{c}$ signifies the effect of the source term. Various methods are applied to solve different types of NWS equations in physics [31, 46,47,48,49].

Theorem 1.1

Let f be a function represented by a fractional power series (FPS) at $t=t_{0}$

$$ \sum_{k=0}^{\infty }\sum _{l=0}^{m-1} d_{kl}(\eta ) (t-t_{0})^{k\lambda + l},\quad 0\leq m-1< \lambda \leq m, t_{0} \leq t < t_{0}+\mathbb{R}. $$

If $D^{k\lambda + l} f(t)$ are continuous on $(t_{0},t_{0}+\mathbb{R})$, $k=0,1,2,\ldots$ , then the coefficients $d_{kl}$ are given by

$$ d_{kl}=\frac{D^{k\lambda + l} f(t_{0})}{\varGamma (k \lambda + l+1)},\quad k=0,1,2,\ldots, $$

where $D^{k \lambda } = D^{\lambda }$, $D^{\lambda },\ldots,D^{\lambda }$ (k times), and the radius of convergence is $\mathbb{R}$.

2 Basic idea of MHATM

2.1 The analytical procedure

The fundamental scheme of the MHATM is illustrated by taking common appearance of FDEs:

$$ D^{\lambda }_{t} \xi (\eta ,t)+ K[\eta ] \xi (\eta ,t)+M[\eta ] \xi (\eta ,t)= Q(\eta ,t), \quad t>0, \eta \in \mathbb{R}, 0< \lambda \leq 1, $$

(2.1)

where $K[\eta ]$ and $M[\eta ]$ are linear and nonlinear terms, respectively, and $Q(\eta ,t)$ and $\xi (\eta ,t)$ are continuous and unknown functions, respectively. For clearness, we neglect all conditions.

Now the methodology consists of first applying the Laplace transform to both sides of equation (2.1):

$$ L\bigl[D^{\lambda }_{t} \xi (\eta ,t)+ K[ \eta ] \xi (\eta ,t)+M[\eta ] \xi (\eta ,t)\bigr]= L\bigl[Q(\eta ,t)\bigr]. $$

(2.2)

Next, using the differentiation property of the Laplace transform, we have

$$ L\bigl[\xi (\eta ,t)\bigr]-\frac{1}{s^{\lambda }}\sum _{k=0}^{n-1} s^{\lambda -k-1}\xi ^{k}(\eta ,0)+\frac{1}{s^{ \lambda }} L \bigl(K[\eta ] \xi (\eta ,t)+M[\eta ] \xi (\eta ,t)- Q( \eta ,t) \bigr)=0. $$

(2.3)

We define the nonlinear operator

$$ \begin{aligned}[b] N\bigl[\aleph (r,t;z)\bigr]&= L\bigl[\aleph (\eta ,t;z)\bigr]-\frac{1}{s^{\lambda }} \sum_{k=0}^{n-1} s^{\lambda -k-1}\xi ^{k}(\eta ,0)\\ &\quad {}+\frac{1}{s^{\lambda }}L \bigl(K[\eta ] \xi (\eta ,t)+M[\eta ] \xi (\eta ,t)- Q(\eta ,t) \bigr), \end{aligned} $$

(2.4)

where $z \in [0,1]$ is an embedding parameter, and $\aleph (\eta ,t;z)$ is a real function of η, t, and z. Generalizing the traditional homotopy analysis methods [50], we construct the zero-order deformation equation

$$ (1-z)L\bigl[\aleph (\eta ,t;z)-\xi _{0}(\eta ,t)\bigr]=\hbar z H(\eta ,t)N\bigl[ \aleph (\eta ,t;z)\bigr], $$

(2.5)

where ħ is a nonzero auxiliary parameter, which helps us to increase the convergence, $H(\eta ,t)$ is an auxiliary function, $\xi _{0}(\eta ,t)$ is an initial guess of $\xi (\eta ,t)$, and $\aleph (\eta ,t;z)$ is an unknown function.

Consequently, we obtain the mth-order deformation equation

$$\begin{aligned} \xi _{m}(\eta ,t) &=(\chi _{m}+ \hbar ) \xi _{m-1}- \hbar (1-\chi _{m}) \sum_{i=0}^{j-1} t^{i} \xi ^{(i-1)}(0) \\ &\quad {}+\hbar L^{-1} \Biggl(\frac{1}{s^{\lambda }} L \Biggl(K_{m-1}[t] \xi _{m-1}(t)+ \sum _{k=0}^{m-1} P_{k}(\xi _{0},\xi _{1},\ldots ,\xi _{m})-Q( \eta ,t) \Biggr) \Biggr), \end{aligned}$$

(2.6)

where $P_{k}$ is the HP given by [15].

For the expediency point of view, the appearance of nonlinear operator form has been customized in HATM, that is, the nonlinear term $M[\eta ,t] \xi (\eta ,t)$ is stretched in the form of HP as

$$ M\bigl[\xi (\eta ,t)\bigr]= M \Biggl(\sum_{k=0}^{m-1} \xi _{m}(\eta ,t) \Biggr)= \sum_{m=0}^{\infty }P_{m} \xi ^{m}. $$

(2.7)

The innovation of our planned algorithm is to construct and escalate the nonlinear expression as a sequence of HP in equation (2.6). Next, from equation (2.6) we can compute different values of $\xi _{m}(\eta ,t)$ for $m\geq 1$. Consequently, we find the whole series solution of equation (2.1) as

$$ \xi (\eta ,t)= \xi _{0} (\eta ,t)+ \sum_{m=1}^{\infty } \xi _{m} (\eta ,t). $$

(2.8)

To illustrate the efficiency and accuracy of the MHATM, we consider two examples.

Example 1

Taking the constant values $k=-1$, $a=-2$, and $b=0$ in Eq. (1.1). Therefore Eq. (1.1) is reduced to the linear TFNWS equation [30]

$$ D^{\lambda }_{t} \xi (\eta ,t)= D ^{2}_{\eta } \xi (\eta ,t) - 2 \xi (\eta ,t), \quad 0< \lambda \leq 1, $$

(2.9)

with initial condition $\xi (\eta ,0)= e^{\eta }$ and exact solution $\xi _{\mathrm{exact}}(\eta ,t)=e^{\eta -t}$, respectively [30].

Taking the Laplace transform of both sides of equation (2.9), we get

$$ s^{\lambda } L\bigl[\xi (\eta ,t)\bigr]-s^{\lambda -1} \xi (\eta ,0)- L \bigl[D^{2} _{\eta } \xi - 2 \xi \bigr]=0. $$

(2.10)

In this case the nonlinear operator defined as

$$ N\bigl[\aleph (\eta ,t;z)\bigr]= L \bigl[\aleph (\eta ,t;z)\bigr]- \frac{1}{s} e^{\eta }-s ^{-\lambda } L \bigl[D^{2}_{\eta } \aleph (\eta ,t;z) - 2 \aleph (\eta ,t;z)\bigr]. $$

(2.11)

Thus we obtain the mth-order deformation equation

$$ L\bigl[\xi (\eta ,t)-\chi _{m} \xi _{m-1}(\eta ,t)\bigr]= \hbar R_{m}(\vec{\eta } _{m-1},\eta ,t). $$

(2.12)

Taking the inverse Laplace transform of both sides in equation (2.12), we get

$$ \xi (\eta ,t)=\chi _{m} \xi _{m-1}(\eta ,t) + \hbar L^{-1} \bigl[R_{m}( \vec{\eta }_{m-1},\eta ,t) \bigr], $$

(2.13)

where

$$\begin{aligned} R_{m}(\vec{\eta }_{m-1},\eta ,t) &= L[\xi _{m-1}]- \frac{1-\chi _{m}}{s} e^{\eta }-s^{-\lambda }L\bigl[D^{2}_{\eta } \xi - 2 \xi \bigr],\quad m \ge 1. \end{aligned}$$

(2.14)

Now the solution of the mth-order deformation equation is

$$\begin{aligned} \xi _{m}(\eta ,t) &=(\chi _{m} +\hbar ) \xi _{m-1}(\eta ,t)-\hbar (1-\chi _{m}) e^{\eta }-\hbar L^{-1}\bigl[s^{-\lambda } L\bigl[D^{2}_{\eta } \xi - 2 \xi \bigr]\bigr]. \end{aligned}$$

(2.15)

With means of $\xi _{0}(\eta ,t)=\xi (\eta ,0)= e^{\eta }$ and equation (2.15) we obtain

$$\begin{aligned} \xi _{1}(\eta ,t) &=\frac{\hbar e^{\eta } t^{\lambda }}{\varGamma ( \lambda +1)}, \\ \xi _{2}(\eta ,t) &= \frac{\hbar (1+\hbar ) e^{\eta } t^{\lambda }}{ \varGamma (\lambda +1)}+ \frac{\hbar ^{2} e^{\eta } t^{2\lambda }}{ \varGamma (2\lambda +1)}, \\ \xi _{3}(\eta ,t) &= \frac{\hbar (1+\hbar )^{2} e^{\eta } t^{\lambda }}{\varGamma (\lambda +1)}+ 2 \frac{\hbar ^{2} (1+\hbar ) e^{\eta } t ^{2\lambda }}{\varGamma (2\lambda +1)}+ \frac{\hbar ^{3} e^{\eta } t ^{3\lambda }}{\varGamma (3\lambda +1)}, \\ \xi _{4}(\eta ,t) &= \frac{\hbar (1+\hbar )^{3} e^{\eta } t^{\lambda }}{\varGamma (\lambda +1)}+ 3 \frac{\hbar ^{2} (1+\hbar )^{2} e^{\eta } t ^{2\lambda }}{\varGamma (2\lambda +1)}+ 3 \frac{\hbar ^{3} (1+\hbar ) e ^{\eta } t^{3\lambda }}{\varGamma (3\lambda +1)}+ \frac{\hbar ^{4} e ^{\eta } t^{4\lambda }}{\varGamma (4\lambda +1)},\qquad \dots . \end{aligned}$$

With the help of Mathematica-7 software, the rest of the components $\xi _{n}(\eta ,t)$ for $n\geq 5$ can be completely obtained. Hence, the solution of equation (2.9) is given as

$$\begin{aligned} \xi (\eta ,t)= \xi _{0}(\eta ,t)+ \xi _{1}(\eta ,t) + \xi _{2}(\eta ,t) + \xi _{3}(\eta ,t)+\cdots . \end{aligned}$$

(2.16)

If we choose $\hbar =-1$, then

$$\begin{aligned} \xi _{m}(\eta ,t) & = e^{\eta } \biggl(1+ \frac{(-t^{\lambda })}{\varGamma ( \lambda +1)}+ \frac{(-t^{\lambda })^{2}}{\varGamma (2\lambda +1)}+ \frac{(-t ^{\lambda })^{3}}{\varGamma (3\lambda +1)} +\frac{(-t^{\lambda })^{4}}{ \varGamma (4\lambda +1)}+\cdots \biggr) \\ & =e^{\eta } \sum^{\infty }_{k=0}{ \frac{(-t^{\lambda })^{k}}{ \varGamma (k\lambda +1)}} \\ & =e^{\eta } E_{\lambda } \bigl(-t^{\lambda }\bigr). \end{aligned}$$

If we choose $\lambda =1$, then we evidently find that $\sum^{\infty }_{m=0}{\xi _{m}(\eta ,t)}$ converges to the exact solution $\xi ( \eta ,t)= e^{\eta -t}$. Also, this outcome is entirely conform to Saravanan and Magesh [30].

Example 2

Here taking the constant values $k=1$, $a=2$, $b=3$, and $c=2$ in Eq. (1.1), we get the nonlinear TFNSW equation [30]

$$ D^{\lambda }_{t} \xi (\eta ,t)= D ^{2}_{\eta } \xi (\eta ,t) + 2 \xi (\eta ,t) -3 \xi ^{2}(\eta ,t), \quad 0< \lambda \leq 1, $$

(2.17)

with initial condition $\xi (\eta ,0)= \beta$ and exact solution $\xi _{\mathrm{exact}}(t)= \frac{\frac{-2}{3} \beta e^{2t}}{ \frac{-2}{3}+ \beta - \beta e^{2t}}$, respectively [30].

Now, applying the technique as in Example 1, in this case the nonlinear operator is

$$ N\bigl[\aleph (\eta ,t;z)\bigr]= L \bigl[\aleph (\eta ,t;z)\bigr]- \frac{1}{s} \beta -s ^{-\lambda } L \bigl[D^{2}_{\eta } \aleph (\eta ,t;z) + 2 \aleph (\eta ,t;z)-3 \aleph ^{2}(\eta ,t;z) \bigr]. $$

(2.18)

Consequently, we get the solution of mth-order deformation equation:

$$\begin{aligned} \xi _{m}(\eta ,t) &=(\chi _{m} +\hbar ) \xi _{m-1}(\eta ,t)-\hbar (1-\chi _{m}) \beta -\hbar L^{-1} \bigl[s^{-\lambda } L \bigl[D^{2}_{\eta } \xi _{m-1} + 2 \xi _{m-1}-3 P_{k} \bigr] \bigr], \end{aligned}$$

(2.19)

where $P_{k}$ is the HP given by

$$\begin{aligned} P_{k}= \frac{1}{\varGamma (m+1)} \biggl[\frac{\partial ^{m}}{\partial q ^{m}} N \bigl[\bigl(q \phi (\eta ,t;q)\bigr) \bigl(q\phi (\eta ,t;q)\bigr)_{\eta } \bigr] \biggr] _{q=0}. \end{aligned}$$

(2.20)

Using $\xi _{0}(\eta ,t)=\xi (\eta ,0)=\beta$, we obtain the following values:

$$\begin{aligned}& \xi _{1}(\eta ,t) =-\frac{\beta (2-3\beta ) \hbar t^{\lambda }}{ \varGamma (\lambda +1)}, \\& \xi _{2}(\eta ,t) = -\frac{\beta (2-3\beta ) \hbar (1+\hbar ) t^{ \lambda }}{\varGamma (\lambda +1)}+ \frac{ (2\beta (2-9\beta )+18\beta ^{3} ) \hbar ^{2} t^{2\lambda }}{\varGamma (2\lambda +1)}, \\& \begin{aligned} \xi _{3}(\eta ,t) &= -\frac{\beta (2-3\beta ) \hbar (1+\hbar )^{2} t ^{\lambda }}{\varGamma (\lambda +1)}+ \frac{4 \beta (2-9\beta +9\beta ^{2}) \hbar ^{2}(1+\hbar ) t^{2\lambda }}{\varGamma (2\lambda +1)} \\ &\quad {}-\frac{4\beta (2-3\beta )(1-3\beta )^{2} \hbar ^{3} t^{3\lambda }}{ \varGamma (3\lambda +1)},\qquad \dots . \end{aligned} \end{aligned}$$

With the help of Mathematica-7 software we can obtain the remaining terms of $\xi _{n}(\eta ,t)$ for $n\geq 4$.

2.2 Convergence analysis

Theorem 2.1

The obtained series solution (2.8) converges if

$$\begin{aligned} \sum^{+\infty }_{m=0}{R_{m}(\vec{\xi }_{m-1}, \eta , t)}=0. \end{aligned}$$

(2.21)

Proof

Since the series (2.8), that is, $\xi (\eta ,t)= \xi _{0} ( \eta ,t)+\sum_{m=1}^{\infty }\xi _{m} (\eta ,t)$, converges, we can write $S(t)= \sum_{m=0}^{\infty }\xi _{m} (\eta ,t)$, and by the necessary condition for the convergence of the series we have that $\lim_{m\rightarrow +\infty } \xi _{m} (\eta ,t)=0$.

Now the mth-order deforming equation is

$$ \mathcal{L}\bigl[\xi _{m}(\eta ,t)-\chi _{m} \xi _{m-1}(\eta ,t)\bigr]=\hbar R_{m}( \vec{\xi }_{m-1}, \eta ,t). $$

(2.22)

Summing both sides from $m=1$ to +∞, we get

$$ \sum^{+\infty }_{m=1}{\mathcal{L}\bigl[\xi _{m}(\eta ,t)-\chi _{m} \xi _{m-1}( \eta ,t)\bigr]} = \sum^{+\infty }_{m=1} \hbar R_{m}( \vec{\xi }_{m-1}, \eta ,t), $$

(2.23)

which becomes

$$\begin{aligned}& \mathcal{L} \Bigl[\lim_{m\rightarrow +\infty }\xi _{m} (\eta ,t) \Bigr] = \sum^{+\infty }_{m=1} \hbar R_{m}(\vec{\xi }_{m-1},\eta ,t) \end{aligned}$$

(2.24)

$$\begin{aligned}& \quad \Rightarrow\quad \sum^{+\infty }_{m=1} \hbar R_{m}(\vec{\xi }_{m-1}, \eta ,t)= 0. \end{aligned}$$

(2.25)

Since $\hbar \neq 0$, we have

$$\begin{aligned} \sum^{+\infty }_{m=0}{R_{m}(\vec{\xi }_{m-1}, \eta , t)}=0. \end{aligned}$$

(2.26)

 □

Theorem 2.2

If the series solution (2.8) converges, then it is a solution of equation (2.1).

Proof

Let $\mu (\eta ,t;q)= N[\phi (\eta ,t;q)]$ denote the residual error of equation (2.1). The residual error at $q = 1$ can be extended by a Taylor formula at $q = 0$:

$$\begin{aligned} \mu (\eta ,t;q=1) &= \sum^{+\infty }_{m=0} \frac{1}{m!} \frac{\partial ^{m} N[\phi (\eta ,t;q)]}{\partial q^{m}}\bigg|_{q=0} \\ & =\sum^{+\infty }_{m=0}{R_{m}(\eta ,t)} \\ & = 0. \end{aligned}$$

Thus the series solution (2.8) converges and so is a solution of equation (2.1). □

3 Basic idea of residual power series method

3.1 The analytical procedure

The method is discussed through the FDEs

$$ D^{\lambda }_{t} \xi (\eta ,t)+ K[\eta ] \xi (\eta ,t)+M[\eta ] \xi (\eta ,t)= Q(\eta ,t),\quad t>0, \eta \in \mathbb{R} , n-1< n\lambda \leq n, $$

(3.1)

where $K[\eta ]$, $M[\eta ]$, and $Q(\eta ,t)$ are defined as before. Let

$$ f_{0}(\eta )=\xi (\eta ,0)= f(\eta ),\qquad f _{n-1}(\eta )=D^{t}_{(n-1)\lambda }\xi (\eta ,0)= h(\eta ). $$

(3.2)

The final solution for equation (3.1) can be written as

$$ \xi (\eta ,t)= {\sum_{k=0}^{\infty } \sum_{l=0}^{m-1}} f_{kl}(\eta ) \frac{ (t-t_{0} )^{k\lambda +l}}{\varGamma (k\lambda +l+1 )}, \quad m-1< \lambda \leq m, \eta \in \mathbb{R}, 0 \leq t < \mathbb{R}, $$

(3.3)

where

$$ \xi _{(0,m-1)}(\eta ,t)= \sum_{l=0}^{m-1} \frac{\phi _{l}(\eta )}{l!} (t-t_{0} )^{l}, \quad \eta \in \mathbb{R}, t_{0}\leq t < t_{0}+\mathbb{R}. $$

(3.4)

By equation (3.4) we can write equation (3.3) as

$$ \xi (\eta ,t)= \sum_{l=0}^{m-1} \frac{\phi _{l}(\eta )}{l!} (t-t _{0} )^{l}+ \sum _{k=1}^{\infty } \sum_{l=0}^{m-1} f_{kl}(\eta ) \frac{ (t-t_{0} )^{k\lambda +l}}{\varGamma (k\lambda +l+1)} , \quad \eta \in \mathbb{R}, t_{0}\leq t < t_{0}+\mathbb{R}. $$

(3.5)

By the procedure described in [19,20,21] we get the following $(a,b)$-truncated residual function:

$$ \begin{aligned}[b] \mathrm{Res}_{(a,b)}(\eta ,t)&= D^{n \lambda }_{t} \xi _{(a,b)}(\eta ,t)+ K[\eta ] \xi _{(a,b)}(\eta ,t)\\ &\quad {}+m[\eta ] \xi _{(a,b)}(\eta ,t)- Q(\eta ,t),\quad \eta \in \mathbb{R}, t\geq t_{0}. \end{aligned} $$

(3.6)

By the procedure described in [19,20,21] we get the following equation:

$$\begin{aligned} &D^{(k-1)\lambda }_{t} D^{l}_{t} \mathrm{Res}( \eta ,t)=D^{(k-1)\lambda } _{t} D^{l}_{t} \mathrm{Res}_{(k,l)}(\eta ,t)=0,\quad \eta \in \mathbb{R}, \\ &\quad k=1,2,3,\ldots,a, l=0,1,2,\ldots,b. \end{aligned}$$

(3.7)

An iterative process is taken until the random order coefficients of the multiple FPS solution are obtained. Finally, a complete solution of equation (3.1) can be found from equation (3.3).

We consider the following problems for the applications of the RPS technique.

Example 3

Consider equation (2.9). According to RPSM technique, by taking $\phi _{0}(\eta )= e^{\eta }$ the series solution of equation (2.9) can be written as

$$ \xi (\eta ,t)= f(\eta )+ \sum_{k=1}^{\infty } f_{k0}(\eta ) \frac{ (t )^{k\lambda }}{\varGamma (k\lambda +1)}, $$

(3.8)

where $\xi _{0,0}(\eta ,t)=f(\eta )$ is the initial value. Next, the $(a,b)$-truncated residual function of equation (2.9) is

$$\begin{aligned}& \xi _{(a,b)}(\eta ,t)= f(\eta )+ \sum _{k=1}^{\infty } f_{k0}(\eta ) \frac{ (t )^{k\lambda }}{\varGamma (k\lambda +1)}, \quad a=1,2,3,\ldots, b=0, \end{aligned}$$

(3.9)

$$\begin{aligned}& \mathrm{Res}_{(a,b)}(\eta ,t)= D^{\lambda }_{t} \xi _{(a,b)} - D_{xx} \xi _{(a,b)}-2 \xi _{(a,b)} , \quad a=1,2,3,\ldots, b=0. \end{aligned}$$

(3.10)

Now according to the methodology of [19], in case of $(k,l)=(1,0)$, putting $t=0$, we get the first coefficient

$$\begin{aligned} f_{10}(\eta ) = -e^{\eta }. \end{aligned}$$

(3.11)

Therefore the $(1,0)$-truncated series of (2.9) is

$$\begin{aligned} \xi _{(1,0)}(\eta ,t) &= e^{\eta } - e^{\eta } \biggl( \frac{t^{\lambda }}{ \varGamma (1+\lambda )} \biggr). \end{aligned}$$

(3.12)

In a similar fashion, we get the remaining terms of $f_{k0}(x)$ for $k \geq 2$: $f_{20}(\eta ) = e^{\eta }$, $f_{30}(\eta ) = -e^{\eta }$, $f _{40}(\eta ) = e^{\eta },\dots$. Therefore the complete solution of (2.9) is

$$\begin{aligned} \xi (\eta ,t) & = e^{\eta } - e^{\eta } \frac{t^{\lambda }}{\varGamma (1+ \lambda )} + e^{\eta } \frac{t^{2\lambda }}{\varGamma (1+2\lambda )} -e ^{\eta } \frac{t^{3\lambda }}{\varGamma (1+3\lambda )}+ e^{\eta } \frac{t ^{4\lambda }}{\varGamma (1+4\lambda )}+\cdots \\ & = e^{\eta } \biggl(1-\frac{t^{\lambda }}{\varGamma (1+\lambda )}+\frac{t ^{2\lambda }}{\varGamma (1+2\lambda )}- \frac{t^{3\lambda }}{\varGamma (1+3 \lambda )} +\frac{t^{4\lambda }}{\varGamma (1+4\lambda )}+\cdots \biggr). \end{aligned}$$

(3.13)

For $\lambda =1$, we get $\xi (\eta ,t)= e^{\eta -t}$, which is an exact solution [30].

Example 4

Consider equation (2.17), According to RPSM technique by taking $\phi _{0}(\eta )= \beta$, we similarly get

$$\begin{aligned}& \xi _{(a,b)}(\eta ,t)= f(\eta )+ \sum _{k=1}^{\infty } f_{k0}(\eta ) \frac{ (t )^{k\lambda }}{\varGamma (k\lambda +1)}, \quad a=1,2,3,\ldots, b=0, \end{aligned}$$

(3.14)

$$\begin{aligned}& \mathrm{Res}_{(a,b)}(\eta ,t)= D^{\lambda }_{t} \xi _{(a,b)} - D_{\eta \eta } \xi _{(a,b)} + 2 \xi _{(a,b)}-3 \xi ^{2}_{(a,b)} , \quad a=1,2,3,\ldots, \quad b=0. \end{aligned}$$

(3.15)

Now from the results of RPSM, in case of $(k,l)=(1,0)$, putting $t=0$, we get

$$\begin{aligned} f_{10}(\eta ) = 2\beta -3 \beta ^{2}. \end{aligned}$$

(3.16)

Hence, the first solution of equation (2.17) is

$$\begin{aligned} \xi _{(1,0)}(\eta ,t) &= \beta - \bigl(2\beta -3 \beta ^{2} \bigr) \biggl(\frac{t ^{\lambda }}{\varGamma (1+\lambda )} \biggr). \end{aligned}$$

(3.17)

In a similar fashion, for the remaining terms $f_{k0}(x)$ for $k \geq 2$, we get $f_{20}(\eta ) = 2\beta (2-3\beta ) (1-3\beta )$, $f _{30}(\eta ) = 2\beta (2-3\beta ) (27\beta ^{2}-18\beta +2),\dots$.

Therefore the complete solution of equation (2.17) is

$$\begin{aligned} \xi (\eta ,t) & =\beta + \bigl(2\beta -3 \beta ^{2}\bigr) \frac{t^{\lambda }}{ \varGamma (1+\lambda )} + 2\beta (2-3\beta ) (1-3\beta )\frac{t^{2\lambda }}{\varGamma (1+2\lambda )} \\ &\quad {} +2\beta (2-3\beta ) \bigl(27\beta ^{2}-18\beta +2\bigr) \frac{t^{3\lambda }}{\varGamma (1+3\lambda )}+\cdots . \end{aligned}$$

(3.18)

For $\lambda =1$, we find $\xi (\eta ,t)=\frac{\frac{-2}{3} \beta e ^{2t}}{\frac{-2}{3}+ \beta - \beta e^{2t}}$, which is an exact one.

3.2 Convergence analysis

Theorem 3.1

(Convergence Theorem)

Suppose that $f_{kl}(\eta )$ has an FPS representation of the form $f_{kl}(\eta )=\sum_{k=0}^{\infty }\sum_{l=0}^{m-1} c_{kl}(\eta )t^{l+k\lambda }$, $0\leq m-1 < \lambda \leq m$, with radius of convergence $\Re (>0)$. Then the series uniformly converges on $[-s, s]$, where $0< s<\Re$.

Proof

Let $\xi _{kl}(\eta )= c_{kl}(\eta )t^{l+k\lambda }$. Since ℜ is the radius of convergence of the FPS, the series absolutely converges for all t such that $\vert t \vert <\Re$.

Hence the series is absolute convergent for all t such that $\vert t \vert \leq s <\Re$ (as $0< s<\Re$).

Therefore the series $\sum_{k=0}^{\infty }\sum_{l=0}^{m-1} c_{kl}( \eta )s^{l+k\lambda }$ converges.

Now $\vert \xi _{kl}(\eta ) \vert = \vert c_{kl}(\eta )t^{l+k \lambda } \vert \leq \vert c_{kl}(\eta ) \vert s^{l+k\lambda }$ for all t such that $\vert t \vert \leq s$.

Let $M_{kl}= \vert c_{kl}(\eta ) \vert s^{l+k\lambda }$ for $k,l,\lambda \in \mathbb{N}$.

Then $\sum_{k=0}^{\infty }\sum_{l=0}^{m-1}M_{kl}$ is a convergent series of positive real numbers, and for all $k,l,\lambda \in \mathbb{N}$, $\vert \xi _{kl}(\eta ) \vert \leq M_{kl}$ for all $t\in [-s,s]$.

By Weierstrass’ M test the series $\sum_{k=0}^{\infty }\sum_{l=0} ^{m-1}\xi _{kl}(\eta )$ uniformly converges on $[-s,s]$.

Consequently, the fractional power series $\sum_{k=0}^{\infty }\sum_{l=0}^{m-1} c_{kl}(\eta )t^{l+k\lambda }$ uniformly converges on $[-s,s]$. □

4 Numerical output and discussion

In this subsection, we discuss the obtained results through the different three-dimensional and two-dimensional figures.

Figure 1 reflects the assessment among the exact solution and 4th-order estimated solution by means of the proposed MHATM method, whereas Fig. 2 shows the corresponding two-dimensional case.

Figure 1

The 4th-order approximate solution of the TFNWS equation: (a) $\eta _{4}(x,t)$ when $\beta =1$. (b) $\eta _{4}(x,t)$ when $\beta =0.75$. (c) $\eta _{4}(x,t)$ when $\beta =0.5$. (d) $\eta _{4}(x,t)$ when $\beta =0.25$. (e) Exact solution $u(x,t)$ when $\beta =1$

Figure 2

Comparison of the 4th term MHATM solution and the exact solution of the TFNWS equation when $x=1$

To confirm the effectiveness and correctness of the MHATM for solving NWS equation, absolute error curves are given in Figs. 3–5. All figures show that our method converges quickly to the original solution only at the 4th-order approximation. Figures 3–5 illustrate that for $\hbar =-1$, the convergence is optimal.

Figure 3

Plot of the absolute error of TFNWS equation when $\hbar =-1$. (a) $E_{4}(\eta )= \vert \eta (x,t)-\eta _{4}(x,t) \vert$. (b) The corresponding $E_{4}(\eta )$ when $t=1$

Figure 4

Plot of the absolute error of TFNWS equation when $\hbar =-1.2$. (a) $E_{4}(\eta )= \vert \eta (x,t)-\eta _{4}(x,t) \vert$. (b) The corresponding $E_{4}(\eta )$ when $t=1$

Figure 5

Plot of the absolute error of TFNWS equation when $\hbar =-0.8$. (a) $E_{4}(\eta )= \vert \eta (x,t)-\eta _{4}(x,t) \vert$. (b) The corresponding $E_{4}(\eta )$ when $t=1$

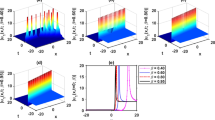
Figure 6 reflects the performance of the estimated solution $\xi _{\mathrm{app}}(\eta ,t)$. Here we find that solution gradually decreases when $\eta =1$ and $\hbar =-1$.

Figure 6

Plot of $\eta _{4}(x,t)$ vs. time t at $x=1$ and different values of β

Table 1 $L_{2}$ and $L_{\infty }$ error norm when $\beta =1$

Table 2 $L_{2}$ and $L_{\infty }$ error norm when $\beta =1$

Figure 7 shows the ħ-curve of TFNSW Eq. (1.1) for different values of λ. We see that the adequate range of ħ is $-1.9\leq \hbar <0$.

Figure 7

Plot of ħ-curve for different values of β

Figure 8 shows the two-dimensional assessment among the exact and estimated solutions obtained by MHATM. At the same time, Figs. 9, 10, and 11 show the absolute error curve for $\hbar =-1$, $\hbar =-1.2$, and $\hbar =-0.8$, respectively.

Figure 8

Comparison of the 4th term MHATM solution and the exact solution of the TFNWS equation when $\lambda =1$

Figure 9

Plot of the absolute error of TFNWS equation when $\hbar =-1$ and $\lambda =1$

Figure 10

Plot of the absolute error of TFNWS equation when $\hbar =-1.2$ and $\lambda =1$

Figure 11

Plot of the absolute error of TFNWS equation when $\hbar =-0.8$ and $\lambda =1$

Figure 12 reflects the performance of the estimated solution $\xi (\eta ,t)$ for different values of λ.

Figure 12

Plot of $\eta _{4}(x,t)$ vs. time t at $x=1$ and different value of β

Nexture, in Fig. 13, the ħ-curve is given, which is also known as converging manage parameter. In this case, we can select that parameter in the range of $-1.6< \hbar < -0.4$.

Figure 13

Plot of ħ-curve for different values of β

4.1 Comparison study

In this subsection, we discuss the comparison between the results obtained by MHATM and RPSM. Figure 14 shows for comparison of the results of Example 1, whereas Fig. 15 shows comparison of results of Example 2. From Figs. 14–15 we can see that the solutions obtained by the MHATM and RPSM methods coincide with the exact solution, and both methods are consistent and efficient for solving fractional NSW equations.

Figure 14

The surfaces show (a) the numerical approximate solution of $\eta _{4}(x,t)$ by MHATM when $\lambda =1$, (b) the numerical approximate solution of $\eta _{4}(x,t)$ by RPSM when $\lambda =1$, (c) the exact solution $\eta (x,t)$ when $\lambda =1$

Figure 15

The surfaces show (a) the numerical approximate solution of $\eta _{4}(x,t)$ by MHATM when $\lambda =1$, (b) the numerical approximate solution of $\eta _{4}(x,t)$ by RPSM when $\lambda =1$, (c) the exact solution $\eta (x,t)$ when $\lambda =1$

5 Concluding remarks

In this study, we proposed two powerful analytical methods for the solution of fractional Newell–Whitehead–Segel equations, which have the potential applications in bioengineering. To obtain the estimated solutions of the time-fractional Newell–Whitehead–Segel equations, we successfully applied the MHATM and RPSM. The accuracy and efficiency of the MHATM and RPSM are explained by examples. Moreover, the convergence analysis of both methods is discussed in detail. The results obtained for MHATM and RPSM are compared and plotted. From the figures we observe that the solution obtained by the MHATM and RPSM methods coincide with the exact solution, and both methods are consistent and efficient for solving fractional Newell–Whitehead–Segal equations. The fast convergence to the exact solutions of MHATM and RPSM shows that these methods are very suitable to solve FDEs. We conclude that the MHATM and RPSM methods are very effective and accurate techniques in the field of fractional-order differential equations. As a future work, we can implement the HAM to estimate the analytical solutions of fractional partial differential equations arising in engineering science by replacing the Laplace transform by a natural transform and the Caputo fractional operator by new fractional operators.