Machine Learning–Based Reduce Order Crystal Plasticity Modeling for ICME Applications

Abstract

Crystal plasticity simulation is a widely used technique for studying the deformation processing of polycrystalline materials. However, inclusion of crystal plasticity simulation into design paradigms such as integrated computational materials engineering (ICME) is hindered by the computational cost of large-scale simulations. In this work, we present a machine learning (ML) framework using the material information platform, Open Citrination, to develop and calibrate a reduced order crystal plasticity model for face-centered cubic (FCC) polycrystalline materials, which can be both rapidly exercised and easily inverted. The reduced order model takes crystallographic texture, constitutive model parameters, and loading condition as inputs and returns the stress-strain curve and final texture. The model can also be inverted and take a stress-strain curve, loading condition, and final texture as inputs and return the initial texture and constitutive model parameters as outputs. Principal component analysis (PCA) is used to develop an efficient description of the crystallographic texture. A viscoplastic self-consistent (VPSC) crystal plasticity solver is used to create the training data by modeling the stress-strain behavior and evolution of texture during deformation processing.

Introduction

In recent decades, the development of computationally aided design methodologies has revolutionized the way products are manufactured, from first prototype to final processing, assembly, and testing. The next frontier is the extension of computational design to include material structure, properties, and processing as critical design variables, which can be optimized to deliver superior material and component-scale performance, rather than constraints on the design process. This is the fundamental goal of Integrated Computational Materials Engineering (ICME) [1]. Leveraging the exponential advances in physics-based materials simulation tools, ICME is predicated on replacing expensive, repeated experimentation and testing with optimization through simulation. While offering unprecedented fidelity and predictive power, spatially and temporally resolved material simulation tools can be too computationally expensive or require too much calibration data to be effectively used within the ICME framework [2, 3]. In order to properly utilize these models in design, we must address the problem of developing reduced order models which replicate the fundamental physical behavior of the material system but, which can be rapidly exercised and easily inverted for integration within an optimization framework. Further, given that the statistical confidence in the final design (previously obtained through repeated material and component-scale testing) must now be obtained through simulation, it is critical that the developed reduced order models are integrated with formal uncertainty quantification as part of the validation process [4].

In this work, a reduced order framework for crystal plasticity, developed through machine learning (ML), is presented. Crystal plasticity was chosen as an initial case study as it is a relatively mature and widely utilized simulation area [5,6,7]. Also, crystal plasticity simulations are often computationally expensive and underdetermined with respect to the parameters, as the single crystal constitutive theory requires more model parameters that there are experimental observations for calibration [8,9,10]. Even relatively simple theories require a large amount of parameters to capture the non-linearity in the stress-strain response, particularly with respect to strain rate, temperature, multiple slip and twinning modes, and strain path effects [8]. Thus, demonstration of the ML framework to identify correlations between model parameters during the training of the reduced order model and then correctly predict constitutive theory model parameters from limited input data serves as a good test of the robustness of the proposed framework.

Traditionally, the calibration of crystal plasticity models was performed by manually adjusting model parameters to best match the available experimentally measured stress-strain and crystallographic texture data. This can be a time-consuming process, with large amounts of human intervention due to the large parameter space. This process needs to be repeated anytime the single crystal mechanical properties are changed [6, 8]. The need for expensive manual calibration renders exploration across many materials and processing paths difficult if not intractable. Therefore, it is important to have an automated process to rapidly estimate model parameters at the preliminary stages based on limited stress-strain response and texture data. Previous attempts at the automated optimization of fitting parameters have not been entirely successful due to strongly non-linear and potentially non-unique relationships between the model parameters and the stress-strain response of the polycrystal [11,12,13]. Another contributing factor is the degree of sample-to-sample variability in both initial microstructure and measured properties. Any automated approach to optimization of model parameters must be robust to uncertainty in the single crystal properties due to noise or variance in: (i) the initial texture and microstructure of the sample, (ii) measurement noise due to variability in the mechanical test, and (iii) limitations of the constitutive theory (e.g., missing physics or model assumptions).

The development of reduced order models has the potential for wide application beyond the design process. One of the tenets of the Materials Genome Initiative (MGI) is the development of an infrastructure to accelerate the development of new materials [14]. The construction of large-scale materials structure-processing-properties databases is a critical aspect of this MGI infrastructure [15]. Significant progress towards population of these databases can potentially be made from the automated mining of legacy material data from the existing materials science and engineering literature literature in the form of manuscript, text, tables, graphics, and figures [6,7,8, 14]. However, it is also understood that significant gaps will be left in the databases as legacy sources may not have collected or reported complete microstructure data. For example, initial or final texture data is frequently missing from reports on mechanical testing, due to the historic difficulty of texture measurement before the advent of commercial electron back-scatter diffraction (EBSD) systems. Fully calibrated reduced order models, such as the one presented here, can be invaluable tools to fill these missing gaps. To illustrate this idea, a proof-of-concept example is demonstrated where the initial state of the microstructure (texture) is predicted from the final observed structure in this work.

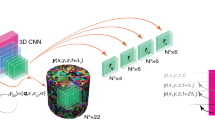
In this study, we apply Open Citrination, a materials informatics platform [15], to establish a “fast-acting reduced order crystal plasticity model” for polycrystalline materials. A viscoplastic self-consistent (VPSC) crystal plasticity formulation with Voce hardening is used as a case study model. Rather than calibrating to isolated mechanical test results either from the lab or literature, the training data is generated by repeatedly exercising VPSC over a range of initial textures and hardening parameters. The trained reduced order model is demonstrated by predicting the stress-strain response and final texture of a sample given the initial texture, strain path, and hardening parameters. The model is inverted to predict the initial texture and optimized hardening parameters given the stress-strain curve and final texture. This process is schematically shown in Fig. 1. The proposed reduced order model can help to quickly predict the behaviors of products in manufacturing design, while providing additional material information according to limited experimental data. Additionally, in order to quantify the high microstructural variance, the dimensionality reduction technique, principal component analysis (PCA), is applied to capture the characteristic microstructural information using a low-dimension description. The correlation between microscale texture/deformation evolution, macroscale stress-strain behavior, and optimal crystal plasticity model will be calibrated through Open Citrination as a case study in this paper.

Fig. 1

Schematic description of the proposed machine learning framework

Methodology

The deformation response of a single-phase, face-centered cubic (FCC) copper, with 12 independent slip systems of type {111} < 110 >, is used as the initial case study. The well-known VPSC framework will be used as the target crystal plasticity model for the machine learning reduced order model [8]. Voce hardening is selected to simulate the plastic hardening response during processing. Representative FCC textures, selected loading conditions, and strain rates are considered as variables in the learning progress. The Open Citrination platform is adopted to learn the complex correlation between the microstructure features and crystal plasticity in this study. Using the computational network established in this study, the deformation behavior and microstructure evolution of FCC copper under arbitrary conditions can be quickly predicted. Additionally, the experimental stress-strain data can also be fitted to identify optimal constitutive model parameters. In order to better focus the discussion on the details of the framework, our initial case study does not extend to multiple materials or multiple deformation mechanisms. Future work will consider more complicated material systems, such as body-centered cubic (BCC) and hexagonal closest packed (HCP) alloys with multiple non-degenerate slip and twinning modes with strong temperature dependence and multi-phase materials.

Viscoplastic Self-Consistent Crystal Plasticity Modeling

There are many well-known constitutive theories and numerical approaches to model the deformation of crystalline materials at the polycrystalline level [5,6,7, 16,17,18]. For brevity, we will only discuss details relevant to this study, readers who require a review of the field are referred to the following references [6,7,8,9,10, 17, 19,20,21,22]. For this work, we will use VPSC as the physics-based model that we wish to replicate. In contrast to crystal plasticity finite elements (CPFE) and the elasto-viscoplastic fast Fourier transform approaches, which are full-field three dimensional spatially resolved solvers, VPSC is a mean field or homogenized model that does not consider the spatial arrangement of grains but computes the effective mechanical response of the polycrystal using the orientation, size, and shape of the individual crystallites [8, 23,24,25].

Self-consistent models are commonly used to estimate the homogenized response of heterogeneous systems [17]. VPSC is routinely used to model the mechanical response of polycrystal aggregates during plastic deformation [8]. Within VPSC, the polycrystal is approximated as an ensemble of weighted statistically representative (SR) grains each with a specific crystallographic orientation. The individual SR grains are modeled as Eshelby inclusions within a homogeneous effective medium [26, 27]. The properties of the effective medium are calculated as an average over the ensemble of SR grains. As the response of the SR grains and the properties of the effective medium are mutually dependent, they must be iteratively updated (starting with an initial estimate of the effective properties) until convergence [6].

The constitutive model applied in this case study is selected as the non-linear rate–dependent power law formulation which relates the viscoplastic strain rate, $\dot {\boldsymbol {\varepsilon }_{p}}$, to the stress σ as

$$ \dot{\boldsymbol{\varepsilon}}_{p}^{r} = \mathbf{M}_{ijkl}^{r}:\boldsymbol{\sigma}_{kl}^{r} = \gamma_{0} \sum\limits_{s} \mathbf{m}^{s}_{ij} \left( \frac{\mathbf{m}^{s}_{kl}:\boldsymbol{\sigma}_{kl}^{r}} {{\tau_{0}^{s}}}\right)^{n} $$

(1)

where $\dot {\boldsymbol {\varepsilon _{p}}}$ and σ are represented as the average viscoplastic strain rate and stress in each SR grain. M^r is the viscoplastic compliance. ${\tau _{0}^{s}}$ is the critical resolved shear stress (CRSS) for slip system s, and m^s is the symmetric Schmid tensor associated with the activated slip/twinning system, s, in homogenized SR grain r. n = 20 is assigned in this case study as a reasonable rate-sensitivity exponent constant. The reference shear rate, γ₀, served as a normalization factor, and the viscoplastic strain rate, $\boldsymbol {\dot {\varepsilon _{p}}}$, can be non-linearly scaled by the magnitude of applied velocity gradient or applied stress components during deforming. Detailed explanation will be provided in “Parameterization of Applied Deformation”.

The Voce hardening model is applied to evolve the slip resistances for each slip system with accumulated deformation [8]. Equation 2 describes the evolution of the threshold stress, $\hat {\tau }^{s}$, that is produced by the accumulated shear strain, ${\Gamma } = {\sum }_{s} {\Delta } \gamma ^{s}$, in each respective grain of a polycrystalline material, where γ^s is the shear activity in a grain. ${\tau _{0}^{s}}$ and ${\tau _{0}^{s}}+{\tau _{1}^{s}}$ are the initial and the back-extrapolated critical shear stress (CRSS) in slip system s, where ${\theta _{0}^{s}}$ and ${\theta _{1}^{s}}$ are the initial and the asymptotic hardening rate. The evolution of plastic hardening behavior for polycrystalline aggregates can be defined using following equations.

$$ \hat{\tau}^{s} = {\tau_{0}^{s}}+({\tau_{1}^{s}}+{\theta_{1}^{s}}{\Gamma})\left( 1-exp\left( -{\Gamma} \left\lvert \frac{{\theta_{0}^{s}}}{{\tau_{1}^{s}}} \right\rvert \right) \right) $$

(2)

$$\begin{array}{@{}rcl@{}} \frac{d \hat{\tau}^{s}}{d{\Gamma}} &=& \theta_{1} +\left( \left|\frac{\theta_{0}}{\tau_{1}}\right| \tau_{1}-\theta_{1}\right) exp\left( -{\Gamma} \left|\frac{\theta_{0}}{\tau_{1}}\right|\right)\\ &&+ \left|\frac{\theta_{0}}{\tau_{1}}\right| \theta_{1} {\Gamma} exp\left( -{\Gamma} \left|\frac{\theta_{0}}{\tau_{1}}\right|\right) \end{array} $$

(3)

As shown in Fig. 2, the standard hardening behavior (defined as “Kosher” Voce hardening in the VPSC manual) demonstrates where the corresponding flow stress increases and hardening rate decreases with increasing strain, requires the condition, 𝜃₀ ≥ 𝜃₁ ≥ 0 [8]. The limiting case of standard is the right-perfectly-plastic hardening, which maintains the relation, 𝜃₀ = 𝜃₁ = 0, where other non-standard situations (defined as “Non-kosher” law in VPSC) are shown in Fig. 2. As an initial case study, we randomly generated data grids for hardening parameters according to the reasonable fitting parameters from existing literature [7, 8].

Fig. 2

Physical interpretation of Voce hardening parameters (Eq. 2)

The increment in threshold stress, Δτ^s, is relative to coupled dislocation interactions when other slip systems, s^′ are activated in a same grain (Eqs. 3 and 4) as,

$$ {\Delta} \tau^{s} = \frac{d \hat{\tau}^{s}}{d{\Gamma}} \sum\limits_{s^{\prime}} h^{ss^{\prime}} {\Delta} \gamma^{s^{\prime}} $$

(4)

The coupling coefficient or hardening matrix, $h_{ss^{\prime }}$, defines the effect of slip on system s^′ on the slip resistance for s. For this case study, we consider both self and latent hardening and take the limiting case of $h_{ss^{\prime }} = 1\quad \forall \quad (s,s^{\prime })$.

Parameterization of Applied Deformation

As the stress-strain response and texture evolution are strong functions of the imposed boundary condition, the complete range of physically meaningful effective velocity gradient tensors for the polycrystal must be parameterized for the machine learning schema described below (see “Machine Learning Algorithm”).¹ Table 1 shows four basic loading conditions with a unit loading rate. Each condition can be fully described in the deformation reference coordinate frame by a nine-component velocity gradient tensor. However, the identical loading/deformation path imposed upon a polycrystalline metal can be more compactly expressed in a principal deformation coordinate frame [28, 29]. Equation 5 details how the loading matrix in reference frame (L_R) is transformed to the one in principal frame (L_P) through multiplication of a stretching tensor, f_P→R (Table 2).

$$ L_{P} = f_{P \to R}^{T} * L_{R} * f_{P \to R} $$

(5)

Table 1 Loading condition in the reference frame (L_R)

Table 2 Loading parameters in the principal frame (L_P)

In the principal frame, the necessary parameters used to describe a loading condition are reduced from an arbitrary nine-component matrix to a three-component diagonal matrix containing a reference strain rate, $\dot {\varepsilon }_{0}^{*}$ (Eq. 6). Varying the effective applied deformation rate can be achieved through multiplication with a reference strain rate, $\dot {\varepsilon }_{0}^{*}$, as

$$\begin{array}{@{}rcl@{}} L_{R} &=& \left[\begin{array}{llll} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{array}\right] \Longleftrightarrow L_{P}\\ &=& \left[\begin{array}{cccc} cos(\beta^{*} -\frac{\pi}{3}) &0 &0\\ 0 &cos(\beta^{*} +\frac{\pi}{3}) &0\\ 0 &0 &-cos(\beta^{*}) \end{array}\right] \dot{\varepsilon}_{0}^{*} \end{array} $$

(6)

The above parameterization reduces the dimension of the description of any applied deformation/loading paths with effective deformation rates into five parameters, where β₁, β₂, β₃, and β^∗ define the transformation stretching tensor between the reference and the principal frame. As an example, Table 2 displays the values of parameterized loading parameters in the principal frame for four corresponding conditions corresponding to Table 1.

Reduced Order Representation of Crystallographic Texture

For this work, crystallographic texture, described by an orientation distribution function (ODF), is assumed to be the controlling microstructure feature for mechanical response. The body of literature on crystal plasticity simulation largely shows that effective stress-stain curves can be well-captured by crystallographic texture while the specific grain structure/geometry affects the stress localization and other fluctuations of the mechanical fields [6,7,8, 30,31,32]. In order to properly calibrate the desired reduced order crystal plasticity model via machine learning, the range of possible ODFs must be sampled. This poses a difficulty as the space of possible crystallographic textures is vast. For example, discretizing the orientation space for cubic materials into 5^∘ bins produces 15,552 ODF components, each of which can be varied individually. Fortunately, these components do not evolve independently during deformation and a more efficient sampling scheme based on experimentally observed texture components can be identified.

Previous work from Raabe and Roters demonstrated that the representation of an arbitrary texture by the weighted mixture of standard texture components was an effective method to capture the effective mechanical response and texture evolution of polycrystals within a crystal plasticity framework [19, 30]. In this study, we follow a similar approach and consider the most important texture components observed to be produced by deformation processing in FCC metals. These include (i) the uniform or random ODF, which has identical values for all orientations, (ii) important unimodal texture components that contain a strong concentration around a preferred orientation including the cube, goss, brass, copper, S1, S2, S3, and Taylor textures often detected in FCC material, and (iii) fiber ODFs which represent all orientations formed by a rotation between two specific orientations including the α, β, and τ fiber textures [31, 33,34,35]. These texture components are defined explicitly in Table 3 and their positions in the Bunge-Euler space are shown in Fig. 3. The figure also highlights the relationship between the unimodal texture components and the fiber textures in cubic crystal structures. Numerical representation of the orientation distribution functions is accomplished via a Fourier series representation utilizing Bunge’s generalized spherical harmonics as a basis set [36]. This choice was simply one of the authors’ preference, as other representations such as direct binning in either the Euler angle or Rodrigues space would also work equally well. The free MATLAB toolbox MTEX is used in this study to carry out all ODF calculations and visualizations in this work [33,34,35].

Table 3 Standard FCC texture components: Miller indices and Euler angles

Fig. 3

Standard texture component representation in Bunge-Euler angle space

The texture components described above form a convenient framework for describing the space of ODFs that need to be considered to adequately train a reduced order model via machine learning. However, each ODF is still expressed as a Fourier series containing thousands of spherical harmonic coefficients [36]. Therefore, individual ODFs still need to be represented in a small number of parameters suitable for the training model. The naïve approach would be used to simply represent any ODF as a vector containing the weights of each of the the texture components. However, this imposes the limitation that the set of final deformation textures and the set of input textures used for model calibration both span the same subspace of the ODF space. As an alternate approach, we could also use the strategy of microstructure-sensitive design (MSD) and consider the set of all possible deformation textures given the set of initial texture components; however, this approach leads to a large parameter set [37,38,39,40,41,42,43,44,45,46]. In order to retain flexibility and reduce the number of parameters, we have adopted principal component analysis (PCA) to identify an appropriate low-dimensional representation. PCA is a dimensionality reduction method that conducts orthogonal decomposition on the high-dimensional raw data and maps to a new low-dimensional orthogonal coordinate frame, i.e., the principal components (PCs) represent as the new coordinate systems [47,48,49].

PCA can be simply explained as projection of the high-dimensional data onto a low-dimensional subspace, defined by a basis set (the principal components), that captures the critical features in the dataset. Each datapoint can be written as a weighted linear combination of the principal components. The new variables, interpreted through PCA, are the weights of the principal components. The basis is defined such that the first PC is the direction of highest variability through the original dataset. Next PC is defined by taking the direction of highest variability orthogonal to the first, and so on. In this way, differences between individual datapoints in the set can be represented by a small number of principal components. Since PCA and the generalized spherical harmonic representation are both linear transformations of the orientation distribution data, the final low-dimensional representation should be identical for both the binned orientation data and the spherical harmonic coefficients of the ODF. Therefore, in this case study, the dimension of each material texture (originally containing thousands of coefficients) is interpreted by PCA since the first couple of PCs can effectively capture the main characteristic of texture.

Similarly, the reconstruction of specific texture can also be completed by picking the corresponding coordinate in PC space [50, 51]. The accuracy and efficiency of the texture reconstruction using PCA has been measured with the L2-norm between the original ODF and the reconstructed one that computed as a function of the number of principal components. Figure 4 shows the PCA reduction based on thousands of initial and final deformation textures, and how the error reduces when using more PCs to reconstruct textures. Both the MTEX synthesized texture and VPSC simulated texture are reconstructed using the same PC basis. The error between the actual and the reconstructed texture converges to zero by picking enough PCs when adding both the linear combinations of the texture components (from Table 3) and deformation textures predicted by VPSC under a range of imposed boundary conditions. Most textures can be represented by using more than 30 PCs with minimum error (Fig. 4). However, as the number of relevant texture components is increased, the number of necessary PCs required to accurately represent the raw data will also increase. In that case, more advanced dimensionality reduction techniques should be recommended, such as kernel PCA, which provides more accuracy when raw data structure is non-linear [52,53,54,55,56]

Fig. 4

Accuracy of texture reconstruction using PCA

In order to simplify the machine learning framework, we would like to use as efficient a representation as possible. Figure 5 shows examples of the reconstruction of both the synthesized and deformation texture using weighted PCs. In Fig. 5b, the ideal simulated ODF (left) shows the orientation distribution resulting from the shearing of an initial cube texture. The main characteristics of the ODF can be captured with acceptable accuracy by reducing the number of PCs to 16. The number of principal components considered is also motivated by the current limitations on the number of degrees of freedom on the Open Citrination platform. Therefore, for this work, we will consider 16 PCs as representative inputs to the machine learning framework, with the understanding that this may not be the optimal choice, but rather a compromise between accuracy and computational resources.

Fig. 5

Example of texture reconstruction using 16 PCs for a MTEX Synthesized unimodel cube texture b VPSC simulated cube under shearing. The initial texture was subsequently deformed to a strain of $\boldsymbol {\varepsilon }_{\mathbf {0}}^{\boldsymbol {*}}= 1$ under shear loading

Machine Learning Algorithm

In the field of material science, ML is usually applied to predict various functional properties/behaviors and calibrate reduced order models from limited experimental data [57,58,59,60,61]. Numeruous ML techniques have been applied across the engineering fields (such as k-nearest neighbors (k-NN), decision trees (DT), random forest (RF), support vector machine (SVC), artificial neural networks (ANN), Bayesian networks, and deep learning) [62,63,64]. Additionally, many convenient toolboxes are developed to analyze and model data on commonly used Integrated Development Environments (IDEs), such as scikit-learn in python, statistics and machine learning toolbox, and neural network toolbox in MATLAB [62, 65, 66]. In this study, we use the Open Citrination platform [15, 67, 68] to construct the ML-based reduced order model for crystal plasticity. The default estimator on Open Citrination is based on random forest [68], which is an ensemble method wherein individual learners are decision trees [69, 70]. More complete description of the Citrination platform and the machine learning model on random forest can be learned from the open-source Lolo scala library [71]. Specific details related to the training of our model such as the number of estimators, minimum samples per leaf, and maximum tree depth used for the reduced order model in this paper are demonstrated on the Open Citrination platform and shown in Appendix [72].

Calibration and Validation of Reduced Order Model

The set of crystal plasticity model parameters and initial conditions (including imposed velocity gradient tensor, material texture, and hardening parameters) were systematically varied in order to build a comprehensive training dataset using VPSC. The details are described in Table 4. Four typical loading conditions are included, pure shear, rolling, uniaxial compression, and tension, while the loading rate varies between 1 × 10^− 3s^− 1 and 1s^− 1. In order to consider the natural randomness at the simulation volume element level, for each ODF, ten different VPSC input grain files were created by discretely sampling 1000 grains. Additionally, ten random combinations of ${\tau _{1}^{s}}$, ${\theta _{0}^{s}}$, and ${\theta _{1}^{s}}$ are picked from the predefined range of normalized Voce hardening parameters for each simulation [8].

Table 4 VPSC model parameters sampling for calibration data

The simulation dataset from VPSC is randomly separated into two groups, the training set and the validation set. The training dataset is used to discover the correlation between the input and output of the predefined configuration, while the validation set is used to check the accuracy of the corresponding mathematical relationship that was built by the training set. In total, approximately two thousand computational results (by picking different parameter sets in Table 4) were used for training and calibration. The reduced order model was trained using one thousand VPSC simulation results out of the complete data set. The remainder of the VPSC simulations was used as validation. Additional validation examples were also created by creating “new” textures, that were not included in the calibration data, as linear combinations of the standard texture components. Results from these additional validation simulations are described below.

Two configurations are defined in this case study as “Property prediction” and “Model calibration” corresponding to the invertible pathway shown in Fig. 6. Property prediction is used as a reduced order simulation tool that quickly generates the stress-strain curve and the processed texture given any initial sample texture and condition. The invertible configuration is used to quickly calibrate the optimal hardening parameters given any strain-stain curve and providing the initial state of a sample based on the EBSD of the processed sample.

Fig. 6

Training configurations of “Property prediction” and “Model calibration”

The prediction of each property is calculated through all inputs; however, each property is predicted mainly through several important features among the training dataset. Open Citrination provides the important score of each feature corresponding to the contribution to model performance of each feature (see Appendix). As an example of model calibration, Voce hardening parameters are mainly determined by features produced from stress-strain curves, while the initial ODF is mainly determined by the input of final ODFs. The accuracy and the uncertainty of the reduced order model model are evaluated during training and validation through different error metrics, such as root mean squared error, and non-dimensional model error. Additionally, the standardized residual measures the difference between ideal and predicted values on Open Citrination.

Results and Discussion

Several examples are presented below to demonstrate the accuracy of predictions from the reduced order model. All of the results presented are from the validation dataset and were not used to calibrate the reduced order model. As mentioned in “Reduced Order Representation of Crystallographic Texture”, both initial and final ODF are represented by the first 16 PCs and the stress-strain behaviors are represented by ten selected points on stress-strain curves. This effectively means that this limited set of 26 variables can efficiently describe the critical microstructural features and the effective mechanical behavior of a FCC sample.

Examples in Fig. 7 show the accuracy of the reduced-order model prediction for the final texture and the stress-strain behavior for a range of different initial textures and loading conditions. The left ODF shown in Fig. 7a is an example of input crystallographic texture ODF, τfiber, used to verify the accuracy of the reduced order model. The middle pole figure shows the VPSC predicted texture resulting from the τ-fiber ODF under a shear loading condition, while the right one shows the predicted ODF from the reduced order model. The intensity of both pole figures are mostly captured when comparing the VPSC simulated results and the reduced order prediction.

Fig. 7

Pole figure of the final texture generated by VPSC simulation (left) and Open Citrination’s prediction (right) for the following: a τ-fiber ODF under shearing; c τ-fiber ODF under tension; e uniform ODF under compression; g 50% cube + 50% brass under shearing; The Von-Mises stress-strain curve generated by VPSC simulation (solid line) and Open Citrination’s prediction (scattering points) for: bτ-fiber ODF under shearing; d τ-fiber ODF under tension; f uniform ODF under compression; (h) 50% cube + 50% brass under shearing;

In Fig. 7b, the red solid line shows the plastic stress-strain curve computed from VPSC for τ-fiber ODF under shear loading while ten blue dots represent the reduced order prediction of stress-strain behavior under the same condition. Most of the predicted points are located very close to the actual stress-strain curve for this case. Figure 7c–f show another two examples of the predicted ODF and plastic stress-strain curve for τ-fiber under tension and uniform ODF under compression. Additionally, Fig. 7g, h shows an example of the prediction of the final texture and the stress-strain curve when input a mixed FCC texture, 50% cube + 50% brass into the reduced order model. These results indicate the calibrated machine learning reduced order model can accurately capture the evolution of crystallographic texture during deformation processing, while the predicted stress-strain curve shows a good correspondence with the VPSC simulation.

The overall expected level of error for the prediction of the stress-strain curve from Open Citrination is quantified in Fig. 8. Both the specific cases for “τ-fiber ODF under shearing (Fig. 7b) ” and “uniform ODF under compression (Fig. 7f)” are shown in Fig. 8. The box plot shows the distribution of the percentage error among the training dataset. The percentage error is defined as $\frac {\sigma _{true}-\sigma _{predicted}}{\sigma _{true}}$ and the average percentage error is limited in 2%. As a good prediction example, “τ-fiber ODF under shearing” has a prediction error within the first and the third quartile (Q1 and Q3), while the percentage is less than 5%. While the percentage error of the worse case (“uniform ODF under compression”) locates around the extreme outlier. Additionally, the standard deviation (SD) of the percentage error of predictions are also shown as a function of the stain, and the overall uncertainty increase along with the strain.

Fig. 8

Error assessment of stress-strain predictions using the reduced order model (The overall percentage error for validation set and the corresponding cases sourced from Fig. 7 are demonstrated). The red line indicates the mean error level and the boxes contain the middle 50% (2nd and 3rd quartile). The error bars indicate 10% and 90% of all samples. Individual extreme values are marked with +

Similarly, the examples in Fig. 9 shows the accuracy of the inverse case: model calibration for the initial texture, and identification of the optimal Voce hardening model parameters. In Fig. 9a, the ground truth initial condition texture, Taylor ODF (middle), is compared with the prediction from the inverse reduced order model. The deformed texture provided as input the to inverse reduced order model is shown on the left. The pole figures demonstrate excellent agreement between the ground truth initial texture and the inverse reduced order model prediction, with both qualitative features and trends in intensities being captured. We believe that the quantitative differences are largely due to truncating the PCA expansion to 16 components, and better agreement can be realized if a more terms could have been used. However, for the future application of identifying missing data in material database the semi-quantitative predictions are likely sufficient. Additional examples are also shown in Fig. 9c, e. Figure 9g shows the inverse reduced order model can also be utilized when the initial texture is not one of the standard ODF components. In this case, the initial texture of 50% goss + 50% brass was subject to rolling.

Fig. 9

Pole figure of the final texture generated by MTEX synthesized (left) and Open Citrination’s calibration (right) for: a Taylor texture; c Goss texture; e Cube texture; g 50% goss+ 50% brass texture; The Von-Mises stress-strain curve generated by VPSC simulation using predefined Voce hardening parameters (solid red line) and Open Citrination’s predicted curves using couple calibrated Voce hardening parameters with variance (dotted lines) for: b Taylor texture under compression; d Goss texture under rolling; f Cube texture under tension; h 50% goss+ 50% brass texture under rolling

The inverse reduced order model can also be utilized to determine optimal Voce hardening parameters from limited stress-strain data. Figure 9b, d, f, and h compares the ground truth VPSC stress-strain curves resulting form the input Voce parameters with stress-strain curves resulting from the inverse reduced order model prediction of the hardening parameters. Stress-strain curves are generated covering the full confidence interval for the Voce parameters to better visualize the expected accuracy resulting from using the reduced order model for parameter estimation.

The accuracy of the validation set for Voce hardening parameters are compared with the exact VPSC simulated value in error bar plot in Fig. 10a. The asymptotic hardening rate is perfectly predicted by the proposed tool. Most of the back-extrapolated CRSS and the initial hardening rates are predicted with some uncertainty. Figure 10b, c shows the cumulative density function (CDF) and the probability density function (PDF) curve of the validation set of normalized hardening parameters from multiple cases. Figure 10b shows the upper predicted boundary (UPB) and the lower predicted boundary (LPB) of Open Citrination’s predicted values that corresponded to the positive and negative variance. Figure 10c shows the probability distribution of the positive variance over the entire training and validation set.

Fig. 10

a The comparison between the ideal and predicted Voce hardening parameters; b Cumulative distribution function (CDF) of predicted Voce hardening parameters using Open Citrination; c Probability distribution function (PDF) of predicted Voce hardening parameters using Open Citrination

For practical applications, crystal plasticity calculations are exercised to predict material response under different conditions (typically either initial texture or strain path) than the calibration data. In order to check whether the uncertainty of the stress-strain behavior that was computed using the estimated hardening parameters is allowable and acceptable for this purpose, the optimal hardening parameters were estimated and used to simulate the stress-strain response under multiple loading conditions. Figures 11 and 12 show the reproduced stress-strain curve of selected texture under different loading conditions. In Figs. 11 and 12, the blue dash line shows the stress-strain data used to estimate the Voce parameters from the inverse reduced order model. The calibrated Voce hardening parameters are then used to predict the stress-strain response under differing loading conditions for the same textures. As can be seen in the figures, the reproduced stress-strain curves are very close to the ground truth response (solid red line).

Fig. 11

Validation of optimal hardening parameters using goss texture under different loading conditions

Fig. 12

Validation of optimal hardening parameters using cube texture under different loading conditions

The case studies above demonstrate that the Open Citrination-trained model successfully captures the underlying physics represented in the VPSC model with Voce hardening, and can be used as a surrogate model for the more computationally expensive crystal plasticity simulation. The model can also be inverted quickly to learn material properties, in this case single crystal yield and hardening parameters, from mechanical tests avoiding manual fitting. This can effectively reduce the cost of large amounts of computational and experimental results at the preliminary design stage with the adoption of the machine learning model.

However, it should be noted that the uncertainty of the calibrated parameters is neither uniform across the three normalized hardening parameters nor constant for a given parameter. As shown in Fig. 10, the calibrated values of the initial hardening rate, 𝜃₀, and the asymptotic hardening rate, 𝜃₁, have smaller variance than the back-extrapolated CRSS, τ₁. This is expected from the form of the Voce hardening law, both 𝜃₀ and 𝜃₁ define slopes of the stress-strain curve which describe the trend of the curve, which means that training data points at multiple strain values contribute to the these parameters. However, τ₁ is the interception of back-extrapolation asymptotic stress as very large strains with the stress axis. This value is not independent of the other parameters and that the calibrated uncertainty of τ₁ will always greater than others. The uncertainty is also not constant in that 𝜃₁ can be determined more accurately when it is numerically small than when it is the parameter takes a large. Or equivalently the hardening parameters can be more accurately determined in systems that display a smaller degree of work hardening.

The quality of the machine learning fit was also found to be sensitive to how the input stress-strain curves were sampled. For initial calibration attempts, we used a uniform (with respect to strain) sampling. However, this found to provide poor fits for parameter sets corresponding to rapid hardening or rapid saturation of stress with increasing strain, i.e., cases where $\tfrac {d\boldsymbol {\sigma }}{d\boldsymbol {\varepsilon }}$ was large. Instead, a non-uniform sampling scheme was applied where a higher density of stress-strain values were taken early in the curve where hardening rates were highest. This scheme is likely to fail for the case of non-kosher Voce parameters (see Fig. 2) as the effective stress-strain response would exhibit curves or inflections in regions not heavily sampled. While a seemingly trivial step in the process, the discretization of the input data can have a large impact on the accuracy and efficacy of the fit machine learning tool.

One potential limitation of this initial implementation is that the texture predictions from the model are all taken at large strains (ε = 1). As shown above, the calibrated machine learning model does a good job of predicting the final texture as a function of initial texture and strain path at large strain, but as it currently stands, has not been calibrated to predict the texture as a function of stress-strain curve for a fixed strain path. Intermediate textures were not used in the calibration process. However, this is a feature that would be reasonably straightforward to add in the future.

Furthermore, this work shows a good prediction of deformation textures resulting from commonly used loading conditions. However, in real-world applications, material may be manufactured by complex loading path, such as bi-axial loading, sequential combination of different paths, or even superposition of strain paths. Analogously to the interim texture predictions, the extension to a broader range of strain paths should also be straightforward.

Overall, as an initial case study, this work only considered the deformation of FCC materials. FCC was chosen for practical reasons, as the plastic response is easier to predict as only one slip mode, containing 12 independent and degenerate {111} < 110 > slip systems, needs to be considered. The “texture-processing-properties” map for materials with BCC is significantly more complex to mine as multiple slip modes and up to 48 slip systems have a opportunity to be activated depending on the deformation path. For other non-cubic structures, such as HCP materials, the deformation behavior is harder to capture because twinning can be an important mechanism for accommodation of plasticity. The inclusion of non-degenerate slip modes drastically increases the number of parameters that need to be estimated in order to predict the stress-strain response and texture evolution. Also for simplicity, the limiting case of uniform latent hardening was considered for the case studies presented above. With non-degenerate slip modes, the form of the hardening matrix (see Eq. 4) also needs to be learned in addition to the hardening parameters for each slip mode. Deformation twinning also usually produces remarkable effect on texture evolution due to grain reorientation. Additionally, the hardening response will be affected since twin lamellae are potent barriers to dislocation motion. This will manifest as a strong degree of latent hardening associated with twin systems. However, in order to become a practical design tool, the framework presented here needs to be extend to both BCC and HCP initially (followed by a wider range of lower symmetry structures).

Conclusion and Future Work

This work demonstrates the feasibility and utility of using a machine learning approach to develop reduced order or fast-acting models to capture the behavior of more complex “physics-based” materials simulations. These reduced order models can then be used in ICME to efficiently explore the relationship between processing, microstructure, and property. The development of the proposed tool can effectively reduce the time and cost of property and performance prediction, and improve the quality of the real-world manufacturing design. Specifically, in this case study, instead of using a crystal plasticity solver to calculate the evolved microstructure and the mechanical properties under different conditions, the proposed tool can predict the result directly. Additionally, the existing material properties can be supplemented without repeatable experiments or simulations. According to the invertible linkage established in this study, the proposed tool can computationally optimize a processing route for a given starting material to meet a set of designer specified criteria.

The initial case study stated in this paper shows that both “Property prediction” and “Model calibration” pathways can be established by training a comprehensive computational database of FCC copper on Open Citrination. This will become a preliminary fast-acting tool that finds the processing path to the desired structure and the macroscale functional properties. The overreaching goal of this project can be extended to the “data-driven material design” for expected microstructures with desired crystal plasticity properties depending upon given element composition, crystal structure, possible activated slip/twining systems, initial texture, and processing techniques and conditions. In the future, we can continue to expand our database by adding experimental data and other textures in various crystal systems and consider other microstructural features as important factors. Moreover, other conditions and model parameters, such as arbitrary loading types, temperature, constitutive sensitive rate, and different crystal plasticity laws can be gradually added as variance in the existing database to complement the current machine learning model.

Appendix: Machine Learnign Details and Hyperparameters

The proposed crystal plasticity reduced order model is built on a random forest model that includes uncertainty estimation. Random forests can be understand as featured bagging of decision trees, where decision trees are basic models that define a piece-wise function that analyzing the input space recursively. Random forests have much better ability than single decision trees when predicting data with noise, and overcome the non-linearity by random draw, and featured bagging of the complete training dataset. The final decision/prediction of random forest is aggregated by voting/averaging of each tree so that limiting the overfitting on dataset without substantially increasing error due to the variance and bias.

Table 5 demonstrates the machine learning algorithm and hyperparameters used for the machine learning training session on Open Citrination, while the estimator is sourced from the open-source machine learning Lolo scala library [71]. The main important features used to train the model are also shown in Table 5. The complete description of the fraction for each important feature used to train the model can be found on Open Citrination [72]. (Importance scores of each feature sums to one and are determined by a given feature’s contribution to the model’s performance.) Moreover, the detailed model reports and summary of the training session for this case study can be reached at Dataviews 5506 (forward configuration) and 5507 (backward configuration) on Open Citrination.

Table 5 Hyperparameter and important features for training session