Skip to main content
SpringerLink
Log in

Design and characteristic analysis of an X-shaped negative stiffness structure

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

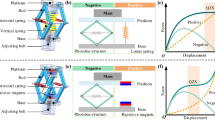
The quasi-zero stiffness (QZS) mechanism is typically implemented by paralleling negative and positive stiffness structures to enhance the vibration isolation effect. As the core component, a novel bistable X-shaped negative stiffness structure (XNSS) is designed. Based on the geometric relationship between angular and displacement coordinates, the single-layer and multilayer mechanical model is derived from the principle of virtual work. After the non-dimensional process, a set of system parameters is summarized. Ensuring that these system parameters satisfy constraints, the comprehensive effects on XNSS are studied in detail. The parallel connection of XNSS and linear stiffness mechanism can constitute a QZS vibration isolator, and the influence of system parameters on loading capacity, stability of equilibriums, and dynamic stiffness are discussed in detail. The amplitude-frequency response and displacement transmissibility of nonlinear QZS vibration isolation model show excellent vibration isolation performance, compared with the corresponding linear system. The results show that the static analysis of the XNSS system parameters can be a good guide to the design of the QZS vibration isolator in order to obtain better dynamic performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35
Fig. 36
Fig. 37
Fig. 38
Fig. 39
Fig. 40

Similar content being viewed by others

Abbreviations

c S :

Viscous damping coefficient in N/m/s

D :

Dissipation function

F NS :

Negative force in N

F NS max, F NS min :

Maximum and minimum value of negative stiffness force in N

F S :

Restoring force in N

h :

Vertical distance between the spring fixing point and the center of rotation of the bar l2 in meter

J :

Jacobian Matrix

k NS :

Spring stiffness for negative stiffness structure in N/m

K NS :

Stiffness of negative stiffness force in N/m

K NS min :

Minimum of negative stiffness in N/m

K NS 1, K NS 2 :

Maximum positive stiffness values in compression and tension stages in N/m

K S :

Dynamical stiffness in N/m

k P S :

Stiffness of linear spring in N/m

l max, l min :

Maximum and minimum value of \(\sqrt s\) in meter

l 1 :

Length of the long bar in meter

l 2 :

Length of the short bar in meter

l NS 0 :

Free length of springs for negative stiffness structure in meter

l PS 0 :

Free length of linear spring in meter

L :

Lagrange function

m :

Mass in kg

n :

Layer number of negative stiffness structure

OB :

Length of spring for negative stiffness structure in meter

r :

Horizontal distance between the spring fixing point and the center of rotation of the bar l2 in meter

R NS :

Relative range of maximum positive stiffness values in compression and tension stages

s :

Square of the distance between highest point of first layer in negative stiffness structure and center of rotation of bar l2 in m2

Skew(F NS):

Skewness of negative stiffness force

t :

Time in s

T :

Kinetic energy

T AD :

Absolute displacement transmissibility in dB

V :

Potential energy

V NS :

Potential energy of negative stiffness structure

x B , y B :

Horizontal and vertical displacement of the free end of the bar l2 in meter

y A :

Vertical displacement of the highest point of negative stiffness structure in meter

y A 0 :

Center position of negative stiffness structure in meter

y AT :

Travel of negative stiffness structure in meter

z :

Displacement of the mass relative to the base in meter

z b :

Vertical excitation from the base in meter

z m :

Absolute displacement response of mass in meter

Z amp :

Amplitude of steady-state response in meter

Z b :

Vertical excitation amplitude from the base in meter

α, β, γ :

Square of root of cubic resolvent equation

α 0, α 1, α 2, α 3 :

Configurative parameters of negative stiffness structure

α 4 :

Static equilibrium position with only linear spring for load bearing

α 5 :

Stiffness ratio

α b :

Dimensionless vertical excitation amplitude from the base

θ :

Angle between l2 and horizontal direction

θ 0, θ 1, θ 2 :

Angle corresponding to the three equilibrium positions in negative stiffness structure

θ max, θ min :

Maximum and minimum value of θ

ξ :

Damping ratio

ω :

Vertical excitation frequency from the base in rad/s

ω 0 :

Cube root of 1

ω n :

Un-damped natural frequency in rad/s

Ω:

Frequency ratio

^:

Denotes dimensionless quantity

•:

Denotes time derivative

′:

Denotes displacement derivative

References

  1. Balaji, P.S., Karthik SelvaKumar, K.: Applications of nonlinearity in passive vibration control: a review. J. Vib. Eng. Technol. 9, 183–213 (2021). https://doi.org/10.1007/s42417-020-00216-3

    Article  Google Scholar 

  2. Ibrahim, R.A.: Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 314, 371–452 (2008). https://doi.org/10.1016/j.jsv.2008.01.014

    Article  Google Scholar 

  3. Wagg, D.J.: A review of the mechanical inerter: historical context, physical realisations and nonlinear applications. Nonlinear Dyn. 104, 13–34 (2021). https://doi.org/10.1007/s11071-021-06303-8

    Article  Google Scholar 

  4. Liu, C., Jing, X., Daley, S., Li, F.: Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 56–57, 55–80 (2015). https://doi.org/10.1016/j.ymssp.2014.10.007

    Article  Google Scholar 

  5. Pishvaye Naeeni, I., Ghayour, M., Keshavarzi, A., Moslemi, A.: Theoretical analysis of vibration pickups with quasi-zero-stiffness characteristic. Acta Mech. 230, 3205–3220 (2019). https://doi.org/10.1007/s00707-019-02465-0

    Article  Google Scholar 

  6. Tobias, S.A.: Design of small isolator units for the suppression of low-frequency vibration. Proc. Inst Mech. Eng. C J. Mech. Eng. Sci. 1, 280–292 (1959). https://doi.org/10.1243/JMES_JOUR_1959_001_032_02

    Article  Google Scholar 

  7. Molyneux, W.G.: The support of an aircraft for ground resonance tests: a survey of available methods. Aircr. Eng. Aerosp. Technol. 30, 160–166 (1958). https://doi.org/10.1108/eb032976

    Article  Google Scholar 

  8. Woodard, S., Housner, J.: Nonlinear behavior of a passive zero-spring-rate suspension system. J. Guid. Control Dyn. 14, 84–89 (1991). https://doi.org/10.2514/3.20608

    Article  Google Scholar 

  9. Shaw, A.D., Gatti, G., Gonçalves, P.J.P., Tang, B., Brennan, M.J.: Design and test of an adjustable quasi-zero stiffness device and its use to suspend masses on a multi-modal structure. Mech. Syst. Signal Process. 152, 107354 (2021). https://doi.org/10.1016/j.ymssp.2020.107354

    Article  Google Scholar 

  10. Li, H., Li, Y., Li, J.: Negative stiffness devices for vibration isolation applications: a review. Adv. Struct. Eng. 23, 1739–1755 (2020). https://doi.org/10.1177/1369433219900311

    Article  Google Scholar 

  11. Platus, D.L.: Negative-stiffness-mechanism vibration isolation systems. In: Vibration Control in Microelectronics, Optics, and Metrology, November 4, 1991–November 6, 1991. pp. 44–54. Publ. by Int Soc for Optical Engineering, San Jose, CA, USA (1992)

  12. Platus, D.L.: Negative-Stiffness-Mechanism vibration isolation systems. In: Proceedings of the 1999 Optomechanical Engineering and Vibration Control, July 20, 1999 - July 23, 1999. pp. 98–105. Society of Photo-Optical Instrumentation Engineers, Denver, CO, USA (1999)

  13. Huang, X.C., Liu, X.T., Hua, H.X.: Effects of stiffness and load imperfection on the isolation performance of a high-static-low-dynamic-stiffness non-linear isolator under base displacement excitation. Int. J. Non-Linear Mech. 65, 32–43 (2014). https://doi.org/10.1016/j.ijnonlinmec.2014.04.011

    Article  Google Scholar 

  14. Dalela, S., Balaji, P.S., Jena, D.P.: Design of a metastructure for vibration isolation with quasi-zero-stiffness characteristics using bistable curved beam. Nonlinear Dyn. 108, 1931–1971 (2022). https://doi.org/10.1007/s11071-022-07301-0

    Article  Google Scholar 

  15. Lee, C.-M., Goverdovskiy, V.N., Temnikov, A.I.: Design of springs with “negative” stiffness to improve vehicle driver vibration isolation. J. Sound Vib. 302, 865–874 (2007). https://doi.org/10.1016/j.jsv.2006.12.024

    Article  Google Scholar 

  16. Yao, H., Wang, Y., Xie, L., Wen, B.: Bi-stable buckled beam nonlinear energy sink applied to rotor system. Mech. Syst. Signal Process. 138, 106546 (2020). https://doi.org/10.1016/j.ymssp.2019.106546

    Article  Google Scholar 

  17. Carrella, A., Brennan, M.J., Waters, T.P., Shin, K.: On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets. J. Sound Vib. 315, 712–720 (2008). https://doi.org/10.1016/j.jsv.2008.01.046

    Article  Google Scholar 

  18. Zhou, N., Liu, K.: A tunable high-static-low-dynamic stiffness vibration isolator. J. Sound Vib. 329, 1254–1273 (2010). https://doi.org/10.1016/j.jsv.2009.11.001

    Article  Google Scholar 

  19. Wang, M., Chen, X., Li, X.: An ultra-low frequency two DOFs’ vibration isolator using positive and negative stiffness in parallel. Math. Probl. Eng. 2016, 3728397 (2016). https://doi.org/10.1155/2016/3728397

    Article  Google Scholar 

  20. Sun, X., Wang, F., Xu, J.: Analysis, design and experiment of continuous isolation structure with Local Quasi-Zero-Stiffness property by magnetic interaction. Int. J. Non. Linear Mech. 116, 289–301 (2019). https://doi.org/10.1016/j.ijnonlinmec.2019.07.008

    Article  Google Scholar 

  21. Shan, Y., Wu, W., Chen, X.: Design of a miniaturized pneumatic vibration isolator with high-static-low-dynamic stiffness. J. Vib. Acoust. Trans. ASME. 137, 045001 (2015). https://doi.org/10.1115/1.4029898

    Article  Google Scholar 

  22. Zheng, Y., Zhang, X., Luo, Y., Yan, B., Ma, C.: Design and experiment of a high-static-low-dynamic stiffness isolator using a negative stiffness magnetic spring. J. Sound Vib. 360, 31–52 (2016). https://doi.org/10.1016/j.jsv.2015.09.019

    Article  Google Scholar 

  23. Zhu, Y., Li, Q., Xu, D., Hu, C., Zhang, M.: Modeling and analysis of a negative stiffness magnetic suspension vibration isolator with experimental investigations. Rev. Sci. Instrum. 83, 095108 (2012). https://doi.org/10.1063/1.4751863

    Article  Google Scholar 

  24. Li, Q., Zhu, Y., Xu, D., Hu, J., Min, W., Pang, L.: A negative stiffness vibration isolator using magnetic spring combined with rubber membrane. J. Mech. Sci. Technol. 27, 813–824 (2013). https://doi.org/10.1007/s12206-013-0128-5

    Article  Google Scholar 

  25. Zheng, Y., Zhang, X., Luo, Y., Zhang, Y., Xie, S.: Analytical study of a quasi-zero stiffness coupling using a torsion magnetic spring with negative stiffness. Mech. Syst. Signal Process. 100, 135–151 (2018). https://doi.org/10.1016/j.ymssp.2017.07.028

    Article  Google Scholar 

  26. Zhou, J., Wang, X., Xu, D., Bishop, S.: Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms. J. Sound Vib. 346, 53–69 (2015). https://doi.org/10.1016/j.jsv.2015.02.005

    Article  Google Scholar 

  27. Zhou, J., Xiao, Q., Xu, D., Ouyang, H., Li, Y.: A novel quasi-zero-stiffness strut and its applications in six-degree-of-freedom vibration isolation platform. J. Sound Vib. 394, 59–74 (2017). https://doi.org/10.1016/j.jsv.2017.01.021

    Article  Google Scholar 

  28. Ye, K., Ji, J.C., Brown, T.: A novel integrated quasi-zero stiffness vibration isolator for coupled translational and rotational vibrations. Mech. Syst. Signal Process. 149, 107340 (2021). https://doi.org/10.1016/j.ymssp.2020.107340

    Article  Google Scholar 

  29. Carrella, A., Brennan, M.J., Waters, T.P.: Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 301, 678–689 (2007). https://doi.org/10.1016/j.jsv.2006.10.011

    Article  Google Scholar 

  30. Carrella, A., Brennan, M.J., Kovacic, I., Waters, T.P.: On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 322, 707–717 (2009). https://doi.org/10.1016/j.jsv.2008.11.034

    Article  Google Scholar 

  31. Carrella, A., Brennan, M.J., Waters, T.P.: Demonstrator to show the effects of negative stiffness on the natural frequency of a simple oscillator. Proc. Inst. Mech Eng. Part C-J. Eng. Mech. Eng. Sci. 222, 1189–1192 (2008). https://doi.org/10.1243/09544062JMES1012

    Article  Google Scholar 

  32. Kovacic, I., Brennan, M.J., Waters, T.P.: A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. J. Sound Vib. 315, 700–711 (2008). https://doi.org/10.1016/j.jsv.2007.12.019

    Article  Google Scholar 

  33. Wang, Y., Li, S., Cheng, C.: Investigation on a quasi-zero-stiffness vibration isolator under random excitation. J. Theor. Appl. Mech. 54, 621–632 (2016). https://doi.org/10.15632/jtam-pl.54.2.621

    Article  Google Scholar 

  34. Le, T.D., Ahn, K.K.: A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vibr. 330, 6311–6335 (2011). https://doi.org/10.1016/j.jsv.2011.07.039

    Article  Google Scholar 

  35. Danh, L.T., Ahn, K.K.: Active pneumatic vibration isolation system using negative stiffness structures for a vehicle seat. J. Sound Vibr. 333, 1245–1268 (2014). https://doi.org/10.1016/j.jsv.2013.10.027

    Article  Google Scholar 

  36. Papaioannou, G., Voutsinas, A., Koulocheris, D., Antoniadis, I.: Dynamic performance analysis of vehicle seats with embedded negative stiffness elements. Veh. Syst. Dyn. 58, 307–337 (2020). https://doi.org/10.1080/00423114.2019.1617424

    Article  Google Scholar 

  37. Xiaozhen, Qu., Hou, G., Liu, H., He, H.: Characteristics analysis of the automobile with negative stiffness suspension. Appl. Mech. Mater. 456, 189–192 (2014). https://doi.org/10.4028/www.scientific.net/AMM.456.189

    Article  Google Scholar 

  38. Suman, S., Balaji, P.S., Selvakumar, K., Kumaraswamidhas, L.A.: Nonlinear vibration control device for a vehicle suspension using negative stiffness mechanism. J. Vib. Eng. Technol. (2021). https://doi.org/10.1007/s42417-020-00275-6

    Article  Google Scholar 

  39. Wu, Q., Huang, G., Liu, C., Xie, S., Xu, M.: Low-frequency multi-mode vibration suppression of a metastructure beam with two-stage high-static-low-dynamic stiffness oscillators. Acta Mech. 230, 4341–4356 (2019). https://doi.org/10.1007/s00707-019-02515-7

    Article  MathSciNet  MATH  Google Scholar 

  40. Valeev, A., Zotov, A., Kharisov, S.: Designing of compact low frequency vibration isolator with quasi-zero-stiffness. J. Low Freq. Noise Vib. Act. Control. 34, 459–473 (2015). https://doi.org/10.1260/0263-0923.34.4.459

    Article  Google Scholar 

  41. Zhou, Y., Chen, P., Mosqueda, G.: Numerical studies of three-dimensional isolated structures with vertical quasi-zero stiffness property. J. Earthq. Eng. (2021). https://doi.org/10.1080/13632469.2020.1813662

    Article  Google Scholar 

  42. Palomares, E., Nieto, A.J., Morales, A.L., Chicharro, J.M., Pintado, P.: Numerical and experimental analysis of a vibration isolator equipped with a negative stiffness system. J. Sound Vibr. 414, 31–42 (2018). https://doi.org/10.1016/j.jsv.2017.11.006

    Article  Google Scholar 

  43. Gatti, G.: A K-shaped spring configuration to boost elastic potential energy. Smart Mater. Struct. 28, 077002 (2019). https://doi.org/10.1088/1361-665X/ab1ec8

    Article  Google Scholar 

  44. Deng, T., Wen, G., Ding, H., Lu, Z.-Q., Chen, L.-Q.: A bio-inspired isolator based on characteristics of quasi-zero stiffness and bird multi-layer neck. Mech. Syst. Signal Process. 145, 106967 (2020). https://doi.org/10.1016/j.ymssp.2020.106967

    Article  Google Scholar 

  45. Liu, C., Jing, X., Li, F.: Vibration isolation using a hybrid lever-type isolation system with an X-shape supporting structure. Int. J. Mech. Sci. 98, 169–177 (2015). https://doi.org/10.1016/j.ijmecsci.2015.04.012

    Article  Google Scholar 

  46. Sun, X., Jing, X., Xu, J., Cheng, L.: Vibration isolation via a scissor-like structured platform. J. Sound Vibr. 333, 2404–2420 (2014). https://doi.org/10.1016/j.jsv.2013.12.025

    Article  Google Scholar 

  47. Sun, X., Jing, X.: Analysis and design of a nonlinear stiffness and damping system with a scissor-like structure. Mech. Syst. Signal Process. 66–67, 723–742 (2016). https://doi.org/10.1016/j.ymssp.2015.05.026

    Article  Google Scholar 

  48. Sun, X., Jing, X.: A nonlinear vibration isolator achieving high-static-low-dynamic stiffness and tunable anti-resonance frequency band. Mech. Syst. Signal Process. 80, 166–188 (2016). https://doi.org/10.1016/j.ymssp.2016.04.011

    Article  Google Scholar 

  49. Song, Y., Sun, X.: Modeling and dynamics of a MDOF isolation system. Appl. Sci.-Basel. 7, 393 (2017). https://doi.org/10.3390/app7040393

    Article  Google Scholar 

  50. Chai, Y., Jing, X., Guo, Y.: A compact X-shaped mechanism based 3-DOF anti-vibration unit with enhanced tunable QZS property. Mech. Syst. Signal Process. 168, 108651 (2022). https://doi.org/10.1016/j.ymssp.2021.108651

    Article  Google Scholar 

  51. Zhang, W., Zhao, J.: Analysis on nonlinear stiffness and vibration isolation performance of scissor-like structure with full types. Nonlinear Dyn. 86, 17–36 (2016). https://doi.org/10.1007/s11071-016-2869-z

    Article  Google Scholar 

  52. Xiong, Y., Li, F., Wang, Y.: A nonlinear quasi-zero-stiffness vibration isolation system with additional X-shaped structure: Theory and experiment. Mech. Syst. Signal Process. 177, 109208 (2022). https://doi.org/10.1016/j.ymssp.2022.109208

    Article  Google Scholar 

  53. Bian, J., Jing, X.: Analysis and design of a novel and compact X-structured vibration isolation mount (X-Mount) with wider quasi-zero-stiffness range. Nonlinear Dyn. 101, 2195–2222 (2020). https://doi.org/10.1007/s11071-020-05878-y

    Article  Google Scholar 

  54. Chai, Y., Jing, X., Chao, X.: X-shaped mechanism based enhanced tunable QZS property for passive vibration isolation. Int. J. Mech. Sci. 218, 107077 (2022). https://doi.org/10.1016/j.ijmecsci.2022.107077

    Article  Google Scholar 

  55. Wu, Z., Jing, X., Bian, J., Li, F., Allen, R.: Vibration isolation by exploring bio-inspired structural nonlinearity. Bioinspir. Biomim. 10, 056015 (2015). https://doi.org/10.1088/1748-3190/10/5/056015

    Article  Google Scholar 

  56. Wang, Y., Jing, X.: Nonlinear stiffness and dynamical response characteristics of an asymmetric X-shaped structure. Mech. Syst. Signal Process. 125, 142–169 (2019). https://doi.org/10.1016/j.ymssp.2018.03.045

    Article  Google Scholar 

  57. Wang, Y., Jing, X., Guo, Y.: Nonlinear analysis of a bio-inspired vertically asymmetric isolation system under different structural constraints. Nonlinear Dyn. 95, 445–464 (2019). https://doi.org/10.1007/s11071-018-4575-5

    Article  Google Scholar 

  58. Jiang, G., Jing, X., Guo, Y.: A novel bio-inspired multi-joint anti-vibration structure and its nonlinear HSLDS properties. Mech. Syst. Signal Process. 138, 106552 (2020). https://doi.org/10.1016/j.ymssp.2019.106552

    Article  Google Scholar 

  59. Yan, G., Wu, Z.-Y., Wei, X.-S., Wang, S., Zou, H.-X., Zhao, L.-C., Qi, W.-H., Zhang, W.-M.: Nonlinear compensation method for quasi-zero stiffness vibration isolation. J. Sound Vib. 523, 116743 (2022). https://doi.org/10.1016/j.jsv.2021.116743

    Article  Google Scholar 

  60. Sun, X., Xu, J., Jing, X., Cheng, L.: Beneficial performance of a quasi-zero-stiffness vibration isolator with time-delayed active control. Int. J. Mech. Sci. 82, 32–40 (2014). https://doi.org/10.1016/j.ijmecsci.2014.03.002

    Article  Google Scholar 

  61. Dhooge, A., Govaerts, W., Kuznetsov, Yu.A., Meijer, H.G.E., Sautois, B.: New features of the software MatCont for bifurcation analysis of dynamical systems. Math. Comput. Model Dyn. Syst. 14, 147–175 (2008). https://doi.org/10.1080/13873950701742754

    Article  MathSciNet  MATH  Google Scholar 

  62. Lu, Z., Brennan, MJ., Chen, L-Q.: On the transmissibilities of nonlinear vibration isolation system. J. Sound Vib 375, 28–37 (2016). https://doi.org/10.1016/j.jsv.2016.04.032

    Article  Google Scholar 

  63. Cheng, C., Li, S., Wang, Y., Jiang, X.: Resonance of a quasi-zero stiffness vibration system under base excitation with load mismatch. Int. J. Struct. Stab. Dyn. 18(01) 1850002 (2018). https://doi.org/10.1142/S0219455418500025

    Article  MathSciNet  Google Scholar 

  64. Karnopp, D., Crosby, M.J., Harwood, R.A.: Vibration control using semi-active force generators. J. Eng. Ind. 96, 619–626 (1974). https://doi.org/10.1115/1.3438373

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Institute of Vibration and Noise Control at Beijing Institute of Technology. The authors would like to thank the reviewers for their precious reviews and comments.

CRediT authorship contribution statement

Bingyi Liu contributed to conceptualization, investigation, methodology, writing—original draft; writing—review and editing. Liang Gu contributed to funding acquisition and supervision. Mingming Dong supervised the study.

Statements and Declarations

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Beijing Institute of Technology, Beijing, 100081, China

    Bingyi Liu, Liang Gu & Mingming Dong

Authors
  1. Bingyi Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liang Gu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mingming Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liang Gu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

The expressions of c, d, and e in Eq. (26) are as follows:

$$\begin{aligned} c & = n^{4} \left[ { - \frac{1}{2}w^{2} + 4\left( {n - 1} \right)^{2} r^{2} w} \right. + 4\left( {n - 1} \right)^{4} r^{4} + 2n^{2} \left( {n - 1} \right)^{2} \left( {l_{\max }^{2} l_{\min }^{2} - 2r^{4} - r^{2} \left( {l_{\max } - l_{\min } } \right)^{2} } \right) \\ &\left. { - 4n\left( {n - 1} \right)\left( {3n - 2} \right)r^{2} l_{\max } l_{\min } } \vphantom{ { - \frac{1}{2}w^{2} + 4\left( {n - 1} \right)^{2} r^{2} w}} \right], \\ \end{aligned}$$
(A.1)
$$\begin{aligned}d = 4n^{6} \left( {n - 1} \right)^{2} r^{2} \left[ {w - n^{2} \left( {l_{\max }^{2} + l_{\min }^{2} } \right)} \right]\left[ {w + 2n\left( {n - 1} \right)l_{\max } l_{\min } - \left( {2n - 1} \right)r^{2} } \right], \end{aligned}$$
(A.2)
$$\begin{aligned} e & = \frac{1}{16}n^{8} w^{4} + n^{8} \left( {n - 1} \right)^{2} r^{2} w^{3} - \frac{1}{2}n^{8} \left( {n - 1} \right)\left[ {n^{2} \left( {n - 1} \right)l_{\max }^{2} l_{\min }^{2} } \right. + 2\left( {2n - 1} \right)\left( {n - 1} \right)r^{4} + 2n\left( {n - 2} \right)r^{2} l_{\max } l_{\min } \\ & \left. + {3n^{2} \left( {n - 1} \right)r^{4} \left( {l_{\max } - l_{\min } } \right)^{2} } \right]w^{2} - 2n^{10} \left( {n - 1} \right)^{2} r^{2} \left[ {2n\left( {n - 1} \right)l_{\max } l_{\min } \left( {l_{\max }^{2} + l_{\min }^{2} } \right)} \right. - \left( {2n - 1} \right)r^{2} \left( {l_{\max }^{2} + l_{\min }^{2} } \right) \\ &\left. { - 2n^{2} l_{\max }^{2} l_{\min }^{2} } \right]w + n^{12} \left( {n - 1} \right)^{4} \left[ {\left( {r^{2} l_{\max }^{2} + r^{2} l_{\min }^{2} - l_{\max }^{2} l_{\min }^{2} } \right)^{2} } \right.\left. { + 4r^{4} l_{\max }^{2} l_{\min }^{2} } \right] + 4n^{13} \left( {n - 1} \right)^{3} r^{2} l_{\max } l_{\min } \left( {r^{2} l_{\max }^{2} } \right. \\ &\left. { + r^{2} l_{\min }^{2} + l_{\max }^{2} l_{\min }^{2} } \right). \\ \end{aligned}$$
(A.3)

Appendix B

The expressions of q and δ in Eq. (31) are as follows:

$$p = - \frac{1}{48}c^{2} - \frac{1}{4}e,$$
(B.1)
$$q = - \frac{1}{864}c^{3} + \frac{1}{24}ec - \frac{1}{64}d^{2},$$
(B.2)
$$\delta = \left( \frac{p}{3} \right)^{3} + \left( \frac{q}{2} \right)^{2}.$$
(B.3)

Appendix C

The coefficient expressions in Eqs. (35)–(44) are as follows:

$$\begin{aligned} a_{1} &= \alpha_{0} \alpha_{2} ,\;a_{2} = \alpha_{0} \alpha_{1} \alpha_{2} ,\;\;a_{3} = 2\alpha_{0} \alpha_{1} \alpha_{2}^{3} ,\;a_{4} = 2\alpha_{1} \alpha_{2}^{2} ,\;a_{5} = \alpha_{1}^{2} \alpha_{2} + \alpha_{2}^{3} + \alpha_{1}^{2} \alpha_{2}^{3} ,\;a_{6} = 2\alpha_{1}^{2} \alpha_{2}^{3} ,\\ a_{7}& = \alpha_{0} \alpha_{2}^{2} \left( {1 + \alpha_{1}^{2} } \right),\;a_{8} = 2\alpha_{0} \alpha_{1}^{2} \alpha_{2}^{2} ,\;a_{9} = \left( 1 \right. + \left. {\alpha_{1}^{2} } \right)\alpha_{2} ,\;a_{10} = 2\alpha_{1}^{2} \alpha_{2} ,\,a_{11} = \alpha_{0}^{2} \alpha_{3}^{2} + \frac{{\alpha_{3}^{2} \left( {1 - \alpha_{1} } \right)^{2} }}{{4\alpha_{2}^{2} }},\\ a_{12}& = \frac{{\alpha_{0} \alpha_{3}^{2} }}{{\alpha_{2} }},\,a_{13} = \frac{{\alpha_{3}^{2} }}{{\alpha_{2} }},\;a_{14} = \alpha_{1} \alpha_{3}^{2} ,a_{15} = \frac{{2\left( {n - 1} \right)^{2} }}{{3n^{2} }}\alpha_{2}^{2} , \end{aligned}$$
$$a_{16} = \frac{{2\left( {n - 1} \right)^{4} }}{{3n^{4} }}\alpha_{2}^{4} + \frac{{\left( {n - 1} \right)^{2} }}{{3n^{2} }}\left[ {\alpha_{1}^{2} } \right. - 2\alpha_{2}^{4} - \left. {\alpha_{2}^{2} \left( {1 - \alpha_{1} } \right)^{2} } \right] - \frac{{2\left( {n - 1} \right)\left( {3n - 2} \right)}}{{3n^{3} }}\alpha_{1} \alpha_{2}^{2} ,a_{17} = \frac{{\left( {n - 1} \right)^{2} }}{{144n^{2} }}\alpha_{2}^{2} ,$$
$$a_{18} = \frac{{\left( {n - 1} \right)^{2} \left( {4n^{2} - 10n + 5} \right)}}{{144n^{4} }}\alpha_{2}^{4} - \frac{{\left( {n - 1} \right)^{2} }}{{72n^{2} }}\alpha_{2}^{2} \left( {1 - \alpha_{1} } \right)^{2} + \frac{{\left( {n - 1} \right)}}{{72n^{3} }}\alpha_{1} \alpha_{2}^{2} - \frac{{\left( {n - 1} \right)^{2} }}{{144n^{2} }}\alpha_{1}^{2} ,$$
$$\begin{aligned} a_{19} & = \frac{{\left( {n - 1} \right)^{4} \left( {2n^{2} - 10n + 5} \right)}}{{54n^{6} }}\alpha_{2}^{6} - \frac{{\left( {n - 1} \right)^{2} \left( {10n^{2} - 26n + 13} \right)}}{{144n^{4} }}\alpha_{2}^{4} \left( {1 - \alpha_{1} } \right)^{2} + \frac{{\left( {n - 1} \right)^{2} \left( {11n - 8} \right)}}{{72n^{5} }}\alpha_{1} \alpha_{2}^{4} \\ & \quad- \frac{{\left( {n - 1} \right)^{3} }}{{24n^{3} }}\alpha_{1} \alpha_{2}^{2} \left( {1 - \alpha_{1} } \right)^{2} - \frac{{\left( {n - 1} \right)^{2} \left( {4n^{2} - 8n + 1} \right)}}{{72n^{4} }}\alpha_{1}^{2} \alpha_{2}^{2} , \\ \end{aligned}$$
$$\begin{aligned} a_{20} & = \frac{{\left( {n - 1} \right)^{4} \left( {2n - 1} \right)\left( {4n^{2} - 10n + 5} \right)}}{{36n^{8} }}\alpha_{2}^{8} + \frac{{\left( {n - 1} \right)^{4} \left( {4n^{2} - 30n + 15} \right)}}{{72n^{6} }}\alpha_{2}^{6} \left( {1 - \alpha_{1} } \right)^{2} - \frac{{\left( {n - 1} \right)^{3} \left( {20n^{2} - 33n + 12} \right)}}{{36n^{7} }}\alpha_{1} \alpha_{2}^{6} \\ & \quad - \frac{{5\left( {n - 1} \right)^{4} }}{{72n^{4} }}\alpha_{2}^{4} \left( {1 - \alpha_{1} } \right)^{4} + \frac{{\left( {n - 1} \right)^{3} \left( {3n^{2} - 12n + 11} \right)}}{{36n^{5} }}\alpha_{1} \alpha_{2}^{4} \left( {1 - \alpha_{1} } \right)^{2} + \frac{{\left( {n - 1} \right)^{2} \left( {32n^{4} - 88n^{3} + 62n^{2} - 11} \right)}}{{72n^{6} }}\alpha_{1}^{2} \alpha_{2}^{4} \\ & \quad- \frac{{\left( {n - 1} \right)^{4} }}{{36n^{4} }}\alpha_{1}^{2} \alpha_{2}^{2} \left( {1 - \alpha_{1} } \right)^{2} + \frac{{\left( {n - 1} \right)^{3} }}{{36n^{5} }}\alpha_{1}^{3} \alpha_{2}^{2} - \frac{{\left( {n - 1} \right)^{4} }}{{36n^{4} }}\alpha_{1}^{4} , \\ \end{aligned}$$
$$\begin{aligned} a_{21} & = \frac{{\left( {n - 1} \right)^{6} \left( {2n - 1} \right)^{2} }}{{9n^{10} }}\alpha_{2}^{10} + \frac{{\left( {n - 1} \right)^{4} \left( {2n - 1} \right)\left( {4n^{2} - 14n + 7} \right)}}{{36n^{8} }}\alpha_{2}^{8} \left( {1 - \alpha_{1} } \right)^{2} + \frac{{\left( {n - 1} \right)^{4} \left( {2n - 1} \right)\left( {6n^{2} - 17n + 8} \right)}}{{18n^{9} }}\alpha_{1} \alpha_{2}^{8} \\ & \quad - \frac{{\left( {n - 1} \right)^{4} \left( {n^{2} + 4n - 2} \right)}}{{18n^{6} }}\alpha_{2}^{6} \left( {1 - \alpha_{1} } \right)^{4} - \frac{{\left( {n - 1} \right)^{3} \left( {12n^{4} - 30n^{3} + 37n^{2} - 32n + 10} \right)}}{{18n^{7} }}\alpha_{1} \alpha_{2}^{6} \left( {1 - \alpha_{1} } \right)^{2} \\ & \quad - \frac{{\left( {n - 1} \right)^{3} \left( {12n^{5} - 40n^{4} + 32n^{3} + 3n^{2} - 15n + 5} \right)}}{{9n^{8} }}\alpha_{1}^{2} \alpha_{2}^{6} + \frac{{\left( {n - 1} \right)^{5} }}{{3n^{5} }}\alpha_{1} \alpha_{2}^{4} \left( {1 - \alpha_{1} } \right)^{4} + \frac{{\left( {n - 1} \right)^{5} }}{{6n^{5} }}\alpha_{1}^{3} \alpha_{2}^{2} \left( {1 - \alpha_{1} } \right)^{2} \\ & \quad + \frac{{\left( {n - 1} \right)^{4} \left( {34n^{2} - 38n - 5} \right)}}{{36n^{6} }}\alpha_{1}^{2} \alpha_{2}^{4} \left( {1 - \alpha_{1} } \right)^{2} + \frac{{\left( {n - 1} \right)^{3} \left( {13n^{2} - 11n + 4} \right)}}{{18n^{7} }}\alpha_{1}^{3} \alpha_{2}^{4} + \frac{{\left( {n - 1} \right)^{4} \left( {2n^{2} - 4n - 1} \right)}}{{18n^{6} }}\alpha_{1}^{4} \alpha_{2}^{2} , \\ \end{aligned}$$
$$\begin{aligned} a_{22} & = \frac{{\left( {n - 1} \right)^{6} \left( {2n - 1} \right)^{3} }}{{27n^{12} }}\alpha_{2}^{12} + \frac{{\left( {n - 1} \right)^{6} \left( {2n - 1} \right)^{2} }}{{18n^{10} }}\alpha_{2}^{10} \left( {1 - \alpha_{1} } \right)^{2} + \frac{{\left( {n - 1} \right)^{5} \left( {2n - 1} \right)^{2} \left( {3n - 2} \right)}}{{9n^{11} }}\alpha_{1} \alpha_{2}^{10} \\ & \quad - \frac{{\left( {n - 1} \right)^{4} \left( {2n - 1} \right)\left( {4n^{2} + 10n - 5} \right)}}{{72n^{8} }}\alpha_{2}^{8} \left( {1 - \alpha_{1} } \right)^{4} - \frac{{\left( {n - 1} \right)^{4} \left( {2n - 1} \right)\left( {12n^{3} - 6n^{2} + 7n - 4} \right)}}{{18n^{9} }}\alpha_{1} \alpha_{2}^{8} \left( {1 - \alpha_{1} } \right)^{2} \\ & \quad - \frac{{\left( {n - 1} \right)^{4} \left( {2n - 1} \right)\left( {24n^{4} - 16n^{3} - 20n^{2} + 28n - 9} \right)}}{{18n^{10} }}\alpha_{1}^{2} \alpha_{2}^{8} - \frac{{\left( {n - 1} \right)^{6} }}{{27n^{6} }}\alpha_{2}^{6} \left( {1 - \alpha_{1} } \right)^{6} + \frac{{\left( {n - 1} \right)^{5} }}{{9n^{7} }}\alpha_{1}^{5} \alpha_{2}^{2} + \frac{{\left( {n - 1} \right)^{6} }}{{27n^{6} }}\alpha_{1}^{6} \\ & \quad- \frac{{\left( {n - 1} \right)^{5} \left( {6n^{2} - 18n + 7} \right)}}{{18n^{7} }}\alpha_{1} \alpha_{2}^{6} \left( {1 - \alpha_{1} } \right)^{4} - \frac{{\left( {n - 1} \right)^{4} \left( {12n^{4} - 58n^{3} + 73n^{2} - 20n - 2} \right)}}{{18n^{8} }}\alpha_{1}^{2} \alpha_{2}^{6} \left( {1 - \alpha_{1} } \right)^{2} \\ & \quad- \frac{{\left( {n - 1} \right)^{3} \left( {72n^{4} - 183n^{3} + 174n^{2} - 78n + 14} \right)}}{{27n^{9} }}\alpha_{1}^{3} \alpha_{2}^{6} - \frac{{7\left( {n - 1} \right)^{6} }}{{18n^{6} }}\alpha_{1}^{2} \alpha_{2}^{4} \left( {1 - \alpha_{1} } \right)^{4} \\ & \quad - \frac{{\left( {n - 1} \right)^{4} \left( {24n^{4} - 52n^{3} + 52n^{2} - 20n + 3} \right)}}{{18n^{8} }}\alpha_{1}^{4} \alpha_{2}^{4} - \frac{{\left( {n - 1} \right)^{6} }}{{9n^{6} }}\alpha_{1}^{4} \alpha_{2}^{2} \left( {1 - \alpha_{1} } \right)^{2} - \frac{{\left( {n - 1} \right)^{5} \left( {15n^{2} - 18n + 2} \right)}}{{9n^{7} }}\alpha_{1}^{3} \alpha_{2}^{4} \left( {1 - \alpha_{1} } \right)^{2} , \\ \end{aligned}$$
$$\begin{aligned} a_{23} &= \frac{{\left( {2n - 1} \right)}}{{n^{2} }}\alpha_{2}^{2} - \frac{{2\left( {n - 1} \right)}}{n}\alpha_{1} ,\;a_{24} = \frac{{2\left( {n - 1} \right)}}{{n^{2} }}\alpha_{1} \alpha_{2}^{2} - \frac{{2\left( {n - 1} \right)}}{n}\alpha_{1}^{2} - \frac{{\left( {n - 1} \right)}}{n}\alpha_{2}^{2} \left( {1 + \alpha_{1} } \right)^{2} ,\;a_{25} = \frac{{\left( {n - 1} \right)^{4} }}{{1728n^{4} }}\alpha_{2}^{4} , \\ a_{26} &= \frac{{\left( {n - 1} \right)^{6} }}{{216n^{6} }}\alpha_{2}^{6} - \frac{{\left( {n - 1} \right)^{5} }}{{864n^{5} }}\alpha_{2}^{4} \left( {1 + \alpha_{1} } \right)^{2} - \frac{{\left( {n - 1} \right)^{4} }}{{1728n^{6} }}\alpha_{2}^{4} \left( {1 + \alpha_{1}^{2} } \right),\\ a_{27} & = \frac{{\left( {n - 1} \right)^{6} }}{{1728n^{6} }}\alpha_{2}^{4} \left( {1 + \alpha_{1}^{2} } \right)^{2} + \frac{{\left( {n - 1} \right)^{5} \left( {2n^{2} - 2n + 1} \right)}}{{432n^{7} }}\alpha_{1} \alpha_{2}^{4} \left( {1 + \alpha_{1}^{2} } \right) + \frac{{\left( {n - 1} \right)^{4} \left( {2n^{2} - 2n + 1} \right)^{2} }}{{1728n^{8} }}\alpha_{1}^{2} \alpha_{2}^{4} \\ & \quad- \frac{{\left( {n - 1} \right)^{6} \left( {16n^{2} - 6n + 3} \right)}}{{864n^{8} }}\alpha_{2}^{6} \left( {1 + \alpha_{1}^{2} } \right) + \frac{{\left( {n - 1} \right)^{5} \left( {4n^{2} + 2n - 1} \right)}}{{432n^{7} }}\alpha_{1} \alpha_{2}^{6} + \frac{{\left( {n - 1} \right)^{6} \left( {2n^{2} - 6n + 3} \right)}}{{216n^{8} }}\alpha_{2}^{8} , \\ \end{aligned}$$
$$\begin{aligned} a_{28} & = \frac{{\left( {n - 1} \right)^{7} }}{{432n^{7} }}\alpha_{1} \alpha_{2}^{4} \left( {1 + \alpha_{1}^{2} } \right)^{2} + \frac{{\left( {n - 1} \right)^{6} \left( {2n^{2} - 2n + 1} \right)}}{{432n^{8} }}\alpha_{1}^{2} \alpha_{2}^{4} \left( {1 + \alpha_{1}^{2} } \right) + \frac{{\left( {n - 1} \right)^{5} \left( {2n - 1} \right)^{2} }}{{432n^{9} }}\alpha_{1}^{3} \alpha_{2}^{4} + \frac{{\left( {n - 1} \right)^{8} \left( {2n - 1} \right)}}{{54n^{10} }}\alpha_{2}^{10} \\ & \quad- \frac{{\left( {n - 1} \right)^{6} \left( {20n^{2} - 22n + 11} \right)}}{{864n^{8} }}\alpha_{2}^{6} \left( {1 + \alpha_{1}^{2} } \right)^{2} + \frac{{\left( {n - 1} \right)^{5} \left( {4n^{2} - 2n + 1} \right)^{2} }}{{864n^{9} }}\alpha_{1} \alpha_{2}^{6} \left( {1 + \alpha_{1}^{2} } \right) + \frac{{\left( {n - 1} \right)^{7} \left( {2n - 1} \right)}}{{54n^{9} }}\alpha_{1} \alpha_{2}^{8} \\ & \quad+ \frac{{\left( {n - 1} \right)^{6} \left( {8n^{4} - 40n^{3} + 32n^{2} - 12n + 3} \right)}}{{432n^{10} }}\alpha_{2}^{8} \left( {1 + \alpha_{1}^{2} } \right) + \frac{{\left( {n - 1} \right)^{6} \left( {2n - 1} \right)\left( {2n^{2} - 2n + 1} \right)}}{{432n^{10} }}\alpha_{1}^{2} \alpha_{2}^{6} , \\ \end{aligned}$$
$$\begin{aligned} a_{29} & = \frac{{\left( {n - 1} \right)^{8} }}{{432n^{8} }}\alpha_{1}^{2} \alpha_{2}^{4} \left( {1 + \alpha_{1}^{2} } \right)^{2} + \frac{{\left( {n - 1} \right)^{6} \left( {2n - 1} \right)^{2} }}{{432n^{10} }}\alpha_{1}^{4} \alpha_{2}^{4} - \frac{{\left( {n - 1} \right)^{8} }}{{108n^{8} }}\alpha_{2}^{6} \left( {1 + \alpha_{1}^{2} } \right)^{3} + \frac{{\left( {n - 1} \right)^{7} \left( {2n - 1} \right)^{2} }}{{36n^{11} }}\alpha_{1} \alpha_{2}^{10} \\ & \quad+ \frac{{\left( {n - 1} \right)^{6} \left( {2n - 1} \right)\left( {2n^{2} - 10n + 5} \right)}}{{432n^{10} }}\alpha_{1}^{2} \alpha_{2}^{6} \left( {1 + \alpha_{1}^{2} } \right) + \frac{{\left( {n - 1} \right)^{5} \left( {2n - 1} \right)^{2} \left( {3n^{2} - 2n + 1} \right)}}{{216n^{11} }}\alpha_{1}^{3} \alpha_{2}^{6} + \frac{{\left( {n - 1} \right)^{8} \left( {2n - 1} \right)^{2} }}{{108n^{12} }}\alpha_{2}^{12} \\ & \quad+ \frac{{\left( {n - 1} \right)^{6} \left( {4n^{2} - 2n + 1} \right)\left( {4n^{2} - 26n + 13} \right)}}{{1728n^{10} }}\alpha_{2}^{8} \left( {1 + \alpha_{1}^{2} } \right)^{2} + \frac{{\left( {n - 1} \right)^{7} \left( {2n - 1} \right)\left( {8n^{2} - 10n + 5} \right)}}{{432n^{11} }}\alpha_{1} \alpha_{2}^{8} \left( {1 + \alpha_{1}^{2} } \right) \\ & \quad+ \frac{{\left( {n - 1} \right)^{6} \left( {2n - 1} \right)^{2} \left( {13n^{2} - 2n + 1} \right)}}{{432n^{12} }}\alpha_{1}^{2} \alpha_{2}^{8} + \frac{{\left( {n - 1} \right)^{8} \left( {2n - 1} \right)\left( {4n^{2} - 2n + 1} \right)}}{{216n^{12} }}\alpha_{2}^{10} \left( {1 + \alpha_{1}^{2} } \right) \\ & \quad+ \frac{{\left( {n - 1} \right)^{7} \left( {4n^{2} - 2n + 1} \right)}}{{432n^{9} }}\alpha_{1} \alpha_{2}^{6} \left( {1 + \alpha_{1}^{2} } \right)^{2} , \\ \end{aligned}$$
$$a_{30} = \frac{1}{{n^{2} }}\alpha_{2}^{2} + \frac{{2\left( {n - 1} \right)}}{n}\left( {\frac{1}{n}\alpha_{2}^{2} - \alpha_{1} } \right),$$
(C.1)

The coefficient expressions in Eq. (53) are as follows:

$$\begin{aligned}a_{31} & = \frac{1}{1728}\left( {\frac{{4\alpha_{2}^{2} }}{{\left( {1 - \alpha_{1} } \right)^{2} }}} \right. - 1\left. { + \frac{{\alpha_{1} }}{{n\left( {n - 1} \right)\left( {1 - \alpha_{1} } \right)^{2} }}} \right)^{3} + \frac{1}{128}\frac{{\left( {2n - 1} \right)^{2} \alpha_{2}^{2} \left( {1 - \alpha_{1}^{2} } \right)^{2} }}{{n^{2} \left( {n - 1} \right)^{2} \left( {1 - \alpha_{1} } \right)^{6} }},\;a_{32} = \frac{1}{384}\frac{{\left( {2n - 1} \right)\alpha_{2} \left( {1 - \alpha_{1}^{2} } \right)}}{{n\left( {n - 1} \right)\left( {1 - \alpha_{1} } \right)^{3} }}, \end{aligned}$$
$$a_{33} = \frac{4}{3}\left( {\frac{{4\alpha_{2}^{2} }}{{\left( {1 - \alpha_{1} } \right)^{2} }}} \right. - 1\left. { + \frac{{\alpha_{1} }}{{n\left( {n - 1} \right)\left( {1 - \alpha_{1} } \right)^{2} }}} \right)^{3} + 9\frac{{\left( {2n - 1} \right)^{2} \alpha_{2}^{2} \left( {1 - \alpha_{1}^{2} } \right)^{2} }}{{n^{2} \left( {n - 1} \right)^{2} \left( {1 - \alpha_{1} } \right)^{6} }},\;a_{34} = \sqrt[3]{{a_{31} + a_{32} \sqrt {a_{33} } }} + \sqrt[3]{{a_{31} - a_{32} \sqrt {a_{33} } }},$$
$$a_{35} = 1 + \frac{{2\alpha_{2}^{2} }}{{\left( {1 - \alpha_{1} } \right)^{2} }} - \frac{{\alpha_{1} }}{{n\left( {n - 1} \right)\left( {1 - \alpha_{1} } \right)^{2} }},\;a_{36} = \frac{{\alpha_{2} }}{{1 - \alpha_{1} }}\left( {2 + \frac{{1 + \alpha_{1}^{2} }}{{n\left( {n - 1} \right)\left( {1 - \alpha_{1} } \right)^{2} }}} \right),\;\;a_{37} = \frac{{\alpha_{2} }}{{1 - \alpha_{1} }}.$$
(C.2)

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, B., Gu, L. & Dong, M. Design and characteristic analysis of an X-shaped negative stiffness structure. Acta Mech 233, 4549–4587 (2022). https://doi.org/10.1007/s00707-022-03343-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-022-03343-y

Search

Navigation