Nonlinear analysis of a bio-inspired vertically asymmetric isolation system under different structural constraints

Abstract

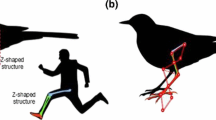
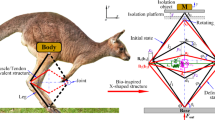
Inspired by the limb configuration of animals in their jumping and landing motions, a systematic investigation on the properties of a class of bio-inspired vertically asymmetric X-shaped (vaX) structures is carried out to explore the advantage of nonlinear characteristics in practical engineering. The nonlinear properties of two different vaX structures are studied under different constraint conditions. Formulations of the nonlinear vibration frequency and absolute displacement transmissibility of the structures are derived by the method of multiple scales. Considering practical conditions, three different constraints (i.e., (a) the same isolations height and assembling angle; (b) the same total rod length and assembling angle; (c) the same total rod length and isolation height) are summarized in this manuscript. Under these conditions, nonlinear properties including nonlinear vibration frequency, isolation performance and static stiffness are systematically discussed. Furthermore, the influences of the assembling pattern (i.e., normal and reverse assembling) on the isolation performance are investigated in detail. The results reveal that there exists rod-length ratio $s_{1}$ such that the nonlinear frequency ratio of the vaX-I vibration system is lowest; the natural frequency of the vaX-I structure is independent of the assembling pattern; however, compared with the normally assembled vaX-I structure, a lower resonant peak of the transmissibility can be obtained for the reverse-assembled structure, which suggests that the nonlinear damping of the vaX-I structure is affected by the assembling pattern. Experiments are carried out to verify the influence of the assembling pattern on the natural frequency and isolation performance of the vaX structures.

Appendices

Appendix A

The symbol descriptions of the bio-inspired isolation system

Symbol	Structural parameters
M	Mass of isolation object (kg)
$k_{l}$	Stiffness of the horizontal spring (N m$^{-1})$
$c_{1}$	Air damping coefficient (Ns m$^{-1})$
$c_{2}$	Damping coefficient of friction in joints
	(Ns m$^{-1})$
n	Number of layers
$a_{1}$, $b_{1}$, $a_{2}$, $b_{2}$	Rod length (m)
$\varphi _{1}$, $\varphi _{2}$	Variation of the assembly angle (Rad)
$\alpha _{1}$, $\alpha _{2}$	Assembly angle (Rad)
$s_{1}$, $s_{2}$	Rod-length ratio

The expressions of the nonlinear functions in Eq. (11) are expressed as:

$$\begin{aligned} h_1 \left( x \right)= & {} \left( \frac{c_2 \left( {2+6 n} \right) }{4 b_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}\right. \nonumber \\&\left. \qquad +\,6 \frac{c_2 n}{4 a_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}} \right) \nonumber \\&\qquad \left( {\frac{1}{2} \frac{\left( {b_1 +b_2 } \right) \left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{b_1 \sqrt{4 b_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}} \right. \nonumber \\&\qquad +\frac{1}{2}\frac{2 b_1 \cos \left( {\alpha _1 } \right) -x}{\sqrt{4 a_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}\nonumber \\&\qquad \left. {+\frac{1}{2}\frac{b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{\sqrt{4 a_2 ^{2}b_2 ^{2}-b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}b_1 }} \right) ^{\mathrm {-}2} \end{aligned}$$

(A.1)

$$\begin{aligned} h_2 \left( x \right)= & {} Mn^{2}\left( -\frac{b_1 +b_2 }{b_1 }\frac{1}{\sqrt{4b_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}\right. \nonumber \\&\left. \qquad -\frac{\left( {b_1 +b_2 } \right) \left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}{b_1 ^{4}} \right. \nonumber \\&\qquad \left( {4-\frac{\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}{b_1 ^{2}}} \right) ^{-3/2}\nonumber \\&\qquad -\frac{1}{\sqrt{4 a_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}\nonumber \\&\qquad -\frac{1}{2}\frac{\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) \left( {4 b_1 \cos \left( {\alpha _1 } \right) -2 x} \right) }{\left( {4 a_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}} \right) ^{3/2}}\nonumber \\&\qquad -\frac{b_2 ^{2}}{b_1 \sqrt{4 a_2 ^{2}b_1 ^{2}-b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}\nonumber \\&\qquad \left. -\frac{b_2 ^{4}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}{b_1 ^{4}}\left( 4 a_2 ^{2}\right. \right. \nonumber \\&\left. \left. \qquad -\frac{b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}{b_1 ^{2}} \right) ^{-3/2} \right) \bigg / \nonumber \\&\qquad \left( { \frac{\left( {b_1 +b_2 } \right) \left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{b_1 \sqrt{4 b_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}} \right. \nonumber \\&\qquad +\frac{2 b_1 \cos \left( {\alpha _1 } \right) -x}{\sqrt{4 a_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}\nonumber \\&\qquad \left. {+\frac{b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{\sqrt{4 a_2 ^{2}b_2 ^{2}-b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}b_1 }} \right) \end{aligned}$$

(A.2)

$$\begin{aligned} h_3 \left( x \right)= & {} {k_l x}\bigg /\left( {\frac{1}{2} \frac{\left( {b_1 +b_2 } \right) \left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{b_1 \sqrt{4 b_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}} \right. \nonumber \\&\qquad +\frac{1}{2}\frac{2 b_1 \cos \left( {\alpha _1 } \right) -x}{\sqrt{4 a_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}\nonumber \\&\qquad \left. {+\frac{1}{2}\frac{b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{\sqrt{4 a_2 ^{2}b_2 ^{2}-b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}b_1 }} \right) \end{aligned}$$

(A.3)

$$\begin{aligned} h_4 \left( x \right)= & {} {Mn}\bigg /\left( {\frac{1}{2} \frac{\left( {b_1 +b_2 } \right) \left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{b_1 \sqrt{4 b_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}} \right. \nonumber \\&\qquad +\frac{1}{2}\frac{2 b_1 \cos \left( {\alpha _1 } \right) -x}{\sqrt{4 a_1 ^{2}-\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}}\nonumber \\&\qquad \left. {+\frac{1}{2}\frac{b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) }{\sqrt{4 a_2 ^{2}b_2 ^{2}-b_2 ^{2}\left( {2 b_1 \cos \left( {\alpha _1 } \right) -x} \right) ^{2}}b_1 }} \right) \end{aligned}$$

(A.4)

Appendix B

The dimensionless variables in Eq. (12) are

$$\begin{aligned} \omega _1= & {} \sqrt{\frac{k_l }{M}} \end{aligned}$$

(B.1)

$$\begin{aligned} \omega _2= & {} \sqrt{\frac{k_{11} }{n^{2}k_l }} \end{aligned}$$

(B.2)

$$\begin{aligned} \xi _0= & {} \frac{1}{2} \frac{C\omega _1 }{n^{2}k_l } \end{aligned}$$

(B.3)

$$\begin{aligned} \xi _1= & {} \frac{1}{2}\frac{p_1 \omega _1 }{n^{2}k_l } \end{aligned}$$

(B.4)

$$\begin{aligned} \xi _2= & {} \frac{1}{2}\frac{p_2 \omega _1 }{n^{2}k_l } \end{aligned}$$

(B.5)

$$\begin{aligned} \xi _1= & {} \frac{1}{2}\frac{p_3 \omega _1 }{n^{2}k_l }\quad 0 \end{aligned}$$

(B.6)

$$\begin{aligned} \gamma _1= & {} \frac{r_1 }{n^{2}k_l } \end{aligned}$$

(B.7)

$$\begin{aligned} \gamma _2= & {} \frac{r_2 }{n^{2}k_l } \end{aligned}$$

(B.8)

$$\begin{aligned} \eta _i= & {} \frac{q_i }{n^{2}M}, \quad i= 0, 1, 2, 3 \end{aligned}$$

(B.9)

$$\begin{aligned} P_i= & {} \frac{F_i }{n^{2}k_l }, \quad i= 1, 2, 3, 4 \end{aligned}$$

(B.10)

where the expressions of the corresponding parameters are

$$\begin{aligned} k_{11}= & {} g_{31} \end{aligned}$$

(B.11)

$$\begin{aligned} C= & {} n^{2}c_1 +g_{10} \end{aligned}$$

(B.12)

$$\begin{aligned} p_i= & {} g_{1i}, \, i = 1, 2, 3 \end{aligned}$$

(B.13)

$$\begin{aligned} r_1= & {} g_{32} \end{aligned}$$

(B.14)

$$\begin{aligned} r_2= & {} g_{33} \end{aligned}$$

(B.15)

$$\begin{aligned} q_i= & {} g_{2i} , \quad i=0, 1, 2, 3 \end{aligned}$$

(B.16)

$$\begin{aligned} F_i= & {} g_{4i} , \quad i=1, 2, 3, 4 \end{aligned}$$

(B.17)

$$\begin{aligned} g_{ij}= & {} {h_i^{(j)} }/{j!}, \quad j = 0, 1, 2, 3 \end{aligned}$$

(B.18)

Here, $g_{ij} ={h_i^{(j)} }/{j!}$ are all complicated functions; $g_{3i}$ is a complicated function of $k_{l}$, $\alpha _{1}$, $a_{1}$, $a_{2}$, $b_{1}$, $b_{2}$; $g_{1i}$ is the function of $c_{2}$, $\alpha _{1}$, $a_{1}$, $a_{2}$, $b_{1}$, $b_{2}$; $g_{2i}$ and $g_{4i}$ are the functions of M, n, $\alpha _{1}$, $a_{1}$, $a_{2}$, $b_{1}$, $b_{2}$, $i= 0, 1, 2, 3$.

Appendix C

The explicit form for dimensionless natural frequency $\omega _{2}$ of the vertical asymmetric structure can be expressed as

$$\begin{aligned} \omega _2= & {} \frac{1}{n^{2}}\left( \frac{\left( {b_1 +b_2 } \right) \cot \left( {\alpha _1 } \right) }{2b_1 }\right. \nonumber \\&\left. +\frac{b_1 \cos \left( {\alpha _1 } \right) }{2\sqrt{a_1^2 -b_1^2 \left( {\cos \left( {\alpha _1 } \right) } \right) ^{2}}}\right. \nonumber \\&\left. + \frac{b_2^2 \cos \left( {\alpha _1 } \right) }{2b_1 \sqrt{a_2^2 -b_2^2 \left( {\cos \left( {\alpha _1 } \right) } \right) ^{2}}} \right) ^{-2} \end{aligned}$$

(C.1)

Then, for vaX-I structure (i.e., $s_{2}=a_{2}/a_{1}=b_{2}/b_{1}=1$), $\omega _{2}$ can be written as

$$\begin{aligned} \omega _2 =\frac{1}{n^{2}}\left( {\cot \left( {\alpha _1 } \right) +\frac{s_1 \cos \left( {\alpha _1 } \right) }{\sqrt{1-s_1^2 \left( {\cos \left( {\alpha _1 } \right) } \right) ^{2}}}} \right) ^{-2} \end{aligned}$$

(C.2)

And for the reverse assembling pattern, the substitution of parameters can be $\alpha _1 \rightarrow \alpha _2$, $s_1 \rightarrow 1/s_1$. Hence, the expression of natural frequency for the reverse-assembled vaX-I structure can be written as

$$\begin{aligned} \omega _2 =\frac{1}{n^{2}}\left( {\cot \left( {\alpha _2 } \right) +\frac{ \cos \left( {\alpha _2 } \right) }{s_1 \sqrt{1-\left( {\cos \left( {\alpha _2 } \right) } \right) ^{2}/s_1^2 }}} \right) ^{-2} \end{aligned}$$

(C.3)

With the relationship of $a_1 \cos \left( {\alpha _2 } \right) =b_1 \cos \left( {\alpha _1 } \right)$, Eq. (C.3) can also be expressed as the form of Eq. (C.2). Hence, this fact means that the same natural frequency of the vaX-I structure holds for different assembling patterns.

The natural frequency of the vaX-II structure (i.e., $s_{1}=b_{1}/a_{1}=b_{2}/a_{2}=1$) can be written as

$$\begin{aligned} \omega _2 =\frac{1}{n^{2}}\left( {\cot \left( {\alpha _1 } \right) +s_2 \cot \left( {\alpha _1 } \right) } \right) ^{-2} \end{aligned}$$

(C.4)

And the natural frequency of vaX-II with reverse assembling pattern can be obtained by substituting $s_2 \rightarrow 1/s_2$ into Eq. C.4), which can be expressed as

$$\begin{aligned} \omega _2 =\frac{1}{n^{2}}\left( {\cot \left( {\alpha _1 } \right) +\frac{\cot \left( {\alpha _1 } \right) }{s_2 }} \right) ^{-2} \end{aligned}$$

(C.5)

Comparison of Eq. (C.4) with Eq. (C.5) illuminates the difference of the natural frequency of vaX-II structure between two assembling patterns.