Tikhonov regularization method for identifying the space-dependent source for time-fractional diffusion equation on a columnar symmetric domain

Abstract

In this paper, we deal with the inverse problem of identifying the unknown source of time-fractional diffusion equation on a columnar symmetric domain. This problem is ill-posed. Firstly, we establish the conditional stability for this inverse problem. Then the regularization solution is obtained by using the Tikhonov regularization method and the error estimates are derived under the a priori and a posteriori choice rules of the regularization parameter. Three numerical examples are presented to illustrate the validity and effectiveness of our method.

1 Introduction

Diffusion equations with fractional order derivatives have been playing more and more important roles. For instance, they appear in mechanics, chemistry, electrical engineering and medicine [1–11]. Time-fractional diffusion equations can be used to describe some anomalous diffusion phenomena in many fields of science [12–15]. These fractional order models are more adequate than the integer order models, because the fractional order derivatives enable the description the properties of different substances [16].

In the past years, many regularization methods have been proposed to deal with the inverse problem for time-fractional diffusion equation, such as the backward problems [17–22], the inverse source problems [23–27], the Cauchy problem [28–31], the initial value problem [32, 33]. In [34], the authors used the quasi-boundary value method to identify the initial value of heat equation on a columnar symmetric domain. In [35], the authors used a quasi-boundary regularization method to identify the initial value of time-fractional diffusion equation on spherically symmetric domain. In this work, we will use the Tikhonov regularization method to identify the space-dependent source for the time-fractional diffusion equation on a columnar symmetric domain. We not only give the a priori choice of the regularization parameter, but also give the a posteriori choice of the regularization parameter which only depends on the measurable date. To the best of our knowledge, there are few papers for the time-fractional diffusion equation on a columnar symmetric domain. In this work, we focus on an inverse problem for the following time-fractional diffusion equation on a columnar symmetric domain:

$$ \textstyle\begin{cases} D_{t}^{\alpha }u(r,t)-\frac{1}{r}u_{r}(r,t)-u_{rr}(r,t)=f(r), & 0< r< r _{0},0< t< T,0< \alpha < 1, \\ u(r,0)=0, &0\leq r\leq r_{0}, \\ u(r_{0},t)=0, & 0\leq t\leq T, \\ \lim_{r\rightarrow 0}u(r,t)\quad \mbox{is bounded}, &0\leq t\leq T, \\ u(r,T)=g(r), & 0\leq r\leq r_{0}, \end{cases} $$

(1.1)

where $r_{0}$ is the radius of the cylinder, $g(r)$ is given, $f(r)$ is unknown source. $D_{t}^{\alpha }$ is the Caputo fractional derivative of order $0<\alpha <1$ defined by

$$ D_{t}^{\alpha }u(r,t)= \textstyle\begin{cases} \frac{1}{\varGamma (1-\alpha )}\int _{0}^{t}\frac{u_{\tau }(r,\tau )}{(t- \tau )^{\alpha }}\,d\tau , & 0< \alpha < 1, \\ u_{t}(r,t), & \alpha =1. \end{cases} $$

(1.2)

We use the final time to identify the unknown source $f(r)$. In applications, the input function $g(r)$ can be measured, and we assume the function $g^{\delta }(r)$ as the measurable data, which satisfies

$$ \bigl\Vert g-g^{\delta } \bigr\Vert \leq \delta , $$

(1.3)

where δ is a noise level of input data.

The rest of this paper is organized as follows. In Sect. 2, we give some preliminaries. In Sect. 3, we analyze the ill-posedness of this problem and give the conditional stability. In Sect. 4, the error estimates are obtained under the a priori and a posteriori parameter choice rules. Three numerical examples are presented to demonstrate the effectiveness of our proposed method in Sect. 5.

2 Preliminaries

In this section, we will give some preliminaries which are very useful for our main conclusion.

Definition 2.1

([6])

The Mittag-Leffler function is

$$ E_{\alpha ,\beta }(z)=\sum_{k=0}^{\infty } \frac{z^{k}}{\varGamma (\alpha k+\beta )}, \quad z\in \mathbb{C}, $$

(2.1)

where $\alpha >0$ and $\beta \in \mathbb{R}$ are arbitrary constants.

Lemma 2.1

([36])

For the Mittag-Leffler function, we have

$$ E_{\alpha ,\beta }(z)=zE_{\alpha ,\alpha +\beta }(z)+ \frac{1}{\varGamma (\beta )}. $$

(2.2)

Lemma 2.2

([6])

For$\gamma >0$, we have

$$ \begin{aligned} &\int _{0}^{\infty }e^{-pt}t^{\gamma k+\beta -1}E_{\gamma ,\beta }^{(k)} \bigl( \pm at^{\gamma }\bigr)\,dt= \frac{k!p^{\gamma -\beta }}{(p^{\gamma }\mp a)^{k+1}}, \\ & \operatorname{Re}(p)> \vert a \vert ^{\frac{1}{\gamma }}, \end{aligned}$$

(2.3)

where$E_{\gamma ,\beta }^{(k)}(y):=\frac{d^{k}}{dy^{k}}E_{\gamma , \beta }(y)$.

Lemma 2.3

([37])

For$0<\alpha <1$, $\eta \geq 0$, we have$0\leq E_{\alpha ,1}(-\eta )\leq 1$. Moreover, $E_{\alpha ,1}(-\eta )$is completely monotonic, that is,

$$ (-1)^{n}\frac{d^{n}}{d\eta ^{n}}E_{\alpha ,1}(- \eta )\geq 0,\quad \eta \geq 0. $$

(2.4)

Lemma 2.4

([38])

For any$\mu _{n}$satisfying$\mu _{n}\geq \mu _{1}> 0$, there exists a positive constantC, depending onα, T, $\mu _{1}$, $r_{0}$such that

$$ \frac{C}{\mu _{n}^{2}T^{\alpha }}\leq E_{\alpha ,1+\alpha }\biggl(-\biggl( \frac{\mu _{n}}{r_{0}}\biggr)^{2}T^{\alpha }\biggr)\leq \frac{r_{0}^{2}}{\mu _{n}^{2}T^{ \alpha }}, $$

(2.5)

where$C(\alpha ,T,\mu _{1},r_{0})=r_{0}^{2}(1-E_{\alpha ,1}(-(\frac{ \mu _{1}}{r_{0}})^{2}T^{\alpha }))$.

Lemma 2.5

For any$p>0$, $\nu >0$, $s\geq \mu _{1}>0$, we have

$$ F(s)=\frac{\nu s^{4-p}}{C^{2}+\nu s^{4}}\leq \textstyle\begin{cases} C_{1}(p,C)\nu ^{\frac{p}{4}}, & 0< p< 4, \\ C_{2}(p, C, \mu _{1})\nu , & p\geq 4, \end{cases} $$

(2.6)

where$C_{1}=C_{1}(p,C)>0$and$C_{2}=C_{2}(p, C, \mu _{1})>0$.

Proof

If $0< p<4$, then $\lim_{s\rightarrow 0}F(s)=\lim_{s\rightarrow +\infty }F(s)=0$, we have

$$ \sup_{s\geq \mu _{1}} F(s)\leq F\bigl(s^{\ast }\bigr), $$

where $s^{\ast }\in (0,\infty )$ such that $F'(s^{\ast })=0$, then $s^{\ast }=(\frac{(4-p)C^{2}}{p\nu })^{\frac{1}{4}}$.

$$ F(s)\leq F\bigl(s^{\ast }\bigr)=\frac{\nu (\frac{(4-p)C^{2}}{p\nu })^{ \frac{4-p}{4}}}{C^{2}+\frac{\nu (4-p)C^{2}}{p\nu }} = \frac{(\frac{(4-p)C ^{2}}{p})^{\frac{4-p}{4}}}{C^{2}+\frac{(4-p)C^{2}}{p}}\nu ^{ \frac{p}{4}}:=C_{1}(p,C)\nu ^{\frac{p}{4}}. $$

If $p\geq 4$, we can obtain

$$ F(s)=\frac{\nu }{(C^{2}+\nu s^{4})s^{p-4}}\leq \frac{\nu }{C^{2}\mu _{1}^{p-4}}:=C_{2}(p, C, \mu _{1})\nu . $$

Lemma 2.5 is proved. □

Lemma 2.6

For any$p>0$, $\nu >0$, $s\geq \mu _{1}>0$, we have

$$ M(s)=\frac{\nu s^{2-p}}{C^{2}+\nu s^{4}}\leq \textstyle\begin{cases} C_{3}(p,C)\nu ^{\frac{p+2}{4}}, & 0< p< 2, \\ C_{4}(p, C, \mu _{1})\nu , & p\geq 2, \end{cases} $$

(2.7)

where$C_{3}=C_{3}(p,C)>0$and$C_{4}=C_{4}(p, C, \mu _{1})>0$.

Proof

If $0< p<2$, then $\lim_{s\rightarrow 0}M(s)=\lim_{s\rightarrow +\infty }M(s)=0$, we have

$$ \sup_{s\geq \mu _{1}} M(s)\leq M\bigl(s^{\ast }\bigr), $$

where $s^{\ast }\in (0,\infty )$ such that $M'(s^{\ast })=0$, then $s^{\ast }=(\frac{(2-p)C^{2}}{(p+2)\nu })^{\frac{1}{4}}$.

$$ M(s)\leq M\bigl(s^{\ast }\bigr)=\frac{\nu (\frac{(2-p)C^{2}}{(p+2)\nu })^{ \frac{2-p}{4}}}{C^{2}+\frac{\nu (2-p)C^{2}}{(p+2)\nu }} = \frac{(\frac{(2-p)C ^{2}}{p+2})^{\frac{2-p}{4}}}{C^{2}+\frac{(2-p)C^{2}}{p+2}} \nu ^{\frac{p+2}{4}}:=C_{3}(p,C)\nu ^{\frac{p+2}{4}}. $$

If $p\geq 2$, we can obtain

$$ M(s)=\frac{\nu }{(C^{2}+\nu s^{4})s^{p-2}}\leq \frac{\nu }{C^{2}\mu _{1}^{p-2}}:=C_{4}(p, C, \mu _{1})\nu . $$

Lemma 2.6 is proved. □

3 Ill-posedness and a conditional stability

We can obtain the solution of the problem (1.1) by the method of separation of variables, as follows [39]:

$$ u(r,t)=\sum_{n=1}^{\infty }t^{\alpha }E_{\alpha ,1+\alpha } \biggl(-\biggl(\frac{ \mu _{n}}{r_{0}}\biggr)^{2}t^{\alpha } \biggr)f_{n}\omega _{n}(r), $$

(3.1)

where $f_{n}=(f(r),\omega _{n}(r))$, $\omega _{n}(r)=\frac{\sqrt{2}}{r _{0}J_{1}(\mu _{n})}J_{0}(\frac{\mu _{n}}{r_{0}})$, $n=1,2,3,\ldots$ , and $\{\omega _{n}(r)\}_{n=1}^{\infty }$ is an orthonormal basis of $L^{2}[0,r_{0}]$, $J_{0}(\cdot )$ and $J_{1}(\cdot )$ are the zeroth order Bessel function and the first order Bessel function, respectively. $\mu _{n}$ is the infinite number real root of the equation

$$ J_{0}(r)=0, $$

(3.2)

and it satisfies

$$ 0< \mu _{1}< \mu _{2}< \mu _{3}< \cdots < \mu _{n}< \cdots ,\qquad \lim _{n\rightarrow \infty }\mu _{n}=\infty . $$

(3.3)

Through this paper, $L^{2}[0,r_{0};r]$ denotes the Hilbert space of Lebesgue measurable functions f with weight r on $[0,r_{0}]$. $(\cdot ,\cdot )$ and $\|\cdot \|$ denote the inner product and norm on $L^{2}[0,r_{0};r]$, respectively, with the norm

$$ \Vert f \Vert =\biggl( \int _{0}^{r_{0}} r \bigl\vert f(r) \bigr\vert ^{2}\,dr\biggr)^{\frac{1}{2}}. $$

(3.4)

We consider the condition $u(r,T)=g(r)$, then we have

$$ g(r)=\sum_{n=1}^{\infty }T^{\alpha }E_{\alpha ,1+\alpha } \biggl(-\biggl(\frac{\mu _{n}}{r_{0}}\biggr)^{2}T^{\alpha } \biggr)f_{n}\omega _{n}(r)=\sum _{n=1}^{\infty }g _{n}\omega _{n}(r), $$

(3.5)

where $g_{n}=(g(r),\omega _{n}(r))$. Defining the operator $K: f\rightarrow g$, we get

$$ g(r)=Kf(r)=\sum_{n=1}^{\infty }T^{\alpha }E_{\alpha ,1+\alpha } \biggl(-\biggl(\frac{ \mu _{n}}{r_{0}}\biggr)^{2}T^{\alpha } \biggr)f_{n}\omega _{n}(r). $$

(3.6)

The operator K is a linear self-adjoint compact operator, its singular value is $\{\sigma _{n}\}_{n=1}^{\infty }$ and

$$ \sigma _{n}=T^{\alpha }E_{\alpha ,1+\alpha } \biggl(-\biggl(\frac{\mu _{n}}{r_{0}}\biggr)^{2}T ^{\alpha } \biggr), $$

(3.7)

and we also have

$$ g_{n}=T^{\alpha }E_{\alpha ,1+\alpha }\biggl(- \biggl(\frac{\mu _{n}}{r_{0}}\biggr)^{2}T ^{\alpha } \biggr)f_{n}. $$

(3.8)

Then we can obtain

$$ f_{n}=\frac{g_{n}}{T^{\alpha }E_{\alpha ,1+\alpha }(-(\frac{\mu _{n}}{r _{0}})^{2}T^{\alpha })}. $$

(3.9)

So

$$ f(r)=\sum_{n=1}^{\infty } \frac{g_{n}}{T^{\alpha }E_{\alpha ,1+\alpha }(-(\frac{\mu _{n}}{r_{0}})^{2}T^{\alpha })}\omega _{n}(r)=\sum _{n=1} ^{\infty }\frac{g_{n}}{\sigma _{n}}\omega _{n}(r). $$

(3.10)

By using Lemma 2.4 and (3.7), we have

$$ \frac{C}{\mu _{n}^{2}}\leq \sigma _{n}\leq \frac{r_{0}^{2}}{\mu _{n}^{2}} $$

(3.11)

and

$$ \frac{1}{\sigma _{n}}=\frac{1}{T^{\alpha }E_{\alpha ,1+\alpha }(-(\frac{ \mu _{n}}{r_{0}})^{2}T^{\alpha })}\geq \frac{\mu _{n}^{2}}{r_{0}^{2}}, $$

we see that $\mu _{n}\rightarrow \infty$ when $n\rightarrow \infty$, so $\frac{1}{\sigma _{n}}\rightarrow \infty$. So the exact data function $g(r)$ must satisfy the property that $(g,\omega _{n}(r))$ decays rapidly. But we cannot ensure the function $g(r)$ decreases, because the function $g(r)$ concerns measurable data, a tiny disturbance of $g(r)$ will cause a great error. So problem (1.1) is ill-posed. Assume for the unknown source $f(r)$ there exists an a priori bound as follows:

$$ \bigl\Vert f(r) \bigr\Vert _{H^{p}}\leq E, \quad p>0, $$

(3.12)

where $E>0$ is a constant and $\|\cdot \|_{H^{p}}$ denotes the norm in Hilbert space which is defined as follows [40]:

$$ \bigl\Vert f(r) \bigr\Vert _{H^{p}}:=\Biggl(\sum _{n=1}^{\infty }u_{n}^{2p} \bigl\vert \bigl(f(r),\omega _{n}(r)\bigr) \bigr\vert ^{2}\Biggr)^{ \frac{1}{2}}. $$

(3.13)

The conditional stability of the inverse source problem can be obtained from Theorem 3.1.

Theorem 3.1

Let the a priori bound condition (3.12) hold, then we have

$$ \bigl\Vert f(r) \bigr\Vert \leq C^{-\frac{p}{p+2}} \Vert g \Vert ^{\frac{p}{p+2}}E^{\frac{2}{p+2}}. $$

(3.14)

Proof

Due to (3.10), (3.11), (3.12), and the Hölder inequality, we obtain

$$\begin{aligned} \bigl\Vert f(r) \bigr\Vert &= \Biggl\Vert \sum _{n=1}^{\infty }\frac{g_{n}}{\sigma _{n}}\omega _{n}(r) \Biggr\Vert \\ &= \Biggl\Vert \sum_{n=1}^{\infty } \frac{1}{\sigma _{n}}\bigl(g_{n}\omega _{n}(r) \bigr)^{ \frac{2}{p+2}}\bigl(g_{n}\omega _{n}(r) \bigr)^{\frac{p}{p+2}} \Biggr\Vert \\ &\leq \Biggl\Vert \sum_{n=1}^{\infty } \biggl(\frac{(g_{n}\omega _{n}(r))^{ \frac{2}{p+2}}}{\sigma _{n}} \biggr)^{\frac{p+2}{2}} \Biggr\Vert ^{\frac{2}{p+2}} \Biggl\Vert \sum_{n=1}^{\infty } \bigl(\bigl(g_{n}\omega _{n}(r)\bigr)^{\frac{p}{p+2}} \bigr)^{ \frac{p+2}{p}} \Biggr\Vert ^{\frac{p}{p+2}} \\ &= \Biggl\Vert \sum_{n=1}^{\infty } \frac{1}{\sigma _{n}^{\frac{p}{2}}}\frac{g _{n}}{\sigma _{n}}\omega _{n}(r) \Biggr\Vert ^{\frac{2}{p+2}} \Biggl\Vert \sum_{n=1}^{\infty }g_{n} \omega _{n}(r) \Biggr\Vert ^{\frac{p}{p+2}} \\ &\leq \Biggl\Vert \sum_{n=1}^{\infty } \biggl(\frac{\mu _{n}^{2}}{C}\biggr)^{\frac{p}{2}}\mu _{n}^{-p}f_{n} \mu _{n}^{p}\omega _{n}(r) \Biggr\Vert ^{\frac{2}{p+2}} \Vert g \Vert ^{ \frac{p}{p+2}} \\ &\leq C^{-\frac{p}{p+2}} \Vert g \Vert ^{\frac{p}{p+2}}E^{\frac{2}{p+2}}. \end{aligned}$$

This completes the proof of Theorem 3.1. □

4 Regularization method and convergence estimate

In this section, we will use the Tikhonov regularization method to obtain the regularization solution for problem (1.1). From Sect. 3, we know that $\{\omega _{n}(r)\}_{n=1}^{\infty }$ is an orthogonal basis of $L^{2}[0,r_{0};r]$, $\{\sigma _{n}\}_{n=1}^{\infty }$ is singular value of the linear self-adjoint compact operator K, and

$$ \sigma _{n}=T^{\alpha }E_{\alpha ,1+\alpha }\biggl(-\biggl( \frac{\mu _{n}}{r_{0}}\biggr)^{2}T ^{\alpha }\biggr). $$

We adopt the Tikhonov regularization method to solve the ill-posed problem, which minimizes the following functional:

$$ \Vert Kf-g \Vert ^{2}+\nu \Vert f \Vert ^{2}, $$

(4.1)

where $\nu >0$ is the regularization parameter. From Theorem 2.12 of [41], we see that the minimum $f_{\nu }(r)$ satisfies

$$ \bigl(K^{*}Kf_{\nu }\bigr) (r)+\nu f_{\nu }(r)=\bigl(K^{*}g\bigr) (r). $$

(4.2)

By a singular value decomposition of the compact self-adjoint operator, we have [42]

$$ f_{\nu }(r)=\sum_{n=1}^{\infty } \frac{\sigma _{n}}{\sigma _{n}^{2}+ \nu }g_{n}\omega _{n}(r). $$

Then we give the regularization solution with measurable data as follows:

$$ f_{\nu }^{\delta }(r)=\sum _{n=1}^{\infty }\frac{\sigma _{n}}{\sigma _{n}^{2}+\nu }g_{n}^{\delta } \omega _{n}(r). $$

(4.3)

4.1 An a priori parameter choice

In this subsection, we will give error estimates for under the suitable choice for the regularization parameter.

Theorem 4.1

Let$f(r)$given by (3.10) be the exact solution of problem (1.1). Let$g^{\delta }(r)$satisfy condition (1.3). Let the a priori condition (3.12) hold for$p>0$. Let$f_{\nu }^{\delta }(r)$given by (4.3) be the Tikhonov regularization solution. If the regularization parameterνsatisfies

$$ \nu = \textstyle\begin{cases} (\frac{\delta }{E})^{\frac{4}{p+2}},& 0< p< 4, \\ (\frac{\delta }{E})^{\frac{2}{3}},& p\geq 4, \end{cases} $$

then the following error estimates hold:

$$ \bigl\Vert f(r)-f_{\nu }^{\delta }(r) \bigr\Vert \leq \textstyle\begin{cases} (\frac{1}{2}+C_{1})E^{\frac{2}{p+2}}\delta ^{\frac{p}{p+2}},& 0< p< 4, \\ (\frac{1}{2}+C_{2})E^{\frac{1}{3}}\delta ^{\frac{2}{3}},& p\geq 4, \end{cases} $$

where$C_{1}$, $C_{2}$are positive constants depending onp, C, $\mu _{1}$.

Proof

By utilizing triangle inequality, we have

$$ \bigl\Vert f_{\nu }^{\delta }(r)-f(r) \bigr\Vert \leq \bigl\Vert f_{\nu }^{\delta }(r)-f_{\nu }(r) \bigr\Vert + \bigl\Vert f_{\nu }(r)-f(r) \bigr\Vert . $$

Using (4.3) and (1.3), we obtain

$$\begin{aligned} \bigl\Vert f_{\nu }^{\delta }(r)-f_{\nu }(r) \bigr\Vert &= \Biggl\Vert \sum_{n=1}^{\infty } \frac{ \sigma _{n}}{\sigma _{n}^{2}+\nu }g_{n}^{\delta }\omega _{n}(r) -\sum_{n=1}^{\infty }\frac{\sigma _{n}}{\sigma _{n}^{2}+\nu }g_{n} \omega _{n}(r) \Biggr\Vert \\ &= \Biggl\Vert \sum_{n=1}^{\infty } \frac{\sigma _{n}}{\sigma _{n}^{2}+\nu }\bigl(g_{n} ^{\delta }-g_{n} \bigr)\omega _{n}(r) \Biggr\Vert \\ &\leq \sup_{n\in \mathbb{N}}\biggl\{ \frac{\sigma _{n}}{\sigma _{n}^{2}+ \nu }\biggr\} \delta \leq \frac{\delta }{2\sqrt{\nu }}. \end{aligned}$$

(4.4)

Considering (3.10) and condition (3.12), we can obtain

$$\begin{aligned} \bigl\Vert f_{\nu }(r)-f(r) \bigr\Vert &= \Biggl\Vert \sum _{n=1}^{\infty }\frac{\sigma _{n}}{\sigma _{n}^{2}+\nu }g_{n} \omega _{n}(r)-\sum_{n=1}^{\infty } \frac{1}{\sigma _{n}}g_{n}\omega _{n}(r) \Biggr\Vert \\ &= \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu }{\sigma _{n}^{2}+\nu }\frac{g_{n}}{ \sigma _{n}}\omega _{n}(r) \Biggr\Vert \\ & = \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu }{\sigma _{n}^{2}+\nu }\mu _{n}^{-p}f _{n}\mu _{n}^{p}\omega _{n}(r) \Biggr\Vert \\ &\leq E\sup_{n\in \mathbb{N}}A(n), \end{aligned}$$

where

$$ A(n)=\frac{\nu \mu _{n}^{-p}}{\sigma _{n}^{2}+\nu }. $$

Using (3.11) and Lemma 2.5, we get

$$ A(n)\leq \frac{\nu \mu _{n}^{-p}}{(\frac{C}{\mu _{n}^{2}})^{2}+\nu }=\frac{ \nu \mu _{n}^{4-p}}{C^{2}+\nu \mu _{n}^{4}}\leq \textstyle\begin{cases} C_{1}(p,C)\nu ^{\frac{p}{4}}, & 0< p< 4, \\ C_{2}(p, C, \mu _{1})\nu , & p\geq 4. \end{cases} $$

So

$$ \bigl\Vert f_{\nu }^{\delta }(r)-f(r) \bigr\Vert \leq \frac{\delta }{2\sqrt{\nu }}+E \textstyle\begin{cases} C_{1}(p,C)\nu ^{\frac{p}{4}}, & 0< p< 4, \\ C_{2}(p, C, \mu _{1})\nu , & p\geq 4. \end{cases} $$

We choose the regularization parameter as follows:

$$ \nu = \textstyle\begin{cases} (\frac{\delta }{E})^{\frac{4}{p+2}}, & 0< p< 4, \\ (\frac{\delta }{E})^{\frac{2}{3}}, & p\geq 4, \end{cases} $$

then we have

$$ \bigl\Vert f(r)-f_{\nu }^{\delta }(r) \bigr\Vert \leq \textstyle\begin{cases} (\frac{1}{2}+C_{1})E^{\frac{2}{p+2}}\delta ^{\frac{p}{p+2}}, & 0< p< 4, \\ (\frac{1}{2}+C_{2})E^{\frac{1}{3}}\delta ^{\frac{2}{3}}, & p\geq 4. \end{cases} $$

Theorem 4.1 is proved. □

4.2 An a posteriori selection rule

In this subsection, we will utilize Morozov’s discrepancy principle to give an a posteriori regularization parameter choice. That is, we will choose the solution ν of the following equation as an a posterior regularization parameter:

$$ \bigl\Vert Kf_{\nu }^{\delta }-g^{\delta } \bigr\Vert =\tau \delta , $$

(4.5)

where $\tau >1$ is constant. We need Lemma 4.1 to obtain the existence and uniqueness of (4.5).

Lemma 4.1

Let$\delta >0$, the function$d(\nu ):= \|Kf_{\nu }^{\delta }-g^{\delta }\|$. If$\|g^{\delta }\|>\tau \delta$, we have some properties, as follows:

• (a) $d(\nu )$is a continuous function;

• (b) $\lim_{\nu \rightarrow 0}d(\nu )=0$;

• (c) $\lim_{\nu \rightarrow \infty }d(\nu )=\|g ^{\delta }\|$;

• (d) $d(\nu )$is a strictly increasing function, for any$\nu \in (0,\infty )$.

The proof of Lemma 4.1 is skipped.

Lemma 4.2

Letνbe the solution of (4.5), we have the following inequality:

$$ \frac{1}{\nu }\leq \textstyle\begin{cases} (\frac{r_{0}^{2}C_{3}}{\tau -1})^{\frac{4}{p+2}}(\frac{E}{\delta })^{ \frac{4}{p+2}}, & 0< p< 2, \\ \frac{r_{0}^{2}C_{4}}{\tau -1}\frac{E}{\delta }, & p\geq 2, \end{cases} $$

where$C_{3}$, $C_{4}$are positive constants depending onp, C, $\mu _{1}$.

Proof

Using (4.5), we have

$$\begin{aligned} \tau \delta &= \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu }{\sigma _{n}^{2}+\nu }g _{n}^{\delta }\omega _{n}(r) \Biggr\Vert \\ & \leq \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu }{\sigma _{n}^{2}+\nu }\bigl(g_{n} ^{\delta }-g_{n} \bigr)\omega _{n}(r) \Biggr\Vert + \Biggl\Vert \sum _{n=1}^{\infty }\frac{\nu }{ \sigma _{n}^{2}+\nu }g_{n} \omega _{n}(r) \Biggr\Vert \\ &\leq \delta + \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu \sigma _{n}}{\sigma _{n} ^{2}+\nu }\mu _{n}^{-p}f_{n}\mu _{n}^{p}\omega _{n}(r) \Biggr\Vert \\ &\leq \delta +E\sup_{n\in \mathbb{N}}B(n), \end{aligned}$$

where

$$ B(n):=\frac{\nu \sigma _{n}}{\sigma _{n}^{2}+\nu }\mu _{n}^{-p}. $$

Utilizing (3.11) and Lemma 2.6, we get

$$ B(n)\leq \frac{\nu \frac{r_{0}^{2}}{\mu _{n}^{2}}}{\frac{C^{2}}{\mu _{n}^{4}}+\nu }\mu _{n}^{-p}= \frac{\nu r_{0}^{2}\mu _{n}^{2-p}}{C^{2}+ \nu \mu _{n}^{4}}\leq \textstyle\begin{cases} r_{0}^{2}C_{3}(p,C)\nu ^{\frac{p+2}{4}}, & 0< p< 2, \\ r_{0}^{2}C_{4}(p, C, \mu _{1})\nu , & p\geq 2, \end{cases} $$

then

$$ (\tau -1)\delta \leq E \textstyle\begin{cases} r_{0}^{2}C_{3}(p,C)\nu ^{\frac{p+2}{4}}, & 0< p< 2, \\ r_{0}^{2}C_{4}(p, C, \mu _{1})\nu , & p\geq 2. \end{cases} $$

So we can obtain

$$ \frac{1}{\nu }\leq \textstyle\begin{cases} (\frac{r_{0}^{2}C_{3}}{\tau -1})^{\frac{4}{p+2}}(\frac{E}{\delta })^{ \frac{4}{p+2}}, & 0< p< 2, \\ \frac{r_{0}^{2}C_{4}}{\tau -1}\frac{E}{\delta }, & p\geq 2. \end{cases} $$

 □

Next, we will give the error estimate for under the a posteriori choice rule.

Theorem 4.2

Let$f(r)$given by (3.10) be the exact solution of problem (1.1). Let$f_{\nu }^{\delta }$given by (4.3) be the Tikhonov regularization solution. Let the solutionνof Eq. (4.5) be regarded as the regularization parameter, then the following error estimates hold:

$$ \bigl\Vert f_{\nu }^{\delta }(r)-f(r) \bigr\Vert \leq \textstyle\begin{cases} (\frac{1}{2}(\frac{r_{0}^{2}C_{3}}{\tau -1})^{\frac{2}{p+2}}+C ^{-\frac{p}{p+2}}(\tau +1)^{\frac{p}{p+2}} )E^{\frac{2}{p+2}} \delta ^{\frac{p}{p+2}} , & 0< p< 2, \\ (\frac{1}{2}(\frac{r_{0}^{2}C_{4}}{\tau -1})^{\frac{1}{2}}+C^{- \frac{1}{2}}(m+m\tau )^{\frac{1}{2}} )E^{\frac{1}{2}} \delta ^{\frac{1}{2}}, & p\geq 2. \end{cases} $$

Proof

Utilizing the triangle inequality, we have

$$ \bigl\Vert f_{\nu }^{\delta }(r)-f(r) \bigr\Vert \leq \bigl\Vert f_{\nu }^{\delta }(r)-f_{\nu }(r) \bigr\Vert + \bigl\Vert f_{\nu }(r)-f(r) \bigr\Vert . $$

(4.6)

Using Lemma 4.1 and (4.4), we get

$$ \bigl\Vert f_{\nu }^{\delta }(r)-f_{\nu }(r) \bigr\Vert \leq \frac{\delta }{2\sqrt{ \nu }}\leq \textstyle\begin{cases} \frac{1}{2}(\frac{r_{0}^{2}C_{3}}{\tau -1})^{\frac{2}{p+2}}E^{ \frac{2}{p+2}}\delta ^{\frac{p}{p+2}} , & 0< p< 2, \\ \frac{1}{2}(\frac{r_{0}^{2}C_{4}}{\tau -1})^{\frac{1}{2}}E^{ \frac{1}{2}}\delta ^{\frac{1}{2}}, & p\geq 2. \end{cases} $$

(4.7)

For the second part of the right side of (4.6), using (1.3) and (4.5), for $0< p<1$, we obtain

$$\begin{aligned} \bigl\Vert K\bigl(f_{\nu }(r)-f(r)\bigr) \bigr\Vert &= \Biggl\Vert \sum_{n=1}^{\infty }\sigma _{n}\biggl(\frac{ \sigma _{n}}{\sigma _{n}^{2}+\nu }-\frac{1}{\sigma _{n}} \biggr)g_{n}\omega _{n}(r) \Biggr\Vert \\ & = \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu }{\sigma _{n}^{2}+\nu }g_{n}\omega _{n}(r) \Biggr\Vert \\ &\leq \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu }{\sigma _{n}^{2}+\nu }\bigl(g_{n}-g _{n}^{\delta } \bigr)\omega _{n}(r) \Biggr\Vert + \Biggl\Vert \sum _{n=1}^{\infty }\frac{\nu }{ \sigma _{n}^{2}+\nu }g_{n}^{\delta } \omega _{n}(r) \Biggr\Vert \\ &\leq \delta +\tau \delta =(\tau +1)\delta . \end{aligned}$$

We have

$$\begin{aligned} \bigl\Vert f_{\nu }(r)-f(r) \bigr\Vert _{H^{p}} & = \Biggl(\sum_{n=1}^{\infty }\biggl( \frac{\nu }{ \sigma _{n}^{2}+\nu }\frac{g_{n}}{\sigma _{n}}\mu _{n}^{p} \biggr)^{2}\Biggr)^{ \frac{1}{2}} \\ &\leq \Biggl(\sum_{n=1}^{\infty }f_{n}^{2} \mu _{n}^{2p}\Biggr)^{\frac{1}{2}} \leq E. \end{aligned}$$

Using Theorem 3.1, we get

$$ \bigl\Vert f_{\nu }(r)-f(r) \bigr\Vert \leq C^{-\frac{p}{p+2}}(\tau +1)^{\frac{p}{p+2}}E ^{\frac{2}{p+2}}\delta ^{\frac{p}{p+2}}. $$

(4.8)

For $p\geq 2$, because $H^{p}$ compacts into $H^{2}$, then there exists a $m\in \mathbb{N}$ such that $\|f(r)\|_{H^{2}}\leq m\|f(r)\|_{H^{p}} \leq mE$, we have

$$\begin{aligned} \bigl\Vert f_{\nu }(r)-f(r) \bigr\Vert ={}& \Biggl\Vert \sum _{n=1}^{\infty }\frac{\nu }{\sigma _{n} ^{2}+\nu } \frac{g_{n}}{\sigma _{n}}\omega _{n}(r) \Biggr\Vert \\ ={}& \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu \sigma _{n}}{\sigma _{n}^{2}+\nu }\frac{f _{n}}{\sigma _{n}}\omega _{n}(r) \Biggr\Vert \\ ={}& \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu \sigma _{n}}{\sigma _{n}^{2}+\nu }\biggl(\frac{f _{n}}{\sigma _{n}}\omega _{n}(r) \biggr)^{\frac{1}{2}}\biggl( \frac{f_{n}}{\sigma _{n}}\omega _{n}(r) \biggr)^{\frac{1}{2}} \Biggr\Vert \\ \leq{}& \Biggl\Vert \sum_{n=1}^{\infty } \biggl(\frac{\nu \sigma _{n}}{\sigma _{n} ^{2}+\nu } \biggl(\frac{f_{n}}{\sigma _{n}}\omega _{n}(r) \biggr)^{ \frac{1}{2}} \biggr)^{2} \Biggr\Vert ^{\frac{1}{2}} \Biggl\Vert \sum_{n=1}^{\infty } \biggl( \biggl(\frac{f_{n}}{\sigma _{n}}\omega _{n}(r) \biggr)^{\frac{1}{2}} \biggr)^{2} \Biggr\Vert ^{\frac{1}{2}} \\ ={}& \Biggl\Vert \sum_{n=1}^{\infty } \biggl(\frac{\nu }{\sigma _{n}^{2}+\nu }\biggr)^{2}\sigma _{n}f_{n} \omega _{n}(r) \Biggr\Vert ^{\frac{1}{2}} \Biggl\Vert \sum _{n=1}^{\infty }\frac{f _{n}}{\sigma _{n}}\omega _{n}(r) \Biggr\Vert ^{\frac{1}{2}} \\ \leq{}& \Biggl( \Biggl\Vert \sum_{n=1}^{\infty } \frac{\nu }{\sigma _{n}^{2}+\nu }\bigl(g _{n}-g_{n}^{\delta } \bigr)\omega _{n}(r) \Biggr\Vert + \Biggl\Vert \sum _{n=1}^{\infty }\frac{ \nu }{\sigma _{n}^{2}+\nu }g_{n}^{\delta } \omega _{n}(r) \Biggr\Vert \Biggr)^{ \frac{1}{2}} \\ & {}\times \Biggl\Vert \sum_{n=1}^{\infty }C^{-1} \mu ^{2}f_{n}\omega _{n}(r) \Biggr\Vert ^{\frac{1}{2}} \\ \leq{}& C^{-\frac{1}{2}}(m+m\tau )^{\frac{1}{2}}\delta ^{\frac{1}{2}}E ^{\frac{1}{2}}. \end{aligned}$$

It is clear that

$$ \bigl\Vert f_{\nu }^{\delta }(r)-f(r) \bigr\Vert \leq \textstyle\begin{cases} (\frac{1}{2}(\frac{r_{0}^{2}C_{3}}{\tau -1})^{\frac{2}{p+2}}+C^{- \frac{p}{p+2}}(\tau +1)^{\frac{p}{p+2}})E^{\frac{2}{p+2}} \delta ^{\frac{p}{p+2}} , & 0< p< 2, \\ (\frac{1}{2}(\frac{r_{0}^{2}C_{4}}{\tau -1})^{\frac{1}{2}}+C^{- \frac{1}{2}}(m+m\tau )^{\frac{1}{2}})E^{\frac{1}{2}}\delta ^{ \frac{1}{2}}, & p\geq 2. \end{cases} $$

The proof of Theorem 4.2 is completed. □

5 Numerical experiments

In this section, we will use three different examples to illustrate the effectiveness and stability of the Tikhonov regularization method under two regularization parameter choice rules. Firstly, we obtain $g(r)$ by solving the direct problem, as follows:

$$ \textstyle\begin{cases} D_{t}^{\alpha }u(r,t)-\frac{1}{r}u_{r}(r,t)-u_{rr}(r,t)=f(r), & 0< r< r _{0},0< t< T,0< \alpha < 1, \\ u(r,0)=0, &0\leq r\leq r_{0}, \\ u(r_{0},t)=0, & 0\leq t\leq T, \\ \lim_{r\rightarrow 0}u(r,t) \quad \mbox{is bounded}, &0\leq t\leq T, \\ u(r,T)=g(r), & 0\leq r\leq r_{0}. \end{cases} $$

(5.1)

Let $r_{0}=\pi$, $T=1$, we discretize the above equation by the finite difference method. Let $\Delta r=\frac{\pi }{M}$, $\Delta t= \frac{1}{N}$ and $r_{i}=(i-1)\Delta r$ ($i=0,1,2,\ldots ,M$), $t_{n}=(n-1)\Delta t$ ($n=0,1,2,\ldots ,N$). In our numerical computations, we will take $M_{1}=M_{2}=50$. The approximate values of each grid point u are denoted $u_{i,j}\approx u(r_{i},t_{j})$. The discrete scheme of time-fractional derivative is given as follows [43, 44]:

$$ D_{t}^{\alpha }u(x_{i}, t_{n})\approx \frac{(\triangle t)^{-\alpha }}{ \varGamma (2-\alpha )}\sum _{j=0}^{n-1}b_{j}\bigl(u_{i}^{n-j}-u_{i}^{n-j-1} \bigr), $$

(5.2)

where $i=1,2,\ldots ,M-1$; $n=1,2,\ldots ,N$ and $b_{j}=(j+1)^{1-\alpha }-j^{1-\alpha }$.

Then we take $g^{\delta }$ as noise by adding a random perturbation, i.e.,

$$ g^{\delta }(r_{i})=g(r_{i})+\varepsilon g(r_{i})\cdot \bigl(2\operatorname{rand}(i)-1\bigr), $$

where ε reflects the relative error level.

Example 1

Take the source function $f(r)=r\sin(r)$.

Example 2

Consider the piecewise smooth function

$$ f(r)= \textstyle\begin{cases} 0, &0\leq r\leq \frac{\pi }{4}, \\ \frac{4}{\pi }(r-\frac{\pi }{4}) , & \frac{\pi }{4}< r\leq \frac{ \pi }{2}, \\ -\frac{4}{\pi }(r-\frac{3\pi }{4}), & \frac{\pi }{2}< r\leq \frac{3 \pi }{4}, \\ 0, &\frac{3\pi }{4}< r\leq \pi . \end{cases} $$

(5.3)

Example 3

Consider the discontinuous function

$$ f(r)= \textstyle\begin{cases} 0 , & 0\leq r\leq \frac{\pi }{3}, \\ 1, & \frac{\pi }{3}< r\leq \frac{2\pi }{3}, \\ 0, & \frac{2\pi }{3}< r\leq \pi . \end{cases} $$

(5.4)

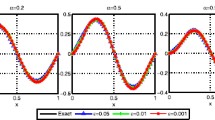
Figure 1 shows the comparisons between the exact solution and the regularization under the a priori and a posteriori regularization parameters choice when $\alpha =0.2$ for $\varepsilon =0.001$, and $\varepsilon =0.0001$ with Example 1. Figure 2 shows the comparisons between the exact solution and the regularization under the a priori and a posteriori regularization parameters choice when $\alpha =0.6$ for $\varepsilon =0.001$, and $\varepsilon =0.0001$ with Example 1. Figure 3 shows the comparisons between the exact solution and the regularization under the priori and posteriori regularization parameters choice when $\alpha =0.2$ for $\varepsilon =0.001$, and $\varepsilon =0.0001$ with Example 2. Figure 4 shows the comparisons between the exact solution and the regularization under the priori and posteriori regularization parameters choice when $\alpha =0.6$ for $\varepsilon =0.001$, and $\varepsilon =0.0001$ with Example 2. Figure 5 shows the comparisons between the exact solution and the regularization under the a priori and a posteriori regularization parameters choice when $\alpha =0.2$ for $\varepsilon =0.001$, and $\varepsilon =0.0001$ with Example 3. Figure 6 shows the comparisons between the exact solution and the regularization under the a priori and a posteriori regularization parameters choice when $\alpha =0.6$ for $\varepsilon =0.001$, and $\varepsilon =0.0001$ with Example 3. From Figs. 1–6, we can find the smaller ε, the better the computed approximation is. Moreover, we can also find the smaller α, the results are also better. Finally, we find that the results of Example 1 are better than that of Examples 2, 3, because in Examples 2, 3, the exact solutions are non-smooth and discontinuous functions, the recover data near the non-smooth and discontinuity points are not accurate. This is the well-known Gibbs phenomenon. But for the ill-posed problem, the results presented in Figs. 3–6 are reasonable.

Figure 1

The comparison of numerical effects between the exact solution and regularization solution for Example 1, $\alpha =0.6$: (a) $\varepsilon =0.001$, (b) $\varepsilon =0.0001$

Figure 2

The comparison of numerical effects between the exact solution and regularization solution for Example 1, $\alpha =0.2$: (a) $\varepsilon =0.001$, (b) $\varepsilon =0.0001$

Figure 3

The comparison of numerical effects between the exact solution and regularization solution for Example 2, $\alpha =0.6$: (a) $\varepsilon =0.001$, (b) $\varepsilon =0.0001$

Figure 4

The comparison of numerical effects between the exact solution and regularization solution for Example 2, $\alpha =0.2$: (a) $\varepsilon =0.001$, (b) $\varepsilon =0.0001$

Figure 5

The comparison of numerical effects between the exact solution and regularization solution for Example 3, $\alpha =0.6$: (a) $\varepsilon =0.001$, (b) $\varepsilon =0.0001$

Figure 6

The comparison of numerical effects between the exact solution and regularization solution for Example 3, $\alpha =0.2$: (a) $\varepsilon =0.001$, (b) $\varepsilon =0.0001$

6 Conclusion

In this paper, we use the Tikhonov regularization method to identify the source of the time-fractional diffusion equation on a columnar symmetric domain. Based on a conditional stability result, the error estimates are obtained under the a priori and a posteriori choice rules of regularization parameter. Meanwhile, the numerical examples verify the efficiency and accuracy of this method. Our original contributions are that we first identify the source of the time-fractional diffusion equation on a columnar symmetric domain. Moreover, we give the a posteriori regularization choice rule which only depends on the measurable data. In future, we will consider the inverse problem of identifying the initial value of the time-fractional diffusion equation on a columnar symmetric domain and give the optimal error estimate analyze. In addition, in this paper, we consider the time-fractional derivative is the Caputo fractional derivative of order $0<\alpha <1$, but in Ref. [45–52], one mentioned the Caputo–Fabrizio fractional integro-differential equation, which is very useful in practice. We will consider the inverse problem of Caputo–Fabrizio fractional integro-differential equations, and use the Tikhonov regularization method to solve this inverse problem.