1 Introduction

In recent years, diffusion equations with fractional-order derivatives play an important role in modeling contaminant diffusion processes. A fractional diffusion equation mainly describes anomalous diffusion phenomena because fractional-order derivatives enable the description of memory and hereditary properties of heterogeneous substances [1]. Replacing the standard time derivative with a time fractional derivative leads to the time fractional diffusion equation, and it can be used to describe superdiffusion and subddiffusion phenomena [1–10]. In some practical problems, the diffusion coefficients, a part of boundary data, initial data, or source term may be unknown. We need additional measurement to identify them, which leads to some fractional diffusion inverse problem. Nowadays there are many research results about fractional diffusion inverse problem. In [11], the authors considered an inverse problem of recovering boundary functions from transient data at an interior point in a 1-D semiinfinite half-order time-fractional diffusion equation. In [12], the authors applied a quasi-reversibility regularization method to solve a backward problem for the time-fractional diffusion equation. In [13–15], the authors studied an inverse problem in a spatial fractional diffusion equation by using the quasi-boundary value method and truncation method. In [16, 17], the authors determined the unknown source in one-dimensional and two-dimensional fractional diffusion equations. In [18], the authors used the dynamic spectral method to consider the inverse heat conduction problem of a fractional heat diffusion equation in 2-D setting. In [19], the authors used an optimal regularization method to consider the inverse heat conduction problem of a fractional heat diffusion equation. In [20, 21], the authors used the quasi-reversibility regularization method and Fourier regularization method to identify the unknown source for a fractional heat diffusion equation.

In this paper, we investigate an inverse problem for the time-fractional diffusion equation with variable coefficients in a general bounded domain[13, 22]:

$$ \textstyle\begin{cases} D_{t}^{\alpha}u-Lu(x,t)=f(x)q(t), & x\in\Omega, t\in(0,T), \alpha \in(0,1),\\ u(x,t)=0, & x\in\partial\Omega,\\ u(x,0)=0, & x\in\Omega, \\ u(x,T)=g(x), & x\in\Omega, \end{cases} $$
(1.1)

where Ω is a bounded domain in \(\mathbb{R}^{d}\) with a sufficient smooth boundary ∂Ω, \(D_{t}^{\alpha}(\cdot )\) is the Caputo fractional derivative of order α (\(0<\alpha\leq1\)), −L is defined on \(D(-L)=H^{2}(\Omega)\cap H_{0}^{1}(\Omega)\) and is a symmetric uniformly elliptic operator:

$$ Lu(x)=\sum_{i=1}^{d} \frac{\partial}{\partial x_{i}}\Biggl(\sum_{j=1}^{d}a_{ij}(x) \frac{\partial}{\partial x_{j}}u(x)\Biggr)+c(x)u(x), \quad x\in \Omega, $$
(1.2)

where the coefficient functions \(a_{ij}\) and \(c(x)\) satisfy

$$ a_{ij}=a_{ji},\quad\quad \nu\sum _{i=1}^{d}\xi_{i}^{2}\leq\sum _{i=1}^{d}\sum_{j=1}^{d}a_{ij}(x) \xi_{i}\xi_{j} \quad \mbox{and} \quad c(x)\leq0,\quad x\in\bar {\Omega}, \xi \in\mathbb{R}^{d}. $$
(1.3)

As in [13], define the Hilbert space

$$ D\bigl((-L)^{p}\bigr)=\Biggl\{ \phi\in L^{2}( \Omega); \sum_{n=1}^{\infty}\lambda _{n}^{2p}\bigl\vert (\phi,X_{n})\bigr\vert ^{2}< \infty\Biggr\} $$
(1.4)

with the norm

$$ \Vert \phi \Vert _{D((-L)^{p})}=\Biggl(\sum _{n=1}^{\infty }\lambda_{n}^{2p}\bigl\vert (\phi,X_{n})\bigr\vert ^{2}\Biggr)^{\frac{1}{2}}. $$
(1.5)

Assume that the time-fractional source term \(q\in C[0,T]\) satisfies \(q(t)\geq q_{0}>0\) for all \(t\in[0,T]\) and is known. The space-dependent source term \(f(x)\) is unknown. We use the data \(u(x,T)=g(x)\) to determine \(f(x)\). The noise data \(g^{\delta}\in L^{2}(\Omega)\) satisfies

$$ \bigl\Vert g^{\delta}-g\bigr\Vert _{L^{2}(\Omega)}\leq \delta, $$
(1.6)

where \(\Vert \cdot \Vert \) denotes the \(L^{2}(\Omega)\) norm, and \(\delta>0\) is a noise level.

In [13], the authors used the modified quasi-boundary value method to solve problem (1.1), but the error estimates between the regularization solution and the exact solution have the saturation phenomenon under the two parameter choice rules, that is, the best convergence rate for the a priori parameter choice method is \(O(\delta ^{\frac{2}{3}})\), and for the a posteriori parameter choice method, it is \(O(\delta^{\frac{1}{2}})\). In [22], the authors used the Tikhonov regularization method to solve problem (1.1), but the error estimates between the regularization solution and the exact solution also have the saturation phenomenon under the two parameter choice rules. In this study, we use the Landweber iterative regularization method to solve this problem. Our error estimates under two parameter choice rules have no saturation phenomenon, and the convergence rates are all \(O(\delta^{\frac{p}{p+2}})\).

This paper is organized as follows. Section 2 presents the Landweber iterative regularization method. Section 3 presents the convergence estimates under a priori and a posteriori choice rules. Section 4 presents some numerical examples to show the effectiveness of our method. Section 5 presents a simple conclusion.

2 Landweber iterative regularization method

In this section, we first give some useful lemmas.

Lemma 2.1

([23])

For \(\eta>0\) and \(0<\alpha \leq1\), we have \(0\leq E_{\alpha,1}(-\eta)<1\), and \(E_{\alpha ,1}(-\eta)\) is completely monotonic, that is,

$$ (-1)^{n}\frac{d^{n}}{d\eta^{n}}E_{\alpha,1}(-\eta)\geq0,\quad \forall n\in\mathbb{N}\cup\{0\}. $$
(2.1)

Lemma 2.2

([23])

For \(\beta\in\mathbb{R}\) and \(\alpha>0\), we have

$$ E_{\alpha,\beta}(z)=zE_{\alpha,\alpha+\beta}(z)+\frac{1}{\Gamma (\beta)}, \quad z\in \mathbb{C}. $$
(2.2)

Lemma 2.3

([24])

For \(0<\alpha<1\), \(\lambda >0\), and \(q\in C(0,T)\), we have

$$ \begin{aligned}[b] & D_{t}^{\alpha} \int_{0}^{t}q(\tau) (t-\tau)^{\alpha-1}E_{\alpha ,\alpha} \bigl(-\lambda(t-\tau)^{\alpha}\bigr)\,d\tau \\ &\quad =q(t)-\lambda \int_{0}^{t}q(\tau) (t-\tau)^{\alpha-1}E_{\alpha ,\alpha} \bigl(-\lambda(t-\tau)^{\alpha}\bigr)\,d\tau. \end{aligned} $$
(2.3)

Moreover, if \(\lambda=0\), then

$$ D_{t}^{\alpha} \int_{0}^{t}q(\tau) (t-\tau)^{\alpha-1}\,d\tau =\Gamma(\alpha)q(t), \quad 0< t\leq T. $$

Lemma 2.4

([13])

For any \(\lambda_{n}\) satisfying \(\lambda_{n}\geq\lambda_{1}>0\), there exists a positive constant \(C_{1}\) depending on α, T, \(\lambda_{1}\) such that

$$ \frac{C_{1}}{T^{\alpha}\lambda_{n}}\leq E_{\alpha,\alpha +1}\bigl(-\lambda_{n}T^{\alpha} \bigr)\leq\frac{1}{T^{\alpha}\lambda_{n}}. $$
(2.4)

Lemma 2.5

For any \(0< x<1\), we have

$$ x< \sqrt{x} $$
(2.5)

and

$$ (1-x)^{h}\geq1-hx,\quad h>0. $$
(2.6)

Due to Lemma 2.3, using the separation of variables, we obtain the solution of problem (1.1)

$$ u(x,t)=\sum_{n=1}^{\infty} \biggl(f_{n} \int_{0}^{t}q(\tau) (t-\tau )^{\alpha-1}E_{\alpha,\alpha} \bigl(-\lambda_{n}(t-\tau)^{\alpha}\bigr)\, d\tau \biggr)X_{n}(x), $$
(2.7)

where \(\lambda_{n}\) are the eigenvalues of the operator −L, and the corresponding eigenfunctions are \(X_{n}(x)\), \(f_{n}=(f(x),X_{n}(x))\). Using \(u(x,T)=g(x)\), we have

$$ g(x)=\sum_{n=1}^{\infty} \biggl(f_{n} \int_{0}^{T}q(\tau) (T-\tau)^{\alpha -1}E_{\alpha,\alpha} \bigl(-\lambda_{n}(T-\tau)^{\alpha}\bigr)\,d\tau \biggr)X_{n}(x), $$
(2.8)

where \(g_{n}=(g(x),X_{n}(x))\). Since −L is a symmetric uniformly elliptic operator, we get [25]

$$ 0< \lambda_{1}\leq\lambda_{2}\leq\cdots\leq \lambda_{n}\leq\cdots , \quad\quad \lim_{n \rightarrow\infty} \lambda_{n}=+\infty. $$
(2.9)

Let \(h_{n}(T):=\int_{0}^{T}q(\tau)(T-\tau)^{\alpha-1}E_{\alpha ,\alpha}(-\lambda_{n}(T-\tau)^{\alpha})\,d\tau\).

So we obtain

$$ g_{n}=f_{n}h_{n}(T). $$
(2.10)

Then

$$ f_{n}=\frac{g_{n}}{h_{n}(T)}, $$
(2.11)

that is,

$$ f(x)=\sum_{n=1}^{\infty}f_{n}X_{n}(x)= \sum_{n=1}^{\infty}\frac {g_{n}}{h_{n}(T)}X_{n}(x). $$
(2.12)

We only need to solve the following first kind integral equation to obtain \(f(x)\):

$$ (Kf) (x)= \int_{\Omega}k(x,\xi)f(\xi)\,d\xi=g(x), \quad x\in\Omega, $$
(2.13)

where the kernel is

$$ k(x,\xi)=\sum_{n=1}^{\infty}h_{n}(T)X_{n}(x)X_{n}( \xi). $$

For \(k(x,\xi)=k(\xi,x)\), K is a self-adjoint operator. If \(f\in L^{2}(\Omega)\), then \(g\in H^{2}(\Omega)\) from [25]. Because \(H^{2}(\Omega)\) is compactly embedded in \(L^{2}(\Omega)\), we have that \(K:L^{2}(\Omega)\rightarrow L^{2}(\Omega)\) is a compact operator. So problem (1.1) is ill-posed [26]. Assume that \(f(x)\) has the following a priori bound:

$$ \bigl\Vert f(x)\bigr\Vert _{D((-L)^{\frac{p}{2}})}\leq E, \quad p>0, $$
(2.14)

where \(E>0\) is a constant. We first give conditional stability results about ill-posed problem (1.1).

Theorem 2.6

([13])

Let \(q(t)\in C[0,T]\) satisfy \(q(t)\geq q_{0}>0\) for all \(t\in[0,T]\), and let \(f(x)\in D((-L)^{-\frac{p}{2}})\) satisfy the a priori bound condition

$$ \bigl\Vert f(\cdot)\bigr\Vert _{ D((-L)^{-\frac{p}{2}})}\leq E, \quad p>0. $$

Then we have

$$ \bigl\Vert f(\cdot)\bigr\Vert \leq C_{2}E^{\frac{2}{p+2}} \bigl\Vert g(x)\bigr\Vert ^{\frac{p}{p+2}}, $$
(2.15)

where \(C_{2}:=(C_{1}q_{0})^{-\frac{p}{p+2}}\).

Now we use the Landweber iterative method to obtain the regularization solution for (1.1) and rewrite the equation \(Kf=g\) in the form \(f=(I-aK^{*}K)f+aK^{*}g\) for some \(a>0\). Iterate this equation:

$$ f^{0,\delta}(x):=0, \quad\quad f^{m,\delta}(x)=\bigl(I-aK^{*}K \bigr)f^{m-1,\delta }(x)+aK^{*}g^{\delta}(x), \quad m=1,2,3,\dots, $$

where m is an iterative step number, and the selected regularization parameter a is called the relaxation factor and satisfies \(0< a<\frac {1}{\Vert K\Vert ^{2}}\). Since K is a self-adjoint operator, we obtain

$$ f^{m,\delta}(x)=a\sum_{k=1}^{m} \bigl(I-aK^{*}K\bigr)^{k-1}Kg^{\delta}(x). $$
(2.16)

We get

$$ f^{m,\delta}(x)=R_{m}g^{\delta}(x)=\sum _{n=1}^{\infty}\frac {1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}g_{n}^{\delta}X_{n}(x), $$
(2.17)

where \(g_{n}^{\delta}=(g^{\delta},X_{n}(x))\).

3 Error estimate under two parameter choice rules

In this section, we give two convergence estimates under an a priori regularization parameter choice rule and an a posteriori regularization parameter choice rule, respectively.

3.1 An a priori regularization parameter choice rule

Theorem 3.1

Let \(f(x)\) be the exact solution of problem (1.1), and let \(f^{m,\delta}(x)\) be the regularization Landweber iterative approximation solution. Choosing the regularization parameter \(m=[r]\), where

$$ r=\biggl(\frac{E}{\delta}\biggr)^{\frac{4}{p+2}}, $$
(3.1)

we have the following convergence rate estimate:

$$ \bigl\Vert f^{m,\delta}(\cdot)-f(\cdot)\bigr\Vert \leq C_{3}E^{\frac {2}{p+2}}\delta^{\frac{p}{p+2}}, $$
(3.2)

where \([r]\) denotes the largest integer less than or equal to r, and \(C_{3}=\sqrt{a}+(\frac{aC_{1}^{2}q_{0}}{p})^{-\frac{p}{4}}\) is a positive constant depending on a, p, and \(q_{0}\).

Proof

By the triangle inequality we have

$$ \bigl\Vert f^{m,\delta}(\cdot)-f(\cdot)\bigr\Vert \leq \bigl\Vert f^{m,\delta}(\cdot)-f^{m}(\cdot)\bigr\Vert +\bigl\Vert f^{m}(\cdot )-f(\cdot)\bigr\Vert . $$
(3.3)

We first give an estimate for the first term. From conditions (1.6) and (2.17) we have

$$\begin{aligned} \bigl\Vert f^{m,\delta}(\cdot)-f^{m}(\cdot)\bigr\Vert ^{2} &=\Biggl\Vert \sum_{n=1}^{\infty} \frac {1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}g_{n}^{\delta}X_{n}(x)-\sum _{n=1}^{\infty}\frac {1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}g_{n}X_{n}(x) \Biggr\Vert ^{2} \\ &=\Biggl\Vert \sum_{n=1}^{\infty} \frac {1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}\bigl(g_{n}^{\delta}-g_{n} \bigr)X_{n})\Biggr\Vert ^{2} \\ &\leq\sup_{n\geq1}H(n)^{2}\delta^{2}, \end{aligned}$$

where \(H(n):=\frac{1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}\).

By Lemma 2.5 we get

$$ \frac{1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}\leq\sqrt{am}, $$
(3.4)

that is,

$$ H(n)\leq\sqrt{am}. $$

So

$$ \bigl\Vert f^{m,\delta}(\cdot)-f^{m}(\cdot)\bigr\Vert \leq\sqrt {am}\delta. $$
(3.5)

Now we estimate the second term in (3.3). By (2.4), (2.14), and (2.17) we have

$$\begin{aligned} \bigl\Vert f^{m}(\cdot)-f(\cdot)\bigr\Vert ^{2} &= \Biggl\Vert \sum_{n=1}^{\infty} \frac {1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}g_{n}X_{n}(x)-\sum _{n=1}^{\infty }\frac{1}{h_{n}(T)}g_{n}X_{n}(x) \Biggr\Vert ^{2} \\ &=\Biggl\Vert \sum_{n=1}^{\infty} \frac {(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}g_{n}X_{n}(x)\Biggr\Vert ^{2} \\ &=\Biggl\Vert \sum_{n=1}^{\infty} \bigl(1-ah_{n}^{2}(T)\bigr)^{m} \lambda_{n}^{-\frac {p}{2}}\lambda_{n}^{\frac{p}{2}}f_{n}X_{n} \Biggr\Vert ^{2} \\ &\leq \sum_{n=1}^{\infty}\biggl(1-a \frac{C_{1}^{2}}{\lambda _{n}^{2}}\biggr)^{2m}\lambda_{n}^{-p} \lambda_{n}^{p}f_{n}^{2} \\ &\leq\sup_{n\geq1}Q(n)^{2}E^{2}, \end{aligned}$$

where \(Q(n):=(1-ah_{n}^{2}(T))^{m}\lambda_{n}^{-\frac{p}{2}}\).

Using Lemma 2.2 and Theorem 2.6, we have

$$\begin{aligned} Q(n)\leq\bigl(1-aq_{0}^{2}T^{2\alpha}E_{\alpha,\alpha +1}^{2} \bigl(-\lambda_{n}T^{\alpha}\bigr)\bigr)^{m} \lambda_{n}^{-\frac{p}{2}} &\leq \biggl(1-aq_{0}^{2} \frac{C_{1}^{2}}{\lambda_{n}^{2}}\biggr)^{m}\lambda_{n}^{-\frac{p}{2}}. \end{aligned}$$

Let \(\lambda_{n}:=t\) and

$$ F(t):=\biggl(1-aq_{0}^{2}\frac{C_{1}^{2}}{t^{2}} \biggr)^{m}t^{-\frac{p}{2}}. $$
(3.6)

Let \(t_{0}\) satisfy \(F'(t_{0})=0\). Then we easily get

$$ t_{0}=\biggl(\frac{aq_{0}^{2}C_{1}^{2}(4m+p)}{p}\biggr)^{\frac{1}{2}}>0. $$
(3.7)

Thus

$$ F(t_{0})=\biggl(1-\frac{p}{4m+p}\biggr)^{m}\biggl( \frac {aq_{0}^{2}C_{1}^{2}(4m+p)}{p}\biggr)^{-\frac{p}{4}}, $$

that is,

$$ F(t)\leq\biggl(\frac{aq_{0}^{2}C_{1}^{2}}{p}\biggr)^{-\frac{p}{4}}(m+1) ^{-\frac{p}{4}}. $$
(3.8)

Thus we obtain

$$ Q(n)\leq\biggl(\frac{aq_{0}^{2}C_{1}^{2}}{p}\biggr)^{-\frac{p}{4}}(m+1) ^{-\frac{p}{4}}. $$
(3.9)

Hence

$$ \bigl\Vert f^{m}(\cdot)-f(\cdot)\bigr\Vert \leq \biggl(\frac {aq_{0}^{2}C_{1}^{2}}{p}\biggr)^{-\frac{p}{4}}(m+1)^{-\frac{p}{4}}E. $$
(3.10)

Combining (3.5) and (3.10) and choosing the regularization parameter \(m=[r]\), we get

$$ \bigl\Vert f^{m,\delta}(\cdot)-f(\cdot)\bigr\Vert \leq C_{3}E^{\frac {2}{p+2}}\delta^{\frac{p}{p+2}}, $$
(3.11)

where \(C_{3}:=\sqrt{a}+(\frac{aq_{0}^{2}C_{1}^{2}}{p})^{-\frac{p}{4}}\).

We complete the proof of Theorem 3.1. □

3.2 An a posteriori regularization parameter choice rule

We consider the a posteriori regularization parameter choice in the Morozov discrepancy and construct regularization solution sequences \(f^{m,\delta}(x)\) by the Landweber iterative regularization method. Let \(\tau>1\) be a given fixed constant. Stop the algorithm at the first occurrence of \(m=m(\delta)\in\mathbb{N}_{0}\) with

$$ \bigl\Vert Kf^{m,\delta}(\cdot)-g^{\delta}(\cdot)\bigr\Vert \leq \tau\delta, $$
(3.12)

where \(\Vert g^{\delta} \Vert \geq\tau\delta\) is constant.

Lemma 3.2

Let \(\gamma(m)=\Vert Kf^{m,\delta}(\cdot)-g^{\delta}(\cdot)\Vert \). Then we have:

  1. (a)

    \(\gamma(m)\) is a strictly decreasing function for any \(m\in (0,+\infty)\);

  2. (b)

    \(\lim_{m\rightarrow+\infty}\gamma(m)=\Vert g^{\delta }\Vert \);

  3. (c)

    \(\lim_{m\rightarrow0}\gamma(m)=0\);

  4. (d)

    \(\gamma(m)\) is a continuous function.

Lemma 3.3

For fixed \(\tau>1\), combining Landweber’s iteration method with stopping rule (3.12), we obtain that the regularization parameter \(m=m(\delta,g^{\delta})\in\mathbb {N}_{0}\) satisfies

$$ m\leq\biggl(\frac{p+2}{aq_{0}^{2}C_{1}^{2}}\biggr) \biggl(\frac{q_{0}}{\tau-1} \biggr)^{\frac {4}{p+2}}\biggl(\frac{E}{\delta}\biggr)^{\frac{4}{p+2}}. $$
(3.13)

Proof

From (2.17) we get the representation

$$ R_{m}g=\sum_{n=1}^{\infty} \frac {1-(1-ah_{n}^{2}(T))^{m}}{h_{n}(T)}g_{n}X_{n}(x) $$
(3.14)

and

$$ \Vert KR_{m}g-g\Vert ^{2}=\sum _{n=1}^{\infty }\bigl(1-ah_{n}^{2}(T) \bigr)^{2m}\bigl\vert (g,X_{n})\bigr\vert ^{2}. $$

Since \(\vert 1-ah_{n}^{2}(T)\vert <1\), we conclude that \(\Vert KR_{m-1}-I\Vert \leq1\).

On the other hand, it is easy to see that m is the minimum value and satisfies

$$ \bigl\Vert KR_{m}g^{\delta}-g^{\delta}\bigr\Vert = \bigl\Vert Kf^{m,\delta}-g^{\delta}\bigr\Vert \leq\tau\delta. $$

Hence

$$\begin{aligned} \Vert KR_{m-1}g-g\Vert &\geq\bigl\Vert KR_{m-1}g^{\delta}-g^{\delta} \bigr\Vert -\bigl\Vert (KR_{m-1}-I) \bigl(g-g^{\delta}\bigr) \bigr\Vert \\ &\geq\tau\delta-\Vert KR_{m-1}-I\Vert \delta \\ &\geq(\tau-1)\delta. \end{aligned}$$

On the other hand, using (2.14), we obtain

$$\begin{aligned} \Vert KR_{m-1}g-g\Vert &=\Biggl\Vert \sum _{n=1}^{\infty}\bigl(1-\bigl(1-ah_{n}^{2}(T) \bigr)^{m-1}\bigr)g_{n}X_{n}-\sum _{n=1}^{\infty}g_{n}X_{n}\Biggr\Vert \\ &=\Biggl\Vert \sum_{n=1}^{\infty}- \bigl(1-ah_{n}^{2}(T)\bigr)^{m-1}(g,X_{n}) \Biggr\Vert \\ &=\Biggl\Vert \sum_{n=1}^{\infty} \bigl(1-ah_{n}^{2}(T)\bigr)^{m-1}h_{n}(T)f_{n} \lambda _{n}^{\frac{p}{2}}\lambda_{n}^{-\frac{p}{2}}X_{n} \Biggr\Vert \\ &\leq \sup_{n\geq1}\bigl(1-ah_{n}^{2}(T) \bigr)^{m-1}h_{n}(T)\lambda_{n}^{-\frac{p}{2}}E. \end{aligned}$$

Let

$$ S(n):=\bigl(1-ah_{n}^{2}(T)\bigr)^{m-1}h_{n}(T) \lambda_{n}^{-\frac{p}{2}}, $$

so that

$$ (\tau-1)\delta\leq S(n)E. $$
(3.15)

Using Lemma 2.4, we have

$$\begin{aligned} S(n) &\leq\bigl(1-aq_{0}^{2}T^{2\alpha}E_{\alpha,\alpha +1} \bigl(-\lambda_{n}T^{\alpha}\bigr)\bigr)^{m-1}q_{0}T^{\alpha}E_{\alpha,\alpha +1} \bigl(-\lambda_{n}T^{\alpha}\bigr)\lambda_{n}^{-\frac{p}{2}} \\ &\leq q_{0}\biggl(1-aq_{0}^{2}\frac{C_{1}^{2}}{\lambda_{n}^{2}} \biggr)\lambda _{n}^{-\frac{p}{2}-1}. \end{aligned}$$

Let \(t:=\lambda_{n}\) and

$$ G(t):=\biggl(1-aq_{0}^{2}\frac{C_{1}^{2}}{t^{2}} \biggr)^{m-1}t^{-\frac{p}{2}-1}. $$
(3.16)

Suppose that \(t_{\ast}\) satisfies \(G'(t_{\ast})=0\). Then we easily get

$$ t_{\ast}=\biggl(\frac{aq_{0}^{2}C_{1}^{2}(4m+p-2)}{(p+2)} \biggr)^{\frac{1}{2}}, $$
(3.17)

so that

$$ \begin{aligned} G(t_{\ast})&\leq\biggl(1-\frac{p+2}{4m+p-2} \biggr)^{m-1}\biggl(\frac {aq_{0}^{2}C_{1}^{2}(4m+p-2)}{(p+2)}\biggr)^{-\frac{p+2}{4}} \\ & \leq\biggl(\frac{aq_{0}^{2}C_{1}^{2}}{p+2}\biggr)^{-\frac{p+2}{4}}. \end{aligned} $$

Then

$$ S(n)\leq q_{0}\biggl(\frac{p+2}{aq_{0}^{2}C_{1}^{2}} \biggr)^{\frac{p+2}{4}}m^{-\frac {p+2}{4}}. $$
(3.18)

Combining (3.15) with (3.17), we obtain

$$ m\leq\biggl(\frac{p+2}{aq_{0}^{2}C_{1}^{2}}\biggr) \biggl(\frac{q_{0}}{\tau-1} \biggr)^{\frac {4}{p+2}}\biggl(\frac{E}{\delta}\biggr)^{\frac{4}{p+2}}. $$

The proof of lemma is completed. □

Theorem 3.4

Let \(f(x)\) be the exact solution of problem (1.1), and let \(f^{m,\delta}(x)\) be the Landweber iterative regularization approximation solution. Choosing the regularization parameter by Landweber’s iterative method with stopping rule (3.12), we have the following error estimate:

$$ \bigl\Vert f^{m,\delta}(\cdot)-f(\cdot)\bigr\Vert \leq \bigl(C_{2}(\tau +1)^{\frac{2}{p+2}}+C_{4} \bigr)E^{\frac{2}{p+2}}\delta^{\frac{p}{p+2}}, $$
(3.19)

where \(C_{4}=(\frac{p+2}{q_{0}^{2}C_{1}^{2}})^{\frac{1}{2}}(\frac {q_{0}}{(\tau-1)})^{\frac{2}{p+2}}\) is a constant.

Proof

Using the triangle inequality, we obtain

$$ \bigl\Vert f^{m,\delta}(\cdot)-f^{m}(\cdot)\bigr\Vert \leq\bigl\Vert f^{m,\delta}(\cdot)-f^{m}(\cdot)\bigr\Vert +\bigl\Vert f^{m}(\cdot)-f(\cdot)\bigr\Vert . $$
(3.20)

Applying (3.2) and Lemma 3.3, we get

$$ \bigl\Vert f^{m,\delta}(\cdot)-f^{m}(\cdot)\bigr\Vert \leq\sqrt {am}\delta\leq C_{4}E^{\frac{2}{p+2}} \delta^{\frac{p}{p+2}}, $$
(3.21)

where \(C_{4}=(\frac{p+2}{q_{0}^{2}C_{1}^{2}})^{\frac{1}{2}}(\frac {q_{0}}{\tau-1})^{\frac{2}{p+2}}\).

For the second part of the right side of (3.20), we get

$$\begin{aligned} K\bigl(f^{m}(\cdot)-f(\cdot)\bigr) &=\sum _{n=1}^{\infty }-\bigl(1-ah_{n}^{2}(T) \bigr)^{m}g_{n}X_{n}(x) \\ &=\sum_{n=1}^{\infty }-\bigl(1-ah_{n}^{2}(T) \bigr)^{m}\bigl(g_{n}-g_{n}^{\delta} \bigr)X_{n}(x) \\ &\quad{} +\sum_{n=1}^{\infty}-\bigl(1-ah_{n}^{2}(T) \bigr)^{m}g_{n}^{\delta}X_{n}(x). \end{aligned}$$

Combining (1.6) and (3.12), we have

$$ \bigl\Vert K\bigl(f^{m}(\cdot)-f(\cdot)\bigr)\bigr\Vert \leq(\tau+1)\delta. $$
(3.22)

Using Theorem 2.6 and (2.14), we have

$$\begin{aligned} \bigl\Vert f^{m}(\cdot)-f(\cdot)\bigr\Vert _{D((-L)^{\frac{p}{2}})} &= \Biggl(\sum_{n=1}^{\infty }-\bigl(1-ah_{n}^{2}(T) \bigr)^{2m}f_{n}^{2}\lambda_{n}^{p} \Biggr)^{\frac{1}{2}} \\ &\leq E. \end{aligned}$$

So

$$ \bigl\Vert f^{m}(\cdot)-f(\cdot)\bigr\Vert \leq C_{2}(\tau+1)^{\frac {p}{p+2}}E^{\frac{2}{p+2}}\delta^{\frac{p}{p+2}}. $$
(3.23)

Hence

$$ \bigl\Vert f^{m,\delta}(\cdot)-f(\cdot)\bigr\Vert \leq \bigl(C_{2}(\tau +1)^{\frac{p}{p+2}}+C_{4} \bigr)E^{\frac{2}{p+2}}\delta^{\frac{p}{p+2}}. $$
(3.24)

The theorem is proved. □

4 Numerical implementation and numerical examples

In this section, we provide numerical examples to illustrate the usefulness of the proposed method. Since analytic solution of problem (1.1) is difficult, we first solve the forward problem to obtain the final data \(g(x)\) using the finite difference method. For details of the finite difference method, we refer to [27–30]. Assume that \(\Omega=(0,1)\) and take \(\Delta t=\frac{T}{N}\) and \(\Delta x=\frac {1}{M}\). The grid points on the time interval \([0,T]\) are labeled \(t_{n}=n\Delta t\), \(n=0,1,\ldots,N\), and the grid points in the space interval \([0,1]\) are \(x_{i}=i\Delta x\), \(i=0,1,2,\ldots,M\). Noise data are generated by adding random perturbation, that is,

$$ g^{\delta}(x)=g(x)+g(x)\varepsilon\cdot\bigl(2\operatorname{rand}\bigl(\operatorname{size}(g)\bigr)-1 \bigr), $$

where ε reflects the noise level. The total error level g can be given as follows:

$$ \delta=\bigl\Vert g^{\delta}-g\bigr\Vert =\sqrt{ \frac{1}{M+1}\sum_{i=1}^{M+1} \bigl(g_{i}-g_{i}^{\delta}\bigr)^{2}}. $$

In our numerical experiments, we take \(T=1\). When computing the Mittag-Leffler function, we need a better algorithm in [29]. In applications, the a priori bound E is difficult to obtain, and thus we only give the numerical results under the a posteriori parameter choice rule. In the following three examples, the regularization parameter is given by (3.12) with \(\tau=1.1\). To avoid the ‘inverse crime,’ we use a finer grid to computer the forward problem, that is, we take \(M=100\), \(N=200\) and choose \(M=50\), \(N=100\) for solving the regularized inverse problem. In the computational procedure, we let \(a(x)=x^{2}+1\), \(c(x)=-(x+1)\), and the time-dependent source term \(q(t)=e^{-t}\).

Example 1

Take function \(f(x)=[x(1-x)]^{\alpha }\sin5\pi x\).

Example 2

Consider the following piecewise smooth function:

$$ f(x)= \textstyle\begin{cases} 0, & 0\leq x\leq\frac{1}{4},\\ 4(x-\frac{1}{4}), &\frac{1}{4}< x\leq\frac{1}{2},\\ -4(x-\frac{3}{4}), &\frac{1}{2}< x\leq\frac{3}{4},\\ 0, &\frac{3}{4}< x\leq1. \end{cases} $$
(4.1)

Example 3

Consider the following initial function:

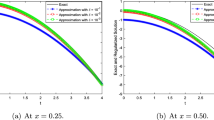
$$ f(x)= \textstyle\begin{cases} 0, & 0\leq x\leq\frac{1}{3},\\ 1, &\frac{1}{3}< x\leq\frac{2}{3},\\ 0, &\frac{2}{3}< x\leq1. \end{cases} $$
(4.2)

Figure 1 indicates the exact and regularized source terms given by the a posteriori parameter choice rule for Example 1. Figure 2 indicates the exact and regularized source terms given by the a posteriori parameter choice rule for Example 2. Figure 3 indicates the exact and regularized source terms given by the a posteriori parameter choice rule for Example 3. According to these three examples, we can find that the smaller ε and α, the better effect between the exact solution and regularized solution. From Figures 2 and 3 we can see that the numerical solution is not better than that of Example 1. Figures 2 and 3 presented worse numerical results because due to the common finite element or high-order finite element, it is difficult to describe a piecewise function. However, the numerical result is reasonable. Moreover, numerical examples show that the Landweber iterative method is efficient and accurate.

Figure 1
figure 1

The exact and regularized terms given by the a posteriori parameter choice rule for Example  1 : (a)  \(\pmb{\alpha=0.2}\) , (b)  \(\pmb{\alpha=0.5}\) , (c)  \(\pmb{\alpha=0.9}\) .

Full size image
Figure 2
figure 2

The exact and regularized terms given by the a posteriori parameter choice rule for Example  2 : (a)  \(\pmb{\alpha=0.2}\) , (b)  \(\pmb{\alpha=0.5}\) , (c)  \(\pmb{\alpha=0.9}\) .

Full size image
Figure 3
figure 3

The exact and regularized terms given by the a posteriori parameter choice rule for Example  3 : (a)  \(\pmb{\alpha=0.2}\) , (b)  \(\pmb{\alpha=0.5}\) , (c)  \(\pmb{\alpha=0.9}\) .

Full size image
Table 1 The posteriori regularization parameter m under different α and ε for Example  1
Full size table
Table 2 The posteriori regularization parameter m under different α and ε for Example  2
Full size table
Table 3 The posteriori regularization parameter m under different α and ε for Example  3
Full size table

5 Conclusion

In this paper, we solve an inverse problem for identifying the unknown source of a separable-variable form in a time-fractional diffusion equation with variable coefficients in a general domain. We propose the Landweber iterative method to obtain a regularization solution. The error estimates are obtained under the a priori regularization parameter choice rule and the a posteriori regularization parameter choice rule. Comparing the error estimated obtained by [13, 22], our error estimates have no saturation phenomenon, and the convergence rates are all \(O(\delta^{\frac{p}{p+2}})\) under two parameter choice rules. Meanwhile, numerical examples verify that the Landweber iterative regularization method is efficient and accurate. In the future work, we will continue to study some source terms that depend on both time and space variables.