Abstract
We propose and study a Lotka–Volterra predator–prey system incorporating both Michaelis–Menten-type prey harvesting and fear effect. By qualitative analysis of the eigenvalues of the Jacobian matrix we study the stability of equilibrium states. By applying the differential inequality theory we obtain sufficient conditions that ensure the global attractivity of the trivial equilibrium. By applying Dulac criterion we obtain sufficient conditions that ensure the global asymptotic stability of the positive equilibrium. Our study indicates that the catchability coefficient plays a crucial role on the dynamic behavior of the system; for example, the catchability coefficient is the Hopf bifurcation parameter. Furthermore, for our model in which harvesting is of Michaelis–Menten type, the catchability coefficient is within a certain range; increasing the capture rate does not change the final number of prey population, but reduces the predator population. Meanwhile, the fear effect of the prey species has no influence on the dynamic behavior of the system, but it can affect the time when the number of prey species reaches stability. Numeric simulations support our findings.
Similar content being viewed by others
1 Introduction
The aim of this paper is investigating the dynamic behavior of the following Lotka–Volterra predato–prey system incorporating both Michaelis–Menten-type harvesting and fear effect of the prey:
where u and v are the density of the prey and predator species at time t, respectively. \(r_{0}\) and d are the birth and death rates of the prey species, respectively, a is the density-dependent coefficient, m is the death rate of the predator species, p denotes the strength of interspecific between prey and predator, c is the conversion efficiency of ingested prey into new predators, k is the level of fear, which is due to antipredator behavior of the prey, E is the fishing effort used to harvest, q is the catchability coefficient, and \(m_{1}\) and \(m_{2}\) are suitable constants.
The predator–prey relationship has been highly valued by scholars because of its widespread existence [1–39]. Such topics as the influence of the stage structure [6–8, 11–15], the influence of refuge [17, 18, 20, 21], the influence of mutual interferences [10], the fear effect of the prey species [1–5], the influence of cannibalism [16], and the influence of the Allee effect [19] are extensively studied by scholars.
Wang, Zanette, and Zou [1] argued that in the predator–prey relationship, the predators cannot only directly kill the prey, but also affect the behavior of the prey, and the latter is more lethal than the former. To describe this phenomenon, we propose the following Lotka–Volterra predator–prey system incorporating the fear effect of the prey:
The system admits three nonnegative equilibria, \(E_{0}(0,0)\), \(E_{1}( \frac{r_{0}-d}{a},0)\), and \(E_{2}(\overline {u},\overline{v})\), where \(\overline{u}= \frac{m}{cp}\), and v̅ satisfies
Concerned with the dynamic behavior of system (1.3), the authors obtained the following result.
Theorem A
If\(r_{0}< d\), then\(E_{0}\)is globally asymptotically stable. The boundary equilibrium\(E_{1}\)is globally asymptotically stable if\(r_{0}\in(d, d+ \frac{am}{cp})\), and the unique positive equilibrium\(E_{2}\)is globally asymptotically stable if\(r_{0}> d+ \frac{am}{cp}\).
Previously, the authors did not consider the influence of human harvesting. The study of resource management including fisheries, forestry, and wildlife management has great importance. It is important to control the harvesting so that both ecological sustainability and conservation of the species can be implemented in a long run. There are also many scholars [22–36] who investigated the influence of harvesting.
In the past decade, two kinds of harvesting were considered by scholars. The first one is the linear harvesting [23, 30–34], and the second one is the Michaelis–Menten-type harvesting ([10, 22, 24–26, 36]).
Generally speaking, the dynamic behavior of a system with linear harvesting is comparatively simple. For example, Lin [33] investigated the dynamic behavior of the following two-species commensal symbiosis model with nonmonotonic functional response and nonselective harvesting in a partial closure:
The author showed that if the system admits a unique positive equilibrium, then it is globally asymptotically stable. Xiao and Lei [31] investigated the dynamic behavior of the following single-species stage structure system incorporating partial closure for the populations and nonselective harvesting:
The authors showed that the system may have a globally asymptotically stable boundary equilibrium or the globally asymptotically stable positive equilibrium. Their results indicated that the system cannot have the bifurcation phenomenon.
On the other hand, the dynamic behavior of the system with Michaelis–Menten-type harvesting becomes complicated. Chen [26] studied the following Lotka–Volterra commensal symbiosis model of two populations with Michaelis–Menten-type harvesting for the first species:
For the limited harvesting case, the author showed that the system admits a unique globally stable positive equilibrium. For the overharvesting case, if the cooperate intensity of both species and the capacity of the second species are large enough, then the two species can coexist in a stable state; otherwise, the first species will be driven to extinction. Gupta, Chandra, and Banerjee [10] incorporated the Michaelis–Menten-type harvesting to the predator–prey model, which has led to the following model:
They showed that the system has at most two interior equilibria and can have saddle-node, transcritical, Hopf–Andronov, and Bogdanov–Takens bifurcations. Furthermore, system (1.7) has an origin, which is always a saddle point, and undergoes a transcritical bifurcation around the semitrivial equilibrium. Finally, they gave the maximum threshold for continuous harvesting without the extinction risk of predator population and concluded that harvesting has no any impact on the prey species. Besides, Hu and Cao [36] studied the influence of Michaelis–Menten-type harvesting to a predator–prey system and found that the dynamic behavior of the system is very complicate.
To the best of our knowledge, to this day, still no scholars investigated the dynamic behavior of the predator–prey system incorporating both fear effect and Michaelis–Menten-type harvesting, which motivated us to propose system (1.1).
The aim of this paper is to give a detail analysis of the dynamic behavior of system (1.1) and to find out the influence of Michaelis–Menten-type harvesting.
The rest of the paper is arranged as follows. In next section, we investigate the existence and local stability of the equilibria of system (1.1). In Sect. 3, we discuss the global stability of the trivial equilibrium by using the differential inequality theory and discuss the global asymptotic stability of the positive equilibrium by applying the Dulac criterion. In Sect. 4, we analyze and verify the condition of Hopf-bifurcation around the positive equilibrium. Numeric simulations are presented in Sect. 5 to show the feasibility of the main results. We end this paper with a brief discussion, including the impact of the Michaelis–Menten-type harvesting and fear effect on system (1.1).
2 The existence and local stability of the equilibria of system (1.1)
2.1 The existence of equilibria of system (1.1)
The equilibria of system (1.1) satisfy the equation system
From the second equation of (2.1) we have \(v=0\) or \(u = \frac{m }{cp}\).
(1) Substituting \(v=0\) into the first equation of (2.1) leads to
which is equivalent to
so equation (2.3) has the solution \(u_{1}=0 \). Hence, system (1.1) admits the boundary equilibrium \(E_{0}(0,0)\).
Other positive solutions of (2.3) can be expressed as
where
(i) If \(B_{2}>0\) and \(B_{3}<0\), then (2.3) has a unique positive solution
(ii) If \(B_{2}=0\) and \(B_{3}<0\), then (2.3) has a unique positive solution
(iii) For \(B_{2}<0\),
(a) when \(B_{3}>0\), if \(B_{2}^{2}-4B_{1}B_{3}>0\), then (2.3) has two positive solutions
if \(B_{2}^{2}-4B_{1}B_{3}=0\), then (2.3) has a unique positive solution
and if \(B_{2}^{2}-4B_{1}B_{3}<0\), then (2.3) has no positive solution;
(b) for \(B_{3}=0\), (2.3) has a unique positive solution
(c) for \(B_{3}<0\), (2.3) has a unique positive solution
Consequently, system (1.1) has the boundary equilibria \(E_{i}(\overline {u_{i}},0)\).
(2) Next, substituting \(u= \frac{m }{cp}\) into the first equation of (2.5) leads to
Set
Then from (2.2) we have
Hence, by the zero point theorem of continuous function, \(F(v)=0\) has at least one positive solution on the interval \((0,+\infty)\). Also,
implies that F is a strictly decreasing function of v, and hence F has at most one positive solution on the interval \((0,+\infty)\). This analysis shows that under the assumption \(r_{0}>d+ \frac{am }{cp}+ \frac{qE}{m_{1}E+ \frac {mm_{2}}{cp}}\), (2.13) admits a unique positive solution \(v^{*}\), and, consequently, system (1.1) admits a unique positive equilibrium \(E^{*}(u^{*},v^{*})\).
2.2 The local stability of the equilibria of system (1.1)
Consider the Jacobian matrix of system (1.1)
where
We have the following results.
Theorem 2.1
The trivial equilibrium\(E_{0}(0,0)\)is a stable node if
or
\(E_{0}(0,0)\)is a saddle if
\(E_{0}(0,0)\)is a saddle-node if
Proof
The Jacobian matrix of system (1.1) about the equilibrium \(E_{0}(0,0)\) is
The eigenvalues of \(J(E_{0})\) are \(\lambda_{1}=r_{0}-d- \frac {q}{m_{1}}\) and \(\lambda_{2}= -m<0\). Thus, if (2.19) holds, then \(\lambda _{1}<0\), and, consequently, \(E_{0}(0,0)\) is a stable node; if (2.21) holds, then \(\lambda_{1}>0\), and, consequently \(E_{0}(0,0)\) is a saddle; if \(q=m_{1}(r_{0}-d)\), then \(\lambda _{1}=0\). So, when \(\lambda_{1}=0\) and \(\lambda_{2}= -m<0\), that is, \(q=m_{1}(r_{0}-d)\), we introduce the time transformation \(dt= \frac{d\tau}{-m}\) and expand system (1.1) in power series up to the third order around \(E_{0}(0,0)\) to consider the stability of \(E_{0}(0,0)\). Then system (1.1) can be changed into
where \(P_{1}(u,v)\) is a power series in \((u,v)\) with terms \(u^{i}v^{j}\) satisfying \(i+j\geq4\).
From equation (2.24) and Theorem 7.1 in Chap. 2 of [40] we know that if (2.22) holds, then \(E_{0}(0,0)\) is a saddle-node; if (2.20) holds, then because of \(\frac{(r_{0}-d){m_{2}}^{2}}{m{m_{1}}^{2}E^{2}}\neq0\), we have that \(E_{0}(0,0)\) is a stable node. □
Theorem 2.2
The semitrivial equilibriaum \(E_{i}(\overline{u_{i}},0)\) is a stable node if
\(E_{i}(\overline{u_{i}},0)\) is a saddle if
Proof
It follows from (2.6) that the Jacobian matrix of system (1.1) about the equilibrium \(E_{i}(\overline{u_{i}},0)\) is
where
Consequently, if (2.25) holds, then \(E_{i}\) is a stable node; if (2.26) holds, then \(E_{i}\) is a saddle. □
Theorem 2.3
The interior equilibrium \(E^{*}(u^{*},v^{*})\) is a stable node if
and
Proof
Noting that \(v^{*}\) satisfies equation (2.13), we get that the Jacobian matrix of system (1.1) about the equilibrium \(E^{*}(u^{*},v^{*})\) is
where
Then we have
and from (2.29) we also have
so that both eigenvalues of \(J (E^{*}(u^{*},v^{*}))\) have negative real parts, and \(E^{*}(u^{*},v^{*})\) is a stable node.
This ends the proof of Theorem 2.3. □
Remark 2.1
As was pointed out by Wang, Zanette, and Zou [1], for system (1.2), the positive equilibrium is locally asymptotically stable as long as it exists (see Theorem 3.1 in [1]). Compared with the system without harvesting, we found that the conditions that ensure the local stability of the positive equilibrium and boundary equilibrium of system (1.1) become complicated.
Remark 2.2
If \(r_{0}>d\), then the boundary equilibrium \(E_{0}(0,0)\) in system (1.3) is unstable, whereas depending on the range of \(r_{0}\), the boundary equilibrium \(E_{1}\) or the positive equilibrium \(E_{2}\) maybe locally asymptotically stable. That is, under the assumption \(r_{0}>d\), at least one of the species in system (1.3) survives. However, if the catchability coefficient q is large enough so that inequality (2.19) or (2.20) holds, then \(E_{0}(0,0)\) in system (1.1) becomes locally asymptotically stable, which means the extinction of both predator and prey species. Hence harvesting plays an important role on changing the dynamic behavior of the system, and overharvesting may lead to the extinction of the species.
3 Global stability
The aim of this section is investigating the global stability property of the equilibria of system (1.1).
As a direct corollary of Lemma 2.2 of Chen [38], we have the following:
Lemma 3.1
If\(a>0\), \(b>0\), and\(\dot{x}\geq x(b-ax)\), then for\(t\geq{0}\)and\(x(0)>0\), we have
If\(a>0\), \(b>0\), and\(\dot{x}\leq x(b-ax)\), then for\(t\geq{0}\)and\(x(0)>0\), we have
Concerned with the global stability property of the equilibria of system (1.1), we have the following result.
Theorem 3.1
-
(1)
Assume that (2.19) or (2.20) holds. Then
$$ \lim_{t\rightarrow+\infty}u(t)=0, \qquad\lim_{t\rightarrow+\infty}v(t)=0, $$(3.1)that is, the trivial equilibrium\(E_{0}(0,0)\)is globally attractive.
-
(2)
The positive equilibrium \(E^{*}(u^{*},v^{*}) \) is globally asymptotically stable if
$$ r_{0}>d+ \frac{am }{cp}+ \frac {qE}{m_{1}E+ \frac{mm_{2}}{cp}} $$(3.2)and
$$ q< \frac{a{m_{1}}^{2}E}{m_{2}}. $$(3.3)
Proof
(1) From the first equation of system (1.1) we have
and hence, because of (2.19) or (2.20),
that is,
For \(\varepsilon>0\) satisfying \(\varepsilon< \frac {m}{2cp}\), from (3.5) it follows that there exists \(T_{1}>0\) such that
Hence from the second equation of system (1.1) and (3.6), for \(t\geq T_{1}\), we have
so that
that is,
The limits (3.5) and (3.9) show that \(E_{0}(0,0)\) is globally attractive if inequality (2.19) or (2.20) holds.
(2) Note that the inequality
implies that
Hence (2.25) and (3.10) imply that \(E^{*}(u^{*},v^{*})\) is locally asymptotically stable. To show that \(E^{*}(u^{*}, v^{*})\) is globally asymptotically stable, it suffices to show that the system admits no limit cycle in the first quadrant. Let u consider the Dulac function \(B(u,v)= \frac{1}{uv}\). Then from (3.3) it follows that
where
By the Dulac theorem [37] there is no closed orbit in the first quadrant. Consequently, \(E^{*}(u^{*}, v^{*})\) is globally asymptotically stable.
The proof of Theorem 3.1 is finished. □
Remark 3.1
Theorem A shows that for system (1.2), the positive equilibrium is globally asymptotically stable as long as it exists. However, for the system with harvesting, the situation becomes complicated. To ensure the positive equilibrium to be globally asymptotically stable, we need some additional requirement on the coefficients; see (3.3) for more detail. If the species in a system without harvesting can coexist in a stable state, then Theorem 3.1(2) shows that for small enough catching ability q, the system can still coexist in a stable state.
4 Hopf bifurcation
In the previous section, we have presented the conditions required for local asymptotic stability of \(E^{*}\), and under these conditions, the other equilibrium is a saddle. In addition, we can conclude that the equilibrium \(E^{*}\) may lose its stability through Hopf bifurcation under certain parameter circumstances. Considering q as the bifurcation parameter, the Hopf bifurcation threshold is a positive root of \(\operatorname{Tr}(J(E^{*}))=0\), denoted \(q=q_{H}= \frac {a}{m_{2}E} (m_{1}E+ \frac{mm_{2}}{cp} )^{2}\), which satisfies \(\operatorname{Det}(J(E^{*})) |_{q=q_{H}}>0\). When q passes through the critical magnitude \(q=q_{H}\), the stability property of \(E^{*}\) changes. So we can obtain the following theorem.
Theorem 4.1
Assume that the system parameters satisfy the conditions for existence of a positive equilibrium\(E^{*}\)given in condition (2.28). Then the positive equilibrium\(E^{*}\)changes its stability through the Hopf bifurcation threshold\(q=q_{H}\).
Proof
The characteristic equation of matrix \(J(E^{*})\) is
and the Hopf bifurcation occurs if and only if \(q=q_{H}\) satisfies
-
(i)
\([\operatorname{Tr}(J(E^{*}))] |_{q=q_{H}}=0\);
-
(ii)
\([\operatorname{Det}(J(E^{*}))] |_{q=q_{H}}>0\), which means the characteristic equation
$${\lambda}^{2}+\operatorname{Det}\bigl(J\bigl(E^{*}\bigr) \bigr)\big|_{q=q_{H}}=0, $$whose roots are purely imaginary;
-
(iii)
\(\frac{d}{dq} [\operatorname{Tr} (J(E^{*}) ) ] |_{q=q_{H}}= \frac{mm_{2}E}{cp (m_{1}E+ \frac{mm_{2}}{cp} )^{2}}\neq0\).
To discuss the stability (or direction) of a limit cycle, we compute the first Lyapunov number \(l_{1}\) at the interior equilibrium \(E^{*}\) of system (1.1).
Firstly, we transfer the equilibrium \(E^{*}\) of system (1.1) to the origin by using the transformation \(u=U+u^{*}\) and \(v=V+v^{*}\). Hence system (1.1) in a neighborhood of the origin can be rewritten as
where \(\alpha_{10}\), \(\alpha_{01}\), \(\beta_{10}\), and \(\beta_{01}\) are the elements of Jacobian matrix calculated at the equilibrium \(E^{*}\). Because the system undergoes the Hopf bifurcation, we have \(\alpha_{10}=0\), \(\beta_{01}=0\), and \(\Delta=\alpha_{10} \beta _{01}- \alpha_{01} \beta_{10}=-\alpha_{01} \beta_{10}>0\). The coefficients \(\alpha_{ij}\) and \(\beta_{ij}\) are determined by
and \(P_{2}(U,V)\) is a power series in \((U,V)\) with terms \(U^{i}V^{j}\) satisfying \(i+j\geq4\).
The first Lyapunov number \(l_{1}\) identifying the stability of a limit cycle for a planar system is given by the formula
where
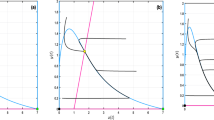
If \(l_{1}>0\), then the equilibrium \(E^{*}\) is destabilized through a subcritical Hopf bifurcation. However, if \(l_{1}<0\), then the Hopf bifurcation is supercritical (see Figs. 1, 2, 3).
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(k=1\), \(d=1\), \(a=0.51234\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=2\), \(c=0.5\), \(q=2<2.30553=q_{H}\), \(E^{*}\) is stable
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(k=1\), \(d=1\), \(a=0.51234\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=2\), \(c=0.5\), \(q=2.30553=q_{H}\), stable periodic orbits bifurcate through Hopf bifurcation around \(E^{*}\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(k=1\), \(d=1\), \(a=0.51234\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=2\), \(c=0.5\), \(q=3.1>2.30553=q_{H}\), \(E^{*}\) is unstable
□
5 Numeric simulations
Example 5.1
Now let us consider the following model:
In the corresponding to system (1.1), we take \(r_{0}=4\), \(d=1\), \(k=a=m=1\), \(c=0.5\), \(p=2\), \(m_{1}=1\), \(m_{2}=0.1\).
(1) Take \(q=4\) and \(E=1\). Then
Hence it follows from Theorem 2.1 and 3.1(i) that the system admits a trivial equilibrium, which is a stable node. Furthermore, \(E_{0}\) is globally asymptotically stable. Figure 4 supports this statement.
Dynamic behavior of system (5.1) with \(r_{0}=4\), \(d=1\), \(k=a=m=1\), \(c=0.5\), \(p=2\), \(m_{1}=1\), \(m_{2}=0.1\), \(q=4\), and \(E=1\)
(2) Take \(q=3\) and \(E=0.3\). Then
and
and from Theorem 2.1 and 3.1(i) it follows that \(E_{0}(0,0)\) is globally attractive. Figure 5 supports this statement.
Dynamic behavior of system (5.1) with \(r_{0}=4\), \(d=1\), \(k=a=m=1\), \(c=0.5\), \(p=2\), \(m_{1}=1\), \(m_{2}=0.1\), \(q=3\), and \(E=0.3\)
(3) Take \(q=2.5\) and \(E=1\). Then
and from Theorem 2.1 it follows that \(E_{0}(0,0)\) is a saddle. Figure 6 supports this statement.
Dynamic behavior of system (5.1) with \(r_{0}=4\), \(d=1\), \(k=a=m=1\), \(c=0.5\), \(p=2\), \(m_{1}=1\), \(m_{2}=0.1\), \(q=2.5\), and \(E=1\)
(4) Take \(q=3\) and \(E=1\). Then
and
and from Theorem 2.1 it follows that \(E_{0}(0,0)\) is a saddle-node. Figure 7 supports this statement.
Dynamic behavior of system (5.1) with \(r_{0}=4\), \(d=1\), \(k=a=m=1\), \(c=0.5\), \(p=2\), \(m_{1}=1\), \(m_{2}=0.1\), \(q=3\), and \(E=1\)
Example 5.2
Now let us consider the following model:
Here in the corresponding system (1.1), we take \(r_{0}=4\), \(d=1\), \(k=a=m=1\), \(c=0.5\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\).
Then for \(q=1.1\), we have
and
and from Theorem 2.1 it follows that the system also admits a unique positive equilibrium \(E^{*}(u^{*}, v^{*})\), which is globally asymptotically stable. Figure 8 supports this statement.
Dynamic behavior of system (5.2) with \(r_{0}=4\), \(d=1\), \(k=a=m=1\), \(c=0.5\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), and \(q=1.1\)
6 Conclusion and discussions
In this paper, we have discussed the dynamics of a prey–predator system where the prey is provided with fear effect and harvesting at Michaelis–Menten-type rate. Firstly, we compare our system (1.1) with system (1.7) without the fear effect in the prey, which was extensively studied in [10]. For system (1.7) without the fear effect, we obtained that the trivial equilibrium was always a saddle, the axial equilibrium was unique, and the number of the interior equilibria depended on the expression \(\eta+\alpha\epsilon-\epsilon\), where \(\alpha= \frac{d}{amr_{1}}\), \(\eta= \frac {qE}{mm_{2}rr_{1}}\), and \(\epsilon= \frac{am_{1}E}{rm_{2}}\). However, if we incorporate the fear effect in the prey species, that is, system (1.1), then we can see that the trivial equilibrium may be a stable node, a saddle, or a saddle-node, even globally attractive. The number of the axial equilibria depends on the expression (2.4). Under condition (2.28), system (1.1) admits a unique positive equilibrium, and in other cases, it has no positive equilibrium. Then we compare our system (1.1) with system (1.2) without Michaelis–Menten-type prey harvesting term. Wang et al. [1] showed the existence of a unique positive equilibrium, which was globally asymptotically. stable However, for system (1.1) with rate of harvesting in the prey, the unique positive equilibrium, when it exists, is globally asymptotically stable, and q satisfies certain conditions.
Moreover, system (1.7) with Michaelis–Menten-type predator harvesting term can exhibit many types of bifurcation; for example, system (1.7) undergoes a Bogdanov–Takens bifurcation around the interior equilibrium and a transcritical bifurcation around the axial equilibrium, respectively. In [10], it is shown that the rate of harvesting was independent of Hopf bifurcation. However, for system (1.2) with fear effect in the prey, it has no any bifurcation. System (1.1) where prey is provided with harvesting at Michaelis–Menten-type rate and fear effect can exhibit only Hopf bifurcation around the interior equilibrium. We find that the rate of harvesting does not only affect the existence of Hopf bifurcation, but also changes the stability (direction) of Hopf bifurcation. So, these facts differ from the results of [1] and [10].
Finally, in the case of fixed fear effect value, via mathematical analysis, we conclude that harvesting has no any negative effect on prey species. However, the study also shows that the rate of harvesting may affect the survival of the predator population. When the rate of harvesting is too heavy, the number of prey population at the positive equilibrium also decreases (see Figs. 9, 10, 11, 12, 13). For system (1.1) with Michaelis–Menten-type prey harvesting and system (1.7) with Michaelis–Menten-type predator harvesting, the above results are the same. On the other hand, in the case of the fixed value of the rate of harvesting, we can find that fear effect does not change the dynamical behavior of the system. The conclusion is the same as in [1]. Furthermore, as the value of fear effect increases, the more time it takes for the number of prey population to stabilize to a constant, the greater the maximum value of prey population, and the smaller the number of predator population (see Figs. 14, 15, 16, 17).
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(k=1\), and \(q=0\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(k=1\), and \(q=1.1\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(k=1\), and \(q=11\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(k=1\), and \(q=18\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(k=1\), and \(q=23\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(q=1.1\), and \(k=0\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(q=1.1\), and \(k=1\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(q=1.1\), and \(k=5\)
Dynamic behavior of system (1.1) with \(r_{0}=4\), \(d=1\), \(a=1\), \(p=2\), \(E=1\), \(m_{1}=1\), \(m_{2}=0.1\), \(c=0.5\), \(q=1.1\), and \(k=30\)
References
Wang, X., Zanette, L., Zou, X.: Modelling the fear effect in predator–prey interactions. J. Math. Biol. 73(5), 1179–1204 (2016)
Wang, X., Zou, X.: Modeling the fear effect in predator–prey interactions with adaptive avoidance of predators. Bull. Math. Biol. 79(6), 1325–1359 (2017)
Xiao, Z.W., Li, Z.: Stability analysis of a mutual interference predator–prey model with the fear effect. J. Appl. Sci. Eng. 22(2), 205–211 (2019)
Kundu, K., Pal, S., Samanta, S.: Impact of fear effect in a discrete-time predator–prey system. Bull. Calcutta Math. Soc. 110(3), 245–264 (2019)
Sasmal, S.K.: Population dynamics with multiple Allee effects induced by fear factors—A mathematical study on prey–predator interactions. Appl. Math. Model. 64, 1–14 (2018)
Chen, F.D., Chen, W.L., et al.: Permanence of a stage-structured predator–prey system. Appl. Math. Comput. 219(17), 8856–8862 (2013)
Chen, F.D., Xie, X.D., et al.: Partial survival and extinction of a delayed predator–prey model with stage structure. Appl. Math. Comput. 219(8), 4157–4162 (2012)
Chen, F.D., Wang, H.N., Lin, Y.H., Chen, W.L.: Global stability of a stage-structured predator–prey system. Appl. Math. Comput. 223, 45–53 (2013)
Yu, S.: Global stability of a modified Leslie–Gower model with Beddington–DeAngelis functional response. Adv. Differ. Equ. 2014, Article ID 84 (2014)
Yu, S., Chen, F.D.: Almost periodic solution of a modified Leslie–Gower predator–prey model with Holling-type II schemes and mutual interference. Int. J. Biomath. 7(3), Article ID 1450028 (2014)
Li, Z., Han, M.A., et al.: Global stability of stage-structured predator–prey model with modified Leslie–Gower and Holling-type II schemes. Int. J. Biomath. 6(1), Article ID 1250057 (2012)
Li, Z., Han, M., et al.: Global stability of a predator–prey system with stage structure and mutual interference. Discrete Contin. Dyn. Syst., Ser. B 19(1), 173–187 (2014)
Lin, X., Xie, X., et al.: Convergences of a stage-structured predator–prey model with modified Leslie–Gower and Holling-type II schemes. Adv. Differ. Equ. 2016, Article ID 181 (2016)
Xiao, Z., Li, Z., Zhu, Z., et al.: Hopf bifurcation and stability in a Beddington–DeAngelis predator–prey model with stage structure for predator and time delay incorporating prey refuge. Open Math. 17(1), 141–159 (2019)
Yue, Q.: Permanence of a delayed biological system with stage structure and density-dependent juvenile birth rate. Eng. Lett. 27(2), 1–5 (2019)
Deng, H., Chen, F., Zhu, Z., et al.: Dynamic behaviors of Lotka–Volterra predator–prey model incorporating predator cannibalism. Adv. Differ. Equ. 2019, Article ID 359 (2019)
Chen, L., Wang, Y., et al.: Influence of predator mutual interference and prey refuge on Lotka–Volterra predator–prey dynamics. Commun. Nonlinear Sci. Numer. Simul. 18(11), 3174–3180 (2013)
Chen, F.D., Lin, Q.X., Xie, X.D., et al.: Dynamic behaviors of a nonautonomous modified Leslie–Gower predator–prey model with Holling-type III schemes and a prey refuge. J. Math. Comput. Sci. 2017, 266–277 (2017)
Chen, F., Guan, X., Huang, X., et al.: Dynamic behaviors of a Lotka–Volterra type predator–prey system with Allee effect on the predator species and density dependent birth rate on the prey species. Open Math. 17(1), 1186–1202 (2019)
Ma, Z., Chen, F., Wu, C., et al.: Dynamic behaviors of a Lotka–Volterra predator–prey model incorporating a prey refuge and predator mutual interference. Appl. Math. Comput. 219(15), 7945–7953 (2013)
Chen, F., Ma, Z., Zhang, H.: Global asymptotical stability of the positive equilibrium of the Lotka–Volterra prey–predator model incorporating a constant number of prey refuges. Nonlinear Anal., Real World Appl. 13(6), 2790–2793 (2012)
Lin, Q., Xie, X., et al.: Dynamical analysis of a logistic model with impulsive Holling type-II harvesting. Adv. Differ. Equ. 2018, Article ID 112 (2018)
Xie, X.D., Chen, F.D., et al.: Note on the stability property of a cooperative system incorporating harvesting. Discrete Dyn. Nat. Soc. 2014, Article ID 327823 (2014)
Xue, Y., Xie, X., Lin, Q.: Almost periodic solutions of a commensalism system with Michaelis–Menten type harvesting on time scales. Open Math. 17(1), 1503–1514 (2019)
Liu, Y., Xie, X., Lin, Q.: Permanence, partial survival, extinction, and global attractivity of a nonautonomous harvesting Lotka–Volterra commensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018, Article ID 211 (2018)
Chen, B.: The influence of commensalism on a Lotka–Volterra commensal symbiosis model with Michaelis–Menten type harvesting. Adv. Differ. Equ. 2019, Article ID 43 (2019)
Wu, R., Li, L., Zhou, X.: A commensal symbiosis model with Holling type functional response. J. Math. Comput. Sci. 16(3), 364–371 (2016)
Zhang, N., Chen, F., Su, Q., et al.: Dynamic behaviors of a harvesting Leslie–Gower predator–prey model. Discrete Dyn. Nat. Soc. 2011, Article ID 473949 (2011)
Chen, F., Wu, H., Xie, X.: Global attractivity of a discrete cooperative system incorporating harvesting. Adv. Differ. Equ. 2016, Article ID 268 (2016)
Lei, C.: Dynamic behaviors of a nonselective harvesting May cooperative system incorporating partial closure for the populations. Commun. Math. Biol. Neurosci. 2018, Article ID 12 (2018)
Xiao, A., Lei, C.: Dynamic behaviors of a nonselective harvesting single species stage-structured system incorporating partial closure for the populations. Adv. Differ. Equ. 2018, Article ID 245 (2018)
Chen, B.: Dynamic behaviors of a nonselective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018, Article ID 111 (2018)
Lin, Q.: Dynamic behaviors of a commensal symbiosis model with nonmonotonic functional response and nonselective harvesting in a partial closure. Commun. Math. Biol. Neurosci. 2018, Article ID 4 (2018)
Su, Q., Chen, F.: The influence of partial closure for the populations to a nonselective harvesting Lotka–Volterra discrete amensalism model. Adv. Differ. Equ. 2019, Article ID 281 (2019)
Gupta, R.P., Chandra, P.: Bifurcation analysis of modified Leslie–Gower predator–prey model with Michaelis–Menten type prey harvesting. J. Math. Anal. Appl. 398(1), 278–295 (2013)
Hu, D.P., Cao, H.J.: Stability and bifurcation analysis in a predator–prey system with Michaelis–Menten type predator harvesting. Nonlinear Anal., Real World Appl. 33, 58–82 (2017)
Zhou, Y.C., Jin, Z., Qin, J.L.: Ordinary Differential Equation and Its Application. Science Press, Beijing (2003)
Chen, F.D.: On a nonlinear nonautonomous predator–prey model with diffusion and distributed delay. J. Comput. Appl. Math. 180, 33–49 (2005)
Chen, L.S.: Mathematical Models and Methods in Ecology. Science Press, Beijing (1988) (in Chinese)
Zhang, Z.F., Ding, T.R., Huang, W.Z., Dong, Z.X.: Qualitative Theory of Differential Equation. Science Press, Beijing (1992) (in Chinese)
Acknowledgements
The authors would like to thank Dr. Chaoquan Lei for giving us his publication on nonselective harvesting.
Availability of data and materials
Data sharing not applicable to this paper as no datasets were generated or analyzed during the current study.
Funding
The research was supported by the Natural Science Foundation of Fujian Province (2019J01841).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that there is no conflict of interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lai, L., Yu, X., He, M. et al. Impact of Michaelis–Menten type harvesting in a Lotka–Volterra predator–prey system incorporating fear effect. Adv Differ Equ 2020, 320 (2020). https://doi.org/10.1186/s13662-020-02724-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02724-8