Abstract
A predator-prey model with modified Leslie-Gower and Beddington-DeAngelis functional response is studied. The local stability of the equilibria and the permanence of the system are investigated. By applying the fluctuation lemma, qualitative analysis and Lyapunov direct method, respectively, three sufficient conditions on the global asymptotic stability of a positive equilibrium are obtained.
MSC:34D23, 92D25, 34D20, 34D40.
Similar content being viewed by others
1 Introduction
As pointed out by Berryman [1], the dynamic relationship between predators and their prey has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance. Leslie [2, 3] introduced the following famous Leslie predator-prey system:
where , stand for the population (the density) of the prey and the predator at time t, respectively. The parameters and are the intrinsic growth rates of the prey and the predator, respectively. measures the strength of competition among individuals of species x. The value is the carrying capacity of the prey in the absence of predation. The predator consumes the prey according to the functional response and carries capacity . The parameter is a measure of the food quantity that the prey provides converted to predator birth. The term is the Leslie-Gower term which measures the loss in the predator population due to rarity (per capita ) of its favorite food. Leslie model is a predator-prey model where the carrying capacity of the predator is proportional to the number of prey, stressing the fact that there are upper limits to the rates of increase in both prey x and predator y, which are not recognized in the Lotka-Volterra model. These upper limits can be approached under favorable conditions: for the predators, when the number of prey per predator is large; for the prey, when the number of predators (and perhaps the number of prey also) is small [4]. For more details of the model, one can see [4–9] and the references cited therein. Holling [10] suggested three different kinds of functional response for different kinds of species to model the phenomena of predation, which made the standard Lotka-Volterra system more realistic. When , the functional response is called Holling-type II.
Recently, Aziz-Alaoui and Daher Okiye [11] pointed out that in the case of severe scarcity, y can switch over to other populations but its growth will be limited by the fact that its most favorite food x is not available in abundance. To solve such a problem, they suggested to add a positive constant d to the denominator and proposed the following predator-prey model with modified Leslie-Gower and Holling-type II schemes:
where , , , have the same meaning as in models (1.1). is the maximum value of the per capita reduction rate of x due to y, (respectively, ) measures the extent to which the environment provides protection to prey x (respectively, to the predator y). The authors studied the boundedness and global stability of positive equilibrium of system (1.2). Since then, system (1.2) and its non-autonomous versions have been studied by incorporating delay and impulses, harvesting and so on (see, for example, [12–29]). In [12], we studied the structure, linearized stability and the global asymptotic stability of equilibria of (1.2). Nindjin et al. [13] incorporated time delay to system (1.2) and studied the global stability and persistence of the delayed system by using the Lyapunov functional. Yafia et al. [14] and [15] further studied the occurrence of Hopf bifurcation at equilibrium by using the time delay as a parameter of bifurcation. Nindjin and Aziz-Alaoui [16] studied uniform persistence and global stability of three Leslie-Gower-type species food chain system. Gakkhar and Singh [17] studied the dynamic behaviors of a modified Leslie-Gower predator-prey system with seasonally varying parameters. Guo and Song [18], Song and Li [19] further considered the influence of impulsive effect. Zhu and Wang [20] obtained sufficient conditions for the existence and global attractivity of positive periodic solutions of system (1.2) with periodic coefficients. Liu and Wang [21] considered a stochastic predator-prey system with modified Leslie-Gower and Holling-type II schemes with Lévy jumps. The results showed that the Lévy jumps can change the properties of the population systems significantly. Kar and Ghorai [22] obtained local stability, global stability, influence of harvesting and bifurcation of a delayed predator-prey system in the presence of harvesting. Two stage-structured predator-prey models with modified Leslie-Gower and Holling-type II schemes were studied in [23–25]. Gupta and Chandra [26] discussed the permanence, stability and bifurcation (saddle-node bifurcation, transcritical, Hopf-Andronov and Bogdanov-Takens) of a modified Leslie-Gower prey-predator model with Michaelis-Menten type prey harvesting. Ji et al. [27, 28] showed there was a stationary distribution of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with stochastic perturbation and it has ergodic property. Lian and Xu [29] discussed the Hopf bifurcation of a predator-prey system with Holling type IV functional response and time delay.
As we all know, the functional response can be classified into two types: prey-dependent and predator-dependent. Prey-dependent depends on prey density only, while predator-dependent means that the functional response is a function of both the preys and the predators densities. Recently, the prey-dependent functional responses have been challenged by several ecologists. There is a growing explicit biological and physiological evidence [30–32] that in many situations, especially when the predator has to search for food (and therefore has to shave or compete for food), a more suitable general predator-prey theory should be predator-dependent. This is supported by numerous fields and laboratory experiments and observations [33, 34]. Starting from this argument and the traditional prey-dependent-only model, Arditi and Ginzburg [33] first proposed the ratio-dependent predator-prey model. Many authors have observed that the ratio-dependent models can exhibit much richer, more complicated and more reasonable or acceptable dynamics, but it has somewhat singular behavior at low densities which has been the source of controversy [35]. For the ratio-dependent predator-prey models, one can refer to [36–39].
Beddington-DeAngelis functional response was first proposed by Beddington and DeAngelis [40, 41]. Predator-prey model with Beddington-DeAngelis functional response has rich dynamical features, which can describe the species and the ecological systems more reasonably. Beddington-DeAngelis functional response is similar to the well-known Holling type II functional response but has an extra term cy in the denominator modeling mutual interference among predators and has some of the same qualitative features as the ratio-dependent form but avoids some of the singular behaviors of ratio-dependent models at low densities.
On the other hand, in 2001, Skalski and Gilliam [42] have presented statistical evidence from nineteen predator-prey systems that three predator-dependent functional responses (Beddington-DeAngelis, Crowley-Martin, and Hassell-Varley) can provide better description of predator feeding over a range of predator-prey abundances. In some cases, the Beddington-DeAngelis type preformed even better. Theoretical studies have shown that the dynamics of models with predator-dependent functional responses can differ considerably from those with prey-dependent functional responses. Although much progress has been seen in the study of predator-prey models with modified Leslie-Gower (see [11–29]), to the best of the authors’ knowledge, seldom did scholars consider the modified Leslie-Gower model with Beddington-DeAngelis functional response. Stimulated by above reasons, in this paper we will incorporate the Beddington-DeAngelis functional response into model (1.2) and consider the following model which is the generalization of model (1.2):
with initial conditions and . The parameters , p, α, a, b, c, , β and k are positive constants and have the same meaning as in model (1.2).
It is easy to see that both the first quadrant and the positive first quadrant are invariant for system (1.3). As a result, solutions to (1.3) with are all positive solutions.
The rest of this paper is organized as follows. In Section 2, we discuss the structure of nonnegative equilibria to (1.3) and their local stability, which motivates us to study permanence and global stability of (1.3) respectively in Section 3 and Section 4.
For more works on this direction, one could refer to [43–51] and the references cited therein.
2 Nonnegative equilibria and their local stability
The Jacobian matrix of system (1.3) is
An equilibrium E of (1.3) is (linearly) stable if the real parts of both eigenvalues of are negative, and therefore a sufficient condition for stability is
Obviously, (1.3) has three boundary equilibria, , and , whose Jacobian matrices are
and
respectively. As a direct consequence of (2.1), we have the following result.
Proposition 2.1
-
(i)
Both and are unstable.
-
(ii)
is locally asymptotically stable if , while it is unstable if .
Besides the three boundary equilibria, (1.3) may have (componentwise) positive equilibria. Suppose that is such an equilibrium. Then
One can easily see that satisfies
where . Moreover, for convenience, we denote
Hence, we have the following result.
Proposition 2.2 Suppose that
holds, then system (1.3) has a unique positive equilibrium , where
We now want to study the stability of the positive equilibrium . It follows from the Jacobian matrix of systems (1.3) and (2.2) that
and
Thus, if , we have
Hence, the following proposition follows from (2.1).
Proposition 2.3 Assume that
holds, then the positive equilibrium is locally asymptotically stable.
Proposition 2.1 and Proposition 2.3 naturally motivate us to seek sufficient conditions on the global stability of and the unique positive equilibrium to (1.3). To achieve it, we need the bounds for positive solutions.
3 Boundedness and permanence
The following result can be proved by slightly modifying the proof of Lemma 3.2 of Chen [52] and it will play an important role in finding the bounds for positive solutions to (1.3).
Lemma 3.1 If , and , when and , we have
If , and , when and , we have
Proposition 3.1 Let be any positive solution of (1.3). Then
and
where and .
Proof Since is a positive solution of (1.3), we have
Then (3.1) and follow directly from Lemma 3.1. Thus, for any , there exists such that
This combined with the second equation of (1.3) leads to
Using Lemma 3.1 again, one has
Thus by letting . □
Proposition 3.2 Suppose that
If is a positive solution to system (1.3), then
Proof Denote
Then, for , we have
According to Proposition 3.1, there exists such that
This, combined with the first equation of (1.3), produces
It follows from Lemma 3.1 that
This gives by letting . □
Combing Proposition 3.1 with Proposition 3.2 gives the permanence of (1.3).
Theorem 3.1 Suppose that (H2) holds, then (1.3) is permanent.
4 Global asymptotic stability
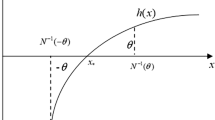
The goal of this section is to establish sufficient conditions on the global asymptotic stability of equilibrium to (1.3). The first two results are proved by employing the fluctuation lemma, which is cited below for the convenience of the readers. See Hirsch et al. [53] or Tineo [54] for more details on the fluctuation lemma.
Lemma 4.1 (Fluctuation lemma)
Let be a bounded differentiable function on . Then there exist sequences and such that
-
(i)
and as ;
-
(ii)
and as .
Theorem 4.1 Assume that
Then is globally asymptotically stable for system (1.3).
Proof Let be any positive solution of (1.3). According to (H3), we can choose such that
It follows from Proposition 3.1 that there exists such that
These inequalities combined with the first equation of (1.3) give us
or
Integrating both sides of (4.2) on interval leads to
Due to (4.1), one has . Hence
Proposition 3.1 again tells us that is bounded and . By Lemma 4.1, there exist sequences , such that , , , and , as .
It follows from the second equation of (1.3) and that
Similarly, one can show that
Equation (4.4) combined with (4.5) implies that
It follows from (4.3) and (4.6) that is globally asymptotically stable. □
Theorem 4.2 In addition to (H2), further suppose that
where is defined in Proposition 3.2. Then system (1.3) has a unique positive equilibrium which is globally asymptotically stable.
Proof Note that (H2) implies (H0), thus (1.3) has a unique positive equilibrium according to Proposition 2.2. Let be any positive solution of (1.3). By the results in Section 3, (>0) and .
We claim that . Suppose that . According to Lemma 4.1, there exist sequences , , and , such that , , and , , , and , as . First, it follows from the second equation of (1.3) that
and
Letting gives us
and
Hence
Similar arguments as above also produce
Second, from the first equation of (1.3), we have
Equation (4.9) implies
Taking limit as , one obtains
This, combined with (4.8), gives us
It follows that
Similarly, one can show that
Multiplying (4.10) by −1 and adding it to (4.11), we have
Due to , one gets
On the other hand,
which contradicts with (4.12). Therefore, and the claim is proved. The claim implies that exists and we denote it by . Then it follows from (4.7) and (4.8) that exists and . Letting in (4.9) gives us
Thus satisfies
That is, is a positive equilibrium of (1.3). This completes the proof as the positive equilibrium is unique and so the unique equilibrium point is globally asymptotically stable. □
The following results in this section are proved by qualitative method and applying the Lyapunov direct method with the Lyapunov function.
Theorem 4.3 Assume that (H0) and (H1) hold, then (1.3) has a unique positive equilibrium which is globally asymptotically stable.
Proof According to Proposition 2.2, (1.3) has a unique positive equilibrium . Taking Dulac function , we obtain
where is the vector field of (1.3). By the positivity of x, y, it is easy to obtain that if (H1) holds. Then, by the Dulac criteria, (1.3) admits no limit cycles or separatrix cycles. Proposition 2.3 shows that is locally asymptotically stable when (H1) holds. On the other hand, (1.3) admits only four equilibria () and . Also, Proposition 2.1 shows that () are all unstable when holds. So, according to Proposition 3.1 and the Poincaré-Bendixson theorem, is globally asymptotically stable. □
Theorem 4.4 Suppose that (H0) holds, further assume that
hold, then (1.3) has a unique positive equilibrium which is globally asymptotically stable.
Proof Let be any positive solution of (1.3). According to Proposition 2.2, (1.3) has a unique positive equilibrium . From (H5), we can choose an such that
Moreover, it follows from Proposition 3.1 that there exists such that
Let , where and . Calculating the derivative of V along the solution of system (1.3), we have
According to (4.13) and (4.14), strictly for all except the positive equilibrium , where . Thus, satisfies Lyapunov’s asymptotic stability theorem, and the positive equilibrium of system (1.3) is globally asymptotically stable. This ends the proof of Theorem 4.4. □
Conclusion
In this paper, we consider a predator-prey model with modified Leslie-Gower and Beddington-DeAngelis functional response. We discuss the structure of nonnegative equilibria and their local stability. Also, the permanence of the system is investigated. By applying the fluctuation lemma, qualitative analysis and Lyapunov direct method, respectively, three sufficient conditions on the global asymptotic stability of a positive equilibrium are obtained. Compare Theorem 4.2 with Theorem 4.3. Since (H2) contains (H0), what will happen when (H0) and (H4) hold? This is a further problem, which can be studied in the future.
References
Berryman AA: The origins and evolution of predator-prey theory. Ecology 1992, 75: 1530–1535.
Leslie PH: Some further notes on the use of matrices in population mathematics. Biometrika 1948, 35: 213–245. 10.1093/biomet/35.3-4.213
Leslie PH: A stochastic model for studying the properties of certain biological systems by numerical methods. Biometrika 1958, 45: 16–31. 10.1093/biomet/45.1-2.16
Korobeinikov A: A Lyapunov function for Leslie-Gower predator-prey models. Appl. Math. Lett. 2001, 14: 697–699. 10.1016/S0893-9659(01)80029-X
Hsu SB, Hwang TW: Global stability for a class of predator-prey systems. SIAM J. Appl. Math. 1995, 55: 763–783. 10.1137/S0036139993253201
Hsu SB, Hwang TW: Uniqueness of limit cycles for a predator-prey system of Holling and Leslie type. Can. Appl. Math. Q. 1998, 6: 91–117.
Hsu SB, Hwang TW: Hopf bifurcation analysis for a predator-prey system of Holling and Leslie type. Taiwan. J. Math. 1999, 3: 35–53.
Yuan S, Song Y: Bifurcation and stability analysis for a delayed Leslie-Gower predator-prey system. IMA J. Appl. Math. 2009, 74: 574–603. 10.1093/imamat/hxp013
May RM: Stability and Complexity in Model Ecosystems. Princeton University Press, Princeton; 2001.
Holling CS: The functional response of predator to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 1965, 45: 1–60.
Aziz-Alaoui MA, Daher Okiye M: Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes. Appl. Math. Lett. 2003, 16: 1069–1075. 10.1016/S0893-9659(03)90096-6
Yu SB: Global asymptotic stability of a predator-prey model with modified Leslie-Gower and Holling-type II schemes. Discrete Dyn. Nat. Soc. 2012., 2012: Article ID 208167
Nindjin AF, Aziz-Alaoui MA, Cadivel M: Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay. Nonlinear Anal., Real World Appl. 2006, 7: 1104–1118. 10.1016/j.nonrwa.2005.10.003
Yafia R, El Adnani F, Talibi Alaoui H: Stability of limit cycle in a predator-prey model with modified Leslie-Gower and Holling-type II schemes with time delay. Appl. Math. Sci. 2007, 1: 119–131.
Yafia R, El Adnani F, Talibi Alaoui H: Limit cycle and numerical similations for small and large delays in a predator-prey model with modified Leslie-Gower and Holling-type II schemes. Nonlinear Anal., Real World Appl. 2008, 9: 2055–2067. 10.1016/j.nonrwa.2006.12.017
Nindjin AF, Aziz-Alaoui MA: Persistence and global stability in a delayed Leslie-Gower type three species food chain. J. Math. Anal. Appl. 2008, 340: 340–357. 10.1016/j.jmaa.2007.07.078
Gakkhar S, Singh B: Dynamics of modified Leslie-Gower-type prey-predator model with seasonally varying parameters. Chaos Solitons Fractals 2006, 27: 1239–1255. 10.1016/j.chaos.2005.04.097
Guo HJ, Song XY: An impulsive predator-prey system with modified Leslie-Gower and Holling type II schemes. Chaos Solitons Fractals 2008, 36: 1320–1331. 10.1016/j.chaos.2006.08.010
Song XY, Li YF: Dynamic behaviors of the periodic predator-prey model with modified Leslie-Gower Holling-type II schemes and impulsive effect. Nonlinear Anal., Real World Appl. 2008, 9: 64–79. 10.1016/j.nonrwa.2006.09.004
Zhu Y, Wang K: Existence and global attractivity of positive periodic solutions for a predator-prey model with modified Leslie-Gower Holling-type II schemes. J. Math. Anal. Appl. 2011, 384: 400–408. 10.1016/j.jmaa.2011.05.081
Liu M, Wang K: Dynamics of a Leslie-Gower Holling-type II predator-prey system with Lévy jumps. Nonlinear Anal. 2013, 85: 204–213.
Kar TK, Ghorai A: Dynamic behaviour of a delayed predator-prey model with harvesting. Appl. Math. Comput. 2011, 217: 9085–9104. 10.1016/j.amc.2011.03.126
Huo H, Wang X, Chavez C: Dynamics of a stage-structured Leslie-Gower predator-prey model. Math. Probl. Eng. 2011., 2011: Article ID 149341
Li Z, Han M, Chen F: Global stability of a stage-structured predator-prey model with modified Leslie-Gower and Holling-type II schemes. Int. J. Biomath. 2012., 5: Article ID 1250057
Liu C, Zhang Q, Huang J: Stability analysis of a harvested prey-predator model with stage structure and maturation delay. Math. Probl. Eng. 2013., 2013: Article ID 329592 10.1155/2013/329592
Gupta RP, Chandra P: Bifurcation analysis of modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting. J. Math. Anal. Appl. 2013, 398: 278–295. 10.1016/j.jmaa.2012.08.057
Ji CY, Jiang DQ, Shi NZ: Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with stochastic perturbation. J. Math. Anal. Appl. 2009, 359: 482–498. 10.1016/j.jmaa.2009.05.039
Ji CY, Jiang DQ, Shi NZ: A note on a predator-prey model with modified Leslie-Gower and Holling-type II schemes with stochastic perturbation. J. Math. Anal. Appl. 2011, 377: 435–440. 10.1016/j.jmaa.2010.11.008
Lian F, Xu Y: Hopf bifurcation analysis of a predator-prey system with Holling type IV functional response and time delay. Appl. Math. Comput. 2009, 215: 1484–1495. 10.1016/j.amc.2009.07.003
Arditi R, Saiah H: Empirical evidence of the role of heterogeneity in ratio-dependent consumption. Ecology 1992, 73: 1544–1551. 10.2307/1940007
Arditi R, Ginzburg LR, Akcakaya HR: Variation in plankton densities among lakes: a case for ratio-dependent models. Am. Nat. 1991, 138: 1287–1296. 10.1086/285286
Gutierrez AP: The physiological basis of ratio-dependent predator-prey theory: A metabolic pool model of Nicholson’s blowflies as an example. Ecology 1992, 73: 1552–1563. 10.2307/1940008
Arditi R, Ginzburg LR: Coupling in predator-prey dynamics: ratio-dependence. J. Theor. Biol. 1989, 139: 311–326. 10.1016/S0022-5193(89)80211-5
Arditi R, Perrin N, Saiah H: Functional response and heterogeneities: an experiment test with cladocerans. Oikos 1991, 60: 69–75. 10.2307/3544994
Yao Z, Xie S, Yu N: Dynamics of cooperative predator-prey system with impulsive effects and Beddington-DeAngelis functional response. J. Egypt. Math. Soc. 2013, 21: 213–223. 10.1016/j.joems.2013.04.008
Beretta E, Kuang Y: Global analysis in some delayed ratio-dependent predator-prey systems. Nonlinear Anal. 1998, 32: 381–408. 10.1016/S0362-546X(97)00491-4
Liang Z, Pan H: Qualitative analysis of a ratio-dependent Holling-Tanner mode. J. Math. Anal. Appl. 2007, 334: 954–964. 10.1016/j.jmaa.2006.12.079
Saha T, Chakrabarti C: Dynamical analysis of a delayed ratio-dependent Holling-Tanner predator-prey model. J. Math. Anal. Appl. 2009, 358: 389–402. 10.1016/j.jmaa.2009.03.072
Liu J, Zhang Z, Fu M: Stability and bifurcation in a delayed Holling-Tanner predator-prey system with ratio-dependent functional response. J. Appl. Math. 2012., 2012: Article ID 384293
Beddington JR: Mutual interference between parasites or predators and its effect on searching efficiency. J. Anim. Ecol. 1975, 44: 331–340. 10.2307/3866
DeAngelis DL, Goldstein RA, O’Neill RV: A model for trophic interaction. Ecology 1975, 56: 881–892. 10.2307/1936298
Skalski GT, Gilliam JF: Functional responses with predator interference: viable alternatives to the Holling type II model. Ecology 2001, 82: 3083–3092. 10.1890/0012-9658(2001)082[3083:FRWPIV]2.0.CO;2
Lu Z, Liu X: Analysis of a predator-prey model with modified Holling-Tanner functional response and time delay. Nonlinear Anal., Real World Appl. 2008, 9: 641–650. 10.1016/j.nonrwa.2006.12.016
Zhang J: Bifurcation analysis of a modified Holling-Tanner predator-prey model with time delay. Appl. Math. Model. 2012, 36: 1219–1231. 10.1016/j.apm.2011.07.071
Cantrell R, Cosner C: On the dynamics of predator-prey models with the Beddington-DeAngelis functional response. J. Math. Anal. Appl. 2001, 257: 206–222. 10.1006/jmaa.2000.7343
Liu ZH, Yuan R: Stability and bifurcation in a delayed predator-prey system with Beddington-DeAngelis functional response. J. Math. Anal. Appl. 2004, 296: 521–537. 10.1016/j.jmaa.2004.04.051
Dimitrov DT, Kojouharov HV: Complete mathematical analysis of predator-prey models with linear prey growth and Beddington-DeAngelis functional response. Appl. Math. Comput. 2005, 162: 523–538. 10.1016/j.amc.2003.12.106
Lin G, Hong Y: Delay induced oscillation in predator-prey system with Beddington-DeAngelis functional response. Appl. Math. Comput. 2007, 190: 1296–1311. 10.1016/j.amc.2007.02.012
Chen WY, Wang MX: Qualitative analysis of predator-prey models with Beddington-DeAngelis functional response and diffusion. Math. Comput. Model. 2005, 42: 31–44. 10.1016/j.mcm.2005.05.013
Xiao HB: Positive equilibrium and its stability of the Beddington-DeAngelis’s type predator-prey dynamical system. Appl. Math. J. Chin. Univ. Ser. B 2006, 21: 429–436. 10.1007/s11766-006-0007-2
Hwang T: Uniqueness of limit cycles of the predator-prey system with Beddington-DeAngelis functional response. J. Math. Anal. Appl. 2004, 290: 113–122. 10.1016/j.jmaa.2003.09.073
Chen FD: On a nonlinear non-autonomous predator-prey model with diffusion and distributed delay. J. Comput. Appl. Math. 2005, 180: 33–49. 10.1016/j.cam.2004.10.001
Hirsch W, Hanisch H, Gabriel J: Differential equation models of some parasitic infection: methods for the study of asymptotic behavior. Commun. Pure Appl. Math. 1985, 38: 733–753. 10.1002/cpa.3160380607
Tineo A: Asymptotic behaviour of positive solutions of the nonautonomous Lotka-Volterra competition equations. Differ. Integral Equ. 1993, 6: 419–457.
Acknowledgements
The author would like to thank the two anonymous referees for their constructive suggestions on improving the presentation of the paper. This research is supported by the Foundation of Fujian Education Bureau (JA13365).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that he has no competing interests.
Author’s contributions
The author wrote the manuscript carefully, read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yu, S. Global stability of a modified Leslie-Gower model with Beddington-DeAngelis functional response. Adv Differ Equ 2014, 84 (2014). https://doi.org/10.1186/1687-1847-2014-84
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-84