Stability analysis of Filippov prey–predator model with fear effect and prey refuge

Abstract

Mathematical ecosystems play a crucial role in our comprehension and conservation of ecology. Within these ecosystems, prey exhibits protective instincts that compel refuging behaviors to avoid predation risk. When the ratio of prey to predators falls below a threshold, prey seeks refuge. However, when prey is abundant relative to predators, these protective instincts are overridden as prey ventures out to forage. Therefore, this study develops a Filippov prey–predator model with fear effect on prey and switching of prey refuge behavior based on the ratio of prey to predators. Analytical and numerical approaches are used to address the dynamic behaviors, bifurcation sets, existence, and stability of various equilibria in this model. Additionally, the regions of sliding and crossing segments are analyzed. The bifurcation sets of pseudo-equilibrium and local and global sliding bifurcations are investigated. The numerical simulations are conducted to investigate the interplay between fear factor and other relevant parameters within the Filippov model, such as the threshold ratio and prey refuge. These investigations shed light on the influence of them in the model. The results indicate that increasing the fear factor results in a decrease in both prey and predator densities, thereby changing the behavior of the dynamics from a limit cycle oscillation to a stable state and vice versa. Notably, despite these population changes, neither species faces complete extinction.

1 Introduction

Ecology, in essence, encompasses the scientific exploration and aesthetic examination of the intricate interplay between organisms and their environments. It encompasses not only the organisms themselves but also the communities they form and the nonliving constituents of their environment, all engaged in dynamic interactions. Throughout history, the relationship between predators and their prey has held a prominent position within the realm of ecology and mathematical ecology, owing to its universal significance [1,2,3]. The interaction between these two entities serves as a pivotal aspect of population dynamics.

In nearly all vertebrates, the perception of predation risk triggers a range of anti-predator responses, such as physiological adaptations, foraging behaviors, changes in habitat usage, and vigilance [4,5,6,7,8,9,10,11]. For instance, birds may abandon their nests and leave their young unprotected when they sense danger, leading to a temporary increase in survival probability but potentially causing long-term consequences for the population [4]. In 2011, Zanette et al. [12] performed a field experiment where they manipulated predation risk in song sparrow populations by playing predator sounds near some nesting sites but not others. The researchers ensured that the direct killing of sparrows was prevented so that any effects were solely from fear. They found that the perceived threat of predators, even without direct attacks, led song sparrow females to produce $40\%$ fewer offspring. Specifically, fearful females laid fewer eggs, had lower hatching rates, and had more baby sparrow deaths in the nests. Scared parent birds fed their young less, resulting in weaker and more vulnerable baby birds. This dramatic effect on demography has been supported by correlational evidence in other hares, birds, dugongs, snowshoe and elk [13,14,15,16,17]. Mathematically, Wang et al. [18] delved into the intriguing role of fear in predator–prey relationships. They crafted a model where fear was represented as a decreasing function of fear parameter and predator biomass. Their analysis revealed that intense fear can stabilize the predator–prey system by eliminating recurring patterns, while low fear levels can cause periodic oscillations through a phenomenon called subcritical Hopf bifurcations, leading to dual stability. This pioneering work has inspired further research into fear’s role in various ecological systems [19,20,21]. Thanks to these previous works, we introduce the following model

$$\begin{aligned} F_{S_{1}}(x,y):\left\{ \begin{aligned}&\frac{dx}{dt}=rx(t)\left( \frac{1}{1+\varphi y(t)}-\frac{x(t)}{k}\right) -\frac{\mu x(t)y(t)}{\alpha x(t)+\beta y(t)+\gamma }, \\&\frac{dy}{dt}=\frac{\eta \mu x(t)y(t)}{\alpha x(t)+\beta y(t)+\gamma } -\delta y(t), \end{aligned} \right. \end{aligned}$$

(1)

where x(t) denotes the prey population at time $t\ge 0$ and y(t) denotes the predator population at time $t\ge 0.$ $r>0$ is the intrinsic growth rate of the prey, $\varphi >0$ represents the degree of fear level induced by predator, $k>0$ is the carrying capacity of the prey, $\mu >0$ is the maximum predation rate, $\alpha >0$ is the abundance of prey, $\beta >0$ be interference of predator, $\gamma >0$ is the saturation constant for Beddington–DeAngelis (BD) type functional response [22,23,24,25], $\eta \in (0,1]$ denotes the conversion predator rate and $\delta >0$ is the death rate of predator. While the expression $\frac{1}{1+\varphi y(t)}$ represents the cost associated with anti-predator defence triggered by fear and $\frac{\mu x(t)y(t)}{\alpha x(t)+\beta y(t)+\gamma }$ is the BD functional response [22, 23].

The fear-induced refuge is a captivating and vital element acquired by prey populations within an ecological community, exerting a profound influence on the dynamics of food web systems and playing a pivotal role in maintaining the delicate ecological balance between prey and predator. The significance of refuge was initially demonstrated by Gause [26] through his experiments involving the protozoan organisms Paramecium and Didinium. Recent years have seen numerous researchers delve into mathematical models that incorporate the impact of prey refuge [27,28,29,30]. Wang et al. [31] conducted a comprehensive investigation, both analytically and numerically, to explore the impacts of anti-predator behavior arising from fear of predators and prey refuge. Prey refuges typically come in two forms: either the amount of refuge scales with prey population size, or there is a fixed maximum capacity [31,32,33,34,35,36,37]. For our model, we consider the first type, specifically, if m (where $0\le m<1$) represents the fixed maximum refuge availability for prey. Then model (1) can be written to include this as:

$$\begin{aligned} F_{S_{2}}(x,y):\left\{ \begin{aligned}&\frac{dx}{dt}=rx(t)\left( \frac{1}{1+\varphi y(t)}-\frac{x(t)}{k}\right) -\frac{\mu (1-m)x(t)y(t)}{\alpha (1-m)x(t)+\beta y(t)+\gamma }-\nu x(t), \\&\frac{dy}{dt}=\frac{\eta \mu (1-m)x(t)y(t)}{\alpha (1-m)x(t)+\beta y(t)+\gamma }-\delta y(t), \end{aligned} \right. \end{aligned}$$

(2)

where $\nu$ is the migration rate of prey due to fear of predator risk [38].

In these models, the response of prey to fear is a focal point. When prey experiences fear, it elicits various reactions, including seeking refuge or potentially migrating, even in the presence of relatively mild fear. However, this response is not constant; the prey’s inclination to seek refuge is triggered predominantly when the fear factor reaches significant levels. For instance, in the case of elk, they exhibit this behavior by seeking refuge in forest cover when wolf packs are numerous. Conversely, when wolf populations decline, they tend to forage more openly in grasslands [39,40,41]. These patterns are underpinned by the innate protective instincts of prey, which play a crucial role in mitigating predation risks. When the prey-to-predator ratio is low, these protective instincts drive prey to employ refuge-seeking as a defensive strategy. Conversely, in situations with a high prey-to-predator ratio, these instincts stimulate active foraging behavior among prey. Inspired by this motivation, we present a Filippov model for predator–prey interactions, incorporating the influence of fear on prey and switching of prey refuge upon the prey-to-predator ratio, denoted as $\frac{x }{y}$. It is assumed that prey seek refuge when the ratio falls below a certain threshold, that is $\frac{x}{y}<\zeta$. However, if the ratio exceeds the threshold, refuge utilization is forbidden, that is $\frac{x}{y} <\zeta$. By elucidating these dynamics and highlighting the importance of fear and refuge effects, our research aims to contribute to the broader understanding of the complexities involved in prey-predator interactions within Filippov systems [35, 36, 42,43,44,45,46]. We consider the following Filippov system:

$$\begin{aligned} {\dot{X}}(t)=\left\{ \begin{array}{ll} F_{S_{1}}(x,y),&{}\quad (x,y){\in S_{1}}, \\ F_{S_{2}}(x,y),&{}\quad (x,y){\in S_{2}}, \end{array} \right. \end{aligned}$$

(3)

where

$$\begin{aligned} F_{S_{1}}(x,y)= & {} \left( \begin{array}{c} rx(t)\left( \frac{1}{1+\varphi y(t)}-\frac{x(t)}{k}\right) -\frac{\mu x(t)y(t)}{\alpha x(t)+\beta y(t)+\gamma } \\ \frac{\eta \mu x(t)y(t)}{\alpha x(t)+\beta y(t)+\gamma }-\delta y(t) \end{array} \right) ,\end{aligned}$$

(4)

$$\begin{aligned} F_{S_{2}}(x,y)= & {} \left( \begin{array}{c} rx(t)\left( \frac{1}{1+\varphi y(t)}-\frac{x(t)}{k}\right) -\frac{\mu (1-m)x(t)y(t)}{\alpha (1-m)x(t)+\beta y(t)+\gamma }-\nu x(t) \\ \frac{\eta \mu (1-m)x(t)y(t)}{\alpha (1-m)x(t)+\beta y(t)+\gamma }-\delta y(t) \end{array} \right) .\\ S_{1}= & {} \{X\in {{\mathbb {R}}}_{+}^{2}|B(x)>0\},\;S_{2}=\{X\in {{\mathbb {R}}} _{+}^{2}|B(x)<0\}\nonumber \\{} & {} \text {and}\;\Sigma =\{X\in {{\mathbb {R}}}_{+}^{2}|\;B(X)=0\},\;\text {with} \;B(X)=x-\zeta y.\nonumber \end{aligned}$$

(5)

The non-intersecting areas $S_{1}$ and $S_{2}$ are partitioned by a switching line $\Sigma$ in such a way that $S_{1}\cup \Sigma \cup S_{2}={ {\mathbb {R}}}_{+}^{2}.$ By scrutinizing these underlying assumptions and investigating the dynamics inherent in our proposed model, our objective is to elucidate the complex interplay between various parameters on the dynamics of predator–prey relationships. This endeavor represents a significant contribution to the comprehension of ecological systems. Furthermore, we will explore the impact of altering parameter values, such as the fear factor, prey refuge availability, and the ratio threshold, on the behavior of the Filippov model (3), elucidating how these changes can potentially shift the model between stable and unstable states, or vice versa.

The subsequent sections of this paper are structured as follows. In Sect. 2, we delve into the analysis of the dynamics of the Filippov subsystems, and we also examine the local stability of the equilibria. Section 3 is dedicated to investigating the sliding region and the sliding mode dynamics on the discontinuity surface $\Sigma$. For a comprehensive understanding for the Filippov model, local and global sliding bifurcations are investigated through numerical simulations in Sect. 4. Finally in the last section, we present our concluding remarks.

2 Basic properties and dynamics of the subsystems $S_{1},S_{2}$

In this section, we examine the equilibria of the system (3) and identify the parameter values that guarantee the stability of the subsystems. It is evident that system (3) possesses two distinct structures, one without a refuge (4) and another with a refuge that provides protection for the prey (5). An equilibrium E of system (3) that satisfies $F_{S_{1}}(E)=0,B(E)>0$ or $F_{S_{2}}(E)=0,B(E)<0$ is called a regular equilibrium [47, 48]. Moreover, it is called virtual equilibrium if $F_{S_{1}}(E)=0,B(E)<0$ or $F_{S_{2}}(E)=0,B(E)>0.$

2.1 Dynamics of the subsystem $S_{1}$

The equilibria of subsystem $S_{1}$ (4) can be expressed by solving the following equations:

$$\begin{aligned} \left\{ \begin{aligned}&rx(t)\left( \frac{1}{1+\varphi y(t)}-\frac{x(t)}{k}\right) -\frac{\mu x(t)y(t)}{\alpha x(t)+\beta y(t)+\gamma }=0, \\&\frac{\eta \mu x(t)y(t)}{\alpha x(t)+\beta y(t)+\gamma }-\delta y(t)=0, \end{aligned} \right. \end{aligned}$$

(6)

then we see that the system has the following equilibria:

• (a) The trivial equilibrium $E_{S_{1}}^{0}(0,0).$

• (b) The axil equilibrium $E_{S_{1}}^{1}(k,0)$ and always regular.

• (c) The interior equilibria are the intersection points of the system (6) in the interior of the first quadrant. So, from the second equation of (6), we get:

  $$\begin{aligned} y_{S_{1}}^{*}=\frac{x_{S_{1}}^{*}}{\beta \delta }(\eta \mu -\alpha \delta )-\frac{\gamma }{\beta }. \end{aligned}$$

  Moreover, from the first equation of (6), we have

  $$\begin{aligned} r\left( \frac{1}{1+\varphi y_{S_{1}}^{*}}-\frac{x_{S_{1}}^{*}}{k}\right) =\frac{ \mu y_{S_{1}}^{*}}{\alpha x_{S_{1}}^{*}+\beta y_{S_{1}}^{*}+\gamma }, \end{aligned}$$

  then

  $$\begin{aligned}{} & {} P_{0}(y_{S_{1}}^{*})^{2}+P_{1}y_{S_{1}}^{*}+P_{2}=0,\nonumber \\{} & {} y_{S_{1}}^{*}=\frac{-P_{1}\pm \sqrt{P_{1}^{2}-4P_{0}P_{2}}}{2P_{0}}, \end{aligned}$$

  (7)

  where $P_{0}=(r\beta x_{S_{1}}^{*}+k\mu )\varphi ,\;P_{1}=rx_{S_{1}}^{*}\left( \beta +\varphi (\alpha x_{S_{1}}^{*}+\gamma )\right) -k(r\beta -\mu ),\;P_{2}=-r(k-x_{S_{1}}^{*})(\alpha x_{S_{1}}^{*}+\gamma ).$ So, the interior equilibria of the system (6) are the intersection points of the following two nullclines.

  $$\begin{aligned} y_{S_{1}}^{*}=\frac{x_{S_{1}}^{*}}{\beta \delta }(\eta \mu -\alpha \delta )-\frac{\gamma }{\beta }, \end{aligned}$$

  (8)
  $$\begin{aligned} y_{S_{1}}^{*}=\frac{-P_{1}+\sqrt{P_{1}^{2}-4P_{0}P_{2}}}{2P_{0}}. \end{aligned}$$

  (9)

  We take the positive square root in the Eq. (7), because $P_{1}^{2}-P_{0}P_{2}$ is nonnegative, and if we take the negative root then $y_{S_{1}}^{*}<0$, and hence any branch in the positive quadrant does not appear. The first nullcline (8) is a line and it lies on the first quadrant of the $x-y$ plane for $\eta \mu -\alpha \delta >0.$ The second nullcline (9) intersects the positive $x-$axis at (k, 0) and positive $y-$axis at $\left( 0,\frac{r\beta -\mu +\sqrt{(r\beta -\mu )^{2}+4r\gamma \mu \varphi }}{2\mu \varphi }\right) .$ Therefore we conclude that there is a unique interior point in the first quadrant if $k\ge k^{*},$ where $k^{*}=\gamma \delta /(\eta \mu -\alpha \delta ).$ Moreover, it is regular if $\zeta (\eta \mu -\alpha \delta )>\beta \delta$ and $x_{S_{1}}^{*}>\frac{\gamma \zeta \delta }{ \zeta (\eta \mu -\alpha \delta )-\beta \delta }.$ Moreover, there are not any interior points in the first quadrant if $k<k^{*}.$ This suggests that a low carrying capacity k for the prey population may result in the extinction of the predator species.

Examining the Jacobian matrix at all the equilibria yields straightforward results:

Theorem 1

• 1. The trivial equilibrium $E_{S_{1}}^{0}$ is a saddle node.

• 2. The axil equilibrium $E_{S_{1}}^{1}$ is stable node if $k(\eta \mu -\alpha \delta )<\gamma \delta$ and it is saddle node if $k(\eta \mu -\alpha \delta )>\gamma \delta .$

• 3. The interior equilibrium $E_{S_{1}}^{*}$ is locally stable (unstable) if $trac(J_{E_{S_{1}}^{*}})<0 (trac(J_{E_{S_{1}}^{*}})>0)$.

Proof

The Jacobian matrix of subsystem $S_{1}$ (4) can be written as

$$\begin{aligned} J=\left( \begin{array}{cc} \frac{-2rx}{k}-\frac{\mu y(\beta y+\gamma )}{(\alpha x+\beta y+\gamma )^{2}}+ \frac{r}{1+\varphi y} &{} -x\left( \frac{\mu (\alpha x+\gamma )}{(\alpha x+\beta y+\gamma )^{2}}+\frac{r\varphi }{(1+\varphi y)^{2}}\right) \\ \frac{\eta \mu y(\beta y+\gamma )}{(\alpha x+\beta y+\gamma )^{2}} &{} -\delta +\frac{\eta \mu x(\alpha x+\gamma )}{(\alpha x+\beta y+\gamma )^{2}} \end{array} \right) . \end{aligned}$$

(10)

• 1. The eigenvalues of the subsystem $S_{1}$ (4) evaluated at $E_{S_{1}}^{0}$ equal $\lambda _{1}=r>0$ and $\lambda _{2}=-\delta <0.$ Therefore it is a saddle node.

• 2. The eigenvalues of the subsystem $S_{1}$ (4) evaluated at $E_{S_{1}}^{1}$ equal $\lambda _{1}=-r<0$ and $\lambda _{2}=-\delta + \frac{\eta \mu k}{\alpha k+\gamma }.$ Therefore, if $k(\eta \mu -\alpha \delta )<\gamma \delta ,$ then $\lambda _{2}<0.$ That means the axil equilibrium $E_{S_{1}}^{1}$ is stable. On the other hand, if $k(\eta \mu -\alpha \delta )>\gamma \delta ,$ then $\lambda _{2}>0.$ Therefore, the equilibrium $E_{S_{1}}^{1}$ is saddle node.

• 3. Let $H(x,y)=xh(x,y)$ and $G(x,y)=yg(x,y)$ where

  $$\begin{aligned} \begin{aligned} h(x,y)&=r\left( \frac{1}{1+\varphi y}-\frac{x}{k}\right) -\frac{\mu y}{\alpha x+\beta y+\gamma }, \\ g(x,y)&=\frac{\eta \mu x}{\alpha x+\beta y+\gamma }-\delta . \end{aligned} \end{aligned}$$

  (11)

  Then we can write the Jacobian matrix (10) as

  $$\begin{aligned} J_{E_{S_{1}}^{*}}=\left( \begin{array}{cc} H_{x} &{} H_{y} \\ G_{x} &{} G_{y} \end{array} \right) =\left( \begin{array}{cc} xh_{x} &{} xh_{y} \\ yg_{x} &{} yg_{y} \end{array} \right) . \end{aligned}$$

  (12)

  If $\frac{dy^{(h)}}{dx}$ and $\frac{dy^{(g)}}{dx}$ refer to the gradients of the tangents of the two nullclines (11) at the interior equilibrium $E_{S_{1}}^{*}$, then using implicit function theorem we get

  $$\begin{aligned} \det (J_{E_{S_{1}}^{*}})=\left[ xyh_{y}g_{y}\left( \frac{dy^{(g)}}{dx}- \frac{dy^{(h)}}{dx}\right) \right] . \end{aligned}$$

  At the interior, the Jacobian matrix can assume one of two possibilities for its sign:

  $$\begin{aligned} \text {sign}(J_{E_{S_{1}}^{*}})=\left\{ \begin{array}{c} \left( \begin{array}{cc} - &{} - \\ + &{} - \end{array} \right) ,\quad x_{h_{\max }}<x_{S_{1}}^{*}, \\ \left( \begin{array}{cc} + &{} - \\ + &{} - \end{array} \right) ,\quad x_{h_{\max }}>x_{S_{1}}^{*}, \end{array} \right. \end{aligned}$$

  where $x_{h_{\max }}$ is the maximum of the curve h(x, y). In the first case, we have $\det (J_{E_{S_{1}}^{*}})>0$ and $trac(J_{E_{S_{1}}^{*}})<0,$ then the interior equilibrium $E_{S_{1}}^{*}$ is locally asymptotically stable. In the second scenario, the slope of the tangent to the first nullcline is steeper than that of the tangent to the second nullcline, i.e. $\frac{dy^{(h)}}{dx}<\frac{dy^{(g)}}{dx}$. That means $\det (J_{E_{S_{1}}^{*}})>0.$ Therefore, $E_{S_{1}}^{*}$ is locally stable (unstable) if $trac(J_{E_{S_{1}}^{*}})<0(trac(J_{E_{S_{1}}^{*}})>0)$.

$\square$

Here, we present numerical examples to demonstrate our previously discussed results. The parameters are set to $k=7,r=1,\varphi =2.3,\mu =2,\beta =2,\gamma =3,\eta =0.7$, and $\delta =0.05$, while $\alpha$ is varied. It is important to mention that the majority of the parameter values used in our study were derived from previous works such as [9, 18, 31]. While the remaining system parameters are assumed. In the first scenario, with $\alpha =18$, the subsystem $S_{{1}}$ has one interior equilibrium $E_{S_{1}}^{*}$, along with the trivial and axial equilibria. According to Theorem 1, it is unstable because $x_{S_{1}}^{*}<x_{h_{\max }}$ and the $trac(J_{E_{S_{1}}^{*}})>0$ as shown in Fig. 1a. In the second scenario, with $\alpha =25$, the subsystem $S_{1}$ has three equilibria and $x_{S_{1}}^{*}>x_{h_{\max }}$, making it stable as seen in Fig. 1b. Finally, with $\alpha =27.6$, the subsystem $S_{1}$ only has the trivial (unstable) and axial (stable) equilibria, as seen in Fig. 1c.

Fig. 1

Phase portraits of the subsystem $S_{1}$ (4) with different values of $\alpha$: a $\alpha = 18$, b $\alpha = 25$, c $\alpha = 27.6$. Blue curves refer to prey nullcline and pink lines refer to predator nullcline. Black dot denotes $E_{S_{1}}^{0}$, green dot denotes $E_{S_{1}}^{1}$, yellow dot denotes $E_{S_{1}}^{*}$ and the other parameters are $k=7,r=1, \varphi =2.3,\mu =2,\beta =2,\gamma =3,\eta =0.7$, and $\delta =0.05$

The bifurcation diagram for subsystem $S_{1}$ can be seen in Fig. 2 using the XPPAUT software [49]. This diagram provides an understanding of changes in stability of fixed points as the parameter $\alpha$ varies, offering valuable insight into the behavior of systems undergoing these transitions. In the diagram, unstable equilibria are represented by black lines and stable equilibria by red lines, while stable limit cycles are shown as green filled circles. As $\alpha$ increases, three equilibria appear in the model (4): $E_{S_{1}}^{0}$ (unstable), $E_{S_{1}}^{1}$ (unstable) and $E_{S_{1}}^{*}$ (stable). With further increase in $\alpha$, the interior equilibrium $E_{S_{1}}^{*}$ becomes unstable, when $\alpha$ passes through the Hopf bifurcation point HB1 and a stable periodic solution emerges. However, this $E_{S_{1}}^{*}$ turns into be stable again as $\alpha$ crosses the Hopf bifurcation point HB2. With the continuation of increasing $\alpha ,$ the interior equilibrium $E_{S_{1}}^{*}$ vanishes and the axial equilibrium $E_{S_{1}}^{1}$ becomes stable through a transcritical bifurcation (TB) at $k_{TB}=\frac{ \gamma \delta }{\eta \mu -\alpha \delta }$.

To better understand the overall behavior of the subsystem $S_{1}$, a bifurcation diagram with two parameters $(\alpha ,\varphi )$ has been generated and presented in Fig. 3 by using the XPPAUT software [49]. The red and black curves in the figure correspond to the Hopf and transcritical bifurcation curves, respectively. The equilibrium point $E_{S_{1}}^{*}$ is stable in the gray region of the diagram and unstable in the blue region, while both the trivial and axial equilibria $E_{S_{1}}^{0}$ and $E_{S_{1}}^{1}$ are unstable. When the value of $\alpha$ passes through $\alpha _{TP}=27.57$, a transcritical bifurcation occurs and the interior equilibrium disappears in the pink area, while the axial equilibrium becomes stable.

Fig. 2

Bifurcation diagram of the subsystem $S_{1}$ with $\alpha$. Black line: unstable equilibria; red line: stable equilibria; green circles: stable limit cycle. HB1 and HB2 are Hopf bifurcation points and TB is transcritical bifurcation point

Fig. 3

Bifurcation diagram of the subsystem $S_{1}$ in the plane $(\alpha , \varphi )$ with fixed parameters $k=7,r=1,\mu =2, \beta =2,\gamma =3,\eta =0.7$, and $\delta =0.05$

2.2 Dynamics of the subsystem $S_{2}$

Similarly, the equilibria of subsystem $S_{2}$ (5) can be expressed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&rx(t)\left( \frac{1}{1+\varphi y(t)}-\frac{x(t)}{k}\right) -\frac{\mu (1-m)x(t)y(t)}{ \alpha (1-m)x(t)+\beta y(t)+\gamma }-\nu x(t)=0, \\&\frac{\eta \mu (1-m)x(t)y(t)}{\alpha (1-m)x(t)+\beta y(t)+\gamma }-\delta y(t)=0, \end{aligned} \right. \end{aligned}$$

then the subsystem $S_{2}$ (5) has the following equilibria

• (a) The trivial equilibrium $E_{S_{2}}^{0}(0,0).$

• (b) The axil equilibrium $E_{S_{2}}^{1}(\frac{k(r-\nu )}{r},0)$ with $r>\nu$ and always virtual.

• (c) As we did for the subsystem $S_{1}$ (4), the interior equilibrium for the subsystem $S_{2}$ (5) can be determined as $E_{S_{2}}^{*}(x_{S_{2}}^{*},y_{S_{2}}^{*})$ where

  $$\begin{aligned}{} & {} y_{S_{2}}^{*}=\frac{(1-m)}{\beta \delta }(\eta \mu -\alpha \delta )x_{S_{2}}^{*}-\frac{\gamma }{\beta },\end{aligned}$$

  (13)
  $$\begin{aligned}{} & {} Q_{0}(y_{S_{2}}^{*})^{2}+Q_{1}y_{S_{2}}^{*}+Q_{2}=0,\nonumber \\{} & {} y_{S_{2}}^{*}=\frac{-Q_{1}+\sqrt{Q_{1}^{2}-4Q_{0}Q_{2}}}{2Q_{0}} \end{aligned}$$

  (14)

  where $Q_{0}=(r\beta x_{S_{2}}^{*}+k(1-m)\mu +k\beta \nu )\varphi ,\;Q_{1}=\varphi (rx_{S_{2}}^{*}+k\nu )(\alpha (1-m)x_{S_{2}}^{*}+\gamma )-r\beta (k-x_{S_{2}}^{*})+k((1-m)\mu +\beta \nu ),Q_{2}=(k\nu -r(k-x_{S_{2}}^{*}))(\alpha x_{S_{2}}^{*}+\gamma ).$ Thus a unique interior point exists in the first quadrant if $k\left( 1-\frac{\nu }{r} \right) (1-m)(\eta \mu -\alpha \delta )\ge \gamma \delta$ and it is regular if $\zeta (\eta \mu -\alpha \delta )(1-m)<\beta \delta$ and $x_{S_{2}}^{*}<\frac{\gamma \zeta \delta }{\zeta (1-m)(\eta \mu -\alpha \delta )-\beta \delta }.$

Analogously to Theorem 1, there is another result that follows, whose proof will be omitted.

Theorem 2

• 1. The trivial equilibrium $E_{S_{2}}^{0}$ is a saddle node if $r>\nu$.

• 2. The axil equilibrium $E_{S_{2}}^{2}$ is stable node if $k(1-m)(r-\nu )(\eta \mu -\alpha \delta )<r\gamma \delta$. Moreover, it is saddle node if $k(1-m)(r-\nu )(\eta \mu -\alpha \delta )>r\gamma \delta .$

• 3. The interior equilibrium $E_{S_{2}}^{*}$ is locally stable (unstable) if $trac(J_{E_{S_{2}}^{*}})<0(trac(J_{E_{S_{2}}^{*}})>0)$.

A bifurcation diagram for subsystem $S_2$ (5), generated using XPPAUT, is presented in Fig. 4. This diagram showcases variations in two parameters, namely $(\alpha , \varphi )$. A noteworthy observation, when comparing Figs. 4 to 3, is the expansion of the stability region surrounding the interior equilibrium. Additionally, the figure highlights the occurrence of a transcritical bifurcation at the critical value of $\alpha _{TP}=27.44$.

Fig. 4

Bifurcation diagram of the subsystem $S_{2}$ in the plane $(\alpha , \varphi )$ with fixed parameters $k=7,r=1,\mu =2, \beta =2,\gamma =3,\eta =0.7, \delta =0.05, m=0.2$ and $\nu =0.05$

3 Sliding regions and sliding mode dynamics on the discontinuity surface $\Sigma$

Although the right-hand side of (3) is undefined on the switching plane $\Sigma$, a unique solution can still be obtained using Filippov’s convex method [47, 48]. To investigate the dynamics of system (3) on the switching plane $\Sigma$, it is crucial to analyze the existence of sliding regions and the sliding mode dynamics inherent in the Filippov model (3).

Assume that

$$\begin{aligned} \sigma (X)=\langle \nabla B(X),F_{S_{1}}(X)\rangle \langle \nabla B(X),F_{S_{2}}(X)\rangle , \end{aligned}$$

(15)

where $\langle \cdot ,\cdot \rangle$ represents the scalar product. The sliding segments $\Sigma ^{S}$ and crossing segments $\Sigma ^{C}$ on the discontinuity surface $\Sigma$ are exist if $\sigma (X)\le 0,\sigma (X)>0,$ respectively. The sliding mode domain $\Sigma ^{S}$ can be characterized as the union of the following two regions:

• Attracting region if $\Sigma _{A}^{S}=\{X\in \Sigma ^{S}\;|\langle \nabla B(X),F_{S_{1}}(X)\rangle <0$ and $\langle \nabla B(X),F_{S_{2}}(X)\rangle >0\}.$

• Repulsive region if $\Sigma _{R}^{S}=\{X\in \Sigma ^{S}\;|\langle \nabla B(X),F_{S_{1}}(X)\rangle >0$ and $\langle \nabla B(X),F_{S_{2}}(X)\rangle <0\}.$

To identify the sliding regions, we assume

$$\begin{aligned} \sigma (X)=\sigma _{1}(X)\sigma _{2}(X)=(G(y)-G_{S_{1}}(y))(G(y)-G_{S_{2}}(y)), \end{aligned}$$

(16)

where

$$\begin{aligned} \sigma _{1}(X)= & {} G(y)-G_{S_{1}}(y), \\ \sigma _{2}(X)= & {} G(y)-G_{S_{2}}(y), \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} G(y)&=r\zeta y\left( \frac{1}{1+\varphi y}-\frac{\zeta y}{k}\right) , \\ G_{S_{1}}(y)&=\frac{\mu \zeta y^{2}}{\alpha \zeta y+\beta y+\gamma }(1+\eta \zeta )-\zeta \delta y, \\ G_{S_{2}}(y)&=\frac{\mu (1-m)\zeta y^{2}}{\alpha (1-m)\zeta y+\beta y+\gamma }(1+\zeta \eta )+\nu \zeta -\zeta \delta y). \end{aligned} \end{aligned}$$

(17)

Since there are two types of sliding mode domain $\Sigma ^{S}$ which are defined as $\Sigma _{A}^{S},\Sigma _{R}^{S},$ then the Filippov system (3) has attracting region if $\sigma _{1}(X)<0,\sigma _{2}(X)>0$ i.e. $G_{S_{2}}(y)<G(y)<G_{S_{1}}(y),$ and it has repulsive region if $\sigma _{1}(X)>0,\sigma _{2}(X)<0$ i.e. $G_{S_{1}}(y)<G(y)<G_{S_{2}}(y).$The endpoints of attracting and repulsive sliding segments are called tangent points of subsystem $S_{1}$ and $S_{2}$ and they are given as the following:

• The tangent point of subsystems $S_{1}$ is given as $E_{S_{1}}^{T}=\{X\in \Sigma ^{S}\;|\sigma _{1}(X)=0\},$

• The tangent point of subsystems $S_{2}$ is given as $E_{S_{2}}^{T}=\{X\in \Sigma ^{S}\;|\sigma _{2}(X)=0\}.$

As we are unable to solve the two algebra inequalities analytically, we can get the solution numerically. The refuge parameter m is chosen as the bifurcation parameter, while other parameters are fixed $r=1,\varphi =2.3,k=3.6,\mu =2,\alpha =3.0937,\beta =2,\gamma =3,\eta =0.385,\nu =0.17,\delta =0.05,\zeta =0.5$. As a result, we have three cases as follows:

Case 1: when $m=0.2$, then the Filippov system has one attracting sliding region given as:

$$\begin{aligned} \Sigma ^S_A=\{y\in \Sigma ^S \;| E^T_{S_1}<y<E^T_{S_2} \}, \end{aligned}$$

and two crossing region sets given as the following:

$$\begin{aligned} \begin{aligned} \Sigma ^C_1&=\{y\in \Sigma ^C \;| 0<y<E^T_{S_1} \}, \\ \Sigma ^C_2&=\{y\in \Sigma ^C \;| E^T_{S_2}<y<\infty \}, \end{aligned} \end{aligned}$$

as shown in Fig. 5a.

Case 2: when $m=0.5958$, then the Filippov system does not have attracting regions and has two crossing regions, which are defined as:

$$\begin{aligned} \Sigma _{3}^{C}= & {} \{y\in \Sigma ^{C}\;|0<y<E_{S_{1}}^{T}\}, \\ \Sigma _{4}^{C}= & {} \{y\in \Sigma ^{C}\;|E_{S_{1}}^{T}<y<\infty \}, \end{aligned}$$

as shown in Fig. 5b.

Case 3: if $m=0.9$, then the Filippov system has one repulsive region given as:

$$\begin{aligned} \Sigma _{R}^{S}=\{y\in \Sigma ^{S}\;|E_{S_{2}}^{T}<y<E_{S_{1}}^{T}\}, \end{aligned}$$

and two crossing region sets given as the following:

$$\begin{aligned} \begin{aligned} \Sigma _{5}^{C}&=\{y\in \Sigma ^{C}\;|0<y<E_{S_{2}}^{T}\}, \\ \Sigma _{6}^{C}&=\{y\in \Sigma ^{C}\;|E_{S_{1}}^{T}<y<\infty \}, \end{aligned} \end{aligned}$$

as shown in Fig. 5c.

Fig. 5

Visualizing the presence of sliding and crossing regions for the Filippov system (3)

Filippov’s convex method [47, 50] suggests extending the system’s vector field by defining the sliding vector field $F_{S}(X)$ on $\Sigma ^{S}$. This can be achieved by combining the two vector fields through the following:

$$\begin{aligned} F_{\Sigma ^{S}}(X)=(1-\alpha _{S}(X))F_{S_{1}}(X) + \alpha _{S}(X)F_{S_{2}}(X), \end{aligned}$$

(18)

where

$$\begin{aligned} \alpha _{S}(X)=\frac{\langle \nabla B(X),F_{S_{1}}(X)\rangle }{\langle \nabla B(X),F_{S_{1}}(X)-F_{S_{2}}(X)\rangle }. \end{aligned}$$

Therefore,

$$\begin{aligned} \alpha _{S}(X)=\frac{A}{B}, \end{aligned}$$

where,

$$\begin{aligned} \begin{aligned} A&= rx\left( \frac{1}{1+\varphi y}-\frac{x}{k}\right) -\frac{\mu xy}{\alpha x+\beta y+\gamma }(1+\eta \zeta )+\zeta \delta y, \\ B&= \frac{m\mu xy((1-\alpha )x-\beta y-\gamma )}{\alpha (1-m)x+\beta y+\gamma }(1+\eta \zeta )+\nu x. \end{aligned} \end{aligned}$$

Hence, the sliding mode differential equation can be written as:

$$\begin{aligned} \left( \begin{array}{c} \frac{dx}{dt} \\ \frac{dy}{dt} \end{array} \right) =\left( \begin{array}{c} \frac{-\zeta Cy}{k(y\phi +1)\left( \alpha ^{2}m\nu x^{2}+m(\gamma +\beta y)(\alpha \nu x+y(\eta \mu \psi +\mu ))-\nu (\gamma +\alpha x+\beta y)^{2}\right) } \\ \frac{-Cy}{k(y\phi +1)\left( \alpha ^{2}m\nu x^{2}+m(\gamma +\beta y)(\alpha \nu x+y(\eta \mu \psi +\mu ))-\nu (\gamma +\alpha x+\beta y)^{2}\right) } \end{array} \right) =F_{\Sigma ^{S}}(X), \nonumber \\ \end{aligned}$$

(19)

where, $x=\zeta y,y\in \Sigma ^{S}$, and

$$\begin{aligned} C= & {} \eta \mu mrx^{2}(y\phi +1)(\gamma +\beta y)-k\nu (y\phi +1)(\gamma +\alpha x+\beta y)(\delta (\gamma +\alpha x+\beta y)-\eta \mu x) \\{} & {} +km\left( x(\alpha \nu (\gamma \delta +\alpha \delta x-\eta \mu x)-\gamma \eta \mu r)+\delta y^{2}(\gamma \mu \phi +\beta (\mu +\alpha \nu x\phi ))\right) \\{} & {} +km\left( y(\gamma \delta \mu -\beta \eta \mu rx+\alpha \beta \delta \nu x+\alpha \nu x\phi (\gamma \delta +\alpha \delta x-\eta \mu x))+\beta \delta \mu y^{3}\phi \right) . \end{aligned}$$

As known, Filippov systems have various types of equilibria, including regular (or virtual) equilibria, tangent points, boundary equilibria, and pseudo equilibria [48]. Until now, we have discussed the first two types and we will investigate the existence of the others. An equilibrium point $E^{P}(\zeta y^{P},y^{P})$ that satisfies $F_{\Sigma ^{S}}(X)=0$ and lies on the sliding mode $\Sigma ^{S}$ is called a pseudo equilibrium of the Filippov system (3) [48]. The point $E \in \Sigma ^{S}$ is a called singular sliding point if $\langle \nabla B(E),F_{S_{1}}(E)-F_{S_{2}}(E)\rangle =0$ [48].

Define

$$\begin{aligned} g(y)=(A_{1}y^{4}+A_{2}y^{3}+A_{3}y^{2}+A_{4}y+A_{5})y=0, \end{aligned}$$

(20)

where

$$\begin{aligned} \begin{aligned} A_{1}&= \beta \zeta ^{2}\eta m\mu r\varphi , \\ A_{2}&= \beta \zeta ^{2}\eta m\mu r-\beta ^{2}\nu \delta k\varphi +\beta k(\alpha \nu \delta \zeta (m-2)(\nu \zeta \eta +\delta m)\mu )\varphi \\&\quad +\zeta ^{2}(\alpha \nu k(m-1)(\alpha \delta -\eta \mu )+\eta \gamma m\mu r)\varphi , \\ A_{3}&= -\beta ^{2}\nu \delta k+\zeta ^{2}(\alpha \nu k(m-1)(\alpha \delta -\eta \mu )+\eta \gamma m\mu r)+\gamma k(\alpha \nu \delta \zeta (m-2) \\&\quad +\beta k(\alpha \nu \delta \zeta (m-2)+\nu \zeta \eta \mu +(\nu \zeta \eta +\delta m)\mu )\varphi +\delta m\mu -\zeta \eta m\mu r-2\nu \delta \gamma \varphi ), \\ A_{4}&= \gamma k(-2\beta \nu \delta +\alpha \nu \delta \zeta (m-2)+\nu \zeta \eta \mu +\delta m\mu -\zeta \eta m\mu r-\nu \delta \gamma \varphi ), \\ A_{5}&= -\nu \delta \gamma ^{2}k. \end{aligned} \end{aligned}$$

We seek to find all roots of $g(y)=0.$ Obviously, $y=0$ is one of the roots of $g(y)=0$. To get the other roots of (20), we assume that $\epsilon _{1}=\frac{A_{2}}{A_{1}},\epsilon _{2}=\frac{A_{3}}{A_{1}},\epsilon _{3}=\frac{A_{4}}{A_{1}},$ and $\epsilon _{4}=\frac{A_{5}}{A_{1}},$ thus Eq. (20) can be written as

$$\begin{aligned} g_{1}(y)=y^{4}+\epsilon _{1}y^{3}+\epsilon _{2}y^{2}+\epsilon _{3}y+\epsilon _{4}=0. \end{aligned}$$

(21)

Based on the findings in [51], the following lemma holds.

Lemma 1

For equation (21), we have the followings:

• 1. If $\epsilon _{4}<0$, equation (21) has at least one positive root

• 2. If $\epsilon _4\ge 0$, equation (21) has no positive root if one of the following conditions holds:

  • (a) $\Delta >0$ and $y_{1}^{*}\le 0$;

  • (b) $\Delta =0$ and $y_{2}^{*}\le 0$;

  • (c) $\Delta <0$ and $y_{3}^{*}\le 0$,

  where $\Delta =(\frac{8\epsilon _{2}-3\epsilon _{1}^{2}}{48})^{3}+(\frac{ 4\epsilon _{1}\epsilon _{2}-8\epsilon _{3}-\epsilon _{1}^{3}}{64})^{2}$, and $y_{i}^{*}=\max {(y_{1}^{*},y_{2}^{*},y_{3}^{*})},i=1,2,3$ and $y_{i}^{*}$ are the real roots of $g^{\prime }(y)=4y^{3}+3\epsilon _{1}y^{2}+2\epsilon _{2}y+\epsilon _{3}.$

• 3. If $\epsilon _{4}\ge 0$, equation (21) has one positive root if one of the following conditions holds:

  • (a) $\Delta >0$, $y_{1}^{*}>0$ and $g(y_{1}^{*})<0$;

  • (b) $\Delta =0$, $y_{2}^{*}>0$ and $g(y_{2}^{*})<0$;

  • (c) $\Delta <0$, $y_{3}^{*}>0$ and $g(y_{3}^{*})<0$.

According to the above lemma then the sliding vector filed $F_{\Sigma ^{S}}(X)$ has at least one positive equilibrium and it is pseudo equilibrium if $y^{P}\in \Sigma ^{S}.$

By using the Routh-Hurwitz stability criterion, the pseudo equilibrium $E^{P}$ is stable if $\epsilon _{1}>0,\epsilon _{2}>0,\epsilon _{3}>0,$ and $3\epsilon _{1}\epsilon _{2}>2\epsilon _{3}$.

On the other hand, the equilibrium $E^{B}$ of (19) is called a boundary equilibrium if $F_{S_{i}}(E^{B})=0,i=1,2$ [48]. Clearly, the trivial equilibrium (0, 0) is a boundary equilibrium and always exists.

Fig. 6

Bifurcation diagram of Filippov system’s (3) equilibria with respect to $\zeta$. The other parameters are $r=1,k=7, \varphi =3,\mu =2,\alpha =1,\beta =2,\gamma =3,\eta =0.7,\nu =0.05,\delta =0.05,m=0.7$

To highlight the significance of the critical threshold $\zeta$ in the Filippov system (3) and its equilibria, a bifurcation diagram is presented in Fig. 6. The diagram shows the existence of pseudo-equilibria, boundary equilibria, and tangent points with respect to the threshold $\zeta$. The green and blue curves represent the tangent points of subsystems $S_{1}$ and $S_{2}$, respectively, while the brown lines refer to the interior equilibria of the two subsystems $S_{1}$ and $S_{2}$. The black curve represents the roots of Eq. (21) (i.e. $g_{1}(y)=0$). The diagram reveals that the sliding segment $\Sigma ^{S}$ decreases as the threshold $\zeta$ increases and is bounded by the two tangent curves $E_{S_{1}}^{T}$ and $E_{S_{2}}^{T}$. Additionally, the boundary equilibrium $E_{S_{2}}^{B}$ appears when the interior equilibrium $E_{S_{2}}^{*}$ intersects with the curve $g_{1}(y)=0$ at $\zeta =0.23$, leading to the appearance of the pseudo-equilibrium $y^{P}$ in the sliding mode. As the threshold $\zeta$ increases further, the boundary equilibrium $E_{S_{1}}^{B}$ manifests at $\zeta =0.62$, when the interior equilibrium $E_{S_{1}}^{*}$ intersects with the curve $g_{1}(y)=0,$ and the pseudo-equilibrium $y^{P}$ disappears.

Fig. 7

Sliding mode bifurcation of the Filippov system (3) in the plane $(\zeta ,\alpha )$

For further investigations about the existence of these equilibria of the Filippov system (3), we employ the bifurcation diagram of them in the $(\zeta ,\alpha )$ plane in Fig. 7. In this figure, we see that the interior equilibria being regular or virtual are determined by their position relative to the boundary curves $E_{S_{i}}^{B}$, $(i=1,2).$ We observe that the equilibrium $E_{S_{1}}^{*}$ is regular above the boundary curve $E_{S_{1}}^{B}$ and virtual below it. On the other hand, the equilibrium $E_{S_{2}}^{*}$ is regular below the boundary curve $E_{S_{2}}^{B}$ and virtual above it and it does not exist for $\alpha >26.497$. However, when both equilibria are virtual, the pseudo equilibrium appears between the two boundary curves $E_{S_{i}}^{B}$, $(i=1,2).$

4 Numerical simulation

In this section, we present a numerical simulation to study the different types of bifurcation that can exhibit for the Filippov system (3). To perform the numerical simulations, we carefully selected values for the attributes in the suggested systems. Many of the system parameters were obtained from reputable sources, specifically referenced in our study as [9, 18, 31]. These sources provided established values that are widely accepted in the field. Due to the importance of parameters $\varphi , m$ and $\zeta$ which represent the rate of fear, the constant rate of refuge, and the density rate of the prey and predator, we will choose them as the bifurcation parameters, and fixed all the other parameters.

4.1 Local sliding bifurcation of Filippov system (3)

The local sliding bifurcation is a result of the collision of many equilibria at the discontinuity surface when one parameter hits a critical value [48]. The Filippov system (3) has three types of local bifurcations which are given as the following.

4.1.1 Boundary node and boundary focus bifurcations

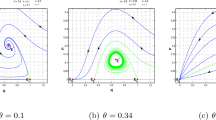
The Filippov system (3) undergoes boundary node bifurcation when $\varphi$ is chosen as the bifurcation parameter while fixing all other parameters as $r=1,k=10,\mu =2,\alpha =5,\beta =2,\gamma =3,\eta =0.7,\nu =0.05,\delta =0.05,m=0.51,\zeta =0.3$. The closed circle means that the equilibrium is regular while the open circle means that the equilibrium is virtual. When $\varphi =0.6,$ the Filippov system has regular stable node $E^{*}_{S_2}$ and the tangent point $E^T_{S_2}$ is visible as shown in Fig. 8a. If $\varphi =0.842747,$ then the equilibrium $E^{*}_{S_2}$, $E^T_{S_2}$ and the pseudo equilibrium $E^P$ collect together at the boundary as seen in Fig. 8b. While when $\varphi =1.6,$ the $E^{*}_{S_2}$ convert to virtual and $E^P$ is a visible and stable node as shown in Fig. 8c. Furthermore if we continue increasing $\varphi$ the boundary focus bifurcation occurs as shown in Figs. 8d–f. When $\varphi =4$, we observe that $E^P$ becomes a visible and stable node. While when $\varphi =4.73537,$ then the $E^P$ and a visible tangent point $E^T_{S_1}$ collect together at the boundary and the equilibrium $E^{*}_{S_1}$ is invisible. If $\varphi =6,$ then the Filippov system has regular stable focus $E^{*}_{S_1}$ and the tangent point $E^T_{S_1}$ is visible.

Fig. 8

Boundary bifurcation for the Filippov system (3) with $r=1,k=10,\mu =2,\alpha =5,\beta =2,\gamma =3,\eta =0.7,\nu =0.05,m=0.51, \delta =0.05,\zeta =0.3$

4.1.2 Collisions of two invisible tangencies bifurcation

The collisions of two invisible tangencies bifurcation is one of the double tangency bifurcations and it occurs when the quadratic tangent points $E^T_{S_1}$ and $E^T_{S_2}$ delimit a single sliding segment [48]. This segment converts from an attractive sliding segment to a repulsive sliding segment when the bifurcation parameter changes. Moreover, the attractive sliding segment contains a pseudo-node $E^P$, and a repulsive sliding segment contains an unstable pseudo. The Filippov system (3) has two invisible tangencies bifurcation if we choose m as the bifurcation parameter and fixed all other parameters as $r=1,k=5.6,\varphi =3,\mu =2,\alpha =3.0937,\beta =2,\gamma =3,\eta =0.358,\nu =0.05,\delta =0.17,\zeta =0.8,$ as shown in Fig. 9. When $m=0.4,$ the Filippov system (3) has a repulsive sliding segment with unstable pseudo equilibrium $E^P$. While if $m=0.66728,$ the tangent points $E^T_{S_1}, E^T_{S_2}$ and $E^P$ collect together and become a singular point [48], as seen in Fig. 9b. If $m=0.8,$ then the Filippov system (3) has attractive sliding segment with stable node pseudo equilibrium $E^P.$

Fig. 9

Collisions of two invisible tangencies bifurcation for the Filippov system (3) with $r=1,k=5.6, \varphi =3,\mu =2,\alpha =3.0937,\beta =2,\gamma =3, \eta =0.358,\nu =0.05,\delta =0.17,\zeta =0.8$

4.2 Global sliding bifurcation

In this section, we investigate the global sliding bifurcations which result from periodic solutions of the Filippov system (3) with the discontinuity surface including sliding and crossing regions. The bifurcation diagram 3 and 4 of subsystems $S_1$ and $S_2$, respectively, shows that the Filippov model (3) has standard periodic solutions. Due to existing of discontinuity surface in the Filippov systems, our model (3) may have other kinds of periodic solutions which lie in $S_1$ or (and) $S_2$ including the pieces of sliding or crossing segments.

4.2.1 Touching bifurcations

The touching sliding bifurcation takes place when a limit cycle comes into contact with the boundary of the sliding segment at a critical value of the bifurcation parameter [48]. The Filippov system (3) has touching bifurcation as shown in Fig. 10 where we choose m as the bifurcation parameter and the other parameters are fixed. At the critical value of the bifurcation parameter, $m^*=0.7051$, the Filippov system exhibits a limit cycle that touches a tangent point, as seen in Fig. 10b. While if $m>m^*,$ then the limit cycle lies entirely in regions $S_1$, and the limit cycle has piece of the sliding segment when $m<m^*$.

Fig. 10

Touching bifurcation for the Filippov system (3) with $r=1,k=10, \varphi =2,\mu =2,\alpha =1,\beta =0.001,\gamma =1,\eta =0.7,\nu =0.05,\delta =0.05,\zeta =1$

4.2.2 Buckling bifurcations

Figure 11 illustrates that the Filippov system (3) has buckling bifurcations when we choose $\zeta$ as the bifurcation and fixed all other parameters as $r=1,k=10, \varphi =2,\mu =2,\alpha =1,\beta =0.001,\gamma =1,\eta =0.7,\delta =0.05, m=0.3, \nu =0.05.$ At the critical value $\zeta =0.35$, the Filippov system has a limit cycle with a full piece of the sliding segment, as depicted in Fig. 11b. While for $\zeta =0.28,$ the limit cycle has a piece of the sliding segment, as shown in Fig. 11a. While the Filippov system (3) has a sliding crossing limit cycle when $\zeta =0.5$, as seen in Fig. 11c.

Fig. 11

Buckling bifurcation for the Filippov system (3)

4.2.3 Sliding crossing bifurcation

In Filippov systems, a sliding crossing bifurcation takes place when a stable crossing limit cycle becomes tangent to the sliding segment at a single point [48]. The behavior of the stable limit cycle depends on the value of the bifurcation parameter relative to its critical value. When the parameter equals its critical value at the bifurcation point, the stable limit cycle just touches the sliding segment tangentially. The stable limit cycle includes a portion of the sliding segment for parameter values below the critical value.

Therefore, if $\zeta$ is used as the bifurcation parameter and $\zeta$ has a critical value of $\zeta ^*=0.3272$, the Filippov system (3) has sliding crossing bifurcation as seen in Fig. 12. If $\zeta >\zeta ^*,$ then therefore the Filippov system (3) has a stable crossing limit cycle as seen in Fig. 12c. When $\zeta =\zeta ^*,$ the stable crossing limit cycle passes through a tangent point, as illustrated in Fig. 12b. If $\zeta <\zeta ^*,$ the stable crossing limit cycle has a piece of the sliding segment, as shown in Fig. 12a.

Fig. 12

Sliding crossing bifurcation for the Filippov system (3) with $r=1,k=10, \varphi =2,\mu =2, \alpha =1,\beta =0.001,\gamma =1,\eta =0.7, \nu =0.05,\delta =0.05,m=0.2$

4.3 Impact of fear factor on the Filippov model (3)

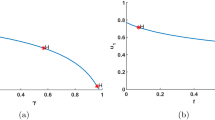
In this subsection, we present a bifurcation diagram exploring the dynamical changes in the Filippov model (3). The fear factor $\varphi$ is the parameter of interest, while other parameters are held constant at $r=1,k=10,\mu =2,\alpha =4,\beta =2,\gamma =3,\eta =0.7,\nu =0.05,\delta =0.05,\zeta =0.33$ and $m=0.5$ (Fig. 13). The bifurcation diagram depicts unstable equilibria as black lines and stable equilibria as red lines. Figure 13a illustrates that for small values of $\varphi$, the Filippov model (3) approaches the stable equilibrium $E^{*}_{S_{2}}$, indicating that the prey find refuge. This behavior occurs because the number of prey caught per predator is small, and the fear level is low. However, as the fear factor increases, the number of prey caught per predator also increases. With the further increase of $\varphi$, the Filippov model (3) reaches the sliding segment $\Sigma ^{S}$, where the number of caught prey per predator becomes fixed, with a ratio of $\frac{x}{y}=\zeta .$ Continuing to increase $\varphi$, the Filippov model (3) approaches the unstable equilibrium $E^{*}_{S_{1}}$, indicating that the prey come out of their refuge to seek food, leading to an increase in the number of prey caught per predator. Finally, as $\varphi$ further increases, the model approaches the stable equilibrium $E^{*}_{S_{1}}$, signifying a state where the prey and predators coexist in a stable manner under the influence of fear. Upon examining the Fig. 13b, c, it becomes evident that a rise in the fear factor leads to a decline in the density of both species x and y. This decrease in prey density can be attributed to the increase in fear levels, consequently causing a reduction in the predator’s density as well. Nevertheless, it is essential to note that despite this decline in densities, the interaction between the two species does not result in their complete annihilation.

Fig. 13

Bifurcation diagram of system (3) with the fear factor $\varphi$. a The variation of x/y with $\varphi$; b the variation of x with $\varphi$; c the variation of y with $\varphi$

Fig. 14

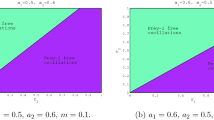
a Depiction of the existence and stability regions for various equilibrium points of the Filippov model (3) within the $(\zeta ,\varphi )$ plane, featuring a prey refuge value of $m=0.5$. In region $R_1$: $E_{S_{1}}^{*}$ exhibits regularity and stability, while $E_{S_{2}}^{*}$ is virtual, and $E^P$ is non-existent. Within region $R_2$: $E_{S_{1}}^{*}$ retains regularity but becomes unstable, $E_{S_{2}}^{*}$ is virtual, and $E^P$ remains non-existent. Region $R_3$ showcases both $E_{S_{1}}^{*}$ and $E_{S_{2}}^{*}$ as virtual, with $E^P$ in existence and stable. Finally, in region $R_4$: $E_{S_{2}}^{*}$ stands as regular and stable, $E_{S_{1}}^{*}$ is virtual, and $E^P$ is absent. b–e Depiction of phase portraits for the Filippov model (3), illustrating the bifurcation regions $R_i, i=1,2,3,4$, across diverse combinations of $\zeta$ and $\varphi$ values

To further explore the dynamics of the Filippov model (3), we have examined the presence and stability regions of different equilibrium points within the $\zeta -\varphi$ plane. These regions are depicted in Figs. 14 and 15, showcasing varying values of the prey refuge parameter m, Fig. 14 corresponds to $m=0.1$, and Fig. 15 to $m=0.5$. The threshold parameter $\zeta$ spans from 0 to 2, while the fear factor varies between 0 and 15, with the remaining parameter values outlined in Fig. 13. Different colors are employed to delineate stability regions for distinct equilibrium points, maintaining consistency in color representation across both figures. Moreover, phase portrait diagrams corresponding to each region are thoughtfully included alongside their respective figures for visual clarity.

Fig. 15

a Representation of existence and stability regions for various equilibrium points of the Filippov model (3) in the $(\zeta ,\varphi )$ plane, with a prey refuge value of $m=0.1$. The descriptions for regions $R_{1}$, $R_{2}$, $R_{3}$, and $R_{4}$ are the same as those in Fig. 14. In region $R_{5}$, $E^{P}$ exists but is unstable, and both $E_{S_{1}}^{*}$ and $E_{S_{2}}^{*}$ are virtual. In region $R_{6}$, $E_{S_{2}}^{*}$ is regular but unstable, $E_{S_{1}}^{*}$ is virtual, and $E^{P}$ does not exist. b, c Depiction of phase portraits for the Filippov model (3), illustrating the bifurcation regions $R_{5}$ and $R_{6}$, for various combinations of $\zeta$ and $\varphi$ values

In Fig. 14a, for the case when $m=0.5$, the bifurcation diagram is divided into four colored regions: $R_{1},R_{2},R_{3}$, and $R_{4}$. In region $R_{1}$, the Filippov model (3) possesses a stable equilibrium point $E_{S_{1}}^{*}$, which is a regular point, while the equilibrium point $E_{S_{2}}^{*}$ is a virtual point. The corresponding phase portrait for region $R_{1}$ in Fig. 14b shows the solution trajectories of the Filippov model (3) converge towards the stable equilibrium $E_{S_{1}}^{*}$. Therefore, the Filippov model (3) is stable in region $R_{1}$. Moving on to region $R_{2}$, the Filippov model (3) has an unstable equilibrium point $E_{S_{1}}^{*}$, which is a regular point, while the equilibrium point $E_{S_{2}}^{*}$ is virtual. The phase portrait for region $R_{2}$ reveals that the solution trajectories of the Filippov model (3) has a limit cycle around the coexisting equilibrium point $E_{S_{1}}^{*}$, as shown in Fig. 14c. In region $R_{3}$, both interior equilibria $E_{S_{1}}^{*}$ and $E_{S_{2}}^{*}$ are virtual, and there exists a pseudo equilibrium point $E^{P}$ that is stable. As seen in Fig. 14d, the trajectories starting from initial points converge to the stable pseudo equilibrium $E^{P}$ on the $x-y$ plane. Lastly, in region $R_{4}$, the Filippov model (3) has a stable equilibrium point $E_{S_{2}}^{*}$, which is a regular point, while the equilibrium point $E_{S_{1}}^{*}$ is virtual. Hence, the trajectories starting from various initial points converge to the stable equilibrium $E_{S_{2}}^{*}$, which lies on the $S_{2}$ region, as depicted in Fig. 14e. It is worth noting that the axial equilibrium $E_{S_{1}}^{1}$ exists in all regions, but it is a saddle-node according to Theorem 1. Also, the pseudo equilibrium point $E^{P}$ does not exist in the regions $R_{1},R_{2}$ and $R_{4}.$

Figure 15a in the plane $(\zeta ,\varphi )$ shows the existence and stability regions, as well as the corresponding phase diagram, when the value of the prey refuge m is reduced to 0.1. Comparing Figs. 14a and 15a, we observe that there is no change in the regions $R_{1}$ and $R_{2}$. However, regions $R_{3}$ and $R_{4}$ have decreased. This suggests that reducing the value of the prey refuge m leads to a reduction in the stability region for both $E_{S_{2}}^{*}$ and $E^{P}$. Additionally, two new regions, $R_{5}$ and $R_{6}$, emerge, as seen in Fig. 15a. In region $R_{5}$, the Filippov model (3) has a stable limit cycle oscillation around the unstable pseudo equilibrium $E^{P}$, while the interior equilibria $E_{S_{1}}^{*}$ and $E_{S_{2}}^{*}$ are virtual. The phase portrait for region $R_{5}$ in Fig. 15b shows that starting from various initial points, the the Filippov model (3) has a limit cycle solution that oscillates around $E^{P}$, indicating instability in this region. In region $R_{6}$, the Filippov model (3) also has a stable limit cycle, but this time around the unstable equilibrium $E_{S_{2}}^{*}$. The equilibrium $E_{S_{1}}^{*}$ is virtual, and $E^{P}$ does not exist in this region. Starting from initial points, the solution of the Filippov model (3) demonstrates limit cycle oscillations around the coexisting equilibrium $E_{S_{2}}^{*}$, as depicted in Fig. 15c. The phase portrait figures for regions $R_{1},R_{2},R_{3},$ and $R_{4}$ are omitted since they are the same as in Fig. 14.

4.4 Impact of prey refuge on the Filippov model (3)

We still need to generate a bifurcation diagram to examine how the prey refuge m, in combination with the fear factor $\varphi$, influences the dynamics of prey x(t) and predators y(t) within the Filippov model (3). In Fig. 16, we present the bifurcation diagram in the $(\varphi ,m)$ plane, considering two distinct threshold values, specifically $\zeta =0.5$ (indicating that prey density is half that of the predators) and $\zeta =1$ (indicating equal prey and predator densities). Subsequently, Fig. 16 provides phase portraits that depict each bifurcation region.

Fig. 16

Representation of existence and stability regions for various equilibrium points of the Filippov model (3) in the $(\varphi ,m)$ plane, with different values of $\zeta$. a $\zeta =0.5$, b $\zeta =1.$ The other parameters are $r=1,k=10, \mu =2, \alpha =10, \beta =2,\gamma =3,\eta =0.7, \nu =0.05,\delta =0.05.$ In region $R_1$, $E_{S_{2}}^{*}$ is regular and unstable, while $E_{S_{1}}^{*}$ is virtual, and $E^P$ is non-existent. Within region $R_2$, $E_{S_{2}}^{*}$ retains regularity but becomes stable, $E_{S_{1}}^{*}$ is virtual, and $E^P$ remains non-existent. Region $R_3$ showcases both $E_{S_{1}}^{*}$ and $E_{S_{2}}^{*}$ as virtual, with $E^P$ in existence and stable. In region $R_4$: $E^P$ exists and stable, $E_{S_{1}}^{*}$ is virtual, $E_{S_{2}}^{*}$ is absent. In region $R_5$, $E^P$ exists and unstable and both $E_{S_{1}}^{*}$ and $E_{S_{2}}^{*}$ are virtual. In region $R_6$: $E_{S_{1}}^{*}$ exhibits regularity and stability, while $E_{S_{2}}^{*}$ is virtual, and $E^P$ is non-existent. In region $R_7$, $E_{S_{1}}^{*}$ exhibits regularity and stability, while both $E_{S_{2}}^{*}$ and $E^P$ are non-existent. The phase diagrams illustrating the bifurcation regions $R_1 - R_7$ are depicted in Fig. 17

Fig. 17

Phase portraits illustrating bifurcation regions $R_i, i=1,2,\ldots ,7$ for the Filippov model (3), as depicted in Fig. 16 with different values of the prey refuge m and fear factor $\varphi$

In the first scenario, where $\zeta =0.5$, the transition between the two subsystems (4) and (5) occurs when the predator density y becomes half that of the prey density x. In region $R_{1}$ of Fig. 16a, as the refuge level m increases, the prey density x rises along with a corresponding increase in predator density y. However, this increase in both densities causes the prey to predator ratio to remain less than 0.5. Consequently, the Filippov model (3) oscillates around the unstable equilibrium $E_{S_{2}}^{*}$, as evident when $m=0.1$ and $\varphi =1$ in Fig. 17a. As the prey refuge m continues to increase, the previously unstable equilibrium $E_{S_{2}}^{*}$ becomes stable within region $R_{2}$. Thus, the Filippov model (3) tends toward the stable equilibrium $E_{S_{2}}^{*}$, as shown in Fig. 17b for $m=0.5$ and $\varphi =1$. As the prey refuge m continues to increase, the prey density increases to half that of the predators. Consequently, the Filippov model (3) approaches the threshold and gravitates toward the stable equilibrium $E^{P}$ in region $R_{3}$, as illustrated in Fig. 17c for $m=0.8$ and $\varphi =1$. In this case, solution trajectories converge to the pseudo equilibrium $E^{P}$ on the $x-y$ plane. In region $R_{5}$, characterized by a large fear factor, increasing the refuge m once again results in prey density approaching half that of the predators. However, in this scenario, the Filippov model (3) oscillates around the unstable equilibrium $E^{P}$, as seen in Fig. 17e for $m=0.1$ and $\varphi =10$. Then the Filippov model (3) reaches stability when the prey refuge increases sufficiently to re-enter region $R_{3}$. It is noteworthy that for substantial fear factors $(\varphi >13.82)$, when the double density of prey exceeds that of predators in region $R_{6}$, it remains fixed with respect to the prey refuge m. In this case, the Filippov model (3) oscillates around the unstable equilibrium $E_{S_{1}}^{*}$, as demonstrated in Fig. 17f for $m=0.5$ and $\varphi =14.5$. Moreover, as the prey refuge m closes to 1, in region $R_{4}$, equilibrium $E_{S_{2}}^{*}$ becomes virtual for $\varphi <13.82$ and disappears in region $R_{7}$, as evident in Fig. 17g, d, respectively.

In the second scenario, characterized by $\zeta =1$, the transition between the two subsystems (4) and (5) occurs when the prey density x equals that of the predator density y. Contrasting this with the previous scenario, illustrated in Fig. 16b, we observe the disappearance of regions $R_{5}$, $R_{6}$, and $R_{7}$, accompanied by an expansion of areas $R_{i}$, where $i=1,2,3,4$. In region $R_{1}$, marked by lower refuge levels m, the prey population remains smaller than that of the predators. Within this context, both species can coexist, exhibiting a limit cycle pattern centered around the unstable equilibrium $E_{S_{2}}^{*}$. Moving to region $R_{2}$, achieved by increasing the prey refuge, results in a reduction of interaction between prey and predators. This shift causes the previously unstable equilibrium $E_{S_{2}}^{*}$ to stabilize. Consequently, they coexist in a stable state. As the prey refuge continues to rise into region $R_{3}$, the prey density increases, eventually equaling that of the predators. In this region, both populations can coexist at the pseudo equilibrium $E^{P}$. Notably, as the prey refuge m closes to 1, in region $R_{4}$, equilibrium $E_{S_{2}}^{*}$ becomes virtual, and the Filippov model (3) approaches $E^{P}$.

5 Conclusion

The preservation of our natural environment depends on our ability to comprehend the complexities of ecology. The ecology system gives us a comprehensive understanding of the interactions between living things and their environment, enabling us to appreciate the delicate balance and interdependence of varied ecosystems. Also, sustainability is promoted, and long-term viability is promoted, enabling us to satisfy our needs today without jeopardizing the ability of future generations to do the same. By mathematical models, we can grasp the complex web of interactions among plants, animals, and their habitats, recognizing the vital roles each species plays [10, 11, 25]. This understanding enables us to identify potential threats to ecological stability, such as species extinction, habitat destruction, pollution, and climate change, and develop effective conservation strategies to mitigate these challenges. In earlier studies [27,28,29, 31], the influence of fear and the availability of prey refuges on prey-predator systems was explored, typically assuming that refuges are consistently accessible to prey due to their fear of predators. However, this scenario does not always hold, as prey tend to seek refuge when they perceive themselves or their population as significantly smaller in comparison to the predator population. Thus, in this paper, we introduced a Filippov prey-predator model with fear effect on prey and prey refuge. For the scenario where the ratio of prey to predators is low, the natural instincts of prey organisms compel them to adopt refuge-seeking as a defensive tactic. Conversely, when the ratio of prey to predators is high, these instincts trigger proactive foraging behavior among the prey population. The incorporation of switching of prey refuge, along with the inclusion of predator-induced fear, in the Filippov system has proven to be effective. This system description has resulted in the establishment of stability and coexistence between the prey and predator populations, thereby ensuring ecosystem stability and preventing species extinction.

Using qualitative analysis methods of non-smooth Filippov dynamic systems and numerical techniques, the dynamics of the proposed Filippov prey–predator model with fear effect on prey ans prey refuge have been studied in detail. The existence and stability of several types of equilibria have been discussed, including the equilibria of subsystems $S_1$, $S_2$, and pseudo equilibria of Filippov system (3). In the discussion about sliding and crossing regions and sliding mode dynamics, there is a connection between the presence of pseudo-equilibria and the bifurcation parameter $\zeta$, as depicted in Fig. 6. The results obtained in Sect. 5 indicate that the Filippov system (3) can give rise to three types of local sliding bifurcation as boundary node and boundary focus bifurcations as seen in Fig. 8 and collisions of two invisible tangencies bifurcation as seen in Fig. 9. As well three types of global sliding bifurcation such as touching bifurcations, as seen in Fig. 10, buckling bifurcations, as seen in Fig. 11 and sliding crossing bifurcation as shown in Fig. 12.

We conducted numerical simulations to explore the potential impact of factors such as fear, prey refuge, and threshold ratio on the Filippov model (3). Our investigation revealed that an increase in the fear factor resulted in a decrease in both prey and predator densities, causing a transition from a limit cycle oscillation to a steady state (as illustrated in Fig. 13). To further investigate this phenomenon, we constructed a bifurcation diagram in the $\zeta -\varphi$ plane, considering different values of the prey refuge parameter m as depicted in Figs. 14 and 15. The diagram displayed four distinct regions $R_1, R_2, R_3$ and $R_4$, illustrating the influence of the fear factor on the equilibria of the Filippov model (3) and their respective stability. Notably, when we reduced the prey refuge parameter m to 0.1 in Fig. 15a, we observed changes in the stability regions. Specifically, regions $R_3$ and $R_4$ decreased in size, while two new regions $R_5$ and $R_6$ emerged. These findings suggest that the prey refuge parameter also plays a role in determining the stability of equilibrium points within the Filippov model.

Moreover, we explored the interplay between prey refuge m and the fear factor $\varphi$ within the Filippov model (3), considering two different threshold values $\zeta$. Our findings, as depicted in Figs. 16 and 17, revealed that changes in prey refuge significantly influenced the dynamics of the Filippov model. Specifically, as the prey refuge m increased, the model transitioned from oscillatory behavior to a stable state. Notably, for the case when $\zeta$ was set to 0.5, we observed that at higher fear factor values, the Filippov system exhibited oscillations around the equilibrium $E^{*}_{S_1}$, indicating that prey ventured out from refuge to forage. This behavior emerges because increasing fear reduces prey and predator densities. Thus, at sufficiently high fear levels, predator density becomes much smaller than prey density, prompting prey to leave refuge in search of sustenance to avoid extinction.

In summary, our findings highlight the intricate ecological dynamics that arise when considering adaptive prey behavior in the face of predation risk. The incorporation of prey-refuging strategy switching based on the prey-to-predator density ratio in the proposed Filippov model offers a more realistic ecological representation. These results underscore the importance of threshold-based refuge seeking for preserving species and maintaining ecosystem stability.