1 Introduction

Nonlinear evolution equations are well used to describe various significant nonlinear phenomena in nature, which display significant prosperities as the soliton solution, infinite number of conservation laws, symmetries, and Hamiltonian structures. Searching for exact solutions of nonlinear evolution equations is important in scientific and engineering applications because it offers rich knowledge on the mechanism of the complicated physical phenomena. A set of systematic methods have been used in the literature to obtain reliable treatments of nonlinear evolution equations. So far, researchers have established several methods to find the exact solutions, including the inverse scattering transform [1], the Bäcklund transformation [2,3,4,5], the Darboux transformation [6,7,8,9,10,11,12,13,14], the Riemann–Hilbert approach [15,16,17] and Hirota’s bilinear method [18,19,20,21,22,23,24,25,26,27,28], Jacobian elliptic function method and modified tanh-function method [29,30,31,32,33]. Each of these approaches has its features, Hirota’s bilinear method is widely popular due to its simplicity and directness. In Refs. [34, 35], some lump solutions and interaction solutions of Hirota–Satsuma–Ito equation are computed via Hirota’s bilinear form through conducting symbolic computations. In Ref. [36], two kinds of lump solutions are constructed explicitly through Hirota’s bilinear method. Hirota’s bilinear method can be used usually to construct the exact localized wave solutions such as soliton, breather (alias periodic soliton), and lump. Soliton has the property of stability caused by the balance of nonlinear and dispersive effects on the medium [31, 32, 37]. Breather is the partially localized breathing waves with a periodic structure in a certain direction [38,39,40]. Lump is a kind of rational function solutions in all space directions, which have some physical applications in shallow water wave, plasma, optic media, and Bose–Einstein condensate [41, 42].

In this paper, we consider the following (\(2+1\))-dimensional asymmetrical Nizhnik–Novikov–Veselov (ANNV) equation:

$$\begin{aligned} u_{t}+u_{xxx}+3\biggl( u \int u_{x}\,\mathrm{d}y\biggr)_{x}=0, \end{aligned}$$
(1)

where the subscripts respectively denote the partial derivatives with respect to the two scaled space coordinates \(x, y\) and time t, u is the functions of \(x, y\), and t, and u is the physical field. The ANNV equation, which is an isotropic Lax integrable extension of the KdV equation, has been proposed in the modern string theory and theory of biological membranes. Many papers focus on analyzing the exact solutions of Eq. (1). Boiti et al. [43] have first derived Eq. (1) and solved it by the inverse scattering transformation. Dai et al. [44] have derived the variable separation solutions of Eq. (1) by using extended tanh-function method. Wazwaz [45] has investigated the multiple soliton solutions for generalized, asymmetric, and modified NNV equation with the help of a simplified form of Hirota’s bilinear method. Fan [46] has investigated the quasi-periodic wave solutions and established the relations between the quasi-periodic wave solutions and soliton solutions of Eq. (1) based on a multi-dimensional Riemann theta function and Hirota’s bilinear method. Zhao et al. [47] have presented the lump stripe solution of Eq. (1) by using bilinear form. As far as we know, the M-lump solutions and different types of localized wave interaction solutions including lump-soliton and lump-soliton-breather solutions have not been reported before.

The rest of this paper is arranged as follows. In Sect. 2, we firstly present the N-soliton solutions of Eq. (1) by using Hirota’s bilinear method. Section 3 is devoted to the M-lump solutions by using long wave limit to even N-soliton solutions. In Sect. 4, we take odd five-soliton solution as an example and give some mixed lump-soliton and lump-soliton-breather solutions by using long wave limit and choosing special parameters. Some conclusions are given in the last section.

2 The N-soliton solution of the (\(2+1\))-dimensional ANNV equation

Taking the transformation

$$\begin{aligned} u=u_{0}+2(\ln f)_{xy}, \end{aligned}$$
(2)

Equation (1) is converted into the following bilinear formulism:

$$\begin{aligned} \bigl(D_{y} D_{t}+D_{x}^{3} D_{y}+3u_{0} D_{x}^{2}\bigr)f \cdot f=0, \end{aligned}$$
(3)

where the bilinear differential operator D is defined [48] by

$$\begin{aligned} D_{x}^{m} D_{y}^{n} D_{t}^{p} (a\cdot b)={}&(\partial _{x} -\partial _{x'})^{m}( \partial _{y} -\partial _{y'})^{n}(\partial _{t} -\partial _{t'})^{p} \\ &{}\times a(x, y, t)b\bigl(x', y', t' \bigr)|_{x=x', y=y', t=t'}, \end{aligned}$$
(4)

then Eq. (3) is equivalent to

$$\begin{aligned} &2f_{yt}-2f_{t} f_{y}+ 2f_{xxxy}f-2f_{xxx} f_{y}-6f_{xxy}f_{x} \\ &\quad{}+6f_{xx}f_{xy}+6u_{0} f_{xx}f -6u_{0} f_{x}^{2}=0. \end{aligned}$$
(5)

Based on Hirota’s bilinear method, the N-soliton solution of Eq. (1) is obtained by substituting

$$\begin{aligned} f ={}&1+\sum_{s=1} ^{N} \exp (\eta _{s})+\sum_{s< j} ^{N} A_{sj}\exp (\eta _{s} +\eta _{j})+\sum_{s< j< k} ^{N} A_{sj}A_{sk}A_{jk} \\ &{}\times \exp (\eta _{s} +\eta _{j}+\eta _{k})+\cdots + \biggl(\prod_{s< j} A _{sj} \biggr) \exp \Biggl\{ \sum_{s=1} ^{N} \eta _{s} \Biggr\} \end{aligned}$$
(6)

into Eq. (2) with

$$\begin{aligned} & \eta _{s}=a_{s} x+b_{s} y+c_{s} t+\eta _{0s},\quad c_{s}=-\frac{ a_{s}^{3} b_{s}+3u_{0} a_{s}^{2}}{b_{s}}, \end{aligned}$$
(7)
$$\begin{aligned} &A_{sj}=-\frac{(a_{s}-a_{j})^{3}(b_{s}-b_{j})+3u_{0} (a_{s}-a_{j})^{2}+(b _{s}-b_{j})(c_{s}-c_{j})}{(a_{s}+a_{j})^{3}(b_{s}+b_{j})+3u_{0} (a _{s}+a_{j})^{2}+(b_{s}+b_{j})(c_{s}+c_{j})}, \\ &\quad s,j=1,2,\ldots, N, \end{aligned}$$
(8)

where the parameters \(a_{s}, b_{s}\), and \(\eta _{0s} \) are constants related to the amplitude and phase of the Nth soliton, respectively. Motivated by the work of [9, 21], we have the following theorem.

Theorem 1

Let \(b_{s}=p_{s} a_{s}\ (s=1,\ldots, N), a_{j}=l _{j} \epsilon,\exp (\eta _{0j})=-1\ (j=1,\ldots, 2M),p_{n}=p_{n+M} ^{*}\ (n=1,\ldots, M)\), \(a_{2M+l}=a_{2M+P+l}^{*}\ (l=1,\ldots, P)\), and \(a_{2M+2P+k}\ (k=1,\ldots, Q)\) be real constants. When \(\epsilon \rightarrow 0\), the N-soliton solution of Eq. (1) can reduce to the interaction solutions of M-lump, P-breather, and Q-soliton, where \(N=2M+2P+Q\), in which \(M, P, Q\) are nonnegative integers and represent the numbers of lump, breather, and soliton, respectively.

Next, we will apply the above conclusion in Theorem 1 to give the M-lump, mixed lump-soliton, and lump-soliton-breather solutions of Eq. (1).

3 M-lump solutions

In this section, we let \(P=Q=0\) (i.e., \(N=2M\)) in Theorem 1, we can obtain M-lump solutions of Eq. (1). By choosing parameters \(b_{s}=p_{s}a_{s}, a_{s}=l_{s} \epsilon \) in Eq. (6) with the provision \(\exp (\eta _{0s})=-1, s=1, 2, \ldots, N\) (N is an even number), and then taking long wave limit as \(\epsilon \rightarrow 0\), the function f in Eq. (6) is translated into pure rational function. Therefore, the general higher-order rational functions of Eq. (1) can be presented as [49, 50]

$$\begin{aligned} f_{N} ={}&\prod _{s=1} ^{N}\omega _{s}+ \frac{1}{2}\prod_{s,j}^{N} B_{sj} \sum_{l\neq s,j}^{N} \omega _{l}+\cdots \\ &{}+\frac{1}{M!2^{M}}\sum_{s, k,\ldots, m, n}^{N} \overbrace{ B_{sj}B _{kl} \cdots B_{mn}}^{M} \prod_{p\neq s, j,k,l\ldots, m,n}^{N} \omega _{p}+ \cdots, \end{aligned}$$
(9)

where

$$\begin{aligned} {B_{sj}=\frac{2p_{s} p_{j}(p_{s}+p_{j})}{u_{0}(p_{s}-p _{j})^{2}}, \qquad \omega _{j}=x+p_{j} y- \frac{3u_{0}}{p_{j}} t,\quad j=1,2, \ldots, N.} \end{aligned}$$
(10)

If we choose \(p_{n}=p_{n+M}^{*}\ (n=1, 2,\ldots, M)\) for \(N=2M\) with the condition \(B_{sj}>0\), we can get a class of nonsingular M-lump solutions.

(i) Setting \(N=2\) in Eq. (9), we have

$$\begin{aligned} f=\omega _{1}\omega _{2}+ B_{12}. \end{aligned}$$
(11)

Substituting Eq. (11) into the bilinear transformation in Eq. (2), we can obtain one-lump solutions of Eq. (1). Figure 1 shows one lump with one peak and two valleys at \(t=0\) if parameters \(u_{0}=-1, p_{1}=p_{2}^{*}=1+i\). In the following, we always set the parameter \(u_{0}=-1\).

Figure 1
figure 1

One-lump solution with parameters \(p_{1}=p_{2}^{*}=1+i\) at \(t=0\). (a) Surface (top) and density (bottom) plots of one lump; (b) the corresponding counter plot of (a)

Full size image

(ii) Setting \(N=4\) in Eq. (9), we have

$$\begin{aligned} f ={}&\omega _{1} \omega _{2} \omega _{3} \omega _{4}+B_{34} \omega _{1} \omega _{2}+B_{24}\omega _{1} \omega _{3}+B_{23}\omega _{1} \omega _{4} +B _{14}\omega _{2} \omega _{3} \\ &{}+B_{13}\omega _{2} \omega _{4}+B_{12} \omega _{3}\omega _{4}+B_{12}B_{34}+B _{13}B_{24}+B_{14}B_{23}. \end{aligned}$$
(12)

Substituting Eq. (12) into the bilinear transformation in Eq. (2), we can obtain two lumps of Eq. (1). Figure 2 shows the elastic interaction between two lumps at different time with parameters

$$\begin{aligned} p_{1}=p_{2}^{*}=1+i,\qquad p_{3}=p_{4}^{*}=\frac{1}{3}+ \frac{1}{2} i. \end{aligned}$$
(13)

From Fig. 2, we can clearly see that two lumps grow closer with time increasing, they collide at \(t=0\), then separate again, after the interaction, two lumps keep their shapes and amplitudes invariant, so their interaction is elastic.

Figure 2
figure 2

Surface (top) and density (bottom) plots of the interaction between two lumps with parameters in Eq. (13) at different time

Full size image

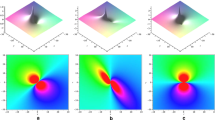
(iii) Setting \(N=6\) in Eq. (9), we can obtain three-lump solution. In this case, there are many soliton parameters and the solution is very complicated, so we omit its expression here. Figure 3 shows the elastic interaction among three lumps at different time with parameters

$$\begin{aligned} p_{1}=p_{2}^{*}= \frac{1}{4}+i,\qquad p_{3}=p_{4}^{*}=1+ i,\qquad p_{5}=p_{6}^{*}=\frac{1}{2}+ \frac{3}{5} i. \end{aligned}$$
(14)

From Fig. 3, we can clearly see that three lumps array a triangle structure at \(t=-50\) and grow closer with time increasing, they interact at \(t=0\), after the interaction, then separate and rearrange a triangle. As time goes on, they are farther and farther away, and their shapes and amplitudes remain the same as before.

Figure 3
figure 3

Surface (top) and density (bottom) plots of the interaction among three lumps with parameters in Eq. (14) at different time

Full size image

4 The lump interacts with soliton or breather

In the previous section, we discussed the M-lump solutions of Eq. (1) by use of long wave limit. In this section, we will consider the interaction solutions of different localized waves such as the interaction of lump and soliton or breather by using long wave limit and choosing conjugate spectral parameters. Here, we take \(N = 5\) in Eq. (6) as an example.

Case 1. One lump interacts with soliton or breather. Putting \(b_{s}=p_{s}a_{s}\ (s=1,2,3,4,5), a_{1}=l_{1}\epsilon, a_{2}=l _{2}\epsilon, \eta _{01}=\eta _{02}^{*}=i\pi \), \(\eta _{03}=\eta _{04}= \eta _{05}=0\) and taking \(\epsilon \to 0\), then the function f in Eq. (6) can be rewritten as

$$\begin{aligned} f ={}&(B_{12}+\omega _{1} \omega _{2})l_{1} l_{2} \epsilon ^{2}+(\omega _{1} \omega _{2}+B_{23} \omega _{1}+B_{13}\omega _{2}+B_{12}+B_{13}B_{23}) \exp (\eta _{3}) \\ & {}\times l_{1} l_{2}\epsilon ^{2}+(\omega _{1} \omega _{2}+B_{24} \omega _{1}+B_{14}\omega _{2}+B_{12}+B_{14}B_{24}) \exp (\eta _{4})l_{1} l_{2} \epsilon ^{2} \\ &{}+B_{34}\bigl[\omega _{1} \omega _{2}+(B_{23}+B_{24})\omega _{1}+(B_{13}+B _{14})\omega _{2}+B_{12}+(B_{13}+B_{14}) \\ &{}\times (B_{23}+B_{24})\bigr]\exp (\eta _{3}+\eta _{4})l_{1} l_{2} \epsilon ^{2}+(\omega _{1} \omega _{2}+B_{25} \omega _{1}+B_{15}\omega _{2}+B_{12} \\ &{}+B_{15}B_{25})\exp (\eta _{5})l_{1} l_{2}\epsilon ^{2}+B_{35}\bigl[\omega _{1} \omega _{2}+(B_{23}+B_{25})\omega _{1}+(B_{13}+B_{15})\omega _{2} \\ &{}+B_{12}+(B_{13}+B_{15}) (B_{23}+B_{25})\bigr]\exp (\eta _{3}+\eta _{5})l _{1} l_{2}\epsilon ^{2}+B_{45}\bigl[\omega _{1} \omega _{2} \\ &{}+(B_{24}+B_{25})\omega _{1}+(B_{14}+B_{15}) \omega _{2}+B_{12}+(B_{14}+B _{15}) (B_{24}+B_{25})\bigr] \\ &{}\times \exp (\eta _{4}+\eta _{5})l_{1} l_{2}\epsilon ^{2}+B_{34}B_{35}B _{45}\bigl[\omega _{1} \omega _{2}+(B_{23}+B_{24}+B_{25}) \omega _{1} \\ &{}+(B_{13}+B_{14}+B_{15})\omega _{2}+B_{12}+(B_{13}+B_{14}+B_{15}) (B _{23}+B_{24} \\ &{}+B_{25})\bigr]\exp (\eta _{3}+\eta _{4}+ \eta _{5})l_{1} l_{2}\epsilon ^{2}+O\bigl( \epsilon ^{3}\bigr), \end{aligned}$$
(15)

where

$$\begin{aligned} &B_{12}=\frac{2p_{1}p_{2}(p_{1}+p_{2})}{u_{0}(p_{1}-p_{2})^{2}},\qquad \omega _{j}=x+p_{j} y- \frac{3u_{0}}{p_{j}} t,\quad j=1,2, \end{aligned}$$
(16)
$$\begin{aligned} &B_{sj}=\frac{2p_{s} a_{j} p_{j}(p_{s}+p_{j})}{u_{0}(p_{s}-p_{j})^{2}-p _{s} p_{j}^{2}a_{j}^{2}} \quad (s=1, 2, j=3, 4, 5), \end{aligned}$$
(17)

and

$$\begin{aligned} B_{sj}=\frac{u_{0}(p_{s}-p_{j})^{2} -p_{s} p_{j}(a_{s}-a_{j})(p_{s} a_{s}-p_{j} a_{j})}{u_{0}(p_{s}-p_{j})^{2}-p_{s} p_{j}(a_{s}+a_{j})(p _{s} a_{s}+p_{j} a_{j})},\quad (3 \leq s< j \leq 5). \end{aligned}$$
(18)

The solution u given by Eq. (15) expresses the interaction solution of lump soliton and breather or line solitons. Here, we will discuss two cases:

(i) When \(M=1, P=0,Q=3\) in Theorem 1, we can derive the interaction solution among one lump and three solitons. Considering

$$\begin{aligned} p_{1}=p_{2}^{*}=1+ i,\qquad a_{3}=a_{4}=\frac{2}{3},\qquad p_{3}=1,\qquad p_{4}=2, \qquad a_{5}= \frac{2}{3},\qquad p_{5}=\frac{2}{3}, \end{aligned}$$
(19)

when \(\epsilon \rightarrow 0\), the solution u given by Eq. (15) expresses the elastic interaction among one lump and three solitons as shown in Fig. 4.

Figure 4
figure 4

Surface (top) and density (bottom) plots of the mixed lump-soliton interaction among one lump and three solitons with parameters in Eq. (19) at different time

Full size image

(ii) When \(M=P=Q=1\) in Theorem 1, we can derive the interaction solution among one lump, one breather, and one soliton. Taking

$$\begin{aligned} p_{1}=p_{2}^{*}=1+ 2i,\qquad a_{3}=a_{4}=\frac{2}{3},\qquad p_{3}= p_{4}^{*}=1+ i,\qquad a_{5}= \frac{2}{3},\qquad p_{5}=1, \end{aligned}$$
(20)

when \(\epsilon \rightarrow 0\), the solution u given by Eq. (15) expresses the elastic interaction among one lump, one breather, and one soliton as shown in Fig. 5.

Figure 5
figure 5

Surface (top) and density (bottom) plots of the mixed lump-soliton-breather interaction among one lump, one breather, and one soliton at different time and parameters in Eq. (20)

Full size image

Case 2. Two lumps interact with one soliton. When \(M=2,P=0,Q=1\) in Theorem 1, we can derive the interaction solution among two lumps and one soliton. Putting \(b_{j}=p_{j}a_{j}, a_{j}=l_{j} \epsilon\ (j=1,2,3,4), b_{5}=p_{5}a_{5}, \eta _{01}=\eta _{02}^{*}=\eta _{03}=\eta _{04}^{*}=i\pi \), \(\eta _{05}=0\) and taking \(\epsilon \to 0\), then the function f in Eq. (6) can be rewritten as

$$\begin{aligned} f ={}&(\omega _{1} \omega _{2} \omega _{3} \omega _{4}+B_{34} \omega _{1} \omega _{2}+B_{24}\omega _{1} \omega _{3}+B_{23}\omega _{1} \omega _{4} +B _{14}\omega _{2} \omega _{3}+B_{13}\omega _{2} \omega _{4} \\ &{}+B_{12}\omega _{3} \omega _{4}+B_{12}B_{34}+B_{13}B_{24}+B_{14}B_{23})l _{1} l_{2} l_{3} l_{4}\epsilon ^{4}+\bigl\{ \omega _{1} \omega _{2} \omega _{3} \omega _{4} \\ &{}+B_{45}\omega _{1} \omega _{2} \omega _{3}+B_{35}\omega _{1} \omega _{2} \omega _{4}+B_{25}\omega _{1} \omega _{3} \omega _{4}+B_{15} \omega _{2} \omega _{3} \omega _{4}+\omega _{1}\bigl[(B_{35}B_{45} \\ &{}+B_{34})\omega _{2}+(B_{25}B_{45}+B_{24}) \omega _{3}+(B_{25}B_{35}+B _{23}) \omega _{4}\bigr]+\omega _{2}\bigl[(B_{15}B_{45} \\ &{}+B_{14}) \omega _{3}+(B_{15}B_{35}+B_{13}) \omega _{4}\bigr]+(B_{15}B_{25}+B _{12})\omega _{3} \omega _{4}+\omega _{1}\bigl[(B_{25}B_{35} \\ &{}+B_{23})B_{45}+B_{24}B_{35}+B_{25}B_{34} \bigr]+\omega _{2}\bigl[(B_{15}B_{35}+B _{13})B_{45}+B_{14}B_{35} \\ &{}+B_{15}B_{34}\bigr]+\omega _{3} \bigl[(B_{15}B_{25}+B_{12})B_{45}+B_{14}B_{25}+B _{15}B_{24}\bigr]+\omega _{4} \\ &{}\times \bigl[(B_{15}B_{25}+B_{12})B_{35}+B_{13}B_{25}+B_{15}B_{23} \bigr]+B _{13}B_{24}+B_{23}B_{14} \\ &{}+B_{34}(B_{15}B_{25}+B_{12})+B_{35}(B_{14}B_{25}+B_{15}B_{24})+B _{45}\bigl[(B_{15}B_{25} \\ &{}+B_{12})B_{35}+B_{13}B_{25}+B_{15}B_{23} \bigr]\bigr\} \exp (\eta _{5})l_{1} l _{2} l_{3} l_{4}\epsilon ^{4}+O\bigl(\epsilon ^{5}\bigr), \end{aligned}$$
(21)

where

$$\begin{aligned} &\omega _{j}=x+p_{j} y- \frac{3u_{0}}{p_{j}} t,\quad j=1,2,3,4, \end{aligned}$$
(22)
$$\begin{aligned} &B_{sj}=\frac{2p_{s} p_{j}(p_{s}+p_{j})}{u_{0}(p_{s}-p_{j})^{2}} \quad (1 \leq s< j \leq 4), \end{aligned}$$
(23)
$$\begin{aligned} &B_{s5}=\frac{2p_{s} a_{5} p_{5}(p_{s}+p_{5})}{u_{0}(p_{s}-p_{5})^{2}-p _{s} p_{5}^{2}a_{5}^{2}}\quad (s=1, 2, 3, 4). \end{aligned}$$
(24)

Taking

$$\begin{aligned} p_{1}=p_{2}^{*}= \frac{1}{2}+ \frac{1}{2}i,\qquad p_{3}= p_{4}^{*}=\frac{1}{3}+ \frac{1}{2}i,\qquad a_{5}=1, \qquad p_{5}=1, \end{aligned}$$
(25)

the solution u given by Eq. (21) expresses the elastic interaction among one soliton and two lumps as shown in Fig. 6.

Figure 6
figure 6

The interaction solution between one line soliton and two lumps at different time and parameters in Eq. (25)

Full size image

5 Conclusions

In this paper, based on Hirota’s bilinear method, we have obtained N-soliton solution of Eq. (1). By using long wave limit and choosing special parameters to N-soliton solution, we have given a general conclusion to obtain mixed lump-breather-soliton interaction solutions. Especially, by using long wave limit to even N-soliton (\(N=2M\)) solution under special parameters, M-lumps and their dynamic properties have been obtained and discussed in Figs. 1–3. In addition, we choose the case \(N=5\) as an example. The mixed lump-soliton interaction solution including one lump and three solitons (see Fig. 4), mixed lump-soliton-breather interaction solution including one lump, one breather, and one soliton (see Fig. 5), and mixed lump-soliton interaction solution including two lumps and one soliton (see Fig. 6) are derived by using long wave limit and choosing special conjugate complex parameters. Table 1 shows some mathematical features to obtain lump-soliton and lump-breather-soliton from five-soliton solutions of Eq. (1) on how to select appropriate parameters. The results given in this paper show that the long wave limit is a direct and powerful mathematical tool to construct mixed interaction solutions of different kinds of localized waves to nonlinear evolution equation, which would be used to investigate other nonlinear models in mathematics and physics.

Table 1 Mixed interaction solutions from five-soliton
Full size table